Abstract
Protein enzymes are highly efficient catalysts that exhibit adaptability and selectivity under diverse biological conditions. In some organisms, such as bacteria, structurally similar enzymes, for instance, shikimate kinase (SK) and adenylate kinase (AK), coexist and act on chemically related ligands. This raises the question of whether these enzymes can accommodate and potentially react with each other’s ligands. In this study, we investigate the stability of non-cognate ligand binding in SK and explore whether external electric fields (EFs) can modulate this interaction, leading to cross-reactivity in SK. Using molecular dynamics simulations, we assess the structural integrity of SK and the binding behavior of ATP and AMP under EF-off and EF-on cases. Our results show that EFs enhance protein structure stability, stabilize non-cognate ligands in the binding pocket, and reduce local energetic frustration near the R116 residue located in the binding site. In addition to this, dimensionality reduction analyses reveal that EFs induce more coherent protein motions and reduce the number of metastable states. Together, these findings suggest that external EFs can reshape enzyme–ligand interactions and may serve as a tool to modulate enzymatic specificity and functional promiscuity. Thus, we provide computational evidence that supports the concept of using an EF as a tunable parameter in enzyme engineering and synthetic biology. However, further experimental investigation would be valuable to assess the reliability of our computational predictions.
1. Introduction
Protein enzymes are fundamental molecules to life, enabling chemical reactions to proceed within biologically relevant timescales [1]. Besides their catalytic efficiency, enzymes demonstrate remarkable adaptability to environmental conditions and perform purpose-driven tasks, which has led researchers to suggest that they exhibit some degree of intelligence [2] and teleonomic behavior [3,4,5].
The proper recognition and binding of cognate ligands (substrates) [6] to enzymes is crucial for catalysis. Through evolutionary optimization, enzymes have developed the ability to distinguish their correct substrates amid the crowded intracellular environment. A compelling example is found in Helicobacter pylori bacteria, where topologically similar enzymes, such as adenylate kinase (AK) and shikimate kinase (SK) [7], coexist yet catalyze distinct reactions. In the presence of a Mg2+ ion, AK converts ATP and AMP to two ADP molecules, while SK catalyzes the phosphorylation of shikimic acid (SKM) using ATP. Both enzymes share conserved structural motifs; for instance, the CORE, binding (SB), and LID domains [8]. Interestingly, they utilize similar binding sites, stabilized by arginine residues oriented towards the substrates.
Given their structural and mechanistic similarities, an intriguing question arises: could one of these enzymes catalyze the reaction of the other? One critical factor in such cross-functionality is the residence time; i.e., the duration a ligand remains within the active site [9]. Under normal physiological conditions, even if non-cognate binding occurs, a short residence time may prevent successful catalysis.
Previously, it was proposed that endogenous electrodynamic fields can be found in living systems in the form of bio-electric phenomena [10]. Thus, owing to their electromagnetic nature, biological systems may be susceptible to modulation by external electric fields (EFs). Recent studies have shown that EFs can influence biological processes at both the tissue level [11] (and references therein) and the molecular level. In the latter, it was shown that EFs affect the binding of SARS-CoV-2 Spike protein to the host angiotensin-converting enzyme 2 (ACE2) receptor [12]. Additionally, in enzymatic systems, external EFs have been found to alter the transition state of the chorismate mutase enzyme by modifying the dipole moment of this state, thereby influencing its catalytic activity [13].
In this study, we explore the potential of external electric fields (EFs) to modulate the binding stability of non-cognate ligands within the active site of the SK enzyme. Using molecular dynamics (MD) simulations, we provide computational evidence that external EFs can enhance ligand stability, which may enable cross-reactivity between similar enzymes. While our findings are preliminary and require experimental validation, they suggest that EFs may represent a tool for modulating enzyme specificity and reactivity, which can lead to modulated promiscuity activities of enzymes [14,15].
2. Materials and Methods
In this section, we describe the protocol that we followed to perform the simulations (Section 2.1) as well as the tools and methodologies that were employed for analyzing the simulation data (Section 2.2).
2.1. Simulation Protocol
We followed a similar protocol adapted from our previous work to perform the present simulations [8]. The structure of SK was obtained from RCSB PDB [16] (PDB ID: 3MUF) (2.3 Å resolution) [17] for Helicobacter pylori. To model ligand binding, the coordinates of the ligands ATP and AMP were obtained by first aligning the SK structure with the AK structure (PDB ID: 1AKE) [18], containing the inhibitor P1,P5-bis(adenosine-5′-) pentaphosphate (Ap5A). The aligned Ap5A ligand was then modified to match the chemical structures of the AMP and ATP molecules. The resulting SK–ligand complex was submitted to the CHARMM-GUI [19] online server to obtain the initial input files for the molecular simulations.
Atomic and molecular interaction parameters were obtained from the CHARMM-36 force field [20,21,22]. The protein complex was solvated with TIP3P waters [23] and Na+ and Cl− ions (at 150 mM concentration) in a cubic box of 66 Å. The resulting solvated system containing 26,689 atoms was ported to GROMACS (v. 2023.3) [24,25,26,27,28,29,30] to solve the Newtonian equations. Long-range electrostatic interactions were computed through the particle mesh Ewald (PME) method [31,32] with a fourth-order cubic interpolation method (grid size of 1.2 Å). The short-range electrostatic interactions were computed explicitly up to 12 Å. Regarding the van der Waals interactions, a force-switching approach was used to truncate interactions at 12 Å, starting smoothing forces at 10 Å.
The simulations followed a standard three-step protocol: energy minimization, equilibration, and production. During the minimization step, harmonic constraints were applied on the backbone, side chains, and dihedral angles, using force constants of 95.6 kcal/(mol nm2), 9.56 kcal/(mol nm2), and 0.956 kcal/(mol rad2), respectively. The maximum force tolerance for the energy minimization step was set to 239 kcal/(mol nm).
In the equilibration step, the system was dynamically propagated during 5 ns (1 fs time step) in the NVT ensemble with the Nosé–Hoover thermostat. The harmonic restraints were kept during the equilibration step. Data production was performed in the NPT ensemble with the Parrinello–Rahman method [33] under standard atmospheric conditions. Three independent replicas were simulated per system using a time step of 2 fs, i.e., in the absence (EF-off) and presence (EF-on) of fields, with a total of 2 μs simulation time per replica.
For the EF-on simulations, similar values for the magnitude of 413 V/m and an angular frequency of 0.0157 ps−1 were used for the EF as in the experimental setup of Pantoja et al. [12]. The equilibrated structure from the EF-off simulation was used as an initial structure in these EF-on simulations.
Regarding the QM/MM simulations, the initial structure was obtained from the NPT classical MD trajectory of the EF-off simulation at time step 40 (80 fs). GROMACS (v. 2022.4) [24,25,26,27,28,29,30] and CP2K (v. 2022.2) [34] were used to solve the Newtonian and Schrödinger equations, respectively. Simulations were run in the NVT ensemble (1 fs time step), where the velocity rescale [35] method was used to maintain a reference temperature of 300 K. Other parameters for the MD part were similar to the classical MD simulations described above. Regarding the QM part, density functional theory (DFT) [36,37] together with the PBE functional [38] was used to solve the interactions from the QM atoms. A double-zeta valence polarized basis set (DZVP-MOLOPT-GTH) [39] was used with Goedecker–Teter–Hutter (GTH) pseudopotentials [40,41]. The total charge of the QM region was −4 with a multiplicity of 1. The excited state energies were computed with the time-dependent density functional perturbation theory (TD-DFPT), where 5 excited states were targeted with an energy threshold of 1 meV.
2.2. Analysis of Results
To perform the alignment, the sequences for SK and AK from Helicobacter pylori were fetched from the UniProt database [42], with IDs T0ERT7 [43] and Q1CTQ6 [44], respectively. The analysis was done with the Blas online server [45,46,47].
The root mean square deviation (RMSD) computations, center-of-mass (COM) distances calculations, and hydrogen bond analysis were done with the built-in tools of VMD (v. 1.9.4) [48]. For the RMSD, the backbone atoms from the equilibrated structure were used as a reference. In the case of the COM, the distances were computed between the COM of the protein Cα atoms and the COM of either ATP or AMP. Regarding the hydrogen bond analysis, bonds were computed between the protein and ATP/AMP with donor–acceptor distance and angle cutoff set to 3 Å and , respectively. Note that reported occupancies, i.e., persistence of a bond during the trajectory, can exceed 100% because several bonds can be formed per residue.
Dimensionality reduction of the dynamical trajectories was achieved through principal component analysis (PCA) [49] and the variational approach for Markov processes (VAMP) [50] as implemented in the Deeptime Python library (v. 0.4.5) [51]. Sine and cosine functions of the dihedral angles of the protein structure were used as inputs for the feature matrix to avoid discontinuity at the boundary values of . A lag time of 1 ns was employed for performing the VAMP analysis.
The FrustratometeR package [52,53] was used to evaluate the local energetic frustration within a 5 Å cut-off sphere around the R116 residue of SK. We employed a configurational model with an electrostatic constant of 4.15. Simulation frames were sampled every 1 ns for this analysis. In FrustratometeR, the degree of frustration within a selected region is quantified as a percentage and categorized into three classes: highly frustrated, indicating interactions with significant energetic conflicts; minimally frustrated, representing energetically optimized, stable interactions; and neutrally frustrated, reflecting intermediate cases. This classification is based on a Z-score derived from an ensemble of random conformations, as defined in Ref. [54].
The absorption spectra for the EF-off case were obtained from the QM/MM simulation by convoluting the excitation energies of the 5 selected states using Gaussian functions with a half-width of 0.01 eV.
3. Results and Discussion
This section presents the findings of our simulations involving non-cognate ligands bound to the SK enzyme, with a focus on the influence of external fields on ligand stability.
3.1. Structural Stability of the Protein in the Presence of External Fields
In bacteria, SK and AK can coexist in the same cellular environment, such as the cytoplasm. Sequence alignment, as described in the Section 2, reveals limited similarity between these two enzymes, with only 11% query coverage and 44.4% identity within the aligned region. Despite this low sequence homology, SK and AK are topologically equivalent, sharing conserved structural motifs including the CORE, substrate binding (SB), and the LID domains. Functionally, both enzymes catalyze phosphorylation reactions but on different small molecules: SK phosphorylates SKM, while AK phosphorylates AMP.
Given the structural similarities between these enzymes and their substrates, we assessed whether SK could accommodate ATP and AMP instead of the cognate ligands ATP and SKM. The latter was the topic of our previous work [55]. To evaluate the feasibility of the non-cognate ligands’ binding, we placed ATP and AMP in the SK active site and performed MD simulations to monitor the structural stability of the protein chain, quantified through the RMSD. In Figure 1, we can see the plot of the RMSD as a function of time in the absence of external perturbations (EF-off). We noticed that the RMSD stayed constant up to 1.25 μs and decreased slightly, reaching a plateau for longer times. This finding suggests that SK can stably accommodate non-cognate ATP-AMP ligands without significantly altering its 3D equilibrated structure.
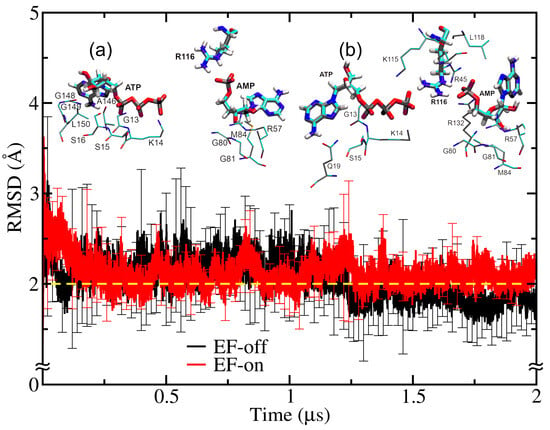
Figure 1.
Root mean square deviation (RMSD) plot of the SK structure in the absence (EF-off) and under the influence of an external electric field (EF-on). A dashed yellow line is added to denote a RMSD of 2 Å. The RMSD of the EF-off case decreases beyond 1.25 μs, while that of EF-on stays constant during the simulation runtime. In the insets (a) and (b), the binding site for the EF-on case is shown at the beginning (0.021 μs) and the end (2 μs) of the simulation, respectively.
Upon application of an external electric field (EF-on), see Figure 1, the RMSD plot remained constant at ~2 Å throughout the simulation, indicating that SK maintains a higher structural integrity than in the EF-off case, where changes in the RMSD during the runtime were observed beyond 1.25 μs. We noticed that in both the EF-off and EF-on simulations, the RMSD values initially started at a higher value of ~2.5 Å than at the end of the trajectory. These initial values can be caused by the different local arrangements of the residues in the binding site, as well as in the positioning of the ATP and AMP ligands. These changes are illustrated in the insets (a) and (b), which show the binding site residues, located within 3 Å of ATP and AMP, at the beginning (0.021 μs) and the end of the MD trajectory (2 μs), respectively.
To further assess the global structural changes of SK under the influence of EFs, we performed principal component analysis (PCA) and projected the MD trajectories onto the first two PCs. The projections for the EF-off and EF-on cases are shown in Figure 2a and Figure 2b, respectively. In both cases, the PCA reveals only partial separation of structural states; however, the EF-on case exhibits slightly more distinct clustering, indicating the emergence of metastable conformations with shared structural features.
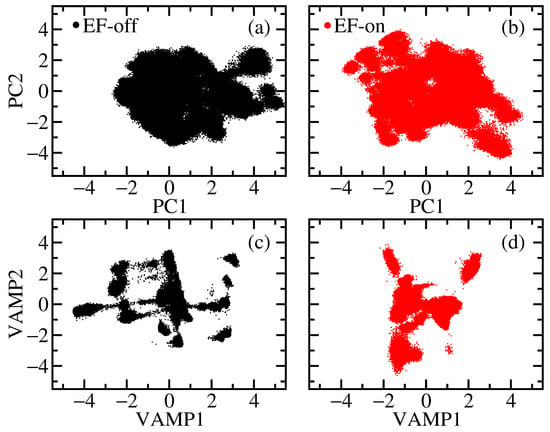
Figure 2.
Dimensionality reduction of the MD trajectories: (a,b) show the PC projections onto the first two components in the EF-off and EF-on cases, respectively; (c,d) display the corresponding VAMP projections for the EF-off and EF-on cases, respectively. MD data is more efficiently clustered with the VAMP method.
The limited ability of PCA to resolve well-defined clusters stems from its focus on capturing the maximal geometric variance to reduce the dimensionality of data. In relatively short trajectories such as those analyzed in the present study, major structural transitions may not be fully sampled, leading to broad, overlapping distributions as seen in Figure 2a. Notably, the EF-on projection spans a larger area in the PC space compared to the EF-off case, suggesting increased conformational flexibility in the presence of EFs. The latter was also observed in the RMSD plot, especially beyond 1.25 μs.
To improve the separation of metastable states in the MD trajectories, we applied the variational approach for Markov processes (VAMP) method, which reduces the dimensionality of time-series data using time-lagged correlations [50]. Unlike PCA, VAMP is well-suited for analyzing off-equilibrium data [56], making it particularly useful in our study, where the conformational space is sparsely sampled and influenced by time-dependent external forces.
Figure 2c,d present the VAMP projections for the EF-off and EF-on cases, respectively. In the absence of an EF (Figure 2c), the analysis reveals multiple metastable states within the chosen lag time. In contrast, the EF-on case (Figure 2d) displays fewer distinct states, indicating that the external EF promotes more coherent and concerted motions in the protein structure [57].
3.2. Ligands’ Stability in the Presence of Fields
In the previous subsection, it was shown that non-native ligands do not disrupt the overall enzyme structure, though they do alter patterns in slow conformational motions. We now focus on assessing the stability of these ligands within the enzyme’s binding pocket. This stability was evaluated by tracking the center-of-mass (COM) distance between the enzyme and each ligand (ATP and AMP) throughout the simulations. Ligand stability can be linked to residence time, which is a critical factor for ensuring the proper substrate binding and enabling catalysis.
As shown in Figure 3a, the COM distance between the enzyme and ATP remains relatively constant over time, indicating stable binding in both EF-off and EF-on cases. In contrast, the COM distance for AMP (Figure 3b) reveals a noticeable stabilizing effect in the presence of the external field. This suggests that the EF enhances the retention of AMP within the binding pocket, potentially increasing its catalytic viability as a non-cognate ligand.
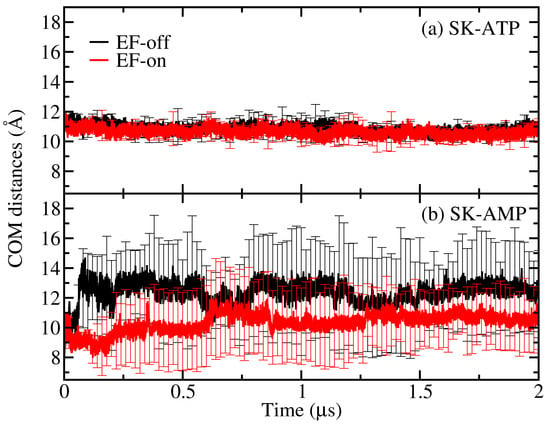
Figure 3.
Stability of the ATP and AMP ligands in the binding pocket of SK measured by the COM distances between the ligands and protein structures. The EF-off and EF-on cases were considered in the COM distances analysis. (a) COM between ATP and SK displaying high stability of this ligand; (b) COM between AMP and SK, showing that in the presence of an EF (EF-on), AMP is stabilized.
The difference in the ligand stability between the EF-off and EF-on cases can be attributed to variations in hydrogen bonding patterns. Specifically, the EF-on case exhibits a higher number of hydrogen bonds (90) compared to the EF-off case (76), including all replicas, suggesting that the external EF can contribute to a more stable ligand–protein complex. Interestingly, the hydrogen bonds between ATP/AMP and residue R116 showed higher occupancies in the EF-on case (64% for ATP and 137% for AMP) compared to the EF-off case (45% for ATP and 84% for AMP), highlighting the crucial role of R116 in stabilizing the ligands under the influence of an external field. These findings also suggest that the external field can modify the preorganized electrostatic environment of the binding site [15,58].
Interactions in the binding pocket can give rise to frustrated interactions; i.e., conditions where not all interactions can be simultaneously optimized due to conflicting energetic constraints. In proteins, frustration often reflects regions where the native structure must balance competing interactions, which can be functionally important, especially in dynamic sites like binding sites [55,59].
The stabilization of the AMP ligand observed under an external field, as shown in Figure 3b, may be linked to altered patterns in slow conformational motions, which can reshape intramolecular interactions in the protein structure, including the binding pocket. These structural rearrangements may, in turn, modulate local frustration patterns.
To explore this hypothesis, we quantified the degree of frustration around the R116 residue, which is located in the binding site of SK; see Figure 1 insets (a) and (b). This analysis provides insight into how ligand binding and external perturbations influence the energetic landscape of the binding pocket. In the absence of an external field, a high degree of frustration is observed, which is displayed in the region enclosed by the blue square in Figure 4a.
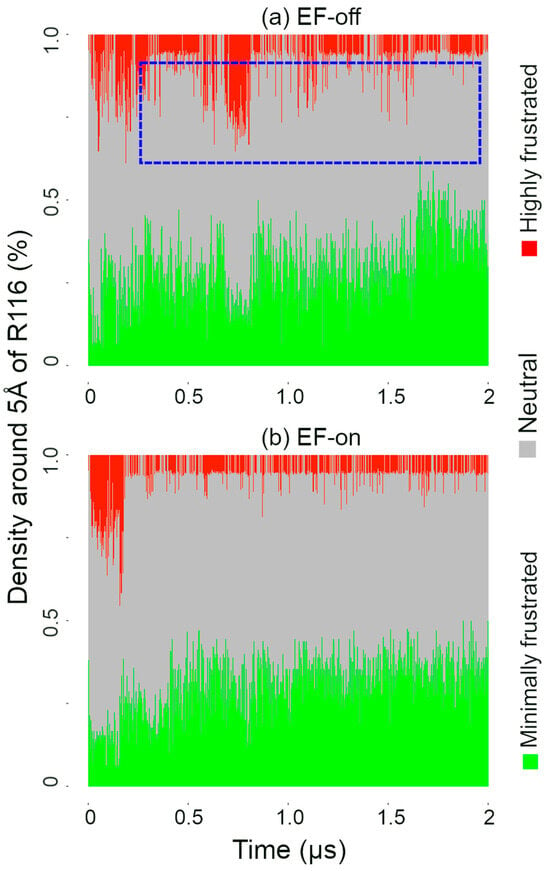
Figure 4.
Density plot showing the degree of frustrated interactions near the binding pocket: (a) EF-off case; (b) EF-on case. In the blue dashed rectangle, the area for the highly frustrated interactions in the EF-off case is highlighted.
In the presence of the EF, the area covered by the highly frustrated interactions decreases; see Figure 4b. Interestingly, the degree of highly frustrated interactions in the EF-on case was comparable to that observed when the native products ADP and shikimate-3-phosphate (S3P) were used as ligands [55]. To illustrate the frustrated interactions at the binding site in the EF-on case, snapshots of the binding site (including residues close to ATP and AMP) from the beginning (0.021 μs, with a high degree of frustration) and the end of the simulation (2 μs, with a low degree of frustration) are presented in Figure 1, insets (a) and (b), respectively. Notably, hydrogen bonds between ATP and R116 are absent in the snapshot at the beginning of the trajectory, which can be associated with the high degree of frustration observed at this stage.
To assess the validity of our results, we conducted simulations with two replicas for both the EF-off and EF-on cases. The plot with the frustration analysis for these cases can be seen in Figure S1a–d in the Supplementary Materials. In these simulations, we notice that the region related to the highly frustrated interactions was similar in the EF-off (Figure S1a,b) and EF-on (Figure S1c,d) cases. However, the region corresponding to the minimally frustrated interactions increased, as can be seen in the area enclosed by the blue rectangle in Figure S1c,d. Thus, taken together, these results suggest that the effect of the external field is to reduce the level of frustration for the selected region around R116 residue either by decreasing the number of highly frustrated interactions or by increasing the minimally frustrated interactions.
It is important to note that the external EF used in the previous simulations was treated classically, via standard Coulombic interactions between point charges. However, external fields can also interact with electronic densities of molecules, which may be particularly relevant for the ligands within the binding site. For example, the absorption spectra computed for ATP and AMP ligands using QM/MM simulations combined with the TDDFPT method revealed possible electronic excitations corresponding to angular frequencies in the range of ; see Figure S2. An external time-dependent EF oscillating at these frequencies could induce such excitations. This may result in conformational changes in ATP and/or AMP that alter the structure and electrostatic environment of the binding site. We think that these effects merit further investigation in future studies.
4. Conclusions
In this study, we explored the use of external electric fields as a potential tool to modulate enzyme–ligand interactions, focusing on the SK enzyme and its response to non-cognate ligands. Despite its low sequence similarity with AK, SK exhibits topological features that enable it to accommodate ATP and AMP. MD simulations revealed that SK maintains structural integrity even with non-native ligands, and that external EFs further enhance this stability, as evidenced by the stable RMSD values (~2 Å) and emergence of coherent metastable states.
Interestingly, EFs were found to improve the stability of AMP in the SK active site, which can contribute to increasing the residence time, which is a key factor for catalysis. This suggests that electric fields could be harnessed to fine-tune substrate binding, opening new possibilities for reprogramming enzyme specificity. Our analysis further indicates that these stabilizing effects are linked to reduced local energetic frustration, particularly around catalytically important residues, such as R116. This suggests that EFs, for this particular SK and ligands case, can reorganize the local energetic landscape in favor of ligand retention in the binding pocket.
Overall, our findings provide computational evidence that external EFs can be used to influence enzymatic behavior by enhancing binding stability and modulating conformational dynamics. This offers a possible tool for enzyme design and synthetic biology, where precise control over substrate specificity and promiscuity is critical. Future experimental validation will be essential to translate these insights into practical applications.
Supplementary Materials
The following supporting information can be downloaded at https://www.mdpi.com/article/10.3390/biophysica5030033/s1, Figure S1: Density plot showing the degree of frustrated interactions near the binding pocket: (a,b) display the results of the replica simulations for the EF-off case; (c,d) show the frustration analysis results for the EF-on case. The minimally frustrated area is highlighted with a blue dashed rectangle. Figure S2. Absorption spectra for the ATP and AMP molecules after 0.02 ps (red line) and 0.1 ps (black line) using QM/MM simulations combined with the TDDFPT method.
Funding
This research received no external funding.
Data Availability Statement
Data are already contained in the present article.
Acknowledgments
This research was conducted using the resources of High Performance Computing Center North (HPC2N). Supported by the eSSENCE Programme under the Swedish Government’s Strategic Research Initiative.
Conflicts of Interest
The author declares no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| VAMP | Variational approach for Markov processes |
| COM | Center of mass |
| PCA | Principal component analysis |
| AK | Adenylate kinase |
| SK | Shikimate kinase |
References
- Wolfenden, R.; Snider, M.J. The Depth of Chemical Time and the Power of Enzymes as Catalysts. Acc. Chem. Res. 2001, 34, 938–945. [Google Scholar] [CrossRef] [PubMed]
- Tripathi, T.; Uversky, V.N.; Giuliani, A. ‘Intelligent’ Proteins. Cell. Mol. Life Sci. 2025, 82, 239. [Google Scholar] [CrossRef] [PubMed]
- Mayr, E. Cause and Effect in Biology. Science 1961, 134, 1501–1506. [Google Scholar] [CrossRef]
- Pross, A. On the Chemical Nature and Origin of Teleonomy. Orig. Life Evol. Biosph. 2005, 35, 383–394. [Google Scholar] [CrossRef]
- Pittendrigh, C.S. Adaptation, Natural Selection, and Behavior. In Behavior and Evolution; Roe, A., Simpson, G.G., Eds.; Yale Univ. Press, Inc.: New Haven, CT, USA, 1958; pp. 390–416. [Google Scholar]
- Das, S.; Orengo, C. Choosing the Best Enzyme Complex Structure Made Easy. Structure 2018, 26, 528–530. [Google Scholar] [CrossRef]
- Krell, T.; Coggins, J.R.; Lapthorn, A.J. The Three-Dimensional Structure of Shikimate Kinase1. J. Mol. Biol. 1998, 278, 983–997. [Google Scholar] [CrossRef]
- Ojeda-May, P. Exploring the Dynamics of Shikimate Kinase through Molecular Mechanics. Biophysica 2022, 2, 194–202. [Google Scholar] [CrossRef]
- Kordylewski, S.K.; Bugno, R.; Podlewska, S. Residence Time in Drug Discovery: Current Insights and Future Perspectives. Pharmacol. Rep. 2025, 77, 851–873. [Google Scholar] [CrossRef]
- Burr, H.S.; Northrop, F.S.C. The Electro-Dynamic Theory of Life. Q. Rev. Biol. 1935, 10, 322–333. [Google Scholar] [CrossRef]
- Zhang, G.; Levin, M. Bioelectricity Is a Universal Multifaced Signaling Cue in Living Organisms. Mol. Biol. Cell 2025, 36, pe2. [Google Scholar] [CrossRef]
- Pantoja, C.; Acosta, F.M.; Granatir, S.; Anderson, M.; Wyr, M.; Tailor, J.; Fuori, A.; Dower, W.; Marr, H.B.; Ramirez, P.W. Electromagnetic Waves Destabilize the SARS-CoV-2 Spike Protein and Reduce SARS-CoV-2 Virus-Like Particle (SC2-VLP) Infectivity. Sci. Rep. 2025, 15, 16836. [Google Scholar] [CrossRef]
- Ali Siddiqui, S.; Dutta Dubey, K. Can the Local Electric Field Be a Descriptor of Catalytic Activity? A Case Study on Chorismate Mutase. Phys. Chem. Chem. Phys. 2022, 24, 1974–1981. [Google Scholar] [CrossRef]
- Hult, K.; Berglund, P. Enzyme Promiscuity: Mechanism and Applications. Trends Biotechnol. 2007, 25, 231–238. [Google Scholar] [CrossRef]
- Fried, S.D.; Boxer, S.G. Electric Fields and Enzyme Catalysis. Annu. Rev. Biochem. 2017, 86, 387–415. [Google Scholar] [CrossRef] [PubMed]
- Burley, S.K.; Bhikadiya, C.; Bi, C.; Bittrich, S.; Chen, L.; Crichlow, G.V.; Christie, C.H.; Dalenberg, K.; Di Costanzo, L.; Duarte, J.M.; et al. RCSB Protein Data Bank: Powerful New Tools for Exploring 3D Structures of Biological Macromolecules for Basic and Applied Research and Education in Fundamental Biology, Biomedicine, Biotechnology, Bioengineering and Energy Sciences. Nucleic Acids Res. 2021, 49, D437–D451. [Google Scholar] [CrossRef] [PubMed]
- Cheng, W.-C.; Chen, Y.-F.; Wang, H.-J.; Hsu, K.-C.; Lin, S.-C.; Chen, T.-J.; Yang, J.-M.; Wang, W.-C. Structures of Helicobacter pylori Shikimate Kinase Reveal a Selective Inhibitor-Induced-Fit Mechanism. PLoS ONE 2012, 7, e33481. [Google Scholar] [CrossRef] [PubMed]
- Müller, C.W.; Schulz, G.E. Structure of the Complex between Adenylate Kinase from Escherichia Coli and the Inhibitor Ap5A Refined at 1.9 Å Resolution: A Model for a Catalytic Transition State. J. Mol. Biol. 1992, 224, 159–177. [Google Scholar] [CrossRef]
- Jo, S.; Kim, T.; Iyer, V.G.; Im, W. CHARMM-GUI: A Web-Based Graphical User Interface for CHARMM. J. Comput. Chem. 2008, 29, 1859–1865. [Google Scholar] [CrossRef]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.M.; Mittal, J.; Feig, M.; MacKerell, A.D. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain Χ1 and Χ2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef]
- Mackerell, A.D.; Feig, M.; Brooks, C.L. Extending the Treatment of Backbone Energetics in Protein Force Fields: Limitations of Gas-Phase Quantum Mechanics in Reproducing Protein Conformational Distributions in Molecular Dynamics Simulations. J. Comput. Chem. 2004, 25, 1400–1415. [Google Scholar] [CrossRef]
- Foloppe, N.; MacKerell, A.D., Jr. All-Atom Empirical Force Field for Nucleic Acids: I. Parameter Optimization Based on Small Molecule and Condensed Phase Macromolecular Target Data. J. Comput. Chem. 2000, 21, 86–104. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Chandrasekhar, J.; Madura, J.D.; Impey, R.W.; Klein, M.L. Comparison of Simple Potential Functions for Simulating Liquid Water. J. Chem. Phys. 1983, 79, 926–935. [Google Scholar] [CrossRef]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A High-Throughput and Highly Parallel Open Source Molecular Simulation Toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High Performance Molecular Simulations through Multi-Level Parallelism from Laptops to Supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Páll, S.; Abraham, M.J.; Kutzner, C.; Hess, B.; Lindahl, E. Tackling Exascale Software Challenges in Molecular Dynamics Simulations with GROMACS. In Solving Software Challenges for Exascale; Springer: Cham, Switzerland, 2014; pp. 3–27. [Google Scholar]
- Van Der Spoel, D.; Lindahl, E.; Hess, B.; Groenhof, G.; Mark, A.E.; Berendsen, H.J.C. GROMACS: Fast, Flexible, and Free. J. Comput. Chem. 2005, 26, 1701–1718. [Google Scholar] [CrossRef]
- Lindahl, E.; Hess, B.; van der Spoel, D. GROMACS 3.0: A Package for Molecular Simulation and Trajectory Analysis. J. Mol. Model. 2001, 7, 306–317. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; van der Spoel, D.; van Drunen, R. GROMACS: A Message-Passing Parallel Molecular Dynamics Implementation. Comput. Phys. Commun. 1995, 91, 43–56. [Google Scholar] [CrossRef]
- Essmann, U.; Perera, L.; Berkowitz, M.L.; Darden, T.; Lee, H.; Pedersen, L.G. A Smooth Particle Mesh Ewald Method. J. Chem. Phys. 1995, 103, 8577–8593. [Google Scholar] [CrossRef]
- Darden, T.; York, D.; Pedersen, L. Particle Mesh Ewald: An N·log(N) Method for Ewald Sums in Large Systems. J. Chem. Phys. 1993, 98, 10089–10092. [Google Scholar] [CrossRef]
- Nosé, S.; Klein, M.L. Constant Pressure Molecular Dynamics for Molecular Systems. Mol. Phys. 1983, 50, 1055–1076. [Google Scholar] [CrossRef]
- Kühne, T.D.; Iannuzzi, M.; Del Ben, M.; Rybkin, V.V.; Seewald, P.; Stein, F.; Laino, T.; Khaliullin, R.Z.; Schütt, O.; Schiffmann, F.; et al. CP2K: An Electronic Structure and Molecular Dynamics Software Package-Quickstep: Efficient and Accurate Electronic Structure Calculations. J. Chem. Phys. 2020, 152, 194103. [Google Scholar] [CrossRef] [PubMed]
- Bussi, G.; Donadio, D.; Parrinello, M. Canonical Sampling through Velocity Rescaling. J. Chem. Phys. 2007, 126, 014101. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- VandeVondele, J.; Hutter, J. Gaussian Basis Sets for Accurate Calculations on Molecular Systems in Gas and Condensed Phases. J. Chem. Phys. 2007, 127, 114105. [Google Scholar] [CrossRef]
- Goedecker, S.; Teter, M.; Hutter, J. Separable Dual-Space Gaussian Pseudopotentials. Phys. Rev. B 1996, 54, 1703–1710. [Google Scholar] [CrossRef]
- Hartwigsen, C.; Goedecker, S.; Hutter, J. Relativistic Separable Dual-Space Gaussian Pseudopotentials from H to Rn. Phys. Rev. B 1998, 58, 3641–3662. [Google Scholar] [CrossRef]
- The UniProt Consortium. UniProt: The Universal Protein Knowledgebase. Nucleic Acids Res. 2017, 45, D158–D169. [Google Scholar] [CrossRef]
- Rehvathy, V.; Tan, M.H.; Gunaletchumy, S.P.; Teh, X.; Wang, S.; Baybayan, P.; Singh, S.; Ashby, M.; Kaakoush, N.O.; Mitchell, H.M.; et al. Multiple Genome Sequences of Helicobacter pylori Strains of Diverse Disease and Antibiotic Resistance Backgrounds from Malaysia. Genome Announc. 2013, 1, e00687-13. [Google Scholar] [CrossRef]
- Oh, J.D.; Kling-Bäckhed, H.; Giannakis, M.; Xu, J.; Fulton, R.S.; Fulton, L.A.; Cordum, H.S.; Wang, C.; Elliott, G.; Edwards, J.; et al. The Complete Genome Sequence of a Chronic Atrophic Gastritis Helicobacter pylori Strain: Evolution during Disease Progression. Proc. Natl. Acad. Sci. USA 2006, 103, 9999–10004. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.F.; Madden, T.L.; Schäffer, A.A.; Zhang, J.; Zhang, Z.; Miller, W.; Lipman, D.J. Gapped BLAST and PSI-BLAST: A New Generation of Protein Database Search Programs. Nucleic Acids Res. 1997, 25, 3389–3402. [Google Scholar] [CrossRef] [PubMed]
- Altschul, S.F.; Wootton, J.C.; Gertz, E.M.; Agarwala, R.; Morgulis, A.; Schäffer, A.A.; Yu, Y.-K. Protein Database Searches Using Compositionally Adjusted Substitution Matrices. FEBS J. 2005, 272, 5101–5109. [Google Scholar] [CrossRef] [PubMed]
- Camacho, C.; Coulouris, G.; Avagyan, V.; Ma, N.; Papadopoulos, J.; Bealer, K.; Madden, T.L. BLAST+: Architecture and Applications. BMC Bioinform. 2009, 10, 421. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On Lines and Planes of Closest Fit to Systems of Points in Space. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Wu, H.; Noé, F. Variational Approach for Learning Markov Processes from Time Series Data. J. Nonlinear Sci. 2020, 30, 23–66. [Google Scholar] [CrossRef]
- Hoffmann, M.; Scherer, M.; Hempel, T.; Mardt, A.; de Silva, B.; Husic, B.E.; Klus, S.; Wu, H.; Kutz, N.; Brunton, S.L.; et al. Deeptime: A Python Library for Machine Learning Dynamical Models from Time Series Data. Mach. Learn. Sci. Technol. 2021, 3, 015009. [Google Scholar] [CrossRef]
- Parra, R.G.; Schafer, N.P.; Radusky, L.G.; Tsai, M.-Y.; Guzovsky, A.B.; Wolynes, P.G.; Ferreiro, D.U. Protein Frustratometer 2: A Tool to Localize Energetic Frustration in Protein Molecules, Now with Electrostatics. Nucleic Acids Res. 2016, 44, W356–W360. [Google Scholar] [CrossRef]
- Rausch, A.O.; Freiberger, M.I.; Leonetti, C.O.; Luna, D.M.; Radusky, L.G.; Wolynes, P.G.; Ferreiro, D.U.; Parra, R.G. FrustratometeR: An R-Package to Compute Local Frustration in Protein Structures, Point Mutants and MD Simulations. Bioinformatics 2021, 37, 3038–3040. [Google Scholar] [CrossRef]
- Ferreiro, D.U.; Hegler, J.A.; Komives, E.A.; Wolynes, P.G. Localizing Frustration in Native Proteins and Protein Assemblies. Proc. Natl. Acad. Sci. USA 2007, 104, 19819–19824. [Google Scholar] [CrossRef]
- Ojeda-May, P. Exploring the Dynamics of Holo-Shikimate Kinase through Molecular Mechanics. Biophysica 2023, 3, 463–475. [Google Scholar] [CrossRef]
- Koltai, P.; Wu, H.; Noé, F.; Schütte, C. Optimal Data-Driven Estimation of Generalized Markov State Models for Non-Equilibrium Dynamics. Computation 2018, 6, 22. [Google Scholar] [CrossRef]
- Chvykov, P.; Berrueta, T.A.; Vardhan, A.; Savoie, W.; Samland, A.; Murphey, T.D.; Wiesenfeld, K.; Goldman, D.I.; England, J.L. Low Rattling: A Predictive Principle for Self-Organization in Active Collectives. Science 2021, 371, 90–95. [Google Scholar] [CrossRef] [PubMed]
- Warshel, A.; Sharma, P.K.; Kato, M.; Xiang, Y.; Liu, H.; Olsson, M.H.M. Electrostatic Basis for Enzyme Catalysis. Chem. Rev. 2006, 106, 3210–3235. [Google Scholar] [CrossRef]
- Parra, R.G.; Ferreiro, D.U. Frustration, Dynamics and Catalysis. arXiv 2025, arXiv:2505.00600. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).