Quantitative Characterization of Nonspecific Interactions Between Macromolecules in Complex Media: Comparison of Experiment, Theory, and Simulation
Abstract
1. Introduction
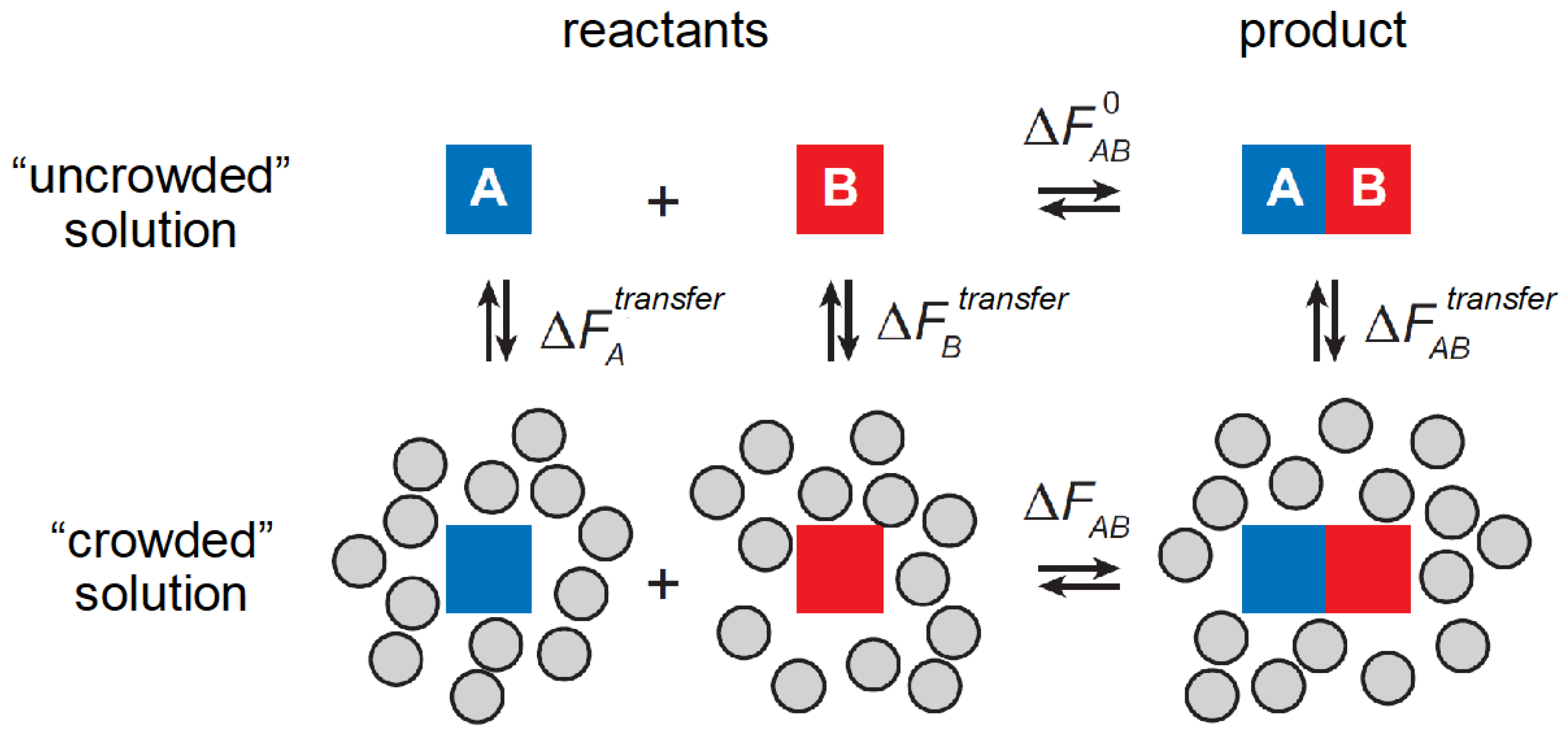
2. Introduction to the Thermodynamic Characterization of Nonspecific Interactions
3. Experimental Measurement of the Free Energy of Transfer in Solutions of One and Two Macrosolutes
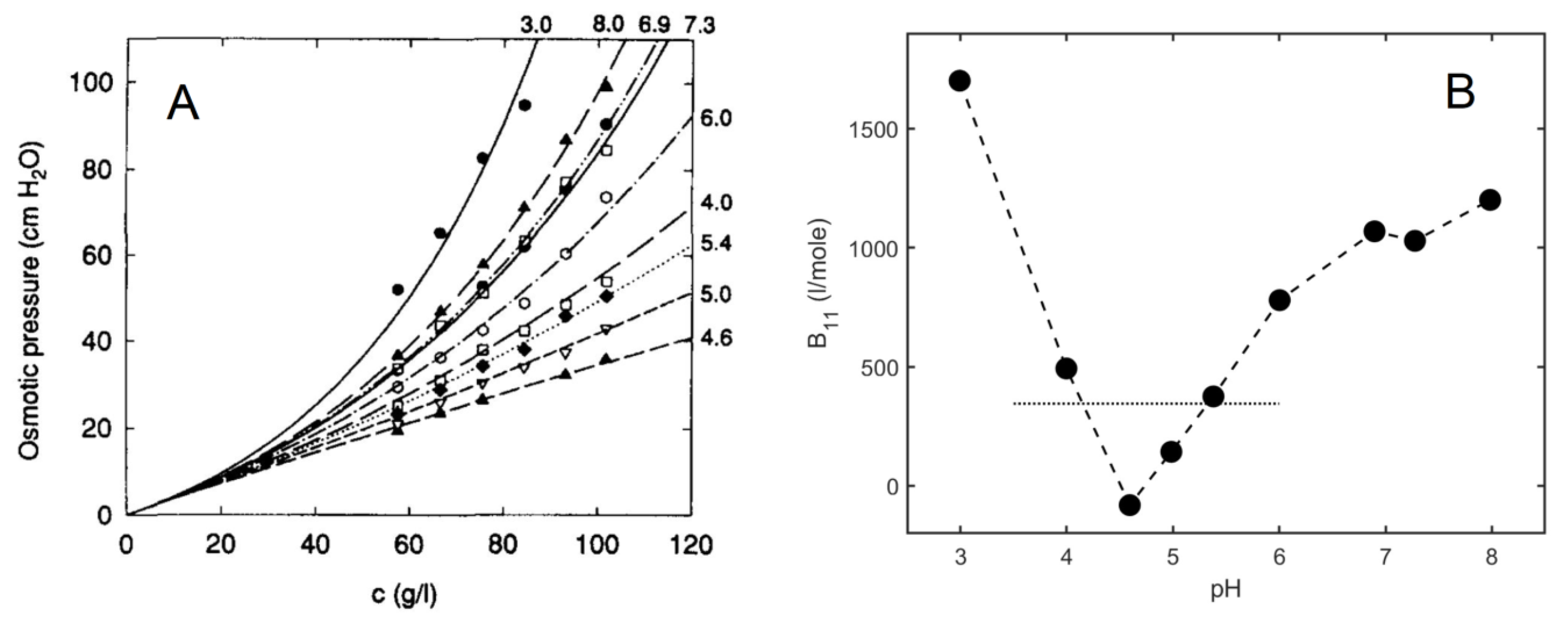
3.1. Osmotic Pressure
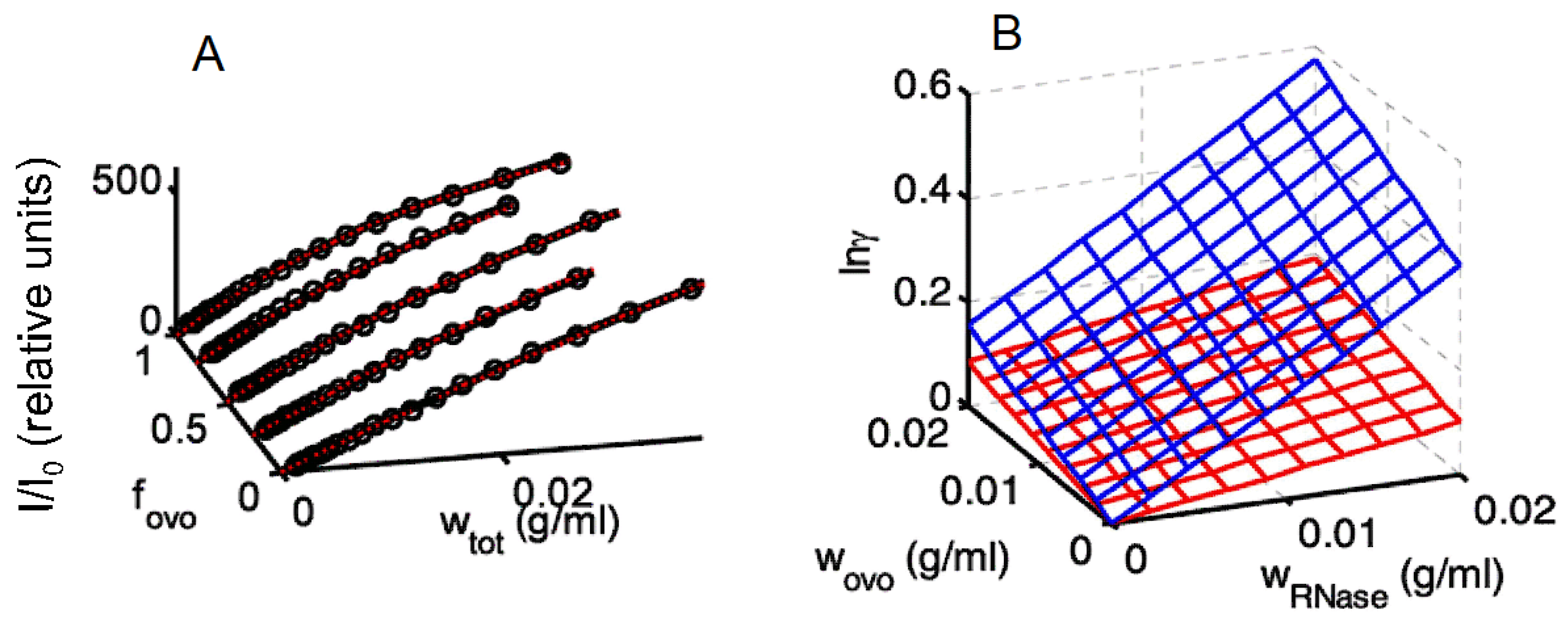
3.2. Static Light Scattering
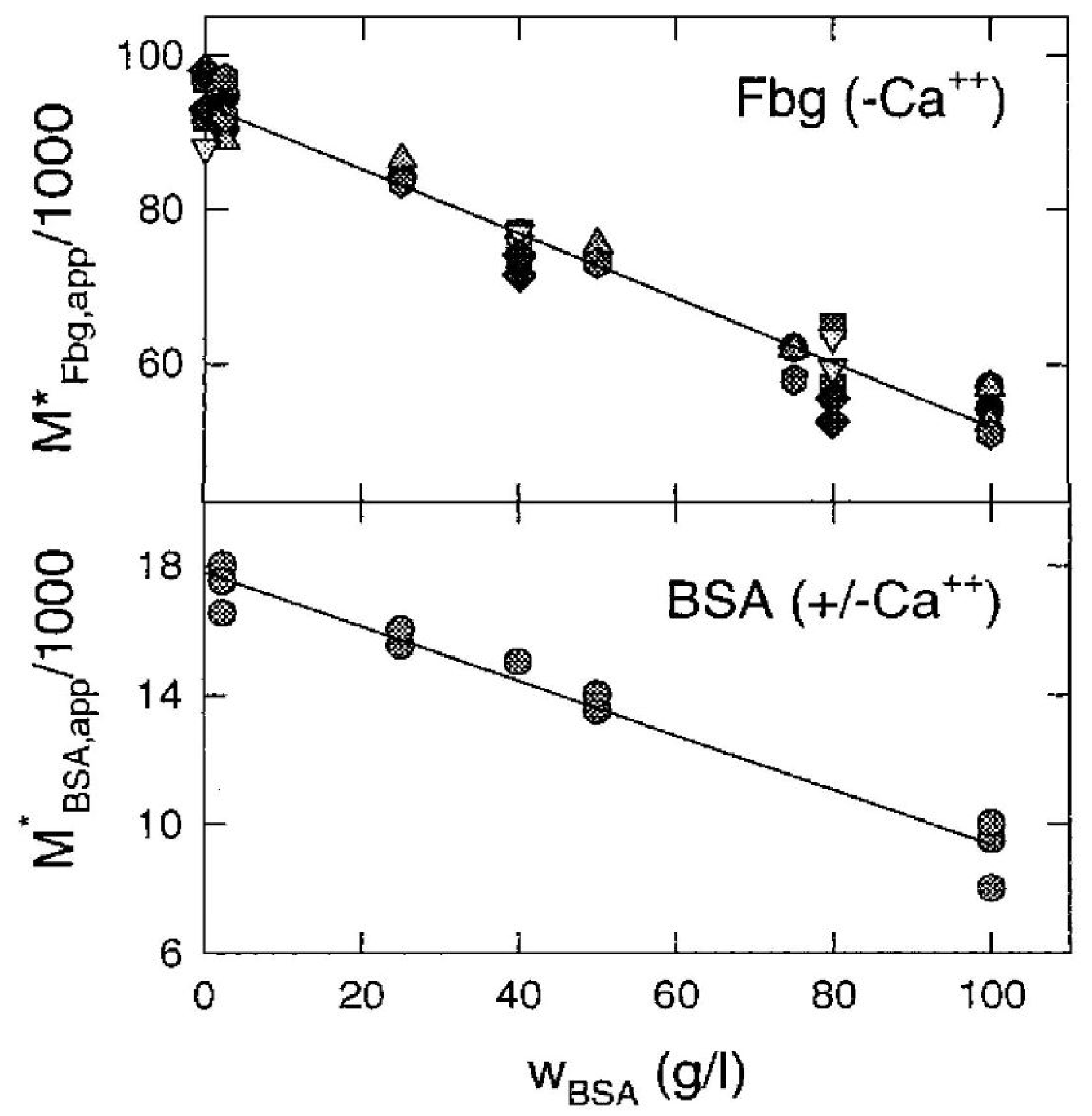
3.3. Nonideal Tracer Sedimentation Equilibrium
4. Quantitative Characterization of Nonspecific Interactions via Theory and Computer Simulation
4.1. Two-Body Interaction Coefficient
4.2. Higher-Order Interactions
5. Conclusions: Recommendations for Advancement in the Quantitative Characterization of Nonspecific Interactions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
References
- Rivas, G.; Minton, A.P. Influence of Nonspecific Interactions on Protein Associations: Implications for Biochemistry In Vivo. Annu. Rev. Biochem. 2022, 91, 321–351. [Google Scholar] [CrossRef] [PubMed]
- Phizicky, E.M.; Fields, S. Protein-protein interactions: Methods for detection and analysis. Microbiol. Rev. 1995, 59, 94–123. [Google Scholar] [CrossRef] [PubMed]
- Schwikowski, B.; Uetz, P.; Fields, S. A network of protein-protein interactions in yeast. Nat. Biotechnol. 2000, 18, 1257–1261. [Google Scholar] [CrossRef]
- Rivas, G.; Minton, A.P. Toward an understanding of biochemical equilibria within living cells. Biophys. Rev. 2017, 10, 241–253. [Google Scholar] [CrossRef]
- Cantor, C.R.; Schimmel, P.R. Biophysical Chemistry Part III: The Behavior of Biological Macromolecules; W. H. Freeman: San Francisco, CA, USA, 1980; p. 1371. [Google Scholar]
- Tanford, C. Physical Chemistry of Macromolecules; Wiley & Sons: New York, NY, USA, 1963; p. 710. [Google Scholar]
- Minton, A.P. Molecular crowding: Analysis of effects of high conceentrations of inert cosolutes on biochemical equilibria and rates in terms of volume exclusion. Methods Enzymol. 1998, 295, 127–149. [Google Scholar] [PubMed]
- Pasquier, C.; Midtgaard, S.R.; Polimeni, M.; Jorgensen, C.I.; Arleth, L.; Callisen, T.H.; Lund, M. Anisotropic protein-protein interactions in dilute and concentrated solutions. J. Colloid Interface Sci. 2023, 629, 794–804. [Google Scholar] [CrossRef]
- Laurent, T.C. Enzyme reactions in polymer media. Eur. J. Biochem. 1971, 21, 498–506. [Google Scholar] [CrossRef]
- Minton, A.P. Excluded volume as a determinant of protein structure and stability. Biophys. J. 1980, 32, 77–79. [Google Scholar] [CrossRef]
- McMillan, W.G., Jr.; Mayer, J.E. The statistical thermodynamics of multicomponent systems. J. Chem. Phys. 1945, 13, 276–305. [Google Scholar] [CrossRef]
- Velev, O.D.; Kaler, E.W.; Lenhoff, A.M. Protein interactions in solution characterized by light and neutron scattering: Comparison of lysozyme and chymotrypsinogen. Biophys. J. 1998, 75, 2682–2697. [Google Scholar] [CrossRef]
- Stradner, A.; Cardinaux, F.; Schurtenberger, P. A small-angle scattering study on equilibrium clusters in lysozyme solutions. J. Phys. Chem. B 2006, 110, 21222–21231. [Google Scholar] [CrossRef] [PubMed]
- Blanco, M.A.; Perevozchikova, T.; Martorana, V.; Manno, M.; Roberts, C.J. Protein-Protein Interactions in Dilute to Concentrated Solutions: α-Chymotrypsinogen in Acidic Conditions. J. Phys. Chem. B 2014, 118, 5817–5831. [Google Scholar] [CrossRef]
- Petsev, D.N.; Wu, X.; Galkin, O.; Vekilov, P.G. Thermodynamic functions of concentrated protein solutions from phase equilibri. J. Phys. Chem. B 2003, 107, 3921–3926. [Google Scholar] [CrossRef]
- Adair, G.S. A theory of partial osmotic pressures and membrane equilibria, with special reference to the application of Dalton’s law to haeoglobin solutions in the presence of salts. Proc. R. Soc. Lond. Ser. A 1928, 120, 573–603. [Google Scholar]
- Briehl, R.W.; Ewert, S. Effects of pH, 2,3-diphosphoglycerate and salts on gelation of sickle cell hemoglobin. J. Mol. Biol. 1973, 80, 445–458. [Google Scholar] [CrossRef]
- Ross, P.D.; Briehl, R.W.; Minton, A.P. Temperature dependence of nonideality in concentrated solutions of hemoglobin. Biopolymers 1978, 17, 2285–2288. [Google Scholar] [CrossRef] [PubMed]
- Ross, P.D.; Minton, A.P. Analysis of non-ideal behavior in concentrated hemoglobin solutions. J. Mol. Biol. 1977, 112, 437–452. [Google Scholar] [CrossRef]
- Williams, R.C., Jr. Concerted formation of the gel of hemoglobin S. Proc. Natl. Acad. Sci. USA 1973, 70, 1506–1508. [Google Scholar] [CrossRef]
- Fodeke, A.A.; Minton, A.P. Quantitative characterization of temperature-independent and temperature-dependent protein-protein interactions in highly nonideal solutions. J. Phys. Chem. B 2011, 115, 11261–11268. [Google Scholar] [CrossRef]
- Minton, A.P.; Lewis, M.S. Self-association in highly concentrated solutions of myoglobin: A novel analysis of sedimentation equilibrium of highly nonideal solutions. Biophys. Chem. 1981, 14, 317–324. [Google Scholar] [CrossRef]
- Rivas, G.; Fernandez, J.A.; Minton, A.P. Direct observation of the self-association of dilute proteins in teh presence of inert macromolecules at high concentration via tracer sedimentation equilibrium: Theory, experiment, and biological significance. Biochemistry 1999, 38, 9379–9388. [Google Scholar] [CrossRef] [PubMed]
- Minton, A.P. The effect of volume occupancy upon the thermodynamic activity of proteins: Some biochemical consequences. Mol. Cell. Biochem. 1983, 55, 119–140. [Google Scholar] [CrossRef] [PubMed]
- Fodeke, A.A.; Minton, A.P. Quantitative characterization of polymer-polymer, protein-protein, and polymer-protein interaction via tracer sedimentation equilibrium. J. Phys. Chem. B 2010, 114, 10876–10880. [Google Scholar] [CrossRef]
- Wu, J.Z.; Prausnitz, J.M. Osmotic pressures of aqueous bovine serum albumin solutions at high ionic strength. Fluid Phase Equilibria 1999, 155, 139–154. [Google Scholar] [CrossRef]
- Atha, D.H.; Ingham, K.C. Mechanism of precipitation of proteins by poyethylene glycols. J. Biol. Chem. 1981, 256, 12108–12117. [Google Scholar] [CrossRef]
- Fodeke, A.A. Quantitative characterization of non-specific interactin of two globular proteins with Dextran T70 in a binary mixture. Eur. Biophys. J. 2024, 53, 465–472. [Google Scholar] [CrossRef]
- Wu, D.; Minton, A.P. Quantitative characteriation of nonspeific self- and hetero-interactions of proteins in nonideal solutions via static light scattering. J. Phys. Chem. B 2015, 119, 1891–1898. [Google Scholar] [CrossRef] [PubMed]
- Fernández, C.; Fodeke, A.A.; Minton, A.P. Quantitative characterization of the concentration-dependent interaction between molecules of Dextran 70 in aqueous solution: Measurement and analysis in the context of thermodynamic and compressible sphere models. Biopolymers 2019, 110, e23284. [Google Scholar] [CrossRef]
- Fernández, C.; Minton, A.P. Static light scattering from concentrated protein solutions II: Experimental test of theory for protein mixtures and weakly self-associating proteins. Biophys. J. 2009, 96, 1992–1998. [Google Scholar] [CrossRef]
- Fodeke, A.A. Quantitative characterization of temperature-independent polymer-polymer interaction and temperature-dependent protein-protein and protein-polymer interactions in concentrated polymer solutions. Eur. Biophys. J. 2019, 48, 189–202. [Google Scholar] [CrossRef]
- Scherer, T.M.; Liu, J.; Shire, S.J.; Minton, A.P. Intermolecular interactions of IgG1 monoclonal antibodies at high concentrations characterized by light scattering. J. Phys. Chem. B 2010, 114, 12948–12957. [Google Scholar] [CrossRef] [PubMed]
- Kimball, W.D.; Lanzaro, A.; Hurd, C.; Jhaveri, N.; Huang, J.; Lewandowski, J.; Qian, K.K.; Woldeyes, M.A.; Majumdar, R.; Witek, M.A.; et al. Growth of Clusters toward Liquid-Liquid Phase Separation of Monoclonal Antibodies as Characterized by Small-Angle X-ray Scattering and Molecular Dynamics Simulation. J. Phys. Chem. B 2025, 129, 2856–2871. [Google Scholar] [CrossRef] [PubMed]
- Lilyestrom, W.G.; Yadav, S.; Shire, S.J.; Scherer, T.M. Monoclonal antibody self-association, cluster formation, and rheology at high concentrations. J. Phys. Chem. B 2013, 117, 6373–6384. [Google Scholar] [CrossRef]
- Gulotta, A.; Polimeni, M.; Lenton, S.; Starr, C.G.; Stradner, A.; Zaccarelli, E.; Schurtenberger, P. Combining Scattering Experiments and Colloid Theory to Characterize Charge Effects in Concentrated Antibody Solutions. Mol. Pharm. 2024, 21, 2250–2271. [Google Scholar] [CrossRef] [PubMed]
- Woldeyes, M.A.; Calero-Rubio, C.; Furst, E.M.; Roberts, C.J. Light Scattering to Quantify Protein-Protein Interactions at High Protein Concentrations. Methods Mol. Biol. 2019, 2039, 23–37. [Google Scholar]
- Stradner, A.; Cardinaux, F.; Egelhaaf, S.U.; Schurtenberger, P. Do equilibrium clusters exist in concentrated lysozyme solutions? Proc. Natl. Acad. Sci. USA 2008, 105, E75–E76. [Google Scholar] [CrossRef]
- Winzor, D.J.; Wills, P.R. Molecular crowding effects of linear polymers in protein solutions. Biophys. Chem. 2006, 119, 186–195. [Google Scholar] [CrossRef]
- Woldeyes, M.A.; Calero-Rubio, C.; Furst, E.M.; Roberts, C.J. Predicting Protein Interactions of Concentrated Globular Protein Solutions Using Colloidal Models. J. Phys. Chem. B 2017, 121, 4756–4767. [Google Scholar] [CrossRef]
- Laurent, T.C.; Ogston, A.G. The interaction between polysaccharides and other macromolecules 4. The osmotic pressure of mixtures of serum albumin and hyaluronic acid. Biochem. J. 1963, 89, 249–253. [Google Scholar] [CrossRef]
- Madden, M.J.; Ellis, S.N.; Riabtseva, A.; Wilson, A.D.; Cunningham, M.F.; Jessop, P.G. Comparison of vapour pressure osmometry, freezing point osmometry and direct membrane osmometry for determining the osmotic pressure of concentrated solutions. Desalination 2022, 539, 276–305. [Google Scholar] [CrossRef]
- Parsegian, V.A.; Rand, R.P.; Fuller, N.L.; Rau, D.C. Osmotic stress for the direct measurement of intermolecular forces. Methods Enzymol. 1986, 127, 400–416. [Google Scholar] [PubMed]
- Jiménez, M.; Rivas, G.; Minton, A.P. Quantitative characterization of weak self-association in concentrated solutions of immunoglobulin G via the measurement of sedimentation equilibrium and osmotic pressure. Biochemistry 2007, 46, 8373–8378. [Google Scholar] [CrossRef] [PubMed]
- Kanal, K.M.; Fullerton, G.D.; Cameron, I.L. A study of the molecular sources of nonideal osmotic pressure of bovine serum albumin solutions as a function of pH. Biophys. J. 1994, 66, 153–160. [Google Scholar] [CrossRef] [PubMed]
- Minton, A.P. A molecular model for the dependence of the osmotic pressure of bovine serum albumin upon concentration and pH. Biophys. Chem. 1995, 57, 65–70. [Google Scholar] [CrossRef]
- Minton, A.P. Recent applications of light scattering measurement in the biological and biopharmaceutical sciences. Anal. Biochem. 2016, 501, 4–22. [Google Scholar] [CrossRef]
- Wyatt, P.J. Light scattering and the absolute characterization of macromolecules. Anal. Chim. Acta 1993, 272, 1–40. [Google Scholar] [CrossRef]
- Minton, A.P. Static light scattering from concentrated protein solutions, I: General theory for protein mixtures and application to self-associating proteins. Biophys. J. 2007, 93, 1321–1328. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Light scattering in multi-component systems. J. Chem. Phys. 1950, 18, 58–61. [Google Scholar] [CrossRef]
- Stacey, K.A. Light-Scattering in Physical Chemistry; Academic Press: New York, NY, USA, 1956; p. 230. [Google Scholar]
- Teller, D.C. Characterization of proteins by sedimentation equilibrium in the analytical ultracentrifuge. Methods Enzymol. 1973, 27, 346–441. [Google Scholar]
- Zorrilla, S.; Jiménez, M.; Lillo, P.; Rivas, G.; Minton, A.P. Sedimentation equilibrium in a solution containing an arbitrary number of solute species at arbitrary concentrations: Theory and application to concentrated solutions of ribonuclease. Biophys. Chem. 2004, 108, 89–100. [Google Scholar] [CrossRef]
- Rivas, G.; Minton, A.P. Tracer sedimentation equilibrium: A powerful tool for the quantitative characterization of macromolecular self- and hetero-associations in solution. Biochem. Soc. Trans. 2003, 31, 1015–1019. [Google Scholar] [CrossRef] [PubMed]
- Rivas, G.; Minton, A.P. Non-ideal tracer sedimentation equilibrium: A powerful tool for the characterization of macromolecular interactions in crowded solutions. J. Mol. Recognit. 2004, 17, 362–367. [Google Scholar] [CrossRef]
- Rivas, G.; Minton, A.P. Beyond the second virial coefficient: Sedimentation equilibrium in highly non-ideal solutions. Methods 2011, 54, 167–174. [Google Scholar] [CrossRef] [PubMed]
- Nguemaha, V.; Qin, S.; Zhou, H.-X. Transfer free energies of test proteins into crowded protein solutions have simple dependence on crowder concentration. Front. Mol. Biosci. 2019, 6, 39. [Google Scholar] [CrossRef]
- Qin, S.; Zhou, H.X. Fast method for computing chemical potentials and liquid-liquid phase equilibria for macromolecular solutions. J. Phys. Chem. B 2016, 120, 8164–8174. [Google Scholar] [CrossRef] [PubMed]
- Qin, S.; Zhou, H.X. Further Development of the FFT-based Method for Atomistic Modeling of Protein Folding and Binding under Crowding: Optimization of Accuracy and Speed. J. Chem. Theory Comput. 2014, 10, 2824–2835. [Google Scholar] [CrossRef]
- Widom, B. Some topics in the theory of fluids. J. Chem. Phys. 1963, 39, 2808–2812. [Google Scholar] [CrossRef]
- Binder, K. Applications of Monte Carlo methods to statistical physics. Rep. Prog. Phys. 1997, 60, 487–559. [Google Scholar] [CrossRef]
- Hoppe, T.; Minton, A.P. Incorporation of hard and soft protein-protein interactions into models for crowding effects in binary and ternary protein mixtures. Comparison of approximate analytical solutions with numerical simulation. J. Phys. Chem. B 2016, 120, 11866–11872. [Google Scholar] [CrossRef]
- Hoppe, T.; Minton, A.P. Non-specific Interactions Between Macromolecular Solutes in Concentrated Solution: Physico-Chemical Manifestations and Biochemical Consequences. Front. Mol. Biosci. 2019, 6, 10. [Google Scholar] [CrossRef]
- Minton, A.P. Explicit Incorporation of Hard and Soft Protein-Protein Interactions into Models for Crowding Effects in Protein Mixtures. 2. Effects of Varying Hard and Soft Interactions upon Prototypical Chemical Equilibria. J. Phys. Chem. B 2017, 121, 5515–5522. [Google Scholar] [CrossRef] [PubMed]
- Minton, A.P. Simple Calculation of Phase Diagrams for Liquid-Liquid Phase Separation in Solutions of Two Macromolecular Solute Species. J. Phys. Chem. B 2020, 124, 2363–2370. [Google Scholar] [CrossRef]
- Xia, J.-Z.; Wang, Q.; Tatarkova, S.; Aerts, T.; Clauwaert, J. Structural basis of eye lens transpareny: Light scattering by concentrated solutions of bovine α-crystallin proteins. Biophys. J. 1996, 71, 2815–2822. [Google Scholar] [CrossRef] [PubMed]
- Yousef, M.A.; Datta, R.; Ridgers, V.G. Free-solvent model of osmotic pressure revisited: Application to concentrated IgG solution under physiological conditions. J. Coll. Interf. Sci. 1998, 197, 108–118. [Google Scholar] [CrossRef]
- Reiche, K.; Hartl, J.; Blume, A.; Garidel, P. Liquid-liquid phase separation of a monoclonal antibody at low ionic strength: Influence of anion charge and concentration. Biophys. Chem. 2017, 220, 7–19. [Google Scholar] [CrossRef] [PubMed]
- Boublík, T. Statistical thermodynamics of convex molecule fluids. Mol. Phys. 1974, 27, 1415–1427. [Google Scholar] [CrossRef]
- Lund, M. Anisotropic protein-protein interactions due to ion binding. Colloids Surf. B-Biointerfaces 2016, 137, 17–21. [Google Scholar] [CrossRef]
- Hoppe, T. A simplified representation of anisotroic charge distributions within proteins. J. Chem. Phys. 2013, 138, 174110. [Google Scholar] [CrossRef]
- Grünberger, A.; Lai, P.-K.; Blanco, M.A.; Roberts, C.J. Coarse-grained modeling of protein second osmotic virial coefficients: Sterics and short-ranged attractions. J. Phys. Chem. B 2012, 117, 763–770. [Google Scholar] [CrossRef]
- Calero-Rubio, C.; Saluja, A.; Roberts, C.J. Coarse-Grained Antibody Models for “Weak” Protein-Protein Interactions from Low to High Concentrations. J. Phys. Chem. B 2016, 120, 6592–6605. [Google Scholar] [CrossRef]
- Le Coeur, C.; Teixeira, J.; Busch, P.; Longeville, S. Compression of random coils due to macromolecular crowding: Scaling effects. Phys. Rev. E Stat. Nonlin Soft Matter Phys. 2010, 81, 061914. [Google Scholar] [CrossRef] [PubMed]
- Minton, A.P. Models for excluded volume interaction between an unfolded protein and rigid macromolecular cosolutes: Macromolecular crowding and protein stability revisited. Biophys. J. 2005, 88, 971–985. [Google Scholar] [CrossRef] [PubMed]

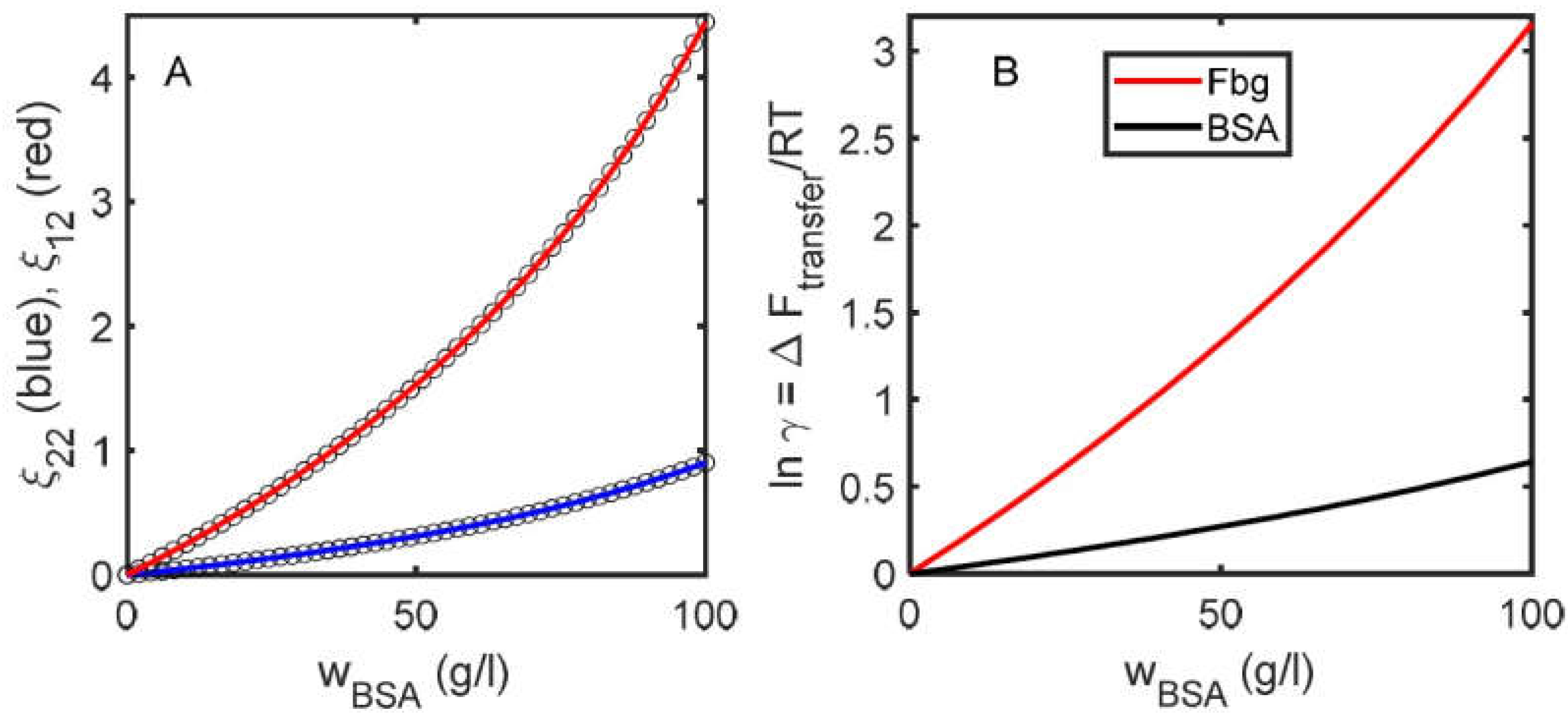
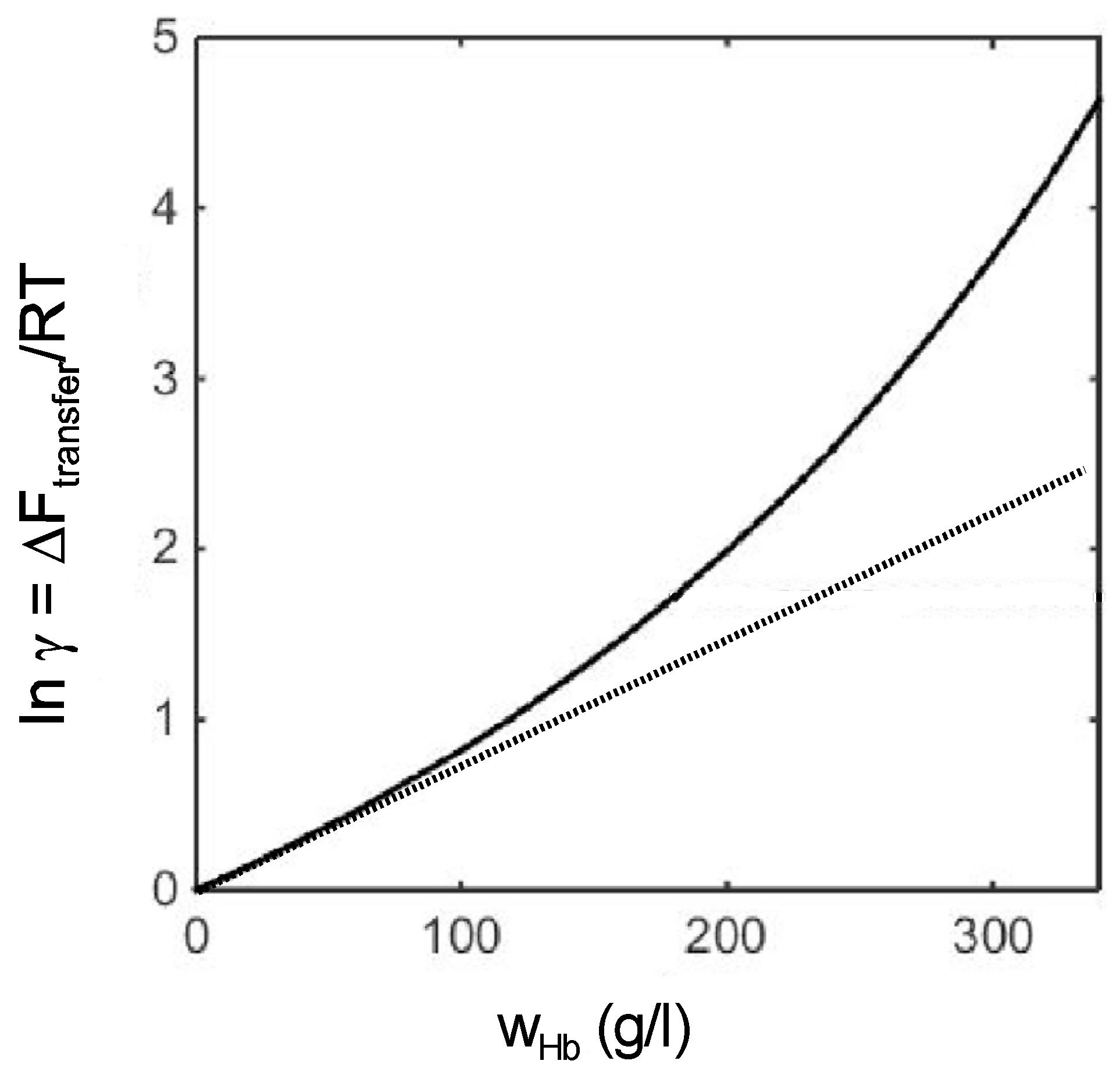

| Self-Interaction Pairs | References | Hetero-Interaction Pairs | References |
|---|---|---|---|
| Hb—Hb | [16,17,18,19,20] | BSA—ovo | [21] |
| Mb—Mb | [22] | BSA—Fbg | [23] |
| BSA—BSA | [21,23,24,25,26] | BSA—SOD | [21] |
| BSA—PEG | [27] | ||
| BSA—Dex 70 | [28] | ||
| Oval—oval | [29] | Ovo—oval | [29] |
| Ovo—ovo | [21,29] | Ovo—RNase | [29] |
| RNase—RNase | [29] | Oval—RNase | [29] |
| Dex 70—Dex 70 | [30] | BSA—Fic 70 | [25] |
| SOD—ovo | [21] | ||
| Fic 70—Fic 70 | [25] | SOD—Dex 70 | [31,32] |
| mAb—mAb | [33,34,35,36,37] | SOD—Fic 70 | [32] |
| Lys—Lys | [12,13,15,38] | CA—Dex (various MW) | [39] |
| α-chym—α-chym | [12,14,40] | CytC—Dex (various MW) | [39] |
| BSA—HA | [41] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Minton, A.P. Quantitative Characterization of Nonspecific Interactions Between Macromolecules in Complex Media: Comparison of Experiment, Theory, and Simulation. Biophysica 2025, 5, 25. https://doi.org/10.3390/biophysica5030025
Minton AP. Quantitative Characterization of Nonspecific Interactions Between Macromolecules in Complex Media: Comparison of Experiment, Theory, and Simulation. Biophysica. 2025; 5(3):25. https://doi.org/10.3390/biophysica5030025
Chicago/Turabian StyleMinton, Allen P. 2025. "Quantitative Characterization of Nonspecific Interactions Between Macromolecules in Complex Media: Comparison of Experiment, Theory, and Simulation" Biophysica 5, no. 3: 25. https://doi.org/10.3390/biophysica5030025
APA StyleMinton, A. P. (2025). Quantitative Characterization of Nonspecific Interactions Between Macromolecules in Complex Media: Comparison of Experiment, Theory, and Simulation. Biophysica, 5(3), 25. https://doi.org/10.3390/biophysica5030025






