Differential Scanning Calorimetry of Proteins and the Two-State Model: Comparison of Two Formulas

Abstract

Differential Scanning Calorimetry (DSC) is a regular and powerful tool to measure the specific heat profile of various materials. In order to connect the measured profile to the properties of a particular protein, a model is required to fit. We discuss here the application of an exact two-state formula with its approximation and process the DSC experimental data on protein folding in water. The approximate formula relies on the smallness of the transition interval, which is different for each protein. With an example of the set of 33 different proteins, we show the practical validity of the approximation and the equivalence of exact and approximate two-state formulas for processing DSC data.

1. Introduction

Differential Scanning Calorimetry (DSC) is a powerful technique used to measure the temperature dependence of specific heat for various solid [1] and soft materials, including biopolymer solutions [2]. Structural transformations taking place in the material of study show up as peaks in the heat capacity. Strictly speaking, only the transition temperature ($T_m$) can be determined from the position of the peak maximum if no model assumptions are invoked. For anything beyond this point, one needs additional assumptions to be made in order to process the DSC data.

If the baselines before and after the transition are parallel, their difference is temperature-independent (constant), and the baseline subtraction can be performed. The area under the specific heat peak can be thus numerically estimated, giving us the enthalpic cost ($\Delta H$) of transformation.

Quite often, it happens that a typical protein undergoing unfolding in solution does not have constant baselines. Sometimes, baselines are linear [3,4,5], and the (unjustified) subtraction gives a closed contour with the area enclosed equal to $\Delta H$. Not only is it unjustified but such a procedure is also not unique: each particular choice of the baseline points fits to a different line, which closes a different contour with a different $\Delta H$. Sometimes, the baselines are not linear at all [6,7,8,9,10], and no analysis is possible beyond the transition temperature determination.

Let us assume it is possible to perform the baseline subtraction. Then, the time comes to decide about the model which is going to be fit to the specific heat profile. The most common approach to analyze the DSC unfolding data is the two-state model [11]. It assumes that a protein exists in either a fully folded or fully unfolded state, and that the unfolding transition is reversible and cooperative [12]. The approach essentially relies on the temperature-independent (constant) difference of specific heats $\Delta C_P=C_P^U-C_P^N$ between the unfolded (U) and native (N) states and allows to derive a formula for the Gibbs free energy cost of protein (un)folding ($\Delta G$). The obtained formula allows to process the experimental data in terms of fitting.

While powerful and general, the two-state model is limited in its ability to accurately describe the complex thermodynamics of protein folding, especially for proteins with more than one domain or subunit [12].

Yet, another well-known approach, suggested by Hawley [13,14], is applicable to describe protein folding. It reproduces the elliptic phase diagram of protein (un)folding and allows for cold denaturation to happen. Hawley assumes the free energy difference between the native and denatured states in a protein is a quadratic function of pressure and temperature [13]. The resulting bell-shaped three-dimensional curve $\Delta G(P,T)$ is sliced at the zero surface to obtain an elliptical phase diagram. The approach was quite successful not only for protein folding but was later applied to describe the re-entrant melting transition in DNA [15] as well.

If we disregard the pressure-dependent terms in Hawley’s approach [13], it becomes very similar to the expressions suggested by Privalov for the two-state model [11]. As shown by Smeller [14], under the assumption of a small transition interval, the logarithmic term in the free energy expression can be resolved into a Taylor series and truncated at the second order, resulting in a quadratic expression. The assumption of the smallness of the transition interval depends on the particular protein: some have slightly wider, and some slightly narrower, temperature intervals. To which extent the approximate formula will be equivalent to the exact one can only become clear after the same two-state approach is applied to a set of data and the fitted parameters are compared.

In this publication, we compare the use of logarithmic and square formulas for the free energy of protein folding within the two-state model. We first discuss the theoretical foundations, review the derivations and later apply both formulas to process the set of 33 experimental DSC curves. Despite the obvious differences in transition intervals for each of proteins, the obtained values of fitted quantities for both methods are very similar. We thus conclude that the assumption of a small transition interval is often valid, at least for the random set of 33 proteins of our choice. It means that the proposed two formulas can be identically used to fit DSC data.

2. Materials and Methods

The extensively adopted two-state model for analyzing heat capacity profiles [2,11,12] is fundamentally based on the premise that folding constitutes a phase transition between the native and denatured states. While protein folding could be theoretically conceptualized as a coil–globule transition, the presence of limited system sizes and the heterogeneous composition of polypeptides results in a finite temperature range that deviates significantly from the idealized notion of a phase transition, which the two-state model is specifically designed to accommodate.

The process of determining the free energy difference between the native (N) and unfolded (U) states begins with formulating expressions for the enthalpies and entropies of each of the phases. The specific heat at constant pressure can be equivalently expressed for both the $\alpha =U,N$ phases as follows:

$$\begin{array}{c}\hfill C_P^{\alpha }={\left(\frac{d{H}^{\alpha }\left(T\right)}{dT}\right)}_P\\ \hfill C_P^{\alpha }=T{\left(\frac{d{S}^{\alpha }\left(T\right)}{dT}\right)}_P,\end{array}$$

(1)

and the estimations for enthalpy and entropy can be expressed as

$$\begin{array}{c}\hfill H^{\alpha }\left(T\right)=H^{\alpha }\left(T_0\right)+{\int }_{T_0}^{T}dT{C}_P^{\alpha }\left(T\right),\\ \hfill S^{\alpha }\left(T\right)=S^{\alpha }\left(T_0\right)+{\int }_{T_0}^{T}dT{C}_P^{\alpha }\left(T\right)/T,\end{array}$$

(2)

where the subscript 0 denotes the values of quantities at the transition point (chosen for convenience, although any reference temperature would work). This facilitates the formulation of expressions for the differences in enthalpy and entropy between the native and denatured phases as

$$\begin{array}{c}\hfill {\Delta }_N^{U}H\left(T\right)=H^U\left(T\right)-H^N\left(T\right)=\Delta H_0+{\int }_{T_0}^{T}dT{\Delta }_N^U{C}_P\left(T\right),\end{array}$$

(3a)

$$\begin{array}{c}\hfill {\Delta }_N^{U}S\left(T\right)=S^U\left(T\right)-S^N\left(T\right)=\Delta S_0+{\int }_{T_0}^{T}dT{\Delta }_N^U{C}_P\left(T\right)/T.\end{array}$$

(3b)

Up to this point, no assumptions have been made apart from the existence of two phases. To proceed, following Privalov [11], we adopt the assumption that the difference in specific heat between the two phases remains constant and can be substituted by its value at transition point, e.g., ${\Delta }_N^U{C}_P=\Delta C_P^0=const$. In other words, within the transition region, the difference in specific heats between the two phases does not vary with temperature. This is often interpreted as parallel baselines as proposed by Privalov [11]. The implications and consequences of such an assumption are not entirely clear, but once it is accepted, it leads to

$$\begin{array}{c}\hfill {\Delta }_N^{U}H\left(T\right)=\Delta H_0+(T-T_0)\Delta C_P^0,\\ \hfill {\Delta }_N^{U}S\left(T\right)=\Delta S_0+ln(T/T_0)\Delta C_P^0.\end{array}$$

(4)

Therefore,

$$\begin{array}{c}\hfill {\Delta }_N^{U}G\left(T\right)={\Delta }_N^{U}H\left(T\right)-T{\Delta }_N^{U}S\left(T\right)\\ \hfill =\Delta H_0\left(1-\frac{T}{T_0}\right)-T_0\Delta C_P^0\left(1-\frac{T}{T_0}+\frac{T}{T_0}ln(T/T_0)\right).\end{array}$$

(5)

Here, we utilize the fact that at the transition point $T_0$, the free energy difference equals zero, implying $\Delta S_0=\frac{\Delta H_0}{T_0}$. Conversely, considering a phase transition in proteins, which are finite-length heteropolymers, the transition interval should not be zero but cannot be excessively large either. This justifies the approximation $\frac{T}{T_0}\approx 1$ (for any temperature T within the transition interval), enabling the expansion of the last term of Equation (5) into a Taylor series. The resulting expression is quadratic in temperature:

$$\begin{array}{c}\hfill \Delta G_{NU}\left(T\right)=\Delta H_{NU}\left(T\right)-T\Delta S_{NU}\left(T\right)\\ \hfill =\Delta H_0\left(1-\frac{T}{T_0}\right)-T_0\Delta C_P^0{\left(1-\frac{T}{T_0}\right)}^2.\end{array}$$

(6)

Hawley was the pioneer in employing such a formula to describe the cold denaturation of chymotrypsinogen [13,14]. However, the Formulas (5) or (6) representing the Gibbs free energy expenditure for unfolding are not suitable for interpreting experimental DSC data on protein folding. Recall that we assumed a constant jump in heat capacity to derive Equation (5). Now, the bad news is that unfolding DSC experiments yield a temperature-dependent dome-shaped curve rather than the fixed jump as modeled with ${\Delta }_N^U{C}_P=\mathrm{const}$. To effectively fit this curve, an adjustment [12] to the aforementioned two-state model is necessary. Specifically, the enthalpy difference Equation (3a) is multiplied by the fraction of unfolded units in the protein

$$\begin{array}{cc}\hfill {\theta }_U\left(T\right)& =\frac{K_{NU}}{1+K_{NU}}\hfill \\ \hfill K_{NU}& =exp[-\Delta G_{NU}\left(T\right)/RT],\hfill \end{array}$$

(7)

where ${\theta }_U$ is the degree of denaturation and $K_{NU}$ represents the equilibrium constant between the native (N) and unfolded (U) states. The modified expression for the enthalpy reads:

$$\Delta H\left(T\right)=\Delta H_{NU}\left(T\right){\theta }_U\left(T\right),$$

(8)

resulting in the specific heat

$$C_P\left(T\right)={\Delta }_N^{U}H\left(T\right)\frac{d{\theta }_U}{dT}+\Delta C_P^0{\theta }_U\left(T\right).$$

(9)

The ansatz in Equation (8) disrupts the equivalence between the two specific heat formulas in Equation (1). Anyway, Equation (9) is used to fit the experimental data within the two-state model [12]. It involves three fitting parameters: $T_0$, $\Delta H_0$, and $\Delta C_P^0$.

3. Results and Discussion

With the detailed derivation we performed above, we can now proceed to the main goal of this paper: the comparison of fitting procedures based on Equation (5) and its approximation Equation (6).

To analyze experimental data, we converted heat capacity plots from various publications into the digital format (see

Table 1. The results of the fits using the logarithmic and square formulas.

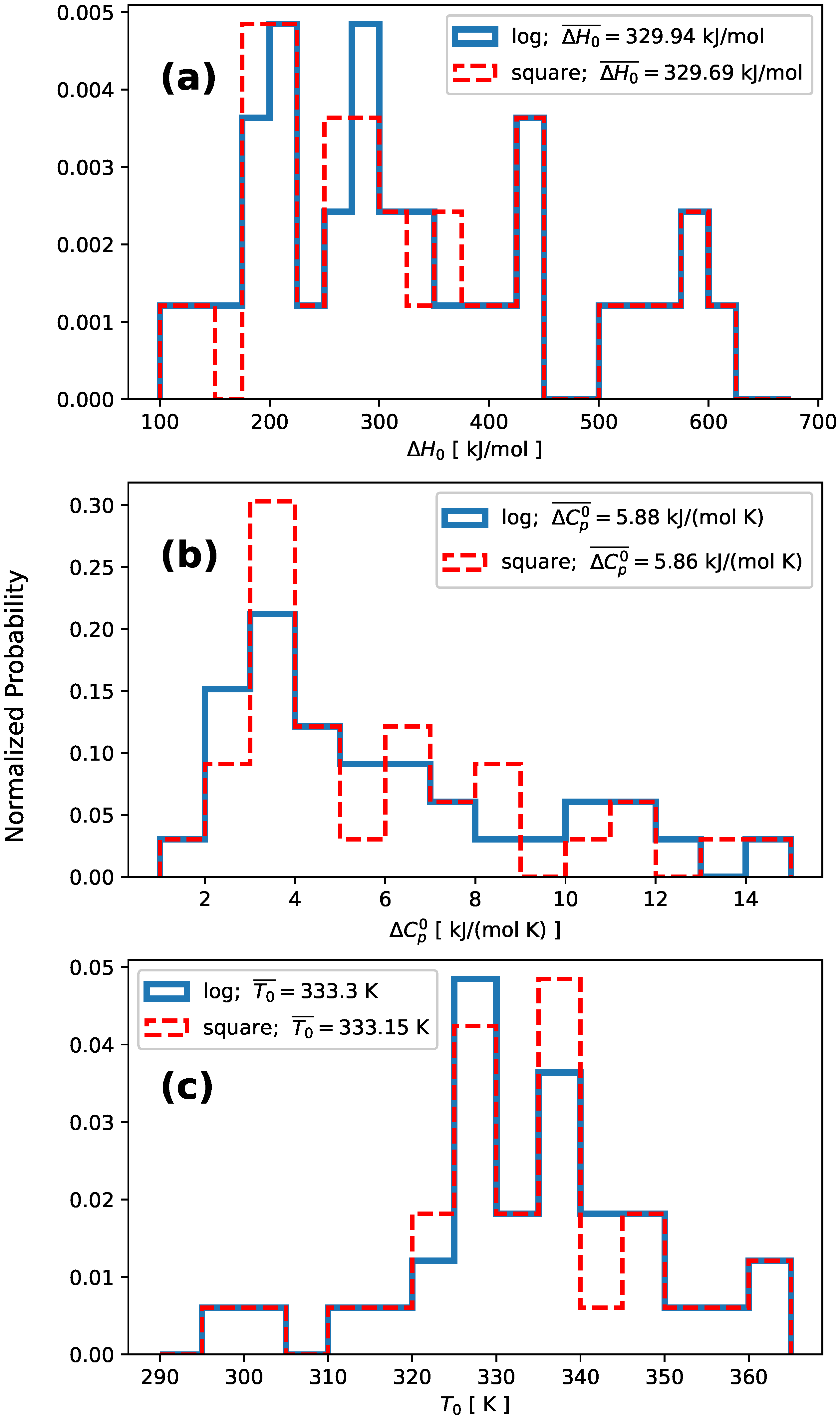
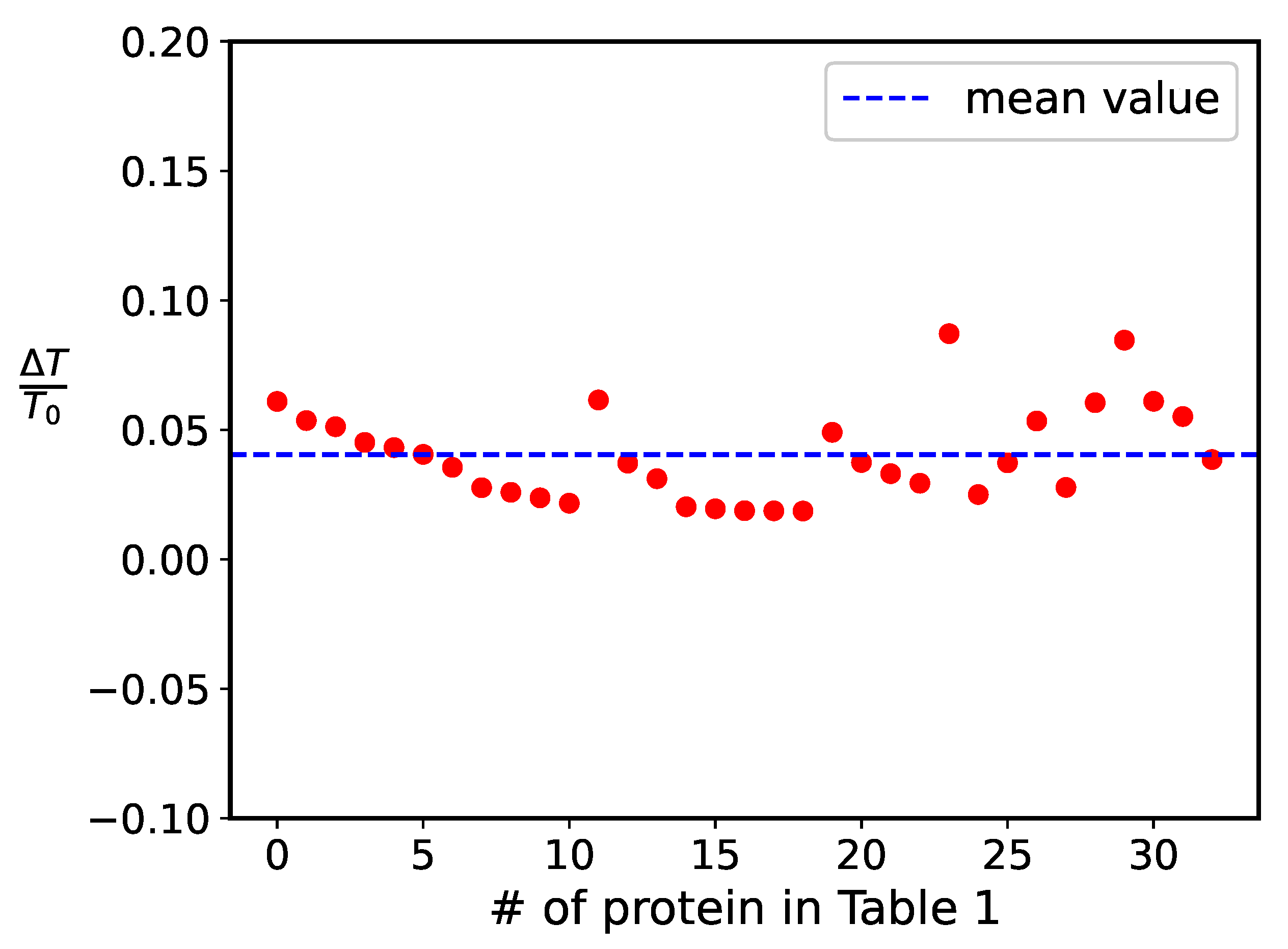
#	Protein	Reference	N	2-State (square)	${\mathit{R}}^{\mathbf{2}}$	2-State (log )	${\mathit{R}}^{\mathbf{2}}$
1	gpW	Ref. [17], Figure 4a	62	$T_0$: 338 (0.2) K $\Delta H_0$: 185 (3.8) kJ/mol $\Delta C_p^0$: 3.3 (8.8) kJ/(mol K)	0.897	$T_0$: 338 (0.2) K $\Delta H_0$: 184.1 (3.3) kJ/mol $\Delta C_p^0$: 3.4 (7.6) kJ/(mol K)	0.908
2	ubiquitin pH 2.0	Ref. [5], Figure 1b	76	$T_0$: 328 (0.02) K $\Delta H_0$: 203.9 (0.4) kJ/mol $\Delta C_p^0$: 3.96 (1) kJ/(mol K)	0.995	$T_0$: 328 (0.02) K $\Delta H_0$: 203.3 (0.4) kJ/mol $\Delta C_p^0$: 4.2 (1.3) kJ/(mol K)	0.998
3	ubiquitin pH 2.5	Ref. [5], Figure 1b	76	$T_0$: 333 (0.02) K $\Delta H_0$: 214 (0.5) kJ/mol $\Delta C_p^0$: 4.1 (1.3) kJ/(mol K)	0.994	$T_0$: 333 (0.02) K $\Delta H_0$: 216 (0.5) kJ/mol $\Delta C_p^0$: 4 (2) kJ/(mol K)	0.995
4	ubiquitin pH 3.0	Ref. [5], Figure 1b	76	$T_0$: 346 (0.03) K $\Delta H_0$: 253.2 (0.8) kJ/mol $\Delta C_p^0$: 3.9 (3.7) kJ/(mol K)	0.988	$T_0$: 346 (0.03) K $\Delta H_0$: 254.5 (0.7) kJ/mol $\Delta C_p^0$: 3.85 (3.1) kJ/(mol K)	0.990
5	ubiquitin pH 3.5	Ref. [5], Figure 1b	76	$T_0$: 357 (0.05) K $\Delta H_0$: 274.6 (1.4) kJ/mol $\Delta C_p^0$: 4 (6.6) kJ/(mol K)	0.969	$T_0$: 357 (0.04) K $\Delta H_0$: 274.86 (1.2) kJ/mol $\Delta C_p^0$: 4 (5.7) kJ/(mol K)	0.972
6	ubiquitin pH 4.0	Ref. [5], Figure 1b	76	$T_0$: 362 (0.03) K $\Delta H_0$: 295.4 (0.7) kJ/mol $\Delta C_p^0$: 3.5 (4.7) kJ/(mol K)	0.992	$T_0$: 362 (0.02) K $\Delta H_0$: 296.7 (0.6) kJ/mol $\Delta C_p^0$: 3.4 (4.6) kJ/(mol K)	0.992
7	barnase pH 1.8	Ref. [5], Figure 1a	110	$T_0$: 295 (0.02) K $\Delta H_0$: 271.4 (0.5) kJ/mol $\Delta C_p^0$: 6.2 (2.9) kJ/(mol K)	0.996	$T_0$: 295 (0.02) K $\Delta H_0$: 275.96 (0.5) kJ/mol $\Delta C_p^0$: 5.6 (3.6) kJ/(mol K)	0.993
8	barnase pH 2.5	Ref. [5], Figure 1a	110	$T_0$: 303 (0.009) K $\Delta H_0$: 363 (0.3) kJ/mol $\Delta C_p^0$: 5.7 (3.2) kJ/(mol K)	0.996	$T_0$: 303 (0.007) K $\Delta H_0$: 364 (0.3) kJ/mol $\Delta C_p^0$: 5.5 (2.7) kJ/(mol K)	0.997
9	barnase pH 2.8	Ref. [5], Figure 1a	110	$T_0$: 314 (0.008) K $\Delta H_0$: 402.8 (0.3) kJ/mol $\Delta C_p^0$: 3.15 (7) kJ/(mol K)	0.995	$T_0$: 314 (0.007) K $\Delta H_0$: 403.2 (0.3) kJ/mol $\Delta C_p^0$: 3.07 (6.7) kJ/(mol K)	0.996
10	barnase pH 3.45	Ref. [5], Figure 1a	110	$T_0$: 320 (0.009) K $\Delta H_0$: 448 (0.4) kJ/mol $\Delta C_p^0$: 6 (4.6) kJ/(mol K)	0.992	$T_0$: 320 (0.008) K $\Delta H_0$: 448 (0.4) kJ/mol $\Delta C_p^0$: 6 (4.1) kJ/(mol K)	0.993
11	barnase pH 5.5	Ref. [5], Figure 1a	110	$T_0$: 329 (0.007) K $\Delta H_0$: 504.33 (0.4) kJ/mol $\Delta C_p^0$: 3.9 (7.3) kJ/(mol K)	0.994	$T_0$: 329 (0.006) K $\Delta H_0$: 504.67 (0.3) kJ/mol $\Delta C_p^0$: 3.8 (7.2) kJ/(mol K)	0.994
12	Sox-5	Ref. [5], Figure 3a	81	$T_0$: 315 (0.1) K $\Delta H_0$: 185.5 (2.3) kJ/mol $\Delta C_p^0$: 4.7 (3.2) kJ/(mol K)	0.893	$T_0$: 315 (0.1) K $\Delta H_0$: 170 (3) kJ/mol $\Delta C_p^0$: 5.7 (4) kJ/(mol K)	0.932
13	bovine $\beta$-lactoglobulin A	Ref. [18], Figure 2a	162	$T_0$: 352 (0.01) K $\Delta H_0$: 313.87 (0.3) kJ/mol $\Delta C_p^0$: 3 (3.6) kJ/(mol K)	0.995	$T_0$: 352 (0.01) K $\Delta H_0$: 314.95 (0.3) kJ/mol $\Delta C_p^0$: 2.9 (3.3) kJ/(mol K)	0.995
14	S44[A] mutant of T4 lysozyme	Ref. [4], Figure 3a	164	$T_0$: 327 (0.02) K $\Delta H_0$: 350.5 (0.8) kJ/mol $\Delta C_p^0$: 8.8 (3.5) kJ/(mol K)	0.948	$T_0$: 327 (0.02) K $\Delta H_0$: 349 (0.8) kJ/mol $\Delta C_p^0$: 9.03 (3.1) kJ/(mol K)	0.949
15	pseudo-WT T4 lysozyme pH 2.8	Ref. [4], Figure 2	164	$T_0$: 323 (0.008) K $\Delta H_0$: 528.7 (0.5) kJ/mol $\Delta C_p^0$: 10.9 (3.5) kJ/(mol K)	0.988	$T_0$: 323 (0.007) K $\Delta H_0$: 529.3 (0.4) kJ/mol $\Delta C_p^0$: 10.8 (3.3) kJ/(mol K)	0.989
16	pseudo-WT T4 lysozyme pH 3.0	Ref. [4], Figure 2	164	$T_0$: 327 (0.007) K $\Delta H_0$: 557.1 (0.4) kJ/mol $\Delta C_p^0$: 8.4 (4.6) kJ/(mol K)	0.991	$T_0$: 327 (0.006) K $\Delta H_0$: 557.45 (0.4) kJ/mol $\Delta C_p^0$: 8.34 (4.4) kJ/(mol K)	0.991
17	pseudo-WT T4 lysozyme pH 3.3	Ref. [4], Figure 2	164	$T_0$: 332 (0.006) K $\Delta H_0$: 588 (0.4) kJ/mol $\Delta C_p^0$: 11.6 (3.8) kJ/(mol K)	0.993	$T_0$: 332 (0.005) K $\Delta H_0$: 587.85 (0.3) kJ/mol $\Delta C_p^0$: 11.44 (3.4) kJ/(mol K)	0.993
18	pseudo-WT T4 lysozyme pH 3.5	Ref. [4], Figure 2	164	$T_0$: 335 (0.006) K $\Delta H_0$: 593.7 (0.4) kJ/mol $\Delta C_p^0$: 13 (3.2) kJ/(mol K)	0.993	$T_0$: 335 (0.005) K $\Delta H_0$: 595 (0.3) kJ/mol $\Delta C_p^0$: 12.75 (3) kJ/(mol K)	0.994
19	pseudo-WT T4 lysozyme pH 3.7	Ref. [4], Figure 2	164	$T_0$: 337 (0.008) K $\Delta H_0$: 601 (0.5) kJ/mol $\Delta C_p^0$: 14.8 (3.8) kJ/(mol K)	0.991	$T_0$: 338 (0.007) K $\Delta H_0$: 602.69 (0.4) kJ/mol $\Delta C_p^0$: 14.4 (3.4) kJ/(mol K)	0.992
20	metmyoglobin pH 3.9	Ref. [3], Figure 3a	153	$T_0$: 333 (0.05) K $\Delta H_0$: 230 (1.3) kJ/mol $\Delta C_p^0$: 6.8 (2) kJ/(mol K)	0.972	$T_0$: 333 (0.04) K $\Delta H_0$: 225.57 (1.2) kJ/mol $\Delta C_p^0$: 7.33 (2) kJ/(mol K)	0.988
21	metmyoglobin pH 4.08	Ref. [3], Figure 3a	153	$T_0$: 340 (0.02) K $\Delta H_0$: 297.5 (0.6) kJ/mol $\Delta C_p^0$: 7 (2) kJ/(mol K)	0.994	$T_0$: 340 (0.02) K $\Delta H_0$: 302 (0.7) kJ/mol $\Delta C_p^0$: 6.67 (2.7) kJ/(mol K)	0.994
22	metmyoglobin pH 4.2	Ref. [3], Figure 3a	153	$T_0$: 345 (0.01) K $\Delta H_0$: 344 (0.4) kJ/mol $\Delta C_p^0$: 6.6 (2.3) kJ/(mol K)	0.998	$T_0$: 345 (0.01) K $\Delta H_0$: 346.5 (0.4) kJ/mol $\Delta C_p^0$: 6.37 (2.5) kJ/(mol K)	0.997
23	metmyoglobin pH 4.44	Ref. [3], Figure 3a	153	$T_0$: 349 (0.02) K $\Delta H_0$: 391.3 (0.6) kJ/mol $\Delta C_p^0$: 7.7 (2.7) kJ/(mol K)	0.991	$T_0$: 349 (0.02) K $\Delta H_0$: 394.7 (0.8) kJ/mol $\Delta C_p^0$: 7.28 (5.7) kJ/(mol K)	0.989
24	mutant SpA(L20A + Y15W)	Ref. [19], Figure 6	58	$T_0$: 324 (0.09) K $\Delta H_0$: 107.8 (2) kJ/mol $\Delta C_p^0$: 3 (2) kJ/(mol K)	0.975	$T_0$: 327 (0.09) K $\Delta H_0$: 124.6 (1.5) kJ/mol $\Delta C_p^0$: 2.5 (2.9) kJ/(mol K)	0.954
25	Lysozyme pH 2.5	Ref. [12], Figure 8	129	$T_0$: 335 (0.006) K $\Delta H_0$: 441.6 (0.3) kJ/mol $\Delta C_p^0$: 11.1 (1.6) kJ/(mol K)	0.996	$T_0$: 335 (0.006) K $\Delta H_0$: 444.85 (0.3) kJ/mol $\Delta C_p^0$: 10.6 (1.7) kJ/(mol K)	0.995
26	Apolipoprotein A-1	Ref. [12], Figure 7	245	$T_0$: 326 (0.04) K $\Delta H_0$: 315 (1.5) kJ/mol $\Delta C_p^0$: 8 (2.4) kJ/(mol K)	0.825	$T_0$: 325 (0.03) K $\Delta H_0$: 289.8 (1) kJ/mol $\Delta C_p^0$: 11.3 (1.4) kJ/(mol K)	0.942
27	ubiquitin	Ref. [20], Figure 1	76	$T_0$: 329 (0.009) K $\Delta H_0$: 201.5 (0.2) kJ/mol $\Delta C_p^0$: 2.9 (0.8) kJ/(mol K)	0.999	$T_0$: 329 (0.004) K $\Delta H_0$: 204.6 (0.08) kJ/mol $\Delta C_p^0$: 2.66 (0.4) kJ/(mol K)	0.999
28	thioredoxin	Ref. [21], Figure 2a	104	$T_0$: 362 (0.02) K $\Delta H_0$: 431.5 (0.7) kJ/mol $\Delta C_p^0$: 4.6 (9.8) kJ/(mol K)	0.996	$T_0$: 362 (0.02) K $\Delta H_0$: 433.33 (0.7) kJ/mol $\Delta C_p^0$: 4.3 (10.3) kJ/(mol K)	0.995
29	Cold shock protein CspB	Ref. [22], Figure 2	67	$T_0$: 327 (0.05) K $\Delta H_0$: 177.5 (0.8) kJ/mol $\Delta C_p^0$: 2.3 (3.4) kJ/(mol K)	0.996	$T_0$: 327 (0.04) K $\Delta H_0$: 179.55 (0.8) kJ/mol $\Delta C_p^0$: 2.2 (3.5) kJ/(mol K)	0.995
30	villin headpiece	Ref. [23], Figure 3	35	$T_0$: 339 (0.2) K $\Delta H_0$: 132.7 (2.9) kJ/mol $\Delta C_p^0$: 1.6 (8.4) kJ/(mol K)	0.955	$T_0$: 340 (0.2) K $\Delta H_0$: 133.4 (2.4) kJ/mol $\Delta C_p^0$: 1.64 (7.4) kJ/(mol K)	0.960
31	gpW	Ref. [24], Figure 1a	58	$T_0$: 338 (0.2) K $\Delta H_0$: 184.5 (3.5) kJ/mol $\Delta C_p^0$: 3.3 (8.4) kJ/(mol K)	0.911	$T_0$: 338 (0.2) K $\Delta H_0$: 183.95 (3) kJ/mol $\Delta C_p^0$: 3.37 (7.2) kJ/(mol K)	0.920
32	SH3	Ref. [24], Figure 1b	57	$T_0$: 339 (0.02) K $\Delta H_0$: 202.8 (0.4) kJ/mol $\Delta C_p^0$: 2.4 (1.9) kJ/(mol K)	0.998	$T_0$: 340 (0.009) K $\Delta H_0$: 204.8 (0.2) kJ/mol $\Delta C_p^0$: 2.3 (1.1) kJ/(mol K)	0.999
33	thioredoxin h	Ref. [25], Figure 1b	113	$T_0$: 335 (0.01) K $\Delta H_0$: 288 (0.4) kJ/mol $\Delta C_p^0$: 3.3 (3.2) kJ/(mol K)	0.996	$T_0$: 335 (0.01) K $\Delta H_0$: 288.84 (0.3) kJ/mol $\Delta C_p^0$: 3.22 (2.7) kJ/(mol K)	0.996

for references). For digitization, we took the graphs from the original papers and uploaded them to an online digitization tool system [16] that is an opensource software leveraging computer vision technology to assist in extracting numerical data from images, including plots, maps, and various other visual materials. WebPlotDigitizer ensures an accurate data extraction of information by employing a combination of computer vision algorithms and manual techniques.

All data are expressed in molar units, with specific heat measured per residue. The data we digitized primarily originate from curves with baselines subtracted by the original authors who conducted the measurements, and only once did we use the linear extrapolation of the initial slope of the heat capacity function to perform the subtraction. Consequently, we refrain from deliberating on the efficacy or limitations of the baseline subtraction procedures employed by other authors. Here, we focus on comparing how two different approaches of the two-state model fit the heat capacity data, reported by other authors. Least-square fit was performed with the domestic code in Python, using the ‘optimize.curve_fit’ function of the ‘scipy’ library.

The results of fitting 33 experimental data to both the logarithmic (Equation (5)) and square (Equation (6)) formulas (see Appendix A) are shown in Table 1. In general, both formulas result in very similar fits. As shown in Figure 1, the qualitative similarity between the fitted curves can be seen visually. However, it is not clear what the statistical consequences would be of using the approximate formula while processing a dataset of experimental points. In order to study the statistical quantitative similarity, in Figure 2, we compare the histograms of fitted parameters and their mean values for 33 proteins in Table 1. The histograms were constructed with a domestic code in Python (https://www.python.org/), with the help of the ‘histogram’ function of the ‘numpy’ library.

As we can see from Figure 2, although the historgams differ a little, the mean values of fitting parameters (see the legends) for both the logarithmic and square equations show a very high degree of proximity. Additionally, the two datasets of fitted values can be compared using the concept of the Root Mean Square Deviation (RMSD):

$$RMSD=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(x_1-x_2\right)}^2}$$

(10)

and the Normalized Root Mean Square Deviation (NRMSD)

$$NRMSD=\frac{RMSD}{\overline{x}},$$

(11)

where

$$\overline{x}=\frac{\overline{x_1}+\overline{x_2}}{2}.$$

(12)

These measures allow to quantify how far the two datasets are from each other. Usually, such analysis is used in the context of the comparison of two conformations of a protein, but nothing stops us from using it for our purposes. The analysis has shown that the NRMSD($\Delta H_0$) = 0.02, NRMSD($\Delta C_P^0$) = 0.11 and NRMSD($T_0$) = 0.002, which means the parameter values obtained from the fit performed with two formulas are very close to each other.

With the results of the fitting summarized in Table 1, we can answer the question posed: is the condition of smallness of the reduced transition interval $\Delta T/T_0$ satisfied for the 33 randomly chosen globular proteins from our set? Under the assumption that all the proteins considered are two-state, we can re-write Equation (12) of Ref. [26] as

$$\frac{\Delta T}{T_0}=\frac{4R{T}_0}{\Delta H_0},$$

(13)

where $R=8.314J/molK$ is the gas constant, and estimate the reduced interval using fitted values from Table 1. The results of such an estimate, presented in Figure 3, indicate a certain span of values around the mean value of $0.04$ for the members of the set. Nevertheless, the parameter remains small, justifying the validity of series expansion and resulting in the equivalence of the logarithmic (Equation (5)) and square (Equation (6)) formulas.

4. Conclusions

We fit the specific heat experimental data (33 samples) using two formulas for the free energy difference between the native and the unfolded states within the two-state model. Despite the fact that the square formula is just an approximation of the logarithmic one, valid for small transition intervals, they both result in very similar outcomes, at least for the random pick of experimental data we have used. Fitted curves often coincide visually, with the coefficients of determination at least $R^2>0.9$ and mostly $R^2>0.99$, indicating very good fits to data points for both formulae. Although there are some differences in histograms of fitted parameters, depending on the type of the formula used in fit, the averages are very close to each other. The comparison of the two datasets of fitted parameters performed with the help of NRMSD analysis has also shown a high degree of similarity. Although the estimate of reduced transition intervals indicates some span of values around the mean value of $0.04$, values remain small and justify the use of series expansion. To summarize, the analysis above allows to consider both the exact logarithmic and the approximate square formulae for the free energy difference of (un)folding to be practically equivalent and suggests the use of Equation (5) or Equation (6) at one’s convenience.