Abstract
This paper outlines the methodology and results for a two-species finite volume scalar computational drug transport model developed for simulating the mass transport of Poly(lactic-co-glycolic acid (PLGA)) from a half-embedded single strut implanted in a coronary arterial vessel wall. The mathematical drug transport model incorporates the convection-diffusion equation in scalar form (dimensionless) with a two-species (free-drug and bound-drug) mass transport setup, including reversible equilibrium reaction source terms for the free and bound-drug states to account for the pharmaco-kinetic reactions in the arterial wall. The relative reaction rates of the added source terms control the interconversion of the drug between the free and bound-drug states. The model is solved by a 2D finite-volume method for discretizing and solving the free and bound drug transport equations with anisotropic vascular drug diffusivities. This model is an improvement over previously developed models using the finite-difference and finite element method. A dimensionless characteristic scaling pre-analysis was conducted a priori to evaluate the significance of implementing the reaction source terms in the transport equations. This paper reports the findings of an investigation of the interstitial flow profile into the arterial wall and the free and bound drug diffusion profiles with a parametric study of varying the polymer drug concentration (low and high), tortuosity, porosity, and Peclet and DamKöhler numbers over the course of 400 h (16.67 days). The results also reveal how a single species drug delivery model that neglects both a reversible binding reaction source term and the porosity and tortuosity of the arterial wall cannot accurately predict the distribution of both the free and bound drug.
1. Introduction
Cardiovascular disease remains to be the leading cause of death worldwide [1,2,3,4,5,6,7,8]. Drug eluting stents have demonstrated exceptional benefits in reducing in-stent restenosis [9,10]. These stents are commonly used in coronary angioplasty procedures to provide structural support and release drug molecules locally at the implanted arterial site to prevent adverse outcomes (such as in-stent restenosis) in patients. Although drug-eluting stents are now the main choice of treatment in coronary interventions, questions regarding their longevity and safety are still prominent [11]. In the United States, present drug-eluting stent designs incorporate sirolimus and paclitaxel and release these drugs into the arterial wall from the eluting struts [12,13,14]. Both sirolimus and paclitaxel eluting stents appear to have comparable clinical benefits.
Initial drug eluting stent treatments were prone to washout by transmural plasma flow, which lowered the drug residence time in the arterial vessel wall. This was a major hindrance since these implants were designed to provide local drug delivery to the diseased site. Hydrophobic drugs, such as sirolimus and paclitaxel, were reported to have higher retention times as compared to other drugs because they can bind to structural elements and intracellular targets in the vessel wall [15,16]. Hydrophobic drugs, such as these, exist in both bound and unbound states within the vessel wall. These states are in equilibrium, and the binding is reversible. Consequently, the diffusion of a hydrophobic drug into the arterial wall from a stent cannot be modeled without interaction of both the bound and free drug forms in the vessel wall.
Several experimental and numerical investigations have been carried out recently with the aim of quantifying the capability of this device to reduce in-stent restenosis after stent implantation. Lovich et al. [17,18,19] studied the behavior of heparin in implanted arteries and concluded that the presence of binding sites changes along the transmural direction, being higher in the endothelium and lower in the adventitia. Lovich and Edelman studied the effects of specific binding sites inside the arterial wall on drug uptake [20], where the presence of specific binding site action was modeled using the reversible chemical reaction. Sakharov et al. [21] disregarded the convective effects on the transport of free drugs. Hwang et al. [22] predicted the free and bound drug concentrations by solving for the distribution of the free drug, then using a multiplicative factor (partition approach) to predict the concentration of the bound drug. Migliavacca et al. [23] studied the drug release pattern in the vascular wall from drug-eluting stents using a single species approach in addition to a partition coefficient approach to relate the free and the bound drug concentrations. Borghi et al. [24] stated that the inclusion of reversible binding leads to delayed release and that the erosion of the polymer affects the drug release from a single strut. Horner et al. [25] considered a two-species drug delivery model including reversible binding sites, and their model predicted that a single species drug delivery model cannot accurately predict the distribution of bound drugs. They also concluded that a two-species approach that includes reversible binding is the way forward for future stent-based drug delivery systems.
Following Tzafriri et al. [26], a second-order dynamic model that describes a saturating reversible binding process by treating the bound drug as a dynamic variable has been taken into account to explore drug interaction with cells of the arterial wall. In most of the studies cited above, transient drug release has been modeled as a uniform release, which is unrealistic and not representative of actual stent-based delivery. Instead, a simple time-dependent Dirichlet boundary condition is often applied on the surface of the struts [27,28,29]. Arterial properties, such as porosity and tortuosity, dictate the transport of drugs within the arterial tissue. When an endovascular drug-eluting stent is implanted, it has a major impact on the structure of the arterial wall, eventually influencing the overall rates of diffusion through tissues [30]. For diffusion in a porous medium, the effective diffusion coefficient is assumed to depend on two factors: porosity (a dimensionless parameter, which is the ratio of pore volume to the total material volume) and diffusion path tortuosity (ratio of the actual pore length to the distance between its ends; i.e., arc-chord ratio) [31]—these parameters change the free diffusivity of the drug eluted from a pair of struts [32].
The goal of this work is to develop a two-dimensional two-species scalar finite volume computational model that can model the reversible binding characteristics of poly(lactic-co-glycolic acid) (PLGA) released into a coronary artery wall from a single drug eluting strut. The model described in this work is an improvement over previous works and considers the integrated process of the drug release in the PLGA coating, the free and bound drug diffusion profiles with varying polymer drug concentration (low and high), vascular diffusivities, tortuosity, porosity, and Peclet and Dahmokoler numbers over the course of 400 h (16.67 days) [33]. The mechanism of diffusion in the PLGA is adapted from the work of Zhu and Braatz [34] and couples the drug diffusion to degradation and erosion along with the drug pharmacokinetics taking place in the arterial wall from the work of Saha and Mandal [35]. The main contributions of the proposed work include:
- A theoretical methodology for computational modeling of the diffusion of PLGA into a coronary arterial wall from a single half-embedded drug eluting stent strut.
- A computational drug diffusion model that considers the pharmaco-kinetic reactions in the arterial wall as equilibrium reversible binding reaction source terms for the free and bound-drug.
- Validation of the reported computational model via simulation-based results from a finite difference model developed from methods reported in previous works.
- A computational drug diffusion model that provides an understanding of the relationship between drug physicochemical properties and the local transport environment which is crucial to the success of new stent designs.
- The model reported in this work is the second reported model in literature that successfully uses an ANSYS FLUENT user-defined scalar (UDS) model to model the diffusion of the free and bound drug in the arterial wall with reversible binding source terms. Additionally, this is the first reported model to use a UDS model to incorporate the polymer layer in the computational domain.
The next section presents the methodology of this work.
2. Material and Methods
2.1. Model Development
In this work, an implanted drug eluting coronary stent (as shown in Figure 1a) is analyzed in the coronary artery where the stent struts are evenly placed and half-embedded in the cross-section of the lumen (as shown in Figure 1b).
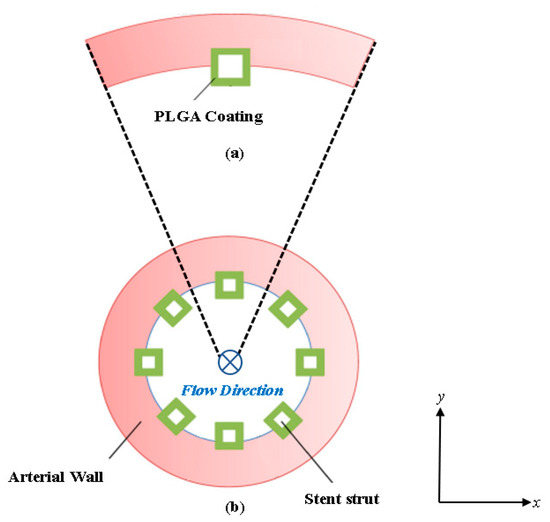
Figure 1.
Cross-sectional view diagram of the arterial stented model: (a) Schematic of a single PLGA coated half-embedded stent strut implanted into the arterial wall and (b) the full stented (all stent struts included) arterial model.
The strut and arterial wall configuration is based on a previous study by Xiaoxiang and Braatz [36] involving a bio-durable polymer coating and is common for drug eluting stent diffusion analysis applications. The blood flow is moving in the direction of the paper plane, as labeled in Figure 1b. Standard square-shaped stent struts are considered in this work [37,38,39]. Due to symmetry, a single stent strut with its surrounding arterial wall domain is extracted for the study to simplify the computational domain and reduce computational costs. The model was developed in ANSYS SpaceClaim (2022) and deployed in ANSYS Meshing (2022) for meshing.
The extracted model domain is illustrated in Figure 1a, where half of the stent strut is embedded into the arterial wall. Distinct from previous works, here, the curvature of the arterial wall is kept intact, and the computational domain consists of a cartesian coordinate system (observed as x and y). The mathematical models for describing the drug delivery process are described in Section 2.2 and Section 2.3. The model for describing drug transport and pharmacokinetics in the arterial wall was developed based on the works of Xiaoxiang and Braatz [36] and Saha and Mandal [35]. The next section describes the boundary conditions for the developed domain model.
2.2. Boundary Conditions and Meshing
The names for each boundary zone are provided in Figure 2. The “inlet” zone represents the exposed inner surface of the artery where plasma flow enters the arterial domain. The “stent surface” represents the location where the stent is in contact with the vessel wall.
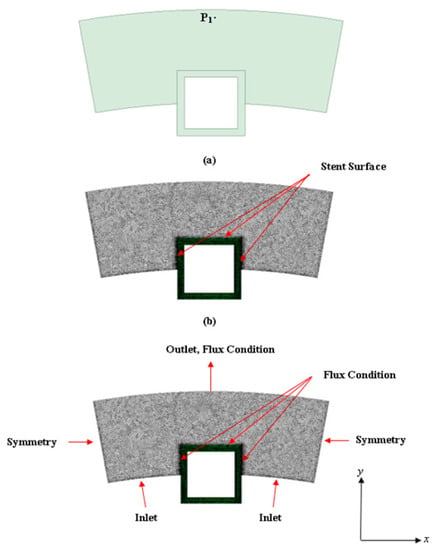
Figure 2.
Model diagram of the half-embedded stented arterial model: (a) Surface model created in ANSYS SpaceClaim and (b) mesh computational domain (model used in the simulations is a finer meshed model). P1 is the location point of interest for evaluating the concentration profiles over time). At the PLGA coating and artery wall interface, the following flux condition is applied:
ANSYS Meshing (2022) was used for meshing the computational domain. The meshing scheme used is a tetrahedral cell mesh type which is applied to all surfaces with the surface size meshed based on the edge spacing selection and an inflation scheme applied to rectify meshing irregularities. The next section describes the plasma flow modeling methodology.
2.3. Plasma Flow
In this work, ANSYS FLUENT (2022 R1 (ver. 21.1)) computational fluid dynamic (CFD) software was used to model both the fluid flow (plasma flow) and the convection-diffusion of the free, bound, and internalized drug. For plasma flow in the arterial domain, a pressure drop filtration is implemented to simulate the steady flow of plasma through the domain. The arterial domain tissue is assumed to behave as a porous media. The Darcy Law model was used to solve the plasma flow field. FLUENT allows implementation of the Darcy Law equation as a source term in the Navier–Stokes equations as shown below in Equation (2):
where v is the velocity vector, P is the pressure, K is the permeability of the vessel wall, and ρ and µ are the density and dynamic viscosity of plasma, respectively. The density of plasma is 1020 kg/m3, and the dynamic viscosity is 0.0035 Pa∙s [2,3,4,5,6,7] at the standard body temperature (37 °C) Whale et al. [40] examined the effects of aging and pressure on the Darcy permeabilities of human aortic walls. A representative value of 2.0 × 10−18 m2 was implemented for this work. Equation (2) is subject to the incompressibility constraint. As described above, the vessel lumen is not a part of the computational domain. This introduces an additional assumption because luminal flow decreases axial non-uniformity of the drug in the artery wall [37,41]. The degree of non-uniformity was observed to increase with increasing the aspect ratio of the stent strut [41]. The impact of this assumption is therefore minimized in the case of square struts and/or stents with an abluminal coating. The next sections discuss the drug transport modeling methodology.
2.4. Drug Transport in the PLGA Coating and Arterial Domains
When the drug is released into the arterial wall, the drug molecules are exposed and interact with the physiological environment. Various drug-tissue interactions occur that affect the arterial wall drug transport, distribution, and drug uptake. The drug-arterial wall interaction has been commonly modeled as a reversible binding reaction of the drug molecules with binding sites present in the arterial wall. During this process, the bound drug Cb is formed by associating the free drug Cf with the available binding sites S0. The bound drug is immobilized, and only the free drug can diffuse. The reversible binding process, however, does not provide a mechanism for drug consumption (e.g., drug uptake by tissue cells), which can be characterized by drug internalization. This work did not take into consideration the internalization of the drug.
- Drug Binding:
- Free Drug in the PLGA Coating Domain:
- Free Drug in the Arterial Domain:
- Bound Drug in the Arterial Domain:
- Drug Transport Boundary Conditions:
ε and τ are the porosity and the tortuosity of the wall material, respectively. Dfree and Deff (Equations (9) and (10)) are the coefficients of free and effective diffusivity, respectively. Rd = (kd/ka) is the equilibrium dissociation constant.
As mentioned in Section 2.2, symmetry boundary conditions for both the free and bound drug are imposed at the proximal and distal walls of the computational domain. An impermeable boundary condition for the bound drug is also imposed at the perivascular wall, lumen-tissue, and strut-tissue interfaces (Equation (7)). For the free drug, a perfect sink condition is imposed at the perivascular end (Equation (8)). In this work, we considered two situations, either that flowing blood is extremely efficient at washing out the mural-adhered drug, modeled as a zero-concentration interface condition [42], or that mural-adhered drug is insensitive to flowing blood, modeled as a zero-flux boundary condition (Equation (6)). As a substitute to modeling the uniform release of drug from a single strut, a simple time-dependent release kinetics with a flux condition (Equation (9)) is assumed at the strut eluting surface.
In this work, the contribution of the true diffusion term was minimized by setting Db = 1.0 × 10−7 Du. The 1.0 × 10−7 pre-factor was adopted from the study of Horner et al. [25] and was used to decrease the true drug diffusivity until the bound drug distribution became independent of the diffusivity results. A cartesian coordinate system was used to specify the components of the diffusion tensor D in the x and y directions, corresponding to Dxx and Dyy, respectively. Both Du and Db have two independent components:
PLGA tends to localize within elastic sheathes in the vessel wall. Hwang and Edelman [22] have proven this experimentally. In our study, we assume that Dyy is larger than Dxx.
- User Defined Scalar and Numerical Modelling
In this work, we implemented the user-defined scalar (UDS) model available in ANSYS FLUENT for solving Equations (5)–(7). A fluent UDS model allows a user to define up to fifty UDS transport equations in a single computational model. The general (UDS) transport equation is shown below in Equation (12) with the four terms (transient, flux, diffusivity, and source terms) that can be customized. The UDS model allows the user to set boundary conditions for the variables within cells of a fluid or solid zone for a particular scalar equation. This is done by fixing the value of ϕk. When ϕk is fixed in a given cell, the UDS scalar transport is not solved, and the cell is not included when the residual sum is computed. For the present work, the value of the initial drug concentration, C0, was fixed, and the coating diffusivity was allowed to vary as a function of ϕ, time, and molecular weight, also allowed to vary with time. For the bound drug transport equation, the mass transport was deselected, which allowed the convection term to be neglected, thus making the bound drug immobile. The same was done for the internalized drug transport equation. The source terms Sϕk include the reversible binding reactions in Equations (6) and (7).
For the drug transport and plasma flow simulations, the drug concentration was assumed to be low enough that it does not affect the plasma velocity field. Therefore, the velocity and scalar transport equations were decoupled and solved sequentially. The velocity field in the tissue was solved using a steady-state formulation. FLUENT’s pressure-based segregated solver was used with the pressure-implicit with splitting of operators (PISO) scheme to couple pressure and velocity degrees of freedom. The standard pressure interpolation scheme was used along with second order up-winding for discretizing the velocity degrees of freedom. The default under-relaxation factor (URF) for pressure was increased to 0.5, and the URF for momentum was lowered to 0.4.
The convergence criterion for the steady fluid flow problem was 10−6 for the momentum equations. The drug transport problem was solved using a transient solver, with the velocity field fixed for all time steps. A first-order implicit time integrator was used along with the QUICK up-winding scheme for spatial discretization of the scalar transport equations. Smooth convergence was observed when using the default URFs of 1.0 for both transport equations. The convergence criterion for concentration at each time. All plasma flow and drug concentration simulations were conducted with a time step of 1 picosecond and resulted in a simulation run time of at least 15 days. All simulations were conducted on an ASUS ROG STRIX desktop computer (ASUS ROG; Taiwan) with 12 cores and an NVIDIA GeForce GTX 1660 TI graphics card. All simulations were conducted in parallel with 11 CPU cores and the NVIDIA graphics card.
2.5. Non-Dimensional Pre-Analyses
Similar to our previous work, we began by performing a dimensionless characteristic scaling analysis to gain insight into the dominant mechanisms of transport throughout the arterial wall. The dimensionless scaling parameters for scaling Equations (2) and (3) are shown below:
Using these characteristic dimensionless terms, the drug transport equations take the following form:
where Vy is the transmural filtration velocity, PeT = [Vyδ/(DT)], and Da = [(kaS0δ2)/(DT)] are the Peclet and DamKöhler numbers in the tissue. Here, ε1 = (Rd/C0), ε2 = (C0/S0), and ε3 = (Rd/S0) are three scaling parameters. Pec = [Vy(h2/δ)]/Dc is the Peclet number in the coating of the strut, and h is the thickness of the coating of the strut.
In these dimensionless equations, three characteristic time scales appear, τ1, τ2, and τ3, corresponding to diffusion coating, transmural diffusion, and the binding reaction. The characteristic time’s scales are shown below:
and
The evaluation of the magnitude of the three groups gives τ1, 103–105 s, τ2, 103–105 s, and τ3 102 s, which indicate that reversible binding is very fast compared to diffusion. The relative significance of diffusion and reversible binding in the wall is also implied by their corresponding dimensionless groups DamKohler and Peclet numbers. Compared with the coefficient of the transmural diffusion component (which is one), the reaction components have very large DamKöhler numbers on the order of 102–104, which also implies that the binding reactions perform a very strong role in the spatiotemporal dynamics. The non-dimensional analysis is provided in the Appendix A of this paper.
2.6. Grid Independence Analysis, Modelling Parameters, and Validation and Verification
A grid independence analysis was conducted on the developed computational domains for obtaining a mesh that produces results independent of the mesh size for model simulations. The grid independent analysis results are shown in Table 1. The grid independence analysis was performed with constant drug diffusivities in the coating and in the arterial wall, and the relative error was calculated for the drug release profile. The reference mesh uses a 0.1 µm element size for the coating and a 5 µm element size for the arterial wall. During the analysis, the relative errors were similar and remained under 5% error for different mesh sizes of the arterial wall domain, while the mesh size of the coating remained the same at 0.1 µm. Although not shown, the final mesh yielded a relative error of less than 5% and contained 372,125 cells. The chosen mesh was approximately 3.3 times the size of the previous mesh of 113,114 cells in which the results were well under a 5% difference which signifies grid independence. A mesh inflation was also applied to the final mesh to create high-quality geometry-aligned elements within the computational domain and along the boundaries.

Table 1.
Table of grid independent study results.
The physiological and pharmacokinetic parameters modeled in Equations (1)–(20) are listed in Table 2. These values were obtained from other relevant works [35,36].

Table 2.
Model description table. Parameters from this work are obtained from prior works [35,36].
For validation and verification of the developed finite volume scalar model, we compared the free drug concentration profiles in the arterial domain of the developed finite volume scalar model with a MATLAB finite difference code developed in our previous work [33]. Similar to the finite volume scalar model, the MATLAB finite difference model uses a cartesian coordinate system that describes the arterial domain, including the square-shaped stent strut. A rectangular domain is used as opposed to a curvature domain, as shown in Figure 3a. The same dimensions for the arterial domain are used for the finite difference and finite volume simulations. The same boundary conditions are imposed in the MATLAB finite difference code. Additionally, the same dimensionless diffusion equations are implemented in the MATLAB finite difference code. The PLGA coating is not modeled in the finite difference code. For the finite difference solution, a numerical grid with a size of 400 × 200 and an initial time step value of δt = 0.00001 s was used for the sake of computational power and time.
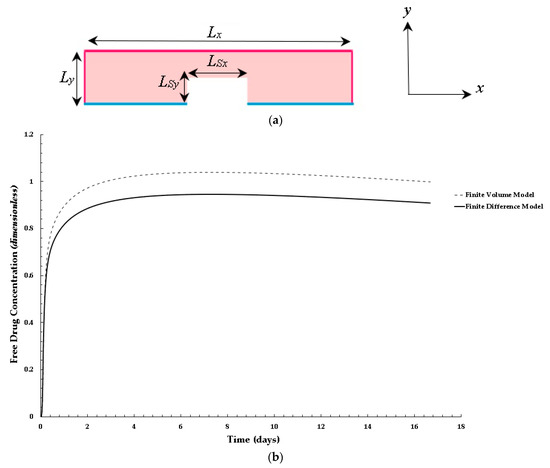
Figure 3.
Validation results for the finite volume model using a finite difference model developed in reference to the work of Saha and Mandal [35]: (a,b) Distribution of normalized mean bound drug concentration for values of: PeT = 2, Da = 40, and ε2 = 100.
Figure 3b shows a comparison of the finite difference and finite volume free drug concentration solution within the arterial domain at point 1 with values of PeT = 2, Da = 40, and ε2 = 100. As shown in the plot in Figure 3b, the overall trend in the growth of the plots is similar; however, the finite volume model has a higher concentration profile (approximately 10 percent higher). This could be attributed to the fine mesh used in the finite volume model, the implementation of the PGLA layer, the application of a diffusion pre-factor, and the application of the diffusive tensor. The key takeaway is that the free drug concentration trend behaves as expected when compared to a finite difference model that was developed based on work reported in the literature. The next section discusses the results of this work.
3. Results
This section of the paper presents the results of the interstitial plasma flow profile into the arterial wall, the initial diffusion flow modeling results using an eroding polymer coating (free and bound drug concentration profile with the interstitial flow), and the parametric study results of varying polymer drug concentration (low and high), tortuosity, porosity, and PeT and Da numbers over the course of 400 h (16.67 days). The next section discusses the initial diffusion flow modeling results.
3.1. Interstitial Flow into the Arterial Wall
The steady flow of plasma through the cross-section of the coronary arterial vessel wall is shown in Figure 4. The stent strut obstructs the plasma flow due to the no-slip boundary condition being applied at the boundaries of the polymer coating. There are two small regions of high velocity due to the energy loss incurred by the sharp regions on the top edges of the strut. The flow magnitude dampens out away from the top and middle region of the strut. There were three drug concentration analyses that were conducted in this work: (1) a plasma flow and drug concentration analysis conducted without the no-slip condition applied at the polymer and arterial wall interface (polymer erosion analysis), (2) a plasma flow and drug concentration analysis conducted with the no-slip condition, and (3) a drug concentration analysis conducted without plasma flow.
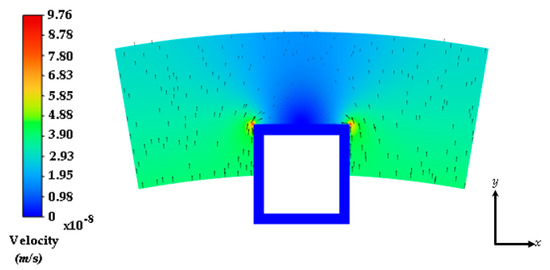
Figure 4.
Interstitial flow profile into the half-embedded strut arterial wall. Black arrows represent the velocity vectors.
The next section discusses the free and bound drug concentration with erosion and interstitial flow results.
3.2. Free and Bound Drug Concentration Profiles with Erosion and Interstitial Flow
Figure 5a,b show the free and bound drug concentration profiles with erosion and interstitial plasma flow. The interstitial flow within the arterial wall is induced by the pressure difference between the lumen and the perivascular space and is typically very small (in the range of 0.01–0.1 µm/s [43]) in reference to the centerline pulsatile flow and the convective transport term for the arterial wall is often left out in the drug transport models of drug-eluting stents [44,45]. In this scenario, the no-slip condition is not applied at the boundaries of the stent, and the plasma flow is allowed to flow through the polymer, which is modeled as a porous medium. In this case, the average free and bound drug concentrations in the arterial wall are significantly impacted by the presence of convection and cause the polymer region to erode, as shown in both Figure 5a,b. The peaking of the average drug concentrations also suggests an early expected resident time, as the transient time of the bound drug is within 2 days. This is again due to the high convection due to plasma flow and the eroding effect of the polymer.
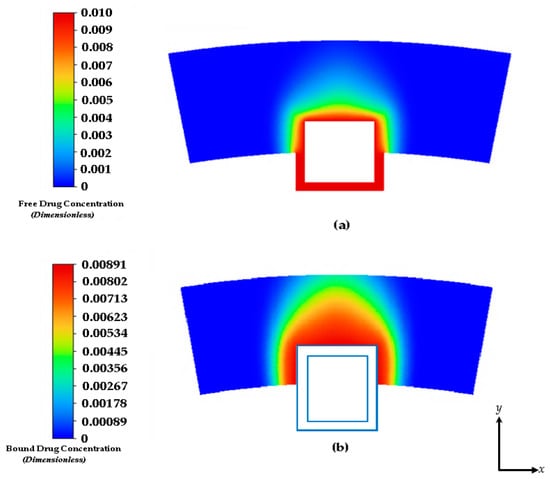
Figure 5.
Drug concentration contours at 2 days: (a) free drug and (b) bound drug. With an initial concentration of C0 = 0.01. The light blue lines incorporate the stent strut boundaries.
Figure 6 shows the free and bound drug concentration contours at 8 days. Similar to the results shown in Figure 5a,b at 2 h, the high convection due to plasma flow and the eroding effect of the polymer has a significant effect on the transit time and diffusion profile. It also appears that when modeling the polymer boundary as porous media without the no-slip condition, washing out of the polymer tends to lower the concentration magnitudes. It is evident that the presence of interstitial flow increases the transport in the transmural direction and leads to faster drug clearance at the perivascular interface using this modeling method. In an effort to compare other works, we continued this study by applying the no-slip condition at the boundaries of the polymer and arterial wall interface and not incorporating interstitial flow with plasma flow through the inlet. Convection is modeled with the tissue Peclet number.
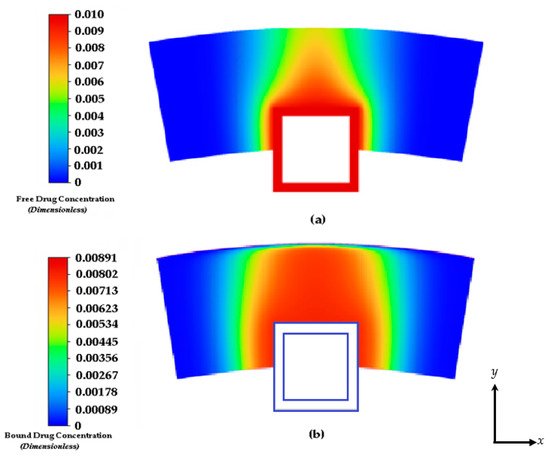
Figure 6.
Drug concentration contours at 8 days: (a) free drug and (b) bound drug. The light blue lines incorporate the stent strut boundaries.
3.3. Free and Bound Drug Concentration Profiles with Erosion and Convection
As mentioned previously, the results shown in this section are results from the simulation by applying the no-slip condition at the boundaries of the polymer and the arterial wall interface and neglecting the interstitial flow with plasma flow through the inlet. Convection, in this case is modelled with the tissue Peclet number. Figure 7a,b show the free drug diffusion contours in the arterial wall with convection modeled with the tissue Peclet number. The drug release contour profiles have similar release rates in the first 4 to 8 days when the PLGA diffusion, degradation, and erosion are insignificant. In Figure 7b, a lower concentration of the free drug in the polymer coating is observed in the case of time-dependent release of the drug from the coating. This is due to the time-dependent boundary condition of Equation (21). The effect of release kinetics on the spatial distribution of the free drug can be visualized clearly in Figure 8. In this case, the heterogeneous distribution and retention of the drug are found to be observed throughout the domain.
The characteristics of the release profiles in the intravascular delivery reported here are in good correspondence to what was reported for in vitro release in previously reported works [46]. In the simulation comparison, significant drug release is achieved in the PLGA coating at around day 17. The arterial bound drug distributions are shown in Figure 8 for the PLGA coating on day 17, shortly after the drug levels have peaked in the arterial wall. The bound drug distribution is close to uniform in the circumferential direction, whereas in the transmural direction, a gradient is clearly observed closer to the perivascular interface. Improved uniformity in the circumferential direction is expected with the anisotropic drug diffusivity, which results in fast drug diffusion in the circumferential direction. This is an improvement over the results shown previously in Figure 5 and Figure 6. In Figure 7, the observed arterial drug distribution pattern for the PLGA coating case is similar to previous studies of a bio-durable coating [34].
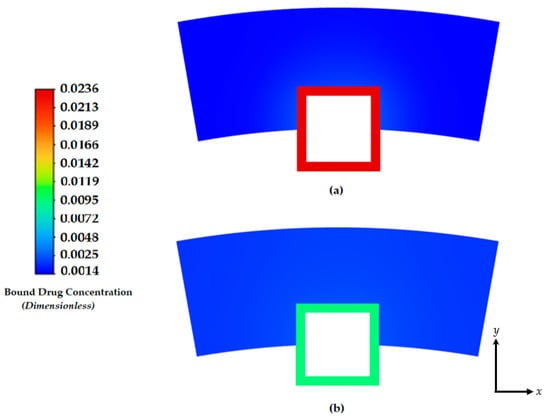
Figure 7.
Contours of the free drug diffusion into the arterial wall at: (a) 4 days and (b) 8 days.
Although the free and bound drug concentration cases are shown here, the internalized drug is neglected. Although not modeled in this work, drug internalization describes the cellular uptake of drug molecules after they associate with the binding sites. This is an important mechanism for drug metabolism in the physiological environment [47,48]. Only limited studies have considered the impact of the internalization process on stent-based drug delivery. While the drug internalization rate may vary for the different drugs, and such data are lacking in the literature, the model discussed in this paper only considers the free and bound drug case. Future work will involve examining the internalized drug.
The distributions of the average weighted free and bound drug concentrations for varying values of the scaling parameter ε1 = (Rd/C0) are presented in Figure 9 and Figure 10, respectively, and the same for different values of ε2 = (C0/BM), which are shown in Figure 11 and Figure 12, respectively. The value of the scaling parameter ε1, decreases with a decrease in the dissociation rate constant kd and with an increase in the association rate constant ka depending on Rd = (kd/ka). Additionally, ε2 increases with decreasing S0 (while keeping c0 fixed).
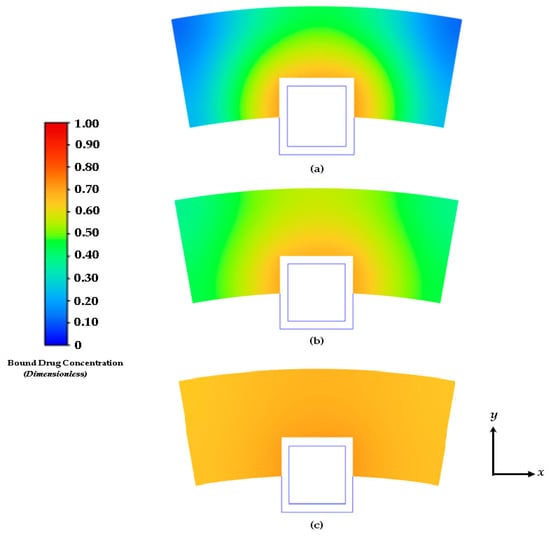
Figure 8.
Contours of drug diffusion into the arterial wall at: (a) 4 days, (b) 8 days, and (c) 16.67 days.
Figure 4a shows that the normalized mean free drug concentration decreases with decreasing ε1 for PeT = 2, Da = 40, ε2 = 100, up to a certain time and, thereafter, no significant changes occurred. It can be concluded and justified that, as ε1 decreases, the rate of reversible binding (kd) decreases and/or the rate of forward binding increases, which lowers the mean concentration of the free drug.
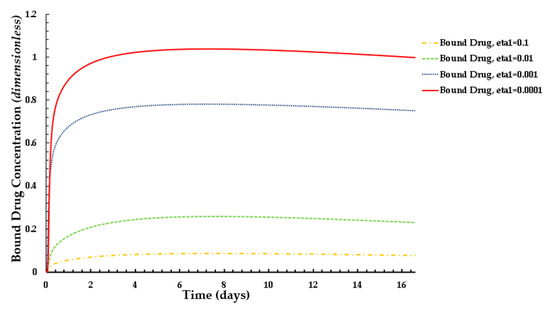
Figure 9.
Distribution of normalized mean bound drug concentration for different values of ε1 at PeT = 2, Da = 40, ε2 = 100.
Figure 10 shows how the rates of forward and reversible binding affect the average weighted concentration of bound drug within the arterial tissue. It can be concluded that the average weighted concentration is increased with the decrease in ε1, which is attributed to the increase in the rate of forward binding and/or to the decrease in the rate of reversible binding.
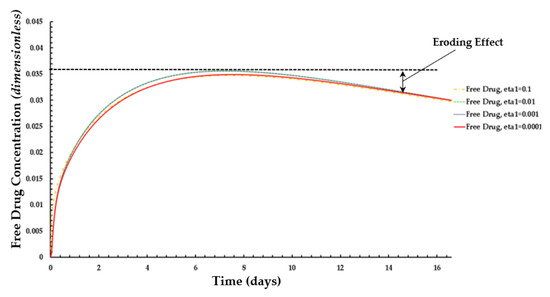
Figure 10.
Distribution of normalized weighted average free drug concentration for different values of ε1 at PeT = 2, Da = 40, ε2 = 100.
The effects of ε2 (i.e., net tissue binding potential on the mean concentrations of free and bound drug) are displayed in Figure 11 and Figure 12, respectively. As previously mentioned, ε2 increases with decreasing binding potential.
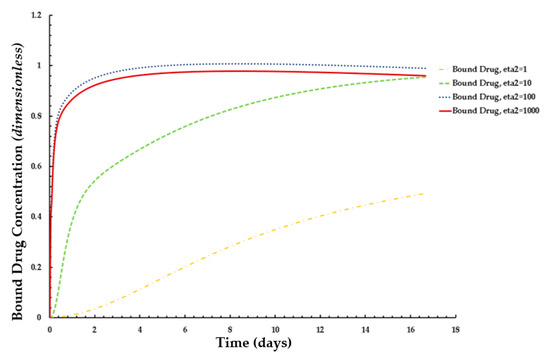
Figure 11.
Distribution of normalized weighted averaged bound drug concentration for different values of ε2 at PeT = 2, Da = 40, ε1 = 0.001.
The results of these figures indicate that the average weighted concentration of free drug increases with decreasing binding potential up to ε2 = 100, but the concentration reaches a quasi-steady state for weaker binding capacity (ε2 = 1000) as compared to the other cases.
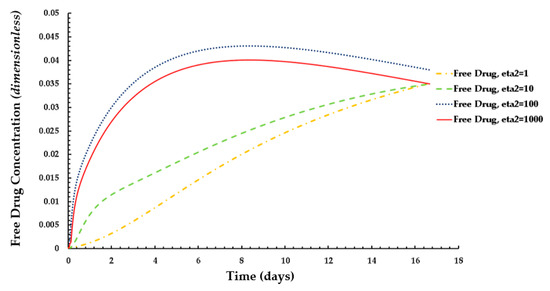
Figure 12.
Distribution of normalized weighted averaged free drug concentration for different values of ε2 at PeT = 2, Da = 40, ε1 = 0.001.
In the case of the free drug for ε2 ≤ 100, the quasi-equilibrium is not fully established until approximately 17 days, while the PLGA coating has eroded significantly. On the other hand, in the case that bound drug for ε2 ≥ 10, the quasi-equilibrium is attained very rapidly.
3.4. Average Weighted Concentration Results for Varying Tortuosity
We also conducted a simple analysis to demonstrate the effect of tortuosity (τ as listed in Equation (11)) on the average weighted concentration. We observed that a decrease in the mean concentration of free drug took place with while increasing tortuosity (i.e., an inverse relationship between free drug concentration and tortuosity is revealed) as shown in Figure 13. A similar pattern is also observed for bound drug in Figure 14.
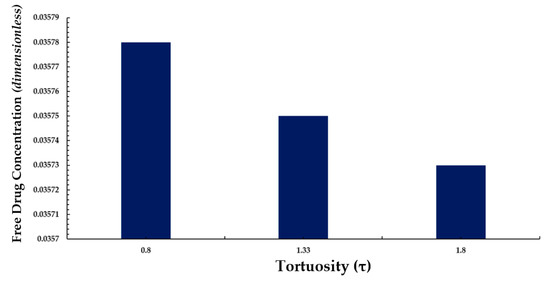
Figure 13.
Normalized average weighted free drug concentration for varying tortuosity (τ).
The above observation may be justified in the sense that as the tortuosity increases so too does the effective distance over which diffusion has to take place (i.e., the progression of diffusion eventually lowering the mean concentration of both drug forms is impeded).
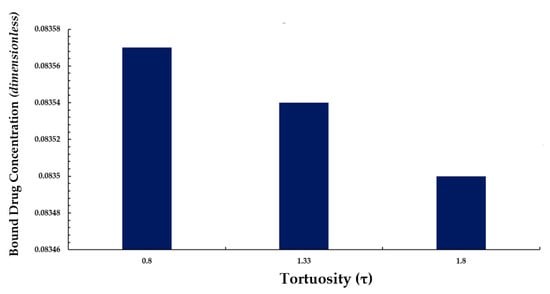
Figure 14.
Normalized average weighted bound drug concentration for varying tortuosity (τ).
4. Conclusions
This paper reports the findings of an investigation of the interstitial flow profile into the arterial wall and the free and bound drug diffusion profiles with a parametric study of varying polymer drug concentration (low and high), tortuosity, porosity, and Peclet and DamKöhler numbers over the course of 400 h (16.67 days). Acquiring an understanding of the relationship between drug physicochemical properties and the local transport environment is crucial to the success of new stent designs. Computational studies can provide highly detailed predictions of the drug distribution in the vessel wall over time. Most computational investigations of drug delivery include only one drug form. This has the drawback of not accounting for binding and convective diffusive transport directly. The developed mathematical model discussed in this paper provides the basis for evaluating and studying diffusion characteristics for drug-eluting stent applications.
Future work will be carried out to enhance this model to characterize the internalized drug, evaluate further the eluting behavior of the PGLA coating, compare PLGA to other bio durable coatings, describe the anisotropic behavior of the diffusion coefficient within the arterial wall with the ease of adaptation to more sophisticated scenarios (e.g., consideration of more pathological conditions) and compare the effect of stent position on drug diffusion profiles (i.e., half, full, and partial embedment). Simulations using the presented model can help provide insight into the drug release and distribution by a stent with PLGA coating, and the potential impacts of various factors that can affect the efficacy of drug delivery. With the developed preliminary model, optimization of the model parameters, such as different stent strut geometries and coating thickness, can also be performed for exploration on the design of drug-eluting stents.
Author Contributions
Conceptualization, R.L.H.J., M.E. and J.P.K.; methodology, R.L.H.J. and J.P.K.; software, R.L.H.J.; validation, R.L.H.J. and M.E.; formal analysis, R.L.H.J., M.E. and J.P.K.; investigation, R.L.H.J., M.E. and J.P.K.; resources, R.L.H.J.; data curation, R.L.H.J.; writing—original draft preparation, R.L.H.J.; writing—review and editing, R.L.H.J.; visualization, R.L.H.J.; supervision, R.L.H.J.; project administration, R.L.H.J.; funding acquisition, R.L.H.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the University of North Carolina at Charlotte (UNC-C) Faculty Research Grant (FRG).
Data Availability Statement
The data from this work will be shared and made available upon request to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Cf | Free drug |
| Cb | Bound drug |
| Cp | Perivascular drug concentration |
| Cw | Wall drug concentration |
| C0 | Initial drug concentration |
| D | Outer diameter of the artery |
| DC | Coefficient of the coating diffusion |
| Da | Dimensionless DamKöhler number in the tissue |
| Dfree | Coefficient of free diffusivity |
| Deff | Coefficient of effective diffusivity |
| DT | True diffusivity of the free drug |
| Jwp | PLGA flux parameter |
| Lx | Arterial domain length |
| Ly | Arterial domain wall thickness |
| Lsx | Stent length |
| Lsy | Stent thickness |
| ka | Tissue binding capacity |
| kd | Dissociation rate constant |
| PeC | Dimensionless Peclet number in the coating |
| PeT | Dimensionless Peclet number in the tissue |
| Rd | Equilibrium dissociation constant |
| Rwp | Mass transfer resistance |
| S0 | Available binding sites |
| T | Time |
| Vy | Transmural filtration velocity |
| x | x-coordinate |
| y | y-coordinate |
| δ | Strut dimension |
| ε | Porosity of the arterial wall |
| ε1 and ε2 | Dimensionless scaling parameters |
| τ | Tortuosity of the arterial wall |
| τ1, τ2, and τ2 | Characteristic time scales |
| PLGA | Poly(lactic-co-glycolic acid) |
| UDS | User defined scalar |
Appendix A
This section provides an overview of the characteristic scaling methodology implemented to dimensionless Equations (4)–(6). In this method, we begin with stating the free and bound drug transport equations as mentioned previously:
- Free-drug in the PLGA Coating Domain:
- Free-drug in the Arterial Domain:
- Bound-drug in the Arterial Domain:
The dimensionless scaling parameters used for scaling Equation (A1) through (A3) are shown below:
The first order free and bound drug concentration derivatives are first non-dimensionalized using the characteristic dimensionless parameters as shown below:
- Scaled free-drug concentration time derivative:
- Scaled bound-drug concentration time derivative:
- Scaled free-drug concentration first-order x-direction derivative:
- Scaled free-drug concentration first-order y-direction derivative:
The second-order derivatives are scaled as shown below:
- Scaled free-drug concentration second-order x-direction derivative:
- Scaled free-drug concentration second-order y-direction derivative:
The dimensionless derivatives are now substituted into Equation (A1) as shown below:
Dividing Equation (A11) through on both sides by C0Vy/δ yields the following:
The finalized dimensionless form of the free-drug transport into the PLGA coating is shown below:
where PeC = [Vyδ/(DC)]. The scaled free-drug concentration derivatives (Equations (A5) and (A7) are now substituted into the free drug transport equation into the arterial wall domain:
Dividing Equation (A14) through on both sides by C0Vy/δ, factoring out the first- and second-order derivative constants, and substituting the equilibrium constant Rd = (kd/ka) yields the following:
Recognizing that the Peclet and DamKöhler numbers are PeT = [Vyδ/(DT) and Da = [(kaS0δ2)/(DT)] are in the tissue and that ε1 = (Rd/C0) is an additional scaling parameter and yields the final non-dimensional form of the free-drug transport equation in the arterial domain as shown below:
The scaled bound-drug concentration derivative (Equation (A6) and the scaling parameters are now substituted into the free drug transport equation into the arterial wall domain:
Dividing through by S0Vy/δ and entering the relations for ε2, Da, and Pe yields.
References
- Edwards, M.; Hewlin, R.L., Jr.; Smith, M. A 2-D Transient Computational Multi-Physics Model for Analyzing Magnetic and Non-Magnetic (Red Blood Cells and E. Coli Bacteria) Particle Dynamics in a Travelling Wave Ferro-Magnetic Microfluidic Device. ASME J. Eng. Sci. Med. Ther. Diagn. 2023, 1–47. [Google Scholar] [CrossRef]
- Hewlin, R.L., Jr.; Edwards, M. Continuous Flow Separation of Red Blood Cells and Platelets in a Y-Microfluidic Channel Device with Saw-Tooth Profile Elec-trodes via Low Voltage Dielectrophoresis. Curr. Issues Mol. Biol. 2023, 45, 3048–3067. [Google Scholar] [CrossRef] [PubMed]
- Hewlin, R.L., Jr.; Ciero, A.; Kizito, J.P. Development of a Two-Way Coupled Eulerian-Lagrangian Computational Magnetic Nanoparticle Targeting Model for Pulsatile Flow in a Patient-Specific Diseased Left Carotid Bifurcation Artery. Cardiovasc. Eng. Technol. 2019, 10, 299–313. [Google Scholar] [CrossRef] [PubMed]
- Stanley, N.; Ciero, A.; Timms, W.; Hewlin, R.L., Jr. A 3-D Printed Optically Clear Rigid Diseased Carotid Bifurcation Arterial Mock Vessel Model for Particle Image Velocimetry Analysis in Pulsatile Flow. ASME Open J. Eng. ASME 2023, 2, 021010. [Google Scholar] [CrossRef]
- Hewlin, R.L., Jr.; Tindall, J.M. Computational Assessment of Magnetic Nanoparticle Targeting Efficiency in a Simplified Circle of Willis Arterial Model. Int. J. Mol. Sci. 2023, 24, 2545. [Google Scholar] [CrossRef] [PubMed]
- Hewlin, R.L., Jr.; Kizito, J.P. Comparison of Carotid Bifurcation Hemodynamics in Patient-Specific Geometries at Rest and During Exercise. In Proceedings of the Fluids Engineering Division Summer Meeting. American Society of Mechanical Engineers, Volume 1A, Symposia: Advances in Fluids Engineering Education; Advances in Numerical Modeling for Turbomachinery Flow Optimization; Applications in CFD; Bio-Inspired Fluid Mechanics; CFD Verification and Validation; Development and Applications of Immersed Boundary Methods; DNS, LES, and Hybrid RANS/LES Methods, Incline Village, NV, USA, 7–11 July 2013; p. V01AT04A001. [Google Scholar] [CrossRef]
- Stanley, N.; Ciero, A.; Timms, W.; Hewlin, R.L., Jr. Development of 3-D Printed Optically Clear Rigid Anatomical Vessels for Particle Image Velocimetry Analysis in Cardiovascular Flow. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers, Volume 7: Fluids Engineering, Salt Lake City, UT, USA, 11–14 November 2019; p. V007T08A004. [Google Scholar] [CrossRef]
- Hewlin, R.L., Jr.; Kizito, J.P. Development of an Experimental and Digital Cardiovascular Arterial Model for Transient Hemodynamic and Postural Change Studies: “A Preliminary Framework Analysis”. Cardiovasc. Eng. Tech. 2018, 9, 1–31. [Google Scholar] [CrossRef]
- Daemen, J.; Serruys, P.W. Drug-Eluting Stent Update 2007 Part I: A Survey of Current and Future Generation Drug-Eluting Stents: Meaningful Advances or More of the Same. Circulation 2007, 116, 316–328. [Google Scholar] [CrossRef]
- Beshchasna, N.; Saqib, M.; Kraskiewicz, H.; Wasyluk, Ł.; Kuzmin, O.; Duta, O.C.; Ficai, D.; Ghizdavet, Z.; Marin, A.; Ficai, A.; et al. Recent Advances in Manufacturing Innovative Stents. Pharnaceutics 2020, 12, 349. [Google Scholar] [CrossRef]
- Conway, C. Clinical Evidence vs. the Testing Paradigm. Cardiovasc. Eng. Technol. 2018, 9, 752–760. [Google Scholar] [CrossRef]
- Beckman, J.A.; White, C.J. Paclitaxel-Coated Balloons and Eluting Stents: Is There a Mortality Risk in Patients with Peripheral Artery Disease. Circulation 2019, 140, 1342–1351. [Google Scholar] [CrossRef]
- Capell, W.H.; Bonaca, M.P.; Nehler, M.R.; Kittelson, J.M.; Anand, S.S.; Berkowitz, S.D.; Debus, E.S.; Fanelli, F.; Haskell, L.; Patel, M.R.; et al. Rationale and Desitn for the Vascular Outcomes Study of ASA Along with Rivaroxaban in Endovascular or Surgical Limb Revascularization for Peripheral Artery Disease. Am. Heart J. 2018, 199, 83–91. [Google Scholar] [CrossRef]
- US Food and Drug Administration. Update: Treatment of Peripheral Arterial Disease with Paclitaxel-Coated Ballons and Paclitaxel-Eluting Stents Potentiall Associated with Increased Mortality: Letter to Health Care Providers. Available online: https://www.fda.gov/medical-devices/letters-health-care-providers/update-treatment-peripheral-arterial-disease-paclitaxel-coated-balloons-and-paclitaxel-eluting (accessed on 5 May 2022).
- Levin, A.; Jonas, M.; Hwang, C.W.; Edelman, E. Local and Systemic Drug Competition in Drug-Eluting Stent Tissue Deposition Properties. J. Control. Release 2005, 109, 226–243. [Google Scholar] [CrossRef] [PubMed]
- Granada, J.F.; Stenoien, M.; Buszman, P.P.; Tellez, A.; Langanki, D.; Kaluza, G.L.; Leon, M.B.; Gray, W.; Jaff, M.R.; Schwartz, R.S. Mechanisms of Tissue Uptake and Retention of Paclitaxel-Coated Balloons: Impact on Neointimal Proliferation and Healing. Open Heart 2014, 1, e000117. [Google Scholar] [CrossRef]
- Lovich, M.A.; Philbrook, M.; Sawyer, S.; Weselcouch, E.; Edelman, E.R. Arterial Heparin Deposition: Role of Diffusion, Convection, and Extravascular Space. Am. J. Physiol. 1998, 275, H2236–H2242. [Google Scholar] [CrossRef]
- Moses, J.W.; Stone, G.W.; Nikolsky, E.; Mintz, G.S.; Dangas, G.; Grube, E. Drug-eluting Stents in the Treatment of Intermediate Lesions: Pooled Analysis from four Randomized Trials. J. Am. Coll. Cardiol. 2006, 47, 2164–2171. [Google Scholar] [CrossRef]
- Serruys, P.W.; Sianos, G.; Abizaid, A.; Aoki, J.; den Heijer, P.; Bonnier, H. The Effect of Variable Dose and Release Kinetics on Neointimal Hyperplasia using a Novel Paclitaxel-eluting Stent Platform: The Paclitaxel In-Stent Controlled Elution Study (Pices). J. Am. Coll. Cardiol. 2005, 46, 253–260. [Google Scholar] [CrossRef] [PubMed]
- Lovich, M.A.; Edelman, E.R. Computational Simulations of Local Vascular Heparin Deposition and Distribution. Am. J. Physiol. 1996, 271, H2014–H2024. [Google Scholar] [CrossRef]
- Sakharov, D.V.; Kalachev, L.V.; Rijken, D.C. Numerical Simulation of Local Pharmcokinetics of a Drug after Intervascular Delivery with an Eluting Stent. J. Drug Target. 2002, 10, 507–513. [Google Scholar] [CrossRef] [PubMed]
- Hwang, C.; Wu, D.; Edelman, E. Physiological Transport Forces Govern Drug Distribution for Stent-Based Delivery. Circulation 2001, 104, 600–605. [Google Scholar] [CrossRef]
- Migiliavacca, F.; Gervaso, F.; Prosi, M.; Zunino, P.; Minisini, S.; Formaggia, L. Expansion and Drug Elution Model of a Coronary Stent. Comput. Methods Biomech. Biomed. Eng. 2007, 10, 63–73. [Google Scholar] [CrossRef]
- Borghi, A.; Foa, E.; Balossino, R.; Migliavacca, F.; Dubini, G. Modelling Drug Elutiogn from Stents: Effects of Reversible Binding in the Vascular Wall and Degradable Polymeric Matrix. Comput. Methods Biomech. Biomed. Eng. 2008, 11, 367–377. [Google Scholar] [CrossRef]
- Horner, M.; Joshi, S.; Dhruva, V.; Sett, S.; Stewart, S.F.C. A Two-Species Drug Delivery Model is Required to Predict Deposition from Drug-Eluting Stents. Cardiovasc. Eng. Technol. 2010, 1, 225–234. [Google Scholar] [CrossRef]
- Tzafriri, A.R.; Levin, A.D.; Edelman, E.R. Diffusion-limited Binding Explains Binary Dose Response for Local Arterial and Tumor Drug Delivery. Cell Prolif. 2009, 42, 348–363. [Google Scholar] [CrossRef]
- Higuchi, T. Theoretical Analysis of Rate of Release of Solid Drugs Dispersed in Solid Matrices. J. Pharm. Sci. 1963, 52, 1145–1149. [Google Scholar] [CrossRef] [PubMed]
- Mandal, A.P.; Mandal, P.K. An Unsteady Analysis of Arterial Drug Transport from Half-Embedded Drug Eluting Stent. Appl. Math. Comput. 2015, 266, 968–981. [Google Scholar] [CrossRef]
- Mandal, A.P.; Mandal, P.K. Computational Modelling of Three-Phase Stent-Based Delivery. J. Explor. Res. Pharm. 2017, 2, 31–40. [Google Scholar] [CrossRef]
- Saltzman, W.M. Drug Delivery: Engineering Principles for Drug Therapy; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Sarifuddin; Mandal, P.K. Effect of Diffusivity on the Transport of Drug Eluted from Drug Eluting Stent. Int. J. Appl. Comput. Math. 2016, 2, 291–301. [Google Scholar] [CrossRef]
- O’Connel, B.M.; Walsh, M.T. Demonstrating the Influence of Compression on Artery Wall Mass Transport. Ann. Biomed. Eng. 2010, 38, 1354–1366. [Google Scholar] [CrossRef]
- Edwards, M.; Kizito, J.P.; Hewlin, R.L., Jr. A Time-Dependent Two Species Explicit Finite Difference Computational Model for Analyzing Diffusion in a Drug Eluting Stented Coronary Artery Wall: A Phase I Study. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers, Volume 4: Biomedical and Biotechnology; Design, Systems, and Complexity, Columbus, OH, USA, 30 October–3 November 2022; p. V004T05A009. [Google Scholar] [CrossRef]
- Zhu, X.; Pack, D.W.; Braatz, R.D. Modelling Intravascular Delivery from Drug-Eluting Stents with Biodegradable Coating: Investigation of Anisotropic Vascular Drug Diffusivity and Arterial Drug Distribution. Comput. Methods Biomech. Biomed. Eng. 2014, 17, 187–198. [Google Scholar] [CrossRef]
- Saha, R.; Mandal, P.K. Modelling Time-dependent Release Kinetics in Stent-based Delivery. J. Explor. Res. Pharmacol. 2018, 3, 61–70. [Google Scholar] [CrossRef]
- Zhu, X.; Braatz, R.D. Modelling and Analysis of Drug-Eluting Stents With Biodegradable PLGS Coating: Consequences on Instravascular Drug Delivery. J. Biomech. Eng. 2015, 136, 111004. [Google Scholar] [CrossRef]
- Balakrishnan, B.; Tzafriri, A.R.; Arifin, D.Y.; Edelman, E.R. Intravascular Drug Release Kinetics Dictate Arterial Drug Deposition, Rentention and Distribution. J. Control. Release 2007, 123, 100–108. [Google Scholar] [CrossRef] [PubMed]
- Vairo, G.; Cioffi, M.; Cottone, R.; Dubini, G.; Migliavacca, F. Drug Release From Coronary Eluting Stents: A Multidomain Approach. J. Biomech. Eng. 2010, 43, 1580–1589. [Google Scholar] [CrossRef]
- Hewlin, R.L., Jr. Transient Cardiovascular Hemodynamics in a Patient-Specific Arterial System. Ph.D. Thesis, North Carolina Agricultural and Technical State University, Greensboro, NC, USA, 2015. [Google Scholar]
- Whale, M.; Grodzinsky, A.; Johnson, M. The Effect of Aging and Pressure on the Specific Hydraulic Conductivity of the Aortic Wall. Biorheology 1996, 33, 17–44. [Google Scholar] [CrossRef]
- Kolachalama, V.; Tzafriri, A.; Arifin, D.; Edelman, E. Luminal Flow Patterns Dictate Arterial Drug Deposition in Stent-Based Delivery. J. Control. Release 2009, 133, 24–30. [Google Scholar] [CrossRef]
- Baldwin, A.L.; Wilson, I.; Gardus-Pizlo, R.; Wilensky, R.; March, K. Effect of Atherosclerosis on Transmural Convection and Arterial Ultrastructure: Implications for Loacl Vascualr Drug Delivery. Aterioscler. Thromb. Vasc. Biol. 1997, 17, 3365–3375. [Google Scholar] [CrossRef]
- Wang, D.; Tarbell, J. Modelling Interstitial Flow in an Artery Wall Allows Estimation of Wall Shear Stress on Smooth Muscle Cells. ASME J. Biomech. Eng. 1995, 117, 358–363. [Google Scholar] [CrossRef]
- Santin, M.; Colombo, P.; Brushci, G. Interfacial Biology of In-Stent Restenosis. Expert Rev. Med. Dev. 2005, 2, 429–443. [Google Scholar] [CrossRef]
- Balakrishnan, B.; Tzafriri, A.R.; Seifert, P.; Groothuis, A.; Rogers, C.; Edelman, E.R. Strut Position, Blood Flow, and Drug Deposition-Implications for Single and Overlapping Drug-Eluting Stents. Circulation 2005, 111, 2958–2965. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.T.; Venkatraman, S.S.; Boey, F.Y.C.; Loo, J.S.C.; Tan, L.P. Controlled Release of Sirolimus from a Multilayered PLGA Stent Matrix. Biomaterials 2006, 27, 5588–5595. [Google Scholar] [CrossRef] [PubMed]
- Castellot, J.J.; Wong, K.; Herman, B.; Hoover, R.L.; Albertini, D.F.; Wright, T.C.; Caleb, B.L.; Karnovsky, M.J. Binding and Internalization of Heparin by Vascular Smooth Muscle Cells. J. Cell. Physiol. 1985, 124, 13–20. [Google Scholar] [CrossRef] [PubMed]
- Deux, J.-F.; Meddahi-Pelle, A.; Le Blanche, A.F.; Feldman, L.J.; Colliec-Jouault, S.; Brée, F.; Boudghène, F.; Michel, J.-B.; Letourneur, D. Low Molecular Weight Fucoidan Prevents Neointimal Hyperplasia in Rabbit Iliac Artery In-Stent Restenosis Model. Arter. Thromb. Vasc. Biol. 2002, 22, 1604–1609. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).