Computational Modeling of the Neurofibromin-Stimulated Guanosine Triphosphate Hydrolysis by the KRas Protein
Abstract
1. Introduction
2. Materials and Methods
3. Results
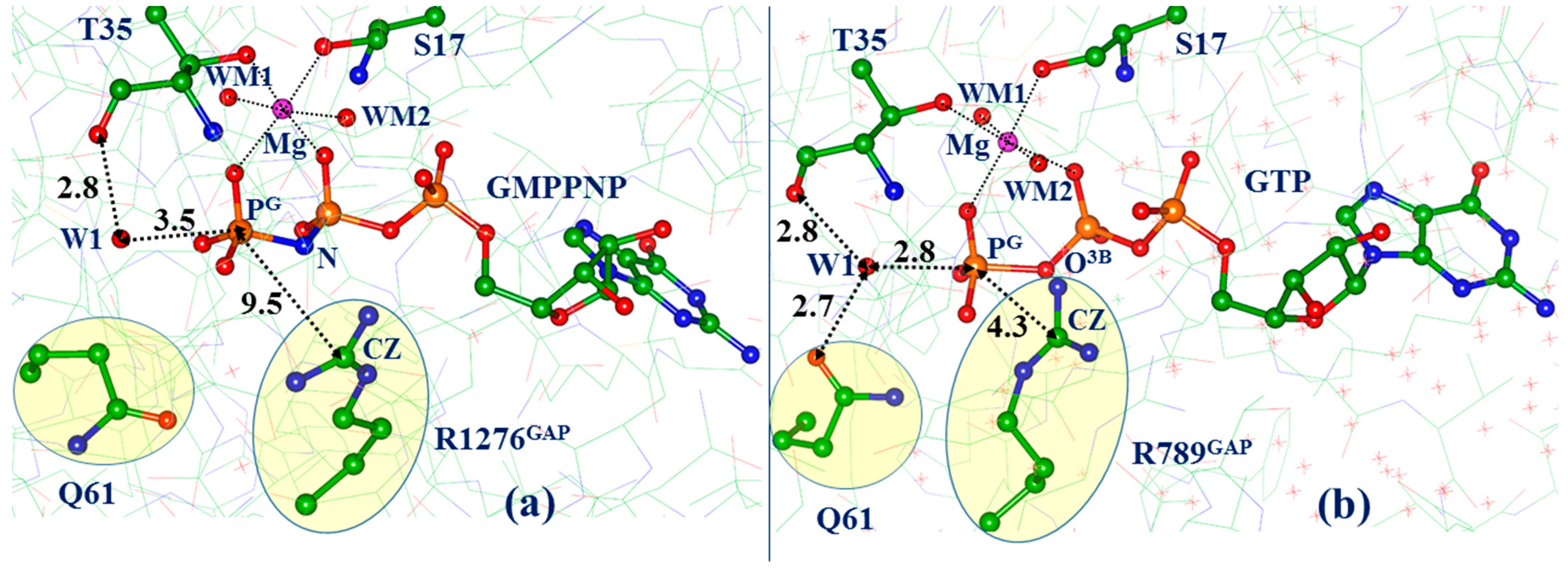
3.1. Classical Molecular Dynamics Reveals Non-Reactive and Reactive ES Complexes
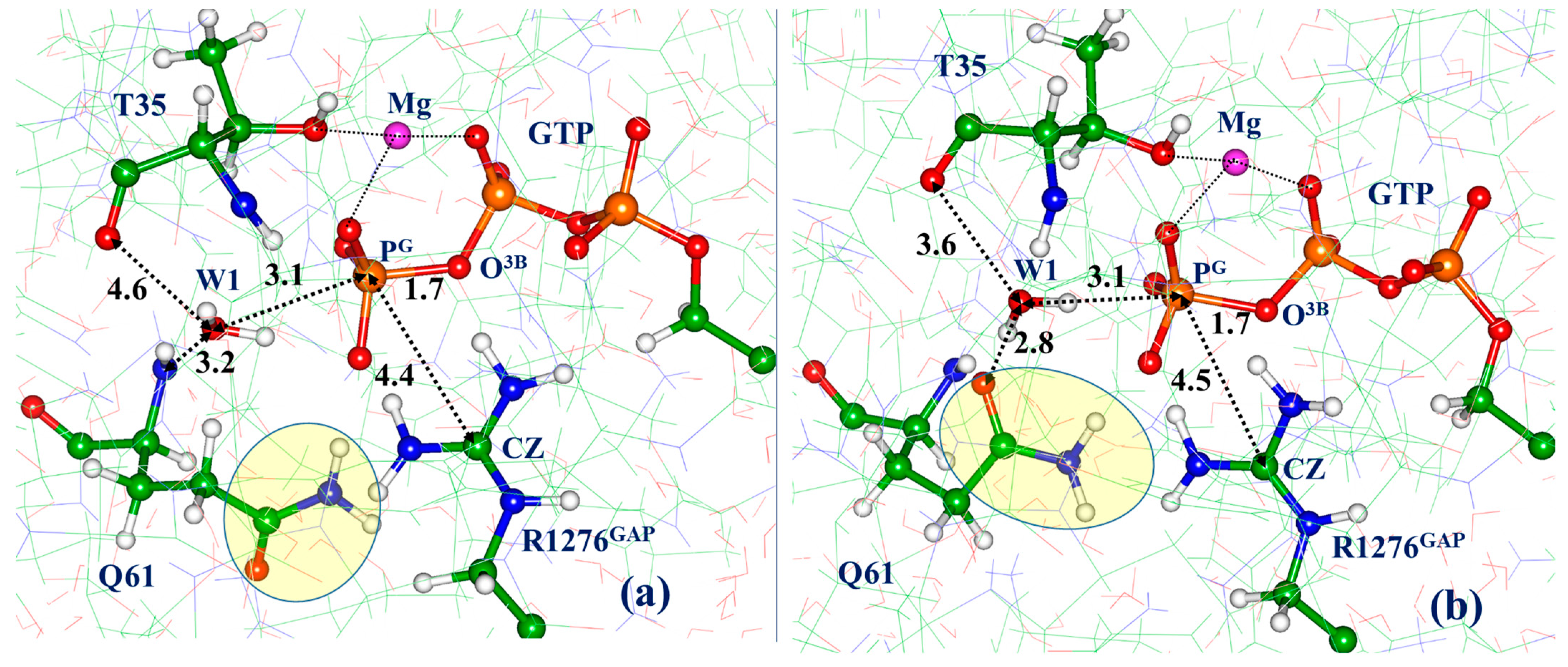
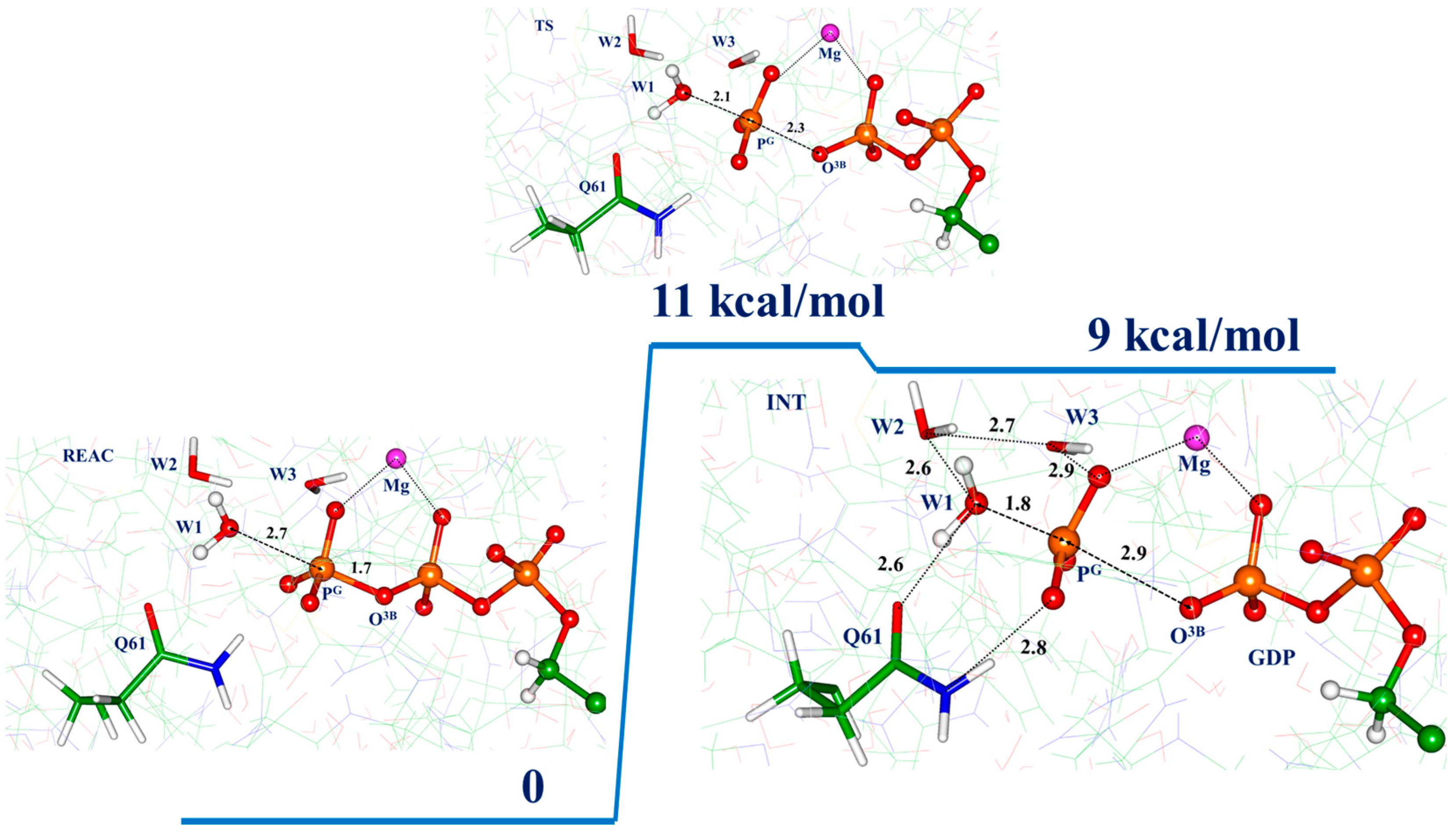
3.2. Molecular Dynamics with QM/MM Potentials Initiated with Non-Reactive ES
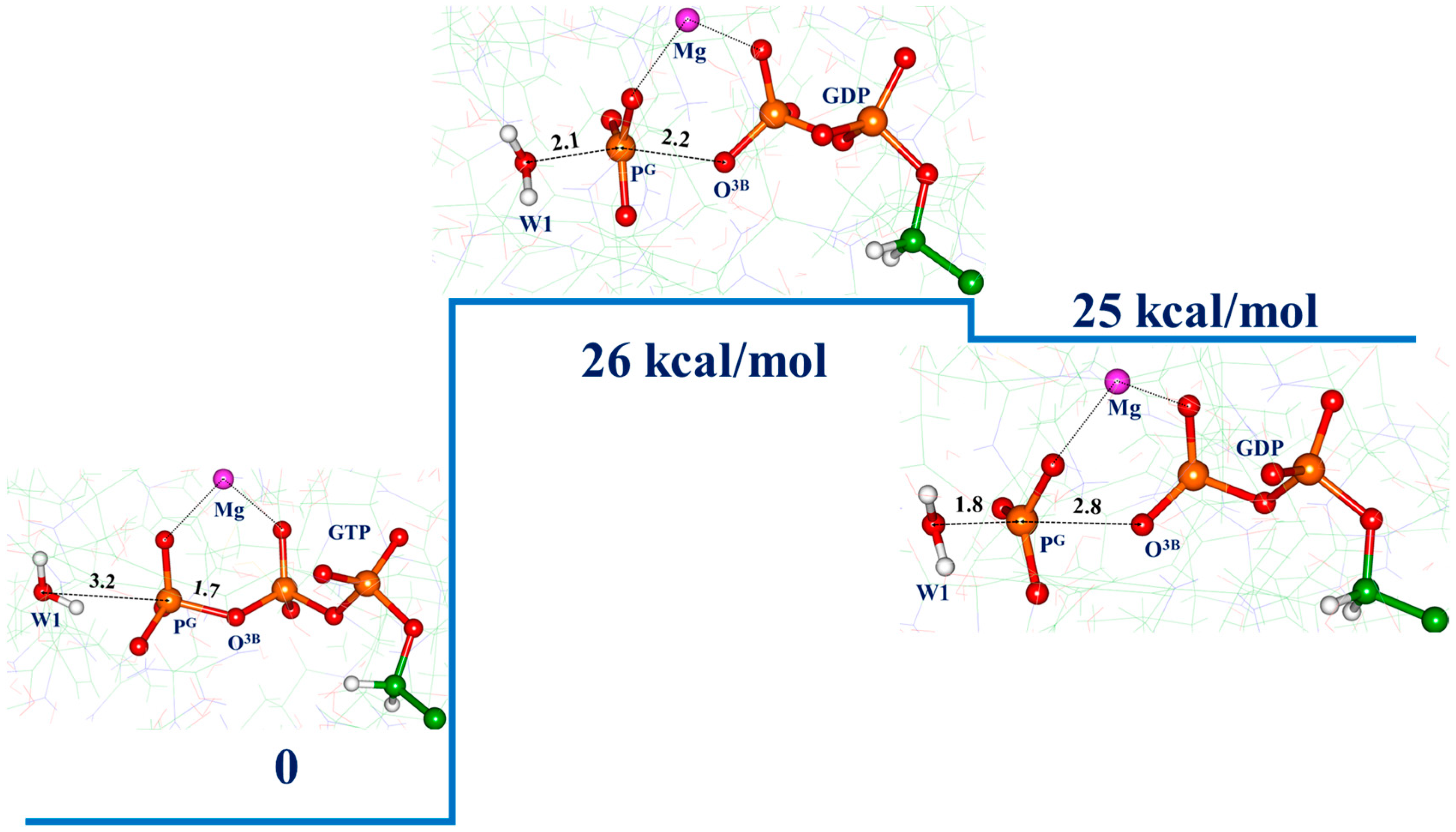
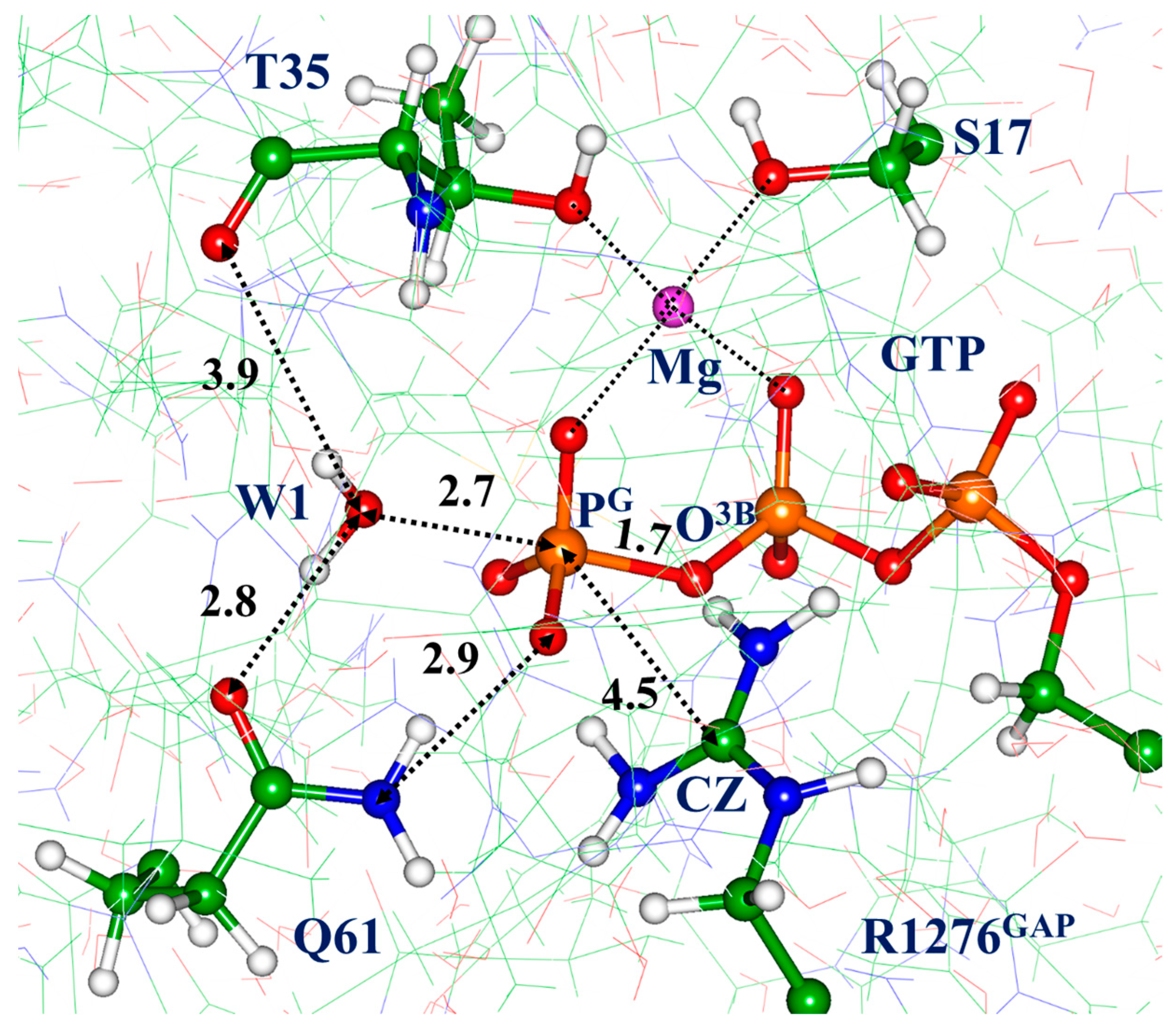
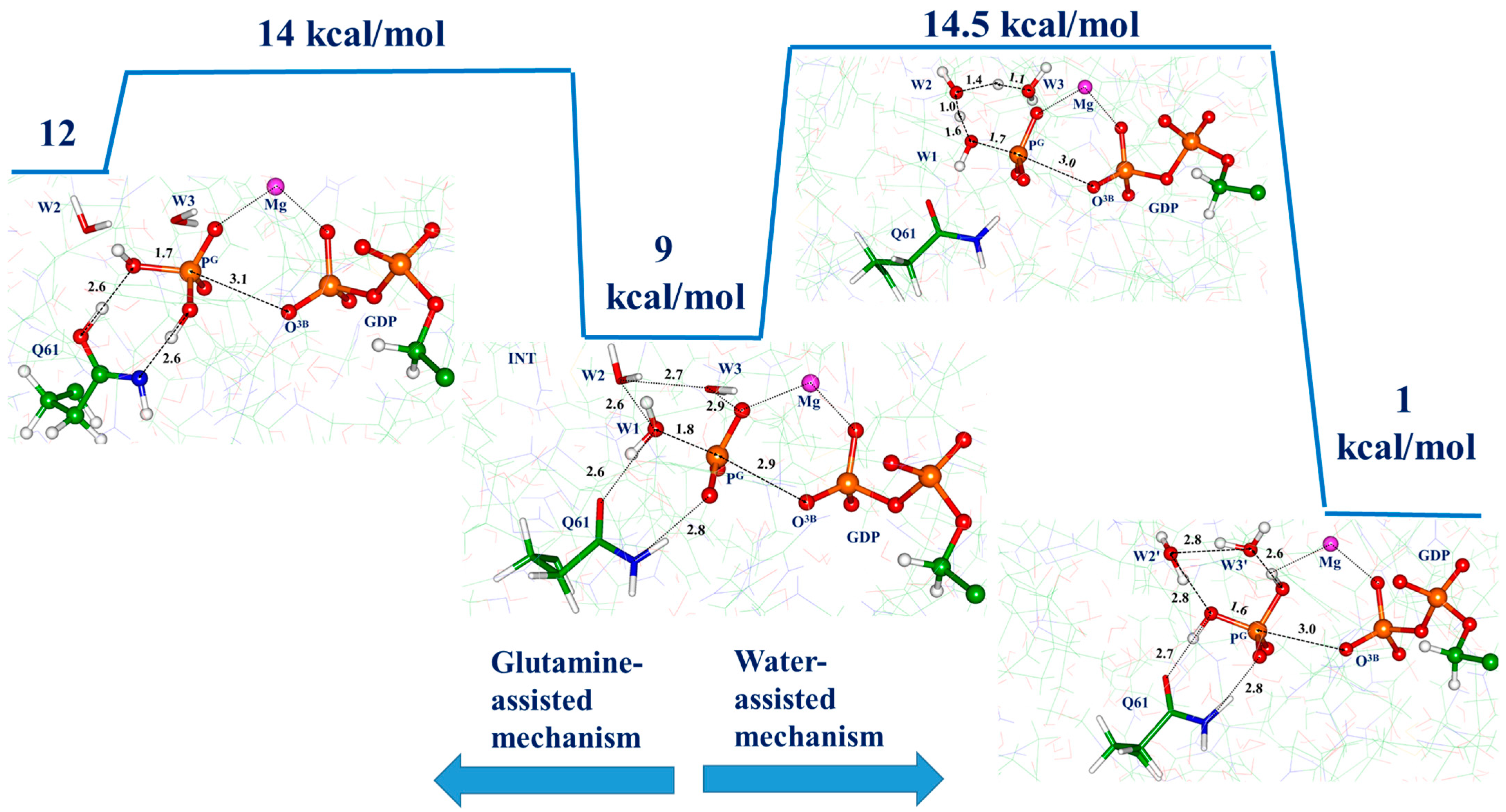
3.3. Molecular Dynamics with QM/MM Potentials Initiated with Reactive ES
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fernández-Medarde, A.; De Las Rivas, J.; Santos, E. 40 Years of RAS—A Historic Overview. Genes 2021, 12, 681. [Google Scholar] [CrossRef] [PubMed]
- Hobbs, G.A.; Der, C.J.; Rossman, K.L. RAS isoforms and mutations in cancer at a glance. J. Cell Sci. 2016, 129, 1287–1292. [Google Scholar] [CrossRef]
- Cox, A.D.; Der, C.J. Ras History: The Saga Continues. Small GTPases 2010, 1, 2–27. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Jang, H.; Muratcioglu, S.; Gursoy, A.; Keskin, O.; Nussinov, R.; Zhang, J. Ras Conformational Ensembles, Allostery, and Signaling. Chem. Rev. 2016, 116, 6607–6665. [Google Scholar] [CrossRef] [PubMed]
- Lu, S.; Jang, H.; Nussinov, R.; Zhang, J. The Structural Basis of Oncogenic Mutations G12, G13 and Q61 in Small GTPase K-Ras4B. Sci. Rep. 2016, 6, 21949. [Google Scholar] [CrossRef] [PubMed]
- Mishra, A.K.; Lambright, D.G. Small GTPases and Their GAPs. Biopolymers 2016, 105, 431–448. [Google Scholar] [CrossRef] [PubMed]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, N.; Bourne, P.E. The protein data bank. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef]
- Scheffzek, K.; Ahmadian, M.R.; Kabsch, W.; Wiesmuller, L.; Lautwein, A.; Schmitz, F.; Wittinghofer, A. The Ras-RasGAP Complex: Structural Basis for GTPase Activation and its Loss in Oncogenic Ras Mutants. Science 1997, 277, 333–338. [Google Scholar] [CrossRef]
- Glennon, T.M.; Villà, J.; Warshel, A. How Does GAP Catalyze the GTPase Reaction of Ras?: A Computer Simulation Study. Biochemistry 2000, 39, 9641–9651. [Google Scholar] [CrossRef]
- Prasad, B.R.; Plotnikov, N.V.; Lameira, J.; Warshel, A. Quantitative Exploration of the Molecular Origin of the Activation of GTPase. Proc. Natl. Acad. Sci. USA 2013, 110, 20509–20514. [Google Scholar] [CrossRef]
- Carvalho, A.T.P.; Szeler, K.; Vavitsas, K.; Åqvist, J.; Kamerlin, S.C.L. Modeling the Mechanisms of Biological GTP Hydrolysis. Arch. Biochem. Biophys. 2015, 582, 80–90. [Google Scholar] [CrossRef] [PubMed]
- Calixto, A.R.; Moreira, C.; Pabis, A.; Kötting, C.; Gerwert, K.; Rudack, T.; Kamerlin, S.C.L. GTP Hydrolysis Without an Active Site Base: A Unifying Mechanism for Ras and Related GTPases. J. Am. Chem. Soc. 2019, 141, 10684–10701. [Google Scholar] [CrossRef]
- Calixto, A.R.; Moreira, C.; Kamerlin, S.C.L. Recent Advances in Understanding Biological GTP Hydrolysis through Molecular Simulation. ACS Omega 2020, 5, 4380–4385. [Google Scholar] [CrossRef]
- Kotting, C.; Blessenohl, M.; Suveyzdis, Y.; Goody, R.S.; Wittinghofer, A.; Gerwert, K. A Phosphoryl Transfer Intermediate in the GTPase Reaction of Ras in Complex with its GTPase-Activating Protein. Proc. Natl. Acad. Sci. USA 2006, 103, 13911–13916. [Google Scholar] [CrossRef] [PubMed]
- te Heesen, H.; Gerwert, K.; Schlitter, J. Role of the Arginine Finger in Ras.RasGAP Revealed by QM/MM Calculations. FEBS Lett. 2007, 581, 5677–5684. [Google Scholar] [CrossRef]
- Kötting, C.; Kallenbach, A.; Suveyzdis, Y.; Wittinghofer, A.; Gerwert, K. The GAP Arginine Finger Movement into the Catalytic Site of Ras Increases the Activation Entropy. Proc. Natl. Acad. Sci. USA 2008, 105, 6260–6265. [Google Scholar] [CrossRef] [PubMed]
- Rudack, T.; Xia, F.; Schlitter, J.; Kötting, C.; Gerwert, K. Ras and GTPase-Activating Protein (GAP) Drive GTP into a Precatalytic State as Revealed by Combining FTIR and Biomolecular Simulations. Proc. Natl. Acad. Sci. USA 2012, 109, 15295–15300. [Google Scholar] [CrossRef]
- Nagy, G.N.; Suardíaz, R.; Lopata, A.; Ozohanics, O.; Vékey, K.; Brooks, B.R.; Leveles, I.; Tóth, J.; Vértessy, B.G.; Rosta, E. Structural Characterization of Arginine Fingers: Identification of an Arginine Finger for the Pyrophosphatase DUTPases. J. Am. Chem. Soc. 2016, 138, 15035–15045. [Google Scholar] [CrossRef]
- Grigorenko, B.L.; Nemukhin, A.V.; Topol, I.A.; Cachau, R.E.; Burt, S.K. QM/MM Modeling the Ras−GAP Catalyzed Hydrolysis of Guanosine Triphosphate. Proteins Struct. Funct. Genet. 2005, 60, 495–503. [Google Scholar] [CrossRef] [PubMed]
- Grigorenko, B.L.; Nemukhin, A.V.; Shadrina, M.S.; Topol, I.A.; Burt, S.K. Mechanisms of Guanosine Triphosphate Hydrolysis by Ras and Ras-GAP Proteins as Rationalized by Ab Initio QM/MM Simulations. Proteins Struct. Funct. Genet. 2007, 66, 456–466. [Google Scholar] [CrossRef]
- Khrenova, M.G.; Grigorenko, B.L.; Kolomeisky, A.B.; Nemukhin, A.V. Hydrolysis of Guanosine Triphosphate (GTP) by the Ras·GAP Protein Complex: Reaction Mechanism and Kinetic Scheme. J. Phys. Chem. B 2015, 119, 12838–12845. [Google Scholar] [CrossRef]
- Grigorenko, B.L.; Kots, E.D.; Nemukhin, A.V. Diversity of Mechanisms in Ras–GAP Catalysis of Guanosine Triphosphate Hydrolysis Revealed by Molecular Modeling. Org. Biomol. Chem. 2019, 17, 4879–4891. [Google Scholar] [CrossRef]
- Cavalli, A.; Carloni, P. Enzymatic GTP Hydrolysis: Insights from an Ab Initio Molecular Dynamics Study. J. Am. Chem. Soc. 2002, 124, 3763–3768. [Google Scholar] [CrossRef]
- Rabara, D.; Tran, T.H.; Dharmaiah, S.; Stephens, R.M.; McCormick, F.; Simanshu, D.K. Holderfield. Proc. Natl. Acad. Sci. USA 2019, 116, 22122–22131. [Google Scholar] [CrossRef]
- Phillips, R.A.; Hunter, J.L.; Eccleston, J.F.; Webb, M.R. The Mechanism of Ras GTPase Activation by Neurofibromin. Biochemistry 2003, 42, 3956–3965. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Zhu, X.; Shim, J.; Lopes, P.E.M.; Mittal, J.; Feig, M.; MacKerell, A.D. Optimization of the Additive CHARMM All-Atom Protein Force Field Targeting Improved Sampling of the Backbone ϕ, ψ and Side-Chain χ1 and χ2 Dihedral Angles. J. Chem. Theory Comput. 2012, 8, 3257–3273. [Google Scholar] [CrossRef] [PubMed]
- Yu, W.; He, X.; Vanommeslaeghe, K.; MacKerell, A.D. Extension of the CHARMM general force field to sulfonyl-containing compounds and its utility in biomolecular simulations. J. Comp. Chem. 2012, 33, 2451–2468. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.C.; Hardy, D.J.; Maia, J.D.C.; Stone, J.E.; Ribeiro, J.V.; Bernardi, R.C.; Buch, R.; Fiorin, G.; Hénin, J.; Jiang, W.; et al. Scalable Molecular Dynamics on CPU and GPU Architectures with NAMD. J. Chem. Phys. 2020, 153, 044130. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef]
- Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the damping function in dispersion corrected density functional theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Melo, M.C.R.; Bernardi, R.C.; Rudack, T.; Scheurer, M.; Riplinger, C.; Phillips, J.C.; Maia, J.D.C.; Rocha, G.B.; Ribeiro, J.V.; Stone, J.E.; et al. NAMD Goes Quantum: An Integrative Suite for Hybrid Simulations. Nat. Methods 2018, 15, 351–354. [Google Scholar] [CrossRef]
- Seritan, S.; Bannwarth, C.; Fales, B.S.; Hohenstein, E.G.; Isborn, C.M.; KokkilaSchumacher, S.I.L.; Li, X.; Liu, F.; Luehr, N.; Snyder, J.W., Jr.; et al. Terachem: A graphical processing unit-accelerated electronic structure package for large-scale ab initio molecular dynamics. WIREs Comput. Mol. Sci. 2021, 11, e1494. [Google Scholar] [CrossRef]
- Khrenova, M.G.; Polyakov, I.V.; Nemukhin, A.V. Molecular Dynamics of Enzyme-Substrate Complexes in Guanosine Trifosphate-Binding Proteins. Rus. J. Phys. Chem. B 2022, 16, 455–460. [Google Scholar] [CrossRef]
- Kästner, J.; Thiel, W. Bridging the Gap between Thermodynamic Integration and Umbrella Sampling Provides a Novel Analysis Method: “Umbrella Integration”. J. Chem. Phys. 2005, 123, 144104. [Google Scholar] [CrossRef]
- Michaud-Agrawal, N.; Denning, E.J.; Woolf, T.B.; Beckstein, O. MDAnalysis: A Toolkit for the Analysis of Molecular Dynamics Simulations. J. Comput. Chem. 2011, 32, 2319–2327. [Google Scholar] [CrossRef]
- Schweins, T.; Geyer, M.; Scheffzek, K.; Warshel, A.; Kalbitzer, H.R.; Wittinghofer, A. Substrate-Assisted Catalysis as a Mechanism for GTP Hydrolysis of p21ras and other GTP-Binding Proteins. Nat. Struct. Biol. 1995, 2, 36–44. [Google Scholar] [CrossRef]
- Seo, H.S.; Jeong, J.Y.; Nahm, M.Y.; Kim, S.W.; Lee, S.Y.; Bahk, J.D. The effect of pH and various cations on the GTP hydrolysis of rice heterotrimeric G-protein alpha subunit expressed in Escherichia coli. J. Biochem. Mol. Biol. 2003, 36, 196–200. [Google Scholar] [CrossRef]
- Stivers, J.T.; Abeygunawardana, C.; Mildvan, A.S.; Hajipour, G.; Whitman, C.P. 4-Oxalocrotonate Tautomerase: pH Dependence of Catalysis and pKa Values of Active Site Residues. Biochemistry 1996, 35, 814–823. [Google Scholar] [CrossRef] [PubMed]
- Sham, Y.Y.; Chu, Z.T.; Warshel, A. Consistent Calculations of pKa’s of Ionizable Residues in Proteins: Semi-microscopic and Microscopic Approaches. J. Phys. Chem. B 1997, 101, 4458–4472. [Google Scholar] [CrossRef]
- Czerwinski, R.M.; Harris, T.K.; Massiah, M.A.; Mildvan, A.S.; Whitman, C.P. The structural basis for the perturbed pKa of the catalytic base in 4-oxalocrotonate tautomerase: Kinetic and structural effects of mutations of Phe-50. Biochemistry 2001, 40, 1984–1985. [Google Scholar] [CrossRef]
- Repič, M.; Purg, M.; Vianello, R.; Mavri, J. Examining Electrostatic Preorganization in Monoamine Oxidases A and B by Structural Comparison and pKa Calculations. J. Phys. Chem. B 2014, 118, 4326–4332. [Google Scholar] [CrossRef] [PubMed]
- Straatsma, T.P.; Berendsen, H.J.C. Free energy of ionic hydration: Analysis of a thermodynamic integration technique to evaluate free energy differences by molecular dynamics simulations. J. Chem. Phys. 1988, 89, 5876–5886. [Google Scholar] [CrossRef]
- Ȧqvist, J. Ion-water interaction potentials derived from free energy perturbation simulations. J. Phys. Chem. B 1990, 94, 8021–8024. [Google Scholar] [CrossRef]
- Warshel, A. Computer Modelling of Chemical Reactions in Enzymes and Solutions; John Wiley and Sons: New York, NY, USA, 1991. [Google Scholar]
- Bauer, P.; Barrozo, A.; Purg, M.; Amrein, B.A.; Eguerra, M.; Barrie Wilson, P.; Major, D.T.; Åqvist, J.; Kamerlin, S.C.L. Q6: A comprehensive toolkit for empirical valence bond and related free energy calculations. SoftwareX 2018, 7, 388–395. [Google Scholar] [CrossRef]
- Prah, A.; Purg, M.; Stare, J.; Vianello, R.; Mavri, J. How Monoamine Oxidase A Decomposes Serotonin: An Empirical Valence Bond Simulation of the Reactive Step. J. Phys. Chem. B 2020, 124, 8259–8265. [Google Scholar] [CrossRef]
- Zhao, L.N.; Mondal, D.; Warshel, A. Exploring alternative catalytic mechanisms of the Cas9 HNH domain. Proteins 2020, 88, 260–264. [Google Scholar] [CrossRef]
- Mironov, V.A.; Khrenova, M.G.; Lychko, L.A.; Nemukhin, A.V. Computational Characterization of the Chemical Step in the GTP Hydrolysis by Ras-GAP for the Wild-Type and G13V Mutated Ras. Proteins Struct. Funct. Genet. 2015, 83, 1046–1053. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polyakov, I.; Nemukhin, A. Computational Modeling of the Neurofibromin-Stimulated Guanosine Triphosphate Hydrolysis by the KRas Protein. Biophysica 2023, 3, 373-384. https://doi.org/10.3390/biophysica3020025
Polyakov I, Nemukhin A. Computational Modeling of the Neurofibromin-Stimulated Guanosine Triphosphate Hydrolysis by the KRas Protein. Biophysica. 2023; 3(2):373-384. https://doi.org/10.3390/biophysica3020025
Chicago/Turabian StylePolyakov, Igor, and Alexander Nemukhin. 2023. "Computational Modeling of the Neurofibromin-Stimulated Guanosine Triphosphate Hydrolysis by the KRas Protein" Biophysica 3, no. 2: 373-384. https://doi.org/10.3390/biophysica3020025
APA StylePolyakov, I., & Nemukhin, A. (2023). Computational Modeling of the Neurofibromin-Stimulated Guanosine Triphosphate Hydrolysis by the KRas Protein. Biophysica, 3(2), 373-384. https://doi.org/10.3390/biophysica3020025





