Evaluation of Numerical Methods for Dispersion Curve Estimation in Viscoelastic Plates

Abstract

This study aims to evaluate the effectiveness of five analytical and semi-analytical methods for estimating Lamb wave dispersion in viscoelastic plates—the Rayleigh–Lamb solution, the Global Matrix Method (GMM), the Semi-Analytical Finite Element (SAFE) method, the Scaled Boundary Finite Element Method (SBFEM), and the Legendre Polynomial Method (LPM). The Rayleigh–Lamb equations are solved using an optimized Newton–Raphson algorithm, enhancing computational efficiency while maintaining comparable accuracy. The SAFE method exhibited a remarkable balance between computational efficiency and physical accuracy, outperforming SBFEM at high frequencies. For epoxy and high-performance polyethylene (HPPE) plates, the SAFE method and the LPM significantly outperform the GMM in relation to computational efficiency, with errors below $1\%$ for fundamental symmetric and antisymmetric modes across the tested frequency range of 0 to 100 kHz. In addition, the ability of the SAFE method to accurately predict both phase velocity and attenuation in viscous media supports their use in guided-wave-based structural health monitoring applications. Among the investigated approaches, the SAFE method emerges as the most robust and accurate for viscoelastic plates, while the SBFEM and LPM show limitations at higher frequencies. This study provides a quantitative and methodological foundation for selecting and implementing numerical methods for guided wave analysis, emphasizing the dual necessity of physical fidelity and numerical stability.

1. Introduction

Ultrasonic testing represents a cornerstone of non-destructive testing (NDT) methodologies, which are widely employed for the identification of material discontinuities. This technique uses low-range ultrasonic frequency waves to probe the internal structure of materials, allowing for the detection of flaws without compromising the integrity of the inspected specimen [1]. Guided waves propagate along the longitudinal axis of the structure, distributing their energy across the cross-sectional area. This unique propagation characteristic facilitates the efficient and rapid assessment of large-scale components, such as pipelines, plates, and other prismatic geometries, over extended distances [2].

The detection of defects, including surface notches, internal cracks, corrosion-induced material loss, and erosion, is achieved by analyzing wave echoes, which arise from variations in acoustic impedance at the defect interfaces. These impedance changes cause the partial reflection or scattering of guided waves, producing waves that can be correlated with the presence, location, and severity of anomalies. Additionally, guided waves propagate via multiple modes—including symmetric and antisymmetric Lamb modes, as well as shear horizontal modes for the specific case of plates—each with distinct sensitivities to specific defect types and structural features [1]. The selection of an appropriate propagation mode can be tailored to optimize the detection of defects based on critical factors such as the structural geometry, spatial orientation, and depth of the defect, as well as prevailing environmental conditions, including temperature, humidity, and the presence of coatings or surrounding media [3]. Furthermore, the versatility of guided wave techniques extends to their adaptability for complex inspection scenarios, e.g., the ability to assess hard-to-access regions, such as buried pipelines or elevated structural components, thereby reducing inspection time and operational costs.

The analysis and interpretation of guided wave signals constitute a fundamental component of ultrasonic guided wave testing. Guided waves engage in complex interactions with the geometry, material properties, boundary conditions, and any structural discontinuities or defects present [4]. The precise characterization of Lamb wave packets, which includes parameters such as amplitude, dispersion characteristics, attenuation, phase velocity, group velocity, and waveform morphology, is indispensable to ensure robust and reliable inspection results. Nevertheless, the multi-modal propagation and inherent attenuation of these waves in viscoelastic media pose substantial challenges to signal extraction and interpretation, complicating the identification and differentiation of defect-related signatures from background noise or other wave interactions [5].

In greater detail, guided wave propagation enables their interaction with a wide array of structural features, including interfaces, welds, and material heterogeneities, in addition to defects such as cracks, corrosion, or delaminations. These interactions result in phenomena such as reflection, scattering, mode conversion, and energy dissipation, which collectively contribute to the complexity of the received signal. To address this complexity, advanced signal processing techniques, including time–frequency analysis, wavelet transforms, and deconvolution methods, are often employed to unravel overlapping wave modes and isolate defect-induced responses [1,6]. Furthermore, the viscoelastic properties of certain materials introduce frequency-dependent attenuation and dispersion, which alter the shape and amplitude of the wave packet over a distance, further obscuring critical diagnostic information [4]. Thus, accurate signal interpretation requires a comprehensive understanding of wave propagation physics, coupled with robust computational models, in order to predict wave behavior under varying material and environmental conditions. These models, often based on finite element analysis or semi-analytical approaches [7], facilitate the correlation of observed signal features with specific defect characteristics, such as size, orientation, and depth.

In numerous industrial sectors, particularly within the oil and gas industry, protective coatings such as bitumen and various viscoelastic materials are extensively employed to safeguard metallic plates, pipelines, and other structural components against corrosion, chemical degradation, erosion, and harsh environmental conditions [8]. These coatings, while critical for structural longevity, deeply influence the propagation characteristics of ultrasonic guided waves, thereby complicating the non-destructive evaluation of structurally sound systems [9].

Conventional ultrasonic testing methods typically require direct contact between transducers and the surface of the inspected component, requiring the removal of protective coatings—a process that is both impractical and economically demanding. In contrast, guided waves offer a significant advantage by propagating through coated structures without requiring coating removal, as their energy is distributed across the cross-sectional area of the waveguide [1]. This capability enables the efficient and long-range inspection of coated metallic structures, positioning guided wave techniques as a more viable and cost-effective alternative to traditional approaches. However, the presence of lossy coatings introduces significant challenges, as these materials attenuate guided wave signals through viscoelastic damping, whereby wave energy is dissipated as heat. This attenuation reduces the amplitude of the propagating waves, potentially limiting the inspection range and compromising the sensitivity of defect detection [10].

Consequently, a thorough characterization of guided wave attenuation in coated metallic structures is imperative to optimize the inspection process. This characterization involves quantifying the energy loss induced by the viscoelastic properties of the coating [8], which depends on factors such as coating thickness, material composition, frequency of guided waves, and environmental conditions. Advanced methodologies, including experimental measurements and computational modeling (e.g., finite element analysis or dispersion curve analysis [11]), are employed to predict attenuation behavior and identify wave modes that minimize energy loss while maintaining sensitivity to defects. By understanding and mitigating the effects of coating-induced attenuation, the inspection range can be maximized and the reliability of flaw detection can be significantly enhanced. Ongoing research into low-attenuation wave modes, advanced signal processing, and adaptive transducer designs continues to advance the efficacy of guided wave inspections in coated structures, ensuring robust structural health monitoring under challenging industrial conditions [12,13].

Dispersion curves are critical for understanding guided wave propagation in waveguides, providing essential data for non-destructive testing and structural health monitoring. These curves can be derived through multiple methodologies, including experimental approaches [1], analytical techniques [14,15], numerical methods [9,11,16,17,18,19], and semi-analytical frameworks [7,20,21]. Semi-analytical methods are particularly effective for modeling complex materials, such as composites or multilayered structures, and intricate geometries where analytical solutions are difficult to derive. These approaches address numerical complexities and simplify implementation. However, a significant limitation is the challenge of distinguishing between wave modes, aggravated by numerical issues and non-physical solutions resulting from discretization and the choice of approximation functions [21]. We selected analytical and semi-analytical techniques for this study because they are physics-based, computationally efficient, and directly interpretable, in contrast to deep learning or other data-driven models that require large training datasets and may lack generalizability outside their training domain.

Although most studies focus on the elastic approach, the viscoelastic effect due to material damping [22] has received significantly less attention than the elastic case. This is likely due to the challenges in numerically solving the governing equations, which involve complex roots due to material damping, or in experimentally analyzing the phenomenon [8]. Recent studies have introduced advanced formulations to enhance dispersion curve analysis in complex media. For example, Liu et al. [23] presented an open-source implementation of the SAFE method for acousto-elastic and multilayered waveguides, significantly improving accessibility and modeling versatility. Similarly, Wang and Shen [24] proposed a seamlessly integrated framework for simulating guided wave propagation in arbitrarily shaped elastic waveguides, demonstrating high compatibility across geometric configurations. Mekkaoui et al. [25] conducted a detailed comparative analysis of the Semi-Analytical Finite Element (SAFE) method, spectral collocation, and the Dispersion Calculator, highlighting their respective strengths and limitations in handling generally anisotropic multilayered composites. These contributions underscore the growing sophistication of dispersion modeling tools and reinforce the importance of evaluating their applicability to viscoelastic media.

In this study, we aim to assess the effectiveness of various analytical and semi-analytical methods in computing complex wavenumber–frequency pairs in viscoelastic plates, prioritizing the physical reliability of the solutions over computational speed. To this end, the performance of each method is examined in terms of its ability to provide a reliable characterization of Lamb wave propagation in dissipative media. Consequently, emphasis is placed on the ability of each method to resolve dispersion relations within the specified domain of analysis. Software implementations, such as GUIGUW v2.1, Dispersion Box v0.01, and Dispersion Calculator v3.1, are employed to validate numerical methods for dispersion curve estimation, ensuring robust comparisons with analytical solutions. To evaluate the practical performance of these methods, we conduct a comparative analysis of Lamb wave dispersion in two viscoelastic materials commonly used in structural applications—epoxy and high-performance polyethylene (HPPE). The study focuses on predicting phase velocity and attenuation for symmetric and antisymmetric modes over a frequency range according to the thickness of the samples. Accuracy, numerical stability, and computational cost are assessed for each method, providing a foundation for selecting appropriate modeling strategies in guided-wave-based structural health monitoring. Although the computational performance of the methods—measured in terms of execution time—is not directly evaluated in this study, reference will be made to previously published works that have quantitatively addressed this aspect. Additionally, the relative complexity of each approach will be discussed qualitatively. The conclusions drawn from the analysis focus on identifying the most practical methodology in terms of computational simplicity and robustness to capture dispersion behavior. From the authors’ perspective, the ability to compute comprehensive and physically consistent dispersion solutions in viscoelastic plates takes precedence over computational cost.

2. Materials and Methods

This study examines Lamb wave dispersion in viscoelastic plates, comparing analytical and semi-analytical methods for computing dispersion and attenuation characteristics. Analytical approaches, such as the Rayleigh–Lamb equations and Global Matrix Method (GMM), provide exact solutions but face challenges with complex root-finding in viscoelastic cases. Semi-analytical methods, including the Scaled Boundary Finite Element Method (SBFEM), Semi-Analytical Finite Element (SAFE) method, and Legendre Polynomial Method (LPM), mitigate these issues by transforming the problem into manageable eigenvalue systems.

2.1. Viscoelastic Material Model

A hysteretic viscoelastic model with frequency-independent damping is adopted across all methods. The complex longitudinal and shear wave velocities are defined in Equation (1) [26], as follows:

$${\tilde{c}}_L=c_L{\left(1+i{\displaystyle \frac{{\alpha }_L}{2\pi }}\right)}^{-1},{\tilde{c}}_T=c_T{\left(1+i{\displaystyle \frac{{\alpha }_T}{2\pi }}\right)}^{-1},$$

(1)

where $c_L$ and $c_T$ are the bulk velocities; ${\alpha }_L$ and ${\alpha }_T$ are the longitudinal and shear attenuation factors (Nepers per wavelength). These velocities yield the complex modulus $\tilde{E}$, Poisson’s ratio $\tilde{\nu }$, and stiffness matrix $\tilde{\mathbf{D}}$, which encapsulates storage and loss moduli. The complex Young’s modulus, $\tilde{E}$, and Poisson’s ratio, $\tilde{v}$, can be obtained as follows (2):

$$\tilde{E}=\rho {\tilde{c}}_T^2\left({\displaystyle \frac{3{\tilde{c}}_L^2-4{\tilde{c}}_T^2}{{\tilde{c}}_L^2-{\tilde{c}}_T^2}}\right),\tilde{\nu }={\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{\tilde{c}}_L^2-2{\tilde{c}}_T^2}{{\tilde{c}}_L^2-{\tilde{c}}_T^2}}\right).$$

(2)

The attenuation model was applied using constant complex velocities for both longitudinal and shear waves. These coefficients are assumed to be frequency-independent and were selected based on representative values from experimental studies on viscoelastic materials. The complex Lamé constants can be calculated as follows (3):

$$\tilde{\lambda }={\displaystyle \frac{\tilde{E}\tilde{\nu }}{(1+\tilde{\nu })(1-2\tilde{\nu })}},\tilde{\nu }={\displaystyle \frac{\tilde{E}}{2(1+\tilde{\nu })}}.$$

(3)

Alternatively, the velocities can be expressed using Lamé coefficients $\lambda$ and $\mu$ as follows (4):

$${\tilde{c}}_L=\sqrt{{\displaystyle \frac{\lambda +2\mu -i({\lambda }^{\prime }+2{\mu }^{\prime })}{\rho }}},{\tilde{c}}_T=\sqrt{{\displaystyle \frac{\mu -i{\mu }^{\prime }}{\rho }}},$$

(4)

where ${\lambda }^{\prime }$ and ${\mu }^{\prime }$ are the loss components, and $\rho$ is the density.

2.2. Analytical Approaches

The general solution for damped waves is given in Equation (5), as follows:

$$\varphi ,\psi =C_{1,2}{e}^{i(kx-\omega t)}{e}^{-k_{i}x},$$

(5)

where $k=k_r+i{k}_i$, with $k_r$ and $k_i$ denoting the real and imaginary parts of the complex wavenumber, corresponding to propagation and attenuation, respectively, and $C_{1,2}$ are constants. The attenuation is governed by the imaginary component $k_i$, which determines the exponential decay of the wave amplitude in space.

2.2.1. Rayleigh–Lamb Equations for Viscoelastic Plates

For viscoelastic plates, Lamb wave dispersion is governed by the complex Rayleigh–Lamb equations [1] for symmetric and antisymmetric modes, as shown in Equation (6), as follows:

$$\begin{array}{cc}\hfill {\displaystyle \frac{tan\left(q^{*}h\right)}{tan\left(p^{*}h\right)}}+{\displaystyle \frac{4p^{*}{q}^{*}{k}^2}{{(q^{*2}-k^2)}^2}}& =0,\left(\mathrm{symmetric}\right)\hfill \\ \hfill {\displaystyle \frac{tan\left(q^{*}h\right)}{tan\left(p^{*}h\right)}}+{\displaystyle \frac{{(q^{*2}-k^2)}^2}{4p^{*}{q}^{*}{k}^2}}& =0,\left(\mathrm{antisymmetric}\right)\hfill \end{array}$$

(6)

where $h=d/2$ is half the plate thickness, k is the wavenumber, and the complex velocities ${\tilde{c}}_L$ and ${\tilde{c}}_T$ yield the complex wavenumbers $p^{*}$ and $q^{*}$, given in Equation (7), as follows:

$$p^{*2}={\left({\displaystyle \frac{\omega }{{\tilde{c}}_L}}\right)}^2-k^2,q^{*2}={\left({\displaystyle \frac{\omega }{{\tilde{c}}_T}}\right)}^2-k^2.$$

(7)

These equations are reformulated into a dispersion function $D(k,\omega )$ in Equation (8), as follows:

$$D(k,\omega )=\left\{\begin{array}{c}sin\left(p^{*}h\right)cos\left(q^{*}h\right){(p^{*2}-k^2)}^2+4p^{*}{q}^{*}{k}^{2}cos\left(p^{*}h\right)sin\left(q^{*}h\right),\left(\mathrm{symmetric}\right),\hfill \\ sin\left(q^{*}h\right)cos\left(p^{*}h\right)4p^{*}{q}^{*}{k}^2+{(q^{*2}-k^2)}^{2}cos\left(q^{*}h\right)sin\left(p^{*}h\right),\left(\mathrm{antisymmetric}\right).\hfill \end{array}\right.$$

(8)

2.2.2. Global Matrix Method

The GMM is an analytical approach that assembles interface and boundary conditions into a single matrix derived from elasticity theory. By employing analytical solutions within individual layers and directly enforcing continuity conditions, the GMM avoids spatial discretization in single-layer homogeneous viscoelastic plates, as well as avoiding numerical instability issues that are inherent in recursive methods like the Transfer Matrix Method [10]. However, solving the resulting global matrix equation requires computationally intensive 2D root-search algorithms (e.g., across frequency–wavenumber domains or the complex wavenumber plane) to identify propagating or leaky modes. These challenges are exacerbated in complex media, such as anisotropic or viscoelastic materials, where isolating closely spaced modes or resolving energy-leaking modes with complex wavenumbers demands high-resolution parameter scans. While the GMM offers theoretical rigor and stability, its practical implementation often incurs significant computational costs.

2.3. Mathematical Formulation

The 3D Navier equations govern wave motion in a viscoelastic medium. Under the assumption of harmonic time dependence $e^{-i\omega t}$ and plane wave propagation in the x-direction, the displacement field reduces to a two-dimensional problem in the $xz$-plane. The displacement components can be expressed as shown in Equation (9), as follows:

$$\mathbf{u}(x,z,t)=\mathbf{U}\left(z\right)e^{i(kx-\omega t)},$$

(9)

where k is the complex wavenumber (encoding both phase velocity and attenuation), $\omega$ is the angular frequency, and $\mathbf{U}\left(z\right)$ represents the mode shape along the thickness (z) direction. By substituting this into the Navier equations, the problem is converted into a first-order state-space ordinary differential Equation (10), as follows:

$${\displaystyle \frac{d\mathbf{Y}\left(z\right)}{dz}}=\mathbf{Q}(k,\omega )\mathbf{Y}\left(z\right),$$

(10)

where $\mathbf{Y}\left(z\right)={[u_x,u_z,{\sigma }_{xz},{\sigma }_{zz}]}^T$ is the state vector (containing displacements and stresses), and $\mathbf{Q}(k,\omega )$ is a $4\times 4$ system matrix for isotropic layers. For viscoelastic materials, the elastic moduli in $\mathbf{Q}$ are replaced by complex-valued quantities to account for energy dissipation. At the free surfaces ($z=\pm h$), the following traction-free boundary conditions are imposed:

$${\sigma }_{xz}={\sigma }_{zz}=0.$$

Enforcing these conditions leads to a nonlinear eigenvalue problem in k for each $\omega$, which can be solved by scanning the complex wavenumber plane. Valid roots (wavenumbers) are identified using numerical techniques such as contour integration or the Newton–Raphson method. Similar to the Rayleigh–Lamb equations for plate waves, the GMM serves as a critical benchmark for validating semi-analytical methods (e.g., SAFE and LPM).

2.4. Root-Finding for Complex Wavenumbers

In this study, the Newton–Raphson scheme is employed due to its simplicity and efficiency, iteratively solving for the complex roots $k\in \mathbb{C}$ of the Rayleigh–Lamb equations for a given real-valued angular frequency $\omega \in \mathbb{R}$, within a specified frequency range $[{\omega }_1,{\omega }_2]$. Real-valued roots correspond to non-attenuating wave propagation, purely imaginary roots represent evanescent (non-propagating) modes, and complex roots indicate attenuated propagating waves, which are crucial for modeling viscoelastic plates.

The iterative scheme is defined by Equation (11), as follows:

$$k_{n+1}=k_n-{\displaystyle \frac{D(k_n,\omega )}{D^{\prime }(k_n,\omega )}},$$

(11)

where the derivative $D^{\prime }(k,\omega )$ is approximated using centered finite differences, as shown in Equation (12), as follows:

$$D^{\prime }(k,\omega )\approx {\displaystyle \frac{D(k+h,\omega )-D(k-h,\omega )}{2h}}.$$

(12)

Convergence is achieved when the stopping criterion $|k_{n+1}-k_n|<\epsilon$ is satisfied. The root-finding process is conducted in the complex wavenumber plane, constrained to the physically meaningful domain where $\mathrm{Re}\left[k\right]\ge 0$ and $\mathrm{Im}\left[k\right]\le 0$.

Alternative approaches for root-finding in complex dispersion problems include the winding number method [9], global optimization strategies [22], Bairstow’s method [27], and homotopy continuation techniques [28].

To distinguish physical from non-physical roots, the algorithms apply multiple filters, whereby roots must exhibit continuity across frequency steps, non-negative attenuation (i.e., $\Im \left(k\right)\ge 0$), and positive phase velocity.

2.5. Semi-Analytical Methods

Semi-analytical methods combine analytical formulations with numerical discretization to approximate guided wave propagation problems as eigenvalue systems. These approaches reduce computational complexity compared to fully analytical root-finding methods while maintaining physical interpretability.

2.5.1. Semi-Analytical Finite Element Method

The SAFE method discretizes the waveguide’s cross-sectional thickness using 1D isoparametric elements. The displacement field within an element $\left(e\right)$ is expressed as shown in Equation (13) [4], as follows:

$${\mathbf{u}}^{\left(e\right)}(x,y,z,t)=\mathbf{N}(y,z){\mathbf{q}}^{\left(e\right)}{e}^{i(kx-\omega t)},$$

(13)

where $\mathbf{N}(y,z)$ is the shape function matrix and ${\mathbf{q}}^{\left(e\right)}$ are nodal displacements.

The corresponding strain field is obtained as shown in Equation (14), as follows:

$${ϵ}^{\left(e\right)}=\left({\mathbf{B}}_1+ik{\mathbf{B}}_2\right){\mathbf{q}}^{\left(e\right)}{e}^{i(kx-\omega t)},$$

(14)

with ${\mathbf{B}}_1=\partial \mathbf{N}/\partial y$ and ${\mathbf{B}}_2=\mathbf{N}$.

Substituting into Hamilton’s principle yields the quadratic eigenvalue problem, as shown in Equation (15), as follows:

$$\left({\mathbf{K}}_1+ik{\mathbf{K}}_2+k^2{\mathbf{K}}_3-{\omega }^2\mathbf{M}\right)\mathbf{U}=0,$$

(15)

where the element matrices are defined as shown in Equation (16), as follows:

$$\begin{array}{cc}\hfill {\mathbf{K}}_1^{\left(e\right)}& ={\int }_{{\Omega }_e}{\mathbf{B}}_1^T\tilde{\mathbf{D}}{\mathbf{B}}_{1}d{\Omega }_e,{\mathbf{K}}_2^{\left(e\right)}={\int }_{{\Omega }_e}\left({\mathbf{B}}_1^T\tilde{\mathbf{D}}{\mathbf{B}}_2-{\mathbf{B}}_2^T\tilde{\mathbf{D}}{\mathbf{B}}_1\right)d{\Omega }_e,\hfill \\ \hfill {\mathbf{K}}_3^{\left(e\right)}& ={\int }_{{\Omega }_e}{\mathbf{B}}_2^T\tilde{\mathbf{D}}{\mathbf{B}}_{2}d{\Omega }_e,{\mathbf{M}}^{\left(e\right)}={\int }_{{\Omega }_e}{\mathbf{N}}^T\rho \mathbf{N}d{\Omega }_e,\hfill \end{array}$$

(16)

where $\tilde{\mathbf{D}}$ denotes the complex-valued constitutive matrix for viscoelasticity and $\rho$ is the material density.

2.5.2. Scaled Boundary Finite Element Method

The SBFEM discretizes the waveguide boundary along the thickness using high-order spectral elements with Gauss–Lobatto–Legendre (GLL) nodes. For a layer parameterized by $\eta \in [-1,1]$, the displacement field is given as follows [29]:

$$\mathbf{u}(\eta ,z,t)=\mathbf{N}\left(\eta \right)\mathbf{U}{e}^{i(kz-\omega t)},$$

(17)

where $\mathbf{N}\left(\eta \right)$ are Lagrange polynomial shape functions.

The strain–displacement relation is obtained as follows:

$$ϵ(z,\eta )={\mathbf{B}}_1{\mathbf{u}}_{,z}\left(z\right)+{\mathbf{B}}_2{\mathbf{u}}_{,\eta }\left(z\right),$$

(18)

with ${\mathbf{B}}_1={\mathbf{b}}_1\mathbf{N}$ and ${\mathbf{B}}_2={\displaystyle \frac{1}{y_{,\eta }}}{\mathbf{b}}_2{\mathbf{N}}_{,\eta }$, where $y_{,\eta }$ is the Jacobian determinant $\left|\mathbf{J}\right|$.

Substituting the strain relation into the variational formulation yields the following quadratic eigenvalue problem:

$$\left(k^2{\mathbf{E}}_0+k({\mathbf{E}}_1^T-{\mathbf{E}}_1)-{\mathbf{E}}_2+{\omega }^2{\mathbf{M}}_0\right)\mathbf{U}=0,$$

(19)

where the matrices are defined as follows:

$$\begin{array}{cc}\hfill {\mathbf{E}}_0& ={\int }_{-1}^1{\mathbf{B}}_1^T\tilde{\mathbf{D}}{\mathbf{B}}_1\left|\mathbf{J}\right|d\eta ,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill {\mathbf{E}}_1& ={\int }_{-1}^1{\mathbf{B}}_2^T\tilde{\mathbf{D}}{\mathbf{B}}_1\left|\mathbf{J}\right|d\eta ,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill {\mathbf{E}}_2& ={\int }_{-1}^1{\mathbf{B}}_2^T\tilde{\mathbf{D}}{\mathbf{B}}_2\left|\mathbf{J}\right|d\eta ,\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill {\mathbf{M}}_0& ={\int }_{-1}^1{\mathbf{N}}^T\rho \mathbf{N}\left|\mathbf{J}\right|d\eta .\hfill \end{array}$$

(23)

Equations (17)–(23) define the SBFEM formulation for viscoelastic waveguides. Due to its boundary-only discretization, the SBFEM is especially effective in modeling media with geometric or material singularities.

2.5.3. Legendre Polynomial Method

The LPM approximates the through-thickness displacement field using orthogonal Legendre polynomials $P_l\left(r\right)$. The displacement field in the i-th layer is given as follows:

$${\mathbf{u}}^{\left(i\right)}(z,t)=\sum _{l=0}^{N_l-1}{\mathbf{U}}_l^{\left(i\right)}{P}_l\left(r\right)e^{i(kx-\omega t)},$$

(24)

where the coordinate transformation

$$r={\displaystyle \frac{2}{h_i}}(z-z_m^i)$$

(25)

maps the physical coordinate z in layer i to the standard interval $r\in [-1,1]$, with $h_i$ being the thickness and $z_m^i$ being the center of the i-th layer.

Substituting Equation (24) into the weak form of the governing elastodynamic equations, followed by Galerkin projection, leads to the following quadratic eigenvalue problem:

$$\left({\mathbf{H}}_1{k}^2+ik{\mathbf{F}}_1+\mathbf{G}\right)\mathbf{X}=0,$$

(26)

where ${\mathbf{H}}_1$, ${\mathbf{F}}_1$, and $\mathbf{G}$ are system matrices that include the complex viscoelastic constitutive matrix $\tilde{\mathbf{D}}$, which captures the damping behavior of the material.

The LPM achieves spectral convergence, which means that it can reach high accuracy with relatively few basis functions. In practice, it requires approximately three times fewer degrees of freedom than the SAFE method for similar levels of accuracy [11].

2.6. Comparative Analysis of Analytical and Semi-Analytical Methods for Dispersion Curve Computation in Viscoelastic Isotropic Plates

Analytical techniques such as the Rayleigh–Lamb equations and the Global Matrix Method (GMM) provide exact solutions for wave dispersion but require complex root-finding procedures, especially in the context of viscoelastic plates. In contrast, semi-analytical methods—including SBFEM, SAFE, and LPM—transform the problem into an eigenvalue formulation, enhancing computational efficiency.

Each of these semi-analytical approaches computes the complex wavenumber k, from which the phase velocity $c_{\mathrm{ph}}=\omega /\mathrm{Re}\left(k\right)$ and attenuation $\mathrm{Im}\left(k\right)$ can be extracted. Among them, the SBFEM is noted for its efficiency, the SAFE method is noted for its flexibility, and the LPM is valued for its speed. However, the SBFEM’s high-order spectral elements may overestimate attenuation in viscoelastic media due to the high order of the basis function.

However, the numerical solution of the eigenvalue problem for Lamb waves in viscoelastic plates often introduces spurious or non-physical solutions that must be filtered to ensure physical consistency. Discretization techniques—such as those based on finite elements, spectral elements, or polynomial expansions—can generate artificial eigenvalues that do not correspond to real wave modes. In particular, high-order approximations, as employed in the LPM or SBFEM, may lead to extraneous solutions due to the truncation of the functional basis.

Moreover, semi-analytical formulations inherently couple multiple wave types (e.g., propagating, evanescent, symmetric, and antisymmetric), which can result in numerical solutions that violate expected symmetry or decay behavior. For instance, evanescent modes should exhibit exponential decay, but numerical errors may produce growing modes that are physically inadmissible.

Additionally, formulations such as the LPM may involve rank-deficient matrices (e.g., ${\mathbf{H}}_1$ and ${\mathbf{F}}_1$), leading to linearly dependent or redundant solutions that fail to satisfy essential boundary conditions. Finally, semi-analytical methods only approximate stress-free and interface boundary conditions. This approximation can be imperfect—particularly for constraints such as ${\sigma }_{13}={\sigma }_{23}={\sigma }_{33}=0$—resulting in solutions that do not align with the physical problem.

Thus, root filtering based on criteria such as decay behavior, physical symmetry, and numerical stability is essential. Roots are typically classified into propagating ($\mathrm{Re}\left(k\right)\ne 0,\mathrm{Im}\left(k\right)\le 0$), evanescent ($\mathrm{Re}\left(k\right)=0,\mathrm{Im}\left(k\right)<0$), and non-physical types.

2.6.1. Computational Performance

The computational efficiency of the primary methods (GMM, SAFE, and LPM) has been benchmarked in [11], with SBFEM performance being evaluated in [3]. Execution time per frequency for isotropic plates was used as the key metric.

The GMM, which requires a two-dimensional root search in the complex wavenumber plane, is computationally expensive. For a $2000\times 2000$ point grid, the GMM required 88.63 s per frequency (C/E Case 1). Despite its exactness and unconditional stability, the computational burden renders the GMM impractical for routine evaluations.

In contrast, the SAFE method and LPM offer substantial gains. The SAFE method requires 0.007 s (5 elements/layer) to 0.043 s (15 elements/layer), while the LPM achieves 0.002 s at order 5 and 0.013 s at order 15. The LPM’s efficiency stems from its smaller global matrices and simpler implementation. For instance, the SAFE method at 10 elements/layer (0.016 s) is over three orders of magnitude faster than the GMM.

The SBFEM further reduces computational cost by using spectral elements with Gauss–Lobatto–Legendre quadrature. With fewer nodes per wavelength (e.g., one high-order element through the thickness), the SBFEM demonstrates thickness-independent execution time, unlike the SAFE method, which scales quadratically with thickness. For plates up to 50 mm thick, the SBFEM maintains accuracy while outperforming the SAFE method in relation to speed and convergence.

2.6.2. Implementation Complexity

From an implementation standpoint, the GMM requires full matrix assembly with the exact enforcement of boundary conditions, but its dependence on complex root-finding presents challenges. The SAFE method simplifies matrix construction for isotropic materials but becomes more complex with viscoelastic damping and finer mesh discretization.

The LPM approximates the displacement field with orthogonal polynomials, simplifying coefficient matrix construction, but requires an additional filtering step to eliminate non-physical modes. The SBFEM, by discretizing only the boundary, reduces the problem size significantly and offers a more straightforward implementation—particularly in isotropic configurations.

In conclusion, for isotropic viscoelastic plates, the SAFE method and LPM significantly outperform the GMM in computational efficiency while maintaining comparable accuracy, as will be demonstrated in the next section. The LPM offers an implementation advantage due to its simplicity and smaller matrices. The SBFEM, leveraging spectral discretization, exhibits favorable convergence and computational time scaling, particularly for thick plates. While the GMM remains the benchmark for accuracy, its practical use is limited by computational demands. Thus, the SAFE method, LPM, and SBFEM are more suitable for structural health monitoring (SHM) applications requiring fast and accurate dispersion curve evaluations.

In semi-analytical methods such as the SAFE method and SBFEM, the discretization scheme and the choice of basis functions can lead to the appearance of spurious or non-physical modes. To address this, our implementation includes a physical filtering criterion to distinguish valid guided wave modes from numerical artifacts.

In practice, all numerical schemes can yield spurious or non-physical solutions, particularly in viscoelastic plates where damping complicates root-finding. To ensure consistency, we applied standard admissibility checks (positive phase velocity, non-negative attenuation, and traction-free boundary conditions) together with method-specific filters. A summary of these criteria and their implementation across Rayleigh–Lamb, the GMM, the SAFE method, the SBFEM, and the LPM is provided in

Table 1. Comparison of spurious solution tendencies and filtering techniques across methods.

Method	Spurious Solutions	Filtering Technique	Notes
Rayleigh–Lamb (reference)	Few, exact roots	Sign checks and domain constraint	Gold standard for validation
GMM	High due to root search	$k_r/k_i$ ratio filter, symmetry filters	Missing solutions
SAFE	Low	Attenuation filter	Robust for viscoelastic plates
SBFEM	Moderate	Remove redundant roots, enforce decay and domain constraint	May overestimate attenuation
LPM	High (truncation)	$k_r/k_i$ ratio filter, smoothness	Missing solutions

.

3. Results

To evaluate the performance of the described numerical methods (GMM, SAFE, SBFEM, and LPM), various implementations are selected based on their underlying numerical methods, and their results are compared against those obtained from the Rayleigh–Lamb equations solved using the Newton–Raphson approach. For the two materials considered—high-performance polyethylene (HPPE) and epoxy—the attenuation parameters used in the viscoelastic model were selected from the literature and applied using the same frequency-independent complex velocity formulation described in Section 2.

The first specimen under investigation is a viscoelastic, high-damping, isotropic HPPE plate with stress-free boundaries. The material has been extensively studied in [4,5] using DISPERSE v2.0 software, which is based on the Semi-analytical Propagating Bulk Wave (SPBW) method.

The physical and geometric properties of the HPPE plate are as follows: density $\rho =953{\mathrm{kg}/\mathrm{m}}^3$, thickness $h=12.7\mathrm{mm}$, longitudinal wave velocity $c_L=2344\mathrm{m}/\mathrm{s}$, shear wave velocity $c_T=953\mathrm{m}/\mathrm{s}$, longitudinal wave attenuation ${\eta }_L=0.055\mathrm{Np}$/wavelength, and shear wave attenuation ${\eta }_T=0.286\mathrm{Np}$/wavelength. Dispersion analyses are conducted over a frequency range of 0–250 kHz in order to capture the behavior of guided wave modes in this specific viscoelastic material for the assessed thickness.

The HPPE material dispersion curves are compared with the results obtained using GUIGUW [30]. GUIGUW employs the SAFE method, which enables the modeling of waveguides with arbitrary cross-sections. The SAFE method discretizes the cross-section of the waveguide into finite elements, facilitating the analysis of guided waves in complex geometries. In contrast, the wave propagation direction is solved analytically, enhancing computational efficiency. In 2022, Orta et al. [11] introduced ’The Dispersion Box’, which is a Matlab-based software that is capable of computing dispersion curves for multilayered, viscoelastic, and orthotropic plates. This software supports various methods, including the GMM, the Stiffness Matrix Method (SMM), the Hybrid Compliance–Stiffness Matrix Method (HCSMM), the SAFE method, and the LPM. This software has implemented the complex root search algorithm developed by Kowalczyk in [22]. Furthermore, Armin Huber developed the software ’Dispersion Calculator’ in [19]. This tool efficiently calculates dispersion curves for isotropic plates using the Rayleigh–Lamb equations and root-finding based on the Bisection Method for the case of isotropic plates.

3.1. Comparative Analysis of Dispersion Methods

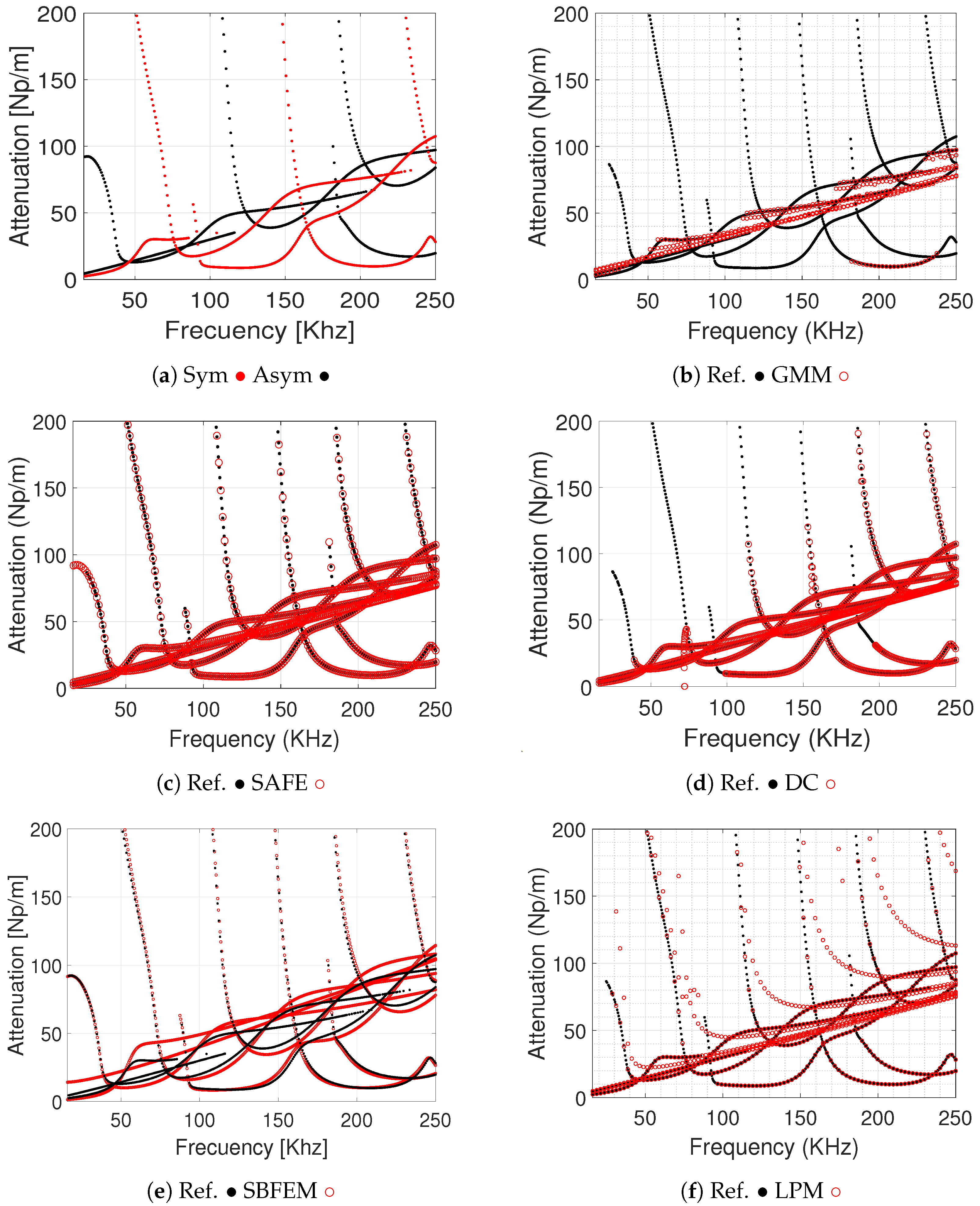
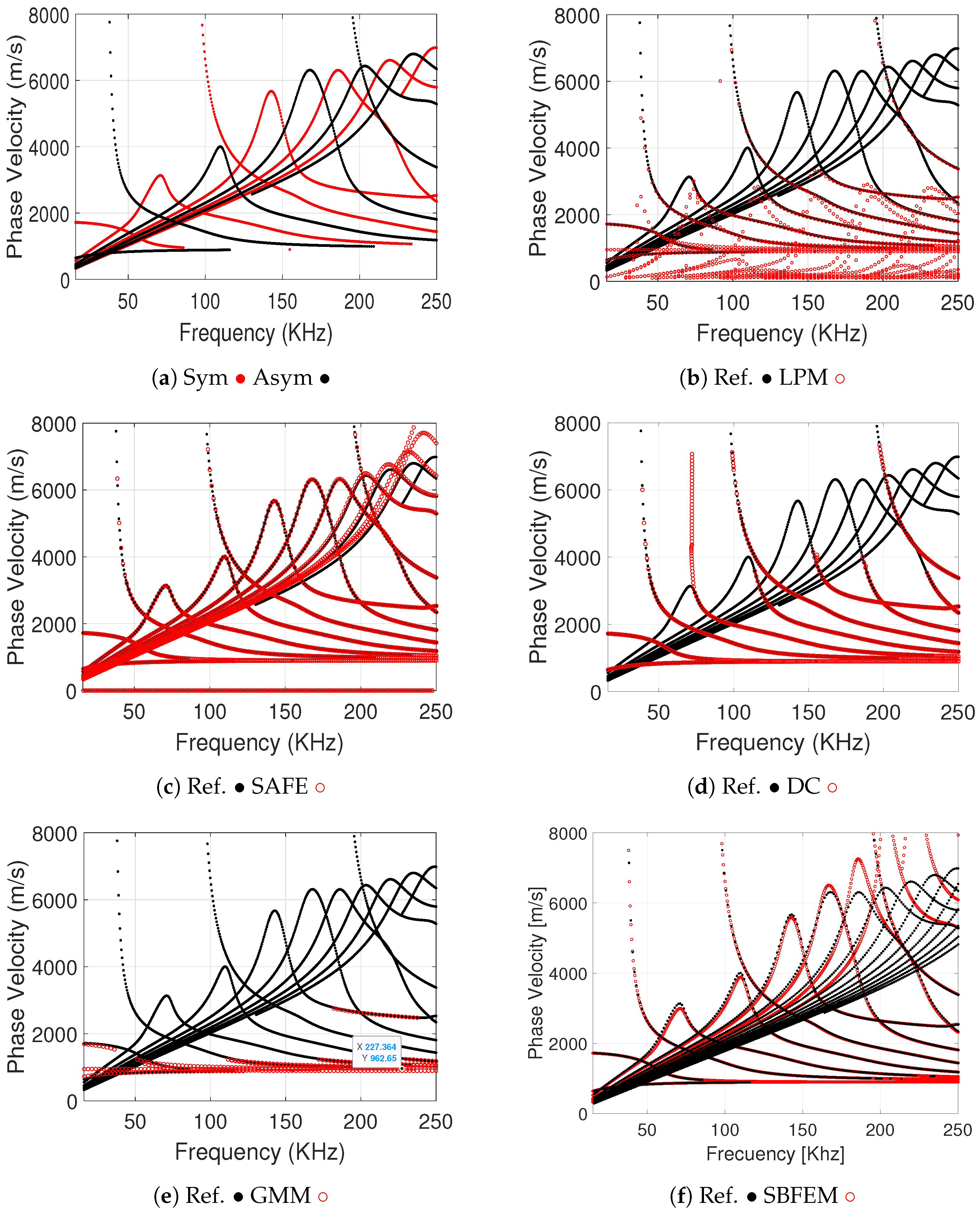
In Figure 1, Figure 2 and Figure 3, we compare the Rayleigh–Lamb reference solution for wave dispersion, implemented by the authors using the Newton–Raphson complex root-finding approach, with five numerical methods implemented in various software tools. These methods are (1) the GMM with 500 elements and the LPM with polynomial order 56, both implemented in Dispersion Box; (2) the SAFE method using 28 isoparametric elements in GUIGUW; (3) the Rayleigh–Lamb equations solved via the Bisection Method in Dispersion Calculator; and (4) the SBFEM with Lagrange polynomials of order 26, implemented by the authors. The number of elements and the polynomial order were optimized through multiple runs in order to ensure solution convergence. These comparisons evaluate three key metrics—wavenumber dispersion ($k\left(\omega \right)$), attenuation ($\alpha \left(\omega \right)$), and phase velocity ($v_{\varphi }\left(\omega \right)$). Only the Rayleigh–Lamb reference solution and Dispersion Calculator inherently distinguish between symmetric (S) and antisymmetric (A) propagation modes, while the other methods require post-processing to separate these mode families.

Following the comparison of five numerical methods, Figure 1 and Figure 2 show that the Rayleigh–Lamb, SAFE, and SBFEM schemes demonstrate superior accuracy in identifying propagation modes characterized by low wavenumbers (i.e., long wavelengths) and highly attenuative regions, corresponding to low real and high imaginary parts of the complex wavenumber $k\in \mathbb{C}$, compared to the GMM, LPM, and Dispersion Calculator (DC). The semi-analytical approaches of the SAFE method and SBFEM, combined with the iterative root-finding of the Rayleigh–Lamb scheme, enable the effective resolution of complex roots without requiring adaptive grid refinement. In contrast, DC, despite using Rayleigh–Lamb equations, misses many roots due to its inability to adjust the solution search domain.

In Figure 1, the Rayleigh–Lamb, SAFE, and SBFEM schemes accurately capture low-k (long wavelength) branches. The GMM and LPM exhibit spurious oscillations at high frequencies due to root-finding sensitivity; finally, Disperse Calculator omits heavily attenuated modes (low real part) because of its filtering threshold.

With respect to the attenuation curves, as shown in Figure 2, the SAFE method and SBFEM correctly predict the peak attenuation near cutoff frequencies. The GMM underestimates attenuation for $f>150$ kHz, likely from insufficient grid resolution, while the LPM shows non-physical negative attenuation regions, indicating numerical artifacts.

Finally, in the case of the phase velocity, the previous results of $k\left(\omega \right)$ show that all methods converge to the Rayleigh–Lamb curve at low frequencies (<100 kHz). At higher frequencies, only the SAFE method and the Newton–Raphson Rayleigh–Lamb schemes maintain accuracy; others deviate by up to 10%. The SBFEM remains stable across the full range, demonstrating its robustness for viscoelastic damping.

In contrast, as verified in the Dispersion Box, the postprocessing stage imposes a threshold on the $k_r/k_i$ ratio (Imaginary filter), which limits the obtained solutions. In particular, when an inappropriate value is used, the solutions fail to identify attenuation regions and low-wavenumber values. As a result, these methods fail to estimate certain phase velocity values, as evidenced in Figure 3b,c,f. Here, the reference scheme effectively identifies most phase velocity values across the analyzed frequency range, closely matching the phase velocity curves established by Bartoli [4] and Chan [5], which are omitted from this article for brevity. The missing modes observed in Figure 3e result from the limitations of the GMM formulation under high attenuation conditions. Specifically, the root-finding algorithm struggles to identify weak or highly damped modes in the presence of strong viscoelastic effects, as is the case for the epoxy plate. This behavior is expected and depends on the root-finding strategy, particularly the search domain and filtering criteria. While the GMM provides physically consistent results, its computational cost increases in complex or highly damped media due to the need for dense root-search grids. To improve efficiency, several techniques can be applied, such as adaptive meshing of the search domain, use of surrogate models to estimate initial root positions, and reduced-order formulations that maintain modal accuracy while lowering computational demand. These strategies are particularly useful when resolving energy-leaking modes with complex wavenumbers or closely spaced branches in viscoelastic and anisotropic materials.

A second material, epoxy, is used to evaluate the performance of the schemes studied, focusing on the SAFE and SBFEM approaches, which were previously shown to excel in low-wavenumber and attenuative regions, as demonstrated in Figure 1, Figure 2 and Figure 3. The epoxy material is characterized according to [8], with the following properties: density $\rho =1390{\mathrm{kg}/\mathrm{m}}^3$, thickness $h=2\mathrm{mm}$, longitudinal wave velocity $c_L=2748.7\mathrm{m}/\mathrm{s}$, shear wave velocity $c_T=1378.7\mathrm{m}/\mathrm{s}$, longitudinal wave attenuation ${\eta }_L=0.0867\mathrm{Np}/\mathrm{wavelength}$, and shear wave attenuation ${\eta }_T=0.1636\mathrm{Np}/\mathrm{wavelength}$. For this new specimen, 24 isoparametric elements were used in the SAFE scheme, and a 21th-order polynomial was employed in the SBFEM approach. The assessment involves comparing predicted wavenumber dispersion and attenuation to experimental data from [8]. The two materials—High-Performance Polyethylene (HPPE) and epoxy—differ significantly, whereby HPPE is lighter with higher damping, while epoxy is denser with lower damping, especially in shear wave attenuation; this makes them suitable for testing the methodology across diverse viscoelastic materials.

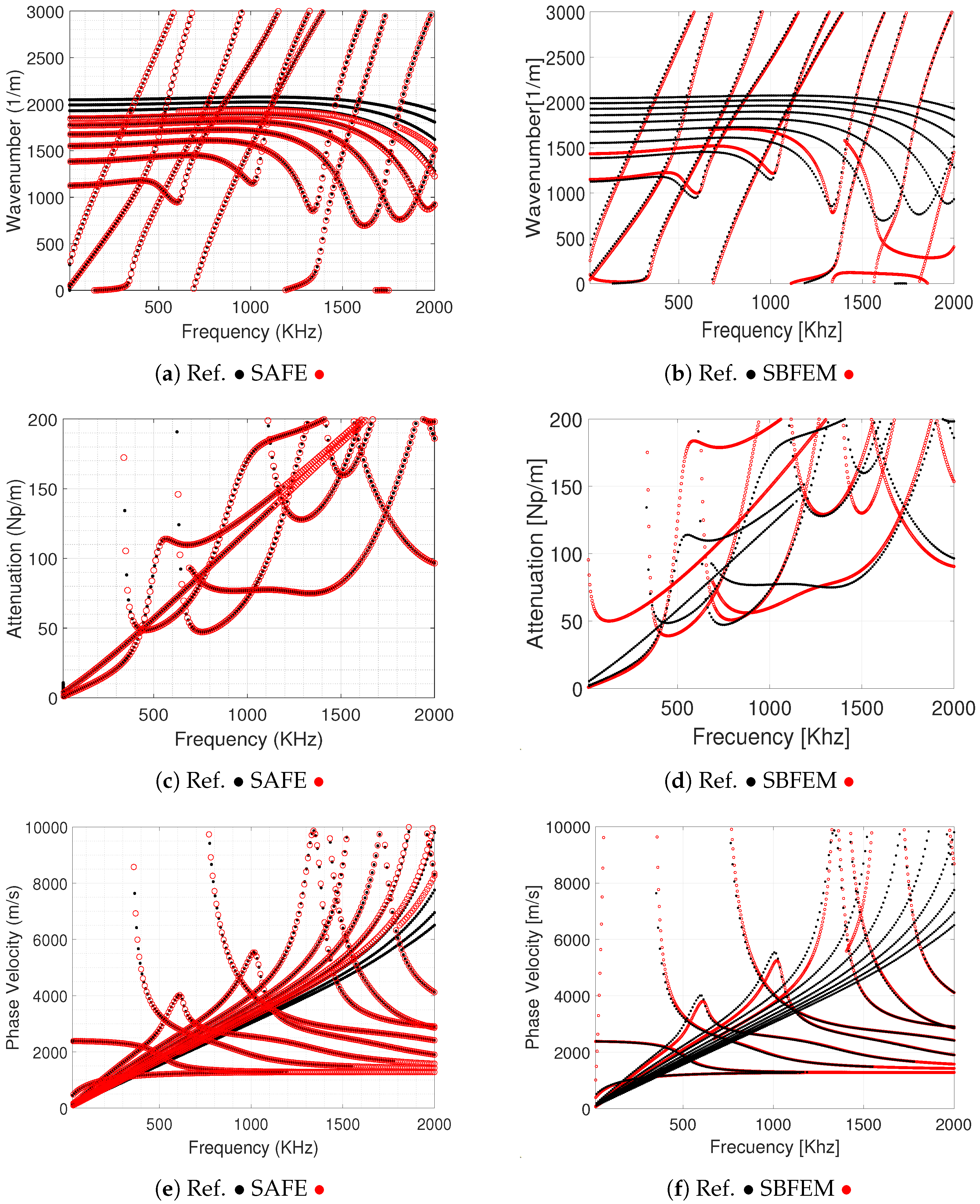
Figure 4a,b depict the real wavenumber ($k_r$) versus frequency for the SAFE method and SBFEM, respectively. Both methods exhibit excellent agreement with the Rayleigh–Lamb solution at low frequencies ($f<150$ kHz), accurately resolving long-wavelength modes ($k_r<500$ rad/m). However, minor deviations emerge at higher frequencies ($f>200$ kHz), where the SBFEM slightly underestimates $k_r$ by $\sim 1.5\%$ compared to the SAFE method, which maintains closer alignment with the analytical reference. The attenuation curves ($\alpha =\mathrm{Im}\left(k\right)$) in Figure 4c,d reveal different behaviors between the SAFE method and SBFEM. Both methods successfully capture the attenuation peaks near cutoff frequencies (e.g., at $f\approx 320$ kHz and $f\approx 620$ kHz), aligning with the Rayleigh–Lamb predictions. However, the SBFEM marginally overestimates attenuation ($\Delta \alpha \approx 70$ Np/m) in the 500–1000 kHz range, whereas the SAFE method maintains tighter agreement. Comparisons of phase velocity ($c_{\mathrm{ph}}=\omega /k_r$) in Figure 4e,f demonstrate that the SAFE method and SBFEM converge to the Rayleigh–Lamb solution throughout the frequency spectrum. At low frequencies ($f<100$ kHz), discrepancies are negligible (<0.3%), confirming the reliability of the methods for long-wavelength inspections. At higher frequencies ($f>250$ kHz), the SBFEM exhibits a gradual velocity underestimation (∼2%), whereas the SAFE method sustains sub-1% error.

Although the SAFE method achieves high accuracy and SBFEM estimation is relatively closer to the analytical scheme, their computational efficiencies differ. As noted previously, the SBFEM’s spectral elements require fewer degrees of freedom than the SAFE method’s isoparametric meshes, reducing matrix sizes and accelerating eigenvalue computations. For the epoxy plate (thickness $h=2$ mm), the execution time of the SBFEM is ∼40% lower than that of the SAFE method. This efficiency advantage becomes more pronounced in thicker or multilayered structures, where the SBFEM’s boundary discretization scales favorably.

The analysis of Figure 4 corroborates the efficacy of the SAFE method and SBFEM in modeling guided wave dispersion in viscoelastic plates. The key findings include the following: Both methods closely match Rayleigh–Lamb solutions, with the SAFE method outperforming the SBFEM at high frequencies because of reduced numerical dispersion. The minor overestimation by the SBFEM highlights the impact of the use of high-order spectral elements in the discretization on damping characterization. Neither method produces non-physical modes, affirming the utility of eigenvalue filtering in semi-analytical frameworks.

For applications requiring high-frequency resolution or computational efficiency, the SAFE method emerges as the preferred choice. The SBFEM remains a versatile alternative, particularly for complex geometries requiring cross-sectional meshing. The Rayleigh–Lamb solution retains its role as the gold standard for validation, although its computational cost limits its practicality in iterative industrial applications. The results for epoxy and HPPE plates demonstrate excellent agreement between the numerical schemes (SBFEM and SAFE) and the analytical Rayleigh–Lamb solutions, with errors below $1\%$ for fundamental symmetric ($S_0$) and antisymmetric ($A_0$) modes across the tested frequency range of 0 to 100 kHz. As frequency increases, higher-order modes emerge and both schemes maintain high fidelity, converging with Rayleigh–Lamb predictions within 0.5% error. Figure 4 confirms the reliability of the SBFEM and SAFE method for modeling guided wave propagation in viscoelastic plates, confirming their suitability for applications in non-destructive evaluation and structural health monitoring, where accurate wave dispersion modeling is critical.

3.2. Analysis of Performance

The superior performance of the SAFE method comes from several factors. First, the uniform isoparametric discretization of its elements provides a dense and consistent mesh across the plate thickness, which effectively captures the exponential decay of attenuative modes. With a sufficient number of elements, the SAFE method offers high spatial resolution and minimizes discretization errors.

Regarding numerical stability, the high-order polynomials used in the SBFEM may lead to rank-deficient matrices, which can produce non-physical solutions and overestimate the imaginary part of the wavenumber $k_i$.

In contrast, for viscoelastic wave fields in highly attenuative materials (e.g., HPPE with ${\eta }_T=0.286\mathrm{Np}/\mathrm{wavelength}$), spectral elements struggle to model the rapid decay of waves accurately, as their basis functions are optimized for smooth, slowly varying solutions. In such cases, isoparametric elements are more effective in resolving steep spatial gradients.

At higher frequencies, where short-wavelength modes become dominant, both the SAFE method and SBFEM are more sensitive to discretization. The accuracy of the SAFE method can be improved by increasing the number of through-thickness elements or by using higher-order isoparametric functions to better resolve steep displacement gradients. For the SBFEM, attenuation bias may be reduced by employing adaptive polynomial orders and optimized spectral bases, which mitigate rank deficiencies. These refinements have been shown in the literature to improve the resolution of short-wavelength branches, thereby enhancing the accuracy of both methods in the high-frequency regime.

It should also be noted that mesh discretization in the SAFE method and the polynomial order in the SBFEM directly influence the computed phase velocity at high frequencies, since short-wavelength modes require finer spatial resolution to avoid dispersion errors. Time-step resolution is not applicable here because the study was carried out entirely in the frequency domain. Material dispersion, however, is inherently included through the viscoelastic constitutive model, and its effects on phase velocity are consistently reflected in the results.

In the present study, the SAFE method employed a uniform through-thickness mesh, while the SBFEM used a fixed spectral order. These configurations are sufficient for general accuracy but at higher frequencies, they contribute to numerical dispersion in the SAFE method and a tendency to overestimate damping in the SBFEM. Future applications can address these limitations by adopting adaptive mesh refinement or higher-order elements in the SAFE method, as well as by implementing adaptive spectral order or optimized basis functions in the SBFEM. Such strategies have been shown to improve the resolution of short-wavelength modes and enhance high-frequency performance.

In the SBFEM, very-high polynomial orders can lead to nearly linearly dependent basis functions, causing rank deficiency in the matrix of the system. This introduces redundant eigenvalues that distort the imaginary part of the wavenumber, thereby reducing the accuracy of attenuation ($k_i$) predictions. The Dispersion Calculator mitigates such issues with continuity and sign checks, while the LPM applies a $k_r/k_i$ ratio and smoothness filter to suppress spurious branches.

4. Conclusions

This comparative study has evaluated the performance of five numerical methods and a reference analytical scheme to estimate dispersion curves in viscoelastic plates. The results allow us to draw several key conclusions regarding the accuracy, stability, and suitability of each method for modeling guided wave propagation in dissipative media.

The complex Rayleigh–Lamb dispersion formulation, solved using an optimized Newton–Raphson algorithm, demonstrated a superior capability of identifying highly attenuative modes, particularly in complex domain regions characterized by components of a low real wave and a high imaginary wavenumber. This approach served as a reliable reference against which numerical schemes were evaluated.

Among the numerical methods evaluated, the Semi-Analytical Finite Element (SAFE) method exhibited a remarkable balance between computational efficiency and physical accuracy. Its uniform isoparametric discretization across the thickness of the plate provided sufficient resolution to capture evanescent behaviors, resulting in errors below $1\%$ in both the wavenumber and frequency for configurations with at least 28 elements. This makes the SAFE method a robust candidate for the industrial-scale characterization of the propagation of guided waves in viscoelastic media.

The Scaled Boundary Finite Element Method (SBFEM) also showed generally stable behavior, but its use of high-order polynomial bases occasionally resulted in rank-deficient matrices, leading to non-physical solutions and overestimated attenuation values ($k_i$). Additionally, methods such as the Local Polynomial Method (LPM) and the Dispersion Calculator were found to omit modes with strong attenuation due to internal filtering criteria based on the $k_r/k_i$ ratio. While computationally efficient, this limitation could impair their reliability when analyzing high-loss materials such as reinforced polymers or multilayered composites.

The comparative results indicate that the SAFE method offers the most robust performance across the frequency spectrum, the SBFEM provides useful accuracy but may overestimate attenuation, and the LPM is computationally efficient yet requires strong filtering. These findings not only benchmark the relative strengths and weaknesses of the methods but also provide future researchers with clear directions, such as employing adaptive refinement in the SAFE method or optimized basis functions in the SBFEM to improve high-frequency accuracy.

Finally, the ability of the SAFE method and SBFEM to accurately predict both phase velocity and attenuation in viscoelastic environments supports their use in guided-wave-based structural health monitoring applications. Their performance in modeling frequency-dependent damping mechanisms ensures the reliable characterization of wave behavior in realistic scenarios. Although the present study focuses on mathematical formulations, its outcomes have direct engineering relevance. Reliable dispersion predictions are fundamental for guided-wave-based NDT and SHM, as well as advanced material characterization. By benchmarking multiple methods, this study provides practical guidance on which approaches are most suitable for engineering applications involving viscoelastic plates.

In summary, this study provides a quantitative and methodological foundation for selecting and implementing numerical dispersion techniques in viscoelastic wave analysis, emphasizing the dual necessity of physical fidelity and numerical stability.