Regularities of Brittle Fracture Zone Formation in the Zone of Dyke Around Horizontal Mine Workings
Abstract
1. Introduction
2. Materials and Methods
- Initial stress initialization: The in situ stress field was applied to the undisturbed rock mass.
- Excavation simulation: Sequential removal of elements corresponding to the advancing excavation.
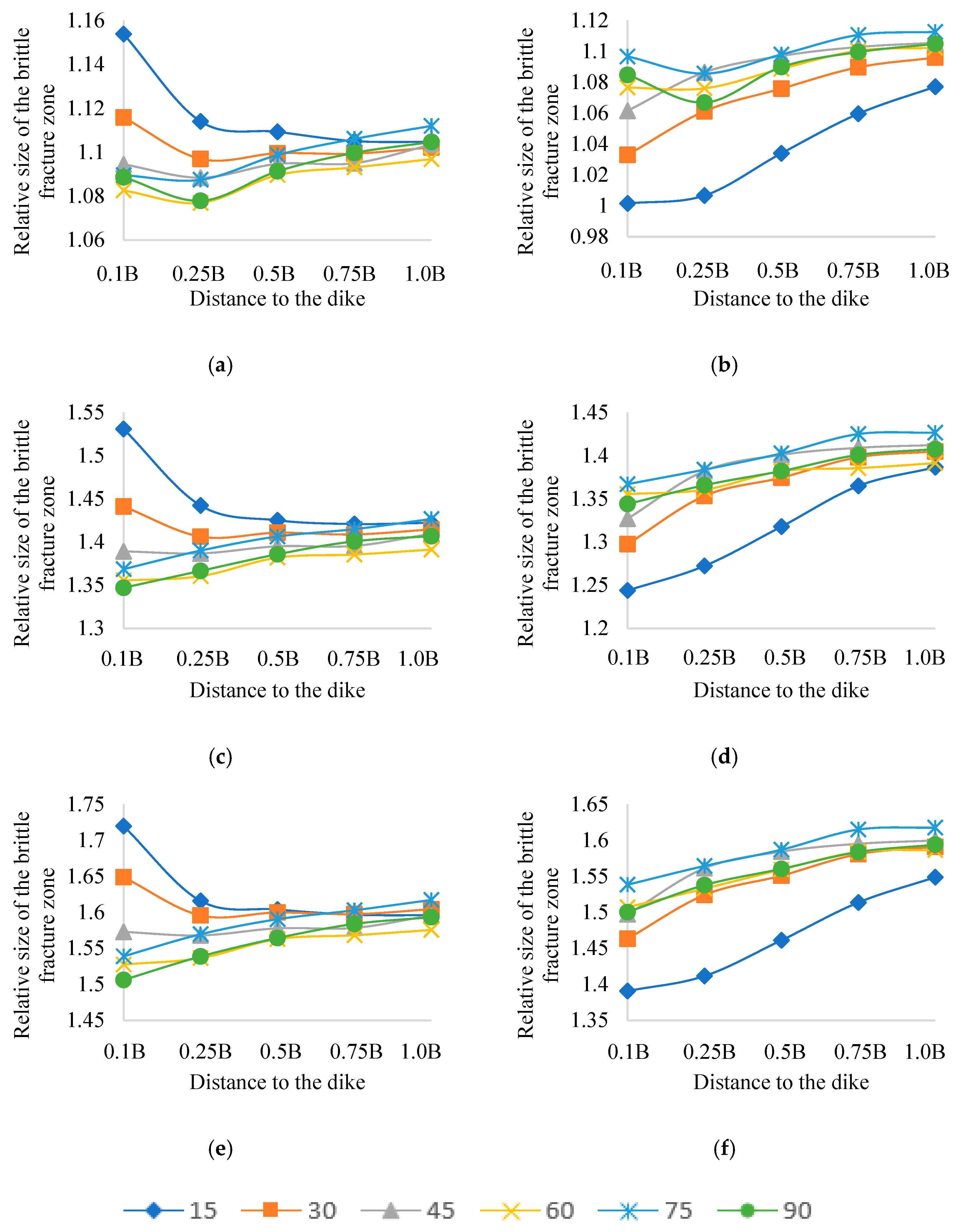
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhang, J.; Kuang, M.; Zhang, Y.; Feng, T. Evaluation and analysis of the causes of a landslide and treatment measures during the excavation of a tunnel through a soil-rock interface. Eng. Fail. Anal. 2021, 130, 105784. [Google Scholar] [CrossRef]
- Do, N.A.; Dias, D.; Dinh, V.D.; Tran, T.T.; Dao, V.C.; Dao, V.D.; Nguyen, P.N. Behavior of noncircular tunnels excavated in stratified rock masses—Case of underground coal mines. J. Rock Mech. Geotech. Eng. 2019, 11, 99–110. [Google Scholar] [CrossRef]
- Yin, X.; Zhang, A.; Zhang, X. A Review of the Influence of Microscopic Characteristics on the Progressively Brittle Failure of Foliated Rocks Subjected to Compression Loading. Geotech. Geol. Eng. 2022, 40, 1663–1673. [Google Scholar] [CrossRef]
- Belyakov, N.A.; Emelyanov, I.A. Inclusion of rock mass fracturing in determination of in situ stress state by overcoring using multi-component displacement sensor. MIAB Min. Inf. Anal. Bull. 2024, 145–164. (In Russian) [Google Scholar] [CrossRef]
- Besimbayeva, O.G.; Khmyrova, E.N.; Tutanova, M.S.; Flindt, N.; Sharafutdinov, R.R. Modern data analysis technologies used for geomechanical monitoring. Review. Kompleks. Ispolz. Miner. Syra = Complex Use Miner. Resour. 2023, 326, 5–15. [Google Scholar] [CrossRef]
- Falmagne, V.; Doucet, C.; Yergeau, D.; St-Onge, N.; Durham, C.; Jacobs, R.; Pyy, A.; Heller, A. Seismic response of large-scale to medium-scale geological structures in deep mines. Deep Mining 2024. In Proceedings of the 10th International Conference on Deep and High Stress Mining, Australian Centre for Geomechanics, Perth, Australia, 24–26 September 2024; Andrieux, P., Cumming-Potvin, D., Eds.; pp. 153–170. [Google Scholar] [CrossRef]
- Thiele, S.T.; Cruden, A.R.; Micklethwaite, S. Failure of load-bearing dyke networks as a trigger for volcanic edifice collapse. Commun. Earth Environ. 2023, 4, 382. [Google Scholar] [CrossRef]
- Thiele, S.T.; Cruden, A.R.; Zhang, X.; Micklethwaite, S.; Matchan, E.L. Reactivation of Magma Pathways: Insights from Field Observations, Geochronology, Geomechanical Tests, and Numerical Models. J. Geophys. Res. Solid Earth 2021, 126, e2020JB021477. [Google Scholar] [CrossRef]
- Bakhtavar, E.; Abdollahisharif, J.; Mohammadi, D. Analysis and improvement of blasting operation in porphyry, diorite dyke, and trachyte Sungun zones: In-situ investigations. Int. J. Min. Geo-Eng. 2022, 56, 19–24. [Google Scholar] [CrossRef]
- Gay, N.C. In-situ stress measurements in Southern Africa. Tectonophysics 1975, 29, 447–459. [Google Scholar] [CrossRef]
- Sudhishna, P.N.R.L.; Mondal, S.; Mondal, T.K.; Das, G. Study of restricted fractures in veins and dykes, and associated stress distribution. J. Earth Syst. Sci. 2024, 133, 31. [Google Scholar] [CrossRef]
- Alekseev, A. Face deformation in tunneling in the zone of structural and mechanical heterogeneity. Min. Inf. Anal. Bull. 2018, 12, 48–56. [Google Scholar] [CrossRef]
- Basalaeva, P.; Kuranov, A.D. Influence of dip angle of lithologically nonuniform interburden on horizontal mine opening stability during driving. MIAB Min. Inf. Anal. Bull. 2024, 3, 17–30. (In Russian) [Google Scholar] [CrossRef]
- Pospehov, G.B.; Norova, L.P.; Izotova, V.A. Comparing the methods of grain size analysis of gypsum-containing sulfuric acid wastes neutralized with limestone. Sustain. Dev. Mt. Territ. 2024, 16, 1729–1742. (In Russian) [Google Scholar] [CrossRef]
- Belikov, A.A.; Beliakov, N.A. Method of numerical modeling of rheological processes on the contour of single mine working. MIAB Min. Inf. Anal. Bull. 2024, 1, 94–108. [Google Scholar] [CrossRef]
- Yang, L.; Sharafisafa, M.; Shen, L. On the fracture mechanism of rock-like materials with interbedded hard-soft layers under Brazilian tests. Theor. Appl. Fract. Mech. 2021, 116, 103102. [Google Scholar] [CrossRef]
- Wang, J.; Deng, X.; Cao, W. Numerical Analysis on the Stability of Layered Surrounding Rock Tunnel Under the Conditions of Different Inclination Angle and Thickness. Am. J. Traffic Transp. Eng. 2019, 4, 67–74. [Google Scholar] [CrossRef][Green Version]
- Sun, X.; Chen, F.; Miao, C.; Song, P.; Li, G.; Zhao, C.; Xia, X. Physical modeling of deformation failure mechanism of surrounding rocks for the deep-buried tunnel in soft rock strata during the excavation. Tunn. Undergr. Space Technol. 2018, 74, 247–261. [Google Scholar] [CrossRef]
- Rong, P.; Zuo, Y.; Lin, J.; Chen, Q.; Zheng, L.; Jin, K. Study of mechanical properties and failure characteristics of combined rock mass with weak interlayer. Géoméch. Geophys. Geo-Energy Geo-Resour. 2022, 8, 89. [Google Scholar] [CrossRef]
- Nunes, M.; Meguid, M. A study on the effects of overlying soil strata on the stresses developing in a tunnel lining. Tunn. Undergr. Space Technol. 2009, 24, 716–722. [Google Scholar] [CrossRef]
- Protosenya, A.G.; Veselova, A.V.; Kotikov, D.A. Assessment of stress concentration in neighborhood of karst voids during ore mining. MIAB Min. Inf. Anal. Bull. 2024, 2, 5–22. (In Russian) [Google Scholar] [CrossRef]
- Zhang, D.-M.; Huang, H.-W.; Hu, Q.-F.; Jiang, F. Influence of multi-layered soil formation on shield tunnel lining behavior. Tunn. Undergr. Space Technol. 2015, 47, 123–135. [Google Scholar] [CrossRef]
- Karasev, M.A.; Petrushin, V.V. Methodological issues in determination of initial parameters for modeling deformation of rock salt as a polycrystalline discrete medium. MIAB Min. Inf. Anal. Bull. 2024, 9, 47–64. [Google Scholar] [CrossRef]
- Kozyrev, A.A.; Enyutin, A.N.; Maltsev, V.A.; Semenova, I.E. Procedure for regional prediction of rockburst hazard and rock mass behavior, and for selection of technical solutions towards safe and efficient mining. In Innovatsionnyy Potentsial Kol’skoy Nauki [The Innovative Potential of the Kola Science]; Izd-vo KNTS RAN: Apatity, Russia, 2005; pp. 52–56. [Google Scholar]
- Trushko, V.L.; Baeva, E.K.; Blinov, A.A. Experimental Investigation on the Mechanical Properties of the Frozen Rocks at the Yamal Peninsula, Russian Arctic. Eng 2025, 6, 76. [Google Scholar] [CrossRef]
- Wawersik, W.; Fairhurst, C. A study of brittle rock fracture in laboratory compression experiments. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1970, 7, 561–575. [Google Scholar] [CrossRef]
- Kota, V.K.; Juneja, A.; Bajpai, R.K.; Srivastava, P. Stability Assessment of Cross-Tunnels in Jointed Rock Using Discrete Element Method. In Proceedings of the Indian Geotechnical Conference, Surat, India, 19–21 December 2019; Lecture Notes in Civil Engineering. Patel, S., Solanki, C.H., Reddy, K.R., Shukla, S.K., Eds.; Springer: Singapore, 2021; Volume 137. [Google Scholar] [CrossRef]
- Griffith, A.A. VI. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. Lond. Ser. A Contain. Pap. A Math. Or Phys. Character 1921, 221, 582–593. [Google Scholar]
- Irwin, G.R. Analysis of Stresses and Strains Near the End of a Crack Traversing a Plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Hoek, E.; Brown, E.T. The Hoek–Brown failure criterion and GSI–2018 edition. J. Rock Mech. Geotech. Eng. 2019, 11, 445–463. [Google Scholar] [CrossRef]
- Hoek, E.; Carranza-Torres, C.; Corkum, B. Hoek-Brown failure criterion—2002 edition. In Proceedings of the Fifth North American Rock Mechanics Symposium, Toronto, ON, Canada, 7–10 July 2002; Volume 1, pp. 267–273. [Google Scholar]
- Verbilo, P.E.; Iovlev, G.A.; Belyakov, N.A. Parameter selection for the Hoek–Brown model with softening of rock mass based on laboratory experiments on rock samples and discrete numerical simulations of jointed rock mass. MIAB Min. Inf. Anal. Bull. 2025, 2, 57–77. (In Russian) [Google Scholar] [CrossRef]
- Suresh, S. Fatigue of Materials, 2nd ed.; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- Anderson, T.L.; Anderson, T.L. Fracture Mechanics: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Lisjak, A.; Liu, Q.; Zhao, Q.; Mahabadi, O.K.; Grasselli, G. Numerical simulation of acoustic emission in brittle rocks by two-dimensional finite-discrete element analysis. Geophys. J. Int. 2013, 195, 423–443. [Google Scholar] [CrossRef]
- Trushko, V.L.; Rozanov, A.O.; Saitgaleev, M.M.; Petrov, D.N.; Ilinov, M.D.; Karmanskii, D.A.; Selikhov, A.A. Acoustic emission criteria for analyzing the process of rock destruction and evaluating the formation of fractured reservoirs at great depths. J. Min. Inst. 2024, 269, 848–858, EDN EGOJFL. [Google Scholar]
- Bieniawski, Z. Determining rock mass deformability: Experience from case histories. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1978, 15, 237–247. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, Q.; Li, Y.; Pan, Z.; Liu, B. Hydraulic Fracture Vertical Propagation Mechanism in Interlayered Brittle Shale Formations: An Experimental Investigation. Rock Mech. Rock Eng. 2023, 56, 199–220. [Google Scholar] [CrossRef]
- Joughin, W. Managing geotechnical uncertainty and risk in mining. J. S. Afr. Inst. Min. Met. 2023, 123, 435–444. [Google Scholar] [CrossRef]
- Karasev, M.; Astapenka, T. Assessment of the Influence of Formation Conditions of Embankments and Spoil Heaps on Their Stability When Dumped on Clay-Salt Slurries. Eng 2025, 6, 2. [Google Scholar] [CrossRef]
- Garashchenko, Z.; Teremetskaya, V.; Gabov, V. Mining of coal pillars using unified excavation modules with local faces. Min. Ind. J. (Gorn. Promishlennost) 2024, 5S, 151–157. (In Russian) [Google Scholar] [CrossRef]
- Bažant, Z.P.; Zi, G. Microplane constitutive model for porous isotropic rocks. Int. J. Numer. Anal. Methods Géoméch. 2002, 27, 25–47. [Google Scholar] [CrossRef]
- Loseva, E.; Lozovsky, I.; Zhostkov, R. Refining Low Strain Pile Integrity Testing for Minor Flaw Detection with Complex Wavelet Transform. Civ. Eng. J. 2024, 10, 3194–3207. [Google Scholar] [CrossRef]
- Protosenya, A.G.; Kumov, V.V. Effect of soil body structure of mixed-type tunnel face on shape and size of subsidence trough on ground surface. Min. Informational Anal. Bull. 2024, 4, 5–21. (In Russian) [Google Scholar] [CrossRef]
- Chen, J.; Gu, S.; Zhou, X. The effects of weak interlayers on the dynamic mechanical properties and failure behaviours of rocks: A combined numerical and experimental analysis. Int. J. Impact Eng. 2023, 180, 104680. [Google Scholar] [CrossRef]
- Collins, I. A systematic procedure for constructing critical state models in three dimensions. Int. J. Solids Struct. 2003, 40, 4379–4397. [Google Scholar] [CrossRef]
- Vermeer, P.A.; De Borst, R. Non-Associated Plasticity for Soils, Concrete and Rock. In Physics of Dry Granular Media; NATO ASI Series; Herrmann, H.J., Hovi, J.P., Luding, S., Eds.; Springer: Dordrecht, The Netherlands, 1998; Volume 350, pp. 163–196. [Google Scholar]
- Cai, M.; Kaiser, P.; Tasaka, Y.; Minami, M. Determination of residual strength parameters of jointed rock masses using the GSI system. Int. J. Rock Mech. Min. Sci. 2007, 44, 247–265. [Google Scholar] [CrossRef]
- Alejano, L.; Alonso, E.; Rodríguez-Dono, A.; Fernández-Manín, G. Application of the convergence-confinement method to tunnels in rock masses exhibiting Hoek–Brown strain-softening behaviour. Int. J. Rock Mech. Min. Sci. 2010, 47, 150–160. [Google Scholar] [CrossRef]
- Hajiabdolmajid, V.; Kaiser, P.; Martin, C. Modelling brittle failure of rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 731–741. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, D.; Xu, H.; Zhao, T.; Hou, W. Effect of interlayer mechanical properties on initiation and propagation of hydraulic fracturing in laminated coal reservoirs. J. Pet. Sci. Eng. 2022, 208, 109381. [Google Scholar] [CrossRef]
- Cai, W.; Deng, J.; Feng, Y.; Lin, H.; Tanko, M.O.; Ma, C. Developing a geomechanics-modeling based method for lost circulation risk assessment: A case study in Bohai Bay, China. J. Pet. Sci. Eng. 2022, 210, 110045. [Google Scholar] [CrossRef]
- Huang, Y.; Yin, X.; Yan, E.-C.; Li, Y.; Song, K. Brittle Failure Modes and Mechanisms in Foliated Rock Under Uniaxial Compression: Laboratory Testing and Particle Flow Modeling. Geotech. Geol. Eng. 2024, 42, 2861–2880. [Google Scholar] [CrossRef]
- Zhao, H.; Deng, B.; Zhang, D.; Li, M.; Song, Z. Influence of weak interlayer thickness on mechanical response and failure behavior of rock under true triaxial stress condition. Eng. Fail. Anal. 2024, 162, 108419. [Google Scholar] [CrossRef]
- Cong, R.; Yang, R.; Li, G.; Huang, Z.; Gong, Y.; Jing, M.; Lu, M. Geomechanical Properties of Thinly Interbedded Rocks Based on Micro- and Macro-Scale Measurements. Rock Mech. Rock Eng. 2023, 56, 5657–5675. [Google Scholar] [CrossRef]
- Wang, H.; Zhao, W.; Sun, D.; Guo, B. Mohr-Coulomb Yield Criterion in Rock Plastic Mechanics. Chin. J. Geophys. 2012, 55, 733–741. [Google Scholar] [CrossRef]
- Gospodarikov, A.P.; Trofimov, A.V.; Kirkin, A.P. Evaluation of deformation characteristics of brittle rocks beyond the limit of strength in the mode of uniaxial servohydraulic loading. J. Min. Inst. 2022, 256, 539–548. [Google Scholar] [CrossRef]
- Korchak, P. Geomechanical prediction of growth of brittle fracture zones in the vicinity of underground excavations in over-stress rock mass. Min. Informational Anal. Bull. 2021, 5, 85–98. [Google Scholar] [CrossRef]
- Renani, H.R.; Martin, C.D. Cohesion degradation and friction mobilization in brittle failure of rocks. Int. J. Rock Mech. Min. Sci. 2018, 106, 1–13. [Google Scholar] [CrossRef]
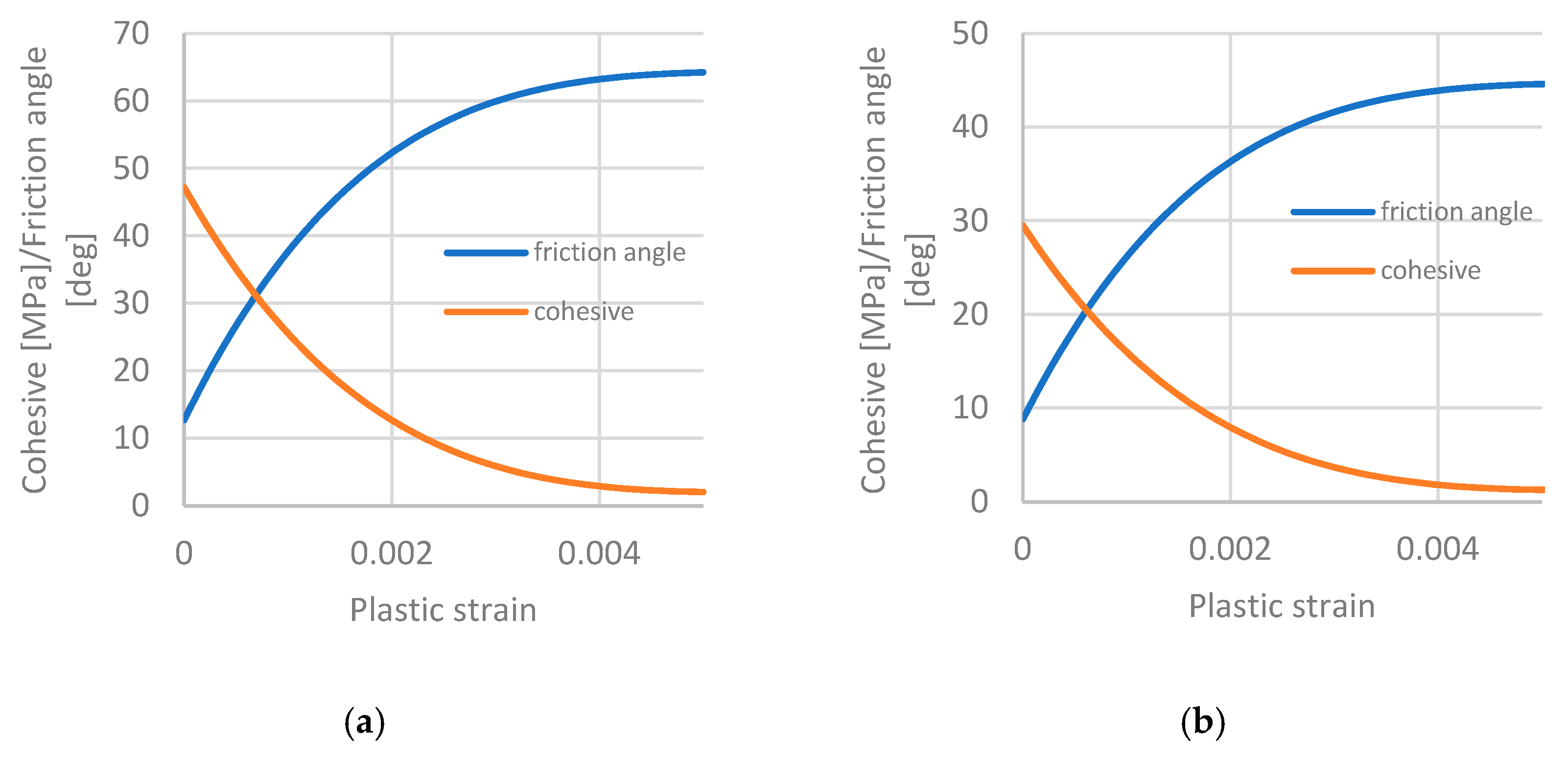
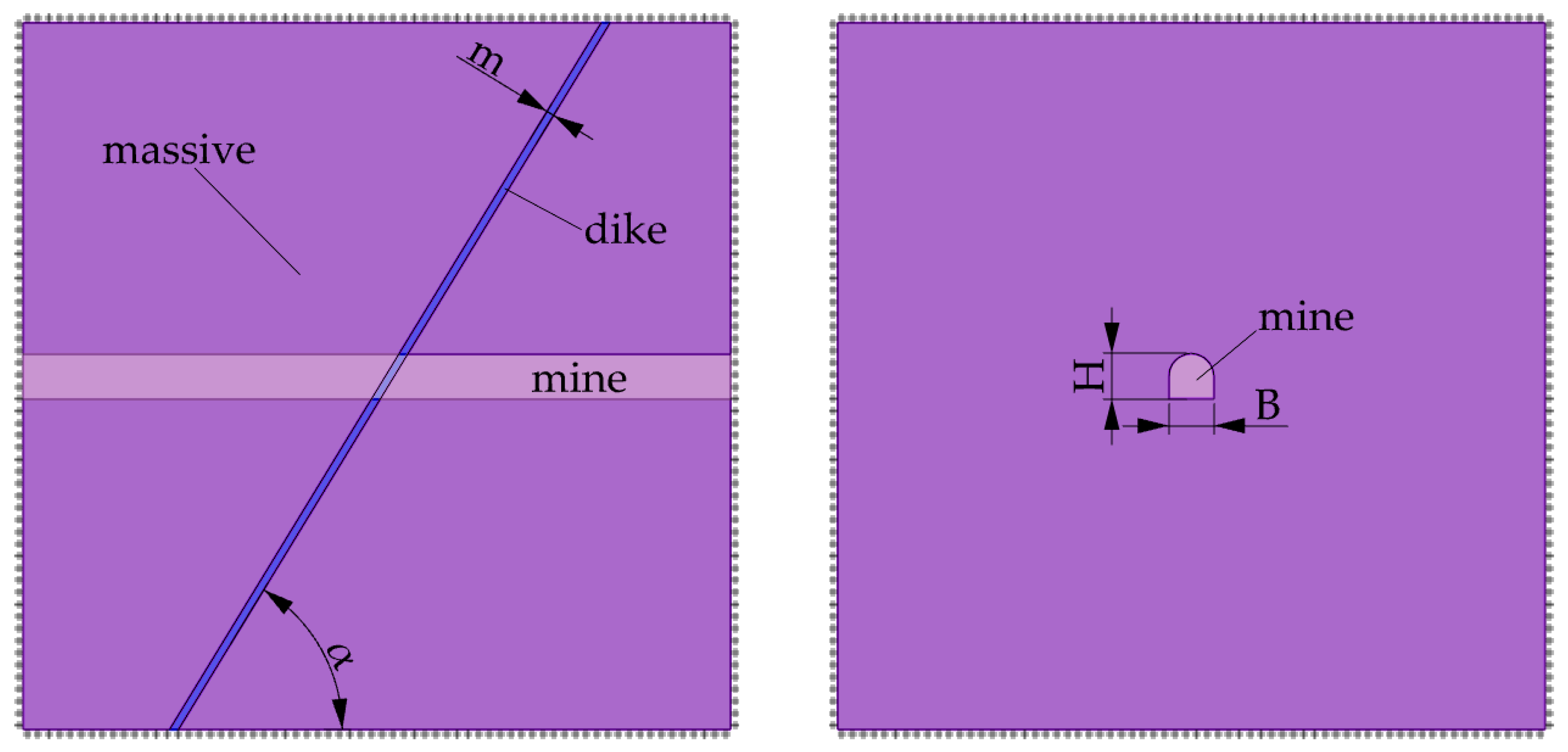

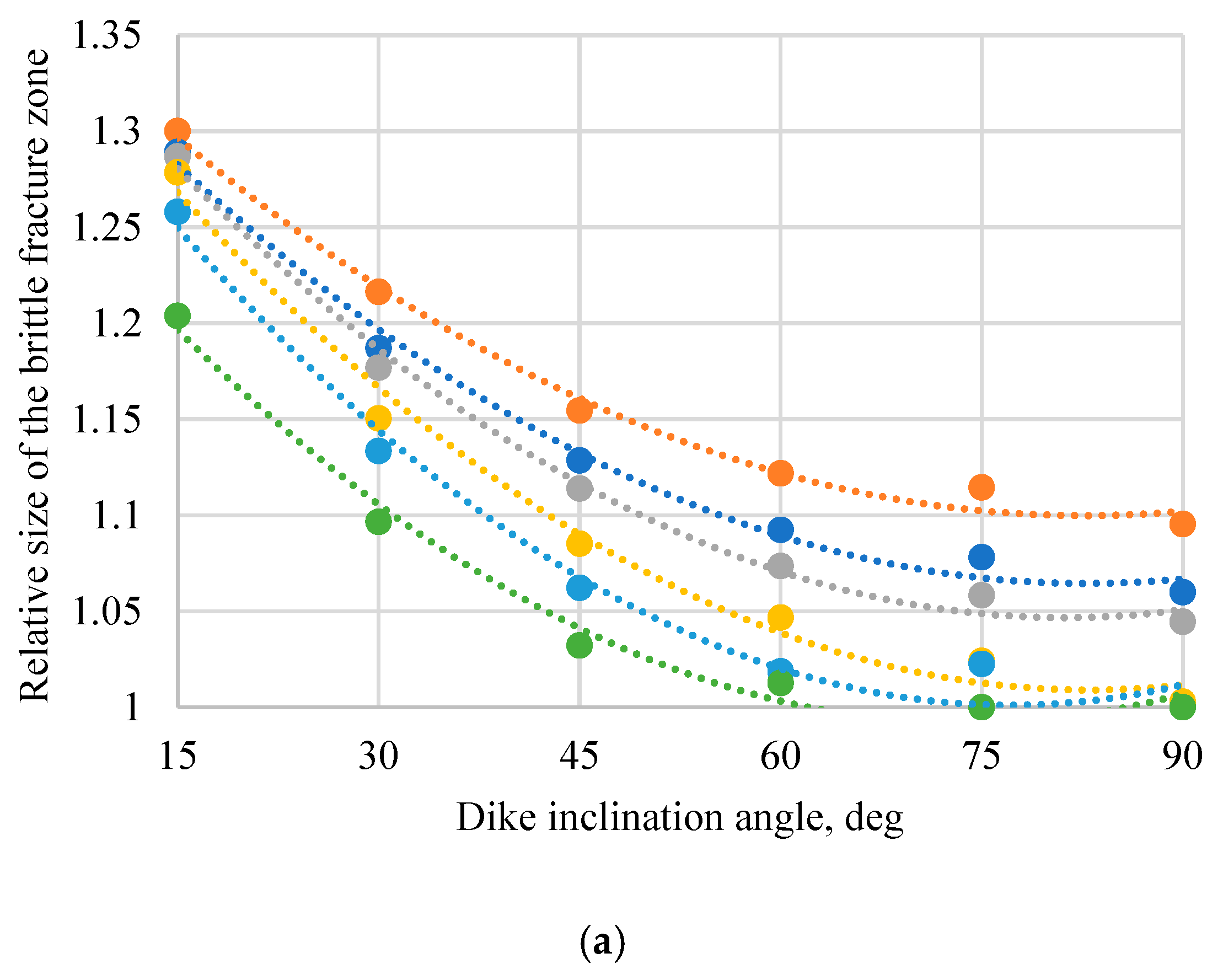
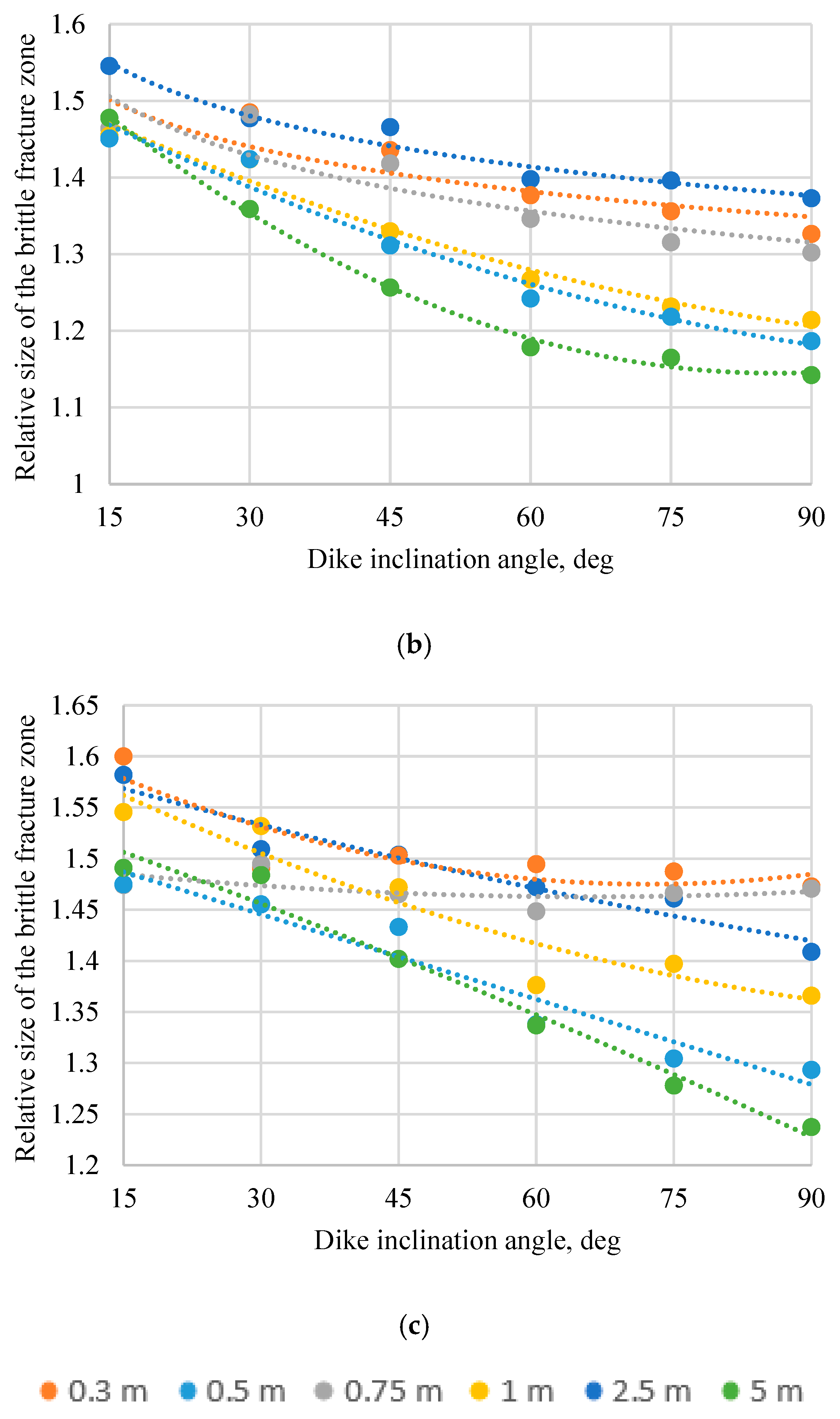
| Rock Parameter | Unit | Massive | Dyke |
|---|---|---|---|
| Modulus of deformation of rock, E | GPa | 10 | 70 |
| Poisson’s ratio, υ | - | 0.23 | 0.23 |
| Compressive strength, σ | Mpa | 120 | 300 |
| Initial cohesion, ci | Mpa | 29.5 | 47.2 |
| Residual cohesion, cr | Mpa | 1.2 | 2.06 |
| Initial friction angle, φi | degrees | 8.8 | 12.7 |
| Residual friction angle, φr | degrees | 44.8 | 64.2 |
| Thickness of the Dyke | ||||||
|---|---|---|---|---|---|---|
| 0.3 m | 0.5 m | 0.75 m | 1.0 m | 2.5 m | 5.0 m | |
| 0.1 B | 1.08–1.16/ 1.00–1.085 | 1.07–1.165/ 0.96 | 1.059–1.168/ 0.95–1.06 | 1.11–1.24/ 0.99–1.108 | 1.02–1.15/ 0.91–1.02 | 1.00–1.11/ 0.91–1.2 |
| 0.25 B | 1.06–1.11/ 1.00–1.067 | 1.07–1.11/ 0.99 | 1.06–1.109/ 0.97–1.059 | 1.121–1.18/ 1.03–1.123 | 1.028–1.109/ 0.93–1.026 | 1.02–1.07/ 0.93–1.015 |
| 0.5 B | 1.09–1.10/ 1.03–1.09 | 1.07–1.10/ 1.01–1.07 | 1.077–1.099/ 1.002–1.076 | 1.147–1.17/ 1.06–1.148 | 1.05–1.08/ 0.97–1.05 | 1.043–1.057/ 0.96–1.04 |
| 0.75 B | 1.10/ 1.05–1.099 | 1.09–1.10/ 1.03–1.09 | 1.088–1.097/ 1.034–1.089 | 1.17/ 1.099–1.159 | 1.066–1.079/ 1.00–1.068 | 1.055–1.058/ 0.99–1.059 |
| 1.0 B | 1.105–1.11/ 1.077–1.11 | 1.10/ 1.06–1.10 | 1.095–1.1/ 1.049–1.1 | 1.17–1.176/ 1.12–1.176 | 1.075–1.077/ 1.02–1.08 | 1.053–1.068/ 1.01–1.078 |
| Thickness of the Dyke | ||||||
|---|---|---|---|---|---|---|
| 0.3 m | 0.5 m | 0.75 m | 1.0 m | 2.5 m | 5.0 m | |
| 0.1 B | 1.53–1.346/ 1.24–1.344 | 1.52–1.54/ 1.19–1.53 | 1.52–1.30/ 1.17–1.30 | 1.52–1.31/ 1.15–1.30 | 1.44–1.37/ 1.10–1.43 | 1.37–1.20/ 1.08–1.19 |
| 0.25 B | 1.44–1.366/ 1.27–1.365 | 1.42–1.599/ 1.24–1.592 | 1.41–1.34/ 1.21–1.33 | 1.41–1.34/ 1.21–1.33 | 1.36–1.48/ 1.14–1.22 | 1.33–1.26/ 1.13–1.25 |
| 0.5 B | 1.425–1.375/ 1.32–1.369 | 1.39–1.63/ 1.29–1.62 | 1.39–1.36/ 1.26–1.36 | 1.39–1.36/ 1.25–1.36 | 1.34–1.32/ 1.19–1.31 | 1.31–1.30/ 1.17–1.29 |
| 0.75 B | 1.42–1.38/ 1.32–1.39 | 1.39–1.638/ 1.32–1.65 | 1.39–1.38/ 1.31–1.38 | 1.39–1.38/ 1.30–1.38 | 1.34/ 1.25–1.35 | 1.31–1.33/ 1.23–1.33 |
| 1.0 B | 1.422–1.406/ 1.386–1.407 | 1.39–1.65/ 1.36–1.65 | 1.387–1.385/ 1.33–1.384 | 1.39/ 1.33–1.40 | 1.34–1.36/ 1.27–1.37 | 1.31–1.34/ 1.25–1.36 |
| Thickness of the Dyke | ||||||
|---|---|---|---|---|---|---|
| 0.3 m | 0.5 m | 0.75 m | 1.0 m | 2.5 m | 5.0 m | |
| 0.1 B | 1.72–1.51/ 1.39–1.50 | 1.82–1.54/ 1.39–1.54 | 1.74–1.47/ 1.27–1.46 | 1.79–1.49/ 1.33–1.48 | 1.69–1.37/ 1.20–1.37 | 1.59–1.34/ 1.17–1.34 |
| 0.25 B | 1.61–1.54/ 1.41–1.54 | 1.69–1.60/ 1.46–1.59 | 1.60–1.51/ 1.33–1.50 | 1.66–1.56/ 1.39–1.56 | 1.55–1.43/ 1.26–1.43 | 1.50–1.41/ 1.23–1.40 |
| 0.5 B | 1.60–1.564/ 1.46–1.56 | 1.66–1.63/ 1.52–1.62 | 1.58–1.61/ 1.39–1.61 | 1.65–1.62/ 1.44–1.62 | 1.53–1.48/ 1.32–1.47 | 1.48–1.46/ 1.30–1.46 |
| 0.75 B | 1.59–1.58/ 1.51–1.58 | 1.66–1.64/ 1.56–1.65 | 1.57–1.65/ 1.46–1.64 | 1.64–1.66/ 1.51–1.64 | 1.53–1.51/ 1.40–1.51 | 1.48–1.49/ 1.37–1.49 |
| 1.0 B | 1.59/ 1.55–1.59 | 1.66–1.65/ 1.61–1.65 | 1.57–1.67/ 1.49–1.67 | 1.64–1.67/ 1.56–1.67 | 1.52–1.54/ 1.42–1.55 | 1.48–1.52/ 1.40–1.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demenkov, P.A.; Basalaeva, P. Regularities of Brittle Fracture Zone Formation in the Zone of Dyke Around Horizontal Mine Workings. Eng 2025, 6, 91. https://doi.org/10.3390/eng6050091
Demenkov PA, Basalaeva P. Regularities of Brittle Fracture Zone Formation in the Zone of Dyke Around Horizontal Mine Workings. Eng. 2025; 6(5):91. https://doi.org/10.3390/eng6050091
Chicago/Turabian StyleDemenkov, Petr A., and Polina Basalaeva. 2025. "Regularities of Brittle Fracture Zone Formation in the Zone of Dyke Around Horizontal Mine Workings" Eng 6, no. 5: 91. https://doi.org/10.3390/eng6050091
APA StyleDemenkov, P. A., & Basalaeva, P. (2025). Regularities of Brittle Fracture Zone Formation in the Zone of Dyke Around Horizontal Mine Workings. Eng, 6(5), 91. https://doi.org/10.3390/eng6050091






