An Enhanced Cloud Network Integrity and Fair Compensation Scheme Through Data Structures and Blockchain Enforcement

Abstract

The expansion of cloud-based storage has intensified concerns about integrity, security, and fair compensation for third-party auditors. Existing authentication methods often compromise privacy with high computational costs, punctuating the need for an efficient and transparent verification system. This study proposes a privacy-preserving authentication framework that combines blockchain-driven smart contracts with an optimized ranked-based Merkle hash tree (RBMHT). Experimental results demonstrated that our approach lowers computational costs by 24.02% and reduces communication overhead by 86.22% compared to existing solutions. By minimizing redundant operations and limiting auditor–cloud interactions, the systems improve reliability and scalability. This makes it well-suited for applications where privacy and trust are critical. Beyond performance gains, the scheme constitutes self-executing smart contracts, preventing dishonest collusions. By bridging security, dependability, and fairness, our findings set a new standard for reliable cloud attestation for a more secure and transparent auditing system.

1. Introduction

The exponential growth of mobile communication, particularly the Internet of Things (IoT), in the information age caused a massive surge in data generation. Experts estimate that by 2025, global data could reach 175 zettabytes [1,2], far exceeding personal storage capacities. As a result, adopting cloud storage (CS) has become essential. Building on cloud computing (CC) principles, CS tackles storage challenges by connecting thousands of devices across networks using cluster applications, advanced networking technologies, and distributed file systems. The global CS market is expected to grow annually by 22.30% from 2021 to 2016 [3]. This transition marks a fundamental shift in data management, enabling efficient and accessible solutions. Users can easily retrieve files from the cloud anytime, anywhere, making access convenient and cost-effective. However, these benefits come with trade-offs. Once data are outsourced, direct control is lost, leading to significant risks. Studies show that third-party exposure increases data vulnerabilities and the potential for exploitation [4,5,6]. Additionally, there is no comprehensive legal or technical framework to fully safeguard client data [7,8]. These experiences advocate for full-proof protocols to maintain data integrity (DI) and trust, essential for securely outsourcing data without compromising privacy or security.

To lessen the risk of illegal access to CS servers (CSSs), researchers developed DI verification. Traditionally, this requires the principal data owner (PDO) to download the entire dataset from CSS for local verification. While apparently simple, this is highly inefficient, as it consumes substantial network bandwidth and storage, both of which are already scarce resources in large-scale systems. Furthermore, neither the PDO nor the CSS can consistently ensure unbiased and credible authentication results [9]. Thus, it is unsuitable for maintaining DI, especially as modern security demands more precise and dependable validation techniques. Integrating cryptographic techniques like homomorphic hashing or proof of retrievability preserves sanctity without requiring full data access [10]. Third-party auditors (TPAs) have been proposed as neutral entities to increase trustworthiness and provide objective confirmation. This boosts efficiency and answers scalability issues inherent in conventional cloud systems. Figure 1 illustrates a TPA-based model.

The PDO sends local resource data to the CSS, taking advantage of its large storage and processing power. To assure DI, the PDO assigns confirmation to the TPA and requests credibility proofs from the CSS. The TPA employs advanced computational tools to examine evidence, confirm its authenticity, and report the findings to the PDO. Recent research highlights this as a best practice [11,12,13]. It curtails bias and errors that could arise if certification were processed solely by the cloud provider [14]. The study in [15] made a minor adjustment to the existing provable data possession (PDP) protocol to support dynamic update verification. Expanding on this, the authors in [16] introduced a more comprehensive PDP control using a skip table structure to accurately locate data blocks (DBs). The labels attached to each block warrant content accuracy, improving data management flexibility and reliability in dynamic environments. However, while this evolution meets the needs of complex data systems, it also creates lengthy authentication paths that add auxiliary data. The extra communication burden strains system resources, causing delays and possible bottlenecks [17]. To solve this issue, optimization is necessary to shorten the path and minimize data requirements.

2. Related Literature

Article [18] presents a framework for dynamic data operations with public auditing. It employs a Merkle hash tree (MHT) to track data segments despite frequent modifications to religiously verify DI, surpassing the limitations of static models by adding adaptability. However, the credibility of TPAs can jeopardize data privacy. Research has stressed these concerns, pointing to the dangers of relying on them without safeguards. For instance, Reference [19] suggests a strategy using homomorphic key random masking to secure data while maintaining usability. The modality used two hidden servers as intermediaries, obscuring data to prevent TPAs from extracting sensitive information. By restricting unauthorized access, it addresses a critical vulnerability stated in previous works. Another proposal by [20] offers secure, dynamic validation for concurrent users and servers in shared environment. Article [21] introduced a more advanced model that supports fluid updates and protects data anonymity. It employs a dual-index information table and a positional array (PA). To pinpoint a specific DB, the PA tracks its exact location. Meanwhile, the directional lookup index table (DLIT) preserves record integrity during DB insertions or deletions, diminishing computational costs while minimizing errors and corruption. Another concern was raised by [22] in terms of verification process. When the PDO challenges the cloud service provider (CSP), it issues a certificate to the TPA, confirming proper data storage. The system assumes that the TPA will act independently. However, if collusion with the CSP happens, it creates a new predicament.

Blockchain technology (BCT), with its decentralized design and data immutability, offers a new perspective for tamper-resistant yet transparent data. Various works [23,24,25,26,27] put forward blockchain-based methods to avoid the risks of single-point failures common in centralized architectures by storing a full copy of the database on each network node. The BCT prevents unauthorized alterations and deletions by linking each block to the previous one to accurately store information, widely recognized for digital records’ preservation. Scientists [28] designed an outsourced dynamic PDP (ODPDP) that uses cryptography to prove that data remain unaltered. It is then verified by TPAs who generate challenges at agreed intervals and use log audits to prevent dishonesty. Unlike ODPDP, the secure identity-based aggregate signature (SIBAS) combines multiple signatures into a single heap. It works by using a trusted execution environment (TEE), creating a secure and isolated space that prevents data leaks and tampering. SIBAS is considered a better option than ODPDP because it improves efficiency by reducing communication and storage demands while still ensuring a strong data security.

Most schemes implicitly assume fair and honest interactions between the PDO and CSP or TPA [29,30]. In practice, this is not the case. In prepay-based payment models, the CSP or TPA may act dishonestly, undermining transaction fairness and reliable verification. Our threat model assumes that the PDO is fully trusted since they generate keys and upload data. By contrast, both CSS and the TPA are honest but curious (attempting to glean sensitive data) or even connive to forge integrity proofs. Thus, our system neither trusts both entities with the underlying plaintext context. In terms of data storage, the PDO stores an encrypted version of the data in the CSS so that no direct plaintext is available. Communication between the PDO, CSS, and TPA during the data transit uses standard secure channels, preventing eavesdroppers from intercepting or tampering with messages. Only the PDO is fully trusted. Thus, cryptographic commitments, ranked-based structures, and verifiable proofs are caught with high probability.

For this work, we prevented the TPA from manipulating authentication results by implementing measures that guarantee fair payment while maintaining privacy and security. Our framework achieves this by using a ranked-based MHT (RBMHT) for data validation. This design improves data localization, supports dynamic updates, and simplifies the probity process. Based on these justifications, we proposed a non-interactive dynamic DI proof (NDDIP) to bolster user data privacy by removing traditional challenge–response-based interactions between participants. Further, we embedded NDDIP to leverage the blockchain’s (BlkChn) inherent immutability. These fusions form the foundations of our model to protect privacy and enforce fair transactions through smart contracts (SCs) by punishing dishonest behavior from either the CSP or TPA. Unlike prior approaches that rely heavily on repetitive TPA challenges and full Merkle tree recalculations, we leverage ranked-based structures and partial, non-interactive verification. This minimizes roundtrips to drastically cut cryptographic overhead specifically in mid-scale scenarios while still delivering superior privacy protection and automated fairness enforcement.

3. Rationale for Investigation

3.1. Verification Process Overview

The data trustworthiness in the cloud is about assurance in its accuracy and completeness over time. This relies on cryptographic processes to confirm data that do not change. Key elements include generating encryption keys and assigning unique identifiers to DBs. The PDO can periodically challenge the CSP for authentication. The CSP responds by generating proof which is validated either by the owner or any trusted third party. In systems that allow for dynamic operations, the checking procedure is extended to reassure that updates (insertion, deletion, and modification) of DB are correctly and securely performed without compromising credibility. Each entity is described below.

Key generation: The process starts with the PDO running a probabilistic algorithm to create unique public (PubK) and private (PriK) keys. Each pair is distinctive to guarantee strong security for the data. The PubK is shared openly to allow authentication through metadata like digital signatures or encryption protocols without yielding safety. In contrast, the PriK is securely retained by the PDO for generating proof of ownership. By publishing the PubK, auditors can independently verify the probity of cloud-stored data without exposing sensitive information.

Label generation: During outsourcing, the PDO divides the primary data into smaller pieces. Each segment gets a unique label, along with the original data. These labels and data are then securely stored in the cloud after which the PDO deletes the local copies. This reduces storage needs and still allows for data verification.

Challenge request: The TPA checks the integrity of the data segments by completing tasks assigned by the PDO, using sampling methods. A random challenge number (CN) and selected indices create dispute sets forwarded to the CSP. This step allows the TPA to validate large datasets by examining small random samples instead of the entire data.

Evidence generation: The CSP responds to the TPA’s challenge by producing cryptographic proofs (CPs) using homomorphic hashing that is not easily tampered, thus improving the trust and reliability of the CS systems.

Evidence verification: In this stage, the TPA reviews the CP provided by the CSP and reports its findings to the PDO, increasing attestation reliability among all involved parties.

Data update execution: When the PDO requests its data updates, the CSP also makes changes to provide a new set of CPs. The proofs are then sent to the TPA to confirm that the revisions match the PDO’s response to maintain data credibility.

Update verification: The final procedure is for the TPA to review the new CPs via an updated attestation process, completing the cycle of data vetting.

3.2. Privacy Leakage Risk

A TPA-based integrity certification scheme can create privacy risks because auditors can access repeated data challenges. In the case that PDO hands it over to an untrusted TPA, they might intentionally send the same request to the same data over multiple rounds. By collecting these responses, the TPA could try to exploit and rebuild the user’s data using Gaussian elimination. These equations, when applied over time to challenge responses, can uncover contents, leading to breaches [31]. The specific attack process can be described in detail as follows:

Repetitive challenges: A TPA checks the DBs multiple times, at specific positions, $p_1, p_2\dots , p_n$, as depicted in Equation (1). By constantly issuing challenges, they can collect sets of information based on the responses from the CSS.

$$\left\{\begin{array}{c}{v}_{p_1}^{\left(1\right)}{m}_{s_1}+v_{p_2}^{\left(1\right)}{m}_{p_2}+\dots +v_{p_n}^{\left(1\right)}{m}_{p_n}={\mu }^{\left(1\right)},\\ v_{p_1}^{\left(2\right)}{m}_{s_1}+v_{p_2}^{\left(2\right)}{m}_{p_2}+\dots +v_{p_n}^{\left(2\right)}{m}_{p_n}={\mu }^{\left(2\right)},\\ :\\ v_{p_1}^{\left(n\right)}{m}_{s_1}+v_{p_2}^{\left(n\right)}{m}_{p_2}+\dots +v_{p_n}^{\left(n\right)}{m}_{p_n}={\mu }^{\left(n\right)}\end{array}\right\}$$

(1)

Equation system formulation: The CSS responds with a reliability proof element, $u^{\left(n\right)}$, for each specific position during the verification cycle. As these results build up, it creates a system of equations.

Solution extraction: In the case that the determinant of the coefficient matrix is non-zero, the application of Gaussian elimination can determine the values $\left\{m_{p1}, m_{p2}, \dots m_{pn}\right\}$ related to the DBs. The TPA can then reconstruct sensitive file contents, compromising security and privacy [32]. Mitigating this scenario needs a mechanism like randomized masking, probabilistic techniques, and homomorphic encryptions to be integrated into the process so that it can increase security [33].

3.3. Privacy-Preserving Verification Strategies

Several studies put forward methods to augment data privacy in the authentication processes by using homomorphic keys [34]. This technology adds a random parameter during the audit stage to obscure the underlying data in the evidence produced by the server. As a result, the TPA receives fidelity proofs without accessing the actual data, thus diminishing the risk of breaches. It specifically hides the specifications used in the audit request without sacrificing confidentiality. The design employs masking to introduce randomness denoted by a dishonesty $\gamma$ (gamma) and $r$ in the algorithm. Mathematically, instead of producing a straightforward integrity proof, $\mu$, it generates a modified masked proof, ${\mu }^{\prime }$, from a linear mix of block values and random parameters. The calculation process changes based on Equation (2):

$${\mu }^{\prime }=\sum \left(data block\ast \gamma \right)+r$$

(2)

These address privacy concerns effectively, but they have limitations in regard to the fairness or equitability payment process. If the CSS and TPA are unscrupulous, they could manipulate the audit results, permitting false-trustworthiness proofs regardless of the actual stored data state. Since PDOs usually pay the CSS and TPA upfront for their services, the collusion can undermine the equability of the system since there is no way to confirm if the TPA is acting honestly. As a result, PDOs risks overpaying for services that may fail to guarantee accurate data verification. To solve this dilemma, BlkChn technology or SC can facilitate fair payment and accountability. For instance, BlkChn systems record each transaction between participants publicly, increasing transparency. It can automatically punish fraudulent behavior by deducting a set amount from the CSS or TPA’s accounts. This makes sure that PDOs only pay for truthful checks and motivates auditors to act responsibly, balancing privacy protection with equitable compensation practices.

4. Proposed Privacy Protection and Equitable Payment Scheme

In this section, we present the authentication model to overcome the reliability issues with TPA in a practical scenario. Our model operates to deliver equitable compensation by integrating privacy protection with payment fairness composed of initialization, audit, and penalty stages. Figure 2 shows four key entities.

In the first phase, the PDO creates a cryptographic key and tags the data in preparation for verification. Afterward, it will be uploaded to the CSS with a well-defined SC penalty in case it is compromised. The audit level uses NDDIP for privacy preservation. If disparities are found, the SC imposes a punishment on either the CSS or TPA depending on the conditions set beforehand. This framework promises fair payment for all parties and forces respondents to perform faithful audits.

4.1. Ranked-Based Merkle Hash Tree

We put a new data structure of RBMHT for DB integrity and dynamic updates averment in cloud storage. Unlike traditional table-based methods, the RBMHT solves existing issues of additional communication overheads caused by redundant authentication information. Research shows that variations in MHT advance security against dishonest cloud providers and improves scalability [35]. Each node (called W) in architecture has three main parts: rank value (r), edge information (s), and hash value (h). First, the r shows how deep the node is in the tree and tells how many leaves can be reached. Second, the s indicates if the node is the left or right child of its parents, helping the tree’s structure become organized. Third, the h is computed by combining the h and r values. Finally, the combined result is then re-hashed, represented by W, via calculation of Equation (3):

$$h(W)=\left\{\begin{array}{c}h\left(m_i\right),\\ h\left(h\left(L\right)\parallel h\left(R\right)\parallel r\right),\end{array} \right\}{\displaystyle \genfrac{}{}{0pt}{}{if W is a leaf node holding data block m_i}{if W is an internal node with children L and R}}$$

(3)

where h(L) and h(R) are the h values of the left and right nodes, respectively. Here, $\parallel$ denotes concatenation. Incorporating $r$ and $s$ (implicit node’s designation) assures that structural tampering, such as subtree rearrangements, cannot pass authentication without being detected, providing forge-proofing. A key advantage of our model lies in how it handles dynamic updates, as traditional MHTs require partial recalculation of node hashes along the path from the modified leaf to the root. By integrating rank information, our approach avoids unnecessary re-computations because tree balancing and structural changes can be localized. It allows us to more precisely check on whether sibling subtrees can remain intact to minimize the cascade effect of updates, as stated in the detailed verification process below:

Step 1: Compute the hash $h_d=H\left(h_l \left|\right| h_r \left|\right| r_d\right)$ for node d, where $h_l$ (left-child) and $h_r$ (right-child) represent child hashes (or DBs), and $r_d$ is the rank of node d.

Step 2: Compute the hash $h_a=H\left(h_c \left|\right| h_d \left|\right| r_a\right)$ for node a similarly, concatenating the child hashes and node rank.

Step 3: At the root node, compute the following:

$$h_{root}=\left(h_a \left|\right| h_b \left|\right| r_{root}\right),$$

(4)

where $h_a$ and $h_b$ are the hashes on the left and right subtrees under the root, and $r_{root}$ is the rank of the root node. The resulting node $W_{root}^{\prime }$ is then compared with the stored reference $W_{root}^{\prime }$.

Step 4: If $W_{root}^{\prime }=W_{root}^{\prime }$, the integrity of the entire tree is confirmed; otherwise, any mismatch indicates corrupt data or unauthorized modification.

When the PDO initiates an update by sending a request to the CSS, it is depicted by the term $Info=\left(Update, i·m_{i }^{*}, {\sigma }_1^{*} \right)$. It identifies which DBs or index positions are being targeted (i). The variable $m_{i }^{*}$ is the new updated DB version that should replace an existing block, and ${\sigma }_1^{*}$ is the PDO’s signature. At this stage, the request is simply declaring what changes need to be performed on the stored data. Once the CSS receives the update request, it processes it in three distinct stages to modify the RBMHT accordingly.

Request parsing: The CSS first parses $Info$, extracting the specific operation, such as the target block index I, and the accompanying metadata, ${\sigma }_1^{*}$. This stage checks the validity of the request, verifying any signature or other cryptographic checks before making changes to the data or structure.

RBMHT update: Based on the parsing results, the CSS updates the RBHMT that depends on the operations. In the DB modification, the CSS replaces the content of the block $m_{i }^{*}$ with $m_{i }^{*}$ at the corresponding leaf node. Because ranks and hashes depend on the internal structure, the node’s hash filed and its rank are updated if the size of the subtree changes. Parent nodes along the path to the root also have their hashes recalculated for the overall chain preservation. In deletion mode, the CSS removes the specified leaf node from the tree. If necessary, it rebalances the RBHMT using information so that the tree remains efficiently structured and that any newly vacant node is handled appropriately. Updated rank values propagate up the tree, requiring partial re-computation of the parent node hashed. For the insertion, the CSS inserts the new leaf node, $m_{i }^{*}$, into the RBMHT at index $i$ or in a designated position. The rank, $r$, of the new node is computed, and higher-level internal nodes adjust their rank and re-hash accordingly. Only the path from the leaf to the root requires hash recalculation to keep its invasiveness at a minimum.

Returning the new root and authentication data: After the update is applied, the CSS produces a new root node, $W_{root}^{*}$, reflecting all changes in hash values. The auxiliary information of $\Omega$ includes node paths (e.g., $\left\{w_b, w_c, w_4\right\}$), sibling hashes, or any necessary proof elements that the verifier can use to validate the correctness and location of the update, as illustrated in Figure 3. These are then returned to confirm that the CSS performed it correctly and to make sure that updated data still pass authentication checks.

Embedding RBHMT’s root hash within a BlkChn further bolsters security by leveraging the immutable ledger properties of decentralized networks. In practice, periodic anchoring of the root to a public consortium prevents retroactive tampering in off-chain data and offers auditability of cloud-data states over time.

4.2. Zero-Challenged Dynamic Integrity Proof Framework

In a traditional interactive integrity-proof scheme, a trusted TPA must send dispute messages to the CSS each time data verification is performed. This scheme is time-consuming and introduces extra communication overhead. To answer these drawbacks, we proposed an NDDIP framework, as illustrated in Figure 4. In this setup, the TPA and the CSS do not exchange the challenge message during audit. Both parties use a shared pseudo-random function (PRF) and synchronized parameters to generate a match without direction interaction. The CSS precomputes the required proof and makes it available to the TPA, along with any metadata needed to demonstrate DI. Through this method, the TPA can verify data correctness without needing to wait for or send custom challenge requests. Its core components include a pseudo-random function (PRF), ${\varphi }_2$; a cryptographic function with a secret seed; and an input. Both the TPA and the CSS share the same PRF and the key so that, at time $t$, they produce the same values. Next, a homomorphic hash with a tree-based structure generates a root representing the entire dataset. We follow a standard PDP practice often attributed to Shacham–Walters in which each file block is encoded by a function with homomorphic properties where partial values from different blocks can be combined without revealing the entire plaintext. Concretely, we used a pairing-friendly cryptosystem (Type-A curves from JPBC library) that provides bilinear-map and hash-group capabilities. In some of the PDP literature, these labels are also called “homomorphic signatures” because each block’s tag is effectively a signature over that block. When parts of the data are changed, the tree is updated accordingly, and new proofs can still be produced efficiently. Third, the metadata includes information necessary to verify integrity, such as block indices, cryptographic signatures, auxiliary (Merkle paths), and the root hash.

The NDDIP processes are split into audit preparation (AP) and verification phases (VPs). In the first stage of AP, pre-computation of challenges is initiated. The CSS knows that, at a time $t$, the shared PRF ${\varphi }_{2}t$ will be used. It computes any challenge-dependent components in advance. In the next stage, non-interactive proofs are generated as stored files and are conceptually divided into $n$ blocks of $\left\{b_{1 },b_{2 }\dots b_{2 }\right\}$. A CSS computes a single aggregated proof containing an aggregator value derived from ${\varphi }_{2}t$. For instance, if ${\varphi }_{2}t$ outputs a set $S=\left\{s_{1 }, s_{2 }, \dots s_{n }\right\}$ of random block indices, the CSS will gather the block hashed and combine them into a single identity proof. The final stage is composed of metadata and storage so that any dynamic structure changes to the data will trigger a recalculation of the root hash. Once updated, it ascertains that the new tokens are stored securely and are readily available for TPA retrieval.

In the verification phase, an independent challenge approximation is established wherein, at the same time $t$, the TPA autonomously runs the PRF ${\varphi }_{2}t$. This yields the same index set, $S$, without needing any interaction. It then accesses the pre-computed proof from the CSS for retrieval proof and metadata. It includes aggregated hash and cryptographic signature. The last step is to use the proof, the challenge set $S$, and the public key for the TPA to check its genuineness. If valid, the TPA concludes that all challenged blocks remain unmodified. Below is a more concrete representation behind NDDIP. Assume that ${\varphi }_{2}t$ is the shared PRF at discrete time steps, $t$, while $H$ is a cryptographic hash function. Equation (5) shows the computation.

$$ChallengeSet\left(t\right)=S=\left\{{\varphi }_{2}t mod n\right\}$$

(5)

where ${\varphi }_{2}t mod n$ can yield the block indices in a range of $\left[1, n\right]$. For multiple blocks, it can expand as follows:

$$S=\left\{{\varphi }_{2}t mod n_1,{\varphi }_2\left(t+1\right) mod n_2\dots \right\}$$

(6)

with proof generation (CSS) of

$$\prod =AggProof\left(\left\{b_i:i ϵ S\right\}\right)=\prod _{i ϵ S }H\left(b_i\right)$$

(7)

and for a Merkle tree of

$$\prod = \left\{MerkePath\left(b_i\right)\right\}::i ϵ S$$

(8)

Given $\prod$ and the root hash, $W_r$, the TPA checks the verification; if the condition holds true, the TPA deems the data to be intact:

$$Verify \left(\prod ,S, W_r\right)=True$$

(9)

4.3. Game-Based Security Model

For the security model, our goal is to make certain that no malicious CSS or adversarial party can deceive the substantiation mechanism without being detected. To formalize this, we employ a game-based security model (GBSM) where the assailant is challenged to generate false proofs. The system is deemed secure if the adversary’s probability of success is negligibly small. First, we define a DI proof game between the challenger ( $C$) and adversary ( $A$). The challenger generates a public key and system parameter (via a key generation algorithm), which the adversary obtains. Both parties then use a PRF to produce a random contest set, denoted by the following:

$$Chal=\left\{s_1, s_{2,}\dots s_k\right\} \subseteq \left\{1, 2, \dots , n\right\}$$

(10)

where $n$ is the total number of DBs. The $A$ uses this information, $\mathrm{C}\mathrm{h}\mathrm{a}\mathrm{l}$, to generate proofs over the specified blocks. Concretely, for each challenged block, ${\mathrm{m}}_1$, the $A$ derives a block label, ${\mathsf{\alpha }}_i$, and a proof element based on cryptographic hashing or homomorphic signatures. The formula is described in Equation (11) as follows:

$${\alpha }_i=H{\left({Frame}_i\right)}^{\lambda }$$

(11)

where ${\mathrm{F}\mathrm{r}\mathrm{a}\mathrm{m}\mathrm{e}}_{\mathrm{i}}$ is a unique identifier of the ith block, $\mathrm{H}(·)$ is a secure hash function, and $\lambda$ relates to a secret or random value. The adversary submits these proof elements back to $C$. Using the public key, the set of ${\mathsf{\alpha }}_i$ and any additional metadata accepts the proofs as correct. If this is the case, the $A$ is said to have “won” the game.

Next, we define a similar proof game for the TPA. Here, the TPA is treated as the potential $A$, while the trusted entities act as the $C$. Again, $A$ and $C$ use a PRF to select indices in the stored data, creating $\mathrm{C}\mathrm{h}\mathrm{a}\mathrm{l}$. For each index, ${\mathrm{s}}_1$, in $\mathrm{C}\mathrm{h}\mathrm{a}\mathrm{l}$, the TPA must compute an integrity proof, $v_{si}$. An example construction incorporates a secret key at upload time, described by Equation (12):

$$v_{si}=\prod _{jϵI{s}_i}{H}^{\prime }\left(m_j\right)$$

(12)

where $I_{si}$ is the set of segments within block $m_{si}$, and $H^{\prime }$ is a hash function combined with additional cryptographic operations. Once computed, the TPA returns a proof to $C$.

Then, it runs a verification procedure to check whether

$$\pi =\prod _{s_iϵChal}{v}_{si}$$

(13)

holds for the expected values. If the authentication accepts, the TPA “wins” this game. In turn, if the TPA attempts to cheat, the authentication mechanism detects the inconsistency with overwhelming probability.

4.4. Blockchain Selection and Deployment

We implemented the prototype using a private Ethereum test network (Ganache) and basic Solidity smart contacts. Each time a new RBMHT root is produced, the CSS submits a signed transaction to the SC, thereby anchoring the updated hash. The TPA, upon verification, calls another function in the same contract, logging a verified or dishonest event. If dishonest behavior is detected, the SC reduces the relevant stake from the misbehaving party’s on-chain balance. In our proof of concept (PoC), each on-chain update required storing just 32 bytes plus a signature. Gas usage for these small writes remained low. To avoid high costs in a public-chain scenario, one can batch updates periodically or adopt a rollup. In permissioned setups, the transaction fees are negligible by design. The SC is the arbiter of fairness, with the primary role for stake and deposit, and verification calls.

4.5. Punishment and Smart Contracts

To further reinforce fairness, a punishment section is defined to penalize dishonest behavior by CSS or TPA whenever a verification failure occurs. In this stage, a BlkChn-based reference SC continuously monitors the results of the integrity checks. Formally, we let $Fail$ denote an event where the challenger’s checking algorithm outputs a failure, $\pi \ne expected$. Whenever $Fail$ arises, the system transitions to a penalty enforcement procedure. This can be illustrated via a function:

$$Penalty\left(Fail\right)=\left\{{\displaystyle \frac{C_{fine \cdot \left(1+\Phi \right),} }{C_{fine }}}\right. {\displaystyle \genfrac{}{}{0pt}{}{if repeated failures occur,}{otherwise }}$$

(14)

where $C_{fine}$ is a base cost (e.g., monetary or token-based amount), and $\mathsf{\Phi }$ is an additional multiplier for repeated or severe misbehavior. When the punishment stage is triggered, the BlkChn contract checks whether the dishonest party has accrued a failure count, $fc$. If $fc$ exceeds a threshold, $\tau$, higher penalties can be enforced to reflect an escalating cost for persistent dishonesty. We can depict this as follows:

$$fc=fc+1, if Fail is detected$$

(15)

If $fc \ge \tau$, the BlkChn contract modifies $\mathsf{\Phi }$ accordingly, leading to a larger penalty in Equation (14). Once calculated, it is automatically deducted from a stake or deposit that the CSS or TPA committed in advance. Thus, the threat of losing tokens or collateral affirms that rational actors have a strong incentive to remain honest.

Our SC is employed to automate both reward and punishment within the system. Upon each challenge–response cycle, a contract invocation is performed with the $C$ by submitting the authentication results $vr \in \left\{0, 1\right\}$, where 1 indicates a successful proof, and 0 indicates a failure. The on-chain validation checks any relevant metadata to confirm that the dispute was legitimate and that the response was computed correctly. During state update, if $vr=1$, the contract releases or maintains the stake of the verifying party. If $vr=0$, it executes the punishment and accounts the penalty via Equation (14). It then updates the failure count, $fc$, as shown in Equation (15). The entire transaction is immutably logged into a ledger comprising the verification results, penalty or reward, and any incremental changes to $fc$. A single transaction on a typical EVM-based hyperledger amounts to approximately 200 to 300 bytes. In a private or permissioned consortium network, the fees are near zero or entirely waived because nodes are run by a federation. Because we are only storing 32-byte digest each time, it is practical from a BlkChn bloat perspective, ensuring unchanged proof of record without the prohibitive cost of storing large files directly. This provides transparency and non-repudiation, as all network participants can audit the outputs. Figure 5 represents the detailed processes of the proposed scheme.

5. Performance Assessments

5.1. Correctness Analysis

Theorem 1.

If CSS honestly stores user data and returns the corresponding evidence, then the content evidence can pass the verification of TPA.

Proof. 

Theorem 1 can be proved as follows: We begin the expression of

$$\pi \cdot e\left(\sigma , g\right)$$

(16)

with the assumptions of bilinear paring, $e=G_1\times G_2⟶ G_T$, where $\mathsf{\pi }$ is the aggregated integrity proof for all challenged segments, $\mathsf{\sigma }$ is a signature-type component or commitment from the CSS, and $\mathrm{g}$ is a generator of bilinear group $G_1$. By substituting definitions into the pairing, we rewrite Equation (16) as a product of two pairings:

$$\pi ·e\left(\sigma , g\right)=e\left({\prod }_{j=1}^s{u}_j^{{\lambda }_j}, H_2\right)\times e\left({\prod }_{i=1}^s{\sigma }_i^{{\gamma }_i}, g\right)$$

(17)

where ${\prod }_{\mathrm{j}=1}^{\mathrm{s}}{\mathrm{u}}_{\mathrm{j}}^{{\mathsf{\lambda }}_{\mathrm{j}}}$ is an aggregation of elements, ${\mathrm{u}}_{\mathrm{j}}$; ${\mathrm{H}}_2$ is a fixed element in $G_1$ used to transform ${\mathrm{u}}_{\mathrm{j}}$ components; and ${\prod }_{\mathrm{i}=1}^{\mathrm{s}}{\mathsf{\sigma }}_{\mathrm{i}}^{{\mathsf{\gamma }}_{\mathrm{i}}}$ is an aggregation of per-block signatures, ${\mathsf{\sigma }}_{\mathrm{i}}$. Each ${\mathsf{{\rm Y}}}_i$ is a random secret exponent introduced during the challenge. Using the bilinear property $e\left(XY, Z\right)=e\left(X,Z\right) e\left(Y,Z\right)$, this can be separated as a product of pairings. Next, each ${\mathsf{\sigma }}_{\mathrm{i}}$ is expanded according to its definition:

$${\sigma }_i=(H{(Fname \parallel i)}^{\alpha } \cdot {\prod }_j\left(g_j^{{\tau }_j}{m}_{j,i,j}^{\beta }\right))$$

(18)

where $\left(H\left(Fname\parallel \right. i\right)$ is a hash of the filename and block index, a factor capturing the file segments, ${\mathrm{m}}_{\mathrm{j},\mathrm{i},\mathrm{j}}$, raised to a cryptographic exponent, $\mathsf{\beta }$; a generator, ${\mathrm{g}}_{\mathrm{j}}$; and a random salt of ${\mathsf{\tau }}_{\mathrm{j}}$. When each ${\mathsf{\sigma }}_{\mathrm{i}}$ is raided to ${\gamma }^i$ and placed inside the pairing $e\left(·, g\right)$, we use bilinearity to separate exponents. Symbolically,

$${\prod }_{i=1}^{s_c}{\sigma }_i^{{\gamma }_i}={\prod }_{i=1}^{s_c}{\left(H{\left(Fname\parallel i\right)}^{\alpha } \cdot {\prod }_j\left(g_j^{{\tau }_j}{m}_{j,i,j}^{\beta }\right)\right)}^{{\gamma }_i}$$

(19)

Applying pairing properties to each factor with $g$, the bilinear map breaks it down as follows:

$$e\left({\prod }_{i=1}^{s_c}{\left[\dots \right]}^{{\gamma }_i}, g\right)={\prod }_{i=1}^{s_c}e\left[{\left(H\left(Fname\parallel i\right), g\right)}^{\alpha {\gamma }_i}\times {\prod }_{j}e{\left(g_j^{{\tau }_j}{m}_{j,i,j}^{\beta }, g\right)}^{{\gamma }_i}\right]$$

(20)

Within the exponent, we can sum or multiply the exponents $\mathsf{\alpha }{\mathsf{\gamma }}_{\mathrm{i}}, \beta {\mathsf{\gamma }}_{\mathrm{i}}$, and $\tau {\mathsf{\gamma }}_{\mathrm{i}}$. By collecting terms, we further expand to reflect the DBs $m_{j,i,j}$. In a transformation involving ${\prod }_{j=1}^s{u}_j^{{\lambda }_j}$ and the term $e\left({\prod }_{j=1}^s{u}_j^{{\lambda }_j}\right), { H}_2$ encodes partial commitments to the user’s data. It remaps the $\left\{u_j\right\}$ to the group element, $H_2$, to inject randomness from the client’s side. By applying bilinear expansion again, we derive Equation (21):

$$e\left({\prod }_{j=1}^s{u}_j^{{\lambda }_j}, H_2\right)={\prod }_{j=1}^{s}e{\left(u_j, H_2\right)}^{{\lambda }_j}$$

(21)

The exponents align with the expansions from the ${\mathsf{\sigma }}_{\mathrm{i}}$ side, assuring that “honest data” satisfy the equation exactly. Under trustworthy behavior, all partial products either match up or cancel correctly. Hence, we reach a concluding expression in Equation (22) to show consistency and precisely represent that verification passes without any leftover terms, demonstrating correctness:

$$e\left({\prod }_{j=1}^s{u}_j^{{\lambda }_j}, H_2\right)={\prod }_{j=1}^{s}e{\left(u_j, H_2\right)}^{{\lambda }_j}$$

(22)

□

5.2. Security Analysis

Theorem 2.

If the label-generation algorithm of the scheme is unforgeable under the random oracle model or RNOM (where every hash function behaves like a truly random function for anyone who queries it), and if Discrete Log (DL) and Computational Diffie–Hellman (CDH) problems are hard in the chosen groups, then no polynomial-time adversary can produce valid but fraudulent data-integrity labels with non-negligible probability. Simply, the adversary’s success probability in “destroying” security is negligible.

Proof. 

To prove the veracity of the theorem, the following was considered. Let $G_1$ be a cyclic group of prime order, $p$, with generator, $g$, denoted by the following:

$$H: {\left\{0, 1\right\}}^{*}⟶G_1$$

(23)

Here, a RNOM maps arbitrary strings to elements of $G_1$. We define $LabelGen$, which takes a secret key, $sk$ (ephemeral exponent), and identifier, $ID$, and produces $\alpha \in G_1$. A simplified form is expressed in Equation (24):

$$\alpha =LabelGen\left(sk, ID\right)={\left(H\left(ID\right)\right)}^x\cdot \left(ht\right),$$

(24)

where $x$ is derived from $sk$, and $ht$ represents homomorphic terms. When a user submits a label, $\mathsf{\alpha }$, for verification (associated with ID), the algorithm checks its consistency with the condition:

$$Verify\left(\alpha , ID\right)=1 ⟺ \alpha =LabelGen(sk, ID),$$

(25)

in equivalence in a bilinear pairing expression or a group equality check. If $\mathsf{\alpha }$ matches the genuine label, validation succeeds.

An adversary, $A$, can query an oracle, $LabelGen$, on selected IDs $\left({ID}_1, \dots {ID}_q\right)$ to obtain the corresponding labels ${\mathsf{\alpha }}_i$. However, to fake a label on the new identifier, ${ID}^{*}$ (one it never requested), $A$ must create ${\mathsf{\alpha }}^{*}$ that passes authentication with no knowledge of $sk$. This event can be formulated by Equation (26):

$${\alpha }^{*}=LabelGen(sk, I{D}^{*})$$

(26)

even though ${ID}^{*}\notin \left\{{ID}_1, \dots {ID}_q\right\}$. If $\mathrm{V}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{f}\mathrm{y}\left(\mathsf{\alpha },\mathrm{I}\mathrm{D}\right)=1$, then $A$ has won. Next, we capture the probability of winning this event as adversary’s advantage, ${Adv}_A^{forge}\left(\lambda \right)$, where $\lambda$ is the security parameter (bit-length controlling $p$ and the random oracle). Equation (27) shows its standard form:

$${Adv}_A^{forge}\left(\lambda \right)=Pr\left[Verify\left({\alpha }^{*}, I{D}^{*}\right)=1 \bigwedge I{D}^{*}\in \left\{{ID}_1, \dots {ID}_q\right\}\right]$$

(27)

Under the RNOM, producing a valid label, ${\alpha }^{\mathrm{*}}$, for a new $I{D}^{*}$ requires either inverting the exponent, $x$, linked to the $sk$ or colliding the hash output, $H\left({ID}^{*}\right)$, with the already obtained $A$. However, inverting $x$ in $g^x$ is the DL problem in $G_1$. Constructing valid exponentiations that match ephemeral Diffie–Hellman tuples is akin to solving CDH. The collisions in $H$ for new ${ID}^{*}$ would require controlling the random finding collisions, assumed negligible if $H$ behaves like a truly random function. One technique to achieve this is reduction. If $A$ can break the label generation unforgeability with non-negligible probability, then $A$ can solve DL or CDH with non-negligible probability. Formally, a simulation of $B$ uses $A\prime s$ forgery to solve a known instance of $g^x$ in polynomial time, summarized by a reduction argument of the following:

$${Adv}_A^{forge}\left(\lambda \right) \ge {Adv}_B^{DL/CDH}\left(\lambda \right),$$

(28)

meaning if $A$ can counterfeit with high probability, then $B$ can solve DL or CDH with comparably high probability, contrary to the assumption that ${\mathrm{A}\mathrm{d}\mathrm{v}}_{\mathrm{B}}^{\mathrm{D}\mathrm{L}/\mathrm{C}\mathrm{D}\mathrm{H}}\left(\mathsf{\lambda }\right)$ is negligible.

To show that ${\mathrm{A}\mathrm{d}\mathrm{v}}_{\mathrm{B}}^{\mathrm{D}\mathrm{L}/\mathrm{C}\mathrm{D}\mathrm{H}}\left(\mathsf{\lambda }\right)$ is insignificant, our scheme uses hybrid games. In each game, the adversary tries a more refined strategy. A concrete illustration of different variants is stated below:

Game 1: The adversary tries to produce a correct label for a block index that $i$. Probability of success: ${\in }_1$.

Game 2: Adversary uses altered label evidence, ${\mathsf{\alpha }}^{\prime }$, while keeping partial data from older queries. Probability of success: ${\in }_2$.

Game 3: Adversary tries a “combine-and-conquer” approach with multiple label queries, forging a brand-new label at the end. Probability of success: ${\in }_3$. A union bound shows that the adversary’s overall success, $\in ={\in }_1+{\in }_2+{\in }_3$, is still dominated by hardness assumptions. Equation (29) simplifies this union bound forgery probability with

$${Adv}_A^{forge}\left(\lambda \right) \le {\in }_1+{\in }_2+{\in }_3 \le negl\left(\lambda \right),$$

(29)

under the premise that forging a new label in any of these game scenarios leads to solving DL/CDH or breaking the random oracle’s resistance. Putting all of the above together, we can confidently conclude that no polynomial-time $A$ can produce a new valid label, ${\mathsf{\alpha }}^{*}$, for $\mathrm{I}{\mathrm{D}}^{\mathrm{*}}\in \left\{{\mathrm{I}\mathrm{D}}_1,\dots {\mathrm{I}\mathrm{D}}_{\mathrm{q}}\right\}$ without essentially solving a known hard problem or finding a random oracle collision. Therefore, ${\mathrm{A}\mathrm{d}\mathrm{v}}_{\mathrm{A}}^{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{e}}\left(\mathsf{\lambda }\right)$ is negligible. Since forging these labels is the core of “destroying security” for the integrity procedure, it follows that the entire scheme retains its security properties under the stated assumptions. We thus arrive at the formal and final security claim of ${\mathrm{A}\mathrm{d}\mathrm{v}}_{\mathrm{A}}^{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{g}\mathrm{e}}\left(\mathsf{\lambda }\right)\le \mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(\mathsf{\lambda }\right)$, validating Theorem 1. Equivalently, there is no polynomial-time algorithm that can break label unforgeability with more than negligible probability. This confirms the algorithm’s reliability under a RNOM and the hardness of DL/CDH. □

5.3. Privacy Analysis

Theorem 3.

In the data authentication scheme that supports privacy and equitable payment, given the content evidence, $\theta =\left\{\sigma ,\mu \right\}$, returned by the CSS for a randomly selected challenge, a dishonest TPA cannot feasibly reconstruct the user’s data $\left\{m_1, m_2\dots m_n\right\}$.

Proof. 

In cloud-based systems, protecting integrity while securing user privacy is critical. During the audit stage, the TPA uses the evidence provided by the CSS to confirm the correctness of stored data. Our mechanism incorporates cryptographic principles and non-interactive protocols so that TPA cannot infer sensitive data while still fulfilling its verification role.

When a TPA questions a subset of blocks, $S_c \subseteq \left\{1, \dots , n\right\}$, the CSS returns two main pieces of evidence. A product type or tag-based component is present,

$$\sigma ={\prod }_{i \in S_c}{\left({\sigma }_i^{\prime }\right)}^{{{\rm Y}}_i}$$

(30)

where each ${\mathsf{\sigma }}_{\mathrm{i}}^{\prime }$ is a tag for the ith block, and ${{\rm Y}}_i$ is a randomly generated exponent linked to the challenge. An aggregate component of the following is present:

$$\mu ={\sum }_{i\in S_c}\left(v_i \cdot m_i\right)$$

(31)

where $m_i$ is the content of block $i$, and $v_i$ is another randomly generated challenge coefficient. Primarily, $\mathsf{\sigma }$ and $\mu$ are checked via function $Verify\left(\theta \right)$ that confirms authenticity without exposing the raw $m_i$.

A fraudulent TPA might try to reconstruct ${\left\{m_i\right\}}_{i=1}^n$ by collecting multiple pairs $\left({\sigma }^{\left(t\right)}, {\mu }^{\left(t\right)}\right)$ from repeated audits $\left(t=1, 2, \dots \right)$. However, two properties of Equations (30) and (31) prevent direct data recovery. For random exponents in $\sigma$, each ${\mathsf{{\rm Y}}}_i^{\left(t\right)}$ is fresh and unpredictable, even if ${\mathsf{\sigma }}_{\mathrm{i}}^{\prime }$ encodes $m_i$ internally or raising it to different powers, ${\mathsf{{\rm Y}}}_i^{\left(t\right)}$, scrambles any consistent relationship across audits. If this is the case, there will be no fixed linear system in $\mu$. For each audit, the subset $S_c^{\left(t\right)}$ of challenged blocks can change. Its random coefficients $\left\{v_i^{\left(t\right)}\right\}$ also change each time. Hence, even if the TPA tries to form linear equations such as

$${\mu }^{\left(t\right)}={\sum }_{i \in S_c^{\left(t\right)}}{v}_i^{\left(t\right)}{m}_i$$

(32)

they do not align into a single global system solvable for every $m_i$. The subsets and multipliers obfuscate the individual values. Suppose the TPA collect $T$ audits in an attempted linear-algebra attack with pairs $\left({\sigma }^{\left(1\right)}, {\mu }^{\left(1\right)}\right), \left({\sigma }^{\left(2\right)}, {\mu }^{\left(2\right)}\right), \dots , \left({\sigma }^{\left(T\right)}, {\mu }^{\left(T\right)}\right)$. They may attempt to treat this as a linear system in the variables $\left\{m_i\right\}$. However, with different subsets, the set $S_c^{\left(t\right)}$ can vary across audits, with $m_i$ disappearing in certain sums. This will yield inconsistent coverage of $\left\{m_{i,}\dots , m_n\right\}$. For random coefficients, even for blocks that do appear, the multipliers, $v_i^{\left(t\right)}$, are independently created each time. This prevents direct linear combination to isolate $m_i$. If the TPA tries to invert these relationships, it will need to solve Equation (33):

$$\left[\begin{array}{ccc}⋮& \cdots & ⋮\\ v_1^{\left(t\right)}& \cdots & v_1^{\left(t\right)}\\ ⋮& \cdots & ⋮\end{array}\right] \left[\begin{array}{c}{m}_1\\ ⋮\\ m_n\end{array}\right]=\left[\begin{array}{c}{\mu }^{\left(1\right)}\\ ⋮\\ {\mu }^{\left(T\right)}\end{array}\right]$$

(33)

But since each row (for each audit) is both partially zero (due to missing blocks in $S_c^{\left(t\right)}$ and includes random $v_i^{\left(t\right)}$), the system is neither complete nor stable. In practice, it is underdetermined, and the TPA cannot reliably solve for the exact $m_1$ unless it breaks the random exponents.

As an added security, we introduced cryptographic barriers. Even ignoring or bypassing the above linear-algebra difficulty, the TPA still faces further barriers such as discrete-log (DisLog) and collision-resistance in hashing (CRH). In DisLog, if ${\sigma }_i^{\prime }$ is based on a function like $H{\left({BlockID}_i\right)}^{m_i}$ or a bilinear pairing encoding, then obtaining $m_1$ from ${\sigma }_i^{\prime }$ requires solving a DisLog-type problems or forging a signature, assumed infeasible. On the other hand, if the TPA (in CRH) tries to guess or re-map the hash outputs used in ${\sigma }_i^{\prime }$, it would need to break the RNOM or find collisions; and doing so is, again, presumed to be impossible. Even in the best scenario, collecting various ${\sigma }^{\left(1\right)}, {\mu }^{\left(1\right)}$ pairs, the TPA still lacks the necessary handles to “peel off” the exponents and isolate the raw block, $m_1$.

With the inclusion of SC to enforce pair payment or penalties, the TPA cannot unilaterally demand repeated identical challenges or manipulate the random seeds to make them “just right” for solving for $\left\{m_1\right\}$. In another scenario, if the TPA colludes with CSS to attempt a “replay attack” or “fixed challenge,” the contract and the system’s protocol detect mismatches, triggering punishments. This decentralized security enforcement further reduces the TPA’s ability to gather the precise data needed for a cryptanalytic attack. Bringing all the pieces together, Theorem 3 follows that no consistent linear system for $\mu$ can be formed due to random subsets and coefficients. The product tags, $\sigma$, rely on exponentiations or pairings that are secured by DisLog assumptions. Lastly, fair payment/penalty protocols prevent manipulations that could reveal additional information. Thus, from $\theta =\left\{\sigma , \mu \right\}$ alone, an unscrupulous TPA cannot reconstruct $\left\{m_{i,}\dots , m_n\right\}$ with non-negligible probability. The scheme effectively guarantees user data privacy against any polynomial-time adversary under standard cryptographic assumptions. □

6. Results and Discussions

In this section, we evaluate the overall performance of our proposed system by examining two primary metrics, computational and communication overhead. The experiments were conducted on a Window 11 system equipped with an Intel Core i7 processor running at 3.4 GHz, with 8 GB of random-access memory (RAM). We implemented the scheme using the Java pairing-based cryptography (JPBC) library for encryption and decryption routines. Each reported result represents an average of ten independent runs.

6.1. Computational Overhead

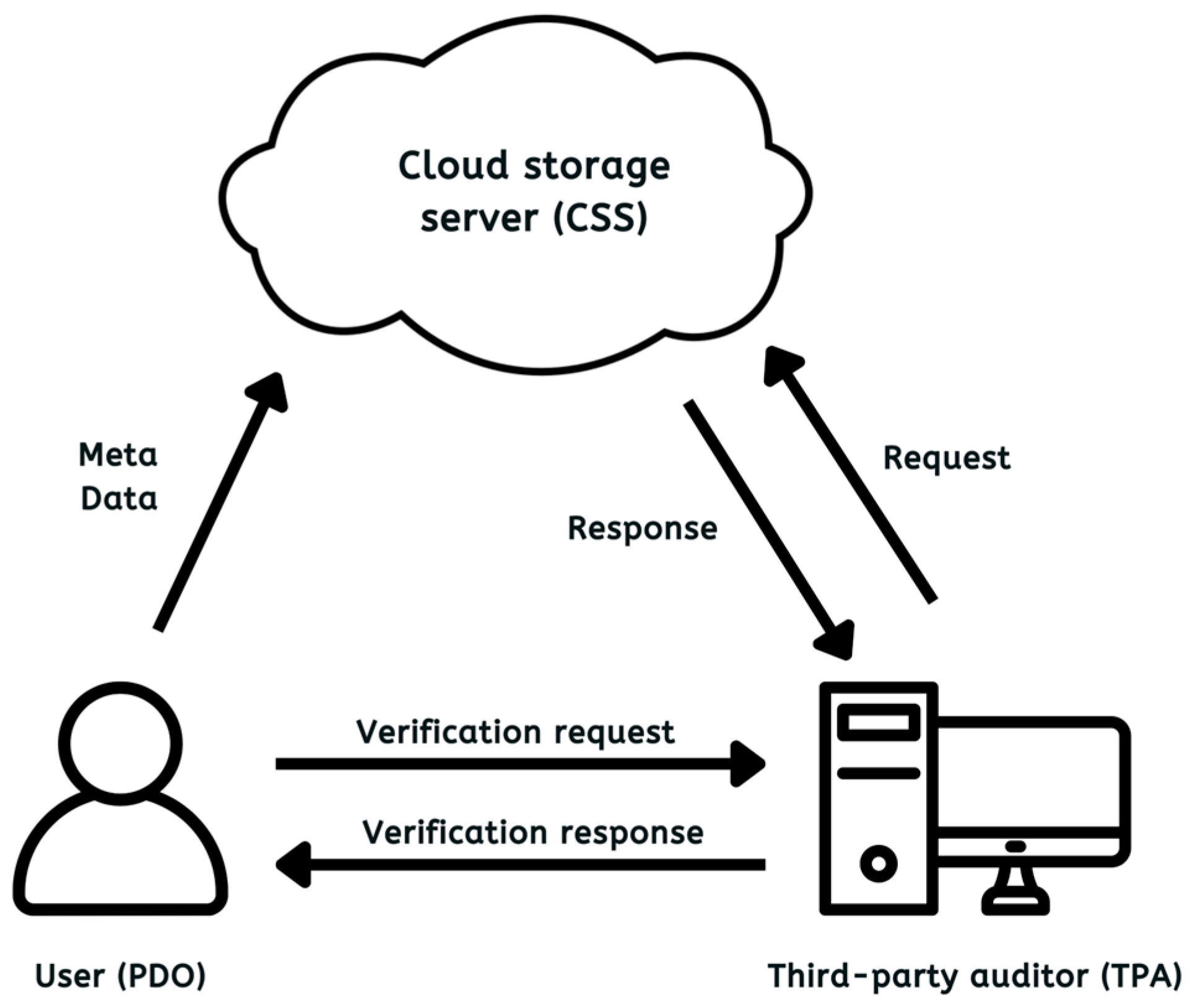
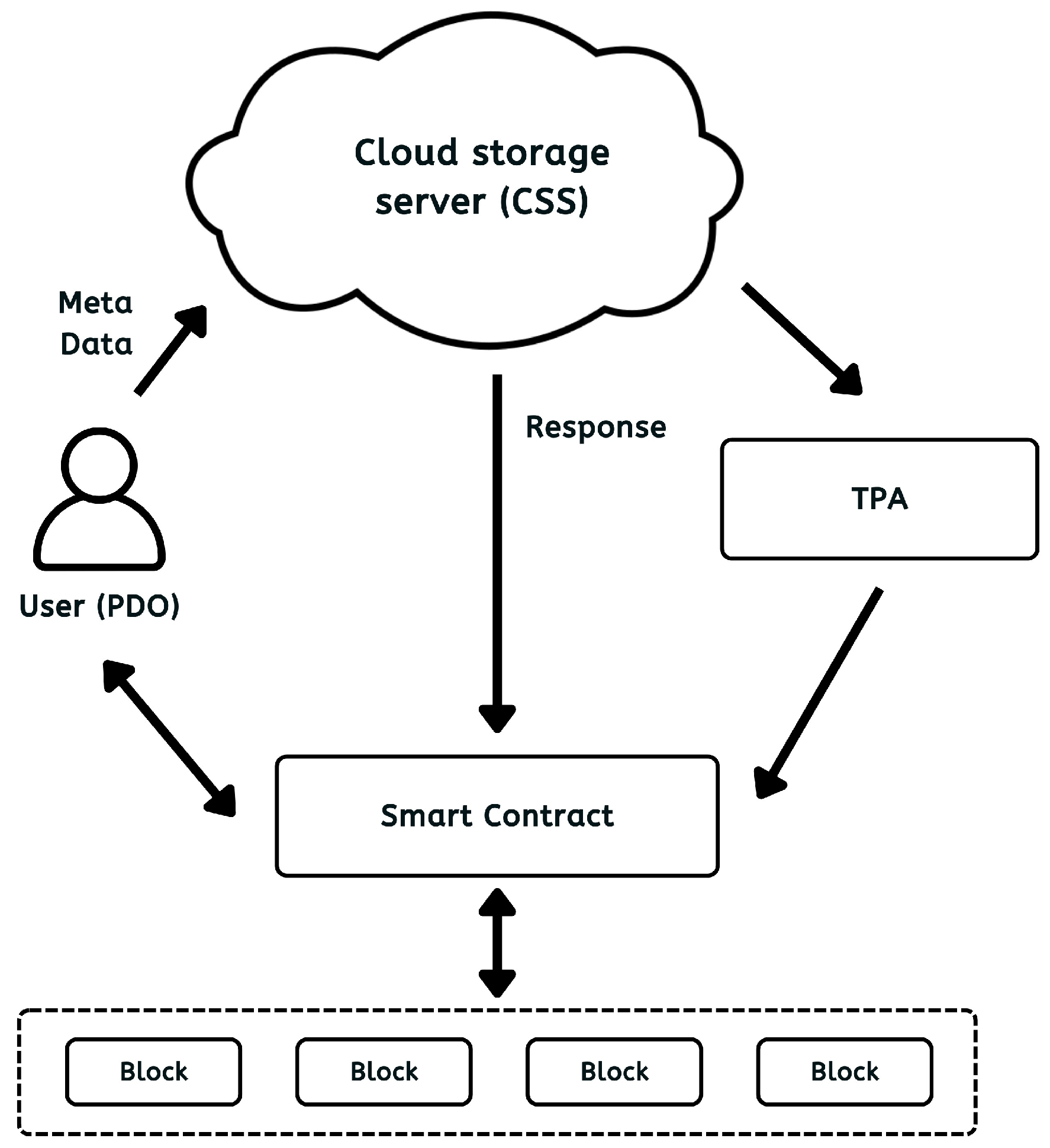
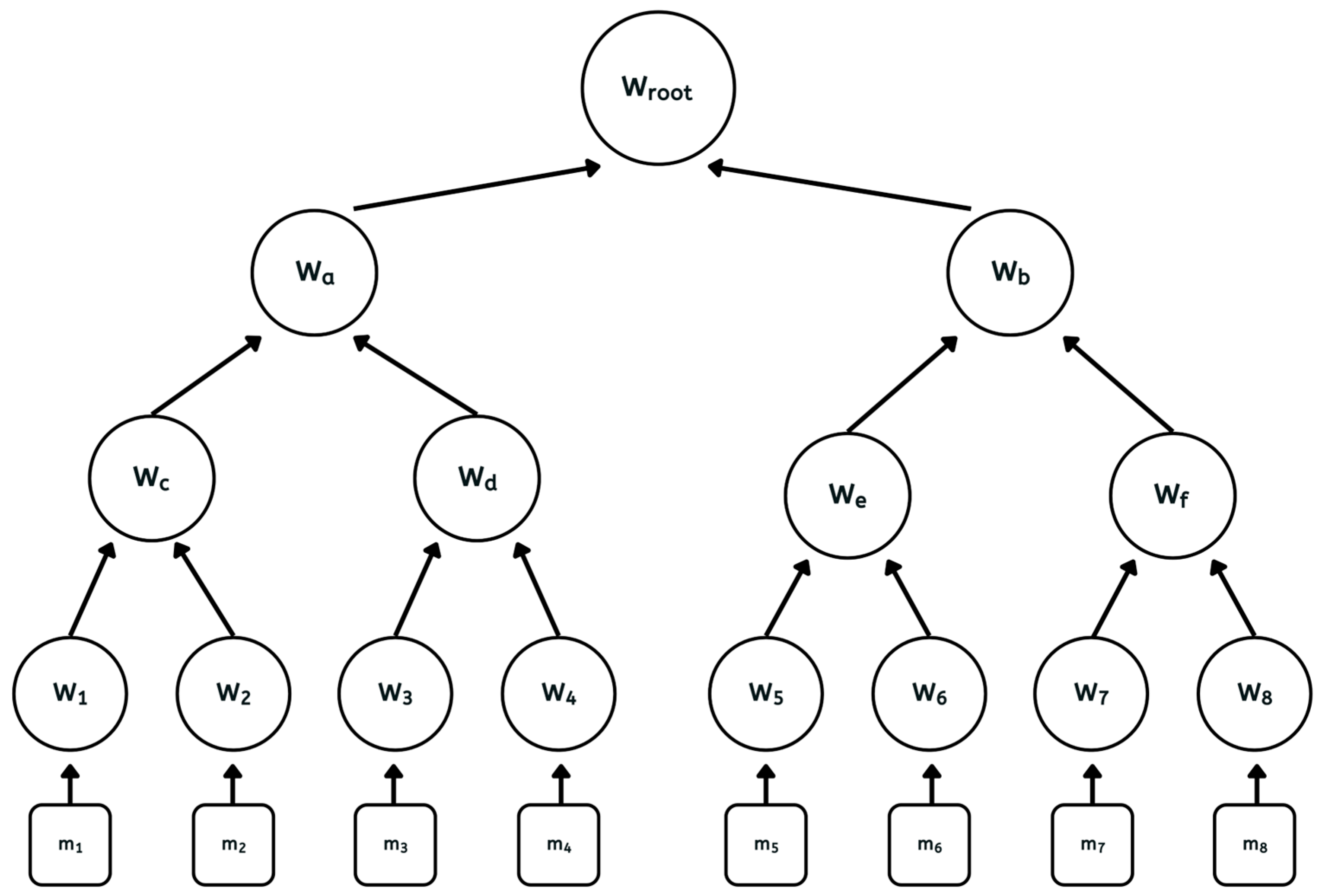
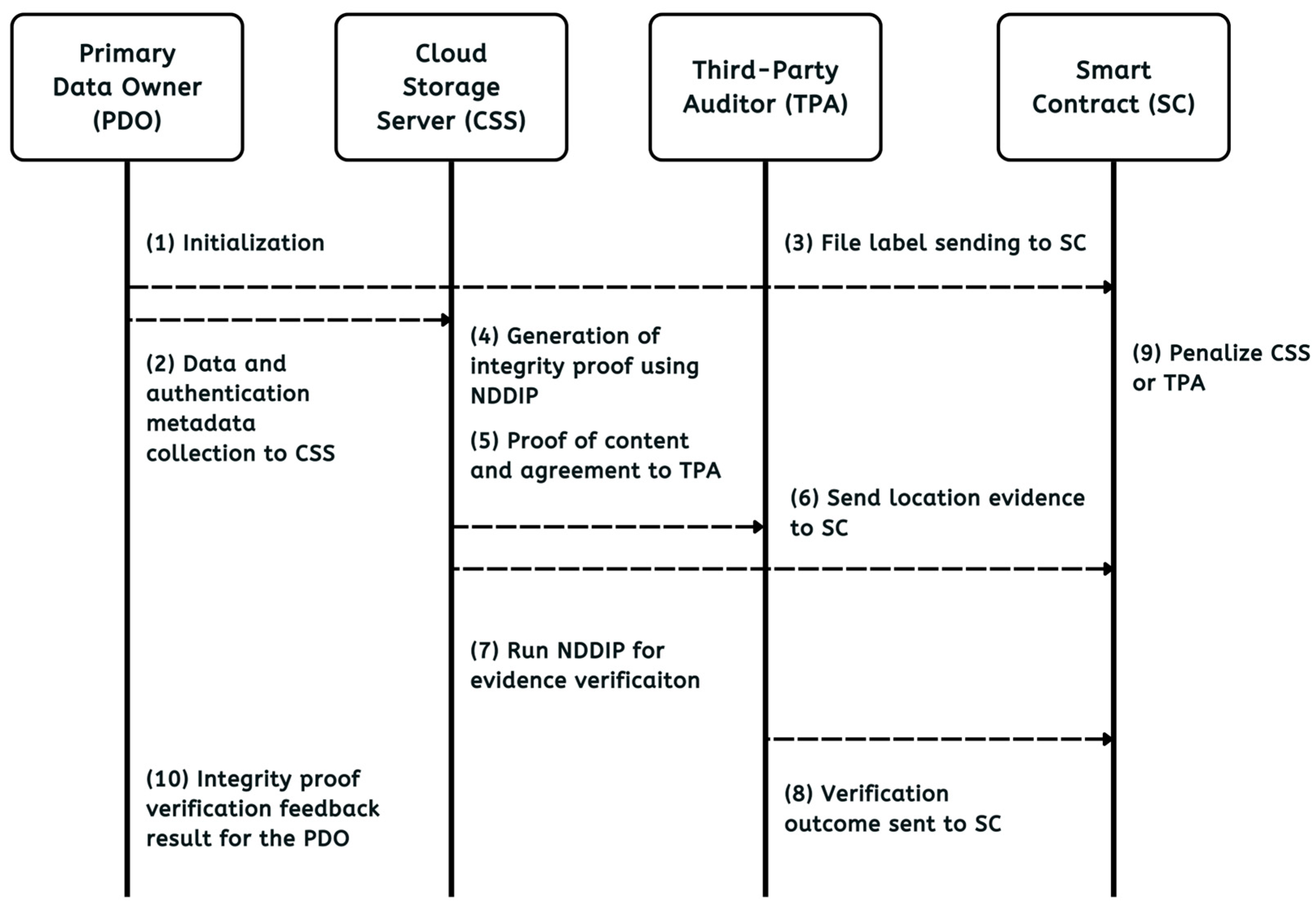
Our framework involves three core entities, namely PDO, CSS, and TPA, each contributing to the system’s computational costs at different phases. The initialization phase involves the PDO to generate authentication tags for each DB before uploading. The audit stage comprises the CSS to create cryptographic evidence in response to challenges with the TPA processing evidence for attestation. To assess how DB size affects these overheads, we performed multiple tests using file blocks of various lengths, ranging from 30 KB (kilobytes) up to 300 KB. In addition, larger files spanning 64 MB (megabytes) to 1024 MB were split into blocks from further stress testing. Throughout the audit stage, we employed a sampling strategy selecting 4.6% of the total blocks as CB [36].

Table A1. Data block size versus time complexity in seconds.

Block Size (KB)	File Size (MB)
	1024	512	256	128	64
30	34.16	27.17	11.18	5.14	1.12
60	19.12	22.18	10.17	4.68	1.06
90	17.25	16.15	9.14	4.25	0.84
120	15.14	14.12	8.64	3.33	0.73
150	12.17	10.11	8.16	3.12	0.67
180	8.16	7.15	6.15	2.52	0.55
210	6.15	4.15	3.14	2.11	0.44
240	4.26	3.25	1.12	1.49	0.35
270	3.15	1.19	0.16	1.11	0.26
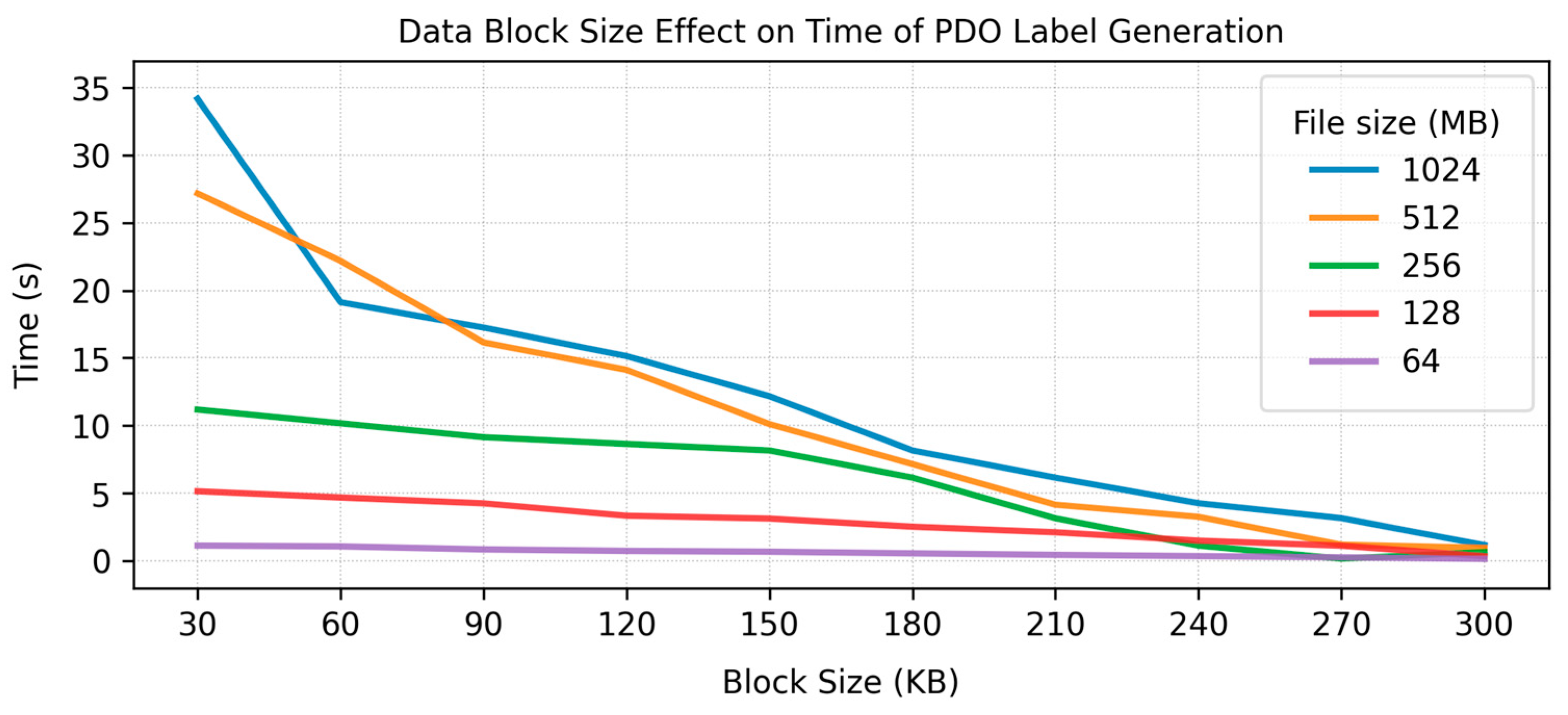
300	1.16	0.95	0.65	0.34	0.14

and Figure 6 illustrate how DB size influences the time required by the PDO to produce authentication metadata. At the onset, as the block size grows from smaller values (30 KB) to moderate-sized values (240 KB), the time spent on generating tags tends to drop. This situation occurs because larger blocks reduce the total number of blocks that need tagging. However, once the DB size passes a certain threshold, each individual tag operation grows more expensive. The total time begins to level off rather than continuing to decrease. In simple words, tag generation stabilizes once the size of the block and the number of segments within it reach an equilibrium in computational costs.

Similarly, when observing the CSS’s time to generate proof data, the performance is influenced by both the size and the number of segments included in each block. As larger blocks are used, the total segment count within those blocks and the consequent components in the integrity proof rise [37]. This leads to an overall increase in the time required for evidence generation, as demonstrated in

Table A2. CSS generation data versus time complexity in seconds.

Block Size (KB)	File Size (MB)
	1024	512	256	128	64
30	2.42	2.14	1.03	0.82	0.63
60	2.63	2.23	1.24	0.91	0.82
90	3.15	2.41	1.44	1.12	0.93
120	3.54	2.50	1.55	1.24	1.03
150	3.82	2.82	1.82	1.24	1.24
180	4.12	3.32	1.91	1.33	1.32
210	4.54	3.51	2.02	1.41	1.41
240	5.41	3.62	2.22	1.54	1.52
270	6.86	3.84	2.41	1.73	1.52
300	7.51	4.25	2.62	1.72	1.53

and Figure 7. The pattern stems from two competing factors. First, increasing the block size means that each contains more data segments. Thus, more cryptographic elements must be processed. Secondly, fewer total blocks are needed for the same dataset when those blocks are larger. The net effect is that while the per-block overhead climbs, the overall quantity to be processed decreases. As a result, the measured CSS generation time, although trending upward, remains manageable within practical bounds versus the block complexity. Therefore, the evidence-generation phase does not become a serious bottleneck in actual deployments.

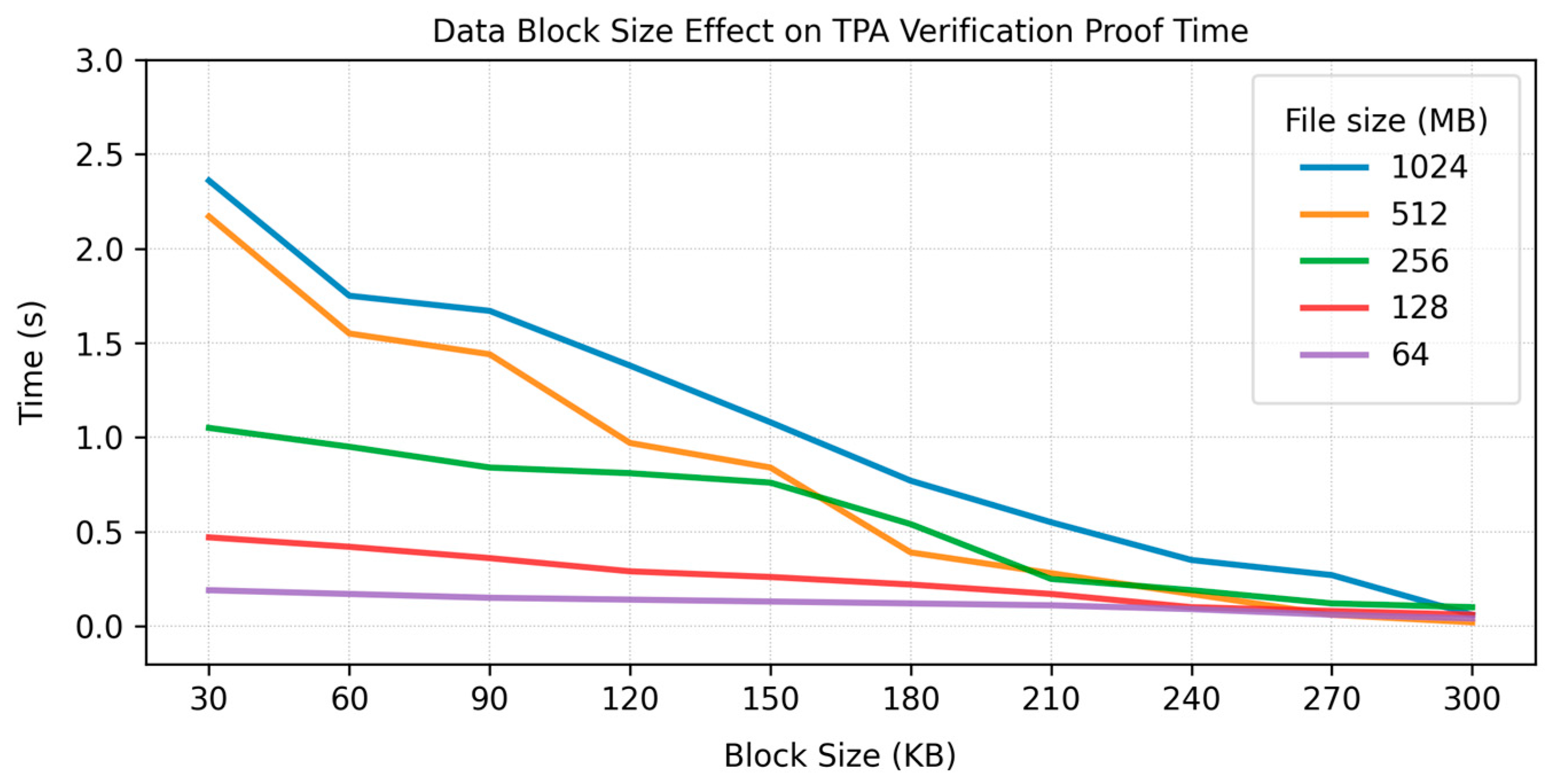
As shown in

Table A3. TPA verification proof data.

Block Size (KB)	File Size (MB)
	1024	512	256	128	64
30	2.36	2.17	1.05	0.47	0.19
60	1.75	1.55	0.95	0.42	0.17
90	1.67	1.44	0.84	0.36	0.15
120	1.38	0.97	0.81	0.29	0.14
150	1.08	0.84	0.76	0.26	0.13
180	0.77	0.39	0.54	0.22	0.12
210	0.55	0.28	0.25	0.17	0.11
240	0.35	0.17	0.19	0.10	0.09
270	0.27	0.06	0.12	0.08	0.06
300	0.06	0.02	0.10	0.06	0.04

and Figure 8, the time required for the TPA to verify the integrity evidence inclines to decrease as the size of each DB increases. An important reason for this behavior is that fewer total blocks exist in larger block configurations, so the number of CSs goes down. To make this clearer, we can model the TPA’s overhead in terms of Equation (34):

$${Cost}_{TPA}=\left(c+2\right)M+\left(s+c+1\right)E+2P,$$

(34)

where $c$ is the challenged blocks in a given audit; $s$ is the segments within each block; $M$ is the computational cost per block for certain multiplication, hashing, or message authentication procedures; $E$ represents the encryption cost per label verification step; and $P$ represents any additional pairing operation costs needed to finalize the proof check. Under most parameter settings, $c$ decreases more sharply with larger block sizes than $s$ increases. Consequently, the term $\left(c+2\right)M$ sees a notable reduction, while $\left(s+c+1\right)E$ gradually rises. It does not offset the savings gained from having fewer blocks in entirety. Thus, the net effect is that TPA verification time generally goes down for bigger blocks until extremely large blocks could potentially start increasing $\left(s+c+1\right)E$ to a point that can limit these gains. Based also on the graph, for smaller blocks (e.g., 30 KB), $c$ can be relatively large, ensuing higher values for the $\left(c+2\right)M$ term, an initial high time for small blocks. It is also observed that when block size grows (150 to 300 KB), the TPA verification times drop to under 1 s in most cases. This is because fewer challenge blocks (CBs) are needed, which makes $\left(c+2\right)M$ and $\left(s+c+1\right)E$ converge to smaller values. A variation in overall file size is also noted, with 1024 KB, 512 KB, 256 KB, 128 KB, and 64 KB constituting different total file magnitudes. Each line shows a downward slope. The differences among these curves reflect how large files involve more blocks but also benefit more from consolidation when scaled up. In a practical setting, moderately sized blocks appear to strike an optimal balance between overhead reduction and data granularity. This outcome guarantees that verifying proof remains efficient while maintaining sufficient data segmentation for reliability and security.

Article [36] developed a TPA-based verification method composed of two phases, an initialization and audit stage. In order to highlight the performance gains, we compare both overheads against the selected benchmark. Notably, the work supports both global and sampling authentication with the same adoption of a fixed 4.6% probability of challenged blocks.

Table 1. Computational cost comparison.

Index	Existing Method	Our Method
PDO generation mark	$nM+2nE$	$n\left(s+1\right)M+2nE$
CSP generation evidence	$\left(2c-1\right)M+cE$	$\left(s\times c+c-1\right)M+cE$
TPA verification evidence	$cM+E+\left(c+1\right)P$	$\left(c+2\right)M+\left(s+c+1\right)E+2 P$

provides a theoretical cost comparison between the methods and the mechanism described. In the table, $n$ is the total number of DBs, $c$ is the challenged blocks, and $s$ denotes segments within each block. The parameters $M$, $E$, and $P$ reflect the cost of multiplication, exponentiation, and bilinear pairing operations.

For the existing PDO generation method [36] of $nM+2nE$, each block requires $M$ multiplications plus $2E$ exponentiations for tag creating, multiplied by the $n$ total blocks. We proposed a strategy of $n\left(s+1\right)M+2nE$, where the PDO treats each block as having $s$ segments plus an additional factor to handle a “frame” or label aggregator. Per block, we need $\left(s+1\right)$ multiplications. The $2nE$ term parallels the existing technique to reflect two exponentiations per block. Although this slightly increases the cost for blocks due to segment handling, it lays the groundwork for more efficient auditing in later phases.

Each challenge for the CSP generation evidence of $\left(2c-1\right)M+cE$ in the reference need to aggregate partial proofs requiring multiple processes. The term $\left(2c-1\right)$ indicates that the CSP multiplies intermediate proof elements an additional $\left(2c-1\right)$ times, while $cE$ indicates exponentiations correlated with the CB. Our method $\left(s\times c+c-1\right)M+cE$ factor is in $s$ because each CB can be subdivided into segments that contribute to evidence calculation. The final multiplier is thus $\left(s\times c+c-1\right)$; it embodies the cost of aggregation of segment tags from each of the CB. $cE$ is needed for consistent exponentiation for each segment set. While the numeric front of $M$ appears larger (due to $\left(s\times c\right)$ in practice, having total blocks can (optimized segment size) mitigate the impact. The random sampling fixed value makes sure that $c$ remains a fraction of $n$.

The current procedure uses pairing, P, to check the correctness of each block’s integrity proof, and $\left(c+1\right)P$ precedes an initial pairing for global signature, plus $c$ of additional coupling for CB. A single $E$ correspond to a final check. Our proposal differentiates by integrating further multiplications $\left(c+2\right)M$ to handle the extended label structure. The count $\left(s+c+1\right)E$ connotes that each CB has $s$ sub-checks, plus an overall aggregator and a final exponent for signature verification. Only two pairings, $2 P$, are needed in the designs, one for the global verification step and one for the secondary signature. This is less than $\left(c+1\right)P$ in large datasets. Since the pairing operations are often the bottlenecks, reducing them down to $2 P$ is a substantial improvement for scenarios where $c$ is significant. We derived our method by analyzing the extra sub-block segmentation and partial-tag aggregations introduced in our RBMHT. Concretely, each block is subdivided into $s$ segments, so the label-generation cost grows to $n\left(s+1\right)M+2nE$, and the CSP’s proof-assembly must account for each CB’s segments, giving $(s\times c+c-1)M+cE$. For TPA verification, we decomposed repeated pairings down to a constant $2 P$, but must perform exponentiations to handle each segment’s partial evidence; thus, $\left(c+2\right)M+\left(s+c+1\right)E+2 P$. To demonstrate the calculations for parameters at 64 MB, we split the file into $n$ = 64 blocks, $c$ = 3 (4.6% or 5% of 64), and $s$ = 2 (proposed method only). Time operations clocked in at $M$ = 0.0038 s, $E$ = 0.0059 s, $P$ = 0.0090 s and $M$ = 0.0012 s, $E$ = 0.0023 s, and $M$ = 0.0030 s, respectively. According to the three phases, the existing method and our method results in $PDO$ = 0.9984 s, $CSP$ = 0.0367 s, and $TPA$ = 0.0533 s, with sum of 1.0884 s or 1.10 s and $PDO$ = 0.5248, $CSP$ = 0.0165 s, and $TPA$ = 0.0258 s with sum of 0.5671 s or 0.60 s, respectively.

Table A4. Computational cost.

File Size (MB)	Existing Method	Our Method
64	1.10	0.60
128	2.30	1.60
256	3.20	2.50
512	6.50	5.40
1024	9.20	8.70

and Figure 9 show the experimental results.

In terms of performance trends, our method exhibits consistent factor improvement across all tested file sizes with 1.83 (64 MB, from 1.10/0.60), 1.44 (128 MB), 1.28 (256 MB), 1.20 (512 MB), and 1.06 (1024 MB). When we say the ratio is 1.83, it means that the existing technique takes 1.83 times as long. In other words, if our method needs 0.60 s, then the existing method requires 1.10 s, almost twice as slow. The degree of ratio is larger for smaller files, and it gradually shrinks for bigger files until it belongs 1.06 times faster at 1024 MB. It can be attributed to reduced pairing operations and efficient exponentiation handling. As file size increases from 64 MB to 1024 MB, both show a growth in total time, but our solution scales more gracefully because it limits the linear expansion of cost-intensive bilinear pairings. For mid-range file sizes (128 MB to 512 MB), exponentiation and multiplication dominate total runtime, but our technique’s segmentation strategy prevents theses operations from escalating sharply. A key reason for the performance gap is the relegation of pairing to a nearly constant overhead, whereas the old method applies it more frequently. This causes faster growth in total computational cost. The technical optimization allows us to outperform its counterpart by up to 40% for smaller file sizes and still maintain a competitive edge for 1024 MB, as seen by a near parallel but lower curve in the graph.

6.2. Communication Overhead

The overhead of communication measures the quantity of data exchanged among the CSS, TPA, and SC during integrity checks [38]. In an audit process, the TPA sends dispute information to the CSS. It then replies with certificates, and the TPA returns attestation results to the SC. Our proposed mechanism minimizes these transmissions through an efficient proof generation by omitting TPA-to-CSS challenge messages. Thus, diminishing the number and size of network packets. Below, we detail how each step contributes to the overall overhead and compare our method’s performance against the chosen similar benchmark.

Table 2. Communication overhead comparison.

Index	Existing Method	Our Method
TPA sends challenge information	$O\left(c\right)$	0
CSS returns complete certificate	$O\left(1\right)$	$O\left(log\left(n/c\right)\right)$
TPA returns content verification results	0	$O\left(1\right)$

contrasts these communication steps for the two approaches. We list their complexity as $O\left(c\right), O\left(1\right), O\left(log\left(n/c\right)\right)$, where n is the total DB, $c$ is the audit’s challenged blocks, and $log\left(n/c\right)$ is partial evidence used to prove correctness, requiring logarithmic-size proofs relative to the total and challenged block ratios. For these derivations, we followed the standard practice in [38] of labeling each message exchange with $O\left(·\right)$. We replaced the baseline’s $O\left(c\right)$ challenge transmissions with zero or near-zero overhead by localizing challenge generation (no TPA to CSS roundtrips), introducing a $log\left(n/c\right)$ factor for the size of partial proofs that reference only refuted blocks within a bigger dataset.

For article [36], the $O\left(c\right)$ infers that each block challenge is explicitly transmitted to the CSs, while our procedure (0 overhead) is to allow the TPA to derive the challenge locally and does not need to repeatedly inform the CSS. This design substantially cut back roundtrip communications. The $O\left(1\right)$ returns a single proof while $O\left(log\left(n/c\right)\right)$ is a compressed structure. As $c$ shrinks relative to $n$, the overhead for returning these partial proofs are grown only logarithmically rather than linearly. In the current method, when a TPA returns content, a 0 overhead is established, interpreted as negligible or a fused step. Our $O\left(1\right)$ is for a final acknowledgment that the TPA’s assessments are complete. This include a small extra message to inform a SC.

Table A5. Communication overhead.

File Size (MB)	Existing Method	Our Method
64	7	0.75
128	11	1.73
256	18	3.22
512	28	4.15
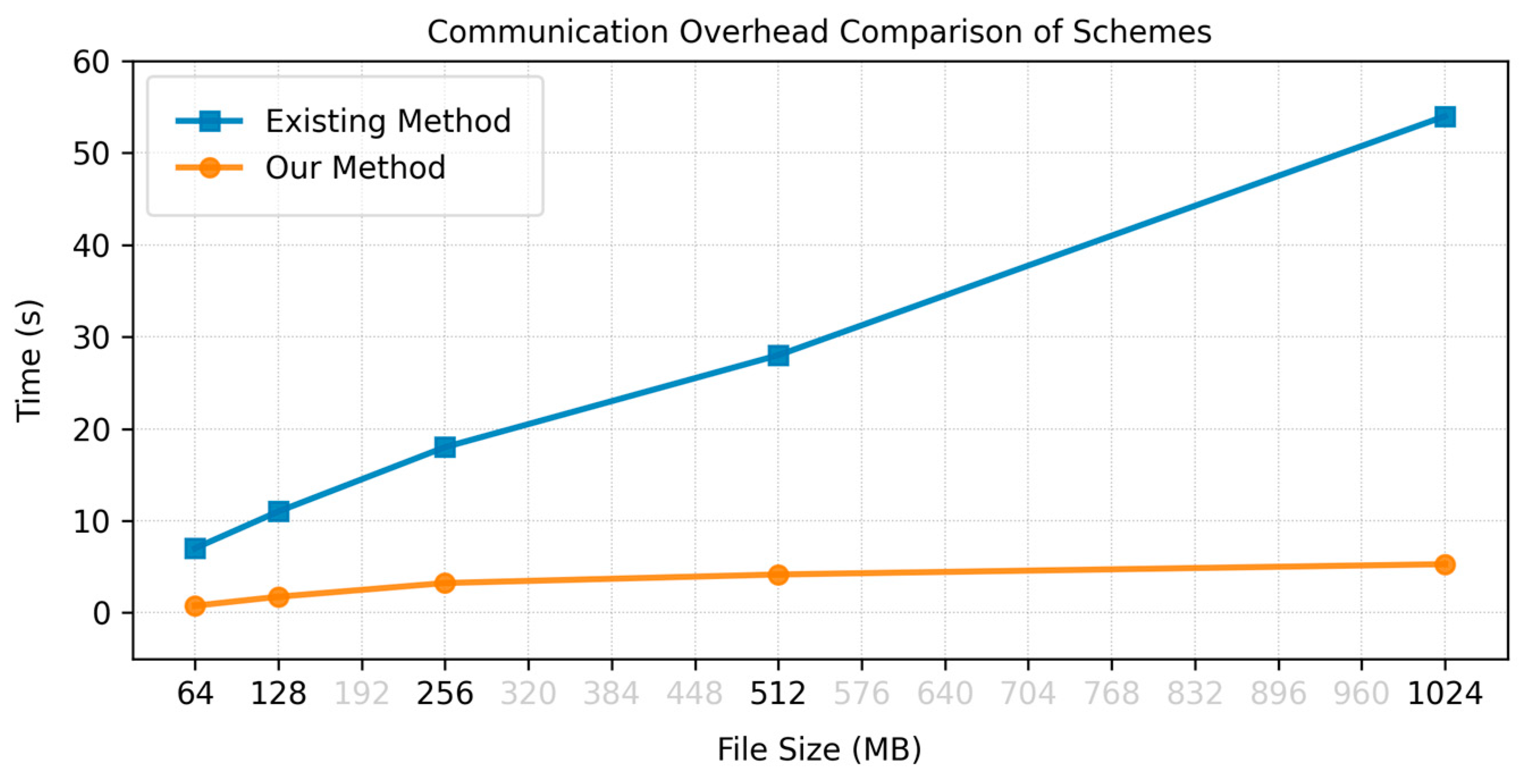
1024	54	5.27

and Figure 10 displays the actual simulation for file sizes ranging from 64 MB to 1024 MB. We observed that the existing method’s overheads grows considerably from 7 units at 64 MB to 54 units at 1024 MB while our proposal remains comparatively low. It only climbs from 0.75 to 5.27. The discrepancy arises mainly because it requires the TPA to send requests $O\left(c\right)$ and do not compress the proofs effectively, whereas we eliminated the back-and-forth concept and used logarithmic-sized certificates.

Both removing repeated, unnecessary communications and compressing proofs greatly streamline data exchange [38]. We achieved a lower mean latency of 86.22%, especially for large datasets, where $n\gg c$, improving scalability in cloud audits where frequent hold-up results in extensive network traffic.

7. Conclusions and Future Works

This study tackles the pressing dilemma of maintaining data credibility in outsourced cloud storage by creating a privacy-preserving authentication model that also enforces fairness. To achieve this, we proposed a RBMHT framework to seamlessly integrate blockchain-driven smart contracts to improve security, optimize verification efficiency, and ensure equitable compensation. The experimental findings indicate that our model outperforms existing similar methodology with smaller computational and communication average overheads of 24.02% and 86.22%, respectively. These results are attained mainly by minimizing the number of costly cryptographic operations and limiting the auditor’s communication with the cloud provider through a more efficient proof-generation process. By relegating expensive pairing routines to a nearly constant factor and using logarithmic-sized certificates, the scheme maintains significant margins across both metrics. Furthermore, as each block grows larger, fewer total blocks are needed to store the same file. When it challenges only a small fraction of blocks (5% to 10%) and sends one compressed proof rather than multiple full-block proofs, the number of messages exchanged drops sharply. Because there are fewer block-level hashes or signatures, the traffic shrinks by more than an order of magnitude compared to the older method.

Our results have practical significance for large-scale applications such as healthcare systems, government records, and corporate data centers, where reliable, privacy-centric authentication can greatly decrease storage and auditing costs while guaranteeing trust. By integrating BlkChn-based smart contracts and minimizing third-party interventions, we are paving the way for fair, tamper-proof environments that better protect user’s data and promote transparent compensation. Despite these promising results, various limitations must be acknowledged. First, the study exclusively relied on simulated data, which may not fully capture the complexity of real-world network environments. Second, it did not examine the scheme’s performance under highly adversarial or multi-tenant scenarios, leaving open questions about security trade-offs in more extreme conditions. Third, real-time user authentication and identity management were not fully implemented, so their impact and overall system throughput remain uncertain.

In future work, we intend to incorporate cutting-edge zero-knowledge proof techniques to further obfuscate data blocks and verification metadata. Such an approach could bolster confidentiality quality assurance and repress the risk of partial information leakage. Moreover, researchers may investigate interoperable or layered BlkChn architectures to dynamically adjust consensus parameters based on workload intensity. This would allow the validation process to scale more efficiently under varying network conditions and client demands while asserting high transaction throughput. Our work lays the foundation for more scalable, adaptive verification methods capable of maintaining trust and fairness in complex cloud environments.