Defect Engineering and Dopant Properties of MgSiO3
Abstract
:1. Introduction
2. Computational Methods
3. Results
3.1. Crystal Structure of MgSiO3
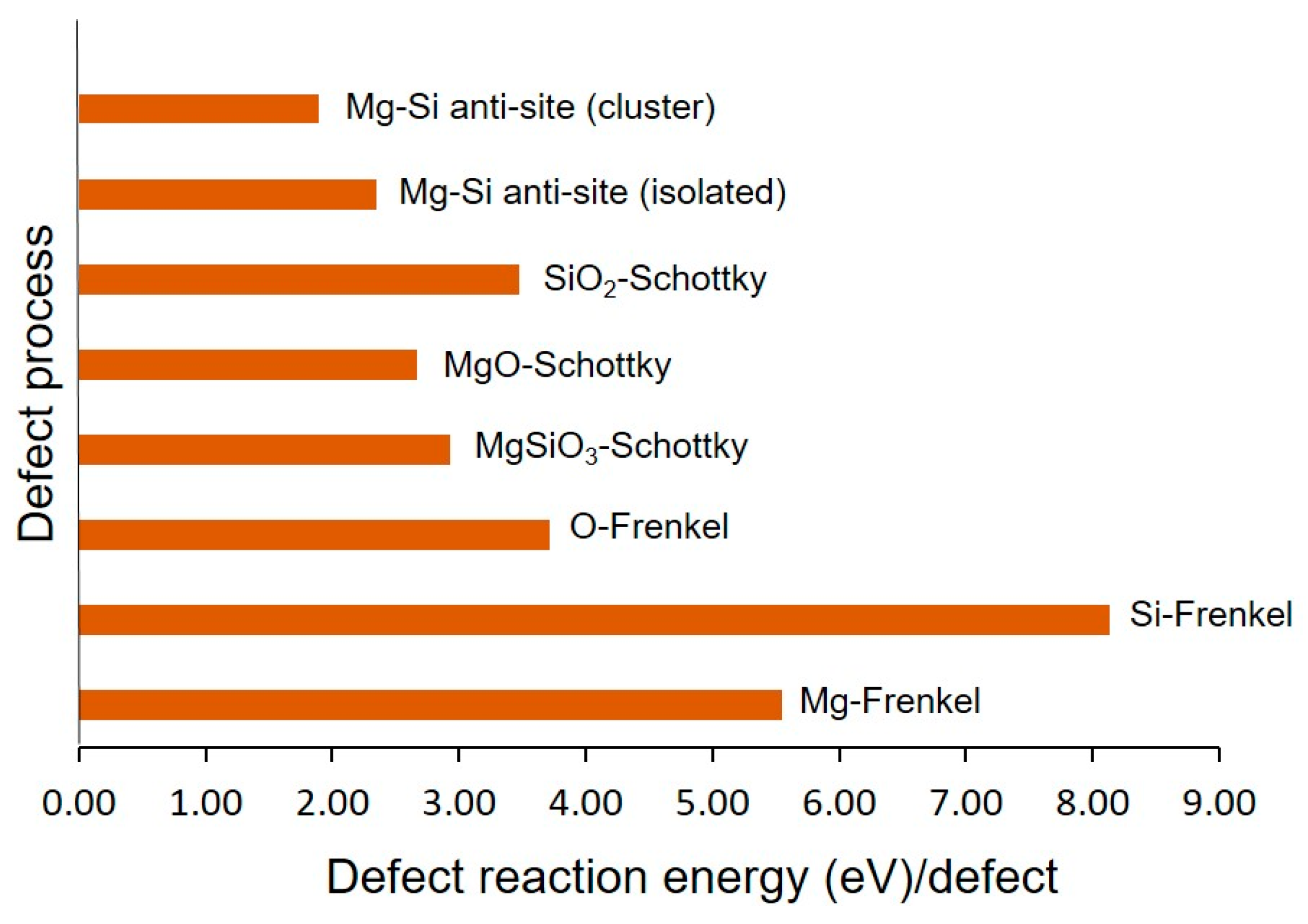
3.2. Intrinsic Defect Formation
3.3. Solution of Dopants
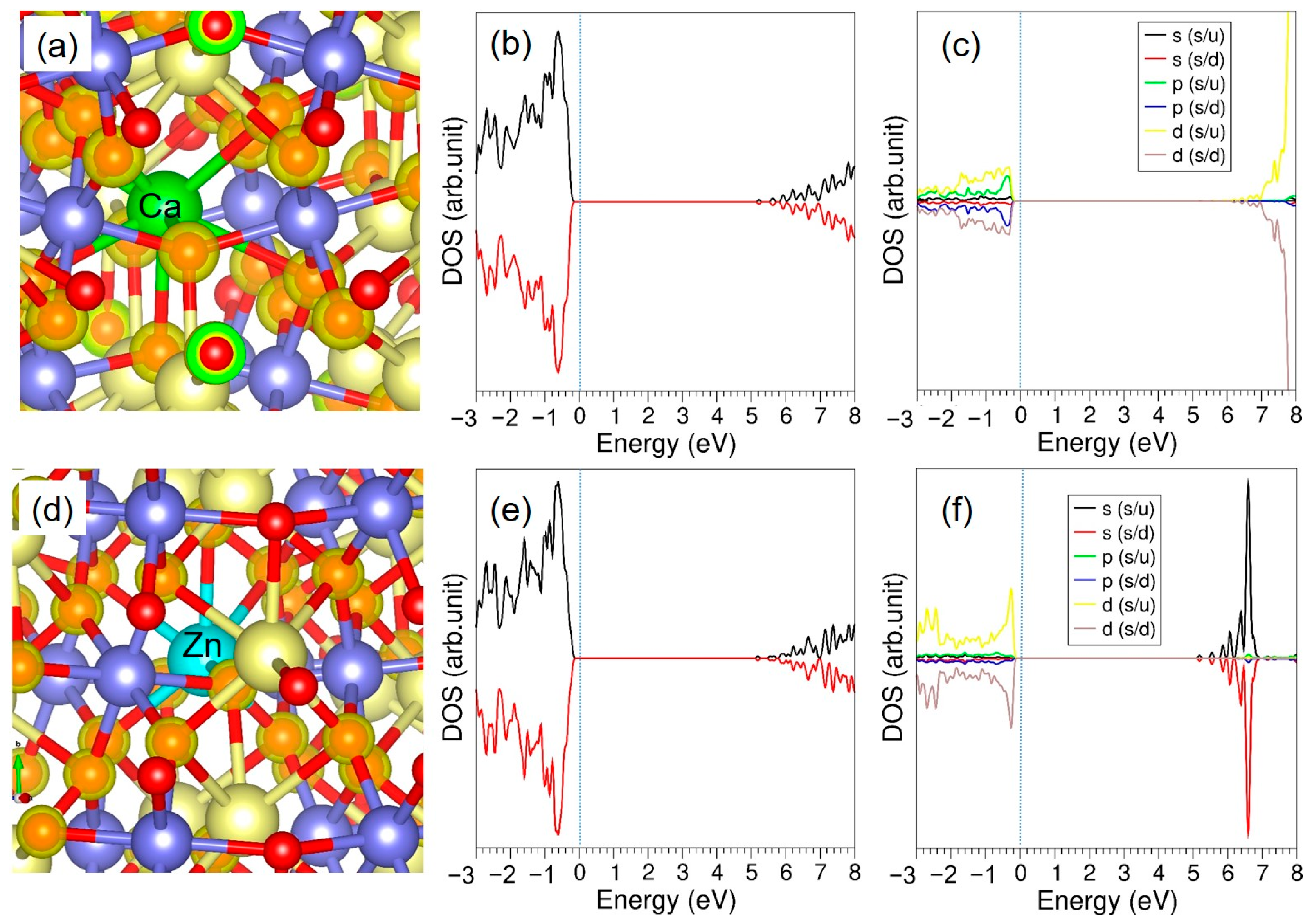
3.3.1. Divalent Dopants

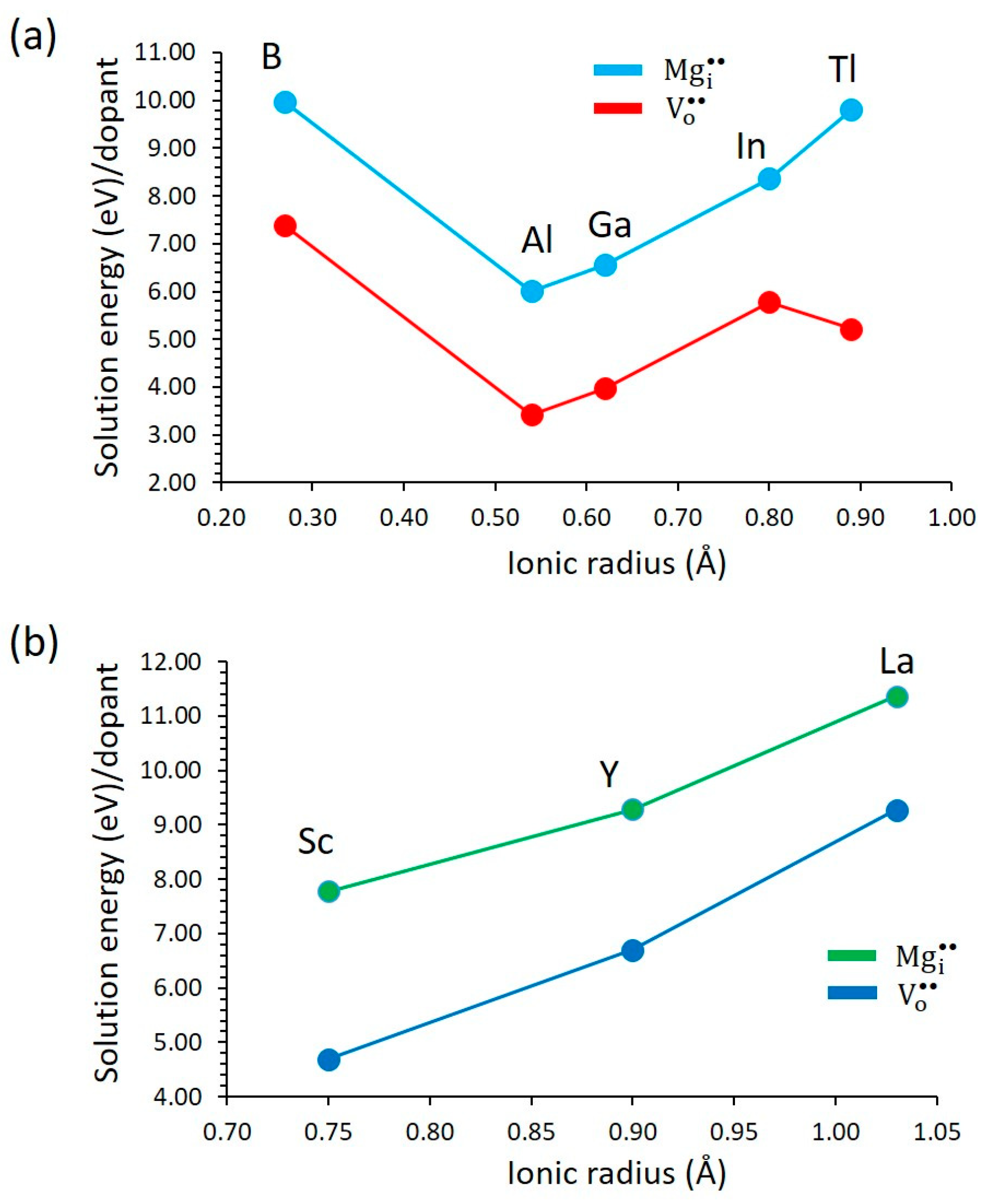
3.3.2. Trivalent Dopants
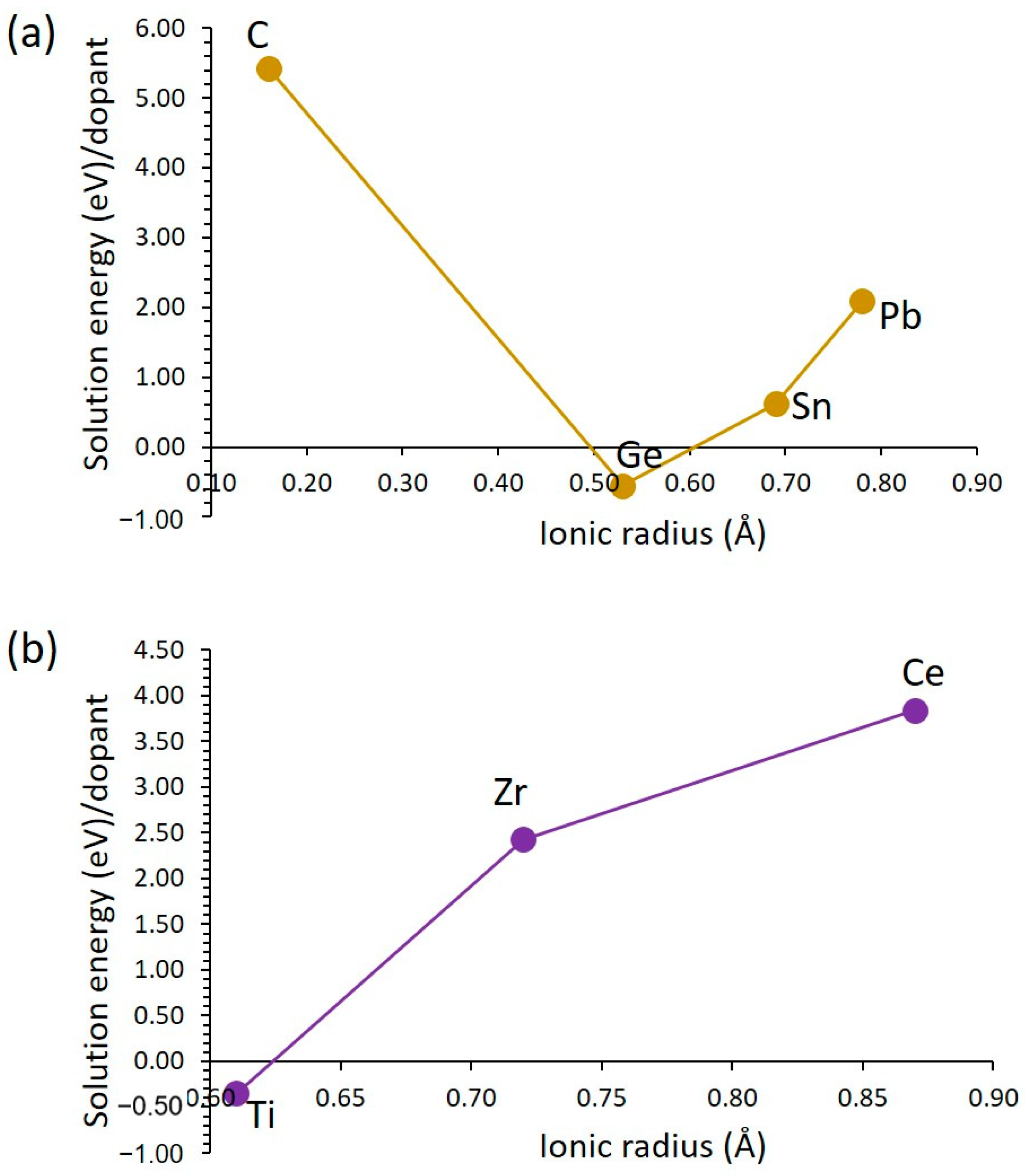
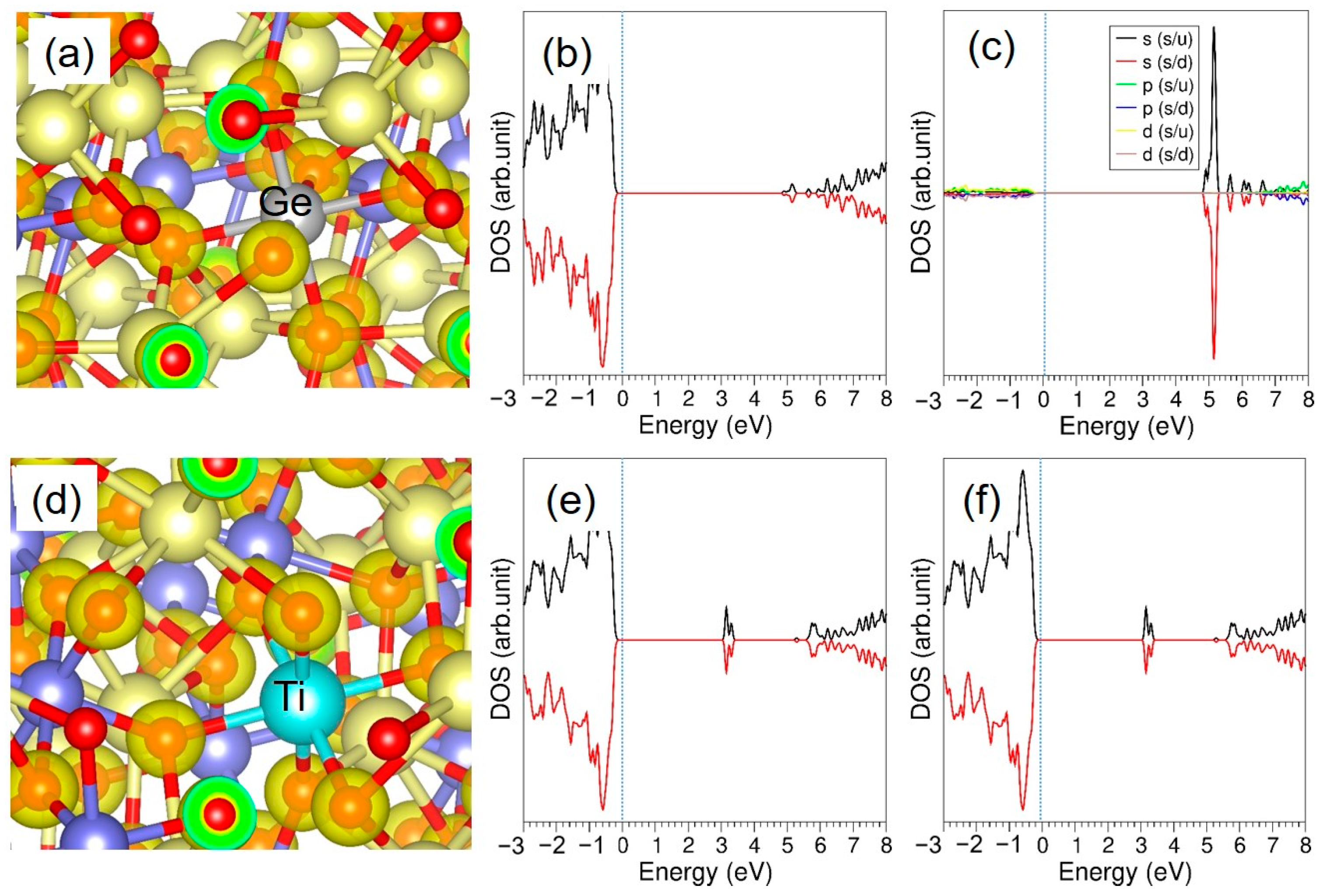
3.3.3. Tetravalent Dopants
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vandeginste, V.; Lim, C.; Ji, Y. Exploratory Review on Environmental Aspects of Enhanced Weathering as a Carbon Dioxide Removal Method. Minerals 2024, 14, 75. [Google Scholar] [CrossRef]
- Ma, D.; Duan, H.; Zhang, J.; Bai, H. A state-of-the-art review on rock seepage mechanism of water inrush disaster in coal mines. Int. J. Coal Sci. Technol. 2022, 9, 50. [Google Scholar] [CrossRef]
- Yao, D.; Jiang, N.; Wang, X.; Jia, X.; Lv, K. Mechanical behaviour and failure characteristics of rocks with composite defects of different angle fissures around hole. Bull. Eng. Geol. Environ. 2022, 81, 290. [Google Scholar] [CrossRef]
- Shi, T.; Fu, J.; Song, W.; Wang, J.; Y, K.M. Effect of internal fractures on mechanical properties and failure of sandstone under multi-physical fields. Heliyon 2024, 10, e24312. [Google Scholar] [CrossRef] [PubMed]
- Criniti, G.; Kurnosov, A.; Boffa Ballaran, T.; Frost, D.J. Single-Crystal Elasticity of MgSiO3 Bridgmanite to Mid-Lower Mantle Pressure. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020967. [Google Scholar] [CrossRef]
- Sharp, T.G.; Lingemann, C.M.; Dupas, C.; Stöffler, D. Natural Occurrence of MgSiO3-Ilmenite and Evidence for MgSiO3-Perovskite in a Shocked L Chondrite. Science 1997, 277, 352–355. [Google Scholar] [CrossRef]
- Vanpeteghem, C.B.; Zhao, J.; Angel, R.J.; Ross, N.L.; Bolfan-Casanova, N. Crystal structure and equation of state of MgSiO3 perovskite. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Howard, C.; Stokes, H. Structures and phase transitions in perovskites—A group-theoretical approach. Acta Crystallogr. Sect. A 2004, 61, 93–111. [Google Scholar] [CrossRef]
- Karki, B.B.; Stixrude, L.; Clark, S.J.; Warren, M.C.; Ackland, G.J.; Crain, J. Elastic properties of orthorhombic MgSiO3 perovskite at lower mantle pressures. Am. Mineral. 1997, 82, 635–638. [Google Scholar] [CrossRef]
- Kim, Y.H.; Yi, Y.S.; Kim, H.I.; Chow, P.; Xiao, Y.; Shen, G.; Lee, S.K. Structural Transitions in MgSiO3 Glasses and Melts at the Core-Mantle Boundary Observed via Inelastic X-ray Scattering. Geophys. Res. Lett. 2019, 46, 13756–13764. [Google Scholar] [CrossRef]
- Kono, Y.; Shibazaki, Y.; Kenney-Benson, C.; Wang, Y.; Shen, G. Pressure-induced structural change in MgSiO3 glass at pressures near the Earth’s core-mantle boundary. Proc. Natl. Acad. Sci. USA 2018, 115, 1742–1747. [Google Scholar] [CrossRef]
- Sinogeikin, S.V.; Zhang, J.; Bass, J.D. Elasticity of single crystal and polycrystalline MgSiO3 perovskite by Brillouin spectroscopy. Geophys. Res. Lett. 2004, 31, 6. [Google Scholar] [CrossRef]
- Goel, A.; Tulyaganov, D.U.; Shaaban, E.R.; Knee, C.S.; Eriksson, S.; Ferreira, J.M.F. Structure and crystallization behaviour of some MgSiO3-based glasses. Ceram. Int. 2009, 35, 1529–1538. [Google Scholar] [CrossRef]
- Mariñoso Guiu, J.; Ghejan, B.-A.; Bernhardt, T.M.; Bakker, J.M.; Lang, S.M.; Bromley, S.T. Cluster Beam Study of (MgSiO3)+-Based Monomeric Silicate Species and Their Interaction with Oxygen: Implications for Interstellar Astrochemistry. ACS Earth Space Chem. 2022, 6, 2465–2470. [Google Scholar] [CrossRef]
- Song, R.; Yang, L.; Luan, J.; Yuan, H.; Ji, S.; Wan, D.; Liu, J.; Hu, W.; Zhong, C. MgSiO3 doped, carbon-coated SiOx anode with enhanced initial coulombic efficiency for lithium-ion battery. J. Energy Storage 2025, 105, 114687. [Google Scholar] [CrossRef]
- Lin, L.; Min, Y.; Chaoshu, S.; Weiping, Z.; Baogui, Y. Synthesis and Luminescence Properties of Red Phosphors: Mn2+ Doped MgSiO3 and Mg2SiO4 Prepared by Sol-Gel Method. J. Rare Earths 2006, 24, 104–107. [Google Scholar] [CrossRef]
- Moncorgé, R.; Capobianco, J.A.; Bettinelli, M.; Cavalli, E.; Girard, S.; Guyot, Y. Cr:MgSiO3, a Cr doped crystal with long fluorescence lifetime and broad-band emission around 1.52 µm. In Advanced Solid State Lasers, Coeur d’Alene, Idaho, 1998/02/02; Bosenberg, W., Fejer, M., Eds.; Optica Publishing Group: Washington, DC, USA, 1998; Volume 19, p. CS16. [Google Scholar]
- Kuganathan, N.; Kordatos, A.; Anurakavan, S.; Iyngaran, P.; Chroneos, A. Li3SbO4 lithium-ion battery material: Defects, lithium ion diffusion and tetravalent dopants. Mater. Chem. Phys. 2019, 225, 34–41. [Google Scholar] [CrossRef]
- Kuganathan, N.; Ganeshalingam, S.; Chroneos, A. Defects, Diffusion, and Dopants in Li2Ti6O13: Atomistic Simulation Study. Materials 2019, 12, 2851. [Google Scholar] [CrossRef]
- Santos, A.L.D.S.; Freire, E.B.; Bispo, G.F.D.C.; Jackson, R.A.; Macedo, Z.S.; Valerio, M.E. A comparison of oxygen Frenkel formation and rare earth doping in the Lu2SiO5 and Y2SiO5 orthosilicates using a computer modelling approach. Comput. Mater. Sci. 2024, 243, 113125. [Google Scholar] [CrossRef]
- Freire, E.B.V.; Santos, A.L.d.S.; Bispo, G.F.d.C.; Macedo, Z.S.; Jackson, R.A.; Valerio, M.E.G. Local modification of the crystalline structure due to co-doping with RE3+ in cadmium metasilicate. Ceram. Int. 2024, 50 Part A, 22534–22543. [Google Scholar] [CrossRef]
- Kuganathan, N.; Kelaidis, N.; Chroneos, A. Defect Chemistry, Sodium Diffusion and Doping Behaviour in NaFeO2 Polymorphs as Cathode Materials for Na-Ion Batteries: A Computational Study. Materials 2019, 12, 3243. [Google Scholar] [CrossRef] [PubMed]
- Karki, B.B.; Khanduja, G. Computer simulation and visualization of vacancy defects in MgSiO3 perovskite. Model. Simul. Mater. Sci. Eng. 2006, 14, 1041. [Google Scholar] [CrossRef]
- Ammann, M.W.; Brodholt, J.P.; Dobson, D.P. DFT study of migration enthalpies in MgSiO3 perovskite. Phys. Chem. Miner. 2009, 36, 151–158. [Google Scholar] [CrossRef]
- Stashans, A.; Rivera, K.; Pinto, H.P. First-principles investigation of Fe-doped MgSiO3-ilmenite. Phys. B Condens. Matter 2012, 407, 2037–2043. [Google Scholar] [CrossRef]
- Stashans, A.; Eras, L.; Chamba, G. Modelling of Al impurity in perovskite and ilmenite structures of MgSiO3. Phys. Chem. Miner. 2010, 37, 191–199. [Google Scholar] [CrossRef]
- Kaushalya, R.; Iyngaran, P.; Kuganathan, N.; Chroneos, A. Defect, Diffusion and Dopant Properties of NaNiO2: Atomistic Simulation Study. Energies 2019, 12, 3094. [Google Scholar] [CrossRef]
- Zhao, Y.; Cormack, A.N.; Wu, Y. Atomistic Simulations of Defect Structures in Rare-Earth-Doped Magnesium Oxide. Crystals 2024, 14, 384. [Google Scholar] [CrossRef]
- Bispo, G.F.C.; Nascimento, D.S.; Santana, L.B.; Ferreira, G.S.; Macedo, Z.S.; Lima, H.R.B.R.; Souza, S.O.; d’Errico, F.; Jackson, R.A.; Valerio, M.E.G. Defects in MgB4O7 (pure and doped with lanthanides): A case study using a computational modelling approach. Phys. B Condens. Matter 2022, 640, 414049. [Google Scholar] [CrossRef]
- Freire, E.B.V.; Santos, A.L.d.S.; Bispo, G.F.d.C.; Macedo, Z.S.; Jackson, R.A.; Valerio, M.E.G. Effect of trivalent rare earth doping in cadmium silicates hosts: A theoretical study. Phys. Scr. 2022, 97, 125829. [Google Scholar] [CrossRef]
- Gale, J.D.; Rohl, A.L. The General Utility Lattice Program (GULP). Mol. Simul. 2003, 29, 291–341. [Google Scholar] [CrossRef]
- Kuganathan, N.; Chroneos, A. Atomic-scale studies of garnet-type Mg3Fe2Si3O12: Defect chemistry, diffusion and dopant properties. J. Power Sources Adv. 2020, 3, 100016. [Google Scholar] [CrossRef]
- Gale, J.D. GULP: A computer program for the symmetry-adapted simulation of solids. J. Chem. Soc. Faraday Trans. 1997, 93, 629–637. [Google Scholar] [CrossRef]
- Mott, N.F.; Littleton, M.J. Conduction in polar crystals. I. Electrolytic conduction in solid salts. Trans. Faraday Soc. 1938, 34, 485–499. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes in C, 2nd ed.; The Art of Scientific Computing; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Kudoh, Y.; Ito, E.; Takeda, H. Effect of pressure on the crystal structure of perovskite-type MgSiO3. Phys. Chem. Miner. 1987, 14, 350–354. [Google Scholar] [CrossRef]
- Spitaler, J.; Estreicher, S.K. Perspectives on the Theory of Defects. Front. Mater. 2018, 5, 70. [Google Scholar] [CrossRef]
- Kim, Y. Theoretical investigation of the cation antisite defect in layer-structured cathode materials for Li-ion batteries. Phys. Chem. Chem. Phys. 2019, 21, 24139–24146. [Google Scholar] [CrossRef] [PubMed]
- Kempaiah Devaraju, M.; Duc Truong, Q.; Hyodo, H.; Sasaki, Y.; Honma, I. Synthesis, characterization and observation of antisite defects in LiNiPO4 nanomaterials. Sci. Rep. 2015, 5, 11041. [Google Scholar] [CrossRef] [PubMed]
- Kröger, F.A.; Vink, H.J. Relations between the Concentrations of Imperfections in Crystalline Solids. In Solid State Physics; Seitz, F., Turnbull, D., Eds.; Academic Press: Cambridge, MA, USA, 1956; Volume 3, pp. 307–435. [Google Scholar]
- Wall, A.; Price, G.D. Defects and diffusion in MgSiO3 perovskite: A computer simulation. In Perovskite: A Structure of Great Interest to Geophysics and Materials Science; American Geophysical Union: Washington, DC, USA, 1989; pp. 45–53. [Google Scholar]
- Smyth, D.M. The effects of dopants on the properties of metal oxides. Solid State Ion. 2000, 129, 5–12. [Google Scholar] [CrossRef]
- Alfredsson, M.; Corà, F.; Brodholt, J.P.; Parker, S.C.; Price, G.D. Crystal morphology and surface structures of orthorhombic MgSiO3 in the presence of divalent impurity ions. Phys. Chem. Miner. 2005, 32, 379–387. [Google Scholar] [CrossRef]
- Ishii, T.; McCammon, C.; Katsura, T. Iron and aluminum substitution mechanism in the perovskite phase in the system MgSiO3-FeAlO3-MgO. Am. Mineral. 2023, 108, 738–743. [Google Scholar] [CrossRef]


| Interaction | A/eV | ρ/Å | C/eV·Å6 | Y/e | K/eV·Å−2 |
|---|---|---|---|---|---|
| Mg2+–O2− | 946.627 | 0.3181 | 0.00 | 2.00 | 99,999 |
| Si4+–O2− | 1283.91 | 0.3205 | 0.00 | 4.00 | 99,999 |
| O2–O2− | 22,764.0 | 0.1490 | 27.89 | −2.86 | 74.92 |
| Lattice Properties | Calculated | Experiment [41] | |∆|(%) | ||
|---|---|---|---|---|---|
| Classical | DFT | Classical | DFT | ||
| a (Å) | 4.86 | 4.82 | 4.75 | 2.32 | 1.47 |
| b (Å) | 4.88 | 4.97 | 4.91 | 0.61 | 1.22 |
| c (Å) | 6.89 | 6.97 | 6.85 | 0.58 | 1.75 |
| α = β = γ (°) | 90.0 | 90.0 | 90.0 | 0.00 | 0.00 |
| V (Å3) | 163.1 | 166.9 | 159.6 | 2.19 | 4.57 |
| Atom | Bader Charge (e) |
|---|---|
| Mg | +2.00 |
| Si | +4.00 |
| O | −2.00 |
| Dopant | Ionic Radius of Dopant Ion (Å) | Bader Charge on Dopant (|e|) | M-O Distance(Å) | |
|---|---|---|---|---|
| Be2+ | 0.59 | +2.00 | 1.69–1.79 | −0.13 |
| Ca2+ | 1.00 | +1.50 | 2.19–2.38 | +0.50 |
| Sr2+ | 1.18 | +1.51 | 2.25–2.47 | +0.89 |
| Ba2+ | 1.35 | +1.49 | 2.49–2.61 | +1.47 |
| Fe2+ | 0.61 | +1.46 | 2.09–2.28 | +0.10 |
| Co2+ | 0.65 | +1.33 | 2.07–2.21 | +0.07 |
| Mn2+ | 0.67 | +1.59 | 2.10–2.36 | +0.21 |
| Ni2+ | 0.69 | +1.26 | 1.98–2.21 | +0.05 |
| Cu2+ | 0.73 | +1.16 | 2.14–2.33 | +0.08 |
| Zn2+ | 0.74 | +1.38 | 2.05–2.16 | +0.10 |
| Dopant | Ionic Radius of Dopant Ion (Å) | Bader Charge on Dopant (|e|) | M-O Distance(Å) | |
|---|---|---|---|---|
| B3+ | 0.27 | +3.00 | 1.74–1.80 | −0.21 |
| Al3+ | 0.54 | +3.00 | 1.89–1.91 | +0.39 |
| Ga3+ | 0.62 | +3.00 | 1.95–1.98 | +0.74 |
| In3+ | 0.80 | +3.00 | 2.09–2.11 | +1.49 |
| Tl3+ | 0.89 | +3.00 | 2.18–2.20 | +1.94 |
| Sc3+ | 0.75 | +1.93 | 2.01–2.03 | +1.14 |
| Y3+ | 0.90 | +2.11 | 2.12–2.14 | +1.82 |
| La3+ | 1.03 | +1.99 | 2.21–2.23 | +2.38 |
| Dopant | Ionic Radius (Å) | Bader Charge (|e|) | M-O Distance (Å) | |
|---|---|---|---|---|
| C | 0.16 | +4.00 | 1.65–1.79 | +0.96 |
| Ge | 0.53 | +4.00 | 2.19–2.38 | +0.46 |
| Sn | 0.69 | +4.00 | 2.25–2.80 | +1.13 |
| Pb | 0.78 | +4.00 | 2.49–2.94 | +1.60 |
| Ti | 0.61 | +2.67 | 1.93, 1.95 | +0.68 |
| Zr | 0.72 | +3.52 | 2.04, 2.05 | +1.39 |
| Ce | 0.87 | +2.19 | 2.12, 2.16 | +1.96 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pathmanathan, K.; Iyngaran, P.; Abiman, P.; Kuganathan, N. Defect Engineering and Dopant Properties of MgSiO3. Eng 2025, 6, 51. https://doi.org/10.3390/eng6030051
Pathmanathan K, Iyngaran P, Abiman P, Kuganathan N. Defect Engineering and Dopant Properties of MgSiO3. Eng. 2025; 6(3):51. https://doi.org/10.3390/eng6030051
Chicago/Turabian StylePathmanathan, Kowthaman, Poobalasuntharam Iyngaran, Poobalasingam Abiman, and Navaratnarajah Kuganathan. 2025. "Defect Engineering and Dopant Properties of MgSiO3" Eng 6, no. 3: 51. https://doi.org/10.3390/eng6030051
APA StylePathmanathan, K., Iyngaran, P., Abiman, P., & Kuganathan, N. (2025). Defect Engineering and Dopant Properties of MgSiO3. Eng, 6(3), 51. https://doi.org/10.3390/eng6030051







