Nonlinear Control of a Permanent Magnet Synchronous Motor Based on State Space Neural Network Model Identification and State Estimation by Using a Robust Unscented Kalman Filter
Abstract
1. Introduction
2. Theoretical Framework
2.1. Discrete State Space Nonlinear Modeling of a PMSM
2.2. Robust Neural Network Training and State Estimation by a Dual UKF
2.3. Exact Feedback Linearization in Discrete Time
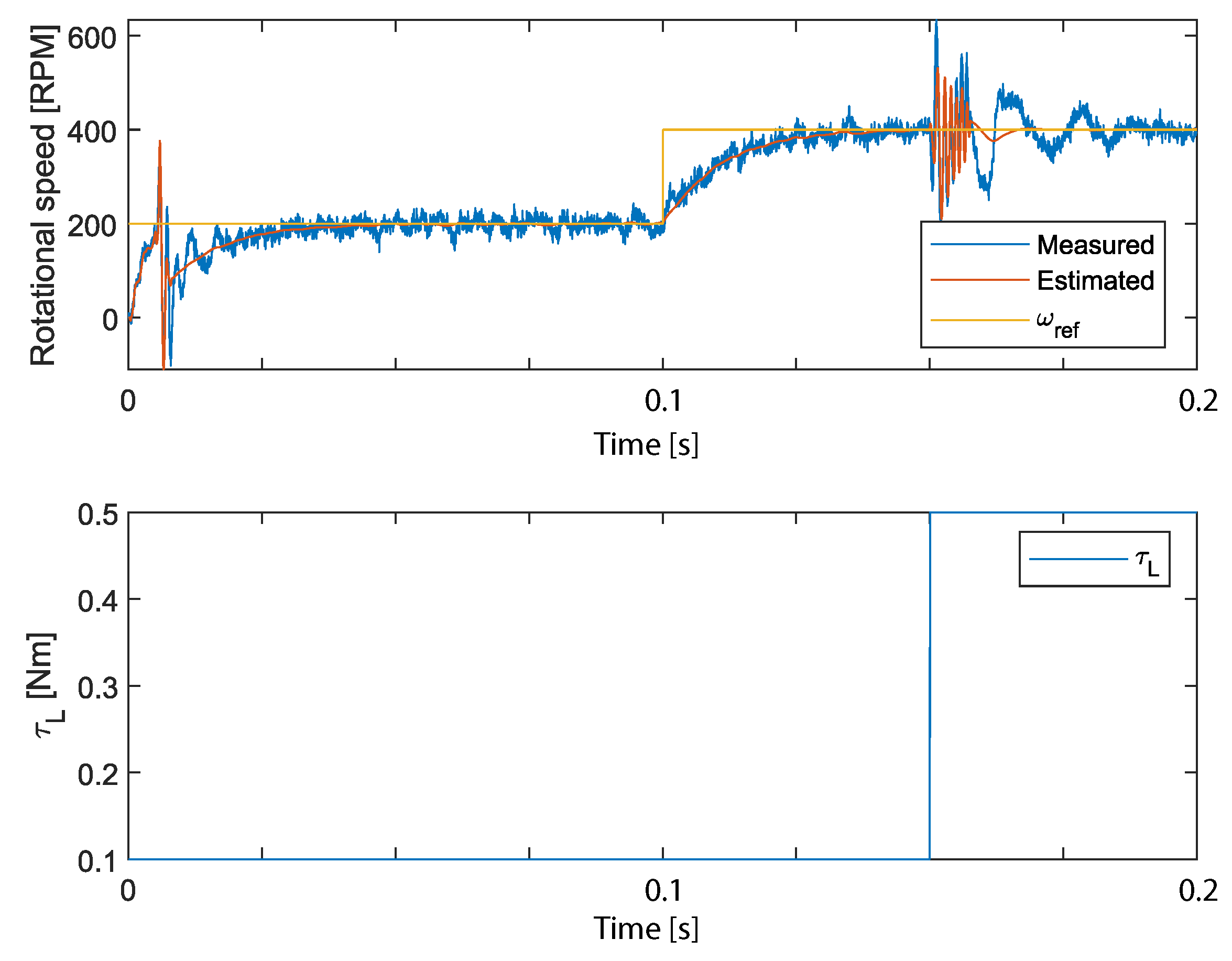
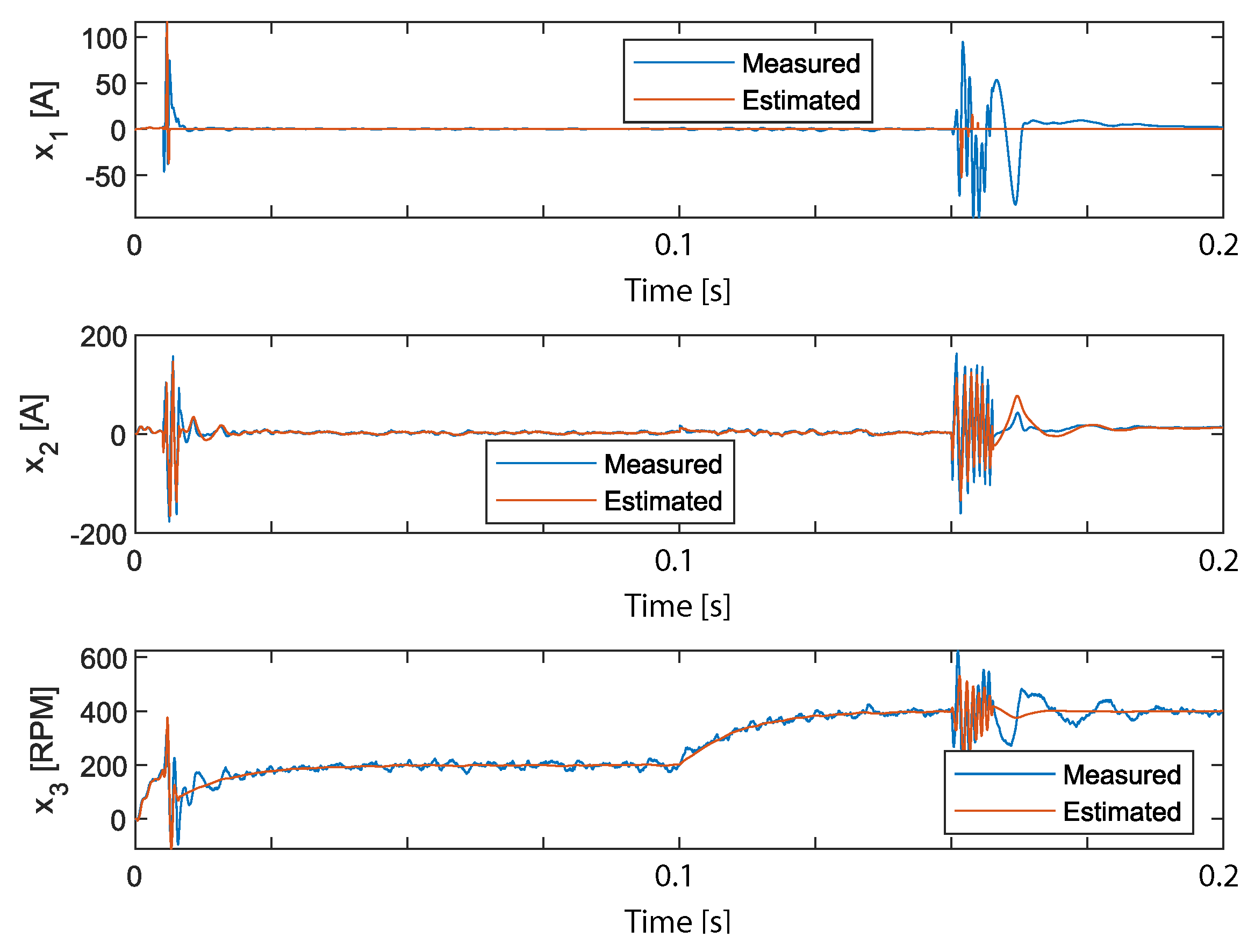
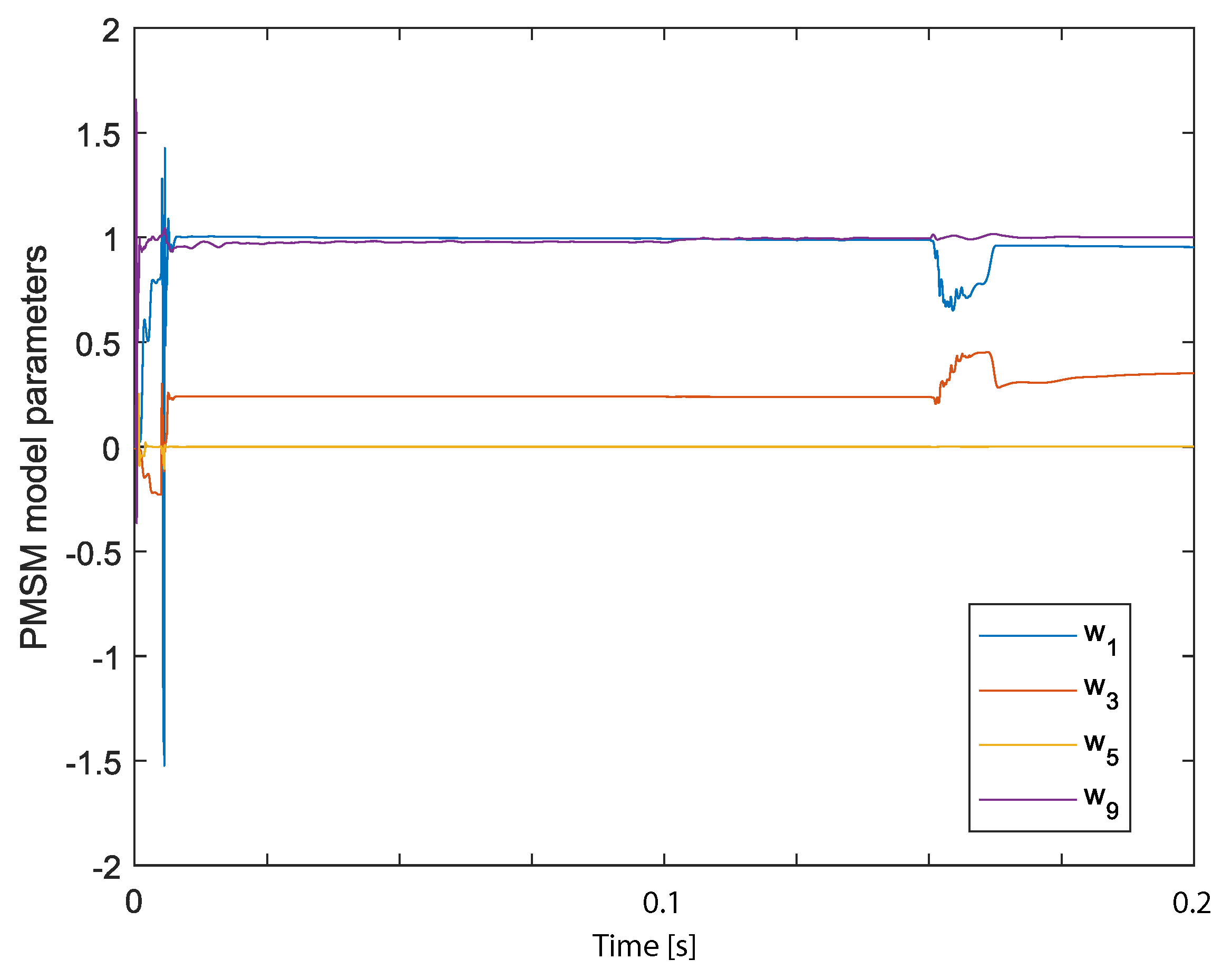
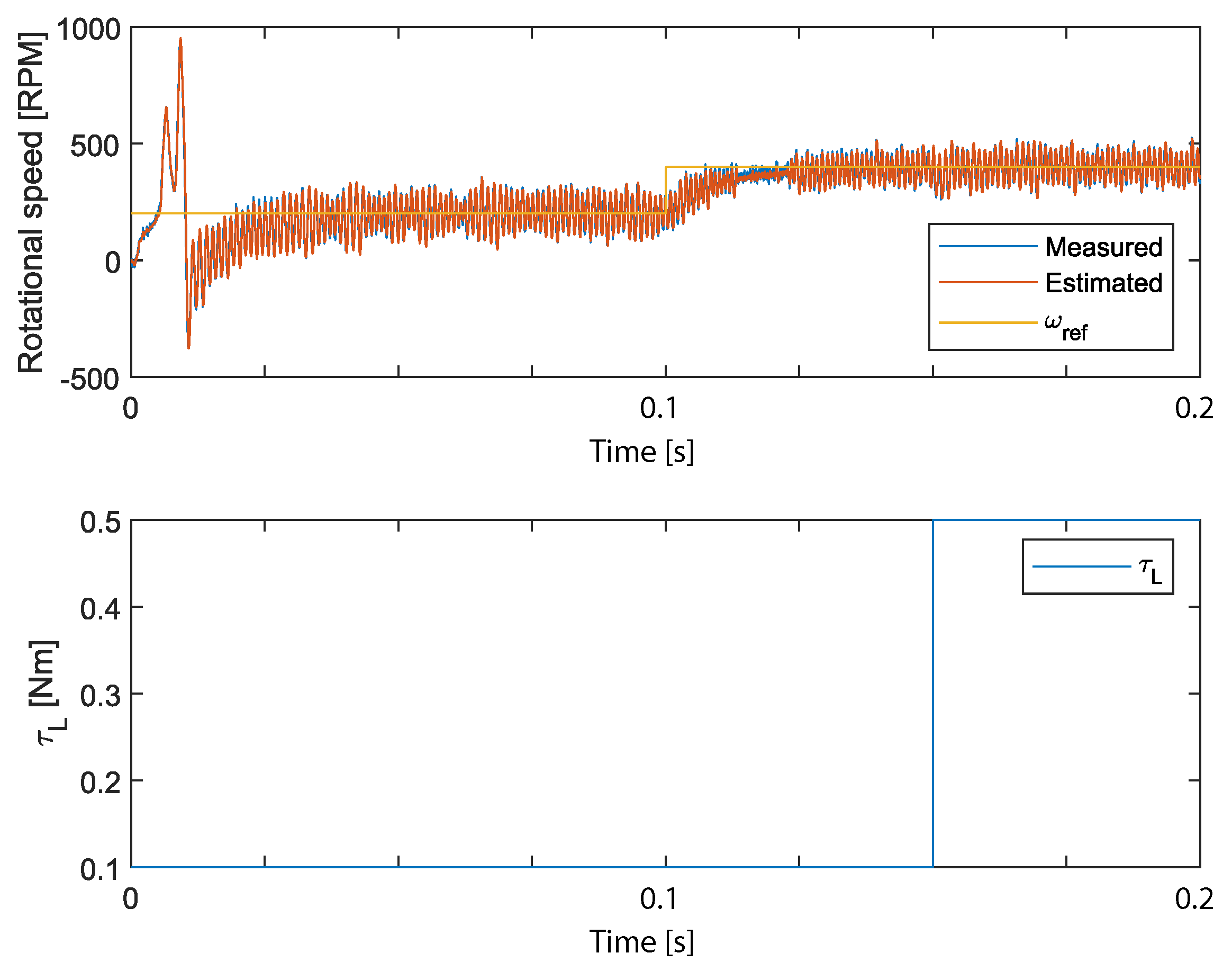
3. Results
Experimental Setup
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Velarde-Gomez, S.; Giraldo, E. Real-Time Identification and Nonlinear Control of a Permanent-Magnet Synchronous Motor Based on a Physics-Informed Neural Network and Exact Feedback Linearization. Information 2024, 15, 577. [Google Scholar] [CrossRef]
- Wan, E.; Van Der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No.00EX373), Lake Louise, AB, Canada, 4 October 2000; pp. 153–158. [Google Scholar] [CrossRef]
- Rouhani, A.; Abur, A. Constrained Iterated Unscented Kalman Filter for Dynamic State and Parameter Estimation. IEEE Trans. Power Syst. 2018, 33, 2404–2414. [Google Scholar] [CrossRef]
- Fang, S.; Zhang, X. A Parameter-Free Model Predictive Current Control for PMSM Drives Based on Motor Parameter Estimation. In Proceedings of the 2024 IEEE 10th International Power Electronics and Motion Control Conference (IPEMC2024-ECCE Asia), Chengdu, China, 17–20 May 2024; pp. 858–862. [Google Scholar] [CrossRef]
- Horváth, K. Load Torque and Permanent Magnet Flux Linkage Estimation of Surface-Mounted PMSM by Using Unscented Kalman Filter. In Proceedings of the 2023 International Conference on Electrical Drives and Power Electronics (EDPE), High Tatras, Slovakia, 25–27 September 2023; pp. 1–8. [Google Scholar] [CrossRef]
- Horváth, K. Position sensorless extended and unscented Kalman filters with permanent magnet flux linkage and load torque estimation for surface-mounted PMSM. Automatika 2024, 65, 1201–1212. [Google Scholar] [CrossRef]
- Moon, C.; Nam, K.H.; Jung, M.K.; Chae, C.H.; Kwon, Y.A. Sensorless speed control of permanent magnet synchronous motor using Unscented Kalman Filter. In Proceedings of the 2012 Proceedings of SICE Annual Conference (SICE), Akita, Japan, 20–23 August 2012; pp. 2018–2023. [Google Scholar]
- Zhou, N.; He, H.; Liu, Z.; Zhang, Z. UKF-based Sensor Fault Diagnosis of PMSM Drives in Electric Vehicles. Energy Procedia 2017, 142, 2276–2283. [Google Scholar] [CrossRef]
- Moon, C.; Park, J.S.; Kwon, Y.A.; Kennel, R.M. Unscented transformnations of UKF for sensorless speed control of PMSM. In Proceedings of the TENCON 2015—2015 IEEE Region 10 Conference, Macao, China, 1–4 November 2015; pp. 1–4. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, L.; Liu, X. Sensorless Direct Torque Control of PMSM using Unscented Kalman Filter*. IFAC Proc. Vol. 2011, 44, 4380–4385. [Google Scholar] [CrossRef]
- Zheng, B.; Fu, P.; Li, B.; Yuan, X. A Robust Adaptive Unscented Kalman Filter for Nonlinear Estimation with Uncertain Noise Covariance. Sensors 2018, 18, 808. [Google Scholar] [CrossRef]
- Ubare, P.; Ingole, D.; Sonawane, D. Nonlinear Model Predictive Control of BLDC Motor with State Estimation. IFAC-PapersOnLine 2021, 54, 107–112. [Google Scholar] [CrossRef]
- Wan, E.A.; Van Der Merwe, R.; Nelson, A.T. Dual estimation and the unscented transformation. In Proceedings of the 12th International Conference on Neural Information Processing Systems, Cambridge, MA, USA, 29 November–4 December 1999; NIPS’99. pp. 666–672. [Google Scholar]
- Kulikov, G.Y.; Kulikova, M.V. Hyperbolic-SVD-Based Square-Root Unscented Kalman Filters in Continuous-Discrete Target Tracking Scenarios. IEEE Trans. Autom. Control 2022, 67, 366–373. [Google Scholar] [CrossRef]
- Zhao, G.; Jiang, Z.; Wang, J.; Gao, S. A Robust SVD-UKF Algorithm and Its Application in Integrated Navigation Systems. Adv. Space Res. 2024, 75, 1902–1912. [Google Scholar] [CrossRef]
- Khodadadi, H.; Jazayeri-Rad, H. Applying a dual extended Kalman filter for the nonlinear state and parameter estimations of a continuous stirred tank reactor. Comput. Chem. Eng. 2011, 35, 2426–2436. [Google Scholar] [CrossRef]



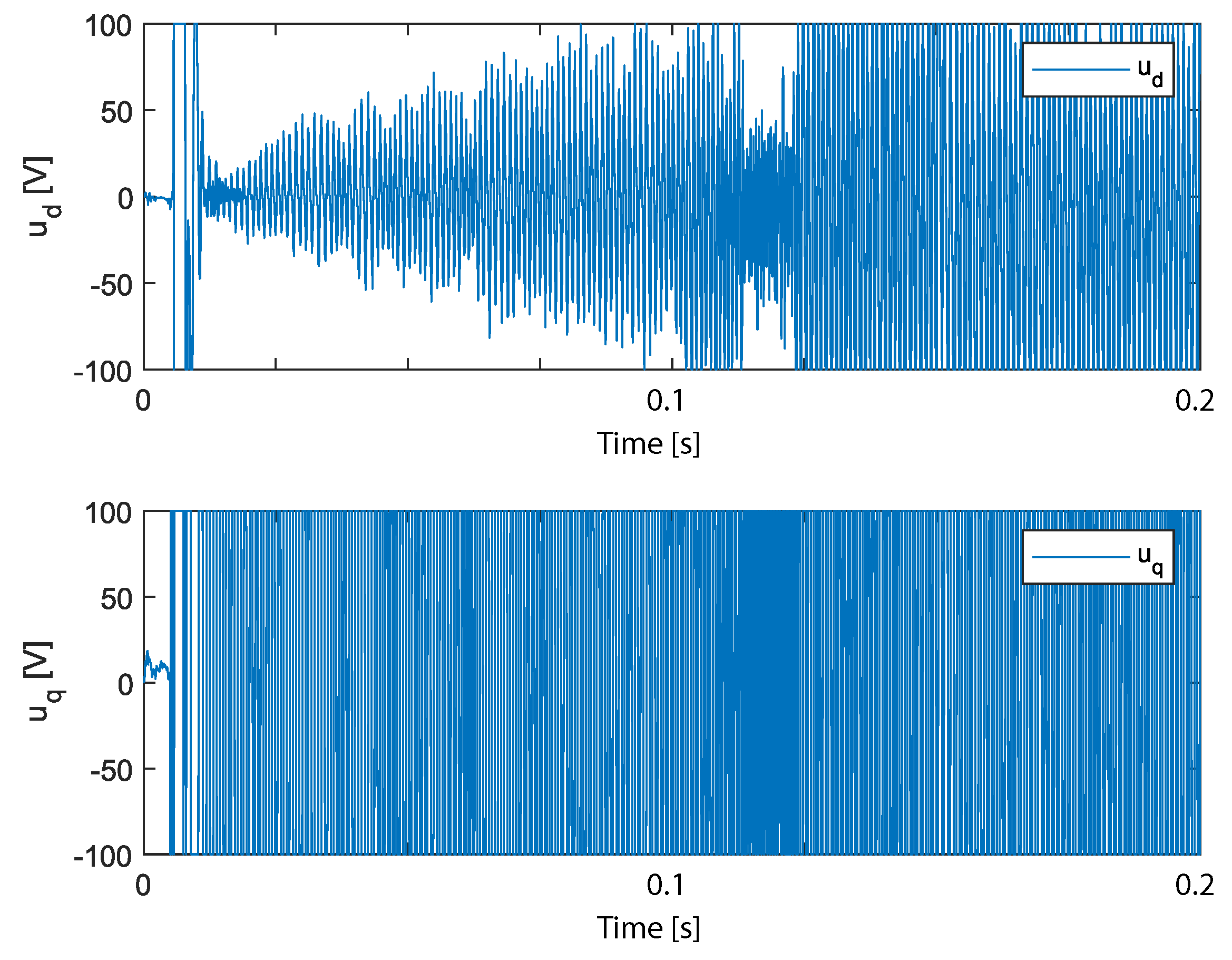


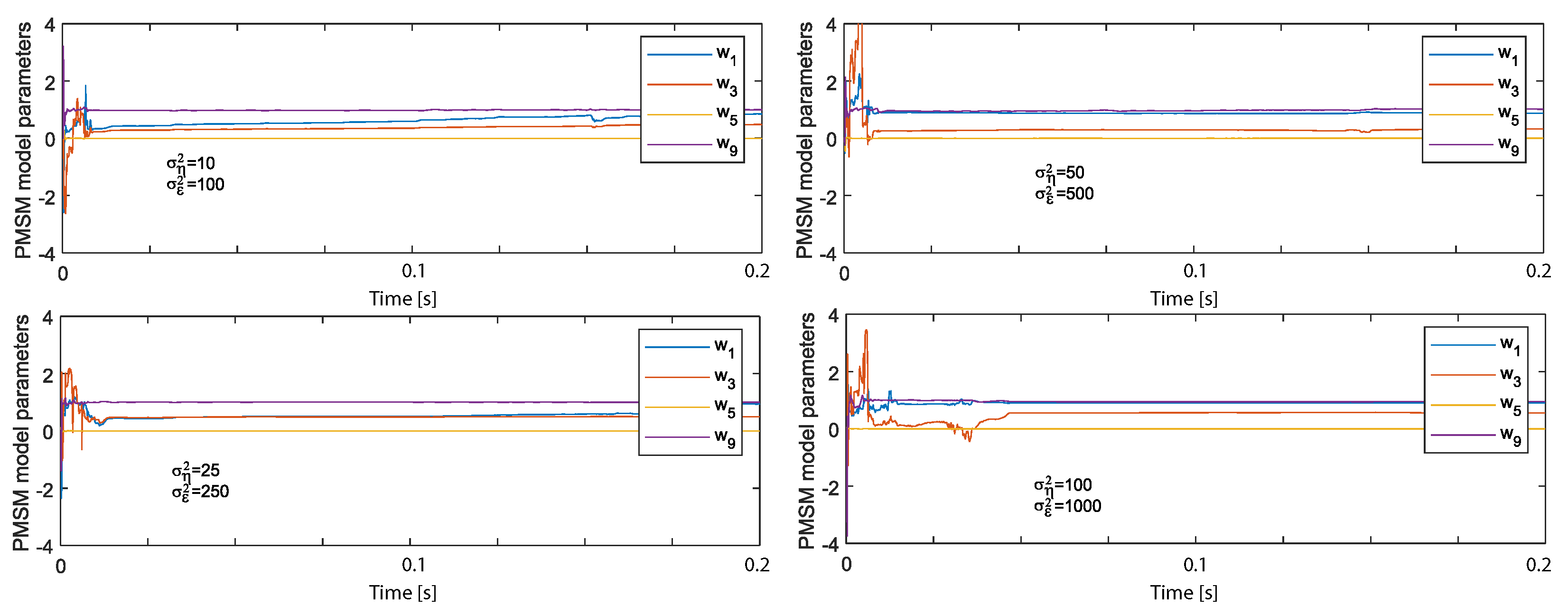
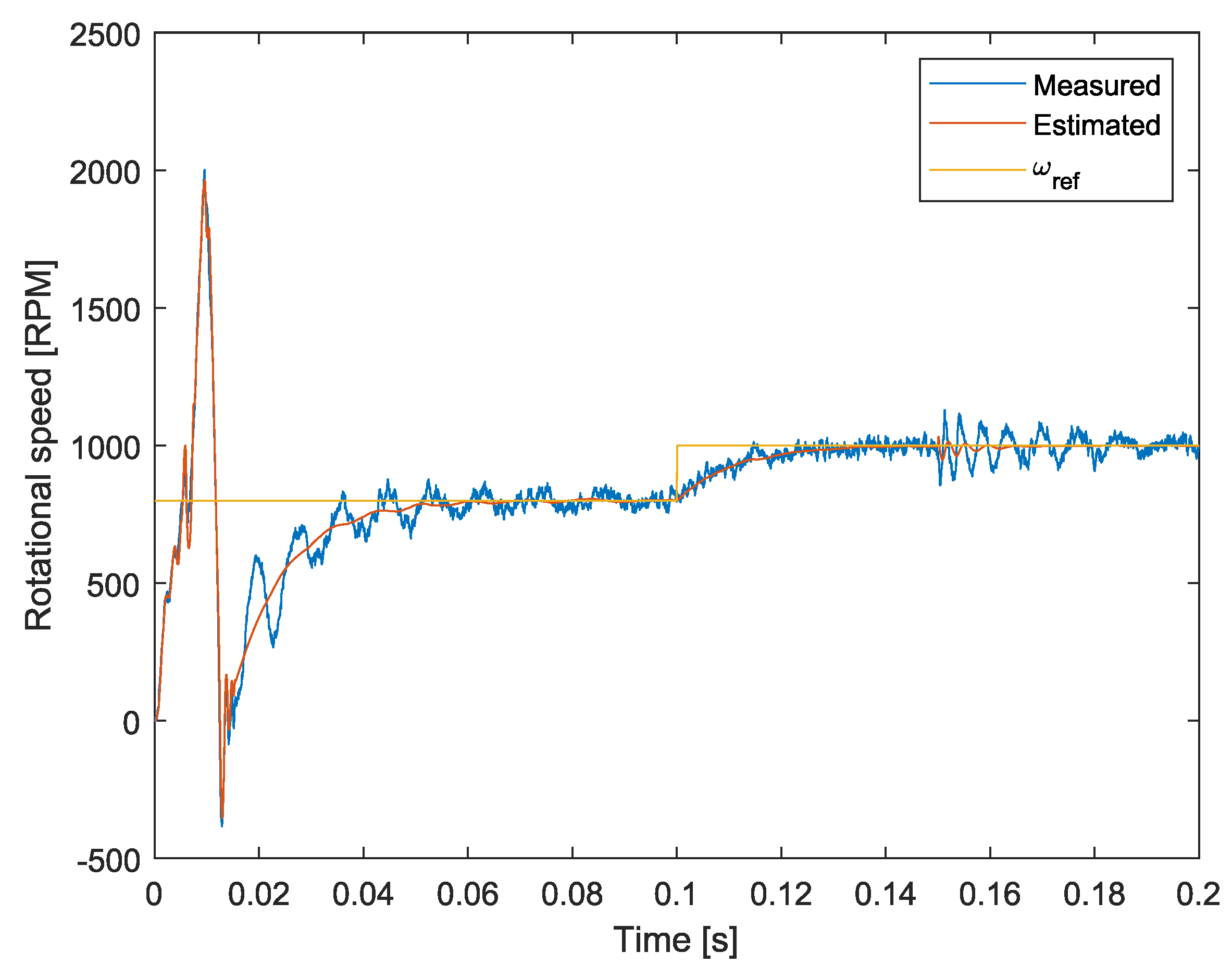
| Parameter | Value |
|---|---|
| Rated torque | |
| Continuous current | |
| Number of pole pairs | |
| Stator resistance per phase | |
| Inductance, phase to phase | |
| Electrical Time Constant | |
| Back EMF | |
| Encoder resolution |
| Noise Variance | RMSE |
|---|---|
| , | |
| , | |
| , | |
| , |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velarde-Gomez, S.; Giraldo, E. Nonlinear Control of a Permanent Magnet Synchronous Motor Based on State Space Neural Network Model Identification and State Estimation by Using a Robust Unscented Kalman Filter. Eng 2025, 6, 30. https://doi.org/10.3390/eng6020030
Velarde-Gomez S, Giraldo E. Nonlinear Control of a Permanent Magnet Synchronous Motor Based on State Space Neural Network Model Identification and State Estimation by Using a Robust Unscented Kalman Filter. Eng. 2025; 6(2):30. https://doi.org/10.3390/eng6020030
Chicago/Turabian StyleVelarde-Gomez, Sergio, and Eduardo Giraldo. 2025. "Nonlinear Control of a Permanent Magnet Synchronous Motor Based on State Space Neural Network Model Identification and State Estimation by Using a Robust Unscented Kalman Filter" Eng 6, no. 2: 30. https://doi.org/10.3390/eng6020030
APA StyleVelarde-Gomez, S., & Giraldo, E. (2025). Nonlinear Control of a Permanent Magnet Synchronous Motor Based on State Space Neural Network Model Identification and State Estimation by Using a Robust Unscented Kalman Filter. Eng, 6(2), 30. https://doi.org/10.3390/eng6020030









