Low-Rank Compensation in Hybrid 3D-RRAM/SRAM Computing-in-Memory System for Edge Computing
Abstract
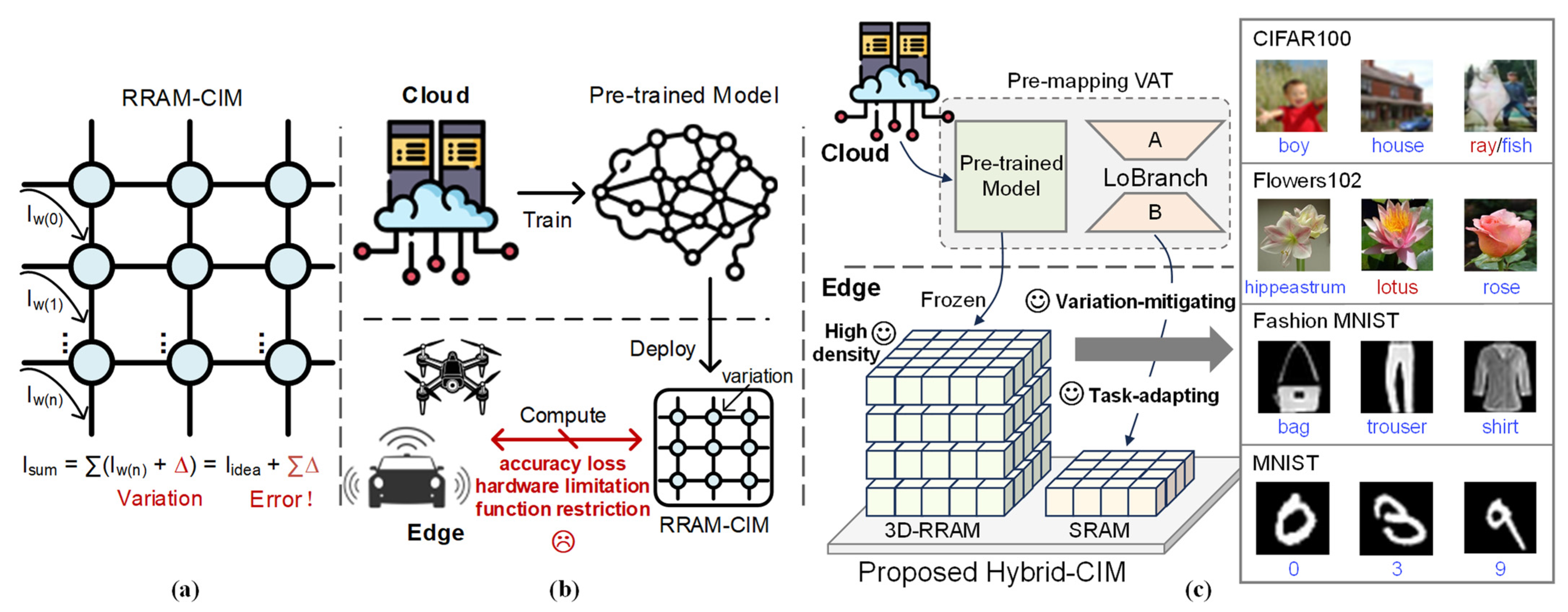
1. Introduction
2. Background and Motivation
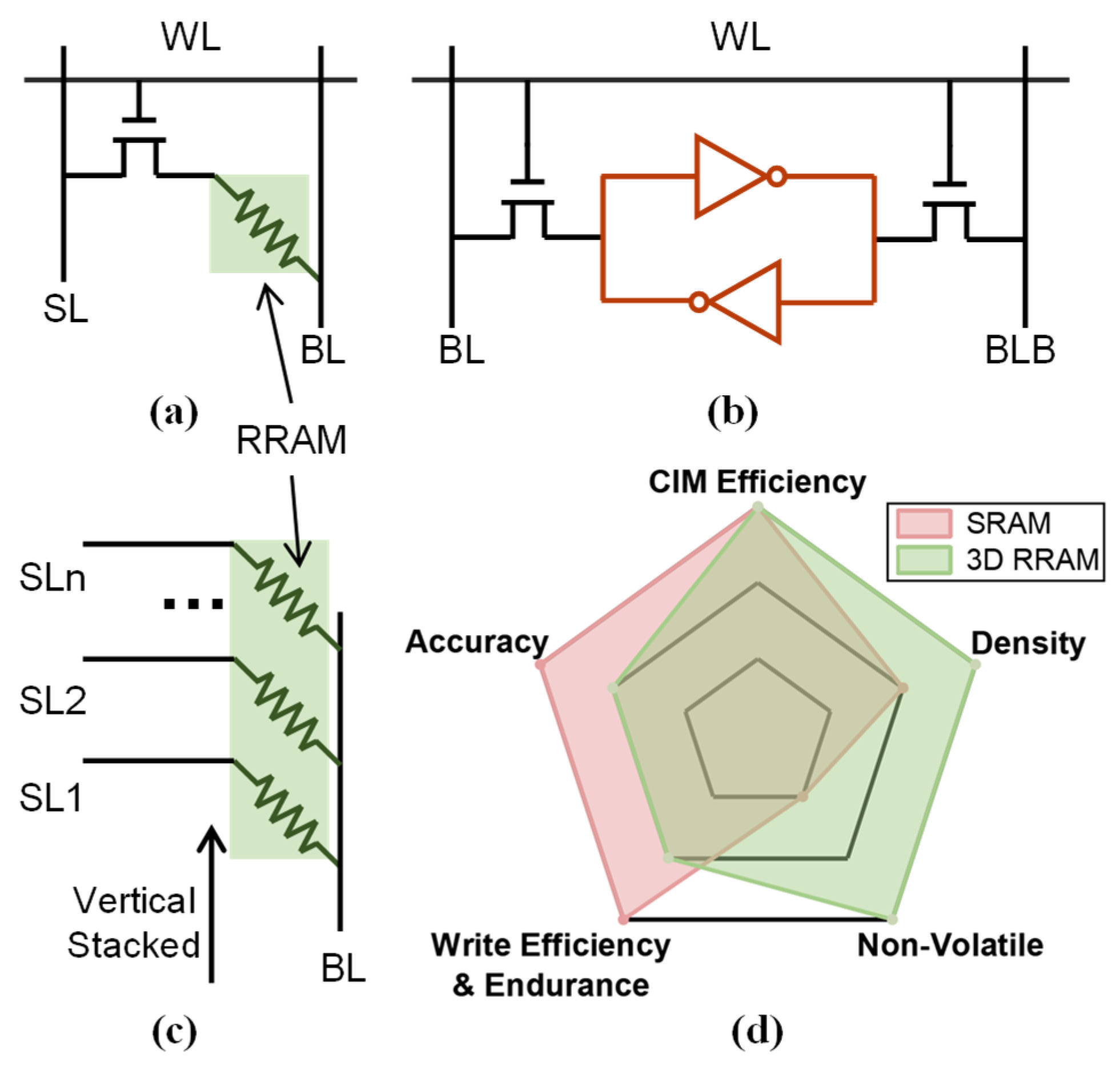
2.1. Three-Dimensional RRAM and SRAM
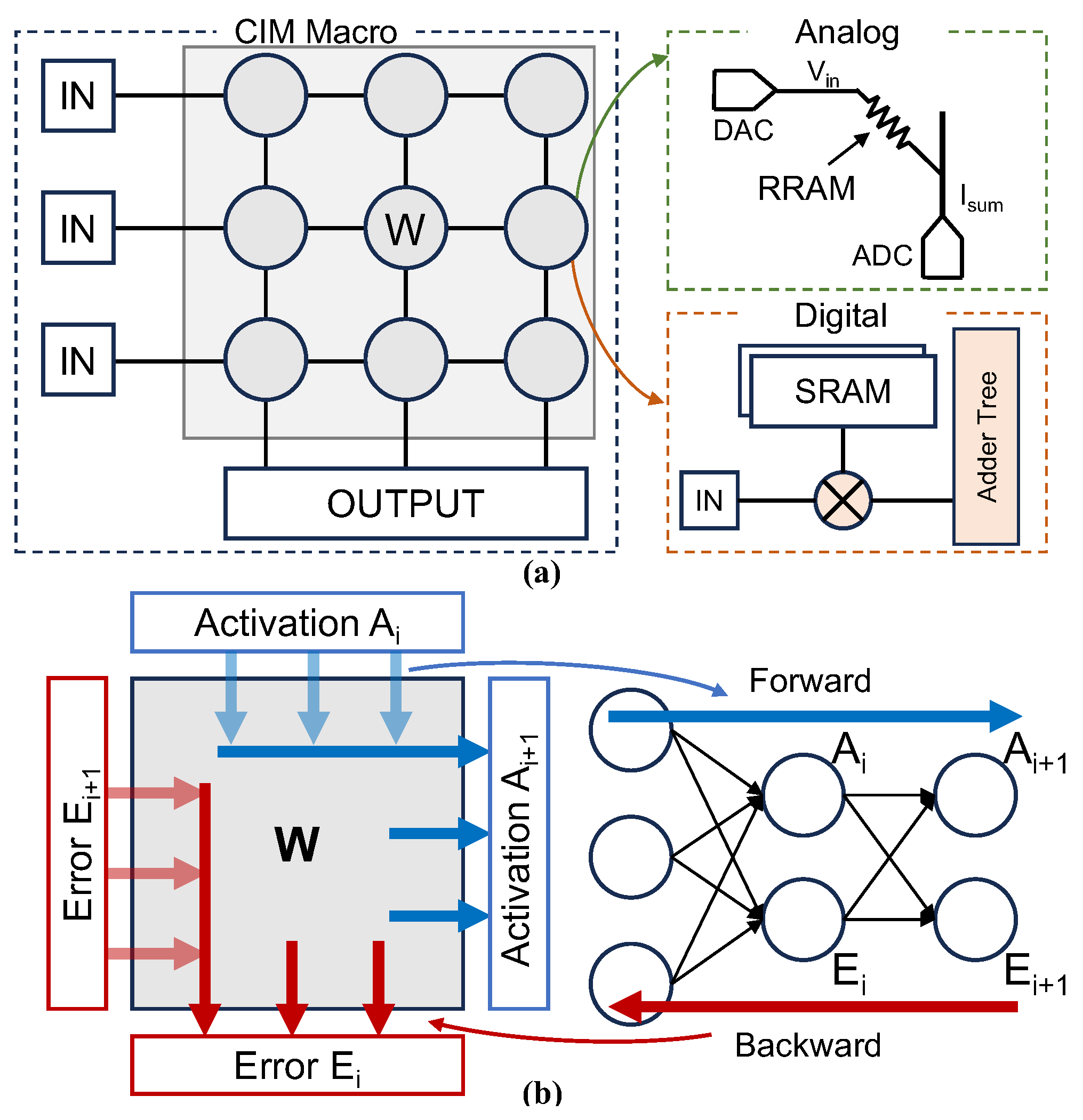
2.2. Computing-in-Memory
2.3. Fine-Tuning and Multi-Task Computing
2.4. Related Work
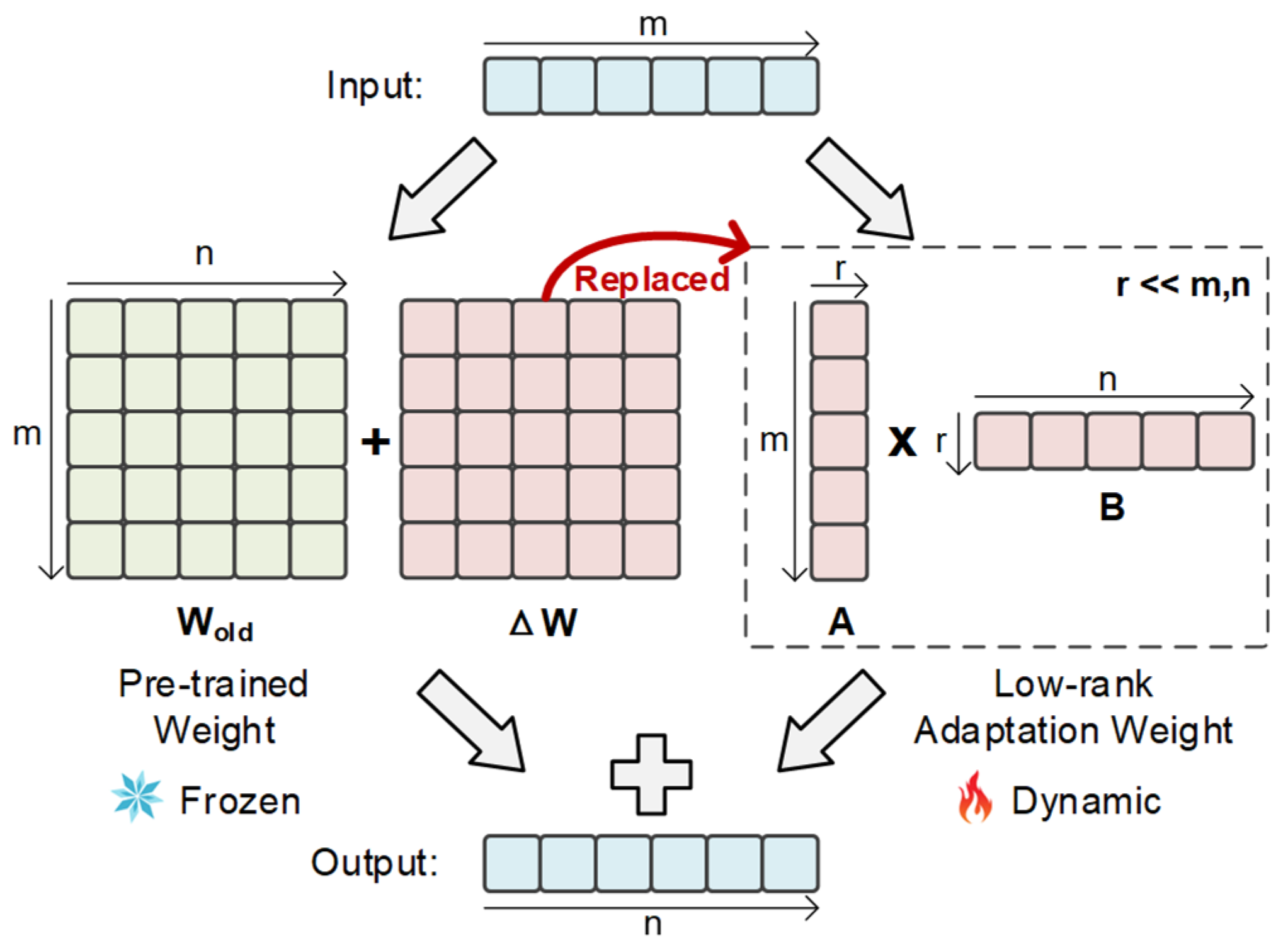
2.4.1. Low-Rank Adaptation
2.4.2. Previous CIM
3. Methodology
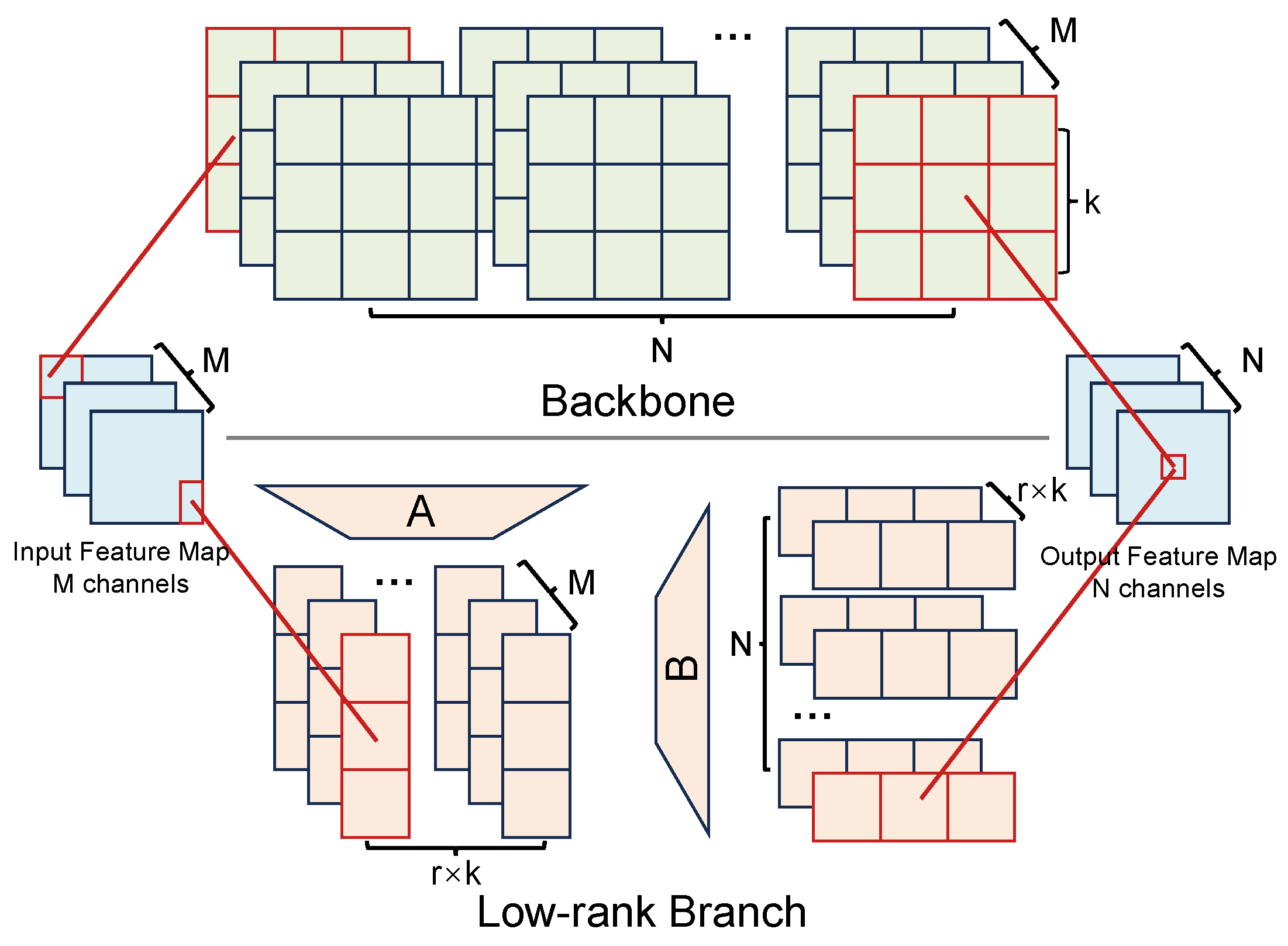
3.1. Low-Rank Adaptation Branch
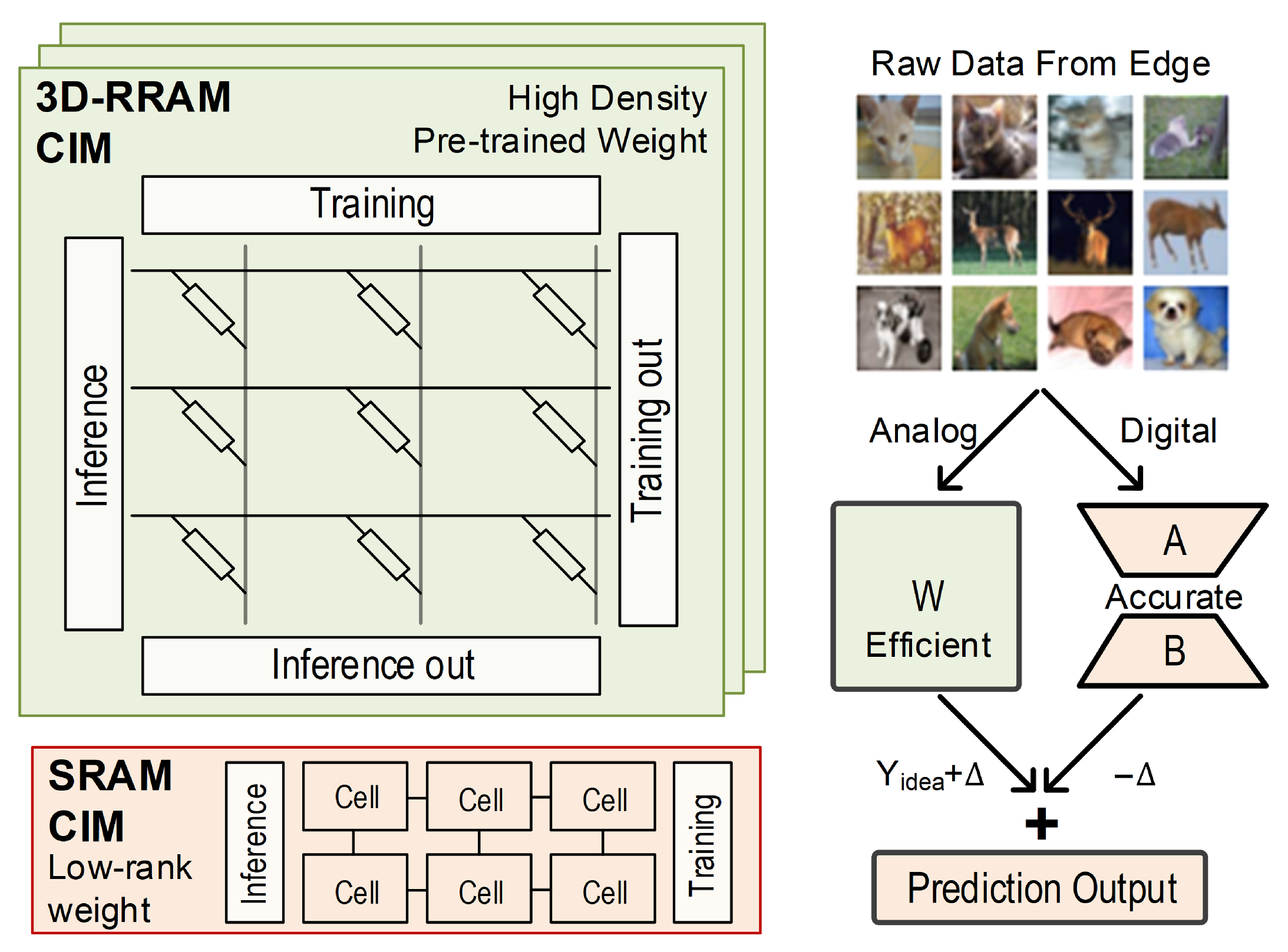
3.2. Hybrid-CIM for LoBranch
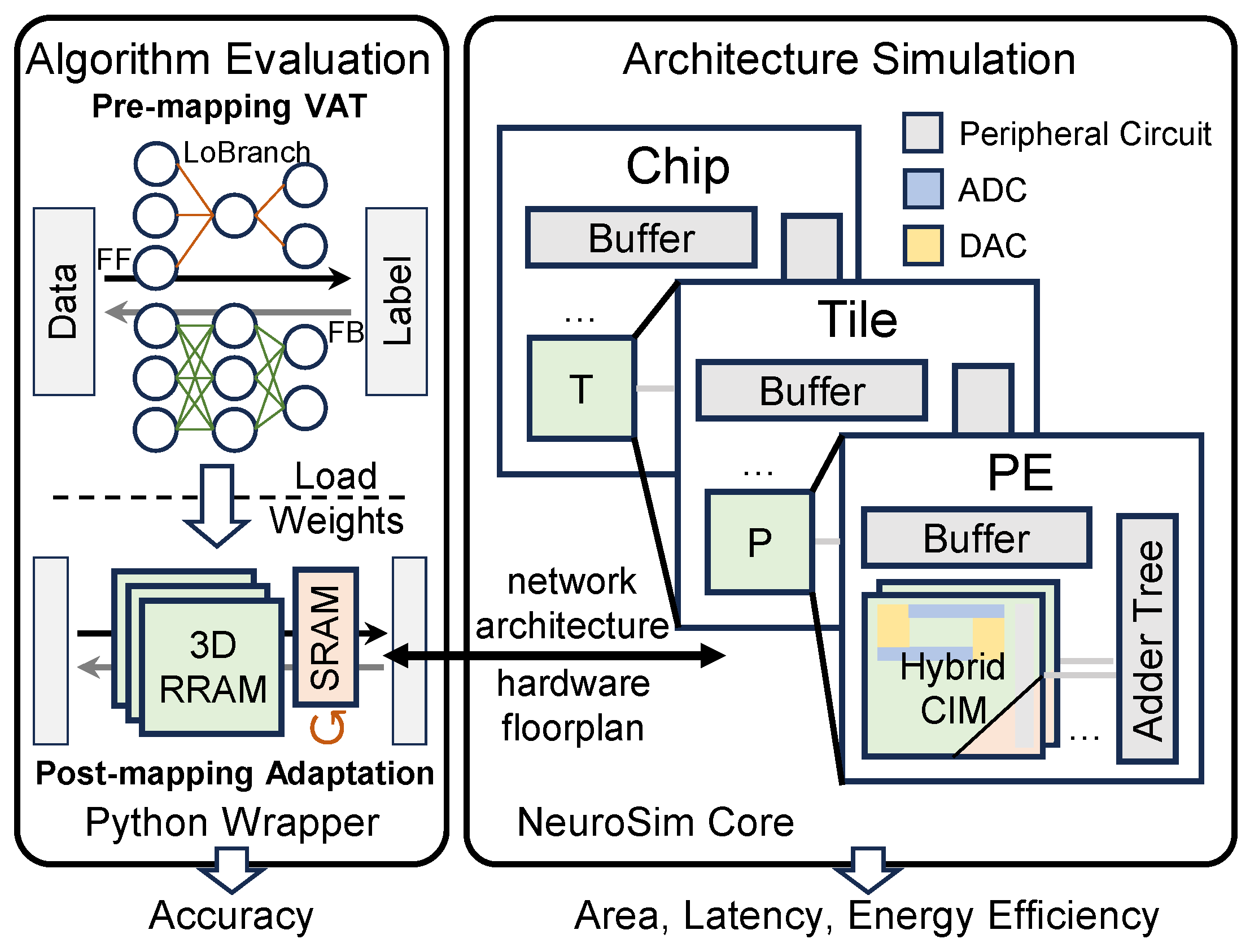
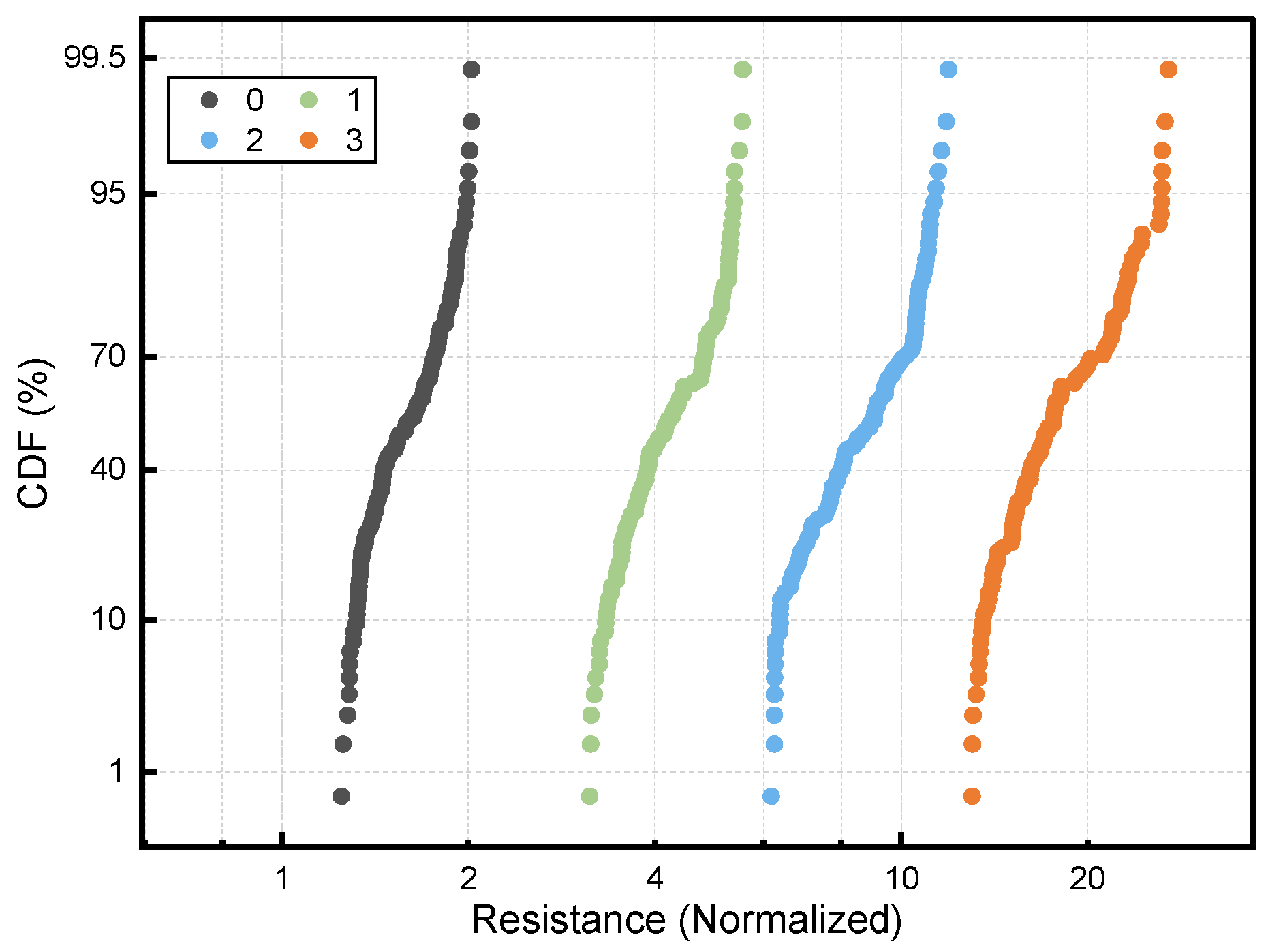
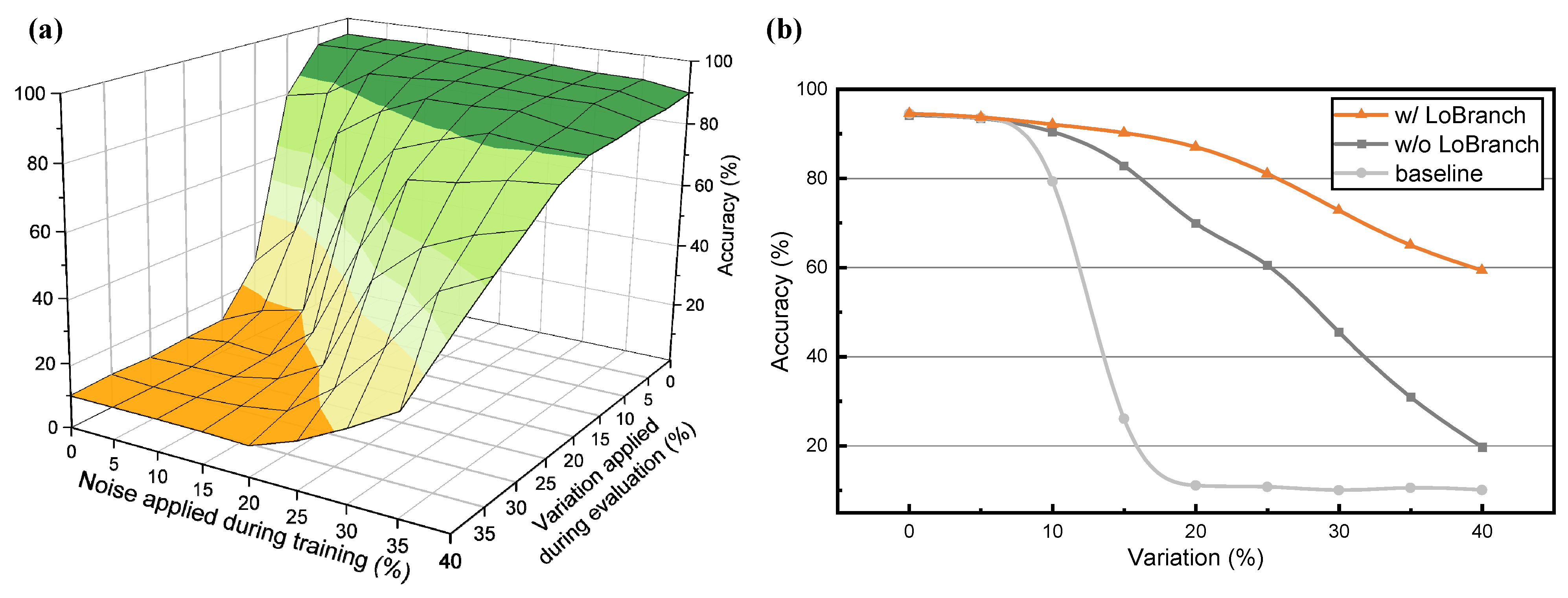
3.3. Simulation on Hybrid-CIM with Variation
- Pre-mapping Variation-Aware Training: The model, incorporating the LoBranch, undergoes training where Gaussian noise is injected into the weights to simulate device-level variation. This stage enhances the model’s inherent robustness before hardware mapping.
- Hybrid-CIM Hardware Mapping: The robust model is then deployed onto the system-level Hybrid-CIM architecture. The pre-trained main weights (W) are mapped to the variation-prone 3D-RRAM macro, while the low-rank LoBranch parameters (A, B) are mapped to the precise SRAM-CIM macro.
- Post-mapping Adaptation: To achieve optimal performance on the specific hardware, the LoBranch weights (A, B) in SRAM are fine-tuned based on the output of the deployed system. This step compensates for write variation, while the main RRAM weights are kept frozen.
- System-Level Performance Evaluation: The final performance of the adapted model is evaluated using a simulation framework calibrated for CIM architectures. This evaluation provides credible estimates for metrics such as accuracy, energy efficiency, latency, and area overhead, representing the optimized system’s capability.
| Algorithm1 Pre-mapping Variation-Aware Training |
| Input: Pre-trained weights W; Rank r; Noise level σ Output: Robust weights W, A, B 1: Initialize low-rank matrices A, B. 2: while not converged do 3: //Inject non-idealities during training 4: Wnoisy = W + N (0, σ2) 5: //Hybrid forward pass with LoBranch 6: Ypred = f (X; Wnoisy) + (A ⋅ B) ⋅ X 7: Compute loss L = Loss (Ypred, Yideal) 8: Compute gradients g with respect to W, A, B. 9: Update W, A, B 10: end while 11: return W, A, B |
| Algorithm 2 Post-mapping Adaptation |
| Input: Frozen weights W; Low-rank matrices A, B Output: Adapted matrices A, B 1: The model is deployed on Hybrid-CIM with variation. 2: while not converged do 3: //Forward pass on the Hybrid-CIM system 4: Yrram = 3DRRAM-CIM (X, W) 5: Ysram = SRAM-CIM (X, A, B) 6: //Layer-wise Hybrid summation 7: Y’ = Yrram + Ysram 8: Compute loss L = Loss (Y’, Yideal) 9: Compute gradients g with respect to A, B. 10: Update A, B stored in SRAM-CIM only. 11: end while 12: return A, B |
3.4. Model and Dataset Selection
4. Results and Discussion
4.1. Implementation of Error Correction
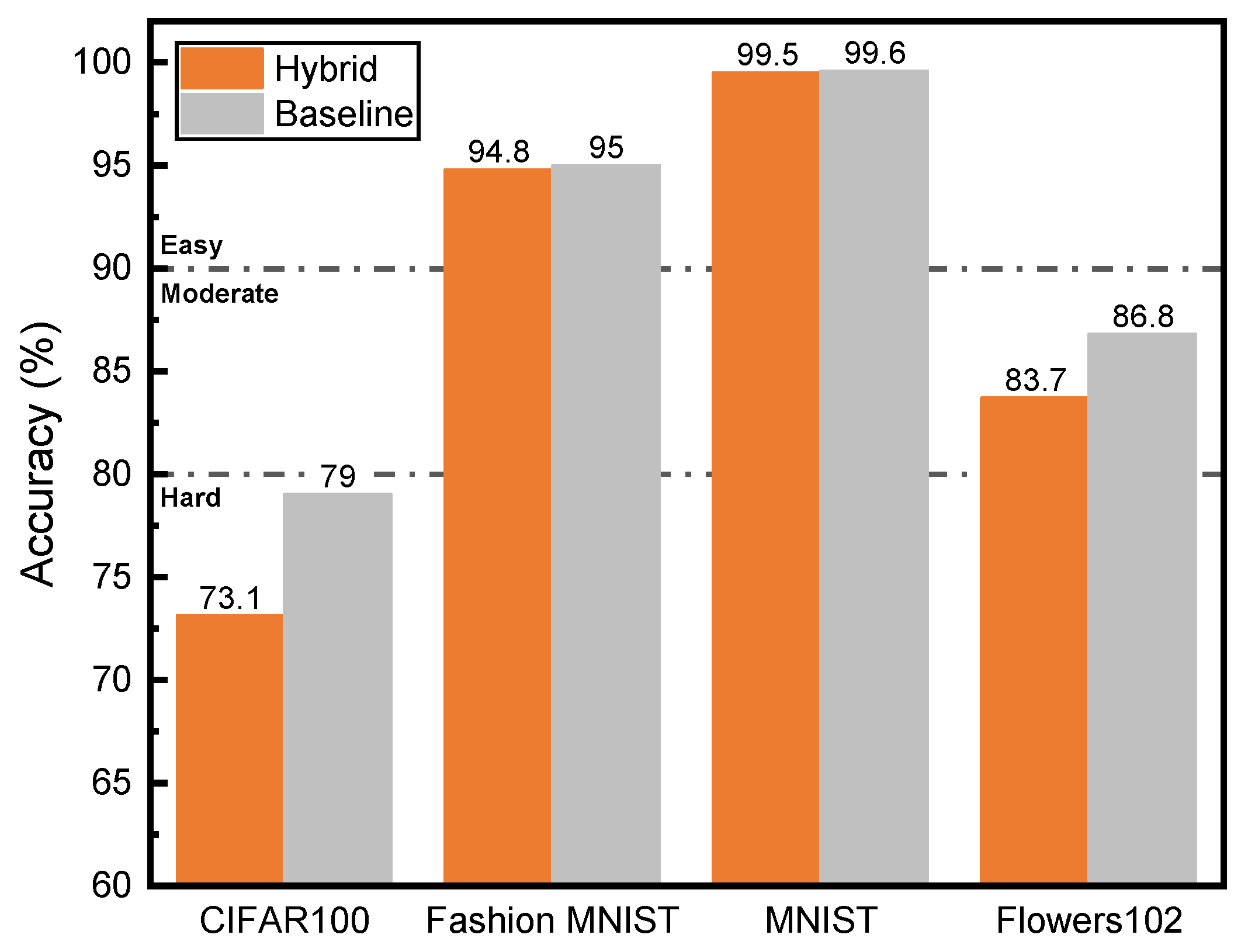
4.2. Implementation of Multi-Task Computing
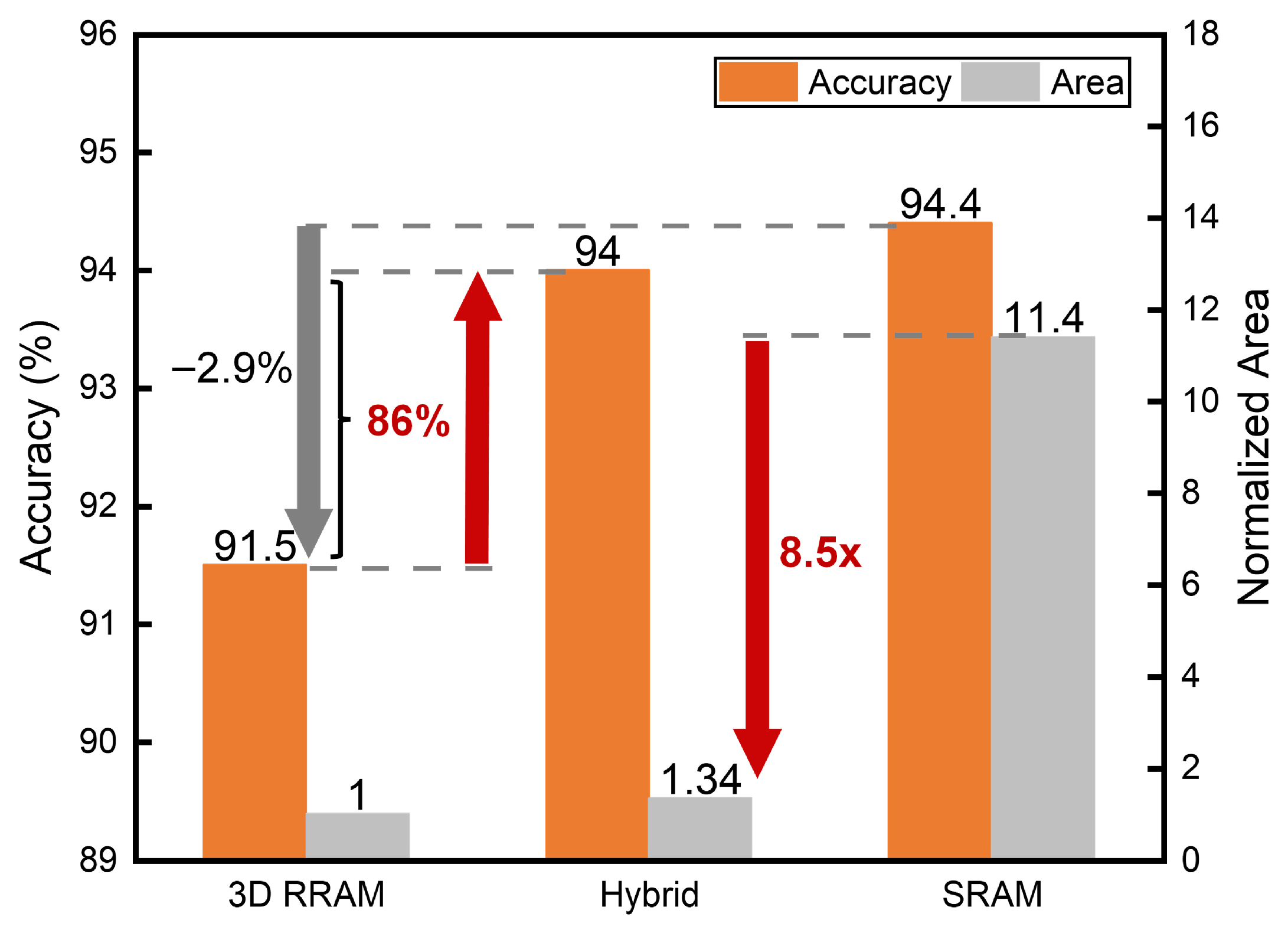
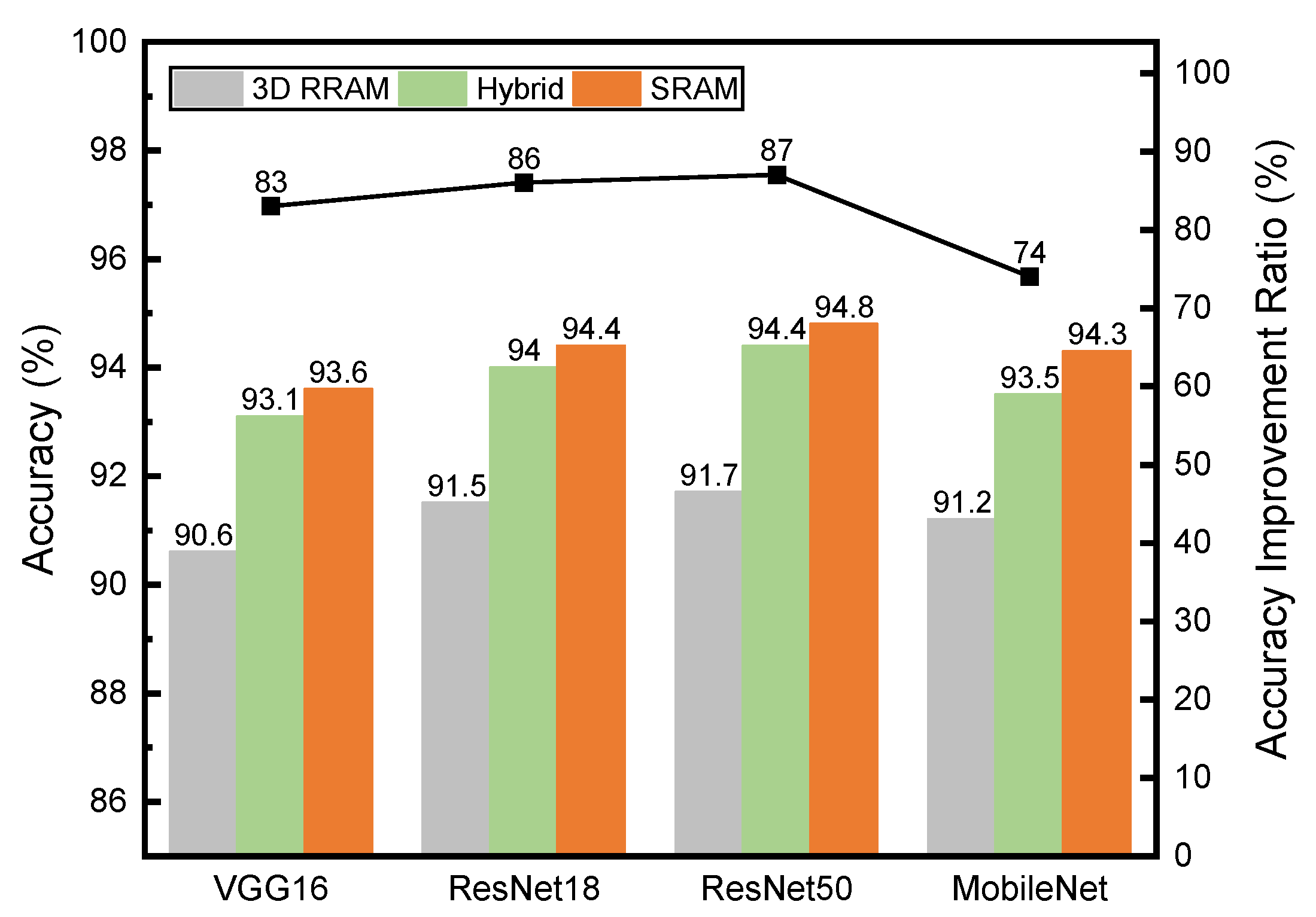
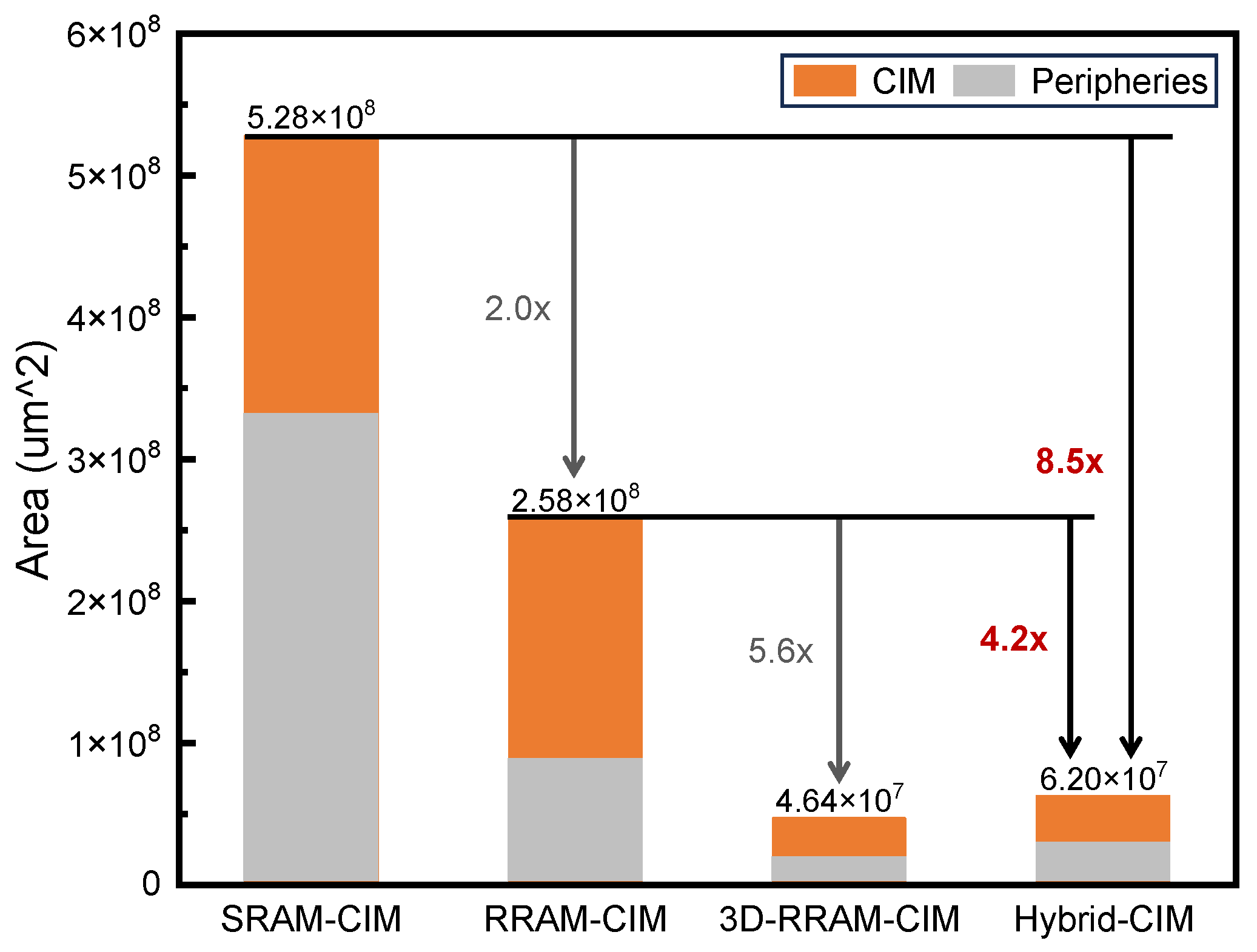
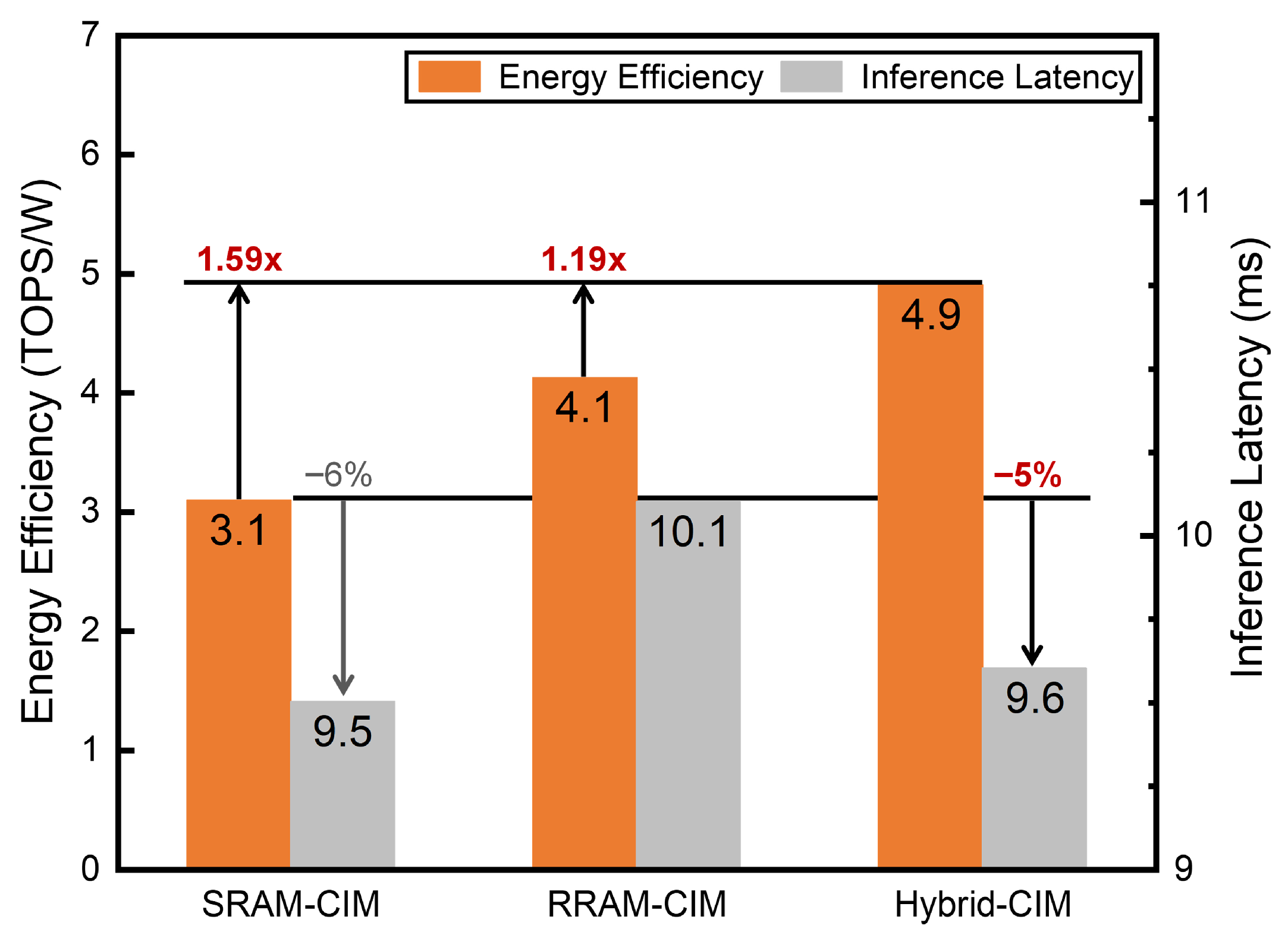
4.3. Comparison and Feasibility Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Hu, E.J.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Wang, L.; Chen, W. LoRA: Low-Rank Adaptation of Large Language Models 2021. In Proceedings of the International Conference on Learning Representations (ICLR), Virtual Event, 25–29 April 2022; pp. 1–13. [Google Scholar]
- Lepri, N.; Glukhov, A.; Cattaneo, L.; Farronato, M.; Mannocci, P.; Ielmini, D. In-Memory Computing for Machine Learning and Deep Learning. IEEE J. Electron Devices Soc. 2023, 11, 587–601. [Google Scholar] [CrossRef]
- Gong, N.; Rasch, M.J.; Seo, S.-C.; Gasasira, A.; Solomon, P.; Bragaglia, V.; Consiglio, S.; Higuchi, H.; Park, C.; Brew, K.; et al. Deep Learning Acceleration in 14nm CMOS Compatible ReRAM Array: Device, Material and Algorithm Co-Optimization. In Proceedings of the 2022 International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2022; pp. 33.7.1–33.7.4. [Google Scholar]
- Jung, S.; Kim, S.J. MRAM In-Memory Computing Macro for AI Computing. In Proceedings of the 2022 International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 3–7 December 2022; pp. 33.4.1–33.4.4. [Google Scholar]
- Su, J.-W.; Chou, Y.-C.; Liu, R.; Liu, T.-W.; Lu, P.-J.; Wu, P.-C.; Chung, Y.-L.; Hung, L.-Y.; Ren, J.-S.; Pan, T.; et al. 16.3 A 28nm 384kb 6T-SRAM Computation-in-Memory Macro with 8b Precision for AI Edge Chips. In Proceedings of the 2021 IEEE International Solid- State Circuits Conference (ISSCC), San Francisco, CA, USA, 13–22 February 2021; pp. 250–252. [Google Scholar]
- Zhang, W.; Yao, P.; Gao, B.; Liu, Q.; Wu, D.; Zhang, Q.; Li, Y.; Qin, Q.; Li, J.; Zhu, Z.; et al. Edge Learning Using a Fully Integrated Neuro-Inspired Memristor Chip. Science 2023, 381, 1205–1211. [Google Scholar] [CrossRef]
- Wan, W.; Kubendran, R.; Schaefer, C.; Eryilmaz, S.B.; Zhang, W.; Wu, D.; Deiss, S.; Raina, P.; Qian, H.; Gao, B.; et al. A Compute-in-Memory Chip Based on Resistive Random-Access Memory. Nature 2022, 608, 504–512. [Google Scholar] [CrossRef]
- Su, J.-W.; Si, X.; Chou, Y.-C.; Chang, T.-W.; Huang, W.-H.; Tu, Y.-N.; Liu, R.; Lu, P.-J.; Liu, T.-W.; Wang, J.-H.; et al. Two-Way Transpose Multibit 6T SRAM Computing-in-Memory Macro for Inference-Training AI Edge Chips. IEEE J. Solid-State Circuits 2022, 57, 609–624. [Google Scholar] [CrossRef]
- Wen, T.-H.; Hung, J.-M.; Huang, W.-H.; Jhang, C.-J.; Lo, Y.-C.; Hsu, H.-H.; Ke, Z.-E.; Chen, Y.-C.; Chin, Y.-H.; Su, C.-I.; et al. Fusion of Memristor and Digital Compute-in-Memory Processing for Energy-Efficient Edge Computing. Science 2024, 384, 325–332. [Google Scholar] [CrossRef]
- Huo, Q.; Yang, Y.; Wang, Y.; Lei, D.; Fu, X.; Ren, Q.; Xu, X.; Luo, Q.; Xing, G.; Chen, C.; et al. A Computing-in-Memory Macro Based on Three-Dimensional Resistive Random-Access Memory. Nat. Electron. 2022, 5, 469–477. [Google Scholar] [CrossRef]
- Rehman, M.M.; Samad, Y.A.; Gul, J.Z.; Saqib, M.; Khan, M.; Shaukat, R.A.; Chang, R.; Shi, Y.; Kim, W.Y. 2D Materials-Memristive Devices Nexus: From Status Quo to Impending Applications. Prog. Mater. Sci. 2025, 152, 101471. [Google Scholar] [CrossRef]
- Huo, Q.; Song, R.; Lei, D.; Luo, Q.; Wu, Z.; Wu, Z.; Zhao, X.; Zhang, F.; Li, L.; Liu, M. Demonstration of 3D Convolution Kernel Function Based on 8-Layer 3D Vertical Resistive Random Access Memory. IEEE Electron Device Lett. 2020, 41, 497–500. [Google Scholar] [CrossRef]
- Peng, X.; Huang, S.; Luo, Y.; Sun, X.; Yu, S. DNN+NeuroSim: An End-to-End Benchmarking Framework for Compute-in-Memory Accelerators with Versatile Device Technologies. In Proceedings of the 2019 IEEE International Electron Devices Meeting (IEDM), San Francisco, CA, USA, 7–11 December 2019; pp. 32.5.1–32.5.4. [Google Scholar]
- Krishnan, G.; Wang, Z.; Yeo, I.; Yang, L.; Meng, J.; Liehr, M.; Joshi, R.V.; Cady, N.C.; Fan, D.; Seo, J.-S.; et al. Hybrid RRAM/SRAM in-Memory Computing for Robust DNN Acceleration. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2022, 41, 4241–4252. [Google Scholar] [CrossRef]
- Jeong, S.; Kim, J.; Jeong, M.; Lee, Y. Variation-Tolerant and Low R-Ratio Compute-in-Memory ReRAM Macro with Capacitive Ternary MAC Operation. IEEE Trans. Circuits Syst. I 2022, 69, 2845–2856. [Google Scholar] [CrossRef]
- Yao, P.; Wu, H.; Gao, B.; Tang, J.; Zhang, Q.; Zhang, W.; Yang, J.J.; Qian, H. Fully Hardware-Implemented Memristor Convolutional Neural Network. Nature 2020, 577, 641–646. [Google Scholar] [CrossRef]
- Wang, Z.; Nalla, P.S.; Krishnan, G.; Joshi, R.V.; Cady, N.C.; Fan, D.; Seo, J.; Cao, Y. Digital-Assisted Analog In-Memory Computing with RRAM Devices. In Proceedings of the 2023 International VLSI Symposium on Technology, Systems and Applications (VLSI-TSA/VLSI-DAT), HsinChu, Taiwan, 17–20 April 2023; pp. 1–4. [Google Scholar]
- Yang, X.; Belakaria, S.; Joardar, B.K.; Yang, H.; Doppa, J.R.; Pande, P.P.; Chakrabarty, K.; Li, H.H. Multi-Objective Optimization of ReRAM Crossbars for Robust DNN Inferencing under Stochastic Noise. In Proceedings of the 2021 IEEE/ACM International Conference On Computer Aided Design (ICCAD), Munich, Germany, 1–4 November 2021; pp. 1–9. [Google Scholar]
- Wang, S.; Zhang, Y.; Chen, J.; Zhang, X.; Li, Y.; Lin, N.; He, Y.; Yang, J.; Yu, Y.; Li, Y.; et al. Reconfigurable Digital RRAM Logic Enables In-Situ Pruning and Learning for Edge AI. arXiv 2025, arXiv:2506.13151. [Google Scholar] [CrossRef]
- Ma, C.; Sun, Y.; Qian, W.; Meng, Z.; Yang, R.; Jiang, L. Go Unary: A Novel Synapse Coding and Mapping Scheme for Reliable ReRAM-Based Neuromorphic Computing. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 1432–1437. [Google Scholar]
- Charan, G.; Mohanty, A.; Du, X.; Krishnan, G.; Joshi, R.V.; Cao, Y. Accurate Inference With Inaccurate RRAM Devices: A Joint Algorithm-Design Solution. IEEE J. Explor. Solid-State Comput. Devices Circuits 2020, 6, 27–35. [Google Scholar] [CrossRef]
- Sun, Y.; Ma, C.; Li, Z.; Zhao, Y.; Jiang, J.; Qian, W.; Yang, R.; He, Z.; Jiang, L. Unary Coding and Variation-Aware Optimal Mapping Scheme for Reliable ReRAM-Based Neuromorphic Computing. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2021, 40, 2495–2507. [Google Scholar] [CrossRef]
- Eldebiky, A.; Zhang, G.L.; Böcherer, G.; Li, B.; Schlichtmann, U. CorrectNet+: Dealing With HW Non-Idealities in In-Memory-Computing Platforms by Error Suppression and Compensation. IEEE Trans. Comput. Aided Des. Integr. Circuits Syst. 2024, 43, 573–585. [Google Scholar] [CrossRef]
- Ye, W.; Wang, L.; Zhou, Z.; An, J.; Li, W.; Gao, H.; Li, Z.; Yue, J.; Hu, H.; Xu, X.; et al. A 28-Nm RRAM Computing-in-Memory Macro Using Weighted Hybrid 2T1R Cell Array and Reference Subtracting Sense Amplifier for AI Edge Inference. IEEE J. Solid-State Circuits 2023, 58, 2839–2850. [Google Scholar] [CrossRef]
- Kosta, A.; Soufleri, E.; Chakraborty, I.; Agrawal, A.; Ankit, A.; Roy, K. HyperX: A Hybrid RRAM-SRAM Partitioned System for Error Recovery in Memristive Xbars. In Proceedings of the 2022 Design, Automation & Test in Europe Conference & Exhibition (DATE), Antwerp, Belgium, 14–23 March 2022; pp. 88–91. [Google Scholar]
- Yang, M.; Chen, J.; Zhang, Y.; Liu, J.; Zhang, J.; Ma, Q.; Verma, H.; Zhang, Q.; Zhou, M.; King, I.; et al. Low-Rank Adaptation for Foundation Models: A Comprehensive Review. arXiv 2024, arXiv:2501.00365. [Google Scholar] [CrossRef]
- Dettmers, T.; Pagnoni, A.; Holtzman, A.; Zettlemoyer, L. QLoRA: Efficient Finetuning of Quantized LLMs. arXiv 2023, arXiv:2305.14314. [Google Scholar] [CrossRef]
- Zhang, Q.; Chen, M.; Bukharin, A.; Karampatziakis, N.; He, P.; Cheng, Y.; Chen, W.; Zhao, T. AdaLoRA: Adaptive Budget Allocation for Parameter-Efficient Fine-Tuning. arXiv 2023, arXiv:2303.10512. [Google Scholar]
- Mao, Y.; Ge, Y.; Fan, Y.; Xu, W.; Mi, Y.; Hu, Z.; Gao, Y. A Survey on LoRA of Large Language Models. Front. Comput. Sci. 2025, 19, 197605. [Google Scholar] [CrossRef]
- Chih, Y.-D.; Lee, P.-H.; Fujiwara, H.; Shih, Y.-C.; Lee, C.-F.; Naous, R.; Chen, Y.-L.; Lo, C.-P.; Lu, C.-H.; Mori, H.; et al. 16.4 An 89TOPS/W and 16.3TOPS/Mm2 All-Digital SRAM-Based Full-Precision Compute-In Memory Macro in 22nm for Machine-Learning Edge Applications. In Proceedings of the 2021 IEEE International Solid- State Circuits Conference (ISSCC), San Francisco, CA, USA, 13–22 February 2021; pp. 252–254. [Google Scholar]
- Fujiwara, H.; Mori, H.; Zhao, W.-C.; Chuang, M.-C.; Naous, R.; Chuang, C.-K.; Hashizume, T.; Sun, D.; Lee, C.-F.; Akarvardar, K.; et al. A 5-Nm 254-TOPS/W 221-TOPS/Mm2 Fully-Digital Computing-in-Memory Macro Supporting Wide-Range Dynamic-Voltage-Frequency Scaling and Simultaneous MAC and Write Operations. In Proceedings of the 2022 IEEE International Solid-State Circuits Conference (ISSCC), San Francisco, CA, USA, 20–26 February 2022; pp. 1–3. [Google Scholar]
- An, J.; Zhou, Z.; Wang, L.; Ye, W.; Li, W.; Gao, H.; Li, Z.; Tian, J.; Wang, Y.; Hu, H.; et al. Write–Verify-Free MLC RRAM Using Nonbinary Encoding for AI Weight Storage at the Edge. IEEE Trans. VLSI Syst. 2024, 32, 283–290. [Google Scholar] [CrossRef]
- Shafiee, A.; Nag, A.; Muralimanohar, N.; Balasubramonian, R.; Strachan, J.P.; Hu, M.; Williams, R.S.; Srikumar, V. ISAAC: A Convolutional Neural Network Accelerator with In-Situ Analog Arithmetic in Crossbars. In Proceedings of the 2016 ACM/IEEE 43rd Annual International Symposium on Computer Architecture (ISCA), Seoul, Republic of Korea, 18–22 June 2016; pp. 14–26. [Google Scholar]
- Lu, A.; Peng, X.; Li, W.; Jiang, H.; Yu, S. NeuroSim Validation with 40nm RRAM Compute-in-Memory Macro. In Proceedings of the 2021 IEEE 3rd International Conference on Artificial Intelligence Circuits and Systems (AICAS), Washington DC, DC, USA, 6–9 June 2021; pp. 1–4. [Google Scholar]
- Li, Y.; Chen, Y.; Dai, X.; Chen, D.; Liu, M.; Yuan, L.; Liu, Z.; Zhang, L.; Vasconcelos, N. MicroNet: Improving Image Recognition with Extremely Low FLOPs. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 11–17 October 2021; pp. 458–467. [Google Scholar]
- Zhu, Y.; Zhang, G.L.; Wang, T.; Li, B.; Shi, Y.; Ho, T.-Y.; Schlichtmann, U. Statistical Training for Neuromorphic Computing Using Memristor-Based Crossbars Considering Process Variations and Noise. In Proceedings of the 2020 Design, Automation & Test in Europe Conference & Exhibition (DATE), Grenoble, France, 9–13 March 2020; pp. 1590–1593. [Google Scholar]
- Long, Y.; She, X.; Mukhopadhyay, S. Design of Reliable DNN Accelerator with Un-Reliable ReRAM. In Proceedings of the 2019 Design, Automation & Test in Europe Conference & Exhibition (DATE), Florence, Italy, 9–13 March 2019; pp. 1769–1774. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2015, arXiv:1409.1556. [Google Scholar] [CrossRef]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.-C. MobileNetV2: Inverted Residuals and Linear Bottlenecks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18–23 June 2018; pp. 4510–4520. [Google Scholar]
- Tang, S.; Gong, R.; Wang, Y.; Liu, A.; Wang, J.; Chen, X.; Yu, F.; Liu, X.; Song, D.; Yuille, A.; et al. RobustART: Benchmarking Robustness on Architecture Design and Training Techniques. arXiv 2022, arXiv:2109.05211. [Google Scholar] [CrossRef]
- Wu, F.; Zhao, N.; Liu, Y.; Chang, L.; Zhou, L.; Zhou, J. A Review of Convolutional Neural Networks Hardware Accelerators for AIoT Edge Computing. In Proceedings of the 2021 International Conference on UK-China Emerging Technologies (UCET), Chengdu, China, 4–6 November 2021; pp. 71–76. [Google Scholar]
| Approach | Precision | Storage Scheme | Heterogeneous | Density | Multi-Task Friendly | Accuracy (%) |
|---|---|---|---|---|---|---|
| VGG-16 on CIFAR-10 | ||||||
| DVA [38] | 8-bit | RRAM | no | medium | no | 80.1 (−13.04) |
| Unary [21] | 8-bit | RRAM | no | medium | no | 87.94 (−5.2) |
| KD + RSA [22] | 4-bit | RRAM and 15% SRAM | yes | limited | no | 92.57 (−0.57) |
| Unary-opt [23] | 6-bit | RRAM | no | medium | no | 92.66 (−0.48) |
| Hybrid IMC [18] | 3-bit | RRAM and 100% SRAM | yes | limited | no | 92.97 (−0.17) |
| CorrectNet+ [24] | 4-bit | RRAM and 0.6% RRAM | yes | medium | no | 91.29 (−1.85) |
| Ours | 8-bit | 3D RRAM and 2% SRAM | yes | high | yes | 93.14 |
| ResNet-18 on CIFAR-10 | ||||||
| DVA [38] | 8-bit | RRAM | no | medium | no | 84.1 (−9.9) |
| Unary-opt [23] | 6-bit | RRAM | no | medium | no | 93.2 (−0.8) |
| Ours | 8-bit | 3D RRAM and 2% SRAM | yes | high | yes | 94.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, W.; Nie, L.; Ma, C.; Wu, H.; Yuan, Y.; Zhang, S.; Liu, Q.; Zhang, F. Low-Rank Compensation in Hybrid 3D-RRAM/SRAM Computing-in-Memory System for Edge Computing. Eng 2025, 6, 332. https://doi.org/10.3390/eng6120332
Tang W, Nie L, Ma C, Wu H, Yuan Y, Zhang S, Liu Q, Zhang F. Low-Rank Compensation in Hybrid 3D-RRAM/SRAM Computing-in-Memory System for Edge Computing. Eng. 2025; 6(12):332. https://doi.org/10.3390/eng6120332
Chicago/Turabian StyleTang, Weiye, Long Nie, Cailian Ma, Hao Wu, Yiyang Yuan, Shuaidi Zhang, Qihao Liu, and Feng Zhang. 2025. "Low-Rank Compensation in Hybrid 3D-RRAM/SRAM Computing-in-Memory System for Edge Computing" Eng 6, no. 12: 332. https://doi.org/10.3390/eng6120332
APA StyleTang, W., Nie, L., Ma, C., Wu, H., Yuan, Y., Zhang, S., Liu, Q., & Zhang, F. (2025). Low-Rank Compensation in Hybrid 3D-RRAM/SRAM Computing-in-Memory System for Edge Computing. Eng, 6(12), 332. https://doi.org/10.3390/eng6120332






