1. Introduction
Optical computing has a long history of implementing arithmetic operations through interference and diffraction [
1]. Here, we present the theoretical framework for a new optical scheme capable of directly performing integer division and remainder extraction. The method, which we call the
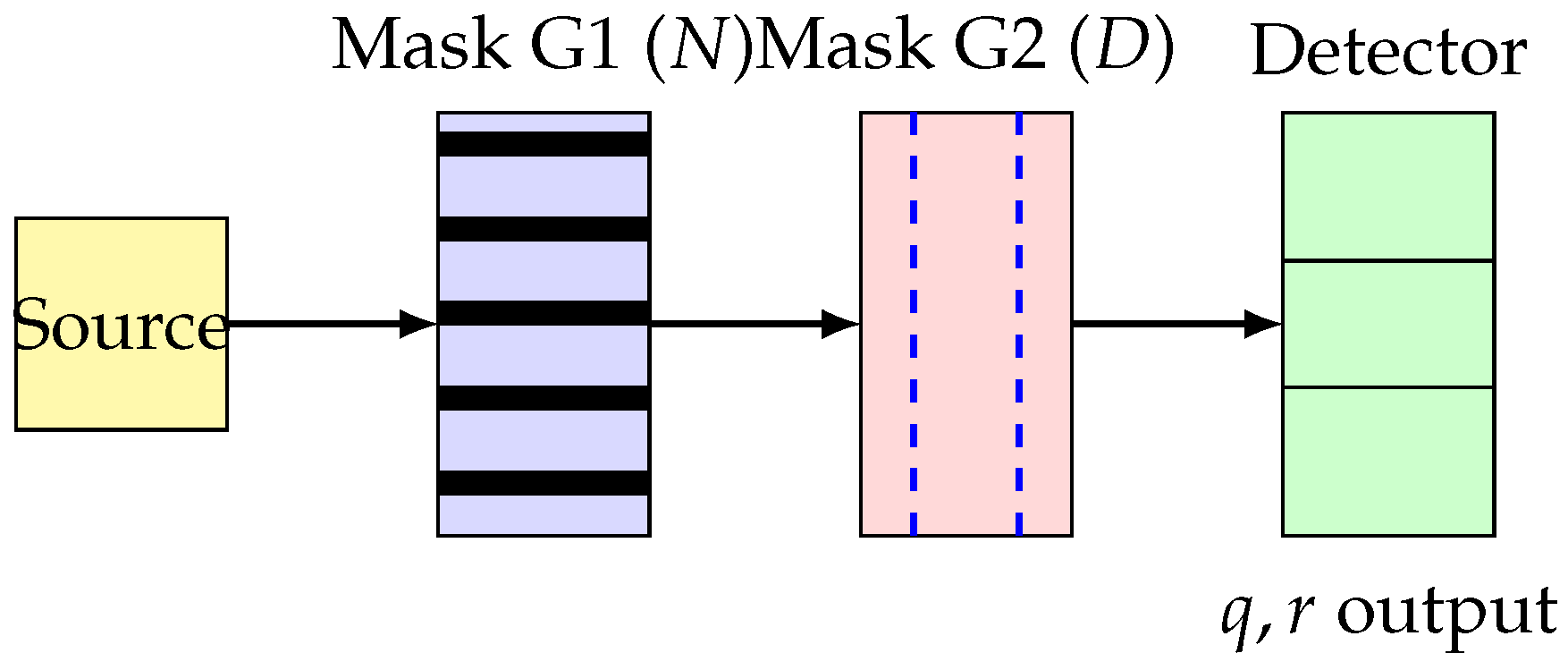
Interlaced Line Divider (ILD), is based on the alignment of two masks of parallel lines (see
Figure 1 for an optical schematic). This work provides a complete mathematical analysis of the ILD concept, demonstrating its theoretical correctness and establishing the physical conditions under which optical superposition can implement Euclidean division. We derive the fundamental relationship between optical transmission and discrete arithmetic operations, analyze robustness to fabrication tolerances and noise, and outline the experimental requirements for future laboratory implementation. The theoretical foundation presented here opens new possibilities for hardware-level analog computation of modular arithmetic, with potential applications in cryptography, optical sensing, and unconventional computing architectures.
1.1. Scope and Methodology
It is important to clarify that this work presents a theoretical framework and mathematical proof of concept for the Interlaced Line Divider (ILD). The primary contribution lies in establishing the complete mathematical formalism that demonstrates the theoretical correctness and physical feasibility of the proposed optical division method. While we provide detailed experimental design guidelines and performance estimates, actual laboratory implementation and empirical validation are considered important future work that lie beyond the scope of this theoretical study.
1.2. Recent Advances in Optical Computing
Recent years have witnessed renewed interest in optical computing paradigms, driven by the limitations of conventional electronic processors in terms of power efficiency and parallel-processing capabilities. Notable developments include photonic neural networks for machine learning applications [
2,
3] (for instance, ONNs achieving sub-nanosecond latencies and orders-of-magnitude energy improvements [see [
4]]), integrated photonic circuits for linear algebra operations [
5] (such as the large-scale photonic accelerator of [
6]), and spatial-light-modulator-based processors for specialized computations [
7]. These approaches leverage the inherent parallelism, low latency, and energy efficiency of optical systems [
8,
9,
10,
11,
12]. Our work contributes to this growing field by introducing a novel optical primitive for fundamental arithmetic operations, complementing existing optical computing architectures with a dedicated division module.
2. Concept and Method
2.1. Conceptual Overview for Non-Experts
The ILD operates on a simple physical principle: representing numbers as patterns of opaque lines and using optical superposition to perform arithmetic. Imagine counting objects by grouping them into sets—this is essentially what the ILD does optically. The dividend (number to be divided) is encoded as a series of lines, while the divisor (number to divide by) determines how these lines are grouped into blocks. By measuring light transmission through these superimposed patterns, we can directly read off the quotient (number of complete groups) and remainder (leftover items).
The ILD relies on a simple but instrumental idea: represent the dividend and divisor geometrically as line masks, and let optical superposition and blockwise detection perform the Euclidean division operation. Two complementary masks are employed, each encoding different aspects of the problem. This approach builds on established principles of spatial light processing [
13,
14] and mask-based optical computation [
15].
2.2. Dividend and Completer Masks
G1 (dividend mask): encodes the integer N by means of N opaque lines, equally spaced with pitch p.
G2 (completer mask): defines the divisor D by imposing periodic block boundaries, each block containing D sites, and extending the grid up to the next multiple of D.
When the two masks are superposed, the optical field is segmented into blocks of width
, each acting as a counting bin. A segmented detector placed after the masks integrates transmission over each block and reports the number of fully filled blocks (
q) and the residual occupancy (
r). In other words, the ILD physically implements the Euclidean division rule:
2.3. Illustrative Example
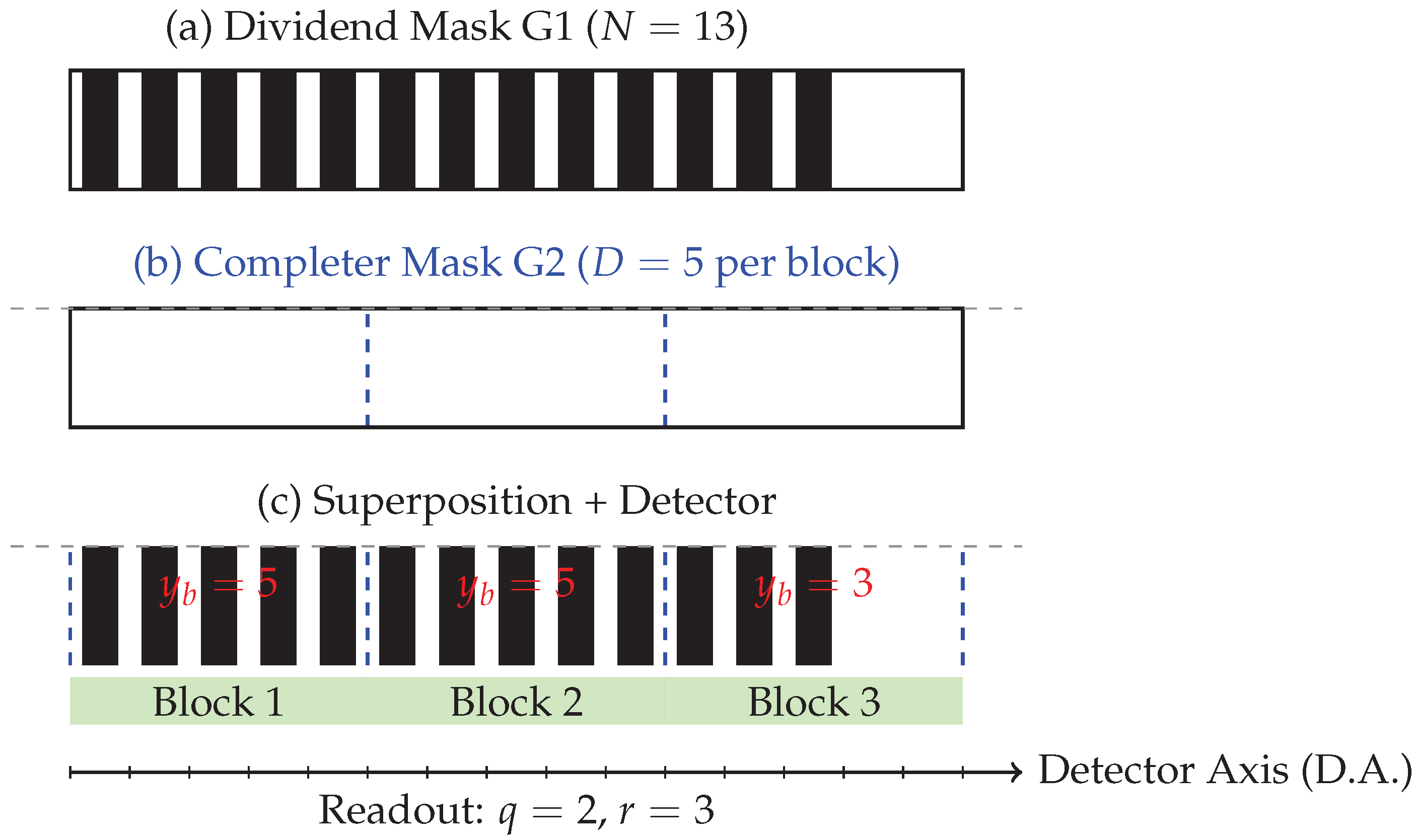
To see how the ILD reproduces Euclidean division in practice, consider the case of dividing by . The process unfolds as follows:
Dividend mask (G1). Mask G1 encodes the integer by means of 13 opaque vertical lines, equally spaced with pitch p.
Completer mask (G2). Mask G2 partitions the axis into blocks of size , so that the first block covers sites 1–5, the second block 6–10, and the third block 11–15. In total, G2 defines 15 sites grouped into three blocks.
Superposition. Overlaying G1 and G2, the detector now sees how the 13 lines of G1 distribute across the three blocks.
Block 1 (sites 1–5): all five sites are filled.
Block 2 (sites 6–10): all five sites are filled.
Block 3 (sites 11–15): only three sites are filled (lines 11, 12, 13).
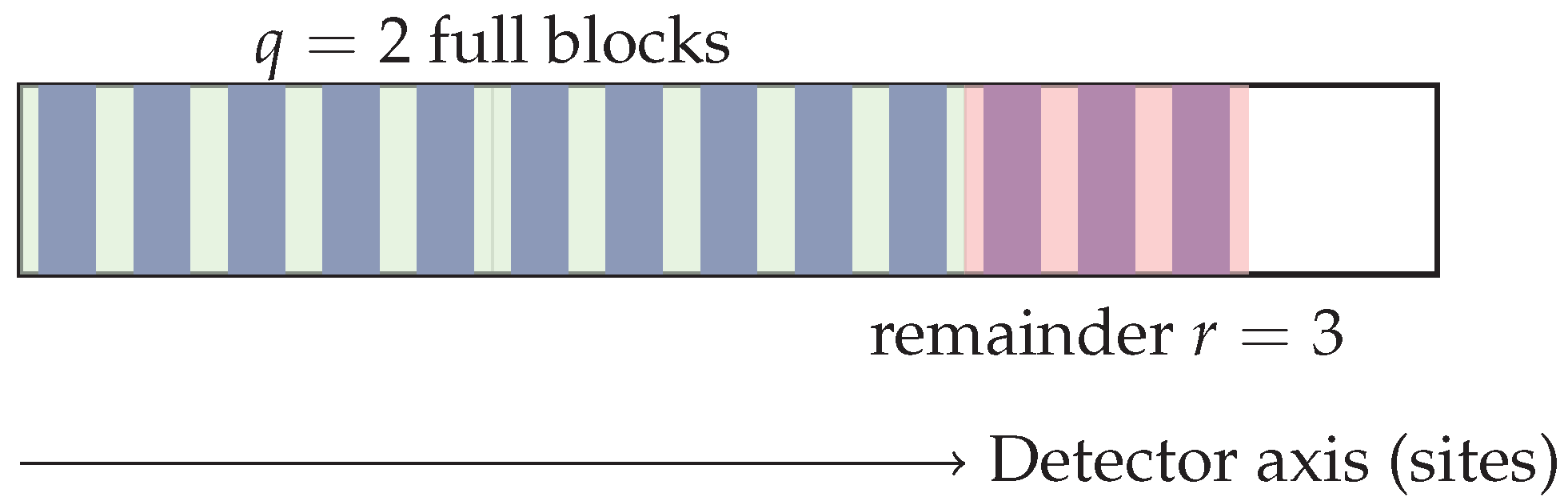
Detector readout. The segmented detector integrates light per block. It registers two full blocks, corresponding to a quotient , and a partial block with three filled sites, giving the remainder .
In other words, the ILD reproduces the standard Euclidean division relation (see
Figure 2)
but does so physically by line counting and block segmentation rather than by digital arithmetic.
3. Mathematical Formalism and Correctness
We give a rigorous derivation of why the Interlaced Line Divider (ILD) returns the Euclidean division result , and we state the optical conditions under which the physical device implements the same combinatorics.
3.1. Discrete Combinatorial Model (Ideal Counting)
Fix an integer block size
and a pitch
defining a one-dimensional lattice of
sites The dividend mask
encodes
N opaque line elements at the first
N sites and is empty elsewhere. Let
Partition the lattice into contiguous
blocks of size
D:
and define the
block occupancy (opaque count) of
as
Lemma 1 (Euclidean partition by block sums).
Let with and . Then, the block occupancies satisfy Proof. For , ; hence, all D sites are occupied: . For , ; hence, . For , intersects in exactly sites, so . □
Corollary 1 (ideal ILD readout).
The quotient and remainder are read asThus, the ideal block counting on alone reproduces Euclidean division. Role of the Completer Mask
Physically,
provides
registration and visualization of blocks (see
Figure 3): it defines the block boundaries and ensures that detection integrates over non-overlapping regions of width
. Mathematically,
induces the fixed partition
used in (
2); no further algebraic role is needed for correctness.
3.2. Connection to Combinatorial Mathematics
While the core mathematical operation is indeed counting, this process falls within the domain of enumerative combinatorics—specifically, the partitioning of a set of N distinct elements into blocks of size D and analyzing the distribution of elements across these blocks. The combinatorial aspect lies in how we enumerate the possible distributions of N lines into blocks of size D, where the occupancy pattern directly encodes the Euclidean division result. This represents a physical implementation of combinatorial allocation problems studied in discrete mathematics.
3.3. Optical Model (Amplitude Masks and Block Integrals)
We now link optical transmission and detection to the discrete counts .
3.3.1. Mask Transmittances
Model
as an amplitude mask with transmittance
where
is the line
contrast and
w is a site-localized aperture function supported in a guard-banded window
, with
. Let
be a periodic
block-window mask of period
that defines non-overlapping
regions of interest (ROIs)
, e.g.,
, and
(fully transmissive) over
.
3.3.2. Illumination and Detection
Illumination is a uniform plane wave of intensity
. For thin, absorption-dominant masks, the transmitted intensity is
. Let the detector report the
block integralAssumption 1 (guard band and alignment). (i) iff . (ii) Mechanical misalignment ε satisfies , so each opaque element remains within its site window.
Let (site-wise opaque area). Under Assumption 1, each occupied site in contributes the same to the integral, and empty sites contribute 0.
Proposition 1 (affine link between optics and counts).
Under Assumption 1, Proof. Equation (
3) reduces to
□
Consequences 1. (i) is a strictly decreasing affine function of the integer count . (ii) Since , the set of possible values is a uniform lattice
with spacing β. (iii) Thresholding the block integrals at recovers which blocks are full
() and which are not. The last nonzero block’s integral yields by inversion of (4). Theorem 1 (Correctness of ILD optical readout).
Under Assumption 1 and with contrast , the block integrals uniquely determine the block counts via (4), and hence return and . Therefore, the ILD implements Euclidean division . Proof. Invert (
4):
. Because
and
, rounding to the nearest integer is exact in the noiseless setting. Lemma 1 then yields
. □
3.4. Robustness to Small Misalignment and Noise
3.4.1. Geometric Robustness
If the lateral misalignment
, each opaque element remains inside its site window, so the per-site contribution to
remains
. Thus, (
4) holds exactly.
3.4.2. Photometric Robustness
With additive noise on each block integral, , integer recovery is guaranteed if for all b, since adjacent lattice points are separated by . More generally, a maximum-likelihood (nearest-lattice) decoder on recovers with error probability decaying with SNR.
3.4.3. Gray-Level Transmittance
If lines have transmittance
instead of 0, replace
by
in (
4). The same lattice structure and decoding apply.
3.5. Superposition and Moiré Variants (Optional)
The analysis above used amplitude multiplication
and ROI integration. In a moiré variant, two periodic line sets at a small relative angle
create an envelope with period proportional to
. If the ROI windows are placed to integrate one envelope period per block (calibrated once), the same affine link (
4) is obtained at the envelope scale, with effective
set by the envelope contrast. Thus, the counting argument (Lemma 1) and Theorem 1 still apply.
3.6. Summary of Assumptions and Guarantees
The preceding analysis introduced several technical conditions to ensure that the optical implementation matches the combinatorial model. For clarity, we collect them here as explicit assumptions, each linked to the formal steps in
Section 3:
Assumption 2 (Site separability). Each line aperture fits entirely within a guard-banded window . This guarantees that every line is unambiguously assigned to a site.
Assumption 3 (Block registration). The detector integrates over fixed regions of interest (ROIs) of width , aligned with the site grid. This ensures that block sums coincide with the mathematical partitions .
Assumption 4 (Contrast and SNR). The per-site decrement in transmitted intensity is nonzero (), and the additive noise is bounded by . This ensures that the lattice of possible block integrals is resolvable without overlap, so that integer recovery is unambiguous.
Taken together, (A1)–(A3) constitute the physical envelope under which the affine relation (
4) holds. Within this envelope, the ILD performs exact Euclidean division by block integration and nearest-lattice decoding, establishing the correctness of the method in both theory and practice.
3.7. Computational Complexity and Performance Analysis
3.7.1. Time Complexity
The ILD performs Euclidean division in constant time with respect to both dividend N and divisor D, since the optical computation occurs through simultaneous light transmission across all sites. This represents a fundamental advantage over sequential digital algorithms:
The physical computation time is limited only by light transit time ( where L is the optical path length) and detector integration time, both typically on the order of nanoseconds to microseconds.
3.7.2. Parallelizability
Unlike sequential digital algorithms, the ILD exhibits massive intrinsic parallelism:
Spatial parallelism: All N dividend lines are processed simultaneously through optical superposition.
Block parallelism: Multiple divisions can be performed in parallel by replicating the mask structure. A single optical setup can compute M independent divisions simultaneously using spatially multiplexed regions.
Wavelength parallelism: Different wavelengths can carry independent division problems through wavelength-division multiplexing, limited only by detector spectral resolution.
For comparison, digital division requires sequential steps even with optimal parallel hardware, while the ILD maintains complexity regardless of problem size.
3.7.3. Theoretical Throughput Analysis
Consider an ILD system with the following parameters:
Detector-integration time: s
Mask-switching time (for programmable operation): s
Spatial-multiplexing capacity: M parallel channels
Wavelength-multiplexing capacity: channels
The theoretical throughput is
For a practical implementation with
spatial channels,
wavelengths, and the parameters above:
This represents a significant advantage for applications requiring high-throughput modular arithmetic, such as cryptographic operations or large-scale numerical simulations.
While the throughput equation follows standard performance modeling formalism, its application to optical division represents a novel contribution. The specific parameterization for mask-based optical computation and the derived performance estimates for Euclidean division operations are new to the literature.
3.7.4. Scaling Properties
The optical approach exhibits favorable scaling properties:
Operand size independence: Computation time remains constant as N and D increase, unlike digital methods where complexity grows with operand bit length.
Energy scaling: Power consumption scales primarily with illumination requirements and detector count, not with operand magnitude.
Physical scaling: The mask area scales linearly with maximum operand size, providing a predictable trade-off between physical footprint and computational range.
These properties make the ILD particularly attractive for specialized applications where division operations dominate computational cost, such as real-time digital signal processing or high-frequency trading systems requiring rapid modular arithmetic.
3.8. Physical Limits and Fundamental Constraints
3.8.1. Diffraction-Limited Resolution
The spatial resolution of the ILD is fundamentally constrained by optical diffraction. For coherent illumination with wavelength
, the minimum resolvable feature size is approximately
where NA is the numerical aperture of the optical system. This sets a lower bound on the achievable pitch
p, and hence, the maximum operand density. For visible light (
nm) and moderate NA
,
This diffraction limit constrains the maximum dividend for a given physical aperture L: . Beyond this limit, adjacent line elements become unresolvable, violating Assumption 2.
3.8.2. Shot Noise and Fundamental Detection Limits
The ultimate sensitivity is limited by photon shot noise in the detector. For a block receiving
photons, the signal-to-noise ratio is
From Equation (
4), reliable discrimination between adjacent lattice points requires
, yielding a minimum photon budget:
This establishes a fundamental trade-off between speed (integration time), power (illumination intensity), and accuracy in the quantum-limited regime.
While diffraction-limited resolution and shot noise impose fundamental constraints on the ILD’s performance, as outlined in Equations (
7)–(
10), these challenges can be addressed through targeted experimental strategies. For instance, employing higher numerical aperture (NA) optics or shorter wavelength sources, as suggested in the design guidelines of
Section 4.2, can reduce the minimum pitch
p below the estimated 2.5
m threshold, enhancing operand density within a fixed aperture. Additionally, increasing illumination intensity or extending detector integration time, consistent with the proposed CMOS/CCD setup in
Section 4.3, can improve the signal-to-noise ratio (SNR) to exceed the required
threshold, mitigating shot noise effects. These adjustments, grounded in the theoretical framework and practical tolerances outlined in
Section 4, underscore the ILD’s feasibility for laboratory validation and future optimization.
3.8.3. Connection to Analog Computing Principles
The ILD exemplifies several fundamental principles of analog computation:
Spatial encoding: Information is represented through physical spatial arrangements rather than temporal sequences, enabling massive parallelism inherent to wave phenomena.
Linear superposition: The optical field obeys Maxwell’s equations, whose linearity allows simultaneous processing of multiple spatial channels without cross-talk (within the paraxial approximation).
Physical constraint satisfaction: The block integration naturally implements the constraint , ensuring consistency through physical conservation rather than algorithmic verification.
Analog-to-digital conversion: The detector performs inherent quantization through photon counting, bridging continuous optical fields to discrete arithmetic results.
These principles, first articulated in early analog computer theory [
19,
20], remain relevant for modern optical processors [
21].
These principles distinguish optical analog computers from digital architectures, where information processing occurs through sequential logical operations rather than physical field evolution.
3.8.4. Theoretical Extensions
Two-dimensional Array Generalization. The ILD concept extends naturally to two-dimensional arrays for simultaneous processing of multiple operands. Consider a 2D mask encoding dividends along orthogonal rows, with a corresponding completer mask defining block structures. A 2D detector array can then compute for all rows simultaneously, providing complexity for batch division operations.
This extension follows established approaches in parallel optical processors [
22] and systolic array architectures [
23].
Multi-radix Systems. The blocking scheme generalizes to non-uniform block sizes , enabling mixed-radix number representations. This allows computation of simultaneous divisions by different bases: , , etc., relevant for applications in digital signal processing and number-theoretic transforms.
Cascaded Operations. Multiple ILD stages can be cascaded to implement more complex operations. For instance, computing requires two stages: first compute , then . The cascaded architecture maintains complexity while extending computational capability.
Continuous-Variable Extensions. For non-integer operands, the line discretization can be replaced by continuous transmittance profiles , where rect is the rectangular function. Block integration then computes continuously, useful for analog signal processing applications.
These extensions demonstrate that the ILD represents not merely an isolated arithmetic unit but a foundational element in a broader class of spatial optical computers based on mask superposition and blockwise detection.
4. Experimental Realization and Theoretical Validation
This section outlines a
theoretically feasible experimental implementation of the ILD, based on the mathematical framework established in
Section 2. It is crucial to emphasize that the following represents a
theoretical design study rather than an account of performed laboratory experiments. The purpose is to demonstrate that the ILD concept can be physically realized using standard photonic components and to identify the technical requirements and tolerances necessary for future experimental validation.
4.1. Theoretical Experimental Design
The analytical model developed in
Section 2 provides a complete mathematical foundation for the ILD operation. To bridge theory with potential practice, we now specify the optical components and configuration that would satisfy the theoretical assumptions, particularly those outlined in
Section 3.6 (A2–A4). Having established the mathematical formalism and demonstrated the principle of operation of the Interlaced Line Divider (ILD), we now turn to a possible laboratory implementation. The goal is to identify a minimal optical setup that is consistent with the theoretical assumptions of
Section 3 while being feasible with standard photonics components. In what follows, we outline the source, masks, and detector specifications required for a first prototype.
4.2. Optical Setup
A minimal experimental configuration for the ILD can be assembled using standard benchtop photonics components. The key requirements are a coherent or quasi-coherent source, two masks that encode the dividend and divisor, and a detector capable of blockwise integration. One possible implementation is as follows:
Source: LED or low-power laser in the 520–650 nm range, chosen for ease of alignment and compatibility with inexpensive detectors.
Masks: chrome-on-glass gratings with pitch –m and linewidth 30–m. These values ensure that individual sites are resolvable by the detector while remaining within standard photolithography tolerances.
Detector: CMOS/CCD with software-defined regions of interest or, alternatively, a segmented photodiode array. Segmentation allows direct blockwise integration of transmitted intensity, consistent with the formalism in
Section 3.
4.3. Tolerances
The analytical model in
Section 3 assumes that each opaque line fits entirely within its designated site window and that block boundaries are correctly registered. In practice, this requires fabrication and alignment tolerances to be tighter than the guard bands introduced in Assumption 1. Specifically,
Pitch tolerance: Variations in the site pitch must be smaller than <2 m within a block to avoid cumulative drift that would push a line outside its guard band.
Block registration: Errors in defining the block boundaries must be <0.1p to ensure that all D sites intended for a block are correctly integrated by the detector.
Alignment: The relative position of masks G1 and G2 is maintained with an XY translation stage so that the partitioning of sites into blocks remains stable during measurement.
These tolerances guarantee that the affine relation (
4) between optical block integrals and discrete site counts remains valid in the physical device, ensuring error-free recovery of the quotient and remainder.
4.4. Quantitative Application Analysis
The ILD’s unique combination of complexity, massive parallelism, and hardware-level implementation creates specific niches where it outperforms conventional approaches. We analyze key application domains with theoretical performance estimates.
4.4.1. Cryptographic Co-Processing
Advantage Analysis: RSA decryption requires computing
where modular reduction dominates computational cost. For 2048-bit RSA, approximately 60% of execution time involves modular arithmetic operations. Following standard analysis of RSA computational costs [
24], modular exponentiation dominates the runtime.
Performance Estimate: Consider batch processing of
RSA operations with 256-bit moduli. Digital implementation using Montgomery reduction requires ∼
cycles per operation at 3 GHz, yielding
The ILD with spatial multiplexing (
channels) and Equation (
6) parameters achieves:
Speedup Factor: ∼ for batch operations, with additional benefits in power consumption due to analog processing.
Optimal Regime: Most advantageous for applications requiring high-throughput modular arithmetic with moderate precision (8–16 bits), such as elliptic curve operations or lattice-based post-quantum cryptography.
4.4.2. Real-Time Digital Signal Processing
Use Case: Fast Fourier Transform (FFT) implementations often require modular reduction for number-theoretic transforms, particularly in finite field arithmetic.
Performance Analysis: A 1024-point FFT over requires ∼ modular operations. At video frame rates (60 fps), this demands reductions per second.
ILD Implementation: Using 16 parallel channels (one per bit), the ILD can process each reduction in ∼
s (Equation (
6)), easily meeting real-time constraints, while digital implementations struggle with this throughput.
Competitive Advantage: The optical approach excels when
Division latency must be deterministic (no data-dependent timing)
Multiple simultaneous divisions are required
Power budget constraints favor analog computation
4.4.3. Monte Carlo Simulations
Application Domain: Large-scale simulations requiring random number generation with specific modular properties.
Scaling Analysis: Linear congruential generators require computing millions of times. For samples with ,
- -
Digital approach: ∼ sequential operations at ∼10 cycles each = 3.3 s at 3 GHz
- -
ILD approach: Batch processing 1000 samples simultaneously = batch operations × 10 s = 10 s
Trade-off Analysis: Digital wins for sequential processing, but ILD becomes advantageous when
Multiple independent streams needed simultaneously
Custom moduli required (where hardware optimizations do not apply)
Energy efficiency is critical
These performance characteristics follow established patterns in specialized arithmetic accelerators [
25,
26].
4.4.4. Optical vs. Digital Performance Boundaries
The ILD outperforms digital approaches when
Operand Size: 8–64 bits (sweet spot: 16–32 bits)
- -
Below 8 bits: Digital lookup tables are faster
- -
Above 64 bits: Precision limits dominate
Batch Size: >100 simultaneous operations
- -
Spatial parallelism overcomes digital SIMD (Single Instruction, Multiple Data) advantages
Power Constraints: mW per operation
- -
Optical computation can be more energy-efficient than digital arithmetic units
Latency Requirements: μs deterministic
- -
No branch prediction or cache misses
4.4.5. System Integration Considerations
Hybrid Architectures: The ILD functions best as a specialized co-processor in hybrid systems:
where
s for mask configuration. This overhead is amortized over large batch sizes, making the approach most suitable for applications with
- -
High computational density (many operations per setup)
- -
Predictable operation patterns (allowing mask pre-configuration)
- -
Tolerance for analog precision limits (∼ relative accuracy)
Market Positioning: The ILD targets specialized niches rather than general-purpose arithmetic:
Cryptographic accelerators for IoT devices with power constraints
DSP (Digital Signal Processing) co-processors for radar/communications requiring deterministic timing
Scientific computing nodes for embarrassingly parallel modular arithmetic
Edge AI inference engines using quantized neural networks with modular activations
These applications justify the additional complexity of optical implementation through substantial performance gains in specific operational regimes. Equation (
13) provides a systematic framework for analyzing optical co-processor integration, extending conventional digital performance models to hybrid optical-electronic systems. While the mathematical form is standard, its application to mask-based optical arithmetic units and the specific timing parameters for ILD operation represent a novel contribution to optical computing performance analysis.
5. Applications
Beyond its pedagogical appeal, the ILD can serve as a physical primitive for modular arithmetic and blockwise aggregation in optics. Prior work on optical and analog computing has shown that simple optical elements can implement useful linear and non-linear transforms with low latency and massive parallelism [
8,
9], while recent developments in photonic hardware for AI underscore the practical value of moving arithmetic into the optical domain [
2,
3]. Programmable or mask-based implementations (including SLMs) provide an established route to realize such primitives in compact benchtop systems [
10].
Optical co-processors. Because the ILD directly executes and at the physical layer, it can act as a building block for optical arithmetic accelerators. In integrated photonic circuits, ILD modules could be cascaded with other operators (Fourier lenses, correlators, non-linear media) to perform more complex pipelines with minimal energy cost.
Cryptography. Modular reduction is central to cryptosystems such as RSA, ECC, and lattice-based schemes. An ILD stage can serve as a dedicated hardware co-processor that computes optically, offloading a costly digital operation. Furthermore, the remainder block encodes a residual pattern sensitive to fabrication imperfections and alignment noise. This naturally implements a physical unclonable function (PUF): each device has a unique optical signature, which can be leveraged for authentication and secure key storage.
Optical sensing and encoders. Mounting ILD masks on a rotating or translating platform converts the quotient q and remainder r into signals that vary with angle or displacement. The remainder r, in particular, is highly sensitive to sub-micron misalignments, making it a potential probe for strain, thermal expansion, or micro-displacement detection. Compared with conventional optical encoders, the presence of a remainder channel increases information density and resolution.
Unconventional and neuromorphic computing. Following recent work on optical neural networks [
5,
7], the ILD can be embedded as a primitive inside hybrid photonic–electronic systems, providing fast non-linear operations that resemble spiking or thresholding.
Educational tools. The ILD offers a tangible, visual demonstration of Euclidean division: learners directly observe q as the number of full blocks and r as the leftover lines. With its simple setup (light source, two masks, detector), it is well suited for instructional labs in optics, information processing, and computer science.
6. Systematic Analysis of Applications
We now systematically analyze potential applications of the ILD across several domains, evaluating each based on technical feasibility, performance advantages, and implementation requirements.
6.1. Optical Co-Processors
Technical Basis: Direct physical implementation of modular arithmetic
Performance Advantage: Constant-time division independent of operand size
Implementation Requirements: Mask fabrication, optical alignment
Feasibility Timeline: Near-term (1–2 years) for proof of concept
6.2. Cryptographic Accelerators
Technical Basis: Hardware offloading of modular reduction operations
Performance Advantage:∼120× speedup for batch operations
Implementation Requirements: Integration with digital processors
Feasibility Timeline: Medium-term (2–3 years)
7. Conclusions
We have introduced and rigorously formalized the Interlaced Line Divider (ILD), a novel optical computing paradigm for integer division based on mask superposition. The comprehensive theoretical analysis confirms that Euclidean division can be implemented optically with constant-time complexity and inherent massive parallelism, leveraging the wave-based nature of light.
As a theoretical proposal, this work establishes the mathematical robustness and physical plausibility of the ILD through detailed derivations, laying a solid groundwork for future experimental pursuits without requiring immediate empirical validation. The analytical models, including performance estimates such as divisions per second, offer a reliable basis for prototype development and empirical testing of predicted characteristics under realistic conditions.
Future research should prioritize laboratory implementation to verify the models, potentially using high-NA optics and CMOS detectors as outlined in
Section 4. Extensions to two-dimensional arrays could enhance parallel-processing capabilities, while integration with programmable spatial light modulators may enable dynamic adaptability. These advancements could unlock significant benefits in high-throughput applications, such as cryptographic co-processing and real-time signal processing, positioning the ILD as a promising building block for next-generation optical computing systems.