Development of a Methodology for Seismic Design of Framed Steel Structures Incorporating Viscous Dampers
Abstract
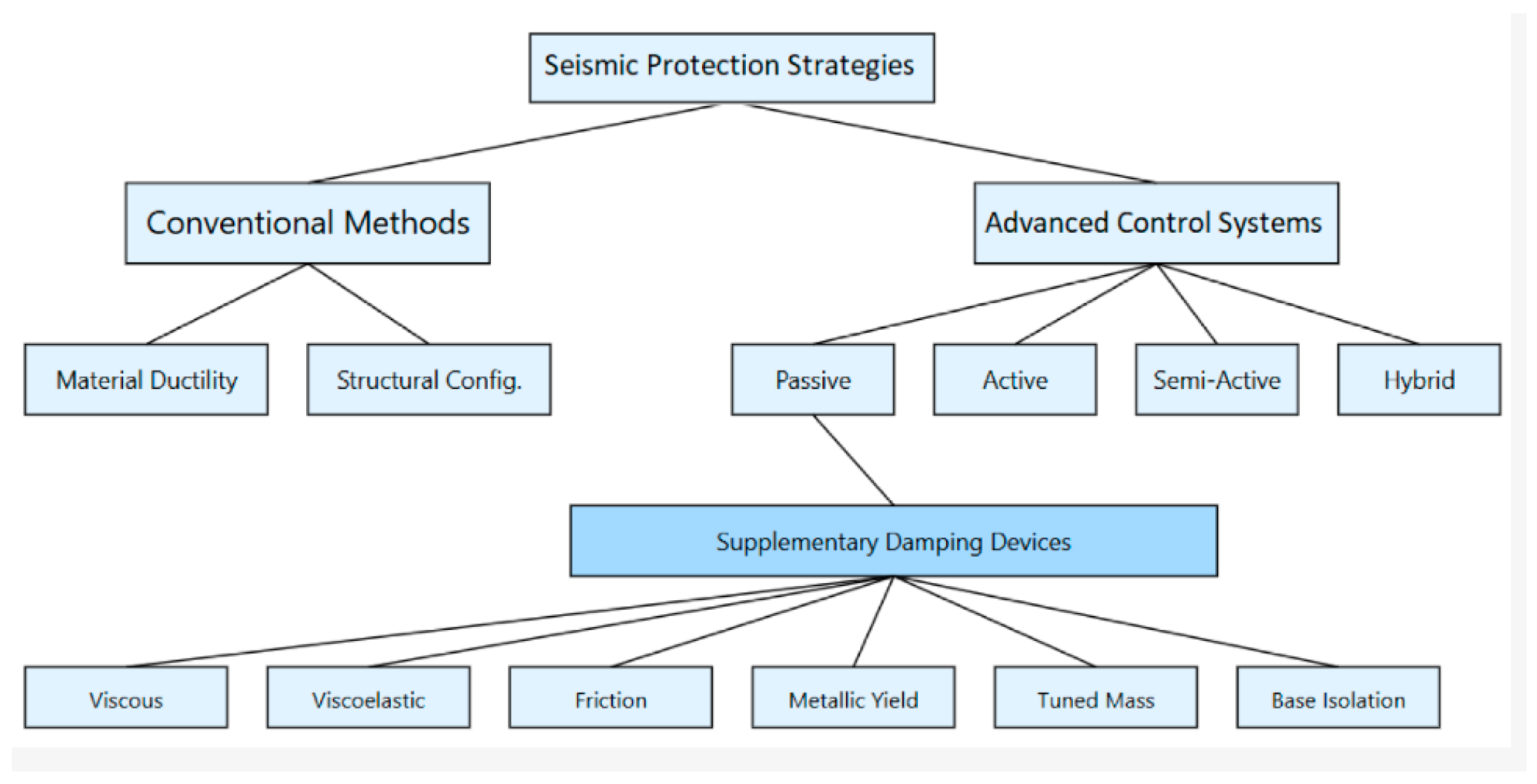
1. Introduction
2. Description of Structures
3. Modelling of Viscous Dampers
4. Results
5. Comparison with Existing Methods and Discussion
5.1. Comparison with Hatzigeorgiou [36] Method
5.2. Comparison with Logotheti et al.’s [38] Approach
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kitayama, S.; Constantinou, M.C. Seismic Performance of Buildings with Viscous Damping Systems Designed by the Procedures of ASCE/SEI 7-16. J. Struct. Eng. 2018, 144, 4018050. [Google Scholar] [CrossRef]
- Christopoulos, C.; Filiatrault, A. Principles of Passive Supplemental Damping and Seismic Isolation; IUSS Press: Pavia, Italy, 2006. [Google Scholar]
- Wang, S.; Mahin, S.A. Seismic retrofit of a high-rise steel moment-resisting frame using fluid viscous dampers. Struct. Des. Tall Spec. Build. 2017, 26, e1367. [Google Scholar] [CrossRef]
- Lavan, O. A methodology for the integrated seismic design of nonlinear buildings with supplemental damping. Struct. Control Health Monit. 2015, 22, 484–499. [Google Scholar]
- Constantinou, M.C.; Tadjbakhsh, I.G. Optimum design of a first story damping system. Comput. Struct. 1983, 17, 305–310. [Google Scholar] [CrossRef]
- Symans, M.D.; Charney, F.A.; Whittaker, A.S.; Constantinou, M.C.; Kircher, C.A.; Johnson, M.W.; McNamara, R.J. Energy dissipation systems for seismic applications: Current practice and recent developments. J. Struct. Eng. ASCE 2008, 134, 3–21. [Google Scholar] [CrossRef]
- Mahjoubi, S.; Maleki, S. Seismic performance evaluation and design of steel structures equipped with dual-pipe dampers. J. Constr. Steel Res. 2016, 122, 25–39. [Google Scholar] [CrossRef]
- Zhu, X.; Jing, X.; Cheng, L. Magnetorheological fluid dampers: A review on structure design and analysis. J. Intell. Mater. Syst. Struct. 2012, 23, 839–873. [Google Scholar]
- Salaas, B.; Bekdaş, G.; Ibrahim, Y.E.; Nigdeli, S.M.; Ezzat, M.; Nawar, M.; Kayabekir, A.E. Design optimization of a hybrid vibration control system for buildings. Buildings 2023, 13, 934. [Google Scholar]
- Zhang, H.; Li, A.; Su, Y.; Xu, G.; Sha, B. Viscoelastic Dampers for Civil Engineering Structures: A Systematic Review of Constructions, Materials, and Applications. J. Build. Eng. 2024, 96, 110597. [Google Scholar]
- Yuan, X.; Tian, T.; Ling, H.; Qiu, T.; He, H. A review on structural development of magnetorheological fluid damper. Shock Vib. 2019, 2019, 1498962. [Google Scholar] [CrossRef]
- Papagiannopoulos, G.A.; Hatzigeorgiou, G.D.; Beskos, D.E. Design Using Supplemental Dampers. In Seismic Design Methods for Steel Building Structures; Springer: Berlin/Heidelberg, Germany, 2021; pp. 463–508. [Google Scholar]
- Landi, L.; Lucchi, S.; Diotallevi, P.P. A procedure for the direct determination of the required supplemental damping for the seismic retrofit with viscous dampers. Eng. Struct. 2014, 71, 137–149. [Google Scholar] [CrossRef]
- Lavan, O. Optimal design of viscous dampers and their supporting members for the seismic retrofitting of 3D irregular frame structures. J. Struct. Eng. 2015, 141, 04015026. [Google Scholar] [CrossRef]
- Nuzzo, I.; Losanno, D.; Caterino, N. Seismic design and retrofit of frame structures with hysteretic dampers: A simplified displacement-based procedure. Bull. Earthq. Eng. 2019, 17, 2787–2819. [Google Scholar] [CrossRef]
- Marioni, A. Seismic retrofitting of existing structures. In Anti-Seismic Devices: A Reference Manual for Structural Engineers; Springer International Publishing: Cham, Switzerland, 2024; pp. 145–168. [Google Scholar]
- Marioni, A. Testing Requirements of Anti-seismic Devices and Available Testing Facilities. In Anti-Seismic Devices: A Reference Manual for Structural Engineers; Springer International Publishing: Cham, Switzerland, 2024; pp. 85–109. [Google Scholar]
- Stanikzai, M.H.; Elias, S.; Chae, Y. Recent advances in hybrid vibration-control systems. Pract. Period. Struct. Des. Constr. 2022, 27, 03122003. [Google Scholar] [CrossRef]
- Shu, Z.; You, R.; Xie, Y. Viscoelastic Dampers for Vibration Control of Building Structures: A State-of-Art Review. J. Earthq. Eng. 2024, 28, 3558–3585. [Google Scholar] [CrossRef]
- Patil, A.Y.; Patil, R.D. A review on seismic analysis of a multi-storied steel building provided with different types of damper and base isolation. Asian J. Civ. Eng. 2024, 25, 3277–3283. [Google Scholar] [CrossRef]
- Almajhali, K.Y.M.; Alhaddad, W. A systematic review of hybrid passive energy dissipating devices. Proc. Inst. Civ. Eng. Struct. Build. 2024, 1–43. [Google Scholar]
- Silwal, B.; Michael, R.J.; Ozbulut, O.E. A superelastic viscous damper for enhanced seismic performance of steel moment frames. Eng. Struct. 2015, 105, 152–164. [Google Scholar] [CrossRef]
- Lavan, O.; Amir, O. Simultaneous topology and sizing optimization of viscous dampers in seismic retrofitting of 3D irregular frame structures. Earthq. Eng. Struct. Dyn. 2014, 43, 1325–1342. [Google Scholar] [CrossRef]
- Güllü, A.; Körpeoğlu, S.G.; Selek Kılıçarslan, E.S. Multi-objective optimal sizing of energy dissipative steel cushions for longitudinal loading. Struct. Multidiscip. Optim. 2021, 63, 2955–2967. [Google Scholar] [CrossRef]
- Nabid, N.; Hajirasouliha, I.; Petkovski, M. Adaptive low computational cost optimisation method for Performance-based seismic design of friction dampers. Eng. Struct. 2019, 198, 109549. [Google Scholar] [CrossRef]
- Wang, S.; Mahin, S.A. High-performance computer-aided optimization of viscous dampers for improving the seismic performance of a tall building. Soil Dyn. Earthq. Eng. 2018, 113, 454–461. [Google Scholar] [CrossRef]
- Kang, J.D.; Tagawa, H. Experimental evaluation of dynamic characteristics of seesaw energy dissipation system for vibration control of structures. Earthq. Eng. Struct. Dyn. 2014, 43, 1889–1895. [Google Scholar] [CrossRef]
- Tagawa, H.; Yamanishi, T.; Takaki, A.; Chan, R.W. Cyclic behavior of seesaw energy dissipation system with steel slit dampers. J. Constr. Steel Res. 2016, 117, 24–34. [Google Scholar] [CrossRef]
- Kang, J.D.; Tagawa, H. Comparison between experimental and analytical results for seesaw energy dissipation systems using fluid viscous dampers. Earthq. Eng. Eng. Vib. 2016, 15, 79–90. [Google Scholar] [CrossRef]
- Katsimpini, P.S.; Askouni, P.K.; Papagiannopoulos, G.A.; Karabalis, D.L. Seismic drift response of seesaw-braced and buckling-restrained braced steel structures: A comparison study. Soil Dyn. Earthq. Eng. 2020, 129, 105925. [Google Scholar] [CrossRef]
- Katsimpini, P.S.; Papagiannopoulos, G.A.; Askouni, P.K.; Karabalis, D.L. Seismic response of low-rise 3-D steel structures equipped with the seesaw system. Soil Dyn. Earthq. Eng. 2020, 128, 105877. [Google Scholar] [CrossRef]
- Katsimpini, P.S.; Papagiannopoulos, G.A. Effectiveness of the seesaw system as a means of seismic upgrading in older, non-ductile reinforced concrete buildings. Vibration 2023, 6, 102–112. [Google Scholar] [CrossRef]
- Mo, Z.; Shu, G.; Lai, B.; Ventura, C.E.; Yang, T. Experimental behavior, numerical modeling and parameters evaluation of three-dimensional seismic isolation device. J. Constr. Steel Res. 2024, 220, 108817. [Google Scholar] [CrossRef]
- Mo, Z.; Lai, B.; Shu, G.; Chen, P.; Yang, T. Performance-based seismic design method of stacked modular steel building based on three-dimensional seismic isolation. Eng. Struct. 2025, 336, 120438. [Google Scholar] [CrossRef]
- Banazadeh, M.; Ghanbari, A. Seismic performance assessment of steel moment-resisting frames equipped with linear and nonlinear fluid viscous dampers with the same damping ratio. J. Constr. Steel Res. 2017, 136, 215–228. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G.D. Damping modification factors for SDOF systems subjected to near-fault, far-fault and artificial earthquakes. Earthq. Engng. Struct. Dyn. 2010, 39, 1239–1258. [Google Scholar] [CrossRef]
- Hatzigeorgiou, G.D.; Pnevmatikos, N.G. Maximum damping forces for structures with viscous dampers under near-source earthquakes. Eng. Struct. 2014, 68, 1–13. [Google Scholar] [CrossRef]
- Logotheti, V.E.; Kafetzi, T.C.; Papagiannopoulos, G.A.; Karabalis, D.L. On the use of interstorey velocity for the seismic retrofit of steel frames with viscous dampers. Soil Dyn. Earthq. Eng. 2020, 129, 105312. [Google Scholar] [CrossRef]
- Mavroeidakos, P.; Katsimpini, P.; Papagiannopoulos, G. Effect of Viscous Dampers with Variable Capacity on the Response of Steel Buildings. Vibration 2025, 8, 11. [Google Scholar] [CrossRef]
- Kolour, N.A.; Basim, M.C.; Chenaghlou, M. Multi-objective optimum design of nonlinear viscous dampers in steel structures based on life cycle cost. Structures 2021, 34, 3776–3788. [Google Scholar] [CrossRef]
- Gharagoz, M.M.; Noureldin, M.; Kim, J. Machine learning-based design of a seismic retrofit frame with spring-rotational friction dampers. Eng. Struct. 2023, 292, 116053. [Google Scholar]
- Wen, J.; Han, Q.; Xie, Y.; Du, X.; Zhang, J. Performance-based seismic design and optimization of damper devices for cable-stayed bridge. Eng. Struct. 2021, 237, 112043. [Google Scholar] [CrossRef]
- Takewaki, I. Building Control with Passive Dampers: Optimal Performance-Based Design for Earthquakes; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Aydin, E.; Boduroglu, M.H.; Guney, D. Optimal damper distribution for seismic rehabilitation of planar building structures. Eng. Struct. 2007, 29, 176–185. [Google Scholar] [CrossRef]
- Lavan, O. On the efficiency of viscous dampers in reducing various seismic responses of wall structures. Earthq. Eng. Struct. Dyn. 2012, 41, 1673–1692. [Google Scholar] [CrossRef]
- Palermo, M.; Muscio, S.; Silvestri, S.; Landi, L.; Trombetti, T. On the dimensioning of viscous dampers for the mitigation of the earthquake-induced effects in moment-resisting frame structures. Bull. Earthq. Eng. 2013, 11, 2429–2446. [Google Scholar] [CrossRef]
- Montuori, R.; Muscati, R. Plastic design of seismic resistant reinforced concrete frame. Earthq. Struct. 2015, 8, 205–224. [Google Scholar] [CrossRef]
- Montuori, R.; Muscati, R. Smart and simple design of seismic resistant reinforced concrete frame. Compos. Part B Eng. 2017, 115, 360–368. [Google Scholar] [CrossRef]
- Peng, Y.; Sun, P. Reliability-based design optimization of tuned mass-damper-inerter for mitigating structural vibration. J. Sound Vib. 2024, 572, 118166. [Google Scholar] [CrossRef]
- Song, C.; Xiao, R.; Jiang, Z.; Sun, B. Active-learning Kriging-assisted robust design optimization of tuned mass dampers: Vibration mitigation of a steel-arch footbridge. Eng. Struct. 2024, 303, 117502. [Google Scholar]
- Sanati, S.H.; Karamodin, A. Optimum seismic design of frame structures with and without metallic yielding dampers considering life-cycle cost. J. Build. Eng. 2023, 76, 107335. [Google Scholar] [CrossRef]
- Li, Y.; Tan, P.; Li, S.; He, H. A novel tuned inerter eddy current damper: Modeling, optimization, and evaluation. Eng. Struct. 2023, 285, 116026. [Google Scholar] [CrossRef]
- Wang, L.; Zhou, Y.; Shi, W. Seismic control of a smart structure with semiactive tuned mass damper and adaptive stiffness property. Earthq. Eng. Resil. 2023, 2, 74–93. [Google Scholar] [CrossRef]
- Jafarzadeh, O.; Mousavi Ghasemi, S.A.; Zahrai, S.M.; Mohammadzadeh, A.; Vafaei Poursorkhabi, R. Online adaptive neurochaotic fuzzy controller design to reduce the seismic response of buildings equipped with active tuned mass damper system. Int. J. Intell. Syst. 2023, 2023, 8460498. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, L.; Shi, W. Seismic control of adaptive variable stiffness intelligent structures using fuzzy control strategy combined with LSTM. J. Build. Eng. 2023, 78, 107549. [Google Scholar] [CrossRef]
- Ghanemi, N.E.; Abdeddaim, M.; Ounis, A. Artificial Intelligence-Driven Active Tuned Mass Damper for Enhanced Seismic Resilience of Shear Frame Smart Structures. J. Vib. Eng. Technol. 2024, 12, 1577–1599. [Google Scholar] [CrossRef]
- Jafarzadeh, O.; Sabetahd, R.; Ghasemi, S.A.M.; Zahrai, S.M. Design of a novel intelligent adaptive fractional-order proportional-integral-derivative controller for mitigation of seismic vibrations of a building equipped with an active tuned mass damper. Smart Mater. Struct. 2024, 33, 095020. [Google Scholar] [CrossRef]
- Wani, Z.R.; Tantray, M.; Farsangi, E.N. Adaptive System Supervising the Response Control for Smart Structures. In Automation in Construction toward Resilience; CRC Press: Boca Raton, FL, USA, 2023; pp. 277–316. [Google Scholar]
- Ghasemi, S.; Hosseini, M.; Hu, S.; Shahram, A. Seismic isolation strategy via controlled soft first story with innovative multi-stage yielding damper: Experimental and numerical insights. Structures 2024, 70, 107553. [Google Scholar] [CrossRef]
- Bruschi, E.; Zoccolini, L.; Cattaneo, S.; Quaglini, V. Experimental characterization, modeling, and numerical evaluation of a novel friction damper for the seismic upgrade of existing buildings. Materials 2023, 16, 1933. [Google Scholar] [CrossRef]
- Almajhali, K.Y.M. Review on passive energy dissipation devices and techniques of installation for high rise building structures. Structures 2023, 51, 1019–1029. [Google Scholar] [CrossRef]
- Ahmadi, M.; Ebadi-Jamkhaneh, M. Seismic upgrading of existing steel buildings built on soft soil using passive damping systems. Buildings 2023, 13, 1587. [Google Scholar] [CrossRef]
- Yang, Y.; Xu, Z.D.; Huang, X.H.; Dong, Y.R.; Dai, J.; Li, Y.J. Ant colony-inspired cooperative control of multi-magnetorheological dampers system for coupled vibration mitigation of spatial irregular structures. Eng. Struct. 2025, 334, 120241. [Google Scholar] [CrossRef]
- Ding, L.; Jiao, H. Performance Analysis of Yielding Tubular Dampers in Steel Frame Knee Braces: A Finite Element Study. Int. J. Steel Struct. 2025, 25, 95–110. [Google Scholar]
- Zhang, P.; Yam, M.C.; Ke, K.; Song, Y.; Zhu, M. Experimental study of a self-centering damper with multistage energy-dissipation mechanism. J. Struct. Eng. 2024, 150, 04024166. [Google Scholar]
- Saeedi, A.; Khatibinia, M.; Mohtashami, E. Optimum distribution and design of friction-damped diagonal brace for reducing seismic damage of steel moment-resisting frames. Struct. Infrastruct. Eng. 2025, 1–21. [Google Scholar] [CrossRef]
- Sattari, A.; Maleki, A.; Lotfollahi-Yaghin, M.A. Seismic Evaluation of Composite Steel Moment Frames with Brace Members and Rotational Friction Dampers under Near-Fault Earthquakes. Numer. Methods Civ. Eng. 2025, 9, 9–23. [Google Scholar] [CrossRef]
- Kye, S.; Jung, H.; Jung, H.J. Experimental investigation on the hysteretic dynamics of a regenerative hybrid electrodynamic cable damper. Struct. Infrastruct. Eng. 2024, 20, 407–420. [Google Scholar] [CrossRef]
- Karami, M.; Estekanchi, H.E.; Hajirasouliha, I.; Mirfarhadi, S.A. Optimal properties of nonlinear viscous dampers in steel structures considering the life cycle cost. J. Earthq. Eng. 2024, 28, 1685–1708. [Google Scholar] [CrossRef]
- Katsimpini, P.; Papagiannopoulos, G.; Hatzigeorgiou, G. A Thorough Examination of Innovative Supplementary Dampers Aimed at Enhancing the Seismic Behavior of Structural Systems. Appl. Sci. 2025, 15, 1226. [Google Scholar] [CrossRef]
- SAP 2000. Static and Dynamic Finite Element Analysis of Structures: Version 25.0; Computers and Structures: Berkeley, CA, USA, 2023. [Google Scholar]
- EN 1993-1; Eurocode 3. Design of Steel Structures—Part 1.1: General Rules and Rules for Buildings. Committee for Standardization (CEN): Brussels, Belgium, 2009.
- Eurocode 8. Design of Structures for Earthquake Resistance, Part 1–1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardization (CEN): Brussels, Belgium, 2005. [Google Scholar]
- National Research Institute for Earth Science and Disaster Resilience. NIED K-NET, KiK-Net; National Research Institute for Earth Science and Disaster Resilience: Tsukuba, Japan, 2019. [Google Scholar]
- Available online: https://www.taylordevices.com/products/fluid-viscous-dampers/ (accessed on 23 April 2025).
- Microsoft Corporation. Microsoft Excel, version 2021. Microsoft 2021. Available online: www.microsoft.com/en-us/microsoft-365/excel (accessed on 23 April 2025).
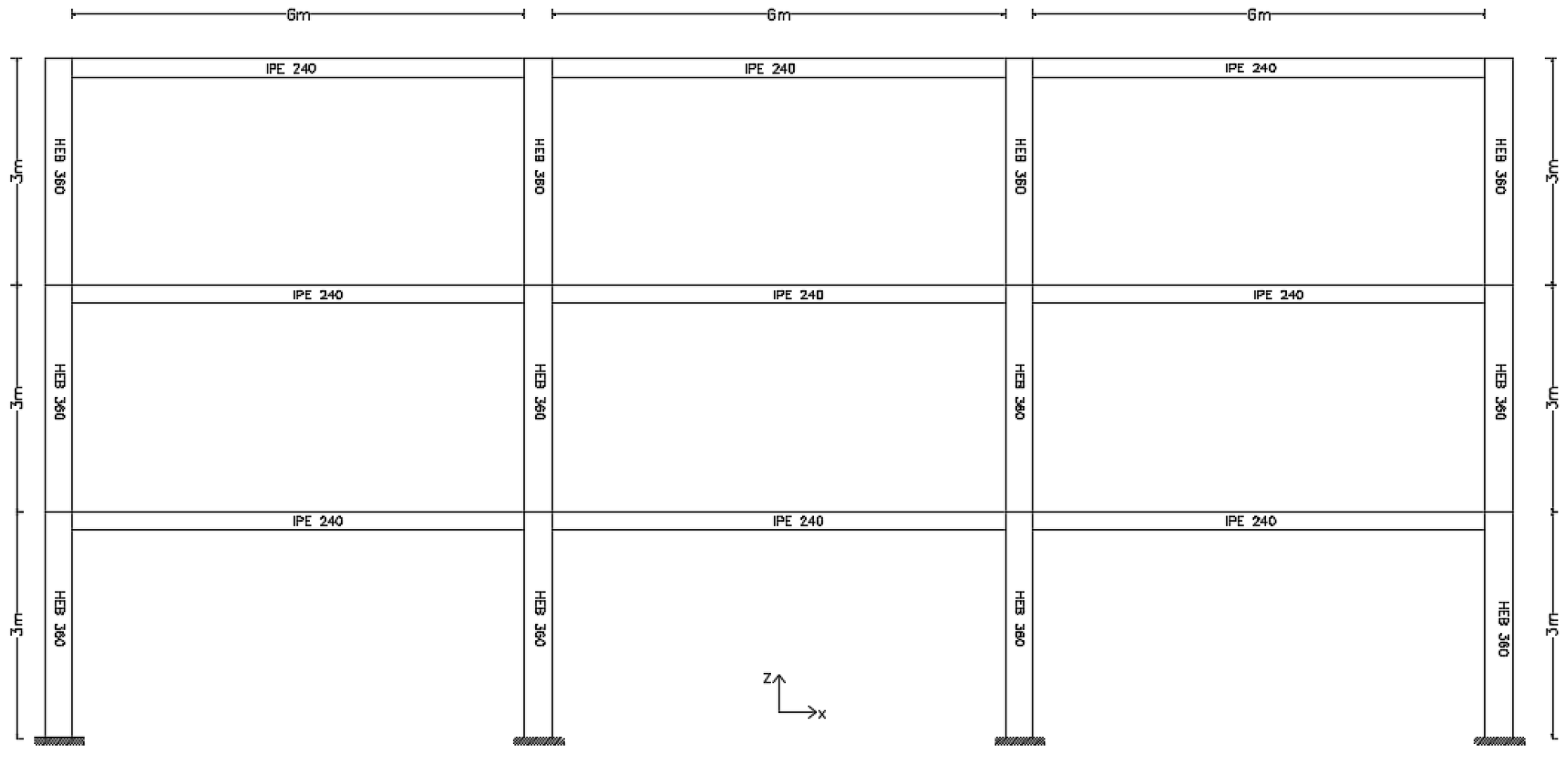

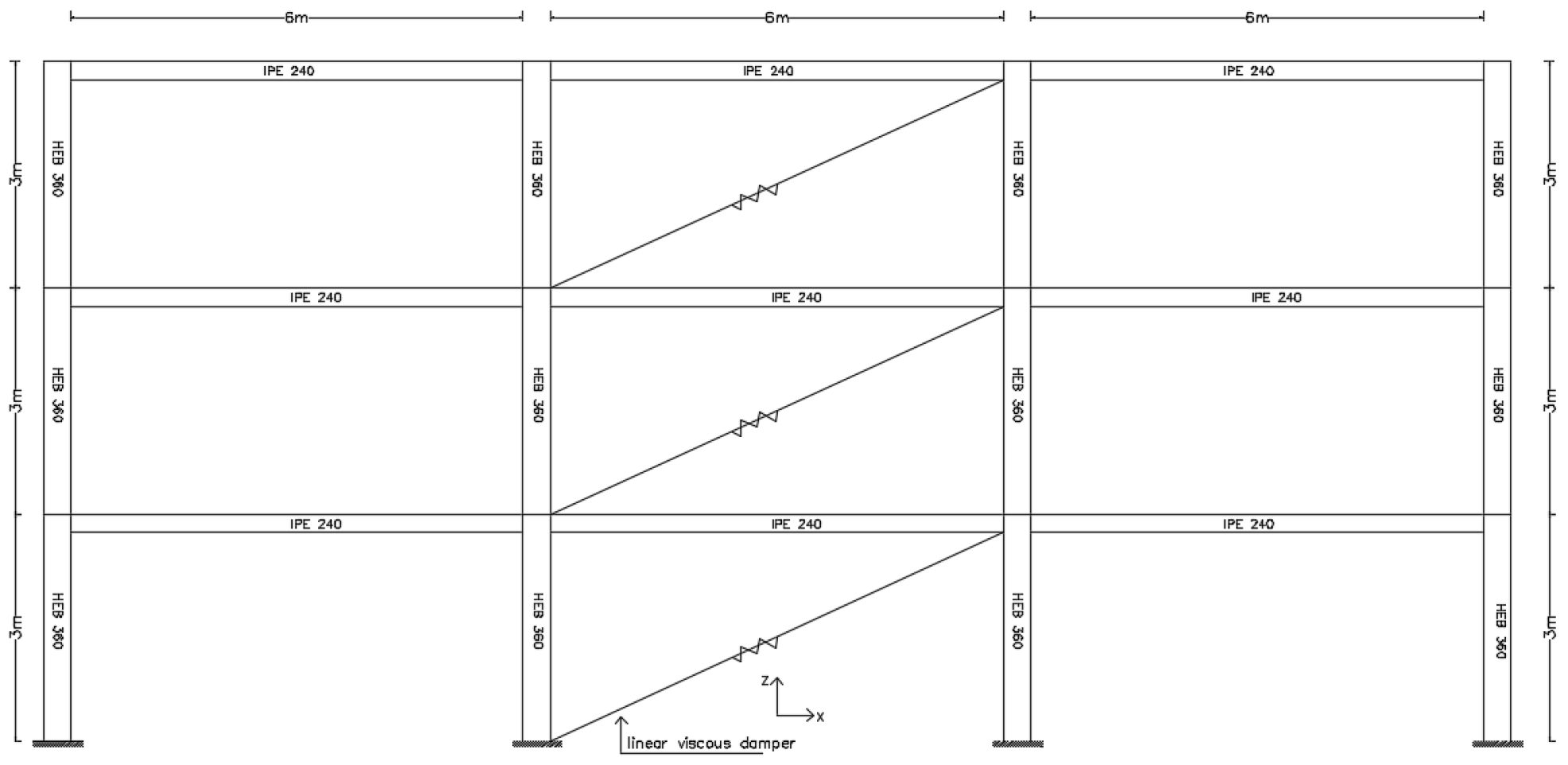





| Three-Story Building | Six-Story Building | |||
|---|---|---|---|---|
| beams | columns | Beams | columns | |
| Floor 1–2 | ΙΡΕ240 | HΕ360Β | ΙΡΕ360 | HΕ360Β |
| Floor 3 | ΙΡΕ240 | HΕ360Β | ΙΡΕ300 | HΕ360Β |
| Floor 4 | - | - | ΙΡΕ300 | HΕ300Β |
| Floors 5–6 | - | - | ΙΡΕ270 | HΕ300Β |
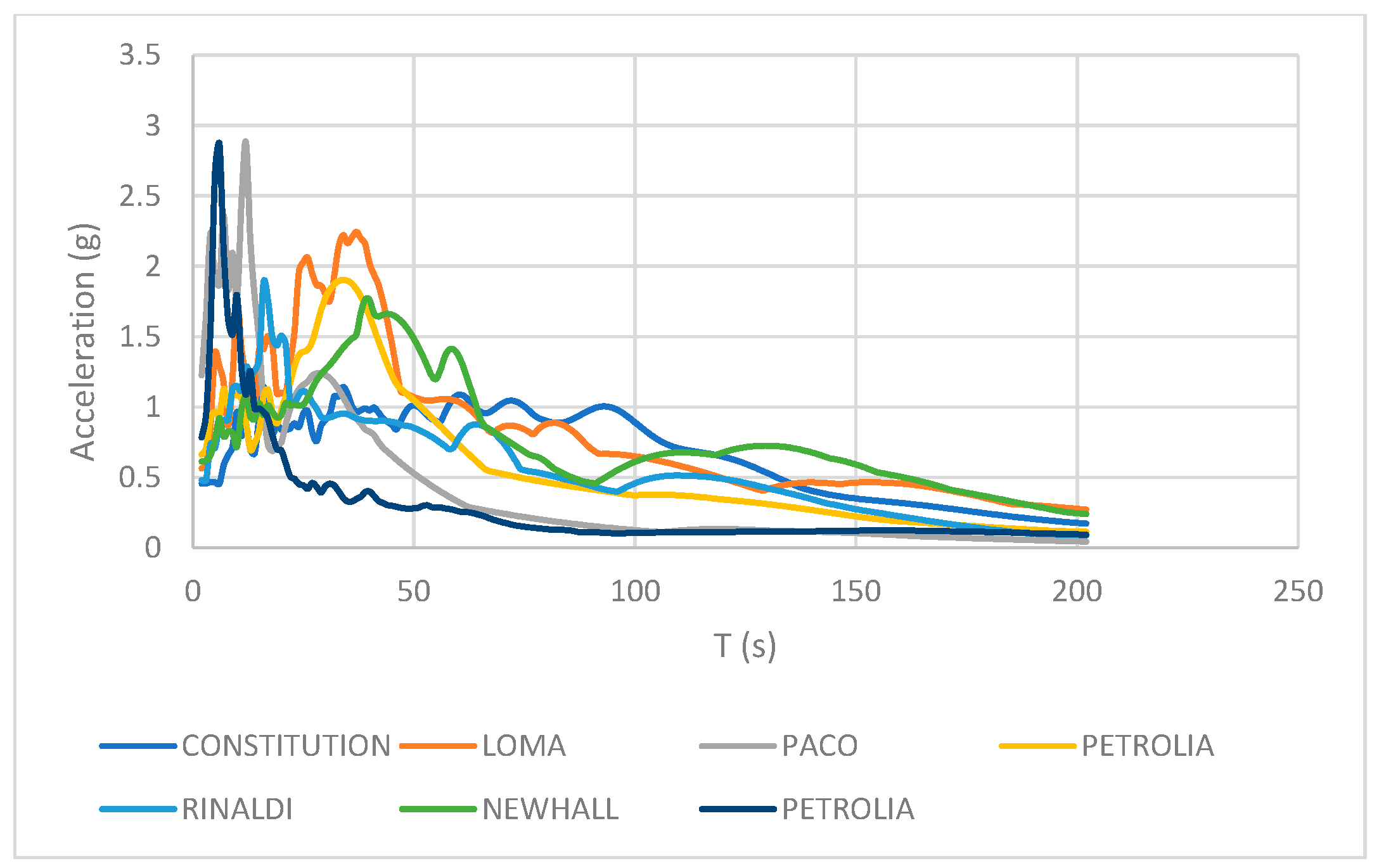
| No. | Earthquake, Location | Date | Recording Station | Mw | Soil Type | PGA (m/s2) |
|---|---|---|---|---|---|---|
| 1 | Loma Prieta, USA | 17 October 1989 | Los Gatos | 7 | HR | 5.53 |
| 2 | San Fernando, USA | 9 February 1971 | Pacoima Dam | 6.6 | HR | 12.03 |
| 3 | Northridge, USA | 17 January 1994 | Rinaldi Receiving St. | 6.7 | SL | 8.22 |
| 4 | Northridge, USA | 17 January 1994 | Newhall | 6.7 | SL | 5.72 |
| 5 | Maule, Chile | 27 February 2010 | Constitución | 8.8 | SR | 6.40 |
| 6 | Christchurch, New Zealand | 22 February 2011 | Resthaven | 6.3 | SL | 6.99 |
| 7 | Cape Mendocino, CA, USA | 25 October 1992 | Petrolia | 6.9 | SR | 14.69 |
| 3-story building | ||||
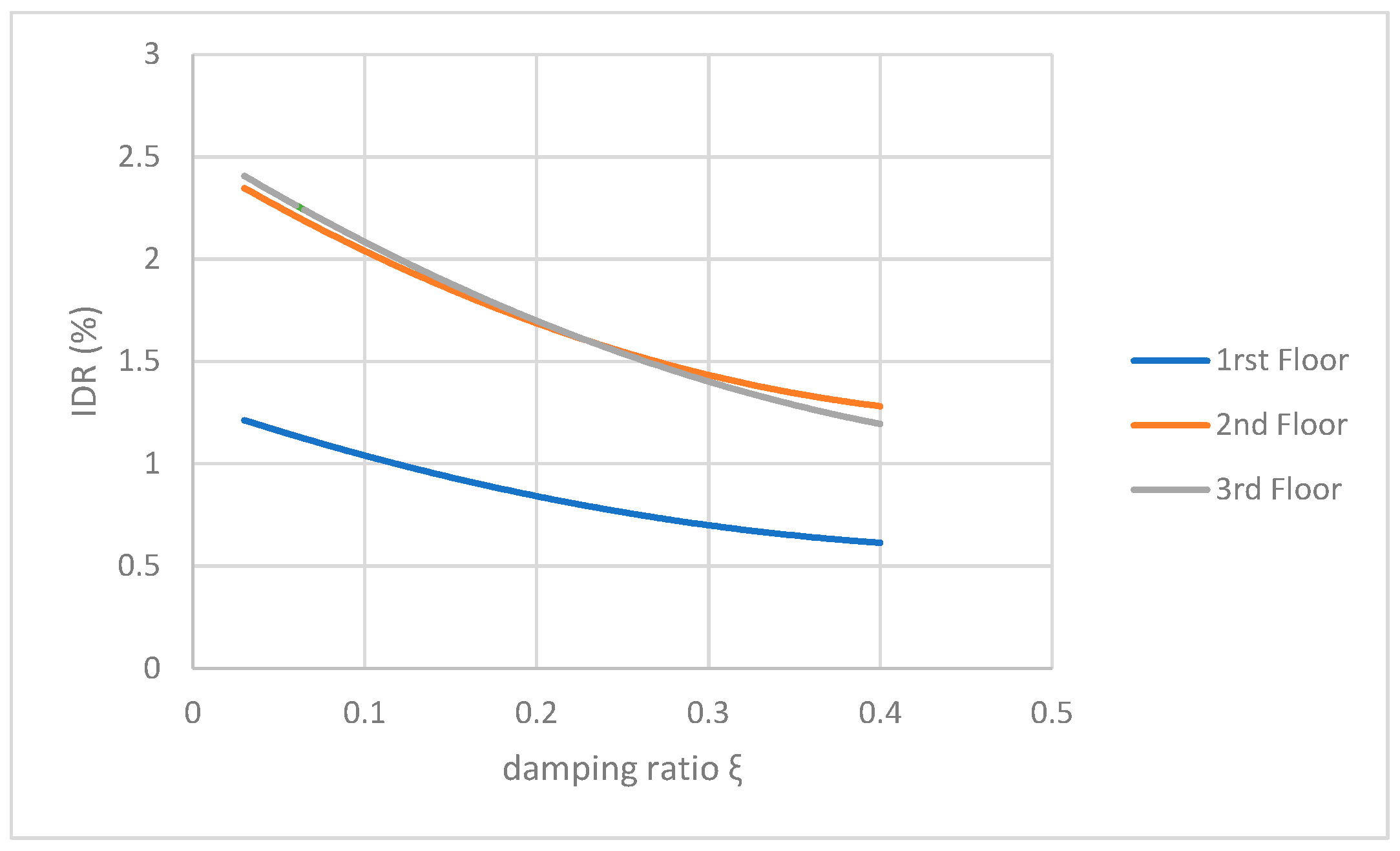
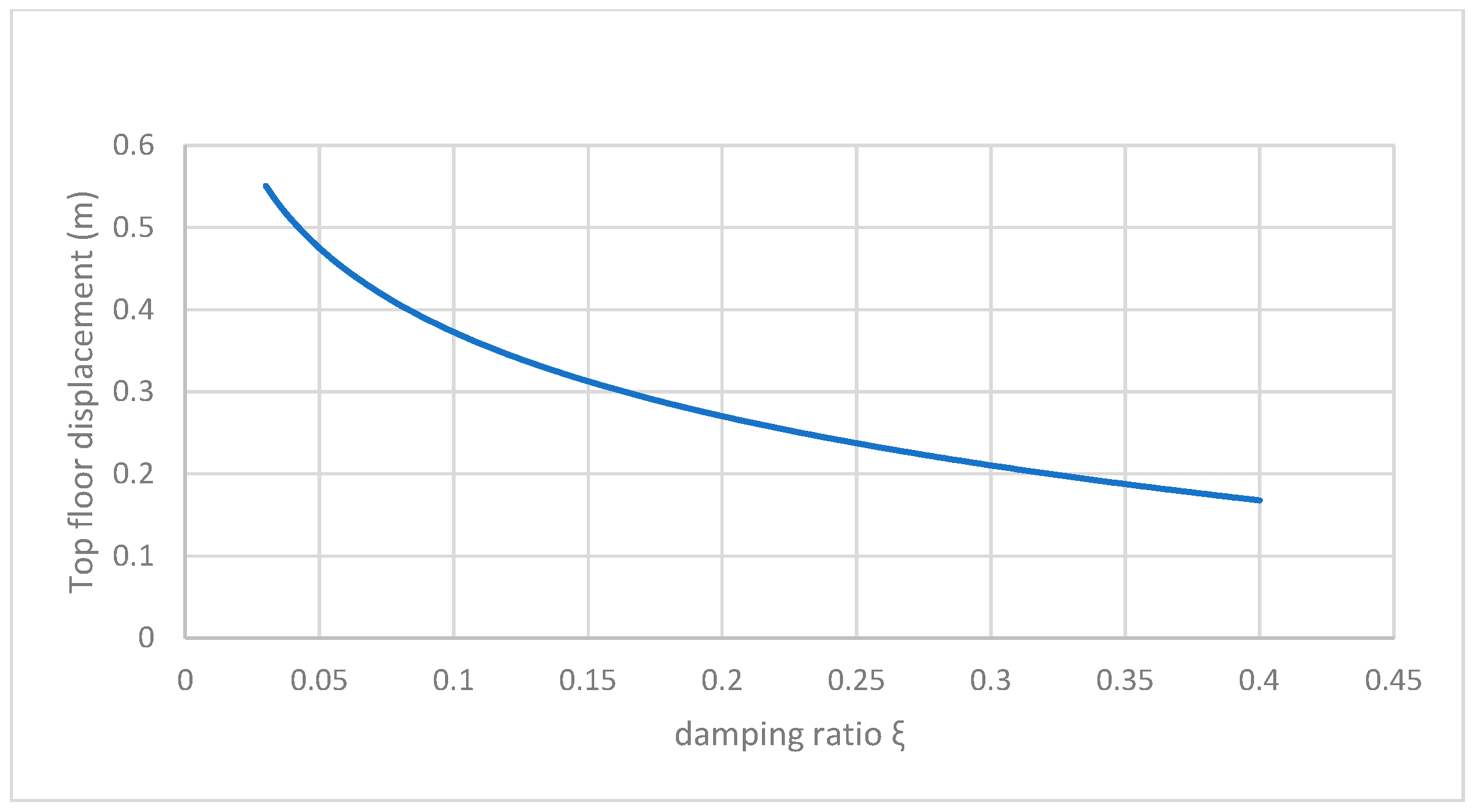
| Damping ratio (ξ)/Top floor displacement (y) | y = 1.1632ξ2 − 0.8816ξ + 0.2535 | |||
| 1st floor | 2nd floor | 3rd floor | ||
| Damping ratio (ξ)/IDR% | IDR = 2.8271ξ2 − 2.8340ξ + 1.2954 | y = 5.0140ξ2 − 5.0362ξ + 2.493 | y = 4.4403ξ2 − 5.1848ξ + 2.5580 | |
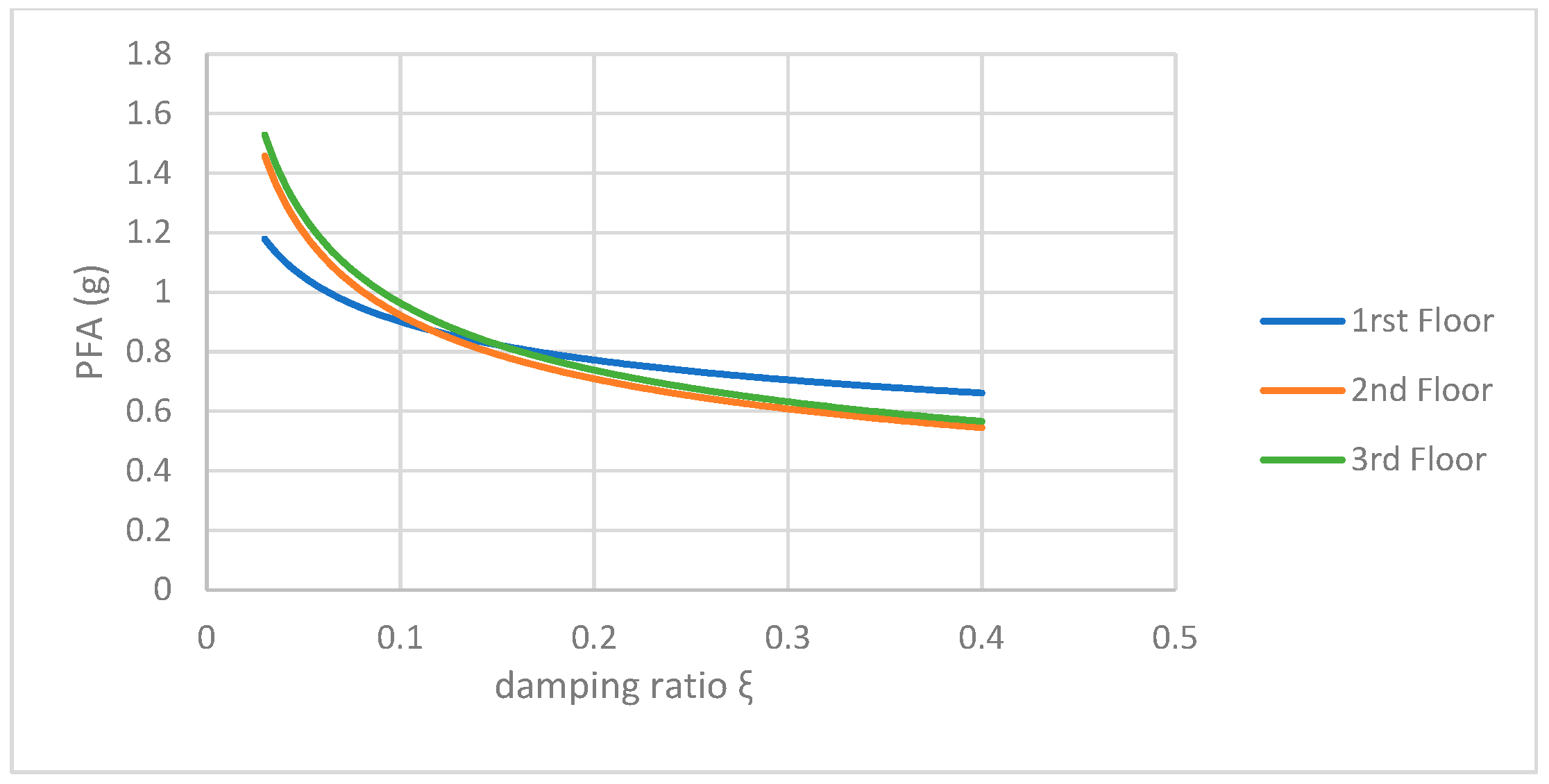
| Damping ratio (ξ)/PFA | PFA = 0.5395ξ−0.2228 | PFA = 0.3851ξ−0.3795 | PFA = 0.3985ξ−0.3833 | |
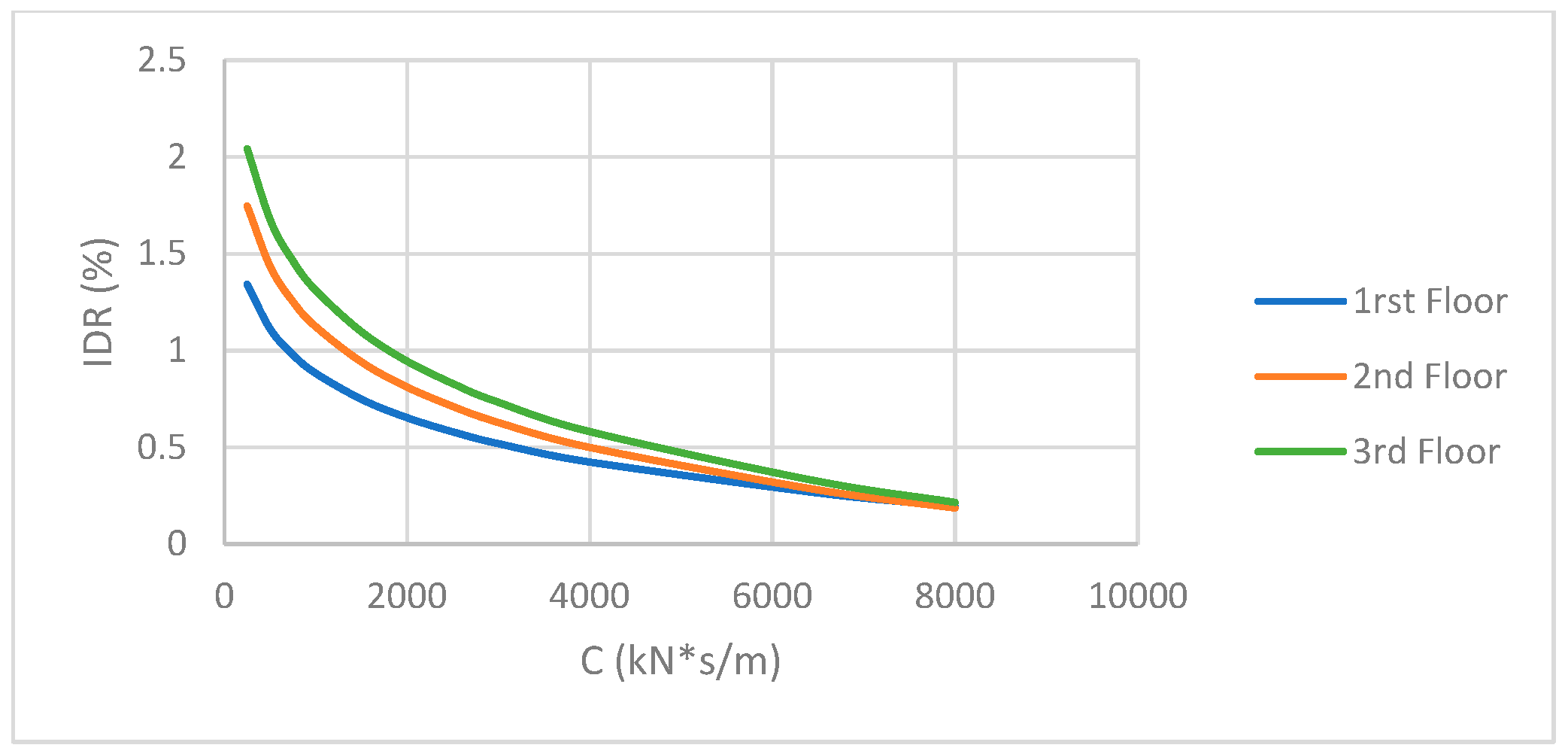
| Dampers’ coefficient c—IDR(%) | IDR = −0.3305ln(c) + 3.1657 | IDR = −0.5268ln(c) + 4.9499 | IDR = −0.4503ln(c) + 4.2315 | |
| Dampers’ coefficient c—PFA | PFA = 0.5598c−0.0003 | PFA = 1.4303c−0.0799 | PFA = 3.6262c−0.1495 | |
| 6-story building | ||||
| Damping ratio (ξ)/Top floor displacement (y) | y = −0.14775ln(ξ) + 0.032375 | |||
| 1st floor | 2nd floor | 3rd floor | ||
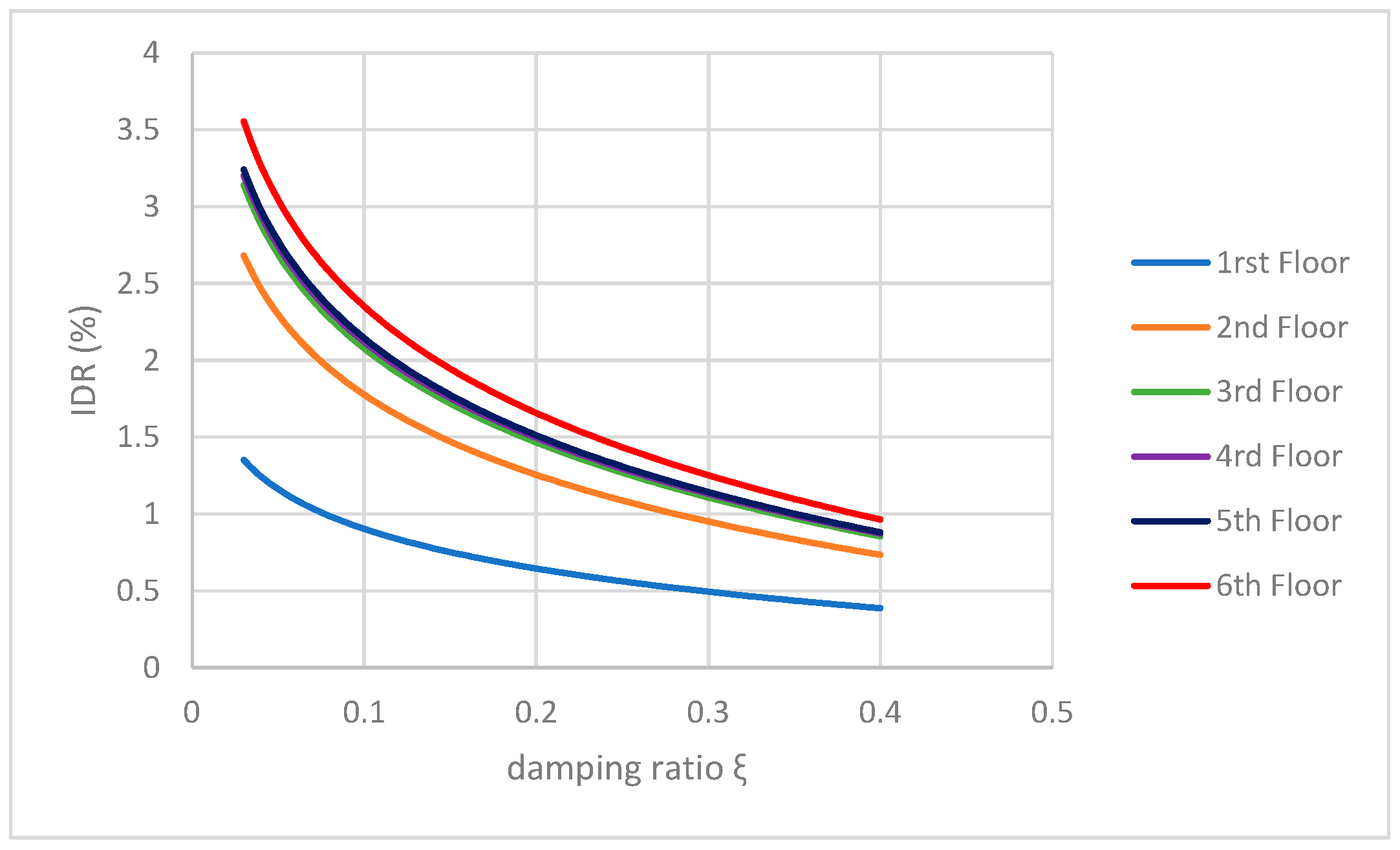
| Damping ratio (ξ)/IDR (%) | IDR = −0.3723ln(ξ) + 0.0461 | IDR = −0.7516ln(ξ) + 0.0461 | IDR = −0.8823ln(ξ) + 0.0462 | |
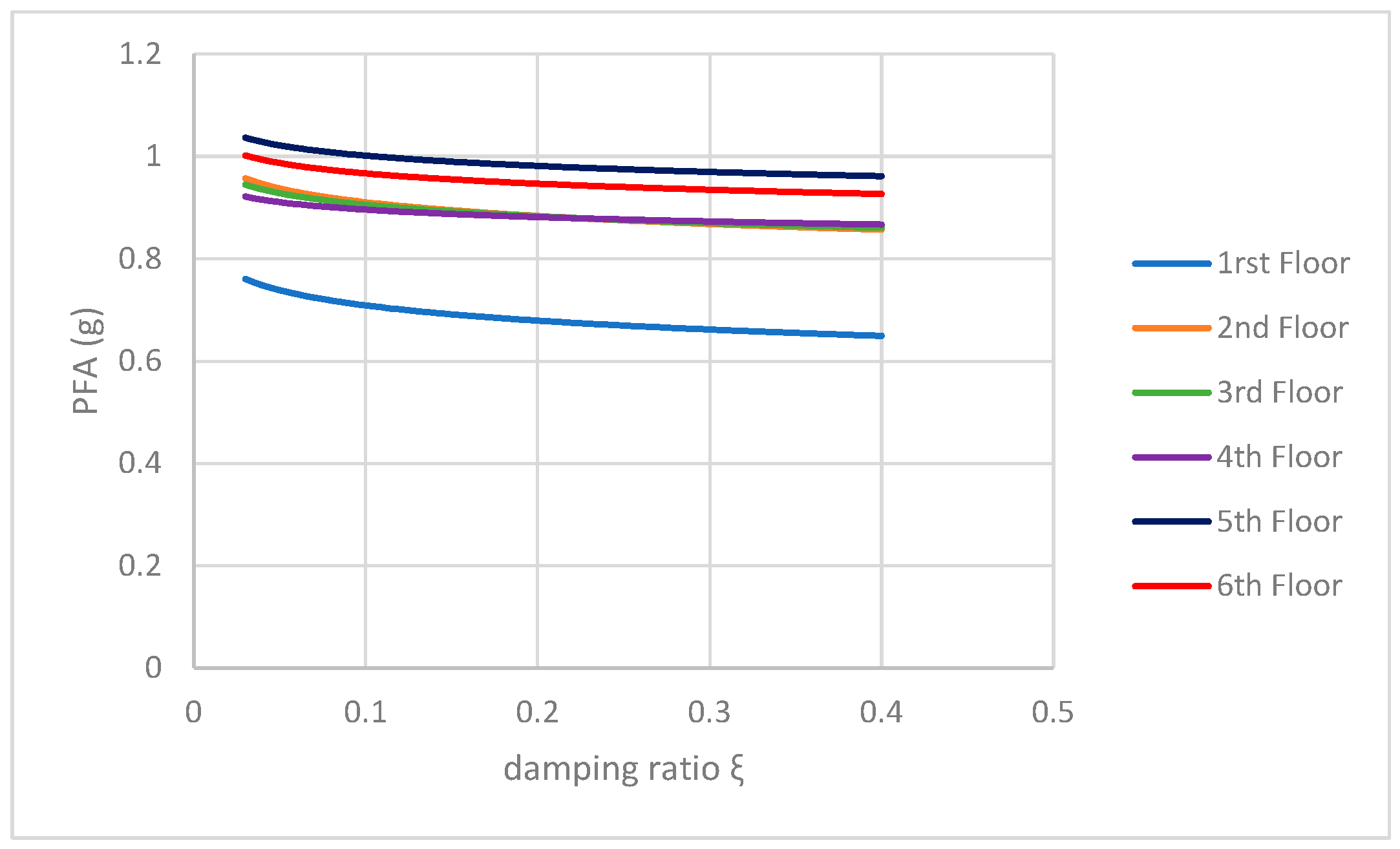
| Damping ratio (ξ)/PFA | PFA = −0.0429ln(ξ) + 0.6100 | PFA = −0.0387ln(ξ) + 0.8214 | PFA = −0.0324ln(ξ) + 0.8309 | |
| Dampers’ coefficient c—IDR | IDR = −0.2730ln(c) + 3.0733 | IDR = −0.5772ln(c) + 6.0520 | IDR = −0.7950ln(c) + 7.9303 | |
| Dampers’ coefficient c—PFA | PFA = 0.6877c−0.0098 | PFA = 0.9515c−0.0531 | PFA = 0.8849c−0.0611 | |
| 4th floor | 5th floor | 6th floor | ||
| Damping ratio (ξ)/IDR (%) | IDR = −0.8995ln(ξ) + 0.0486 | IDR = −0.9113ln(ξ) + 0.0461 | IDR = −1.0003ln(ξ) + 0.0483 | |
| Damping ratio (ξ)/PFA | PFA = −0.0210ln(ξ) + 0.8477 | PFA = −0.0290ln(ξ) + 0.9348 | PFA = −0.02902ln(ξ) + 0.9002 | |
| Dampers’ coefficient c—IDR (%) | IDR = −0.8203ln(c) + 7.9177 | IDR = −0.7358ln(c) + 6.9222 | IDR = −0.4857ln(c) + 4.8054 | |
| Dampers’ coefficient c—PFA | PFA = 1.1327c−0.0992 | PFA = 1.5456c−0.1108 | PFA = 2.70705c−0.1840 | |
| Case | c (kN·s/m) | Present Study ξ | Hatzigeorgiou ξ | Difference (%) |
|---|---|---|---|---|
| 3-story, 1st floor | 1000 | 0.142 | 0.158 | 11.3 |
| 3-story, 1st floor | 3000 | 0.287 | 0.271 | −5.6 |
| 6-story, 3rd floor | 2000 | 0.195 | 0.203 | 4.1 |
| 6-story, 6th floor | 4000 | 0.341 | 0.328 | −3.8 |
| Average absolute difference: 6.2% | ||||
| Building | Floor | IDR (%) | Present c (kN·s/m) | Logotheti-Based c | Ratio |
|---|---|---|---|---|---|
| 3-story | 1st | 1.5 | 1250 | 1180 | 1.06 |
| 3-story | 2nd | 2.0 | 1580 | 1620 | 0.98 |
| 6-story | 3rd | 1.8 | 2100 | 2280 | 0.92 |
| 6-story | 6th | 2.2 | 2850 | 2650 | 1.08 |
| Average ratio: 1.01 (±6%) | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diamantis, P.; Katsimpini, P.; Hatzigeorgiou, G.D. Development of a Methodology for Seismic Design of Framed Steel Structures Incorporating Viscous Dampers. Eng 2025, 6, 308. https://doi.org/10.3390/eng6110308
Diamantis P, Katsimpini P, Hatzigeorgiou GD. Development of a Methodology for Seismic Design of Framed Steel Structures Incorporating Viscous Dampers. Eng. 2025; 6(11):308. https://doi.org/10.3390/eng6110308
Chicago/Turabian StyleDiamantis, Panagiotis, Panagiota Katsimpini, and George D. Hatzigeorgiou. 2025. "Development of a Methodology for Seismic Design of Framed Steel Structures Incorporating Viscous Dampers" Eng 6, no. 11: 308. https://doi.org/10.3390/eng6110308
APA StyleDiamantis, P., Katsimpini, P., & Hatzigeorgiou, G. D. (2025). Development of a Methodology for Seismic Design of Framed Steel Structures Incorporating Viscous Dampers. Eng, 6(11), 308. https://doi.org/10.3390/eng6110308








