Identification of Critical and Post-Critical States of a Drill String Under Dynamic Conditions During the Deepening of Directional Wells
Abstract
1. Introduction
2. Materials and Methods
3. Results
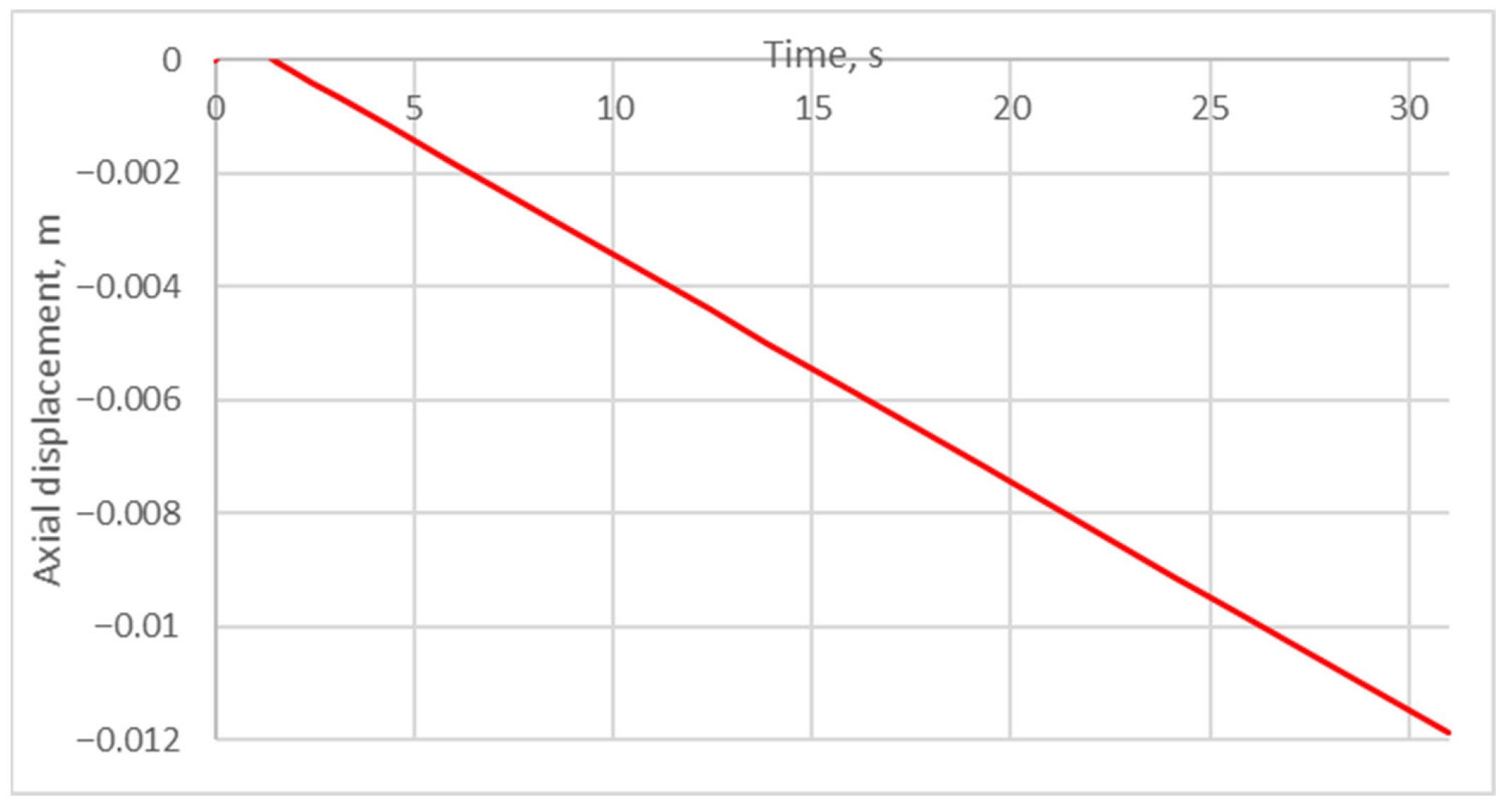
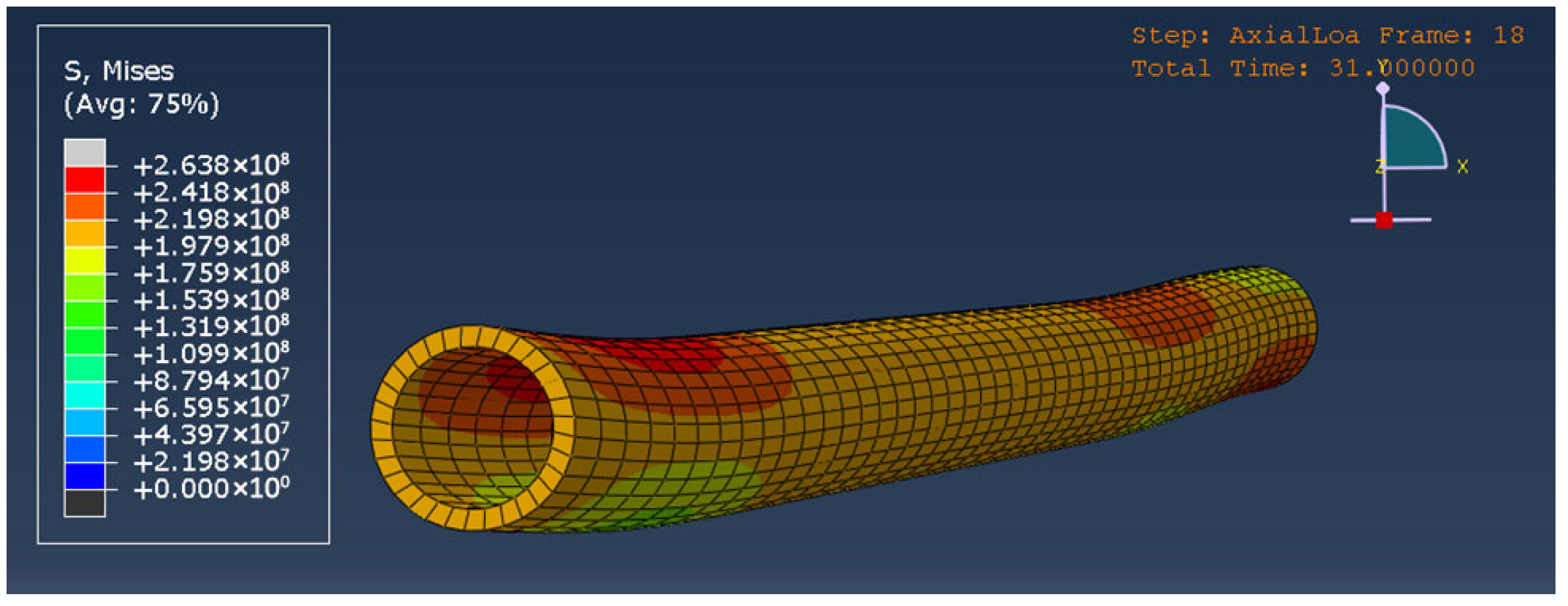
3.1. Reference Experiments
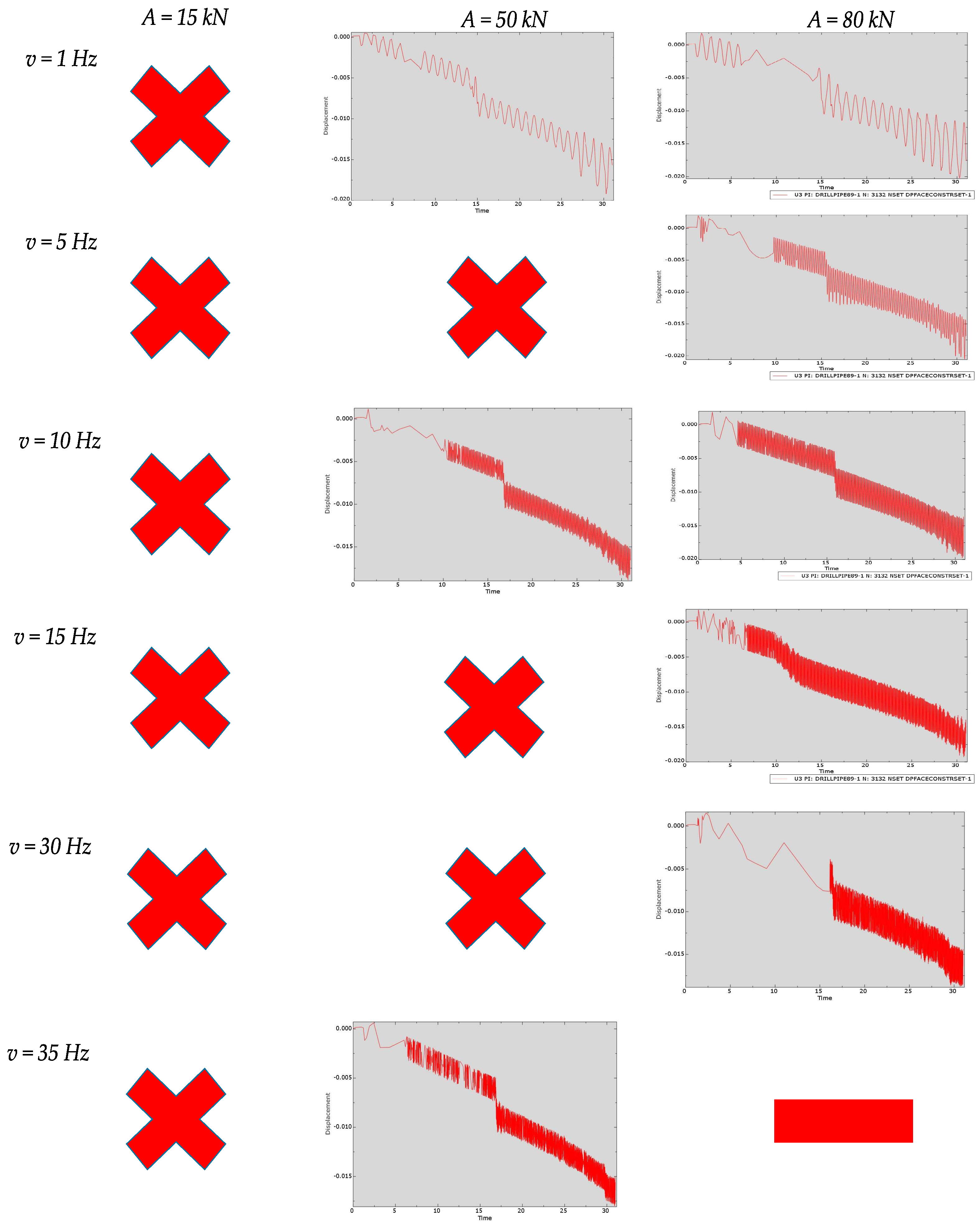
3.2. Series of Experiments with Axial Vibrations Without Friction
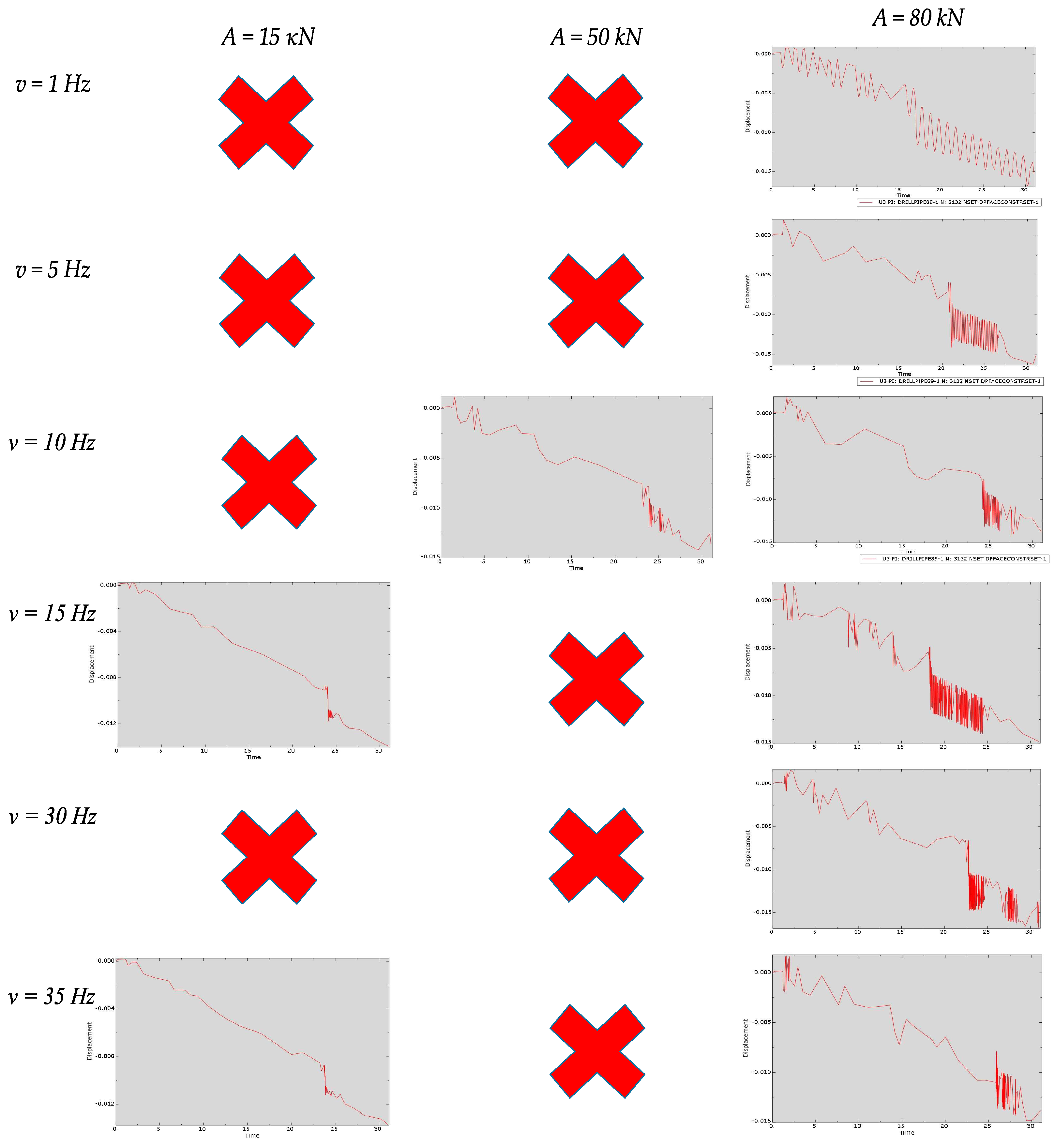
3.3. Series of Experiments with Axial Vibrations with Friction
3.4. Series of Experiments with Lateral Vibrations Along the OX-Axis Without Friction
3.5. Series of Experiments with Lateral Vibrations Along the OX-Axis with Friction
3.6. Series of Experiments with Lateral Vibrations Along the OY-Axis Without Friction
3.7. Series of Experiments with Lateral Vibrations Along the OY-Axis with Friction
4. Discussion
5. Conclusions
- It has been demonstrated that frictional forces exert a stabilizing effect on the drill string, and the influence of friction effect cannot be neglected when predicting critical loads.
- The presence of tool joints may exert a stabilizing effect due to the formation of an additional contact force from the deflection of the string and the formation of bending stresses in the tool body.
- The influence of vibrations on the buckling behavior of the drill string has been refined. Different combinations of vibration frequency and amplitude of the acting force form zones of stability and instability. In zones of instability, the critical load is significantly reduced, while in zones of stability the reduction in critical load is relatively small or there is an increase in critical load compared to the value predicted in the static formulation of the problem. The presence of stability zones allows us to reconsider the drilling technology from the point of view of not avoiding vibrations, but selecting the frequency of vibrations and the amplitude of the variable acting force, which are inevitably formed during the drilling process, in order to increase the efficiency of drilling. The use of vibrators to stabilize the drill string may be expedient.
- Lateral vibrations in a plane perpendicular to the vertical reduce the critical load by forming eccentricity, which facilitates the drill string losing its equilibrium. An increase in the amplitude of vibrations generally leads to a decrease in the critical load, but certain combinations of amplitude and frequency of vibrations can lead to localized zones of stabilization and significant destabilization.
- Lateral vibrations aligned with the vertical may negate the stabilizing effect of drill string bending caused by gravity and tool joints when the vibration amplitude is >1 g. Certain frequencies, for example 5 Hz in the series of experiments conducted, can destabilize the drill string at an amplitude of 1 g. Certain frequencies, for example 30 Hz, contribute to significant stabilization of the column even at an amplitude of 1.5 g.
- It has been established that the rate of deformation of the column in a state of sinusoidal buckling from axial loading is many times greater than the rate of deformation according to Hooke’s law and deformation in a helical form. The deformation of the drill string in a helical buckling state is greater than the deformation of a “straight” drill string obeying Hooke’s law. These deformation rate relationships are also observed under dynamic conditions.
- The possibility of identifying and localizing drill string buckling by monitoring traveling block velocity and hook load has been theoretically substantiated and experimentally confirmed. Tracking shocks using downhole accelerometers may improve the accuracy of localizing sections of the drill string that are in a state of buckling. After identifying and localizing the loss of stability, the analytical model should use appropriate formulae for calculating additional side force against the wellbore wall, bending moment, and bending stresses, in order to enhance the accuracy of determining the DS SSS and fatigue wear in the post-buckling state.
- It has been revealed that a column in a state of sinusoidal bending, due to its unstable state, is susceptible to vibrations; therefore, it is recommended to avoid maintaining the drill string in a sinusoidal buckling configuration to prevent wear of the string and tool from multicycle fatigue from vibrations during “sliding” and column rotation, when alternating bending loads occur.
- In future studies, it is necessary to investigate the influence of drill string rotation, including the development of precessional motion and torsional vibrations, as well as to clarify the combined effects of dynamic conditions and the presence of the downhole tool in the drilling fluid environment on the buckling of the drill string.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SSS | Stress–strain state |
| DS | Drill string |
| M/LWD | Measurements/logging while drilling |
| BHA | Bottomhole assembly |
References
- Litvinenko, V. The Role of Hydrocarbons in the Global Energy Agenda: The Focus on Liquefied Natural Gas. Resources 2020, 9, 59. [Google Scholar] [CrossRef]
- Morenov, V.A.; Shchigolev, K.V. Assessment of the Possibility of Carbon Dioxide Utilization for Enhanced Oil Recovery in Oil Field Condition. Neftyanoe Khozyaystvo—Oil Ind. 2025, 4, 76–81. [Google Scholar] [CrossRef]
- Nikolaev, A.; Zhukov, A.; Goluntsov, A.; Shirmaher, E. Evaluation of the Effectiveness of Anti-Turbulence Additives in the Transportation of High-Viscosity Oil at Low Ambient Temperatures. Processes 2025, 13, 1434. [Google Scholar] [CrossRef]
- Wang, F.; Kobina, F. The Influence of Geological Factors and Transmission Fluids on the Exploitation of Reservoir Geothermal Resources: Factor Discussion and Mechanism Analysis. Reserv. Sci. 2025, 1, 3–18. [Google Scholar] [CrossRef]
- Savenok, O.V.; Zharikova, N.K.; Chuykova, E.P.; Verisokin, A.E.; Hadid, M.; Povarova, L.V.; Kalashnikov, D.S.; Domanova, A.S. Justification and Selection of a Method for Restricting Water Inflow to Horizontal Wells in Low-Permeability Terrigenous Reservoir Conditions Using the Example of the YuS2 Formation of an Oil and Gas Condensate Field. Bull. Tomsk. Polytech. Univ. Geo Assets Eng. 2025, 336, 193–205. [Google Scholar] [CrossRef]
- Wu, J.; Ansari, U. From CO2 Sequestration to Hydrogen Storage: Further Utilization of Depleted Gas Reservoirs. Reserv. Sci. 2025, 1, 19–35. [Google Scholar] [CrossRef]
- Blinov, P.A.; Silichev, N.M.; Nikishin, V.V.; Gorelikov, V.G. Justification and Development of a Continuous Deflector with Full Core Sampling for Drilling Exploration Wells. Bull. Tomsk Polytech. Univ. Geo Assets Eng. 2025, 336, 17–28. [Google Scholar] [CrossRef]
- Zhdaneev, O.V.; Zaytsev, A.V.; Prodan, T. Possibilities for Creating Russian High-Tech Bottomhole Assembly. J. Min. Inst. 2021, 252, 872–884. [Google Scholar] [CrossRef]
- Blinov, P.A.; Sadykov, M.I.; Gorelikov, V.G.; Nikishin, V.V. Development and Research of Backfill Compounds with Improved Elastic and Strength Properties for Oil and Gas Well Lining. J. Min. Inst. 2024, 268, 588–598. [Google Scholar]
- Bolshunov, A.V.; Ignatev, S.A.; Serbin, D.V.; Turkeev, A.V. Experimental Ice Drilling with Organosilicon Fluid Using the KEMS-135 Drill in Borehole 5G (Vostok Station, Antarctica). J. Min. Inst. 2025, 273, 147–158. [Google Scholar]
- Serbin, D.V.; Buslaev, G.V.; Lavrik, A.Y.; Kadochnikov, V.G.; Dmitriev, A.N. Study of the Interaction between the Drilling Fluid and Lake Water during the Opening of the Subglacial Lake Vostok in Antarctica. J. Min. Inst. 2025, 273, 136–146. [Google Scholar]
- Buslaev, G.V.; Konoplyannikov, A.V. Mathematical Modeling of a Hydro-Mechanical System with a Positive Displacement Motor and Hydraulic Thruster to Optimize the Drilling Process for Extended-Reach Drilling Wells. Int. J. Eng. Trans. B Appl. 2026, 39, 1077–1087. [Google Scholar] [CrossRef]
- Griguletsky, V.G.; Kuznetsov, A.B. Influence of Bit Size on Stability Bottom Drill Column Balance When Drilling a Horizontal Well. Oil Gas Stud. 2021, 3, 37–51. [Google Scholar] [CrossRef]
- Cunha, J.C. Buckling of Tubulars inside Wellbores: A Review on Recent Theoretical and Experimental Works. SPE Drill. Complet. 2004, 19, 13–19. [Google Scholar] [CrossRef]
- Lubinski, A.; Althouse, W.S. Helical Buckling of Tubing Sealed in Packers. J. Pet. Technol. 1962, 14, 655–670. [Google Scholar] [CrossRef]
- Wang, C.Y. A Critical Review of the Heavy Elastica. Int. J. Mech. Sci. 1986, 28, 549–559. [Google Scholar] [CrossRef]
- Wu, J.; Juvkam-Wold, H.C. Buckling and Lockup of Tubulars in Inclined Wellbores. J. Energy Resour. Technol. 1995, 117, 208–213. [Google Scholar] [CrossRef]
- Paslay, P.R.; Bogy, D.B. The Stability of a Circular Rod Laterally Constrained to Be in Contact with an Inclined Circular Cylinder. J. Appl. Mech. 1964, 31, 605–610. [Google Scholar] [CrossRef]
- Dawson, R.; Rapier, J. Drill Pipe Buckling in Inclined Holes. J. Pet. Technol. 1984, 36, 1734–1738. [Google Scholar] [CrossRef]
- McCann, R.C.; Suryanarayana, P.V.R. Experimental Study of Curvature and Frictional Effects on Buckling. In Proceedings of the Annual Offshore Technology Conference, Houston, TX, USA, 2–5 May 1994; pp. 511–521. [Google Scholar] [CrossRef]
- Miska, S.; Qiu, W.; Volk, L.; Cunha, J.C. An Improved Analysis of Axial Force along Coiled Tubing in Inclined/Horizontal Wellbores. In Proceedings of the SPE Eastern Regional Meeting, Morgantown, WV, USA, 23–25 October 1996; pp. 207–214. [Google Scholar] [CrossRef]
- Wu, J.; Juvkam-Wold, H.C. Coiled Tubing Buckling Implication in Drilling and Completing Horizontal Wells. SPE Drill. Complet. 1995, 10, 16–21. [Google Scholar] [CrossRef]
- Johancsik, C.A.; Friesen, D.B.; Dawson, R. Torque and Drag in Directional Wells—Prediction and Measurement. J. Pet. Technol. 1984, 36, 987–992. [Google Scholar] [CrossRef]
- He, X.; Kyllingstad, A. Helical Buckling and Lock-Up Conditions for Coiled Tubing in Curved Wells. SPE Drill. Complet. 1995, 10, 10–15. [Google Scholar] [CrossRef]
- American Petroleum Institute. API Recommended Practice 7G: Recommended Practice for Drill Stem Design and Operating Limits, 16th ed.; API: Washington, DC, USA, 1998. [Google Scholar]
- Qiu, W.; Miska, S.; Volk, L. Drill Pipe/Coiled Tubing Buckling Analysis in a Hole of Constant Curvature. In Proceedings of the Permian Basin Oil & Gas Recovery Conference, Midland, TX, USA, 23–25 March 1998; pp. 385–389. [Google Scholar] [CrossRef]
- Mitchell, S.; Moore, N.B.; Franks, J.; Liu, G.; Xiang, Y. Comparing the Results of a Full-Scale Buckling-Test Program to Actual Well Data: New Semiempirical Buckling Model and Methods of Reducing Buckling Effects. SPE Drill. Complet. 2011, 26, 578–596. [Google Scholar] [CrossRef]
- Mitchell, R.F.; Weltzin, T. Lateral Buckling—The Key to Lockup. SPE Drill. Complet. 2011, 26, 436–452. [Google Scholar] [CrossRef]
- Wu, J. Slack-Off Load Transmission in Horizontal and Inclined Wells. In Proceedings of the SPE Production Operations Symposium, Oklahoma City, OK, USA, 2–4 April 1995. [Google Scholar] [CrossRef]
- Kuru, E.; Martinez, A.; Miska, S.; Qiu, W. The Buckling Behavior of Pipes and Its Influence on the Axial Force Transfer in Directional Wells. J. Energy Resour. Technol. 2000, 122, 129–135. [Google Scholar] [CrossRef]
- Liang, Z.; Zhu, Z.L. Critical Helical Buckling Load Assessment of Coiled Tubing under Axial Force by Use of the Explicit Finite-Element Method. J. Pet. Sci. Eng. 2018, 169, 51–57. [Google Scholar] [CrossRef]
- Tan, X.C.; Forsman, B. Buckling of Slender String in Cylindrical Tube under Axial Load: Experiments and Theoretical Analysis. Exp. Mech. 1995, 35, 55–60. [Google Scholar] [CrossRef]
- Kuang, Y.; Li, B.; Liu, J.; Lu, H. Research on Buckling Behavior and Analysis of Sensitive Factors in Horizontal Well Drilling. J. Fail. Anal. Prev. 2016, 16, 376–383. [Google Scholar] [CrossRef]
- Wu, L.; Fang, P.; Huang, Y.; Li, G.; Xu, J. Study on the Evolution of Buckling Behavior of Tubular String under Frictional Effects in Horizontal Wells. J. Vibroeng. 2024, 26, 961–982. [Google Scholar] [CrossRef]
- Gao, G.; Miska, S. Effects of Friction on Post-Buckling Behavior and Axial Load Transfer in a Horizontal Well. SPE J. 2010, 15, 1110–1124. [Google Scholar] [CrossRef]
- Dunayevsky, V.A.; Abbassian, F.; Judzis, A. Dynamic Stability of Drillstrings under Fluctuating Weight on Bit. SPE Drill. Complet. 1993, 8, 84–92. [Google Scholar] [CrossRef]
- Jia, P.; Zhou, B.; Xue, S.; Zhang, Y.; Zhu, X.; Sun, F. A Dynamic Method for Post Buckling Analysis of Drill String in Vertical Wells. J. Pet. Sci. Eng. 2022, 214, 110334. [Google Scholar] [CrossRef]
- Tian, J.; Liu, C.; Yang, Y. Dynamic Buckling Characteristics of Drill String in Inclined Straight Well with Friction Effect. Int. J. Struct. Stab. Dyn. 2022, 23, 2350007. [Google Scholar] [CrossRef]
- Ren, F.; Wang, B.; Zhao, L.; Zhu, A. Experimental Investigation and Analysis of Dynamic Buckling of Drill String in Horizontal Well. Shock Vib. 2017, 2017, 1658435. [Google Scholar] [CrossRef]
- Tian, J.; Song, H.; Yang, Y.; Mao, L.; Song, J. Dynamic Buckling Characteristics of Drill String in Horizontal Wells. Int. J. Struct. Stab. Dyn. 2023, 24, 2450121. [Google Scholar] [CrossRef]
- Tian, J.; Song, H.; Yang, Y.; Mao, L.; Song, J. Study on Dynamic Buckling Characteristics of Drill String in Horizontal Well Based on Stochastic Model. Geoenergy Sci. Eng. 2023, 231, 212293. [Google Scholar] [CrossRef]
- Lubkin, S.; Stoker, J.J. Stability of Columns and Strings under Periodically Varying Forces. Q. Appl. Math. 1943, 1, 215–236. [Google Scholar] [CrossRef]
- Taheran, F.; Monfared, V.; Daneshmand, S.; Abedi, E. Nonlinear Vibration Analysis of Directional Drill String Considering Effect of Drilling Mud and Weight on Bit. J. Vibroeng. 2016, 18, 1280–1287. [Google Scholar] [CrossRef]
- Kapitaniak, M.; Vaziri, V.; Wiercigroch, M. Helical Buckling of Drill-Strings. MATEC Web Conf. 2018, 148, 16007. [Google Scholar] [CrossRef]
- Menand, S.; Sellami, H.; Akowanou, J.; Simon, C.; Macresy, L.; Isambourg, P.; Dupuis, D. How Drillstring Rotation Affects Critical Buckling Load? In Proceedings of the SPE/IADC Drilling Conference, Orlando, FL, USA, 4–6 March 2008; pp. 485–497. [Google Scholar] [CrossRef]
- Cao, J.; Zou, D.; Xue, Q.; Wang, J.; Huang, L.; Guo, F.; Wang, C.; Qu, J. Analysis on the Dynamics of Flexible Drillstring under Different Drilling Parameters. Front. Earth Sci. 2024, 12, 1396784. [Google Scholar] [CrossRef]
- Hajianmaleki, M.; Daily, J.S.; Ring, L.; Gandikota, R. Critical Buckling Load Assessment of Drill Strings in Different Wellbores Using the Explicit Finite Element Method. In Proceedings of the SPE Offshore Europe Conference and Exhibition (OE 2013), Aberdeen, UK, 3–6 September 2013; pp. 430–446. [Google Scholar] [CrossRef]
- Che, J.; Qiao, Z.; Chen, L.; Li, M. Dynamic Analysis of Drill String and Wellbore in Ultra Short Radius Wells Based on Abaqus. Proc. Conf. 2025, 2025, 732–740. [Google Scholar]
- Gabdrakhmanov, M.S.; Galeev, A.S.; Khuzina, L.B.; Suleymanov, R.I. Dynamics of the Drilling Tool During the Construction of Vertical, Inclined, and Horizontal Wells; Nedra LLC: Moscow, Russia, 2011. [Google Scholar]
- Miska, S.; Cunha, J.C. An Analysis of Helical Buckling of Tubulars Subjected to Axial and Torsional Loading in Inclined Wellbores. In Proceedings of the SPE Production Operations Symposium, Oklahoma, OK, USA, 2–4 April 1995. [Google Scholar] [CrossRef]
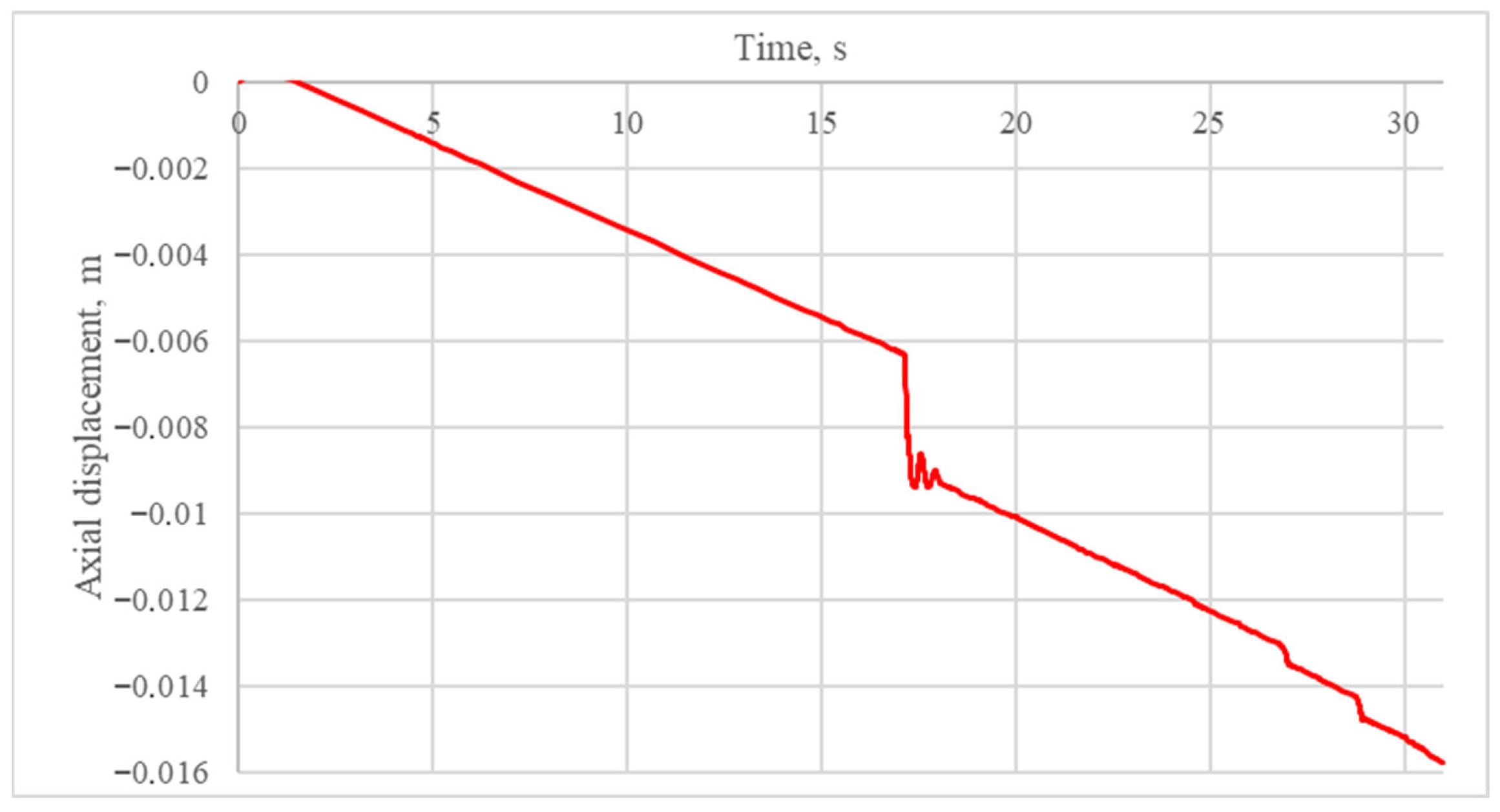
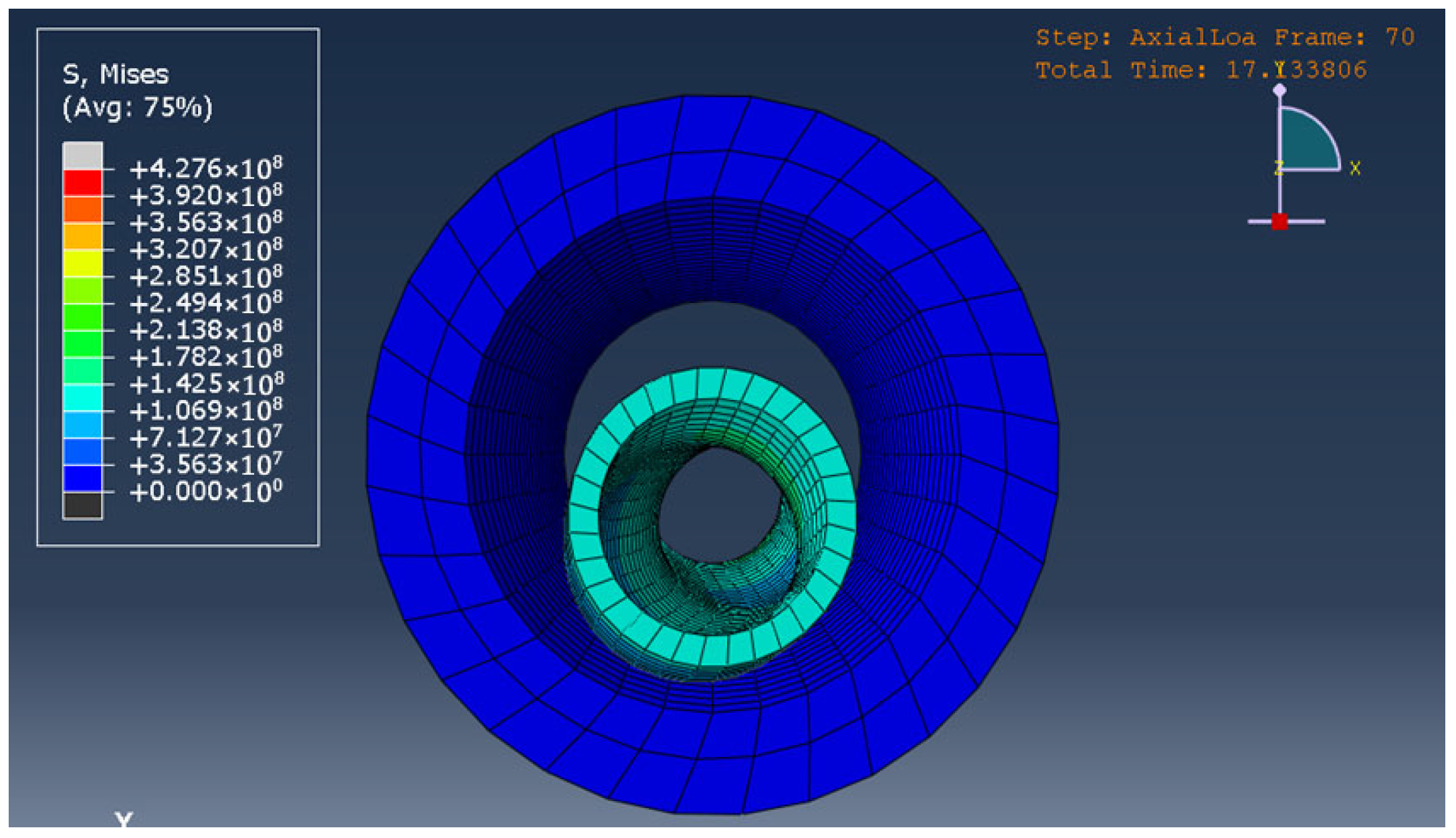
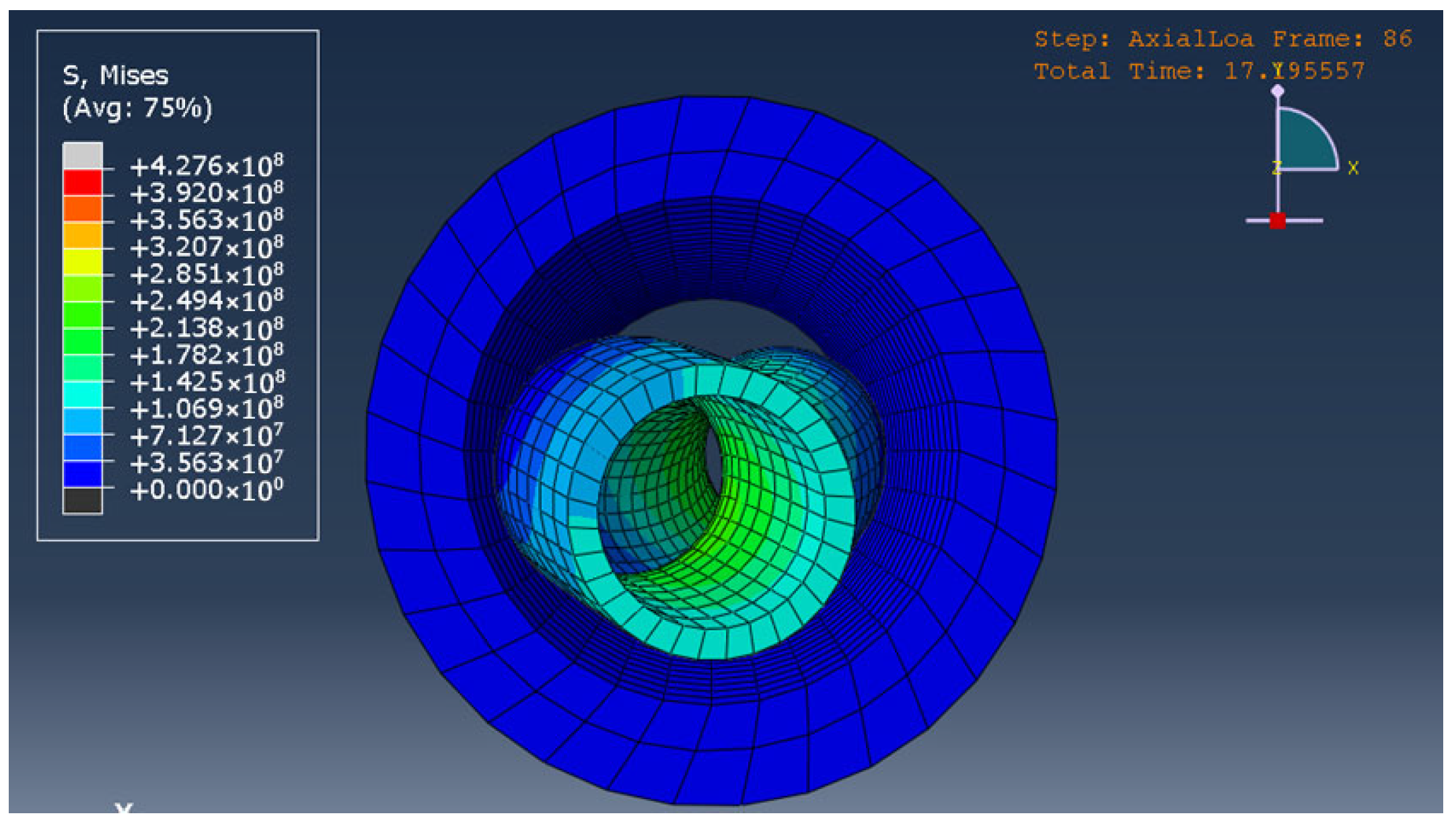
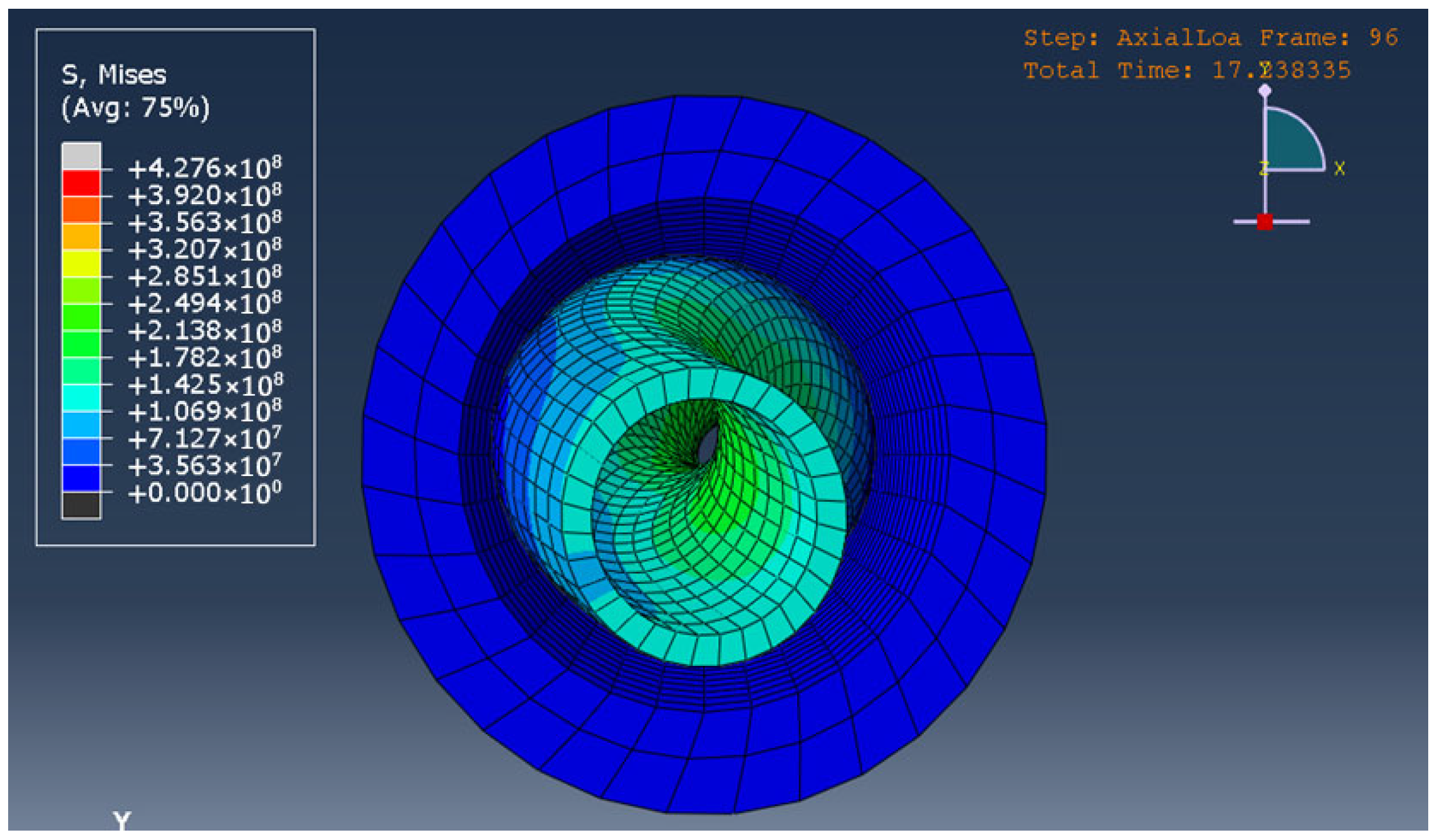
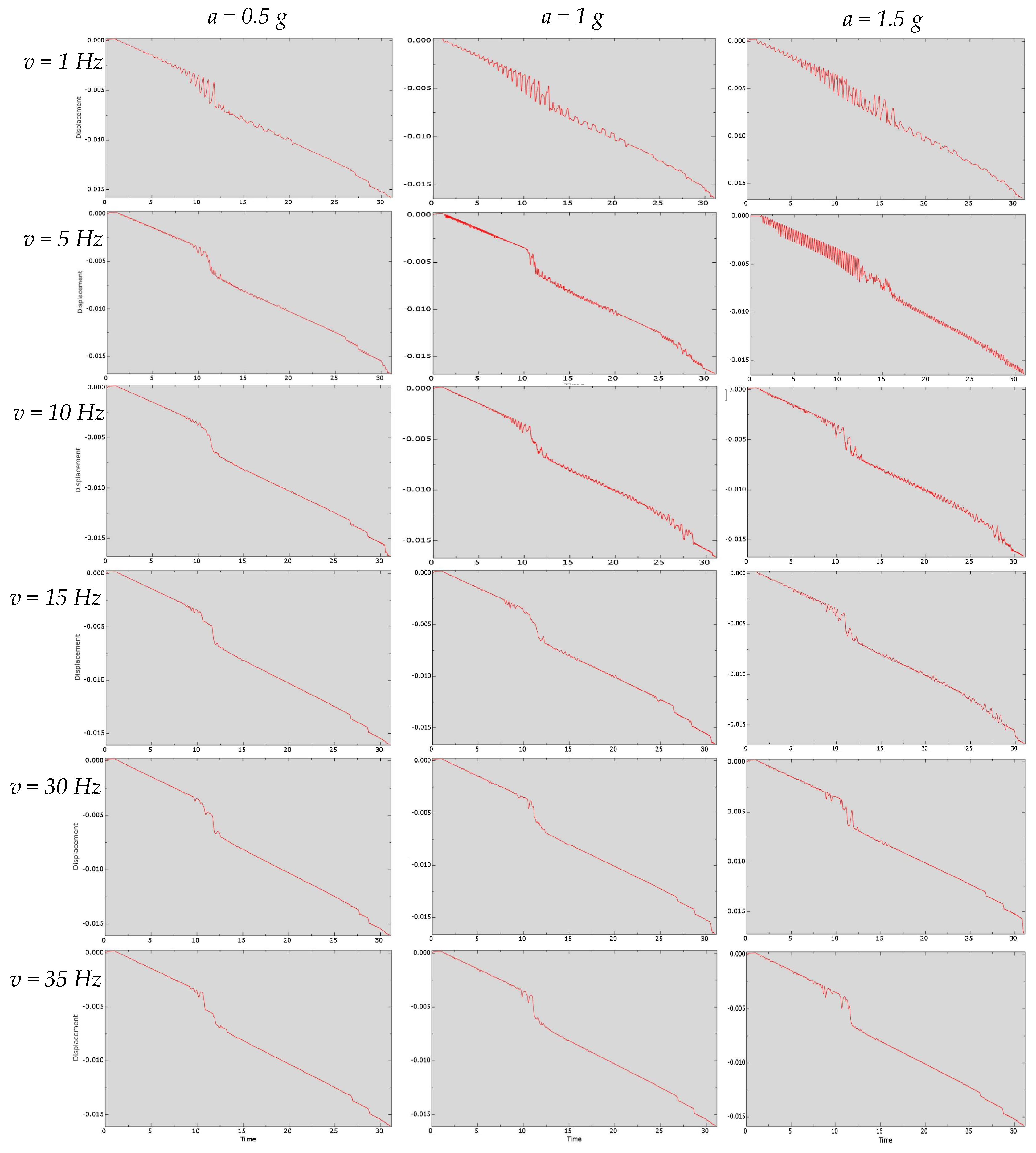
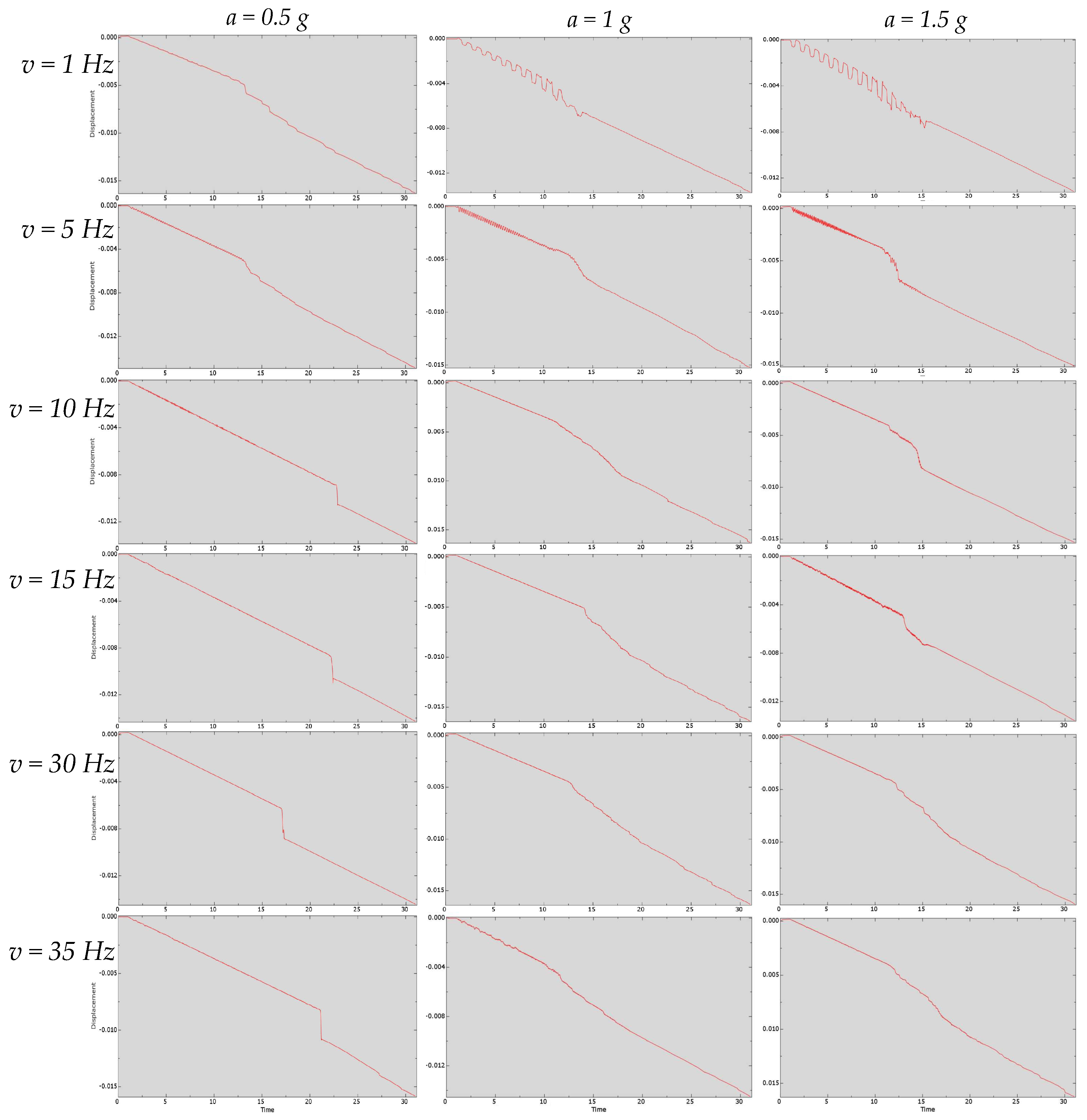
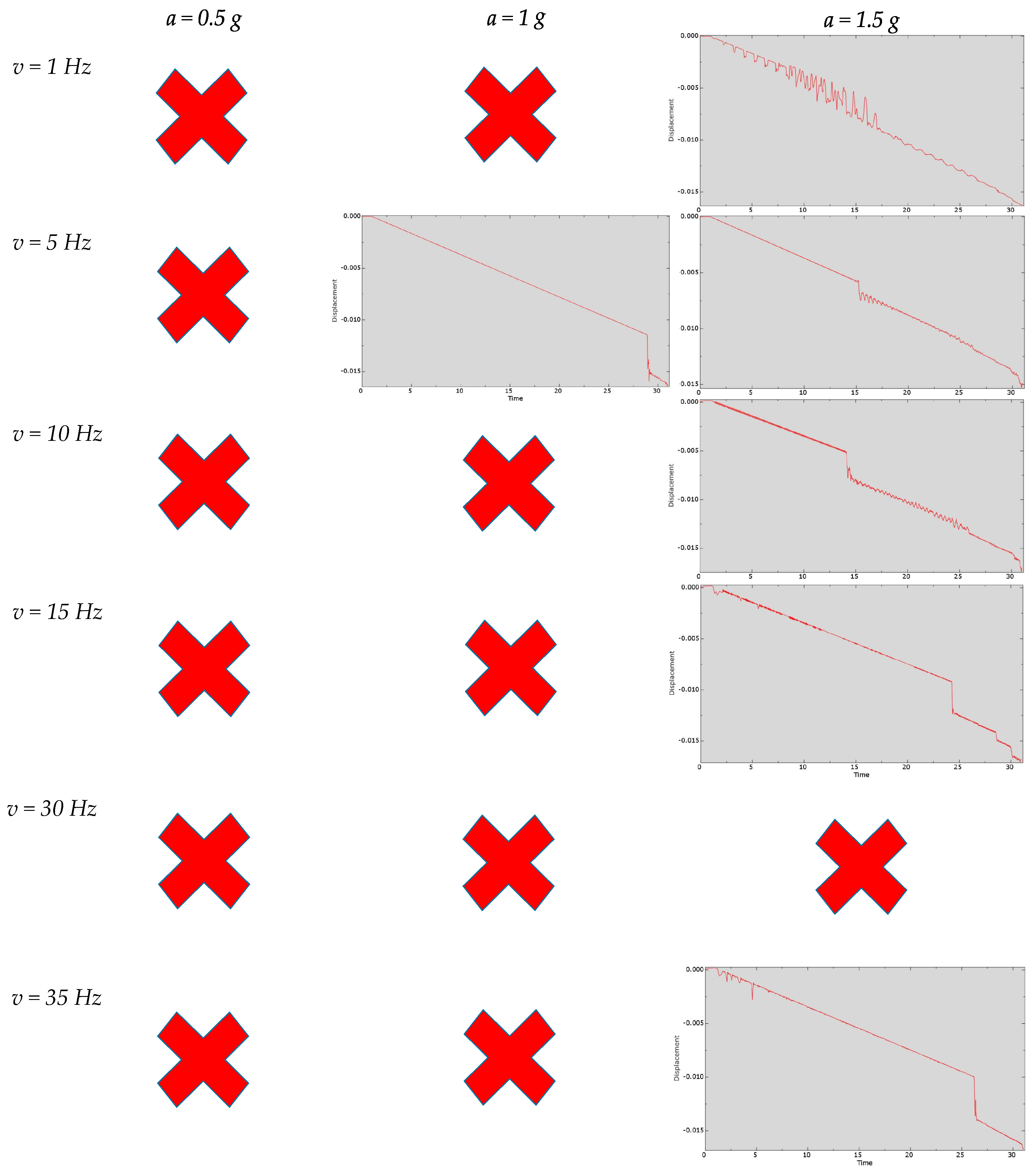
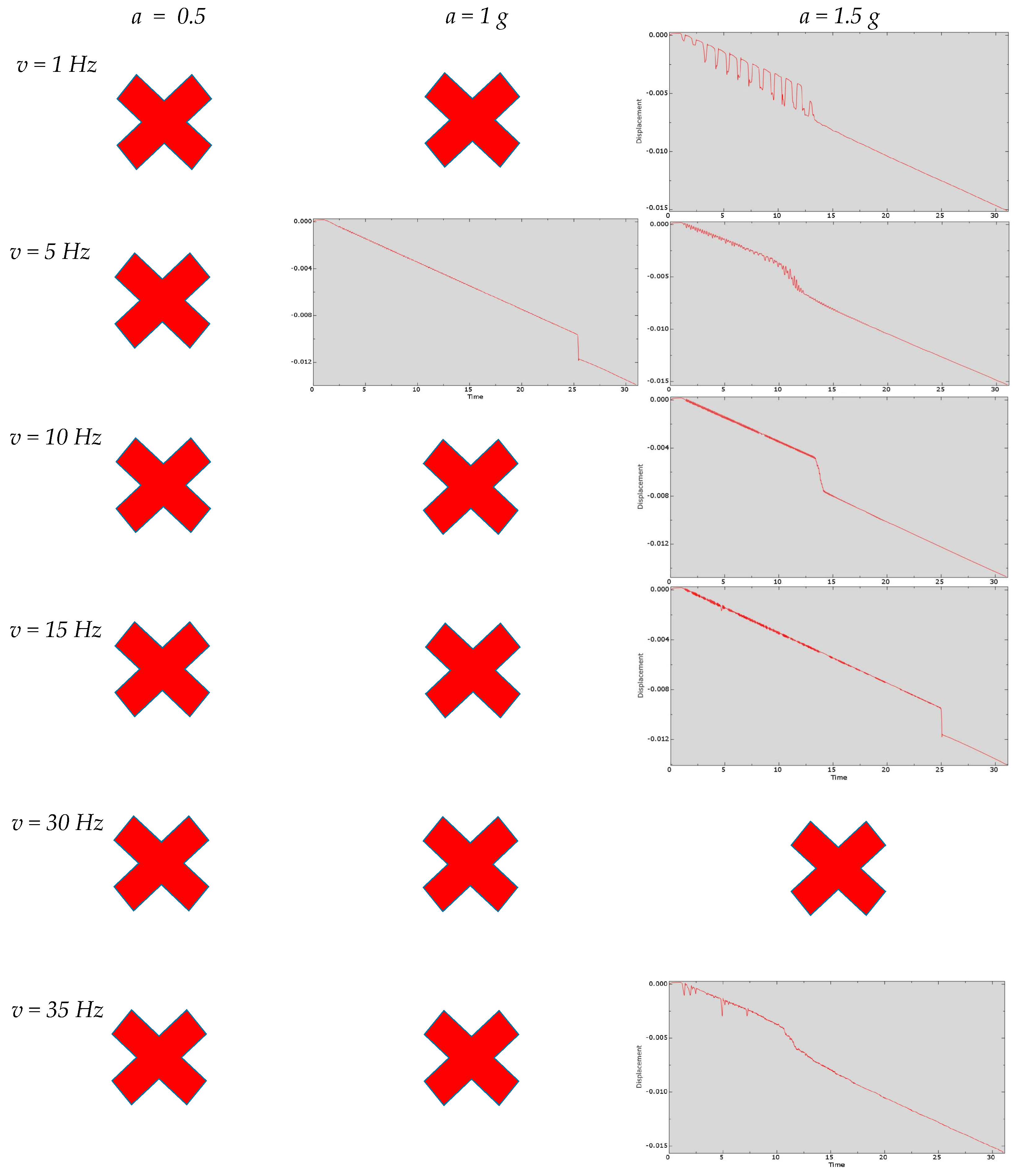
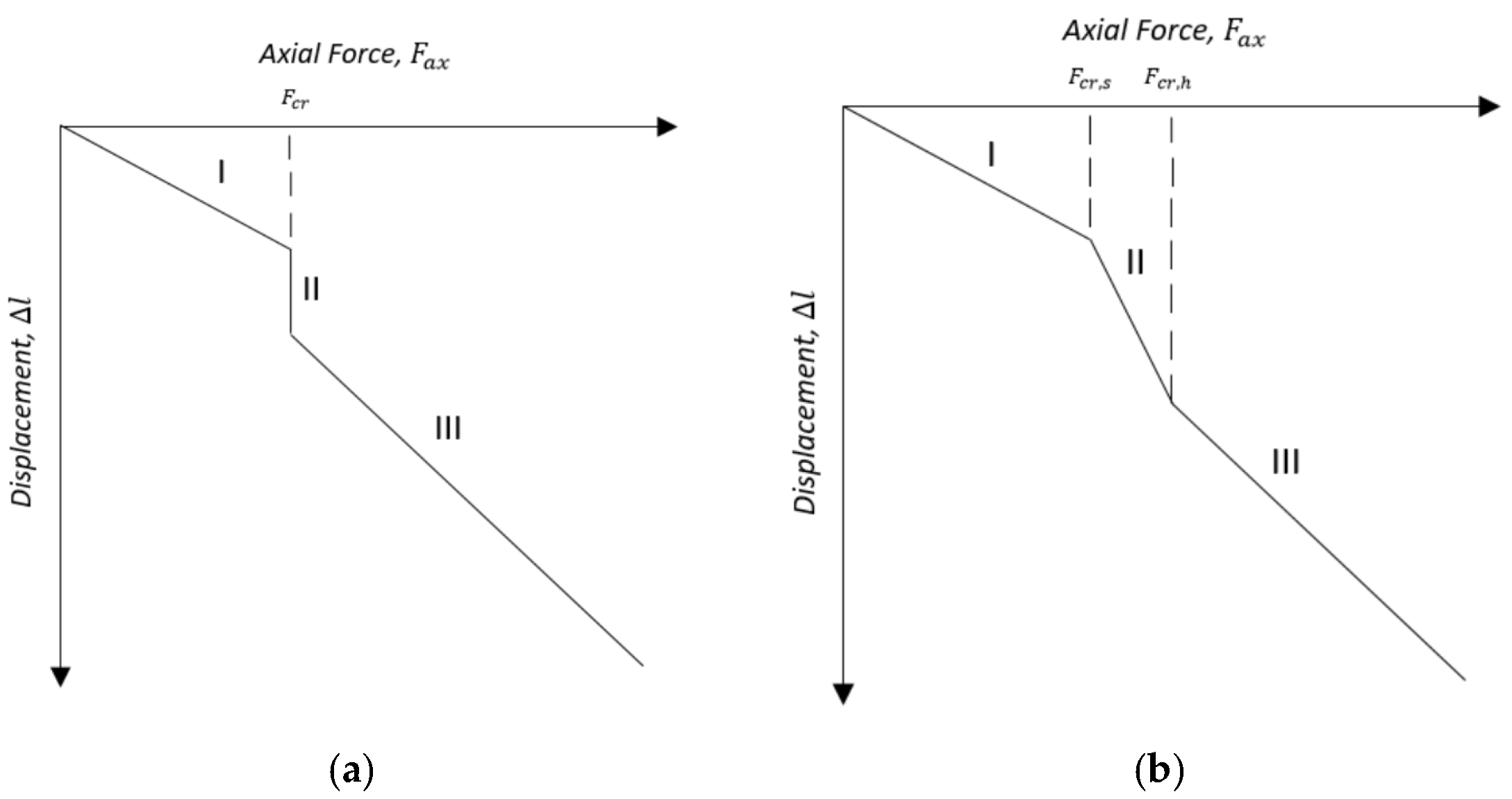
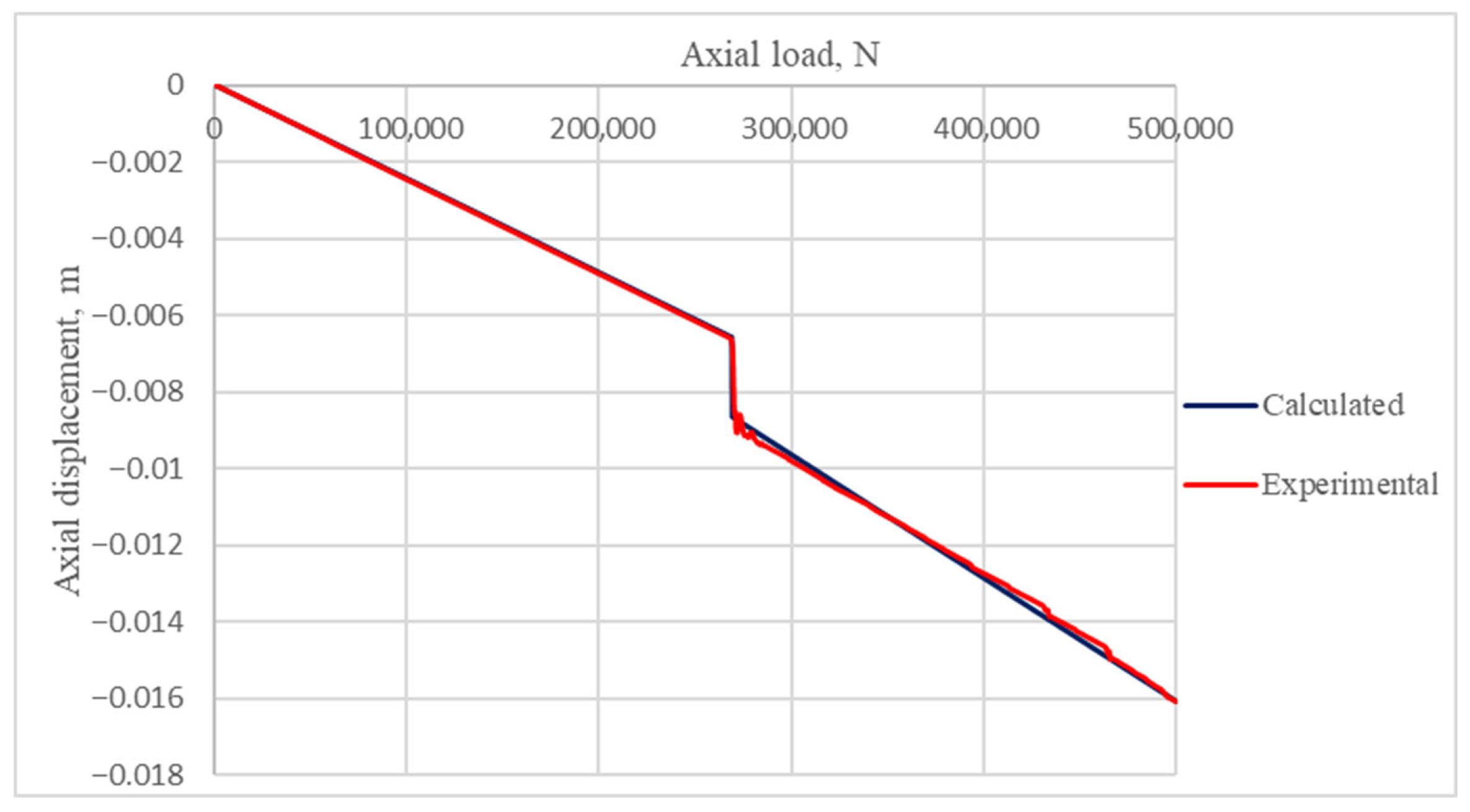
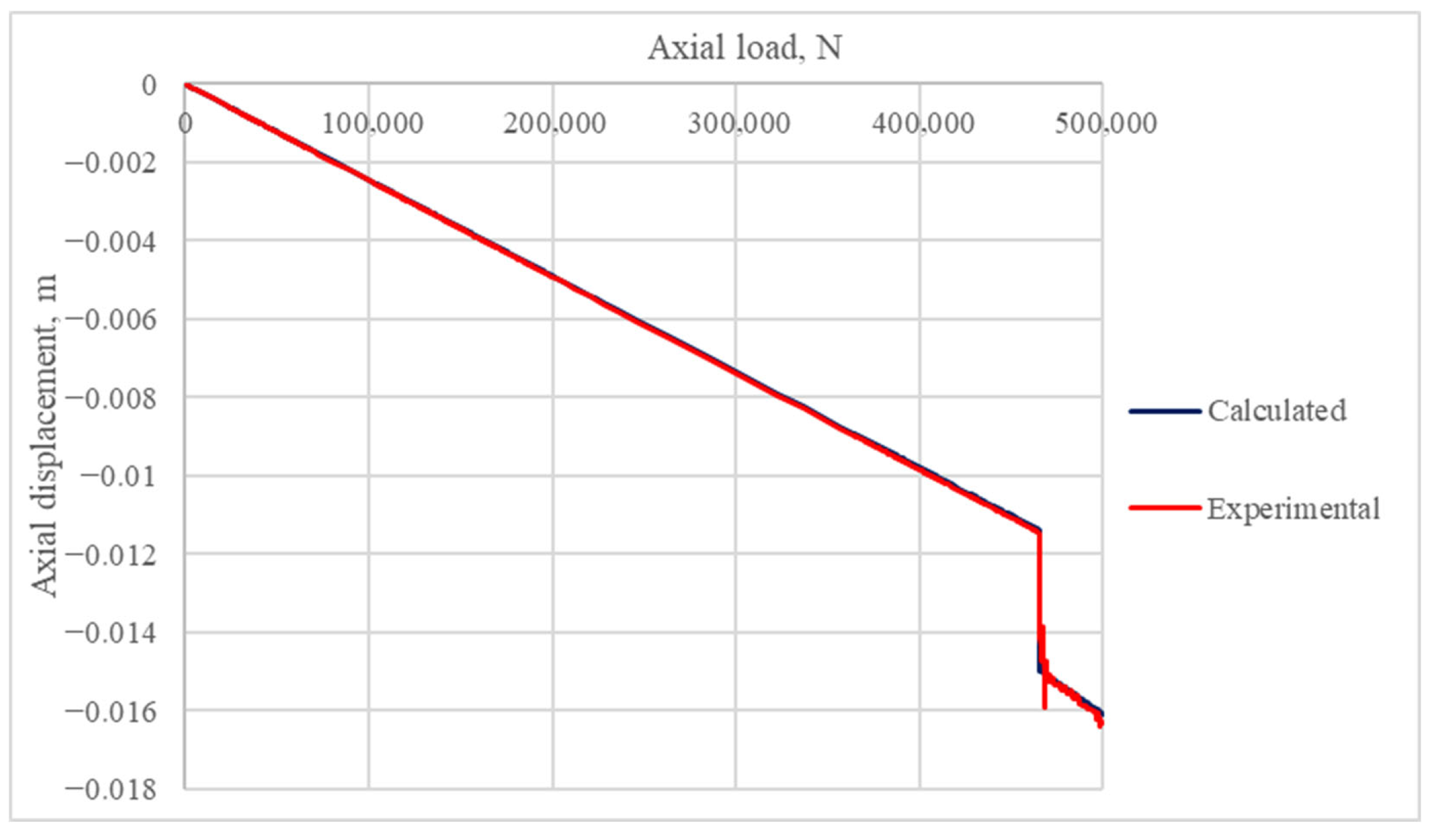
| Researchers | Helical Buckling |
|---|---|
| Chen, Cheatham [20] | |
| Kuru, Cunha, Qu, Martinez Miska, Volk [21] | |
| Wu, Juvkam-Wold [22] |
| Researchers | Unstable Sinusoidal/Helical Buckling |
|---|---|
| Cunha (1995) [14] | |
| Kuru, Cunha, Qu, Martinez, Miska, Volk (1996) [21] | 3.75 |
| Type of Vibration | Frequency, Hz |
|---|---|
| Self-excited vibrations of the drill string caused by contact of tool joints with the borehole wall, hook load fluctuations due to drawworks brake operation, vibrations in the turbodrill thrust bearing due to drilling fluid pulsations | ≈1 |
| Bit bounce, including waviness of a well bottom | 1–40 |
| Bit BHA forward whirl | <5 |
| Bit backward whirl | <50 |
| BHA backward whirl | <20 |
| BHA harmonic resonance | <5 |
| Parametric resonance | <10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dvoynikov, M.; Kutuzov, P. Identification of Critical and Post-Critical States of a Drill String Under Dynamic Conditions During the Deepening of Directional Wells. Eng 2025, 6, 306. https://doi.org/10.3390/eng6110306
Dvoynikov M, Kutuzov P. Identification of Critical and Post-Critical States of a Drill String Under Dynamic Conditions During the Deepening of Directional Wells. Eng. 2025; 6(11):306. https://doi.org/10.3390/eng6110306
Chicago/Turabian StyleDvoynikov, Mikhail, and Pavel Kutuzov. 2025. "Identification of Critical and Post-Critical States of a Drill String Under Dynamic Conditions During the Deepening of Directional Wells" Eng 6, no. 11: 306. https://doi.org/10.3390/eng6110306
APA StyleDvoynikov, M., & Kutuzov, P. (2025). Identification of Critical and Post-Critical States of a Drill String Under Dynamic Conditions During the Deepening of Directional Wells. Eng, 6(11), 306. https://doi.org/10.3390/eng6110306






