Experimental Study on Failure Characteristics and Energy Evolution Law of Coal–Rock Combination Body Under Different Quasi-Static Loading Rates
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Experimental Equipment
2.3. Test Scheme
3. Results
3.1. Strength, Deformation, and Failure Characteristics
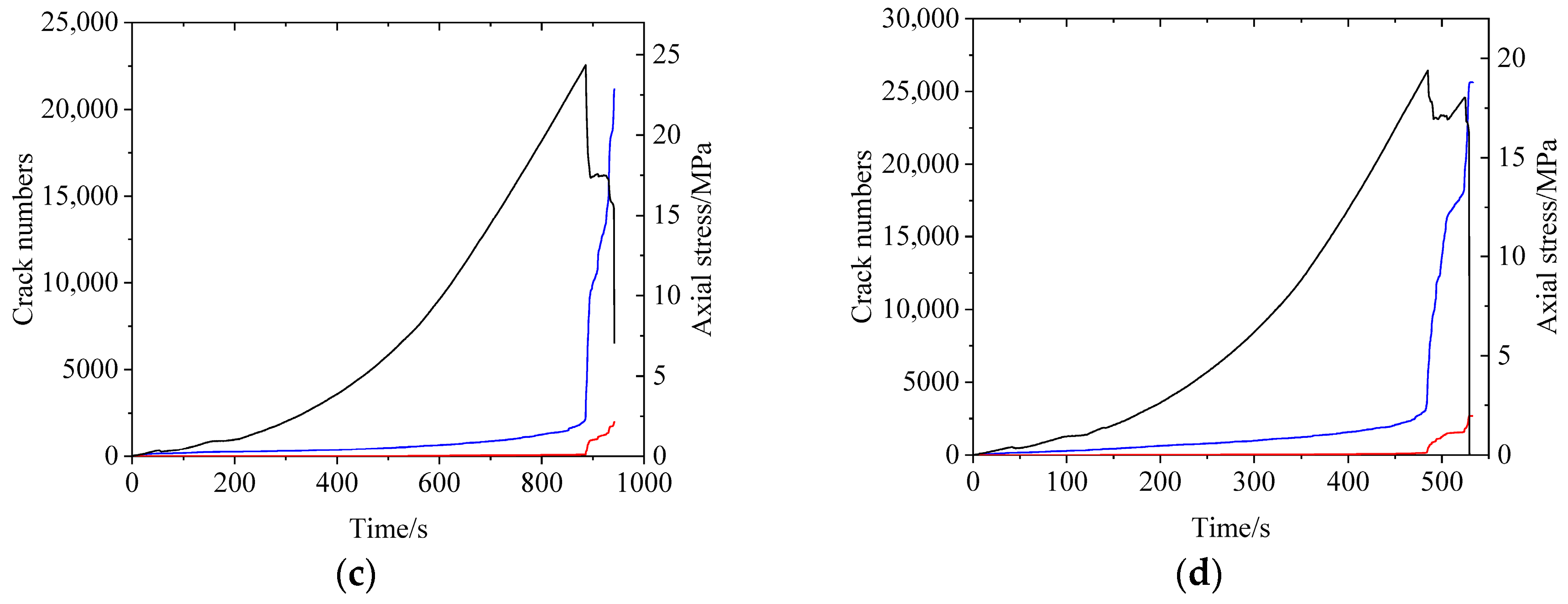
3.2. Damage Evolution Characteristics
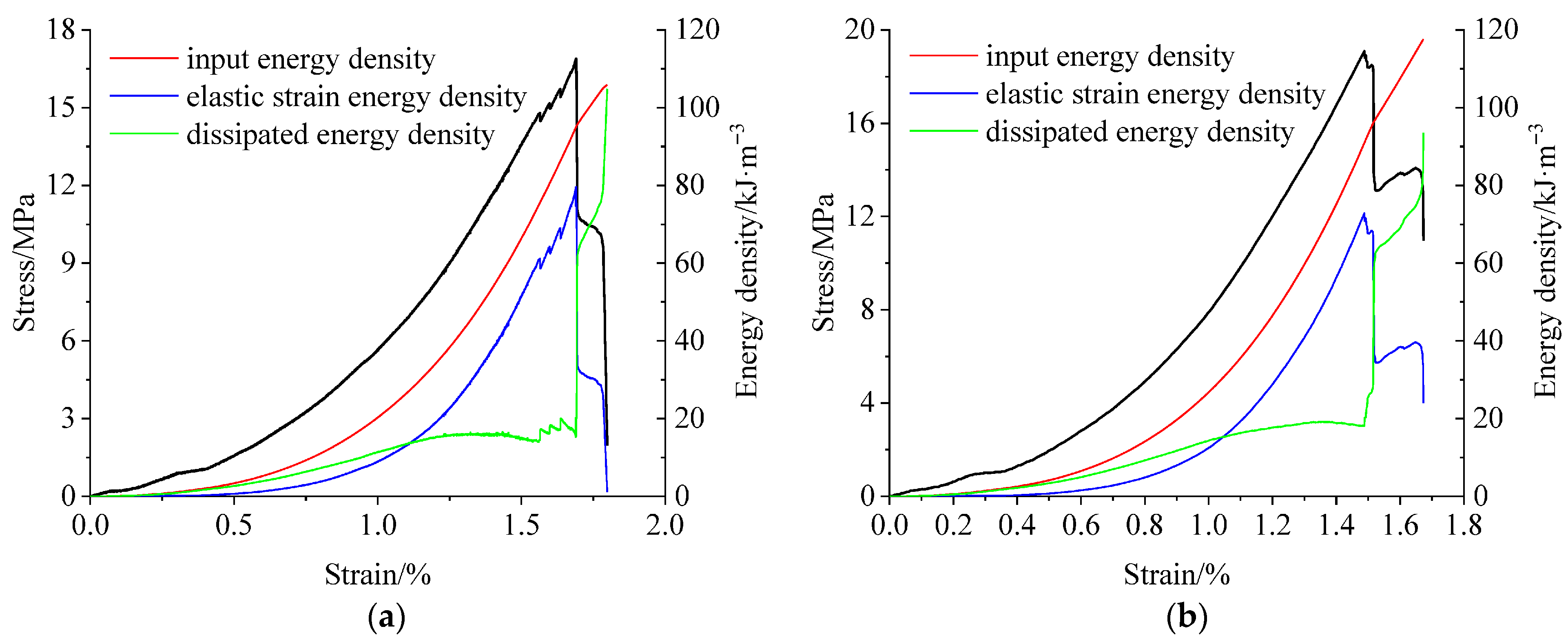
3.3. Energy Evolution Characteristics
4. Discussion
5. Conclusions
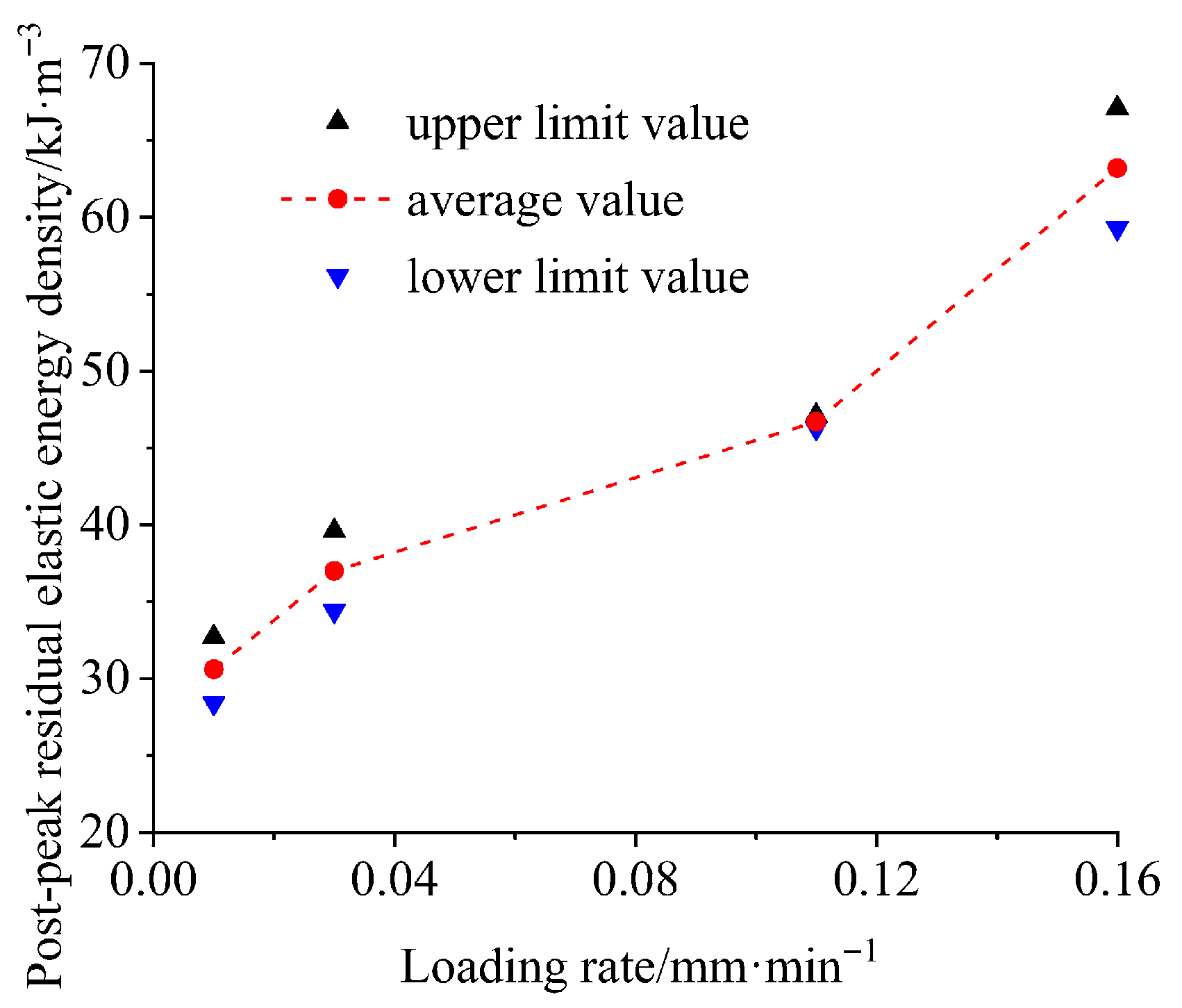
- The uniaxial compressive strength and elastic modulus of the coal–rock combination body show a variation law of first increasing and then decreasing with the increase in loading rate, while the degree of impact failure significantly increases gradually as the loading rate rises. The post-peak residual elastic energy density of the coal–rock combination body increases gradually with the increase in loading rate, which indicates that the post-peak residual elastic energy density of the coal–rock combination body has a positive correlation with its impact failure effect.
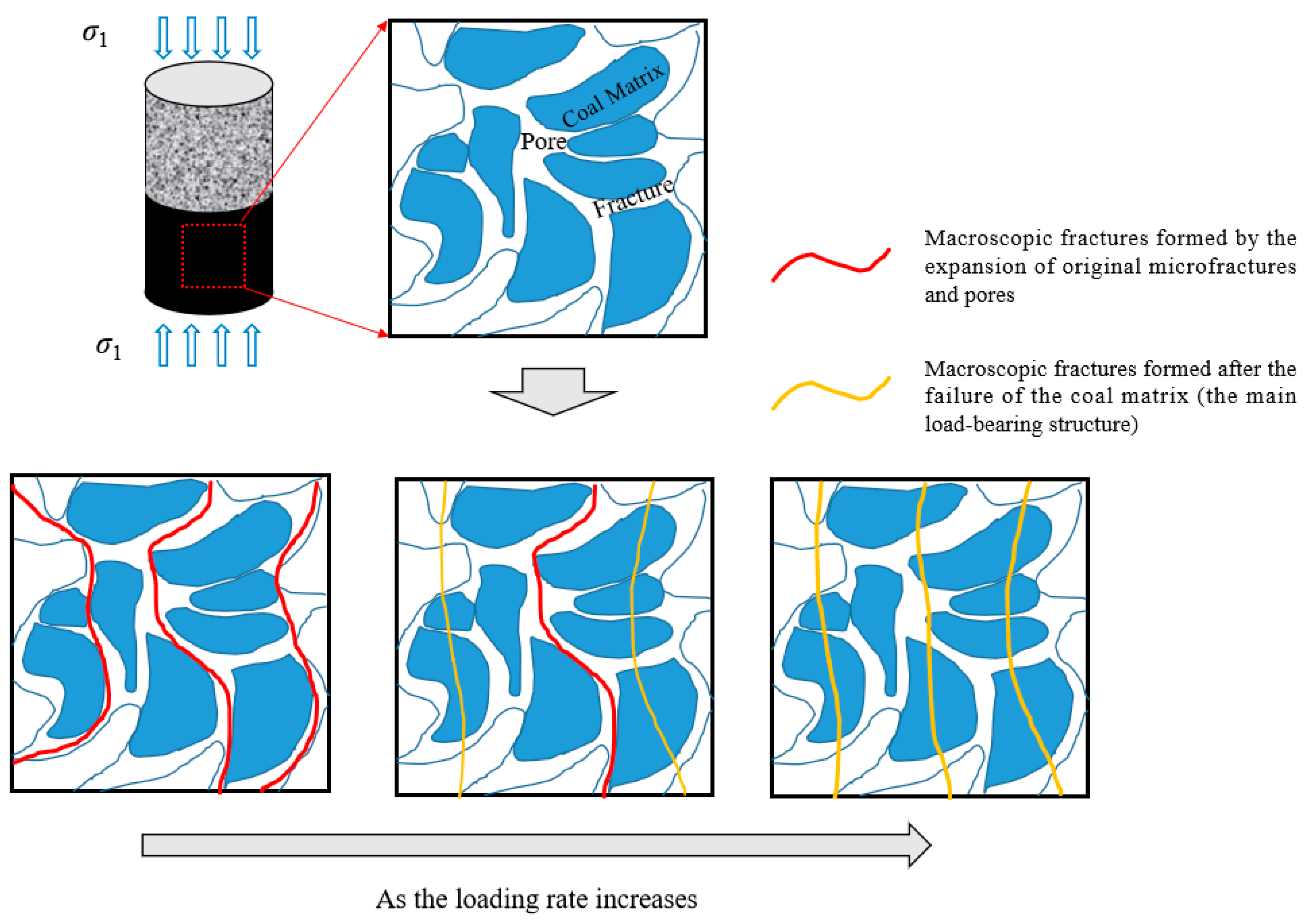
- The formation of the advancing speed effect of mining-induced stress concentration and elastic energy accumulation in coal–rock masses is caused by the “competitive” interaction between fracture propagation and coal matrix damage when the coal component in the coal–rock combination is deformed under stress.
- During low-speed advancing, the loading rate is relatively low, providing sufficient time for the development and propagation of fractures. Consequently, the macroscopic mechanical properties are characterized by low compressive strength, small elastic modulus, high energy dissipation, low energy accumulation, minimal energy release during failure, and a weak impact failure effect.
- The proposed mechanism is consistent with the observed results. In the case of high-speed advancing, the higher loading rate leads to insufficient development and propagation of fractures. The coal matrix, acting as a framework, exerts a significant load-bearing effect. As a result, the macroscopic mechanical properties exhibit increased compressive strength, larger elastic modulus, low energy dissipation, high energy accumulation, substantial energy release during failure, and a strong impact failure effect.
6. Outlook
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Li, W.L.; Tu, S.H.; Tu, H.S.; Liu, X.; Miao, K.J.; Zhao, H.B.; Ma, J.Y.; Tang, L.; Li, Y. A new method to assess thick, hard roof-induced rock burst risk based on mining speed effect on key energy strata. Sustainability 2022, 14, 15054. [Google Scholar] [CrossRef]
- Li, W.L.; Tu, S.H.; Hao, D.Y.; Liu, X.; Miao, K.J. Influence of mining speed and filling ratio on energy accumulation and release of thick and hard roof in deep backfilling working face. J. China Univ. Min. Technol. 2021, 50, 498–506. [Google Scholar]
- Li, W.L.; Tu, S.H.; Zhao, T.B. Study on the tensile failure characteristics and energy calculation model of coal seam hard roof considering the mining speed. Appl. Sci. 2024, 14, 5734. [Google Scholar] [CrossRef]
- Li, H.T.; Song, L.; Zhou, H.W.; Song, F. Experimental study of nonlinear evolution mechanism of coal strength under multi-loading rates and its application. Chin. J. Rock Mech. Eng. 2016, 35, 2978–2989. [Google Scholar]
- Wu, P.; Chen, L.; Chen, Y.L.; Mao, X.B.; Pu, H.; Zhang, K.; Wang, X.F.; Zhang, W. Experimental study on mechanical properties and microcrack fracture of coal specimens under the coupling of loading rate and compression-shear loads. Int. J. Geomech. 2022, 22, 04022028. [Google Scholar] [CrossRef]
- Feng, K.W.; Wang, K.Q.; Zhang, D.M.; Yang, Y.S. Experimental study on mechanical properties and seepage laws of raw coal under variable loading and unloading rates. Geofluids 2021, 2021, 5596858. [Google Scholar] [CrossRef]
- Zhang, M.B.; Cui, L.; Hu, W.J.; Du, J.L.; Zhang, Z.; Wang, C.L. Acoustic emission experimental research of the damage characteristics of raw coal under different loading and unloading rates. Shock Vib. 2020, 2020, 9063929. [Google Scholar] [CrossRef]
- Xiong, Z.Y.; Zhang, D.M.; Lu, J.; Wang, C.Y.; Chen, Y.; Zhang, Y. Mechanical behavior and acoustic emission characteristic response of Macaowan coal samples under different loading rates. Phys. Fluids 2025, 37, 027195. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, Y.X.; Hua, X.Z.; Ling, C.W.; Wang, X.L. Failure characteristic and acoustic emission spatio-temporal evolution of coal under different cyclic loading rates. Energy Sci. Eng. 2023, 11, 2039–2051. [Google Scholar] [CrossRef]
- Liu, B.; Sun, X.; Ling, C.W.; Huang, Z.J.; Zhang, H.W. Mechanical behaviors and acoustic emission fractal characteristics of bump-prone coal under different loading rates. Fractal Fract. 2023, 7, 45. [Google Scholar] [CrossRef]
- Liu, X.W.; Chen, H.X.; Liu, B.; Deng, W.; Liu, Q.S.; Zhang, Z.Z. Experimental and numerical study on failure characteristics and mechanism of coal under different quasi-static loading rates. Theor. Appl. Fract. Mech. 2022, 121, 103478. [Google Scholar] [CrossRef]
- Zhu, C.Q.; Li, S.B.; Luo, Y.; Guo, B. Progressive damage process and failure characteristics of coal under uniaxial compression with different loading rates. Shock Vib. 2021, 2021, 3360738. [Google Scholar] [CrossRef]
- Liu, Y.C.; Ding, L.; Zhao, Y.F.; Fan, Y.; Li, H.F. Experimental investigations on charge induction and microseismic characteristics of the coal and rock under different loading rates. Shock Vib. 2021, 2021, 6242075. [Google Scholar] [CrossRef]
- Li, G.W.; Lu, S.F.; Liu, S.F.; Liu, J.; Shi, P.; Fan, B.W. Application and effect of loading rates on coal sample failure. Shock Vib. 2021, 2021, 6681082. [Google Scholar] [CrossRef]
- Zhou, C.; He, X.Q.; Song, D.Z.; Li, Z.L.; Yang, H.K.; Liu, Y.; Guo, L. Study on signal characteristics of burst tendency coal under different loading rates. Int. J. Coal Sci. Technol. 2024, 11, 73. [Google Scholar] [CrossRef]
- Li, H.T.; Zhou, H.W.; Jiang, Y.D.; Wang, H.W. An evaluation method for the bursting characteristics of coal under the effect of loading rate. Rock Mech. Rock Eng. 2016, 49, 3281–3291. [Google Scholar] [CrossRef]
- Xue, J.H.; Wang, S.L.; Yang, Q.L.; Du, Y.T.; Hou, Z.X. Study on damage characteristics of deep coal based on loading rate effect. Minerals 2022, 12, 402. [Google Scholar] [CrossRef]
- Jing, C.; Ji, X.; Yang, W.; Pang, M.K.; Zhang, T.J.; Pan, H.Y. Crack propagation characteristics of coal body around the borehole under different loading rates. Theor. Appl. Fract. Mech. 2024, 133, 104498. [Google Scholar] [CrossRef]
- Khan, N.M.; Ma, L.; Cao, K.; Spearing, A.J.S.; Liu, W.; Jie, Y.; Yousaf, M. Early violent failure precursor prediction based on infrared radiation characteristics for coal specimens under different loading rates. Rock Mech. Rock Eng. 2022, 55, 6939–6961. [Google Scholar] [CrossRef]
- Li, X.B.; Feng, G.; Xiao, M.L.; Wang, G.F.; Bi, J.; Gao, C.Y.; Liu, H.Z. Experimental study on the effects of loading rates on the fracture mechanical characteristics of coal influenced by long-term immersion in mine water. Appl. Sci. 2025, 15, 8222. [Google Scholar] [CrossRef]
- Wang, D.; Ju, F.; Xu, J.; Yan, C.S.; Xiao, M.; Ning, P.; Wang, T.F.; Si, L.; Wang, Y.B. Effects of moisture content and loading rate on coal samples: Mechanical properties and failure mechanisms. Rock Mech. Rock Eng. 2025, 58, 3391–3416. [Google Scholar] [CrossRef]
- Wang, S.G.; Elsworth, D.; Liu, J.S. Mechanical behavior of methane infiltrated coal: The roles of gas desorption, stress level and loading rate. Rock Mech. Rock Eng. 2013, 46, 945–958. [Google Scholar] [CrossRef]
- Zhang, M.B.; Liu, M.Q.; Zhu, H.Q.; Zhou, D.H.; Wang, L. An experimental study of the damage characteristics of gas-containing coal under the conditions of different loading and unloading rates. J. Loss Prev. Process Ind. 2018, 55, 338–346. [Google Scholar] [CrossRef]
- Cao, Y.L.; Hao, J.F.; Sun, W.J.; Su, W.W.; Tian, F.C. Study on temperature evolution law of coal containing gas under uniaxial loading process with different loading rates. Environ. Prog. Sustain. Energy 2024, 44, 14501. [Google Scholar] [CrossRef]
- Li, Q.W.; Xu, M.J.; Li, W.X.; Pan, C.C.; Yu, M.M. Energy evolution characteristics and failure mechanism of coal confined by CFRP jackets subjected to different loading rates. Polym. Test. 2025, 143, 108723. [Google Scholar] [CrossRef]
- Khan, N.M.; Ahmad, M.; Cao, K.W.; Ali, L.; Liu, W.; Rehman, H.; Hussain, S.; Rehman, F.U.; Ahmed, T. Developing a new bursting liability index based on energy evolution for coal under different loading rates. Sustainability 2022, 14, 1572. [Google Scholar] [CrossRef]
- Ma, Q.; Tan, Y.L.; Liu, X.S.; Zhao, Z.H.; Fan, D.Y.; Purev, L. Experimental and numerical simulation of loading rate effects on failure and strain energy characteristics of coal-rock composite samples. J. Cent. South Univ. 2021, 28, 3207–3222. [Google Scholar] [CrossRef]
- Huang, B.X.; Liu, J.W. The effect of loading rate on the behavior of samples composed of coal and rock. Int. J. Rock Mech. Min. Sci. 2013, 61, 23–30. [Google Scholar] [CrossRef]
- Chen, G.B.; Zhang, J.; Xu, Y.J.; Li, T.; Wang, E.; Zhang, G.H. The influence of loading rate on accumulated energy distribution in coal-rock samples and their failure behavior. J. Min. Sci. 2025, 60, 792–807. [Google Scholar] [CrossRef]
- Zhao, S.K.; Deng, Z.G.; Ji, W.B.; Li, Z.G.; Zhang, G.H.; Li, Y.Z. Effects of multi-stage tectonic movement on regional tectonic stress characteristics and rockburst. J. Min. Saf. Eng. 2019, 36, 306–314. [Google Scholar]
- Shen, Z. Experimental Study on Characteristics of Acoustic Emission and Fractal in Rock. Master’s Thesis, Chengdu University of Technology, Chengdu, China, 2017. [Google Scholar]
- Ma, Y.A.; Ya, C.; Li, H.B.; Liang, Z.Q.; Liu, Y.Q.; Li, S.J. Experimental study on the mechanical properties and energy dissipation of granite during the fracturing process. Chin. J. Rock Mech. Eng. 2025, 44, 1313–1325. [Google Scholar] [CrossRef]
- Hashiba, K.; Okubo, S.; Fukui, K. A new testing method for investigating the loading rate dependency of peak and residual rock strength. Int. J. Min. Sci. Technol. 2006, 43, 894–904. [Google Scholar] [CrossRef]
- Gao, M.Z.; Xie, J.; Gao, Y.N.; Wang, W.Y.; Cong, L.; Yang, B.G.; Liu, J.J. Mechanical behavior of coal under different mining rates: A case study from laboratory experiments to field testing. Int. J. Min. Sci. Technol. 2021, 31, 825–841. [Google Scholar] [CrossRef]
- Yi, Z.Q.; Yin, Y.P.; Li, S.D.; Wang, W.P.; Zhang, M.Z.; Mao, T.Q.; Zhang, Y.X.; Wang, X.B.; Gao, S.H. Research on short-term prediction precursors of bedding-layered sandstone based on strain monitoring. Eng. Fract. Mech. 2025, 320, 111071. [Google Scholar] [CrossRef]
- Lyu, X.F.; Chen, Y.L.; Liao, S.M.; Fernandez-Steeger, T.M. Theoretical and numerical analyses of thermal stresses and temperature variations in disc cutter cutting composite strata under thermal-force multi-fields. Case Stud. Therm. Eng. 2024, 61, 105104. [Google Scholar] [CrossRef]
- Xu, C.; Yang, T.; Wang, K.; Yuan, Y.W.; Guo, L. Influence of primary interface characteristics on mechanical properties and damage evolution of coal-rock combination. Eng. Fail. Anal. 2024, 164, 108658. [Google Scholar] [CrossRef]
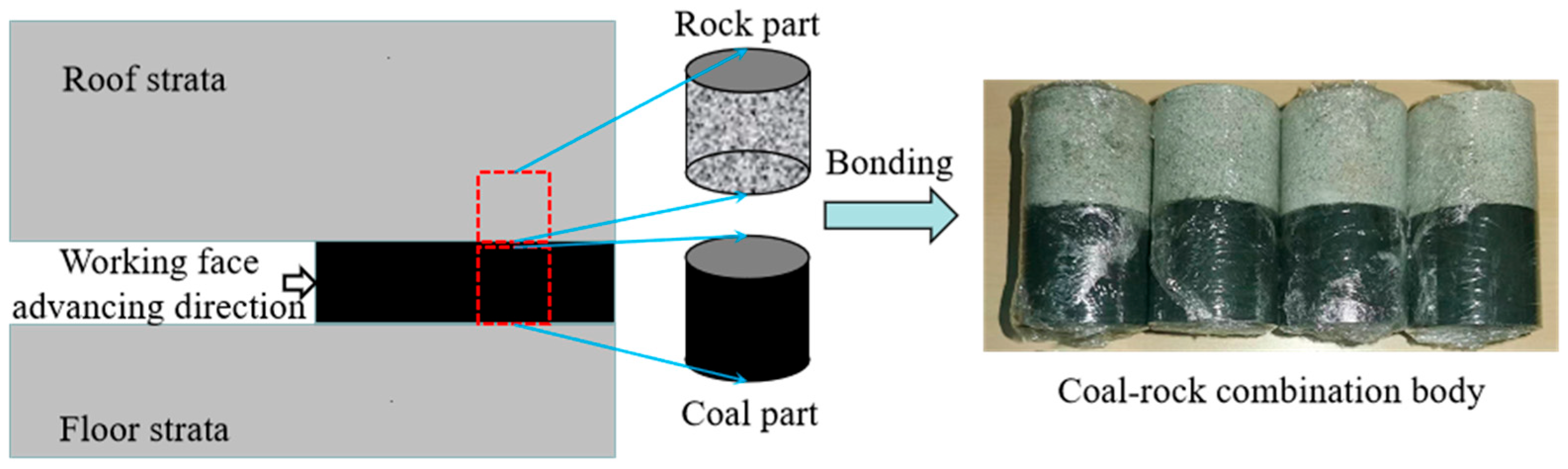

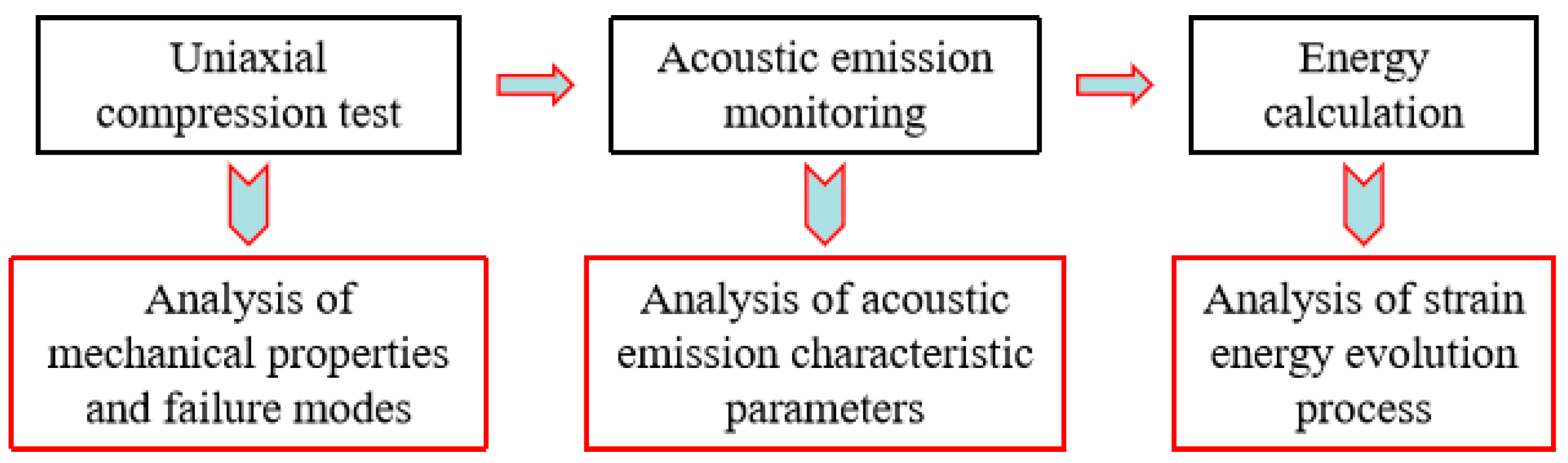
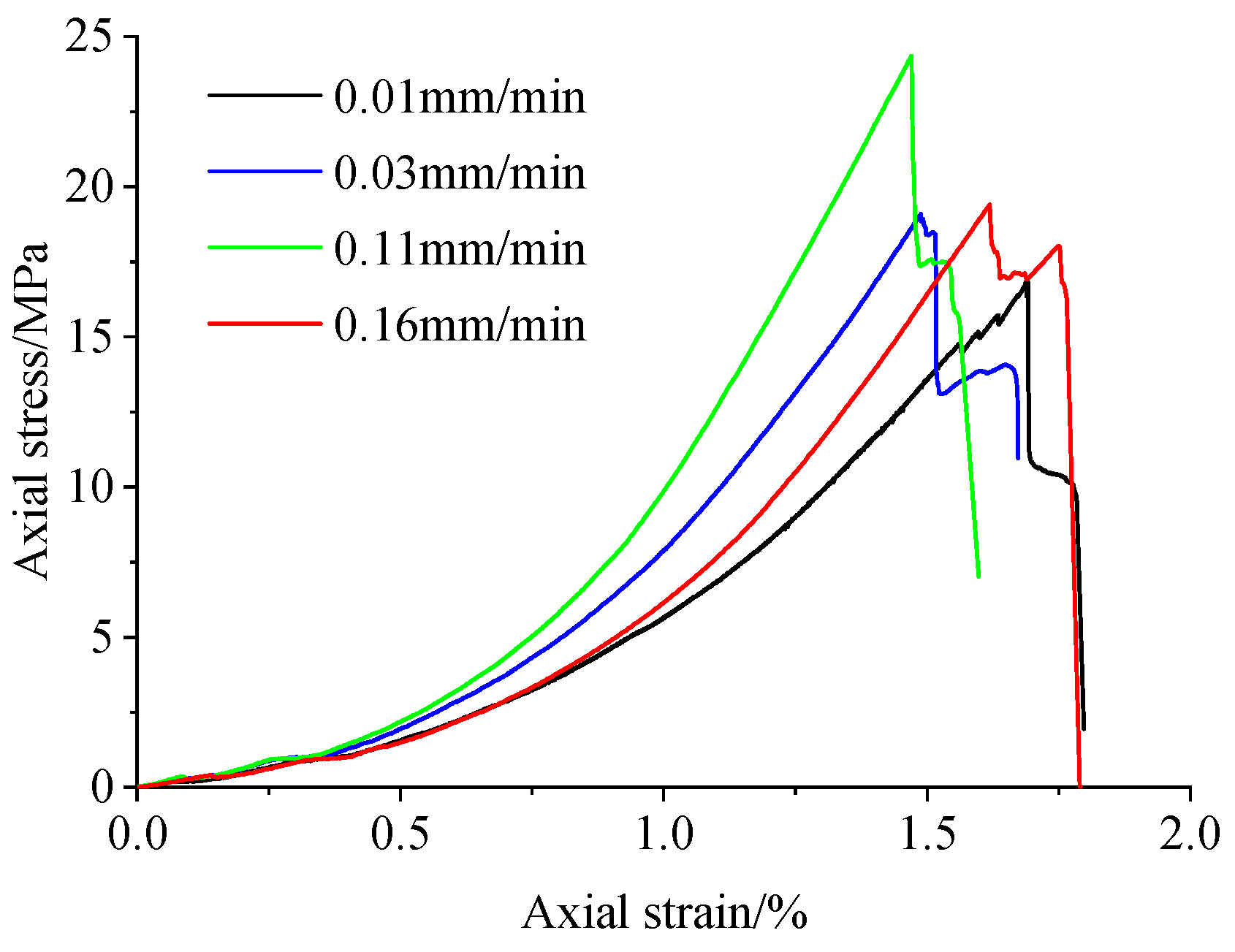
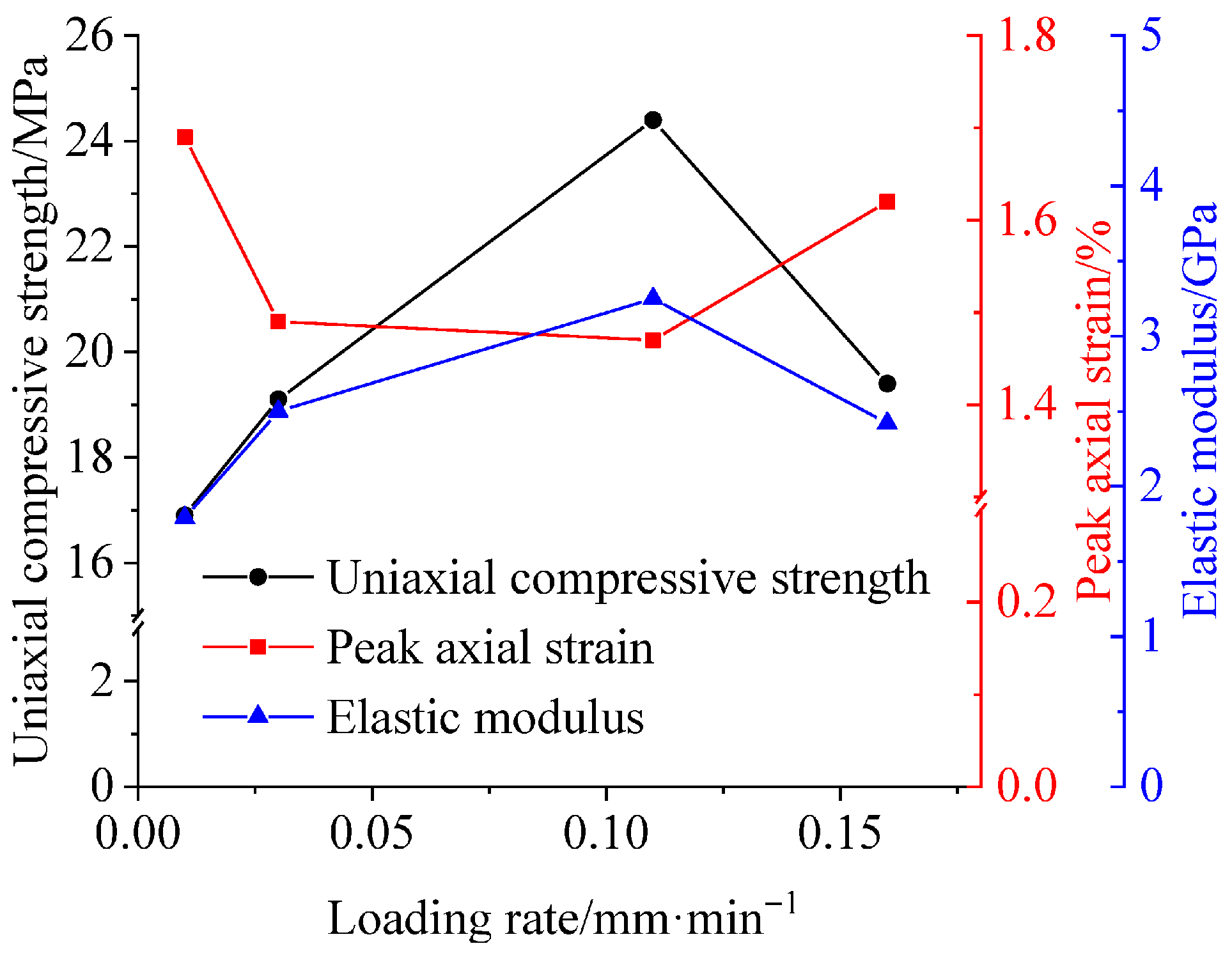


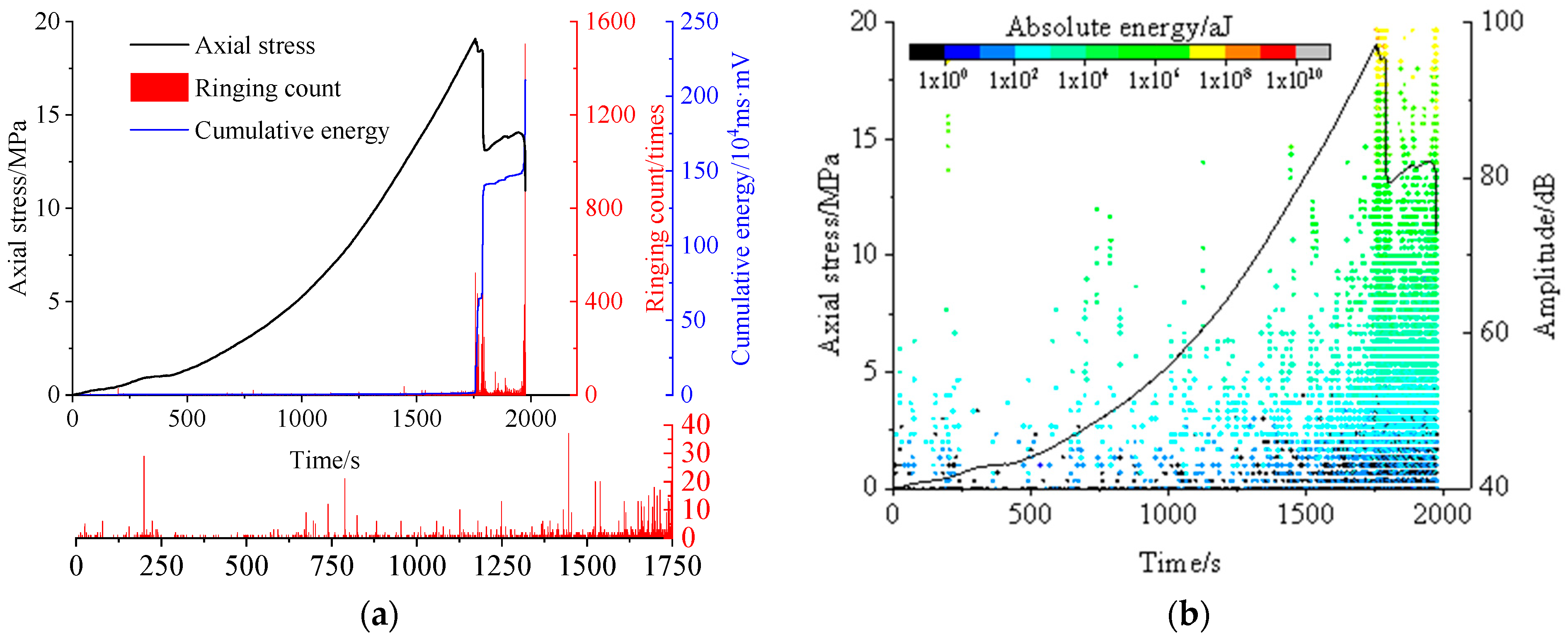
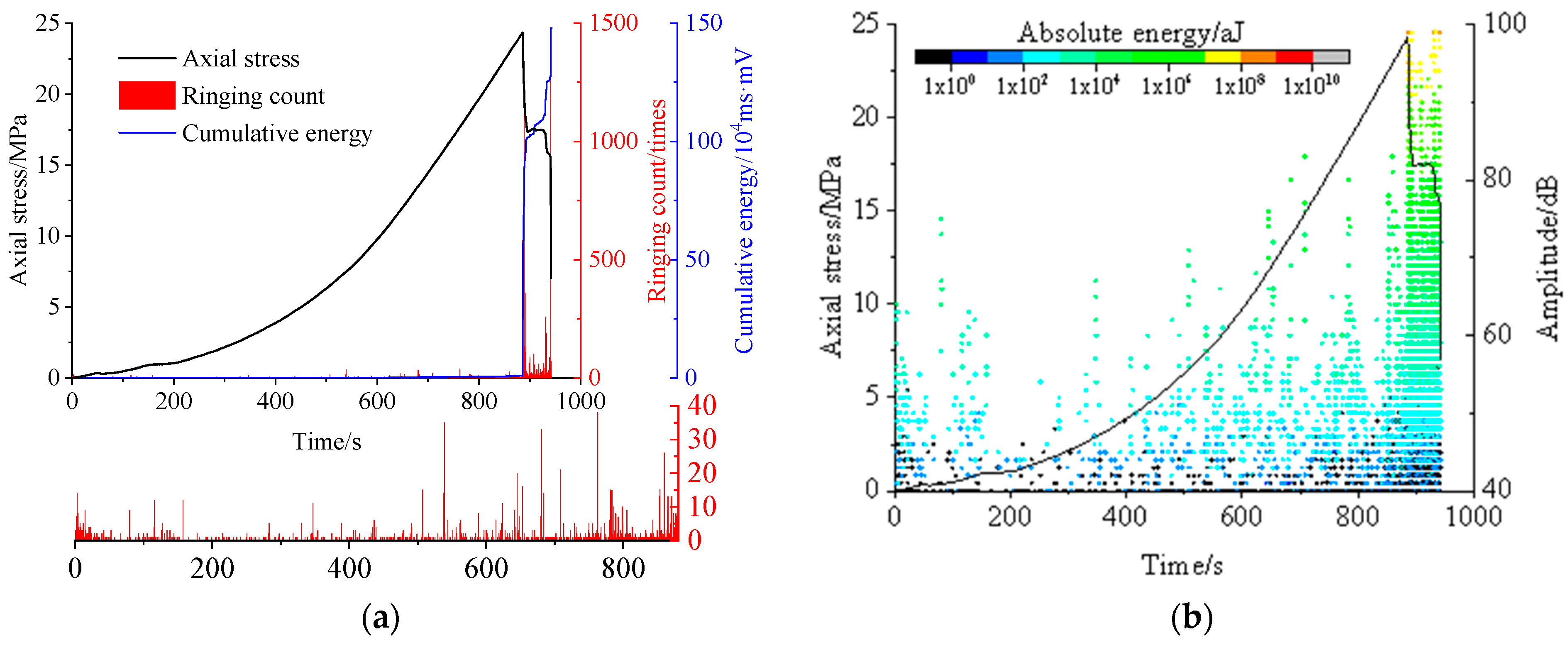
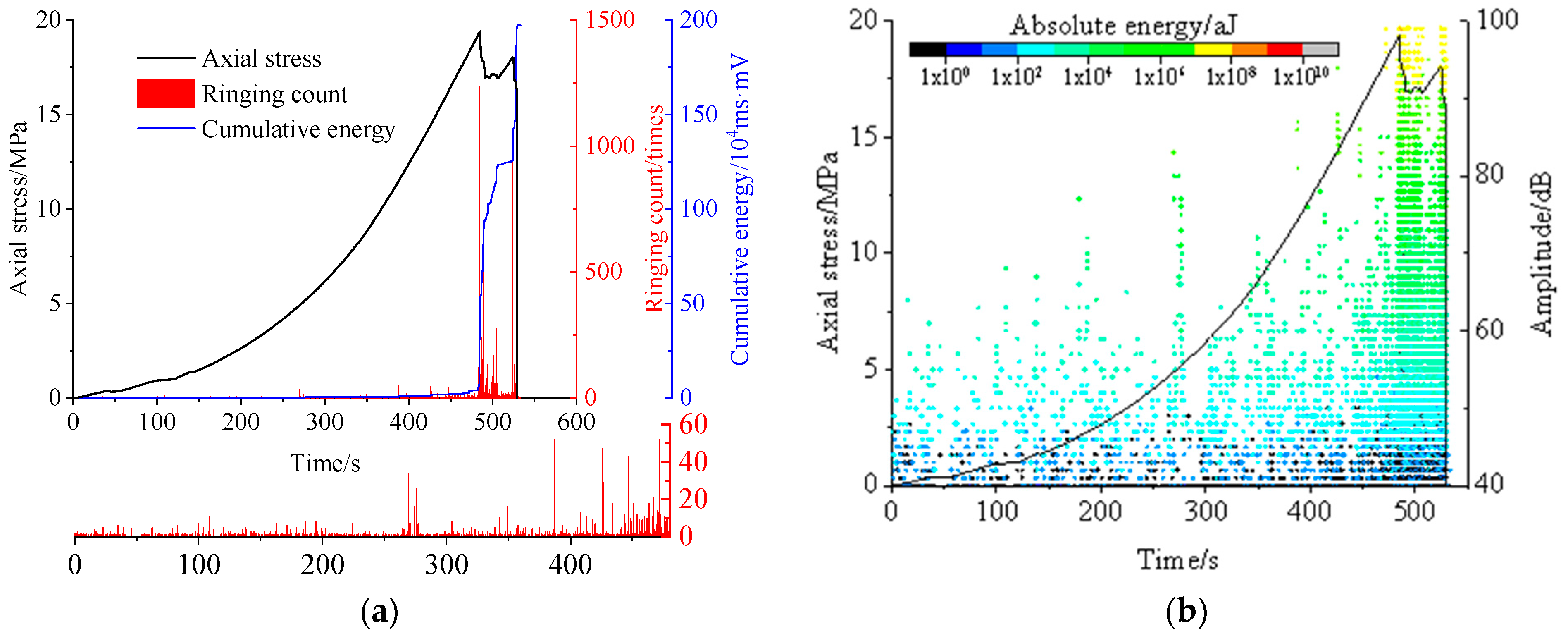
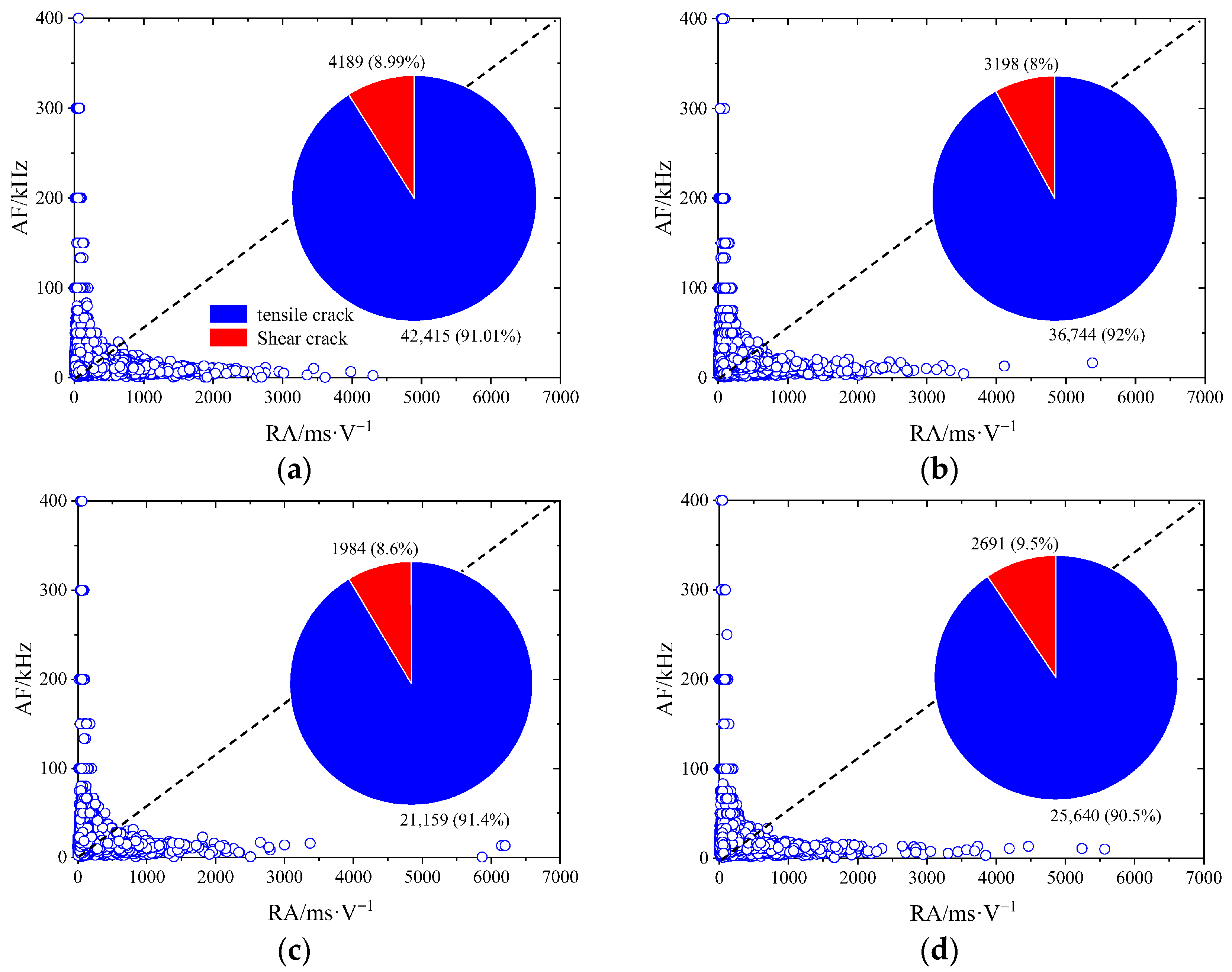


| Sample Number | Quality /kg | Diameter /mm | Height /mm | Density /kg·m−3 |
|---|---|---|---|---|
| UC-1 | 0.369 | 49.67 | 100.21 | 1901 |
| UC-2 | 0.367 | 49.97 | 99.77 | 1877 |
| UC-3 | 0.368 | 49.97 | 100.55 | 1867 |
| UC-4 | 0.366 | 49.62 | 100.08 | 1892 |
| Loading Rate /mm·min−1 | Compressive Strength/MPa | Elastic Modulus/GPa | Post-Peak Residual Elastic Energy Density /kJ·m−3 |
|---|---|---|---|
| 0.01 | 16.9 | 1.8 | 30.6 |
| 0.03 | 19.1 | 2.5 | 37.0 |
| 0.11 | 24.4 | 3.3 | 46.7 |
| 0.16 | 19.4 | 2.4 | 63.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, W.; Zhao, T.; Tu, S. Experimental Study on Failure Characteristics and Energy Evolution Law of Coal–Rock Combination Body Under Different Quasi-Static Loading Rates. Eng 2025, 6, 287. https://doi.org/10.3390/eng6110287
Li W, Zhao T, Tu S. Experimental Study on Failure Characteristics and Energy Evolution Law of Coal–Rock Combination Body Under Different Quasi-Static Loading Rates. Eng. 2025; 6(11):287. https://doi.org/10.3390/eng6110287
Chicago/Turabian StyleLi, Wenlong, Tongbin Zhao, and Shihao Tu. 2025. "Experimental Study on Failure Characteristics and Energy Evolution Law of Coal–Rock Combination Body Under Different Quasi-Static Loading Rates" Eng 6, no. 11: 287. https://doi.org/10.3390/eng6110287
APA StyleLi, W., Zhao, T., & Tu, S. (2025). Experimental Study on Failure Characteristics and Energy Evolution Law of Coal–Rock Combination Body Under Different Quasi-Static Loading Rates. Eng, 6(11), 287. https://doi.org/10.3390/eng6110287







