Prediction of Concrete Compressive Strength Based on Gradient-Boosting ABC Algorithm and Point Density Correction
Abstract
1. Introduction
- This research pioneers the application of this enhanced metaheuristic framework to the complex problem of concrete compressive strength prediction using non-destructive testing data, offering a more robust and reliable approach than conventional methods;
- This study proposes a novel gradient-boosting artificial bee colony algorithm, which effectively integrates gradient descent to significantly accelerate convergence and enhance the precision of concrete compressive strength prediction;
- A unique point density-weighted mechanism, based on Gaussian Kernel Density Estimation, is incorporated into the GB-ABC algorithm to ensure the model’s fitting results are more suitable for real-world scenarios, particularly by preventing small sample data from becoming isolated and improving the representation in sparse or unevenly distributed data regions.
2. Preliminaries
Artificial Bee Colony Algorithm
- ;
- D represents the dimension of the problem to be solved;
- represents the value of the i-th food source in the j-th dimension;
- represents the lower limit of the parameter ;
- represents the upper limit.
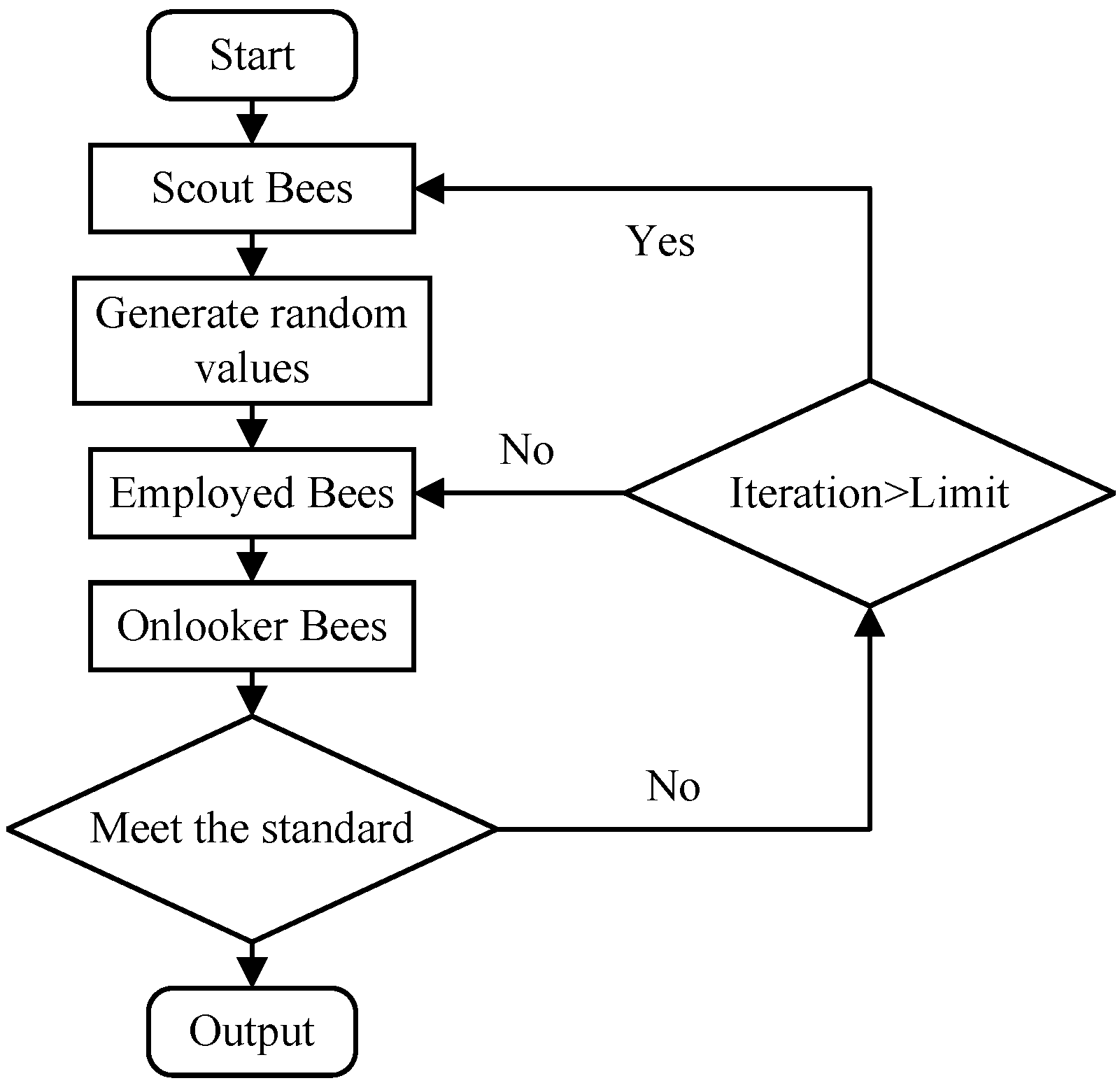
3. Method
3.1. Overall Framework
3.2. Data Preprocessing
3.3. Rebound-Strength Correlation Modeling with GB-ABC
3.3.1. Objective Function
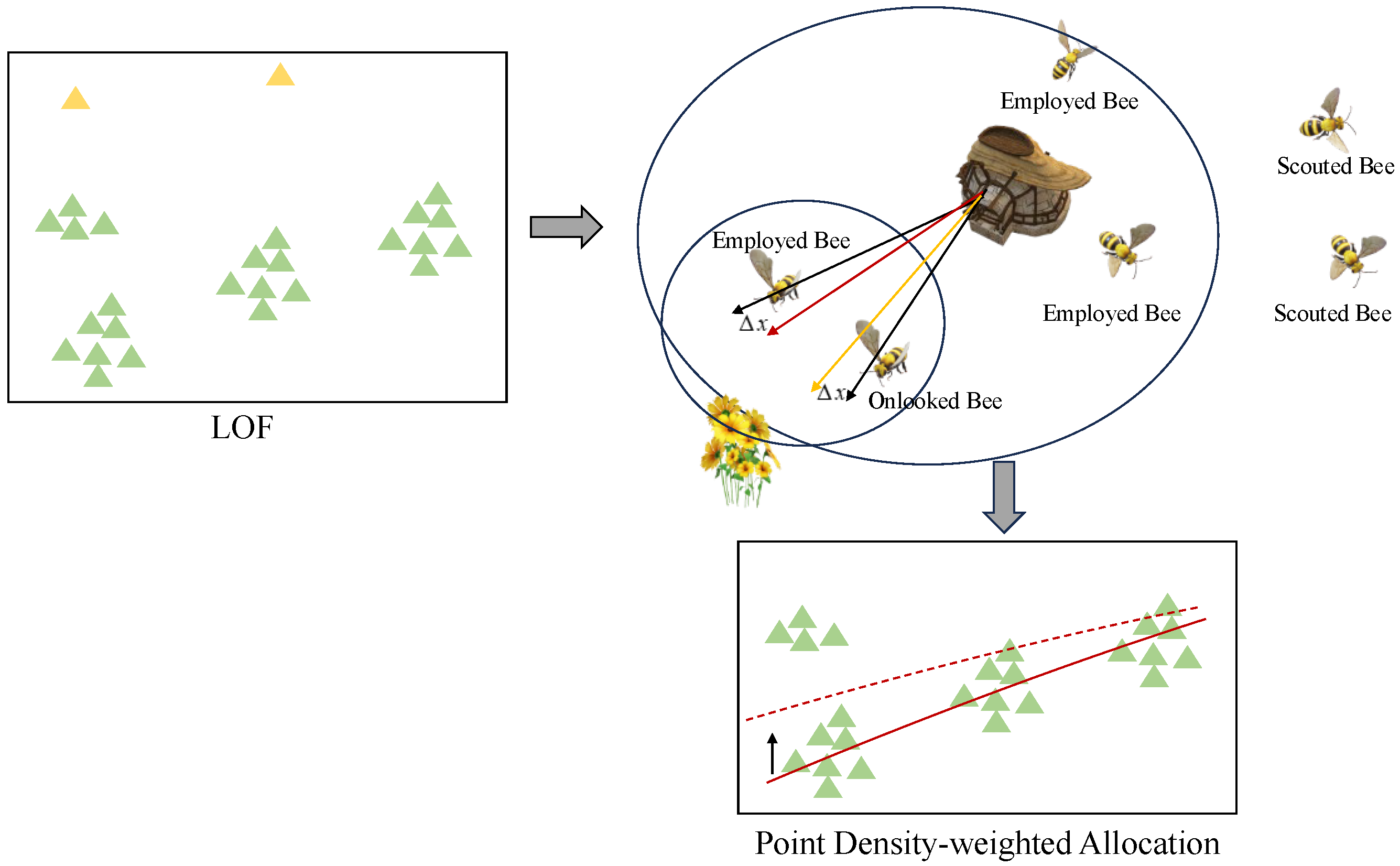
3.3.2. Prior Knowledge Based on Point Density-Weighted Allocation
- 1.
- Spatial Density Field ModelingThis paper aims to modify the trend of the fitted curve by utilizing the spatial distribution of the data, so that the trend is not only to satisfy the minimum mean RER, but also to be closer to the trend direction in the data. Therefore, this study adopts Gaussian kernel density estimation to create a continuous probability density function, because of its non-parametric nature, that is, it does not make any specific assumptions about the underlying distribution of the data. This function leverages the normal distribution’s probability density to smoothly disperse the influence of each data point to surrounding areas, with closer points receiving higher weights, as shown in Figure 3. Ultimately, by integrating discrete data values with spatial distance relationships through Gaussian kernel density estimation, the spatial density assessment is completed.Based on Gaussian Kernel Density Estimation (GKDE), calculate the local density estimate for each data point as shown in Equation (8).where the bandwidth parameters for rebound values and strength are automatically optimized using the Silverman rule.
- 2.
- Density-Weighted MappingDesign an allocation mechanism that assigns higher weights to low-density regions to compensate for their lack of information content, while simultaneously maintaining the influence of high-density regions on the regression trend. The density values are divided into three equal parts. The portion below one-third is considered a low-density region, and the weights of the low-density region are multiplied by , while the weights of other regions remain unchanged.
- 3.
- Weighted Nonlinear RegressionThe updated objective function is as follows:The issue of fitting variation caused by local density differences can be addressed by assigning weights to each scattered point and applying these weights to the objective function.
3.3.3. Local Optimization Strategy Based on Gradient Descent
- 1.
- Dynamic Role Allocation MechanismTo balance the exploration and exploitation capabilities of the algorithm, an adaptive role-switching controller is designed based on the state feedback of the optimization process. This controller dynamically adjusts the dominance weight between GD and ABC by real-time analyzing the population diversity (measured by the fitness standard deviation) and the iteration progress (time decay factor). Specifically, the dominance factor at the t-th iteration is defined as follows:where:
- : Standard deviation of population fitness;
- : Mean population fitness;
- : Maximum iterations.
If D(t) is more than the threshold, the gradient descent strategy is activated; otherwise, the ABC algorithm is used to search for the global optimal solution normally. - 2.
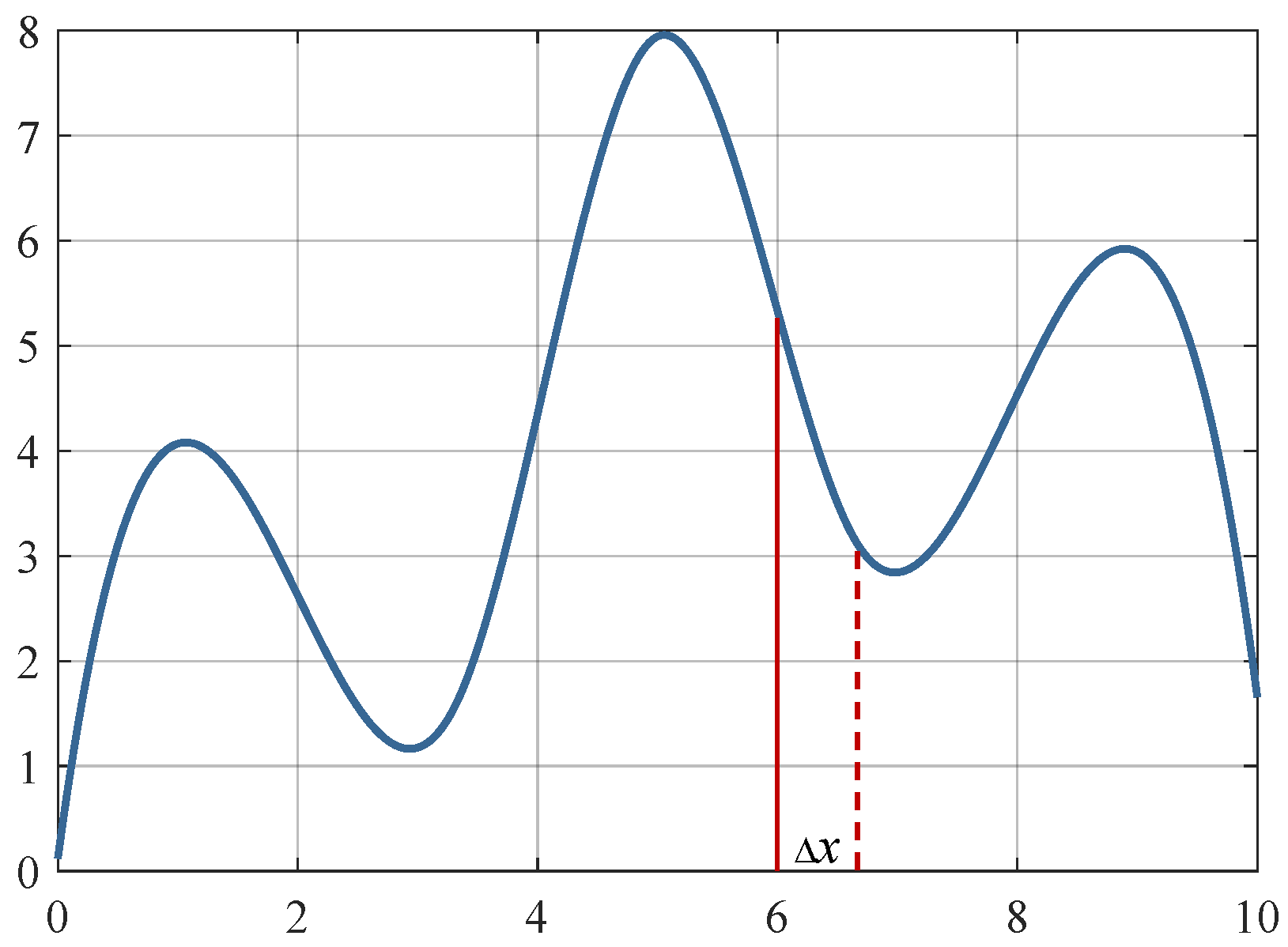
- Gradient-Boosting Neighborhood SearchIn the ABC algorithm, bees are categorized into three types: employed bees, onlooker bees, and scout bees. This paper primarily focuses on incorporating gradient information into the metaheuristic algorithm to conduct local refined searches around the optimal points found by the algorithm, aiming to achieve a more precise local optimum, as shown in Figure 4.Assuming the solution space is D-dimensional, the solution corresponding to the i-th employed bee can be represented as a vector: .The process by which employed bees search for a new solution in the vicinity of their current solution can be expressed with the following formula:The process by which employed bees search for a new solution in the vicinity of their current solution can be expressed with the Equation (2).In the employed bee phase, the traditional random neighborhood search is not effective in finding the optimal direction during the convergence phase. Therefore, gradient information is incorporated to guide the mutation direction, as shown in Equation (11):where is the adaptive fusion coefficient. When the gradient magnitude is large, the direction tends to favor the gradient descent direction; otherwise, it enhances the random exploration of ABC. represents the gradient information, which uses the sub-gradient approximation, as shown in Equation (12):The adaptive fusion coefficient in the employed bee phase is adjusted based on the gradient magnitude, which allows for greater reliance on the GD direction in regions with larger gradients (steep areas), and increased random exploration in regions with smaller gradients (flat areas). Unlike the employed bees, its adaptive fusion coefficient linearly increases the gradient weight over time to ensure local exploitation in the later stages of the algorithm. Its calculation method is shown as Equation (13).
3.4. Algorithm Pseudocode
| Algorithm 1 Point Density-weighted Allocation |
| Require: data—dataset whose second column contains the input feature Ensure: weights—normalized density-based weight vector
|
| Algorithm 2 Gradient Descent |
| Require: solution—current solution vector Require: problem—problem instance containing lower and upper bounds Require: step—finite-difference step size Ensure: gradient—estimated gradient vector
|
4. Experimental Results
4.1. Data Description
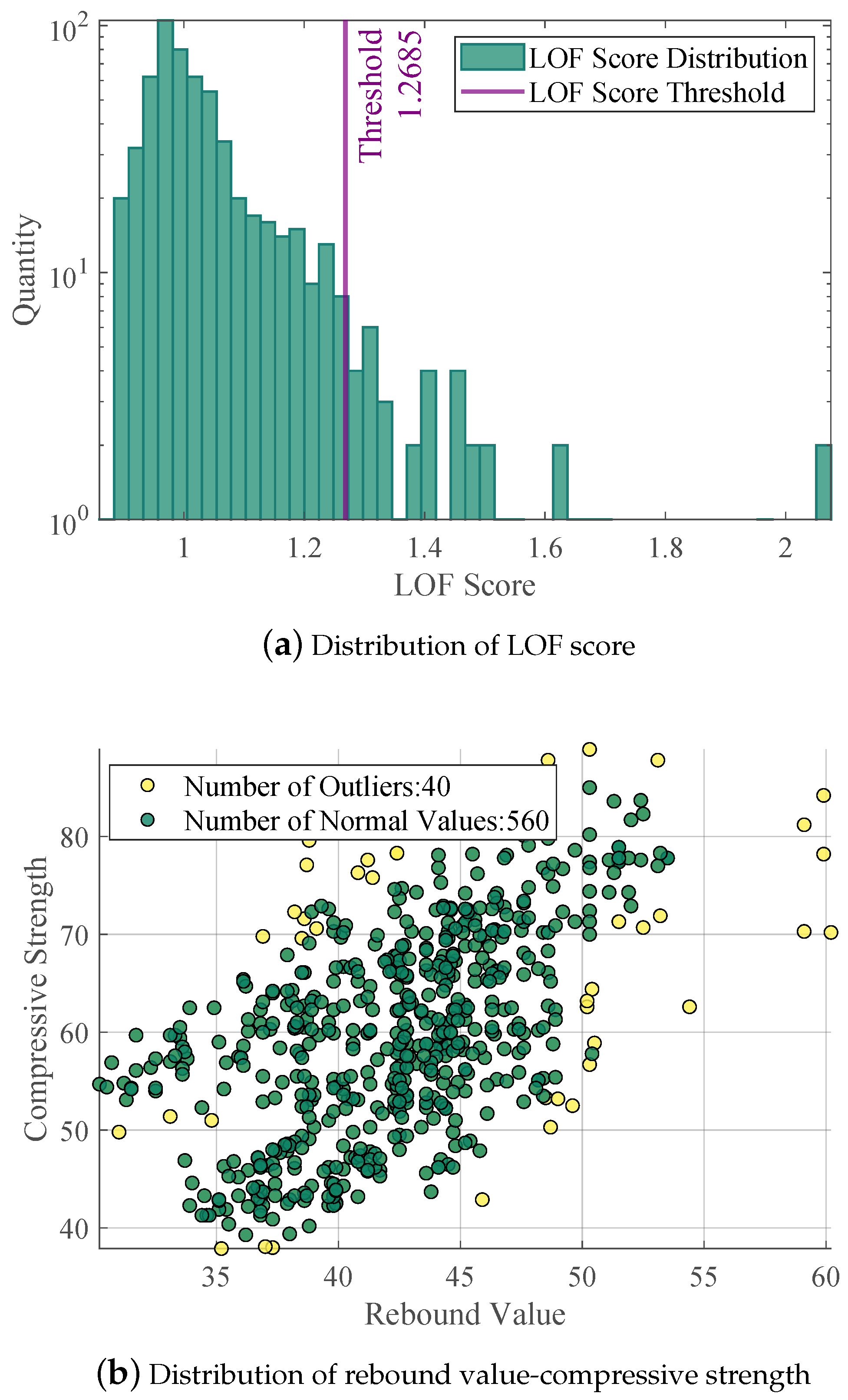
4.2. Results of Data Pre-Process
4.3. Analysis of Experimental Results
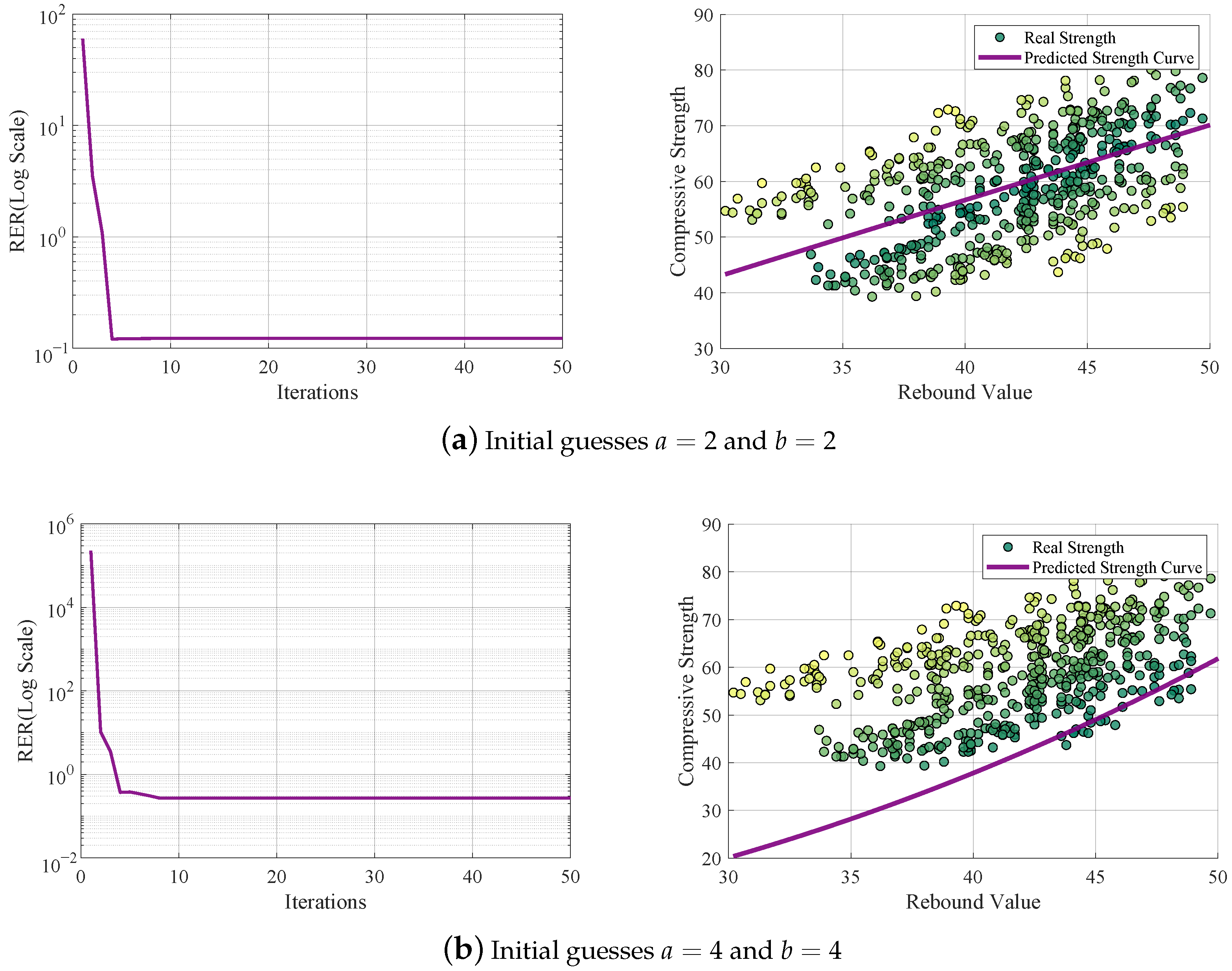
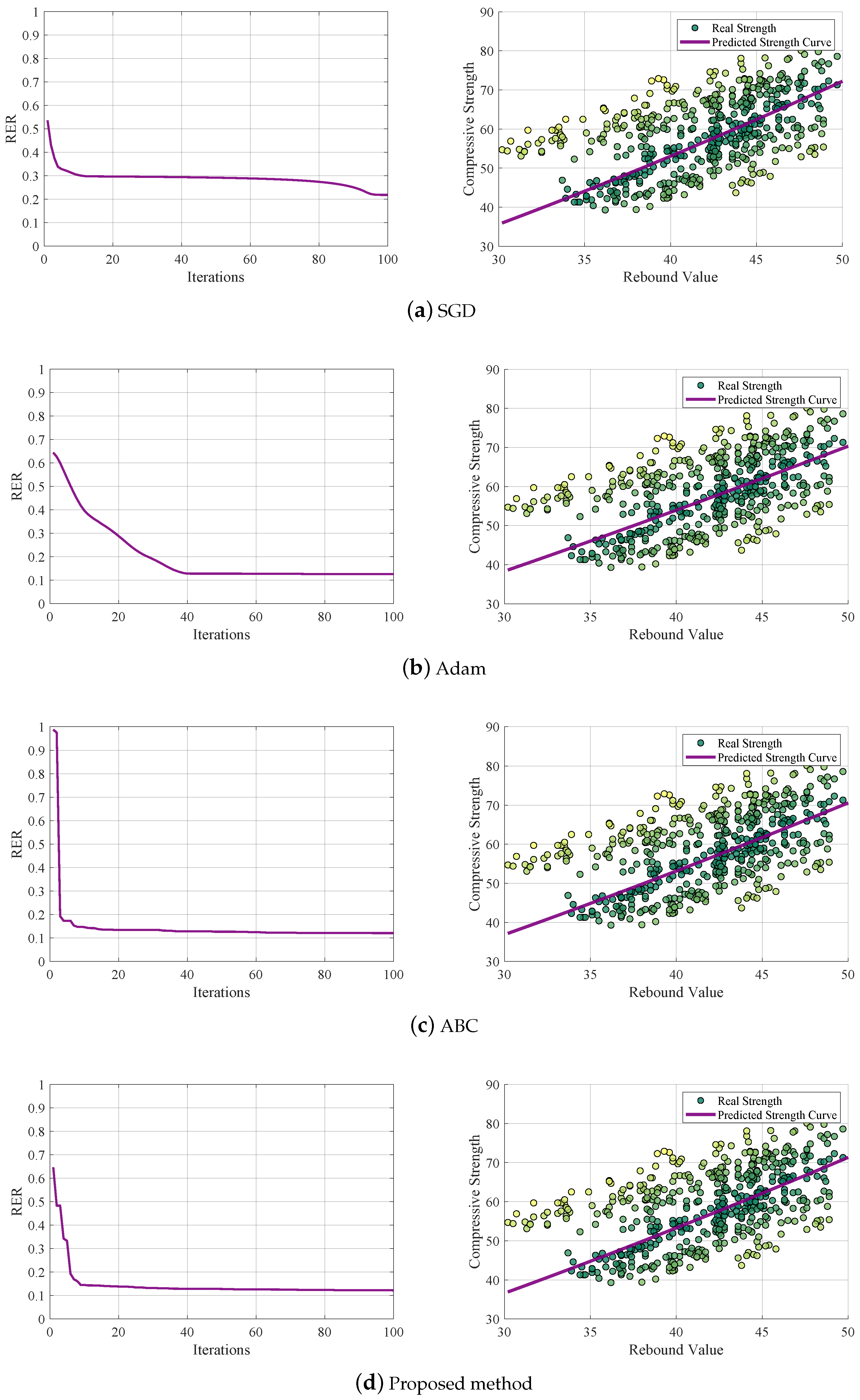
4.3.1. Performance Analysis of Algorithm Results
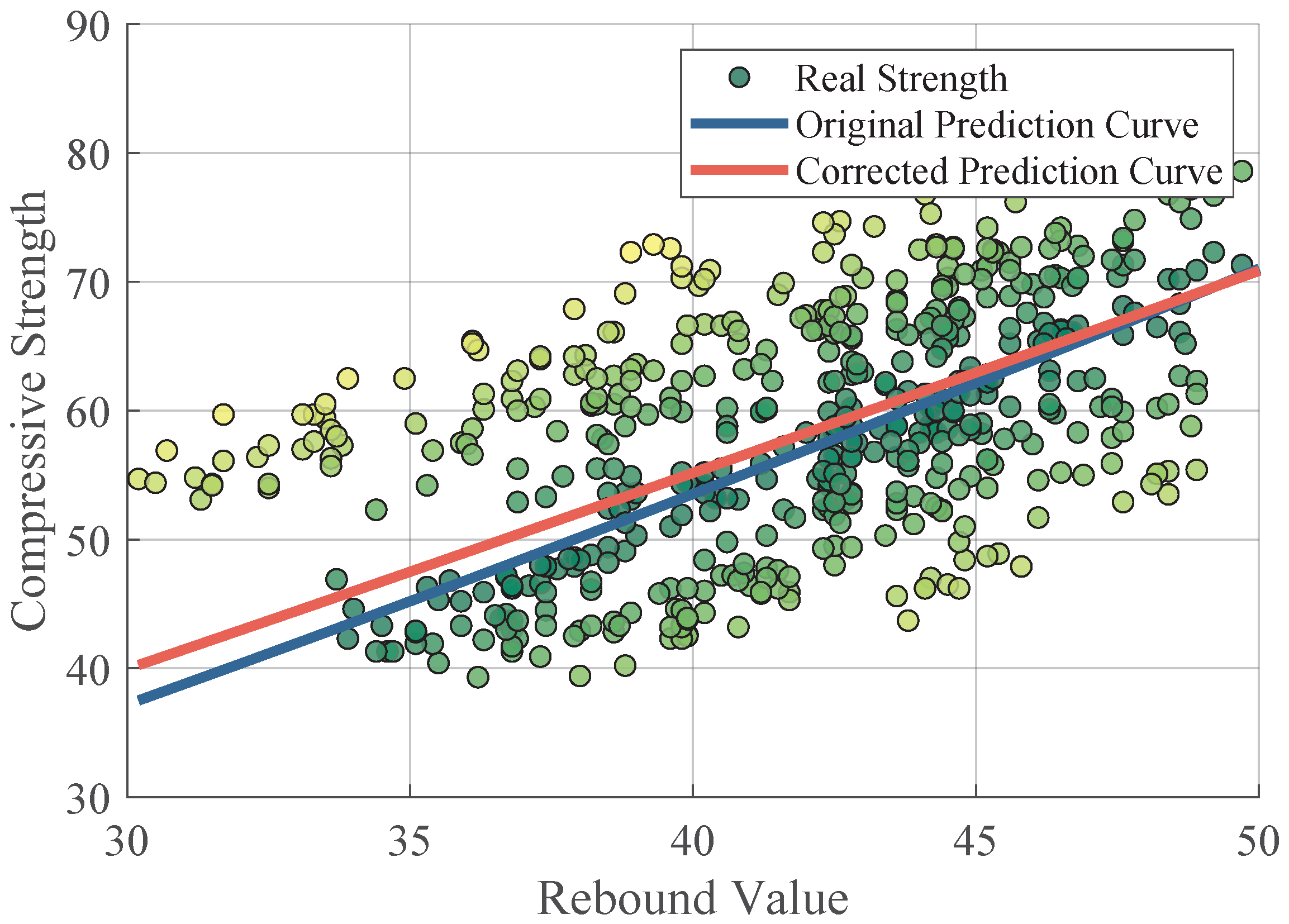
4.3.2. Analysis of Point Density-Weighted Allocation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Neville, A.M.; Brooks, J.J. Concrete Technology; Longman Scientific & Technical: London, UK, 1987; Volume 438. [Google Scholar]
- Khan, K.; Johari, M.A.M.; Amin, M.N.; Khan, M.I.; Iqbal, M. Optimization of colloidal nano-silica based cementitious mortar composites using RSM and ANN approaches. Results Eng. 2023, 20, 101390. [Google Scholar] [CrossRef]
- Khan, M. Robust segmentation of concrete road surfaces via fuzzy entropy modelling and multiscale laplacian texture analysis. Mechatron. Intell. Transp. Syst. 2025, 4, 72–80. [Google Scholar] [CrossRef]
- Hussain, I. An adaptive multi-stage fuzzy logic framework for accurate detection and structural analysis of road cracks. Mechatron. Intell. Transp. Syst. 2024, 3, 190–202. [Google Scholar] [CrossRef]
- Elmansouri, O.; Alossta, A.; Badi, I. Pavement condition assessment using pavement condition index and multi-criteria decision-making model. Mechatron. Intell. Transp. Syst. 2022, 1, 57–68. [Google Scholar] [CrossRef]
- Khan, M.I.; Khan, N.; Hashmi, S.R.Z.; Yazid, M.R.M.; Yusoff, N.I.M.; Azfar, R.W.; Ali, M.; Fediuk, R. Prediction of compressive strength of cementitious grouts for semi-flexible pavement application using machine learning approach. Case Stud. Constr. Mater. 2023, 19, e02370. [Google Scholar] [CrossRef]
- El Mir, A.; Nehme, S.G. Repeatability of the rebound surface hardness of concrete with alteration of concrete parameters. Constr. Build. Mater. 2017, 131, 317–326. [Google Scholar] [CrossRef]
- Helal, J.; Sofi, M.; Mendis, P. Non-destructive testing of concrete: A review of methods. Electron. J. Struct. Eng. 2015, 14, 97–105. [Google Scholar] [CrossRef]
- Lantsoght, E.O.; van der Veen, C.; de Boer, A.; Hordijk, D.A. State-of-the-art on load testing of concrete bridges. Eng. Struct. 2017, 150, 231–241. [Google Scholar] [CrossRef]
- Malhotra, V.M.; Carino, N.J. Handbook on Nondestructive Testing of Concrete; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Bungey, J.H.; Grantham, M.G. Testing of Concrete in Structures; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- Ali-Benyahia, K.; Sbartaï, Z.M.; Breysse, D.; Kenai, S.; Ghrici, M. Analysis of the single and combined non-destructive test approaches for on-site concrete strength assessment: General statements based on a real case-study. Case Stud. Constr. Mater. 2017, 6, 109–119. [Google Scholar] [CrossRef]
- Xu, T.; Li, J. Assessing the spatial variability of the concrete by the rebound hammer test and compression test of drilled cores. Constr. Build. Mater. 2018, 188, 820–832. [Google Scholar] [CrossRef]
- Verma, S.K.; Bhadauria, S.S.; Akhtar, S. Review of nondestructive testing methods for condition monitoring of concrete structures. J. Constr. Eng. 2013, 2013, 834572. [Google Scholar] [CrossRef]
- Maierhofer, C.; Reinhardt, H.W.; Dobmann, G. Non-Destructive Evaluation of Reinforced Concrete Structures: Non-Destructive Testing Methods; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Li, H.; He, Y.; Wang, L.; Li, Z.; Deng, Z.; Zhang, W. Enhancing lateral dynamic performance of HTS Maglev vehicles using electromagnetic shunt dampers: Optimisation and experimental validation. Veh. Syst. Dyn. 2025, 1–20. [Google Scholar] [CrossRef]
- Khan, K.; Jalal, F.E.; Iqbal, M.; Khan, M.I.; Amin, M.N.; Al-Faiad, M.A. Predictive modeling of compression strength of waste pet/scm blended cementitious grout using gene expression programming. Materials 2022, 15, 3077. [Google Scholar] [CrossRef] [PubMed]
- El-Mir, A.; El-Zahab, S.; Sbartaï, Z.M.; Homsi, F.; Saliba, J.; El-Hassan, H. Machine learning prediction of concrete compressive strength using rebound hammer test. J. Build. Eng. 2023, 64, 105538. [Google Scholar] [CrossRef]
- Dong, Y.; Tang, J.; Xu, X.; Li, W.; Feng, X.; Lu, C.; Hu, Z.; Liu, J. A new method to evaluate features importance in machine-learning based prediction of concrete compressive strength. J. Build. Eng. 2025, 102, 111874. [Google Scholar] [CrossRef]
- Chaabene, W.B.; Flah, M.; Nehdi, M.L. Machine learning prediction of mechanical properties of concrete: Critical review. Constr. Build. Mater. 2020, 260, 119889. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Hanandeh, S.; Ulloa, N.; Barba-Vera, R.; Moghal, A.A.B.; Ebid, A.M.; Arunachalam, K.P.; Ur Rehman, A. Developing machine learning frameworks to predict mechanical properties of ultra-high performance concrete mixed with various industrial byproducts. Sci. Rep. 2025, 15, 24791. [Google Scholar] [CrossRef]
- Kocáb, D.; Misák, P.; Cikrle, P. Characteristic curve and its use in determining the compressive strength of concrete by the rebound hammer test. Materials 2019, 12, 2705. [Google Scholar] [CrossRef]
- Amar, M. Comparative use of different AI methods for the prediction of concrete compressive strength. Clean. Mater. 2025, 15, 100299. [Google Scholar] [CrossRef]
- Mohammed, B.S.; Azmi, N.J.; Abdullahi, M. Evaluation of rubbercrete based on ultrasonic pulse velocity and rebound hammer tests. Constr. Build. Mater. 2011, 25, 1388–1397. [Google Scholar] [CrossRef]
- Ziolkowski, P. Influence of Optimization Algorithms and Computational Complexity on Concrete Compressive Strength Prediction Machine Learning Models for Concrete Mix Design. Materials 2025, 18, 1386. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, H.; Guan, T.; Chen, P.; Ren, B.; Guo, Z. Intelligent prediction of compressive strength of concrete based on CNN-BiLSTM-MA. Case Stud. Constr. Mater. 2025, 22, e04486. [Google Scholar] [CrossRef]
- Huang, H.; Lei, L.; Xu, G.; Cao, S.; Ren, X. Machine learning approaches for predicting mechanical properties of steel-fiber-reinforced concrete. Mater. Today Commun. 2025, 45, 112149. [Google Scholar] [CrossRef]
- Kazemi, R.; Golafshani, E.M.; Behnood, A. Compressive strength prediction of sustainable concrete containing waste foundry sand using metaheuristic optimization-based hybrid artificial neural network. Struct. Concr. 2024, 25, 1343–1363. [Google Scholar] [CrossRef]
- Roy, T.; Das, P.; Jagirdar, R.; Shhabat, M.; Abdullah, M.S.; Kashem, A.; Rahman, R. Prediction of mechanical properties of eco-friendly concrete using machine learning algorithms and partial dependence plot analysis. Smart Constr. Sustain. Cities 2025, 3, 2. [Google Scholar] [CrossRef]
- ČSN 73 1373; Non-Destructive Testing of Concrete—Determination of Compressive Strength by Hardness Testing Methods. Czech Technical Standard (ČSN): Prague, Czech Republic, 2011.
- PCTE. SilverSchmidt Reference Curve. 2019. Available online: https://hammondconcrete.co.uk/wp-content/uploads/2020/06/The-SilverSchmidt-Reference-Curve.pdf (accessed on 10 September 2025).
- Tayarani-N, M.H.; Yao, X.; Xu, H. Meta-heuristic algorithms in car engine design: A literature survey. IEEE Trans. Evol. Comput. 2014, 19, 609–629. [Google Scholar] [CrossRef]
- Salgotra, R.; Singh, U.; Singh, G.; Mittal, N.; Gandomi, A.H. A self-adaptive hybridized differential evolution naked mole-rat algorithm for engineering optimization problems. Comput. Methods Appl. Mech. Eng. 2021, 383, 113916. [Google Scholar] [CrossRef]
- Khalid, O.W.; Isa, N.A.M.; Sakim, H.A.M. Emperor penguin optimizer: A comprehensive review based on state-of-the-art meta-heuristic algorithms. Alex. Eng. J. 2023, 63, 487–526. [Google Scholar] [CrossRef]
- Hu, Y.; Dong, J.; Zhang, G.; Wu, Y.; Rong, H.; Zhu, M. Cancer gene selection with adaptive optimization spiking neural p systems and hybrid classifiers. J. Membr. Comput. 2023, 5, 238–251. [Google Scholar] [CrossRef]
- Dong, J.; Zhang, G.; Hu, Y.; Wu, Y.; Rong, H. An optimization numerical spiking neural membrane system with adaptive multi-mutation operators for brain tumor segmentation. Int. J. Neural Syst. 2024, 34, 2450036. [Google Scholar] [CrossRef]
- Luo, W.; Yu, X. Reinforcement learning-based modified cuckoo search algorithm for economic dispatch problems. Knowl.-Based Syst. 2022, 257, 109844. [Google Scholar] [CrossRef]
- Erbas, C.; Cerav-Erbas, S.; Pimentel, A.D. Multiobjective optimization and evolutionary algorithms for the application mapping problem in multiprocessor system-on-chip design. IEEE Trans. Evol. Comput. 2006, 10, 358–374. [Google Scholar] [CrossRef]
- Aslan, S.; Karaboga, D. A genetic Artificial Bee Colony algorithm for signal reconstruction based big data optimization. Appl. Soft Comput. 2020, 88, 106053. [Google Scholar] [CrossRef]
- Dhal, K.G.; Ray, S.; Das, A.; Das, S. A Survey on Nature-Inspired Optimization Algorithms and Their Application in Image Enhancement Domain: KG Dhal et al. Arch. Comput. Methods Eng. 2019, 26, 1607–1638. [Google Scholar] [CrossRef]
- Fong, S.; Deb, S.; Chaudhary, A. A review of metaheuristics in robotics. Comput. Electr. Eng. 2015, 43, 278–291. [Google Scholar] [CrossRef]
- Lu, P.; Ye, L.; Zhao, Y.; Dai, B.; Pei, M.; Tang, Y. Review of meta-heuristic algorithms for wind power prediction: Methodologies, applications and challenges. Appl. Energy 2021, 301, 117446. [Google Scholar] [CrossRef]
- Shaheen, A.M.; Spea, S.R.; Farrag, S.M.; Abido, M.A. A review of meta-heuristic algorithms for reactive power planning problem. Ain Shams Eng. J. 2018, 9, 215–231. [Google Scholar] [CrossRef]
- Karaboga, D. Artificial bee colony algorithm. Scholarpedia 2010, 5, 6915. [Google Scholar] [CrossRef]
- Karaboga, D.; Akay, B. A comparative study of artificial bee colony algorithm. Appl. Math. Comput. 2009, 214, 108–132. [Google Scholar] [CrossRef]
- Gao, W.f.; Liu, S.y. A modified artificial bee colony algorithm. Comput. Oper. Res. 2012, 39, 687–697. [Google Scholar] [CrossRef]
- Bansal, J.C.; Sharma, H.; Jadon, S.S. Artificial bee colony algorithm: A survey. Int. J. Adv. Intell. Paradig. 2013, 5, 123–159. [Google Scholar] [CrossRef]
- Kumar, B.; Kumar, D. A review on Artificial Bee Colony algorithm. Int. J. Eng. Technol. 2013, 2, 175. [Google Scholar] [CrossRef][Green Version]
- Boukerche, A.; Zheng, L.; Alfandi, O. Outlier detection: Methods, models, and classification. ACM Comput. Surv. (CSUR) 2020, 53, 1–37. [Google Scholar] [CrossRef]
- Alghushairy, O.; Alsini, R.; Soule, T.; Ma, X. A review of local outlier factor algorithms for outlier detection in big data streams. Big Data Cogn. Comput. 2020, 5, 1. [Google Scholar] [CrossRef]
- Xu, H.; Zhang, L.; Li, P.; Zhu, F. Outlier detection algorithm based on k-nearest neighbors-local outlier factor. J. Algorithms Comput. Technol. 2022, 16, 17483026221078111. [Google Scholar] [CrossRef]
- Ma, H.; Hu, Y.; Shi, H. Fault detection and identification based on the neighborhood standardized local outlier factor method. Ind. Eng. Chem. Res. 2013, 52, 2389–2402. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Abdel-Fatah, L.; Sangaiah, A.K. Metaheuristic algorithms: A comprehensive review. In Computational Intelligence for Multimedia Big Data on the Cloud with Engineering Applications; Elsevier: Amsterdam, The Netherlands, 2018; pp. 185–231. [Google Scholar]

| Methods | RER | RMSE | MAE | |
|---|---|---|---|---|
| Nonlinear least squares | ||||
| SGD | ||||
| Adam | ||||
| ABC | ||||
| Proposed Method |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Liu, Q.; Tang, Y.; Yang, Y.; Hu, Y.; Wu, Y. Prediction of Concrete Compressive Strength Based on Gradient-Boosting ABC Algorithm and Point Density Correction. Eng 2025, 6, 282. https://doi.org/10.3390/eng6100282
Xie Y, Liu Q, Tang Y, Yang Y, Hu Y, Wu Y. Prediction of Concrete Compressive Strength Based on Gradient-Boosting ABC Algorithm and Point Density Correction. Eng. 2025; 6(10):282. https://doi.org/10.3390/eng6100282
Chicago/Turabian StyleXie, Yaolin, Qiyu Liu, Yuanxiu Tang, Yating Yang, Yangheng Hu, and Yijin Wu. 2025. "Prediction of Concrete Compressive Strength Based on Gradient-Boosting ABC Algorithm and Point Density Correction" Eng 6, no. 10: 282. https://doi.org/10.3390/eng6100282
APA StyleXie, Y., Liu, Q., Tang, Y., Yang, Y., Hu, Y., & Wu, Y. (2025). Prediction of Concrete Compressive Strength Based on Gradient-Boosting ABC Algorithm and Point Density Correction. Eng, 6(10), 282. https://doi.org/10.3390/eng6100282






