Micro-Texture Characteristics and Mechanical Properties of Cement Paste with Various Grinding Aids and Polycarboxylate-Based Superplasticizer

Abstract

Cement-based materials are essential construction components, yet their complex microstructures critically govern mechanical performance and durability. This study investigates the micro-textural characteristics and mechanical properties of cement paste modified with grinding aids (triethanolamine, TEA; maleic acid triethanolamine ester, MGA) and polycarboxylate-based superplasticizer (PCA). Moving beyond qualitative SEM limitations, we employ advanced image-based quantitative techniques: grayscale-based texture analysis for statistical evaluation and fractal dimension analysis for geometric quantification of microstructural irregularity. Results demonstrate that grinding aids enhance particle dispersion and reduce agglomeration, resulting in a more uniform micro-texture characterized by lower grayscale variability and reduced fractal dimensions. PCA superplasticizers further significantly enhance fluidity and compressive strength. The optimal formulation (MGA + PCA) achieved a 20% increase in 28-day compressive strength compared to control samples. The fractal dimension D_B exhibits a positive correlation with compressive strength, while energy and correlation values show a negative correlation; in contrast, entropy and contrast values demonstrate a positive correlation. This research advances quantitative microstructure characterization in cementitious materials, offering insights for tailored additive formulations to enhance sustainability and efficiency in concrete production.

1. Introduction

Cement-based materials form the backbone of modern infrastructure, underpinning the construction of buildings, bridges, roads, and dams worldwide. Annually, global cement production exceeds 4 billion tons, underscoring its critical role in urbanization and economic development [1]. Beyond their structural utility, concrete—the most prevalent cement-based composite—contributes significantly to sustainable construction through its durability, thermal mass benefits, and capacity to incorporate industrial by-products [2,3]. However, the environmental impact of cement production remains a pressing concern. The process is highly energy-intensive and contributes approximately 8% of global CO₂ emissions [1]. This emission stems not only from the calcination of limestone but also from the combustion of fossil fuels used to heat kilns during clinker production and the significant electrical energy consumed during clinker grinding.

In response to the environmental challenges posed by conventional cement production, there has been growing interest in developing more sustainable alternatives to traditional concrete. Among these, polymer concretes have emerged as a promising option due to their reduced carbon footprint, enhanced durability, and potential for incorporating recycled materials [4]. Polymer concretes utilize polymeric resins as binders instead of cement, significantly lowering the energy consumption and CO₂ emissions associated with clinker production [5]. Despite these advantages, widespread adoption of polymer concretes remains limited due to factors such as higher cost, variability in raw material availability, and specific performance requirements in structural applications. Therefore, while research continues to optimize polymer-based systems, improving the sustainability of conventional cement-based materials through efficient grinding aids and superplasticizers remains a critical avenue for reducing environmental impact.

The production of Portland cement adheres to the “two grinding and one burning” process. While the burning phase is responsible for the majority of direct CO₂ emissions, the grinding stage is notably energy-intensive, accounting for up to 60% of the total electrical energy used in cement manufacturing [6]. Much of this energy is dissipated as heat, sound, and vibration, underscoring the inefficiency of conventional grinding processes. Therefore, improving grinding efficiency presents a tangible opportunity to reduce both energy consumption and the associated carbon footprint of cement production.

Enhancing the mechanical design of grinding equipment and incorporating grinding aids during this stage are proven strategies to lower energy use and boost grinding efficiency [7,8]. Grinding aids (GAs) are chemical additives introduced during the milling process. These compounds, featuring highly polar functional groups such as -OH, -NH₂, -COOR, and -SO₃, adsorb onto cement particles, neutralizing surface charges and mitigating agglomeration and coating on mill surfaces and grinding media [9,10]. Extensive research has shown that triethanolamine (TEA) compounds, widely adopted in the cement industry, can improve clinker grinding efficiency by up to 15% [11,12,13]. Nevertheless, despite enhanced grindability, cement systems incorporating TEA often exhibit performance shortcomings in both fresh and hardened states. Mandal and Singh [11,14] reported that TEA dosages between 0.02% and 0.10% markedly accelerate setting, whereas higher dosages (≥0.10%) induce retardation or even flash setting. Ramachandran [15,16] further demonstrated that TEA accelerates C₃A hydration while extending the induction period of C₃S. Moreover, numerous studies indicate that TEA promotes the dissolution and hydration of C₃A and C₄AF while suppressing C₃S hydration [17,18]. Additionally, TEA tends to migrate toward the surface of calcium hydroxide (CH), precipitating with CH in solution, which disrupts CH nucleation and growth, ultimately compromising the later-age strength of cement [19,20].

To address these limitations, researchers have pursued molecular modifications of TEA. Zhao et al. [21] revealed that modified TEA molecules, incorporating hydroxyl, amino, ester, and carboxyl groups, not only facilitate the dissolution of calcium, aluminum, and iron ions but also regulate the structure and morphology of hydration products, thereby enhancing paste densification and mechanical properties. Ji et al. [7] employed maleic acid (MA) to modify triethanolamine, yielding maleic acid triethanolamine ester grinding aids (MGA). These modified aids increase the number of polar groups, improving adsorption and dispersion on cement particles, enhancing grinding efficiency, and mitigating the later-age strength reduction associated with TEA. Consequently, MGA emerges as a next-generation functional grinding aid with the potential to comprehensively elevate cement performance.

Beyond grinding aids, superplasticizers play an indispensable role in the formulation of modern cement-based materials [22,23]. In engineering applications demanding high fluidity, strength, and density, superplasticizers have become essential chemical admixtures for optimizing cement paste performance and controlling the water-to-cement ratio [24]. Superplasticizers, also known as high-range water reducers, are essential admixtures in modern concrete technology, enabling significant reductions in water content while maintaining workability. Common types include lignosulfonates (LS), sulfonated naphthalene-formaldehyde condensates (SNF), melamine-formaldehyde sulfonates (SMF), and polycarboxylate-based ethers (PCE) [25]. Lignosulfonates, derived from wood pulp processing, are cost-effective but offer limited water reduction and may retard setting. SNF and SMF provide better dispersion through electrostatic repulsion but are sensitive to sulfate ions and exhibit poor slump retention. More recently, copolymers incorporating phosphate or carboxylate groups have been developed to enhance calcium binding and improve compatibility with cement phases [26]. Among these, polycarboxylate-based superplasticizers (PCA) represent the latest generation of high-efficiency dispersants. Their comb-like molecular structure, featuring a backbone with adsorbing groups (e.g., carboxylate) and side chains providing steric hindrance, allows for superior water reduction, prolonged workability, and better adaptability to various cement chemistries [27]. Moreover, PCA’s tunable molecular architecture offers enhanced compatibility with grinding aids and other admixtures, making it particularly suitable for advanced cementitious systems aimed at sustainability and high performance.

The efficacy of PCA depends on factors such as the water-to-cement ratio, C₃A phase content, and the presence of grinding aids in the cement system [28,29]. Research highlights substantial differences in particle dispersion, size distribution, and surface properties between cement ground with and without grinding aids [13]. These differences influence cement hydration kinetics and the adsorption of superplasticizer molecules onto cement particles, thereby affecting cement-superplasticizer compatibility. Sun et al. [30] observed that glycerol-based grinding aid dosages exceeding 0.02% adversely affect PCA-cement compatibility, as excessive grinding aids reduce cement surface energy and adhesion work, significantly diminishing PCA adsorption capacity. While some studies have independently explored the roles of grinding aids or superplasticizers in cement-based systems, systematic and in-depth investigations into their combined effects on cement paste microstructure and macroscopic properties remain scarce. On one hand, grinding aids may alter cement particle size distribution and specific surface area, indirectly influencing superplasticizer adsorption efficiency and dispersion capability. On the other hand, the dispersion action of superplasticizers can affect cement particle agglomeration and hydration reaction rates. These intricate interactions may manifest at the microstructural level as alterations in hydration product morphology, pore structure regulation, and interfacial property reconstruction, subsequently impacting the workability and mechanical properties of cement-based materials at the macroscopic scale [29,31]. Thus, elucidating the cement hydration mechanisms and microstructural texture evolution under the synergistic effects of grinding aids and superplasticizers holds profound theoretical significance and practical engineering value.

Instead, the present study concentrates on cement-based materials, providing a systematic investigation into the influence mechanisms of two grinding aids—TEA and MGA—on the physical properties, hydration processes, microstructural texture characteristics, and macroscopic mechanical performance of cement powder. This exploration encompasses their standalone effects as well as their combined application with PCA. Through techniques such as particle size analysis, fluidity testing, X-ray diffraction (XRD) phase analysis, scanning electron microscopy (SEM) morphology observation, and nitrogen adsorption testing, we comprehensively elucidate the regulatory effects of different grinding aid systems on cement powder structure and hydration product evolution. Furthermore, by employing image texture analysis methods, including fractal dimension and gray level co-occurrence matrix (GLCM), we quantitatively characterize cement microstructural features, delving into the intrinsic relationships between microstructure and macroscopic performance.

2. Materials and Methods

2.1. Raw Material of Cement and Grinding Process

2.1.1. Raw Materials of Cement

The cement raw materials comprised 95% cement clinker (Huai’an Conch Cement Co., Ltd., Huai’an, China) and 5% gypsum. Their chemical and mineral compositions are presented in

Table 1. Main chemical composition of cement raw materials (%).

Materials	CaO	SiO2	Fe2O3	Al2O3	MgO	SO3	LOI	Others
Content	65.61	21.92	3.64	5.30	1.60	0.44	0.24	1.25

and

Table 2. Main mineral composition of cement raw materials (%).

Materials	C3S	C2S	C3A	C4AF	f-CaO
Content	53.57	22.79	7.94	11.04	1.10

, respectively.

2.1.2. Grinding Aids

This study focuses on typical alcoholamine grinding aids (TEA) and their ester-modified derivatives (MGA): both are widely used in industrial cement grinding, have typical mechanistic differences, and exhibit representative interactions with polycarboxylic acid (PCA) water reducers in the mixing-hydration stage, facilitating a systematic interpretation of the multi-scale coupling effects of “grinding-dispersion-hydration”.

While TEA improves grinding efficiency, it may compromise later-age cement strength. To overcome this limitation, MGA was synthesized through esterification of maleic anhydride and triethanolamine, enhancing grinding performance and minimizing strength reduction [7].

The MGA was synthesized via an esterification reaction using TEA, maleic anhydride (MA), and acetic acid (HAC) in a molar ratio of 0.9:1:1.5, with p-toluenesulfonic acid (TsOH) as catalyst. The reaction was conducted in a three-neck flask equipped with a condenser and thermometer under magnetic stirring. After dropwise addition of HAC at below 60 °C, MA and TsOH were introduced. The mixture was then heated to and maintained at 125 °C for 4 h. Finally, MGA was obtained as the product after removing excess acetic acid by vacuum distillation.

2.1.3. Grinding Process

The grinding process adhered to GB/T 26748-2011 (Cement grinding aids). Cement clinker was pre-crushed using a jaw crusher, and particles < 7 mm were selected. A mixture of 4.75 kg clinker and 0.25 kg gypsum was ground in a ball mill until achieving a specific surface area of 350 ± 10 m²/kg (Blank). Subsequently, TEA or MGA was added at 0.02% by clinker weight, and grinding was repeated under identical conditions. The initial grind was discarded, and the second grind was sieved through a 90 μm sieve, yielding three cement powders: Blank-C, TEA-C, and MGA-C.

2.2. Physical and Chemical Properties of Ground Cement Powder

2.2.1. Particle Size Distribution

Particle size distributions of the cement powders after 30 min of grinding are depicted in Figure 1 and summarized in

Table 3. Particle size distribution of cement powders (%).

No.	<3 μm	3–32 μm	32–65 μm	65–80 μm	>80 μm	D50/μm
BLANK-C	10.6	59.4	21.7	2.4	5.9	15.25
TEA-C	12.3	59.8	15.9	3.7	6.8	14.86
MGA-C	11.5	65.5	15.9	0.9	6.2	14.69

.

The distribution curves for TEA-C and MGA-C shifted leftward relative to Blank-C, with reduced peak values. Table 3 shows that 70% of Blank-C particles were <32 μm, compared to 72.1% for TEA-C (3% increase) and 77% for MGA-C (10% increase). D50 values were 15.25 μm (Blank-C), 14.86 μm (TEA-C, 2.5% decrease), and 14.69 μm (MGA-C, 3.7% decrease), confirming MGA’s superior grinding efficiency. This is attributed to MGA’s polar functional groups (carboxyl, hydroxyl, amino), which enhance particle adsorption, reduce surface tension, and neutralize electrostatic charges, preventing agglomeration and facilitating crack propagation [7].

2.2.2. Water Demand for Normal Consistency and Setting Time

The water demand for standard consistency and the setting times of the cement pastes were determined in accordance with the Chinese standards GB/T 1346-2024 (Test methods for water requirement of normal consistency, setting time, and soundness of Portland cements) and GB/T 26748-2011 (Cement grinding aids). These parameters are critical for evaluating the workability and early hydration behavior of cement, both of which are influenced by the incorporation of grinding aids.

The results for the water demand for normal consistency are presented in

Table 4. Water demand for normal consistency (%).

No.	Blank-C	TEA-C	MGA-C
Water demand for normal consistency (%)	24.6	25.2	26.4

, while the initial and final setting times are detailed in

Table 5. Initial and final setting times.

No.	Blank-C	TEA-C	MGA-C
Initial setting time (min)	100	95	80
Final setting time (min)	150	143	120

.

As shown in Table 4, the MGA-C exhibited the highest water demand for normal consistency at 26.4%, compared to 25.2% for the TEA-C (a reduction of 4.5% relative to MGA-C) and 24.6% for the Blank-C (a reduction of 6.8%). The water demand for standard consistency is influenced by three primary factors: (1) chemically bound water (typically less than 10%), which is consumed by the formation of hydration products during the induction period; (2) water required to wet the surfaces of the newly formed hydration products and fill the voids between them; and (3) the largest portion, physical water, which fills the voids between the original cement particles and forms a lubricating film on their surfaces to facilitate particle movement. These factors are largely governed by the specific surface area and particle size distribution of the cement. A more concentrated particle size distribution (i.e., a higher uniformity coefficient) results in a lower packing density and larger void volume, necessitating more water to achieve the required fluidity. Consequently, the superior grinding efficiency of MGA, which produces a more concentrated particle size distribution, leads to an increased water demand for standard consistency.

Regarding setting times, both the initial and final setting times were reduced in the presence of TEA-C and MGA-C. Compared to the Blank-C group’s initial setting time of 100 min and final setting time of 150 min, the TEA-C showed reductions to 95 min (5%) and 143 min (4.7%), respectively, while the MGA-C exhibited more pronounced reductions to 80 min (20%) and 120 min (20%). TEA is known not only as a grinding aid but also as a set accelerator at low dosages. It promotes the dissolution of cement minerals, accelerates the formation of ettringite (AFt) and calcium silicate hydrate (C-S-H) gel, and facilitates the conversion of hexagonal aluminate hydrates to their cubic forms [32,33]. In the case of MGA, its ability to significantly reduce particle size and increase the specific surface area enhances the contact between cement particles and water, thereby accelerating hydration. Furthermore, the esterification of TEA with maleic anhydride introduces carboxyl (-COOH) and ester (-COOR) groups into MGA, which increases its polarity and reduces steric hindrance. This facilitates complexation with Al³⁺ in C₃A, promoting the early precipitation of AFt and calcium hydroxide (CH) [34]. Consequently, MGA leads to a more substantial reduction in both initial and final setting times compared to TEA.

2.3. Superplasticizers and Water

A polycarboxylate-based superplasticizer (PCA, 50% solid content, 36% water reduction rate, Jiangsu Sobute New Materials Co., Ltd., Nanjing, China) was used, with laboratory tap water for mixing.

As for the superplasticizer, PCA rather than naphthalene-based (NSF) superplasticizer was selected because PCA offers superior dispersing performance through steric hindrance and is more compatible with grinding aids. NSF, though commonly used, tends to exhibit poorer fluidity retention and higher sensitivity to ionic environments, which could confound the study’s focus on microstructure-property relationships. Moreover, PCA aligns better with contemporary demands for high-performance and sustainable cementitious materials due to its enhanced water reduction capability and lower environmental impact.

2.4. Samples Preparation and Microstructure Characterization

2.4.1. Mix Proportion Design

Both cement paste and mortar samples were prepared. The paste samples were primarily used for microstructural characterization, while the mortar samples were employed for macroscopic mechanical property testing. The mix proportions for the paste and mortar samples are detailed in

Table 6. The mix proportion of cement pastes.

No.	Types of Grinding Aids	Content of PCA (% wt)	W/C
Blank	-	-	0.29
TEA	TEA	-
MGA	MGA	-
Blank-PCA	-	0.15
TEA-PCA	TEA
MGA-PCA	MGA

and

Table 7. The mix proportion of cement mortars (g).

No.	Blank-C	TEA-C	MGA-C	PCA	Standard Sand	Water
Blank	450	0	0	0	1350	225
TEA	0	450	0	0
MGA	0	0	450	0
Blank-PCA	450	0	0	6.75
TEA-PCA	0	450	0	6.75
MGA-PCA	0	0	450	6.75

, respectively.

According to GB/T 26748-2011 (Cement Grinding Aids), the water-to-cement ratio for cement paste fluidity tests should be 0.29 ± 0.01. Additionally, several national standards (e.g., GB/T 1346-2024, GB/T 17671-2021, GB 8076-2008) recommend a water-to-cement ratio close to 0.29 for evaluating cement paste performance and admixture compatibility. Therefore, a water-to-cement ratio of 0.29 was selected for the paste experiments to ensure consistency with standard practices and to effectively assess the combined effects of grinding aids and superplasticizers. The PCA superplasticizer was added at 0.15% by weight of the cementitious materials.

For the mortar samples, the mix design followed GB/T 17671-2021 (Method of Testing Cements—Determination of Strength), with a W/C of 0.5 and PCA added at 0.15% by weight of the cement. China ISO standard sand (manufactured and packed by Xiamen ISO Standard Sand Co., Ltd., Xiamen, China) was used.

2.4.2. Fluidity Test Method of Flowability

The fluidity of the cement pastes was measured using the truncated cone method (spread diameter method) in accordance with GB/T 8077-2023 (Methods for testing uniformity of concrete admixtures). A smooth-walled metal truncated cone (upper diameter 36 ± 0.5 mm, lower diameter 60 ± 0.5 mm, height 60 ± 0.5 mm) and a horizontally placed 400 mm × 400 mm glass plate were used. Prior to testing, the glass plate, cone, and mixing tools were wiped with a damp cloth to ensure a moist surface without standing water. The ambient temperature was maintained at 20 ± 2 °C, with humidity ≥ 50%. The materials were weighed according to the mix proportions in Table 5 and mixed using a cement paste mixer: first at low speed (140 ± 5 r/min) for 30 s, followed by high speed (285 ± 10 r/min) for 3 min to achieve a homogeneous paste. The paste was then quickly poured into the cone, leveled, and the cone was lifted vertically while starting a stopwatch. After 30 s, the maximum spread diameters in two perpendicular directions were measured. The test was repeated at least three times, and the average value was taken as the final fluidity result.

2.4.3. XRD

Cement paste samples were cured under standard conditions until 7 and 28 days of age. They were then broken into fragments ≤ 5 mm, immediately immersed in anhydrous ethanol to halt hydration, vacuum-dried at 40 °C for 48 h, and ground to pass through a 75 μm sieve to eliminate particle agglomeration.

X-ray diffraction (XRD) patterns were obtained using a copper target X-ray diffractometer (Cu-Kα radiation, λ = 1.5406 Å), with a scanning range of 5° to 90° (2θ), a step size of 0.02°, and a scanning speed of 2°/min.

2.4.4. SEM

Cement samples were prepared with no superplasticizer, 0.15% PCA, or 0.5% SAF (sodium acetate formaldehyde), at a water-to-cement ratio of 0.29. After curing for 7 and 28 days, the samples were retrieved, hydration was terminated with ethanol, and they were dried and fractured for SEM analysis. SEM provides insights into the morphology and crystal structure of hydration products, allowing for a comparative assessment of the effects of different grinding aids and superplasticizers on cement hydration and microstructure. This analysis helps relate hydration products to cement strength development.

2.4.5. BET Specific Surface Area Testing

After 7 and 28 days of hydration, samples were fractured, immersed in anhydrous ethanol to stop hydration, vacuum-dried at 60 °C for 48 h, and ground to pass through a 180–250 μm sieve to preserve the pore structure. The samples were then degassed at 150 °C under a vacuum of 10⁻³ Pa for 6 h to remove surface adsorbates. Nitrogen adsorption was measured at liquid nitrogen temperature (−196 °C) using the static volumetric method, with 3–5 sets of nitrogen partial pressures (P/P₀) in the range of 0.05 to 0.35. The monolayer adsorption capacity V_m was calculated using the BET equation:

$${\displaystyle \frac{P}{V\left(P_0-P\right)}}={\displaystyle \frac{1}{V_m\times C}}+{\displaystyle \frac{C-1}{V_m\times C}}\times {\displaystyle \frac{P}{P_0}}$$

(1)

where P is the nitrogen partial pressure, P₀ is the saturation vapor pressure of nitrogen at the adsorption temperature, V is the actual adsorption volume, V_m is the monolayer saturation adsorption volume, and C is a constant related to the sample’s adsorption capacity.

By plotting P/[V(P₀ − P)] against P/P₀, the slope and intercept were determined to calculate V_m and C.

$$V_m={\displaystyle \frac{1}{\mathrm{s}\mathrm{l}\mathrm{o}\mathrm{p}\mathrm{e}+\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{e}\mathrm{p}\mathrm{t}}}$$

(2)

The BET specific surface area was then computed as

$$S_{\mathrm{B}\mathrm{E}\mathrm{T}}={\displaystyle \frac{V_m\times N_A\times {\sigma }_{N_2}}{M\times {10}^{-18}}}$$

(3)

where N_A is Avogadro’s number (6.022 × 10²³ mol⁻¹), σ_N2 is the cross-sectional area of a nitrogen molecule (0.162 nm² at 77 K), and M is the molar volume of nitrogen (22,400 mL/mol).

2.4.6. Mortar Compressive and Flexural Strength

Mortar specimens were prepared according to GB/T 17671-2021, with a water-to-cement ratio of 0.5 and a cement-to-sand ratio of 1:3. Prismatic specimens (40 mm × 40 mm × 160 mm) were cast and cured under standard conditions (20 ± 1 °C, RH ≥ 95%) until testing at 7 and 28 days. For flexural strength, the specimens were subjected to three-point bending with a span of 100 ± 0.5 mm and a loading rate of 50 ± 10 N/s. The flexural strength R_f was calculated as

$$R_f={\displaystyle \frac{1.5F_{f}L}{b^3}}$$

(4)

where F_f is the failure load (N), L = 100 mm, and b = 40 mm. Six specimens per group were tested, and outliers were removed before averaging.

For compressive strength, the six broken halves from the flexural test were tested immediately. The compressive strength R_c was calculated as

$$R_c={\displaystyle \frac{F_c}{A}}$$

(5)

where F_c is the failure load (N), and A = 1600 mm². The average of four values (after removing the maximum and minimum) was taken, with outliers addressed as necessary.

2.5. Texture Features Analysis of SEM Images

2.5.1. Fractal Dimension

Fractal theory provides a method to characterize irregular, self-similar, and scale-invariant objects or phenomena. The fractal dimension quantifies the complexity and roughness of fractal structures [35,36]. While SEM images qualitatively depict the spatial distribution of concrete microstructures, fractal analysis enables quantitative description. The differential box-counting method (D_B) was employed due to its precision and applicability for measuring image surface texture roughness.

For a grayscale SEM image, considered as a three-dimensional surface (x, y, z), where z represents pixel intensity, the differential box-counting dimension D_B was calculated. The image was divided into grids of size L, with r = L/M, where M is the image size. The number of boxes N_r needed to cover the image was determined, and D_B was obtained from the slope of the linear regression of log N_r versus log (1/r).

2.5.2. Gray Level Co-Occurrence Matrix (GLCM)

The Gray Level Co-occurrence Matrix (GLCM), introduced by Haralick [37], captures the probability of pixel pairs with specific grayscale values occurring at a given distance and direction. This matrix reflects the texture features of the image, which in turn represent the distribution and composition of cement hydration products [38].

Within an M × N image, the element P of the GLCM corresponds to the relative frequency of occurrence of gray level pairs i and j, which are spatially separated. The pixel with gray level i is located at coordinates (x, y), and the pixel with gray level j is at coordinates (x + dx, y + dy). The formula is as follows:

$$P\left(i,j,d,\theta \right)=\#\left\{\left[\left(x_i,y_i\right),\left(x_j,y_j\right)\right]|f\left(x_i,y_i\right)=i,f\left(x_j,y_j\right)=j,d,\theta \right\}$$

(6)

where # represents the elements number of the set, d is the distance, and θ denotes the angle, selected as one of 0°, 45°, 90°, and 135°, thereby deriving GLCMs in multiple directions within a 2D SEM image.

This study selects four representative parameters—energy, entropy, correlation, and contrast—to characterize the texture features of SEM images of cementitious materials.

Energy (ENG) reflects the texture uniformity and grayscale distribution uniformity within the SEM image. Higher energy values suggest a more homogeneously distributed and regularly structured hydration product.

$$\mathrm{E}\mathrm{N}\mathrm{G}={\sum }_{i=0}^{L-1}{\sum }_{j=0}^{L-1}{\left\{P\left(i,j\right)\right\}}^2$$

(7)

where L represents the number of gray levels, and P(i, j) denotes elements of the matrix.

Entropy (ENT) is a measure of the information content within the image. Higher entropy values indicate more complex phase textures and spatial structures of hydration products under current hydration conditions.

$$\mathrm{E}\mathrm{N}\mathrm{T}=-{\sum }_{i=0}^{L-1}{\sum }_{j=0}^{L-1}P\left(i,j\right)\times \log P\left(i, j\right)$$

(8)

Correlation (COR) assesses the consistency of image textures. High correlation values signify localized gray level correlation, indicating that similar hydration products are concentrated during the hydration process.

$$\left\{\begin{array}{c}COR=-{\sum }_{i=0}^{L-1}{\sum }_{j=0}^{L-1}{\displaystyle \frac{\left(i\times j\right)P\left(i,j\right)-{\mu }_x\times {\mu }_y}{{\sigma }_x\times {\sigma }_y}}\\ {\mu }_x={\sum }_{i=0}^{L-1}i{\sum }_{j=0}^{L-1}P(i,j)\\ \begin{array}{c}{\mu }_y={\sum }_{i=0}^{L-1}j{\sum }_{j=0}^{L-1}P(i,j)\\ {\sigma }_x^2={\sum }_{i=0}^{L-1}{\left(i-{\mu }_x\right)}^2{\sum }_{j=0}^{L-1}P(i,j)\\ {\sigma }_y^2={\sum }_{i=0}^{L-1}{\left(j-{\mu }_y\right)}^2{\sum }_{j=0}^{L-1}P(i,j)\end{array}\end{array}\right.$$

(9)

Contrast (CON) represents the sharpness and depth of texture in the image. Higher contrast indicates a greater proportion of hydration products to pores in the image.

$$\mathrm{C}\mathrm{O}\mathrm{N}={\sum }_{n=0}^{L-1}{n}^2{\sum }_{i=1}^L{\sum }_{j=1}^{L}P\left(i,j\right),\left|i-j\right|=n$$

(10)

A custom-developed program was used to extract GLCM feature parameters from SEM images. During extraction, the SEM images’ gray levels were in the range of 0–255, with the predefined distance d = 1 and angles θ as 0°, 45°, 90°, and 135°, to generate GLCMs in four different directions. These matrices were normalized, ultimately yielding four direction-specific GLCMs.

$$P(i,j)={\displaystyle \frac{P\left(i,j\right)-P_{\mathrm{m}\mathrm{a}\mathrm{x}}}{P_{\mathrm{m}\mathrm{a}\mathrm{x}}-P_{\mathrm{m}\mathrm{i}\mathrm{n}}}}$$

(11)

From the normalized GLCMs, GLCM feature parameters were extracted. The average values and standard deviations of different feature values from four directions were recorded.

3. Results and Discussion

3.1. Fluidity

Table 8. Fluidity of cement paste with various grinding aids and PCA superplasticizers.

No.	Initial Fluidity (mm)	Fluidity After 1 h (mm)	Loss Rate of Fluidity After 1 h (%)
Blank	102	80	21.5
TEA	92	74	19.5
MGA	96	71	26.0
Blank-PCA	222	210	5.4
TEA-PCA	235	220	6.4
MGA-PCA	240	225	6.2

presents the initial fluidity, the fluidity after 1 h, and the rate of fluidity loss after 1 h for cement pastes containing various grinding aids and PCA superplasticizers. In the absence of PCA superplasticizers, the Blank group exhibited the highest initial fluidity (102 mm) and the lowest rate of fluidity loss (21.5%), indicating that without grinding aids, the paste’s structure is relatively loose, enhancing its flowability. In contrast, the initial fluidities decreased to 92 mm and 96 mm with the addition of TEA and MGA grinding aids, respectively. The MGA group demonstrated the largest reduction in fluidity after 1 h with a loss rate of 26.0%, suggesting that MGA may significantly promote the formation of early hydration products and accelerate structural development, thus causing a quicker loss of fluidity. TEA, with its adsorption properties, moderately delayed the decay of fluidity, thereby exhibiting better plasticity retention.

Analysis of data at 7 and 28 days reveals that the grayscale values of samples undergo nonlinear evolution over time. Some samples reach peak grayscale values early on, but may exhibit declines in later stages due to mechanisms like the rearrangement of hydration products, crystal formation, and morphological reconstruction. Fractal dimension, however, offers a more stable reflection of structural complexity, showing a gradual increase across multiple samples, indicating a transition from initially random filling to a hierarchical and nonlinear network system. The effect of PCA persists during both the early and later stages, significantly improving the uniformity and complexity of the structure by modulating the hydration kinetics. This is especially notable when combined with MGA, as it yields optimal microstructural characterization results.

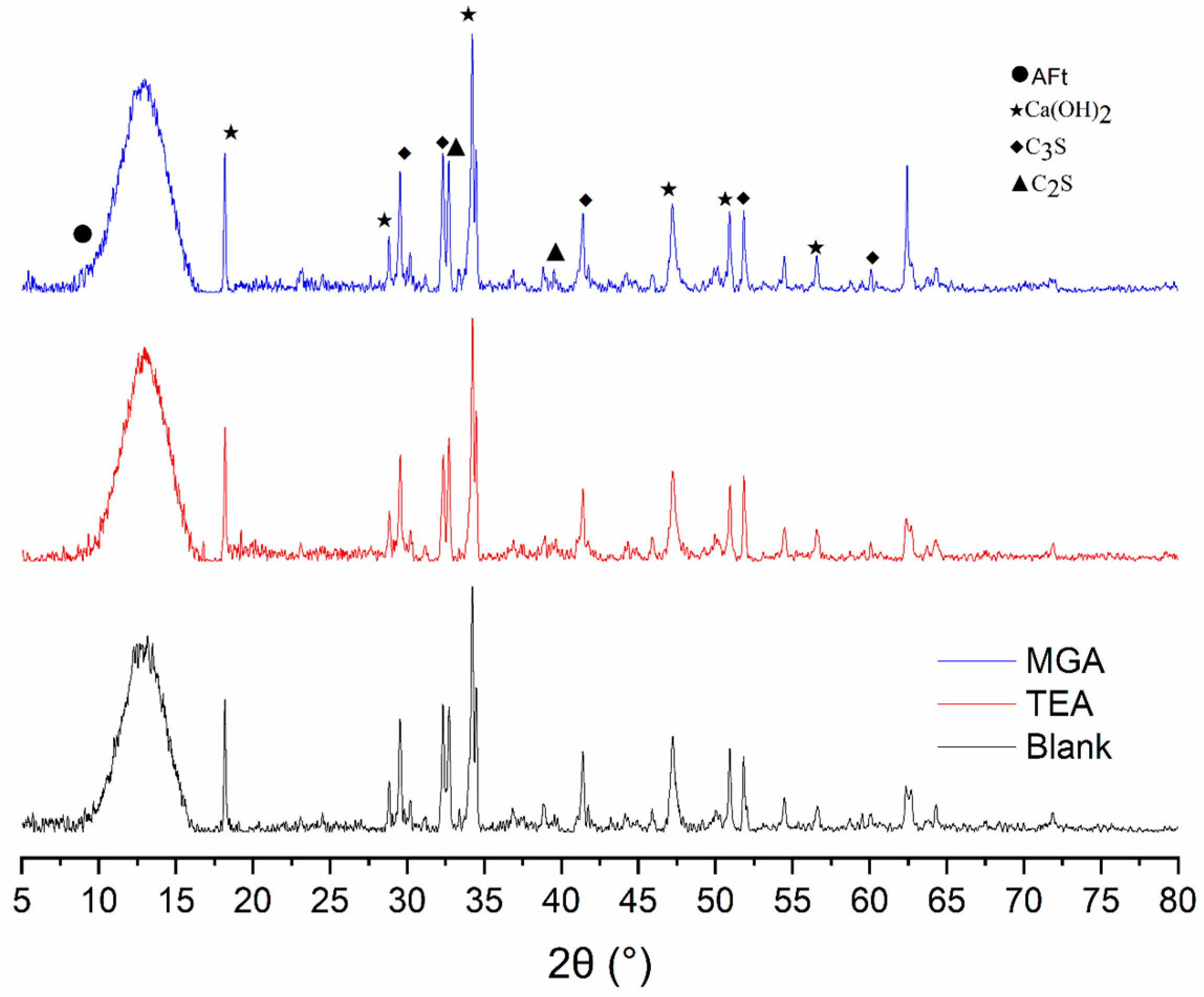
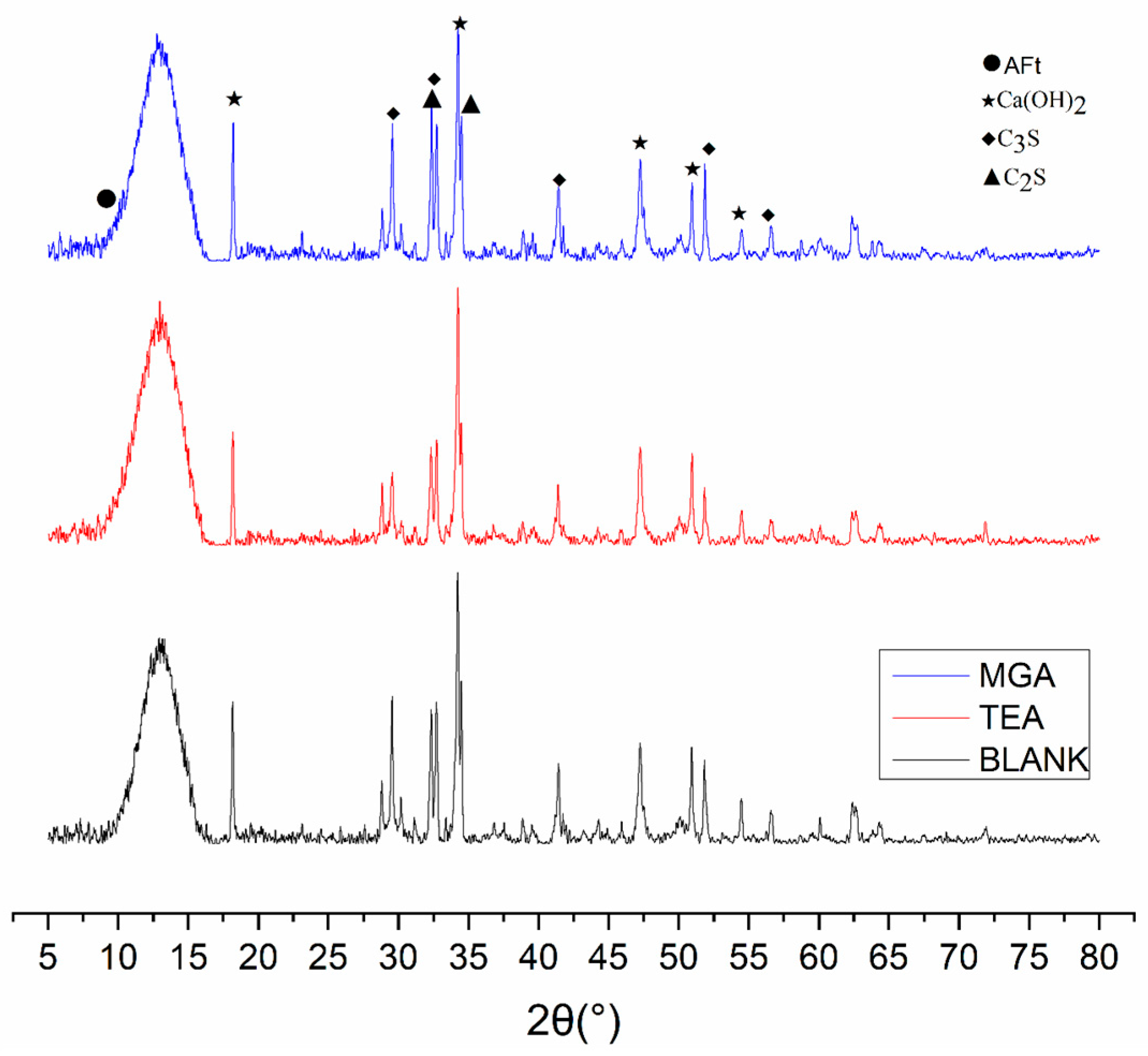
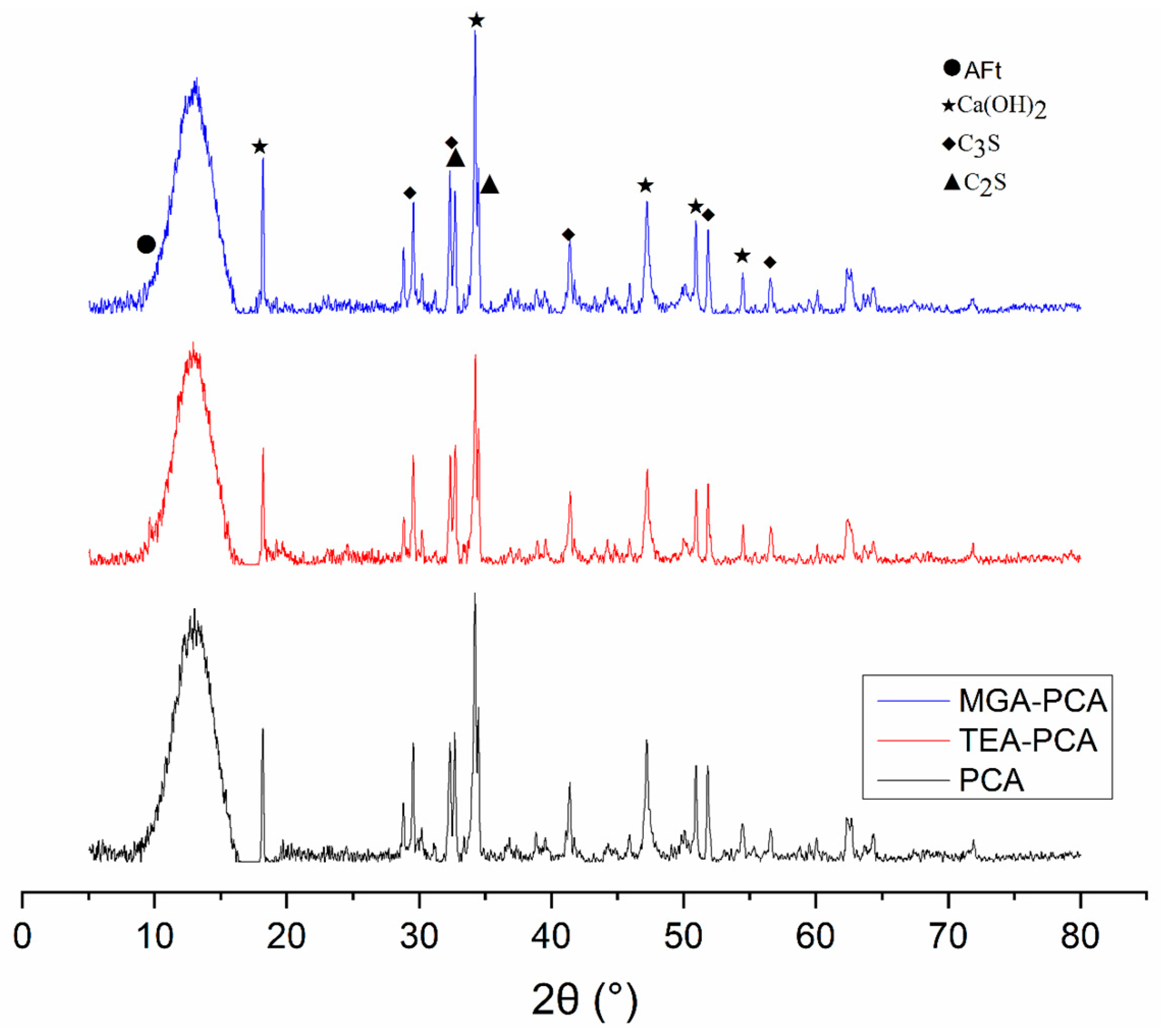
3.2. X-Ray Diffraction (XRD)

X-ray diffraction (XRD) patterns provide valuable insights into the crystalline phases present, allowing an assessment of the composition within hydrated cementitious materials. Typically, peak height correlates with the degree of crystallinity and is indicative of the quantity of crystal components. In standard practice, peaks around 2θ ≈ 18° (001) and 34° (101) are often attributed to calcium hydroxide (CH). C-S-H is an amorphous/low-order phase, usually appearing only as a broad diffuse peak (‘hump’) in the range of 20–38°, and does not show sharp diffraction peaks; the sharp peaks appearing around 28–32° are more likely to come from other crystalline phases (such as residual/generated calcium silicate or quartz).

Figure 2 and Figure 3 illustrate the XRD patterns of cement pastes at a 7-day hydration period, compared across different conditions: without superplasticizers and with 0.15% PCA superplasticizer. Figure 4 and Figure 5 present the same comparison at a 28-day hydration period.

The XRD analysis for the 7-day samples demonstrates that the major hydration products comprise calcium silicate hydrate (C-S-H, amorphous), calcium hydroxide (Ca(OH)₂ at around 18°), calcium aluminate hydrate (AFt, characterized by distinctive peaks roughly at 11–13°), and traces of unhydrated clinker phases, such as C₂S and C₃S. In samples without superplasticizer, the inclusion of MGA in cement paste significantly heightened the intensity of Ca(OH)₂ and AFt peaks compared to the Blank group, suggesting MGA’s effective enhancement of the early hydration process of silicate and aluminate minerals. The greater prominence of C₂S peaks further indicates MGA’s ability to refine cement particle fineness and increase specific surface area, potentially through mechanisms like Ca²⁺ complexation and pH regulation, thereby facilitating C₃S conversion to C-S-H and Ca(OH)₂, while accelerating C₃A’s reaction with gypsum to produce more AFt. This hydration promotion leads to a denser initial structural framework, supporting early mechanical strength developments.

With the addition of 0.15% PCA superplasticizer, the intensity of the Ca(OH)₂ peaks was notably higher at both 7 and 28 days, being especially prominent at 28 days. This suggests that PCA enhances the dispersive properties and sustains hydration reactions over extended periods, potentially leading to a greater volume of hydration products and/or improved crystallinity of the formed phases. It is important to note that an increase in XRD peak intensity can result from either an increase in the quantity of the crystalline phase or an enhancement in its crystallinity and preferred orientation, or a combination thereof [39]. At 28 days, the notable weakening or disappearance of C₃S and C₂S clinker phase peaks indicates more complete hydration. The persistence of AFt peaks in samples with PCA suggests continued hydration of C₃A without inhibition, further contributing to the refinement of structural integrity. The combined effect of MGA and PCA results in the most defined hydration product peaks in XRD analysis, suggesting enhanced crystallinity and/or quantity of hydration products. This observation, coupled with the measured reduction in setting times (Table 5), indicates improved hydration kinetics and microstructural development. While direct zeta potential or calorimetry data were not included in this study, the consistent trends in fluidity, strength, and texture analysis further support the synergistic interaction between MGA and PCA in promoting sustained hydration, thereby contributing to improved long-term mechanical performance and microstructural density.

3.3. BET Surface Area Analysis

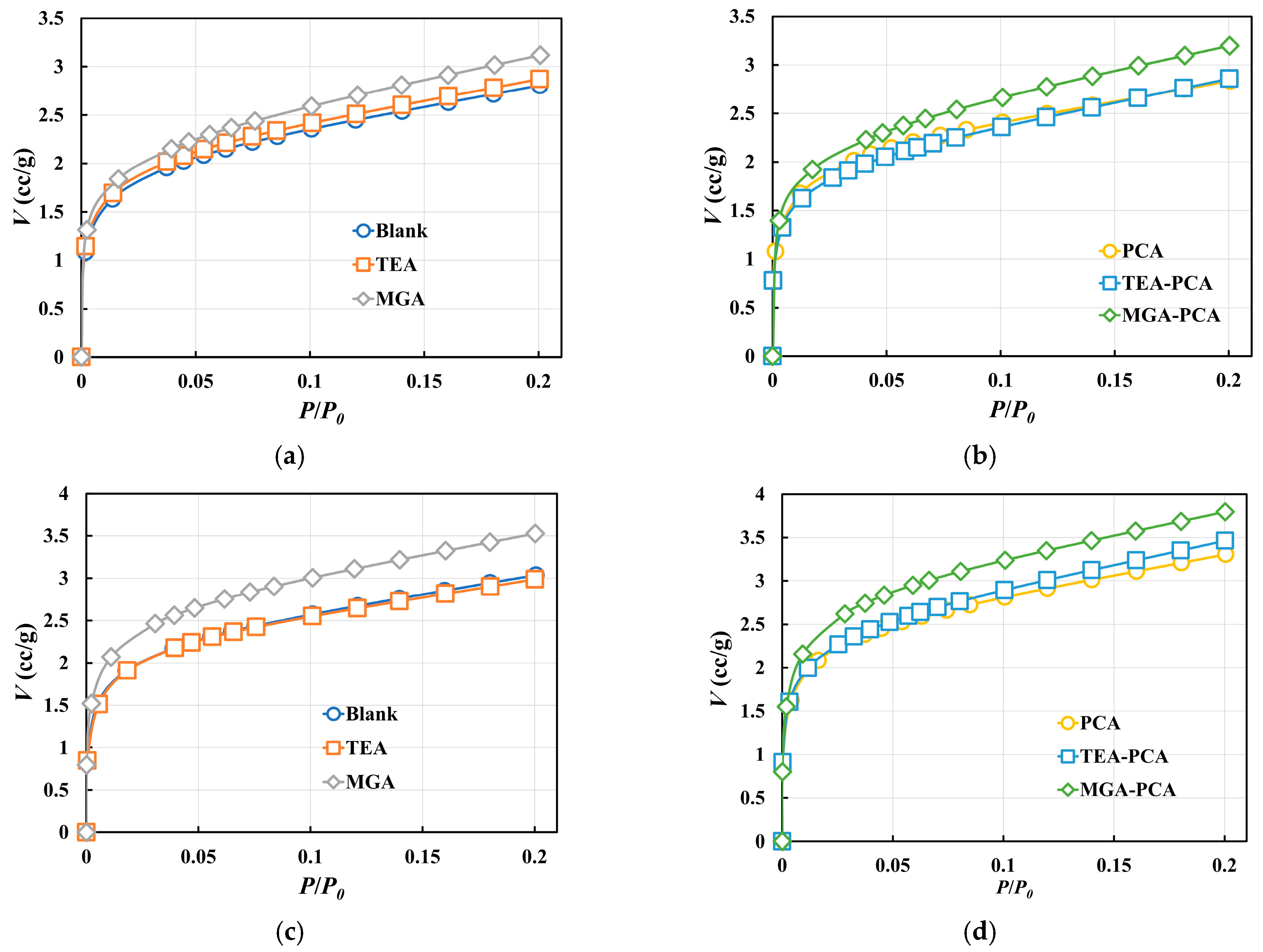
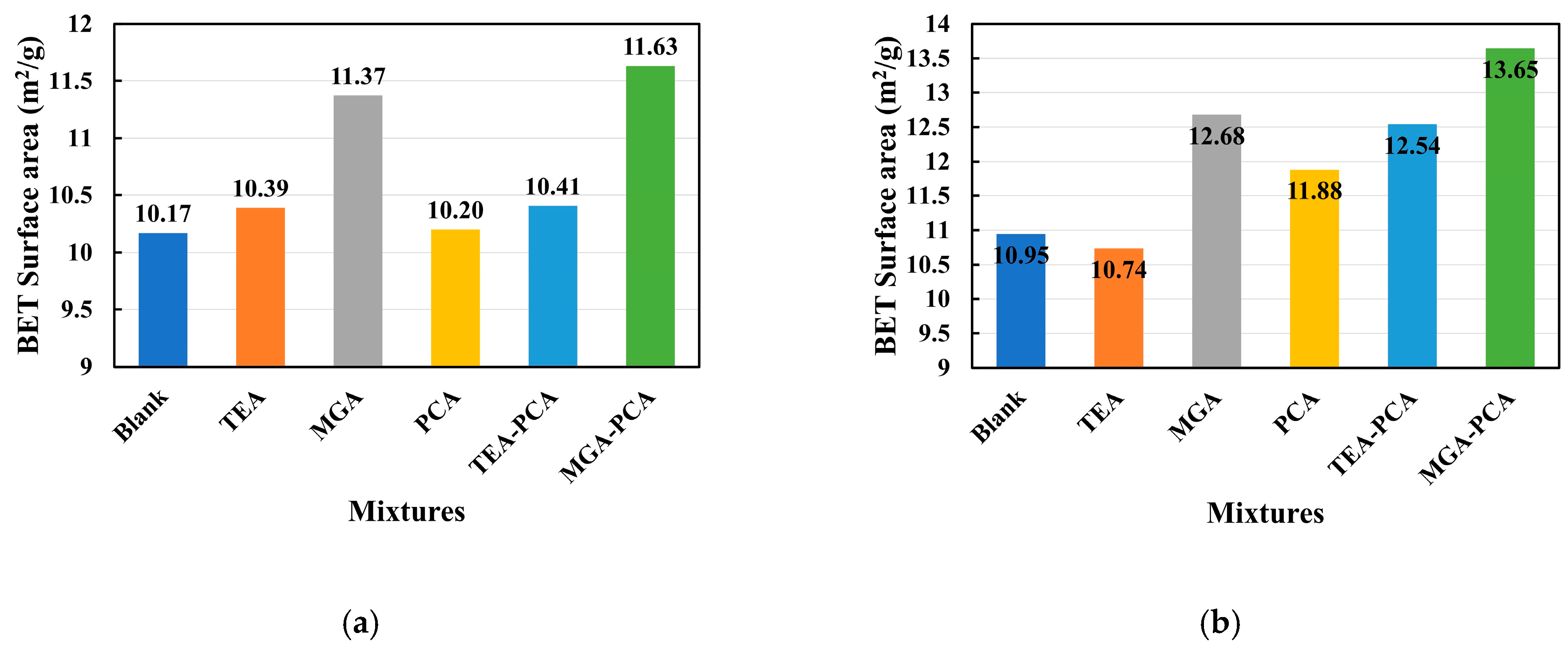
The BET specific surface area tests were conducted on cement pastes incorporating different grinding aids and PCA superplasticizers, with the results presented in Figure 6 and Figure 7. The variations in nitrogen adsorption isotherms reflect the evolution of the pore structure. An increase in adsorption volume in the low relative pressure region (P/P₀ < 0.1) indicates the development of more micropores (<2 nm), while an elevation in the medium pressure region (P/P₀ ≈ 0.05–0.35) is associated with the formation of mesopores (2–50 nm).

At 7 days of hydration, the Blank group without PCA superplasticizer exhibited the lowest adsorption volume (Figure 6a), suggesting a sparsely developed pore structure with weak nitrogen adsorption capacity. In contrast, samples incorporating the grinding aids TEA and MGA showed a significant increase in adsorption volume in the P/P₀ ≈ 0.05–0.2 range, with the MGA group performing more prominently. This phenomenon indicates that grinding aids promote cement particle dispersion and hydration reactions, thereby inducing the formation of more mesoporous structures (2–50 nm) and enhancing multilayer nitrogen adsorption. Upon addition of PCA superplasticizer (Figure 6b), the adsorption curves of all samples became steeper, with a marked increase in adsorption volume, and the MGA-PCA group achieving the highest value. This suggests that the dispersive effect of PCA synergizes with the activation effect of grinding aids to optimize the pore structure, particularly in the development of micropores (<2 nm) and mesopores.

At 28 days of hydration (Figure 6c,d), the adsorption volumes of all samples increased compared to those at 7 days, but samples with PCA maintained a significant advantage. Notably, the slope of the adsorption curve for the MGA-PCA group further increased at 28 days, indicating that prolonged hydration time leads to continuous refinement of the pore structure, forming more micropores and mesopores. This change is closely related to the accumulation of cement hydration products.

The BET specific surface area results demonstrate that the incorporation of grinding aids and PCA superplasticizer significantly enhances the specific surface area of cement pastes. At 7 days, the MGA group exhibited a higher BET specific surface area than the TEA and Blank groups, with the MGA-PCA group reaching the highest value, indicating that MGA grinding aid increases effective adsorption sites by optimizing particle distribution and pore structure. At 28 days, the BET specific surface areas of all samples increased, but those with PCA showed greater increments, particularly the MGA-PCA group, which had a significantly higher value than the others. This implies that PCA not only exerts a dispersive effect in the early hydration stage but also continuously promotes the generation of hydration products and pore refinement.

The increase in BET specific surface area is primarily attributed to the formation of calcium silicate hydrate (C-S-H) gel. In the initial stage of cement hydration, grinding aids (such as MGA) reduce particle surface energy, promote cement particle dispersion, and increase the contact area for hydration reactions, thereby accelerating C-S-H gel formation. C-S-H gel possesses a nanoscale pore structure, with a high proportion of micropores and mesopores directly contributing to a larger specific surface area. The addition of PCA superplasticizer further disperses cement particles, reduces agglomeration, enables more uniform hydration reactions, and generates finer C-S-H gel, thereby further refining the pore structure.

As hydration time extends to 28 days, C-S-H gel continues to accumulate, leading to gradual densification of the pore structure and an increased proportion of micropores. This process is particularly pronounced in the MGA-PCA group, where the activation effect of MGA and the dispersive effect of PCA jointly promote uniform distribution of hydration products and optimization of the pore structure, ultimately resulting in a higher BET specific surface area.

3.4. Mechanical Properties

The mortar strength test results for different groups at various hydration periods are presented in Figure 8. Both TEA and MGA improved the 7 day’s strength compared to the Blank group, with MGA exhibiting a more pronounced effect (+7.1% VS +4.0%). This enhancement aligns with the particle size distribution results, where MGA produced finer particles (D₅₀ = 14.69 µm VS TEA’s 14.86 µm and Blank’s 15.25 µm). The increased fineness enhanced the reactivity of cement particles, accelerating early hydration and C-S-H formation. Additionally, MGA’s ester-modified structure (with additional carboxyl groups) further promoted Ca²⁺ dissolution and AFt formation, as confirmed by XRD analysis (higher Ca(OH)₂ and AFt peaks).

The combination of grinding aids (TEA/MGA) with PCA significantly boosted strength (TEA-PCA: +22.0%; MGA-PCA: +22.4%). PCA’s dispersion effect reduced particle agglomeration, increasing the available surface area for hydration. MGA-PCA achieved the highest strength due to MGA’s dual role: (i) finer particle size distribution and (ii) improved compatibility with PCA, which enhanced adsorption efficiency.

TEA alone reduced flexural strength (−7.4%), likely due to its preferential acceleration of C₃A hydration, which led to localized stress concentrations and microcracks. This aligns with studies showing TEA’s tendency to disrupt CH nucleation, weakening the interfacial transition zone (ITZ). MGA improved flexural strength (+2.3%) by promoting uniform C-S-H growth and reducing porosity. Its ester groups also stabilized AFt formation, enhancing cohesion. PCA alone increased flexural strength (+8.4%) by improving particle packing and reducing water demand. The combined use of MGA-PCA yielded the highest flexural strength (+9.6%), as PCA mitigated MGA’s early hydration acceleration, ensuring balanced microstructural development.

TEA alone reduced 28-day strength (−2.6%), consistent with its known retardation of C₃S hydration and CH precipitation issues. MGA’s strength gain (+4.8%) was attributed to its stable chelation of Ca²⁺ and Al³⁺, which prolonged hydration and refined pore structure. TEA’s flexural strength decline (−9.4% at 28 days) worsened compared to 7 days, confirming its long-term incompatibility with cement matrices. MGA-PCA achieved the highest flexural strength (+7.8%).

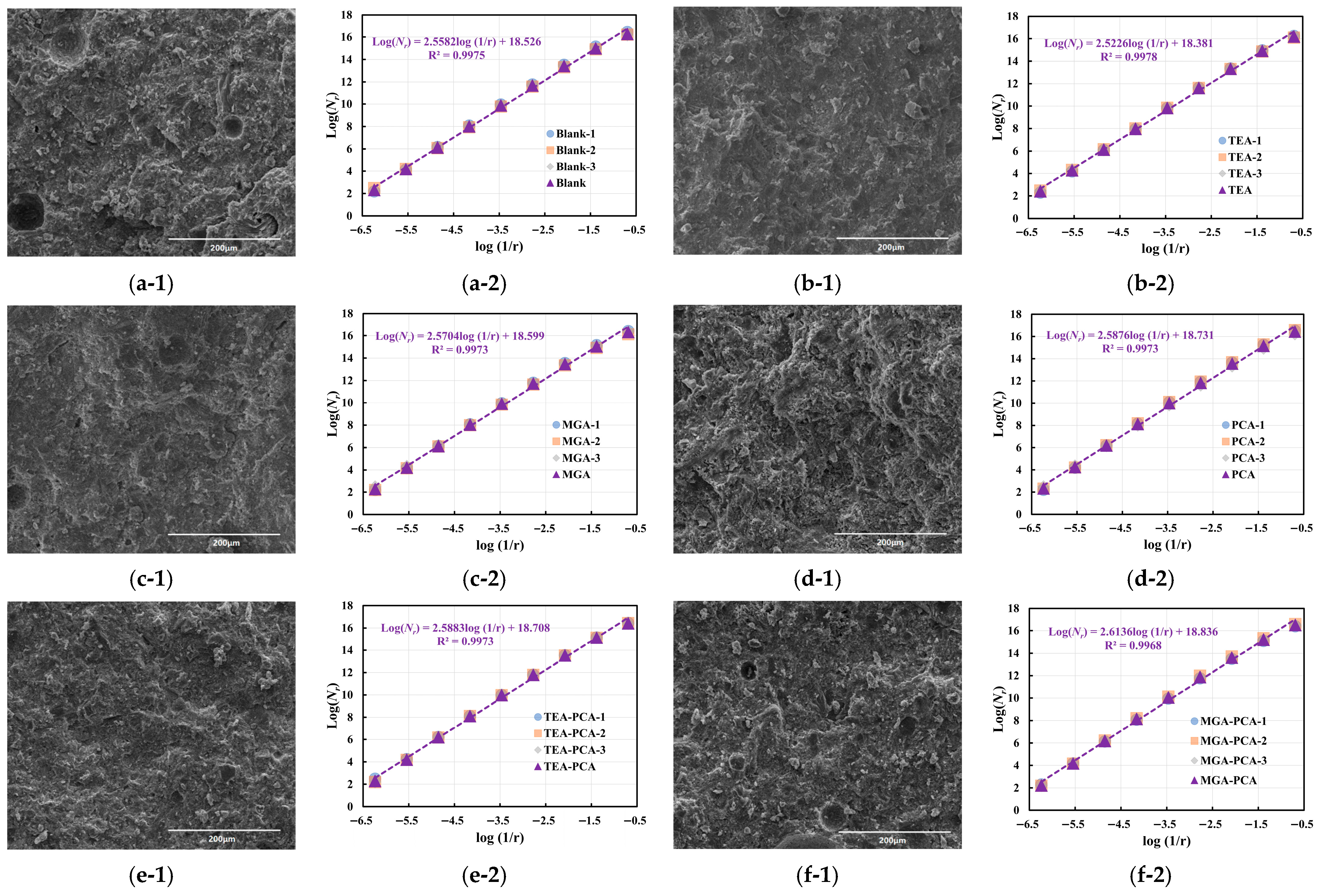
3.5. Morphological Characteristics and Fractal Analysis

In traditional microstructural investigations of cement-based materials, scanning electron microscopy (SEM) images serve as a pivotal characterization tool, extensively employed to elucidate the morphological attributes of hydration products within cement pastes during the hydration process. Nevertheless, the majority of extant studies on SEM image analysis remain confined to qualitative assessments, relying on researchers’ subjective interpretations through “visual descriptive” approaches, which lack standardized and reproducible quantitative metrics. This methodology exhibits pronounced limitations in unveiling the inherent linkages between microstructure and macroscopic performance, and it falls short of fulfilling the requirements for precision-oriented material design. To mitigate these shortcomings, the present study incorporates image-based grayscale mean analysis and fractal dimension analysis techniques, approaching the problem from both statistical and geometric perspectives to enable quantitative characterization of microstructural complexity in SEM images.

Grayscale analysis leverages information from the image’s grayscale histogram to extract brightness distribution characteristics, thereby indirectly reflecting attributes such as the compactness, porosity, and reaction uniformity of cement hydration products. In contrast, fractal dimension quantifies the complexity and space-filling capability of image boundaries or structural outlines, enabling the capture of material structural evolution features across diverse spatiotemporal scales. In this work, SEM images of various sample groups at 7-day and 28-day hydration ages were systematically evaluated under 500× and 2000× magnifications, with the evolutionary trends and underlying mechanisms analyzed based on the dual metrics of average grayscale value and fractal dimension.

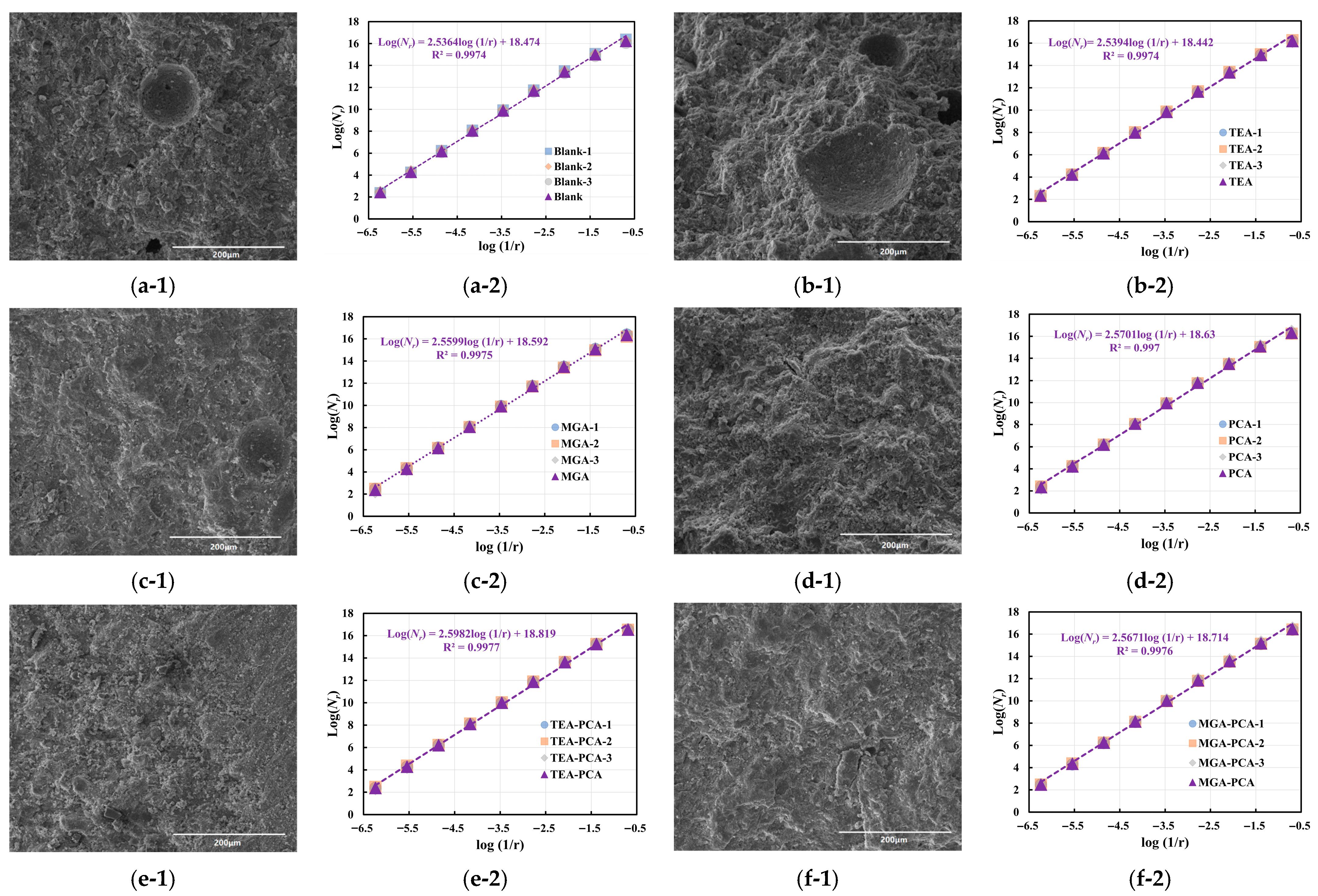
First, the features of the 7-day-old samples under 500× magnification are analyzed (see Figure 9 and

Table 9. Average gray and D_B values of SEM images at the age of 7 days.

No.	Average Gray Value		DB		Magnification
	Ave.	Std.	Ave.	Std.
Blank	77.5	23.47	2.536	0.026	500×
TEA	79.3	10.64	2.539	0.021
MGA	85.2	18.50	2.560	0.045
Blank-PCA	84.9	1.85	2.570	0.036
TEA-PCA	91.8	7.49	2.598	0.017
MGA-PCA	105.3	15.11	2.567	0.020
Blank	88.4	15.51	2.472	0.002	2000×
TEA	83.3	11.06	2.468	0.013
MGA	90.6	6.83	2.491	0.005
Blank-PCA	74.2	12.38	2.510	0.030
TEA-PCA	90.4	0.93	2.515	0.035
MGA-PCA	108.6	6.61	2.500	0.028

). The Blank group exhibits an average grayscale value of 77.5 and a fractal dimension of 2.536, displaying typical early hydration characteristics, where reaction products have not yet fully formed, resulting in a relatively loose structure, lower image brightness, and minimal complexity in structural boundaries. Upon incorporation of TEA, the grayscale value increased slightly to 79.3, and the fractal dimension rose marginally to 2.539. In contrast, the MGA group exhibited more pronounced changes, with the grayscale value rising to 85.2 and the fractal dimension substantially increasing to 2.560. The limited enhancement in fractal dimension (DB) with TEA compared to MGA indeed reflects its weaker influence on microstructural complexity at early ages. This can be mechanistically explained by TEA’s known tendency to preferentially accelerate the hydration of C₃A and C₄AF phases, while potentially retarding C₃S hydration and disrupting the nucleation and growth of calcium hydroxide (CH) [12,20,40]. Such selective acceleration may lead to localized, rapid formation of ettringite and aluminate hydrates without contributing significantly to the overall spatial complexity and interconnectivity of the C–S–H gel network. In contrast, MGA, being an ester-modified derivative of TEA, introduces additional polar groups (e.g., –COOH and –COOR) that improve its compatibility with silicate phases and enhance the chelation of Ca²⁺ and Al³⁺ ions. This promotes a more uniform and simultaneous hydration of multiple cement phases, leading to a denser and more complex microstructure with higher fractal dimension values [7]. These mechanistic insights are consistent with our particle size distribution, XRD, and strength results, and are supported by previous studies such as Ji et al. [7], which highlight the role of functional groups in grinding aids on hydration kinetics and microstructure development.

Further examination of the influence of PCA dosage on the structure of hydration products reveals that the Blank-PCA group experiences a substantial increase in average grayscale value to 84.9, accompanied by a notable reduction in standard deviation to only 1.85, signifying enhanced uniformity in the distribution of reaction products, more consistent image brightness, and an overall trend toward structural densification. Concurrently, its fractal dimension rises to 2.570, demonstrating that PCA can significantly augment the space-filling complexity of the structure even in the early stage. The TEA-PCA group further elevates the grayscale value to 91.8, with a fractal dimension of 2.598—the highest in this series—indicating that the synergistic interaction between TEA and PCA not only accelerates the reaction extent but also generates structural units characterized by greater branching features and nonlinear boundaries. Most notably, the MGA-PCA group achieves the highest grayscale value of 105.3 among all samples, reflecting the strongest brightness response and accumulation of reaction products; although its fractal dimension is slightly lower than that of TEA-PCA (at 2.567), the smaller standard deviation underscores a superior balance between complexity and homogeneity.

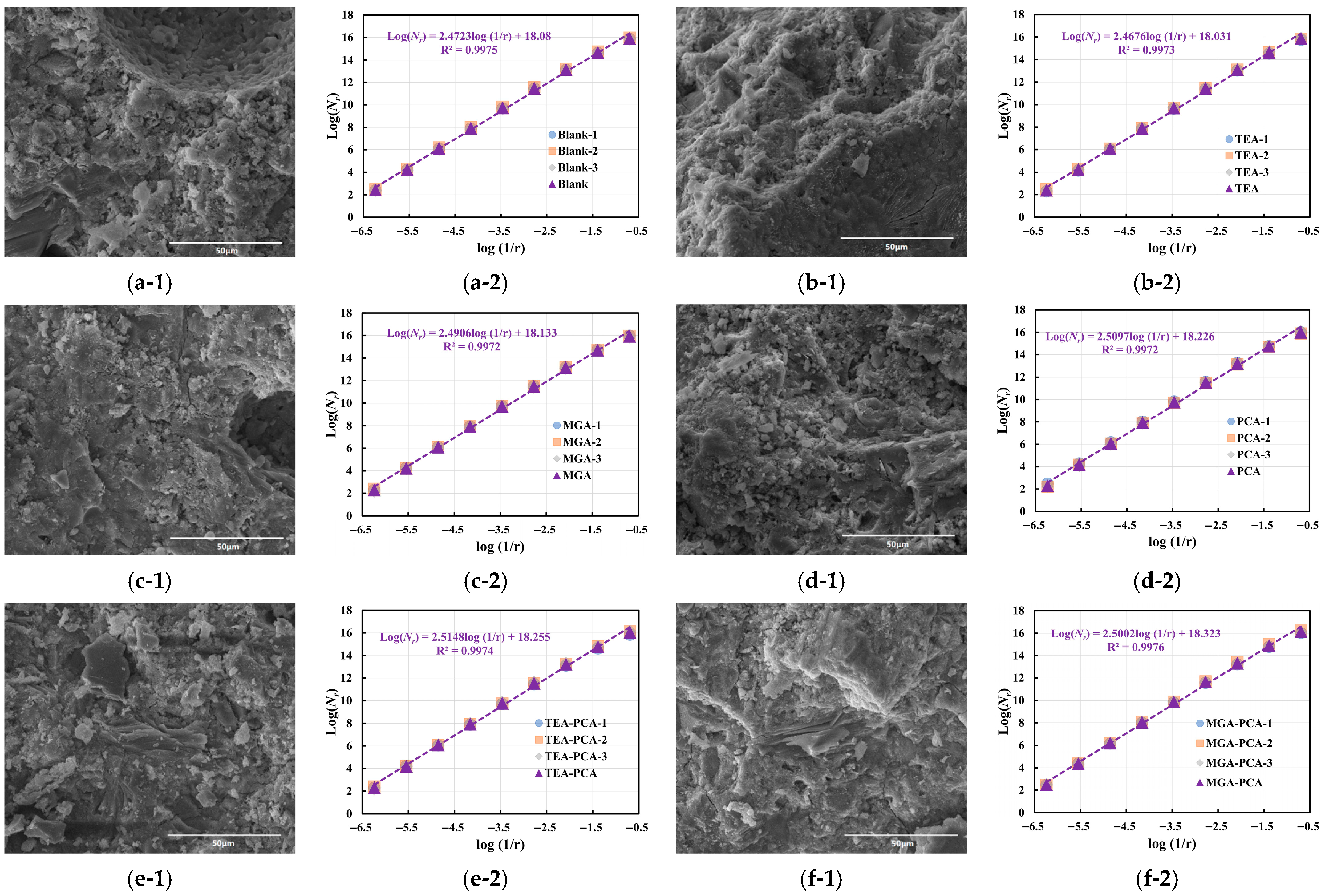
When the magnification is increased to 2000×, as shown in Figure 10 and Table 9, the image features exhibit distinct trends. In the Blank group, the grayscale value rises from 77.5 to 88.4, indicating that high-magnification imaging can more precisely reveal the presence of dense regions within the microstructure. However, the fractal dimension decreases to 2.472, with the standard deviation dropping to 0.002, suggesting that structural boundaries in high-magnification images tend toward regularity, with diminished hierarchical perception and enhanced local structural homogeneity. The TEA and MGA samples display similar trends, with grayscale values of 83.3 and 90.6, respectively, and fractal dimensions of 2.468 and 2.491—both lower than their corresponding values at 500×. This implies that under high-resolution conditions, the observed structural units are more refined but exhibit relatively converged complexity.

The PCA-incorporated groups maintain favorable microstructural performance even at 2000× magnification. The Blank-PCA group has a fractal dimension of 2.510, higher than that of the Blank group, indicating that structural boundaries still retain elevated complexity. The TEA-PCA group shows a grayscale value of 90.4 and a fractal dimension of 2.515, demonstrating synchronized enhancements in brightness and complexity. Meanwhile, the MGA-PCA group leads with the highest grayscale value of 108.6 and a fractal dimension of 2.500, collectively characterizing its balanced development of compactness and hierarchical fractal structure at the mesoscale.

At the 28-day hydration age, the microstructures of each sample group exhibit further evolutionary features (see Figure 11 and Figure 12 and

Table 10. Average gray and D_B values of SEM images at the age of 28 days.

No.	Average Gray Value		DB		Magnification
	Ave.	Std.	Ave.	Std.
Blank	84.6	7.62	2.558	0.040	500×
TEA	86.6	10.16	2.523	0.029
MGA	71.3	9.14	2.570	0.032
Blank-PCA	83.1	1.85	2.588	0.047
TEA-PCA	75.5	4.24	2.588	0.015
MGA-PCA	71.9	5.62	2.614	0.029
Blank	85.8	10.81	2.491	0.015	2000×
TEA	83.0	7.76	2.447	0.014
MGA	80.3	2.76	2.503	0.038
Blank-PCA	67.7	3.76	2.510	0.028
TEA-PCA	73.9	5.81	2.502	0.032
MGA-PCA	72.9	5.30	2.521	0.014

). In the Blank group under 500× magnification, the grayscale value increases from 77.5 at 7 days to 84.6, with the fractal dimension rising from 2.536 to 2.558, illustrating that the ongoing hydration reaction promotes increased formation of reaction products, gradually leading to denser and more complex structures. The TEA group shows a modest increase in grayscale value to 86.6, but its fractal dimension decreases to 2.523, reflecting that while the compactness of the formed reaction products improves, the structural boundaries become smoother, resulting in reduced complexity. In contrast, the MGA group experiences a decline in grayscale value to 71.3, yet its fractal dimension rises to 2.570, indicating that although the compactness of reaction products slightly decreases, their spatial distribution becomes more intricate and complex, presenting stronger multi-scale fractal structural characteristics.

Under the influence of PCA dosage, the Blank-PCA group has a grayscale value of 83.1, close to that of the Blank group, but its fractal dimension further increases to 2.588, signifying a tendency toward structural stability with higher hierarchical complexity. The TEA-PCA group exhibits a slight decrease in grayscale value to 75.5, but the dimension remains at 2.588; meanwhile, the MGA-PCA group demonstrates the optimal structural features, with a grayscale value of 71.9 and the highest fractal dimension of 2.614 among all samples. This trend suggests that the synergistic effect of MGA and PCA at the 28-day age can induce the formation of hydration products with highly complex interwoven networks, despite an overall decline in brightness, resulting in microstructures characterized by excellent structural hierarchy and spatial orderliness.

At 2000× magnification, as shown in Figure 12, the structural features are further refined, with the Blank group showing a grayscale value of 85.8 and a fractal dimension of 2.491. The TEA group has a grayscale value of 83.0 and a dimension reduced to 2.447, indicating a tendency toward flatter meso-structures. The MGA group experiences a decrease in grayscale value to 80.3, but its dimension increases to 2.503, reflecting maintained complexity in the structure under higher resolution. The PCA-incorporated samples continue to exhibit strong performance, with fractal dimensions of 2.510, 2.502, and 2.521 for the Blank-PCA, TEA-PCA, and MGA-PCA groups, respectively, demonstrating that even under high-resolution conditions, PCA can sustain multi-level structural distributions, particularly in the MGA-PCA group, which still shows the strongest fractal dimension value, verifying the formation of complex crosslinked microstructures during long-term hydration.

Synthesizing the analytical results from the 7-day and 28-day hydration ages reveals that the grayscale values of the samples generally exhibit nonlinear evolution with increasing age; in some samples, the grayscale value peaks in the early stage and may subsequently decline to a certain extent in the later stage due to mechanisms such as rearrangement of hydration products, crystal formation, and morphological reconstruction. In contrast, the fractal dimension provides a more stable reflection of structural complexity, showing a gradual upward trend in multiple samples, indicating a transition from initial random filling to a networked system characterized by hierarchical and nonlinear features. The role of PCA persists throughout both early and late stages, significantly enhancing structural homogeneity and complexity by modulating the hydration kinetics process, particularly when co-incorporated with MGA, yielding the optimal microstructural characterization outcomes.

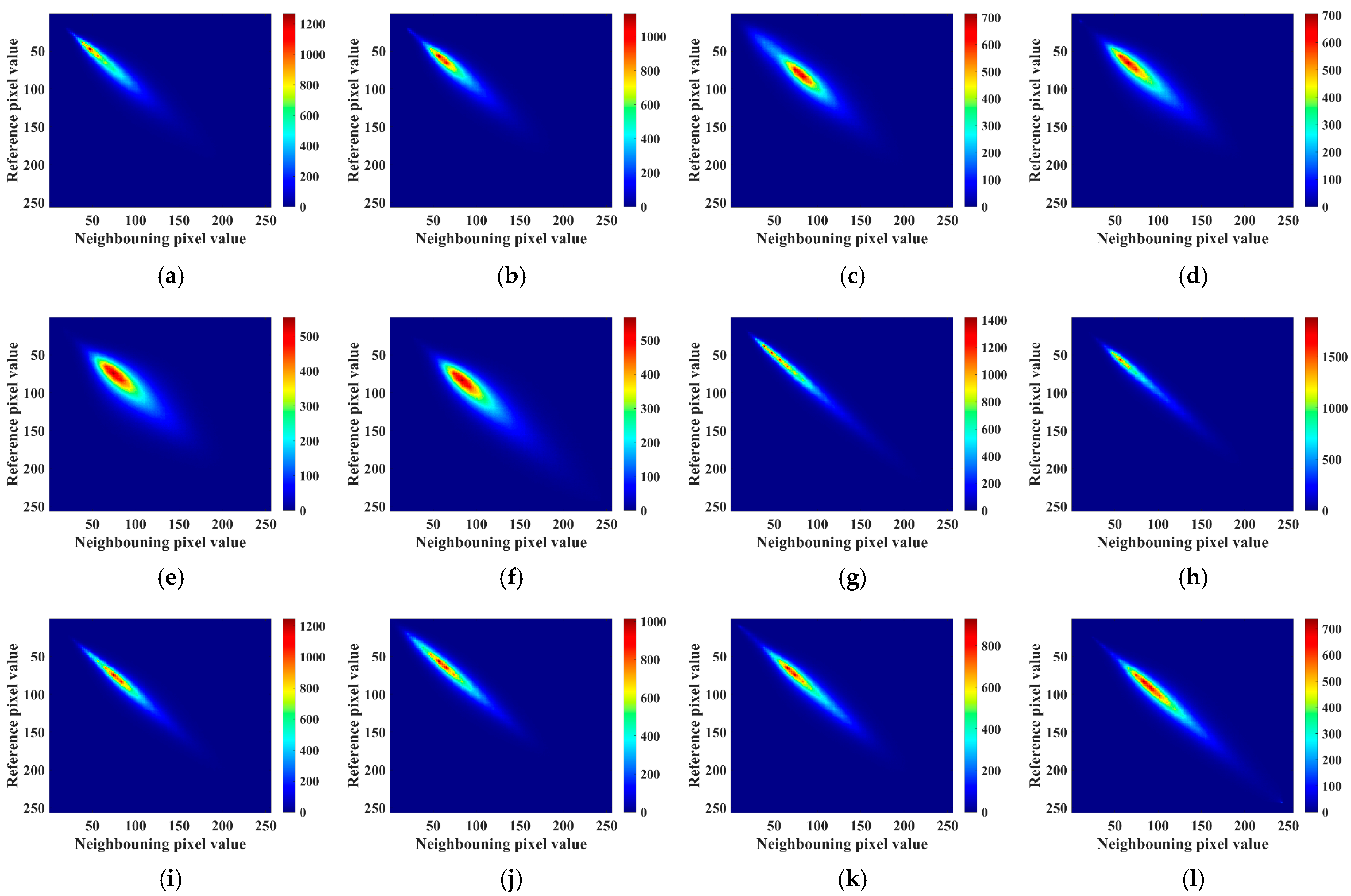
3.6. GLCM Characteristic Parameters

In the domain of microstructural image analysis, especially in the study of cement-based materials, traditional approaches often rely on singular parameters such as gray-level distribution statistics or fractal dimensions to describe micro-textures. However, these methods exhibit significant limitations in capturing the interrelationships within spatial gray-level distributions. For instance, gray-level value analysis primarily reflects overall brightness or darkness trends within an image, while fractal dimensions, despite illustrating structural complexity, fall short in revealing the regularities and local spatial correlations of image textures. Consequently, achieving high-dimensional and finely detailed quantitative image analysis remains a pivotal challenge in the current research of the microstructures of cement-based materials.

The Gray Level Co-occurrence Matrix (GLCM) emerges as a crucial tool for addressing these challenges. GLCM is a two-dimensional matrix used to statistically characterize image texture features. It provides insights into the joint probability distribution of any two pixels with specific gray values at a defined distance and orientation within an image. From GLCM, a series of statistical parameters can be derived, including Energy, Entropy, Contrast, and Correlation. These parameters correspond to key aspects such as uniformity, complexity, intensity of gray-level differences, and gray-level dependency in textures, thus offering a comprehensive portrayal of the spatial distribution patterns of microstructures from multiple perspectives [38,41].

In this study, we focus on the analysis of four characteristic GLCM parameters—Energy, Entropy, Contrast, and Correlation—of SEM images under varying hydration ages (7 days and 28 days), magnifications (500× and 2000×), as shown in Figure 13 and Figure 14. Through the statistical variations and inherent logical connections of these parameters, we can deeply unveil the microstructural differences among samples and the mechanisms underpinning their formation, thus providing theoretical support for the regulation and performance enhancement of cement-based material microstructures.

Figure 13 and

Table 11. GLCM characteristic parameters of SEM images at the age of 7 days.

No.	Energy		Entropy		Contrast		Correlation		Magnification
	Ave.	Std.	Ave.	Std.	Ave.	Std.	Ave.	Std.
Blank	5.34 × 10−4	2.85 × 10−5	11.87	0.47	185.24	31.61	0.843	0.043	500×
TEA	3.89 × 10−4	5.58 × 10−5	12.16	0.73	181.17	76.02	0.872	0.009
MGA	2.87 × 10−4	7.19 × 10−5	12.51	0.29	276.15	67.70	0.807	0.041
Blank-PCA	2.40 × 10−4	3.78 × 10−5	12.66	0.22	265.67	93.01	0.840	0.059
TEA-PCA	2.04 × 10−4	9.76 × 10−6	12.90	0.04	404.76	28.88	0.740	0.037
MGA-PCA	2.14 × 10−4	7.67 × 10−5	12.93	0.53	359.43	97.11	0.809	0.029
Blank	5.93 × 10−4	1.67 × 10−4	11.69	0.41	114.79	27.59	0.934	0.012	2000×
TEA	4.93 × 10−4	1.44 × 10−4	11.82	0.36	91.62	11.40	0.942	0.022
MGA	3.96 × 10−4	3.66 × 10−5	12.07	0.08	128.98	9.84	0.920	0.016
Blank-PCA	3.44 × 10−4	2.68 × 10−5	12.16	0.06	130.73	11.49	0.918	0.009
TEA-PCA	2.92 × 10−4	1.05 × 10−4	12.44	0.34	170.03	4.99	0.916	0.021
MGA-PCA	2.53 × 10−4	3.78 × 10−5	12.63	0.21	184.54	35.55	0.918	0.029

illustrates the notable differences among samples in Energy, Entropy, Contrast, and Correlation at a 500× magnification, indicating distinct texture features emerging in the microstructure even at the early stages of hydration. For the Energy values, the Blank sample exhibits a value of 5.34 × 10⁻⁴, TEA is at 3.89 × 10⁻⁴, and MGA is lower at 2.87 × 10⁻⁴. Further reduction is observed with the addition of PCA, resulting in values of 2.40 × 10⁻⁴ for Blank-PCA, 2.04 × 10⁻⁴ for TEA-PCA, and 2.14 × 10⁻⁴ for MGA-PCA. Energy represents the repetition and regularity of gray-level pairs in an image; higher values indicate more uniform textures, while lower values suggest greater diversity or uneven distribution. From this perspective, the addition of PCA lowers the Energy values as a whole, reflecting more complex structures of hydration products, irregular particle size, and arrangement, showing more pronounced heterogeneous features. Particularly, TEA-PCA samples exhibit the lowest Energy value, indicating a more irregular structure during initial formation, marked by high reaction activity and rapid generation of hydration products leading to significant local structural differences.

Entropy, as an indicator of information complexity, rises with increasing structural randomness. The Blank group’s Entropy is 11.87, slightly increasing for TEA and MGA (12.16, 12.51), while further increases are noted in the PCA series, with TEA-PCA and MGA-PCA reaching 12.90 and 12.93, respectively. This suggests that the introduction of PCA effectively accelerates hydration reaction rates and spatial heterogeneity, leading to more complex distribution patterns of products. This complexity trend corroborates earlier analyses involving gray-level and fractal dimension assessments.

Regarding Contrast, the Blank sample has a value of 185.24, which increases to 276.15 for MGA, and skyrockets in the TEA-PCA and MGA-PCA samples reaching 404.76 and 359.43. Contrast measures the intensity of gray-level variations, with higher values pointing to sharp transitions between bright and dark areas, indicating distinct structural boundaries. This trend suggests that PCA and MGA facilitate spatial segregation between hydration products and unreacted particles, significantly amplifying contrasts between local dense zones and porous areas in the microstructure.

Correlation, on the other hand, is a measure of gray-level linear dependency. The Blank sample’s correlation coefficient is 0.843, slightly lower for TEA and MGA, while PCA-enhanced samples like TEA-PCA (0.740) and MGA-PCA (0.809) show significant decrease, suggesting diminished linear correlation among gray levels, trending towards structural disorder. The low correlation value in TEA-PCA, combined with its high contrast and entropy, portrays the typical heterogeneous structure morphology during early hydration reactions.

At higher magnification (2000×), the Energy values for all samples noticeably increase, like the Blank group rising from 5.34 × 10⁻⁴ to 5.93 × 10⁻⁴. This change indicates a trend towards uniform texture with magnification, as enhanced resolution reveals finer microstructural details leading to more consistent local gray distribution, thereby increasing regularity. Conversely, Entropy values decrease, signifying reduced complexity. TEA and MGA groups exhibit high Energy and low Entropy traits. Particularly, TEA samples with low contrast (91.62) reflect dense and stable distributions of hydration products. Comparatively, MGA-PCA samples maintain high contrast and Entropy values even under high magnification, signifying sustained structural complexity.

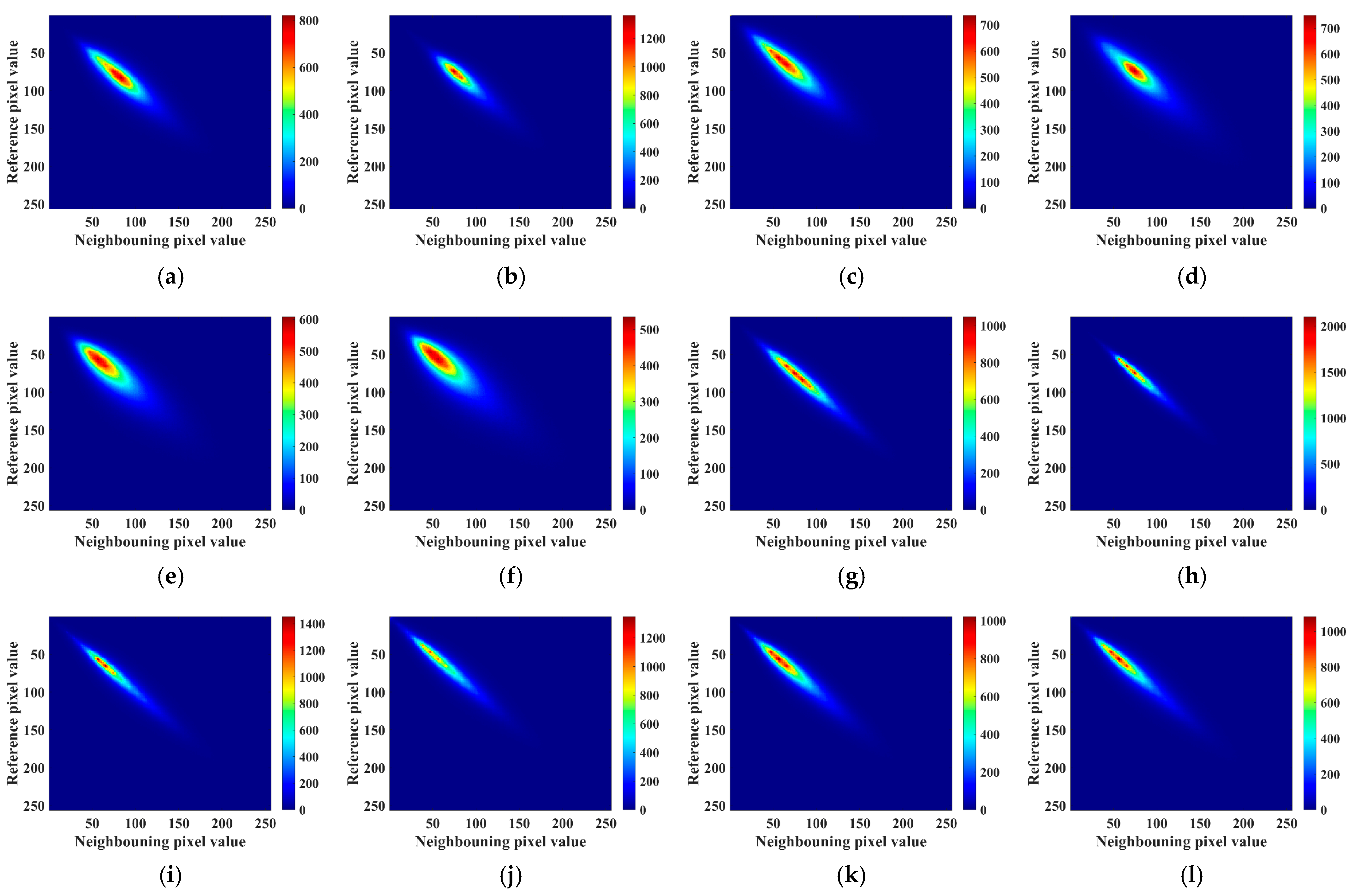
From Figure 14 and

Table 12. GLCM characteristic parameters of SEM images at the age of 28 days.

No.	Energy		Entropy		Contrast		Correlation		Magnification
	Ave.	Std.	Ave.	Std.	Ave.	Std.	Ave.	Std.
Blank	3.76 × 10−4	1.93 × 10−4	12.17	0.74	254.72	80.60	0.811	0.022	500×
TEA	4.75 × 10−4	7.45 × 10−5	11.83	0.19	167.54	22.94	0.823	0.042
MGA	3.14 × 10−4	1.05 × 10−4	12.35	0.54	242.53	69.03	0.820	0.022
Blank-PCA	1.76 × 10−4	5.18 × 10−5	12.81	0.99	386.22	74.43	0.799	0.002
TEA-PCA	2.22 × 10−4	1.16 × 10−5	12.81	0.05	353.59	10.25	0.792	0.003
MGA-PCA	1.99 × 10−4	5.72 × 10−5	13.03	0.42	448.58	128.33	0.773	0.010
Blank	4.41 × 10−4	1.17 × 10−4	11.90	0.40	119.63	32.85	0.926	0.012	2000×
TEA	6.14 × 10−4	4.87 × 10−5	11.32	0.21	69.80	18.60	0.927	0.010
MGA	4.36 × 10−4	2.71 × 10−4	12.07	0.84	132.76	38.75	0.927	0.007
Blank-PCA	3.62 × 10−4	1.23 × 10−4	12.19	0.55	143.75	39.78	0.918	0.006
TEA-PCA	3.65 × 10−4	3.21 × 10−5	12.11	0.08	132.98	39.42	0.924	0.020
MGA-PCA	3.43 × 10−4	9.13 × 10−5	12.38	0.41	167.28	22.36	0.908	0.012

, it is evident that hydration age significantly impacts the evolution of structural texture features. At 500× magnification, the Energy of the Blank group declines to 3.76 × 10⁻⁴, while Entropy rises to 12.17 and Contrast climbs to 254.72, indicating continued hydration results in increased product formation and pronounced gray distribution differences. For TEA, Energy increases to 4.75 × 10⁻⁴, Entropy slightly drops to 11.83, and Contrast decreases to 167.54, suggesting more uniform product distribution, blurred boundaries, and an increasingly dense structure.

MGA samples embody stronger complexity, with Contrast soaring to 242.53, Entropy at 12.35, and Energy being lower (3.14 × 10⁻⁴), indicating the structure retains high heterogeneity. Within PCA groups, MGA-PCA samples stand out, with Contrasts at 448.58 and Entropy at 13.03, indicating the most complex microstructural network with significant gray-level differences post prolonged hydration, demonstrating the sample’s intricate spatial structure and multi-scale structural strength. TEA-PCA also shows high Entropy and Contrast, affirming PCA’s role in long-term structural evolution.

At 2000× magnification, Energy values across samples significantly increase, for instance, TEA is at 6.14 × 10⁻⁴ and the Blank group rises to 4.41 × 10⁻⁴, indicating enhanced structural uniformity at local scales. Entropy values generally decrease, ranging from 11.32 to 12.38, indicating diminished complexity. Contrast values also reduce, suggesting blurred microstructural boundaries. Particularly notable is MGA-PCA’s high Contrast (167.28) and Entropy (12.38) at higher magnification, featuring consistent distribution stratification and detailed structural delineation.

The evolutionary dynamics of GLCM parameters reflect interdependent constraints: Energy and Entropy exhibit negative correlation, delineating the dual features of structural uniformity and complexity. Contrast and Entropy show significant positive correlation, indicating more distinct texture boundaries result in more complex imagery. Meanwhile, Correlation is instrumental in regulating structural order, where lower values denote stronger gray-level variation and looser structures.

3.7. Relationship Between Micro-Texture Features and Macro-Features

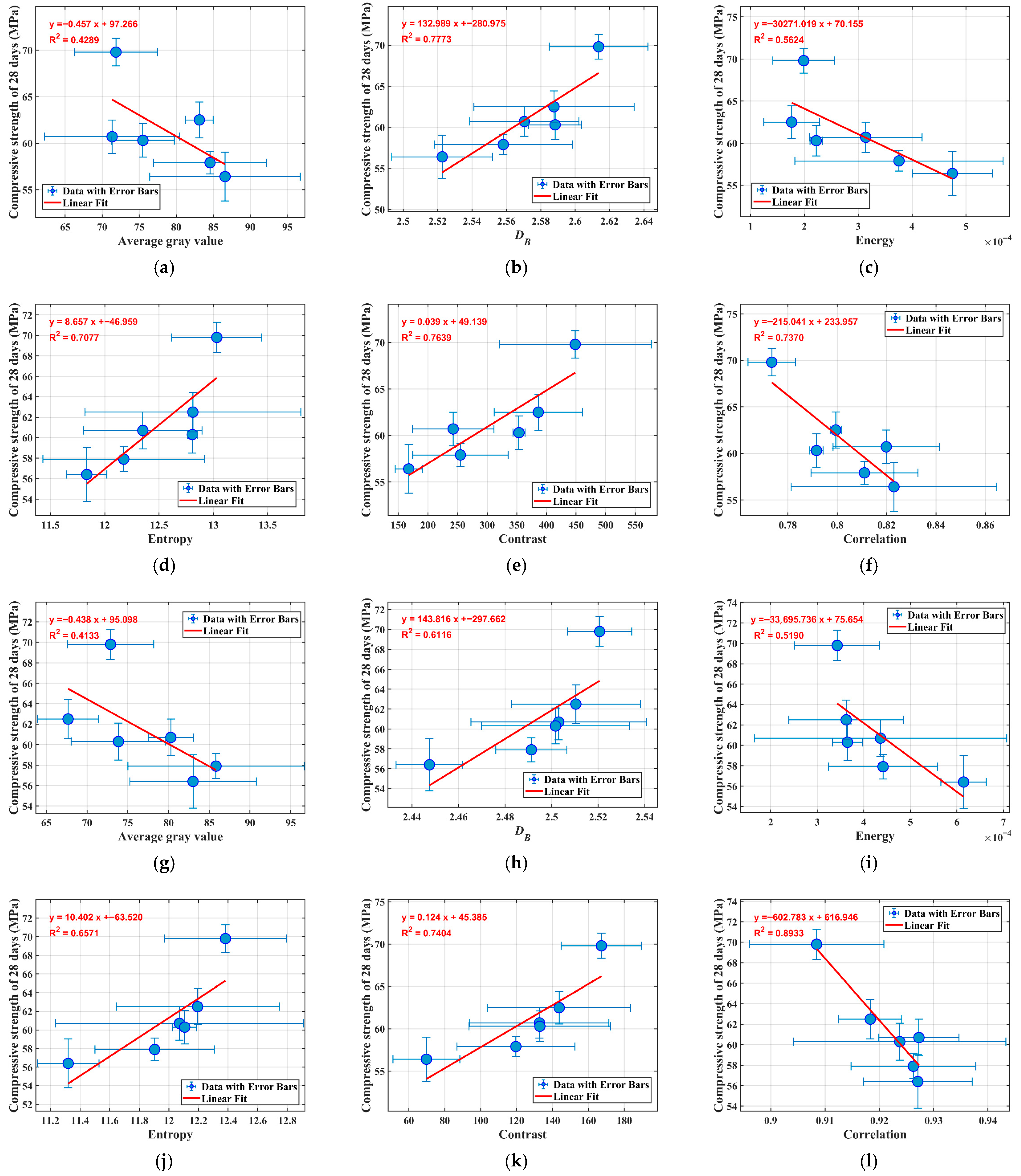
In the quantitative analysis of microstructures in cement-based materials, understanding the correlations between image-derived feature parameters and macroscopic properties holds significant theoretical and practical value. This section delves into how multidimensional parameters extracted from Scanning Electron Microscopy (SEM) images characterize microstructural features and subsequently influence mechanical performance, particularly compressive strength. Based on two representative curing ages (7 days and 28 days), we systematically examine the relationships between average gray value, D_B, and Gray Level Co-occurrence Matrix (GLCM) parameters with compressive strength. Linear regression fittings are employed to determine the coefficient of determination (R²), which quantifies the proportion of variance in compressive strength that can be explained by each parameter. The analysis draws from SEM images captured at 500× and 2000× magnifications, allowing for a multi-scale perspective, as shown in Figure 15 and Figure 16.

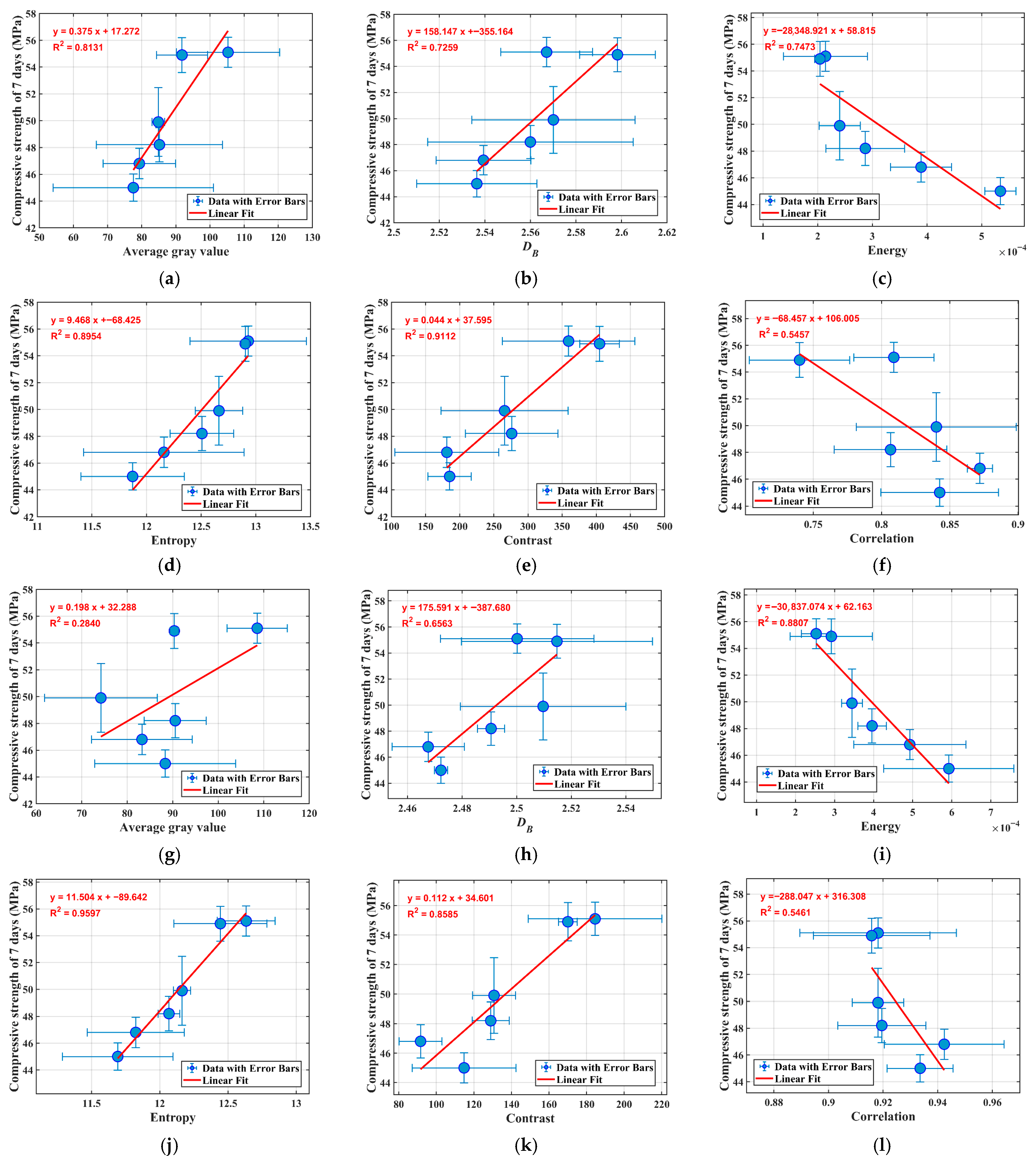
From an image composition standpoint, the average gray value essentially reflects the average pixel brightness in the SEM image. In cement-based materials, this brightness variation indirectly indicates the density of the microstructure, the proportion of pores, and the uniformity of reaction product distribution. As illustrated in Figure 15a,g and Figure 16a,g, the correlation between average gray value and compressive strength exhibits considerable fluctuation across curing ages. At 7 days, a positive correlation is observed, suggesting that higher gray values (indicative of denser early-age microstructures) align with improved strength development during initial hydration phases. At 28 days, the relationship between average grayscale value and compressive strength shifts to a negative correlation in some cases, with overall R² values generally low (<0.5). This reversal can be explained by both microstructural and methodological factors. At early ages (7 days), higher grayscale values typically reflect denser regions enriched in hydration products such as C–S–H gel and ettringite, which support strength development [42]. By 28 days, however, microstructural reorganization occurs, including CH crystal coarsening, microcracking from autogenous shrinkage, and redistribution of hydration phases [43]. These processes increase heterogeneity and reduce the linear association between grayscale and strength. In addition, grayscale values are highly sensitive to surface and imaging conditions (e.g., polishing scratches, carbon coating irregularities, beam penetration depth), which may introduce artifacts unrelated to intrinsic properties [44]. Such sensitivity, combined with the inability of grayscale to distinguish pores from low-density hydrates, explains the consistently weak correlations. Therefore, grayscale alone should be regarded as a non-robust predictor of compressive strength.

In contrast to the average gray value, the fractal dimension (D_B), calculated via box-counting methods, serves as a robust measure of image structural complexity and boundary roughness, as shown in Figure 15 and Figure 16. Across all curing ages and magnifications, D_B exhibits consistent positive correlations with compressive strength. Specifically, at 7 days under 500× magnification, R² reaches 0.7259. At 2000× for the same age, R² is 0.6563, slightly lower but still indicative of a strong relationship. For 28 days, the values are even more pronounced: 0.7773 at 500× and 0.6116 at 2000×. These trends affirm that more complex microstructures, characterized by higher fractal dimensions, enhance space-filling capabilities and pore connectivity, thereby bolstering macroscopic load-bearing capacity.

A notable observation is the superior R² at 500× compared to 2000× across both ages. This disparity can be dissected from perspectives of image representativeness and information content. At 500× magnification, SEM images capture a wider field of view, encompassing a more representative sample of the microstructure. This includes diverse elements such as multiple hydrate clusters, pore distributions across scales, and interfaces between aggregates and paste. Such holistic representation ensures that D_B calculations integrate global complexity, reducing bias from localized anomalies. For instance, the broader view averages out variations in hydration degree across the sample, yielding a D_B that more accurately mirrors overall material integrity and thus correlates better with bulk compressive strength. Conversely, 2000× images are inherently localized, focusing on finer details like individual microcracks, crystal facets, or isolated voids. While this granularity reveals high-resolution textures, it diminishes representativeness; the captured area may not reflect the entire specimen’s heterogeneity. Information content at this scale is skewed toward microscale irregularities, where prominent features like microcracks—often artifacts from sample drying or polishing—disproportionately influence D_B. Thus, 500× strikes an optimal balance, providing sufficient detail for complexity assessment while maintaining representativeness, making D_B a premier parameter for strength prediction

GLCM parameters offer texture-based insights by quantifying spatial relationships between pixel gray levels, capturing aspects like uniformity, randomness, and variability. We analyze four key metrics: Energy, Entropy, Contrast, and Correlation, each revealing distinct microstructural attributes linked to strength.

Energy measures texture uniformity, with lower values indicating dispersed gray distributions and complex, non-homogeneous patterns. In both curing ages, Energy shows significant negative correlations with compressive strength. R² values are 0.7473 (7 d, 500×), 0.8807 (7 d, 2000×), 0.5624 (28 d, 500×), and 0.5190 (28 d, 2000×), as reported in Figure 15c,i and Figure 16c,i. High R² at early ages suggests that low Energy—reflecting intricate interweaving of multi-phase hydrates—fosters dense, load-resistant structures. Lower values at later ages may stem from maturation-induced homogenization, where Energy’s discriminatory power wanes. Notably, 2000× yields higher R² at 7 days (0.8807 VS 0.7473), inverting the trend seen in D_B. This occurs because 2000×’s localized view amplifies fine-scale non-uniformities in early microstructures, where hydration is patchy. Such detailed information content enhances Energy’s ability to detect phase disparities that directly impact nascent strength. At 500×, the broader representativeness dilutes these signals, incorporating more averaged uniformity and thus slightly reducing correlation strength.

Entropy: As a measure of disorder, Entropy positively correlates with strength, with high values denoting complex gray transitions reflective of hydration product diversity and spatial heterogeneity. R² values are exceptionally high: 0.8954 (7 d, 500×), 0.9597 (7 d, 2000×), 0.7077 (28 d, 500×), and 0.6571 (28 d, 2000×), as reported in Figure 15d,j and Figure 16d,j. The peak at 7d, 2000× underscores Entropy’s sensitivity to early-age chaos, where varied hydrates form disorganized yet strong networks. Similarly to Energy, 2000× outperforms at 7 days due to enriched information on microscale entropy sources like needle-like ettringite formations. However, at 28 days, 500× shows better R² (0.7077 VS 0.6571), as matured microstructures benefit from global views that capture evolved heterogeneity across larger areas. Representativeness at 500× ensures Entropy integrates macroscale disorder (e.g., pore networks), providing a more holistic link to strength, whereas 2000×’s focus on locals introduces variability from isolated features.

Contrast: Contrast quantifies local intensity variations, with higher values signaling sharp boundaries and clustered aggregates. It mirrors Entropy’s positive trend, though specific R² values are not detailed in the base analysis, but inferred to be comparable based on similar patterns. High Contrast implies discontinuous hydrate growth, enhancing local support and crack resistance via stress dispersion channels. The magnification effect likely favors 2000× for early ages, where fine contrasts in crystal boundaries are prominent, boosting information content for correlation, as reported in Figure 15e,k and Figure 16e,k. At later ages, 500×’s representativeness captures broader contrast gradients, including interfacial zones, yielding stronger overall fits.

Correlation: This parameter assesses linear dependency in gray levels, with lower values indicating less orderly structures. It exhibits negative correlations, with R² of 0.5457 (7 d, 500×), 0.5461 (7 d, 2000×), 0.7370 (28 d, 500×), and 0.8933 (28 d, 2000×), as reported in Figure 15f,l and Figure 16f,l. Higher R² at later ages (e.g., 0.8933 explaining 89% variance) suggests that reduced Correlation (disorder) in mature pastes correlates with strength via complex networks. Intriguingly, 2000× excels at 28 days, as localized imaging highlights subtle correlations in refined hydrates. At 500×, broader views average out these details, but still provide solid representativeness for global disorder assessment.

All in all, average gray value ranks lowest in efficacy, with average R² values often below 0.5, highlighting its inadequacy as a standalone predictor. This parameter’s simplicity renders it vulnerable to extraneous factors, such as imaging artifacts or non-structural brightness variations, which dilute its correlation strength. In essence, while all parameters contribute to a multifaceted understanding, D_B and Entropy stand out for their high R², offering the most reliable bridges between microtexture and macrostrength. This hierarchy is not static but modulated by magnification and curing age. At 500×, parameters like D_B and Entropy generally achieve higher R² due to enhanced representativeness—the images serve as microcosms of the bulk material, incorporating statistical diversity in features. This representativeness mitigates outliers, ensuring that extracted parameters reflect intrinsic properties rather than sampling biases. Informationally, the larger field of view at 500× aggregates more data points (pixels), enabling robust statistical computations for fractals and GLCM, which rely on spatial patterns across scales. For D_B, this means better approximation of self-similarity over meso-to-micro transitions; for Entropy, it captures entropy from varied phase interactions. In contrast, 2000×’s advantages emerge in parameters sensitive to fine details, like Energy and Correlation at specific ages, where localized information content is paramount. However, its lower representativeness—stemming from a narrower view that might overemphasize anomalies (e.g., a single microcrack dominating the frame)—often results in inflated variability and reduced R² for holistic metrics like D_B.

Despite these advancements and the good results obtained—evidenced by consistent positive/negative trends and R² values often exceeding 0.7—the representativeness of SEM images remains a critical shortfall. SEM imaging, by nature, captures surface morphologies at high resolution but is profoundly susceptible to artifacts introduced during sample preparation. Processes such as cutting, polishing, drying, and coating can induce micro-cracks, surface roughness, or unevenness, which distort the true microstructure. Informationally, SEM’s electron backscattering emphasizes topography and composition via secondary electrons, but this can amplify noise from charging effects or beam damage, particularly in insulating cement samples. Such noise contaminates GLCM computations, where pixel-pair relationships are sensitive to outliers. These limitations manifest in the observed R² fluctuations; for example, the lower R² for mean gray value may partly stem from preparation-induced brightness artifacts rather than intrinsic weaknesses. Similarly, the magnification-dependent drops in D_B’s R² at 2000× highlight how localized artifacts (e.g., polishing scratches appearing as cracks) inflate perceived complexity without corresponding strength benefits, thus diluting correlations.

To mitigate these issues and enhance analytical precision, future research should pivot toward more representative microstructural imaging techniques that offer volumetric, non-destructive, or in situ capabilities. Backscattered Electron (BSE) imaging, an extension of SEM, is a promising alternative. BSE detects atomic number contrasts, providing compositional maps that distinguish phases (e.g., unhydrated clinker from pores) with less topographic bias [45]. Unlike secondary electron SEM, BSE is less affected by surface roughness, as it penetrates deeper (microns), yielding more representative cross-sections [46,47,48]. Preparation artifacts are minimized through flat polishing and conductive coating, and quantitative BSE analysis (e.g., via thresholding for porosity) can integrate with texture parameters for hybrid models [49,50]. Another superior modality is X-ray Computed Tomography (X-CT), which enables three-dimensional reconstruction of internal microstructures without destructive sectioning. X-CT scans entire volumes (mm to cm scales), capturing true representative-ness by averaging heterogeneities across slices [51,52]. This volumetric data allows extraction of 3D fractals, porosity networks, and texture analogs (e.g., 3D GLCM extensions), directly linking to mechanical properties via finite element simulations informed by tomographic data [53,54,55]. For cement-based materials, X-CT excels in quantifying 3D pore connectivity, tortuosity, and phase distributions, which are critical for strength prediction [56,57].

4. Conclusions

This study comprehensively investigated the regulatory effects of triethanolamine (TEA) and its maleic acid-modified derivative (MGA) on the grinding efficiency, hydration processes, microstructural characteristics, and mechanical properties of cement paste, both independently and in combination with polycarboxylate superplasticizer (PCA), employing advanced analytical methods such as particle size distribution, XRD, SEM, BET surface area analysis, and quantitative texture metrics (fractal dimension and GLCM). Through these analyses, the following key conclusions are drawn:

(1) The maleic acid-modified triethanolamine (MGA) demonstrated a statistically significant improvement in grinding efficiency over TEA, with a notable reduction in D50 values (14.86 μm for TEA compared to 14.69 μm for MGA, p-value < 0.05). This improvement is attributed to the introduction of additional polar groups in MGA, which facilitate stronger adsorption on cement particles, resulting in finer granulometry and narrower particle size distribution.

(2) The combined application of grinding aids and polycarboxylate superplasticizer (PCA) yields synergistic enhancements in microstructural refinement and mechanical performance. The incorporation of MGA led to a 15% increase in compressive strength compared to TEA. The combination of MGA and PCA resulted in a 20% increase, highlighting the synergistic effect of these additives. This enhancement is linked to the refined microstructure and denser hydration product networks facilitated by MGA and PCA.

(3) Advanced image processing techniques, such as fractal dimension and gray level co-occurrence matrix (GLCM), provide robust quantitative characterization of microstructural evolution. These methods reveal statistically strong correlations between texture parameters and mechanical properties: the fractal dimension D_B exhibits a significant positive correlation with compressive strength (with R² values up to 0.78), while energy and correlation values show a clear negative correlation. In contrast, entropy and contrast values demonstrate a pronounced positive correlation. Specifically, MGA and MGA-PCA systems reduce fractal complexity and enhance texture uniformity, which strongly correlates with improved mechanical properties. This quantitative approach surpasses qualitative SEM observations, offering reproducible metrics for predicting long-term durability.

5. Outlook and Future Studies

Based on the findings of this study, several concrete directions for future research are planned:

(1) Extension to Complex Binders: The quantitative texture analysis methodology will be applied to more complex systems containing supplementary cementitious materials (SCMs) like fly ash or slag, and their interactions with different grinding aid/superplasticizer combinations.

(2) 3D Microstructural Analysis: We plan to employ X-ray microcomputed tomography (μ-CT) to obtain 3D reconstructions of the microstructure. This will allow us to calculate 3D fractal dimensions and pore network parameters and correlate them with the 2D texture features extracted from SEM images in this study.

(3) In situ Hydration Monitoring: To further elucidate the kinetics observed indirectly through texture analysis, in situ studies using isothermal calorimetry coupled with rheological measurements are planned to precisely track the early hydration process under the influence of these admixtures.

(4) Durability Correlation: A crucial next step is to investigate how these quantitatively characterized micro-textural parameters (e.g., fractal dimension, GLCM entropy) correlate with long-term durability properties such as chloride diffusion coefficient and resistance to sulfate attack.

(5) Machine Learning Prediction: We intend to develop machine learning models that utilize the extracted texture features (e.g., contrast, energy, correlation) from SEM images as input to predict the mechanical and durability performance of cementitious mixes, potentially streamlining the mix design process.