Abstract
This paper provides a recent overview of the exact, approximate, and hybrid optimization methods that handle Multi-Objective Mixed-Integer Non-Linear Programming (MO-MINLP) problems. Both the domains of exact and approximate research have experienced significant growth, driven by their shared goal of addressing a wide range of real-world problems. This work presents a comprehensive literature review that highlights the significant theoretical contributions in the field of hybrid approaches between these research areas. We also point out possible research gaps in the literature. Hence, the main research questions to be answered in this paper involve the following: (1) how to exactly or approximately solve a MO-MINLP problem? (2) What are the drawbacks of exact methods as well as approximate methods? (3) What are the research lines that are currently underway to enhance the performances of these methods? and (4) Where are the research gaps in this field? This work aims to provide enough descriptive information for newcomers in this area about the research that has been carried out and that is currently underway concerning exact, approximate, and hybrid methods used to solve MO-MINLP problems.
1. Introduction
Applications of optimization are countless, with the potential for optimizing every process. It is a ubiquitous task for companies, as there is no organization that does not engage in solving optimization problems [1]. Furthermore, any system design inherently involves an optimization process [2]. In fact, numerous challenging applications in science and industry can be formulated as optimization problems [3,4], where the objective is to minimize time, cost, and risk, or maximize profit, quality, and efficiency.
The inherent complexity and constraints of real-world systems cause the presence of discrete decisions and non-linearities. Such problems are mixed-integer problems, which combine combinatorial and continuous optimization challenges. Solving these problems is exceedingly difficult due to the need to explore a large number of possible solutions in the combinatorial space, ensuring the identification of the best one, and the infinite and potentially unbounded nature of the continuous search space. Consequently, there are limited dedicated algorithms available for dealing with mixed-variable problems [5,6].
Mixed-Integer Non-Linear Programming (MINLP) problems can be classified into two categories: mono-objective problems, which involve one objective function resulting in an optimal solution, and multi-objective problems, which involve multiple objectives to be optimized simultaneously, resulting in a set of solutions called the Pareto Front. In this paper, we specifically focus on multi-objective methods.
1.1. Problem Formulation
The general Multi-Objective MINLP (MO-MINLP) problem is written as
where , and c are the objectives, equality constraints, and inequality constraints functions, respectively, that are not necessarily convex or differentiable, and p and m are the numbers of objectives and constraints, respectively. x and y denote the variables of the problem, where and are the number of continuous and integer variables, respectively.
The optimal solution of a multi-objective problem is a set of non-dominated solutions called the Pareto front . Each non-dominated solution is called a Pareto element. For a given and vector values of the objective function for two given “points” solution in the feasible set, the dominance relation between them is defined by the following.
Definition 1.
dominates , (), when no value of is less than and at least one value value of is strictly greater than [7].
1.2. Applications
Multi-Objective Mixed-Integer Non-Linear Programming (MO-MINLP) problems appear in several real-world applications, such as engineering, chemistry, environmental science, operational research fields, and others. Table 1 shows some application examples in distinct subject areas.

Table 1.
Subject Areas and Applications of MO-MINLP.
Although MO-MINLP problems appear in many fields, this paper highlights especially MO-MINLP problems in the engineering domain. Engineering problems frequently require decisions that can only take on a finite set of values or options such as selecting equipment types, determining the number of components to use, or deciding on routing options. Simultaneously, these problems often involve continuous variables, which can take on any real value within a given range. These variables typically represent the design parameters of a system, such as dimensions or flow rates. In real-world engineering systems, these variables are often related non-linearly. This non-linearity can arise from physical phenomena, process dynamics, or system constraints. Optimization of conflicting objectives appears in various engineering problems where improving one objective may lead to degradation in another. Hence, MO-MINLP has established a significant presence in the engineering field. In [27], the authors design an optimization problem for an integrated bioenergy park that combines algal cultivation with sludge-based bioenergy production. The MO-MINLP problem aims to optimize both economic and environmental objectives by minimizing operational costs, energy production, and carbon emissions simultaneously. In [28], the authors propose a novel MO-MINLP model for the transit network design and frequency-setting problem. The model considers multiple objectives, including minimizing travel time, reducing waiting times, avoiding overcrowding, and optimizing the utilization of the vehicle fleet. The study applies the model to a real-world bus transport network in Kayseri, Turkey, demonstrating its effectiveness in improving transit planning. In [29], the authors develop an MO-MINLP model of optimal conductor selection in direct current (DC) distribution networks with radial topology. The model aims to optimize the total investment in conductors and the total cost of energy losses in one year of operation. In [30], the authors integrate pressure-drop estimation and density prediction into the hydrogen network problem. The resultant MO-MINLP model aims to maximize the flow rate and minimize the total annual cost. In [31], the authors develop an optimization model of an integrated energy system that combines fuel, wind, and solar energies. The MO-MINLP model aims to optimize the system’s performance in terms of energy savings, cost reductions, and carbon emission reductions. The study uses a case study of hospital buildings in Harbin, China, to validate the model and demonstrate its significant improvements.
1.3. State-of-the-Art of Review Articles
Optimization methods can be classified into exact, approximate, or hybrid methods [32]. This classification is based on the type of the resulting solution(s) by the method, i.e., exact (real) solution or approximate (estimated) solution, while hybrid methods acquire their name from the hybridization of different methods to produce better performance. Exact methods are deterministic algorithms that converge towards a solution that satisfies some optimality conditions. These algorithms have been successfully applied to many engineering design problems [33]. Exact methods offer the guarantee of identifying the true optimum of a problem. However, their computational cost becomes prohibitively high when dealing with a large combinatorial space resulting from the inclusion of integer variables. Conversely, approximate methods are characterized by their stochastic nature and employ probabilistic transition rules. These methods have been developed to overcome the limitations of exact methods and are capable of solving complex optimization problems, providing solutions of good quality within a comparatively shorter time frame.
Many academics have presented detailed surveys for multi-objective optimization problems (MOPs) from various angles as the field of MOPs has progressed [34,35]. Existing reviews, however, are more focused on continuous MOPs. Although the MINLP field has received substantial attention, the mono-objective field has received the most attention [36,37,38,39]. Relatively few reviews on MO-MINLPs have been published, even though these problems exist widely in real-world applications (refer to Table 1). Peres and Castelli [40] discussed the main concepts and challenges in the multi-objective combinatorial optimization area and proposed a formalism to classify, design, and code combinatorial optimization problems and metaheuristics. Liu et al. [41] provided a comprehensive review of multi-objective metaheuristics and applications for MO-MINLP including combinatorial optimization problems as well as integer or mixed-integer programs. In [42,43], the authors reviewed and classified the hybrid metaheuristics in the MO-MINLP field. In [44], the authors reviewed both exact and approximate methods for multi-objective combinatorial optimization problems (MOCOPs); yet, this review concerns linear programming only. Table 2 shows the problem and method types covered by several review articles. Although these reviews have significantly contributed to the literature from different aspects, none give a general overview regarding all exact, approximate, and hybrid methods that handle MO-MINLP problems. Such an overview is notably important for newcomers to this domain.

Table 2.
Problem and Solution Methodology Types Handled in Previous Review Articles.
1.4. Contribution
This paper aims to contribute to the literature by providing a recent overview of the exact, approximate, and hybrid optimization methods that handle MO-MINLP problems. This work aims to provide enough descriptive information for newcomers in this area on the research that has been done and that is currently underway concerning the methods used to solve MO-MINLP problems. The main research questions to be answered in this paper involve the following: (1) How to exactly or approximately solve a MO-MINLP problem? (2) What are the drawbacks of exact methods as well as approximate methods? (3) What are the research lines that are currently underway to enhance the performances of these methods? and (4) Where are the research gaps in this field?
1.5. Procedure and Approach
The main scope of this paper is to describe and discuss all paradigms proposed in the literature to solve MO-MINLP problems. Some paradigms are extensively discussed in the literature, so we highlight the review articles that focus on this particular domain. Other paradigms have less attention in the literature, hence, we provide a brief review of these. Some paradigms have not been discussed in the literature, thus, we highlight these as research gaps. Each set of methods that follow a single paradigm has been discussed individually in this paper. To this aim, the literature has been reviewed using the Scopus database based on a combination of five groups of specific keywords. The first group of keywords consists of multi-objective, multi-criteria, and many objectives. The second group consists of evolution, evolutionary, genetic, firefly, ant colony, bee colony, particle swarm, heuristic, and metaheuristic. The third group consists of exact, deterministic, and true Pareto fronts. The fourth group consists of hybrid, tree search, combining metaheuristics, and multi-criteria branch and bound. Furthermore, the last group consists of discrete, combinatorial, and mixed-integer. From the resulting search, publications with a recent publication date and/or having more citations have been preferred.
1.6. Paper Organization
The rest of the paper is organized as follows. Section 2 reviews the exact methods used in the literature to solve MO-MINLP problems. Section 3 presents an overview of approximate methods and their pros and cons. In Section 4, hybrid approaches are classified and reviewed pointing to the research gap in the literature. Finally, an overall conclusion is drawn in Section 5.
2. Exact Methods
Exact methods refer to deterministic algorithms that iteratively converge towards a solution that satisfies specific optimality conditions. These algorithms have demonstrated successful applications in various engineering design problems [33]. The main concept of a multi-objective exact method is to convert the multi-objective problem into a mono-objective one. Each method has its own mechanism to make this conversion. In this section, we show the different types of mechanisms. The main methodologies for the exact solution of multi-objective non-linear problems with mixed-integer variables are the scalarization methods and multi-criteria branch and bound methods [46].
2.1. Scalarization Methods
The most commonly employed technique, found in both exact methods and many heuristic techniques, to identify efficient solutions is known as scalarization [47,48]. Scalarization methods are not dedicated to MO-MINLP problems only; in fact they are general techniques that transform the multi-objective problem into a single-objective one. In [49], the authors have mentioned five scalarization methods that are used to solve MO-MINLP problems. In particular, they transform MO-MINLP into a scalarized MINLP. The scalarized problem pertains to a single-objective MINLP problem that is derived from the MO-MINLP problem by introducing additional variables and/or parameters. Typically, the scalarized problem is solved iteratively to identify a subset of the solutions set of the MO-MINLP problem. Although the literature proposes a variety of scalarization methods (reviewed in [35,48]), this section outlines only some of the most frequently employed scalarization strategies.
2.1.1. The Weighted Sum Method
The scalarization by the weighted sum method entails constructing a convex combination of the p objectives in MO-MINLP, preserving the original feasible set:
where is the weight of each objective function . Conserving the computational complexity is a significant advantage in the weighted sum method. Consequently, it requires an equivalent computational effort for solving the single-objective version of the MO-MINLP problem [48].
2.1.2. The -Constraint Method
The -constraint technique is widely recognized as one of the most popular methods for identifying all efficient solutions. In this method, one of the p objectives (specifically, the j-th objective) is retained for minimization, while the remaining objectives are transformed into constraints:
By appropriately specifying the values of the right-hand side, it is possible to identify all efficient solutions. However, it is important to note that the computational effort required varies significantly depending on the specific problem characteristics [48].
2.1.3. Pascoletti–Serafini Scalarization
This approach, introduced by Pascoletti and Serafini (1984) [50], is commonly known as the goal-attainment method. Given a fixed , Pascoletti–Serafini (PS) scalarization formulates the following problem:
where is a new variable and is an optimal vector. The optimal vector is found by varying the parameters of the scalar problem.
2.1.4. Normal Boundary Intersection (NBI)
The Normal Boundary Intersection (NBI) method, introduced by Das and Dennis (1998) [51], is a valuable tool for solving multi-objective optimization problems and generating Pareto optimal solutions. In comparison to other conventional methods like the weighted sum method, the NBI technique offers two key advantages [52]: (1) Independence from the values of the objective functions: The performance of the NBI method remains unaffected by the scale or magnitude of the objective functions; and (2) Even distribution of Pareto optimal solutions: The NBI method produces Pareto optimal solutions that are evenly spread across the solution space. Recently, the NBI method has been gaining popularity in the field of mixed-integer optimization [52,53,54].
2.2. Multi-Criteria Branch and Bound
Branch and bound (B&B) is a widely recognized and versatile method used for computing optimal solutions in single-objective optimization problems. It employs a “divide and conquer” approach, utilizing an implicit enumeration principle represented as a tree search. The feasible set of the problem is iteratively partitioned to form subproblems of the original one. Generally, in branch and bound, the main problem is divided into subproblems (nodes). Each subproblem is assessed to obtain a lower bound on its objective value. These lower bounds are then utilized to construct a proof of optimality without the need for an exhaustive search. Subproblems that are deemed uninteresting or infeasible are pruned (fathomed) as with the red subproblem in Figure 1, while promising subproblems are selected and instantiated as with the blue problems in Figure 1.
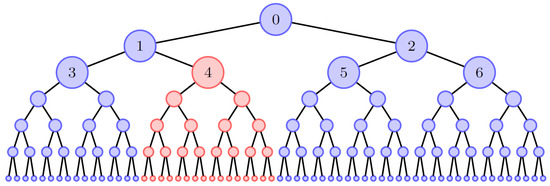
Figure 1.
Implicit enumeration of the domain space by branch and bound algorithm.
While the original branch and bound method was proposed by Land and Doig in 1960 [55], it was not until 1983 that Kiziltan introduced the first complete algorithm incorporating a multi-objective branch and bound approach [56]. This work was later referenced by Przybylski et al. [46]. In 1998, an algorithm for multi-objective mixed binary linear programming (MO-MILP) problems was presented [57]. Mavrotas proposed the Multi-Criteria Branch and Bound (MCBB) method [57], which employs a vector optimization approach to generate all the efficient extreme solutions for Mixed 0–1 multi-objective linear problems. By modifying the conventional branch and bound algorithm to systematically explore feasible combinations of binary variables, the algorithm effectively identifies all non-dominated solutions in multiple objective problems.
MCBB was successfully implemented to solve mixed integer linear problems in the engineering [10], operational research [58] and chemical [59] fields. Moreover, MCBB was used to develop a heuristic method to solve convex MO-MINLP problems in [58]. Later, in [60], the authors proposed the first deterministic MCBB-based method to solve convex MINLP problems.
2.2.1. Branching
Branching is a procedure used to partition a problem domain into subsets, ensuring that the union of these subsets is equivalent to the complete set. When applying a branching strategy, the bounds of integer variables are manipulated, resulting in two distinct types of subspaces:
- •
- Subspaces in which all integer variables are fixed, leading to the creation of leaf nodes associated with multi-objective continuous problems.
- •
- Subspaces that include free integer variables, corresponding to mono-objective mixed-integer problems where the objective is to determine their bounds.
2.2.2. Bounding and Fathoming
Bounding a node involves evaluating its upper and lower bounds. In the case of a single-objective optimization problem, there exists at most one optimal value, and the definition of upper and lower bounds on this value is straightforward. However, in multi-objective optimization problems, upper bounds are considered on the set of non-dominated points. A well-known lower bound is the ideal point of the Pareto front.
Definition 2.
The ideal point refers to a specific point in the objective space that corresponds to the optimal value of all objectives simultaneously.
In MCBB, each node is solved repeatedly for each objective function independently. Consequently, a mono-objective solver is invoked multiple times to obtain an optimal solution for each objective function.
Fathoming in MCBB extends to handle multiple objectives. A node can be fathomed if its lower bound vector is dominated by (at least) one of the non-dominated points in the current incumbent set, or if the node is infeasible.
2.2.3. Discussion
In MCBB, certain components are left unspecified, yet they can significantly influence the algorithm’s performance [61]. These components are illustrated in Figure 2 and are as follows: the separation order, which is the sequential branching of integer variables during the exploration of subproblems in the tree; the branching strategy, which is the partitioning of the solution space to generate new subproblems within the tree; the active node selection strategy such as “deep first” or “breadth first” methods; and the fathoming rules, which are the rules that prevent exploration of sub-optimal regions of the tree. In [46,62], the authors discuss the impact of “separation order” and “choosing the active node” on the performance of MCBB. Moreover, the authors review the existing strategies and the differences between them. In [46,58], the authors review distinct pruning rules used in MCBB. In [61], the authors mention two general frameworks of “branching strategies”; however, these frameworks are dedicated to single-objective branch and bound. To the best of our knowledge, there is a lack in the literature concerning the branching strategies for MCBB.
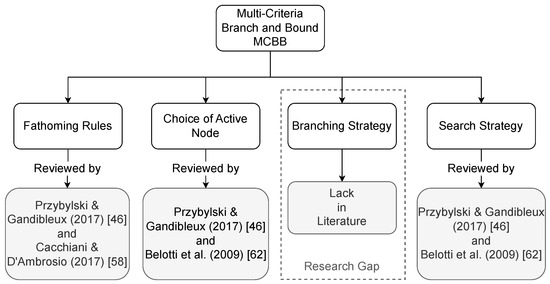
Figure 2.
MCBB components review chart.
2.3. Drawbacks and Conclusions
Figure 3 shows a guideline for newcomers to solving MO-MINLP problems. Exact methods can be categorized into mono-objective or multi-objective methods. Multi-objective methods are enumerative methods that convert the MO-MINLP problem into another type of problem. MCBB converts the MO-MINLP problem into a mono-objective MINLP problem and a multi-objective continuous NLP problem; while scalarization methods convert the MO-MINLP problem into a mono-objective MINLP problem. The methods used to solve multi-objective NLP problems are reviewed in [47], while depending on the type of the problem, i.e., convex or non-convex, the methods used to solve mono-objective MINLP problems are reviewed in [63,64], respectively. In [63], the authors mention six methods that can handle convex MINLPs, including the Outer Approximation and Extended Cutting Plane methods. In [64], the authors mention several techniques—such as factorization, under- and over-estimators, and separable functions—in addition to various branch-and-bound-based methods—such as spatial and branch and bound—to solve non-convex MINLPs.
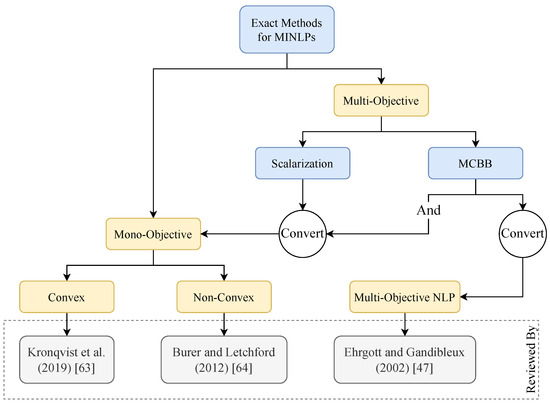
Figure 3.
A review of exact methods.
The main drawback of MINLP exact methods is first that the computation cost increases prohibitively when the combinatorial space is large. Another aspect related to exact methods that solve MINLPs is that most rely on the concept of integer relaxation, which may be undesirable in some cases, especially where categorical variables exist. In such cases, if the problem cannot be relaxed, the only way to solve it is by enumerating all possible combinations of the integer variables, which may lead to “combinatorial explosion” with an increase in the problem size; thus, only small combinatorial spaces can be solved by such an approach. Hence, although there exist exact methods for solving mixed-integer optimization problems, they have their disadvantages. They may not always be employed, either because of the problem formulation or because solving the problems would require excessive time. As a result, metaheuristics and other approximation techniques are gaining popularity.
3. Approximate Methods
In contrast to exact methods, approximate methods offer the advantage of handling large-scale problem instances and providing satisfactory solutions within a reasonable time. However, it is important to note that these methods do not guarantee finding global optimal solutions or even bounded solutions. Given the computational complexity of difficult combinatorial problems, particularly when dealing with large-scale instances, significant research efforts have been dedicated to the development of approximate algorithms in recent decades.
3.1. Metaheuristics Overview
Metaheuristics are a class of approximate approaches used to address computationally hard combinatorial optimization problems in a suboptimal way [1]. The phrase metaheuristic is formed by combining two Greek words: meta and heuriskein. “Meta” means “beyond”, “on a higher level”, and “heuriskein” means “to find”. In reality, metaheuristics are a class of algorithms that attempt to combine simple heuristic methods in higher-level frameworks in order to rapidly explore the set of possible solutions to a given combinatorial problem. Over the last few decades, metaheuristics have grown in popularity. Metaheuristics are now used in a wide range of applications [1,65,66]. Several classifications are proposed in the literature for metaheuristics as shown in Figure 4. However, this paper adopts the classification of metaheuristics proposed in [1,41], which is based on the fitness assignment (selection mechanism) as follows:
- Dominance-based metaheuristics: These metaheuristics employ the concept of Pareto dominance as the primary selection criterion to guide the multi-objective search process.
- Decomposition-based metaheuristics: These metaheuristics decompose the problem into multiple scalar sub-problems and optimize them simultaneously.
- Indicator-based metaheuristics: These metaheuristics prefer to use indicators to guide their search process.
Liu et al. [41] conducted a comprehensive review of 125 recent research papers from 39 journals in the field of MO-MINLP. The review revealed that a majority of studies (70.40%) in the literature have adopted dominance-based metaheuristics. Decomposition-based metaheuristics were found to occupy 18.40% of the related literature. Relatively fewer studies have utilized indicator-based metaheuristics. Hence, dominance-based metaheuristics are significantly the most popular class of metaheuristics to solve MO-MINLP problems. Genetic Algorithms (GAs) occupy the highest percentage (29%) of the dominance-based metaheuristics. The most popular multi-objective GA is the NSGAII [67]. In their review on NSGAII for multi-objective combinatorial optimization problems (MOCOPs), Verma et al. [68] highlighted the remarkable popularity of NSGAII. According to their findings, the original NSGAII article has been cited more than 20,630 times in the IEEE Xplore database, making it one of the most cited journal articles. Additionally, Google Scholar records over 35,240 citations for the original NSGAII article, with more than 19,600 citations from the Web of Science. These statistics demonstrate the widespread recognition and popularity of NSGAII.
In their review of 169 papers, Verma et al. [68] observed that NSGAII was applied to solve MOCOPs in three categories: conventional (8%), modified (58%), and hybrid (34%) forms. The modifications were typically made to address the limitations of the conventional NSGAII for specific problems. Researchers commonly modified NSGAII by adjusting the crossover operator, mutation operator, initialization procedure, parent selection, and constraint handling techniques to enhance its convergence and diversity. Hybridization techniques were also employed to improve the efficiency of NSGAII for particular problems or classes of problems. Among the hybridization approaches, the tabu search algorithm [69] was frequently utilized in conjunction with NSGAII.
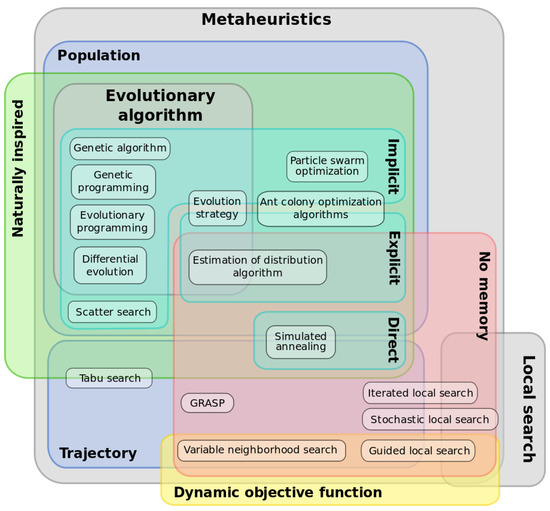
Figure 4.
Classification of metaheuristics [70].
3.2. Drawbacks and Discussion
3.2.1. Best Metaheuristic
The use of metaheuristics in many applications shows their efficiency and effectiveness in solving large and complex problems. However, in the context of mechanical engineering optimization, for example, the literature does not provide a clear conclusion on which metaheuristic has the best performance. In [71], the authors concluded that the best metaheuristic is the moth-flame optimization (MFO) on a benchmark of six mono-objective mixed-integer engineering design problems. In [72], the authors found that the best metaheuristic is the mixed differential evolution (NAMDE) on a benchmark of 13 mono-objective mixed-integer engineering design problems. In [73], the authors observed that EMoSOA—a new evolutionary multi-objective seagull optimization algorithm for global optimization—is the best-performing algorithm on a benchmark of four multi-objective mixed-integer engineering design problems. In [74], the authors concluded that the butterfly metaheuristic is the best on a benchmark of four mono-objective engineering design problems. In [75], a discrete rat swarm optimizer (DRSO) algorithm was proposed to solve the discrete quadratic assignment problem (QAP). The authors demonstrated the effectiveness of the algorithm through extensive simulations and comparisons with other algorithms. The results consistently indicate that DRSO outperforms these algorithms in terms of solution quality and convergence speed. In their work [76], Kaur et al. introduced the Emperor Penguin Optimizer (EPO) as a metaheuristic algorithm for solving multi-objective problems. They extended the capabilities of EPO to handle multi-objective optimization and named the modified algorithm Multi-objective Emperor Penguin Optimizer (MOEPO). Through empirical analysis, the authors demonstrated the superior performance of MOEPO compared to other existing algorithms on seven multi-objective mixed-integer engineering problems. Table 3 summarizes these results in terms of problem type, number of problems, and best metaheuristic. Therefore, the literature does not provide a clear conclusion on which metaheuristic has the best performance on mono-objective/multi-objective MINLP problems even in a single subject area such as engineering applications.

Table 3.
Best Metaheuristic for MINLP Engineering Problems.
3.2.2. Metaheuristics Suitability for MO-MINLP Problems
In their work [79], Giagkiozis et al. conducted a comprehensive review of seven metaheuristic families (GA, Evolution Strategies (ES), Artificial Immune System (AIS), Ant Colony Optimization (ACO), Differential Evolution (DE), Particle Swarm Optimization (PSO), and Estimation of Distribution algorithms (EDA)) to evaluate their capability to handle mixed-variable problems in multi-objective optimization. The authors employed a scale ranging from 1 to 5 to assess the relative strengths and weaknesses of these algorithm families. A rating of 5 indicated high suitability for solving this type of problem, while a rating of 1 indicated poor suitability. Surprisingly, the comparison revealed that although six out of the seven algorithms were capable of handling mixed variables optimization, all six algorithms received a suitability score of 1. In their thesis [11], El Samrout examined five well-known metaheuristics in the field of combinatorial optimization: (1) NSGAII; (2) MOPSO; (3) Cuckoo Search; (4) Bat Algorithm; and (5) Firefly Algorithm. The evaluation was conducted on three MO-MINLP engineering design problems. By comparing the solutions obtained from these metaheuristics with the true Pareto front of each problem, the author concluded that “the traditional metaheuristics were unable to solve the three optimization problems”.
Similarly, in another study by Jaber et al. [10], the same engineering design problems were tackled using NSGAII, resulting in low-quality solutions. Even with the utilization of the best metaheuristic, which in this case was NSGAII, not all Pareto solutions were discovered. The calculated Pareto front remained far from being a satisfactory solution, as indicated by the low percentage of intersection between the true front and the calculated one for all three problems. Furthermore, conventional metaheuristics demonstrated their limited capability in handling mixed-variable constrained problems. Consequently, the need for a more effective approach to address such problems has become a focal point of interest for numerous researchers. In the past few decades, a new line of research has arisen, that of the hybridization of distinct algorithms. In the next section, an overview of these hybrid methods is presented.
4. Hybrid Methods
In recent years, there has been a proliferation of algorithms that go beyond the traditional framework of a single classic metaheuristic, as highlighted by Blum et al. [39]. These algorithms integrate various components derived from optimization research in different fields, giving rise to what is known as hybrid metaheuristics.
The hybridization of metaheuristics has become a prevalent strategy for solving optimization problems. The abundance of efficient hybrid metaheuristics serves as evidence that these approaches are highly effective for both classical and real-life challenging problems, as noted by El Samrout [11]. The rationale behind combining multiple algorithms is to leverage the complementary nature of diverse optimization strategies, aiming to achieve synergy. Selecting the appropriate combination of complementary algorithmic approaches is crucial for achieving improved performance in various challenging optimization problems [39].
Literature reviews on hybrid methods for multi-objective optimization have been conducted by Ehrgott et al. [43,44] and on single-objective hybrids and their classifications by Blum et al. [39]. Different approaches for combining exact algorithms and metaheuristics to solve combinatorial optimization problems have been discussed by Puchinger et al. [32].
4.1. Hybrids Classifications
The initial approach to hybridization involved combining different metaheuristics. Initially, this approach seemed to be the most straightforward, and other methods of hybridizing metaheuristics were overlooked. It was only later that researchers recognized the complementary nature between certain exact methods and metaheuristics, leading to the emergence of this type of hybridization [11]. Consequently, hybrids are classified into two categories in this section: the hybridization of metaheuristics with other metaheuristics and the hybridization of approximate methods with exact methods. In this context, several trials of a combination of metaheuristics and machine learning are proposed; however, these approaches are out of our scope. Interested readers can refer to [11,42].
4.1.1. Metaheuristics with Metaheuristics
A notable observation is that many hybrid metaheuristics in this field are based on the collaboration between trajectory-based (or single-solution-based) metaheuristics and population-based metaheuristics. The reasoning behind this cooperation lies in the complementary nature of these two approaches for multi-objective optimization. Trajectory-based metaheuristics excel at intensifying the search by aggressively converging toward good solutions. However, they require guidance along the non-dominated frontier. Conversely, population-based approaches are proficient explorers of the search space, capable of maintaining a diverse population of solutions along the non-dominated frontier. However, they often converge slowly to the non-dominated frontier. As a result, methods that combine components from both approaches can effectively leverage these features, offering a favorable trade-off. In their works [43,44], the authors propose a classification scheme for hybridizing multi-objective metaheuristics based on the objectives of the hybridization process. The classification includes the following categories:
- Hybridization to enhance search aggressiveness: The objective here is to improve the exploration capability of the approximation procedure. For instance, a common approach is to combine a multi-objective evolutionary algorithm (EA) with a neighbor search algorithm. This combination aims to refine promising solutions obtained from evolutionary operators and maximize their quality.
- Hybridization for guided search: In this category, the goal is to incorporate a guiding mechanism along the non-dominated frontier. Population-based metaheuristics like multi-objective genetic algorithms (GAs) are utilized to extract global information about the current approximation. This information then guides local search processes, ensuring a thorough coverage of the non-dominated frontier.
- Hybridization for leveraging complementary strengths: Here, the focus is on harnessing the complementary strengths of different metaheuristics. For example, a GA algorithm may be employed initially to generate a diverse set of high-quality solutions, followed by the application of an aggressive search method (e.g., tabu search) to further refine the solutions.
4.1.2. Metaheuristics with Exact Methods
In [11,80], the authors classify multi-objective metaheuristics–exact hybrids based on the concept of the algorithm as follows:
- Metaheuristic-based upper bound generation: This approach involves executing a multi-objective metaheuristic to obtain an approximation of the Pareto set. The obtained approximation is then used to initialize a multi-objective exact algorithm. By employing a branch and bound algorithm, a significant number of nodes in the search tree can be pruned, improving the overall efficiency of the hybrid approach.
- Exact algorithm for solving subproblems: In this hybrid strategy, a multi-objective exact algorithm is utilized to solve subproblems that are generated by the multi-objective metaheuristic. Leveraging the strengths of the exact algorithm, these subproblems can be solved optimally or near-optimally.
The combination of metaheuristics/heuristics with tree search techniques is widely recognized as a popular approach for integrating different algorithms in optimization. A fundamental component of any optimization technique is the mechanism for exploring the search space, which refers to the space of valid solutions for the given optimization problem. The hybridization of metaheuristics with branch and bound concepts is rather recent [81]. On one side, it is possible to use branch and bound concepts within metaheuristics in order to increase the efficiency of the metaheuristics search process. On the other side, metaheuristics can be used within branch and bound in order to reduce the space and time consumption of branch and bound. Ideally, such hybrids are expected to obtain higher quality solution(s) than that obtained by metaheuristics with less effort than that consumed by branch and bound as illustrated in Figure 5.
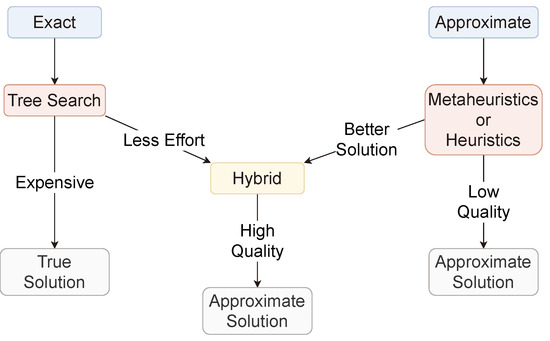
Figure 5.
Combining approximate methods with tree search.
4.2. Combining B&B with Metaheuristics
In [42], the author categorized the hybridization mechanisms between metaheuristics and the mono-objective branch and bound (and its variants) as follows:
- Metaheuristic for generating an upper bound.
- Exact algorithm for exploring very large neighborhoods.
- Exact algorithm for solving subproblems.
- Exact algorithm for achieving one objective improvement.
- Exact algorithm for exploring the infinite region (∞ Region).
In the following, we provide descriptive examples of hybridization mechanisms between metaheuristics and mono-objective branch and bound algorithms, encompassing both mono- and multi-objective trials.
In one of the pioneering works on combining branch and bound with an evolutionary algorithm, the authors of [82] present a two-stage process. The first stage involves executing the branch and bound method up to a predefined tree level, denoted as k. During this stage, lower bounds are evaluated using a heuristic method. The second stage entails executing the evolutionary algorithm on the active nodes identified in the first stage.
Another approach, introduced in [83], incorporates the branch and bound method into the evolutionary algorithm. This framework embeds the branch and bound operator within the evolutionary process, allowing the hybrid operator to explore potential offspring generated through recombination and identify optimal combinations without implicit mutation.
In [84], a chunking-based strategy is proposed to decide at each node of the branch and bound tree whether a metaheuristic should be called to find a better incumbent solution.
In [85], the NSGAII algorithm generates potentially Pareto optimal solutions, which are then used to construct subproblems. These subproblems are subsequently solved using the branch-and-cut algorithm.
The work presented in [86] utilizes an evolutionary algorithm with an order representation, specific recombination and mutation operators, and a decoding heuristic. In one variant, branch and bound is occasionally applied to locally optimize parts of a solution during decoding.
In [39], a portion of the decision variables are fixed to their values in an incumbent solution, while the remaining “free” variables are optimized using a MIP-solver. If an improved solution is found, it becomes the new incumbent, and the process is iterated within a defined large neighborhood.
In [81], branch and bound concepts are employed to enhance the solution construction process of ant colony optimization.
The authors of [87] utilize the constraint programming system, employing the depth-first branch and bound technique to validate solutions and determine the values of constrained variables, rather than searching for solutions.
Extensive literature reviews on this topic can be found in [32,39,43].
4.3. Combining MCBB with Heuristics
Researchers have also conducted several trials implementing MCBB algorithms using heuristic methods.
In [58], the author proposes a heuristic approach based on MCBB. The algorithm initiates with a set of feasible points obtained at the root node of the enumeration tree. These points are obtained iteratively by solving a single-objective model using an -constraint method, where the other objective functions are incorporated as constraints. Lower bounds are derived by optimally solving Non-Linear Programming problems (NLP) problems. Each leaf node of the enumeration tree corresponds to a convex multi-objective NLP problem, which is heuristically solved by varying the weights in a weighted sum approach.
In [88], the authors utilize both exact and approximate algorithms. The exact algorithm is a modified version of MCBB, further customized with appropriate heuristics. Three branching heuristics and a composite branching and construction heuristic are devised to enhance its performance.
In [89], the authors develop a heuristic method based on a branch and bound structure. The proposed method combines several lower bounds, upper bounds, and dominance rules.
4.4. Discussion and Conclusions
The performance of conventional metaheuristics on MO-MINLP problems was discussed in Section 3 with the conclusion that the current performance is not sufficient for this type of problem. Similarly, exact methods are too expensive when they are applied to mid- to large-scale problems. Many researchers have proposed using hybrids of metaheuristics with mono-objective branch and bound algorithms to enhance the performance of metaheuristics. Some have also suggested incorporating heuristics with multi-criteria branch and bound algorithms. However, to the best of our knowledge, there is a noticeable lack of literature on the hybridization of multi-criteria branch and bound algorithms with metaheuristics, in contrast to the extensive research on mono-objective branch and bound algorithms as illustrated in Figure 6. This lack of literature may be due to the apprehension of high computational effort. Hence, any design of such hybrids must consider the “investment” in computational effort, in which, hybrids that combine MCBB with a metaheuristic are expected to consume more effort than the metaheuristic alone. However, what if this investment in the computational effort is added to the metaheuristic itself (as increasing the maximum generations or population size in GA)? In fact, this is an open research question that should be considered when examining the performance of such hybrids. Furthermore, it has been observed by [39] that the effectiveness of hybrid approaches can vary depending on the specific problem at hand, while some hybrids may perform well for certain problems, they may not be as effective for others. Nevertheless, there exist hybridization strategies that have consistently demonstrated success across a wide range of applications. These successful hybrids can serve as valuable references and provide guidance for future developments in the field.
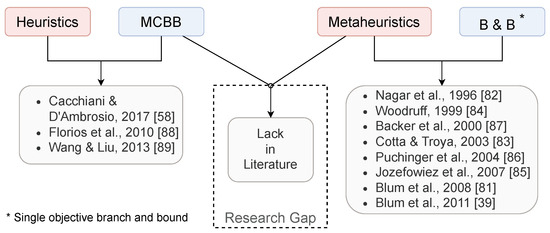
Figure 6.
A review of hybrid tree search with approximate methods.
5. Conclusions
In summary, addressing mixed-variable optimization problems poses significant challenges as it involves the convergence of two distinct types of difficulties. The first challenge arises from the combinatorial nature of these problems, necessitating a comprehensive exploration of the solution space to guarantee the identification of the optimal solution. The second challenge stems from the continuous nature of the problems, where the search space is infinite and potentially unbounded. The main drawback of MINLP exact methods is that the computation cost increases prohibitively when the combinatorial space is large. Unlike exact methods, approximate methods allow the tackling of large-size problem instances by delivering satisfactory solutions in a reasonable time. However, it is not clear what metaheuristic delivers the best performance. Additionally, conventional metaheuristics are not able to handle mixed-variable constrained problems. In this paper, we have provided descriptive information for newcomers in this area on the research that has been done and that is currently underway concerning the methods used to solve MINLP problems. Moreover, we have highlighted the research gaps found in the literature regarding the following: (1) the branching strategies for the Multi-Criteria Branch and Bound (MCBB); and (2) the hybridization of MCBB with metaheuristics.
Author Contributions
Conceptualization, A.J.; Methodology, A.J., R.Y. and P.L.; Project administration, P.L.; Supervision, R.Y. and P.L.; Validation, A.J., R.Y., J.K. and P.L.; Writing—original draft, A.J. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the Lebanese University (LU); the regional council of the “Grand Est” region, France; and the European Regional Development Fund (ERDF).
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Talbi, E.G. Metaheuristics: From Design to Implementation; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Breitkopf, P.; Coelho, R.F. Multidisciplinary Design Optimization in Computational Mechanics; Wiley-ISTE: Hoboken, NJ, USA, 2013. [Google Scholar]
- Bensemlali, M.; Hatimi, B.; Sanad, A.; El Gaini, L.; Joudi, M.; Labjar, N.; Nasrellah, H.; Aarfane, A.; Bakasse, M. Novel Synthesis of Nanocalcite from Phosphogypsum and Cesium Carbonate: Control and Optimization of Particle Size. Eng 2024, 5, 932–943. [Google Scholar] [CrossRef]
- Bikas, H.; Manitaras, D.; Souflas, T.; Stavropoulos, P. Process-Driven Layout Optimization of a Portable Hybrid Manufacturing Robotic Cell Structure. Eng 2024, 5, 918–931. [Google Scholar] [CrossRef]
- Socha, K. Ant Colony Optimisation for Continuous and Mixed-Variable Domains; VDM Verlag: Saarbrücken, Germany, 2009. [Google Scholar]
- Socha, K.; Dorigo, M. Ant colony optimization for continuous domains. Eur. J. Oper. Res. 2008, 185, 1155–1173. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Muiltiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
- Jaber, A.; Lafon, P.; Younes, R. An Application of BnB-NSGAII: Initializing NSGAII to Solve 3 Stage Reducer Problem. In Proceedings of the Optimization and Learning, Sicilia, Italy, 21–23 June 2021; Communications in Computer and Information Science. pp. 337–349. [Google Scholar] [CrossRef]
- Han, L.; Liu, G.; Yang, X.; Han, B. Dimensional and Layout Optimization Design of Multistage Gear Drives Using Genetic Algorithms. Math. Probl. Eng. 2020, 2020, 3197395. [Google Scholar] [CrossRef]
- Jaber, A.; Lafon, P.; Younes, R. A branch-and-bound algorithm based on NSGAII for multi-objective mixed integer nonlinear optimization problems. Eng. Optim. 2021, 54, 1004–1022. [Google Scholar] [CrossRef]
- El Samrout, A. Hybridization of Multicriteria Metaheuristic Optimization Methods for Mechanical Problems. Ph.D. Thesis, Université de technologie de Troyes, Troyes, France, 2019. [Google Scholar]
- Canelas, E.; Pinto-Varela, T.; Sawik, B. Electricity portfolio optimization for large consumers: Iberian electricity market case study. Energies 2020, 13, 2249. [Google Scholar] [CrossRef]
- Syauqi, A.; Purwanto, W.W. Mixed-integer non-linear programming (MINLP) multi-period multi-objective optimization of advanced power plant through gasification of municipal solid waste (MSW). Chem. Prod. Process Model. 2020, 15, 20190126. [Google Scholar] [CrossRef]
- Ghaseminejad, A.; Kazemipoor, H.; Fallah, M. Modeling the robust facility layout problem for unequal space considering health and environmental safety criteria under uncertain parameters. Decis. Mak. Appl. Manag. Eng. 2023, 6, 426–460. [Google Scholar] [CrossRef]
- Monsiváis-Alonso, R.; Mansouri, S.; Román-Martínez, A. Life cycle assessment of intensified processes towards circular economy: Omega-3 production from waste fish oil. Chem. Eng. Process. Process Intensif. 2020, 158. [Google Scholar] [CrossRef]
- Ernst, P.; Zimmermann, K.; Fieg, G. Multi-objective Optimization-Tool for the Universal Application in Chemical Process Design. Chem. Eng. Technol. 2017, 40, 1867–1875. [Google Scholar] [CrossRef]
- Zimmermann, K.; Fieg, G. Development of a Diversity-Preserving Strategy for the Pareto Optimization in Chemical Process Design. Chemie-Ingenieur-Technik 2017, 89, 1297–1305. [Google Scholar] [CrossRef]
- Gargalo, C.; Carvalho, A.; Gernaey, K.; Sin, G. Optimal Design and Planning of Glycerol-Based Biorefinery Supply Chains under Uncertainty. Ind. Eng. Chem. Res. 2017, 56, 11870–11893. [Google Scholar] [CrossRef]
- Brunet, R.; Guillén-Gosálbez, G.; Jiménez, L. Combined simulation–optimization methodology to reduce the environmental impact of pharmaceutical processes: Application to the production of Penicillin V. J. Clean. Prod. 2014, 76, 55–63. [Google Scholar] [CrossRef]
- Zhang, S.; Zhuang, Y.; Tao, R.; Liu, L.; Zhang, L.; Du, J. Multi-objective optimization for the deployment of carbon capture utilization and storage supply chain considering economic and environmental performance. J. Clean. Prod. 2020, 270, 122481. [Google Scholar] [CrossRef]
- Bonnin, M.; Azzaro-Pantel, C.; Domenech, S. Optimization of natural resource management: Application to French copper cycle. J. Clean. Prod. 2019, 223, 252–269. [Google Scholar] [CrossRef]
- Rabbani, M.; Akbarpour, M.; Hosseini, M.; Farrokhi-Asl, H. A multi-depot vehicle routing problem with time windows and load balancing: A real world application. Int. J. Supply Oper. Manag. 2021, 8, 347–369. [Google Scholar] [CrossRef]
- Khodashenas, M.; Najafi, S.E.; Kazemipoor, H.; Sobhani, M. Providing an integrated multi-depot vehicle routing problem model with simultaneous pickup and delivery and package layout under uncertainty with fuzzy-robust box optimization method. Decis. Mak. Appl. Manag. Eng. 2023, 6, 372–403. [Google Scholar] [CrossRef]
- Moheb-Alizadeh, H.; Handfield, R.; Warsing, D. Efficient and sustainable closed-loop supply chain network design: A two-stage stochastic formulation with a hybrid solution methodology. J. Clean. Prod. 2021, 308. [Google Scholar] [CrossRef]
- Mohammadi, S.; Al-e Hashem, S.; Rekik, Y. An integrated production scheduling and delivery route planning with multi-purpose machines: A case study from a furniture manufacturing company. Int. J. Prod. Econ. 2020, 219, 347–359. [Google Scholar] [CrossRef]
- Mzili, T.; Mzili, I.; Riffi, M.; Pamucar, D.; Simic, V.; Abualigah, L. Hybrid Genetic and Penguin Search Optimization Algorithm (GA-PSEOA) for Efficient Flow Shop Scheduling Solutions. Facta Univ. Ser. Mech. Eng. 2023, 22. [Google Scholar] [CrossRef]
- Dhiman, G.; Singh, K.K.; Soni, M.; Nagar, A.; Dehghani, M.; Slowik, A.; Kaur, A.; Sharma, A.; Houssein, E.H.; Cengiz, K. MOSOA: A new multi-objective seagull optimization algorithm. Expert Syst. Appl. 2021, 167, 114150. [Google Scholar] [CrossRef]
- Benli, A.; Akgün, b. A Multi-Objective Mathematical Programming Model for Transit Network Design and Frequency Setting Problem. Mathematics 2023, 11, 4488. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.F. On the mathematical modeling for optimal selecting of calibers of conductors in DC radial distribution networks: An MINLP approach. Electr. Power Syst. Res. 2021, 194, 107072. [Google Scholar] [CrossRef]
- Juwari; Renanto; Arifin, R.; Anugraha, R.P.; Tamimi, F.Q.; Roostewen, K. Multi-objective optimization hydrogen network in refinery expansion with improved transport constraint. Int. J. Hydrogen Energy 2024, 64, 368–380. [Google Scholar] [CrossRef]
- Li, J.; Zhao, H. Multi-Objective Optimization and Performance Assessments of an Integrated Energy System Based on Fuel, Wind and Solar Energies. Entropy 2021, 23, 431. [Google Scholar] [CrossRef] [PubMed]
- Puchinger, J.; Raidl, G.R. Combining Metaheuristics and Exact Algorithms in Combinatorial Optimization: A Survey and Classification. In Proceedings of the Artificial Intelligence and Knowledge Engineering Applications: A Bioinspired Approach; Mira, J., Álvarez, J.R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2005; pp. 41–53. [Google Scholar]
- Rao, R.V.; Savsani, V.J. Mechanical Design Optimization Using Advanced Optimization Techniques; Springer Series in Advanced Manufacturing; Springer: London, UK, 2012. [Google Scholar] [CrossRef]
- Chinchuluun, A.; Pardalos, P.M. A survey of recent developments in multiobjective optimization. Ann. Oper. Res. 2007, 154, 29–50. [Google Scholar] [CrossRef]
- Gunantara, N. A review of multi-objective optimization: Methods and its applications. Cogent Eng. 2018, 5, 1502242. [Google Scholar] [CrossRef]
- Belotti, P.; Kirches, C.; Leyffer, S.; Linderoth, J.; Luedtke, J.; Mahajan, A. Mixed-integer nonlinear optimization. Acta Numer. 2013, 22, 1–131. [Google Scholar] [CrossRef]
- Boukouvala, F.; Misener, R.; Floudas, C.A. Global optimization advances in Mixed-Integer Nonlinear Programming, MINLP, and Constrained Derivative-Free Optimization, CDFO. Eur. J. Oper. Res. 2016, 252, 701–727. [Google Scholar] [CrossRef]
- Harish Kumar, P.; Mageshvaran, R. Methods and solvers used for solving mixed integer linear programming and mixed nonlinear programming problems: A review. Int. J. Sci. Technol. Res. 2020, 9, 1872–1882. [Google Scholar]
- Blum, C.; Puchinger, J.; Raidl, G.R.; Roli, A. Hybrid metaheuristics in combinatorial optimization: A survey. Appl. Soft Comput. 2011, 11, 4135–4151. [Google Scholar] [CrossRef]
- Peres, F.; Castelli, M. Combinatorial Optimization Problems and Metaheuristics: Review, Challenges, Design, and Development. Appl. Sci. 2021, 11, 6449. [Google Scholar] [CrossRef]
- Liu, Q.; Li, X.; Liu, H.; Guo, Z. Multi-objective metaheuristics for discrete optimization problems: A review of the state-of-the-art. Appl. Soft Comput. 2020, 93, 106382. [Google Scholar] [CrossRef]
- Talbi, E.G. Hybrid Metaheuristics for Multi-Objective Optimization. J. Algorithms Comput. Technol. 2015, 9, 41–63. [Google Scholar] [CrossRef]
- Ehrgott, M.; Gandibleux, X. Hybrid Metaheuristics for Multi-objective Combinatorial Optimization. In Hybrid Metaheuristics: An Emerging Approach to Optimization; Blum, C., Aguilera, M.J.B., Roli, A., Sampels, M., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; pp. 221–259. [Google Scholar] [CrossRef]
- Ehrgott, M.; Gandibleux, X. A survey and annotated bibliography of multiobjective combinatorial optimization. Spektrum 2000, 22, 425–460. [Google Scholar] [CrossRef]
- Trespalacios, F.; Grossmann, I.E. Review of Mixed-Integer Nonlinear and Generalized Disjunctive Programming Methods. Chem. Ing. Tech. 2014, 86, 991–1012. [Google Scholar] [CrossRef]
- Przybylski, A.; Gandibleux, X. Multi-objective branch and bound. Eur. J. Oper. Res. 2017, 260, 856–872. [Google Scholar] [CrossRef]
- Ehrgott, M.; Gandibleux, X.; Hillier, F.S. (Eds.) Multiple Criteria Optimization: State of the Art Annotated Bibliographic Surveys. In International Series in Operations Research & Management Science; Springer: Boston, MA, USA, 2002; Volume 52. [Google Scholar] [CrossRef]
- Ehrgott, M. A discussion of scalarization techniques for multiple objective integer programming. Ann. Oper. Res. 2006, 147, 343–360. [Google Scholar] [CrossRef]
- Burachik, R.S.; Kaya, C.Y.; Rizvi, M.M. Algorithms for generating Pareto fronts of multi-objective integer and mixed-integer programming problems. Eng. Optim. 2022, 54, 1413–1425. [Google Scholar] [CrossRef]
- Pascoletti, A.; Serafini, P. Scalarizing vector optimization problems. J. Optim. Theory Appl. 1984, 42, 499–524. [Google Scholar] [CrossRef]
- Das, I.; Dennis, J.E. Normal-Boundary Intersection: A New Method for Generating the Pareto Surface in Nonlinear Multicriteria Optimization Problems. SIAM J. Optim. 1998, 8, 631–657. [Google Scholar] [CrossRef]
- Ahmadi, A.; Kaymanesh, A.; Siano, P.; Janghorbani, M.; Nezhad, A.E.; Sarno, D. Evaluating the effectiveness of normal boundary intersection method for short-term environmental/economic hydrothermal self-scheduling. Electr. Power Syst. Res. 2015, 123, 192–204. [Google Scholar] [CrossRef]
- Simab, M.; Javadi, M.S.; Nezhad, A.E. Multi-objective programming of pumped-hydro-thermal scheduling problem using normal boundary intersection and VIKOR. Energy 2018, 143, 854–866. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, X.; Jiang, C.; Wang, L.; Gong, K. Multi-objective optimal operation of pumped-hydro-solar hybrid system considering effective load carrying capability using improved NBI method. Int. J. Electr. Power Energy Syst. 2021, 129, 106802. [Google Scholar] [CrossRef]
- Land, A.H.; Doig, A.G. An Automatic Method of Solving Discrete Programming Problems. Econometrica 1960, 28, 497–520. [Google Scholar] [CrossRef]
- Kiziltan, G.; Yucaoğlu, E. An Algorithm for Multiobjective Zero-One Linear Programming. Manag. Sci. 1983, 29, 1444–1453. [Google Scholar] [CrossRef]
- Mavrotas, G.; Diakoulaki, D. A branch and bound algorithm for mixed zero-one multiple objective linear programming. Eur. J. Oper. Res. 1998, 107, 530–541. [Google Scholar] [CrossRef]
- Cacchiani, V.; D’Ambrosio, C. A branch-and-bound based heuristic algorithm for convex multi-objective MINLPs. Eur. J. Oper. Res. 2017, 260, 920–933. [Google Scholar] [CrossRef]
- Boix, M.; Montastruc, L.; Pibouleau, L.; Azzaro-Pantel, C.; Domenech, S. Multiobjective optimization of industrial water networks with contaminants. Comput. Aided Chem. Eng. 2010, 28, 859–864. [Google Scholar] [CrossRef][Green Version]
- De Santis, M.; Eichfelder, G.; Niebling, J.; Rocktäschel, S. Solving Multiobjective Mixed Integer Convex Optimization Problems. SIAM J. Optim. 2020, 30, 3122–3145. [Google Scholar] [CrossRef]
- Morrison, D.R.; Jacobson, S.H.; Sauppe, J.J.; Sewell, E.C. Branch-and-bound algorithms: A survey of recent advances in searching, branching, and pruning. Discret. Optim. 2016, 19, 79–102. [Google Scholar] [CrossRef]
- Belotti, P.; Lee, J.; Liberti, L.; Margot, F.; Wächter, A. Branching and bounds tighteningtechniques for non-convex MINLP. Optim. Methods Softw. 2009, 24, 597–634. [Google Scholar] [CrossRef]
- Kronqvist, J.; Bernal, D.E.; Lundell, A.; Grossmann, I.E. A review and comparison of solvers for convex MINLP. Optim Eng 2019, 20, 397–455. [Google Scholar] [CrossRef]
- Burer, S.; Letchford, A.N. Non-convex mixed-integer nonlinear programming: A survey. Surv. Oper. Res. Manag. Sci. 2012, 17, 97–106. [Google Scholar] [CrossRef]
- el Sheshtawy, H.; el Moctar, O.; Natarajan, S. Multi-Point Shape Optimization of a Horizontal Axis Tidal Stream Turbine. Eng 2021, 2, 340–355. [Google Scholar] [CrossRef]
- Bade, S.O.; Meenakshisundaram, A.; Tomomewo, O.S. Current Status, Sizing Methodologies, Optimization Techniques, and Energy Management and Control Strategies for Co-Located Utility-Scale Wind–Solar-Based Hybrid Power Plants: A Review. Eng 2024, 5, 677–719. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Verma, S.; Pant, M.; Snasel, V. A Comprehensive Review on NSGA-II for Multi-Objective Combinatorial Optimization Problems. IEEE Access 2021, 9, 57757–57791. [Google Scholar] [CrossRef]
- Glover, F. Tabu Search—Part II. ORSA J. Comput. 1990, 2, 4–32. [Google Scholar] [CrossRef]
- Dréo, J.; Candan, C. Different Classifications of Metaheuristics. 2007. Available online: https://commons.wikimedia.org/w/index.php?curid=16252087 (accessed on 20 July 2021).
- Yildiz, A.R.; Abderazek, H.; Mirjalili, S. A Comparative Study of Recent Non-traditional Methods for Mechanical Design Optimization. Arch. Comput. Methods Eng. 2020, 27, 1031–1048. [Google Scholar] [CrossRef]
- Abderazek, H.; Yildiz, A.R.; Sait, S.M. Mechanical engineering design optimisation using novel adaptive differential evolution algorithm. Int. J. Veh. Des. 2019, 80, 285. [Google Scholar] [CrossRef]
- Dhiman, G.; Singh, K.K.; Slowik, A.; Chang, V.; Yildiz, A.R.; Kaur, A.; Garg, M. EMoSOA: A new evolutionary multi-objective seagull optimization algorithm for global optimization. Int. J. Mach. Learn. Cybern. 2021, 12, 571–596. [Google Scholar] [CrossRef]
- Assiri, A.S. On the performance improvement of Butterfly Optimization approaches for global optimization and Feature Selection. PLoS ONE 2021, 16, e0242612. [Google Scholar] [CrossRef]
- Mzili, T.; Mzili, I.; Riffi, M.; Pamucar, D.; Simic, V.; Kurdi, M. A Novel Discrete Rat Swarm Optimization Algorithm for the Quadratic Assignment Problem. Facta Univ. Ser. Mech. Eng. 2023, 21, 529–552. [Google Scholar] [CrossRef]
- Kaur, H.; Rai, A.; Bhatia, S.S.; Dhiman, G. MOEPO: A novel Multi-objective Emperor Penguin Optimizer for global optimization: Special application in ranking of cloud service providers. Eng. Appl. Artif. Intell. 2020, 96, 104008. [Google Scholar] [CrossRef]
- Chakraborty, S.; Kumar Saha, A.; Sharma, S.; Mirjalili, S.; Chakraborty, R. A novel enhanced whale optimization algorithm for global optimization. Comput. Ind. Eng. 2021, 153, 107086. [Google Scholar] [CrossRef]
- Sattar, D.; Salim, R. A smart metaheuristic algorithm for solving engineering problems. Eng. Comput. 2021, 37, 2389–2417. [Google Scholar] [CrossRef]
- Giagkiozis, I.; Purshouse, R.C.; Fleming, P.J. An overview of population-based algorithms for multi-objective optimisation. Int. J. Syst. Sci. 2015, 46, 1572–1599. [Google Scholar] [CrossRef]
- Jourdan, L.; Basseur, M.; Talbi, E.G. Hybridizing exact methods and metaheuristics: A taxonomy. Eur. J. Oper. Res. 2009, 199, 620–629. [Google Scholar] [CrossRef]
- Blum, C.; Cotta, C.; Fernández, A.J.; Gallardo, J.E.; Mastrolilli, M. Hybridizations of Metaheuristics with Branch & Bound Derivates. In Hybrid Metaheuristics: An Emerging Approach to Optimization; Blum, C., Aguilera, M.J.B., Roli, A., Sampels, M., Eds.; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2008; pp. 85–116. [Google Scholar] [CrossRef]
- Nagar, A.; Heragu, S.S.; Haddock, J. A combined branch-and-bound and genetic algorithm based approach for a flowshop scheduling problem. Ann. Oper. Res. 1996, 63, 397–414. [Google Scholar] [CrossRef]
- Cotta, C.; Troya, J.M. Embedding Branch and Bound within Evolutionary Algorithms. Appl. Intell. 2003, 18, 137–153. [Google Scholar] [CrossRef]
- Woodruff, D.L. A Chunking Based Selection Strategy for Integrating Meta-Heuristics with Branch and Bound. In Meta-Heuristics: Advances and Trends in Local Search Paradigms for Optimization; Voß, S., Martello, S., Osman, I.H., Roucairol, C., Eds.; Springer: Boston, MA, USA, 1999; pp. 499–511. [Google Scholar] [CrossRef]
- Jozefowiez, N.; Semet, F.; Talbi, E.G. The bi-objective covering tour problem. Comput. Oper. Res. 2007, 34, 1929–1942. [Google Scholar] [CrossRef]
- Puchinger, J.; Raidl, G.R.; Koller, G. Solving a Real-World Glass Cutting Problem. In Proceedings of the Evolutionary Computation in Combinatorial Optimization; Gottlieb, J., Raidl, G.R., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2004; pp. 165–176. [Google Scholar] [CrossRef]
- Backer, B.D.; Furnon, V.; Shaw, P.; Kilby, P.; Prosser, P. Solving Vehicle Routing Problems Using Constraint Programming and Metaheuristics. J. Heuristics 2000, 6, 501–523. [Google Scholar] [CrossRef]
- Florios, K.; Mavrotas, G.; Diakoulaki, D. Solving multiobjective, multiconstraint knapsack problems using mathematical programming and evolutionary algorithms. Eur. J. Oper. Res. 2010, 203, 14–21. [Google Scholar] [CrossRef]
- Wang, S.; Liu, M. A heuristic method for two-stage hybrid flow shop with dedicated machines. Comput. Oper. Res. 2013, 40, 438–450. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).