Determination of Permanent Deformations of Non-Cohesive Soils in Pavement Structures under Repeated Traffic Load
Abstract
1. Introduction
2. Research Methodology
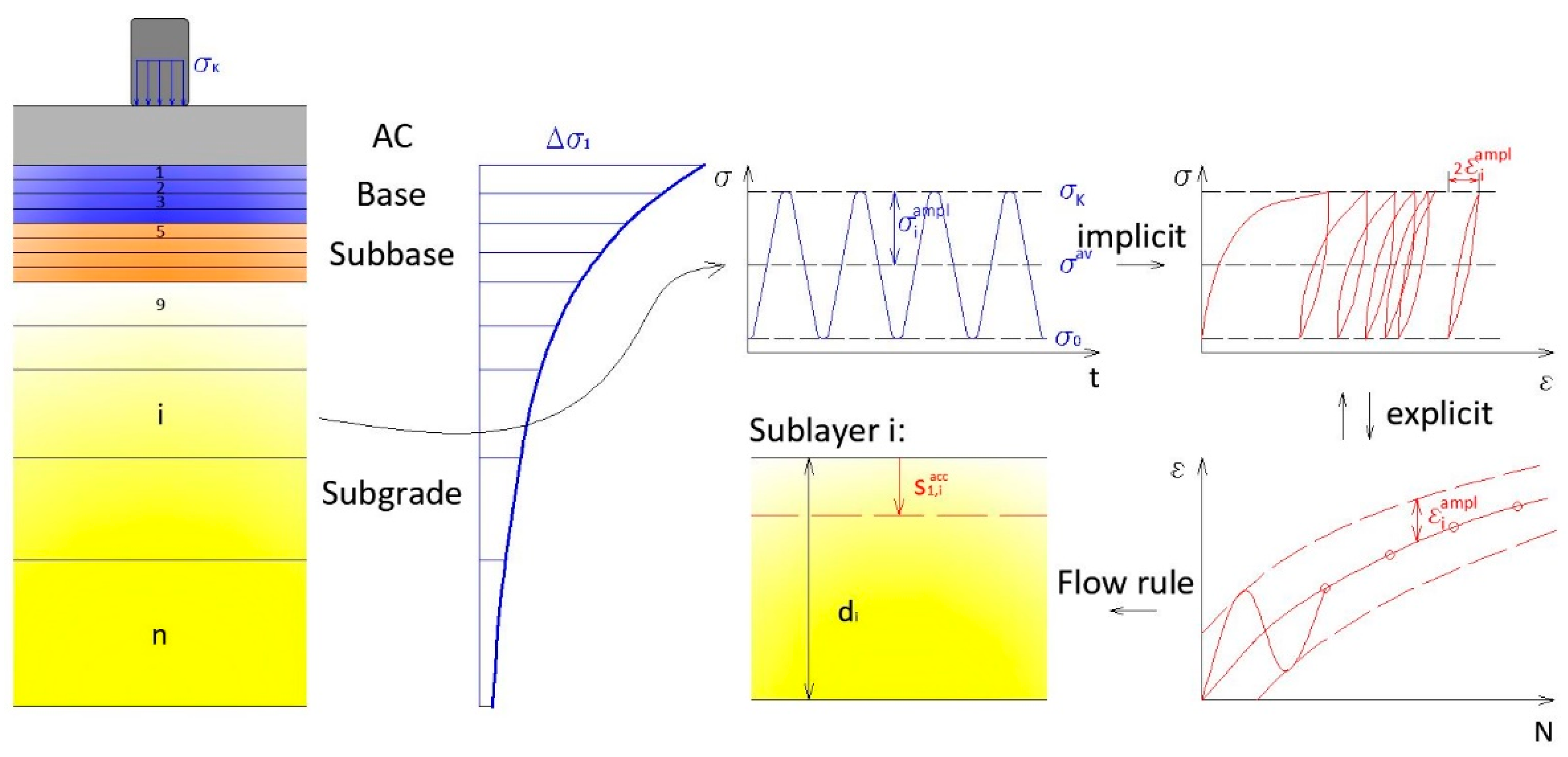
2.1. Explicit Calculation Method and HCA Model
- is the plastic strain rate per load cycle;
- is the function describing the influence of strain amplitude;
- is the function describing the preloading history (memory of soil);
- is the function describing the influence of void ratio (density);
- is the function describing the influence of average mean pressure;
- is the function describing the influence of the average stress ratio;
- is the function describing the influence of polarisation changes.
2.2. Calculation Method
2.3. Analyzed Pavement Structure
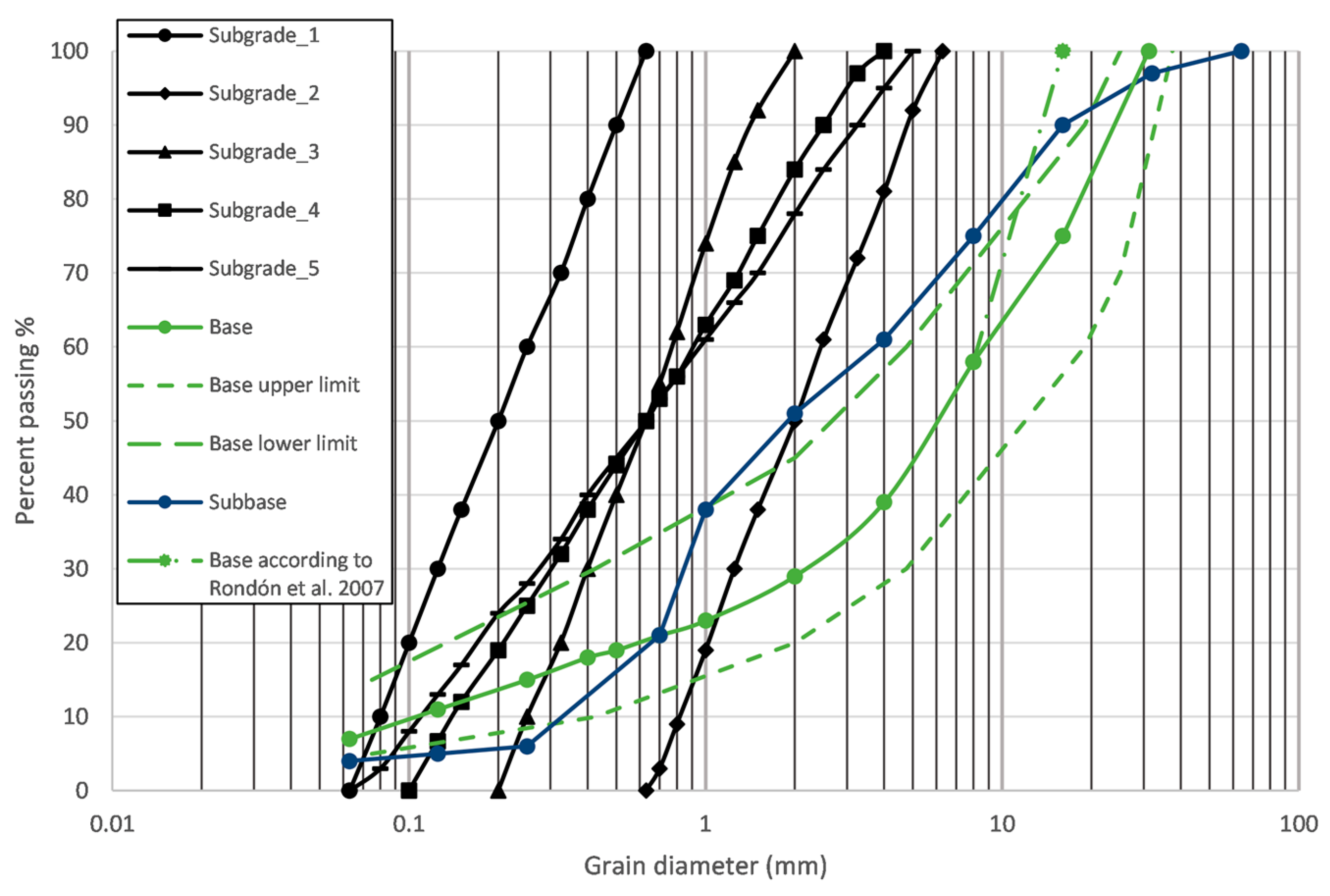
2.4. Analyzed Soils and Their Properties
3. Results and Discussion
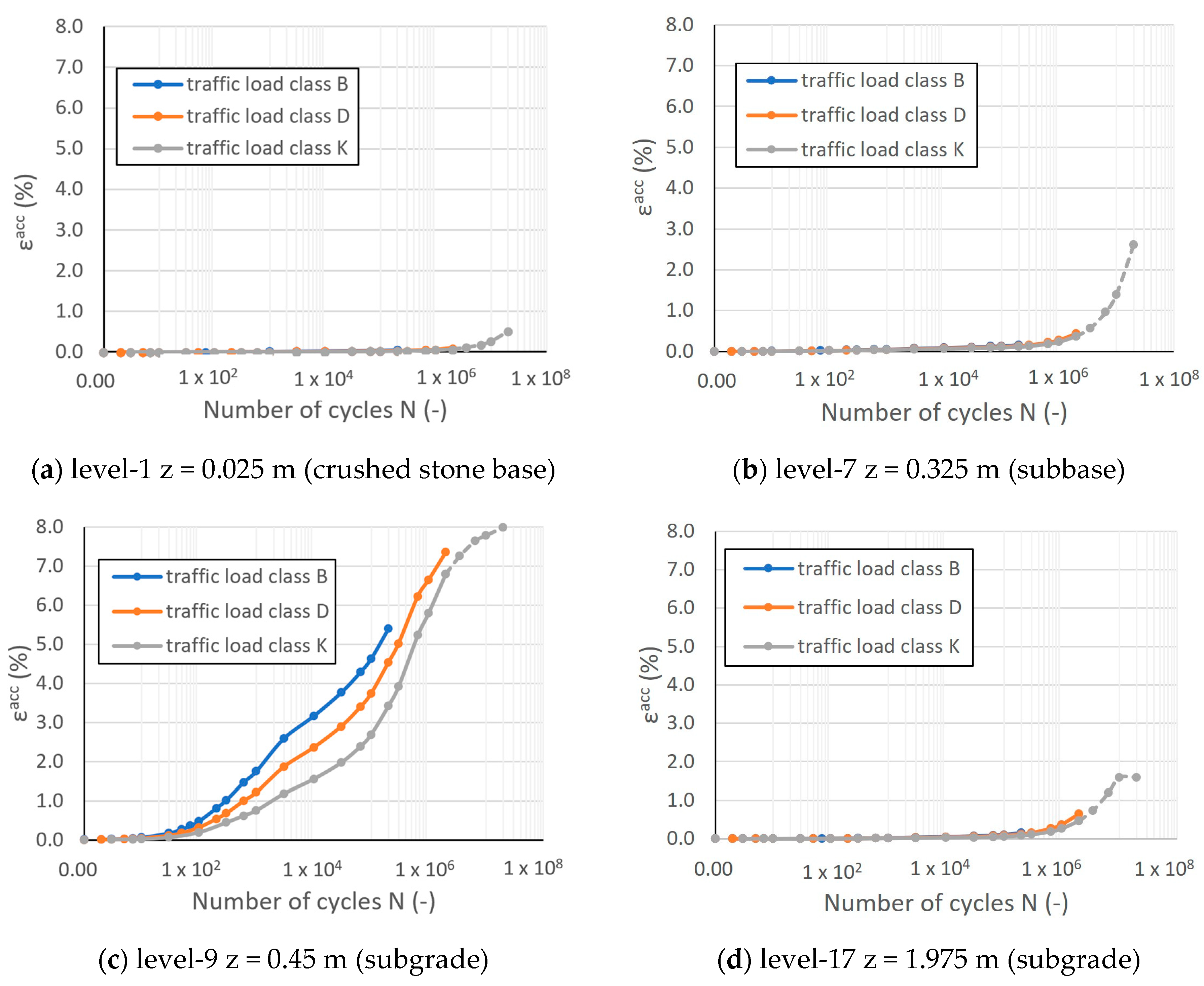
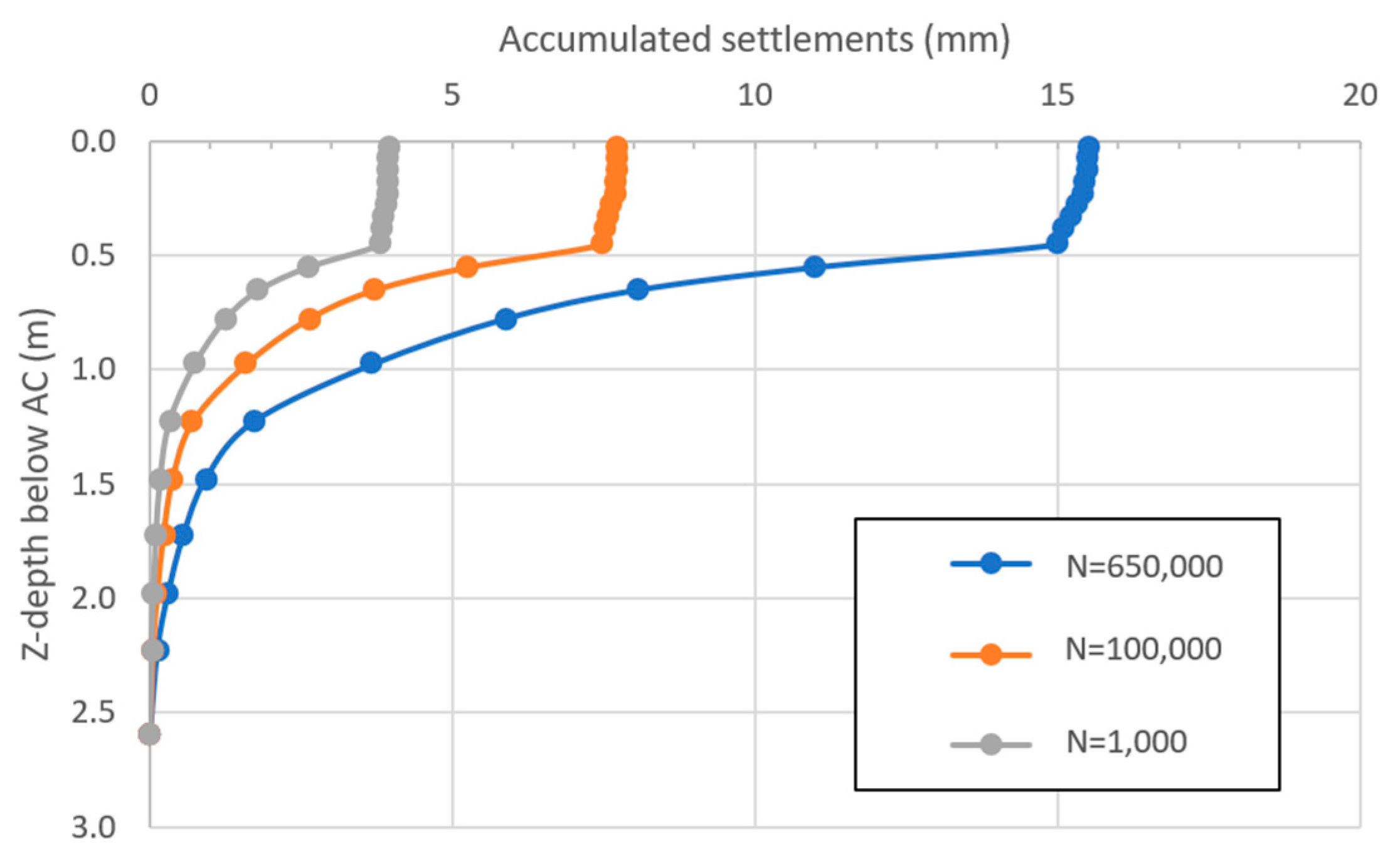
3.1. Distribution of Strains
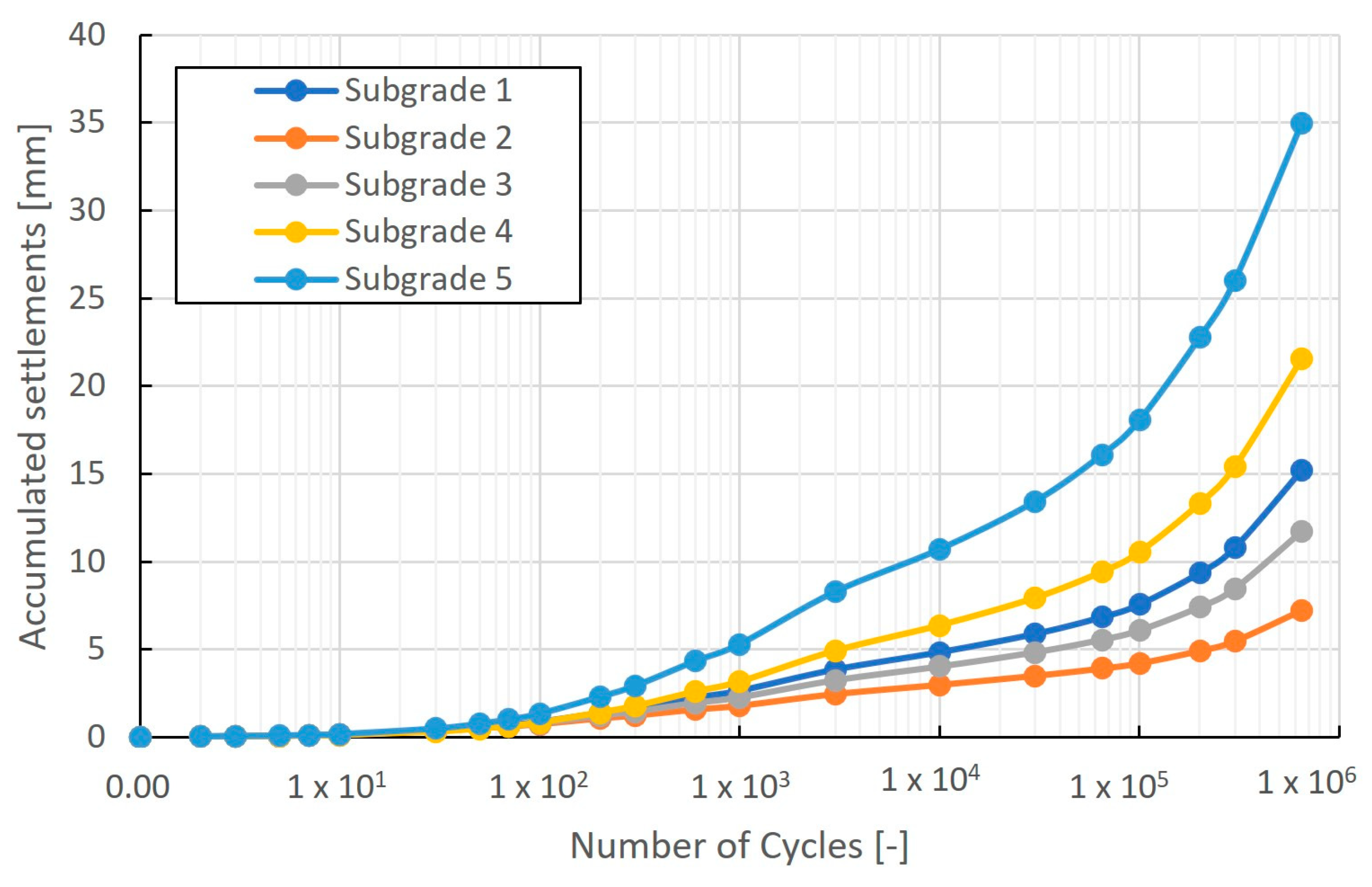
3.2. The Effect of Subgrade
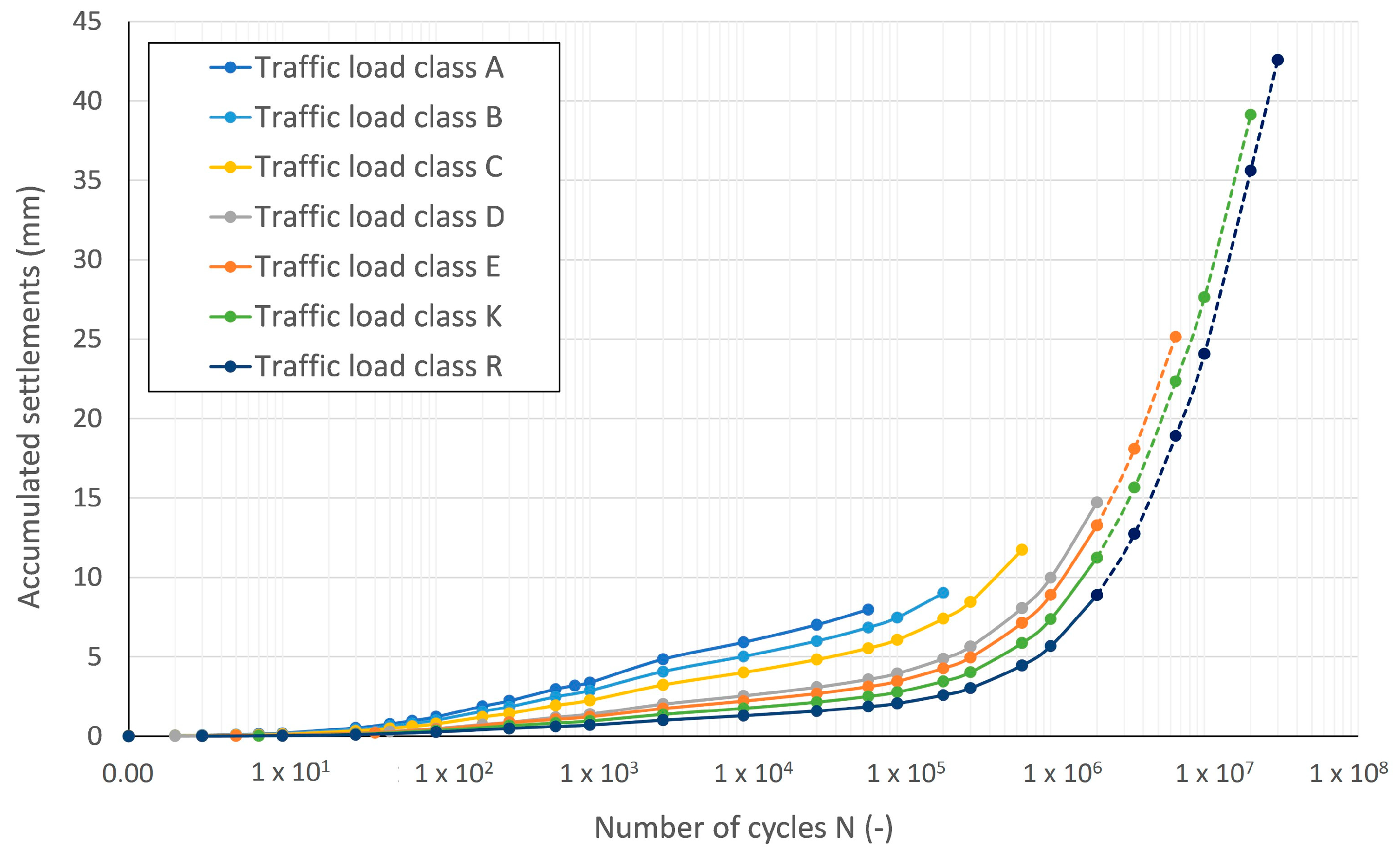
3.3. The Effect of Traffic Load Class
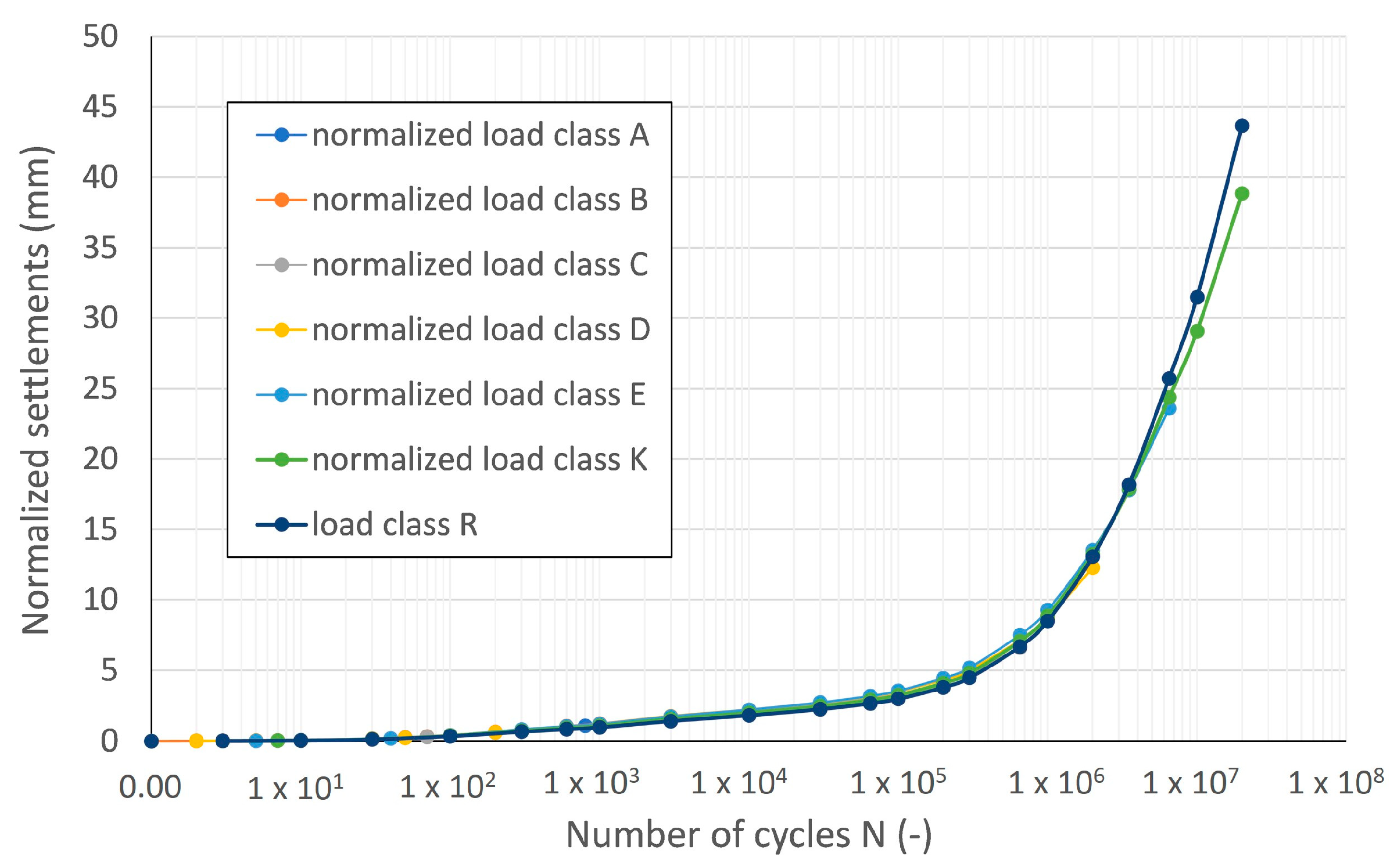
3.4. Ratio of Settlements
4. Conclusions
- Influence of subgrade type: The subgrade grain size distribution characteristic significantly impacts the rutting depth, with well-graded soils showing higher accumulated strains due to better compactability. Increasing the mean particle size (d50) while maintaining a constant coefficient of uniformity (CU) positively affects settlement.
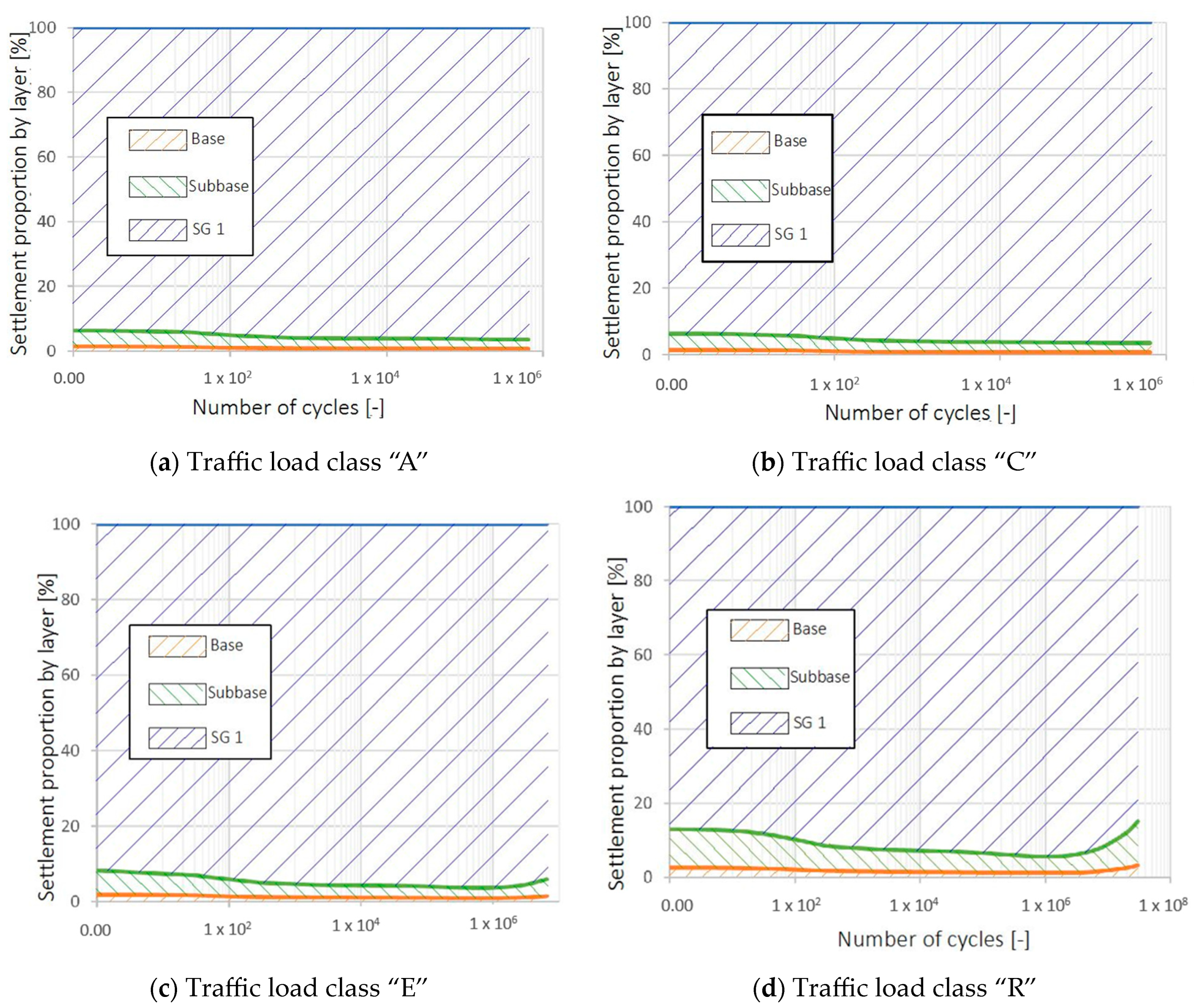
- Layer contribution: The subgrade accounts for the majority of the total settlement (75–98%), though its contribution decreases towards the end of the design lifetime. Most strains originate in the upper part of the subgrade, suggesting that improving this zone can most effectively reduce rutting.
- Traffic Load Class: By a given number of load repetitions the accumulated strains will be smaller in the cross sections with thicker asphalt layers due to a better stress distribution. The settlements, however, towards the end of design lifetime, increase with higher traffic load classes and are proportional to the thickness of the asphalt layer when boundary conditions and cycle numbers are constant.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- AASHTO. AASHTO Guide for Design of Pavement Structures; American Association of State Highway and Transportation Officials: Washington, DC, USA, 1993; ISBN 978-1-56051-055-0. [Google Scholar]
- Albayati, A.H. A Review of Rutting in Asphalt Concrete Pavement. Open Eng. 2023, 13, 20220463. [Google Scholar] [CrossRef]
- Bissada, A.F. Compactibility of Asphalt Paving Mixtures and Relation to Permanent Deformation. Transp. Res. Rec. 1983, 911, 1–10. [Google Scholar]
- Bharath, G.; Kakade, V.; Reddy, K.S.; Tandon, V.; Reddy, M.A. Investigation of Rutting Performance of Dense and Gap Graded Recycled Asphalt Mixtures. Innov. Infrastruct. Solut. 2023, 8, 252. [Google Scholar] [CrossRef]
- Zhang, J.; Cao, J.; Huang, W.; Shi, X.; Zhou, X. Rutting Prediction and Analysis of Influence Factors Based on Multivariate Transfer Entropy and Graph Neural Networks. Neural Netw. 2023, 157, 26–38. [Google Scholar] [CrossRef]
- Aljbouri, H.J.; Albayati, A.H. Effect of Nanomaterials on the Durability of Hot Mix Asphalt. Transp. Eng. 2023, 11, 100165. [Google Scholar] [CrossRef]
- Morris, J. The Prediction of Permanent Deformation in Asphalt Concrete Pavements; USA Transport Group: Bensenville, IL, USA, 1973. [Google Scholar]
- White, T.D.; Haddock, J.E.; Hand, A.J.T.; Fang, H. Contributions of Pavement Structural Layers to Rutting of Hot Mix Asphalt Pavements; NCHRP Report 468; National Academy Press: Washington, DC, USA, 2002; ISBN 978-0-309-06721-8. [Google Scholar]
- Singh, A.K.; Sahoo, J.P. Rutting Prediction Models for Flexible Pavement Structures: A Review of Historical and Recent Developments. J. Traffic Transp. Eng. Engl. Ed. 2021, 8, 315–338. [Google Scholar] [CrossRef]
- Werkmeister, S. Permanent Deformation Behaviour of Unbound Granular Materials in Pavement Constructions. Ph.D. Thesis, Technische Universität Dresden, Dresden, Germany, 2003. [Google Scholar]
- Powell, W.D.; Potter, J.F.; Mayhew, H.C.; Nunn, M.E. The Structural Design of Bituminous Roads; Transport and Road Research Laboratory (TRRL): Wokingham, Berkshire, UK, 1984. [Google Scholar]
- Uzan, J. Permanent Deformation in Flexible Pavements. J. Transp. Eng. 2004, 130, 6–13. [Google Scholar] [CrossRef]
- Qi, H.; Zhang, X.; Liu, J.; Zhang, T.; Lv, G.; Cui, L.; Xie, Q. Study on Deformation Characteristics of Low-Highway Subgrade under Traffic Load. Appl. Sci. 2022, 12, 3406. [Google Scholar] [CrossRef]
- Zhou, P.; Cui, L.; Zhang, X.; Ma, C.; Liu, J.; Shao, Y.; Lv, G.; Xie, Q. Study on Deformation Characteristics of Extended Highway in Operation Period. Adv. Civ. Eng. 2022, 2022, 5496999. [Google Scholar] [CrossRef]
- Leonardi, G.; Suraci, F. A 3D-FE Model for the Rutting Prediction in Geogrid Reinforced Flexible Pavements. Sustainability 2022, 14, 3695. [Google Scholar] [CrossRef]
- Niemunis, A.; Wichtmann, T.; Triantafyllidis, T. A High-Cycle Accumulation Model for Sand. Comput. Geotech. 2005, 32, 245–263. [Google Scholar] [CrossRef]
- Vamos, M.J.; Szendefy, J. Calculation Method for Traffic Load-Induced Permanent Deformation in Soils under Flexible Pavements. Geotechnics 2023, 3, 955–974. [Google Scholar] [CrossRef]
- Niemunis, A. Extended Hypoplastic Models for Soils; Habilitáció, Institutes für Grundbau und Bodenmechanik der Ruhr-Universität Bochum: Bochum, Germany, 2003. [Google Scholar]
- Wichtmann, T. Explicit Accumulation Model for Non-Cohesive Soils under Cyclic Loading; Schriftenreihe des Institutes für Bodenmechanik der Ruhr-Universität Bochum: Bochum, Germany, 2005. [Google Scholar]
- Wichtmann, T. Soil Behaviour under Cyclic Loading—Experimental Observations, Constitutive Description and Applications; Karlsruher Institut für Technologie Institut für Bodenmechanik und Felsmechanik: Karlsruhe, Germany, 2016. [Google Scholar]
- Wichtmann, T.; Niemunis, A.; Triantafyllidis, T. Flow Rule in a High-Cycle Accumulation Model Backed by Cyclic Test Data of 22 Sands. Acta Geotech. 2014, 9, 695–709. [Google Scholar] [CrossRef]
- Wichtmann, T.; Rondón, H.; Niemunis, A.; Triantafyllidis, T.; Lizcano, A. Prediction of Permanent Deformations in Pavements Using a High-Cycle Accumulation Model. J. Geotech. Geoenvironmental Eng. 2010, 136, 728–740. [Google Scholar] [CrossRef]
- Wichtmann, T.; Niemunis, A.; Triantafyllidis, T. Improved Simplified Calibration Procedure for a High-Cycle Accumulation Model. Soil Dyn. Earthq. Eng. 2015, 70, 118–132. [Google Scholar] [CrossRef]
- Wichtmann, T.; Triantafyllidis, T. Inspection of a High-Cycle Accumulation Model for Large Numbers of Cycles (N = 2 Million). Soil Dyn. Earthq. Eng. 2015, 75, 199–210. [Google Scholar] [CrossRef]
- Häcker, A. Erweiterung Eines Lamellenmodells für Zyklisch Belastete Flachgründungen (Extension of a Laminal Modell for Cyclic Loaded Foundations); Karlsruher Institute für Technologie, Institute für Bodenmechanik und Felsmechanik: Karlsruhe, Germany, 2013. [Google Scholar]
- Wöhrle, T. Überprüfung und Entwicklung Einfaher Ingenieurmodelle für Offshore-Windenerigealagen auf Bass Eines Akkumulationsmodells (Examination and Development of Simplified Engineering Oriented Model for Offshore Wind Turbins on the Basis of an Accumulation Modell); Karlsruher Institute für Technologie, Institute für Bodenmechanik und Felsmechanik: Karlsruhe, Germany, 2012. [Google Scholar]
- Zachert, H. Zur Gebrauchstauglichkeit von Gründungen für Offshore-Windenergieanlagen (On the Usability of Foundations for Offshore Wind Turbins). Ph.D. Thesis, Karlsruher Institut für Technologie (KIT), Karlsruhe, Germany, 2015. ISBN 0453-3267. [Google Scholar]
- e-UT06.03.13; Aszfaltburkolatú Útpályaszerkezetek Méretezése és Megerősítése E-UT06.03.13 (ÚT 2-1.202). Útügyi Műszaki Előírás: Budapest, Hungary, 2017.
- Káli, A. Ipari Padlók Ágyazatként És Útépítési Védőrétegként Használt Durvaszemcsés Talaj Sajátmodulusának Numerikus Modellezése. Bachelor’s Thesis, BME, Budapest, Hungary, 2020. [Google Scholar]
- Vámos, M.J.; Szendefy, J. Overconsolidated Stress and Strain Condition of Pavement Layers as a Result of Preloading during Construction. Period. Polytech. Civ. Eng. 2023, 67, 1273–1283. [Google Scholar] [CrossRef]
- Wichtmann, T.; Triantafyllidis, T. Influence of the Grain-Size Distribution Curve of Quartz Sand on the Small Strain Shear Modulus Gmax. J. Geotech. Geoenvironmental Eng. ASCE 2009, 135, 1404–1418. [Google Scholar] [CrossRef]
- Wichtmann, T.; Triantafyllidis, T. On the Influence of the Grain Size Distribution Curve on P-Wave Velocity, Constrained Elastic Modulus Mmax and Poisson’s Ratio of Quartz Sands. Soil Dyn. Earthq. Eng. 2010, 30, 757–766. [Google Scholar] [CrossRef]
- Wichtmann, T.; Triantafyllidis, T. Effect of Uniformity Coefficient on G/Gmax and Damping Ratio of Uniform to Well-Graded Quartz Sands. J. Geotech. Geoenvironmental Eng. 2013, 139, 59–72. [Google Scholar] [CrossRef]
- Rondón, H.A.; Wichtmann, T.; Triantafyllidis, T.; Lizcano, A. Hypoplastic Material Constants for a Well-Graded Granular Material for Base and Subbase Layers of Flexible Pavements. Acta Geotech. 2007, 2, 113–126. [Google Scholar] [CrossRef]
- Útügyi Lapok Kutatási Jelentés: Tervezési Útmutató: Aszfaltburkolatú Útpályaszerkezetek Méretezésének Alternatív Módszere. 2016. Available online: https://utugyilapok.hu/wp-content/uploads/2015/11/Analitikus-TU.pdf (accessed on 28 April 2024).
- Leelantikul, S.; Timmerman, D.H. Deformation of Sand under Cyclic Loading. In Proceedings of the Conference on Soil Dynamics and Earthquake Engineering, Southampton, UK, 13–15 July 1982. [Google Scholar]



| Traffic Load Class | Design Traffic (Million Axles) | Thickness of Base Course (mm) | Thickness of AC-Layer (mm) |
|---|---|---|---|
| A | 0.03–0.1 | 200 | 100 |
| B | 0.1–0.3 | 200 | 120 |
| C | 0.3–1.0 | 200 | 150 |
| D | 1.0–3.0 | 200 | 180 |
| E | 3.0–10.0 | 200 | 220 |
| K | 10.0–30.0 | 200 | 250 |
| R | Over 30 | 200 | 290 |
| Layer | d50 (mm) | CU (-) | emin (-) | emax (-) | ρdmax (g/cm3) | e0 (-) | υ (-) |
|---|---|---|---|---|---|---|---|
| Subgrade 1 | 0.2 | 3.0 | 0.540 | 0.920 | 1.75 | 0.627 | 0.33–0.36 |
| Subgrade 2 | 2.0 | 3.0 | 0.491 | 0.783 | 1.81 | 0.577 | 0.33–0.36 |
| Subgrade 3 | 0.6 | 3.0 | 0.474 | 0.829 | 1.83 | 0.559 | 0.33–0.36 |
| Subgrade 4 | 0.6 | 5.0 | 0.394 | 0.749 | 1.93 | 0.478 | 0.35–0.38 |
| Subgrade 5 | 0.6 | 8.0 | 0.356 | 0.673 | 1.98 | 0.439 | 0.36–0.40 |
| Subbase | 2.0 | 11.9 | 0.364 | 0.513 | 2.06 | 0.340 | 0.40 |
| Base | 6.3 | 100.0 | 0.230 | 0.440 | 2.30 | 0.188 | 0.40 |
| Layer | Campl | Ce | Cp | CY | CN1 | CN2 | CN3 | fcc |
|---|---|---|---|---|---|---|---|---|
| Subgrade 1 (L26) | 1.70 | 0.513 | 0.47 | 2.26 | 5.49 × 10−3 | 1.30 × 10−2 | 2.38 × 10−5 | 32.76° |
| Subgrade 2 (L19) | 1.70 | 0.466 | 0.21 | 2.98 | 2.11 × 10−3 | 2.77 × 10−2 | 1.22 × 10−5 | 34.73° |
| Subgrade 3 (L12) | 1.70 | 0.450 | 0.41 | 2.60 | 3.88 × 10−3 | 1.54 × 10−2 | 2.05 × 10−5 | 33.20° |
| Subgrade 4 (L14) | 1.70 | 0.374 | 0.41 | 2.60 | 8.44 × 10−3 | 6.72 × 10−3 | 3.21 × 10−5 | 33.20° |
| Subgrade 5 (L16) | 1.70 | 0.338 | 0.41 | 2.60 | 1.53 × 10−2 | 5.67 × 10−3 | 4.53 × 10−5 | 33.20° |
| Base | 1.10 | 0.070 | −0.22 | 1.80 | 5.20 × 10−4 | 0.03 | 1.30 × 10−5 | 44° |
| Subbase | 1.10 | 0.204 | −0.22 | 1.80 | 5.20 × 10−4 | 0.03 | 1.30 × 10−5 | 42° |
| Traffic Load Class | Total Settlement (mm) | “Subgrade-5”/“Subgrade-2” | “Subgrade-1”/“Subgrade-2” | ||
|---|---|---|---|---|---|
| “Subgrade-1” | “Subgrade-2” | “Subgrade-5” | |||
| A | 11.0 | 5.8 | 20.6 | 3.6 | 1.9 |
| B | 12.5 | 6.4 | 25.2 | 3.9 | 2.0 |
| C | 15.5 | 7.2 | 35.0 | 4.9 | 2.2 |
| D | 22.8 | 9.1 | 45.6 | 5.0 | 3.2 |
| E | 33.8 | 16.1 | 56.6 | 3.5 | 2.1 |
| K | 47.1 | 27.4 | 67.5 | 2.4 | 1.7 |
| R | 50.4 | 32.1 | 68.2 | 2.1 | 1.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vamos, M.J.; Szendefy, J. Determination of Permanent Deformations of Non-Cohesive Soils in Pavement Structures under Repeated Traffic Load. Eng 2024, 5, 1067-1084. https://doi.org/10.3390/eng5020058
Vamos MJ, Szendefy J. Determination of Permanent Deformations of Non-Cohesive Soils in Pavement Structures under Repeated Traffic Load. Eng. 2024; 5(2):1067-1084. https://doi.org/10.3390/eng5020058
Chicago/Turabian StyleVamos, Mate Janos, and Janos Szendefy. 2024. "Determination of Permanent Deformations of Non-Cohesive Soils in Pavement Structures under Repeated Traffic Load" Eng 5, no. 2: 1067-1084. https://doi.org/10.3390/eng5020058
APA StyleVamos, M. J., & Szendefy, J. (2024). Determination of Permanent Deformations of Non-Cohesive Soils in Pavement Structures under Repeated Traffic Load. Eng, 5(2), 1067-1084. https://doi.org/10.3390/eng5020058





