Snap-Off during Imbibition in Porous Media: Mechanisms, Influencing Factors, and Impacts
Abstract
:1. Introduction
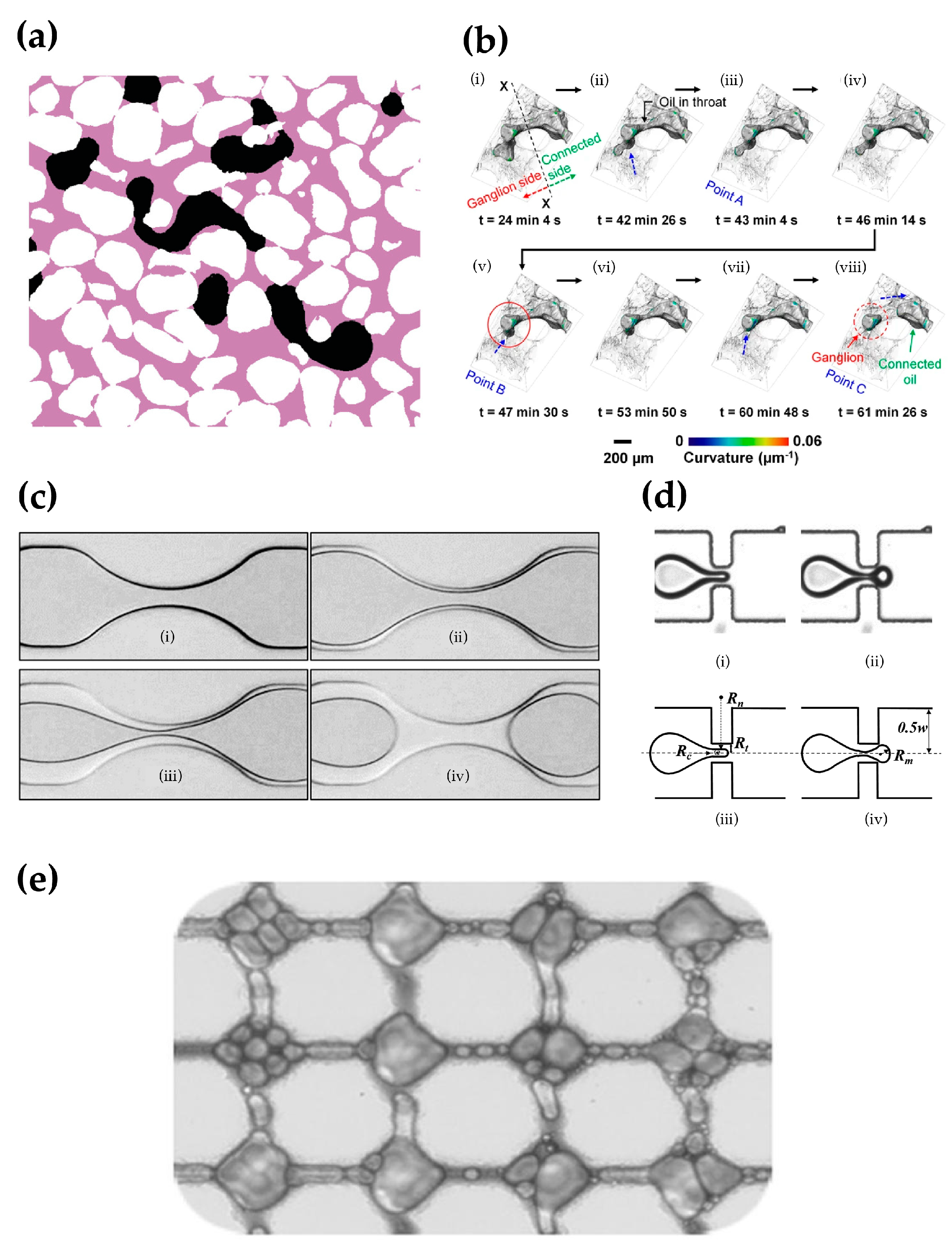
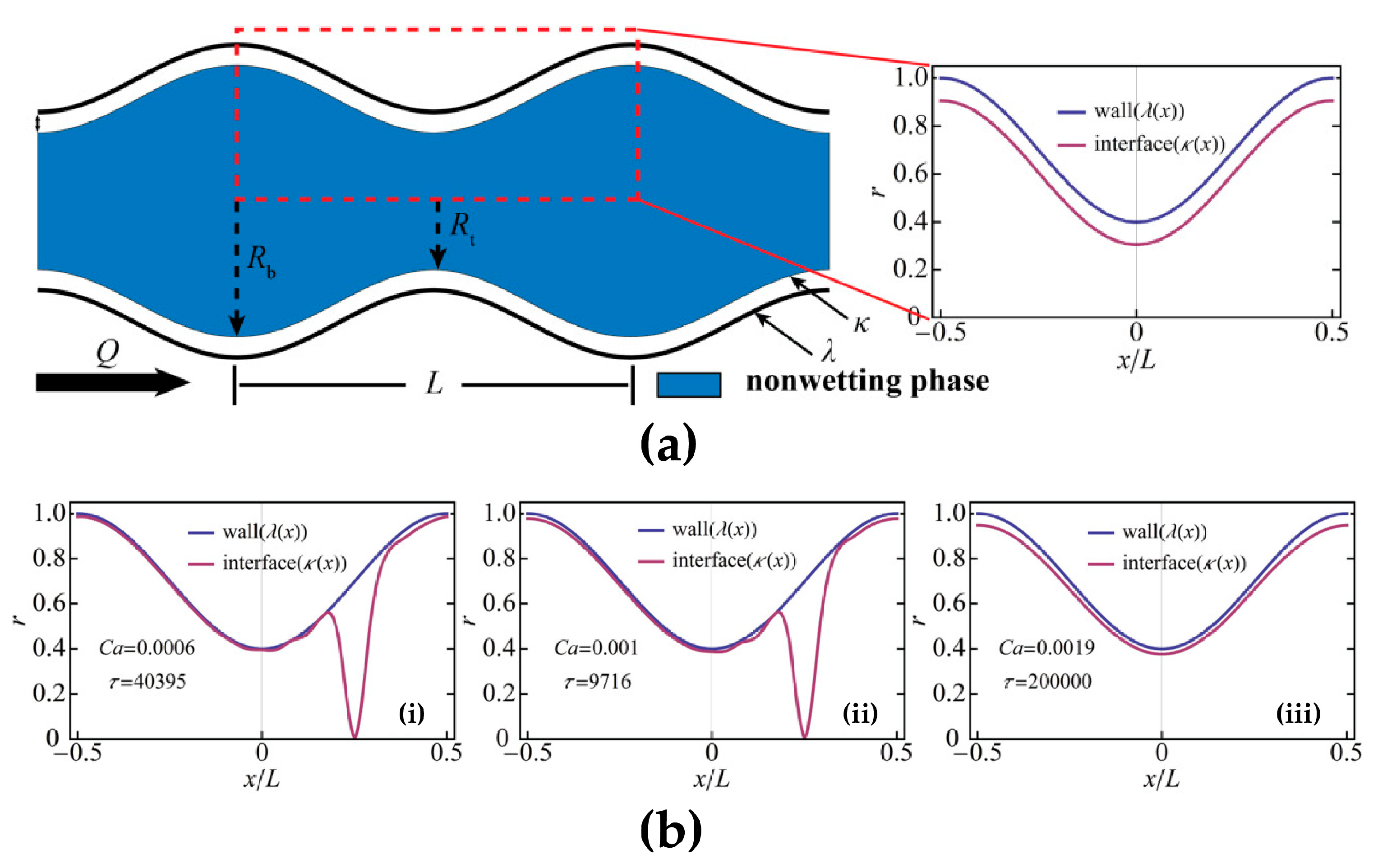
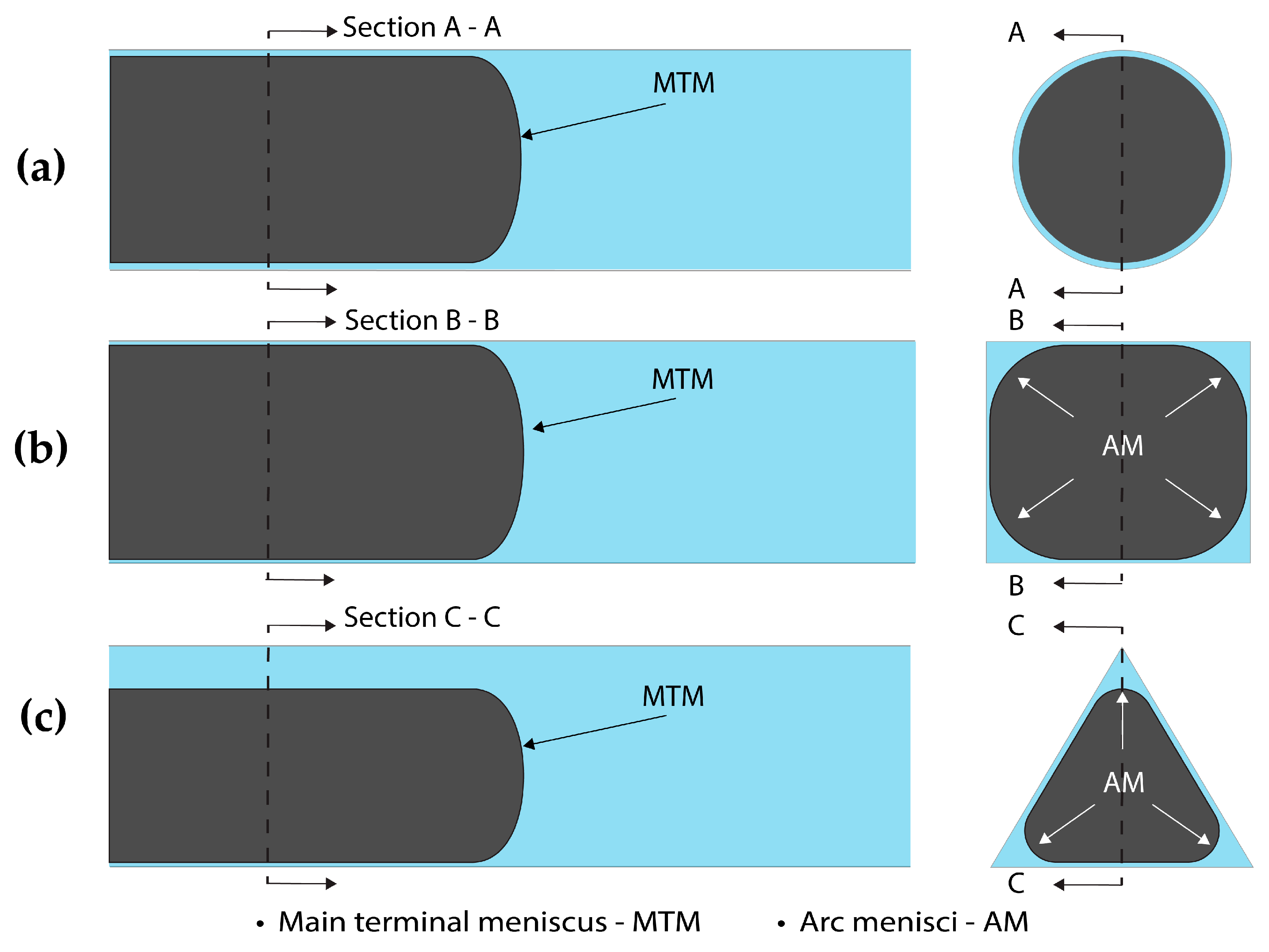
2. Mechanisms of Snap-Off
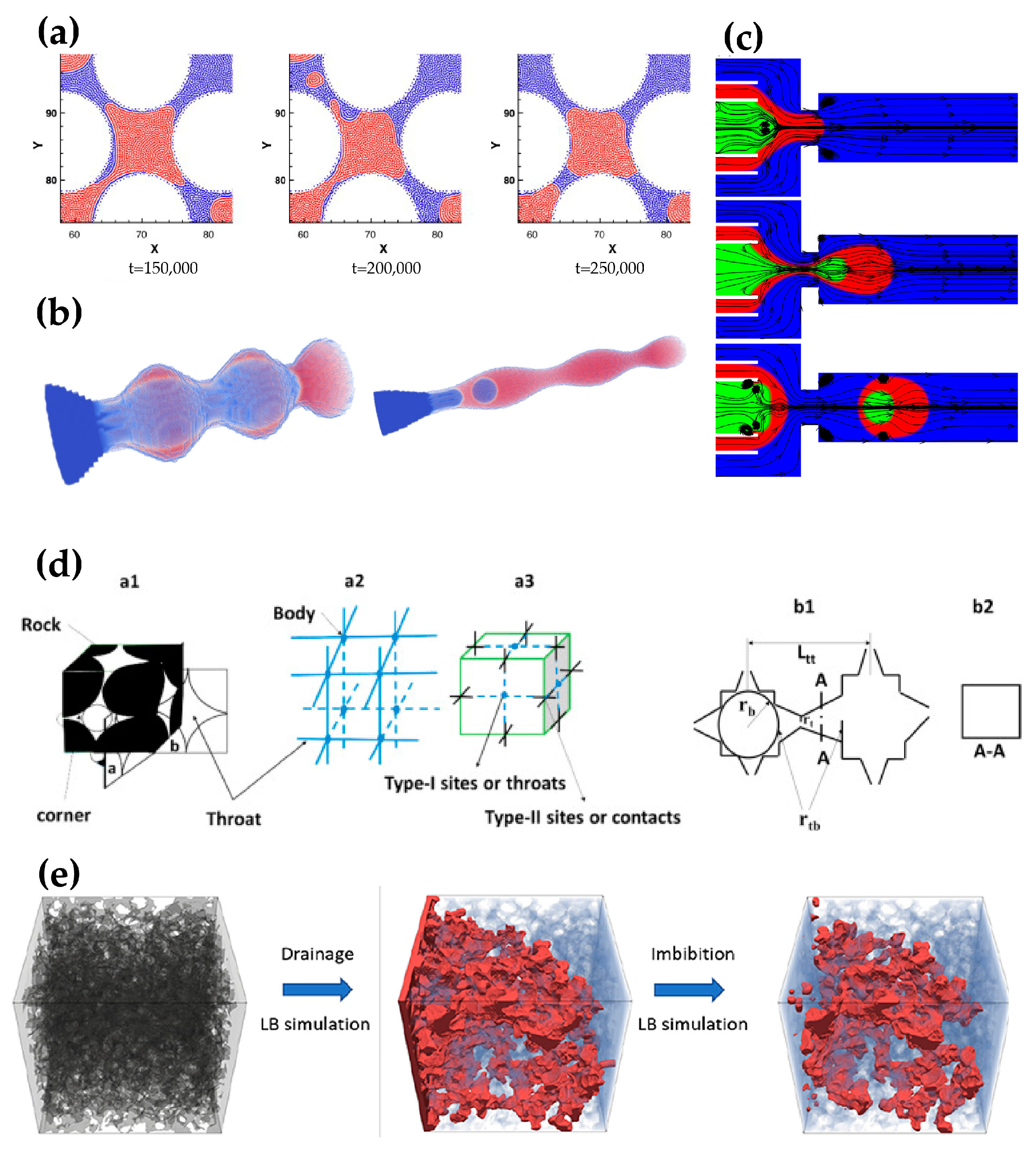
3. Influencing Factors of Snap-Off
3.1. Characteristics of Multiphase Fluids
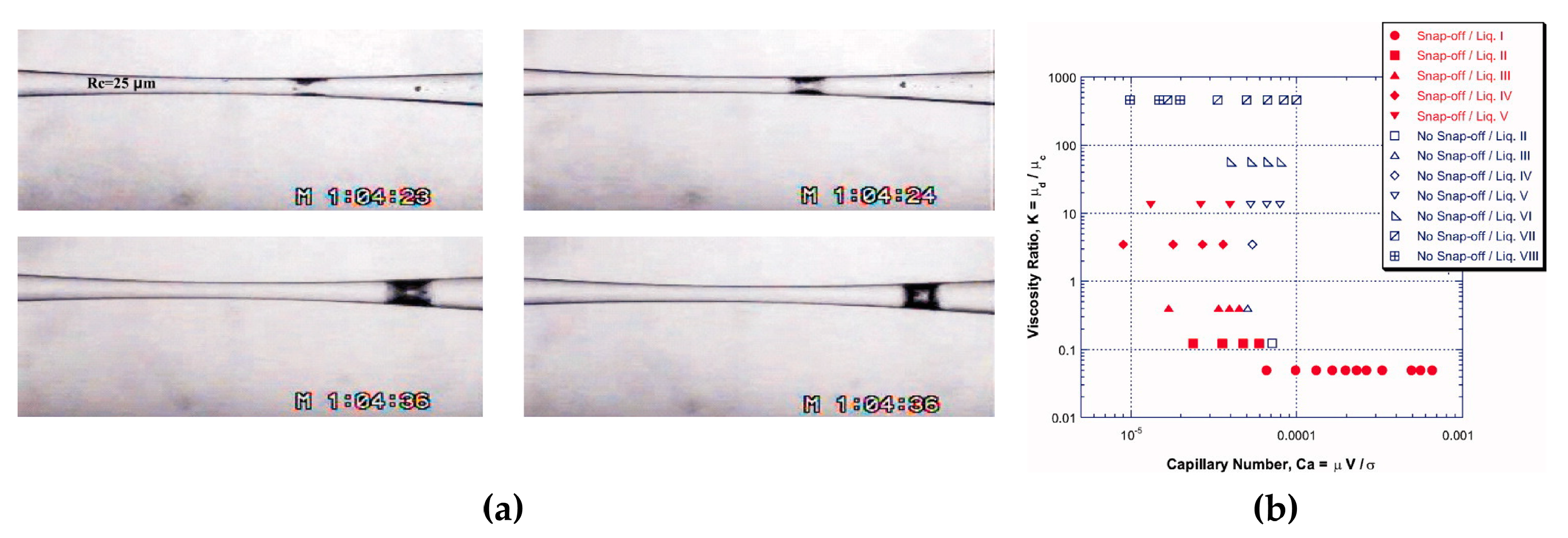
3.1.1. Capillary Number
3.1.2. Viscosity Ratio
3.1.3. Flow Rate Ratio
3.2. Wettability of Porous Media
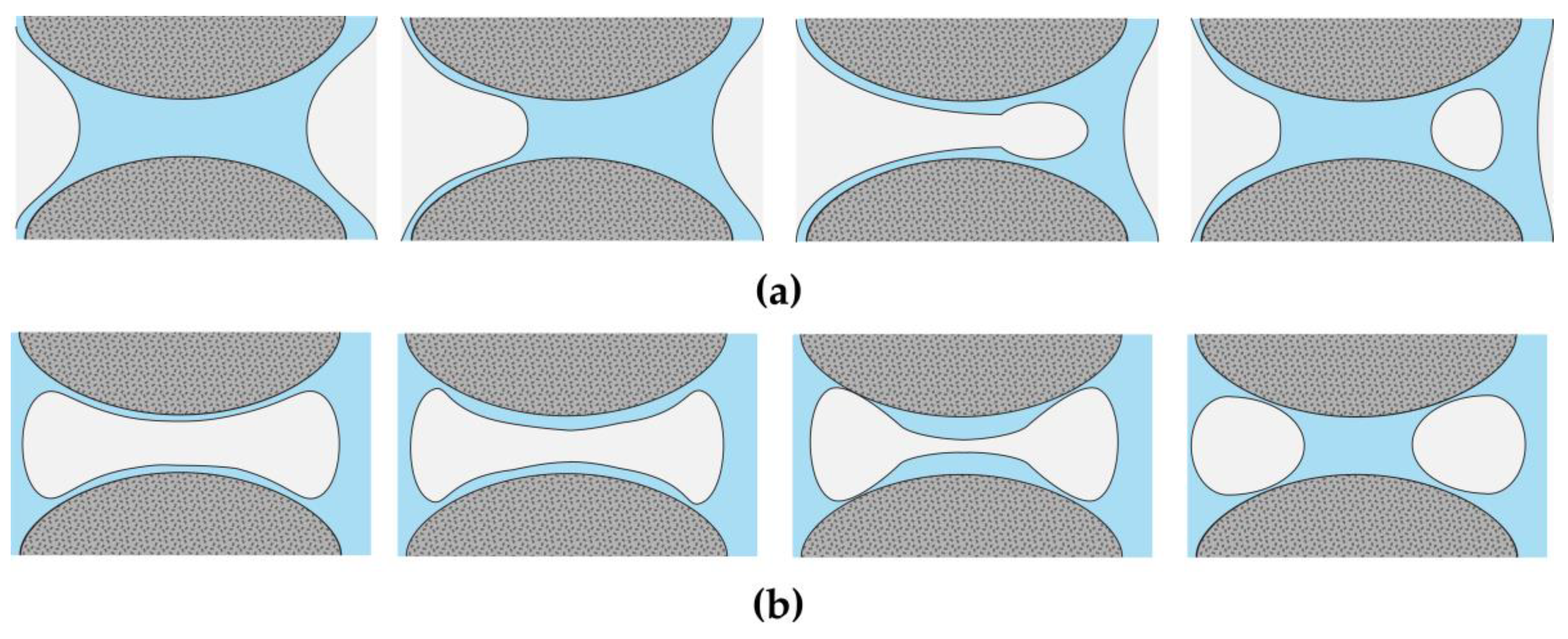
3.3. Pore–Throat Geometry and Topology
3.3.1. Cross-Sectional Shape
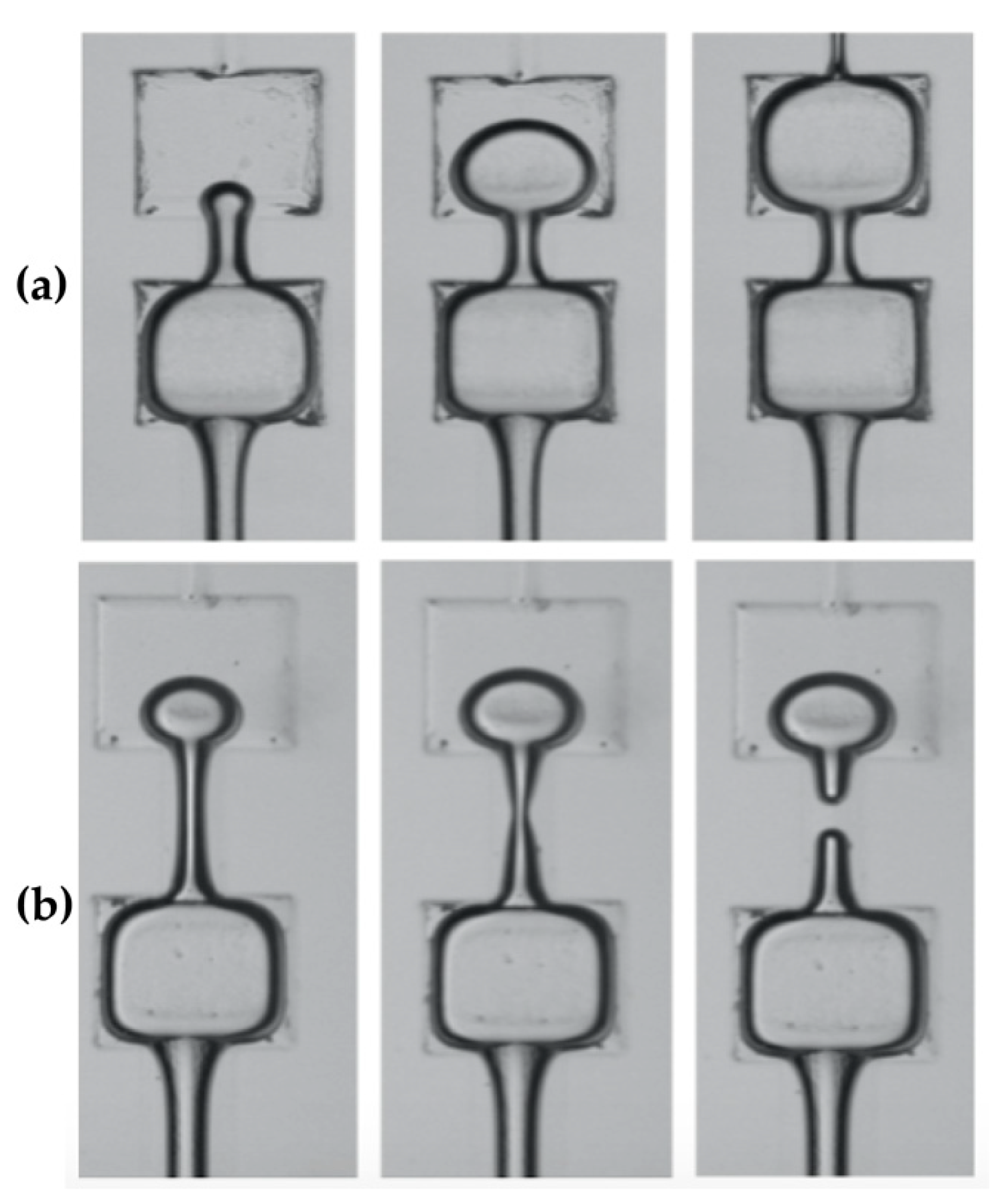
3.3.2. Pore–Throat Connection
4. Impacts of Snap-Off
4.1. Unrecoverable Oil Droplet Formation
4.2. Oil Bridging Effect
4.3. Drainage–Imbibition Hysteresis
4.4. Strong Foam Generation
4.5. Transient/Dynamic Effects
4.6. Interconnections between Effects
5. Prevention and Utilization of Snap-Off
5.1. Prevention of Snap-Off in Waterflooding for Oil Production
5.2. Utilization of Snap-Off in CO2-EOR
5.3. Utilization of Snap-Off in CO2 Storage
6. Limitations and Future Improvements
7. Conclusions
- (1)
- The formation of snap-off is governed by changes in the interface curvature within confined regions and the impact of the capillary pressure, resulting in the destabilization of the meniscus interface between the two-phase fluids. Ultimately, this instability leads to the occurrence of snap-off phenomena at the constrictions.
- (2)
- The snap-off phenomenon is primarily influenced by factors, including the characteristics of multiphase fluids, the wettability of porous media, and the pore–throat geometry and topology within porous media.
- (3)
- Numerous effects are brought about by snap-off, such as the unrecoverable oil droplet formation, the oil bridging effect, drainage–imbibition hysteresis, strong foam generation, and transient/dynamic effects.
- (4)
- During the conventional waterflooding for oil production, the snap-off phenomenon detrimentally impacts oil recovery. It results in unrecoverable oil droplets, the oil bridging effect, and drainage–imbibition hysteresis, significantly reducing crude oil-recovery rates. Therefore, pertinent measures should be implemented to avoid the occurrence of the snap-off phenomenon during waterflooding.
- (5)
- In the CO2-EOR context, snap-off mechanisms facilitate the generation of robust foam structures, which, in turn, serve to improve oil mobility and enhance the sweep efficiency, ultimately leading to an enhancement in crude oil-recovery rates.
- (6)
- In the context of CO2 storage within saline aquifers, large, stable CO2 bubbles are generated through the strong foam generation effect of snap-off within the reservoir porous media. Subsequently, snap-off-induced transient/dynamic effects reduce water saturation and lower the water relative permeability, facilitating stable CO2 storage in saline aquifers.
- (7)
- Experimental studies of snap-off face limitations, such as difficulties in manufacturing microfluidic models with sub-10-micrometer pore structures, and issues related to the high expenses and low resolution of advanced visualization techniques. To address these challenges, future improvements should focus on refining manufacturing techniques for precise models, as well as enhancing the time–space scanning resolution of imaging techniques.
- (8)
- The core challenge in numerical simulation studies of snap-off revolves around the delicate balance between computational efficiency and simulation precision. To address the challenge, future enhancements should focus on the development of more efficient algorithms to support numerical stability, the utilization of parallel and distributed computing to expedite simulations and curtail computational resources, and the refinement of model physical representations for practical applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Morrow, N.R.; Mason, G. Recovery of Oil by Spontaneous Imbibition. Curr. Opin. Colloid Interface Sci. 2001, 6, 321–337. [Google Scholar] [CrossRef]
- Zhou, X.; Torsæter, O.; Xie, X.; Morrow, N.R. The Effect of Crude-Oil Aging Time and Temperature on the Rate of Water Imbibition and Long-Term Recovery by Imbibition. SPE Form. Eval. 1995, 10, 259–265. [Google Scholar] [CrossRef]
- Babadagli, T. Temperature Effect on Heavy-Oil Recovery by Imbibition in Fractured Reservoirs. J. Pet. Sci. Eng. 1996, 14, 197–208. [Google Scholar] [CrossRef]
- Wang, X.; Peng, X.; Zhang, S.; Du, Z.; Zeng, F. Characteristics of Oil Distributions in Forced and Spontaneous Imbibition of Tight Oil Reservoir. Fuel 2018, 224, 280–288. [Google Scholar] [CrossRef]
- Clarkson, C.; Yuan, B.; Zhang, Z.; Tabasinejad, F.; Behmanesh, H.; Hamdi, H.; Anderson, D.; Thompson, J.; Lougheed, D. Anomalous Diffusion or Classical Diffusion in an Anomalous Reservoir? Evaluation of the Impact of Multi-Phase Flow on Reservoir Signatures in Unconventional Reservoirs. In Proceedings of the 7th Unconventional Resources Technology Conference, Denver, CO, USA, 22–24 July 2019. [Google Scholar] [CrossRef]
- Lin, D.; Wang, J.; Yuan, B.; Shen, Y. Review on Gas Flow and Recovery in Unconventional Porous Rocks. Adv. Geo-Energy Res. 2017, 1, 39–53. [Google Scholar] [CrossRef]
- Zhu, D.; Li, B.; Zheng, L.; Lei, W.; Li, B.; Li, Z. Effects of CO2 and Surfactants on the Interface Characteristics and Imbibition Process in Low-Permeability Heavy Oil Reservoirs. Colloids Surf. A Physicochem. Eng. Asp. 2023, 657, 130538. [Google Scholar] [CrossRef]
- Yao, J.; Li, G.; Wu, J. Application of In-Situ Combustion for Heavy Oil Production in China: A Review. J. Oil Gas Petrochem. Sci. 2018, 1, 69–72. [Google Scholar] [CrossRef]
- Yao, J.; Song, Y. Dynamic Analysis Approach to Evaluate In-Situ Combustion Performance for Heavy Oil Production. J. Oil Gas Petrochem. Sci. 2019, 2, 42–47. [Google Scholar] [CrossRef]
- Aghaeifar, Z.; Strand, S.; Puntervold, T. Significance of Capillary Forces during Low-Rate Waterflooding. Energy Fuels 2019, 33, 3989–3997. [Google Scholar] [CrossRef]
- Li, J.; McDougall, S.R.; Sorbie, K.S. Dynamic Pore-Scale Network Model (PNM) of Water Imbibition in Porous Media. Adv. Water Resour. 2017, 107, 191–211. [Google Scholar] [CrossRef]
- Yao, J. A Microfluidic Model for Visualizing Snap-off During Imbibition. Ph.D. Dissertation, University of Wyoming, Laramie, WY, USA, 2017. [Google Scholar]
- Andersen, P.Ø.; Salomonsen, L.; Sleveland, D.S. Characteristic Forced and Spontaneous Imbibition Behavior in Strongly Water-Wet Sandstones Based on Experiments and Simulation. Energies 2022, 15, 3531. [Google Scholar] [CrossRef]
- Liu, Y.; Berg, S.; Ju, Y.; Wei, W.; Kou, J.; Cai, J. Systematic Investigation of Corner Flow Impact in Forced Imbibition. Water Resour. Res. 2022, 58, e2022WR032402. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Sheppard, A.P.; Knackstedt, M.A.; Pinczewski, W.V. A Dynamic Network Model for Imbibition. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004. [Google Scholar] [CrossRef]
- Prodanović, M.; Bryant, S.L. A Level Set Method for Determining Critical Curvatures for Drainage and Imbibition. J. Colloid Interface Sci. 2006, 304, 442–458. [Google Scholar] [CrossRef] [PubMed]
- Meng, Q.; Liu, H.; Wang, J. Entrapment of the Non-Wetting Phase during Co-Current Spontaneous Imbibition. Energy Fuels 2015, 29, 686–694. [Google Scholar] [CrossRef]
- Cai, J.; Yu, B.; Zou, M.; Luo, L. Fractal Characterization of Spontaneous Co-Current Imbibition in Porous Media. Energy Fuels 2010, 24, 1860–1867. [Google Scholar] [CrossRef]
- Takahashi, S.; Kovscek, A.R. Spontaneous Countercurrent Imbibition and Forced Displacement Characteristics of Low-Permeability, Siliceous Shale Rocks. J. Pet. Sci. Eng. 2010, 71, 47–55. [Google Scholar] [CrossRef]
- Kashchiev, D.; Firoozabadi, A. Analytical Solutions for 1D Countercurrent Imbibition in Water-Wet Media. SPE J. 2003, 8, 401–408. [Google Scholar] [CrossRef]
- Pooladi-Darvish, M.; Firoozabadi, A. Cocurrent and Countercurrent Imbibition in a Water-Wet Matrix Block. SPE J. 2000, 5, 3–11. [Google Scholar] [CrossRef]
- Tanino, Y.; Zacarias-Hernandez, X.; Christensen, M. Oil/Water Displacement in Microfluidic Packed Beds under Weakly Water-Wetting Conditions: Competition between Precursor Film Flow and Piston-like Displacement. Exp. Fluids 2018, 59, 35. [Google Scholar] [CrossRef]
- Rezaei Dehshibi, R.; Sadatshojaie, A.; Mohebbi, A.; Riazi, M. A New Insight into Pore Body Filling Mechanism during Waterflooding in a Glass Micro-Model. Chem. Eng. Res. Des. 2019, 151, 100–107. [Google Scholar] [CrossRef]
- Roof, J.G. Snap-Off of Oil Droplets in Water-Wet Pores. Soc. Pet. Eng. J. 1970, 10, 85–90. [Google Scholar] [CrossRef]
- Moreno, R.B.; Bonet, E.J.; Iatchuk, S.; Vieira, M.R.; Correa, A.C. Residual-Oil Saturation for a Very Long Unconsolidated Core, With Live Oil at Reservoir Conditions. In Proceedings of the SPE Latin American and Caribbean Petroleum Engineering Conference, Lima, Peru, 1–3 December 2010. [Google Scholar] [CrossRef]
- Liu, Y.; Iglauer, S.; Cai, J.; Amooie, M.A.; Qin, C. Local Instabilities during Capillary-Dominated Immiscible Displacement in Porous Media. Capillarity 2019, 2, 1–7. [Google Scholar] [CrossRef]
- Zhou, Y.; Yin, D.; Chen, W.; Liu, B.; Zhang, X. A Comprehensive Review of Emulsion and Its Field Application for Enhanced Oil Recovery. Energy Sci. Eng. 2019, 7, 1046–1058. [Google Scholar] [CrossRef]
- Li, Y.; Ranjith, P.G.; Perera, M.S.A.; Yu, Q. Residual Water Formation during the CO 2 Storage Process in Deep Saline Aquifers and Factors Influencing It: A Review. J. CO2 Util. 2017, 20, 253–262. [Google Scholar] [CrossRef]
- Hamza, M.F.; Sinnathambi, C.M.; Aljunid Merican, Z.M.; Soleimani, H.; Karl, D.S. An Overview of the Present Stability and Performance of EOR-Foam. Sains Malays. 2017, 46, 1641–1650. [Google Scholar] [CrossRef]
- Diamantopoulos, E.; Durner, W. Dynamic Nonequilibrium of Water Flow in Porous Media: A Review. Vadose Zone J. 2012, 11, vzj2011.0197. [Google Scholar] [CrossRef]
- Rossen, W.R. A Critical Review of Roof Snap-off as a Mechanism of Steady-State Foam Generation in Homogeneous Porous Media. Colloids Surf. A Physicochem. Eng. Asp. 2003, 225, 1–24. [Google Scholar] [CrossRef]
- Yao, J.; Han, H.; Yang, Y.; Song, Y.; Li, G. A Review of Recent Progress of Carbon Capture, Utilization, and Storage (CCUS) in China. Appl. Sci. 2023, 13, 1169. [Google Scholar] [CrossRef]
- Falls, A.H.; Hirasaki, G.J.; Patzek, T.W.; Gauglitz, D.A.; Miller, D.D.; Ratulowski, T. Development of a Mechanistic Foam Simulator: The Population Balance and Generation by Snap-Off. SPE Reserv. Eng. 1988, 3, 884–892. [Google Scholar] [CrossRef]
- Gauglitz, P.A.; Laurent, C.M.S.; Radke, C.J. Experimental Determination of Gas-Bubble Breakup in a Constricted Cylindrical Capillary. Ind. Eng. Chem. Res. 1988, 27, 1282–1291. [Google Scholar] [CrossRef]
- Goldsmith, H.L.; Mason, S.G. The Movement of Single Large Bubbles in Closed Vertical Tubes. J. Fluid Mech. 1962, 14, 42–58. [Google Scholar] [CrossRef]
- Mast, R.F. Microscopic Behavior of Foam in Porous Media. In Proceedings of the Fall Meeting of the Society of Petroleum Engineers of AIME, San Antonio, TX, USA, 8–11 October 1972. [Google Scholar] [CrossRef]
- Ransohoff, T.C.; Radke, C.J. Laminar Flow of a Wetting Liquid along the Corners of a Predominantly Gas-Occupied Noncircular Pore. J. Colloid Interface Sci. 1988, 121, 392–401. [Google Scholar] [CrossRef]
- Lebedeva, E.V.; Fogden, A. Micro-CT and Wettability Analysis of Oil Recovery from Sand Packs and the Effect of Waterflood Salinity and Kaolinite. Energy Fuels 2011, 25, 5683–5694. [Google Scholar] [CrossRef]
- Singh, K.; Menke, H.; Andrew, M.; Lin, Q.; Rau, C.; Blunt, M.J.; Bijeljic, B. Dynamics of Snap-off and Pore-Filling Events during Two-Phase Fluid Flow in Permeable Media. Sci. Rep. 2017, 7, 5192. [Google Scholar] [CrossRef] [PubMed]
- Tian, J.; Kang, Y.; Xi, Z.; Jia, N.; You, L.; Luo, P. Real-Time Visualization and Investigation of Dynamic Gas Snap-off Mechanisms in 2-D Micro Channels. Fuel 2020, 279, 118232. [Google Scholar] [CrossRef]
- Li, Z.; Gu, Z.; Li, R.; Wang, C.; Chen, C.; Yu, C.; Zhang, Y.; Shu, Q.; Su, J. Investigation on Droplet Dynamic Snap-off Process in a Short, Abrupt Constriction. Chem. Eng. Sci. 2021, 235, 116496. [Google Scholar] [CrossRef]
- Liu, Y.; Block, E.; Squier, J.; Oakey, J. Investigating Low Salinity Waterflooding via Glass Micromodels with Triangular Pore-Throat Architectures. Fuel 2021, 283, 119264. [Google Scholar] [CrossRef]
- Bandara, U.C.; Tartakovsky, A.M.; Palmer, B.J. Pore-Scale Study of Capillary Trapping Mechanism during CO2 Injection in Geological Formations. Int. J. Greenh. Gas. Control. 2011, 5, 1566–1577. [Google Scholar] [CrossRef]
- Starnoni, M.; Pokrajac, D. Numerical Study of the Effects of Contact Angle and Viscosity Ratio on the Dynamics of Snap-off through Porous Media. Adv. Water Resour. 2018, 111, 70–85. [Google Scholar] [CrossRef]
- Kohanpur, A.H.; Chen, Y.; Valocchi, A.J. Using Direct Numerical Simulation of Pore-Level Events to Improve Pore-Network Models for Prediction of Residual Trapping of CO2. Front. Water 2022, 3, 710160. [Google Scholar] [CrossRef]
- Hosseinzadegan, A.; Raoof, A.; Mahdiyar, H.; Nikooee, E.; Ghaedi, M.; Qajar, J. Review on Pore-Network Modeling Studies of Gas-Condensate Flow: Pore Structure, Mechanisms, and Implementations. Geoenergy Sci. Eng. 2023, 226, 211693. [Google Scholar] [CrossRef]
- Aghaei, A.; Piri, M. Direct Pore-to-Core up-Scaling of Displacement Processes: Dynamic Pore Network Modeling and Experimentation. J. Hydrol. 2015, 522, 488–509. [Google Scholar] [CrossRef]
- Zankoor, A.; Khishvand, M.; Mohamed, A.; Wang, R.; Piri, M. In-Situ Capillary Pressure and Wettability in Natural Porous Media: Multi-Scale Experimentation and Automated Characterization Using X-Ray Images. J. Colloid Interface Sci. 2021, 603, 356–369. [Google Scholar] [CrossRef] [PubMed]
- Fulcher, R.A.; Ertekin, T.; Stahl, C.D. Effect of Capillary Number and Its Constituents on Two-Phase Relative Permeability Curves. J. Pet. Technol. 1985, 37, 249–260. [Google Scholar] [CrossRef]
- Guo, H.; Dou, M.; Hanqing, W.; Wang, F.; Yuanyuan, G.; Yu, Z.; Yansheng, W.; Li, Y. Proper Use of Capillary Number in Chemical Flooding. J. Chem. 2017, 2017, 4307368. [Google Scholar] [CrossRef]
- Olbricht, W.L. Pore-Scale Prototypes of Multiphase Flow in Porous Media. Annu. Rev. Fluid. Mech. 1996, 28, 187–213. [Google Scholar] [CrossRef]
- Yao, J.; Oakey, J. Geometrically-Mediated Snap-off of Water-in-Oil Emulsion Droplets in Microfluidic Flow Focusing Devices. J. Oil Gas Petrochem. Sci. 2018, 1, 42–46. [Google Scholar] [CrossRef]
- Peña, T.J.; Carvalho, M.S.; Alvarado, V. Snap-off of a Liquid Drop Immersed in Another Liquid Flowing through a Constricted Capillary. AIChE J. 2009, 55, 1993–1999. [Google Scholar] [CrossRef]
- Tsai, T.M.; Miksis, M.J. Dynamics of a Drop in a Constricted Capillary Tube. J. Fluid Mech. 1994, 274, 197–217. [Google Scholar] [CrossRef]
- Ransohoff, T.C.; Gauglitz, P.A.; Radke, C.J. Snap-off of Gas Bubbles in Smoothly Constricted Noncircular Capillaries. AIChE J. 1987, 33, 753–765. [Google Scholar] [CrossRef]
- Mohanty, K.K.; Davis, H.T.; Scriven, L.E. Physics of Oil Entrapment in Water-Wet Rock. SPE Reserv. Eng. 1987, 2, 113–128. [Google Scholar] [CrossRef]
- Deng, W.; Balhoff, M.; Cardenas, M.B. Influence of Dynamic Factors on Nonwetting Fluid Snap-off in Pores. Water Resour. Res. 2015, 51, 9182–9189. [Google Scholar] [CrossRef]
- Beresnev, I.A.; Deng, W. Theory of Breakup of Core Fluids Surrounded by a Wetting Annulus in Sinusoidally Constricted Capillary Channels. Phys. Fluids 2010, 22, 012105. [Google Scholar] [CrossRef]
- Yao, J. Microfluidic Studies on Snap-Off during Imbibition Process. Master’s Thesis, China University of Petroleum (East China), Qingdao, China, 2014. [Google Scholar]
- Herring, A.L.; Gilby, F.J.; Li, Z.; McClure, J.E.; Turner, M.; Veldkamp, J.P.; Beeching, L.; Sheppard, A.P. Observations of Nonwetting Phase Snap-off during Drainage. Adv. Water Resour. 2018, 121, 32–43. [Google Scholar] [CrossRef]
- Bai, X.; Yan, G.; Kong, S.; Yang, T.; Yao, J.; Wen, P.; Li, G. Study on the Mechanism of the Influence of Surfactant Alkyl Chain Length on the Wettability of Anthracite Dust Based on EDLVO Theory and Inverse Gas Chromatography. Fuel 2023, 353, 129187. [Google Scholar] [CrossRef]
- Bai, X.; Yan, G.; Kong, S.; Yao, J.; Wen, P.; Li, G.; Li, J.; Zhang, J. Suppression of Anthracite Dust by a Composite of Oppositely-Charged Ionic Surfactants with Ultra-High Surface Activity: Theoretical Calculation and Experiments. Fuel 2023, 344, 128075. [Google Scholar] [CrossRef]
- Amirmoshiri, M.; Zhang, L.; Puerto, M.C.; Tewari, R.D.; Bahrim, R.Z.B.K.; Farajzadeh, R.; Hirasaki, G.J.; Biswal, S.L. Role of Wettability on the Adsorption of an Anionic Surfactant on Sandstone Cores. Langmuir 2020, 36, 10725–10738. [Google Scholar] [CrossRef]
- Amott, E. Observations Relating to the Wettability of Porous Rock. Trans. AIME 1959, 216, 156–162. [Google Scholar] [CrossRef]
- Wardlaw, N.C. The Effects of Geometry, Wettability, Viscosity And Interfacial Tension On Trapping In Single Pore-Throat Pairs. J. Can. Pet. Technol. 1982, 21, PETSOC-82-03-01. [Google Scholar] [CrossRef]
- Yu, L.; Wardlaw, N.C. The Influence of Wettability and Critical Pore-Throat Size Ratio on Snap—Off. J. Colloid Interface Sci. 1986, 109, 461–472. [Google Scholar] [CrossRef]
- Al-Futaisi, A.; Patzek, T.W. Impact of Wettability Alteration on Two-Phase Flow Characteristics of Sandstones: A Quasi-Static Description. Water Resour. Res. 2003, 39, 1042. [Google Scholar] [CrossRef]
- Stratford, K.; Adhikari, R.; Pagonabarraga, I.; Desplat, J.-C.; Cates, M.E. Colloidal Jamming at Interfaces: A Route to Fluid-Bicontinuous Gels. Science (1979) 2005, 309, 2198–2201. [Google Scholar] [CrossRef] [PubMed]
- Melle, S.; Lask, M.; Fuller, G.G. Pickering Emulsions with Controllable Stability. Langmuir 2005, 21, 2158–2162. [Google Scholar] [CrossRef] [PubMed]
- Jadhunandan, P.P.; Morrow, N.R. Effect of Wettability on Waterflood Recovery for Crude-Oil/Brine/Rock Systems. SPE Reserv. Eng. 1995, 10, 40–46. [Google Scholar] [CrossRef]
- Yao, J. Microfluidic Studies of Geometrically-Mediated Snap-Off. Master’s Thesis, University of Wyoming, Laramie, WY, USA, 2014. [Google Scholar]
- Sulerud, T.; Sami, A.B.; Li, G.; Kloxin, A.; Oakey, J.; Gatlin, J. Microtubule-Dependent Pushing Forces Contribute to Long-Distance Aster Movement and Centration in Xenopus Laevis Egg Extracts. Mol. Biol. Cell 2020, 31, 2791–2802. [Google Scholar] [CrossRef] [PubMed]
- Li, G. 3D Printed Microfluidic Devices for Controlled Biomaterial Fabrication. Ph.D. Dissertation, University of Wyoming, Laramie, WY, USA, 2020. [Google Scholar]
- Chen, J.D. Measuring the Film Thickness Surrounding a Bubble inside a Capillary. J. Colloid Interface Sci. 1986, 109, 341–349. [Google Scholar] [CrossRef]
- Gauglitz, P.A.; Radke, C.J. The Dynamics of Liquid Film Breakup in Constricted Cylindrical Capillaries. J. Colloid Interface Sci. 1990, 134, 14–40. [Google Scholar] [CrossRef]
- Chatzis, I.; Morrow, N.R.; Lim, H.T. Magnitude and Detailed Structure of Residual Oil Saturation. Soc. Pet. Eng. J. 1983, 23, 311–326. [Google Scholar] [CrossRef]
- Westborg, H.; Hassager, O. Creeping Motion of Long Bubbles and Drops in Capillary Tubes. J. Colloid Interface Sci. 1989, 133, 135–147. [Google Scholar] [CrossRef]
- Yu, L.; Wardlaw, N.C. Mechanisms of Nonwetting Phase Trapping during Imbibition at Slow Rates. J. Colloid Interface Sci. 1986, 109, 473–486. [Google Scholar] [CrossRef]
- Arriola, A.; Willhite, G.P.; Green, D.W. Trapping of Oil Drops in a Noncircular Pore Throat and Mobilization Upon Contact With a Surfactant. Soc. Pet. Eng. J. 1983, 23, 99–114. [Google Scholar] [CrossRef]
- Mohammad Piri Pore-Scale Modeling of Three-Phase Flow. Ph.D. Dissertation, Imperial College London, London, UK, 2003.
- Sedghi, M.; Piri, M.; Goual, L. Molecular Dynamics of Wetting Layer Formation and Forced Water Invasion in Angular Nanopores with Mixed Wettability. J. Chem. Phys. 2014, 141, 194703. [Google Scholar] [CrossRef] [PubMed]
- Anbari, A.; Lowry, E.; Piri, M. Estimation of Capillary Pressure in Unconventional Reservoirs Using Thermodynamic Analysis of Pore Images. J. Geophys. Res. Solid Earth 2019, 124, 10893–10915. [Google Scholar] [CrossRef]
- Ma, S.; Mason, G.; Morrow, N.R. Effect of Contact Angle on Drainage and Imbibition in Regular Polygonal Tubes. Colloids Surf. A Physicochem. Eng. Asp. 1996, 117, 273–291. [Google Scholar] [CrossRef]
- Qu, Z.; Yao, J.; Yang, Y.; Wang, B.; He, L. Laboratory Experiments of a Microfluidic Model for Imbibition. J. Petrochem. Univ. 2014, 37, 64–66. [Google Scholar] [CrossRef]
- Priyadarshi, M.; Srita, K.V.; Bhaskar, V.V.K.N.S.; Khalid, M.; Subramanian, G.; Shankar, V. A New Elastic Instability in Gravity-Driven Viscoelastic Film Flow. Phys. Fluids 2023, 35, 073104. [Google Scholar] [CrossRef]
- Harriott, G.M.; Brown, R.A. Flow in a Differentially Rotated Cylindrical Drop at Moderate Reynolds Number. J. Fluid Mech. 1984, 144, 403–418. [Google Scholar] [CrossRef]
- Ayyaswamy, P.S.; Catton, I.; Edwards, D.K. Capillary Flow in Triangular Grooves. J. Appl. Mech. 1974, 41, 332–336. [Google Scholar] [CrossRef]
- Dullien, F.A.L. Two-Phase Flow in Porous Media. Chem. Eng. Technol.-CET 1988, 11, 407–424. [Google Scholar] [CrossRef]
- Chatzis, I.; Dullien, F.A.L. Dynamic Immiscible Displacement Mechanisms in Pore Doublets: Theory versus Experiment. J. Colloid Interface Sci. 1983, 91, 199–222. [Google Scholar] [CrossRef]
- Larson, R.G. The Influence of Phase Behavior on Surfactant Flooding. Soc. Pet. Eng. J. 1979, 19, 411–422. [Google Scholar] [CrossRef]
- Nayberg, T.M. Laboratory Study of Lost Circulation Materials for Use in both Oil-Based and Water-Based Drilling Muds. SPE Drill. Eng. 1987, 2, 229–236. [Google Scholar] [CrossRef]
- Morrow, N.R. Wettability and Its Effect on Oil Recovery. J. Pet. Technol. 1990, 42, 1476–1484. [Google Scholar] [CrossRef]
- Dickinson, E.; Flint, F.O.; Hunt, J.A. Bridging Flocculation in Binary Protein Stabilized Emulsions. Food Hydrocoll. 1989, 3, 389–397. [Google Scholar] [CrossRef]
- Delshad, M.; Pope, G.A. Comparison of the Three-Phase Oil Relative Permeability Models. Transp. Porous Media 1989, 4, 59–83. [Google Scholar] [CrossRef]
- Fayers, F.J.; Matthews, J.D. Evaluation of Normalized Stone’s Methods for Estimating Three-Phase Relative Permeabilities. Soc. Pet. Eng. J. 1984, 24, 224–232. [Google Scholar] [CrossRef]
- Jerauld, G.R.; Salter, S.J. The Effect of Pore-Structure on Hysteresis in Relative Permeability and Capillary Pressure: Pore-Level Modeling. Transp. Porous Media 1990, 5, 103–151. [Google Scholar] [CrossRef]
- Lenormand, R.; Zarcone, C.; Sarr, A. Mechanisms of the Displacement of One Fluid by Another in a Network of Capillary Ducts. J. Fluid Mech. 1983, 135, 337. [Google Scholar] [CrossRef]
- Rossen, W.R.; Gauglitz, P.A. Percolation Theory of Creation and Mobilization of Foams in Porous Media. AIChE J. 1990, 36, 1176–1188. [Google Scholar] [CrossRef]
- Almajid, M.M.; Kovscek, A.R. Pore-Level Mechanics of Foam Generation and Coalescence in the Presence of Oil. Adv. Colloid Interface Sci. 2016, 233, 65–82. [Google Scholar] [CrossRef]
- Kovscek, A.R.; Radke, C.J. Pressure-Driven Capillary Snap-off of Gas Bubbles at Low Wetting-Liquid Content. Colloids Surf. A Physicochem. Eng. Asp. 2003, 212, 99–108. [Google Scholar] [CrossRef]
- Almajid, M.M.; Kovscek, A.R. Pore Network Investigation of Trapped Gas and Foam Generation Mechanisms. Transp. Porous Media 2020, 131, 289–313. [Google Scholar] [CrossRef]
- Ransohoff, T.C.; Radke, C.J. Mechanisms of Foam Generation in Glass-Bead Packs. SPE Reserv. Eng. 1988, 3, 573–585. [Google Scholar] [CrossRef]
- Yan, G.; Li, Z.; Galindo Torres, S.A.; Scheuermann, A.; Li, L. Transient Two-Phase Flow in Porous Media: A Literature Review and Engineering Application in Geotechnics. Geotechnics 2022, 2, 32–90. [Google Scholar] [CrossRef]
- Hassanizadeh, S.M.; Celia, M.A.; Dahle, H.K. Dynamic Effect in the Capillary Pressure-Saturation Relationship and Its Impacts on Unsaturated Flow. Vadose Zone J. 2002, 1, 38–57. [Google Scholar] [CrossRef]
- Malaya, C.; Sreedeep, S. Critical Review on the Parameters Influencing Soil-Water Characteristic Curve. J. Irrig. Drain. Eng. 2012, 138, 55–62. [Google Scholar] [CrossRef]
- Joekar Niasar, V.; Hassanizadeh, S.M.; Pyrak-Nolte, L.J.; Berentsen, C. Simulating Drainage and Imbibition Experiments in a High-porosity Micromodel Using an Unstructured Pore Network Model. Water Resour. Res. 2009, 45, W02430. [Google Scholar] [CrossRef]
- Kalaydjian, F. A Macroscopic Description of Multiphase Flow in Porous Media Involving Spacetime Evolution of Fluid/Fluid Interface. Transp. Porous Media 1987, 2, 537–552. [Google Scholar] [CrossRef]
- Mirzaei, M.; Das, D.B. Dynamic Effects in Capillary Pressure–Saturations Relationships for Two-Phase Flow in 3D Porous Media: Implications of Micro-Heterogeneities. Chem. Eng. Sci. 2007, 62, 1927–1947. [Google Scholar] [CrossRef]
- Shams, M.; Singh, K.; Bijeljic, B.; Blunt, M.J. Direct Numerical Simulation of Pore-Scale Trapping Events During Capillary-Dominated Two-Phase Flow in Porous Media. Transp. Porous Media 2021, 138, 443–458. [Google Scholar] [CrossRef]
- Barkley, S.; Scarfe, S.J.; Weeks, E.R.; Dalnoki-Veress, K. Predicting the Size of Droplets Produced through Laplace Pressure Induced Snap-Off. Soft Matter 2016, 12, 7398–7404. [Google Scholar] [CrossRef] [PubMed]
- Sukee, A.; Nunta, T.; Haruna, M.A.; Kalantariasl, A.; Tangparitkul, S. Influence of Sequential Changes in the Crude Oil-Water Interfacial Tension on Spontaneous Imbibition in Oil-Wet Sandstone. J. Pet. Sci. Eng. 2022, 210, 110032. [Google Scholar] [CrossRef]
- Gong, Y.; Sedghi, M.; Piri, M. Two-Phase Relative Permeability of Rough-Walled Fractures: A Dynamic Pore-Scale Modeling of the Effects of Aperture Geometry. Water Resour. Res. 2021, 57, e2021WR030104. [Google Scholar] [CrossRef]
- Liu, Y.; Rui, Z. A Storage-Driven CO2 EOR for a Net-Zero Emission Target. Engineering 2022, 18, 79–87. [Google Scholar] [CrossRef]
- Li, G.; Yao, J.; Song, Y.; Tang, J.; Han, H.; Cui, X. A Review of the Metallogenic Mechanisms of Sandstone-Type Uranium Deposits in Hydrocarbon-Bearing Basins in China. Eng 2023, 4, 1723–1741. [Google Scholar] [CrossRef]
- Abdelaal, A.; Aljawad, M.S.; Alyousef, Z.; Almajid, M.M. A Review of Foam-Based Fracturing Fluids Applications: From Lab Studies to Field Implementations. J. Nat. Gas Sci. Eng. 2021, 95, 104236. [Google Scholar] [CrossRef]
- Krevor, S.; Blunt, M.J.; Benson, S.M.; Pentland, C.H.; Reynolds, C.; Al-Menhali, A.; Niu, B. Capillary Trapping for Geologic Carbon Dioxide Storage–From Pore Scale Physics to Field Scale Implications. Int. J. Greenh. Gas Control. 2015, 40, 221–237. [Google Scholar] [CrossRef]
- Suekane, T.; Nobuso, T.; Hirai, S.; Kiyota, M. Geological Storage of Carbon Dioxide by Residual Gas and Solubility Trapping. Int. J. Greenh. Gas Control. 2008, 2, 58–64. [Google Scholar] [CrossRef]
- Bachu, S. Drainage and Imbibition CO2/Brine Relative Permeability Curves at in Situ Conditions for Sandstone Formations in Western Canada. Energy Procedia 2013, 37, 4428–4436. [Google Scholar] [CrossRef]
- Brinckmann, S.A.; Yao, J.; Young, J.C.; Jones, M.H.; Fertig, R.S., III; Frick, C.P. Additive Manufacturing of SiCNO Polymer-Derived Ceramics via Step-Growth Polymerization. Open Ceram. 2023, 15, 100414. [Google Scholar] [CrossRef]
- Brinckmann, S.A.; Patra, N.; Yao, J.; Ware, T.H.; Frick, C.P.; Fertig, R.S. Stereolithography of SiOC Polymer-Derived Ceramics Filled with SiC Micronwhiskers. Adv. Eng. Mater. 2018, 20, 1800593. [Google Scholar] [CrossRef]

| Authors | Content | Year | References |
|---|---|---|---|
| Liu et al. | This paper presents a review of the pore-scale dynamics associated with snap-off, highlighting that capillary-dominated immiscible displacement serves as the predominant mechanism governing the snap-off phenomenon. | 2019 | [26] |
| Zhou et al. | This paper provides a comprehensive review of snap-off-induced emulsions and their application in enhanced oil recovery, elucidating that snap-off represents the fundamental mechanism responsible for emulsion formation within porous media. | 2019 | [27] |
| Li et al. | This paper presents an in-depth review of residual water formation during the CO2 storage process in deep saline aquifers, underscoring the pivotal and determining role that snap-off plays in shaping the CO2 storage capacity. | 2017 | [28] |
| Hamza et al. | This paper offers an overview of the stability and performance of EOR foam, demonstrating snap-off as a critical mechanism for EOR foam generation. | 2017 | [29] |
| Diamantopoulos and Durner | This paper offers an overview of effective modeling approaches for assessing the impact of snap-off on dynamic imbibition at a macroscopic scale. | 2012 | [30] |
| Rossen | This paper provides a critical review on the applicability of the snap-off mechanism in generating foam at steady-state in homogeneous porous media. | 2003 | [31] |
| Authors | Category | Content | Advantages | Disadvantages | Year | References |
|---|---|---|---|---|---|---|
| Lebedeva and Fogden | Imaging technique | This study employed the micro-CT imaging technique to investigate multiphase flow phenomena, such as snap-off and pore–body filling, in the context of saline waterflooding. |
|
| 2011 | [38] |
| Singh et al. | Imaging technique | This paper provides a 3D dynamic visualization study of snap-off occurring during two-phase fluid flow, employing fast synchrotron X-ray microtomography. |
|
| 2017 | [39] |
| Tian et al. | Fabrication technique | This study employed a standard lithography process and hydrofluoric (HF) acid etching to fabricate a glass microfluidic device to investigate the dynamic gas snap-off mechanisms under the capillary dominant flow regime in 2D micro channels. |
|
| 2020 | [40] |
| Li et al. | Fabrication technique | This paper employed soft lithography manufacturing techniques to fabricate a polydimethylsiloxane (PDMS) microfluidic platform for studying the dynamic snap-off process of droplets in short constrictions. |
|
| 2021 | [41] |
| Liu et al. | Fabrication technique | This study employed the femtosecond pulsed-laser direct-writing technique to fabricate 3D microfluidic models with triangular cross-sections for the investigation of snap-off-induced emulsions in low-salinity waterflooding. |
|
| 2021 | [42] |
| Author | Category | Content | Advantages | Disadvantages | Year | References |
|---|---|---|---|---|---|---|
| Bandara et al. | Direct numerical simulations (DNS) | This paper utilizes a smoothed particle hydrodynamics (SPH) model for simulating pore-scale displacement and elucidating the capillary-trapping mechanisms of supercritical CO2. It illustrates that snap-off is the predominant displacement behavior under capillary-dominant conditions. |
|
| 2011 | [43] |
| Starnoni and Pokrajac | Direct numerical simulations (DNS) | This study employed the volume-of-fluid (VOF) method and developed a computational fluid dynamics (CFD) code to numerically simulate snap-off phenomena within pore–throat constrictions characterized by varying cross-sectional geometries. |
|
| 2018 | [44] |
| Zhou et al. | Direct numerical simulations (DNS) | This study elucidates the formation process of snap-off-induced emulsion using a ternary Lattice–Boltzmann method (LBM), which models the streaming of fluids in space. |
|
| 2019 | [27] |
| Kohanpur et al. | Pore space geometrical idealization | This study employs pore–network modeling (PNM) to predict the trapping of CO2 bubbles induced by snap-off. |
|
| 2021 | [45] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Yao, J. Snap-Off during Imbibition in Porous Media: Mechanisms, Influencing Factors, and Impacts. Eng 2023, 4, 2896-2925. https://doi.org/10.3390/eng4040163
Li G, Yao J. Snap-Off during Imbibition in Porous Media: Mechanisms, Influencing Factors, and Impacts. Eng. 2023; 4(4):2896-2925. https://doi.org/10.3390/eng4040163
Chicago/Turabian StyleLi, Guihe, and Jia Yao. 2023. "Snap-Off during Imbibition in Porous Media: Mechanisms, Influencing Factors, and Impacts" Eng 4, no. 4: 2896-2925. https://doi.org/10.3390/eng4040163
APA StyleLi, G., & Yao, J. (2023). Snap-Off during Imbibition in Porous Media: Mechanisms, Influencing Factors, and Impacts. Eng, 4(4), 2896-2925. https://doi.org/10.3390/eng4040163







