Effects of Mean Stress and Multiaxial Loading on the Fatigue Life of Springs

Abstract

In this paper, the effects of mean stress and damage accumulation on the fatigue life of springs are theoretically studied. The study examines the fatigue life of homogeneously stressed material subjected to cyclic loading. The mean stress of a load cycle is non-zero. Goodman and Haigh diagrams are commonly used for estimating fatigue life in engineering applications. Alternatively, conventional hypotheses by Smith–Watson–Topper, Walker and Bergmann have been successfully used to describe uniaxial cyclic fatigue with non-zero mean value over the whole range of the fatigue life. However, the physical characteristics of the mean stress sensitivities in these hypotheses are different. The mean stress sensitivity according to Smith–Watson–Topper is identical for all materials and stress levels. This weakness reduces the applicability of the Smith–Watson–Topper parameter. At first glance, the mean stress sensitivities according to Walker and Bergmann are diverse. The mean stress sensitivities depend upon two different additional correction parameters, namely the Bergmann parameter and the Walker exponent. The possibility of fitting the mean stress sensitivity in these hypotheses overcomes the significant drawback of the Smith–Watson–Topper schema. The principal task of this actual study is to reveal the dependence between the Bergmann parameter and the Walker exponent, which leads to a certain mean stress sensitivity. The manuscript establishes the simple relationship between both fitting parameters, which causes the equivalent mean stress sensitivity for the Bergmann and Walker criteria. As known from the state of the technology, fabrication and operation yield several impacts with a significant influence on the fatigue life of springs. One effect deals with the sequence of low and high stress amplitudes and amplitude-dependent damage accumulation. Particularly, during the load cycle a certain microscopical creep occurs. This creep causes damage. The accumulation hypothesis for creep damage is introduced. The hypothesis can be verified experimentally.

1. Introduction

A proper description of fatigue processes is significant for machinery, in which potential damage can become a danger to people, as a consequence. This applies to the aerospace, energy and automotive industries, among others. Particularly, the fatigue life of springs has not yet been fully evaluated. The merging of the multiaxial stress tensor to the equivalent scalar value is one open question. The mean stress sensitivity is the other question. To answer these questions, diverse strength hypotheses have been proposed. The strength hypotheses lead to associations for a reasonable curve expressed in stress or strain. From this curve, the definitive admissible amplitudes of the stresses or strains are obtained. The definitive admissible amplitudes correspond to a certain number of cycles to failure. The dominant stresses in leaf and disc springs are the normal stresses. For shear compression or helical tension springs, the shear stresses should be used instead of the normal stresses. Fatigue characteristics are determined by analyzing the failure parameters and the fatigue characteristics of the materials. Among the equivalents, stress hypotheses have the greatest potential [1]. For a loading with a fully occupied stress tensor, the application of the magnitudes for the equivalent scalar stress is appropriate. Alternatively, multiaxial stress can be reduced to a certain scalar energy parameter [2,3]. The equivalent scalar stress for isotopic materials can be presented as a function of the stress invariants. If only the second invariant of the stress tensor plays a role, and the corresponding scalar is referred to as the Mises equivalent stress.

Based on the same equivalent stress, higher fatigue strengths typically result for springs made of the same material subjected to normal stress than for springs subjected to shear stress. For this reason, numerous alternative equivalent stress criteria have been proposed, such as the multiaxial fatigue criteria embrace stress criteria, strain criteria and energy criteria (stress–strain). The proper choice depends on the physical nature of the failure parameter. The fatigue criteria describe the failure after a large number of cycles. Accordingly, the plastic deformation is very small, and can be neglected. Alternatively, for large plastic deformations, stress criteria have been proposed that condense the tensor stress state to the uniaxial scalar value. The corresponding equivalent stress $\sigma$ is used for calculations instead of tensor stress functions. For the subsequent fatigue calculations, the equivalent stress $\sigma$ is used.

The aims of the paper are:

(1)

To establish the relationships between the Bergmann, Walker and Smith–Watson–Topper parameters;

(2)

To express the additional fitting parameters of Bergmann and Walker in terms of mean stress sensitivity due to Schütz;

(3)

To present a proposal to incorporate the creep pro stress cycle into sequence-sensitive damage accumulation in order to overcome the sequence neutrality of the Miner rule.

The manuscript presents the possibility to make the proper choice between the traditional Bergmann and Walker criteria. Namely, if the fitting parameters of Bergmann and Walker correspond to the same mean stress sensitivity due to Schütz, the curves of both criteria will be slightly different. With the additional experimental date, it is possible to determine, whether Bergmann or Walker are preferrable.

2. Fatigue Strength Diagrams

Fatigue strength is the stress range or stress amplitude at which a component can endure an infinite number of load cycles. The fatigue strength ${\sigma }_w$ denotes the stress amplitude that can be sustained under alternating stress. On the Wöhler line, this range is marked by the horizontal curve to the right of the inflection point. As soon as a component is subjected to higher stresses, the fatigue check is referred to as the fatigue strength [4]. In addition to fatigue strength ${\sigma }_w$, the analysis of a fatigue strength diagram is based on several static strength parameters. The static strength parameters include tensile strength $R_m$ and yield strength $R_e$.

The Wöhler line for the spring elements depends on different parameters for the following influencing factors:

• Spring material, incl. thermal treatment;
• Notch effect, corrosion, roughness;
• Stress (normal or shear stress, mixed stress);
• Load spectrum;
• Component size and specifically diameter of spring wire;
• Operating temperature;
• Residual stress (shot peening, roller burnishing, laser peening, tapping);
• Mean stress;
• Stress gradient.

In the literature, the correlation of fatigue strength with the certain material properties, such as ductility and strength, was reported. Experience finds that the fatigue strength is nearly proportional to the tensile strength of the material. The higher the tensile strength, the higher the fatigue strength. Other influences of the material condition on the fatigue strength arise from the ductility, grain size, heat treatment, presence of flaws and inclusions in the material.

The notch effect on the surface of the spring has a determining influence on the fatigue strength. Surface defects such as blowholes, hard inclusions, corrosion cavities, hairline cracks, decarburization or grooves act like notches. The sharper the notch, the lower the fatigue strength of the component with respect to the nominal stresses.

Experimental studies show that the fatigue strength declines strongly with the environmental deterioration and corrosion of springs. In fatigue-stressed components, corrosion leads to the expansion of incipient cracks and also to progressive crack growth. The roughness profile on the component surface, generated by the manufacturing process, acts as a notch in conjunction with the microstructure on the surface. The influence of roughness on the reduction of fatigue strength with increasing brittleness (and indirectly with increasing strength) increases, according to VDI 2226 [5]. The effect of microplasticity during the cyclic loading was briefly discussed by VDI 2226.

The influence of the component size is caused by different mechanisms, namely:

• Technological influences (edge layer thickness, edge strength, surface hardening);
• The size of the highly stressed volume or surface of a spring. Depending on how far the stressed area extends over the volume of the spring, there may be an increased influence of statistically distributed flaws and inclusions;
• The higher the stress gradient, the higher the supporting effect of the surrounding material. A higher supporting effect positively influences fatigue behavior. The supporting effect does not play a special role for the springs, since the spatial gradients for the stresses are low and the stress distributions for similar springs are identical;
• With geometrically similar springs and equally high stress maxima, the smaller spring has a higher stress gradient and, thus, more favorable fatigue behavior;
• The wires of smaller diameter possess commonly the higher fatigue resistance.

Both the fatigue and static strengths of most materials commonly increase at low temperatures. However, notch sensitivity and the tendency toward brittle fracture are made stronger. Accordingly, higher temperatures generally result in a reduction in fatigue strength.

There are some special features of spring materials, which are important for fatigue design. Residual stresses occur in springs, as a result of almost all treatments in the manufacturing process. These can assume values up to the yield point. The effects on fatigue strength depend on the value of the residual stresses [6,7]. There are predominantly compressive or predominantly tensile residual stresses. Compressive residual stresses increase the fatigue strength, while the effect of tensile residual stresses on the fatigue strength is usually negative. The tensile residual stresses are added to the mean stresses in each cycle, and cause a higher level of damage in each load cycle.

3. Influence of Mean Stress on Fatigue Strength

Fatigue strength diagrams represent the dependence of fatigue strength on the mean stress. The fatigue strength diagrams according to Smith and Haigh are commonly used in spring industry. In the Smith diagram, the admissible upper stresses ${\sigma }_o$ and lower stresses ${\sigma }_u$ are the functions of the mean stress (${\sigma }_m$). The mean stress is the average value of the upper stress (${\sigma }_o={\sigma }_m+{\sigma }_a$) and the lower stress (${\sigma }_u$) during one load cycle:

$${\sigma }_m=\left({\sigma }_o+{\sigma }_u\right)/2,\hspace{1em}\hspace{1em}{\sigma }_a=\left({\sigma }_o-{\sigma }_u\right)/2.$$

(1)

The ratio of lower stress to upper stress in a cycle is referred to as the stress ratio:

$$R={\sigma }_u/{\sigma }_o.$$

(2)

The compression and shear tests are performed in the stress–positive region: $0<{\sigma }_u<{\sigma }_o$. The tension test is executed in the stress–negative region: ${\sigma }_u<{\sigma }_o<0$.

The tensile strength is plotted as an upper stress on the ordinate and as a mean stress on the abscissa. The resulting point lies with the coordinate origin on a 45° line. From this point, the Goodman straight line for the top stress is generated in the simplified Smith diagram by connecting it to the alternating stress on the ordinate. The same procedure is followed for the Goodman straight line for the lower stress. The resulting fatigue range is bounded at the top by the yield strength. The fatigue range below the 45° line is, consequently, adjusted due to the symmetry between the upper stress and the lower stress. From the Smith diagram, it is possible to read the upper and lower stresses that can be sustained and the stress amplitudes ${\sigma }_a$ as a function of the mean stress ${\sigma }_m$. In general, alloys with increasing tensile strength exhibit higher sensitivity with respect to mean stress. Another correlation is found in the ductility of the materials. Brittle alloys tend to exhibit higher mean stress sensitivity.

In the Haigh diagram, the steady-state stress amplitude over the mean stress can be read directly. Furthermore, the stress ratios can be assigned to the pairs of values from the stress amplitude and mean stress by means of the origin lines. Similar to the Smith diagram, the Goodman straight line is drawn as a simplification, starting from the alternating strength on the ordinate. In the Haigh diagram, however, this point is connected to the point of tensile strength on the mean stress axis (abscissa). Below the Goodman line, the fatigue range is obtained, which is bounded on the right by a straight line passing between the yield strengths on the amplitude axis and on the mean stress axis. In the compression range, the Goodman straight line is extended to the yield point or conservatively replaced by a horizontal line at the level of the alternating fatigue strength (${\sigma }_w$). The fatigue range is also limited here by a straight line between the fatigue and yield strengths (or, in the compression range, the crush limit).

4. Mean Stress Sensitivity

4.1. Mean Stress Sensitivity According to Schütz

As shown above, the inclination of the Goodman straight line determines the mean stress sensitivity. An equivalent slope in the straight line has a similar meaning in the Haigh diagram. The number of load cycles to failure (fatigue life) does not change along the straight lines. In other words, both diagrams use the linear dependence of the ultimate stress amplitude on the mean stress. This approach is traditional in industrial engineering.

The formal definition of mean stress sensitivity is outlined below. The mean stress sensitivity according to Schütz uses only three values ${\sigma }_a\left(R=-1\right), {\sigma }_a\left(R=0\right), {\sigma }_m\left(R=0\right)$ (see

Table 1. Stress ratio.

Stress Ratio	Position of the Origin Straight Line	Stress Range
$R=1$	Positive range of mean stress axis	Constant stress
$R=0$	45° line in the first quadrant (tension area)	Oscillating tension stress ${\sigma }_u=0$
$R=-1$	Positive range of the amplitude axis	Alternating stress ${\sigma }_u=-{\sigma }_o$
$R=-\infty$	45° line in the second quadrant (compression area)	Oscillating compression stress ${\sigma }_o=0$

).

The mean stress sensitivity, according to Schütz [8], designates the tangent of the angle between the horizontal and the Goodman straight line:

$$\mathcal{M}=\frac{{\sigma }_a\left(R=-1\right)-{\sigma }_a\left(R=0\right)}{{\sigma }_m\left(R=0\right)}.$$

(3)

The evaluation of the damage parameter $Ps$ and the mean stress sensitivity according to Schütz is displayed on

Table 2. Damage parameter $Ps$ and the mean stress sensitivity according to Schütz.

Stress Ratio	Lower Stress	Mean Stress	Upper Stress	${\mathit{P}}_{\mathit{S}}={\mathit{\sigma }}_{\mathit{a}}+{\mathit{\sigma }}_{\mathit{m}}\mathit{·}\mathcal{M}\equiv \frac{{\mathit{\sigma }}_{\mathit{o}}-{\mathit{\sigma }}_{\mathit{u}}}{2}+\frac{{\mathit{\sigma }}_{\mathit{o}}+{\mathit{\sigma }}_{\mathit{u}}}{2}\mathcal{M}$
$R=0$	${\sigma }_u=0$	${\sigma }_m={\sigma }_a$	${\sigma }_o=2{\sigma }_a$	$P_S\left(R=0\right)=\left(1+\mathcal{M}\right){\sigma }_a$
$R=-1$	${\sigma }_u\equiv {\sigma }_a=-{\sigma }_o$	${\sigma }_m=0$	${\sigma }_o={\sigma }_a$	$P_S\left(R=-1\right)={\sigma }_a$

.

However, the real materials frequently demonstrate the nonlinear dependence of the stress amplitude on the mean stress. In this case, the simple linear dependence of the ultimate stress amplitude on the mean stress is inappropriate. According to the experimental findings, the amplitude ${\sigma }_a$ approximately follows a hyperbola with the increasing mean stress ${\sigma }_m$. The correction was proposed by FKM [9]. This standard uses the piecewise-linear approximation (Figure 1). The pivot points of the piecewise-linear function are referred to in [4,9] as “overloads”. The overload case describes the relationship between the mean and amplitude stress during a load change. There are the following overload cases, according to the FKM guideline [9]:

• Overload case F1: Constant mean stress (${\sigma }_m= \mathrm{const}$);
• Overload case F2: Constant stress ratio ($R=const)$;
• Overload case F3: Constant minimal stress in cycle (${\sigma }_u= \mathrm{const}$);
• Overload case F4: Constant maximal stress in cycle (${\sigma }_o= \mathrm{const}$).

Figure 1. Visualization of the mean stress sensitivity according to FKM.

Figure 1. Visualization of the mean stress sensitivity according to FKM.

Consequently, the piecewise-linear function, according to FKM, consists of three regions. To determine the pivot points, additional experimental data is necessary.

Three alternative criteria are widely used in industry. These criteria, namely the Smith–Watson–Topper, Walker and Bergmann criteria, demonstrate the analogous hyperbolical dependence between the amplitude and mean stress. In each of these traditional criteria, the additional fitting parameters are used to describe the continuous nonlinear dependence of stress amplitude on mean stress for certain fatigue life. Among them, the Smith–Watson–Topper criteria has no such additional parameter. Each criterion (Walker or Bergmann) uses one fitting parameter. The methodology for the unified evaluation of the mean stress sensitivity is explained below.

4.2. Mean Stress Sensitivity According to Smith–Watson–Topper

The Smith–Watson–Topper parameter ($P_{SWT}$) [10] was proposed for the evaluation of the fatigue life of metallic materials in uniaxial loading conditions. This fatigue parameter characterizes the crack initiation with non-zero mean values. In the above cited paper, the numerous modifications to the original $P_{SWT}$ are summarized. The Smith–Watson–Topper parameters have been widely used to describe uniaxial cyclic fatigue with non-zero mean values over the whole range of the fatigue life. The results from the cyclic tests were presented using the $Pswt$ parameter [11,12,13,14,15,16]. This parameter was used for the description of the fatigue life in a complex loading. Several energy criteria were proposed recently [17].

The determination of the damage parameter $Pswt$ and mean stress sensitivity, according to Smith–Watson–Topper, uses the following schema.

Table 3. Determination of the damage parameter $Pswt$ and the mean stress sensitivity according to Smith–Watson–Topper.

Stress Ratio	Lower Stress	Mean Stress	Upper Stress	${\mathit{P}}_{\mathit{S}\mathit{W}\mathit{T}}=\sqrt{{\mathit{\sigma }}_{\mathit{a}}\mathit{·}{\mathit{\sigma }}_{\mathit{o}}}$
				${\mathit{P}}_{\mathit{S}\mathit{W}\mathit{T}}=\sqrt{{\mathit{\sigma }}_{\mathit{a}}\mathit{·}\left({\mathit{\sigma }}_{\mathit{a}}+{\mathit{\sigma }}_{\mathit{m}}\right)}$
$R=0$	${\sigma }_u=0$	${\sigma }_m={\sigma }_a$	${\sigma }_o=2{\sigma }_a$	$P_{SWT}\left(R=0\right)=\sqrt{2}$${\sigma }_a$
$R=-1$	${\sigma }_u=-{\sigma }_o$	${\sigma }_m=0$	${\sigma }_o={\sigma }_a$	$P_{SWT}\left(R=-1\right)={\sigma }_a$
Mean stress sensitivity according to Smith–Watson–Topper	$\mathcal{M} \stackrel{Eq \left(3\right)}{\overbrace{=}} \frac{P_{SWT}\left(R=-1\right)-\frac{P_{SWT}\left(R=0\right)}{\sqrt{2}}}{P_{SWT}\left(R=0\right)}=1-\frac{1}{\sqrt{2}}=0.29\dots \stackrel{\text{def}}{=}{\mathcal{M}}_{SWT}$
	${\left.\frac{d\mathcal{M}}{d\zeta }\right|}_{\zeta =0}=0$		${\left.\mathcal{M}\right|}_{\zeta =0}=\frac{1}{2}$

displays the steps to link the mean stress sensitivity, according to Schütz [8], to the mean stress sensitivity, according to Smith–Watson–Topper. In the actual study, the mean stress sensitivity uses three values ${\sigma }_a\left(R=-1\right), {\sigma }_a\left(R=0\right),{\sigma }_m\left(R=0\right)$, in accordance with Schütz [8]. Accordingly, two distinct stress ratios $R=0$ and $R=1$ are used. The calculation requires only three experimentally acquired values, namely ${\sigma }_a\left(R=-1\right)$, ${\sigma }_a\left(R=0\right)$ and ${\sigma }_m\left(R=0\right)$. With these values, the values

$$P_{SWT}\left(R=0\right)=\sqrt{2} {\sigma }_a\left(R=0\right),\hspace{1em}\hspace{1em}\hspace{1em}{P}_{SWT}\left(R=-1\right)={\sigma }_a\left(R=-1\right)$$

are calculated for a certain fixed fatigue life. After substitution of these damage parameters, Equation (3) results in the mean stress sensitivity, according to Smith–Watson–Topper. Evidently, this value is the same for all materials and stress levels, namely ${\mathcal{M}}_{SWT}=0.29$. This circumstance reveals a significant drawback to the Smith–Watson–Topper hypothesis, because this criterion has no extra fitting parameters. Thus, the application of the Smith–Watson–Topper criterion for materials with a significantly different mean stress sensitivity is highly questionable.

4.3. Mean Stress Sensitivity According to Walker

An alternative empirical relationship was developed by Walker [18]. This relationship provides more freedom in the description of the mean stress effects and satisfactorily represents the effect of the mean stress. In the relationship by Walker, an additional correction parameter γ is introduced. The parameter γ characterizes the exponent of the stress amplitude. Walker’s parameters were used to fit the experimental data and predict the fatigue life behavior at different mean strain values during cyclic loading. Based on the Walker approach, the authors [19,20,21] evaluated the influence of the mean strain on the fatigue life of the spring material.

The determination of the damage parameter $Pw$ and mean stress sensitivity, according to Walker, is performed analogously (

Table 4. Determination of the damage parameter $P_W$ and the mean stress sensitivity according to Walker.

Stress Ratio	Lower Stress	Mean Stress	Upper Stress		${\mathit{P}}_{\mathit{W}}={\mathit{\sigma }}_{\mathit{a}}{}^{\mathit{\gamma }}\mathit{·}{\mathit{\sigma }}_{\mathit{o}}{}^{1-\mathit{\gamma }}$
					${\mathit{P}}_{\mathit{W}}={\mathit{\sigma }}_{\mathit{a}}{}^{\mathit{\gamma }}\mathit{·}{\left({\mathit{\sigma }}_{\mathit{a}}+{\mathit{\sigma }}_{\mathit{m}}\right)}^{1-\mathit{\gamma }}$
$R=0$	${\sigma }_u=0$	${\sigma }_m={\sigma }_a$	${\sigma }_o=2{\sigma }_a$		$P_W\left(R=0\right)=2^{1-\gamma }{\sigma }_a$
$R=-1$	${\sigma }_u=-{\sigma }_o$	${\sigma }_m=0$	${\sigma }_o={\sigma }_a$		$P_W\left(R=-1\right)={\sigma }_a$
Mean stress sensitivity according to Walker	$\mathcal{M} \stackrel{Eq .\left(3\right)}{\overbrace{=}} \frac{P_W\left(R=-1\right)-\frac{P_W\left(R=0\right)}{2^{1-\gamma }}}{P_W\left(R=0\right)}=\frac{{\sigma }_a-\frac{{\sigma }_a}{2^{1-\gamma }}}{{\sigma }_a}=1-\frac{1}{2^{1-\gamma }}$
	${\left.\frac{d\mathcal{M}}{d\gamma }\right|}_{\gamma =0}=-\frac{ln\left(2\right)}{2}$			${\left.\mathcal{M}\right|}_{\gamma =0}=\frac{1}{2}$

). Two distinct stress ratios are used, namely the ratios according to Schütz $R=0$ and $R=1$. Similarly, the same values as above, namely ${\sigma }_a\left(R=-1\right)$, ${\sigma }_a\left(R=0\right)$ and ${\sigma }_m\left(R=0\right)$, are required for the calculations. With these values, the damage parameters are calculated with the Walker formula as:

$$P_W\left(R=0\right)=2^{1-\gamma }·{\sigma }_a\left(R=0\right),\hspace{1em}\hspace{1em}{P}_W\left(R=-1\right)={\sigma }_a\left(R=-1\right)$$

The substitution of these values in Equation (3) results in the mean stress sensitivity, according to Walker:

$$\mathcal{M}=1-2^{\gamma -1}$$

Importantly, this value is not constant anymore and depends on parameter $\mathsf{\gamma }.$ This feature of the Walker hypothesis overcomes the significant drawback to the Smith–Watson–Topper schema.

It is possible to express the Walker exponent $\gamma$ in terms of the Schütz mean stress sensitivity $\mathcal{M}$ [8]. Crucially, the Walker exponent $\gamma$ depends directly on $\mathcal{M}$:

$$\gamma \left(\mathcal{M}\right)=1+\frac{\ln \left(1-\mathcal{M}\right)}{\ln 2}.$$

(4)

Figure 2 demonstrates the dependence of the cycle amplitude on the mean stress according to Walker, which leads to a certain fixed fatigue life. Each curve matches to a certain value on the parameter $\gamma$, as shown in Equation (4).

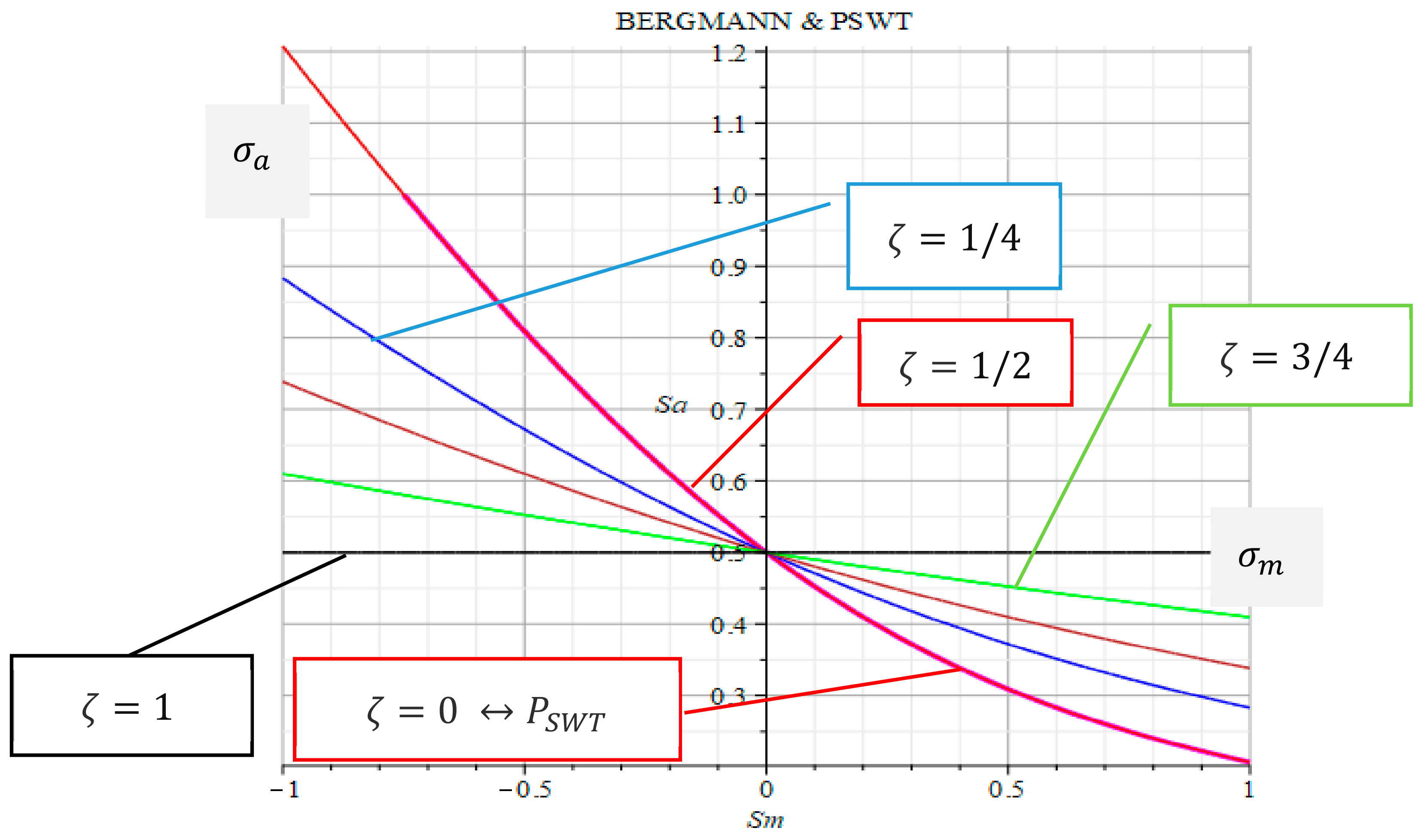
4.4. Mean Stress Sensitivity According to Bergmann

Similar nonlinear approximations were proposed by Bergmann [22,23]. The factor used in this paper slightly differs from the original parameter by Bergmann, $k=1-\zeta$. The sense of the new parameter is the following: the parameter $\zeta$ clearly reveals the similarity with the criterion by Walker (Figure 3). Bergmann’s adaptation assumes the non-zero value of the $\zeta$-factor. For example, for carbon steel $k=0.45$, $\zeta =0.55$. A better agreement with the experiment was obtained for $k=0.4$, $\zeta =0.6$ [24]. For the 1045 steel grade, the best fitting for the experimental data was obtained for $k=1.2, \zeta =-0.2$ [25]. Notably, for the following value in the Bergmann parameter $\zeta =1, k=0$, the mean stress sensitivity fades.

The determination of the damage parameter $P_B$ and mean stress sensitivity, according to Bergmann, is assessed similarly.

Table 5. Determination of the damage parameter $P_B$ and the mean stress sensitivity according to Bergmann.

Stress Ratio	Lower Stress	Mean Stress	Upper Stress		${\mathit{P}}_{\mathit{B}}=\sqrt{{\mathit{\sigma }}_{\mathit{a}}\mathit{·}\left({\mathit{\sigma }}_{\mathit{o}}-\mathit{\zeta }{\mathit{\sigma }}_{\mathit{m}}\right)}$
					${\mathit{P}}_{\mathit{B}}=\sqrt{{\mathit{\sigma }}_{\mathit{a}}\mathit{·}\left[{\mathit{\sigma }}_{\mathit{a}}+\left(1-\mathit{\zeta }\right){\mathit{\sigma }}_{\mathit{m}}\right]}$
$R=0$	${\sigma }_u=0$	${\sigma }_m={\sigma }_a$	${\sigma }_o=2{\sigma }_a$		$P_B\left(R=0\right)={\sigma }_a \sqrt{2-\zeta }$
$R=-1$	${\sigma }_u=-{\sigma }_o$	${\sigma }_m=0$	${\sigma }_o={\sigma }_a$		$P_B\left(R=-1\right)={\sigma }_a$
Mean stress sensitivity according to Bergmann	$\mathcal{M} \stackrel{Eq .\left(3\right)}{\overbrace{=}} \frac{P_B\left(R=-1\right)-\frac{P_B\left(R=0\right)}{\sqrt{2-\zeta }}}{P_B\left(R=0\right)}=1-\frac{1}{\sqrt{2-\zeta }}$
	${\left.\frac{d\mathcal{M}}{d\zeta }\right|}_{\zeta =0}=-\frac{\sqrt{2}}{8}$			${\left.\mathcal{M}\right|}_{\zeta =0}=1-\frac{1}{\sqrt{2}}=0.29.$

uses the stress ratios $R=0$ and $R=1$. Once again, the values ${\sigma }_a\left(R=-1\right)$, ${\sigma }_a\left(R=0\right)$ and ${\sigma }_m\left(R=0\right)$ are evaluated. From these values, the parameters are determined as:

$$P_B\left(R=0\right)=\sqrt{2-\zeta } ·{\sigma }_a\left(R=0\right) \mathrm{and} P_B\left(R=-1\right)={\sigma }_a\left(R=-1\right)$$

In conclusion, Equation (3) results in the mean stress sensitivity, which follows from the Bergmann criterion:

$$\mathcal{M}=1-1/\sqrt{2-\zeta }.$$

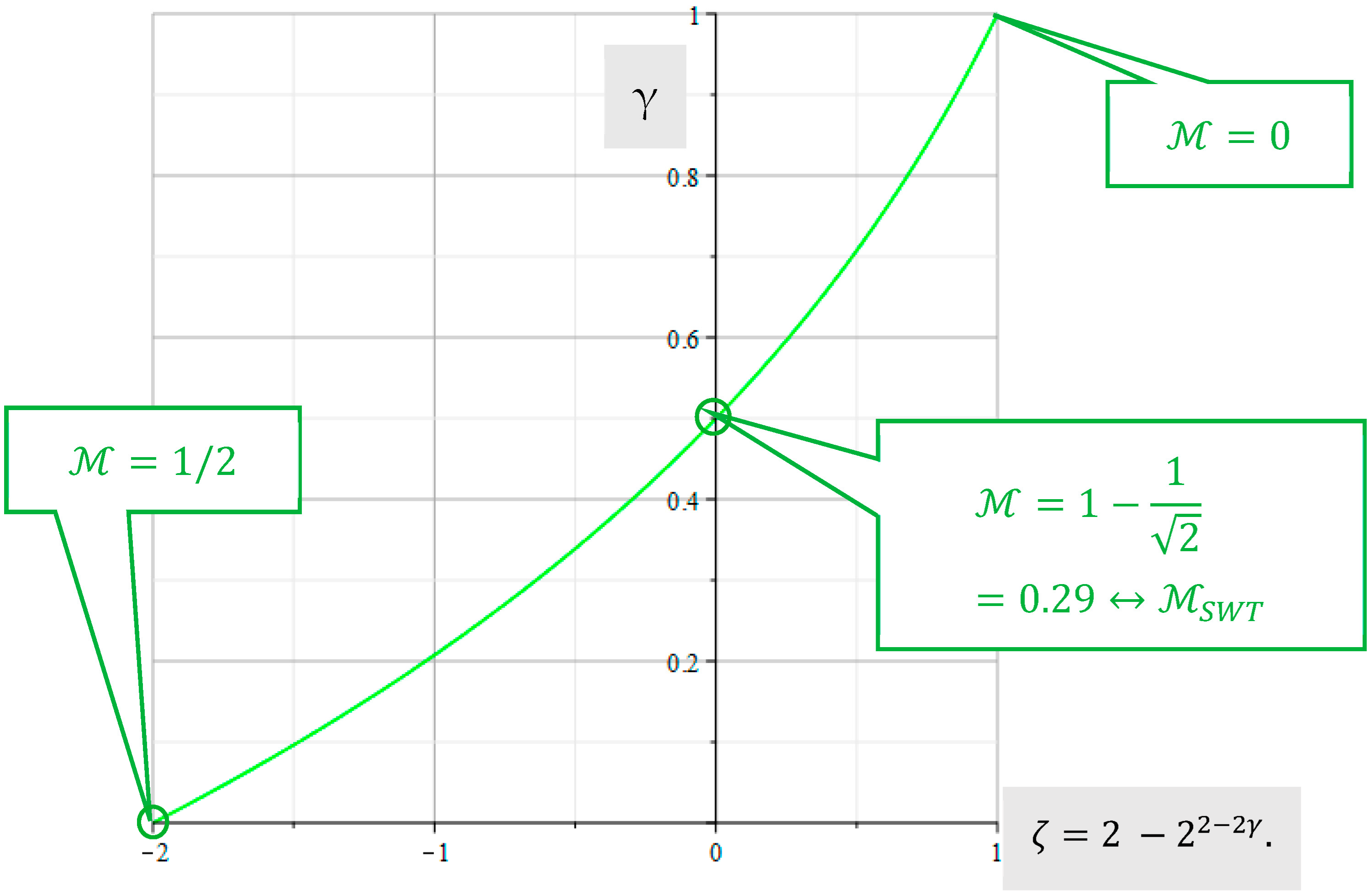
Significantly, this value is the function of another parameter $\mathit{\zeta }.$ This property of the Bergmann hypothesis overcomes the abovementioned disadvantage to the Smith–Watson–Topper schema.

Analogously to Equation (4), the Bergmann parameters are definite functions of the mean stress sensitivity as well:

$$\zeta \left(\mathcal{M}\right)=\frac{2{\mathcal{M}}^2-4\mathcal{M}+1}{{\left(\mathcal{M}-1\right)}^2},\hspace{1em}\hspace{1em}\hspace{1em}k\left(\mathcal{M}\right)=\frac{\mathcal{M} \left(2-\mathcal{M}\right)}{{\left(\mathcal{M}-1\right)}^2},\hspace{1em}\hspace{1em}k=1-\zeta .$$

(5)

Figure 4 demonstrates the graphs for the functions $\zeta \left(\mathcal{M}\right), \gamma \left(\mathcal{M}\right)$. The green vertical line shows the determined mean stress sensitivity $\mathcal{M}={\mathcal{M}}_{SWT}\equiv 1-\frac{1}{\sqrt{2}}=0.29$, which results from the calculation of the damage parameter $P_{SWT}$, according to Smith–Watson–Topper. From the graphs (Figure 4), the reduction of both parameters with the increasing mean stress sensitivity is clearly visible.

4.5. Interrelation between the Bergmann and Walker Criteria

From Equations (4) and (5), follows the correspondence between the Bergmann parameter $\zeta$ and the Walker exponent $\gamma$. The parameters of both criteria match to the identical mean stress sensitivity $\mathcal{M}$:

$$\mathcal{M}=1-\frac{1}{2^{1-\gamma }}=1-\frac{1}{\sqrt{2-\zeta }}.$$

(6)

A resolution of Equation (6) with respect to ζ, gives the looked-for dependence on the Walker exponent $\gamma$ as:

$$2-\zeta =2^{2-2\gamma }.$$

(7)

Figure 3 displays the Bergmann dependence of cycle amplitude on the mean stress, which leads to the equal fatigue life. According to Equation (5), each curve corresponds to a certain value in the parameter $\zeta$. It is also possible to use the quadratic approximation with three unknown coefficients:

$$P_Q=\sqrt{a {\sigma }_a{}^2+b{\sigma }_a{\sigma }_m+c {\sigma }_m{}^2}.$$

Figure 4 shows the parameters of Walker $\gamma$ and Bergmann $\zeta$, which correspond to the same fatigue life, as the functions of mean stress sensitivity $\mathcal{M}$.

The relationship between the parameters of Walker $\gamma$ and Bergmann $\zeta$ for equal fatigue life and for equal mean stress sensitivity $\mathcal{M}$ is demonstrated in Figure 5. The calculation uses Equation (7). Meanwhile, the value $\zeta =0$ corresponds to the mean stress sensitivity ${\mathcal{M}}_{SWT}$, according to Smith–Watson–Topper.

Both parameters by Walker and Bergmann are capable of properly describing the experimentally acquired mean stress sensitivity. The difference between both parameters is the slightly different dependences of the cycle amplitude on the mean stress, as shown in Figure 2 and Figure 3.

The actual study displays the possibility for the simple unification of the nonlinear dependence of the stress amplitude on the mean value of stress with one parameter. The above results clarify the difference and the similarity between the traditional Walker and Bergmann criteria.

The Smith–Watson–Topper rule has no fitting constant and demonstrates the fixed values of damage.

The damage parameters $P_{SWT}, P_B$,$P_B$ for different ratios of lower stress to upper stress in the cycle and the positive ${\sigma }_o$ are shown in

Table 6. Damage parameters, $P_S,P_{SWT},P_B$, $P_B,$ for different stress ratios $R$.

Damage Parameter	$\mathit{R}=0$	$\mathit{R}=-1$	$\mathit{R}=-1/2$
$P_{SWT}=\frac{{\sigma }_o}{\sqrt{2}}\sqrt{1-R}$	$\frac{{\sigma }_o}{\sqrt{2}}$	${\sigma }_o$	$\frac{\sqrt{3 }{\sigma }_o}{2}$
$P_S={\sigma }_o\left( \frac{1-R}{2}+\frac{1+R}{2}\mathcal{M}\right)$	$\left(1+\mathcal{M}\right)\frac{{\sigma }_o}{2}$	${\sigma }_o$	${\sigma }_o\left(\frac{3}{4}+\frac{\mathcal{M}}{4}\right)$
$P_W={\left(\frac{1-R}{2}\right)}^{\gamma }{\sigma }_o$	$2^{-\gamma }{\sigma }_o$	${\sigma }_o$	${\left(\frac{3}{4}\right)}^{\gamma }{\sigma }_o$
$P_B=\frac{\sqrt{\left(R-1\right)·\left(\zeta R+\zeta -2\right)}}{2}{\sigma }_o$	$\frac{{\sigma }_o}{2}\sqrt{2-\zeta }$	${\sigma }_o$	$\frac{{\sigma }_o}{4}\sqrt{3·\left(4-\zeta \right)}$

. The damage values are always equal for pure alternating stress $R=-1$. The fitting constants can be chosen to equalize the damage for $R=0$. As shown above, if the Walker exponent $\gamma$ relates to the Bergmann parameter according to Equation (6), the damage parameters for $R=0$ for the three criteria, $P_S,P_B$,$P_B$, will all be equal. However, for $R=-1/2$ the damage parameters $P_S,P_B$,$P_B$ result in different values. The parameter, which shows the minimal deviation between the acquired and predicted damage in the third case $R=-1/2$, will be preferrable for the fatigue estimation in the full range $0\le R\le -1$.

4.6. Criteria with Equal Initial Sensitivity at Zero Mean Stress

The damage parameters $P_{SWT},P_B$, $P_B$ were evaluated above for the fixed range of the ratios of lower stress to upper stress in the cycle. It is also theoretically possible to derive the relationship between both parameters $\zeta , \gamma$, which results in the same sensitivity at one point, say for zero mean stress ${\sigma }_m=0$. This relationship follows from the formulas of

Table 7. Damage parameters, $P_S,P_B$, $P_W,$ for the same sensitivity at zero mean stress ${\sigma }_m=0$.

Damage Parameter	${\frac{\mathit{d}\mathit{P}}{\mathit{d}{\mathit{\sigma }}_{\mathit{m}}}\rceil }_{{\mathit{\sigma }}_{\mathit{m}}=0}$	Parameters for Equal Mean Stress $\mathbf{Sensitivity} \mathbf{at} {\mathit{\sigma }}_{\mathit{m}}=0$
$P_S={\sigma }_a+\mathcal{M}{\sigma }_m$	${\frac{d{P}_S}{d{\sigma }_m}\rceil }_{{\sigma }_m=0}=\mathcal{M}$	$\mathcal{M}$
$P_W={\sigma }_a{}^{\gamma }·{\left({\sigma }_a+{\sigma }_m\right)}^{1-\gamma }$	${\frac{d{P}_W}{d{\sigma }_m}\rceil }_{{\sigma }_m=0}=1-\gamma$	$\mathcal{M}=1-\gamma$
$P_B=\sqrt{{\sigma }_a·\left[{\sigma }_a+\left(1-\zeta \right){\sigma }_m\right]}$	${\frac{d{P}_B}{d{\sigma }_m}\rceil }_{{\sigma }_m=0}=\frac{1-\zeta }{2}$	$\mathcal{M}=\frac{1-\zeta }{2}$

and reads as follows:

$$\zeta =2\gamma -1$$

.

However, the determination of the mean stress sensitivity at one point is experimentally practically impossible.

5. Accumulation of Damage and Sequence Effects

5.1. Miner Rule

In load spectra where the individual load levels result in stresses above the fatigue strength, the fatigue strength is reduced. Thus, previously uncritical load levels can contribute to damage accumulation. This effect is accounted for by Wöhler lines, which slope down above the fatigue limit by different degrees with the increasing stress. Damage caused during cyclic loading corresponds to the accumulation of partial damage from oscillating equivalent stress. Linear damage accumulation is used to evaluate the influence of a load collective on the service life of a component [26,27,28]. To calculate the service life, the amplitude collective is divided into individual rectangular collectives with constant amplitude and a partial cycle number $n_i$. According to the linear damage accumulation method, partial damage is now calculated for each partial collective by dividing the partial vibration cycle number by the maximum tolerable vibration cycle number in a Wöhler line $N_i$:

$${\mathrm{p}}_i=\frac{n_i}{N_i}.$$

(8)

The partial damages of all the sub-collectives are summed up. According to the Miner rule, the sum of the partial damages characterizes the total damage:

$$D={{\displaystyle \sum }}_{i=1}^n{p}_i.$$

(9)

If the damage $D$ exceeds the value 1, a fracture is to be expected. If one imagines a two-stage loading, according to the linear damage accumulation it does not matter in which order the loadings come. Notably, with the Miner rule Equation (9) sequence effects cannot be explained. The effect of the stress ratio in the damage accumulation rule was discussed in [1] (§10.2 and §10.3). The explanation accounts for the influence of the stress ratio on the accumulated crack growth.

5.2. Relaxation of Damage and Reduction of Cumulative Damage

Frequently, one finds that partial damage reduces continuously with time. The reduction of partial damage is explained by the creep effect. The relaxation of the stresses due to the creep of the material at the tip of the microcracks leads to a reduction in the partial damage. The partial damage now turns into the functions of time. If the instantaneous partial damage ${\mathrm{p}}_i$ with index $i$ is caused at the instant $t_i$, the permanent partial damage $d_i\left(T\right)$ becomes smaller at the later moment $T$. In the simplest case of viscous creep, the relaxation is given as an exponential function of the time between the moment $t_i$ of the partial damage and the observation time $T$:

$$d_i\left(T\right)={\mathrm{p}}_i\exp \left(\frac{t_i-T}{\tau }\right).$$

(10)

The time constant $\tau$ in Equation (10) represents the rapidity of the relaxation. The partial damage $d_i\left(T\right)$ of all the sub-collectives, continuously reduced with time, are added together. The sum of the partial damage characterizes the current total damage in the observation time $T$:

$$D\left(T\right)={{\displaystyle \sum }}_{i=1}^n{d}_i\left(T\right) \equiv {{\displaystyle \sum }}_{i=1}^n{\mathrm{p}}_i\exp \left(\frac{t_i-T}{\tau }\right) .$$

(11)

Sequence effects are appealingly explained by time-dependent cumulative damage reduction $D\left(T\right)$, Equation (11). Clearly, the current total damage (11) reduces exponentially with time $T$ in the simplest case of viscous creep. The sequence of low and high stress amplitudes leads to amplitude-dependent damage accumulation. In the course of one load cycle, occurs a certain microscopical creep. This creep causes definite damage. The accumulation hypothesis for creep damage requires rigorous experimental validation and evaluation.

6. Summary

Numerous models for estimating fatigue life and fatigue failure of materials are known from the literature. Several models are based on the idea of the Smith–Watson–Topper model. Regrettably, the Smith–Watson–Topper model has a significant shortcoming. The mean stress sensitivity in the $Pswt$ model is solely $\mathcal{M}={\mathcal{M}}_{SWT}\equiv 1-\frac{1}{\sqrt{2}}=0.29$.

Corresponding alterations are already known from the literature. The models of Walker and Bergmann include an additional parameter and allow the representation of actual, experimentally determined damage sensitivity on the mean stress. These models, undoubtedly, describe the experimentally observed continuous reduction of the tolerable amplitude with increasing mean stress. The cited models can replace the piecewise-linear representation, which is known from FKM [4]. In this paper, the dependences of the Walker and Bergmann parameters on mean stress sensitivity are established. These dependences allow for the evaluation of the initial slope in the Goodman straight line. Both the Walker and Bergmann parameters demonstrate the different fitting curves, which present the possibility for a better fitting of the experimental data. Finally, a better description of the mean stress effects can be achieved.

Observations indicate that partial damage reduces continuously with time. The reduction in partial damage was explained by the creep effect. The relaxation of stresses as a result of creep in the material at the tip of the microcracks leads to the lessening of partial damage. For the calculation, only a constant τ is needed, which characterizes the characteristic time for stress relaxation. Sequence effects are explained by cumulative exponential damage reduction. The cumulative exponential damage reduction hypothesis can be used to calculate the damage due to complex load spectra.