Abstract
Tunnel Boring Machines (TBMs) have become prevalent in tunnel construction due to their high efficiency and reliability. The proliferation of data obtained from site investigations and data acquisition systems provides an opportunity for the application of machine learning (ML) techniques. ML algorithms have been successfully applied in TBM tunnelling because they are particularly effective in capturing complex, non-linear relationships. This study focuses on commonly used ML techniques for TBM tunnelling, with a particular emphasis on data processing, algorithms, optimisation techniques, and evaluation metrics. The primary concerns in TBM applications are discussed, including predicting TBM performance, predicting surface settlement, and time series forecasting. This study reviews the current progress, identifies the challenges, and suggests future developments in the field of intelligent TBM tunnelling construction. This aims to contribute to the ongoing efforts in research and industry toward improving the safety, sustainability, and cost-effectiveness of underground excavation projects.
1. Introduction
The Tunnel of Eupalinos, the oldest known tunnel, was constructed in the 6th century BC in Greece for transporting water. The Industrial Revolution brought about a significant increase in tunnel construction used for various purposes including mining, defensive fortification, and transportation. The technology continued to evolve in modern times, and tunnel boring machines (TBMs) became widespread for tunnel excavation projects, including transportation tunnels, water and sewage tunnels, and mining operations. TBMs typically consist of a rotating cutterhead that breaks up the rock or soil and a conveyor system that removes the excavated material. TBMs are preferred over traditional drill and blast techniques due to their higher efficiency, safer working conditions, minimal environmental disturbance, and reduced project costs [1,2,3]. The continuous cutting, mucking, and lining installation process enables TBMs to excavate tunnels efficiently. However, the high cost of building and operating TBMs, as well as the need for regular maintenance, remains a significant concern. Most importantly, tunnel collapse, rock bursting, water inrush, squeezing, or machine jamming can pose major challenges in complex geotechnical conditions. Therefore, optimising tunnelling operations is critical for project time management, cost control, and risk mitigation.
Traditionally, TBM operators rely primarily on empiricism based on site geology, operational parameters, and tunnel geometry. While theoretical models enhance a fundamental understanding of TBM cutting mechanics, they fail to reasonably predict field behaviour [4,5]. Empirical models study regressive correlations between TBM performance and related parameters in the field but are limited to similar geological conditions [6,7,8]. The accuracy of theoretical or empirical models is acceptable, but not sufficiently high to meet the demands for safe and efficient construction.
The abundance of data collected by the data acquisition system provides an opportunity for the application of machine learning (ML) in TBM tunnelling. ML techniques are known for their high effectiveness and versatility in capturing complex, non-linear relationships, and have been successfully applied in this field. We conducted a comprehensive analysis of research on ML techniques and TBM tunnelling using the Web of Science search engine. Figure 1 shows 254 published papers, indicating little interest before 2018 but growing popularity between 2018 and 2022. The increasing trend in published papers signifies the growing interest and recognition of the benefits of ML techniques in TBM tunnelling.
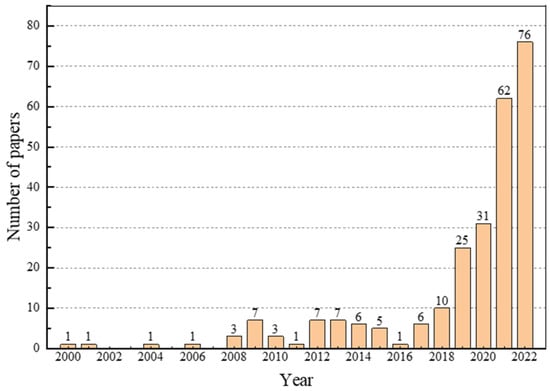
Figure 1.
Number of papers using ML models in TBM tunnelling.
Regarding this, literature reviews on soft computing techniques for TBM tunnelling were conducted. Shreyas and Dey [9] mainly introduced ML techniques and investigated their characteristic and limitations. Shahrour and Zhang [10] discussed predictive issues related to surface settlement, tunnel convergence, and TBM performance. They highlighted the importance of feature selection, model architecture, and data repartition to choose an optimal algorithm. Sheil et al. [11] investigated four main applications–TBM performance prediction, surface settlement prediction, geological forecasting, and cutterhead design optimisation. It is found that the sharing of a complete and high-quality database remains a major challenge in the development of ML techniques in TBM tunnelling [12]. In addition, no paper clearly identified the difference between prediction and time series forecasting, and the latter is much more complex due to known inputs being current and historical information.
In this study, we present a typical framework for ML modelling and review the methodology for data processing, ML algorithm, hyperparameter tuning, and evaluation metrics in Section 2. We then focus on three research topics in TBM tunnelling in Section 3—prediction of TBM performance, prediction of surface settlement, and time series forecasting. Section 4 summarises the application of ML in tunnelling including the current progress, challenges, and future development. The goal is to provide guidance for future research and industry on intelligent TBM tunnelling construction.
2. Machine Learning Modelling
Figure 2 depicts a basic flowchart for building a near-optimal model using machine learning. Prior to modelling, a dataset is processed to select relevant data by outlier detection, interpolation, data smoothing, and feature selection. The processed data are randomly split into training, validation, and test sets. The training and validation set is used to train the model, while the test set is used to evaluate its performance. The choice of algorithm is crucial as it can significantly impact the model’s accuracy and reliability. Hyperparameter tuning aims to find the best combination of hyperparameters, which helps to fine-tune the model’s performance. As a result, the near-optimal model is built and evaluated in the test set. In the ML modelling process, data processing, ML algorithm selection, hyperparameter tuning, and evaluation metrics, four main components, will be briefly described.
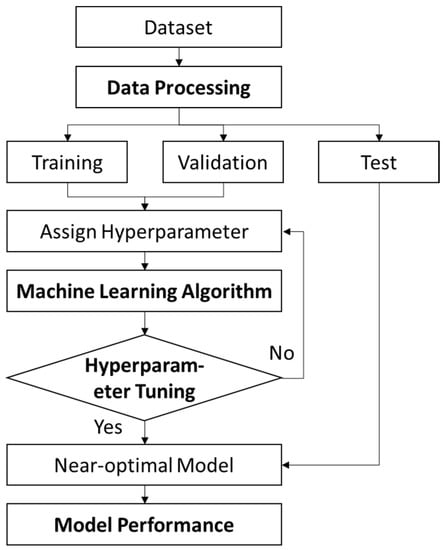
Figure 2.
Typical flowchart of the modelling process in ML studies.
2.1. Data Processing
The data generated during tunnel construction is extensive and diverse, encompassing geological and geotechnical survey data, operational parameters, and monitoring data of surface settlement and structure deformation. For example, the data acquisition system recorded 199 operational parameters per second in the Yingsong water diversion project, accounting for 86,400 data points per day. Since the quality and quantity of data heavily influence the performance of ML models, data processing is essential to delete outliers, interpolate missing values, remove noise, and select features for better applicability.
Outliers are data points that significantly differ from other observations in a dataset which are considered errors and should be removed. There are several methods available to detect and remove outliers in a dataset. Assuming the dataset follows a normal distribution, data points that fall outside the range of the mean plus or minus three standard deviations can be removed according to the three-sigma rule [13,14]. Another method is the interquartile range (IQR) method, which sets up a minimum and maximum fence based on the first quartile (Q1) and the third quartile (Q3), respectively [15]. Any observations that exceed 1.5 times the IQR below Q1 or above Q3 are considered outliers and should be removed. In addition to statistical methods, isolation forest is an unsupervised decision-tree-based algorithm used for outlier detection [16]. It generates partitions recursively by randomly selecting an attribute and a split value between the minimum and maximum values to isolate the data point.
Interpolation is a common technique in data analysis used to estimate unknown values between two known data points. It involves constructing a function that approximates the behaviour of the data within the range of the known values, such as linear, polynomial, and spline interpolation [13]. Another interpolation method, called kriging interpolation, takes into account the spatial correlation between the locations to estimate the value of a variable at an unsampled location using the values at sampled locations [17,18]. Kriging interpolation is particularly useful in geology, hydrology, and environmental science fields for modelling and predicting spatial data.
Data smoothing is a data analysis technique commonly used to eliminate noise and fine-grained variation in time series data to reveal the underlying information. The simple moving average method creates a smoothed version by averaging observations within a specific period, assigning equal weight to each observation [14,19]. In contrast, the exponential moving average method assigns greater weight and significance to the recent data points while gradually reducing the weight of older data points. Wavelet transform is a technique used to decompose signals into basic functions by contracting, expanding, and translating a wavelet function. Wavelet denoising, which applies a threshold to the wavelet coefficients, reduces the contribution of the noisy components in time series data [17,20,21,22,23]. The denoised signal is then reconstructed from the remaining wavelet coefficients, resulting in a signal with reduced noise and preserved features.
Feature selection is a crucial process for handling high-dimensional data, where the primary objective is to identify the most relevant features that can offer valuable insights into the underlying patterns and relationships within the data. However, many selected features are based on prior experience of laboratory tests and field studies, resulting in ignoring the effects of uncertain factors. The variance threshold method removes features that do not meet a specified threshold [2], including zero-variance features that have the same value across all samples. Pearson correlation coefficient (PCC) measures the linear relationship between two or more variables on a scale of −1 to 1 [24,25], where features with a higher absolute value indicate a stronger relationship with the target variable. Alternatively, Principal component analysis (PCA) is a dimensionality reduction method that can transform a large set of variables into a smaller set that contains most of the information in the original set [26,27,28,29].
2.2. Machine Learning Algorithms
‘Artificial intelligence’, ‘Machine Learning (ML)’, and ‘Deep Learning’ are commonly used interchangeably to describe software that can demonstrate intelligent behaviour. Artificial intelligence involves creating algorithms and computational models that enable machines to imitate human cognitive abilities such as decision-making, learning from experience, and adapting to new situations. ML is a subfield of artificial intelligence to develop relationships between inputs and outputs, performing specific tasks without explicit programming. Deep learning is a further subfield of ML that utilises ‘deep’ neural networks with multiple hidden layers to learn from large amounts of data.
Artificial neural networks (ANNs) are deep learning algorithms inspired by the structure and function of the human brain [30,31,32]. ANNs comprise many interconnected nodes, or neurons, that work together to perform a specific task. Each neuron receives input from one or more other neurons and applies a mathematical function to that input to generate an output. The output of one neuron becomes the input to other neurons, and this process continues until the final output is produced. Various ANN variants are developed to improve model accuracy, including the wavelet neural network [33], radial basis function network [24], general regression neural network [34], and extreme learning machine [35].
Convolutional neural networks (CNNs) are powerful deep learning algorithms that are particularly well-suited for image recognition/classification tasks [14,36]. The input to the network is usually an image or a set of images. Convolutional layers apply a set of filters to extract relevant features, with the filters typically being small squares of pixels that slide over the image. Pooling layers reduce the dimensionality of the data to make the network more robust. The output of the final layer is then passed through one or more fully connected layers, which perform a final classification or regression task.
Recurrent neural networks (RNNs) are deep learning algorithms for sequential problems such as speech recognition, natural language processing, or time series forecasting [19,37]. RNNs are characterised by recurrent connections to maintain an internal state or memory, which enables them to capture temporal dependencies. However, RNNs can encounter the vanishing gradient problem when input sequences are too long. Long short-term memory (LSTM) is a type of RNN that includes additional memory cells and gating mechanisms, which selectively store and retrieve information over long periods [2,17,21,23,25,38,39]. In an LSTM, the input gate controls how much new information is stored in the cell, the forget gate controls how much old information is discarded from the cell, and the output gate controls how much information is passed to the next time step.
Fuzzy logic (FL) is a branch of mathematics that deals with reasoning with imprecision and uncertainty [40,41]. FL allows for degrees of truth or falsity to be represented as values between 0 and 1, in contrast to traditional logic that operates on the binary true/false principle. FL is ideal for artificial intelligence, control systems, and decision-making applications. An adaptive neuro-fuzzy inference system (ANFIS) is a hybrid system that combines fuzzy logic and neural network techniques to represent the input–output relationship with a set of fuzzy if-then rules [26,27,42]. The input data is first fuzzified, then the fuzzy rules are applied to generate an output. The neural network component of ANFIS is used to adjust the parameters of the fuzzy rules.
Support vector machine (SVM) is a type of ML algorithm with the ability to handle high-dimensional data and produce accurate results with relatively small datasets [3,17,43,44]. SVM uses a kernel function to map input data into a high-dimensional space where a hyperplane is used to separate the data into different classes. The main goal of SVM is to find the best-fitting hyperplane that maximises the margin between the predicted and actual values. However, SVM can be computationally expensive for large datasets and sensitive to the choice of kernel function and hyperparameters.
Decision tree (DT) is a widely used ML algorithm for classification and regression analysis, which is very effective because of its simplicity, interpretability, and accuracy in handling complex datasets [15,45]. It is based on a hierarchical structure where each node represents a decision or test of a specific feature. The tree is built by recursively splitting the data into smaller subsets based on the feature that provides the most information gain or reduction in entropy. Once the tree is built, it can be used to classify new data by following the path from the root node to the appropriate leaf node.
Random forest (RF) is an extension of the decision tree that uses multiple trees to produce more robust results and reduce the risk of overfitting [18,46,47]. RF combines the results of many decision trees to obtain a more accurate prediction. It has been successfully applied to a wide range of problems including remote sensing, object recognition, and cancer diagnosis. A classification and regression tree (CART) is a decision tree that simultaneously handles categorical and continuous variables [48,49]. A CART output is a decision tree where each fork is split into a predictor variable, and each node at the end has a prediction for the target variable. Another popular extension of the decision tree is extreme gradient boosting (XGBoost), which uses a gradient boosting framework to improve the accuracy and speed of prediction [36,50]. XGBoost uses a regularisation term to prevent overfitting and can handle missing values and sparse data. It also includes several advanced features such as cross-validation, early stopping, and parallel processing, which make it a popular choice for large-scale datasets and competitions on platforms.
2.3. Hyperparameter Tuning
Hyperparameter optimisation techniques aim to find the optimal combination of hyperparameters that are not learned from data but are instead specified by the user before training the model, such as the learning rate, batch size, and the number of hidden sizes.
Grid search is a simple and effective way to find good hyperparameter values for a model, but it can be computationally expensive. With grid search, a range of values is specified for each hyperparameter, and the model is trained and evaluated for every possible combination of hyperparameter values. The optimal combination of hyperparameters is chosen based on the highest performance in a validation set.
Particle swarm optimisation (PSO) is a population-based optimisation algorithm that is inspired by the behaviour of swarms of birds or insects [22,25,35,51,52]. In PSO, a population of candidate solutions, represented by particles, are evaluated according to a fitness function. Each particle moves towards its own best position and the best position found by the swarm, with the speed and direction of each particle being determined by its current position and velocity, as well as the position and velocity of the best particle in the swarm. This process is repeated until a satisfactory solution is found, or a stopping criterion is met.
Bayesian optimisation (BO) is a method used to optimise expensive, black box functions that lack an explicit mathematical form, particularly useful when the evaluation of the function is time-consuming or expensive [44,49,53,54]. It combines the previous knowledge of the target function with the results of previously evaluated points to determine the next point to be evaluated. It works by constructing a probabilistic model of the target function and updating the model as new observations. It allows the algorithm to balance exploration and exploitation to converge to the optimum of the function quickly.
Imperialist competitive algorithm (ICA) is a metaheuristic optimisation algorithm inspired by the concept of empires and colonies in history [30,55,56]. In ICA, each solution in the population represents a colony and the best solution is designated as imperialist. The imperialist expands its territory by attracting other colonies towards it, while the weaker colonies are forced to merge with the stronger ones. ICA balances exploration and exploitation, as weaker colonies explore new regions of the search space while stronger colonies exploit promising regions.
2.4. Evaluation Metrics
Model performance in testing is an indicator of the quality of the trained model. Equations (1)–(6) show various evaluation metrics that quantitatively evaluate prediction errors. In expressions, are measured and predicted values, and is the mean of measured values. Mean absolute error (MAE), mean squared error (MSE), and root mean squared error (RMSE) are dimensional and assess the errors between measured and predicted values, while mean absolute percentage error (MAPE) is non-dimensional and expressed as a percentage. The coefficient of determination (R2) and variance account for (VAF) represent the proportion of the variance in the dependent values between 0 and 1, where a larger value indicates a higher accuracy between predicted and measured values, and vice versa.
3. Application in TBM Tunnelling
Figure 3 summarises the number of studies that have utilised different ML algorithms to address the challenges of predicting TBM performance, predicting surface settlement, and time series forecasting. Specifically, ANN is the most widely used algorithm used in 19 studies to predict TBM performance and surface settlement, followed by SVM in 11 studies and RF in 10 studies. Given the time-dependent nature of the TBM tunnelling process, RNN, LSTM, and gated recurrent unit (GRU) are widely utilised in time series forecasting with studies of 8, 12, and 3, respectively. RNN, LSTM, and GRU models in time series forecasting are highly effective because of a loop structure to capture temporal dependencies, enabling them to outperform SVM and RF models.
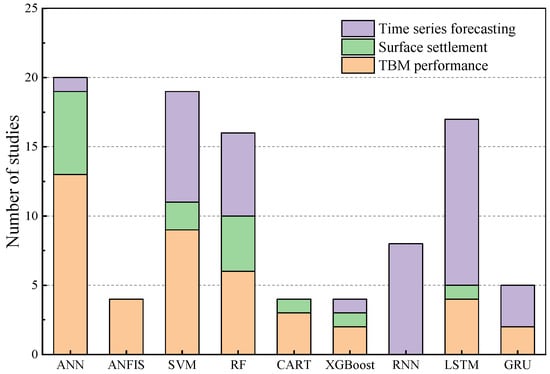
Figure 3.
Summary of ML algorithms in TBM performance, surface settlement and time series forecasting.
Predicting TBM performance or surface settlement is a function of input parameters in Equation (7), while time series forecasting is expressed in Equation (8).
where X is the input vector and Y is the output vector. The weight matrix W and bias b are the arguments to be trained by the activation function σ using ML algorithms. For time series forecasting, input vector comprises historical sequential data and output vector is the target value in the next step .
Typically, penetration rate, revolutions per minute, thrust force, and cutterhead torque are considered as feature vectors in ML models [13,57,58]. In addition to these four operational parameters, Lin et al. [25] used PCC to identify mutually independent parameters such as face pressure, screw conveyor speed, foam volume, and grouting pressure. Zhang et al. [29] applied PCA to reduce dimensionality and found the first eight principal components can capture the main information of 33 input parameters.
3.1. TBM Performance
Extensive research has been conducted on employing ML algorithms to investigate TBM performance in Table 1. TBM performance refers to the effectiveness and efficiency of the machine in excavating a tunnel and involves various indicators such as penetration rate, advance rate, field penetration index, thrust force, and cutterhead torque. Understanding and optimising TBM performance is crucial for project time management, cost control, and risk mitigation.

Table 1.
Summary of literature on ML algorithms and predicting TBM performance.
Since ML models are data-driven, the quality of datasets (e.g., availability to the public, number of samples, input parameters used, etc.) is crucial. Table 2 displays three types of models corresponding to three typical datasets and their respective limitations. It is worth noting that models are categorised according to their input parameters: Model A includes geological conditions, operational parameters, and TBM type and size, Model B only includes geological conditions, and Model C includes geological conditions and operational parameters.

Table 2.
Three types of models based on input parameters and their limitations.
The penetration rate (PR) measures the speed of boring distance divided by the working time, typically quantified in m/h or mm/min. PR plays a crucial role in tunnelling operations as it directly affects overall productivity. A higher penetration rate results in faster tunnel excavation, ultimately reducing project time and costs. For predicting PR, ANIFS, ANN, and SVM models have shown promising results in various studies. For instance, the ANIFS model [26] demonstrated better performance than multiple regression and empirical methods based on a database of 640 TBM projects in rock. The ANIFS model (Model A) is adaptable as it takes into account geological conditions, operational parameters, and even TBM type and size, but most TBM datasets are not available for public access.
The ANN and SVM models [43,59] outperformed linear and non-linear regression when applied to the publicly available Queen water tunnel dataset with 151 samples. In the sensitivity analysis, interestingly, the brittleness index was found to be the least effective parameter in the SVM model [43] but the most sensitive parameter in the RF model [70]. These contrasting results can be attributed to a limited number of samples for training, which leads to overfitting or lack of generalisability of Model B.
In the project of Pahang–Selangor raw water transfer with 1286 samples, ML models for predicting PR were robust and reliable because of more data and adding operational parameters [30,50,63]. However, TBM performance is a real-time operational parameter that cannot be obtained before the start of a project, making it infeasible to apply Model C in practice. For example, although the average thrust force is an effective parameter for predicting PR [63], it is an operational input in Model C and is unavailable as it is collected in real-time as well as PR itself.
Given the expression for predicting PR using statistical analysis, optimisation techniques can be applied to optimise the correlations of weighting in multiple regression [52]. On the other hand, optimisation techniques can be used to fine-tune the hyperparameters of ML models, such as the XGBoost model by Zhou et al. [50]. Figure 4 compares the model performance using different optimisation techniques, with Figure 4a showing the MR model and Figure 4b showing the XGBoost model. The accuracy improves by utilising optimisation techniques, but the difference between different optimisation techniques is small.
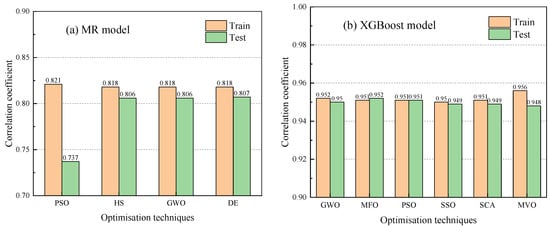
Figure 4.
Comparison optimisation techniques (a) MR model based on dataset from Queen water tunnel; (b) XGBoost model based on dataset from Pahang–Selangor raw water transfer.
Advance rate (AR) is a crucial indicator in tunnelling operations, calculated as the boring distance divided by the working time and stoppages. Compared with PR, AR additionally considers stoppages due to TBM maintenance, cutters change, breakdowns, or tunnel collapses. Comparing AR prediction models, the ANN model by Benardos and Kaliampakos [31] was limited by the small size of the Athens metro dataset. In contrast, the Pahang–Selangor raw water transfer dataset allowed for the development of more robust and reliable ML models for AR prediction [35,54,55,65].
Field penetration index (FPI) evaluates TBM efficiency in the field calculated as the average cutter force divided by penetration per revolution. For predicting FPI, ANIFS and RF models performed well when applied to the Queen water tunnel dataset [3,42]. Furthermore, Salimi et al. [27,48,69] successfully developed ML models to predict FPI in different rock types and conducted a sensitivity analysis to better understand the relationship between FPI and input parameters.
Thrust force (TH) refers to the force that TBM exerts on the excavation face, whereas cutterhead torque (TO) refers to the twisting force applied to the cutterhead. The amount of TH or TO depends on the hardness and strength of the material being excavated and the size and type of TBM being used. Regarding the prediction of TH and TO, Sun et al. [18] built RF models for heterogeneous strata, while Lin et al. [25,68] utilised PSO-LSTM and PSO-GRU models based on the dataset from Shenzhen intercity railway. Bai et al. [45] utilised an SVM classifier to identify the location of interbedded clay or stratum interface and subsequently developed ML models to predict TH, TO, and FP.
Although these ML models offer high accuracy in predicting TBM performance, their applicability is limited due to their project-specific nature (Model B and Model C) and lack of generalisability across different TBM types and geological conditions [71]. Despite these limitations, ML models remain highly flexible in adding or filtering related parameters and implicitly capturing the impact of uncertain parameters, providing valuable insights into TBM performance optimisation.
3.2. Surface Settlement
The surface settlement, the subsidence of the ground surface above a tunnel due to excavation, poses risks to surrounding structures and utilities. Accurate prediction of surface settlement is essential for mitigating potential damages during tunnel construction. Engineers can minimise ground movement and reduce the risk of damage by adjusting excavation parameters and support structures. Table 3 reviews papers on settlement induced by TBM tunnelling and excludes construction methods such as drilling, blasting, and the new Austrian Tunnelling Method [72,73,74].

Table 3.
Summary of literature on ML algorithms and predicting surface settlement.
Suwansawat and Einstein [32] were among the first to use ANN to predict the maximum settlement (Smax) for the Bangkok subway project, considering tunnel geometry, geological conditions, and operational parameters. Pourtaghi and Lotfollahi-Yaghin [33] improved the ANN model by adopting wavelets as activation functions, resulting in higher accuracy than traditional ANN models. In contrast, Goh et al. [77] utilised MARS and Zhang et al. [78] utilised XGBoost to predict Smax for Singapore mass rapid transport lines with 148 samples. Interestingly, the mean standard penetration test showed opposite sensitivities in these two models. It further highlights the unreliability and unrobustness of ML models with limited samples, which may lead to overfitting or lack of generalisability. A comprehensive dataset from Changsha metro line 4, including geometry, geological conditions, and real-time operational parameters, has been used to compare the performance of various ML models such as ANN, SVM, RF, and LSTM [22,24,34,47].
Since the observed settlement showed a Gaussian shape in the transverse profile, Boubou et al. [75] incorporated the distance from the tunnel axis as an input parameter in their ANN model. They identified advance rate, hydraulic pressure, and vertical guidance parameter as the most influential factors in predicting surface settlement.
Various ML models have been employed to predict surface settlement induced by TBM tunnelling. The choice of ML algorithms and feature selection can significantly impact prediction accuracy, and researchers should carefully consider these factors when applying ML to surface settlement prediction in TBM tunnelling.
3.3. Time Series Forecasting
Time series forecasting is a real-time prediction using current and historical data to forecast future unknown values, which means input parameters are available and it does not have the practical problem of Model C. It is crucial in TBM tunnelling for predicting TBM performance, surface settlement, and moving trajectory in real time because operators can make necessary adjustments when potential issues are detected. Several studies using ML techniques for time series forecasting are shown in Table 4. Since the quality and quantity of data heavily influence model performance, moving average or wavelet transform are employed to eliminate noise and fine-grained variation to reveal the underlying information in time series data [14,17,19,21].

Table 4.
Summary of literature on ML algorithms and time series forecasting.
High-frequency data is collected directly from the data acquisition system every few seconds or minutes. High-frequency prediction of next-step TBM performance can be achieved with high accuracy using RNN, LSTM, and GRU. These ML algorithms have been found to outperform others by incorporating both current and historical parameters [21,36,37,53,82]. However, it is less meaningful to predict TBM performance just a few seconds or millimetres in advance, as shown in Table 5. Therefore, multi-step forecasts were explored, and it was found that errors increase significantly with an increasing forecast horizon [39,81,84].

Table 5.
Comparison of time series forecasting on historical data and forecast horizon.
High-frequency data can be preprocessed into low-frequency data, where each data point represents a fixed segment or working cycle spanning 1–2 m. Low-frequency data, such as that from the Yingsong water diversion project, have been used to forecast average operational parameters [2,14] and predict next-step TBM performance in different geological conditions [13]. In contrast, Shan et al. [19] employed RNN and LSTM to predict near-future TBM performance (1.5–7.5 m ahead), focusing on the difference in geological conditions between training data and test data. While one-step forecasts are highly accurate, predictions decrease in accuracy as the forecast horizon increases.
Regarding the number of steps back required to predict future TBM performance, Table 5 demonstrates that the number of steps used for training ranges from 5 to 10, except for those who used data from the last 50 steps. High-frequency prediction normally uses data just a few millimetres beforehand for training, while low-frequency prediction uses data up to seven metres beforehand. Nevertheless, these data are collected a few millimetres to a few meters away from the current cutterhead location and essentially reflect the current operation of the TBM [85].
To account for the surface settlement developing over time in a single point, Guo et al. [20] used an Elman RNN to predict the longitudinal settlement profile, while Zhang et al. [79] integrated wavelet transform and SVM to forecast daily surface settlement. Zhang et al. [83] used historical geometric and geological parameters to build an RF model to predict operational parameters in the next step. They then combined predicted operational parameters with geometric and geological parameters to estimate Smax in the next step based on another RF model.
To improve moving trajectory, current, and historical parameters have been used to predict real-time TBM movements such as horizontal deviation of shield head, horizontal deviation of shield tail, vertical deviation of shield head, vertical deviation of shield tail, roll, and pitch [17,23,29]. When deviations reach the alarm value, the TBM route can be regulated by fine-tuning the thrust force and strokes in the corresponding positions.
Time series forecasting techniques vary in effectiveness depending on the frequency of data collection, the forecast horizon, and the specific application in TBM tunnelling. Understanding these differences and selecting the appropriate ML algorithm is essential for optimising tunnelling operations.
4. Summary and Perspectives
Many studies have reported successful applications of ML techniques in TBM tunnelling, with an increasing trend in Figure 1. This trend is likely to persist as the volume of data continues to grow and the use of ML becomes more common. This paper presents a systematic literature review on using ML techniques in TBM tunnelling. A framework of ML modelling is presented, highlighting the importance of data processing before modelling, ML algorithms, and optimisation techniques used to build near-optimal models, and evaluation metrics for model performance. Furthermore, it identifies three main issues in TBM tunnelling: predicting TBM performance, predicting surface settlement, and time series forecasting.
ANN, SVM, and RF are the most popular algorithms adopted in the prediction of TBM performance and surface settlement. The model performance heavily depends on the selection of ML algorithms and hyperparameter tuning. Availability to the public, number of samples, and input parameters for training are also crucial in ML modelling when applied to tunnel projects. Optimisation techniques can effectively enhance the performance of both multiple regression and ML models.
Given the time-dependent nature of the TBM tunnelling process, RNN, LSTM, and GRU are widely utilised to deal with time series problems. However, high-frequency prediction is less meaningful as it only provides a few seconds or millimetres advance warning, while low-frequency prediction is limited by the number of samples after data preprocessing. One-step forecasts have proven to be highly accurate and play a practical role in warning of possible accidents. However, the accuracy of multi-step forecasts decreases significantly with an increasing forecast horizon, mainly due to the decreased impact of parameters farther away from the TBM cutterhead.
The black box problem is a significant limitation of ML models as they lack interpretability. While ML models are able to make predictions based on complex patterns and relationships within data, it can be difficult to interpret how the model arrived at its results. To address the limitation, researchers are developing more interpretable ML models. Specifically, decision tree-based algorithms can provide insights into the model’s decision-making process through probabilistic sensitivity analysis. Theory-guided machine learning and physics-informed neural networks can incorporate theoretical knowledge or physical laws into the learning process, facilitating the capture of optimal solutions and effective generalisation, even with limited training samples.
Another important challenge is that ML models are developed and validated using only one dataset or similar datasets, which limits their applicability to different projects. Validation and generalisation of ML models across various datasets are necessary for the industry to gain confidence in their effectiveness. As tunnelling data become more accessible, it may be possible to interrogate larger data for training data. This would allow the reliability and robustness of ML models on future projects to improve feedback in the industry.
Author Contributions
Conceptualisation, F.S.; methodology, F.S.; writing—original draft preparation, F.S. and H.X.; writing—review and editing, X.H., D.J.A. and D.S.; supervision, X.H. and D.S.; funding acquisition, D.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analysed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare that they have no known competing financial interest or personal relationships that could have appeared to influence the work reported in this paper.
Abbreviations
| TBM | Tunnel boring machine |
| ML | Machine learning |
| PR | Penetration rate |
| AR | Advance rate |
| FPI | Field penetration index |
| TH | Thrust force |
| TO | Cutterhead torque |
| Smax | Maximum surface settlement |
| PCA | Principal component analysis |
| PCC | Pearson correlation coefficient |
| ANN | Artificial neural network |
| CNN | Convolutional neural network |
| RNN | Recurrent neural network |
| LSTM | Long short-term memory |
| GRU | Gated recurrent unit |
| FL | Fuzzy logic |
| ANIFS | Adaptive neuro-fuzzy inference system |
| SVM | Support vector machine |
| DT | Decision tree |
| RF | Random forest |
| CART | Classification and regression tree |
| XGBoost | Extreme gradient boosting |
| PSO | Particle swarm optimisation |
| BO | Bayesian optimisation |
| ICA | Imperialism competitive algorithm |
References
- Adoko, A.C.; Gokceoglu, C.; Yagiz, S. Bayesian prediction of TBM penetration rate in rock mass. Eng. Geol. 2017, 226, 245–256. [Google Scholar] [CrossRef]
- Li, J.; Li, P.; Guo, D.; Li, X.; Chen, Z. Advanced prediction of tunnel boring machine performance based on big data. Geosci. Front. 2021, 12, 331–338. [Google Scholar] [CrossRef]
- Yang, H.; Wang, Z.; Song, K. A new hybrid grey wolf optimizer-feature weighted-multiple kernel-support vector regression technique to predict TBM performance. Eng. Comput. 2022, 38, 2469–2485. [Google Scholar] [CrossRef]
- Ozdemir, L. Development of Theoretical Equations for Predicting Tunnel Boreability; Colorado School of Mines: Golden, CO, USA, 1977. [Google Scholar]
- Rostami, J. Development of a Force Estimation Model for Rock Fragmentation with Disc Cutters through Theoretical Modeling and Physical Measurement of Crushed Zone Pressure; Colorado School of Mines: Golden, CO, USA, 1997. [Google Scholar]
- Barton, N.R. TBM Tunnelling in Jointed and Faulted Rock; Crc Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Bruland, A. Hard Rock Tunnel Boring. Ph.D. Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 1998. [Google Scholar]
- Yagiz, S. Utilizing rock mass properties for predicting TBM performance in hard rock condition. Tunn. Undergr. Space Technol. 2008, 23, 326–339. [Google Scholar] [CrossRef]
- Shreyas, S.; Dey, A. Application of soft computing techniques in tunnelling and underground excavations: State of the art and future prospects. Innov. Infrastruct. Solut. 2019, 4, 46. [Google Scholar] [CrossRef]
- Shahrour, I.; Zhang, W. Use of soft computing techniques for tunneling optimization of tunnel boring machines. Undergr. Space 2021, 6, 233–239. [Google Scholar] [CrossRef]
- Sheil, B.B.; Suryasentana, S.K.; Mooney, M.A.; Zhu, H. Machine learning to inform tunnelling operations: Recent advances and future trends. Proc. Inst. Civ. Eng. -Smart Infrastruct. Constr. 2020, 173, 74–95. [Google Scholar]
- Li, J.-B.; Chen, Z.-Y.; Li, X.; Jing, L.-J.; Zhangf, Y.-P.; Xiao, H.-H.; Wang, S.-J.; Yang, W.-K.; Wu, L.-J.; Li, P.-Y. Feedback on a shared big dataset for intelligent TBM Part I: Feature extraction and machine learning methods. Undergr. Space 2023, 11, 1–25. [Google Scholar] [CrossRef]
- Feng, S.; Chen, Z.; Luo, H.; Wang, S.; Zhao, Y.; Liu, L.; Ling, D.; Jing, L. Tunnel boring machines (TBM) performance prediction: A case study using big data and deep learning. Tunn. Undergr. Space Technol. 2021, 110, 103636. [Google Scholar] [CrossRef]
- Xu, C.; Liu, X.; Wang, E.; Wang, S. Prediction of tunnel boring machine operating parameters using various machine learning algorithms. Tunn. Undergr. Space Technol. 2021, 109, 103699. [Google Scholar] [CrossRef]
- Hou, S.; Liu, Y.; Yang, Q. Real-time prediction of rock mass classification based on TBM operation big data and stacking technique of ensemble learning. J. Rock Mech. Geotech. Eng. 2022, 14, 123–143. [Google Scholar] [CrossRef]
- Wu, Z.; Wei, R.; Chu, Z.; Liu, Q. Real-time rock mass condition prediction with TBM tunneling big data using a novel rock–machine mutual feedback perception method. J. Rock Mech. Geotech. Eng. 2021, 13, 1311–1325. [Google Scholar] [CrossRef]
- Shen, S.-L.; Elbaz, K.; Shaban, W.M.; Zhou, A. Real-time prediction of shield moving trajectory during tunnelling. Acta Geotech. 2022, 17, 1533–1549. [Google Scholar] [CrossRef]
- Sun, W.; Shi, M.; Zhang, C.; Zhao, J.; Song, X. Dynamic load prediction of tunnel boring machine (TBM) based on heterogeneous in-situ data. Autom. Constr. 2018, 92, 23–34. [Google Scholar] [CrossRef]
- Shan, F.; He, X.; Armaghani, D.J.; Zhang, P.; Sheng, D. Success and challenges in predicting TBM penetration rate using recurrent neural networks. Tunn. Undergr. Space Technol. 2022, 130, 104728. [Google Scholar] [CrossRef]
- Guo, J.; Ding, L.; Luo, H.; Zhou, C.; Ma, L. Wavelet prediction method for ground deformation induced by tunneling. Tunn. Undergr. Space Technol. 2014, 41, 137–151. [Google Scholar] [CrossRef]
- Wang, R.; Li, D.; Chen, E.J.; Liu, Y. Dynamic prediction of mechanized shield tunneling performance. Autom. Constr. 2021, 132, 103958. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, H.; Chen, R.; Dai, T.; Meng, F.; Wang, H. A critical evaluation of machine learning and deep learning in shield-ground interaction prediction. Tunn. Undergr. Space Technol. 2020, 106, 103593. [Google Scholar] [CrossRef]
- Zhou, C.; Xu, H.; Ding, L.; Wei, L.; Zhou, Y. Dynamic prediction for attitude and position in shield tunneling: A deep learning method. Autom. Constr. 2019, 105, 102840. [Google Scholar] [CrossRef]
- Chen, R.-P.; Zhang, P.; Kang, X.; Zhong, Z.-Q.; Liu, Y.; Wu, H.-N. Prediction of maximum surface settlement caused by earth pressure balance (EPB) shield tunneling with ANN methods. Soils Found. 2019, 59, 284–295. [Google Scholar] [CrossRef]
- Lin, S.; Zhang, N.; Zhou, A.; Shen, S. Time-series prediction of shield movement performance during tunneling based on hybrid model. Tunn. Undergr. Space Technol. 2022, 119, 104245. [Google Scholar] [CrossRef]
- Grima, M.A.; Bruines, P.; Verhoef, P. Modeling tunnel boring machine performance by neuro-fuzzy methods. Tunn. Undergr. Space Technol. 2000, 15, 259–269. [Google Scholar] [CrossRef]
- Salimi, A.; Rostami, J.; Moormann, C.; Delisio, A. Application of non-linear regression analysis and artificial intelligence algorithms for performance prediction of hard rock TBMs. Tunn. Undergr. Space Technol. 2016, 58, 236–246. [Google Scholar] [CrossRef]
- Tiryaki, B. Application of artificial neural networks for predicting the cuttability of rocks by drag tools. Tunn. Undergr. Space Technol. 2008, 23, 273–280. [Google Scholar] [CrossRef]
- Zhang, N.; Zhang, N.; Zheng, Q.; Xu, Y.-S. Real-time prediction of shield moving trajectory during tunnelling using GRU deep neural network. Acta Geotech. 2022, 17, 1167–1182. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Mohamad, E.T.; Narayanasamy, M.S.; Narita, N.; Yagiz, S. Development of hybrid intelligent models for predicting TBM penetration rate in hard rock condition. Tunn. Undergr. Space Technol. 2017, 63, 29–43. [Google Scholar] [CrossRef]
- Benardos, A.; Kaliampakos, D. Modelling TBM performance with artificial neural networks. Tunn. Undergr. Space Technol. 2004, 19, 597–605. [Google Scholar] [CrossRef]
- Suwansawat, S.; Einstein, H.H. Artificial neural networks for predicting the maximum surface settlement caused by EPB shield tunneling. Tunn. Undergr. Space Technol. 2006, 21, 133–150. [Google Scholar] [CrossRef]
- Pourtaghi, A.; Lotfollahi-Yaghin, M. Wavenet ability assessment in comparison to ANN for predicting the maximum surface settlement caused by tunneling. Tunn. Undergr. Space Technol. 2012, 28, 257–271. [Google Scholar] [CrossRef]
- Zhang, P.; Wu, H.-N.; Chen, R.-P.; Chan, T.H. Hybrid meta-heuristic and machine learning algorithms for tunneling-induced settlement prediction: A comparative study. Tunn. Undergr. Space Technol. 2020, 99, 103383. [Google Scholar] [CrossRef]
- Zeng, J.; Roy, B.; Kumar, D.; Mohammed, A.S.; Armaghani, D.J.; Zhou, J.; Mohamad, E.T. Proposing several hybrid PSO-extreme learning machine techniques to predict TBM performance. Eng. Comput. 2021, 38, 3811–3827. [Google Scholar] [CrossRef]
- Qin, C.; Shi, G.; Tao, J.; Yu, H.; Jin, Y.; Lei, J.; Liu, C. Precise cutterhead torque prediction for shield tunneling machines using a novel hybrid deep neural network. Mech. Syst. Signal Process. 2021, 151, 107386. [Google Scholar] [CrossRef]
- Gao, X.; Shi, M.; Song, X.; Zhang, C.; Zhang, H. Recurrent neural networks for real-time prediction of TBM operating parameters. Autom. Constr. 2019, 98, 225–235. [Google Scholar] [CrossRef]
- Jin, Y.; Qin, C.; Tao, J.; Liu, C. An accurate and adaptative cutterhead torque prediction method for shield tunneling machines via adaptative residual long-short term memory network. Mech. Syst. Signal Process. 2022, 165, 108312. [Google Scholar] [CrossRef]
- Shi, G.; Qin, C.; Tao, J.; Liu, C. A VMD-EWT-LSTM-based multi-step prediction approach for shield tunneling machine cutterhead torque. Knowl.-Based Syst. 2021, 228, 107213. [Google Scholar] [CrossRef]
- Acaroglu, O.; Ozdemir, L.; Asbury, B. A fuzzy logic model to predict specific energy requirement for TBM performance prediction. Tunn. Undergr. Space Technol. 2008, 23, 600–608. [Google Scholar] [CrossRef]
- Mikaeil, R.; Naghadehi, M.Z.; Sereshki, F. Multifactorial fuzzy approach to the penetrability classification of TBM in hard rock conditions. Tunn. Undergr. Space Technol. 2009, 24, 500–505. [Google Scholar] [CrossRef]
- Parsajoo, M.; Mohammed, A.S.; Yagiz, S.; Armaghani, D.J.; Khandelwal, M. An evolutionary adaptive neuro-fuzzy inference system for estimating field penetration index of tunnel boring machine in rock mass. J. Rock Mech. Geotech. Eng. 2021, 13, 1290–1299. [Google Scholar] [CrossRef]
- Mahdevari, S.; Shahriar, K.; Yagiz, S.; Shirazi, M.A. A support vector regression model for predicting tunnel boring machine penetration rates. Int. J. Rock Mech. Min. Sci. 2014, 72, 214–229. [Google Scholar] [CrossRef]
- Mokhtari, S.; Mooney, M.A. Predicting EPBM advance rate performance using support vector regression modeling. Tunn. Undergr. Space Technol. 2020, 104, 103520. [Google Scholar] [CrossRef]
- Bai, X.-D.; Cheng, W.-C.; Li, G. A comparative study of different machine learning algorithms in predicting EPB shield behaviour: A case study at the Xi’an metro, China. Acta Geotech. 2021, 16, 4061–4080. [Google Scholar] [CrossRef]
- Kannangara, K.P.M.; Zhou, W.; Ding, Z.; Hong, Z. Investigation of feature contribution to shield tunneling-induced settlement using Shapley additive explanations method. J. Rock Mech. Geotech. Eng. 2022, 14, 1052–1063. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, R.; Wu, H. Real-time analysis and regulation of EPB shield steering using Random Forest. Autom. Constr. 2019, 106, 102860. [Google Scholar] [CrossRef]
- Salimi, A.; Rostami, J.; Moormann, C. Application of rock mass classification systems for performance estimation of rock TBMs using regression tree and artificial intelligence algorithms. Tunn. Undergr. Space Technol. 2019, 92, 103046. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, W.; Liu, Z.; Tan, J. TBM performance prediction with Bayesian optimization and automated machine learning. Tunn. Undergr. Space Technol. 2020, 103, 103493. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Armaghani, D.J.; Zhang, W.; Li, C.; Zhu, S.; Tarinejad, R. Predicting TBM penetration rate in hard rock condition: A comparative study among six XGB-based metaheuristic techniques. Geosci. Front. 2021, 12, 101091. [Google Scholar] [CrossRef]
- Yagiz, S.; Karahan, H. Prediction of hard rock TBM penetration rate using particle swarm optimization. Int. J. Rock Mech. Min. Sci. 2011, 48, 427–433. [Google Scholar] [CrossRef]
- Yagiz, S.; Karahan, H. Application of various optimization techniques and comparison of their performances for predicting TBM penetration rate in rock mass. Int. J. Rock Mech. Min. Sci. 2015, 80, 308–315. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, Q.; Liu, Q.; Liu, X.; Liu, B.; Wang, J.; Yin, X. A real-time prediction method for tunnel boring machine cutter-head torque using bidirectional long short-term memory networks optimized by multi-algorithm. J. Rock Mech. Geotech. Eng. 2022, 14, 798–812. [Google Scholar] [CrossRef]
- Zhou, J.; Qiu, Y.; Zhu, S.; Armaghani, D.J.; Khandelwal, M.; Mohamad, E.T. Estimation of the TBM advance rate under hard rock conditions using XGBoost and Bayesian optimization. Undergr. Space 2021, 6, 506–515. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Koopialipoor, M.; Marto, A.; Yagiz, S. Application of several optimization techniques for estimating TBM advance rate in granitic rocks. J. Rock Mech. Geotech. Eng. 2019, 11, 779–789. [Google Scholar] [CrossRef]
- Harandizadeh, H.; Armaghani, D.J.; Asteris, P.G.; Gandomi, A.H. TBM performance prediction developing a hybrid ANFIS-PNN predictive model optimized by imperialism competitive algorithm. Neural Comput. Appl. 2021, 33, 16149–16179. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, Y.; Li, J.; Li, X.; Jing, L. Diagnosing tunnel collapse sections based on TBM tunneling big data and deep learning: A case study on the Yinsong Project, China. Tunn. Undergr. Space Technol. 2021, 108, 103700. [Google Scholar] [CrossRef]
- Liu, B.; Wang, R.; Zhao, G.; Guo, X.; Wang, Y.; Li, J.; Wang, S. Prediction of rock mass parameters in the TBM tunnel based on BP neural network integrated simulated annealing algorithm. Tunn. Undergr. Space Technol. 2020, 95, 103103. [Google Scholar] [CrossRef]
- Yagiz, S. Assessment of brittleness using rock strength and density with punch penetration test. Tunn. Undergr. Space Technol. 2009, 24, 66–74. [Google Scholar] [CrossRef]
- Javad, G.; Narges, T. Application of artificial neural networks to the prediction of tunnel boring machine penetration rate. Min. Sci. Technol. 2010, 20, 727–733. [Google Scholar] [CrossRef]
- Armaghani, D.J.; Faradonbeh, R.S.; Momeni, E.; Fahimifar, A.; Tahir, M. Performance prediction of tunnel boring machine through developing a gene expression programming equation. Eng. Comput. 2018, 34, 129–141. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Tootoonchi, H.; Jahed Armaghani, D.; Tonnizam Mohamad, E.; Hedayat, A. Application of deep neural networks in predicting the penetration rate of tunnel boring machines. Bull. Eng. Geol. Environ. 2019, 78, 6347–6360. [Google Scholar] [CrossRef]
- Koopialipoor, M.; Fahimifar, A.; Ghaleini, E.N.; Momenzadeh, M.; Armaghani, D.J. Development of a new hybrid ANN for solving a geotechnical problem related to tunnel boring machine performance. Eng. Comput. 2020, 36, 345–357. [Google Scholar] [CrossRef]
- Wang, Q.; Xie, X.; Shahrour, I. Deep learning model for shield tunneling advance rate prediction in mixed ground condition considering past operations. IEEE Access 2020, 8, 215310–215326. [Google Scholar] [CrossRef]
- Zhou, J.; Yazdani Bejarbaneh, B.; Jahed Armaghani, D.; Tahir, M. Forecasting of TBM advance rate in hard rock condition based on artificial neural network and genetic programming techniques. Bull. Eng. Geol. Environ. 2020, 79, 2069–2084. [Google Scholar] [CrossRef]
- Bardhan, A.; Kardani, N.; GuhaRay, A.; Burman, A.; Samui, P.; Zhang, Y. Hybrid ensemble soft computing approach for predicting penetration rate of tunnel boring machine in a rock environment. J. Rock Mech. Geotech. Eng. 2021, 13, 1398–1412. [Google Scholar] [CrossRef]
- Lin, S.; Shen, S.; Zhang, N.; Zhou, A. Modelling the performance of EPB shield tunnelling using machine and deep learning algorithms. Geosci. Front. 2021, 12, 101177. [Google Scholar] [CrossRef]
- Lin, S.-S.; Shen, S.-L.; Zhou, A. Real-time analysis and prediction of shield cutterhead torque using optimized gated recurrent unit neural network. J. Rock Mech. Geotech. Eng. 2022, 14, 1232–1240. [Google Scholar] [CrossRef]
- Salimi, A.; Rostami, J.; Moormann, C.; Hassanpour, J. Introducing Tree-Based-Regression Models for Prediction of Hard Rock TBM Performance with Consideration of Rock Type. Rock Mech. Rock Eng. 2022, 55, 4869–4891. [Google Scholar] [CrossRef]
- Yang, J.; Yagiz, S.; Liu, Y.-J.; Laouafa, F. Comprehensive evaluation of machine learning algorithms applied to TBM performance prediction. Undergr. Space 2022, 7, 37–49. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Li, Y.; Liu, H.; Chen, Y.; Ding, X. Application of deep learning algorithms in geotechnical engineering: A short critical review. Artif. Intell. Rev. 2021, 54, 5633–5673. [Google Scholar] [CrossRef]
- Ahangari, K.; Moeinossadat, S.R.; Behnia, D. Estimation of tunnelling-induced settlement by modern intelligent methods. Soils Found. 2015, 55, 737–748. [Google Scholar] [CrossRef]
- Neaupane, K.M.; Adhikari, N. Prediction of tunneling-induced ground movement with the multi-layer perceptron. Tunn. Undergr. Space Technol. 2006, 21, 151–159. [Google Scholar] [CrossRef]
- Santos, O.J., Jr.; Celestino, T.B. Artificial neural networks analysis of Sao Paulo subway tunnel settlement data. Tunn. Undergr. Space Technol. 2008, 23, 481–491. [Google Scholar] [CrossRef]
- Boubou, R.; Emeriault, F.; Kastner, R. Artificial neural network application for the prediction of ground surface movements induced by shield tunnelling. Can. Geotech. J. 2010, 47, 1214–1233. [Google Scholar] [CrossRef]
- Dindarloo, S.R.; Siami-Irdemoosa, E. Maximum surface settlement based classification of shallow tunnels in soft ground. Tunn. Undergr. Space Technol. 2015, 49, 320–327. [Google Scholar] [CrossRef]
- Goh, A.T.C.; Zhang, W.; Zhang, Y.; Xiao, Y.; Xiang, Y. Determination of earth pressure balance tunnel-related maximum surface settlement: A multivariate adaptive regression splines approach. Bull. Eng. Geol. Environ. 2018, 77, 489–500. [Google Scholar] [CrossRef]
- Zhang, W.; Li, H.; Wu, C.; Li, Y.; Liu, Z.; Liu, H. Soft computing approach for prediction of surface settlement induced by earth pressure balance shield tunneling. Undergr. Space 2021, 6, 353–363. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Ji, W.; AbouRizk, S.M. Intelligent approach to estimation of tunnel-induced ground settlement using wavelet packet and support vector machines. J. Comput. Civ. Eng. 2017, 31, 04016053. [Google Scholar] [CrossRef]
- Gao, M.-Y.; Zhang, N.; Shen, S.-L.; Zhou, A. Real-time dynamic earth-pressure regulation model for shield tunneling by integrating GRU deep learning method with GA optimization. IEEE Access 2020, 8, 64310–64323. [Google Scholar] [CrossRef]
- Erharter, G.H.; Marcher, T. On the pointlessness of machine learning based time delayed prediction of TBM operational data. Autom. Constr. 2021, 121, 103443. [Google Scholar] [CrossRef]
- Gao, B.; Wang, R.; Lin, C.; Guo, X.; Liu, B.; Zhang, W. TBM penetration rate prediction based on the long short-term memory neural network. Undergr. Space 2021, 6, 718–731. [Google Scholar] [CrossRef]
- Zhang, P.; Chen, R.; Dai, T.; Wang, Z.; Wu, K. An AIoT-based system for real-time monitoring of tunnel construction. Tunn. Undergr. Space Technol. 2021, 109, 103766. [Google Scholar] [CrossRef]
- Qin, C.; Shi, G.; Tao, J.; Yu, H.; Jin, Y.; Xiao, D.; Zhang, Z.; Liu, C. An adaptive hierarchical decomposition-based method for multi-step cutterhead torque forecast of shield machine. Mech. Syst. Signal Process. 2022, 175, 109148. [Google Scholar] [CrossRef]
- Shan, F.; He, X.; Armaghani, D.J.; Zhang, P.; Sheng, D. Response to Discussion on “Success and challenges in predicting TBM penetration rate using recurrent neural networks” by Georg H. Erharter, Thomas Marcher. Tunn. Undergr. Space Technol. 2023, 105064. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).