Neuroevolution Application to Collaborative and Heuristics-Based Connected and Autonomous Vehicle Cohort Simulation at Uncontrolled Intersection
Abstract
1. Introduction
2. Materials and Methods
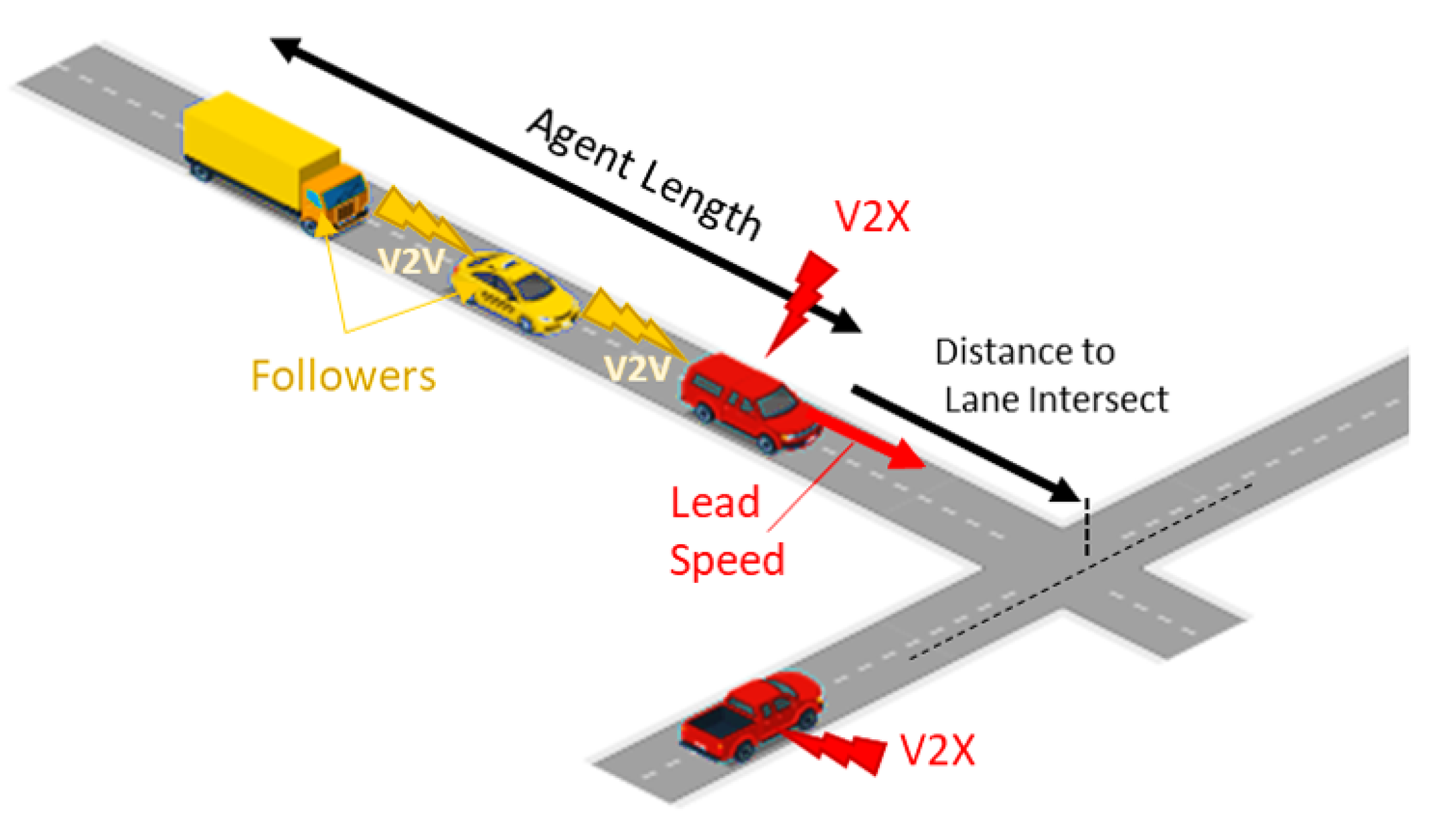
- Current speed of the agent ;
- Current agent distance from the lane intersect ;
- Current agent length ;
- Current speed of the second agent (cross traffic agent) ;
- Current distance of the second agent to the lane intersect ;
- Second agent length .
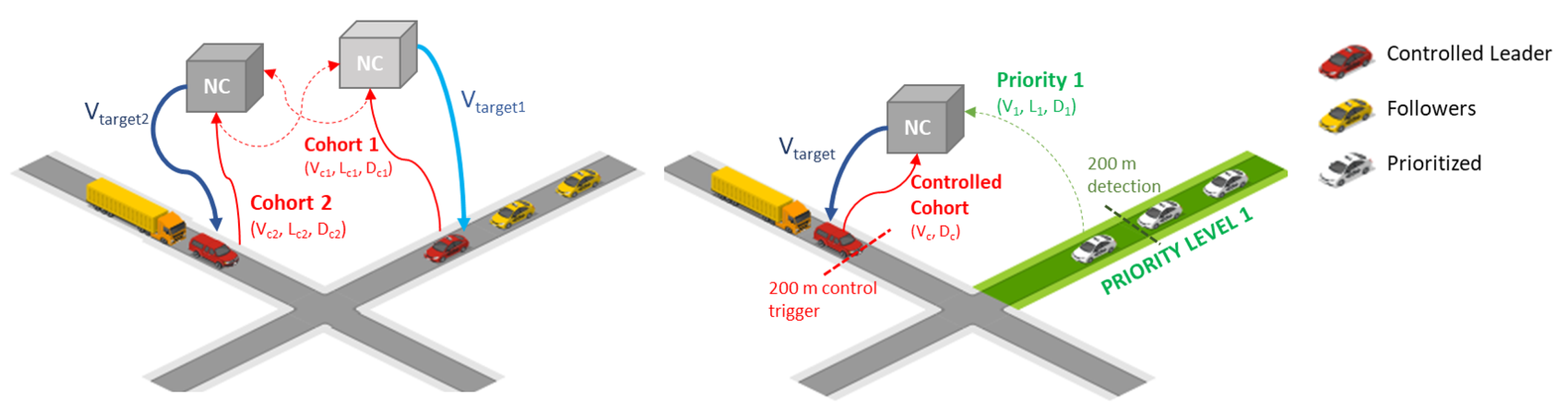
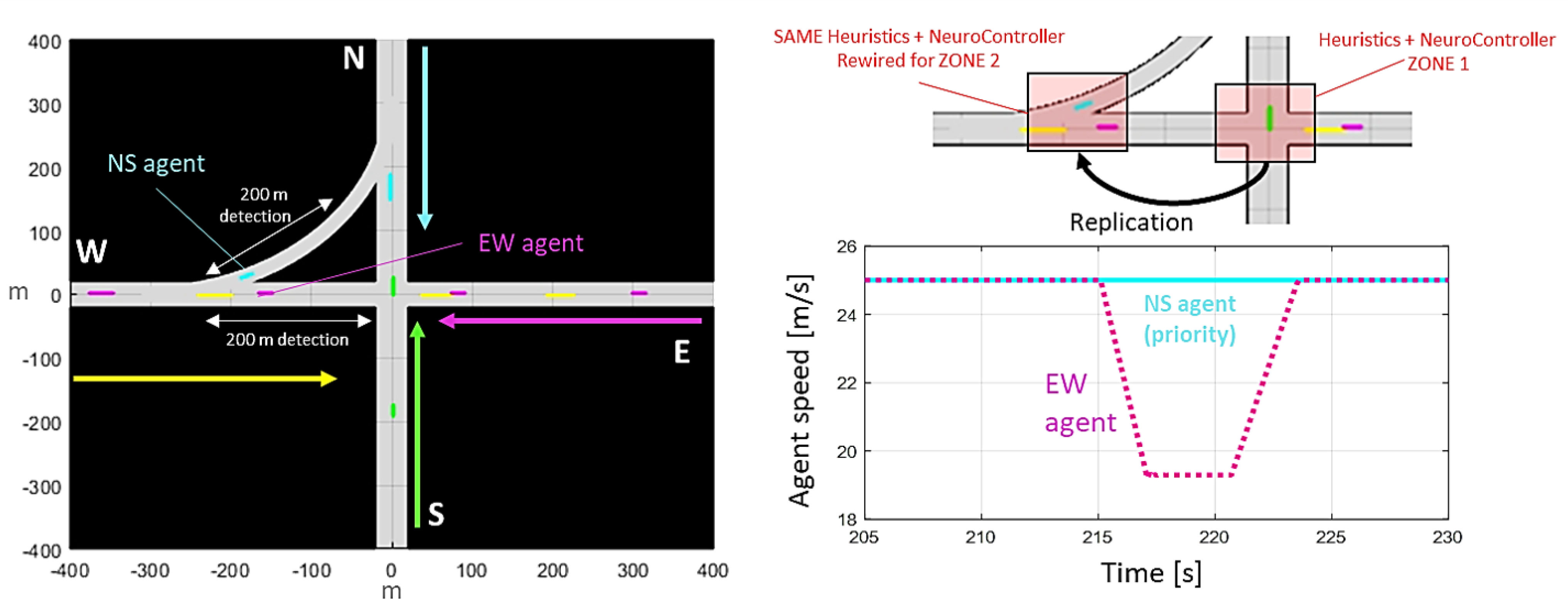
- The first agent within 200 m of the intersection gets to level 1 priority and can remain at the speed limit.
- A second agent entering the 200 m threshold on a cross-traffic road is then set to level 2 priority and is thus requested to modulate its speed to avoid conflict with the level 1 priority agent.
- The third agent entering the 200 m threshold would then be at the lowest priority level 3—requiring it to modulate its speed to avoid conflict with the first and/or second agent depending on the road and lane it is occupying.
- As agents clear the intersection and arrive, the priorities are updated, always combining up to three agents at a time. By design, any lower-priority agent cannot pass the intersection until it becomes a priority level 1 agent. The rolling combination of agents upstream of the intersection permits high traffic density to be simulated.
- Current agent speed ;
- Current agent length ;
- Priority 1 agent speed ;
- Priority 1 distance from the intersection ;
- Priority 1 agent length .
3. Results
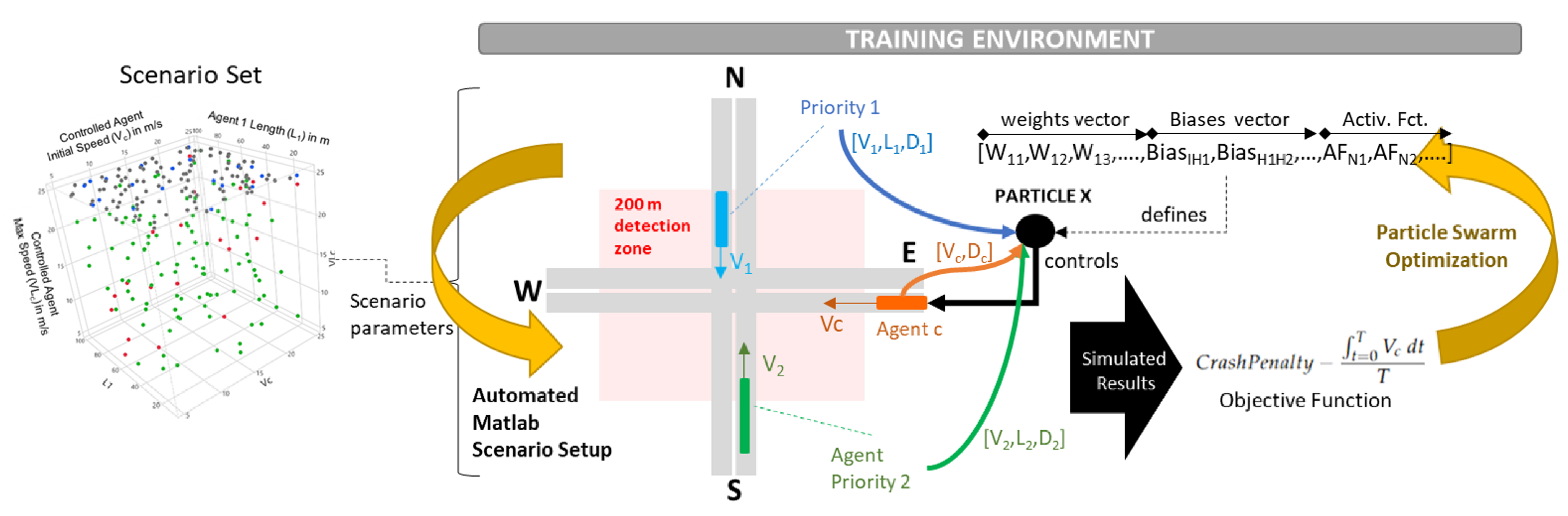
3.1. Training Results
3.2. WANN and Activation Function Optimization Discussion
- ReLu with encoding as 1;
- Linear with encoding as 2;
- Sigmoid with encoding as 3;
- Radial Basis with encoding as 4.
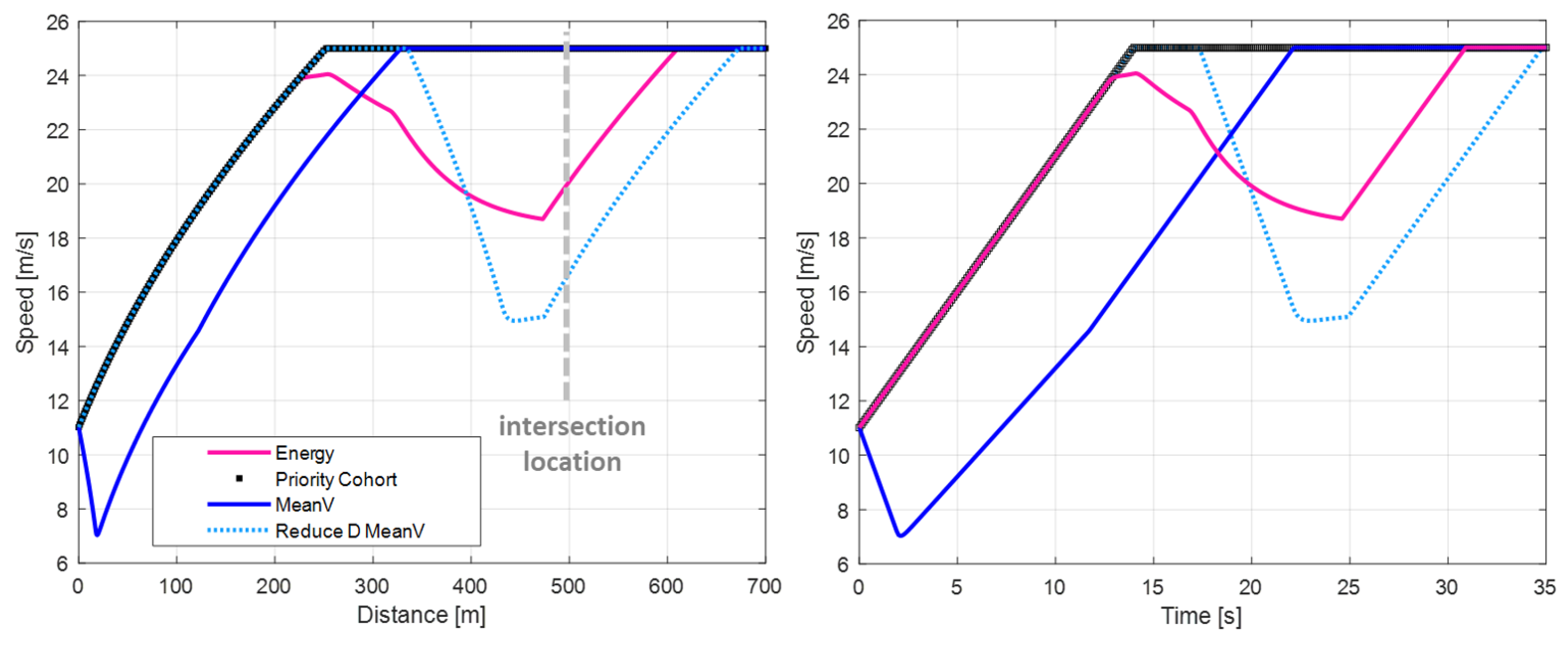
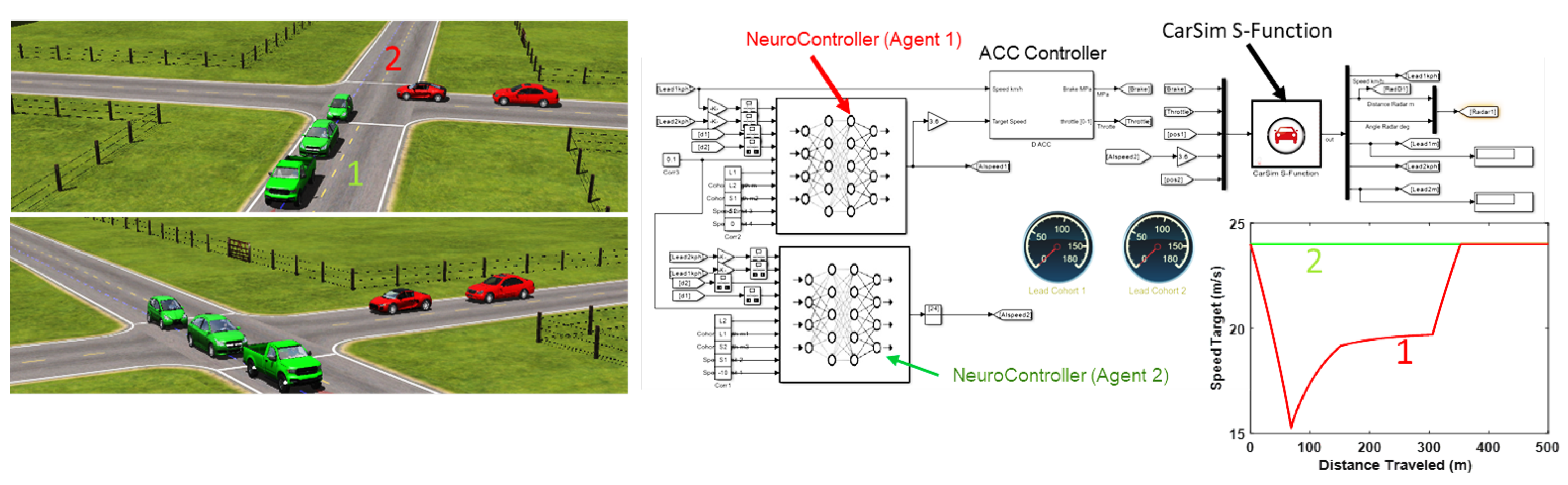
3.3. Full Vehicle Dynamic Validation
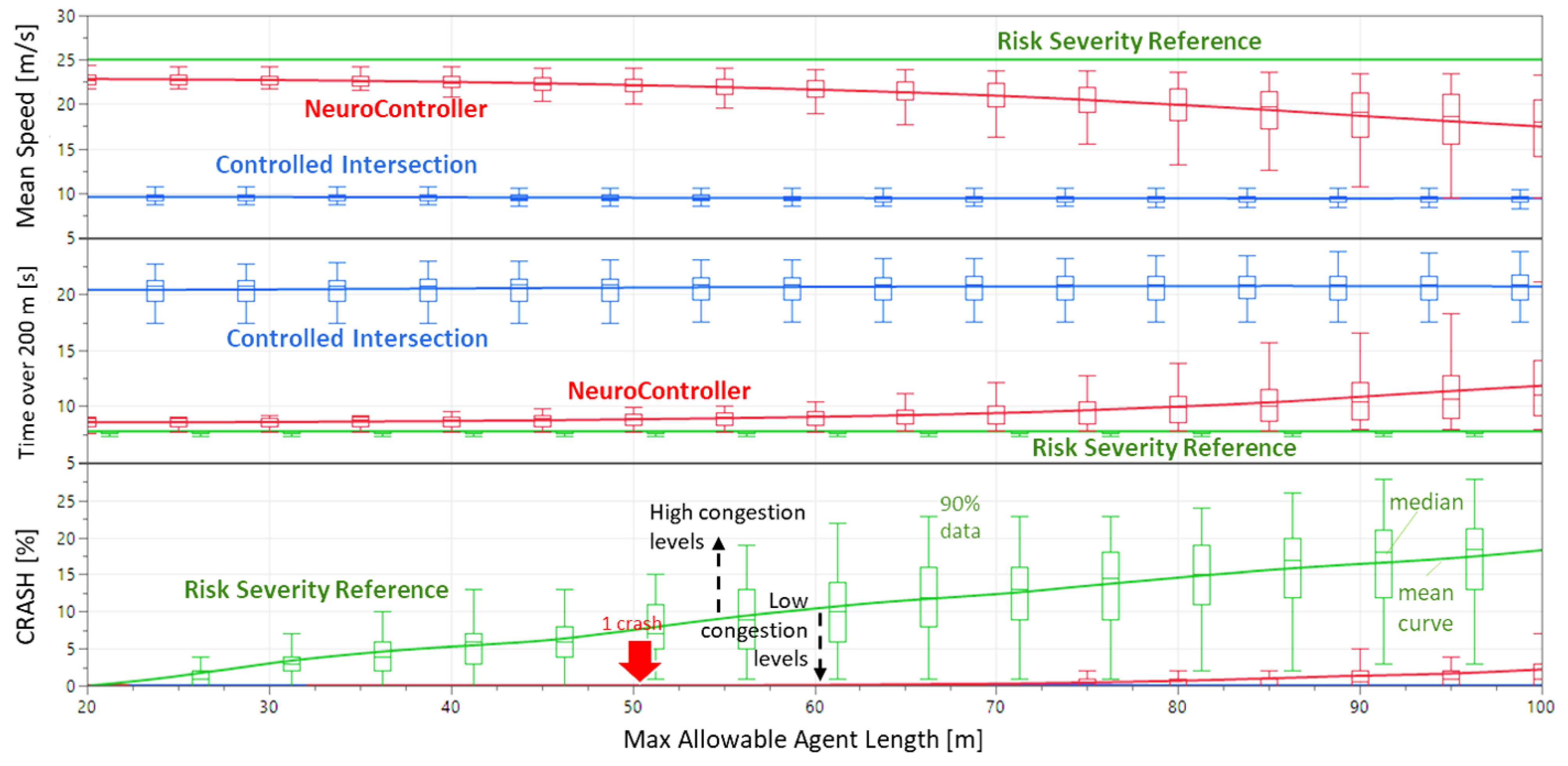
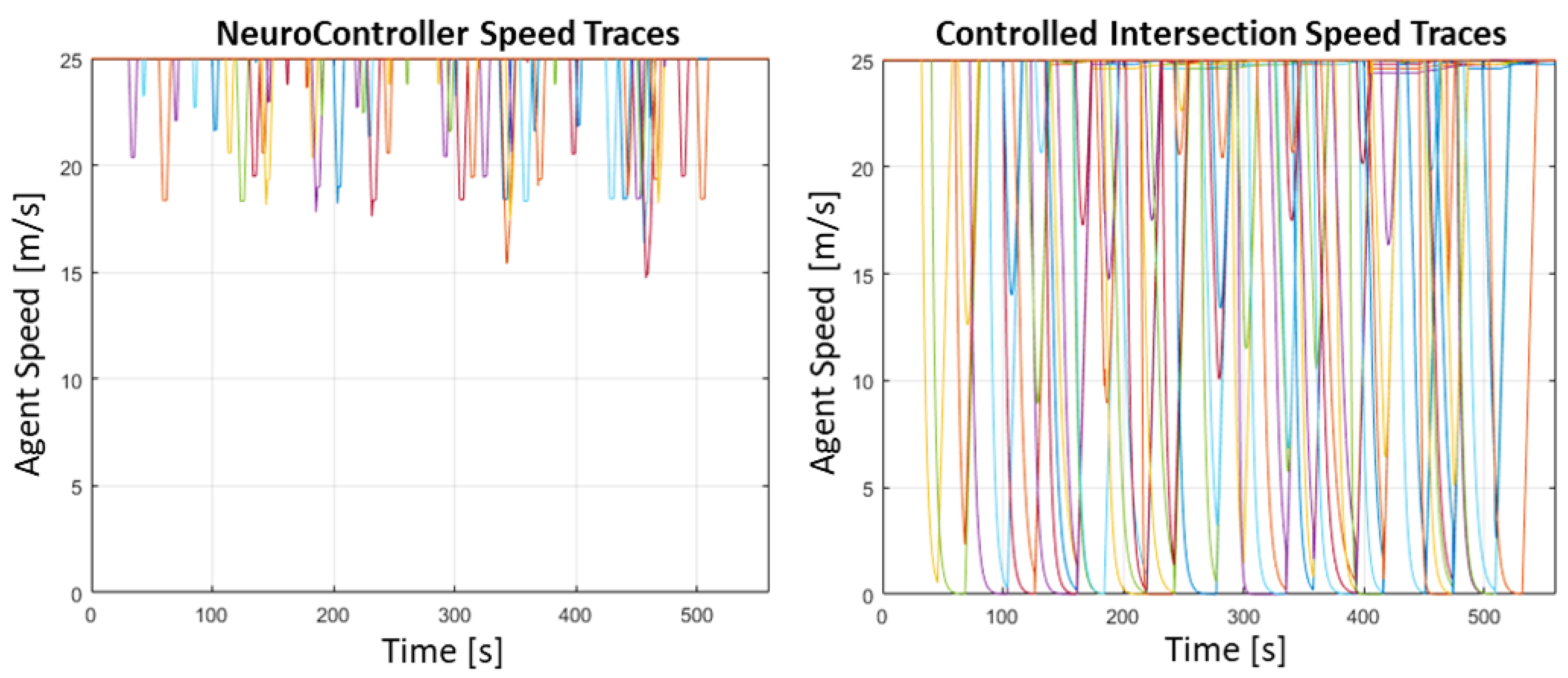
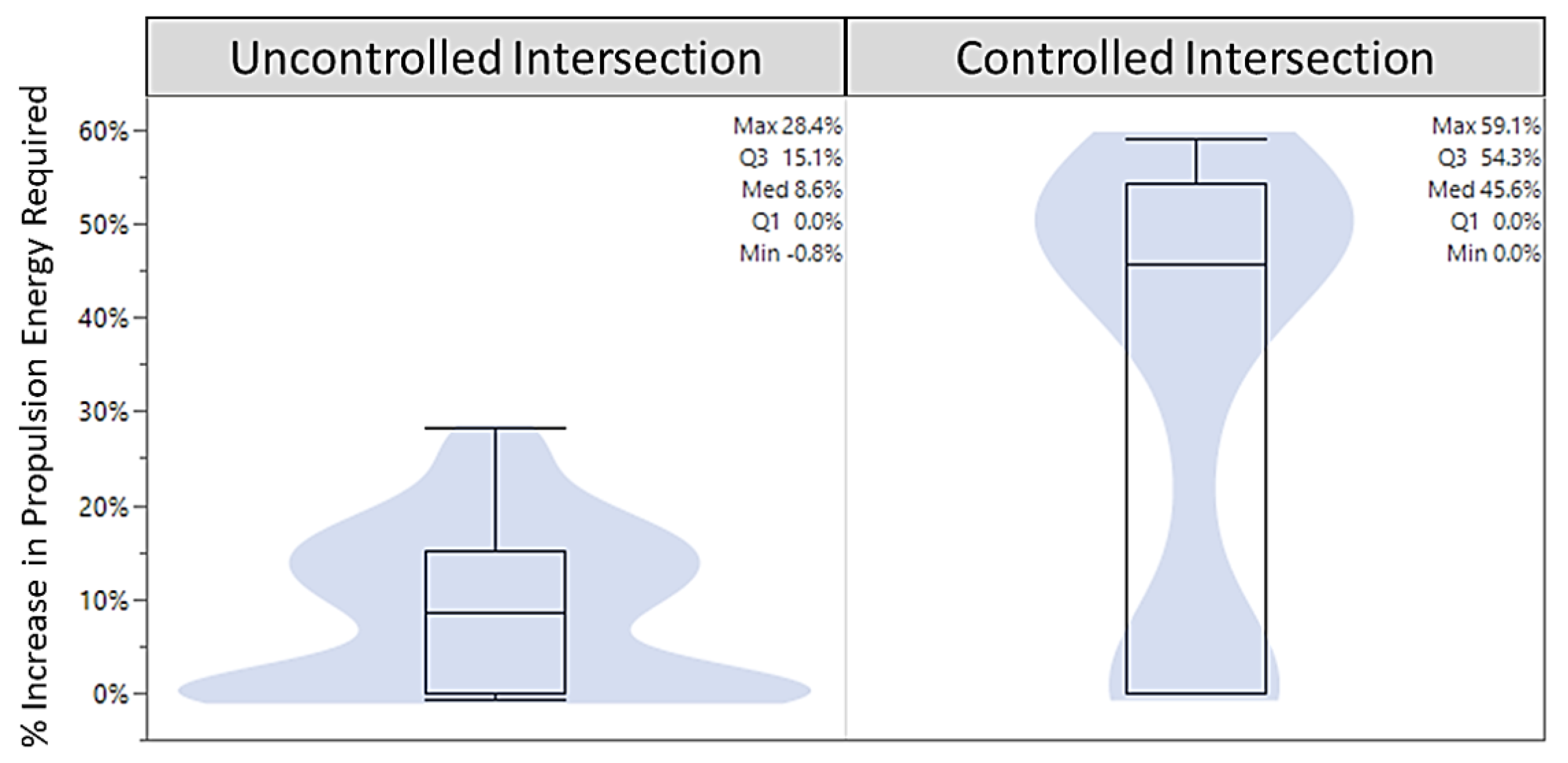
3.4. Traffic Flow Simulation and Results
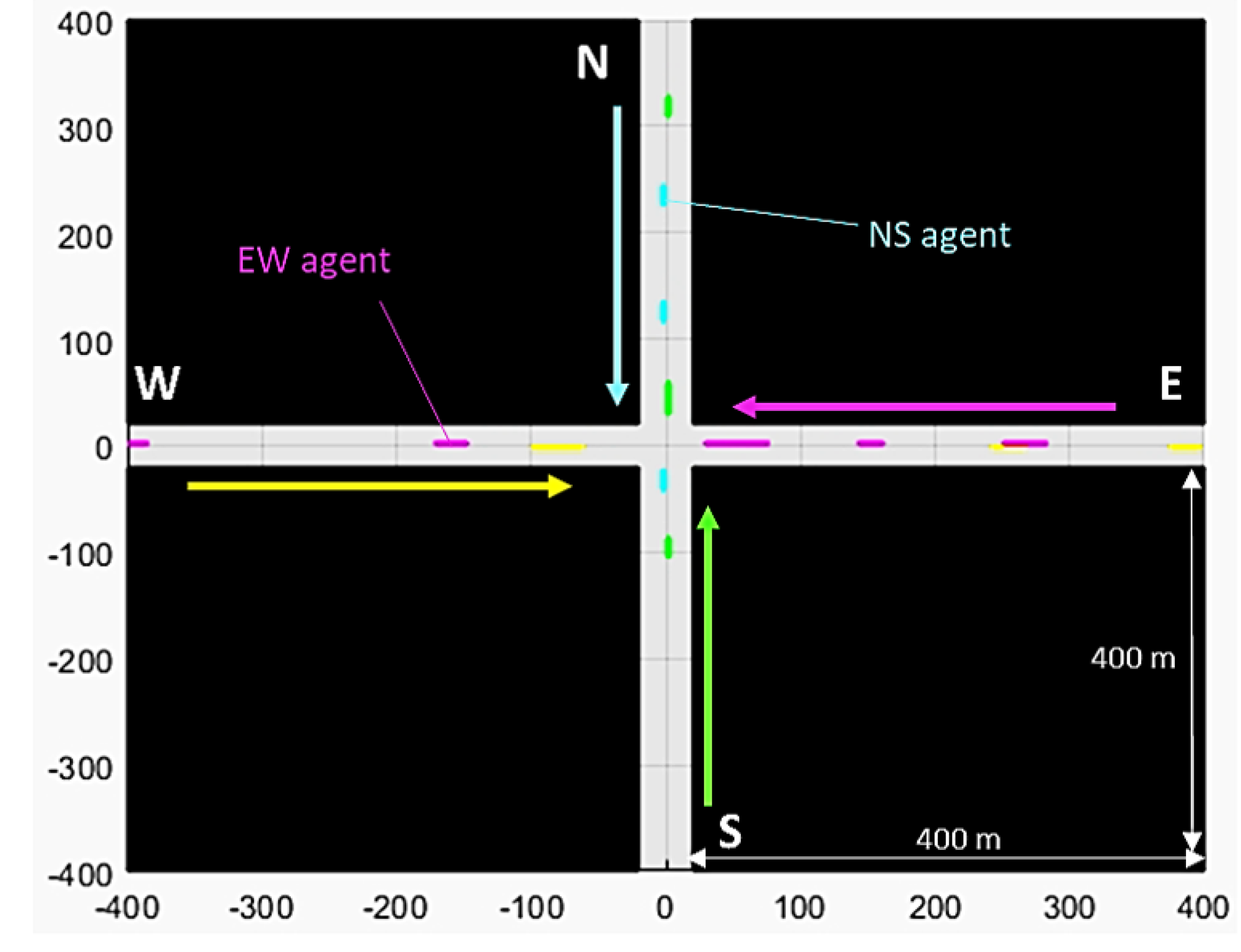
3.4.1. Simple Intersection
3.4.2. Adding Turning Lanes
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karimi, A.; Duggirala, P.S. Formalizing traffic rules for uncontrolled intersections. In Proceedings of the 2020 ACM/IEEE 11th International Conference on Cyber-Physical Systems (ICCPS), Sydney, Australia, 21–25 April 2020; pp. 41–50. [Google Scholar] [CrossRef]
- Ma, Y.; Qin, X.; Grembek, O.; Chen, Z. Developing a safety heatmap of uncontrolled intersections using both conflict probability and severity. Accid. Anal. Prev. 2018, 113, 303–316. [Google Scholar] [CrossRef]
- Datta, S.; Rokade, S.; Rajput, S.P.S. Classification of Uncontrolled Intersections Using Hierarchical Clustering. Arab. J. Sci. Eng. 2020, 45, 8591–8606. [Google Scholar] [CrossRef]
- Safarov, K.; Kent, T.; Wilson, E.; Richards, A. Emergent Crossing Regimes of Identical Autonomous Vehicles at an Uncontrolled Intersection. arXiv 2021, arXiv:2104.04150. [Google Scholar] [CrossRef]
- Treiber, M.; Kesting, A. Traffic flow dynamics. In Traffic Flow Dynamics: Data, Models and Simulation; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Kreutz, K.; Eggert, J. Analysis of the Generalized Intelligent Driver Model (GIDM) for Uncontrolled Intersections. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Online, 16–17 June 2021; The Institute of Electrical and Electronics Engineers, Inc. (IEEE): Piscataway, NJ, USA, 2021; Volume 2021, pp. 3223–3230. [Google Scholar] [CrossRef]
- Song, W.; Xiong, G.; Chen, H. Intention-Aware Autonomous Driving Decision-Making in an Uncontrolled Intersection. Math. Probl. Eng. 2016, 2016, 1–15. [Google Scholar] [CrossRef]
- Li, N.; Yao, Y.; Kolmanovsky, I.; Atkins, E.; Girard, A.R. Game-Theoretic Modeling of Multi-Vehicle Interactions at Uncontrolled Intersections. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1428–1442. [Google Scholar] [CrossRef]
- Nan, J.; Deng, W.; Zheng, B. Intention Prediction and Mixed Strategy Nash Equilibrium-Based Decision-Making Framework for Autonomous Driving in Uncontrolled Intersection. IEEE Trans. Veh. Technol. 2022, 71, 10316–10326. [Google Scholar] [CrossRef]
- Jeong, Y. Stochastic model-predictive control with uncertainty estimation for autonomous driving at uncontrolled intersections. Appl. Sci. 2021, 11, 9397. [Google Scholar] [CrossRef]
- Jeong, Y.; Yi, K. Target Vehicle Motion Prediction-Based Motion Planning Framework for Autonomous Driving in Uncontrolled Intersections. IEEE Trans. Intell. Transp. Syst. 2021, 22, 168–177. [Google Scholar] [CrossRef]
- Park, S.; Jeong, Y. Proactive Motion Planning for Uncontrolled Blind Intersections to Improve the Safety and Traffic Efficiency of Autonomous Vehicles. Appl. Sci. 2022, 12, 11570. [Google Scholar] [CrossRef]
- Jeong, Y.; Yi, K.; Park, S. SVM based intention inference and motion planning at uncontrolled intersection. IFAC PapersOnLine 2019, 52, 356–361. [Google Scholar] [CrossRef]
- Yao, Z.; Jiang, H.; Jiang, Y.; Ran, B. A Two-Stage Optimization Method for Schedule and Trajectory of CAVs at an Isolated Autonomous Intersection. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3263–3281. [Google Scholar] [CrossRef]
- Jiang, H.; Yao, Z.; Jiang, Y.; He, Z. Is All-Direction Turn Lane a Good Choice for Autonomous Intersections? A Study of Method Development and Comparisons. IEEE Trans. Veh. Technol. 2023, 1–16. [Google Scholar] [CrossRef]
- Jacquelin, F.; Bae, J.; Chen, B.; Robinette, D.; Santhosh, P.; Orlando, J.; Knopp, D. Connected and Autonomous Vehicle Cohort Speed Control Optimization via Neuroevolution. IEEE Access 2022, 10, 97794–97801. [Google Scholar] [CrossRef]
- Jacquelin, F.; Bae, J.; Chen, B.; Robinette, D.; Santhosh, P.; Kraemer, T.; Henderson, B. Real Time Predictive and Adaptive Hybrid Powertrain Control Development via Neuroevolution. Vehicles 2022, 4, 942–956. [Google Scholar] [CrossRef]
- Lehman, J.; Miikkulainen, R. Neuroevolution. Scholarpedia 2013, 8, 30977. [Google Scholar] [CrossRef]
- Künzel, S.; Meyer-Nieberg, S. Evolving Artificial Neural Networks for Multi-objective Tasks. In Applications of Evolutionary Computation: 21st International Conference, EvoApplications 2018, Parma, Italy, 4–6 April 2018; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 671–686. [Google Scholar] [CrossRef]
- Silva, F.; Correia, L.; Christensen, A. Dynamics of Neuronal Models in Online Neuroevolution of Robotic Controllers. In Proceedings of the Portuguese Conference on Artificial Intelligence, Azores, Portugal, 9–12 September 2013; pp. 90–101. [Google Scholar] [CrossRef]
- Stanley, K.; Bryant, B.; Miikkulainen, R. Real-time neuroevolution in the NERO video game. IEEE Trans. Evol. Comput. 2005, 9, 653–668. [Google Scholar] [CrossRef]
- Hausknecht, M.; Lehman, J.; Miikkulainen, R.; Stone, P. A Neuroevolution Approach to General Atari Game Playing. IEEE Trans. Comput. Intell. Games 2014, 6, 355–366. [Google Scholar] [CrossRef]
- Kim, H.K.; Becerra, R.; Bolufé, S.; Azurdia-Meza, C.A.; Montejo-Sánchez, S.; Zabala-Blanco, D. Neuroevolution-based adaptive antenna array beamforming scheme to improve the v2v communication performance at intersections. Sensors 2021, 21, 2956. [Google Scholar] [CrossRef]
- Kim, E.J.; Perez, R.E. Neuroevolutionary Control for Autonomous Soaring. Aerospace 2021, 8, 267. [Google Scholar] [CrossRef]
- Galassi, M.; Capodieci, N.; Cabri, G.; Leonardi, L. Evolutionary strategies for novelty-based online neuroevolution in swarm robotics. In Proceedings of the 2016 IEEE International Conference on Systems, Man and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; pp. 002026–002032. [Google Scholar] [CrossRef]
- Gadikar, P.U.; Ganesan, V.; Panda, P.K. Generalized Weight Agnostic Neural Networks for Configurable and Continual Autonomous Systems. In Proceedings of the ACM International Conference Proceeding Series, Online, 12–14 November 2021. [Google Scholar] [CrossRef]
- Berry, I.M. The Effects of Driving Style and Vehicle Performance on the Real-World Fuel Consumption of US Light-Duty Vehicles. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2010. [Google Scholar]
- Mersky, A.C.; Samaras, C. Fuel economy testing of autonomous vehicles. Transp. Res. Part Emerg. Technol. 2016, 65, 31–48. [Google Scholar] [CrossRef]
- Sharer, P.; Leydier, R.; Rousseau, A. Impact of drive cycle aggressiveness and speed on HEVs fuel consumption sensitivity. In Proceedings of the SAE World Congress & Exhibition. SAE International, Sacramento, CA, USA, 9–12 July 2007. [Google Scholar] [CrossRef]
- Gaier, A.; Ha, D. Weight Agnostic Neural Networks. arXiv 2019, arXiv:1906.04358. [Google Scholar] [CrossRef]
- Soni, A.; Hu, H. Formation Control for a Fleet of Autonomous Ground Vehicles: A Survey. Robotics 2018, 7, 67. [Google Scholar] [CrossRef]
- Spyropoulou, I. Simulation using Gipps’ car-following model-An in-depth analysis. Transportmetrica 2007, 3, 231–245. [Google Scholar] [CrossRef]


| Variable | Min | Max |
|---|---|---|
| Agents Initial Speed (, ) | 10 m/s | 25 m/s |
| Agents Length (, ) | 15 m | 100 m |
| Agents Distance (, ) | 50 m | 500 m |
| Variable | Min | Max |
|---|---|---|
| Agents Initial Speed (, ) | 10 m/s | 25 m/s |
| Agents Length () | 15 m | 100 m |
| Agent Distance () | 201 m | 250 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jacquelin, F.; Bae, J.; Chen, B.; Robinette, D. Neuroevolution Application to Collaborative and Heuristics-Based Connected and Autonomous Vehicle Cohort Simulation at Uncontrolled Intersection. Eng 2023, 4, 1320-1336. https://doi.org/10.3390/eng4020077
Jacquelin F, Bae J, Chen B, Robinette D. Neuroevolution Application to Collaborative and Heuristics-Based Connected and Autonomous Vehicle Cohort Simulation at Uncontrolled Intersection. Eng. 2023; 4(2):1320-1336. https://doi.org/10.3390/eng4020077
Chicago/Turabian StyleJacquelin, Frederic, Jungyun Bae, Bo Chen, and Darrell Robinette. 2023. "Neuroevolution Application to Collaborative and Heuristics-Based Connected and Autonomous Vehicle Cohort Simulation at Uncontrolled Intersection" Eng 4, no. 2: 1320-1336. https://doi.org/10.3390/eng4020077
APA StyleJacquelin, F., Bae, J., Chen, B., & Robinette, D. (2023). Neuroevolution Application to Collaborative and Heuristics-Based Connected and Autonomous Vehicle Cohort Simulation at Uncontrolled Intersection. Eng, 4(2), 1320-1336. https://doi.org/10.3390/eng4020077





