Prediction Model for Optimal Efficiency of the Green Corrosion Inhibitor Oleoylsarcosine: Optimization by Statistical Testing of the Relevant Influencing Factors
Abstract
1. Introduction
2. Materials and Methods
2.1. Metal Samples, Inhibitor, and Experimental Setup
2.2. Experimental Design and Optimization
3. Results and Discussion
3.1. Experimental Corrosion Protection Efficiencies According to the BBD Matrix
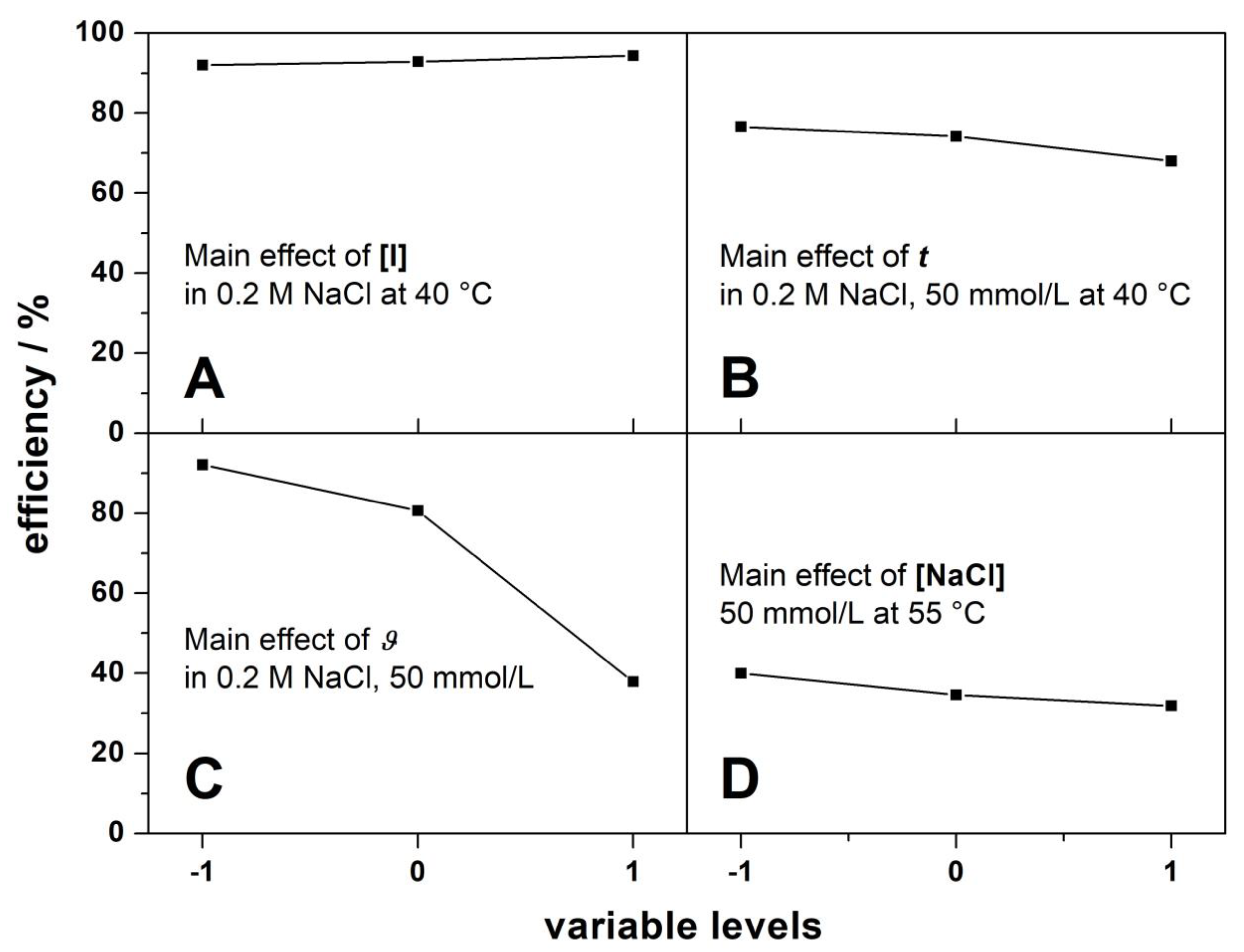
3.2. General Effects of the Variables and Their Levels
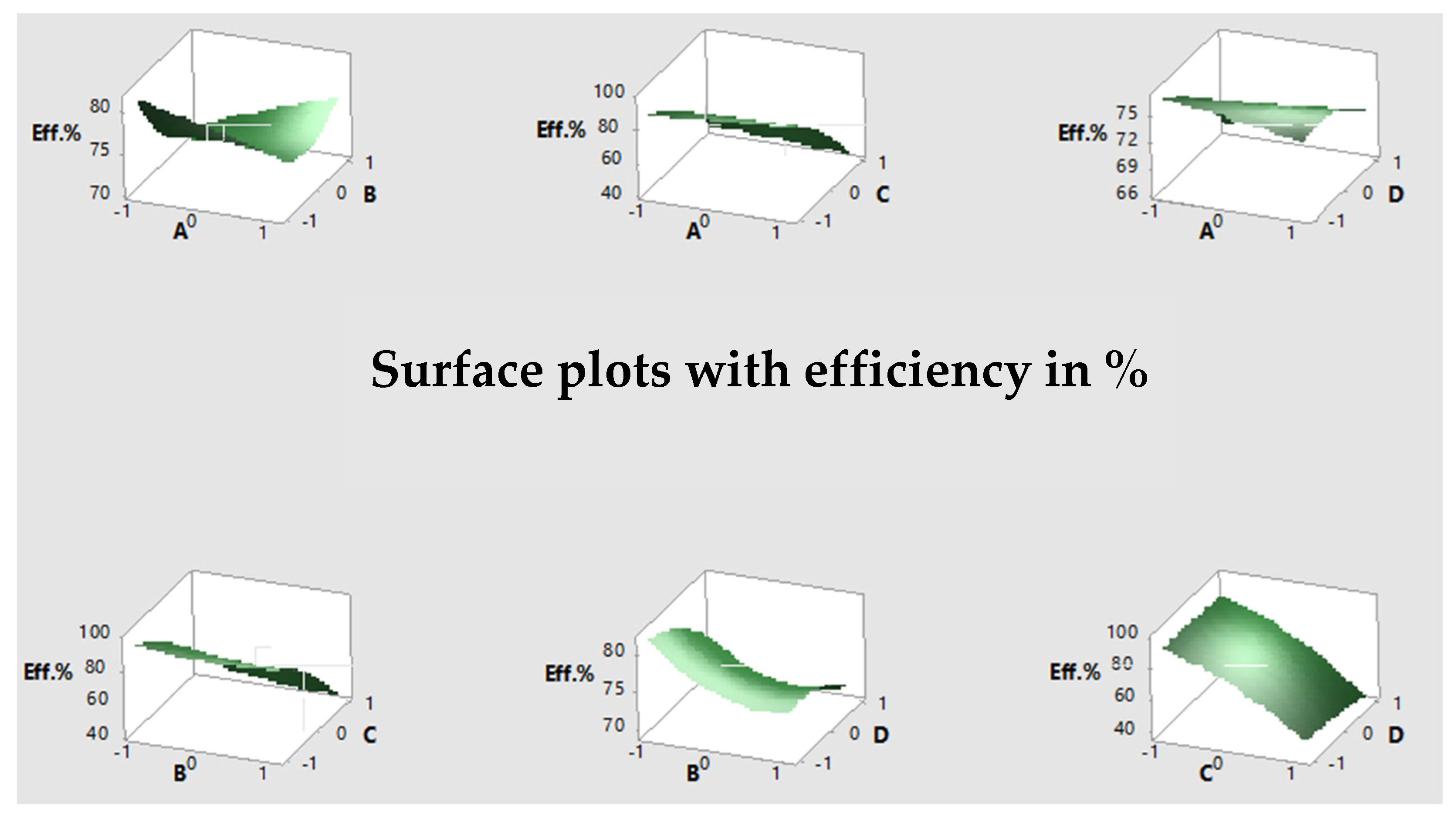
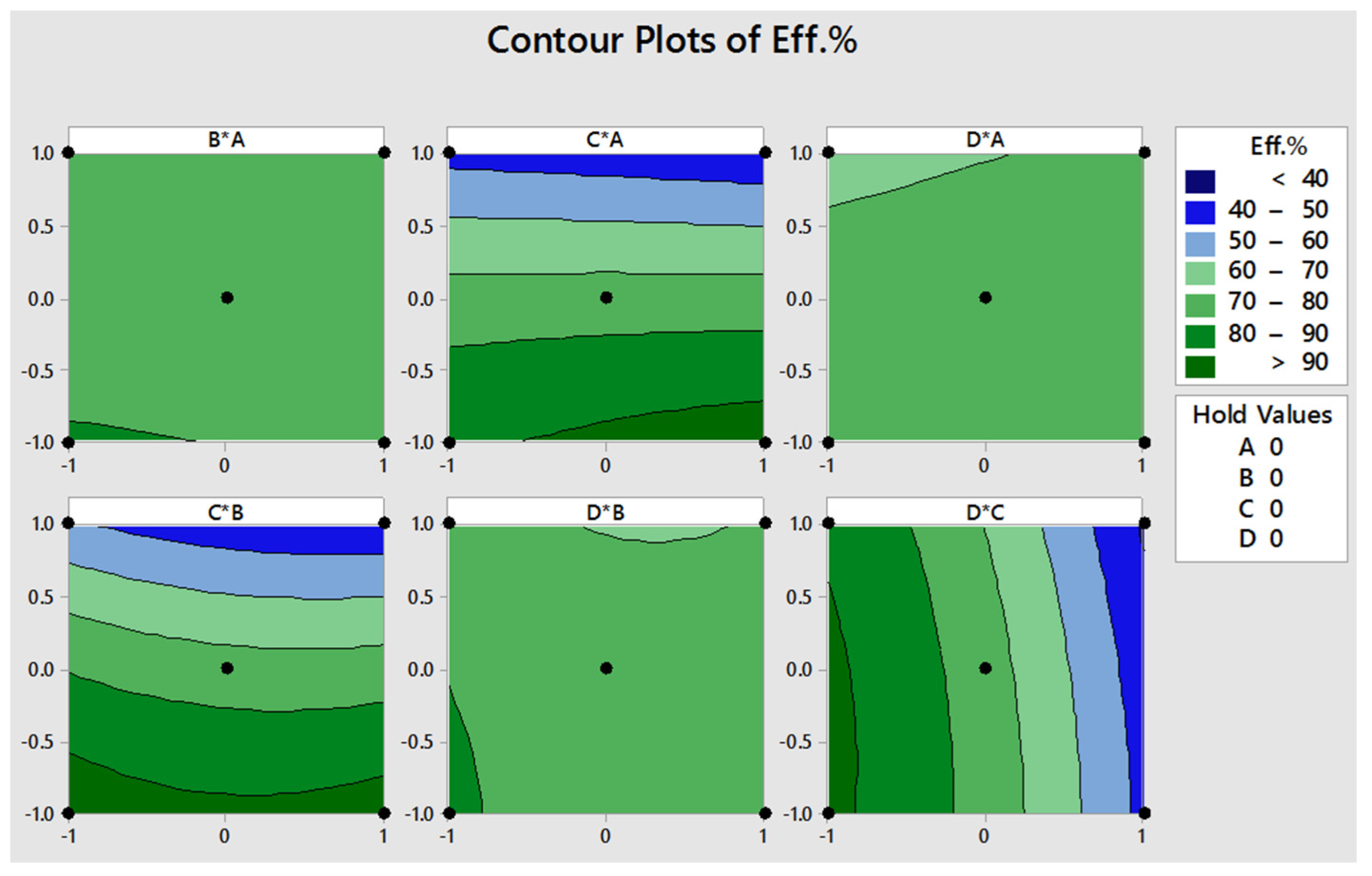
3.3. Response Plot
3.4. Normal Probability Plot
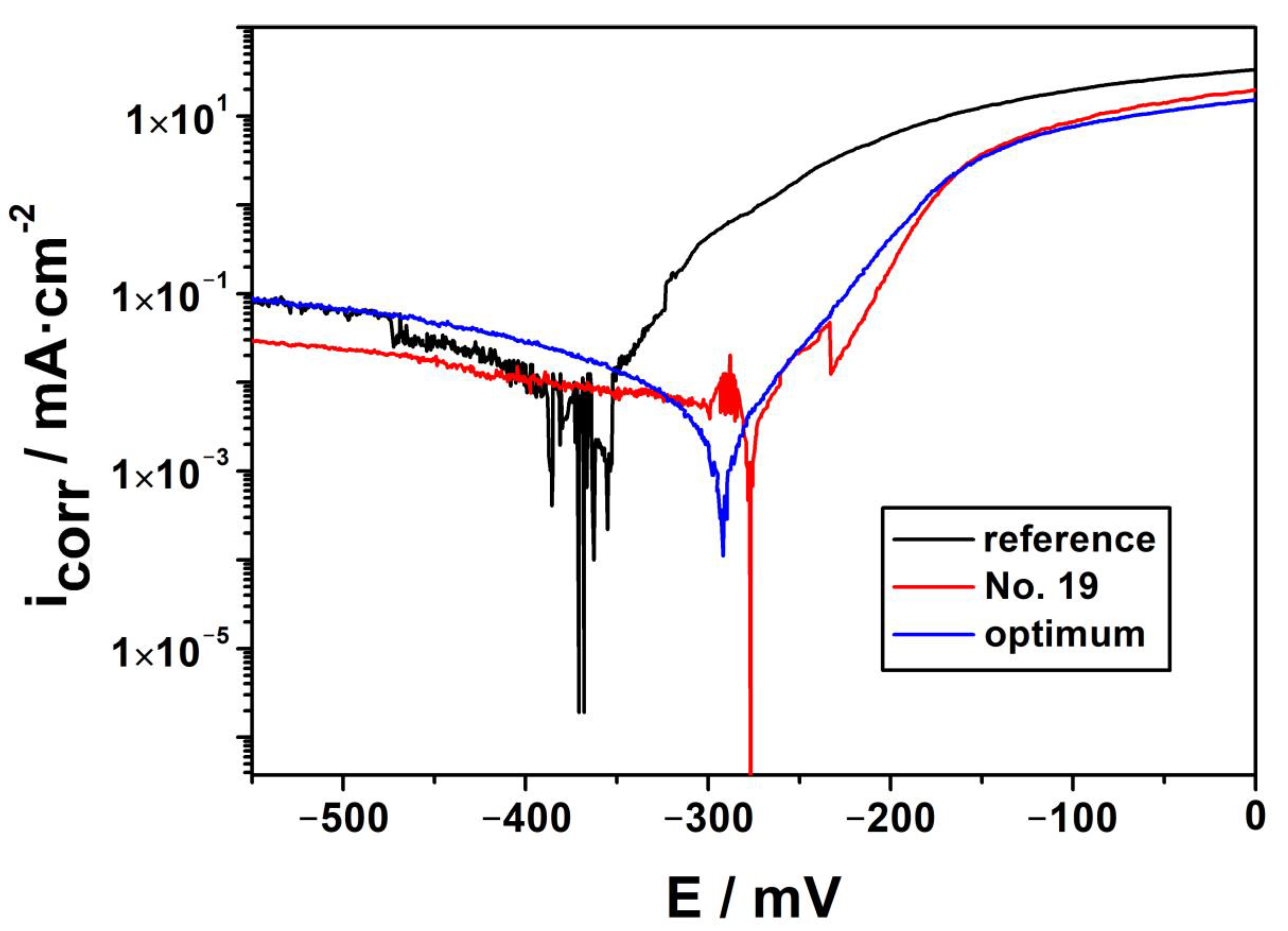
3.5. Optimization
3.5.1. Implementation of the Empirical Model
1.52 × D2 + 2.58 × AB − 2.65 × AC + 1.67 × AD − 1.86 × BC + 0.72 × BD − 1.26 × CD
3.5.2. Statistical Simulation of the RSM
3.5.3. Find the Optimal Levels for Best Prediction
6.07 × (−1)2 −1.52 × (0.1919)2 + 2.58 × (1 × 1) − 2.65 × (1 × −1) + 1.67 × (1 × 0.1919) − 1.86 ×
(1 × −1) + 0.72 × (1 × 0.1919) − 1.26 × (−1 × 0.1919) = 99.4
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kaskah, S.E.; Pfeiffer, M.; Klock, H.; Bergen, H.; Ehrenhaft, G.; Ferreira, P.; Gollnick, J.; Fischer, C.B. Surface protection of low carbon steel with N-acyl sarcosine derivatives as green corrosion inhibitors. Surf. Interfaces 2017, 9, 70–78. [Google Scholar] [CrossRef]
- Rahim, A.A.; Kassim, J. Recent development of vegetal tannins in corrosion protection of iron and steel. Recent Pat. Mater. Sci. 2008, 1, 223–231. [Google Scholar] [CrossRef]
- Zhao, L.; Teng, H.K.; Yang, Y.S.; Tan, X. Corrosion inhibition approach of oil production systems in offshore oilfields. Mater. Corros. 2004, 9, 684–688. [Google Scholar] [CrossRef]
- Moyo, F.; Tandlich, R.; Wilhelm, B.S.; Balaz, S. Sorption of hydrophobic organic compounds on natural sorbent and organoclays from aqueous and non-aqueous solutions: A mini-review. Int. J. Environ. Res. Public Health 2014, 11, 5020–5048. [Google Scholar] [CrossRef] [PubMed]
- Lanigan, S. Final Report on the Safety Assessment of Cocoyl Sarcosine, Lauroyl Sarcosine, Myristoyl Sarcosine, Oleoyl Sarcosine, Stearoyl Sarcosine, Sodium Cocoyl Sarcosinate, Sodium Lauroyl Sarcosinate, Sodium Myristoyl Sarcosinate, Ammonium Cocoyl Sarcosinate, and Ammonium Lauroyl Sarcosinate. Int. J. Toxicol. 2001, 20, 1–14. [Google Scholar] [PubMed]
- Frignani, A.; Trabanelli, G.; Wrubl, C.; Mollica, A. N-Lauroyl sarcosine sodium salt as a corrosion inhibitor for type 1518 carbon steel in neutral saline environments. NACE Int. Corros. 1996, 52, 177–182. [Google Scholar] [CrossRef]
- Salensky, G.A.; Cobb, M.G.; Everhart, D.S. Corrosion-Inhibitor Orientation on Steel. Ind. Eng. Chem. Prod. Res. Dev. 1986, 25, 133–140. [Google Scholar] [CrossRef]
- Popov, B.N. Corrosion Engineering Principles and Solved Problems; Elsevier, B.V.: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Sastri, V.S. Challenges in Corrosion: Cost, Causes, Consequences, and Control; John Wiley: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kaskah, S.E.; Ehrenhaft, G.; Gollnick, J.; Fischer, C.B. Concentration and coating time effects of N-acyl sarcosine derivatives for corrosion protection of low-carbon steel CR4 in salt water—Defining the window of application. Corros. Eng. Sci. Technol. 2019, 3, 216–224. [Google Scholar] [CrossRef]
- Kaskah, S.E.; Ehrenhaft, G.; Gollnick, J.; Fischer, C.B. N-b-Hydroxyethyl Oleyl Imidazole as Synergist to Enhance the Corrosion Protection Effect of Natural Cocoyl Sarcosine on Steel. Corros. Mater. Degrad. 2022, 3, 536–552. [Google Scholar] [CrossRef]
- Nist, N.I. Comparisons of response surface design. In NIST/SEMATECH e-Handbook of Statistical Methods; United States Department of Commerce: Washington, DC, USA, 2012. [Google Scholar] [CrossRef]
- Penteado, R.B.; Hag Ui, J.C.; Faria, J.C.; Ribeiro, M.V. Application of Taguchi Method in process improvement of turning of a Superalloy NIMONIC 80A. Int. J. Innov. Res. Eng. Manag. 2015, 2, 81–88. [Google Scholar]
- Rakić, T.; Kasagić-Vujanović, I.; Jovanović, M.; Jančić-Stojanović, B.; Ivanović, D. Comparison of Full Factorial Design, Central Composite Design, and Box-Behnken Design in Chromatographic Method Development for the Determination of Fluconazole and Its Impurities. Anal. Lett. 2014, 47, 1334–1347. [Google Scholar] [CrossRef]
- Mourabet, M.; El Rhilassi, E.; El Boujaady, H.; Bennani-Ziatni, M.; El Hamri, R.; Taitai, A. Removal of fluorid from aqueous solution by adsorption on apatitic tricalcium phosphate using box-behnken design and desirability function. Appl. Surf. Sci. 2012, 258, 4402–4410. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments; SAS Insitute Inc.: Cary, NC, USA, 2013. [Google Scholar]
- Ferreira, S.L.C.; Bruns, R.E.; Ferreira, H.S.; Matos, G.D.; David, J.M.; Brandao, G.C.; da Silva, E.G.P.; Portugal, L.A.; dos Reis, P.S.; Souza, A.S.; et al. Box-behnken design: An alternative for the optimization of analytical methods. Anal. Chim. Acta 2007, 597, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Rupi, E.; Mawonike, R. Response surface methodology for process monitoring of soft drink: A case of delta beverages in Zimbabwe. J. Math. Stat. Sci. 2015, 2015, 213–233. [Google Scholar]
- Masoumi, H.R.F.; Kassim, A.; Basri, M.; Abdullah, D.K.K. Determining optimum condition for Lipase-Catalyzed synthesis of triethanolamine (TEA)-Based esterquat cationic surfactant by a Taguchi robust design method. Molecules 2011, 16, 4672–4680. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.S.; Malyan, S.K.; Kumar, A.; Bishnol, N.R. Optimization of fenton’s oxidation by box-behnken design of response surface methodology for landfill leachate. J. Mater. Environ. Sci. 2016, 7, 4456–4466. [Google Scholar]
- Ahmadi, M.; Ghanbari, F. Optimizing COD removal from greywater by photoelectro-persulfate process using box-behnken design: Assessment of effluent quality and electrical energy consumption. Environ. Sci. Pollut. Res. 2016, 23, 19350–19361. [Google Scholar] [CrossRef]
- Magdum, V.B.; Naik, V.R. Evaluation and optimization of machining parameter for turning of EN 8 steel. Int. J. Eng. Trends Technol. 2013, 4, 1564–1568. [Google Scholar]
- Khuri, A.I. Response surface methodology and its application in agricultural and food sciences. Biom. Biostat. Int. J. 2017, 5, 1–11. [Google Scholar] [CrossRef]
- Hill, W.J.; Huntar, W.G. Response Surface Methodology: A Review; Technical report; University of Wisconsin: Madison, WI, USA, 1966. [Google Scholar]
- Olivi, L. Response Surface Methodology, Handbook for Nuclear Reactor Safety; Commission of the European Communities: Luxembourg, 1985. [Google Scholar]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology, Process and Product Optimization Using Designed Experiments, 3rd ed.; John Wiley & Sons INC.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Nakhai, B.; Neves, J.S. The challenges of six sigma in improving service quality. Int. J. Qual. Reliab. Manag. 2009, 26, 663–684. [Google Scholar] [CrossRef]
- Li, M.; Feng, C.; Zhang, Z.; Chen, R.; Xue, Q.; Gao, C.; Sugiura, N. Optimization of process parameters for electrochemical nitrate removal using Box-Behnken design. Electrochim. Acta 2010, 56, 265–270. [Google Scholar] [CrossRef]
- Box, G.E.P.; Hunter, W.G.; Hunter, J.S. Statistics for Experimenters, An Introduction to Design, Data Analysis and Model Building; John Wiley & Sons: Hoboken, NJ, USA, 1978. [Google Scholar]
- Bezerra, M.A.; Bruns, R.E.; Ferreira, S.L.C. Statistical design-principal component analysis optimization of a multiple response procedure using cloud point extraction and simultaneous determination of metals by ICP OES. Anal. Chim. Acta 2006, 580, 251–257. [Google Scholar] [CrossRef]
- Vandeginste, B.G.M.; Massart, D.L.; Buydens, L.M.C.; De Jong, S.; Lewi, P.J.; Smeyers-Verbeke, J. Handbook of Chemometrics and Qualimetrics, Part B. In Data Handling in Science and Technology–Volume 20; Vandeginste, B.G.M., Rutan, S.C., Eds.; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Dwivedi, S.P.; Kumar, S.; Kumar, A. Effects of turning parameters on dimensional deviation of A356/5% SiC composite using Box-Behnken design and genetic algorithm. Front. Manuf. Eng. 2014, 2, 8–14. [Google Scholar]
- Qureshi, M.J.; Phin, F.F.; Patro, S. Enhanced solubility and dissolution rate of clopidogrel by nanosuspension: Formulation via high pressure homogenization technique and optimization using Box-Behnken design response surface methodology. J. Appl. Pharm. Sci. 2017, 7, 106–113. [Google Scholar]
- Wegst, C.; Wegst, M. Stahlschlüssel, 22nd ed.; Verlag Stahlschlüssel Wegst GmbH: Marbach am Neckar, Germany, 2010. [Google Scholar]
- DIN EN ISO 9227:2006; Corrosion Tests in Artificial Atmospheres—Salt Spray Tests. European Committee for Standardization: Brussels, Belgium, 2006.
- DIN EN ISO 1514:2005-02; Paints and Varnishes—Standard Panels for Testing. European Committee for Standardization: Brussels, Belgium, 2004.
- Mondal, N.K.; Samanta, A.; Dutta, S.; Chattoraj, S. Optimization of Cr(VI) biosorption onto aspergillus niger using 3-level Box-Behnken design: Equilibrium, kinetic, thermodynamic and regeneration studies. J. Genet. Eng. Biotechnol. 2017, 15, 151–160. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Ma, D.; Li, Y.; Liu, Y.; Wang, Y. Optimization the process of microencapsulation of Bifidobacterium bifidum BB01 by Box-Behnken design. Acta Univ. Cibiniensis Ser. E Food Technol. 2016, 20, 17–28. [Google Scholar] [CrossRef]




| No. | Variable Code | Selected Variable | Coded Level | ||
|---|---|---|---|---|---|
| −1 | 0 | +1 | |||
| 1 | A | Inhibitor concentration [I] (mmol/L) | 25 | 50 | 75 |
| 2 | B | Immersion time t (min) | 1 | 10 | 30 |
| 3 | C | Temperature ϑ (°C) | 25 | 40 | 55 |
| 4 | D | NaCl content [NaCl] (mol/L) | 0.05 | 0.1 | 0.2 |
| Coded Value | ||||
|---|---|---|---|---|
| No. | A | B | C | D |
| 1 | −1 | −1 | 0 | 0 |
| 2 | −1 | +1 | 0 | 0 |
| 3 | +1 | −1 | 0 | 0 |
| 4 | +1 | +1 | 0 | 0 |
| 5 | 0 | 0 | −1 | −1 |
| 6 | 0 | 0 | −1 | +1 |
| 7 | 0 | 0 | +1 | −1 |
| 8 | 0 | 0 | +1 | +1 |
| 9 | −1 | 0 | 0 | −1 |
| 10 | −1 | 0 | 0 | +1 |
| 11 | +1 | 0 | 0 | −1 |
| 12 | +1 | 0 | 0 | +1 |
| 13 | 0 | −1 | −1 | 0 |
| 14 | 0 | −1 | +1 | 0 |
| 15 | 0 | +1 | −1 | 0 |
| 16 | 0 | +1 | +1 | 0 |
| 17 | −1 | 0 | −1 | 0 |
| 18 | −1 | 0 | +1 | 0 |
| 19 | +1 | 0 | −1 | 0 |
| 20 | +1 | 0 | +1 | 0 |
| 21 | 0 | −1 | 0 | −1 |
| 22 | 0 | −1 | 0 | +1 |
| 23 | 0 | +1 | 0 | −1 |
| 24 | 0 | +1 | 0 | +1 |
| 25 | 0 | 0 | 0 | 0 |
| 26 | 0 | 0 | 0 | 0 |
| 27 | 0 | 0 | 0 | 0 |
| Coded Value | Real Value | Efficiency % | |||||||
|---|---|---|---|---|---|---|---|---|---|
| No. | A | B | C | D | A | B | C | D | |
| 1 | −1 | −1 | 0 | 0 | 25 | 1 | 40 | 0.1 | 85.20 ± 4.1 |
| 2 | −1 | +1 | 0 | 0 | 25 | 30 | 40 | 0.1 | 77.99 ± 8.9 |
| 3 | +1 | −1 | 0 | 0 | 75 | 1 | 40 | 0.1 | 66.77 ± 2.1 |
| 4 | +1 | +1 | 0 | 0 | 75 | 30 | 40 | 0.1 | 69.87 ± 3.6 |
| 5 | 0 | 0 | −1 | −1 | 50 | 10 | 25 | 0.05 | 89.11 ± 0.6 |
| 6 | 0 | 0 | −1 | +1 | 50 | 10 | 25 | 0.2 | 92.06 ± 0.8 |
| 7 | 0 | 0 | +1 | −1 | 50 | 10 | 55 | 0.05 | 39.94 ± 0.2 |
| 8 | 0 | 0 | +1 | +1 | 50 | 10 | 55 | 0.2 | 37.86 ± 2.5 |
| 9 | −1 | 0 | 0 | −1 | 25 | 10 | 40 | 0.05 | 70.05 ± 8.0 |
| 10 | −1 | 0 | 0 | +1 | 25 | 10 | 40 | 0.2 | 52.40 ± 6.1 |
| 11 | +1 | 0 | 0 | −1 | 75 | 10 | 40 | 0.05 | 85.57 ± 1.0 |
| 12 | +1 | 0 | 0 | +1 | 75 | 10 | 40 | 0.2 | 74.59 ± 4.8 |
| 13 | 0 | −1 | −1 | 0 | 50 | 1 | 25 | 0.1 | 92.86 ± 0.1 |
| 14 | 0 | −1 | +1 | 0 | 50 | 1 | 55 | 0.1 | 50.15 ± 8.3 |
| 15 | 0 | +1 | −1 | 0 | 50 | 30 | 25 | 0.1 | 91.96 ± 1.0 |
| 16 | 0 | +1 | +1 | 0 | 50 | 30 | 55 | 0.1 | 41.80 ± 9.7 |
| 17 | −1 | 0 | −1 | 0 | 25 | 10 | 25 | 0.1 | 91.98 ± 1.6 |
| 18 | −1 | 0 | +1 | 0 | 25 | 10 | 55 | 0.1 | 54.26 ± 7.9 |
| 19 | +1 | 0 | −1 | 0 | 75 | 10 | 25 | 0.1 | 94.35 ± 0.5 |
| 20 | +1 | 0 | +1 | 0 | 75 | 10 | 55 | 0.1 | 46.03 ± 4.1 |
| 21 | 0 | −1 | 0 | −1 | 50 | 1 | 40 | 0.05 | 86.46 ± 2.3 |
| 22 | 0 | −1 | 0 | +1 | 50 | 1 | 40 | 0.2 | 80.63 ± 0.2 |
| 23 | 0 | +1 | 0 | −1 | 50 | 30 | 40 | 0.05 | 76.51 ± 3.9 |
| 24 | 0 | +1 | 0 | +1 | 50 | 30 | 40 | 0.2 | 73.55 ± 4.6 |
| 25 | 0 | 0 | 0 | 0 | 50 | 10 | 40 | 0.1 | 74.23 ± 0.5 |
| 26 | 0 | 0 | 0 | 0 | 50 | 10 | 40 | 0.1 | 74.23 ± 0.5 |
| 27 | 0 | 0 | 0 | 0 | 50 | 10 | 40 | 0.1 | 74.23 ± 0.5 |
| Variable/ Interaction | Estimated Effect Ef | Rank I | Probability (Pi) = 100(I − 0.5)/10 |
|---|---|---|---|
| C | 47.046 | 1 | 5 |
| CD | 9.805 | 2 | 15 |
| BD | 9.244 | 3 | 25 |
| B | 6.952 | 4 | 35 |
| D | 6.091 | 5 | 45 |
| AB | 6.021 | 6 | 55 |
| AC | 5.300 | 7 | 65 |
| BC | 5.186 | 8 | 75 |
| AD | 3.335 | 9 | 85 |
| A | 1.158 | 10 | 95 |
| Mean | 10.014 | - | - |
| No. | Coefficient | Coefficient Obtained | Symbol |
|---|---|---|---|
| 1 | Constant | 74.23 | ß0 |
| 2 | A | 0.44 | ß1 |
| 3 | B | −2.53 | ß2 |
| 4 | C | −23.52 | ß3 |
| 5 | D | −3.05 | ß4 |
| 6 | AA | −0.23 | ß11 |
| 7 | BB | 2.86 | ß22 |
| 8 | CC | −6.07 | ß33 |
| 9 | DD | −1.52 | ß44 |
| 10 | AB | 2.58 | ß12 |
| 11 | AC | −2.65 | ß13 |
| 12 | AD | 1.67 | ß14 |
| 13 | BC | −1.86 | ß23 |
| 14 | BD | 0.72 | ß24 |
| 15 | CD | −1.26 | ß34 |
| Experiment No. | Experimental Efficiency [%] | Predicted Efficiency [%] | Error [%] |
|---|---|---|---|
| 1 | 85.20 | 81.52 | 2.59 |
| 2 | 77.99 | 71.30 | 4.72 |
| 3 | 66.77 | 77.25 | 7.41 |
| 4 | 69.87 | 77.34 | 5.28 |
| 5 | 89.11 | 91.95 | 2.00 |
| 6 | 92.06 | 88.37 | 2.60 |
| 7 | 39.94 | 47.42 | 5.28 |
| 8 | 37.86 | 38.81 | 0.67 |
| 9 | 70.05 | 76.74 | 4.73 |
| 10 | 52.40 | 67.32 | 10.55 |
| 11 | 85.57 | 74.29 | 7.97 |
| 12 | 74.59 | 71.54 | 2.15 |
| 13 | 92.86 | 95.21 | 1.66 |
| 14 | 50.15 | 51.88 | 1.23 |
| 15 | 91.96 | 93.87 | 1.35 |
| 16 | 41.80 | 43.09 | 0.91 |
| 17 | 91.98 | 88.36 | 2.55 |
| 18 | 54.26 | 46.61 | 5.40 |
| 19 | 94.35 | 94.54 | 0.13 |
| 20 | 46.03 | 42.20 | 2.70 |
| 21 | 86.46 | 81.86 | 3.25 |
| 22 | 80.63 | 74.33 | 4.45 |
| 23 | 76.51 | 75.36 | 0.81 |
| 24 | 73.55 | 70.70 | 2.01 |
| 25 | 74.23 | 74.23 | 0 |
| 26 | 74.23 | 74.23 | 0 |
| 27 | 74.23 | 74.23 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kaskah, S.E.; Ehrenhaft, G.; Gollnick, J.; Fischer, C.B. Prediction Model for Optimal Efficiency of the Green Corrosion Inhibitor Oleoylsarcosine: Optimization by Statistical Testing of the Relevant Influencing Factors. Eng 2023, 4, 635-649. https://doi.org/10.3390/eng4010038
Kaskah SE, Ehrenhaft G, Gollnick J, Fischer CB. Prediction Model for Optimal Efficiency of the Green Corrosion Inhibitor Oleoylsarcosine: Optimization by Statistical Testing of the Relevant Influencing Factors. Eng. 2023; 4(1):635-649. https://doi.org/10.3390/eng4010038
Chicago/Turabian StyleKaskah, Saad E., Gitta Ehrenhaft, Jörg Gollnick, and Christian B. Fischer. 2023. "Prediction Model for Optimal Efficiency of the Green Corrosion Inhibitor Oleoylsarcosine: Optimization by Statistical Testing of the Relevant Influencing Factors" Eng 4, no. 1: 635-649. https://doi.org/10.3390/eng4010038
APA StyleKaskah, S. E., Ehrenhaft, G., Gollnick, J., & Fischer, C. B. (2023). Prediction Model for Optimal Efficiency of the Green Corrosion Inhibitor Oleoylsarcosine: Optimization by Statistical Testing of the Relevant Influencing Factors. Eng, 4(1), 635-649. https://doi.org/10.3390/eng4010038







