Covering Arrays ML HPO for Static Malware Detection
Abstract
1. Introduction
1.1. Malware and Its Detection
1.2. Ml-Based Static Malware Detection Related Literature
1.3. Grid Search and the Curse of Dimensionality
| A | B | C |
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| A | B | C | .. | X | Y | Z |
| 0 | 0 | 0 | .. | 0 | 0 | 0 |
| 1 | 1 | 1 | .. | 1 | 1 | 1 |
| A | B | C |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
1.4. Generating Covering Arrays
1.5. The Cagen Toolset
1.6. Array Indexing
1.7. Structure of the Paper
2. Methodology
2.1. Overall Approach
2.2. Experimental Details
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Pandey, A.K.; Tripathi, A.K.; Kapil, G.; Singh, V.; Khan, M.W.; Agrawal, A.; Kumar, R.; Khan, R.A. Trends in Malware Attacks: Identification and Mitigation Strategies. In Critical Concepts, Standards, and Techniques in Cyber Forensics; IGI Global: Hershey, PA, USA, 2020; pp. 47–60. [Google Scholar]
- Schultz, M.G.; Eskin, E.; Zadok, F.; Stolfo, S.J. Data mining methods for detection of new malicious executables. In Proceedings of the Proceedings 2001 IEEE Symposium on Security and Privacy. S&P 2001, Oakland, CA, USA, 14–16 May 2000; pp. 38–49. [Google Scholar]
- Kolter, J.Z.; Maloof, M.A. Learning to detect and classify malicious executables in the wild. J. Mach. Learn. Res. 2006, 7, 470–478. [Google Scholar]
- Raff, E.; Barker, J.; Sylvester, J.; Brandon, R.; Catanzaro, B.; Nicholas, C.K. Malware detection by eating a whole exe. In Proceedings of the Workshops at the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Anderson, H.S.; Roth, P. elastic/ember. Available online: https://github.com/elastic/ember/blob/master/README.md (accessed on 8 December 2022).
- Pham, H.D.; Le, T.D.; Vu, T.N. Static PE malware detection using gradient boosting decision trees algorithm. In Proceedings of the International Conference on Future Data and Security Engineering; Springer: Berlin/Heidelberg, Germany, 2018; pp. 228–236. [Google Scholar]
- Fawcett, C.; Hoos, H.H. Analysing differences between algorithm configurations through ablation. J. Heuristics 2016, 22, 431–458. [Google Scholar] [CrossRef]
- Malik, K.; Kumar, M.; Sony, M.K.; Mukhraiya, R.; Girdhar, P.; Sharma, B. Static Malware Detection and Analysis Using Machine Learning Methods. 2022. Available online: https://www.mililink.com/upload/article/793128668aams_vol_217_may_2022_a47_p4183-4196_kartik_malik_et_al..pdf (accessed on 8 December 2022).
- Azeez, N.A.; Odufuwa, O.E.; Misra, S.; Oluranti, J.; Damaševičius, R. Windows PE Malware Detection Using Ensemble Learning. Informatics 2021, 8, 10. [Google Scholar] [CrossRef]
- Forbes, M.; Lawrence, J.; Lei, Y.; Kacker, R.N.; Kuhn, D.R. Refining the in-parameter-order strategy for constructing covering arrays. J. Res. Natl. Inst. Stand. Technol. 2008, 113, 287. [Google Scholar] [CrossRef] [PubMed]
- Lei, Y.; Kacker, R.; Kuhn, D.R.; Okun, V.; Lawrence, J. IPOG: A general strategy for t-way software testing. In Proceedings of the 14th Annual IEEE International Conference and Workshops on the Engineering of Computer-Based Systems (ECBS’07), Tucson, AZ, USA, 26–29 March 2007; pp. 549–556. [Google Scholar]
- Seroussi, G.; Bshouty, N.H. Vector sets for exhaustive testing of logic circuits. IEEE Trans. Inf. Theory 1988, 34, 513–522. [Google Scholar] [CrossRef]
- Kitsos, P.; Simos, D.E.; Torres-Jimenez, J.; Voyiatzis, A.G. Exciting FPGA cryptographic Trojans using combinatorial testing. In Proceedings of the 2015 IEEE 26th International Symposium on Software Reliability Engineering (ISSRE), Washington, DC, USA, 2–5 November 2015; pp. 69–76. [Google Scholar]
- Kleine, K.; Simos, D.E. Coveringcerts: Combinatorial methods for X. 509 certificate testing. In Proceedings of the 2017 IEEE International Conference on Software Testing, Verification and Validation (ICST), Toyko, Japan, 13–17 March 2017; pp. 69–79. [Google Scholar]
- Kleine, K.; Simos, D.E. An efficient design and implementation of the in-parameter-order algorithm. Math. Comput. Sci. 2018, 12, 51–67. [Google Scholar] [CrossRef]
- Hartman, A.; Raskin, L. Problems and algorithms for covering arrays. Discret. Math. 2004, 284, 149–156. [Google Scholar] [CrossRef]
- Colbourn, C.J.; Dinitz, J.H. Part VI: Other Combinatorial Designs. In Handbook of Combinatorial Designs; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006; pp. 349–350. [Google Scholar]
- Cohen, D.M.; Dalal, S.R.; Fredman, M.L.; Patton, G.C. The AETG system: An approach to testing based on combinatorial design. IEEE Trans. Softw. Eng. 1997, 23, 437–444. [Google Scholar] [CrossRef]
- Bryce, R.C.; Colbourn, C.J. The density algorithm for pairwise interaction testing. Softw. Test. Verif. Reliab. 2007, 17, 159–182. [Google Scholar] [CrossRef]
- Bryce, R.C.; Colbourn, C.J. A density-based greedy algorithm for higher strength covering arrays. Softw. Testing, Verif. Reliab. 2009, 19, 37–53. [Google Scholar] [CrossRef]
- Lei, Y.; Tai, K.C. In-parameter-order: A test generation strategy for pairwise testing. In Proceedings of the Proceedings Third IEEE International High-Assurance Systems Engineering Symposium (Cat. No. 98EX231), Washington, DC, USA, 13–14 November 1998; pp. 254–261. [Google Scholar]
- Yu, L.; Lei, Y.; Kacker, R.N.; Kuhn, D.R. Acts: A combinatorial test generation tool. In Proceedings of the 2013 IEEE Sixth International Conference on Software Testing, Verification and Validation, Luxembourg, 18–22 March 2013; pp. 370–375. [Google Scholar]
- Torres-Jimenez, J.; Izquierdo-Marquez, I. Survey of covering arrays. In Proceedings of the 2013 15th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, Washington, DC, USA, 23–26 September 2013; pp. 20–27. [Google Scholar]
- Lei, Y.; Kacker, R.; Kuhn, D.R.; Okun, V.; Lawrence, J. IPOG/IPOG-D: Efficient test generation for multi-way combinatorial testing. Softw. Testing, Verif. Reliab. 2008, 18, 125–148. [Google Scholar] [CrossRef]
- Duan, F.; Lei, Y.; Yu, L.; Kacker, R.N.; Kuhn, D.R. Improving IPOG’s vertical growth based on a graph coloring scheme. In Proceedings of the 2015 IEEE Eighth International Conference on Software Testing, Verification and Validation Workshops (ICSTW), Graz, Austria, 13–17 April 2015; pp. 1–8. [Google Scholar]
- Younis, M.I.; Zamli, K.Z. MIPOG-an efficient t-way minimization strategy for combinatorial testing. Int. J. Comput. Theory Eng. 2011, 3, 388. [Google Scholar] [CrossRef]
- Group, M.R. Covering Array Generation. Available online: https://matris.sba-research.org/tools/cagen/#/about (accessed on 21 July 2022).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Mauricio. Benign Malicious. Available online: https://www.kaggle.com/amauricio/pe-files-malwares (accessed on 10 November 2022).
- Carrera, E. Pefile. 2022. Available online: https://github.com/erocarrera/pefile (accessed on 15 January 2022).
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Buitinck, L.; Louppe, G.; Blondel, M.; Pedregosa, F.; Mueller, A.; Grisel, O.; Niculae, V.; Prettenhofer, P.; Gramfort, A.; Grobler, J.; et al. API design for machine learning software: Experiences from the scikit-learn project. arXiv 2013, arXiv:1309.0238. [Google Scholar]
- LightGBM documentation. Available online: https://lightgbm.readthedocs.io/en/latest (accessed on 20 August 2021).
- Sklearn. Sklearn-Accuracy-Metrics. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.metrics.accuracy_score.html (accessed on 21 July 2022).
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]



| ML Algorithms | Hyper-Parameters | Hyper-Parameter IPM Values | T-Strengths Values | IPM Values | Number of Iterations |
|---|---|---|---|---|---|
| RF | n_estimators, max_depth, criterion, min_samples_split, min_samples_leaf, max_features | [[100, 300, 50], [350, 550, 50], [600, 800, 50]] [[1, 10, 1], [11, 15, 1], [16, 20, 1],None] [’entropy’, ’gini’] [[5, 25, 5], [30, 50, 5]] [[5, 25, 5], [30, 50, 5]] [’auto’, ’sqrt’, ’log2’, ’None’] | T-2, 3, 4 | 30 | |
| LightGBM | num_leaves, boosting_type, Subsample_for_bin, Is_unbalance, max_depth | [[], []] [’GBDT’, ’GOSS’] [[], [], []] [True, False] [] | T- | 30 | |
| Xgboost | Min_child_weight gamma max_leaves reg_alpha max_depth | [1, 2, 4, 6, 8, 10, 12, 14] [[1, 4, 1], [5, 8, 1]] [2, 4, 6, 8, 10, 12] [] [] | T- | 30 | |
| DT | max_depth, criterion, min_samples_split, min_samples_leaf, max_features | [[], [11, 15, 1], [16, 20, 1], None] [’entropy’, ’gini’] [[5, 25, 5], [30, 50, 5]] [[5, 25, 5], [30, 50, 5]] [’auto’, ’sqrt’, ’log2’, ’None’] | T- | 0, 1, 2, 3 0, 1 0, 1 0, 1 0, 1, 2, 3 | 30 |
| ML Algorithms | Optimal Values | T-Values/ Grid Search | Time to Complete | No. of Evaluations | Score (min/max Accuracy and Mean) |
|---|---|---|---|---|---|
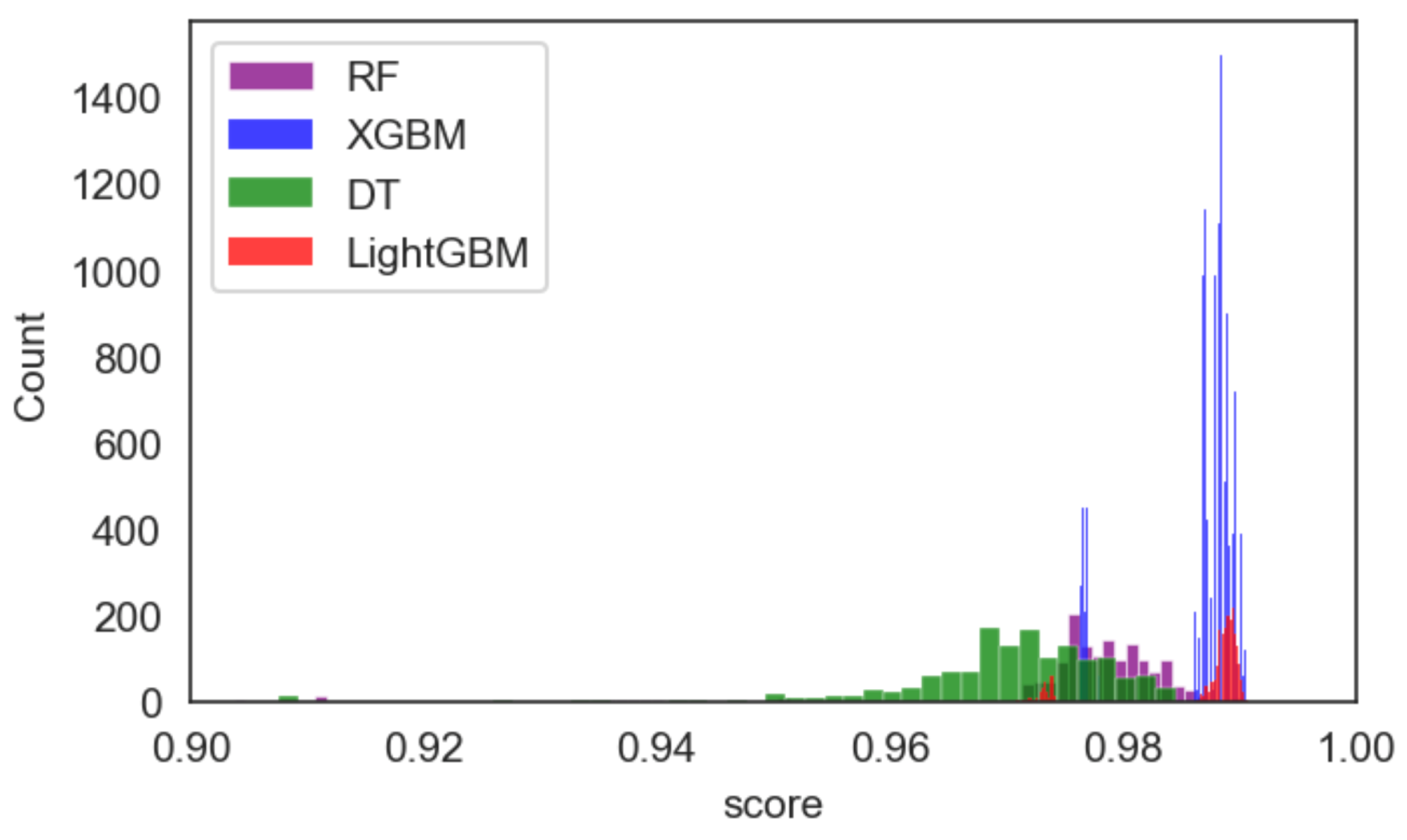
| RF | 400 14 entropy 5 10 None | T2 | 2 h 35 min 21 s | 480 | minmax = (0.9031205384458495, 0.9904140322251682) mean = 0.9743610662231913 |
| 700 None entropy 5 10 None | T3 | 7 h 31 min 17 s | 1500 | minmax = (0.8916989598205181, 0.9902100754640016), mean = 0.9760138690597593 | |
| 150 18 entropy 5 10 None | T4 | 11 h 58 min 4 s | 2880 | minmax = (0.8949622679991842, 0.9902100754640016), mean = 0.975666825299703 | |
| 650 19 entropy 5 5 None | Full Grid Search | 2 Days, 23 h, 58 min and 18 s | 11520 | minmax = (0.8853763002243524, 0.9906179889863349), mean = 0.9755531264871848 |
| ML Algorithms | Optimal Values | T-Values/ Grid Search | Time to Complete | No. of Evaluations | Score (min/max Accuracy and Mean) |
|---|---|---|---|---|---|
| LightGBM | 60 gbdt 9000 False 25 | T2 | 1 h 41 min 18 s | 540 | minmax = (0.9726697940036713 0.9908219457475015), mean = 0.9858956345699156 |
| 60 gbdt 15000 False 25 | T3 | 3 h 4 min 23 s | 1080 | min,max = (0.9702223128696716 0.9908219457475015) mean = 0.985933215491649 | |
| 40 gbdt 1000 False 15 | T4 | 5 h 36 min 55 s | 2160 | min,max = (0.9704262696308382, 0.9912298592698348), mean = 0.9859165023681646 | |
| 140 goss 1000 False 20 | Full Grid Search | 7 h 57 min 14 s | 4320 | min,max = (0.9696104425861717, 0.9910259025086682), mean = 0.985890630075313 |
| ML Algorithms | Optimal Values | T-Values/ Grid Search | Time to Complete | No. of Evaluations | Score (min/max Accuracy and Mean) |
|---|---|---|---|---|---|
| Xgboost | 1 1 10 0.4 20 | T2 | 1 h 9 min 21 s | 1440 | min,max = (0.9763410157046706, 0.9902100754640016), mean = 0.9856683549754118 |
| 2 1 2 0.01 25 | T3 | 5 h 37 min 32 s | 8640 | min,max = (0.9763410157046706, 0.9902100754640016), mean = 0.985969474471412 | |
| 2 1 12 0.1 25 | T4 | 23 h 12 min 33 s | 51840 | min,max = (0.9763410157046706, 0.9906179889863349), mean = 0.9859859987460435 | |
| 1 1 10 0.01 15 | Full Grid Search | 1 d 12 h 21 min 51 s | 103680 | min,max = (0.9763410157046706, 0.9906179889863349), mean = 0.9856382316161938 |
| ML Algorithms | Optimal Values | T-Values/ Grid Search | Time to Complete | No. of Evaluations | Score (min/max Accuracy and Mean) |
|---|---|---|---|---|---|
| DT | Entropy 20 None 5 25 | T2 | 42.5 s | 480 | min,max = (0.744034264735876 0.9836834591066694) mean = 0.9656014174994901 |
| Entropy 11 None 5 15 | T3 | 1 min 28 s | 960 | minmax = (0.7352641240057108, 0.9840913726290027), mean = 0.9662880719287512 | |
| Entropy None None 5 10 | T4 | 2 min 46 s | 1920 | min,max = (0.7352641240057108, 0.9840913426290027), mean = 0.9662736249915017 | |
| Gini None None 10 20 | Full Grid Search | 5 min 43 s | 3840 | min,max = (0.7352641240057108 0.9849071996736691) mean = 0.9660357285505473 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
ALGorain, F.T.; Clark, J.A. Covering Arrays ML HPO for Static Malware Detection. Eng 2023, 4, 543-554. https://doi.org/10.3390/eng4010032
ALGorain FT, Clark JA. Covering Arrays ML HPO for Static Malware Detection. Eng. 2023; 4(1):543-554. https://doi.org/10.3390/eng4010032
Chicago/Turabian StyleALGorain, Fahad T., and John A. Clark. 2023. "Covering Arrays ML HPO for Static Malware Detection" Eng 4, no. 1: 543-554. https://doi.org/10.3390/eng4010032
APA StyleALGorain, F. T., & Clark, J. A. (2023). Covering Arrays ML HPO for Static Malware Detection. Eng, 4(1), 543-554. https://doi.org/10.3390/eng4010032






