Quantifying Small-Scale Hyporheic Streamlines and Resident Time under Gravel-Sand Streambed Using a Coupled HEC-RAS and MIN3P Model
Abstract
:1. Introduction
2. Materials and Methods
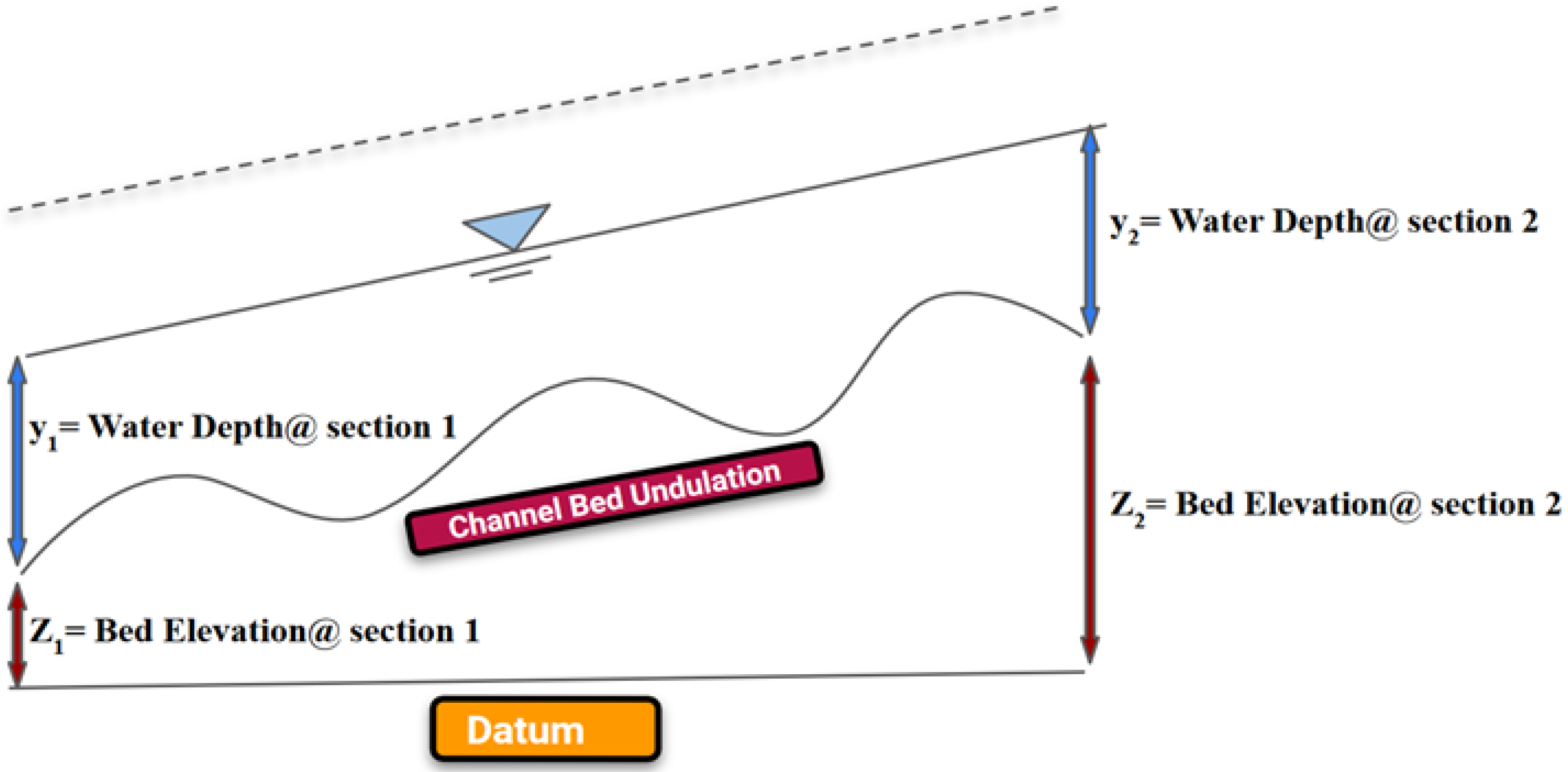
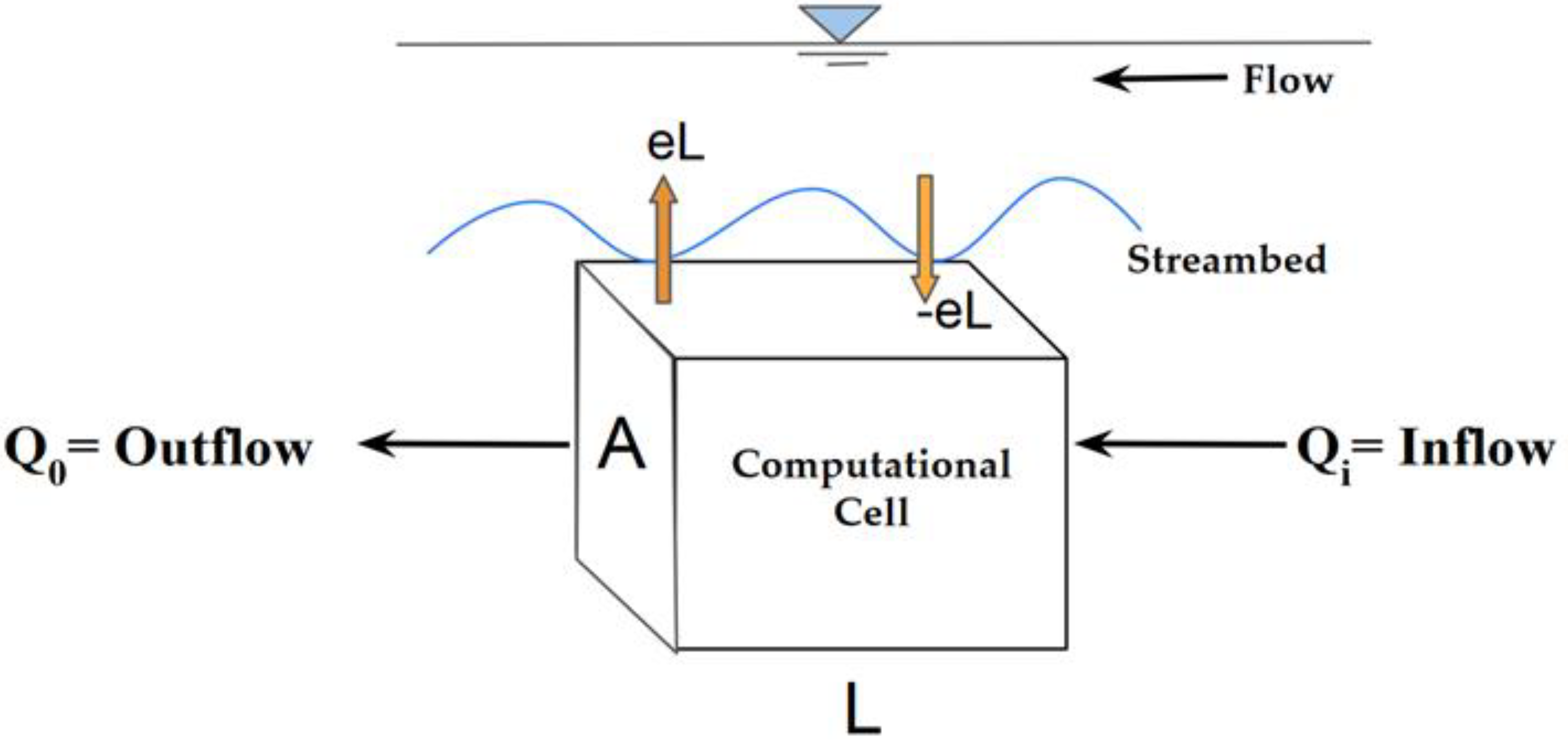
2.1. Formulation of GW-SW Exchange
2.2. Numerical Modelling of Hyporheic Exchange
2.3. Model Parameterization
2.3.1. Base Case
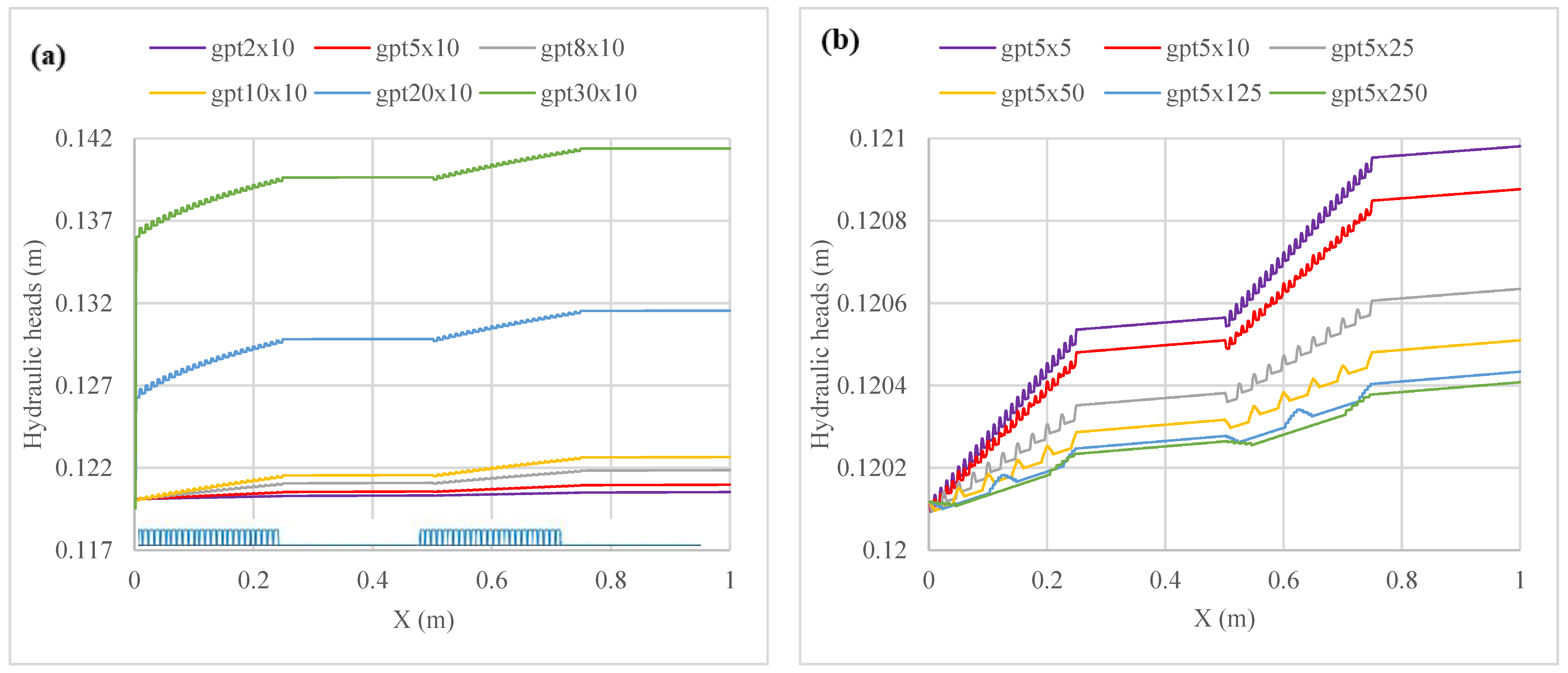
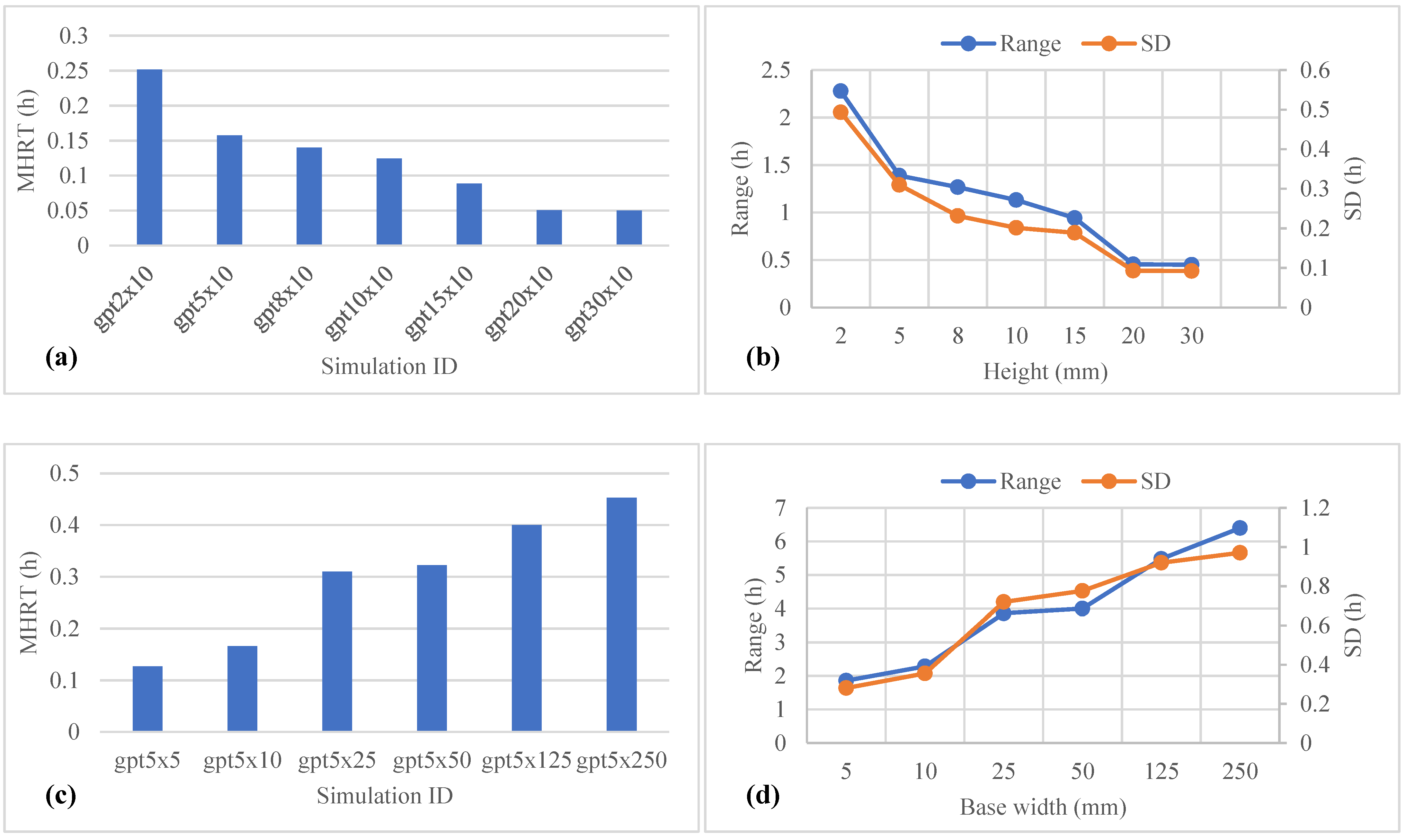
2.3.2. Size of the Gravel Piece: Height
2.3.3. Base Width
2.3.4. Variation in the Distribution of Gravel and Sand Portion
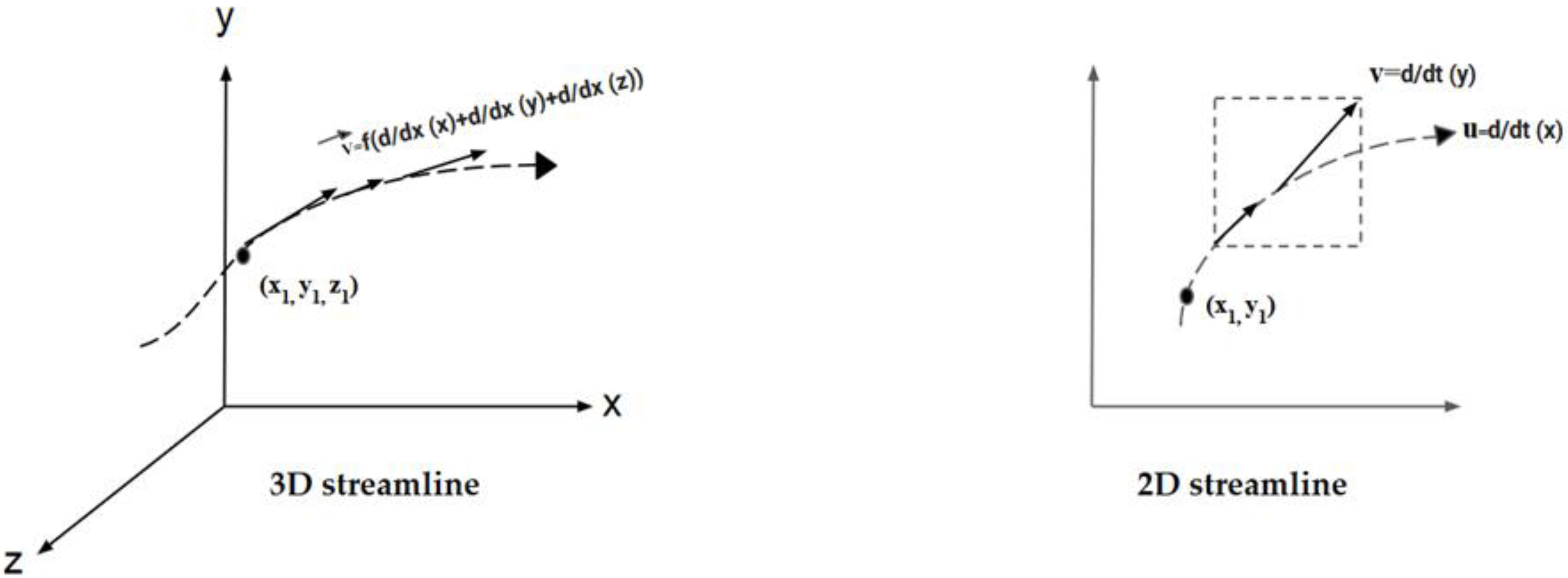
2.4. Automated Generation of Hyporheic Streamlines
Numerical Method of Particle Tracking
3. Results
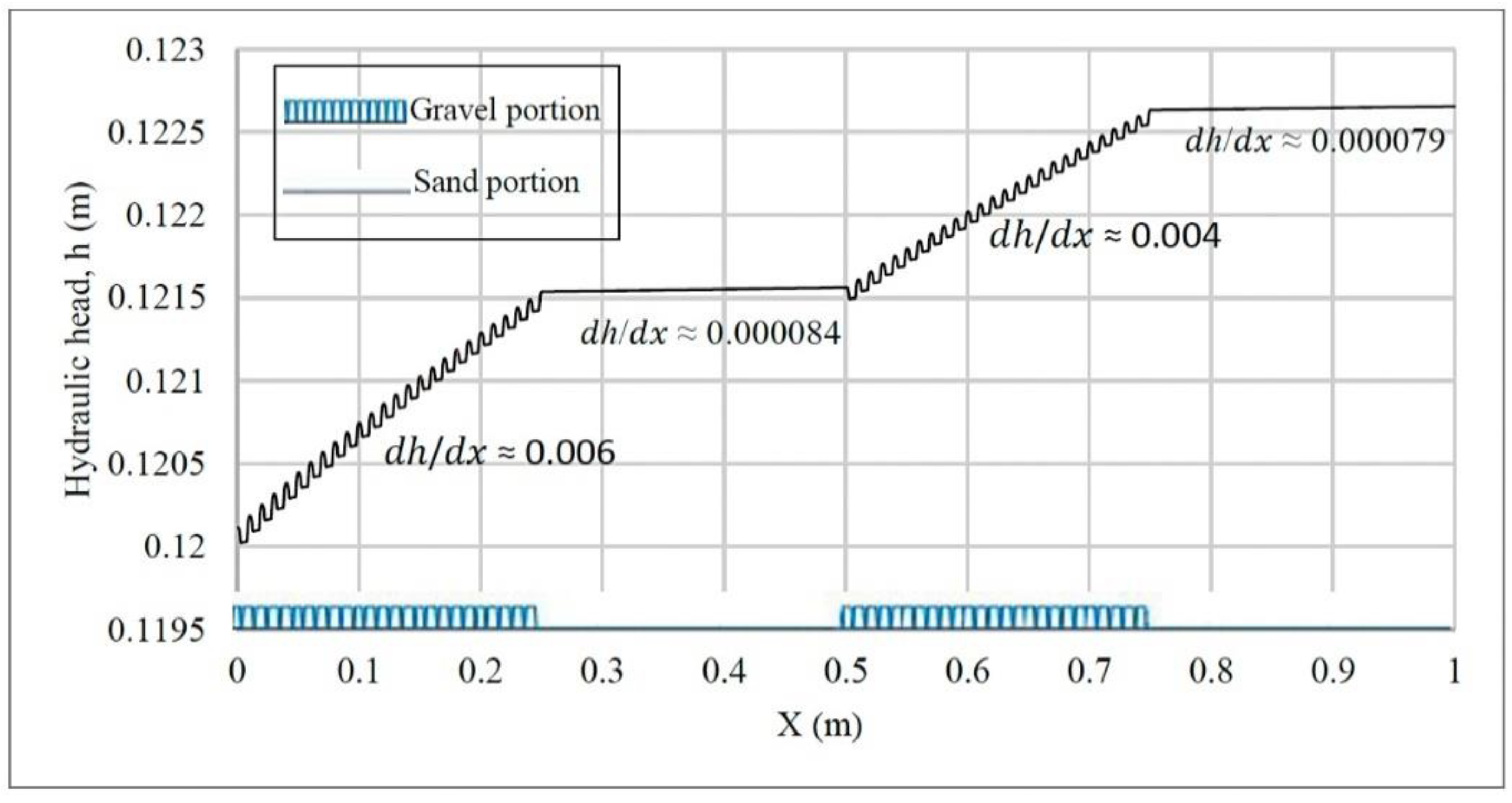
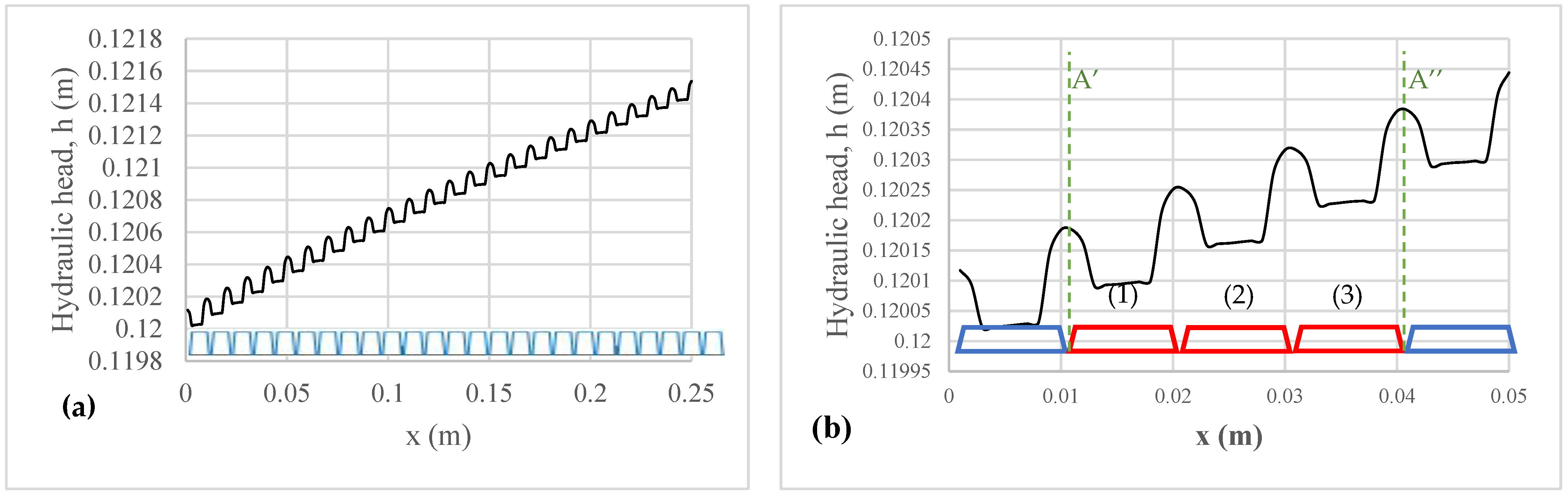
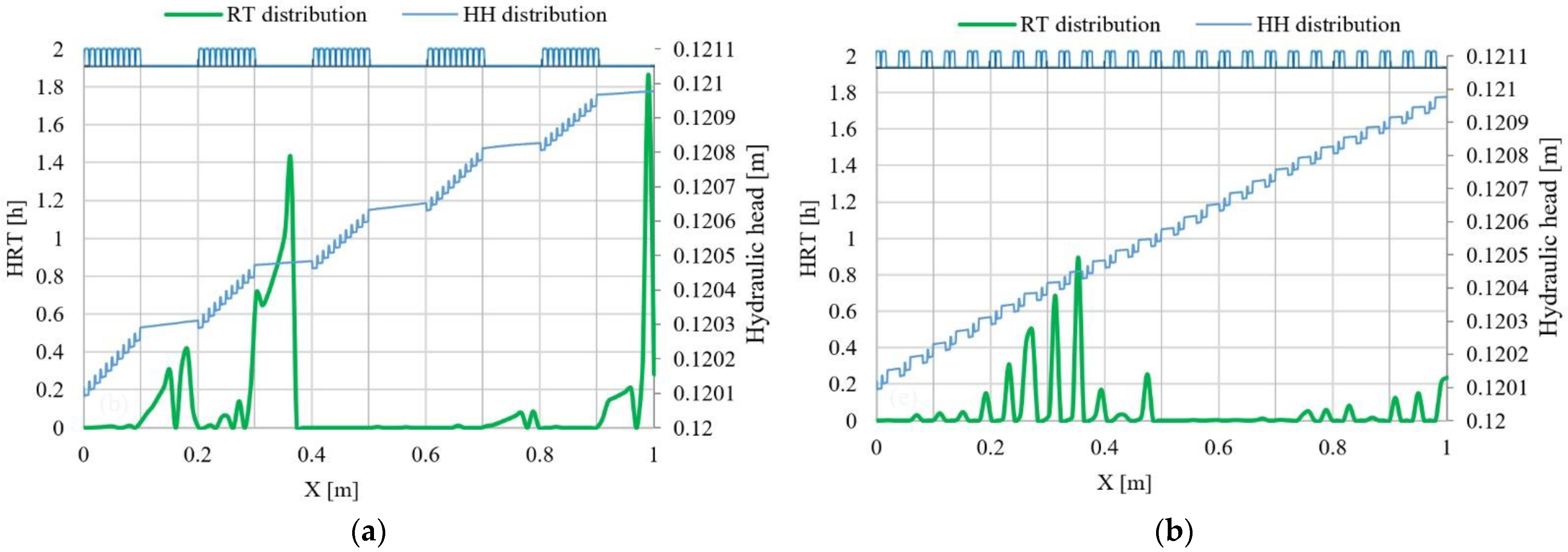
3.1. Hydraulic Head Distribution
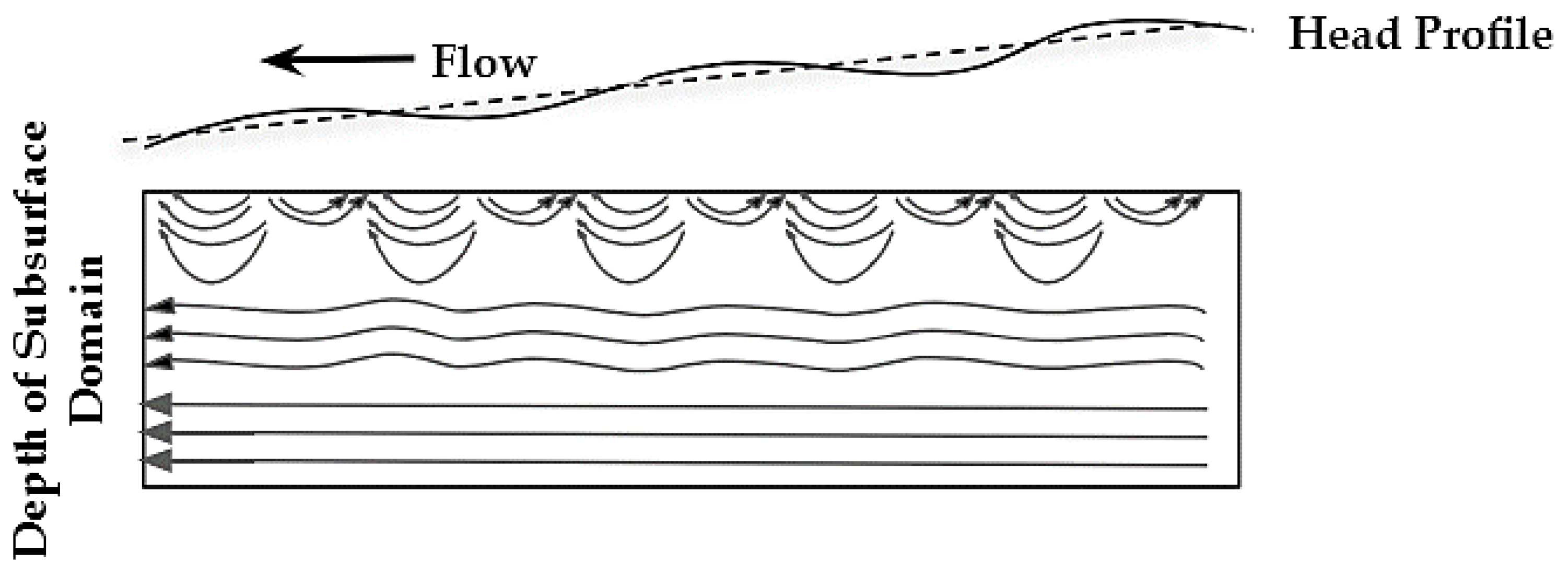
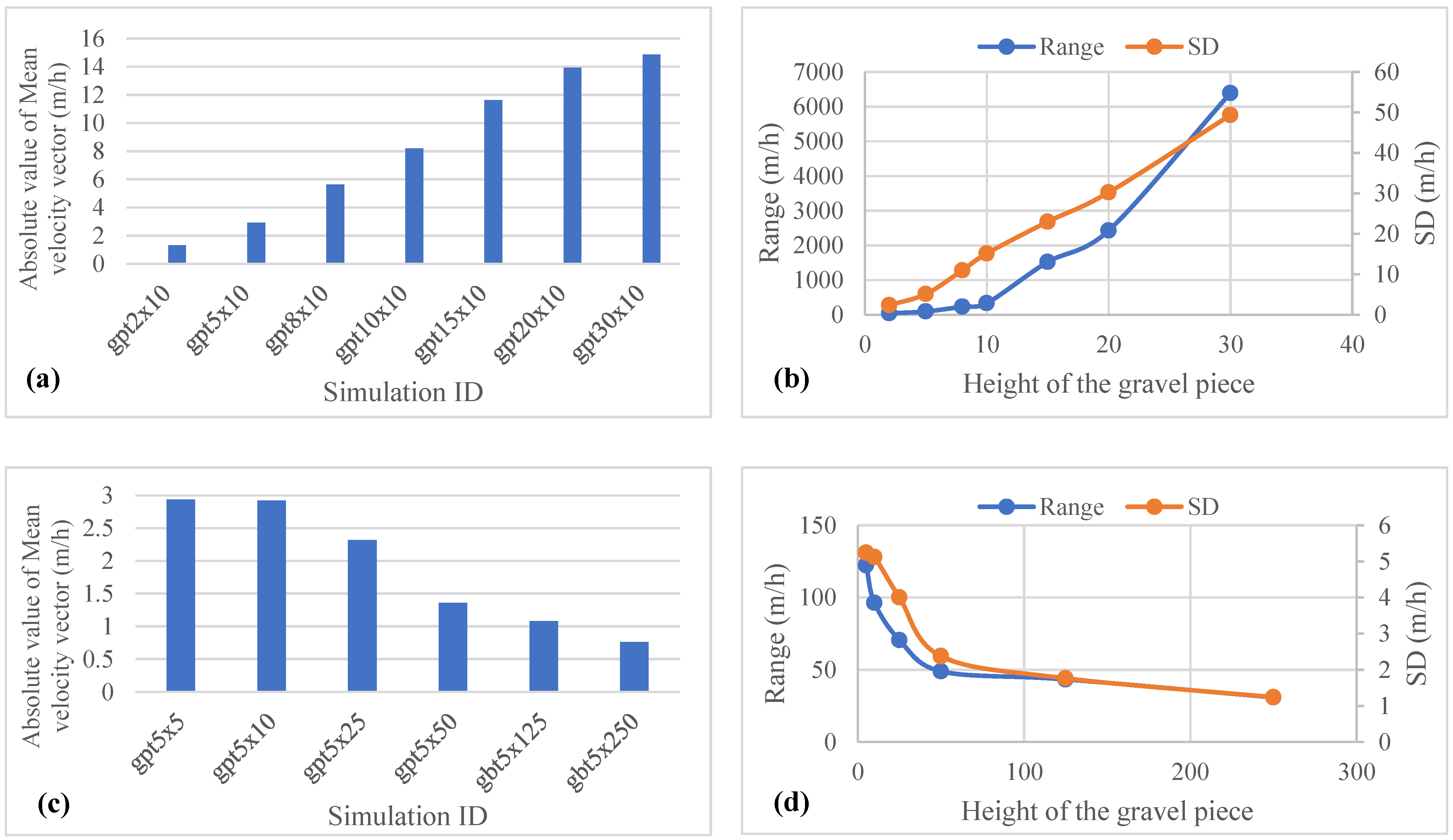
3.2. Subsurface Flow Field
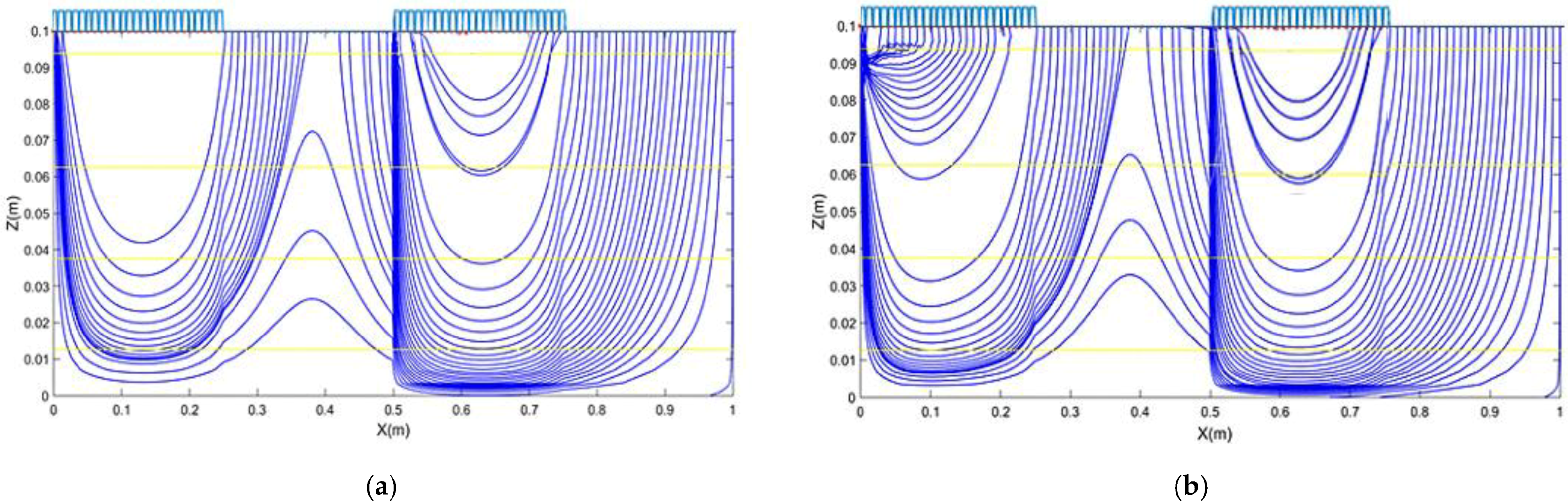
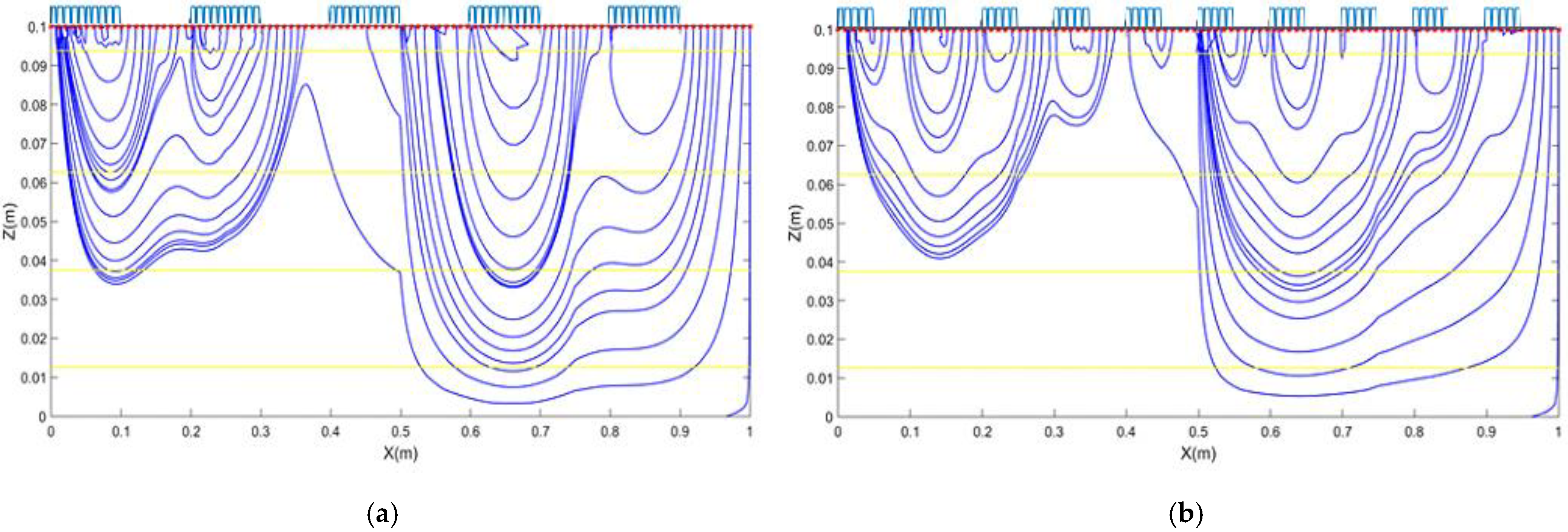
3.3. Hyporheic Streamline Distribution
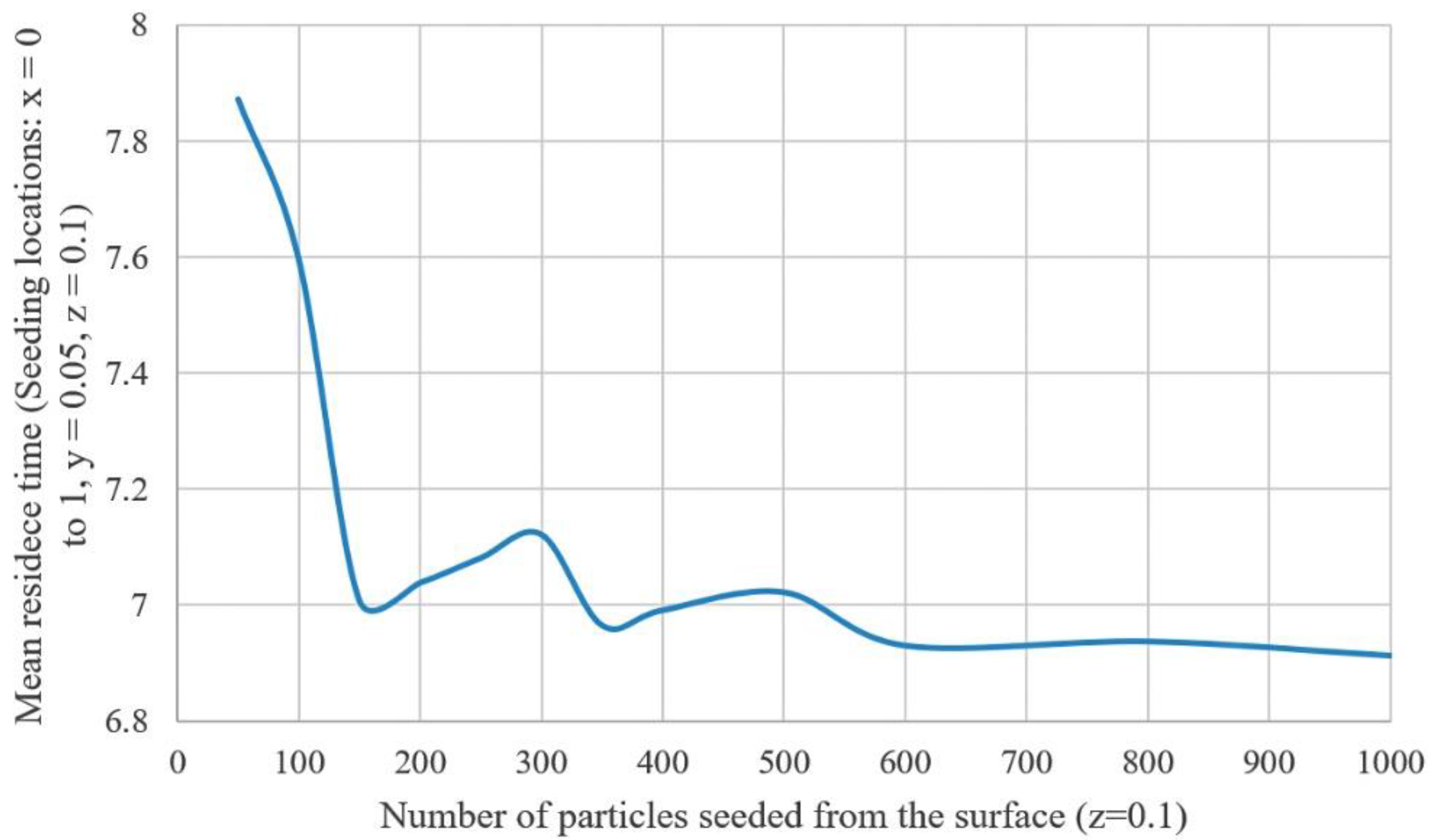
3.4. Residence Time
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Kuriata-Potasznik, A.; Szymczyk, S.; Bęś, A.; Sidoruk, M.; Skwierawski, A.; Kobus, S. Role of River–Lake System Sediments and Microbial Activity in the Hyporheic Zone. Water 2021, 13, 3499. [Google Scholar] [CrossRef]
- Nawalany, M.; Sinicyn, G.; Grodzka-Łukaszewska, M.; Mirosław-Świątek, D. Groundwater–Surface Water Interaction—Analytical Approach. Water 2020, 12, 1792. [Google Scholar] [CrossRef]
- Yazdan, M.M.S.; Ahad, M.T.; Jahan, I.; Mazumder, M. Review on the Evaluation of the Impacts of Wastewater Disposal in Hydraulic Fracturing Industry in the United States. Technologies 2020, 8, 67. [Google Scholar] [CrossRef]
- Fleckenstein, J.H.; Krause, S.; Hannah, D.M.; Boano, F. Groundwater-surface water interactions: New methods and models to improve understanding of processes and dynamics. Adv. Water Res. 2010, 33, 1291–1295. [Google Scholar] [CrossRef]
- Stanford, J.A.; Ward, J.V. The hyporheic habitat of river ecosystems. Nature 1998, 335, 64–66. [Google Scholar] [CrossRef]
- Bencala, K.E. Hyporheic Exchange Flows. In Encyclopedia of Hydrological Sciences v.3; Anderson, M.G., McDonnell, J., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 1733–1740. [Google Scholar]
- Al Mehedi, M.A.; Reichert, N.; Molkenthin, F. Sensitivity Analysis of Hyporheic Exchange to Small Scale Changes In Gravel-Sand Flumebed Using A Coupled Groundwater-Surface Water Model (No. EGU2020-20319). Copernic. Meet. 2020. Available online: https://meetingorganizer.copernicus.org/EGU2020/EGU2020-20319.html (accessed on 13 February 2022).
- Thomle, J.; Strickland, C.; Johnson, T.C.; Zhu, Y.; Stegen, J. A Flux Detection Probe to Quantify Dynamic Groundwater-Surface Water Exchange in the Hyporheic Zone. Groundwater 2020, 58, 892–900. [Google Scholar] [CrossRef]
- Esteve-Llorens, X.; Ita-Nagy, D.; Parodi, E.; González-García, S.; Moreira, M.T.; Feijoo, G.; Vázquez-Rowe, I. Environmental footprint of critical agro-export products in the Peruvian hyper-arid coast: A case study for green asparagus and avocado. Sci. Total Environ. 2021, 818, 151686. [Google Scholar] [CrossRef]
- Al Mehedi, M.A.; Smith, V.; Hosseiny, H.; Jiao, X. Unraveling the Complexities of Urban Flood Hydraulics through AI. 2022. Available online: https://assets.researchsquare.com/files/rs-1602023/v1/17edf6de-a4df-4859-93b8-bbb55b7ce510.pdf?c=1652287364 (accessed on 13 February 2022).
- Hordon, R.M. Hydrological Cycle; Herschy, R.W., Fairbridge, R.W., Eds.; Encyclopedia of Hydrology and Water Resources; Springer: Dordrecht, Switzerland, 1998; pp. 367–371. Available online: https://link.springer.com/referencework/10.1007/1-4020-4497-6 (accessed on 13 February 2022).
- Jekatierynczuk-Rudczyk, E.; Puczko, K.; Żukowska, J.; Sawicka, A. Biota communities influence on nutrients circulation in hyporheic zone—a case study in urban spring niches in Bialystok (NE Poland). Aquat. Sci. 2021, 83, 75. [Google Scholar] [CrossRef]
- Uddin, M.G.; Nash, S.; Olbert, A.I. A review of water quality index models and their use for assessing surface water quality. Ecol. Indic. 2021, 122, 107218. [Google Scholar] [CrossRef]
- Shen, G.; Yuan, J.; Phanikumar, M.S. Quantifying the effects of bed roughness on transit time distributions via direct numerical simulations of turbulent hyporheic exchange. Water Resour. Res. 2022, 58, e2021WR030503. [Google Scholar] [CrossRef]
- Yazdan, M.M.; Ahad, M.T.; Mallick, Z.; Mallick, S.P.; Jahan, I.; Mazumder, M. An Overview of the Glucocorticoids’ Pathways in the Environment and Their Removal Using Conventional Wastewater Treatment Systems. Pollutants 2021, 1, 141–155. [Google Scholar] [CrossRef]
- Di Lorenzo, T.; Fiasca, B.; Di Cicco, M.; Cifoni, M.; Galassi, D.M. Taxonomic and functional trait variation along a gradient of ammonium contamination in the hyporheic zone of a Mediterranean stream. Ecol. Indic. 2021, 132, 108268. [Google Scholar] [CrossRef]
- Karan, S.; Jacobsen, M.; Kazmierczak, J.; Reyna-Gutiérrez, J.A.; Breum, T.; Engesgaard, P. Numerical Representation of Groundwater-Surface Water Exchange and the Effect on Streamflow Contribution Estimates. Water 2021, 13, 1923. [Google Scholar] [CrossRef]
- Liang, D.; Song, J.; Xia, J.; Chang, J.; Kong, F.; Sun, H.; Cheng, D.; Zhang, Y. Effects of heavy metals and hyporheic exchange on microbial community structure and functions in hyporheic zone. J. Environ. Manag. 2022, 303, 114201. [Google Scholar] [CrossRef]
- Conant, B.; Robinson, C.E.; Hinton, M.J.; Russell, H.A.J. A framework for conceptualizing groundwater-surface water interactions and identifying potential impacts on water quality, water quantity, and ecosystems. J. Hydrol. 2019, 574, 609–627. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A comparison of numerical solutions of the one-dimensional unsaturated—saturated flow and mass transport equations. Adv. Water Resour. 1982, 5, 47–55. [Google Scholar] [CrossRef]
- Feng, J.; Liu, D.; Liu, Y.; Li, Y.; Li, H.; Chen, L.; Xiao, J.; Liu, J.; Dong, J. Hyporheic exchange due to in-stream geomorphic structures. J. Freshw. Ecol. 2022, 37, 221–241. [Google Scholar] [CrossRef]
- Dibyanshu, K.; Chhaya, T.; Raychoudhury, T. A review on the fate and transport behavior of engineered nanoparticles: Possibility of becoming an emerging contaminant in the groundwater. Int. J. Environ. Sci. Technol. 2022, 1–24. [Google Scholar] [CrossRef]
- Salehin, M.; Packman, A.I.; Paradis, M. Hyporheic exchange with heterogeneous streambeds: Laboratory experiments and modeling. Water Resour. Res. 2004, 40. Available online: https://agupubs.onlinelibrary.wiley.com/doi/full/10.1029/2003WR002567 (accessed on 13 February 2022). [CrossRef]
- Brunke, M.; Gonser, T.O.M. The ecological significance of exchange processes between rivers and groundwater. Freshw. Biol. 1997, 37, 1–33. [Google Scholar] [CrossRef] [Green Version]
- Haque, A.; Salama, A.; Lo, K.; Wu, P. Surface and Groundwater Interactions: A Review of Coupling Strategies in Detailed Domain Models. Hydrology 2021, 8, 35. [Google Scholar] [CrossRef]
- Wallace, C.D.; Soltanian, M.R. Surface water-groundwater exchange dynamics in buried-valley aquifer systems. Hydrol. Processes 2021, 35, e14066. [Google Scholar] [CrossRef]
- Ikard, S.J.; Briggs, M.A.; Lane, J.W. Investigation of Scale-Dependent Groundwater/Surface-water Exchange in Rivers by Gradient Self-Potential Logging: Numerical Modeling and Field Experiments. J. Environ. Eng. Geophys. 2021, 26, 83–98. [Google Scholar] [CrossRef]
- Boano, F.; Revelli, R.; Ridolfi, L. Bedform-induced hyporheic exchange with unsteady flows. Adv. Water Resour. 2007, 30, 148–156. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Wilson, J.L. Dunes, turbulent eddies, and interfacial exchange with permeable sediments. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Wilson, J.L. Hydrodynamics of coupled flow above and below a sediment–water interface with triangular bedforms. Adv. Water Resour. 2007, 30, 301–313. [Google Scholar] [CrossRef]
- Magliozzi, C.; Grabowski, R.; Packman, A.I.; Krause, S. Scaling down hyporheic exchange flows: From catchments to reaches. Hydrol. Earth Syst. Sci. 2017, 1–53. [Google Scholar]
- Packman, A.I.; Salehin, M.; Zaramella, M. Hyporheic exchange with gravel beds: Basic hydrodynamic interactions and bedform-induced advective flows. J. Hydraul. Eng. 2004, 130, 647–656. [Google Scholar] [CrossRef]
- Smith, J.W.N. Groundwater–Surface Water Interactions in the Hyporheic Zone, Environment Agency. Sci. Rep. 2005, 21, 13943–13955. [Google Scholar] [CrossRef]
- Wilhelmsen, K.; Sawyer, A.H.; Marshall, A.; McFadden, S.; Singha, K.; Wohl, E. Laboratory Flume and Numerical Modeling Experiments Show Log Jams and Branching Channels Increase Hyporheic Exchange. Water Resour. Res. 2021, 57, e2021WR030299. [Google Scholar] [CrossRef]
- Boulton, A.J.; Findlay, S.; Marmonier, P.; Stanley, E.H.; Valett, H.M. The functional significance of the hyporheic zone in streams and rivers. Annu. Rev. Ecol. Syst. 1998, 29, 59–81. [Google Scholar] [CrossRef] [Green Version]
- Frey, S.K.; Miller, K.; Khader, O.; Taylor, A.; Morrison, D.; Xu, X.; Berg, S.J.; Hwang, H.-T.; Sudicky, E.A.; Lapen, D.R. Evaluating landscape influences on hydrologic behavior with a fully-integrated groundwater—Surface water model. J. Hydrol. 2021, 602, 126758. [Google Scholar] [CrossRef]
- Cardenas, M.B.; Wilson, J.L.; Haggerty, R. Residence time of bedform-driven hyporheic exchange. Adv. Water Resour. 2008, 31, 1382–1386. [Google Scholar] [CrossRef]
- Shrivastava, S.; Stewardson, M.J.; Arora, M. Influence of Bioturbation on Hyporheic Exchange in Streams: Conceptual Model and Insights from Laboratory Experiments. Water Resour. Res. 2021, 57, e2020WR028468. [Google Scholar] [CrossRef]
- Tonina, D.; Buffington, J.M. Hyporheic exchange in mountain rivers I: Mechanics and environmental effects. Geogr. Compass 2009, 3, 1063–1086. [Google Scholar] [CrossRef]
- Gatel, L.; Lauvernet, C.; Carluer, N.; Weill, S.; Paniconi, C. Sobol Global Sensitivity Analysis of a Coupled Surface/Subsurface Water Flow and Reactive Solute Transfer Model on a Real Hillslope. Water 2020, 12, 121. [Google Scholar] [CrossRef] [Green Version]
- Cremeans, M.M.; Devlin, J.F.; McKnight, U.S.; Bjerg, P.L. Application of new point measurement device to quantify groundwater-surface water interactions. J. Contam. Hydrol. 2018, 211, 85–93. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bencala, K.E. Simulation of solute transport in a mountain pool-and-riffle stream with a kinetic mass transfer model for sorption. Water Resour. Res. 1983, 19, 732–738. [Google Scholar] [CrossRef]
- Blanco-Coronas, A.M.; López-Chicano, M.; Calvache, M.L.; Benavente, J.; Duque, C. Groundwater-Surface Water Interactions in “La Charca de Suárez” Wetlands, Spain. Water 2020, 12, 344. [Google Scholar] [CrossRef] [Green Version]
- Martone, I.; Gualtieri, C.; Endreny, T. Characterization of Hyporheic Exchange Drivers and Patterns within a Low-Gradient, First-Order, River Confluence during Low and High Flow. Water 2020, 12, 649. [Google Scholar] [CrossRef] [Green Version]
- Vaux, W.G. Interchange of stream and intragravel water in a salmon spawning riffle. U.S. Fish Wildl. Serv. Spec. Sci. Rep. Fish. 1962, 405, 11. [Google Scholar]
- Mantey, J.; Nyarko, K.B.; Owusu-Nimo, F.; Awua, K.A.; Bempah, C.K.; Amankwah, R.K.; Akatu, W.E.; Appiah-Effah, E. Mercury contamination of soil and water media from different illegal artisanal small-scale gold mining operations (galamsey). Heliyon 2020, 6, 4312. [Google Scholar] [CrossRef] [PubMed]
- Mantey, J.; Nyarko, K.B.; Owusu-Nimo, F.; Awua, K.A.; Bempah, C.K.; Amankwah, R.K.; Akatu, W.E.; Appiah-Effah, E. Influence of illegal artisanal small-scale gold mining operations (galamsey) on oil and grease (O/G) concentrations in three hotspot assemblies of Western Region, Ghana. Environ. Pollut. 2020, 263, 114251. [Google Scholar] [CrossRef] [PubMed]
- Laube, G.; Schmidt, C.; Fleckenstein, J.H. A systematic model-based evaluation of the influence of hydraulic conductivity, heterogeneity and domain depth on hyporheic nutrient transformation. Adv. Water Resour. 2022, 159, 104087. [Google Scholar] [CrossRef]
- HEC-RAS Manual. Available online: https://www.hec.usace.army.mil/software/hec-ras/documentation.aspx (accessed on 13 February 2022).
- Atangana, A. Fract. Operators with Constant and Variable Order with Application to Geo-Hydrology; Academic Press: Cambridge, MA, USA, 2017. [Google Scholar]
- Tonina, D.; Buffington, J.M. Hyporheic exchange in gravel bed rivers with pool-riffle morphology: Laboratory experiments and three-dimensional modeling. Water Resour. Res. 2007, 43, W01421. [Google Scholar] [CrossRef] [Green Version]
- Zlatanović, S.; Fabian, J.; Premke, K.; Mutz, M. Shading and sediment structure effects on stream metabolism resistance and resilience to infrequent droughts. Sci. Total Environ. 2018, 621, 1233–1239. [Google Scholar] [CrossRef]
- Jurjovec, J.; Blowes, D.; Ptacek, C.; Mayer, K. Multicomponent reactive transport modeling of acid neutralization reactions in mine tailings. Water Resour. Res. 2004, 40. [Google Scholar] [CrossRef] [Green Version]
- Su, D.; Mayer, K.U.; MacQuarrie, K.T.B. MIN3P-HPC: A High-Performance Unstructured Grid Code for Subsurface Flow and Reactive Transport Simulation. Math. Geosci. 2021, 53, 517–550. [Google Scholar] [CrossRef]
- Su, D.; Mayer, K.U.; MacQuarrie, K.T.B. Numerical investigation of flow instabilities using fully unstructured discretization for variably saturated flow problems. Adv. Water Res. 2020, 143, 103673. [Google Scholar] [CrossRef]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Floodplains. U.S. Geol. Surv.; 1989. Available online: https://pubs.er.usgs.gov/publication/wsp2339 (accessed on 13 February 2022).
- Koiter, A.J.; Owens, P.N.; Petticrew, E.L.; Lobb, D.A. The role of gravel channel beds on the particle size and organic matter selectivity of transported fine-grained sediment: Implications for sediment fingerprinting and biogeochemical flux research. J. Soils Sediments 2015, 15, 2174–2188. [Google Scholar] [CrossRef]
- Aldridge, B.N.; Garrett, J.M. Roughness Coefficients for Stream Channels in Arizona. U.S. Geol. Surv.; 1973. Available online: https://pubs.usgs.gov/of/1973/0003/report.pdf (accessed on 13 February 2022).
- Trauth, N.; Schmidt, C.; Maier, U.; Vieweg, M.; Fleckenstein, J.H. Coupled 3-D stream flow and hyporheic flow model under varying stream and ambient groundwater flow conditions in a pool-riffle system. Water Resour. Res. 2013, 49, 5834–5850. [Google Scholar] [CrossRef]
- Maher, K.; Mayer, K.U. The Art of Reactive Transport Model Building. Elements 2019, 15, 117–118. [Google Scholar] [CrossRef] [Green Version]
- Murphy, B.L.; Morrison, R.D. Introduction to Environmental Forensics. 2014. Available online: https://www.elsevier.com/books/introduction-to-environmental-forensics/murphy/978-0-12-404696-2 (accessed on 13 February 2022).
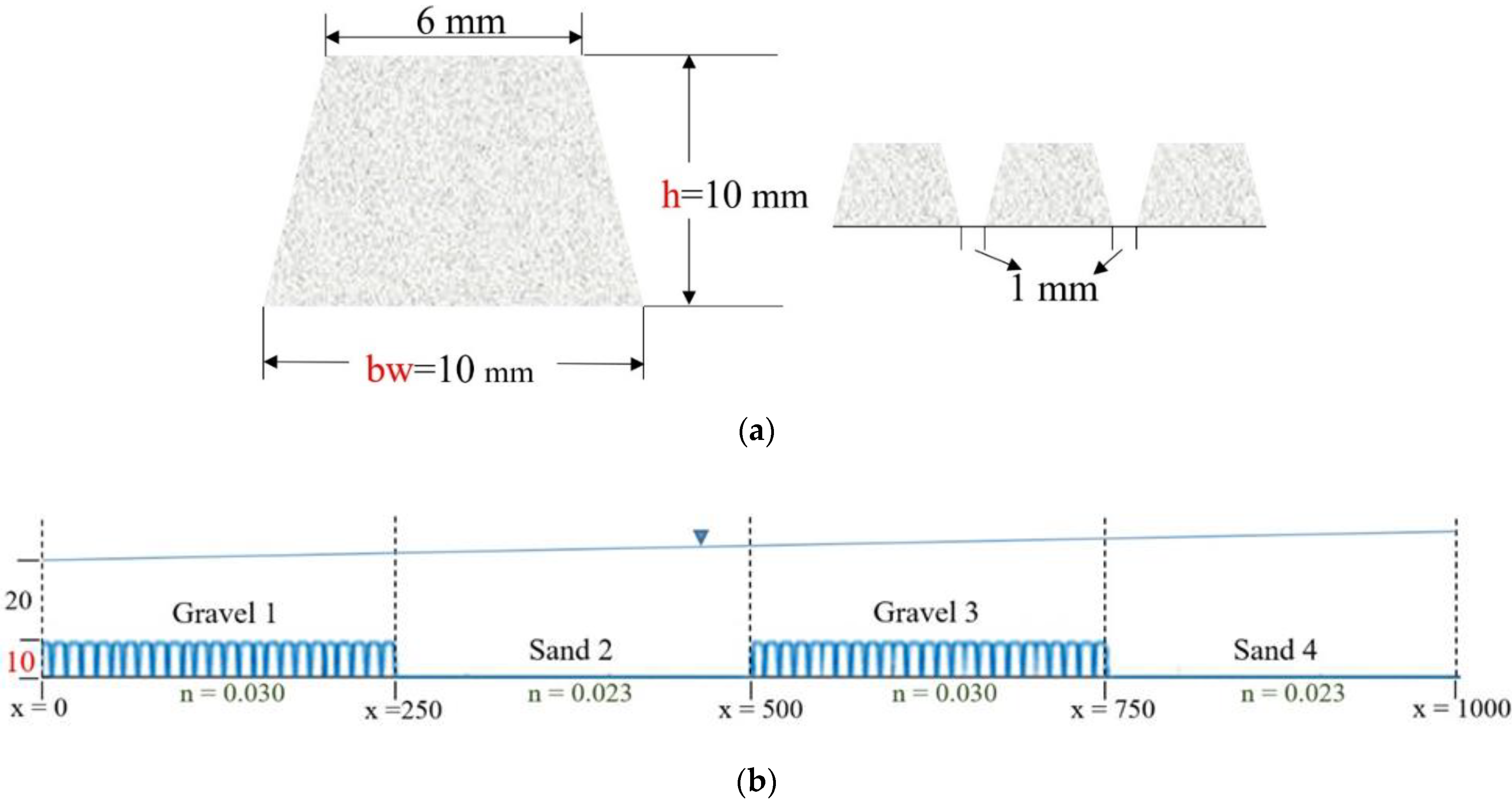
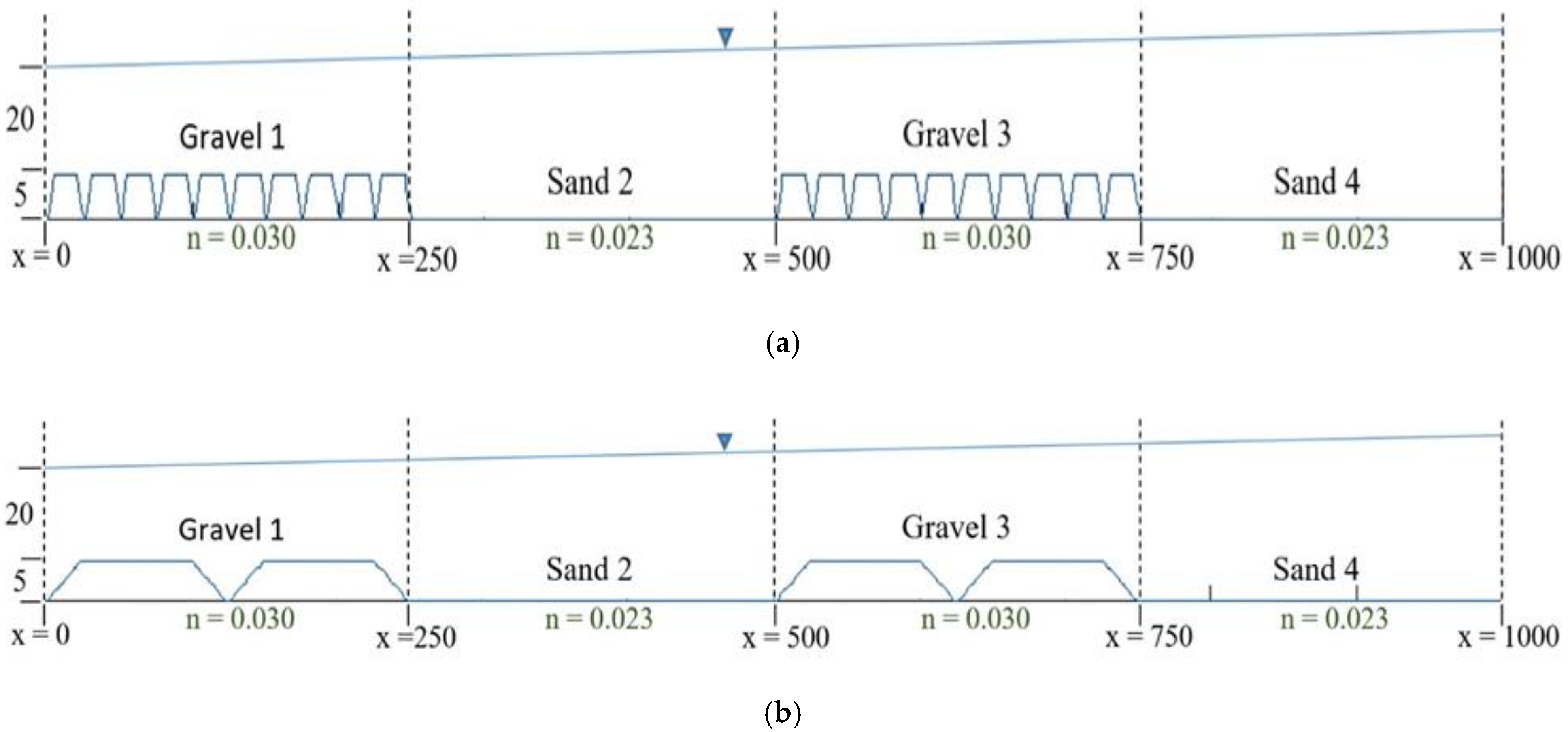
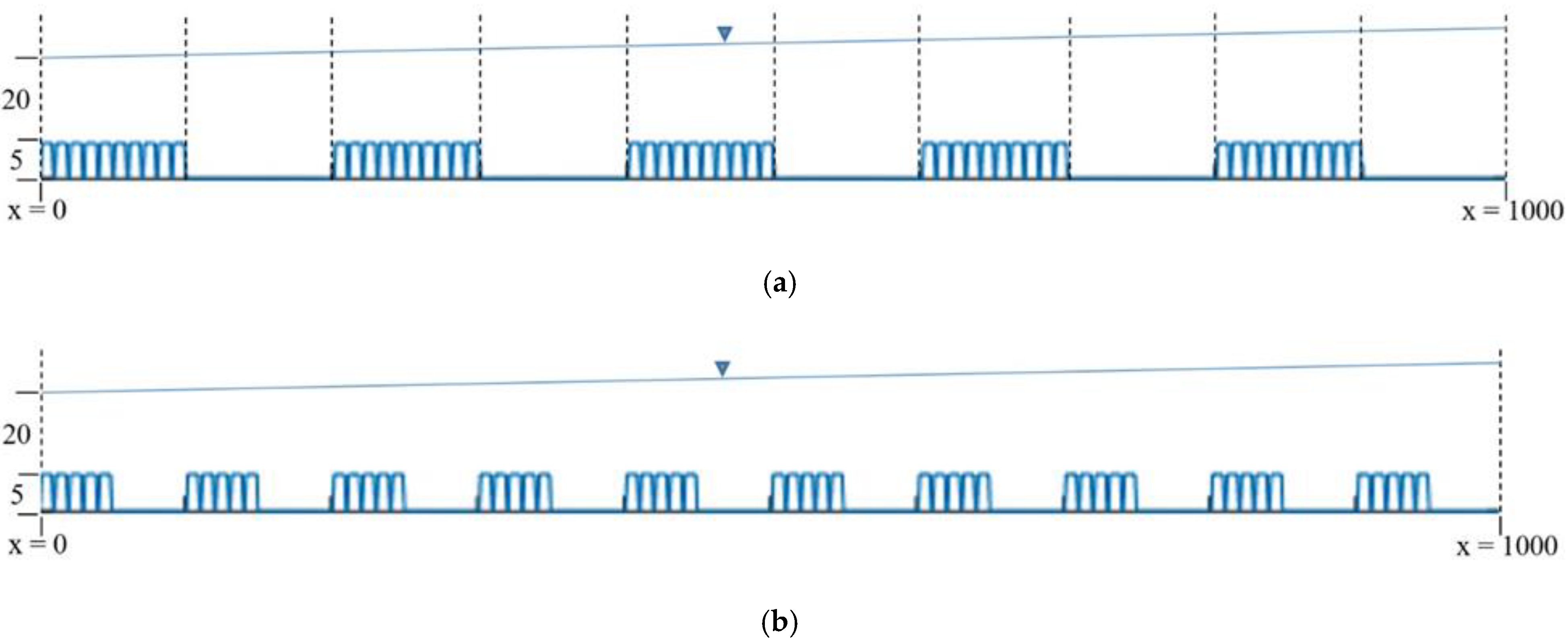
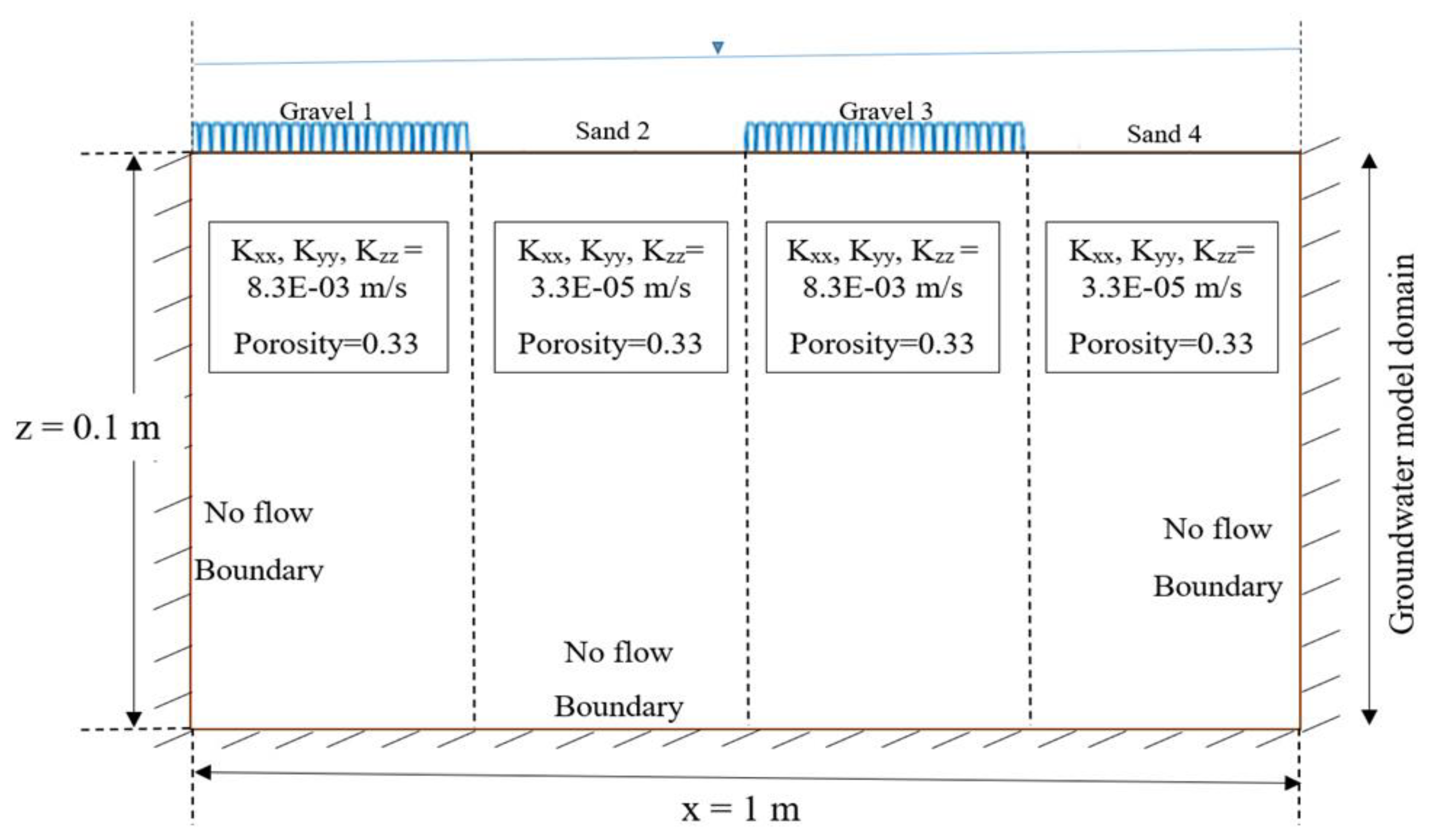


| Group | Simulation ID/Model Setup | Description |
|---|---|---|
| Height of gravel piece (h) | gpt2 × 10 | Trapezoidal gravel particle with h = 2, bw = 10, l= 6 |
| gpt5 × 10 | Trapezoidal gravel particle with h = 5, bw = 10, l = 6 | |
| gpt8 × 10 | Trapezoidal gravel particle with h = 8, bw = 10, l = 6 | |
| gpt10 × 10 | Trapezoidal gravel particle with h = 10, bw = 10, l = 6 | |
| gpt20 × 10 | Trapezoidal gravel particle with h = 20, bw = 10, l = 6 | |
| gpt30 × 10 | Trapezoidal gravel particle with h = 30, bw = 10, l = 6 |
| Group | Simulation ID/Model Setup | Description |
|---|---|---|
| Base width of gravel piece (bw) | gpt5 × 5 | Trapezoidal gravel particle with h = 5, bw = 5 |
| gpt5 × 10 | Trapezoidal gravel particle with h = 5, bw = 10 | |
| gpt5 × 25 | Trapezoidal gravel particle with h = 5, bw = 25 | |
| gpt5 × 50 | Trapezoidal gravel particle with h = 5, bw = 50 | |
| gpt5 × 125 | Trapezoidal gravel particle with h = 5, bw = 125 | |
| gpt5 × 250 | Trapezoidal gravel particle with h = 5, bw = 250 |
| Group | Simulation ID/Model Setup | Description |
|---|---|---|
| Variation in the distribution of gravel and sand portion | zgst5 × 10-2 | Sand and gravel zone with trapezoidal gravel piece, h = 5, bw = 10; no. of zone of gravel = 2, no. of zone of sand = 2. |
| zgst5 × 10-5 | Sand and gravel zone with trapezoidal gravel piece, h = 5, bw = 10; no. of zone of gravel = 5, no. of zone of sand = 5. | |
| zgst5 × 10-10 | Sand and gravel zone with trapezoidal gravel piece, h = 5, bw = 10; no. of zone of gravel = 10, no. of zone of sand = 10. | |
| zgst5 × 10-20 | Sand and gravel zone with trapezoidal gravel piece, h = 5, bw = 10; no. of zone of gravel = 20, no. of zone of sand = 20. | |
| zgst5 × 10-25 | Sand and gravel zone with trapezoidal gravel piece, h = 5, bw = 10; no. of zone of gravel = 25, no. of zone of sand = 25. | |
| zgst5 × 10-50 | Sand and gravel zone with trapezoidal gravel piece, h = 5, bw = 10; no. of zone of gravel = 50, no. of zone of sand = 50. |
| Simulation ID | Zone of Stream Bed | |||
|---|---|---|---|---|
| Gravel1 | Sand2 | Gravel3 | Sand4 | |
| gpt2 × 10 | 0.000177 | 0.000029 | 0.000172 | 0.000029 |
| gpt5 × 10 | 0.000419 | 0.000029 | 0.000388 | 0.000028 |
| gpt8 × 10 | 0.000946 | 0.000027 | 0.000747 | 0.000024 |
| gpt10 × 10 | 0.001420 | 0.000025 | 0.001071 | 0.000021 |
| gpt20 × 10 | 0.009697 | 0.000009 | 0.001708 | 0.000008 |
| gpt30 × 10 | 0.019511 | 0.000004 | 0.001750 | 0.000003 |
| gpt5 × 5 | 0.000419 | 0.000029 | 0.000388 | 0.000028 |
| gpt5 × 10 | 0.000364 | 0.000029 | 0.000339 | 0.000028 |
| gpt5 × 25 | 0.000235 | 0.000029 | 0.000224 | 0.000028 |
| gpt5 × 50 | 0.000170 | 0.000030 | 0.000164 | 0.000029 |
| gpt5 × 125 | 0.000130 | 0.000030 | 0.000127 | 0.000030 |
| gpt5 × 250 | 0.000117 | 0.000030 | 0.000114 | 0.000030 |
| Mean (μ) (m/h) | Standard Deviation (σ) (m/h) | ||||
|---|---|---|---|---|---|
| vx | vy | vz | vx | vy | vz |
| −6.424 | 1.212 × 10−8 | 7.1861 × 10−5 | 13.845 | 3.061 × 10−8 | 7.966 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehedi, M.A.A.; Yazdan, M.M.S.; Ahad, M.T.; Akatu, W.; Kumar, R.; Rahman, A. Quantifying Small-Scale Hyporheic Streamlines and Resident Time under Gravel-Sand Streambed Using a Coupled HEC-RAS and MIN3P Model. Eng 2022, 3, 276-300. https://doi.org/10.3390/eng3020021
Mehedi MAA, Yazdan MMS, Ahad MT, Akatu W, Kumar R, Rahman A. Quantifying Small-Scale Hyporheic Streamlines and Resident Time under Gravel-Sand Streambed Using a Coupled HEC-RAS and MIN3P Model. Eng. 2022; 3(2):276-300. https://doi.org/10.3390/eng3020021
Chicago/Turabian StyleMehedi, Md Abdullah Al, Munshi Md. Shafwat Yazdan, Md Tanvir Ahad, Wisdom Akatu, Raaghul Kumar, and Ashiqur Rahman. 2022. "Quantifying Small-Scale Hyporheic Streamlines and Resident Time under Gravel-Sand Streambed Using a Coupled HEC-RAS and MIN3P Model" Eng 3, no. 2: 276-300. https://doi.org/10.3390/eng3020021
APA StyleMehedi, M. A. A., Yazdan, M. M. S., Ahad, M. T., Akatu, W., Kumar, R., & Rahman, A. (2022). Quantifying Small-Scale Hyporheic Streamlines and Resident Time under Gravel-Sand Streambed Using a Coupled HEC-RAS and MIN3P Model. Eng, 3(2), 276-300. https://doi.org/10.3390/eng3020021








