Design Data and Finite Element Analysis of 3D Printed Poly(ε-Caprolactone)-Based Lattice Scaffolds: Influence of Type of Unit Cell, Porosity, and Nozzle Diameter on the Mechanical Behavior
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. CAD-Based Lattice Structures Design
2.3. Finite Element Method (FEM) Modeling
2.4. Fused Deposition (FDM) Printing
2.5. Spectroscopic Characterizations of 3D Printed Lattice Structures
3. Results and Discussion
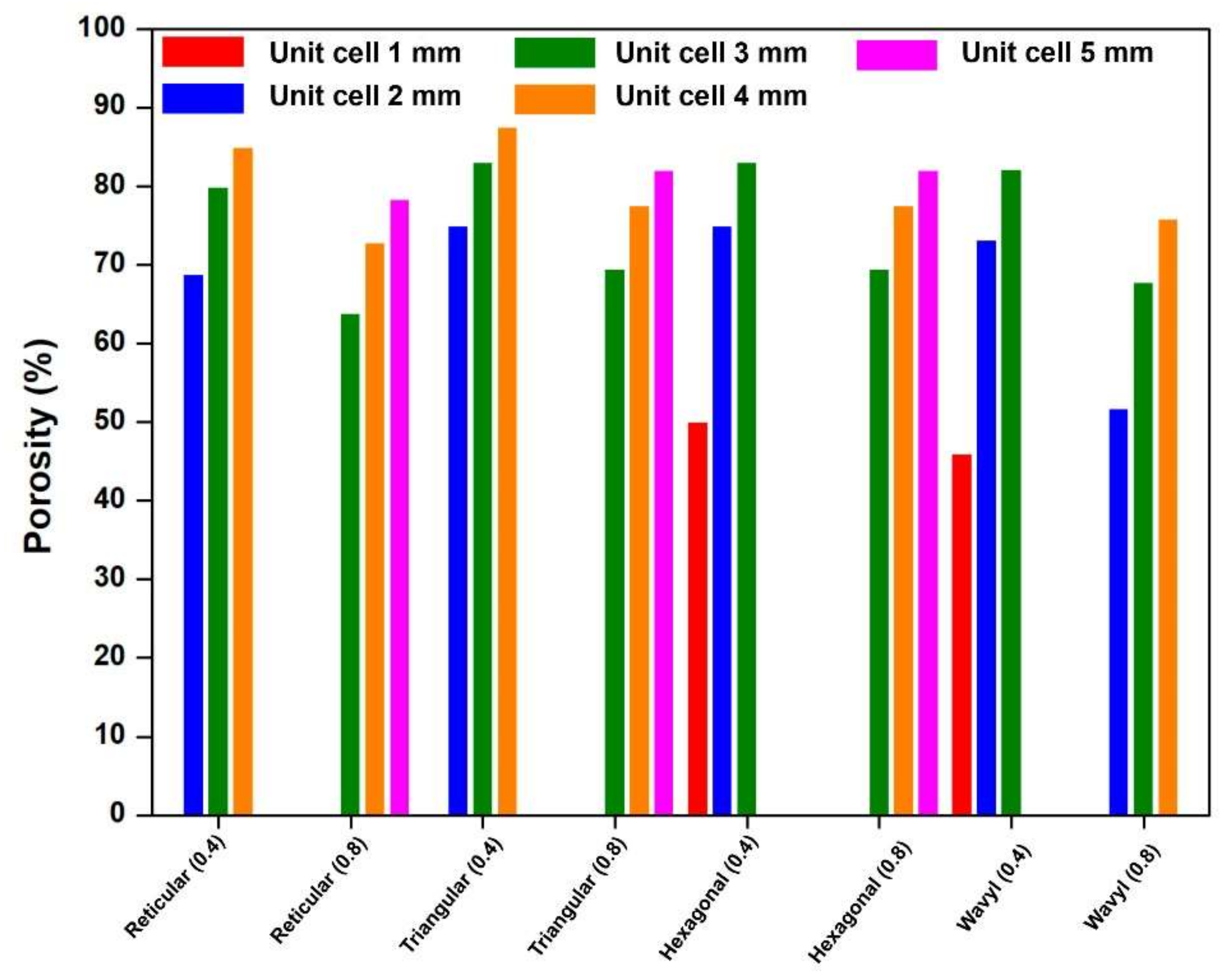
3.1. CAD-Based Scaffolds Design and Printability
3.2. FEM Analysis
3.3. Spectroscopy Characterization of 3D Printed Scaffolds
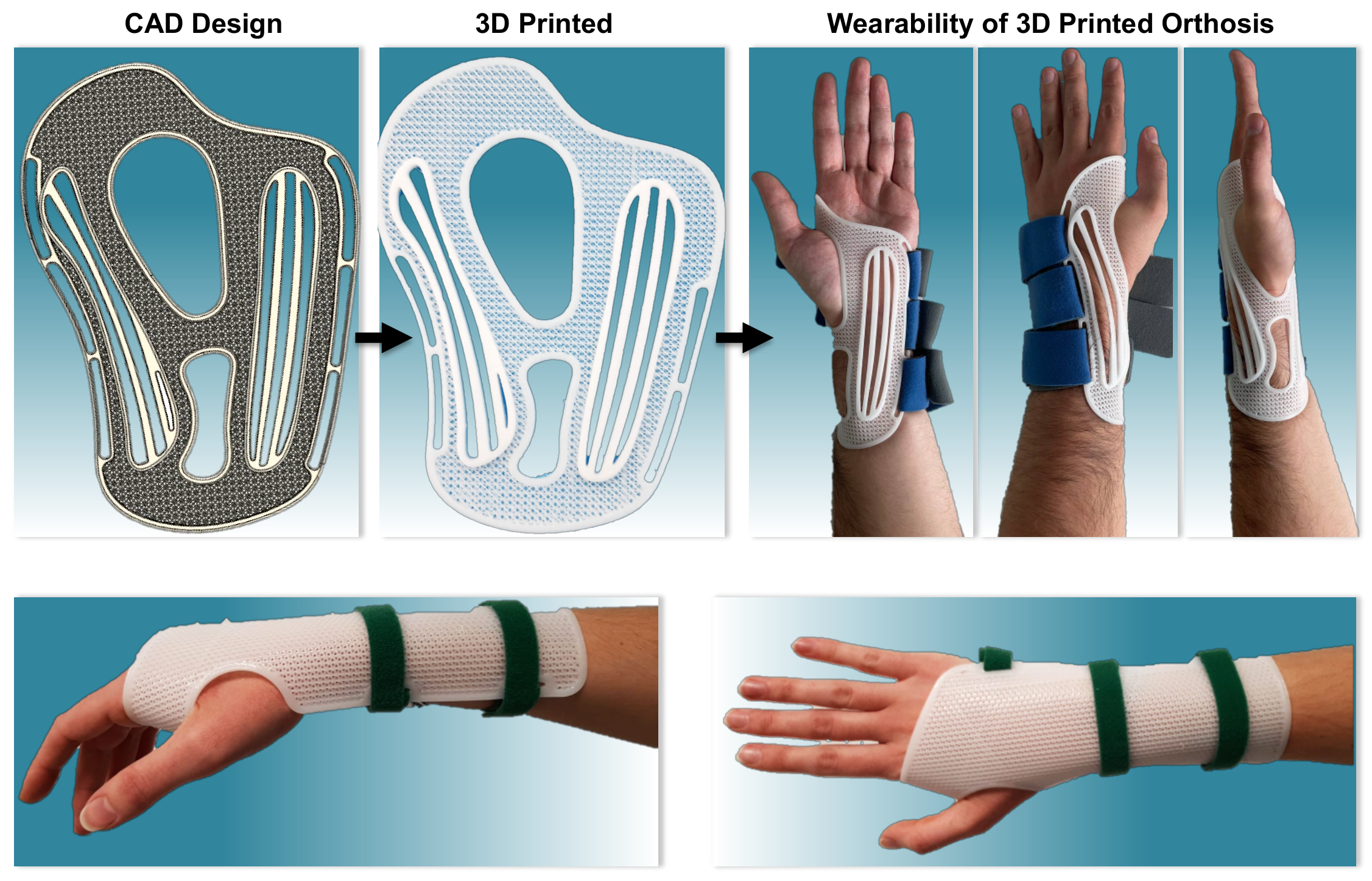
3.4. 3D Printed Wrist Brace Orthosis with Different Lattice Geometries
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Q.; Zhang, K.; Hu, G. Smart three-dimensional lightweight structure triggered from a thin composite sheet via 3D printing technique. Sci. Rep. 2016, 6, 22431. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koteswari, S.; Narayan Yeole, S. Development of 3D printed orthotic device for flat foot problem. Mater. Today Proc. 2021, 44, 2435–2441. [Google Scholar] [CrossRef]
- Martorelli, M.; Gloria, A.; Bignardi, C.; Calì, M.; Maietta, S. Design of additively manufactured lattice structures for biomedical applications. J. Healthc. Eng. 2020, 2020, 2707560. [Google Scholar] [CrossRef] [PubMed]
- Hutmacher, D.W. Scaffold design and fabrication technologies for engineering tissues—State of the art and future perspectives. J. Biomater. Sci. Polym. Ed. 2001, 12, 107–124. [Google Scholar] [CrossRef]
- Vijayavenkataraman, S.; Zhang, L.; Zhang, S.; Fuh, J.Y.H.; Lu, W.F. Triply periodic minimal surfaces sheet scaffolds for tissue engineering applications: An optimization approach toward biomimetic scaffold design. ACS Appl. Bio Mater. 2018, 1, 259–269. [Google Scholar] [CrossRef]
- Zhou, M.; Hou, J.; Zhang, G.; Luo, C.; Zeng, Y.; Mou, S.; Xiao, P.; Zhong, A.; Yuan, Q.; Yang, J.; et al. Tuning the mechanics of 3D-printed scaffolds by crystal lattice-like structural design for breast tissue engineering. Biofabrication 2019, 12, 015023. [Google Scholar] [CrossRef] [PubMed]
- Hollister, S.J. Porous scaffold design for tissue engineering. Nat. Mater. 2005, 4, 518–524. [Google Scholar] [CrossRef]
- Roohani-Esfahani, S.I.; Newman, P.; Zreiqat, H. Design and fabrication of 3D printed scaffolds with a mechanical strength comparable to cortical bone to repair large bone defects. Sci. Rep. 2016, 6, 19468. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Alomar, Z.; Concli, F. Compressive behavior assessment of a newly developed circular cell-based lattice structure. Mater. Des. 2021, 205, 109716. [Google Scholar] [CrossRef]
- Kantaros, A.; Piromalis, D. Fabricating lattice structures via 3D printing: The case of porous bio-engineered scaffolds. Appl. Mech. 2021, 2, 289–302. [Google Scholar] [CrossRef]
- Yoo, D. New paradigms in internal architecture design and freeform fabrication of tissue engineering porous scaffolds. Med. Eng. Phys. 2012, 34, 762–776. [Google Scholar] [CrossRef] [PubMed]
- Bagheri, A.; Buj-Corral, I.; Ferrer, M.; Pastor, M.M.; Roure, F. Determination of the elasticity modulus of 3D-printed octet-truss structures for use in porous prosthesis implants. Materials 2018, 11, 2420. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bennett, I.; Bulterys, P.L.; Chang, M.; DeSimone, J.M.; Fralick, J.; Herring, M.; Kabaria, H.; Kong, C.S.; Larson, B.; Lu, O.; et al. The rapid deployment of a 3D printed “latticed” nasopharyngeal swab for COVID-19 testing made using digital light synthesis. medRxiv 2020, 44, 1361–1368. [Google Scholar]
- Wong, K.C. 3D-printed patient-specific applications in orthopedics. Orthop. Res. Rev. 2016, 8, 57–66. [Google Scholar] [CrossRef] [Green Version]
- Yap, Y.L.; Sing, S.L.; Yeong, W.Y. A review of 3D printing processes and materials for soft robotics. Rapid Prototyp. J. 2020, 26, 1345–1361. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, F.; Zhu, X.; Yong, K.-T.; Gu, G. Stimuli-responsive functional materials for soft robotics. J. Mater. Chem. B 2020, 8, 8972–8991. [Google Scholar] [CrossRef] [PubMed]
- Keneth, E.S.; Kamyshny, A.; Totaro, M.; Beccai, L.; Magdassi, S. 3D printing materials for soft robotics. Adv. Mater. 2021, 33, 2003387. [Google Scholar] [CrossRef]
- Buswell, R.; Soar, R.; Gibb, A.; Thorpe, A. Freeform construction: Mega-scale rapid manufacturing for construction. Autom. Constr. 2007, 16, 224–231. [Google Scholar] [CrossRef] [Green Version]
- Maconachie, T.; Leary, M.; Lozanovski, B.; Zhang, X.; Qian, M.; Faruque, O.; Brandt, M. SLM lattice structures: Properties, performance, applications and challenges. Mater. Des. 2019, 183, 108137. [Google Scholar] [CrossRef]
- Jadayel, M.; Khameneifar, F. Improving geometric accuracy of 3D printed parts using 3D metrology feedback and mesh morphing. J. Manuf. Mater. Process. 2020, 4, 112. [Google Scholar] [CrossRef]
- Austermann, J.; Redmann, A.J.; Dahmen, V.; Quintanilla, A.L.; Mecham, S.J.; Osswald, T.A. Fiber-reinforced composite sandwich structures by co-curing with additive manufactured epoxy lattices. J. Compos. Sci. 2019, 3, 53. [Google Scholar] [CrossRef] [Green Version]
- Tao, W.; Leu, M.C. Design of lattice structure for additive manufacturing. IEEE Xplore 2016, 325–332. [Google Scholar]
- Chen, W.; Zheng, X.; Liu, S. Finite-element-mesh based method for modeling and optimization of lattice structures for additive manufacturing. Materials 2018, 11, 2073. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boniotti, L.; Beretta, S.; Foletti, S.; Patriarca, L. Strain concentrations in BCC micro lattices obtained by AM. Proc. Struct. Integr. 2017, 7, 166–173. [Google Scholar] [CrossRef]
- Gümrük, R.; Mines, R.A.W. Compressive behaviour of stainless steel micro-lattice structures. Int. J. Mech. Sci. 2013, 68, 125–139. [Google Scholar] [CrossRef]
- Pugliese, R.; Beltrami, B.; Regondi, S.; Lunetta, C. Polymeric biomaterials for 3D printing in medicine: An overview. Ann. 3D Print. Med. 2021, 2, 100011. [Google Scholar] [CrossRef]
- Panetta, J.; Zhou, Q.; Malomo, L.; Pietroni, N.; Cignoni, P.; Zorin, D. Elastic textures for additive fabrication. ACM Trans. Graph. 2015, 34, 135. [Google Scholar] [CrossRef] [Green Version]
- Silva, R.; Torres, M.; Viñuela, J.; Zamora, A. Manufacturing and characterization of 3D miniature polymer lattice structures using fused filament fabrication. Polymers 2021, 13, 635. [Google Scholar] [CrossRef]
- Olubamiji, A.D.; Izadifar, Z.; Si, J.L.; Cooper, D.M.; Eames, B.F.; Chen, D.X. Modulating mechanical behaviour of 3D-printed cartilage-mimetic PCL scaffolds: Influence of molecular weight and pore geometry. Biofabrication 2016, 8, 025020. [Google Scholar] [CrossRef]
- Eshraghi, S.; Das, S. Micromechanical finite-element modeling and experimental characterization of the compressive mechanical properties of polycaprolactone-hydroxyapatite composite scaffolds prepared by selective laser sintering for bone tissue engineering. Acta Biomater. 2012, 8, 3138–3143. [Google Scholar] [CrossRef] [Green Version]
- Soufivand, A.A.; Abolfathi, N.; Hashemi, S.A.; Le, S.J. Prediction of mechanical behavior of 3D bioprinted tissue-engineered T scaffolds using finite element method (FEM) analysis. Addit. Manuf. 2020, 33, 101181. [Google Scholar] [CrossRef]
- Şerban, D.A.; Marşavina, L.; Silberschmidt, V. Behaviour of semi-crystalline thermoplastic polymers: Experimental studies and simulations. Comput. Mater. Sci. 2012, 52, 139–146. [Google Scholar] [CrossRef]
- Abbasi, A.A.; Ahmadian, M.T.; Alizadeh, S.T.A. Application of hyperelastic models in mechanical properties prediction of mouse oocyte and embryo cells at large deformations. In Proceedings of the ASME 2016 International Mechanical Engineering Congress and Exposition, Phoenix, AZ, USA, 11–17 November 2016. [Google Scholar]
- Kondo, T.; Hashimoto, R.; Ohrui, Y.; Sekioka, R.; Nogami, T.; Muta, F.; Seto, Y. Analysis of chemical warfare agents by portable Raman spectrometer with both 785nm and 1064nm excitation. Forensic Sci. Int. 2018, 291, 23–38. [Google Scholar] [CrossRef] [PubMed]
- Tlegenov, Y.; Hong, G.S.; Lu, W.F. Nozzle condition monitoring in 3D printing. Robot. Comput. Integr. Manuf. 2018, 54, 45–55. [Google Scholar] [CrossRef]
- Patterson, R.M.; Salatin, B.; Janson, R.; Salinas, S.P.; Mullins, M.J.S. A current snapshot of the state of 3D printing in hand rehabilitation. J. Hand. Ther. 2020, 33, 156–163. [Google Scholar] [CrossRef]




| Unit Cell Size (mm) | Ecomp Reticular (MPa) | Ecomp Triangular (MPa) | Ecomp Hexagonal (MPa) | Ecomp Wavy (MPa) |
|---|---|---|---|---|
| 1 (nozzle 0.4) | - | - | 100.74 | 116.48 |
| 2 (nozzle 0.4) | 33.92 | 27.61 | 3.46 | 28.80 |
| 3 (nozzle 0.4) | 14.47 | 11.93 | 0.34 | 12.80 |
| 4 (nozzle 0.4) | 7.80 | 6.69 | - | - |
| 5 (nozzle 0.4) | - | - | - | - |
| 1 (nozzle 0.8) | - | - | - | |
| 2 (nozzle 0.8) | - | - | - | 88.00 |
| 3 (nozzle 0.8) | 40.25 | 33.05 | 2.25 | 38.40 |
| 4 (nozzle 0.8) | 22.04 | 18.43 | 0.28 | 21.40 |
| 5 (nozzle 0.8) | 14.52 | 11.70 | 0.07 | - |
| Ecomp | Linear | Nonlinear | Linear | Nonlinear | Linear | Nonlinear | Linear | Nonlinear |
|---|---|---|---|---|---|---|---|---|
| Unit Cell Size (mm) | Reticular (MPa) | Triangular (MPa) | Hexagonal (MPa) | Wavy (MPa) | ||||
| 1 (nozzle 0.4) | - | - | - | - | 100.74 | 89.86 | 116.48 | 101 |
| 2 (nozzle 0.4) | 33.92 | 29.85 | 27.61 | 24.07 | 3.46 | 3.39 | 28.80 | 25 |
| 3 (nozzle 0.4) | 14.47 | 11.98 | 11.93 | 10.28 | 0.34 | 0.34 | 12.80 | 11.11 |
| 4 (nozzle 0.4) | 7.80 | 6.38 | 6.69 | 5.74 | - | - | - | - |
| 5 (nozzle 0.4) | - | - | - | - | - | - | - | - |
| 1 (nozzle 0.8) | - | - | - | - | - | - | - | - |
| 2 (nozzle 0.8) | - | - | - | - | - | - | 88.00 | 77.5 |
| 3 (nozzle 0.8) | 40.25 | 35.18 | 33.05 | 28.63 | 2.25 | 2.18 | 38.40 | 33.56 |
| 4 (nozzle 0.8) | 22.04 | 19.18 | 18,43 | 15.9 | 0.28 | 0.29 | 21.4 | 18.73 |
| 5 (nozzle 0.8) | 14.52 | 12.28 | 11.7 | 10.14 | 0.07 | 0.07 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sala, R.; Regondi, S.; Pugliese, R. Design Data and Finite Element Analysis of 3D Printed Poly(ε-Caprolactone)-Based Lattice Scaffolds: Influence of Type of Unit Cell, Porosity, and Nozzle Diameter on the Mechanical Behavior. Eng 2022, 3, 9-23. https://doi.org/10.3390/eng3010002
Sala R, Regondi S, Pugliese R. Design Data and Finite Element Analysis of 3D Printed Poly(ε-Caprolactone)-Based Lattice Scaffolds: Influence of Type of Unit Cell, Porosity, and Nozzle Diameter on the Mechanical Behavior. Eng. 2022; 3(1):9-23. https://doi.org/10.3390/eng3010002
Chicago/Turabian StyleSala, Riccardo, Stefano Regondi, and Raffaele Pugliese. 2022. "Design Data and Finite Element Analysis of 3D Printed Poly(ε-Caprolactone)-Based Lattice Scaffolds: Influence of Type of Unit Cell, Porosity, and Nozzle Diameter on the Mechanical Behavior" Eng 3, no. 1: 9-23. https://doi.org/10.3390/eng3010002
APA StyleSala, R., Regondi, S., & Pugliese, R. (2022). Design Data and Finite Element Analysis of 3D Printed Poly(ε-Caprolactone)-Based Lattice Scaffolds: Influence of Type of Unit Cell, Porosity, and Nozzle Diameter on the Mechanical Behavior. Eng, 3(1), 9-23. https://doi.org/10.3390/eng3010002







