Analysis of Available Components and Performance Estimation of Optical Multi-Band Systems

Abstract

Optical multi-band (OMB) systems exploit the low-loss spectrum of the single mode fiber (SMF) and are key enablers to increase the transportation capacity and node connectivity of already deployed systems. The realization of OMB systems is mainly based on the technological advances on the component and system level, and for this purpose, a broad gamut of various structural elements, such as transceivers, amplifiers, filters, etc. have been commercialized already or are close to commercialization. This wide range of options, which aid in unlocking the concurrent transmission in all amplification bands, is reviewed here for the first time, whilst their pros and cons as well as their limitations are discussed. Furthermore, the needs for additional components in order to fully exploit the ≈390 nm low-loss wavelength range of SMF, which spans from 1260 to 1650 nm, are highlighted. Finally, based on a physical layer formalism, which incorporates the impact of the most important physical layer constraints for an OMB system, the attainable capacity and transparent reach of each amplification band are quantified.

1. Introduction

To meet the increasing demand for higher bandwidth and more dynamic traffic patterns of the emerging Enhanced Fiber Broad Band (eFBB) services, such as ultra-high-definition video streaming, cloud office, and virtual/augmented reality [1], the ultimate bandwidth of the SMF has to be exploited [2,3,4]. A potential solution to this issue is the optical multi-band (OMB) system, which can fully exploit the second and third transmission windows of SMFs (practically, the 1260 to 1650 nm wavelength range) and increase the capacity of currently deployed systems by as much as an order of magnitude. However, research on OMB systems is still in its infancy, and the related work is mainly experimental, focusing more on C and L-bands and lesser on O, E, and S-bands [5,6,7,8,9].

The realization of an OMB system depends on the availability of optical components, such as optical transceivers, amplifiers, filters etc., for a number of optical transmission bands. In this work, we tabulate the state-of-the-art details for these commercially and experimentally available structural elements, and we discuss their specifications and their impact on the overall system performance. We show that using the currently available technology, the deployment of an OMB system is feasible only for a confined spectral range, and an important amount of work has to be carried out, along with the introduction of novel optical components, to unlock the entire low attenuation range of the single-mode optical fiber.

Next, we employ a novel physical layer formalism, which calculates the performance of an OMB transmission system considering an amplification scheme based on commercially available rare-earth doped fiber amplifiers for the S, C and L-bands. The proposed expression is closed-form and incorporates the impact of the main transmission impairments of an OMB system, which are the Amplified Spontaneous Emission (ASE) noise accumulation, the Four-Wave-Mixing (FWM) crosstalk, and the Stimulated Raman Scattering (SRS). Using this formula, we calculate the attainable capacity and transparent reach for each band and for three different modulation formats, namely polarization multiplexing (PM) quadrature phase shift keying (QPSK), PM-16 quadrature amplitude modulation (QAM), and 64QAM, discussing their performance trade-offs.

The paper is organized as follows: Section 2 includes a review of commercially available state-of-the-art components (such as transceivers, amplifiers, and filters), Section 3 attempts a quantification of the capacity and the transparent reach of an OMB system employing commercially available equipment, Section 4 discusses the main findings of our work, and Section 5 concludes the paper.

2. Review of Commercially Available Components

2.1. Transceivers

In this section, we decouple the types of transceivers into two categories based on their target applications. The first category incorporates transceivers for long-reach purposes, e.g., core networks, while the second one includes transceivers for short-reach applications, e.g., access and intra-data center applications. The details of the transceivers for the first category are tabulated in

Table 1. Commercially available transceivers for regional and long-haul transmission.

Type	Modulation Format	Symbol Rate	Channel Spacing	Data Rate	Required OSNIR (for BER = 10−3)
100 G	PM-QPSK	32 Gbaud	37.5 GHz	100 Gb/s	9.8 dB
200 G	PM-16QAM	32 Gbaud	37.5 GHz	200 Gb/s	16.55 dB
400 G	PM-16QAM	63 Gbaud	75 GHz	400 Gb/s	16.55 dB
	PM-64QAM	42 Gbaud	50 GHz	400 Gb/s	22.5 dB
	PCS-16QAM	80–95 Gbaud	100 GHz	400 Gb/s	varies
800 G	PM-16QAM	128 Gbaud	150 GHz	800 Gb/s	16.55 dB
	PM-32QAM	96 Gbaud	112.5 GHz	800 Gb/s	19.5 dB
	PM-64QAM	80 Gbaud	100 GHz	800 Gb/s	22.5 dB
	PCS-64QAM	90 Gbaud	100 GHz	800 Gb/s	N/A
200–800 G	Probabilistic Shaping	60–95 Gbaud	75–100 GHz	200–800 Gb/s	varies

. To compose this table, we are based on both commercially available solutions and experimental components such as [10,11]. The first observation is that a 200 G line rate can be attained by increasing the modulation format, from PM-QPSK to 16QAM, simply doubling the number of bits per symbol. However, this comes with the cost of a higher value of required optical to signal plus interference ratio (OSNIR) in order to attain the same Bit Error Rate (BER), which will directly result in a smaller attainable reach. Secondly, the 400 G and 800 G line rates can be realized using a number of different options. Each alternative has its own trade-offs, e.g., lower modulation formats such as 16QAM, require a lower OSNIR in order to attain the same BER as 64QAM. This will lead to a higher reach for the lower cardinality modulation format; however, this reach is traded for a lower number of channels, as they consume a higher channel bandwidth. In this case, capacity is traded with connectivity, and the optimal solution is based solely on the high-level design set by the network operator. The OSNIR shown in the last column of Table 1 is calculated over the whole channel bandwidth while designating the target pre-Forward Error Correction (FEC) value. The existence of a FEC, e.g., [12], is considered, which can make a pre-FEC BER of 10⁻³ shrink to a post-FEC BER of less than 10⁻¹². The exact resulting performance after the FEC depends on the employed algorithm and its complexity; in commercially available transceivers, a common option is soft-decision FEC.

Next, we tabulate the details of indicative commercially available transceivers for short-reach applications (

Table 2. Commercially available transceivers for data center interconnection and access applications.

Type	Band	Line Rate	Distance	Output Power	Sensitivity
CFP8 Transceiver	O	400 Gb/s	<2 km	N/A	N/A
CFP4/CFP2Transceiver	O	100 Gb/s	<10 km	N/A	N/A
200 G and 400 G Coherent Transceiver CFP2-DCO	C	400 Gb/s	N/A	>−10 dBm	−30/>−20 dBm
100 G Coherent Transceiver CFP-DCO	C	100 Gb/s	N/A	>−5 dBm	>−28 dBm
400 G QSFP-DCO Coherent Transceiver	C	400 Gb/s	<120 km	−10dBm	>−12 dBm
400 G Transceiver DD-QSFP-DCO	C	400 Gb/s	<120 km	−10dBm	>−12 dBm
16G-CWDM SFP+ Transceiver	L	16 Gb/s	<40 km	>−1 dBm	−16 dBm
XFP Transceiver	O	10 Gb/s	<40 km	>−5 dBm	−16 dBm
SFP Transceiver	O, S	1 Gb/s	<40km	>−6 dBm	−23 dBm

). These transceivers are part of the small form-factor pluggable (SFP) category of transceivers, which are mainly dedicated to access and/or shorter reach applications. SFP transceivers are hot-pluggable network interface modules which show some important features such as compactness, flexibility, cost-effectiveness, and high data rates. Based on their characteristics and application, they can be delineated in various categories such as simple SFP, SFP+, XFP, QSPF, and CFP. For example, XFP, where X stands for “10”, and SFP+ are improved versions of simple SPF that can attain significantly higher data rates, e.g., 10 Gb/s compared with the 1 Gb/s rate of the simple SFP. Furthermore, QSFP, where Q stands for “Quad”, and CFP, where C stands for “100”, can extend further the data rate to 100 Gb/s and beyond, as they can employ multiple optical channels.

From Table 2, it is evident that the main operational bands for these commercially available components are the O and C-band. This is expected, as the transmission bands for the upstream direction of important access standards, such as Gigabit-PON (GPON), 10G-EPON, and XG(S)-PON is O-band, while the C-band is also the premium band in current transmission systems due to its low fiber attenuation. Furthermore, the output power is an important parameter that can increase the overall power budget allowing (a) to support a larger number of users, as the number of power splits in a Passive Optical Network (PON) is higher and (b) to extend the transmission reach, as the tolerable link loss can be greater. Finally, a low sensitivity receiver is desirable in an optical system as it can detect an even smaller signal, leading to an improved power budget.

2.2. Amplifiers

Optical amplification is a critical procedure in optical transmission as it can rectify the signal power attenuated within the optical fiber. There are numerous commercially available optical amplifiers that can be exploited for an OMB system, the most indicative of which are illustrated in

Table 3. Commercially available amplifiers and their characteristics.

Amplifier Type	Operating Bands	Flat Gain Wavelength Range	Gain	Gain Flatness	Noise Figure	Max Output Power
EDFA	mainly L	1560–1610 nm	<35 dB	±2 dB	<6 dB	>+22 dBm
	mainly C	1525–1565 nm	<38 dB	±2.5 dB	<5 dB	>+17 dBm
	L	1575–1605 nm	<35 dB	±2 dB	≤7 dB	≥+27 dBm
SOA	S, C, L	1520–1580 nm	<20 dB	±0.3 dB	7 dB	16 dBm
	1050–1080 nm	1050–1080 nm	<40 dB	0.3 dB	8 dB	18 dBm
	O	1280–1300 nm	<25 dB	±1.5 dB	7.5 dB	12 dBm
RAMAN	mainly C, L	1525–1605 nm	<18 dB	<±1.5 dB	N/A	31.8 dBm
	L	1565–1605 nm	<15 dB	<±1.5 dB	N/A	28.7 dBm
YDFA	1055–1075 nm	1055–1075 nm	<30 dB	N/A	<6 dB	>+20 dBm/23 dBm on request
	1025–1075 nm	1025–1075 nm	<22 dB	±5 dB	<8 dB	<+23 dBm
PDFA	O	1280–1320nm	<35dB	±2 dB	<7dB	>+20 dBm
TDFA	S	1470–1520nm	<30dB	±0.25 dB	<7dB	+19 dBm

. In particular, the Doped Fiber Amplifier (DFA) is a family of amplification components that shows desirable characteristics for an OMB system, such as the sufficient flat gain over a large spectral extent, the low noise figure, and the high output power. In Figure 1, we illustrate the attainable gain and the noise figure of indicative commercially available amplifiers for the O, S, C, and L-bands, while for the E-band, the experimental neodymium (N) DFA of [13] is considered. Another considerable DFA solution for the E-band can be the bismuth (B) DFA of [14]. As it is evident from Figure 1, the amplification technology for the S, C, and L-bands is more mature compared with the O and E-bands, as it can provide a higher overall gain and a lower noise figure compared with praseodymium (P) DFA and NDFA. These are important drawbacks for the exploitation of the lower bands, as a network operator may resort to a higher number of PDFAs and NDFAs to restore the optical power compared with thulium (T) and erbium (E) DFAs, which will directly lead to higher CapEx and OpEx costs. Furthermore, due to the increased noise figure, the overall physical layer performance of the channels in the O and E-band is expected to be lower compared with channels in the S, C, and L-bands.

The second family of optical amplification components is the semiconductor optical amplifier (SOA). SOAs can be exploited in all bands, as shown in Table 3; however, they show some important drawbacks compared with the DFA family, such as the low saturated output power, the poor gain flatness, the significant transient effects, and the high-noise figure. On the other hand, SOAs are more compact and cheaper than EDFAs and a single SOA, as in [15], can restore the power of channels that are extended over 100 nm. Finally, SOAs as well as ytterbium (Y) DFAs can be exploited to unlock the beyond 1 μm spectral range of transmission.

The third category is the Raman amplification. This category can be exploited in all low attenuation bands similarly to SOAs. Raman-type amplifiers can achieve a sufficient flat gain activating several high-power pumps. An advantage of Raman amplifiers is that they can create arbitrary gain profiles at will, using machine learning methods, which can generate the desirable output power even in a channel basis. In this way, the gain can be tailored to each band to ensure an optimal physical layer performance in all bands of an OMB system concurrently [16]. Other significant advantages of the Raman-type amplifiers are the distributed amplification and their high output power (about 30 dBm), although such an output power may not be always desirable due to non-linear phenomena and due to safety reasons. Furthermore, due to the smaller gain of Raman amplifiers compared with DFAs, usually a hybrid Raman/EDFA amplification can be considered [17]. Overall, an important advantage of Raman amplifiers and SOAs compared with DFAs is that they offer a seamless gain over a large spectral extend, avoiding a waste of bandwidths for the frequency areas between the bands, e.g., 1510–1530 nm in Figure 1. The selection procedure for the best amplification scheme depends on the system demands. In particular, if a large system capacity is required, amplifiers that can be extended to more than a single band need to be considered. Next, if a large amplification gain is targeted, DFAs seem to be a good option, as they can provide an adequate gain over a large amplification range. Furthermore, if the impact of ASE noise is an important constraint, low-noise figure amplifiers need to be selected.

2.3. Band Filters

Band filters are also key components for the realization of an OMB system as they can segregate and combine the optical bands at the node’s ingress and egress, respectively, as well as at any amplification stage.

Table 4. Commercially available filters for OMB transmission.

Filter Type	Output Wavelength Range (Transmit)	Output Wavelength Range (Reflected)	Insertion Loss	Isolation Transmission Port/ Reflection Port	Return Loss
Band Filter	1570–1610 nm (or 1500–1564 nm)	1500–1564 nm (or 1570–1610 nm)	≤0.5 dB (passband) ≤0.6 dB (reflect)	>30 dB/>12 dB	>50 dB
	1460–1575 nm	1610–1640 nm	<0.8 dB (passband) <0.5 dB (reflect)	30 dB/15 dB	50 dB
	1500–1563 nm	1570–1640 nm	<0.7 dB (passband) <0.6 dB (reflect)	30 dB/15 dB	>50 dB
	1410–1500 nm	1510–1625 nm	<0.7 dB (passband) <0.6 dB (reflect)	30 dB/15 dB	>50 dB
	1310 nm > ±50 nm	1470–1610 nm	≤0.70 dB (passband) ≤0.45 dB (reflect)	≥45 dB/≥15 dB	≥45 dB
	1310 nm ±2 nm	1270–1355 nm, 1317–1355 nm	≤0.80 dB (passband) ≤0.45 dB (reflect)	≥20 dB/≥12 dB	≥45 dB
Passband	1563–1568 nm	1525–1561.5 nm, 1569.5–1620 nm	0.5 dB	>30 dB/>20 dB	50 dB
	1500–1520 nm	1530–1610 nm	0.8 dB (passband) 0.4 dB (reflect)	15 dB/40 dB	50 dB
	1280–1340 nm	1350–1620 nm	<1.1 dB	>50 dB/>20 dB	50 dB
Tunable	varies from 1260 to 1650 nm	varies from 1260 to 1650 nm	4.5 dB	60 dB	N/A
High-Isolation Filter	1510–1590 nm	1270–1350 nm	≤0.8 dB (passband) ≤0.6 dB (reflect)	≥40 dB/≥40 dB	≥45 dB
Pluggable Filter	1260–1360 nm, 1460–1581 nm	1610–1660 nm	<1.2 dB	N/A	>18 dB (1260–1360 nm)/ >17 dB (1460–1581 nm)
Reflector	1260–1570 nm	1610–1680 nm	<0.60 dB	>15 dB/>40 dB	>45 dB

contains indicative band filters along with their key parameters. As it is evident, using a number of them e.g., in tandem, we can obtain a multi-band filter that can multiplex/demultiplex a number of bands. The most important parameters when selecting a band filter are (a) the wavelength range, as a cascade of different band filters may be required to split/combine the bands, (b) the insertion loss, as when a number of different filters are cascaded, the amplification gain should be higher to mitigate this loss, leading to a greater ASE noise, (c) the isolation, as an inadequate value can lead to an important channel crosstalk, degrading the physical layer performance, and (d) the return loss, which has to be as high as possible to avoid filter reflections. All in all, Table 4 reveals that a broad gamut of band filters is available, spanning from static to tunable and from filters with small spectral range of a few tens of nm to hundreds of nm.

3. Quantifying the Capacity and Transparent Reach of an OMB System

3.1. System under Study

In the physical layer study of this section, we consider only Doped Fiber Amplifiers (DFAs) to compensate for the fiber losses as the DFA family shows similar operational and performance features with C-band EDFAs, and at the same time, it is a widely deployed type of amplifier. In particular, the DFAs provide a sufficiently flat gain over a substantial spectral range, allowing the effective exploitation of the low-loss attenuation spectrum of the fiber. Furthermore, they provide a relatively low-noise figure, e.g., 5.5 dB, leading to an improved physical layer performance compared with SOAs. In our case, the DFAs for the new bands are collocated in the same amplifier duct with the EDFAs, and in this way, the operator has the flexibility to add new DFAs on an “as-needed” basis, preserving the investment made on the existing networking infrastructure. Moreover, the S-band is split into S₁ and S₂ sub-bands, since a single Thulium-Doped Fiber Amplifier (TDFA) cannot ensure sufficient power per channel at its output, e.g., higher than −2 dBm, due to the large amplification range (which is ≈55 nm).

The system under investigation is a core network that consists of nodes with an inter-node distance of 150 km and employs commercially available state-of-the-art components (Figure 2). The link consists of three fiber spans of 50 km, where a fiber span is set as the distance between two consecutive amplification stages. Each amplification stage comprises four DFAs to compensate for the fiber losses and the loss induced by the band filters, which in our case is set to 2 dB. For all amplifiers, we consider the presence of Gain-Flattening Filters (GFFs), which can offer an effectively flat gain with <1 dB ripple across the band. This is mandatory in order to maintain similar power levels between the channels of each band and avoid an unpredicted impact of FWM and SRS, which may lead to a significant degradation of the OSNIR on specific channels. Furthermore, the power equalization is performed at the optical nodes, which are Wavelength-Selective-Switch (WSS)-based, maintaining the power at the egress of one node equal to the power at the egress of every other node. These technologies are available today as in [18]. The band details and the corresponding DFAs are shown in

Table 5. Spectral partitioning used in our study.

Band	Used Range (nm)	Range (nm)	Number of Channels	Noise Figure (dB)	Amplifier Type
S1 band	1455–1480	25	92	5.5	TDFA
S2 band	1485–1510	25	89	5.5	TDFA
C band	1530–1565	35	116	5.5	EDFA
L band	1570–1615	45	141	6.0	EDFA

.

3.2. Physical Layer formalism

In an OMB system, the main physical layer impairments are ASE noise, FWM, and SRS [19,20,21,22,23]. ASE noise and FWM are intra-band effects, while SRS is an inter-band effect, as it leads to a power exchange from the lowest bands, such as the S-band, toward the highest ones, such as the L-band. By making the assumption that FWM is a Gaussian Noise (GN) source, statistically independent from ASE noise, then, we can calculate the OSNIR as follows [20]:

$$\mathrm{OSNIR}=\frac{P_{ch}\cdot {\displaystyle \prod _{i=1}^{N_s}{G}_{SRS,i}}}{P_{ASE}+P_{FWM}}$$

(1)

where P_ch is the power of the examined channel, P_FWM is the power of FWM interference, G_SRS,i is the SRS gain/loss effect of the channel under observation at the ith fiber span, and P_ASE is the power of ASE noise. The OSNIR can be directly used to calculate the BER for various modulation formats as follows [24]:

$$\begin{array}{l}{\mathrm{BER}}_{\mathrm{QPSK}}=\frac{1}{2}erfc\left(\sqrt{\frac{\mathrm{OSNIR}}{2}}\right)\\ {\mathrm{BER}}_{16\mathrm{QAM}}=\frac{3}{8}erfc\left(\sqrt{\frac{\mathrm{OSNIR}}{10}}\right)\\ {\mathrm{BER}}_{64\mathrm{QAM}}=\frac{7}{24}erfc\left(\sqrt{\frac{\mathrm{OSNIR}}{42}}\right)\end{array}$$

(2)

Next, the power of ASE noise is given by

$$P_{ASE}={\displaystyle \sum _{i=1}^{N_s}\left[hf\left(N{F}_i\cdot G_i-1\right)B_0{\displaystyle \prod _{r=i+1}^{N_s}{G}_{SRS,r}}\right]}$$

(3)

where G_i is the amplifier gain and NF_i is the noise figure at the ith amplification stage. N_s is the number of fiber spans a channel is traversing before its power is equalized using e.g., a WSS.

The SRS gain/loss effect for the jth wavelength in the ith fiber span, is given by [20,25]:

$$G_{SRS,i}=P_{tot,SRS}\frac{e^{\frac{g^{\prime }\cdot B\cdot L_{eff}}{2A_e}\left(j-1\right)P_{tot,SRS}}}{{\displaystyle \sum _m\left[P_{m,0}{e}^{\frac{g^{\prime }\cdot B\cdot L_{eff}}{2A_e}\left(m-1\right)P_{tot,SRS}}\right]}}$$

(4)

where g′ is the Raman gain slope equal to 4.9 × 10⁻²⁷ m/(W·Hz), A_e is the effective cross-sectional area of the fiber equal to 80 μm², and P_m,0 is the power of the mth interfering channel at fiber input. The term P_tot,SRS sums the power of channels that interact within the SRS gain bandwidth, which in our work is considered as 15 THz, since we use the triangular approximation [26]. This wide SRS gain bandwidth makes the OSNIR of one band a function of the power level of the channels in all other bands.

To estimate the impact of FWM, we use the expression of P_FWM in [27], which was shown in [19] to be in a very good agreement with numerical results across the S, C, and L-bands:

$$\begin{array}{ll}{P}_{FWM}& =\frac{32}{27}\frac{{\gamma }^2{L}_{eff}{}^2{P}_{ch}{}^3{N}_s{}^{2}c}{{\lambda }^2{B}^{2}D\sqrt{z_1}}\left(1+\frac{4e^{-aL}}{{\left(1-e^{-aL}\right)}^2}\right)(asinh\left(\frac{\pi {\lambda }^{2}D{B}^2}{8c}{N}_{ch}{}^{\frac{2B}{B+GB}}\sqrt{z_2}\right)-\frac{5}{3}\Phi Log\left(N_{ch}{}^{\frac{B}{B+GB}}\right))\\ & -\frac{32}{27}\frac{{\gamma }^2{L}_{eff}{}^2{P}_{ch}{}^3{N}_s{}^{2}c}{{\lambda }^2{B}^{2}D\sqrt{z_1+12L^2}}\frac{4e^{-aL}}{{\left(1-e^{-aL}\right)}^2}(asinh\left(\frac{\pi {\lambda }^{2}D{B}^2}{8c}{N}_{ch}{}^{\frac{2B}{B+GB}}\sqrt{z_2+12L^2}\right)-\frac{5}{3}\Phi Log\left(N_{ch}{}^{\frac{B}{B+GB}}\right))\end{array}$$

(5)

where $z_1={\left(\frac{2}{a}\right)}^2+2L^2\left(N_s{}^2-1\right)/{\left({\displaystyle \sum _{k=x_1}^{x_2}\frac{1}{1+{\left(2k\pi /\left(aL\right)\right)}^2}}\right)}^2$, $z_2={\left(\frac{2}{a}\right)}^2+2L^2\left(N_s{}^2-1\right)$, $x_1=-\frac{{\lambda }^2{B}^{2}DL{N}_{ch}{}^2}{16c}$, $x_2=\frac{{\lambda }^2{B}^{2}DL{N}_{ch}{}^2}{2c}$, γ is the non-linear fiber coefficient, which takes the value of 1.31744 W⁻¹·km⁻¹, D is the local dispersion, and a is the fiber attenuation parameter, which are different in each band and can be extracted from Figure 2 of [20].

Table 6. Operational parameters for each amplification band (extracted from [20]).

Parameter/Band	S1	S2	C	L
λ (nm)	1467.5	1497.5	1547.5	1592.5
a (dB/km)	0.246	0.23	0.211	0.209
D (ps/nm/km)	12.1	14	16.9	19.4

illustrates the a, D, and λ for the central wavelength of each band. Next, L is the span length, N_ch is the number of channels of the band, B is the channel bandwidth, and B + GB is the channel spacing, which is equal to 37.5 GHz in this work. Finally, Φ is a parameter that depends on the modulation format and takes the value of 1 for QPSK, 17/25 for 16QAM, and 13/21 for 64QAM.

The next step is to calculate the power of the channels in each band at the beginning of a link, in a way that ensures a balanced OSNIR performance across all channels at the end of the link. For this purpose, we employed closed-form expressions instead of more complex methods, e.g., Split Step Fourier Method, in order to perform power optimizations in a reasonable-time manner. The power arrangement is an important procedure, as it can minimize the impact of SRS, which as an inter-band effect can deplete the power of the channels in the lower bands degrading significantly their OSNIR. At the same time, it can also increase the channel power in the higher bands, stressing them toward the non-linear regime, where the increased FWM can severely degrade their OSNIR. As a result, a collective optimization of the OSNIR performance across all bands is required. For this purpose, we use the method of [23], which minimizes a suitably chosen merit function subject to specific power constraints P_min and P_max as follows:

$$\begin{array}{l}A\left(P_{S_1},P_{S_2},P_C,P_L\right)={\displaystyle \sum _b{\left(\frac{1}{{\mathrm{OSNIR}}_b\left(P_{S_1},P_{S_2},P_C,P_L\right)}\right)}^2}\\ minimize A\left(P_{S_1},P_{S_2},P_C,P_L\right)\\ subject to P_{min}\le P_{S_1},P_{S_2},P_C,P_L\le +1 \mathrm{dBm}\end{array}$$

(6)

where $P_{S_1},P_{S_2},P_C,P_L$ are the wanted quantities, which represent the power of the middle channel of S₁, S₂, C, and L-bands at the beginning of each link. P_min is set in order to avoid a catastrophic OSNIR degradation due the small channel power, while P_max is set to e.g., +1 dB, to avoid a DFA operation in its saturation regime, which can result in insufficient amplification gain and consequently to a severe OSNIR degradation. In essence, Equation (6) minimizes the OSNIR difference between the various exploited bands, providing a more balanced OSNIR performance across the entire spectrum. Using this method, the appropriate values of each band are calculated, allowing each band to swing between the ASE-limited and NL-limited regime, mitigating in this way the catastrophic SRS impact on the S-band. In this work, we calculate the transmission performance for a system where all bands are fully loaded with channels, which is the worst possible scenario in terms of physical layer performance.

3.3. Results

In this section, we employ the physical layer formalism presented in the previous section to investigate the attainable transparent reach and capacity for an OMB system with S, C, and L-bands. Using the power allocation method of Equation (6), the computed optimal power for the middle channel of each band is −0.2, −1.4, −8.3, and −9 dBm for S₁, S₂, C, and L-bands, respectively. From these power levels, it is evident that the S-band requires a significantly higher power compared with C and L in order to compensate for the power depletion due to SRS. Moreover, the power of C and L-bands stresses them to operate in a deeply linear regime, where ASE noise is the dominant effect. Furthermore, three modulation formats are examined, namely PM-QPSK, PM-16QAM, and PM-64QAM, where each one requires a different OSNIR value in order to attain the same BER, as it is obvious from Equation (2). In particular, we target a BER of 10⁻³ for which, from Equation (2), the required OSNIR is 9.8, 16.55, and 22.5 dB for PM-QPSK, PM-16QAM, and PM-64QAM, respectively. Finally, the baud rate is set to 32 Gbaud, and the channel spacing equals 37.5 GHz.

The OSNIR when the signal traverses a different number of optical nodes is illustrated in Figure 3. The inter-node distance is set to 150 km, and this link comprises three fiber spans of 50 km. The target OSNIR, which leads to a BER equal to 10⁻³ for the three modulation formats, is also plotted with dashed lines. As it is evident, the C and L-bands, which are favored due to SRS, show a higher OSNIR performance compared with S₁ and S₂-bands. In particular, the OSNIR of the S₁-band is up to 3.4 dB lower compared with the other three bands, which in turn leads to a smaller attainable transparent reach. Evidently, when PM-QPSK is employed, a transparent reach of more than 2250 km can be attained in all bands. Next, when PM-16QAM is considered, the attainable reach varies significantly between bands, from 600 km for the S₁-band to 1350 km in the C-band. Finally, the PM-64QAM can be employed to interconnect only adjacent nodes, as the OSNIR can hardly clear the threshold of 22.5 dB after 150 km in S₁ and S₂-bands.

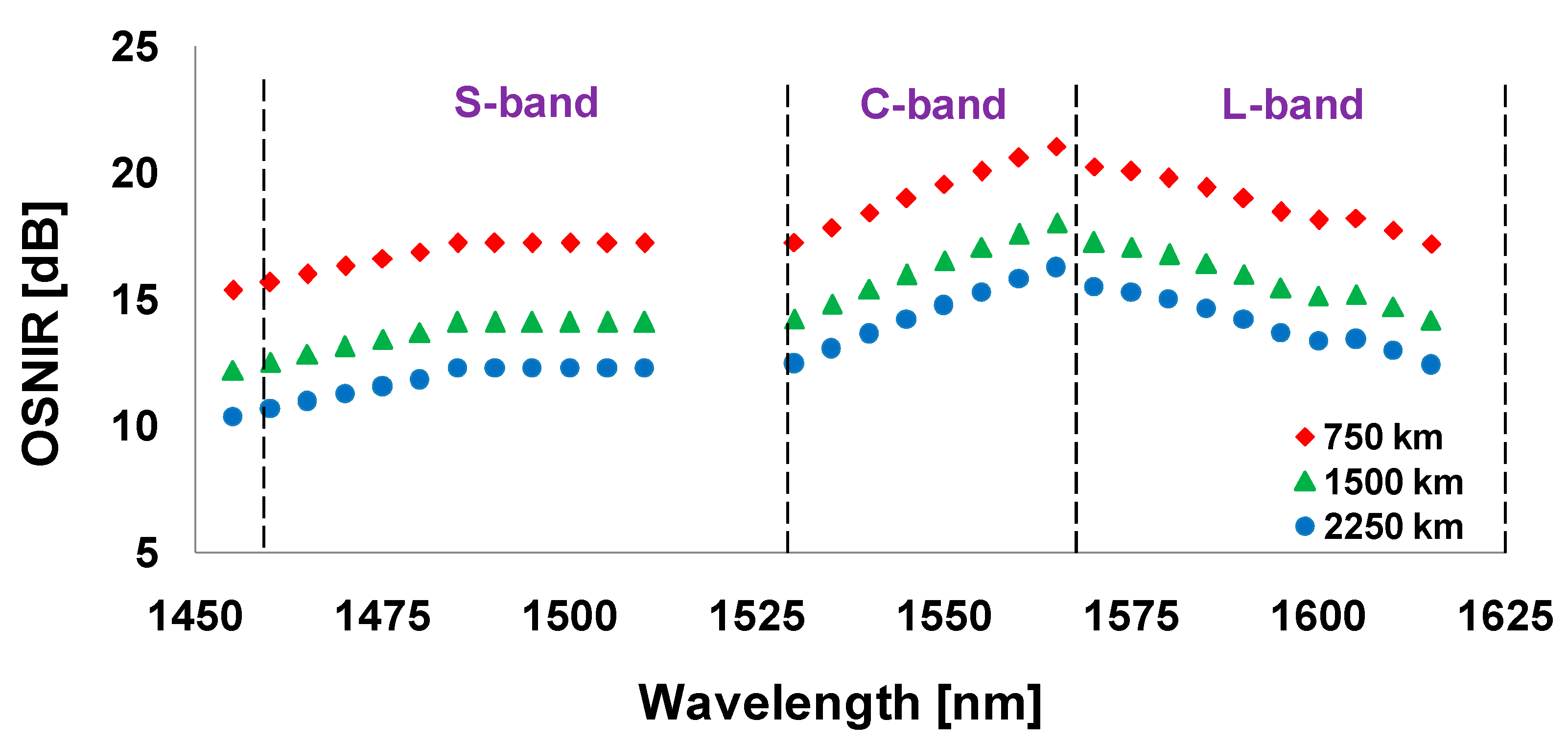
As Figure 3 shows only an instance of OSNIR for the central channel of each band, Figure 4 illustrates the OSNIR for various channels per band. We calculate the OSNIR every 5 nm after 5, 10, and 15 optical nodes. A guard band of 5 nm is also considered between S₁ and S₂-bands and between C and L-bands, whilst a larger guard band of 20 nm is set between the S₂ and C-bands. The latter guard band is set as the commercially available DFAs fail to provide sufficient gain in this spectral region. We can observe that even within the same band, there is a significant OSNIR difference of up to 4 dB between the channels located at the band edges. This clearly indicates that Equation (6) is needed to incorporate a greater number of channels from each band, and not only the central one if a flatter OSNIR over the entire band is the target. Another observation is that in order to increase further the number of channels, the unexploited 20 nm guard band between the S and C-bands has to be filled. For this purpose, the existence of a commercially available amplifier for this amplification range is mandated.

Finally, we tabulate the overall attainable capacity and transmission reach when different modulation formats are employed (

Table 7. Attainable reach and capacity per band when PM-QPSK, PM-16QAM, and PM-64QAM are considered.

Bands	PM-QPSK	PM-16QAM	PM-64QAM
S1 band	L = 2250 km C = 9.2 Tb/s	L = 450 km C = 18.4 Tb/s	L = 150 km C = 27.6 Tb/s
S2 band	L = 2250 km C = 8.9 Tb/s	L = 750 km C = 17.8 Tb/s	L = 150 km C = 26.7 Tb/s
C band	L = 2250 km C = 11.6 Tb/s	L = 750 km C = 23.2 Tb/s	L = 150 km C = 34.8 Tb/s
L band	L = 2250 km C = 14.1 Tb/s	L = 750 km C = 28.2 Tb/s	L = 150 km C = 42.3 Tb/s
Total (C × L)	98.55 (Pb/s)·km	60.18 (Pb/s)·km	19.71 (Pb/s)·km

). In this table, we show the transmission reach for the channel with the lowest OSNIR in each band. For example, the worst channel of the S₁-band attains an OSNIR slightly above 10 dB after 2250 km. This OSNIR value allows supporting a PM-QPSK modulation format for up to 2250 km, which is the attainable reach for this band when PM-QPSK is employed. Next, in order to calculate the overall capacity, we consider line rates of 100 G, 200 G, and 300 G for PM-QPSK, PM-16QAM, and PM-64QAM, respectively. The attainable capacity in each band is the product of the number of channels that clear the OSNIR threshold for a BER of 10⁻³ times the channel line rate. This analysis reveals that when a higher modulation format is enabled, the overall capacity increases; however, the bit rate (C) times transmission reach (L) product decreases. This is expected, since a migration from PM-QPSK to PM-16QAM doubles the overall capacity; however, an about four times higher OSNIR is expected in order to attain the same BER. Finally, with the proposed amplification scheme, a capacity of 43.8 Tb/s can be attained for up to 15 nodes when PM-QPSK is employed, whilst between adjacent nodes, the overall capacity can reach up to 131.4 Tb/s. A direct benchmarking of these results with relevant experimental works [5,8,15,28] is not possible, as we consider different system details, such as the amplification range, existence of WSSs, etc. However, our results are aligned with the general trends in terms of capacity, due to which more than 100 Tb/s can be attained only in short links, e.g., less than a few hundreds of km, while in longer links, a capacity of less than 100 Tb/s can be achieved. It is worth mentioning that in our study, we consider transmission only in the S, C, and L-bands, as there, the amplification technology is more mature compared with the O and E-bands. The overall capacity will be greatly enhanced as more amplifiers with the required features, e.g., flat gain over a spectral region, sufficient gain, low-noise figure, etc. for the O, the E, and even the U-band will become commercially available.

4. Discussion

Our analysis revealed that the transceivers based on the application can be decoupled into two categories, the long-reach applications and access/intra-data center applications. In the first category, there are available transceivers for 100 G to 800 G line rates. However, in order to increase the line rate per channel, we can either consume more optical bandwidth, which will result in a lower number of channels, or migrate to a higher modulation format, which will require a higher OSNIR to attain the same BER, limiting the optical reach. The most suitable solution depends solely on the high-level objective set by the network operator. Furthermore, from the category of the SFP transceivers, there are various commercially available solutions mainly for O and C-bands, as these bands are the main bands for access and short-reach transmission. Finally, the most desirable characteristics for optical transceivers are the high output power and the low receiver sensitivity, as both can lead to a longer transmission length and/or number of supported users.

Based on our study, the commercially available technology of band filters seems to be mature. By placing a number of these filters, e.g., in tandem, we can obtain a filter that can multiplex/demultiplex the desirable bands. The most important characteristics of a band filter are (a) the wavelength range, in order to exploit optimally the low-loss spectrum of the SMF, (b) the insertion loss, which has to be as low as possible to minimize the total losses, (c) the isolation, to be as high as possible, in order to avoid crosstalk, and (d) the return loss, which has to be kept in a high level to avoid the filter reflections.

Next, the amplification technology is mature in S, C, and L-bands, as there, the majority of the optical amplifiers exists. On the other hand, the technology at both the component and system level has to be developed further in O and E-bands in order to exploit the whole extent of the low-attenuation spectrum of the fiber. Our study revealed that SOAs can be employed to attain a wider amplification range; however, they suffer from low gain per channel, low gain flatness, transient effects, and the high noise figure. Furthermore, using Raman amplifiers, we can obtain the desirable gain profiles, which can tune the desirable output power in a channel basis. One significant disadvantage of Raman amplification is the low attainable gain, which compared with DFAs may require a larger number of amplifiers to restore the power of the optical channel. Finally, the rare earth amplification is designated as the winning amplification technology, as it (a) is a well-known technology due to the extensive use of EDFAs in the C-band, (b) allows for a modular engineering, allowing to introduce amplifiers on an as-needed basis, and (c) provides the desirable characteristics such as low noise figure, gain flatness, and high output power.

The proposed physical layer analysis revealed that by using the currently available components and in particular rare earth amplifiers, we can exceed a capacity of 130 Tb/s for shorter distances, e.g., 150 km, and 40 Tb/s for longer ones, e.g., >2000 km. Moreover, we highlighted a trade-off between the modulation format and the attainable reach, as the higher cardinality modulation formats require a higher OSNIR in order to attain the same BER. This resulted in a decrease in the bit rate times reach product, when a higher modulation format is employed. Finally, the adopted physical layer formalism balanced the impact of ASE, FWM, and SRS, leading to small differences of OSNIR between all bands; however, in order to attain a completely flat OSNIR within a band, a large number of channels has to be incorporated in the optimization procedure, which is the scope of an ongoing work.

5. Conclusions

In this work, we studied an OMB link with an amplification scheme based on commercially available rare-earth doped fiber amplifiers for the O, S, C, and L-bands. We derived a closed-form expression for the attainable transparent reach of each band of the link (taking into account the impact of the ASE accumulation and the FWM crosstalk), and then, we proceeded to the calculation of the link’s capacity and the capacity-length product.

The proposed physical layer analysis showed that systems based on currently available components can exceed a capacity of 130 Tb/s for short distances such as 150 km and 40 Tb/s for longer ones, e.g., >2000 km. It also illustrated the fact that there is a trade-off between the modulation format and the attainable reach (as the higher cardinality modulation formats require a higher OSNIR in order to attain the same BER), which resulted in a decreased bit rate times reach product for the higher modulation formats.