Interaction of Particles and Filter Fabric in Ultrafine Filtration
Abstract
:1. Introduction
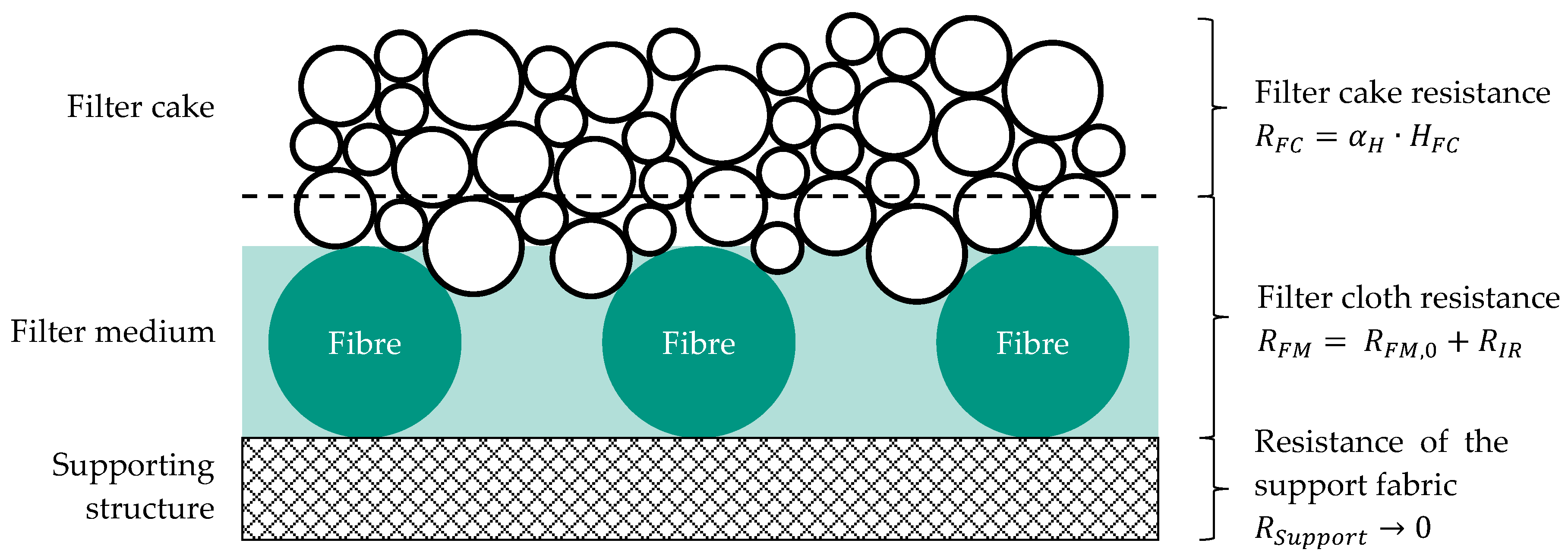
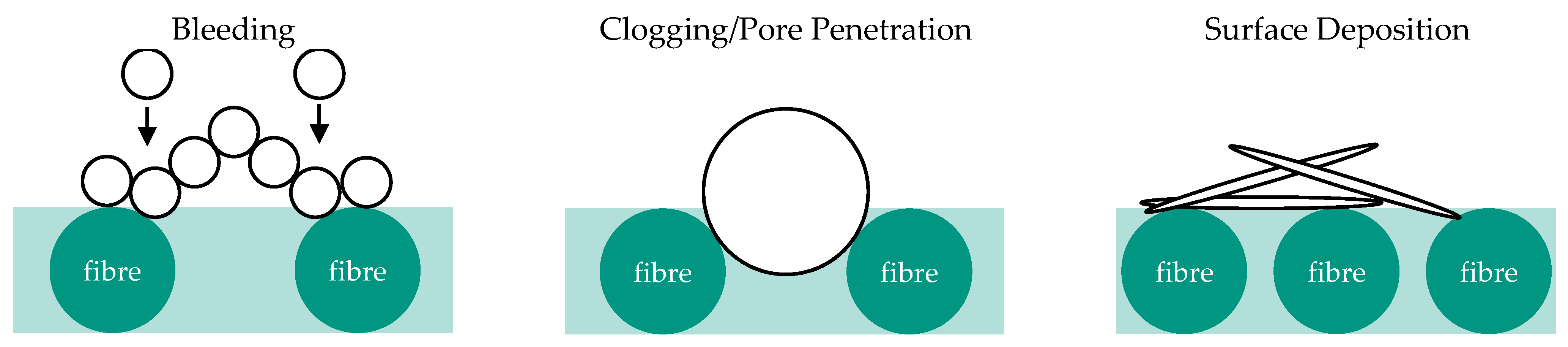
2. Mechanisms of Filtration
- Cake filtration (q = 0);
- Standard filtration (depth filtration; q = 1.5);
- Intermediate filtration (q = 1);
- Clogging filtration (q = 2).
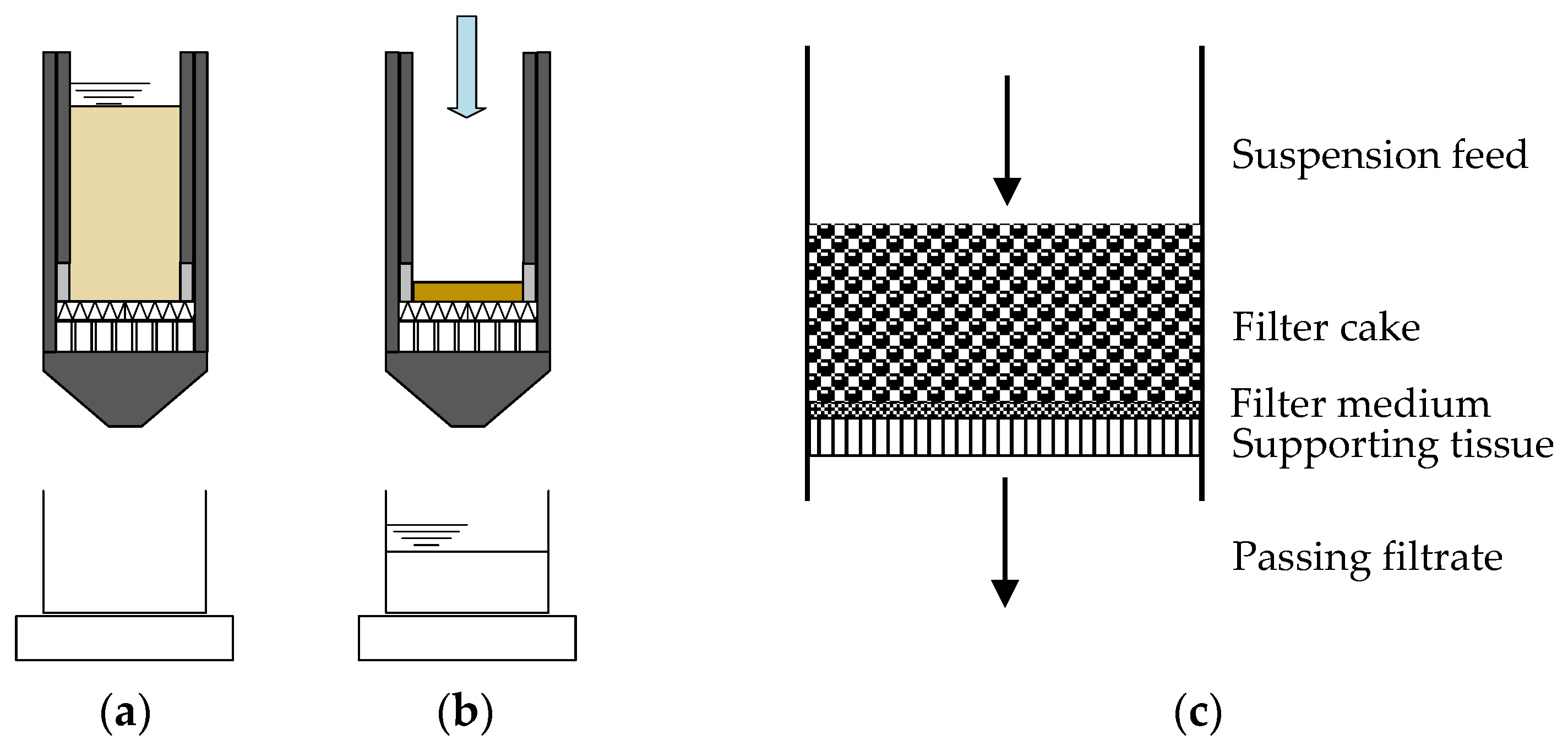
3. Method
4. Materials
- Polymer-based monofilament fabrics (plain, twill, and satin weave)
- Polymer-based multifilament fabrics (plain and twill weave)
- Metal-based monofilament fabrics (plain and twill weave)
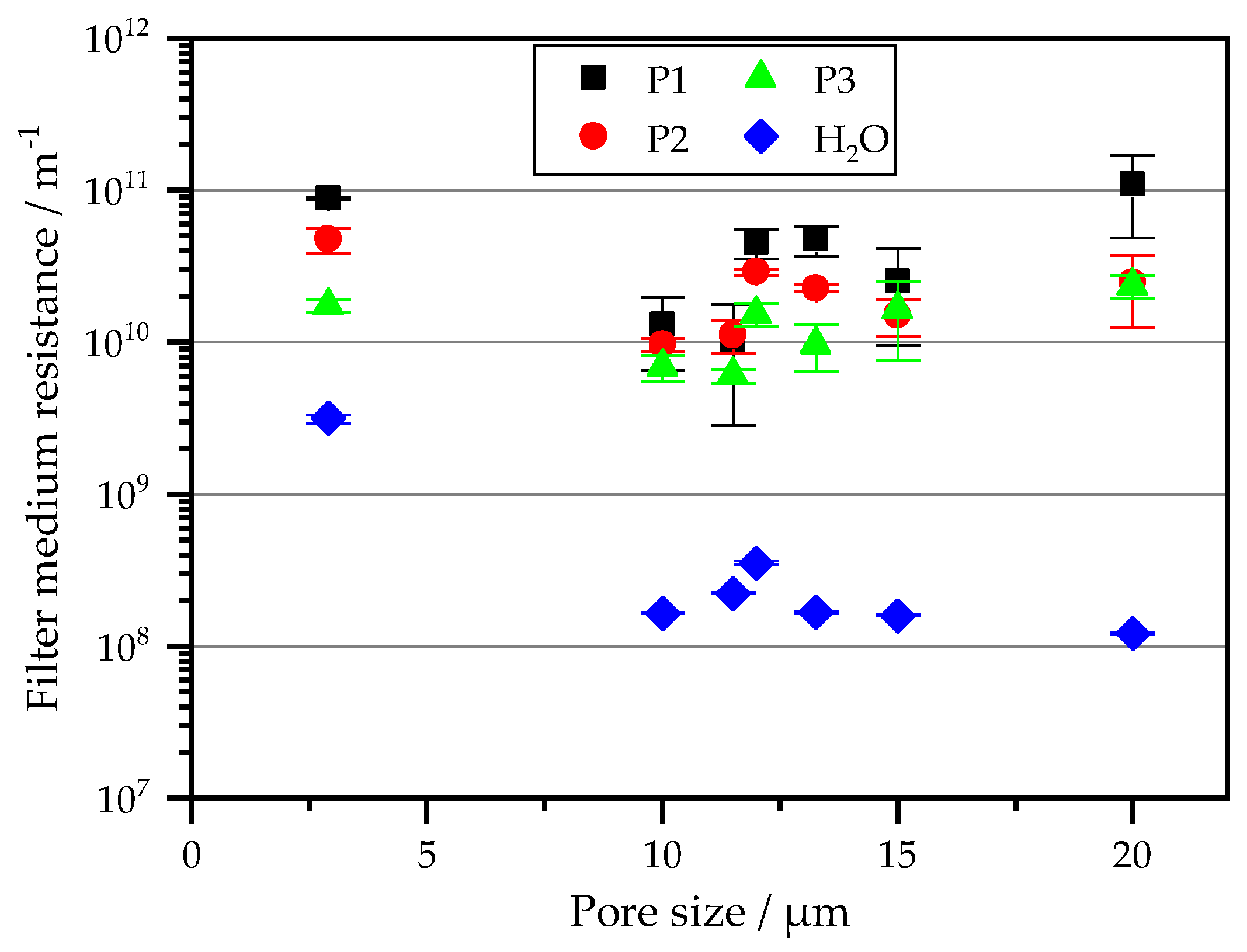
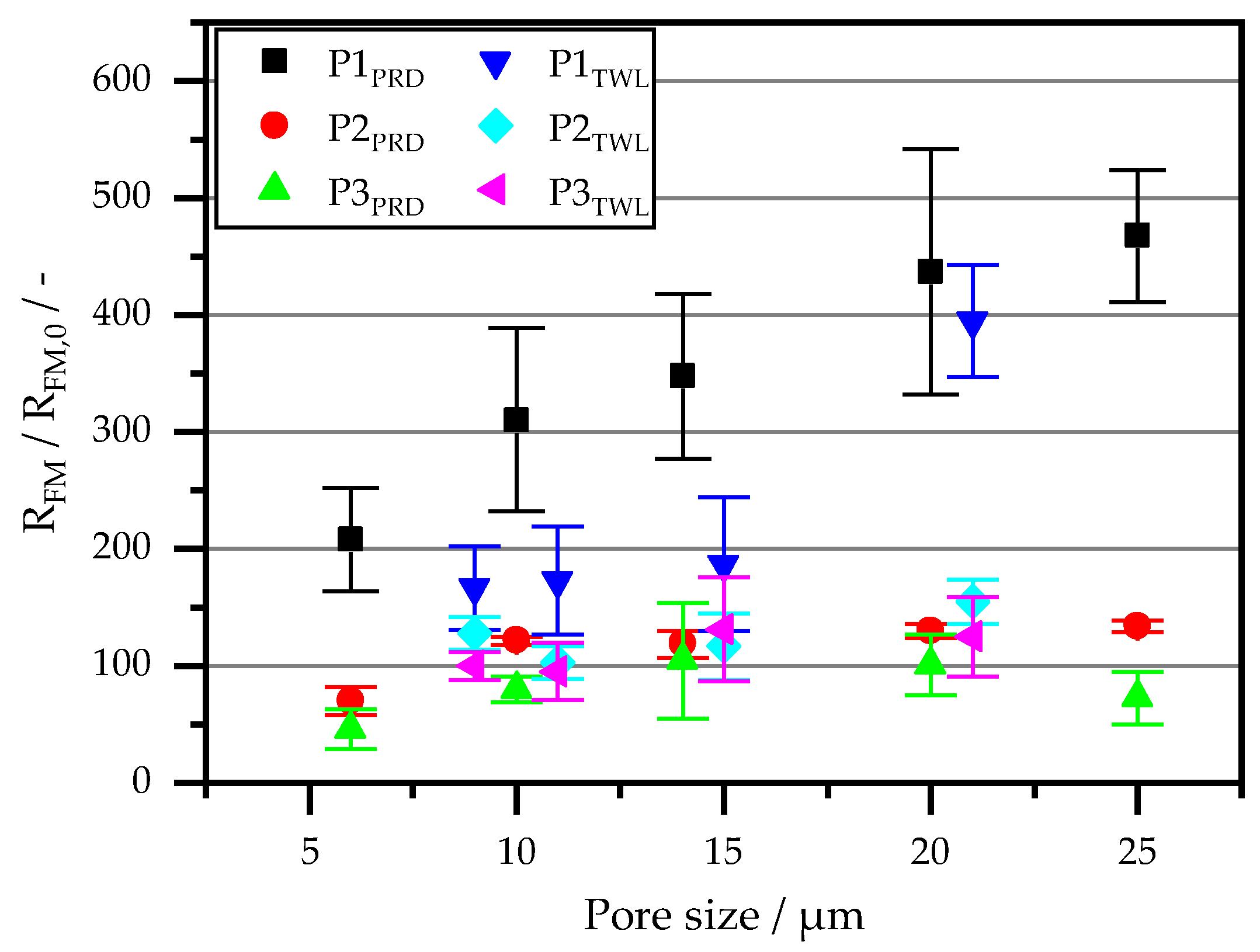
5. Interpretation
5.1. Polymer-Based Monofilament Fabrics
5.2. Polymer-Based Multifilament Fabrics
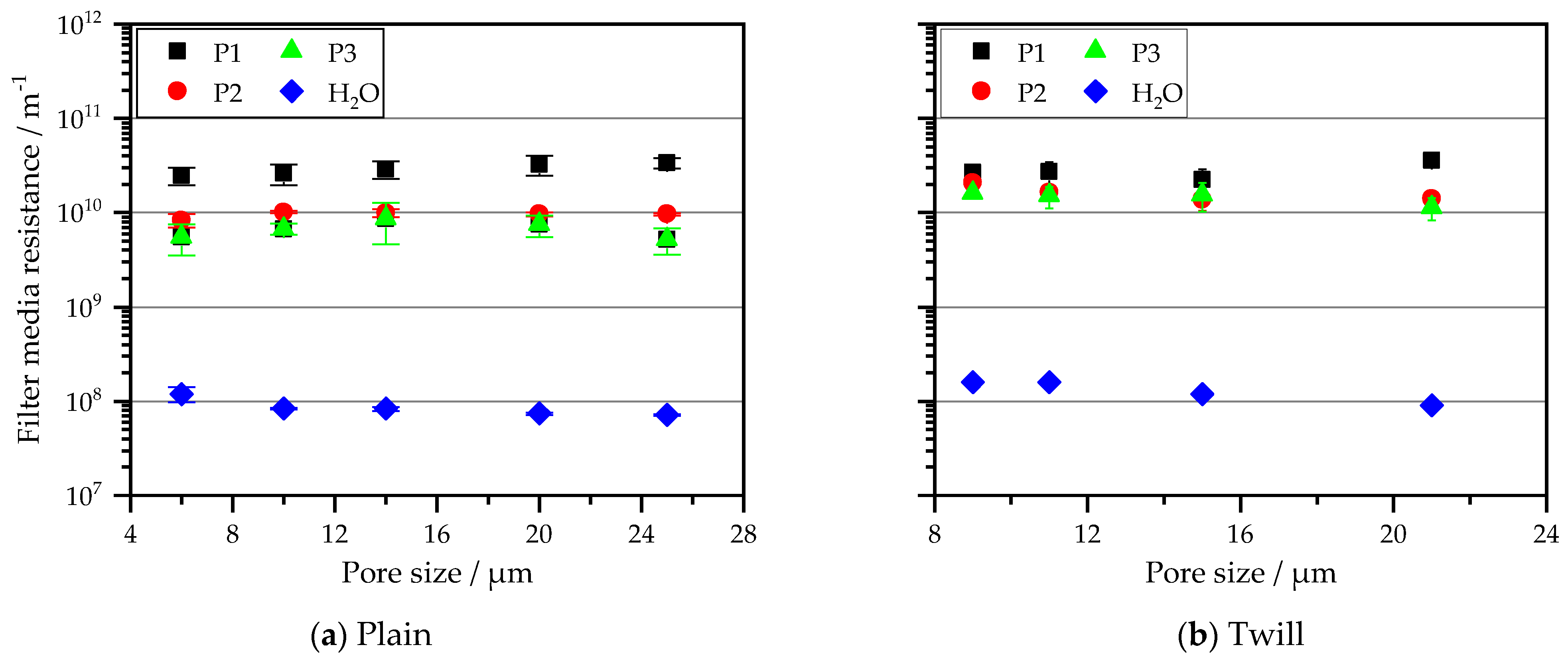
5.3. Metall-Based Monofilament Fabrics
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Description | Unit |
| A | Filter surface | m2 |
| dMesh | Mesh size of filter cloth based on a bubble-point-test | m |
| HFC | Filter cake height | m |
| K | Parameter Filter equation | - |
| q | Parameter Filtration mechanism according to [14] | - |
| RFC | Filter cake resistance | m−1 |
| RF.0 | Initial resistance at the beginning of the Filtration | m−1 |
| RFM | Filter medium resistance | m−1 |
| RFM,0 | Clear water resistance of the filter fabric | m−1 |
| RIR | Interference resistance [19]; Interaction between filter fabric and particles | m−1 |
| RSupport | Resistance of the supporting fabric; Tends to 0 compared to the filter fabric. | m−1 |
| VF | Filtrate volume | m3 |
| V̇F | Filtrate volume flow | m3 ∙ s−1 |
| x50,3 | Mass/volume related modal value | m |
| αH | Specific filter cake resistance | m−2 |
| Δp | Pressure difference | Pa |
| ηf | Viscosity | Pa ∙ s |
| χ = A ∙ HFC/VF | Specific cake volume/filtrate volume | m3 ∙ m−3 |
References
- Rocha, S.M.S.; Bacelos, M.S.; Damasceno, J.J.R.; Vieira, L.; Aguiar, M.L. The Effect of the Dust Cake Resistance on Fluid Flow Passing through the Filter Media. MSF 2012, 727–728, 758–763. [Google Scholar] [CrossRef]
- Jaganathan, S.; Tafreshi, H.V.; Pourdeyhimi, B. A realistic approach for modeling permeability of fibrous media: 3-D imaging coupled with CFD simulation. Chem. Eng. Sci. 2008, 63, 244–252. [Google Scholar] [CrossRef]
- Wakeman, R. The influence of particle properties on filtration. Sep. Purif. Technol. 2007, 58, 234–241. [Google Scholar] [CrossRef]
- Rushton, A.; Griffiths, P.V.R. Role of the cloth in filtration. Chem. Eng. 2004, 4, 47–54. [Google Scholar]
- Rushton, A. Effect of Filter Cloth Structure on Flow Resistance, Bleeding, Blinding and Plant performance. Chem. Eng. 1970, 273, 88–94. [Google Scholar]
- Zhang, Q.; Horst, D.; Schmidt, E. Modellierung der Oberflächenstruktur von Nadelfilz-Filtermedien zur Simulation der kuchenbildenden Staubfiltration. Chem. Ing. Tech. 2020, 92, 275–281. [Google Scholar] [CrossRef]
- Zhang, Q.; Schmidt, E. Simulation der Partikelschichtablösung unter Beachtung transienter kinetischer Effekte. Chem. Ing. Tech. 2008, 80, 587–592. [Google Scholar] [CrossRef]
- Ripperger, S.; Puga, J.F.; Tichy, J.W. Einfluss des Filtermittelwiderstandes und der Strömungswiderstände im Filtratablaufb bbei kontinuierlich betriebenen Filtern mit hohem Feststoffdurchsatz. Filtr. Sep. 2005, 19, 58–62. [Google Scholar]
- Purchas, D.B.; Sutherland, K. Handbook of Filter Media; Elsevier Advanced Technology: Oxford, UK, 2002. [Google Scholar]
- Darcy, H. Les Fontaines Publiques de la Ville de Dijon: Exposition et Application des Principes à Suivre et des Formules à Employer dans les Questions de Distribution d’eau; Victor Dalmont: Paris, France, 1856. [Google Scholar]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Kozeny, J. Über kapillare Leitung des Wassers im Boden. Sitz. Akad. Wiss. Wien. 1927, 136, 271–306. [Google Scholar]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Hermans, P.H.; Bredée, H.L. Zur Kenntnis der Filtrationsgesetze. Recl. Travaux Chim. Pays-Bas. 1935, 54, 680–700. [Google Scholar] [CrossRef]
- Erk, A. Rheologische Eigenschaften Feindisperser Suspensionen Während ihrer Fest-Flüssig-Trennung in Filtern und Zentrifugen; Shaker: Aachen, Germany, 2006. [Google Scholar]
- Morsch, P.; Ginisty, P.; Anlauf, H.; Nirschl, H. Factors influencing backwashing operation in the liquid phase after cake filtration. Chem. Eng. Sci. 2020, 213, 115372. [Google Scholar] [CrossRef]
- Heymann, J.; Böttner, P. Textile Filtermedien—Beschaffenheit und Eigenschaften. Filtr. Sep. 1997, 11, 43–51. [Google Scholar]
- Tung, K.-L.; Li, Y.-L.; Lu’, K.-T.; Lu, W.-M. Effect of calendering of filter cloth on transient characteristics of cake filtration. Sep. Purif. Technol. 2006, 48, 1–15. [Google Scholar] [CrossRef]
- Tichy, J.W. Zum Einfluss des Filtermittels und der Auftretenden Interferenzen Zwischen Filterkuchen und Filtermittel bei der Kuchenfiltration. Ph.D. Thesis, Technische Universität Kaiserslautern, Kaiserslautern, Germany, 2007. Available online: https://kluedo.ub.uni-kl.de/frontdoor/index/index/docId/1856 (accessed on 22 May 2007).
- Anlauf, H. Filtermedien zur Kuchenfiltration—Schnittstelle Zwischen Suspension und Apparat. Chem. Ing. Tech. 2007, 79, 1821–1831. [Google Scholar] [CrossRef] [Green Version]
- Morsch, P.; Ginisty, P.; Anlauf, H.; Nirschl, H. Influence of regeneration variables during backwashing treatment into gas-phase after liquid filtration. Sep. Purif. Technol. 2020, 249, 11707. [Google Scholar] [CrossRef]
- Morsch, P.; Kühn, J.; Werner, R.; Anlauf, H.; Geier, D.U.; Becker, T.; Nirschl, H. Influence of the filter cloth and nozzles type on the in-situ cleaning procedure of filter presses. Chem. Eng. Sci. 2020, 226, 115889. [Google Scholar] [CrossRef]



| Fabric Type/Mesh Size in µm / Material | Weave According to DIN ISO 9354 | Mesh per Filter Area in mm−2 | Weight per Unit Area in g m−2 | Surface Roughness (ISO 25178) in µm | Thread Thickness Warp/Weft in µm | Fabric Thickness (ISO 5084) in µm | Schematic Weaving Patterns, Based on [17] | ||
|---|---|---|---|---|---|---|---|---|---|
| Plain | 12 | PET | 10-01 01-01-00 | 241 | 70 | 9 | 100/45 | 80 |  |
| 14 | PA6.6 | 88 | 120 | 90 | 100/75 | 160 | |||
| 22 | PET | 64 | 175 | 31 | 126/176 | 185 | |||
| Twill | 5 | PP | 20-04 01-01-04 | 5 | 295 | 3 | 212/822 | 420 |  |
| 11 | PET | 20-03 01-01-03 | 29 | 240 | 29 | 132/429 | 265 | ||
| 14 | PP | 20-02 01-01-02 | 40 | 136 | 40 | 168/161 | 200 | ||
| 15 | PET | 20-03 01-01-02 | 26 | 235 | 8 | 175/283 | 265 | ||
| 20 | PET | 20-03 01-01-03 | 35 | 235 | 30 | 128/160 | 260 | ||
| 25 | PP | 20-02 01-01-02 | 11 | 210 | 24 | 61/187 | 320 | ||
| Satin | 6 | PP | 20-02 01-02-01 | 6 | 435 | 11 | 164/898 | 590 |  |
| 11 | PP | 30-04 01-01-02 | 5 | 330 | 13 | 371/572 | 400 | ||
| 18 | PP | 20-08 02-02-04 | 3 | 370 | 13 | 269/294 | 500 | ||
| 18 | PP | 30-04 02-02-02 | 4 | 447 | 7 | 227/443 | 714 | ||
| 22 | PET | 30-06 02-01-03 | 5 | 395 | 11 | 235/604 | 380 | ||
| Fabric Type/Mesh Size in µm /Material | Weave According to DIN ISO 9354 | Mesh per Filter Area in mm−2 | Weight per Unit Area in g m−2 | Surface Roughness (ISO 25178) in µm | Thread Thickness Warp/Weft in µm | Fabric Thickness (ISO 5084) in µm | Schematic Weaving Patterns, Based on [17] | ||
|---|---|---|---|---|---|---|---|---|---|
| Multi Twill | 10 | PP | 20-02 03-01-04 | 8 | 280 | 79 | 146/654 | 560 |  |
| 11,5 | PVDF | 20-02 03-01-04 | 7 | 550 | 82 | 111/738 | 550 | ||
| 13,25 | PPS | 20-02 01-01-01 | 6 | 408 | 11 | 325/323 | 670 | ||
| 15 | PPS | 20-02 02-02-03 | 2 | 248 | 15 | 141/882 | 350 | ||
| 20 | PP | 20-02 02-01-03 | 13 | 170 | 43 | 106/428 | 390 | ||
| Multi Plain | 2,9 | PPS | 10-01 01-01-00 | 3 | 381 | 16 | 275/431 | 690 |  |
| 12 | PPS | 10-01 01-02-00 | 2 | 254 | 20 | 181/922 | 370 | ||
| Fabric Type/Mesh Size in µm /Material | Weave According to DIN ISO 9354 | Mesh per Filter Area in mm−2 | Weight per Unit Area in g m−2 | Surface Roughness (ISO 25178) in µm | Thread Thickness Warp/Weft in µm | Fabric Thickness (ISO 5084) in µm | Schematic Weaving Patterns, Based on [17] | ||
|---|---|---|---|---|---|---|---|---|---|
| Twill | 9 | 1.4404 | 20-02 02-01-02 | 834 | 343 | 4 | 19/30 | 66 |  |
| 11 | 1.4404 | 455 | 425 | 6 | 20/31 | 82 | |||
| 15 | 1.4404 | 206 | 757 | 7 | 21/64 | 144 | |||
| 21 | 1.4306 | 171 | 692 | 6 | 44/47 | 142 | |||
| Plain | 6 | 1.4404/1.4301 | 10-01 01-01-00 | 1452 | 188 | 4 | 13/36 | 65 |  |
| 10 | 1.4404 | 869 | 287 | 5 | 19/45 | 94 | |||
| 14 | 1.4404 | 407 | 444 | 8 | 26/60 | 132 | |||
| 20 | 1.4404 | 309 | 437 | 9 | 27/61 | 145 | |||
| 25 | 1.4404 | 260 | 450 | 9 | 29/60 | 150 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bächle, V.; Morsch, P.; Fränkle, B.; Gleiß, M.; Nirschl, H. Interaction of Particles and Filter Fabric in Ultrafine Filtration. Eng 2021, 2, 126-140. https://doi.org/10.3390/eng2020009
Bächle V, Morsch P, Fränkle B, Gleiß M, Nirschl H. Interaction of Particles and Filter Fabric in Ultrafine Filtration. Eng. 2021; 2(2):126-140. https://doi.org/10.3390/eng2020009
Chicago/Turabian StyleBächle, Volker, Patrick Morsch, Bernd Fränkle, Marco Gleiß, and Hermann Nirschl. 2021. "Interaction of Particles and Filter Fabric in Ultrafine Filtration" Eng 2, no. 2: 126-140. https://doi.org/10.3390/eng2020009
APA StyleBächle, V., Morsch, P., Fränkle, B., Gleiß, M., & Nirschl, H. (2021). Interaction of Particles and Filter Fabric in Ultrafine Filtration. Eng, 2(2), 126-140. https://doi.org/10.3390/eng2020009








