Parametric Study of the Physical Responses of NSM CFRP-Strengthened RC T-Beams in the Negative Moment Region
Abstract
1. Introduction
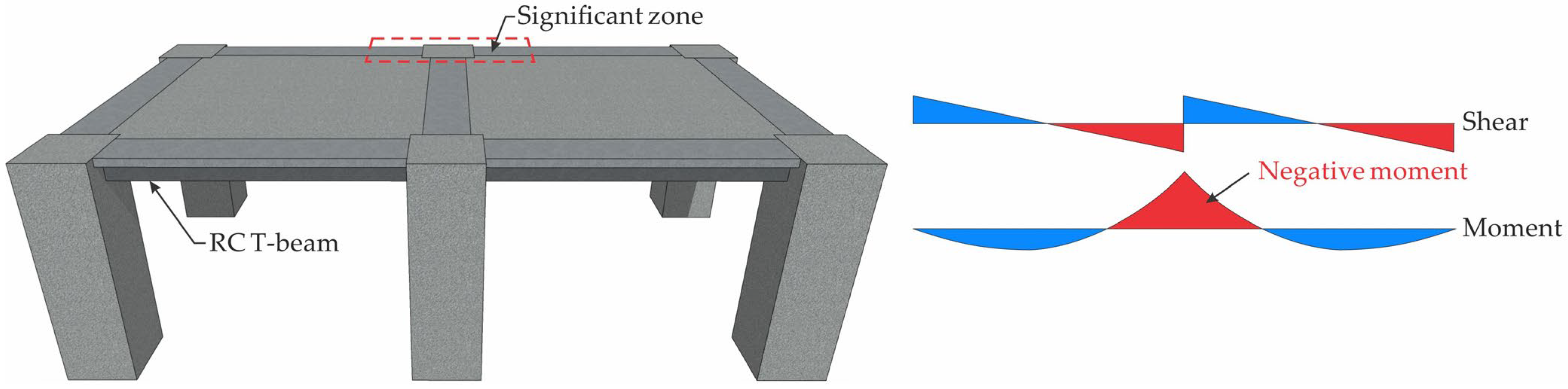
2. Overview of Referenced Experimental Program
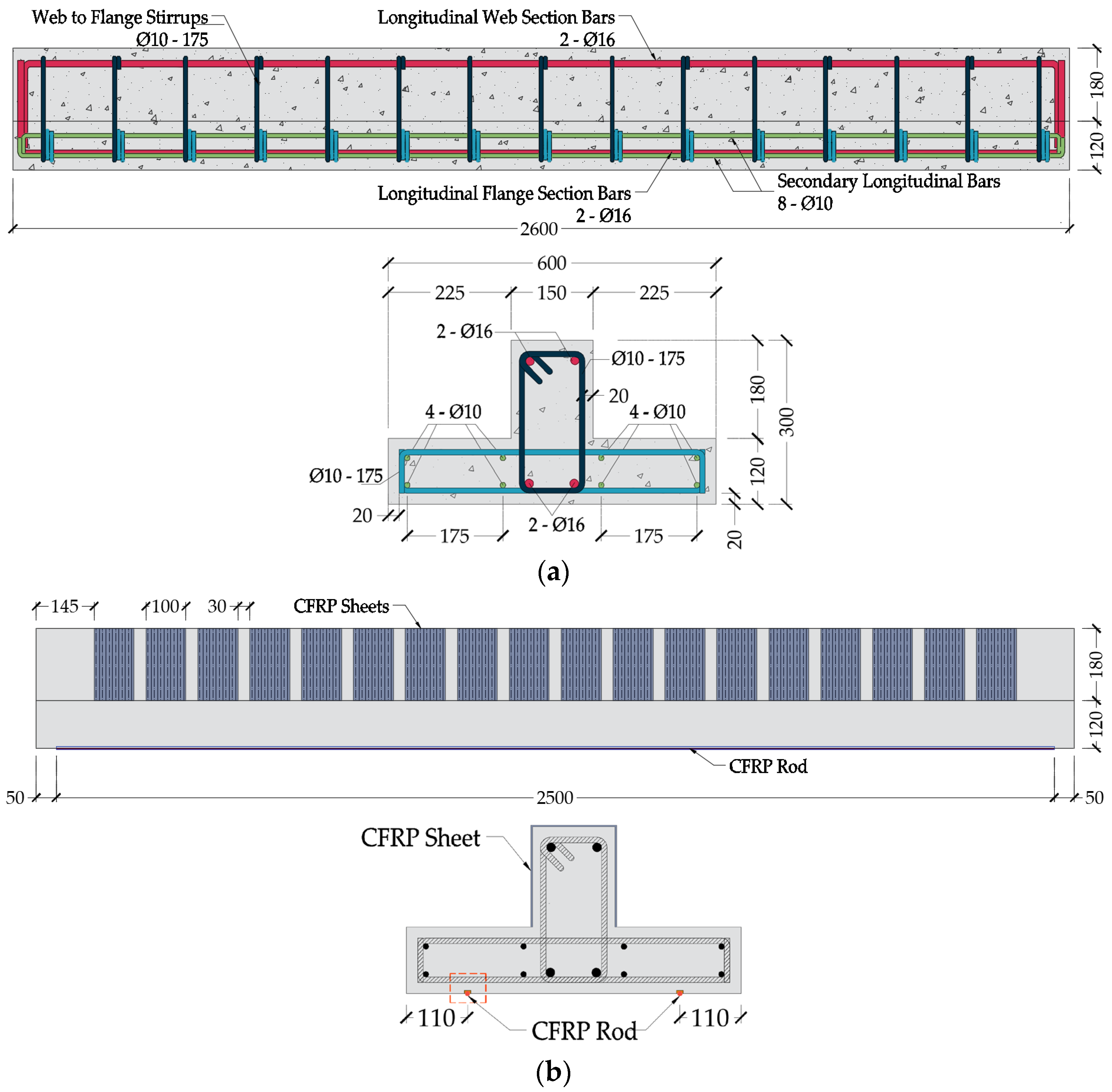
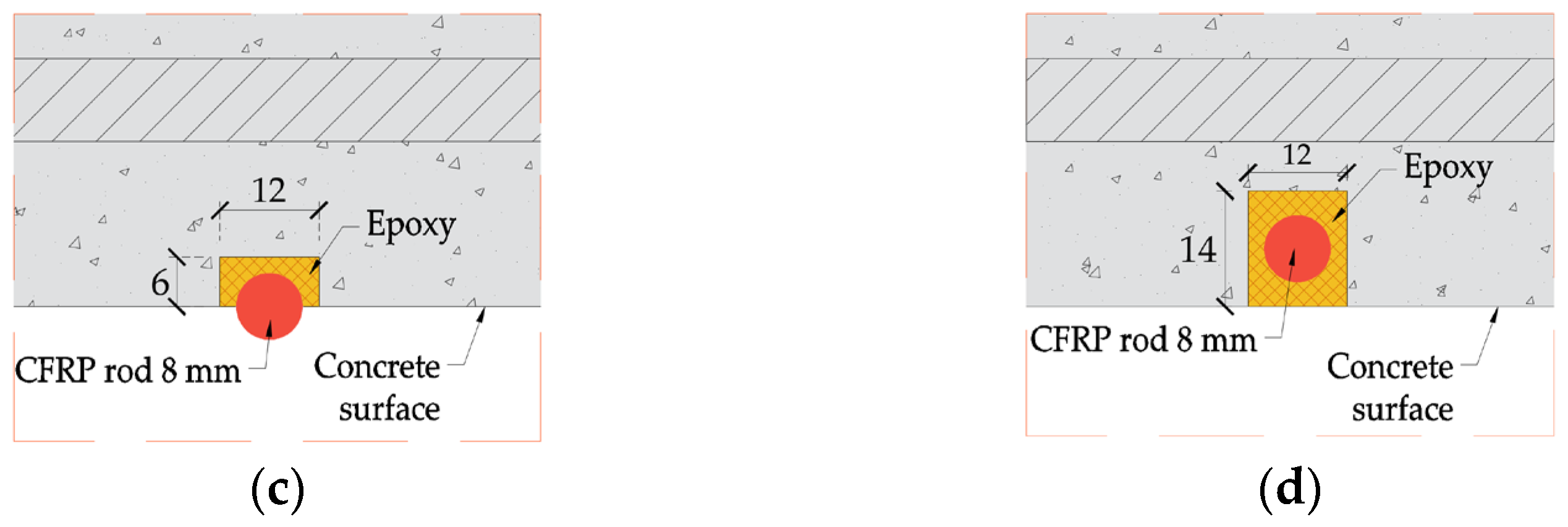
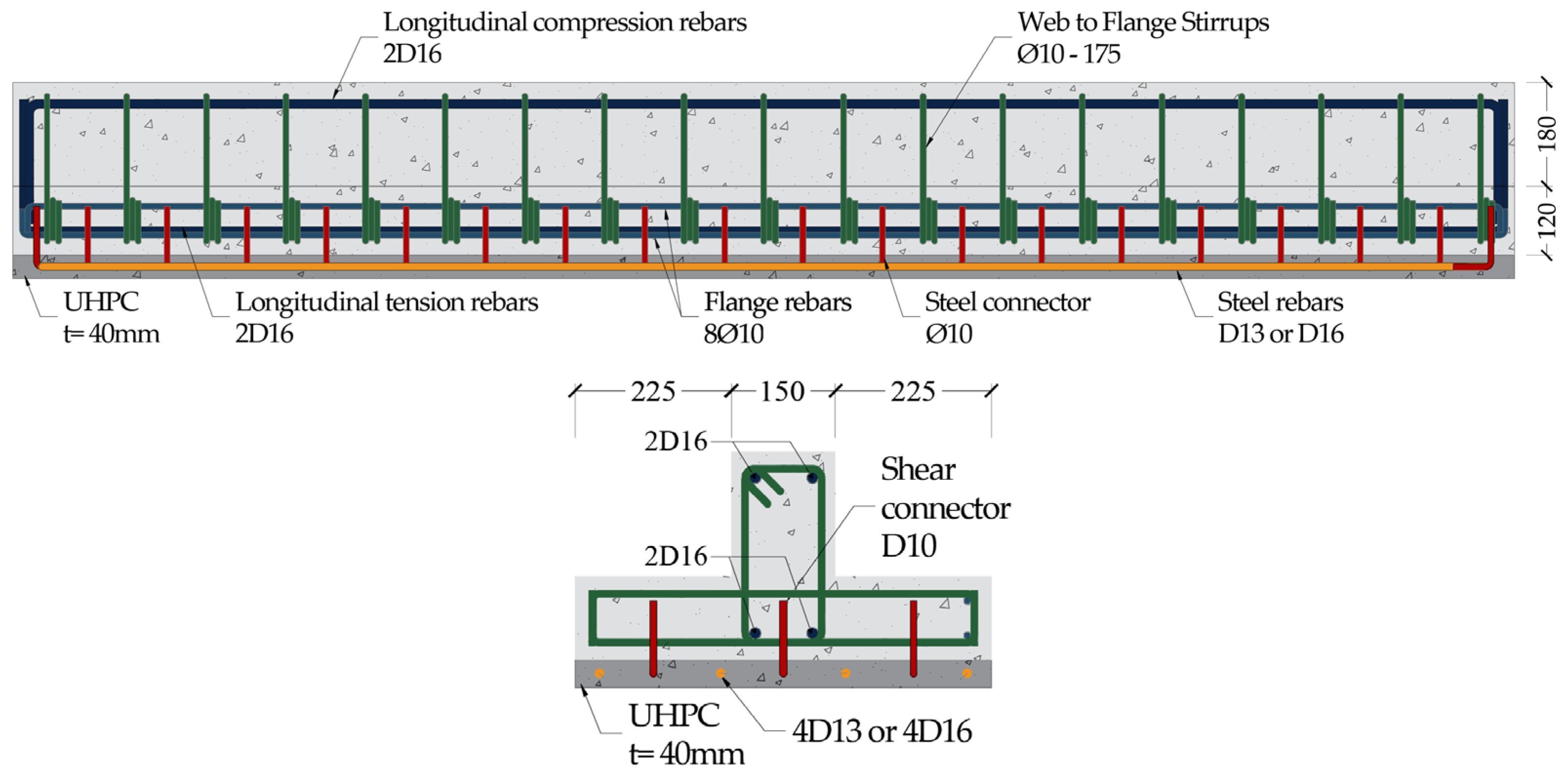
2.1. Specimen Configuration
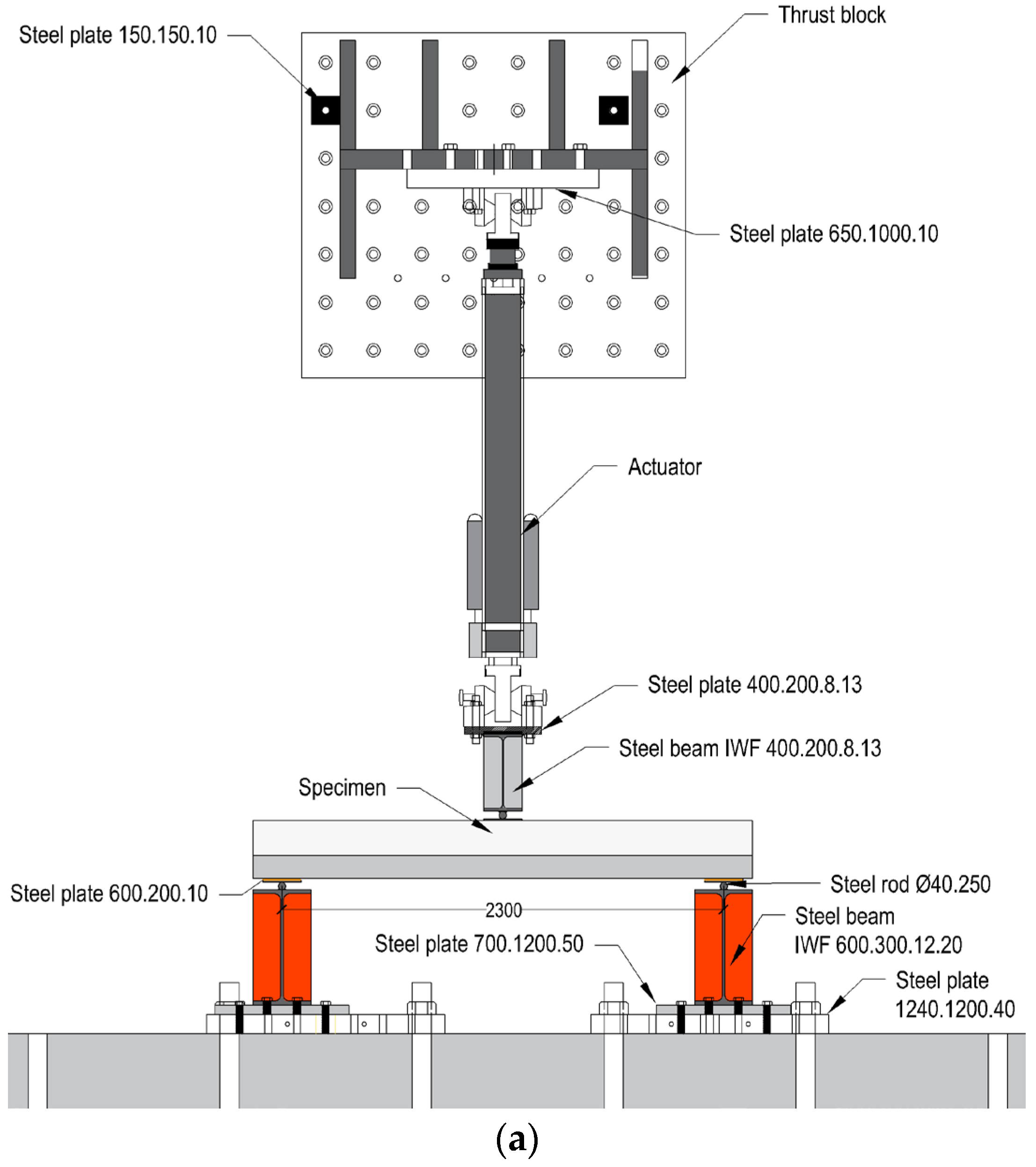
2.2. Test Setup and Instrumentation
3. FE Model Development
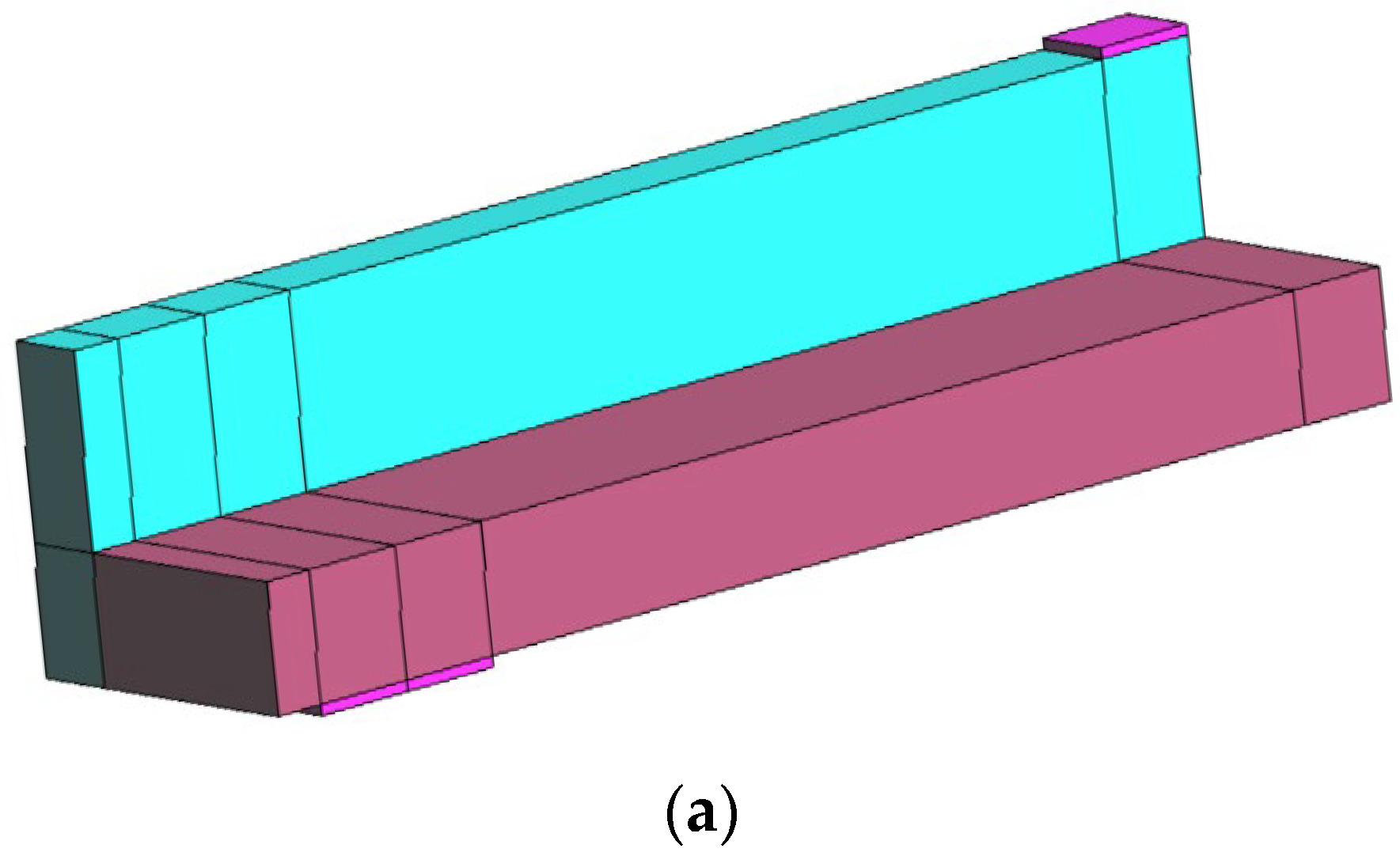
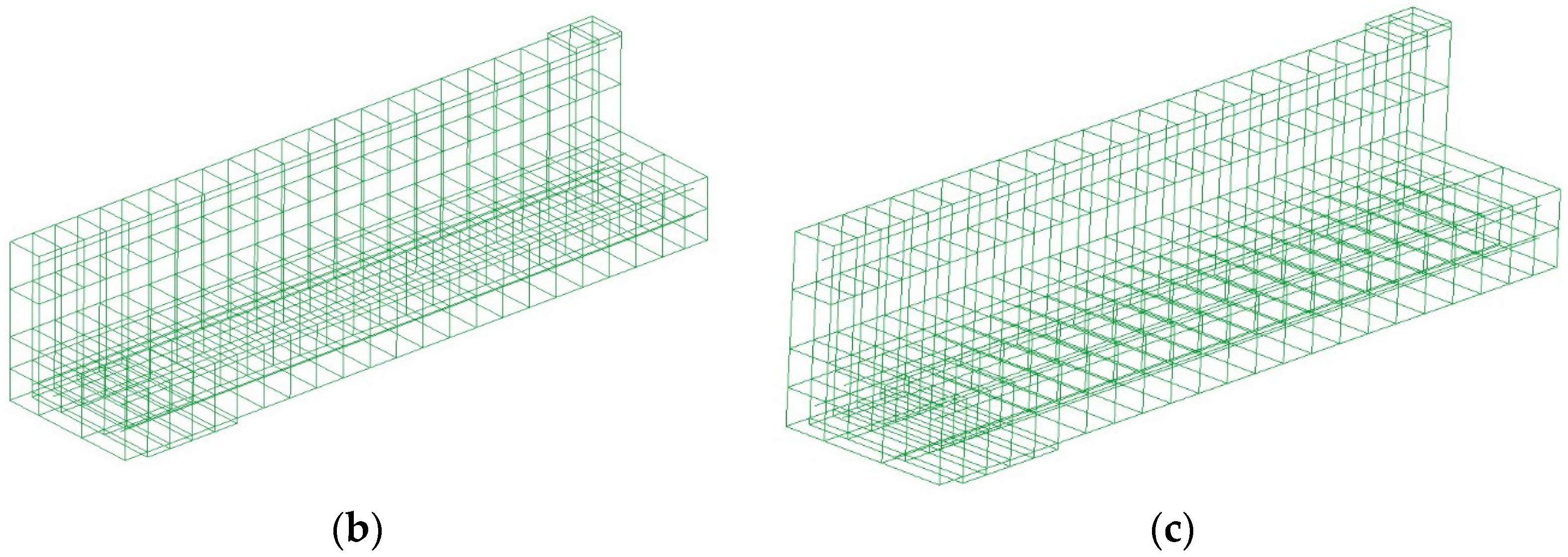
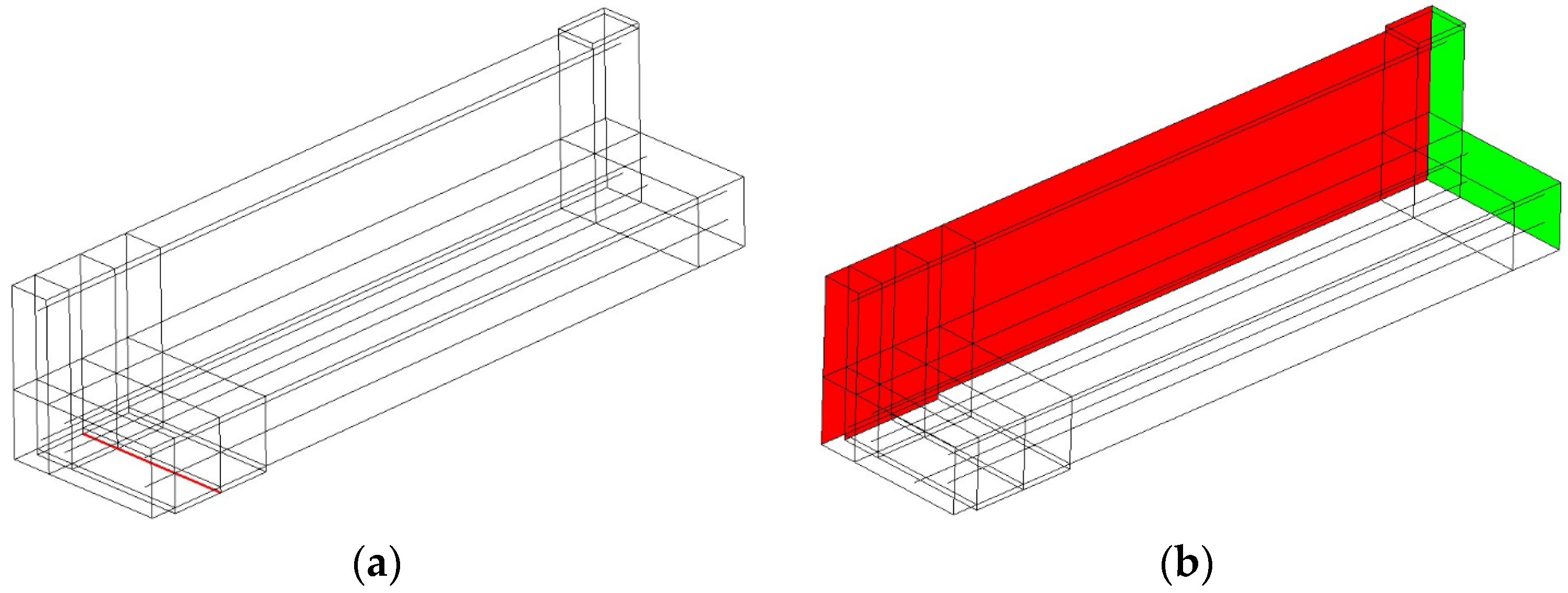
3.1. Geometry Definition
3.2. Material Modeling
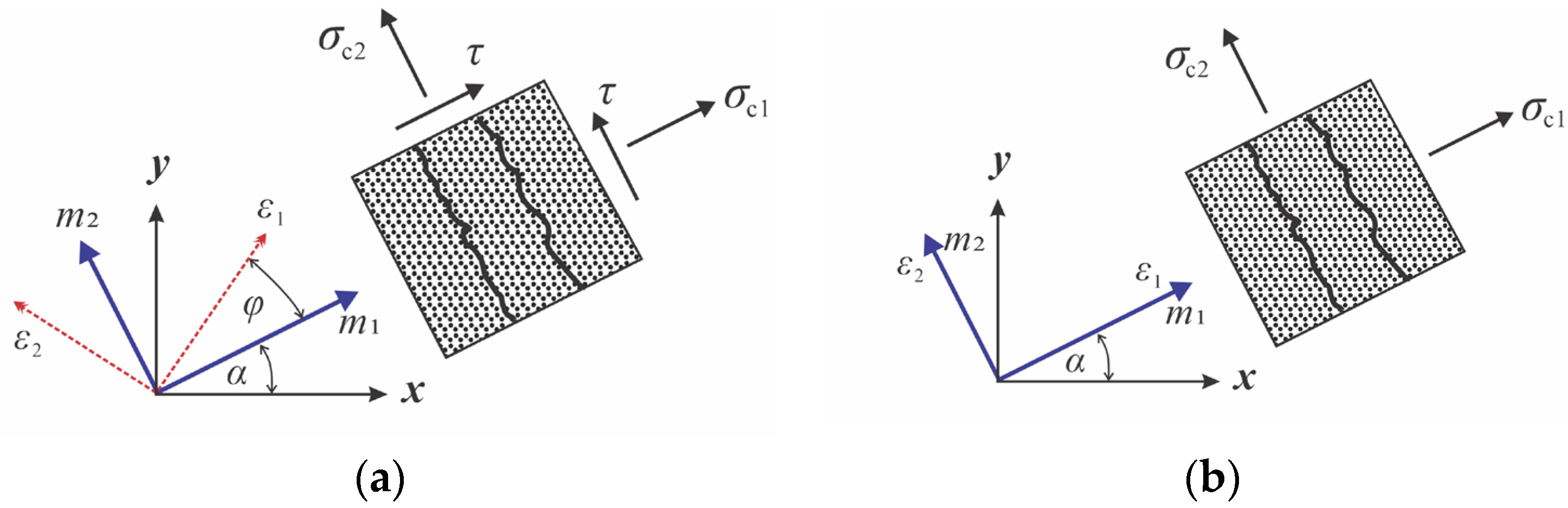
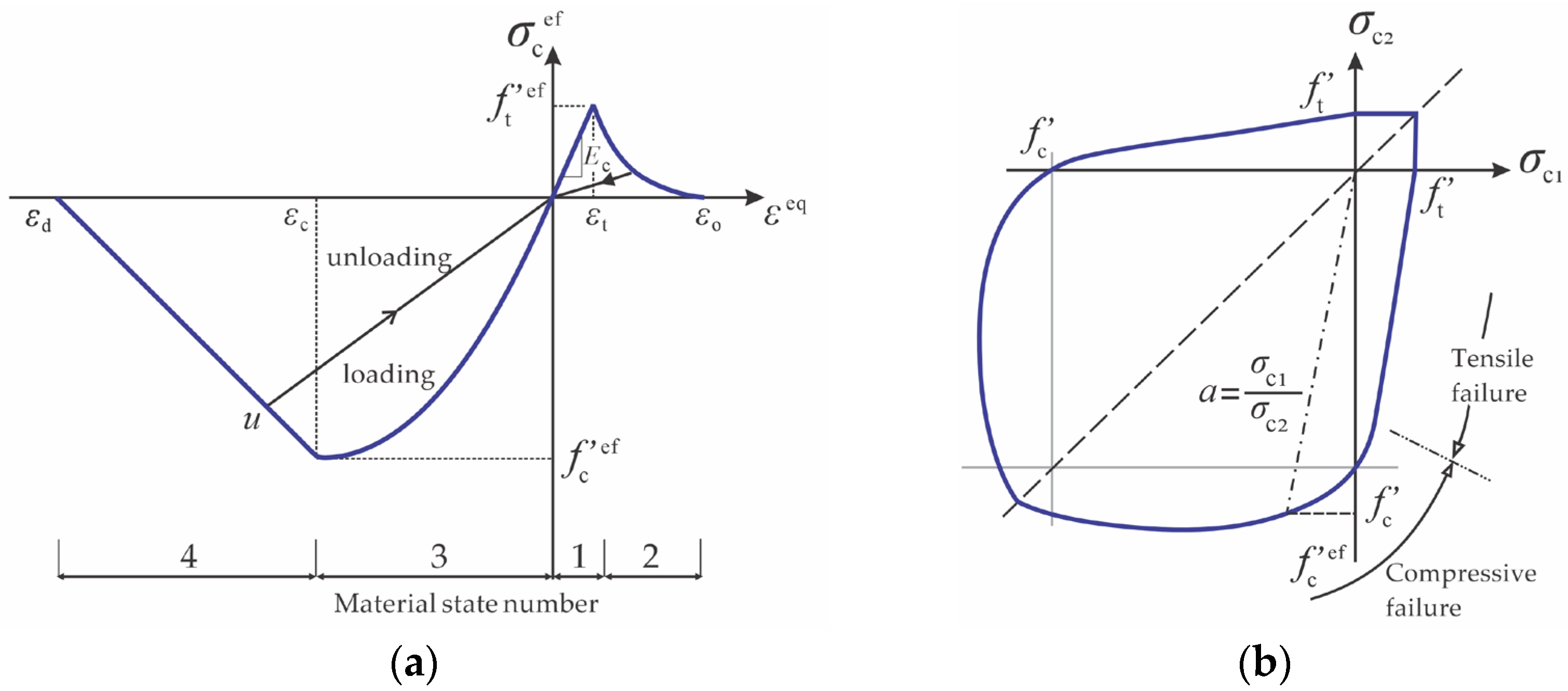
3.2.1. Concrete
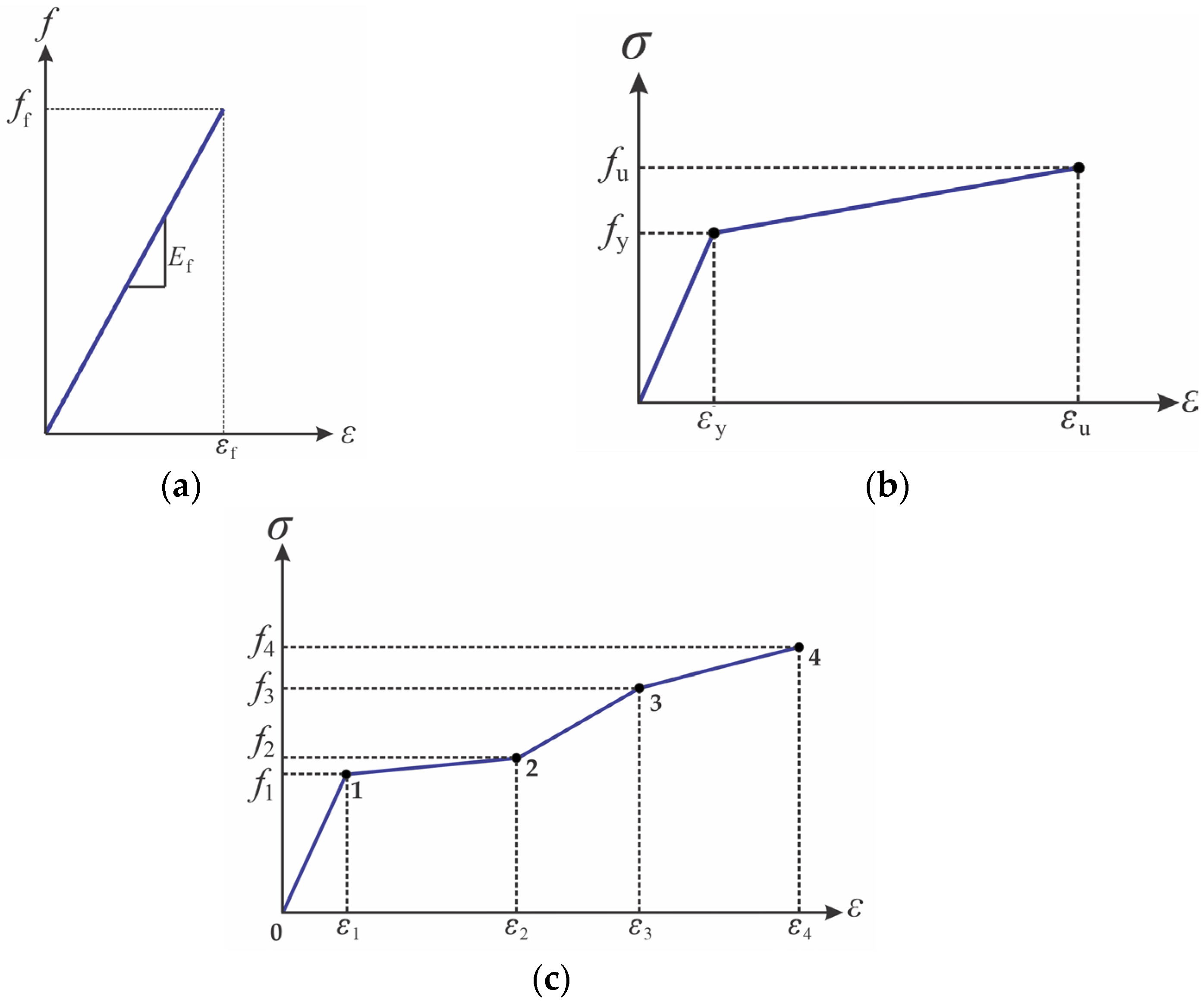
3.2.2. Steel Reinforcement and CFRP Materials
3.2.3. Loading and Supporting Components
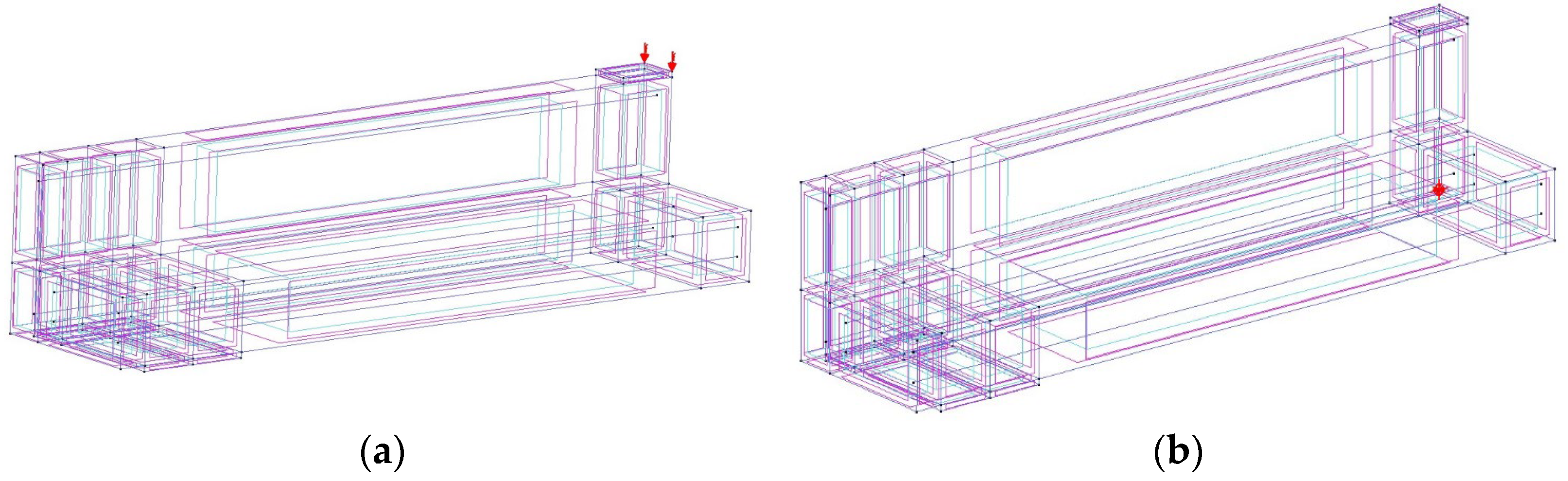
3.3. Boundary Conditions and Output Monitoring
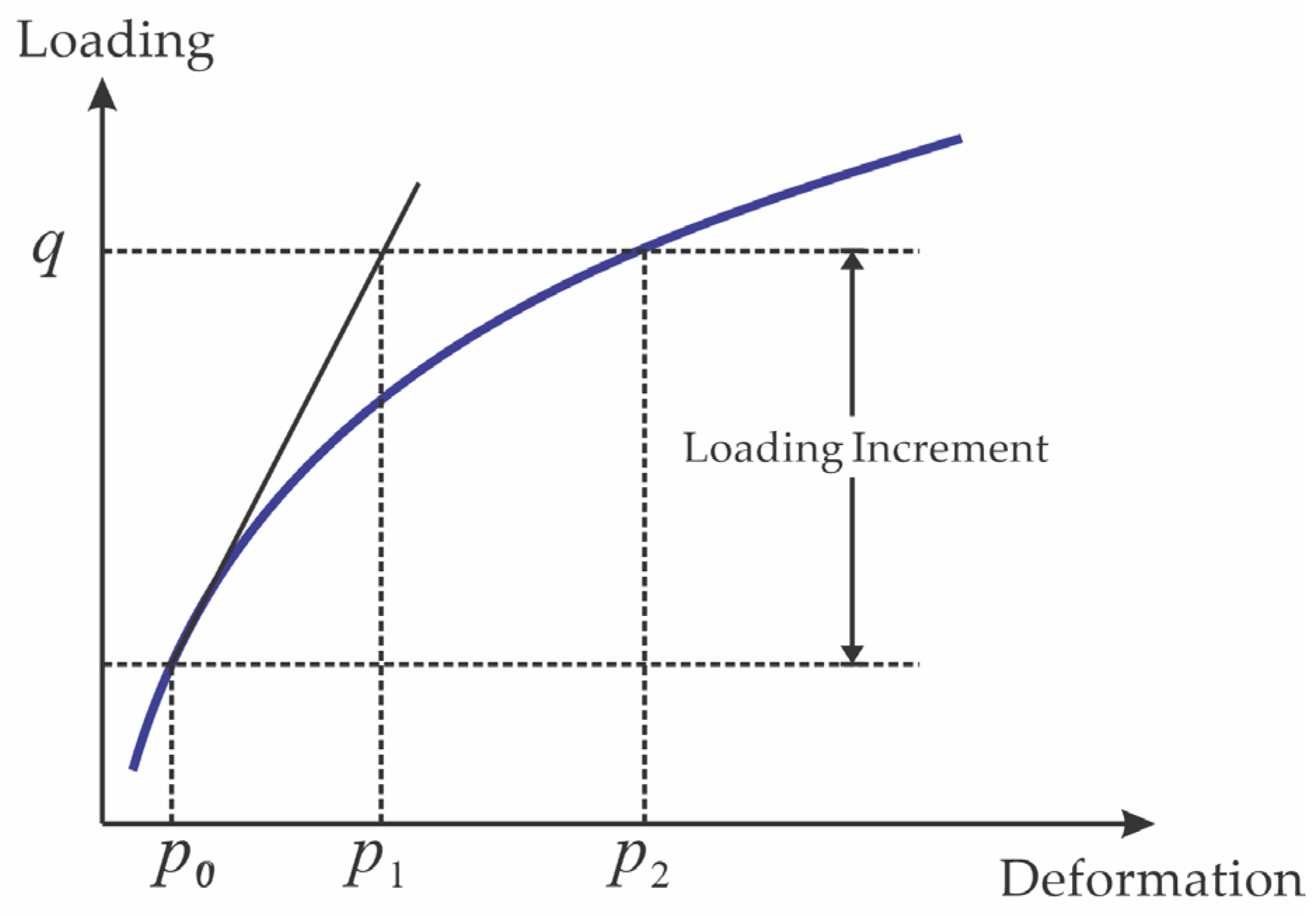
3.4. Solution Strategy
4. Results and Discussion
4.1. Summary of Experimental Findings
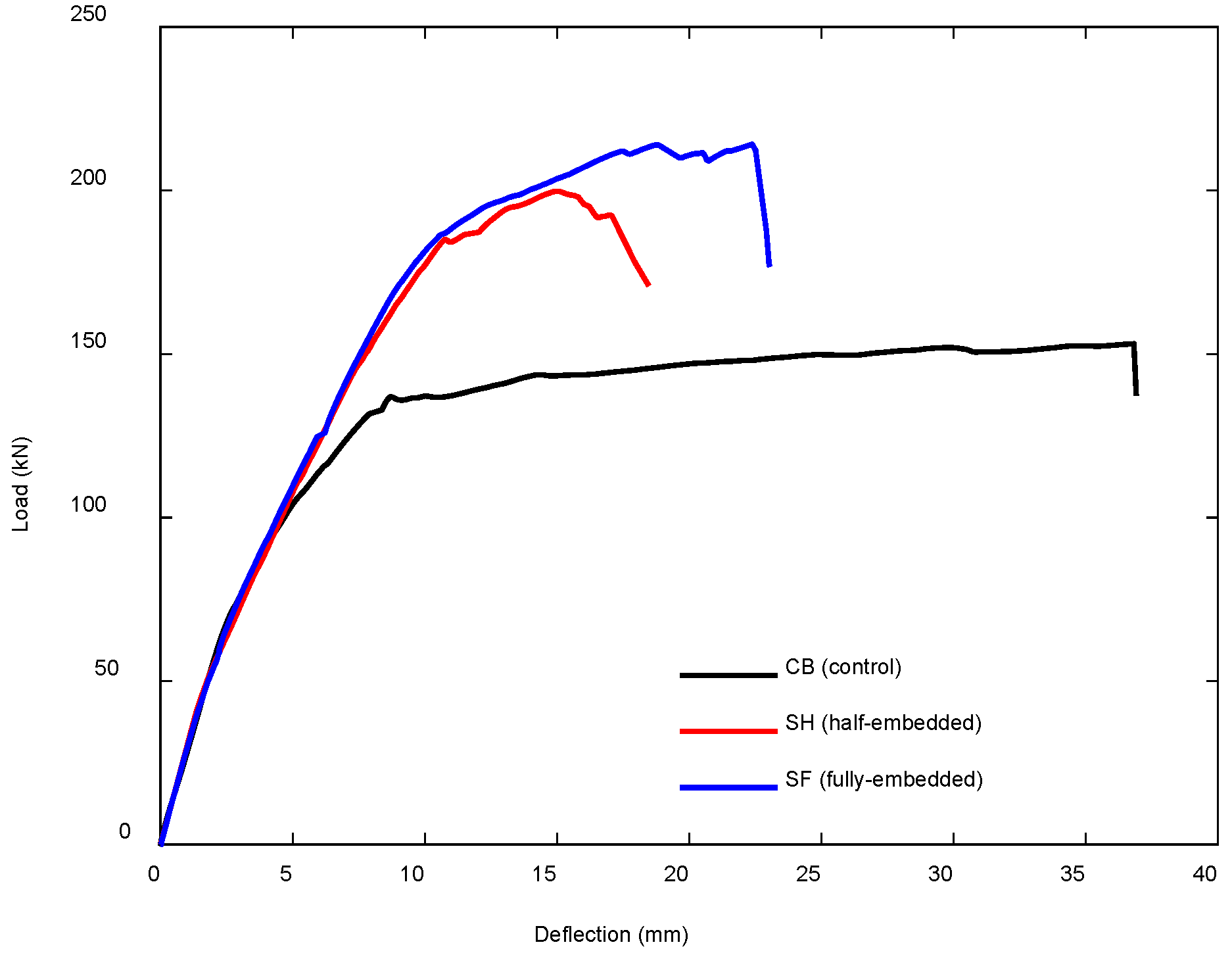
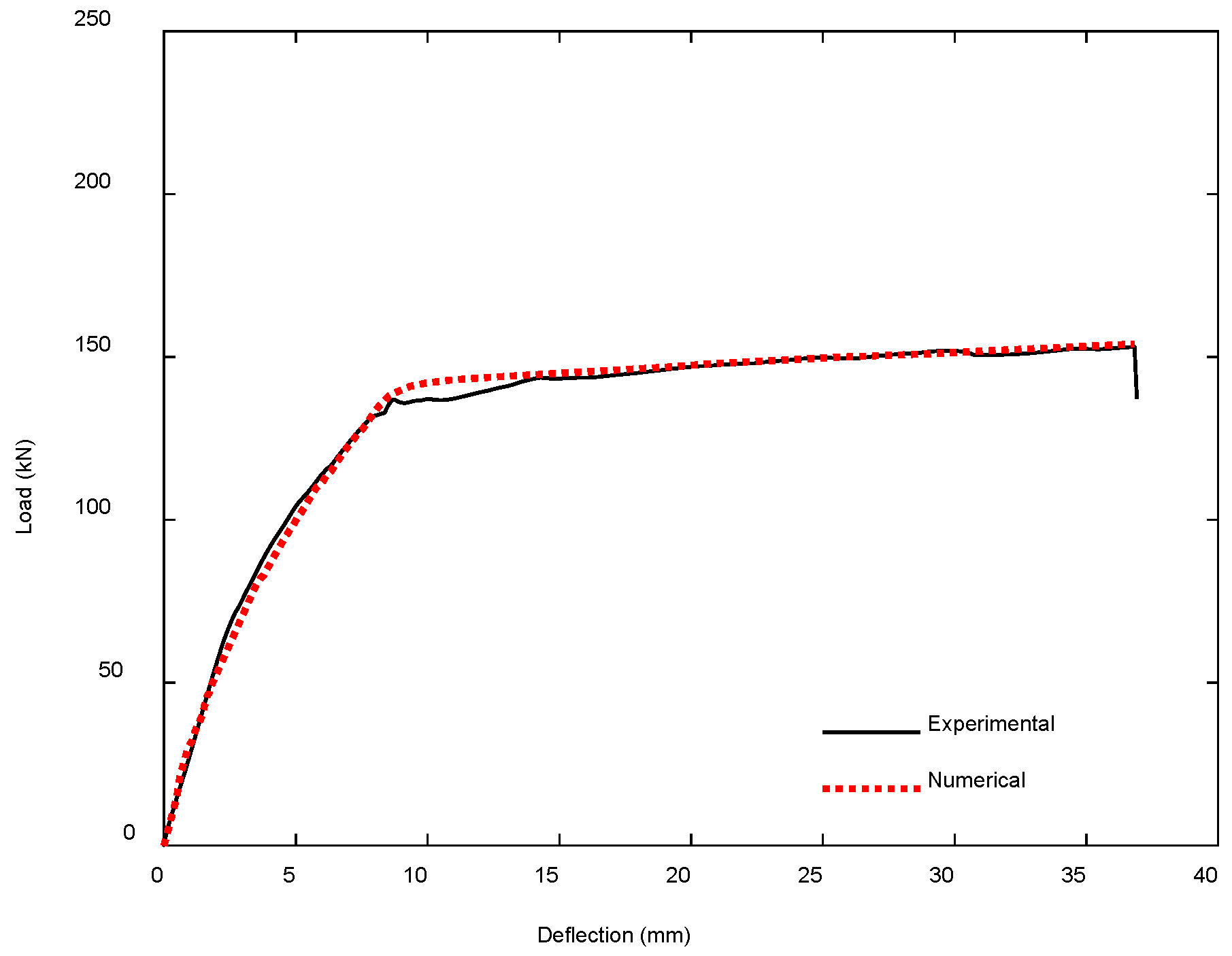
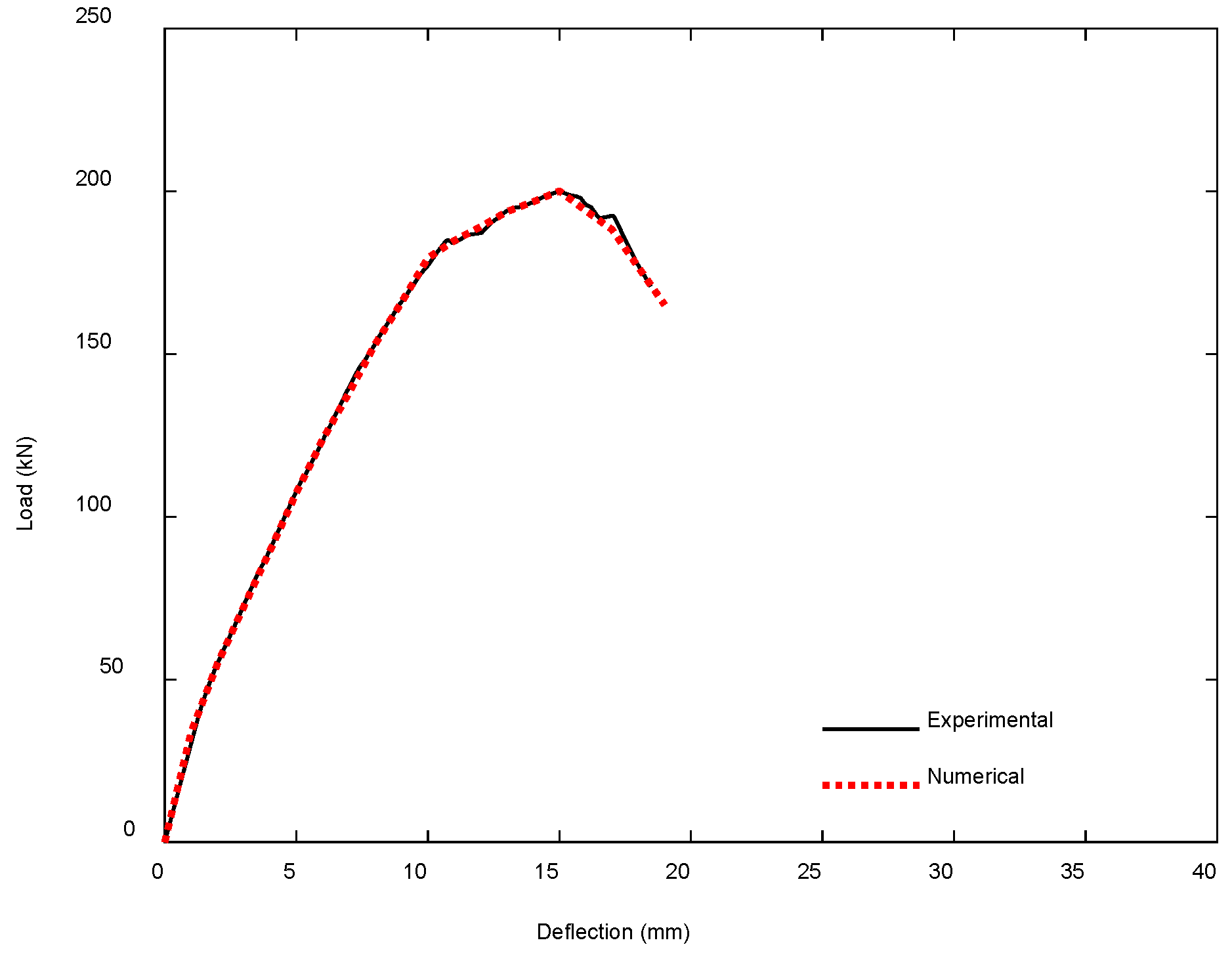
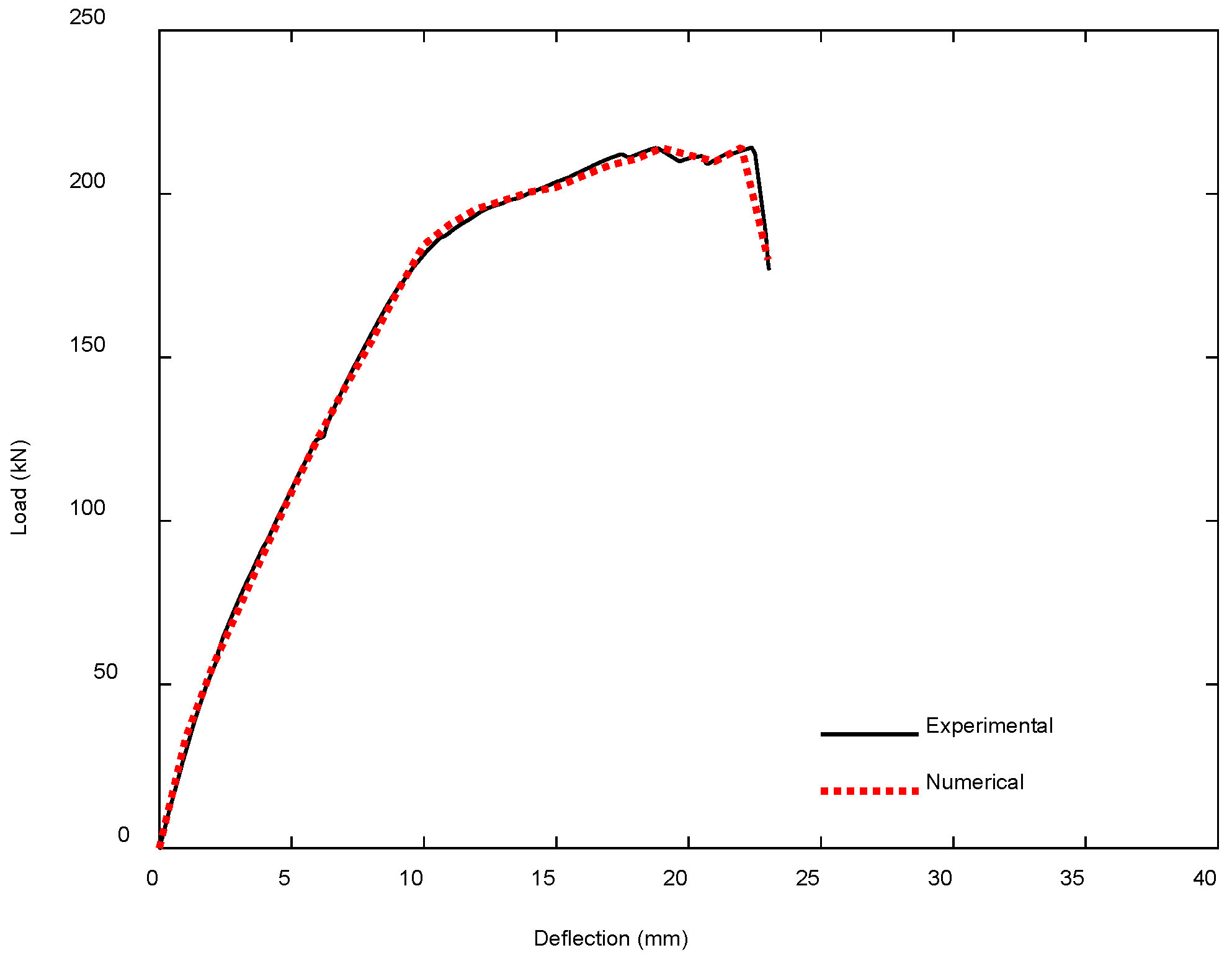
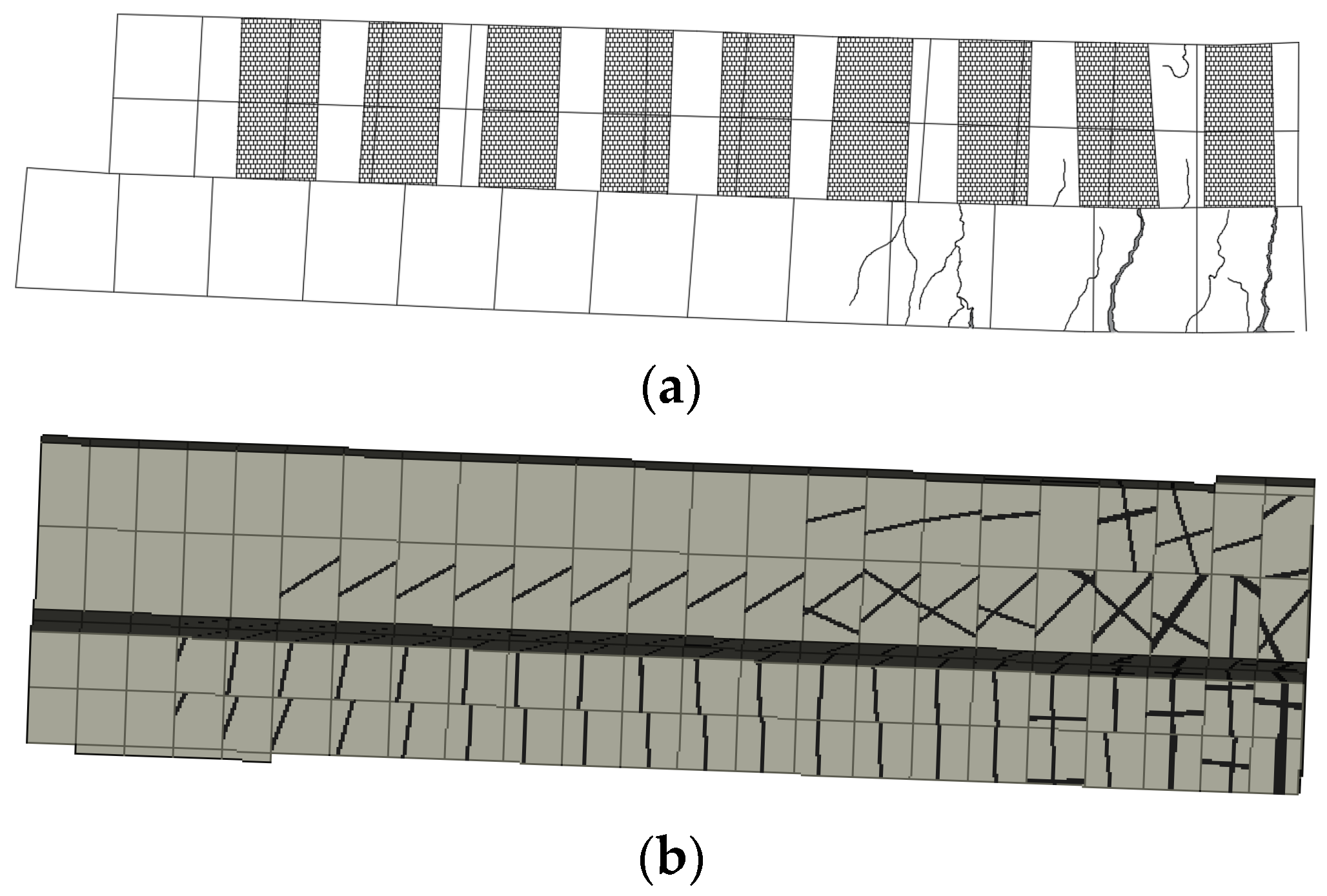
4.2. Comparison Between Numerical and Experimental Results
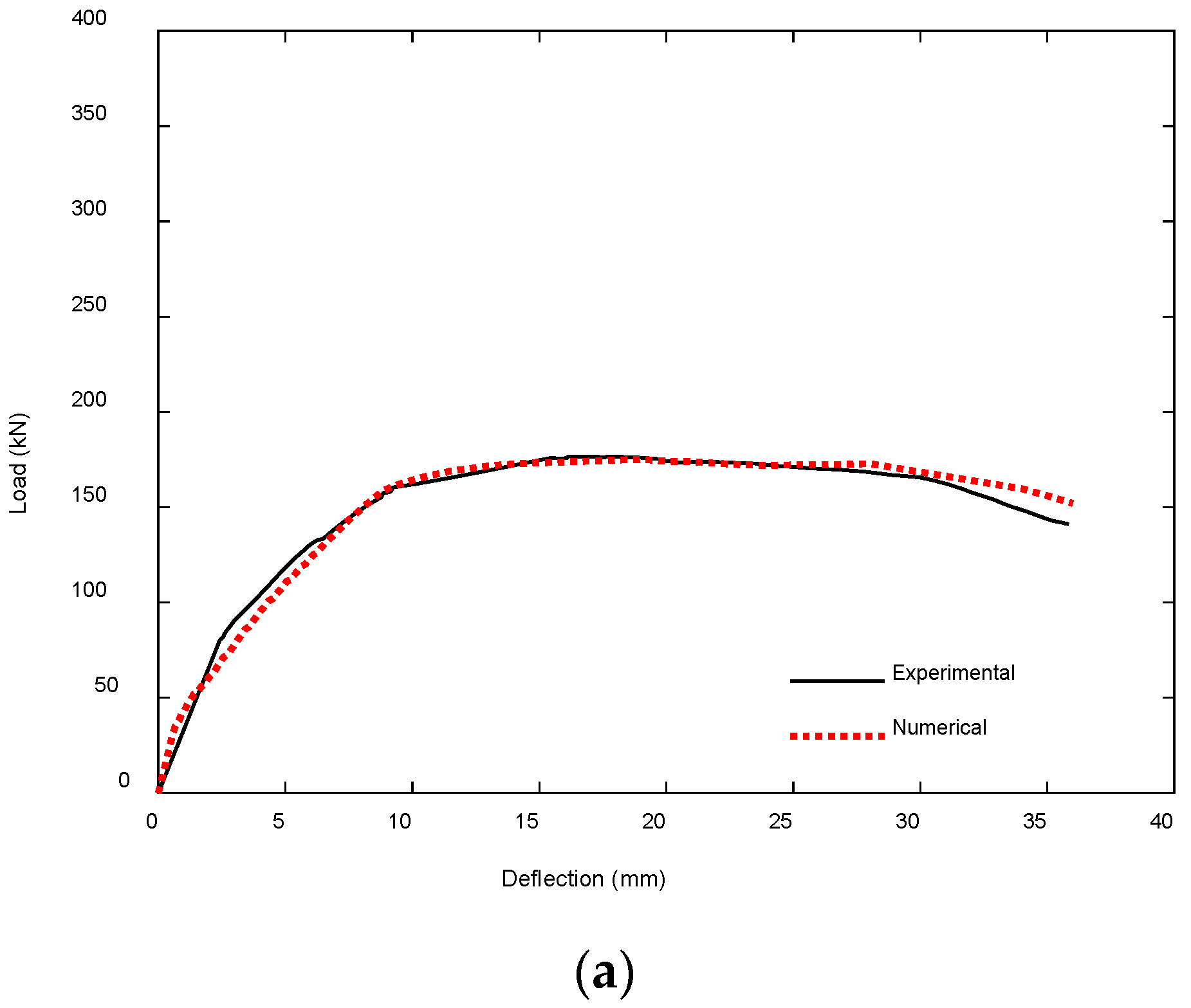
4.2.1. UHPC-Strengthened RC T-Beams by Nugroho et al. [69]
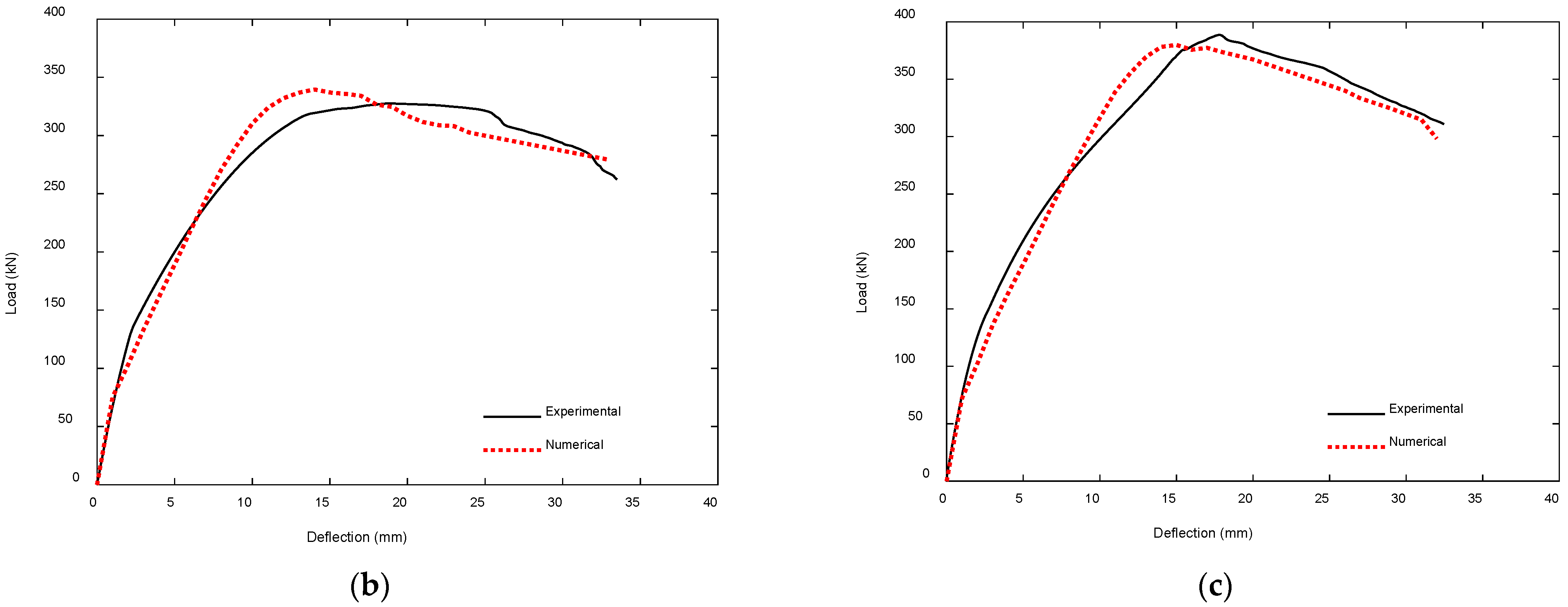
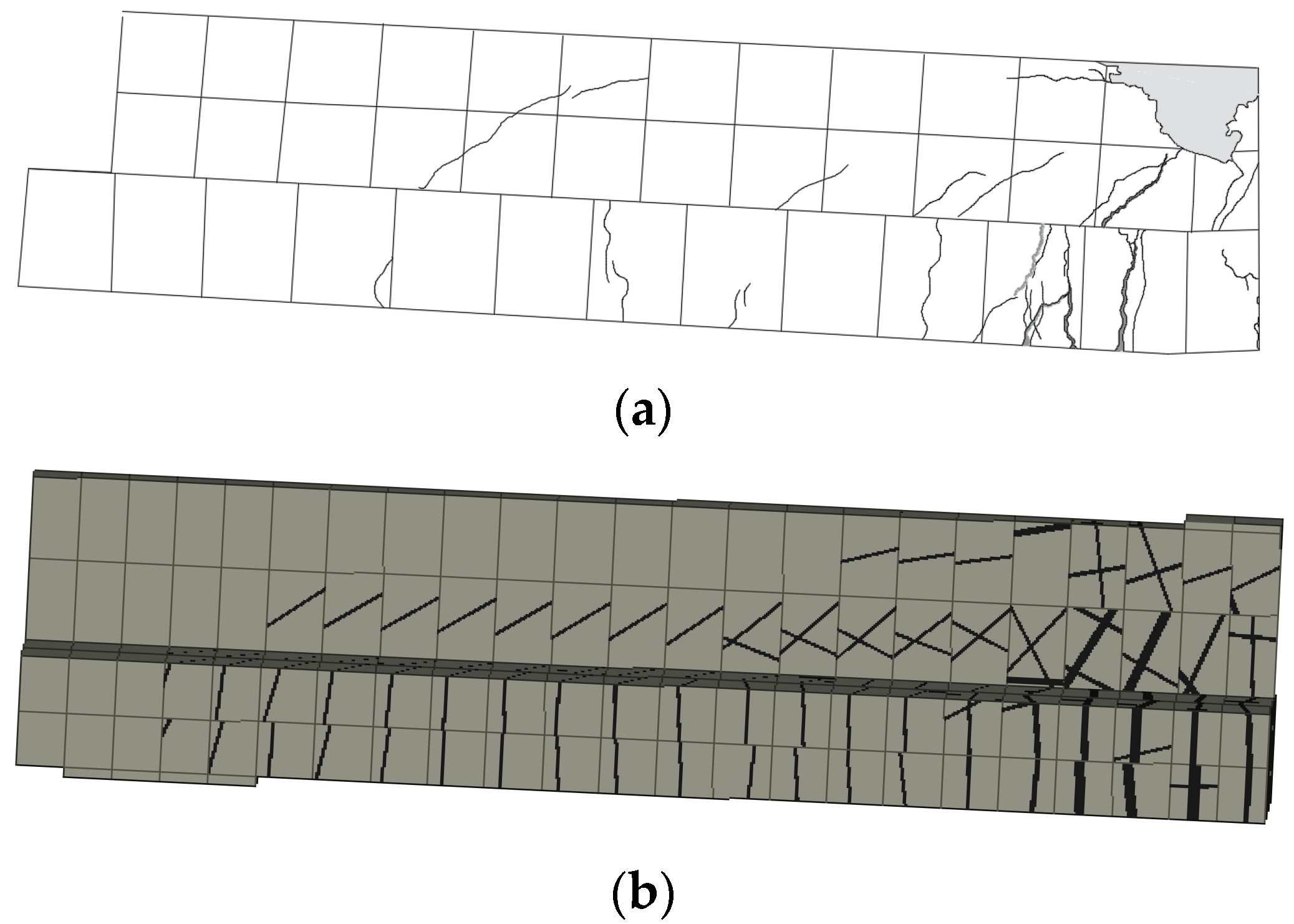
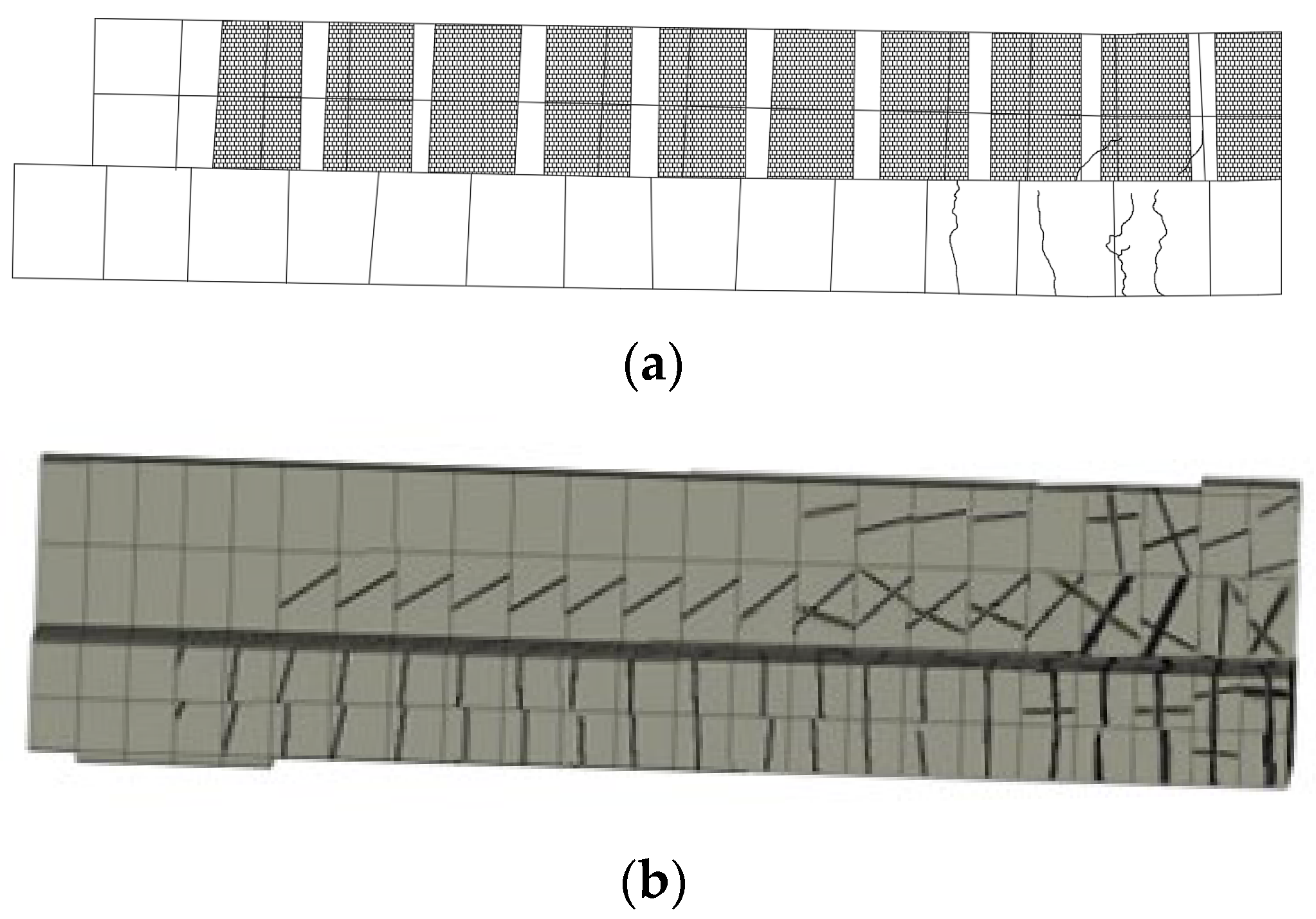
4.2.2. CFRP-Strengthened RC T-Beams by Haryanto et al. [45,54]
- Unstrengthened Control Beam (CB)
- 2.
- Half-Embedded NSM CFRP-Strengthened Beam (SH)
- 3.
- Fully Embedded NSM CFRP-Strengthened Beam (SF)
4.3. Parametric Analysis
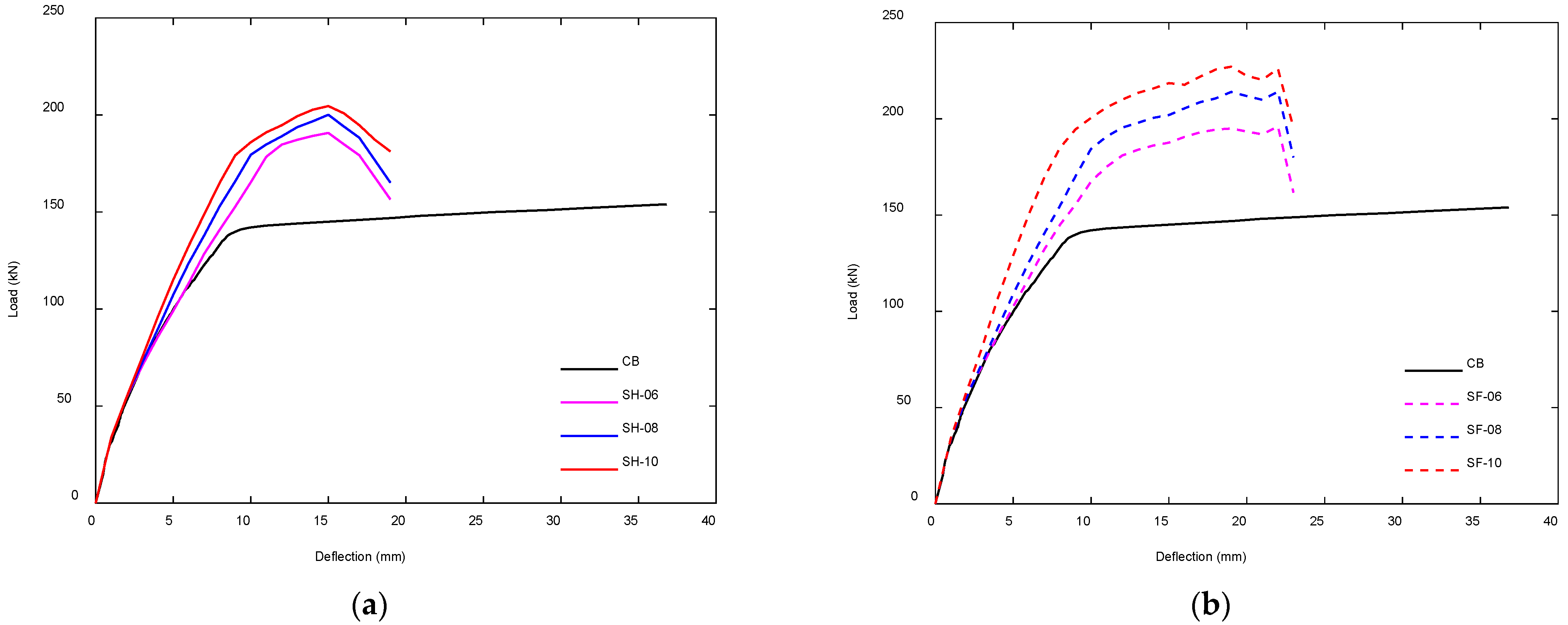
4.3.1. Influence of CFRP Rod Diameter
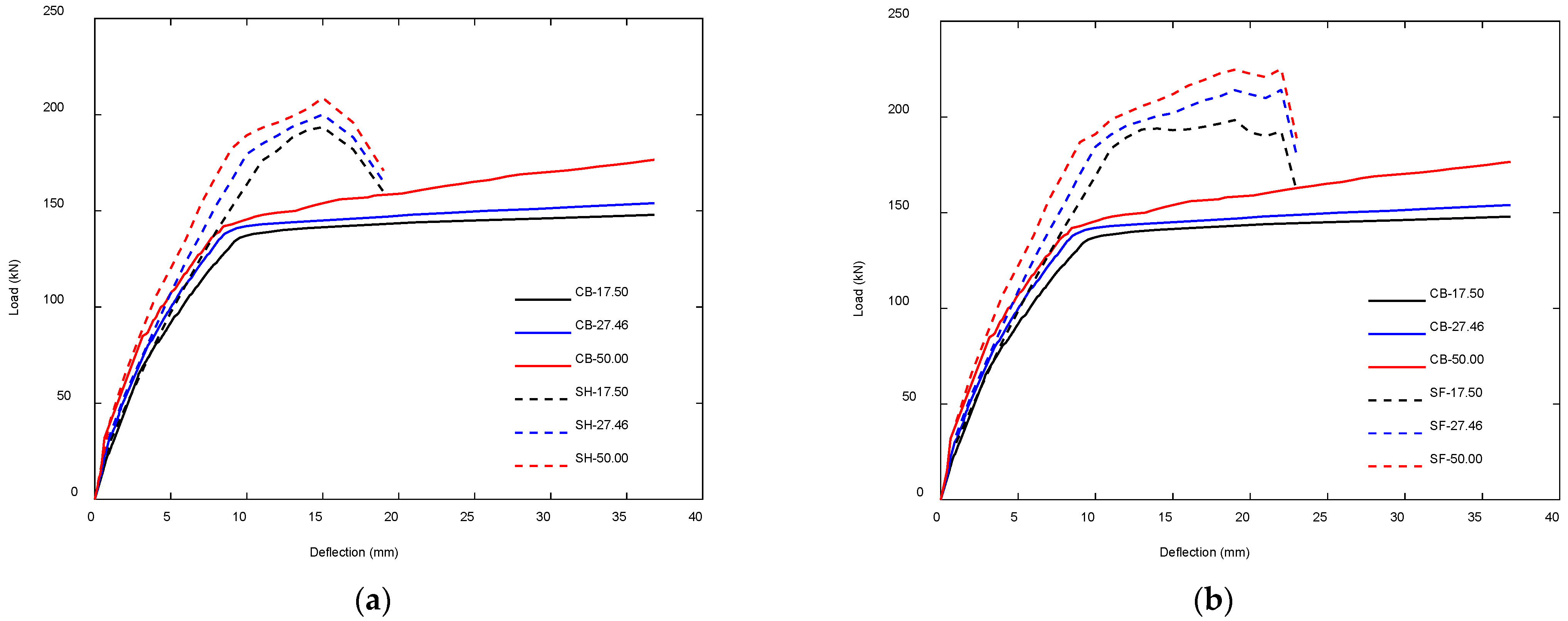
4.3.2. Influence of Concrete Compressive Strength
4.3.3. Influence of Steel Reinforcement Ratio
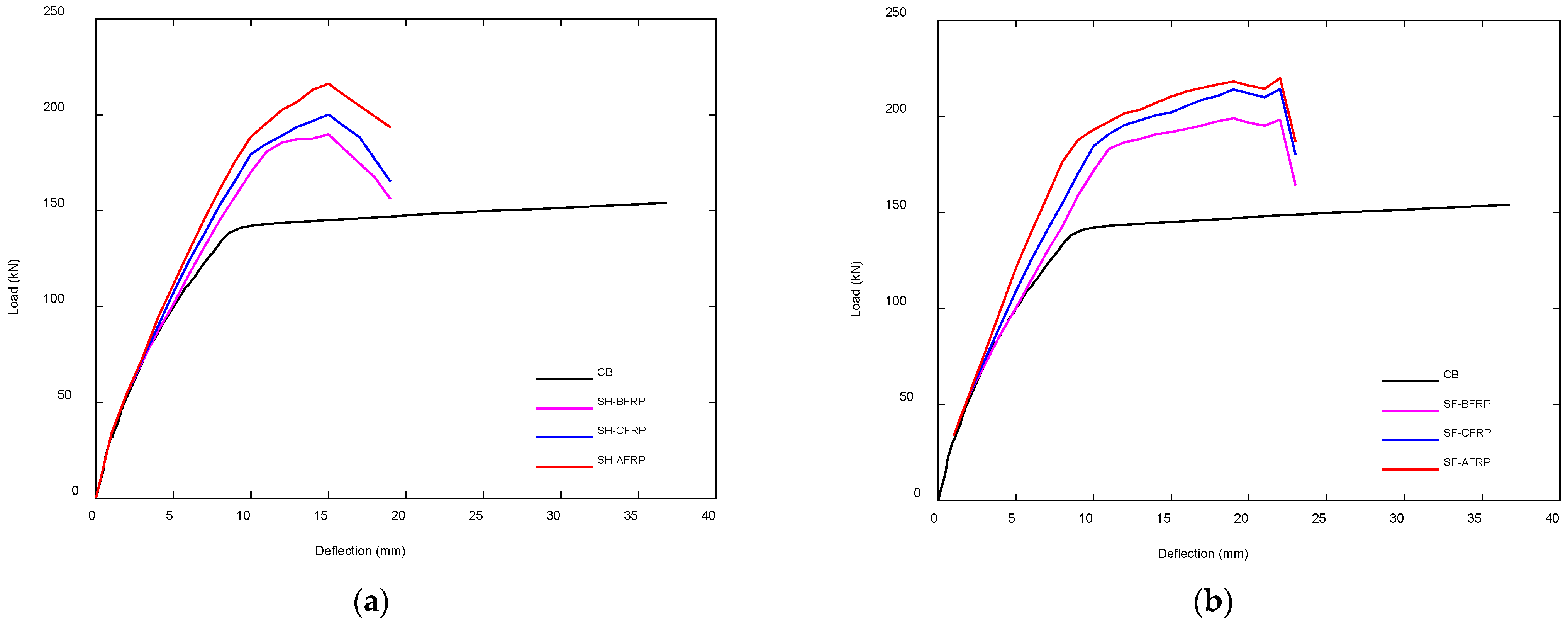
4.3.4. Influence of FRP Material Type
5. Conclusions
- The FE model was successfully validated against experimental results, with load–deflection curves, crack patterns, and response parameters showing excellent agreement (ratios 0.95–1.04; NMSE as low as 0.006).
- Increasing CFRP diameter from 6 to 10 mm enhanced ultimate load and stiffness by up to 47.51% in fully embedded configurations, while undersized rods produced limited improvements.
- Higher concrete compressive strength improved stiffness, energy absorption, and modestly increased ductility, though strengthened beams remained less ductile than the control, a trade-off critical in seismic and thermal applications.
- Beams with reinforcement ratios up to 2.90% achieved peak loads of 309.61 kN, but ductility indices declined from 4.62 to 1.77, indicating more brittle behavior.
- CFRP and AFRP provided the greatest strength and stiffness gains, while BFRP offered more moderate improvements with a better balance between strength and deformability.
- NSM CFRP reinforcement was shown to substantially improve the negative moment performance of RC T-beams even when full groove depth was not achievable. This outcome is highly relevant for retrofit applications where embedment depth is limited by cover or construction constraints, and the results provide quantitative benchmarks that may serve as a basis for future design guidance.
- While the findings demonstrate the effectiveness of NSM CFRP retrofitting, the study did not address cyclic, seismic, or thermal effects, nor did it explicitly model bond–slip behavior. These limitations should be explored in future research to broaden the applicability of the proposed approach and to develop more comprehensive design recommendations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RC | Reinforced concrete |
| FRP | Fiber-reinforced polymers |
| NSM | Near-surface mounted |
| CFRP | Carbon-fiber-reinforced polymers |
| FE | Finite element |
| LVDT | Linear variable differential transformer |
| ATENA | Advanced Tool for Engineering Nonlinear Analysis |
| NMSE | Normalized mean square error |
| BFRP | Basalt-fiber-reinforced polymers |
| AFRP | Aramid-fiber-reinforced polymers |
References
- Hanif, M.U.; Seo, S.-Y.; Tran, H.V.; Senghong, K. Monitoring and characterizing the debonding in CFRP retrofitted RC beams using acoustic emission technology. Dev. Built Environ. 2023, 14, 100141. [Google Scholar] [CrossRef]
- Ayyobi, P.; Barros, J.A.O.; Dias, S.J.E. Numerical assessment of the effect of CFRP anchorages on the flexural and shear strengthening performance of RC beams. J. Compos. Sci. 2024, 8, 348. [Google Scholar] [CrossRef]
- Schwarz, Y.; Sanio, D.; Mark, P. Experimental study of the effectiveness of strengthening reinforced concrete slabs with thermally prestressed reinforcement. CivilEng 2025, 6, 49. [Google Scholar] [CrossRef]
- Baena, M.; Jahani, Y.; Torres, L.; Barris, C.; Perera, R. Flexural performance and end debonding prediction of NSM carbon FRP-strengthened reinforced concrete beams under different service temperatures. Polymers 2023, 15, 851. [Google Scholar] [CrossRef] [PubMed]
- Murad, Y.Z.; Al-Mahmood, H.; Tarawneh, A.; Aljaafreh, A.J.; AlMashaqbeh, A.; Abdel Hadi, R.; Shabbar, R. Shear strengthening of RC beams using fabric-reinforced cementitious matrix, carbon plates, and 3D-printed strips. Sustainability 2023, 15, 4293. [Google Scholar] [CrossRef]
- Hosen, M.A.; Shammas, M.I.; Kaaf, K.A.A.; Jumaat, M.Z.; Alengaram, U.J.; Sulong, N.H.R.; Hashim, H.B. Carbon fiber reinforced polymer (CFRP) for structural capacity enhancement of RC beams incorporating innovative side hybrid (SH) technique. Buildings 2024, 14, 1919. [Google Scholar] [CrossRef]
- Li, W.; Huang, X.; Liu, X.; Wen, T.; Jing, C.; Li, L. Flexural performance of reinforced concrete beams strengthened with a novel high-strength and high-toughness epoxy mortar thin layer. Appl. Sci. 2024, 14, 3999. [Google Scholar] [CrossRef]
- Atmajayanti, A.T.; Haryanto, Y.; Hsiao, F.-P.; Hu, H.-T.; Nugroho, L. Effective flexural strengthening of reinforced concrete T-beams using bonded fiber-core steel wire ropes. Fibers 2025, 13, 53. [Google Scholar] [CrossRef]
- Haryanto, Y.; Hu, H.-T.; Atmajayanti, A.T.; Hsiao, F.-P.; Nugroho, L.; Wariyatno, N.G. Simulation-based study on the performance of NSM-CFRP strengthening in prestressed concrete T-beams under seismic loading. Materials 2025, 18, 4386. [Google Scholar] [CrossRef]
- Bournas, D.A.; Pavese, S.; Tizani, W. Tensile capacity of FRP anchors in connecting FRP and TRM sheets to concrete. Eng. Struct. 2015, 82, 72–81. [Google Scholar] [CrossRef]
- Siddika, A.; Shojib, M.H.H.; Hossain, M.M.; Hossain, M.I.; Al Mamun, M.A.; Alyousef, R.; Amran, Y.H.M. Flexural performance of wire mesh and geotextile-strengthened reinforced concrete beam. SN Appl. Sci. 2019, 1, 1324. [Google Scholar] [CrossRef]
- Siddika, A.; Al Mamun, M.A.; Ferdous, W.; Alyousef, R. Performances, challenges and opportunities in strengthening reinforced concrete structures by using FRPS—A state-of-the-art review. Eng. Fail. Anal. 2020, 111, 104480. [Google Scholar] [CrossRef]
- Alhassan, M.; Al-Rousan, R.; Ababneh, A. Anchoring of the main CFRP sheets with transverse CFRP strips for optimum upgrade of RC beams: Parametric experimental study. Constr. Build. Mater. 2021, 293, 123525. [Google Scholar] [CrossRef]
- Lee, L.S.; Jain, R. The role of FRP composites in a sustainable world. Clean Technol. Environ. Policy 2009, 11, 247–249. [Google Scholar] [CrossRef]
- Al-Rouslan, R. Influence of opening sizes on the flexural behavior of heat-damaged reinforced concrete slabs strengthened with CFRP ropes. Case Stud. Constr. Mater. 2022, 17, e01464. [Google Scholar] [CrossRef]
- Al-Rouslan, R.; Issa, M.A. Flexural behavior of RC beams externally strengthened with CFRP composites exposed to severe environment conditions. KSCE J. Civ. Eng. 2017, 21, 2300–2309. [Google Scholar] [CrossRef]
- Al-Rouslan, R. Effect of CFRP schemes on the flexural behavior of RC beams modeled by using a nonlinear finite-element analysis. Mech. Compos. Mater. 2015, 51, 437–446. [Google Scholar] [CrossRef]
- Al-Rouslan, R. Impact of internal CFRP strips on the flexural behavior of heat-damaged reinforced concrete beams. Heliyon 2023, 9, e17145. [Google Scholar] [CrossRef]
- Al-Rouslan, R. Anchored CFRP ropes for flexural capacity recovering of thermally damaged RC one-way slabs. Alex. Eng. J. 2023, 76, 757–774. [Google Scholar] [CrossRef]
- Su, M.; Gong, S.; Liu, Y.; Peng, H. Flexural behavior of RC beams strengthened with fully or partially prestressed near-surface mounted FRP strips: An experimental investigation. Eng. Struct. 2022, 262, 114345. [Google Scholar] [CrossRef]
- Teng, J.G.; De Lorenzis, L.; Wang, B.; Li, R.; Wong, T.N.; Lam, L. Debonding failures of RC beams strengthened with near-surface mounted CFRP strips. J. Compos. Constr. 2006, 10, 92–105. [Google Scholar] [CrossRef]
- Zhang, S.S.; Yu, T.; Chen, G.M. Reinforced concrete beams strengthened in flexure with Near-Surface Mounted (NSM) CFRP strips: Current status and research needs. Compos. B Eng. 2017, 131, 30–42. [Google Scholar] [CrossRef]
- ACI Committee 440. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures (ACI 440.2R-17); American Concrete Institute: Farmington Hills, MI, USA, 2017. [Google Scholar]
- Badawi, M.; Soudki, K. Flexural strengthening of RC beams with prestressed NSM CFRP rods—Experimental and analytical investigation. Constr. Build. Mater. 2009, 23, 3292–3300. [Google Scholar] [CrossRef]
- Dias, S.J.E.; Barros, J.A.O. Shear strengthening of RC beams with NSM CFRP laminates: Experimental research and analytical formulation. Compos. Struct. 2013, 99, 477–490. [Google Scholar] [CrossRef]
- Almassri, B.; Kreit, A.; Al Mahmoud, F.; François, R. Mechanical behaviour of corroded RC beams strengthened by NSM CFRP rods. Compos. B Eng. 2014, 64, 97–107. [Google Scholar] [CrossRef]
- Capozucca, R.; Domizi, J.; Magagnini, E. Damaged RC beams strengthened with NSM CFRP rectangular rods under vibration in different constrain conditions. Compos. Struct. 2016, 154, 660–683. [Google Scholar] [CrossRef]
- Dias, S.J.E.; Barros, J.A.O.; Janwaen, W. Behavior of RC beams flexurally strengthened with NSM CFRP laminates. Compos. Struct. 2018, 201, 363–376. [Google Scholar] [CrossRef]
- Zhang, S.S.; Ke, Y.; Smith, S.T.; Zhu, H.P.; Wang, Z.L. Effect of FRP U-jackets on the behaviour of RC beams strengthened in flexure with NSM CFRP strips. Compos. Struct. 2021, 256, 113095. [Google Scholar] [CrossRef]
- Abdallah, M.; Al Mahmoud, F.; Tabet-Derraz, M.I.; Kheli, A.; Mercier, J. Experimental and numerical investigation on the effectiveness of NSM and side-NSM CFRP bars for strengthening continuous two-span RC beams. J. Build. Eng. 2021, 41, 102723. [Google Scholar] [CrossRef]
- Hadi, S.; Kazeminezhad, E.; Safakhah, S. Full-scale experimental evaluation of flexural strength and ductility of reinforced concrete beams strengthened with various FRP mechanisms. Structures 2022, 43, 1160–1176. [Google Scholar] [CrossRef]
- Ke, Y.; Zhang, S.S.; Nie, X.F.; Yu, T.; Yang, Y.M.; Jedrzejko, M.J. Finite element modelling of RC beams strengthened in flexure with NSM FRP and anchored with FRP U-jackets. Compos. Struct. 2022, 282, 115104. [Google Scholar] [CrossRef]
- Bouzid, H.; Rabia, B.; Daouadji, T.H. Ultimate behavior of RC beams strengthened in flexure using FRP material. Eng. Struct. 2023, 289, 116300. [Google Scholar] [CrossRef]
- Ahmed, S.; Sharaky, I.A.; Ibrahim, E.Y.E.; Abdo, A. Flexural response of GFRP RC beams strengthened with side and bottom NSM GFRP bars. Case Stud. Constr. Mater. 2023, 18, e01858. [Google Scholar] [CrossRef]
- Sharaky, I.A.; Torres, L.; Comas, J.; Barris, C. Flexural response of reinforced concrete (RC) beams strengthened with near surface mounted (NSM) fiber reinforced polymer (FRP) bars. Compos. Struct. 2014, 109, 8–22. [Google Scholar] [CrossRef]
- Budipriyanto, A.; Han, A.L.; Hu, H.-T. Bond-shear behavior of FRP rods as a function of attachment configuration. J. Adv. Civ. Environ. Eng. 2018, 1, 9–17. [Google Scholar] [CrossRef]
- Haryanto, Y.; Hu, H.-T.; Han, A.L.; Hsiao, F.-P.; Teng, C.-J.; Hidayat, B.A.; Nugroho, L. Nonlinear 3D model of double shear lap tests for the bond of near-surface mounted FRP rods in concrete considering different embedment depth. Period. Polytech. Civ. Eng. 2021, 65, 878–889. [Google Scholar]
- Haryanto, Y.; Hu, H.-T.; Han, A.L.; Hsiao, F.-P.; Teng, C.-J.; Hidayat, B.A.; Wariyatno, N.G. Negative moment region flexural strengthening system of RC T-beams with half-embedded NSM FRP rods: A parametric analytical approach. J. Chin. Inst. Eng. 2021, 44, 553–561. [Google Scholar] [CrossRef]
- Tudjono, S.; Han, A.L.; Gan, B.S. An integrated system for enhancing flexural member’s capacity via combinations of the fiber reinforced plastic use, retrofitting, and surface treatment techniques. Int. J. Technol. 2018, 9, 5–15. [Google Scholar] [CrossRef]
- Haryanto, Y.; Hu, H.-T.; Han, A.L.; Hsiao, F.-P.; Teng, C.-J.; Hidayat, B.A.; Nugroho, L. Numerical investigation on RC T-beams strengthened in the negative moment region using NSM FRP rods at various depth of embedment. Comput. Concr. 2021, 28, 347–360. [Google Scholar]
- Jumaat, M.Z.; Rahman, M.M.; Alam, M.A. Flexural strengthening of RC continuous T-beam using CFRP laminate: A review. Int. J. Phys. Sci. 2010, 5, 619–625. [Google Scholar]
- Al-Khafaji, A.; Salim, H. Flexural strengthening of RC continuous T-beams using CFRP. Fibers 2020, 8, 41. [Google Scholar] [CrossRef]
- Han, A.L.; Hu, H.-T.; Gan, B.S.; Hsiao, F.-P.; Haryanto, Y. Carbon fiber-reinforced polymer rod embedment depth influence on concrete strengthening. Arab. J. Sci. Eng. 2022, 47, 12685–12695. [Google Scholar] [CrossRef]
- Haryanto, Y.; Han, A.L.; Hu, H.-T.; Hsiao, F.-P.; Gan, B.S.; Nugroho, L.; Lin, C.-C. Impact of Non-Reversed Low Cyclic Loading on the Seismic Response of RC T-Beams Strengthened in the Hogging Zone Using NSM-CFRP Rods with Different Embedment Depth. In Proceedings of the 33rd International Ocean and Polar Engineering Conference, Ottawa, ON, Canada, 18–23 June 2023. [Google Scholar]
- Haryanto, Y.; Hsiao, F.-P.; Hu, H.-T.; Han, A.L.; Chua, A.W.; Salim, F.; Nugroho, L. Structural behavior of negative moment region NSM-CFRP strengthened RC T-beams with various embedment depth under monotonic and cyclic loading. Compos. Struct. 2022, 301, 116214. [Google Scholar] [CrossRef]
- Haryanto, Y.; Hermanto, N.I.S.; Hsiao, F.-P.; Hu, H.-T.; Han, A.L.; Nugroho, L.; Salim, F. Predicting the Behavior of RC T-Beams Strengthened with NSM-CFRP Rods in The Negative Moment Region: A Finite Element Approach for Low Cyclic Loading. In Proceedings of the E3S Web Conference, 2nd International Conference on Disaster Mitigation and Management, Padang, Indonesia, 29–30 September 2023. [Google Scholar]
- Nugroho, L.; Haryanto, Y.; Hu, H.-T.; Han, A.L.; Hsiao, F.-P.; Lin, C.-C.; Weng, P.-W.; Widiastuti, E.P. NSM-CFRP rods with varied embedment depths for strengthening RC T-beams in the negative moment region: Investigation on high cyclic response. Compos. Struct. 2024, 331, 117891. [Google Scholar] [CrossRef]
- Nugroho, L.; Haryanto, Y.; Hu, H.-T.; Hsiao, F.-P.; Han, A.L.; Widyaningrum, A.; Prasetijo, H. Flexural Capacity of Negative Moment Region NSM-CFRP Strengthened RC T-beam Under High Loading Rate: An Analytical Prediction. In Proceedings of the E3S Web Conference the 2nd International Conference on Disaster Mitigation and Management, Padang, Indonesia, 29–30 September 2023. [Google Scholar]
- Nguyen, M.H.; Ho, M.H.; Tran, V.R.; Phan, H.N.; Nguyen, D.D.N.; Huynh, P.N. Flexural performance of reinforced concrete beams strengthened with prestressed FRP sheets: Experiments and numerical investigations. Case Stud. Constr. Mat. 2024, 21, e03475. [Google Scholar] [CrossRef]
- Cutolo, A.; Guarracino, F.; Olivieri, C.; Mascolo, I. Nonlinear FE analysis of a masonry spiral staircase in Nisida: A refined numerical case study. Int. J. Multiscale Comput. Eng. 2022, 20, 105–114. [Google Scholar] [CrossRef]
- Verre, S. Numerical strategy for column strengthened with FRCM/SRG system. Buildings 2022, 12, 2187. [Google Scholar] [CrossRef]
- Nugroho, L.; Haryanto, Y.; Hu, H.-T.; Hsiao, F.-P.; Pamudji, G.; Setiadji, B.H.; Hsu, C.-N.; Weng, P.-W.; Lin, C.-C. Prestressed concrete T-beams strengthened with near-surface mounted carbon-fiber-reinforced polymer rods under monotonic loading: A finite element analysis. Eng 2025, 6, 36. [Google Scholar] [CrossRef]
- Haryanto, Y.; Hsiao, F.-P.; Nugroho, L.; Hu, H.-T.; Sudibyo, G.H.; Wariyatno, N.G.; Hidayat, B.A.; Pamudji, G. Enhancing the negative moment flexural capacity of RC T-beams with bonded steel wire ropes—A parametric study. Eng. Fail. Anal. 2025, 180, 109883. [Google Scholar] [CrossRef]
- Haryanto, Y.; Wariyatno, N.G.; Hsiao, F.-P.; Hu, H.-T.; Han, A.L.; Nugroho, L.; Hartono, H. RC T-beams with flexural strengthening in the negative moment region under different configurations of NSM CFRP rods. Eng. Fail. Anal. 2025, 173, 109458. [Google Scholar] [CrossRef]
- ACI Committee 318. Building Code Requirements for Structural Concrete and Commentary (ACI 318-19); American Concrete Institute: Farmington Hills, MI, USA, 2019. [Google Scholar]
- Cervenka, V.; Cervenka, J.; Janda, Z.; Pryl, D. ATENA Program Documentation Part 8: User’s Manual for ATENA-GID Interface; Cervenka Consulting: Prague, Czech Republic, 2021. [Google Scholar]
- Alwash, D.; Kalfat, R.; Al-Mahaidi, R. Numerical modelling of RC beams strengthened in shear using NSM FRP and cement based adhesives. Structures 2023, 57, 105217. [Google Scholar] [CrossRef]
- Palomo, I.R.I.; Frappa, G.; de Almeida, L.C.; Trautwein, L.M.; Pauletta, M. Analytical and numerical models to determine the strength of RC exterior beam–column joints retrofitted with UHPFRC. Eng. Struct. 2024, 312, 118244. [Google Scholar] [CrossRef]
- Zheng, Y.-Z.; Wang, W.-W.; Mosalam, K.M.; Fang, Q.; Chen, L.; Zhu, Z.-F. Experimental investigation and numerical analysis of RC beams shear strengthened with FRP/ECC composite layer. Compos. Struct. 2020, 246, 112436. [Google Scholar] [CrossRef]
- Cervenka, V. Constitutive model for cracked reinforced concrete. J. Proc. 1985, 82, 877–882. [Google Scholar]
- Vecchio, F.J.; Collins, M.P. The modified compression-field theory for reinforced-concrete elements subjected to shear. J. Proc. 1986, 83, 219–231. [Google Scholar]
- Comité Euro-International du Béton. CEB-FIP Model Code 1990: Design Code; Thomas Telford Publishing: London, UK, 1993. [Google Scholar]
- Kupfer, H.; Hilsdorf, H.K.; Rüsch, H. Behavior of concrete under biaxial stresses. J. Proc. 1969, 66, 656–666. [Google Scholar] [CrossRef]
- Scotta, R.; Vitaliani, R.; Saetta, A.; Oñate, E.; Hanganu, A. A scalar damage model with a shear retention factor for the analysis of reinforced concrete structures: Theory and validation. Comput. Struct. 2001, 79, 737–755. [Google Scholar] [CrossRef]
- Vos, E. Influence of Loading Rate and Radial Pressure of Bond in Reinforced Concrete. Ph.D. Thesis, Delft University, Delft, The Netherlands, 1983. [Google Scholar]
- ASTM Committee C09. Standard Test Method for Compressive Strength of Cylindrical Concrete Specimens (ASTM C39/C39M-21); ASTM International: West Conshohocken, PA, USA, 2021. [Google Scholar]
- ASTM Committee A01. Standard Test Methods and Definitions for Mechanical Testing of Steel Products (ASTM A370-18); ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar]
- Dassault Systèmes. P Projectile Impact on a Carbon Fiber Reinforced Plate (TB-06-CRP-1, revised April 2007). Available online: https://www.3ds.com/assets/invest/2023-10/aero-projectile-impact-on-a-carbon-fiber-reinforced-06.pdf (accessed on 15 March 2024).
- Nugroho, L.; Haryanto, Y.; Hsiao, F.-P.; Hu, H.-T.; Weng, P.-W.; Lin, C.-C.; Kristiawan, S.A.; Sangadji, S. Effectiveness of UHPC reinforced with steel rebars for flexural strengthening of RC T-beams in an idealized negative moment region. Structures 2025, 10, 109728. [Google Scholar] [CrossRef]
- Poli, A.A.; Cirillo, M.C. On the use of the normalized mean square error in evaluating dispersion model performance. Atmos. Environ. Part A 1993, 27, 2427–2434. [Google Scholar] [CrossRef]
- Kumar, A.; Luo, J.; Bennett, G.F. Statistical evaluation of lower flammability distance (LFD) using four hazardous release models. Process Saf. Prog. 1993, 12, 1–11. [Google Scholar] [CrossRef]
- Alabdulhady, M.Y.; Ojaimi, M.F.; Chkheiwer, A.H. The efficiency of CFRP strengthening and repair system on the flexural behavior of RC beams constructed with different concrete compressive strength. Results Eng. 2022, 16, 100763. [Google Scholar] [CrossRef]
- Ashour, S.A. Effect of compressive strength and tensile reinforcement ratio on flexural behavior of high-strength concrete beams. Eng. Struc. 2000, 22, 413–423. [Google Scholar] [CrossRef]
- Abbood, I.S.; Odaa, S.A.; Hasan, K.F.; Jasim, M.A. Properties evaluation of fiber reinforced polymers and their constituent materials used in structures—A review. Mater. Today Proc. 2021, 43, 1003–1008. [Google Scholar] [CrossRef]
- Abd el-Hafez, L.M.; Mahmoud, F.R.; Fahmy, N.G.; Tawfic, Y.R. Behavior of large-scale columns strengthened with basalt fiber-reinforced polymers sheets or bars and hybrid FRPs. Case Stud. Constr. Mater. 2023, 19, e02125. [Google Scholar] [CrossRef]




| Properties | Formula | Value |
|---|---|---|
| Compressive strength [45,54] (MPa) | Test result | 27.46 |
| Tensile strength [56] (MPa) | 2.62 | |
| Elastic modulus [56] (MPa) | 24,297.56 | |
| Poisson’s ratio [56] | N/A | 0.2 |
| Specific fracture energy [56] (N/m) | 65.50 | |
| Critical compressive displacement [56] (m) | N/A | −0.0005 |
| Shear retention factor | N/A | Variable |
| Bar Size | Modulus of Elasticity (GPa) | Yield Strength (MPa) | Yield Strain (µε) | Tensile Strength (MPa) |
|---|---|---|---|---|
| 10 | 200 | 350.67 | 1800 | 500.85 |
| 16 | 200 | 492.25 | 2500 | 727.51 |
| Parameter | UB | SB-U13 | SB-U16 |
|---|---|---|---|
| Experimental ultimate load, Pu-exp (kN) [69] | 176.66 | 327.58 | 388.59 |
| Numerical ultimate load, Pu-num (kN) | 175.12 | 339.63 | 379.88 |
| Difference (%) | 0.87 | 3.68 | 2.24 |
| NMSE (%) | 0.2 | 0.3 | 0.3 |
| Investigation | Physical Response Characteristics | ||||
|---|---|---|---|---|---|
| Ultimate Load (kN) | Deflection (mm) | Stiffness (kN/mm) | Ductility index | Energy Absorption (kN.mm) | |
| Experimental | 153.14 | 36.82 | 13.58 | 4.55 | 4901.72 |
| Numerical | 154.00 | 36.81 | 13.39 | 4.33 | 4915.49 |
| Ratio | 1.01 | 1.00 | 0.99 | 0.95 | 1.00 |
| Investigation | Physical Response Characteristics | ||||
|---|---|---|---|---|---|
| Ultimate Load (kN) | Deflection (mm) | Stiffness (kN/mm) | Ductility Index | Energy Absorption (kN.mm) | |
| Experimental | 199.80 | 14.97 | 14.14 | 1.79 | 2639.61 |
| Numerical | 200.12 | 15.00 | 15.10 | 1.83 | 2724.14 |
| Ratio | 1.00 | 1.00 | 0.94 | 0.98 | 0.97 |
| Investigation | Physical Response Characteristics | ||||
|---|---|---|---|---|---|
| Ultimate Load (kN) | Deflection (mm) | Stiffness (kN/mm) | Ductility Index | Energy Absorption (kN.mm) | |
| Experimental | 214.13 | 22.38 | 15.01 | 2.10 | 3708.98 |
| Numerical | 214.14 | 22.00 | 14.87 | 2.06 | 3688.69 |
| Ratio | 1.00 | 0.98 | 0.99 | 0.98 | 0.99 |
| Beam Model | CFRP Rod Diameter (mm) | Physical Response Characteristics | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ultimate Load (kN) | Stiffness (kN/m) | Ductility Index | Energy Absorption (kN.mm) | ||||||
| Value | Ratio | Value | Ratio | Value | Ratio | Value | Ratio | ||
| CB | - | 154.00 | - | 13.39 | - | 4.33 | - | 4915.49 | - |
| SH-06 | 2 Ø6 | 190.78 | 1.24 | 13.76 | 1.03 | 1.74 | 0.40 | 2585.71 | 0.53 |
| SH-08 | 2 Ø8 | 200.12 | 1.30 | 15.10 | 1.13 | 1.83 | 0.42 | 2724.14 | 0.55 |
| SH-10 | 2 Ø10 | 204.61 | 1.33 | 16.77 | 1.25 | 1.96 | 0.45 | 2863.75 | 0.58 |
| SF-06 | 2 Ø6 | 196.10 | 1.27 | 13.89 | 1.04 | 2.10 | 0.48 | 3417.94 | 0.70 |
| SF-08 | 2 Ø8 | 214.14 | 1.39 | 14.87 | 1.11 | 2.06 | 0.48 | 3688.69 | 0.75 |
| SF-10 | 2 Ø10 | 227.17 | 1.48 | 19.76 | 1.48 | 2.45 | 0.57 | 4031.37 | 0.82 |
| Beam Model | Concrete Compressive Strength (MPa) | Physical Response Characteristics | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ultimate Load (kN) | Stiffness (kN/m) | Ductility Index | Energy Absorption (kN.mm) | ||||||
| Value | Ratio | Value | Ratio | Value | Ratio | Value | Ratio | ||
| CB-L | 17.50 | 147.96 | - | 12.24 | - | 4.07 | - | 4712.28 | - |
| CB-B | 27.46 | 154.00 | - | 13.39 | - | 4.33 | - | 4915.49 | - |
| CB-H | 50.00 | 176.56 | - | 14.57 | - | 4.75 | - | 5495.98 | - |
| SH-L | 17.50 | 193.56 | 1.31 | 13.97 | 1.14 | 1.68 | 0.41 | 2565.05 | 0.54 |
| SH-B | 27.46 | 200.12 | 1.30 | 15.10 | 1.13 | 1.83 | 0.42 | 2724.14 | 0.55 |
| SH-H | 50.00 | 208.74 | 1.18 | 15.97 | 1.10 | 1.98 | 0.42 | 2913.52 | 0.53 |
| SF-L | 17.50 | 198.40 | 1.34 | 14.74 | 1.20 | 2.04 | 0.50 | 3426.55 | 0.73 |
| SF-B | 27.46 | 214.14 | 1.39 | 14.87 | 1.11 | 2.06 | 0.48 | 3688.69 | 0.75 |
| SF-H | 50.00 | 225.15 | 1.28 | 15.22 | 1.04 | 2.21 | 0.47 | 3940.45 | 0.72 |
| Beam Model | Steel Reinforcement Ratio (%) | Physical Response Characteristics | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ultimate Load (kN) | Stiffness (kN/m) | Ductility Index | Energy Absorption (kN.mm) | ||||||
| Value | Ratio | Value | Ratio | Value | Ratio | Value | Ratio | ||
| CB-0.6 | 0.6 | 149.96 | - | 11.29 | - | 4.62 | - | 4252.28 | - |
| CB-1.0 | 1.0 | 154.00 | - | 13.39 | - | 4.33 | - | 4915.49 | - |
| CB-2.9 | 2.9 | 176.56 | - | 12.88 | - | 3.21 | - | 6058.84 | - |
| SH-0.6 | 0.6 | 169.88 | 1.13 | 13.20 | 1.17 | 1.96 | 0.42 | 2368.43 | 0.56 |
| SH-1.0 | 1.0 | 200.12 | 1.30 | 15.10 | 1.13 | 1.83 | 0.42 | 2724.14 | 0.55 |
| SH-2.9 | 2.9 | 281.75 | 1.60 | 18.04 | 1.40 | 1.44 | 0.45 | 3490.46 | 0.58 |
| SF-0.6 | 0.6 | 179.38 | 1.20 | 13.02 | 1.15 | 2.26 | 0.49 | 3179.78 | 0.75 |
| SF-1.0 | 1.0 | 214.14 | 1.39 | 14.87 | 1.11 | 2.06 | 0.48 | 3688.69 | 0.75 |
| SF-2.9 | 2.9 | 309.61 | 1.75 | 18.76 | 1.46 | 1.77 | 0.55 | 4979.60 | 0.82 |
| Beam Model | FRP Material | Physical Response Characteristics | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Ultimate Load (kN) | Stiffness (kN/m) | Ductility Index | Energy Absorption (kN.mm) | ||||||
| Value | Ratio | Value | Ratio | Value | Ratio | Value | Ratio | ||
| CB | - | 154.00 | - | 13.39 | 4.33 | - | 4915.49 | - | |
| SH-BFRP | BFRP | 189.78 | 1.23 | 14.23 | 1.06 | 1.83 | 0.42 | 2061.87 | 0.42 |
| SH-CFRP | CFRP | 200.12 | 1.30 | 15.10 | 1.13 | 1.83 | 0.42 | 2724.14 | 0.55 |
| SH-AFRP | AFRP | 216.17 | 1.40 | 15.90 | 1.19 | 1.97 | 0.45 | 2939.22 | 0.60 |
| SF-BFRP | BFRP | 198.98 | 1.29 | 13.97 | 1.04 | 2.05 | 0.47 | 3461.26 | 0.70 |
| SF-CFRP | CFRP | 214.14 | 1.39 | 14.48 | 1.08 | 2.06 | 0.48 | 3688.69 | 0.75 |
| SF-AFRP | AFRP | 219.80 | 1.43 | 17.47 | 1.30 | 2.34 | 0.54 | 3865.82 | 0.79 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Haryanto, Y.; Sudibyo, G.H.; Hu, H.-T.; Hsiao, F.-P.; Nugroho, L.; Saputro, D.N.; Suryanto, H.R.; Haryanto, A.E.C. Parametric Study of the Physical Responses of NSM CFRP-Strengthened RC T-Beams in the Negative Moment Region. CivilEng 2025, 6, 56. https://doi.org/10.3390/civileng6040056
Haryanto Y, Sudibyo GH, Hu H-T, Hsiao F-P, Nugroho L, Saputro DN, Suryanto HR, Haryanto AEC. Parametric Study of the Physical Responses of NSM CFRP-Strengthened RC T-Beams in the Negative Moment Region. CivilEng. 2025; 6(4):56. https://doi.org/10.3390/civileng6040056
Chicago/Turabian StyleHaryanto, Yanuar, Gathot Heri Sudibyo, Hsuan-Teh Hu, Fu-Pei Hsiao, Laurencius Nugroho, Dani Nugroho Saputro, Habib Raihan Suryanto, and Abel Earnesta Christopher Haryanto. 2025. "Parametric Study of the Physical Responses of NSM CFRP-Strengthened RC T-Beams in the Negative Moment Region" CivilEng 6, no. 4: 56. https://doi.org/10.3390/civileng6040056
APA StyleHaryanto, Y., Sudibyo, G. H., Hu, H.-T., Hsiao, F.-P., Nugroho, L., Saputro, D. N., Suryanto, H. R., & Haryanto, A. E. C. (2025). Parametric Study of the Physical Responses of NSM CFRP-Strengthened RC T-Beams in the Negative Moment Region. CivilEng, 6(4), 56. https://doi.org/10.3390/civileng6040056