Experimental Study of the Effectiveness of Strengthening Reinforced Concrete Slabs with Thermally Prestressed Reinforcement
Abstract
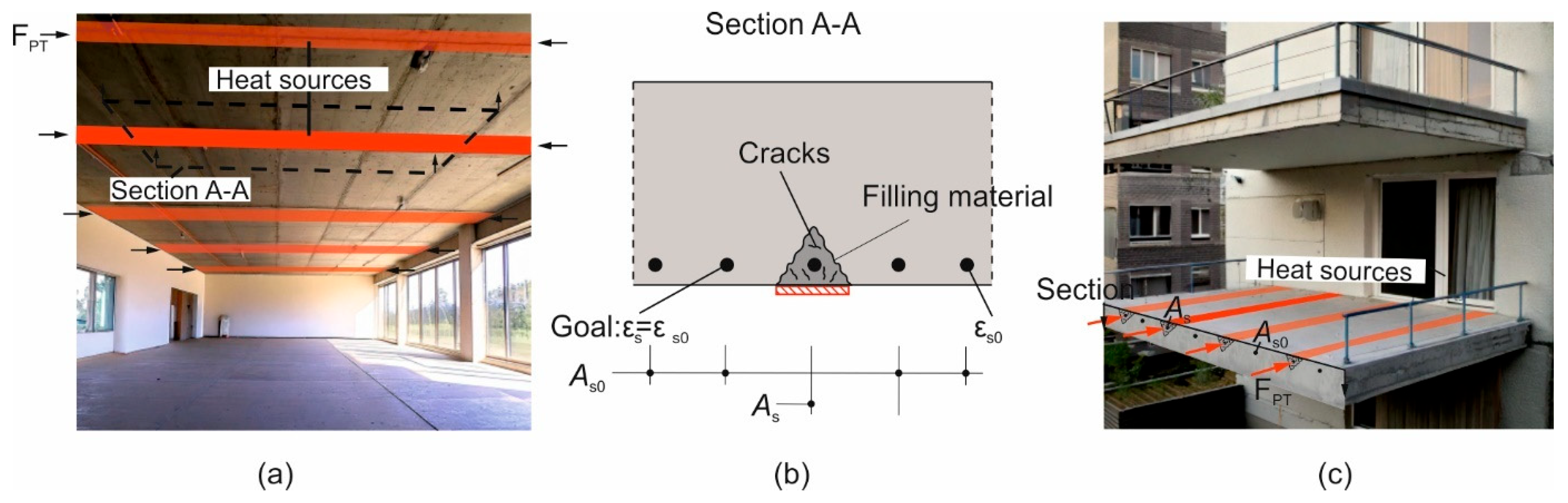
1. Introduction
2. Experimental Investigations
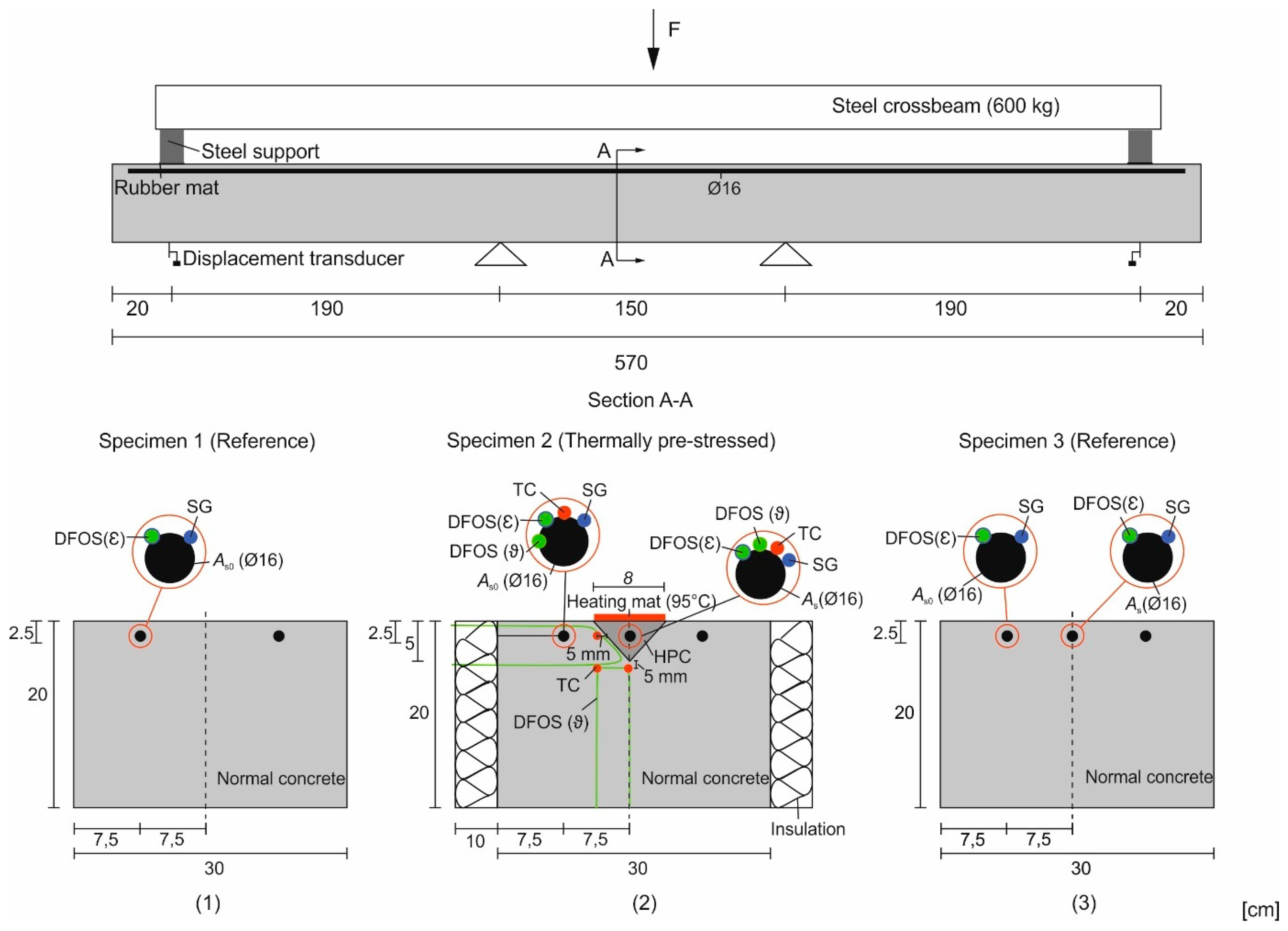
2.1. Key Performance Indicators and Experimental Campaign
2.2. Materials
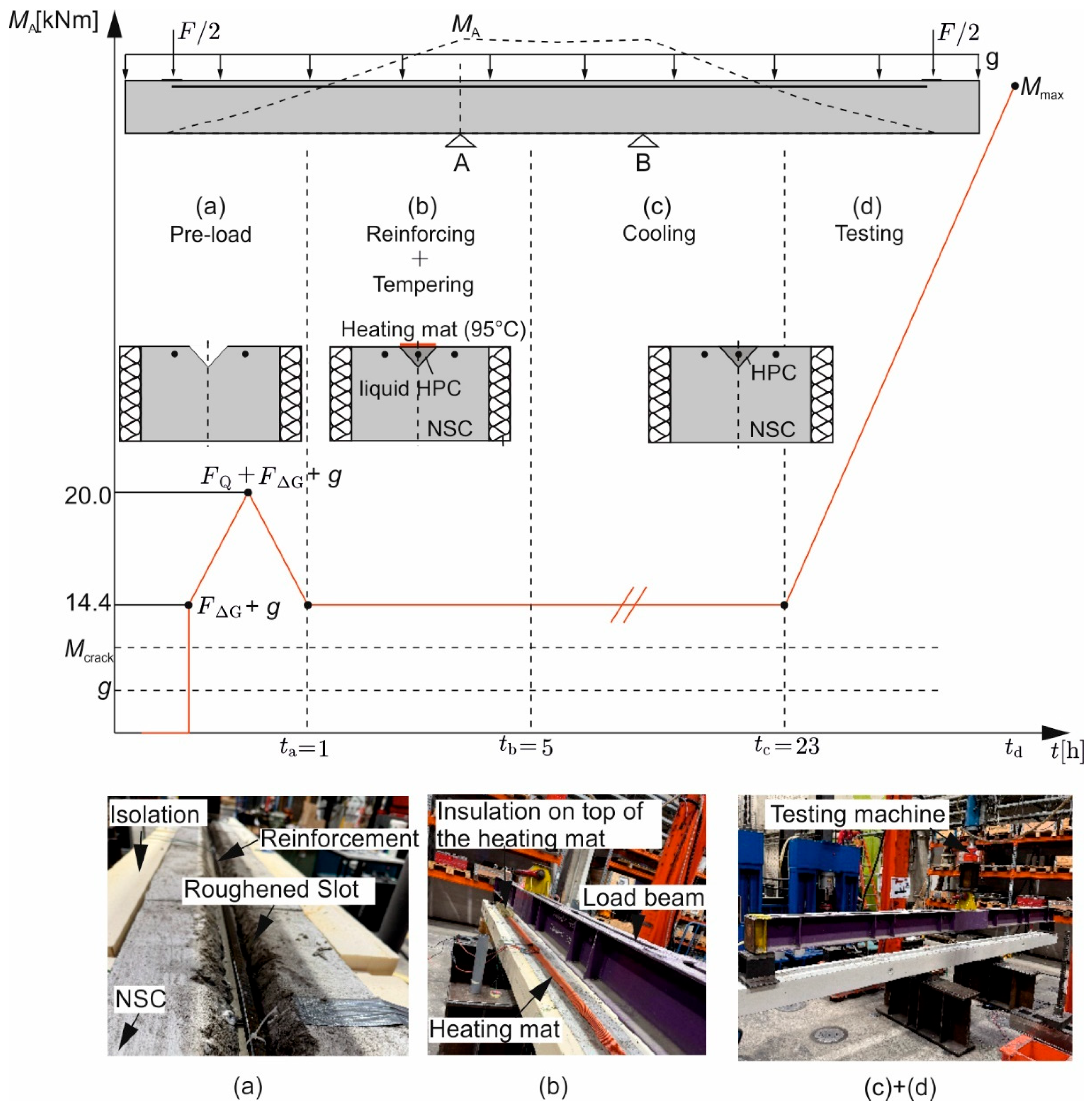
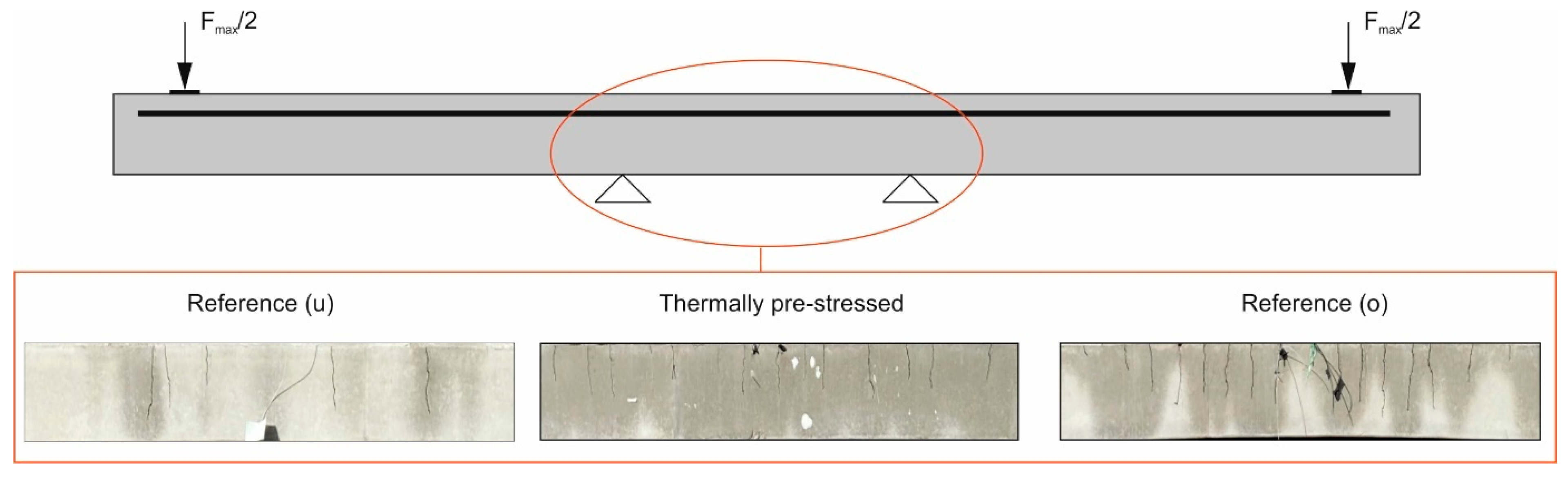
2.3. Test Setup and Execution
3. Experimental Results
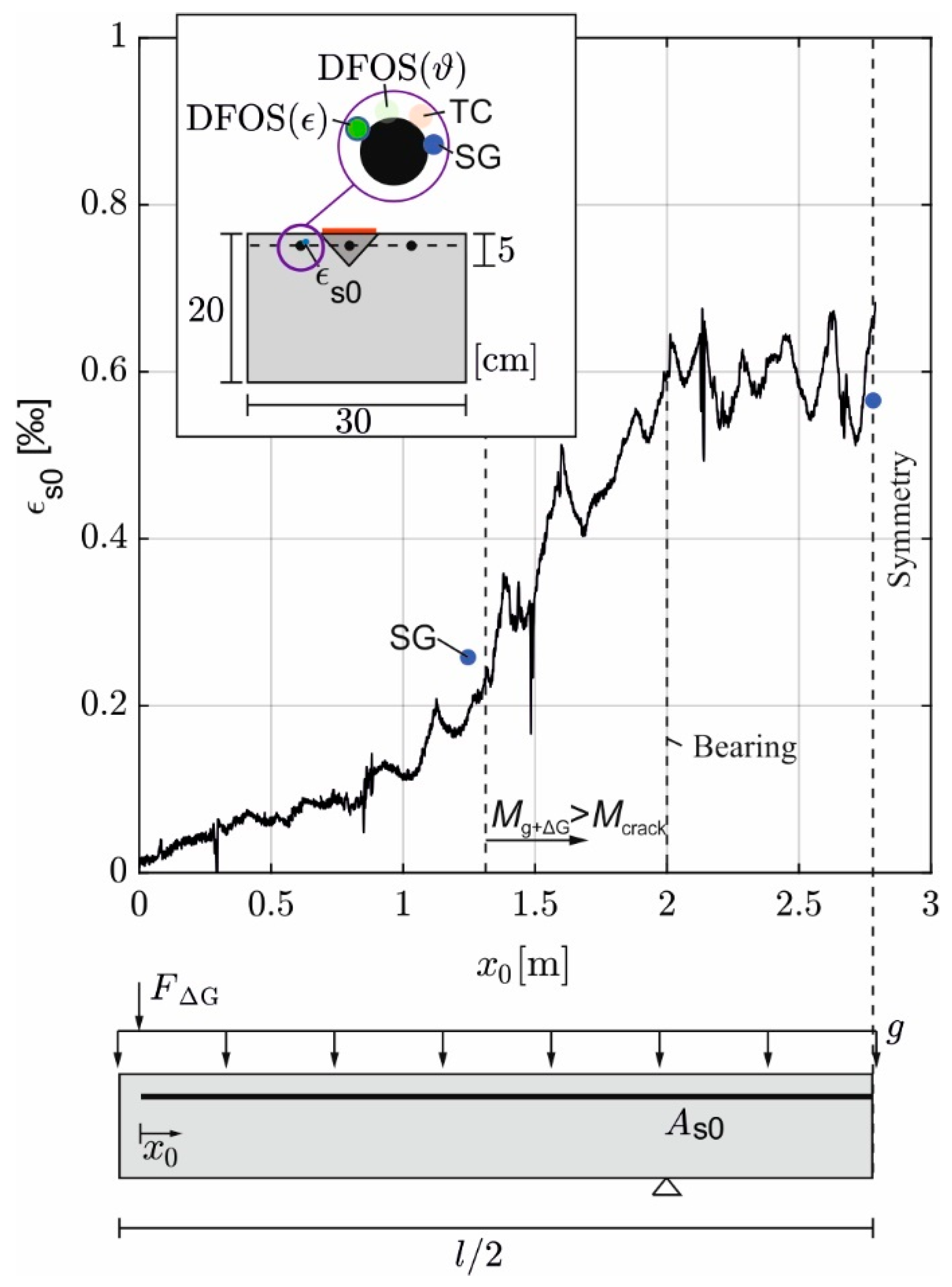
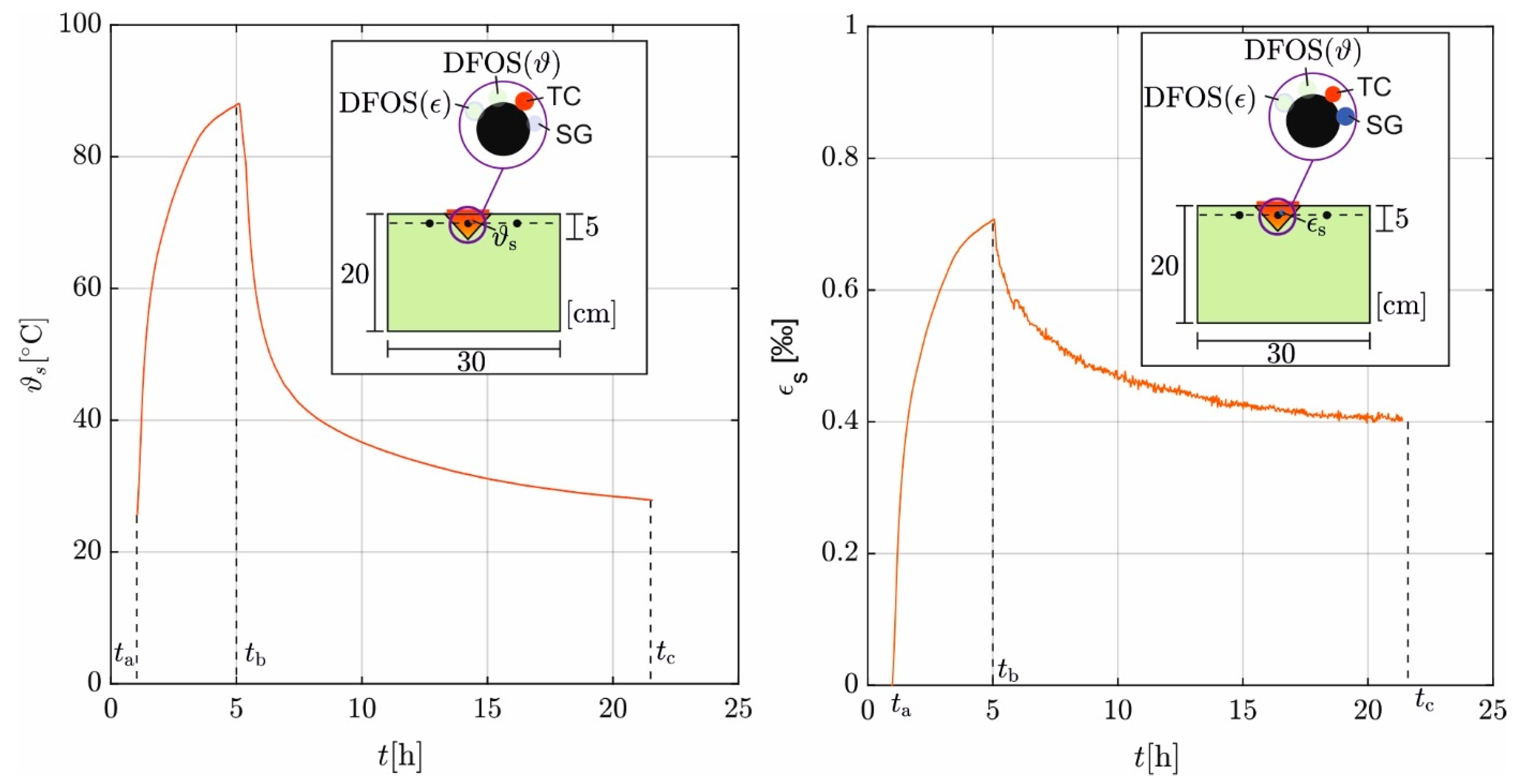
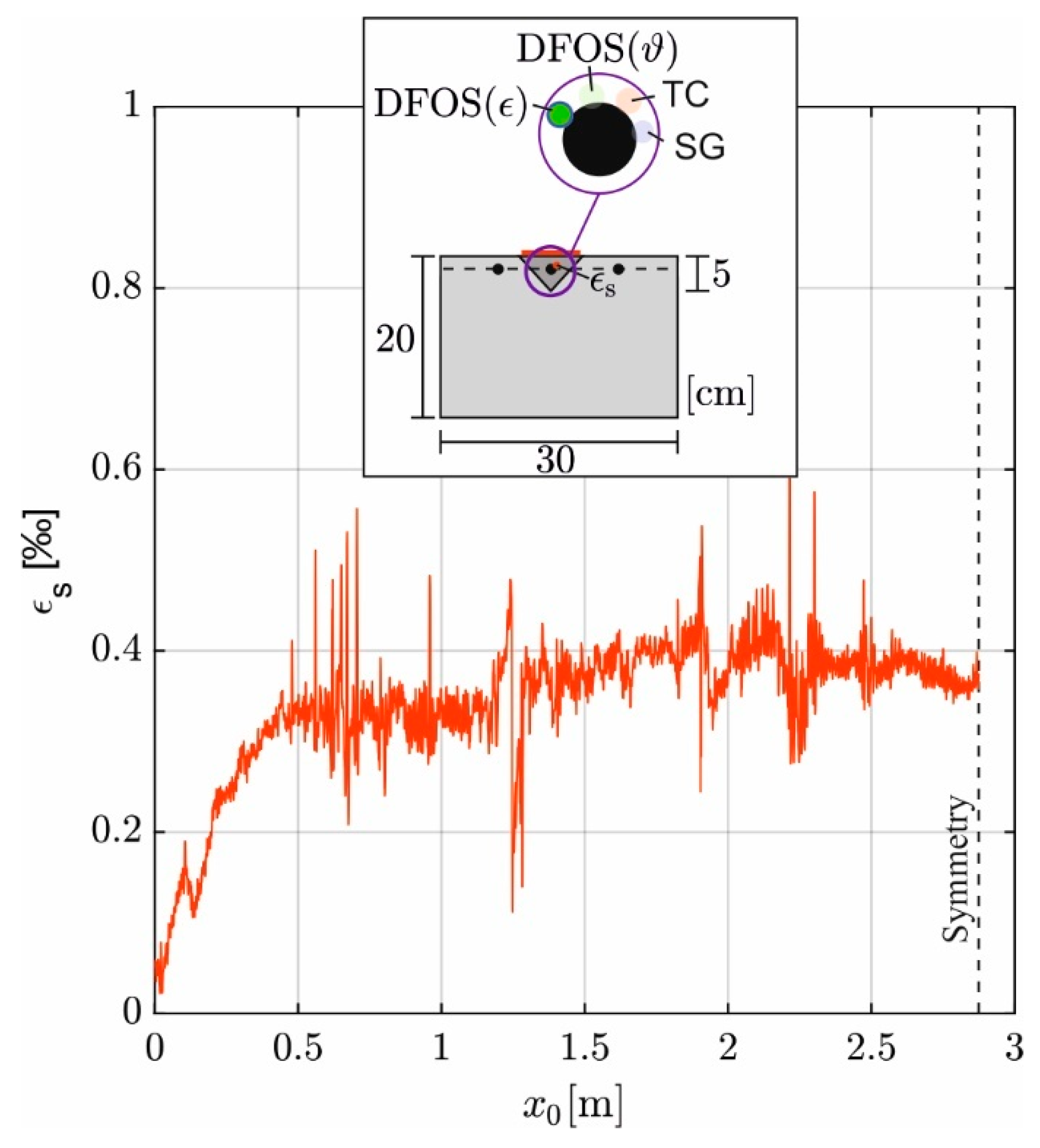
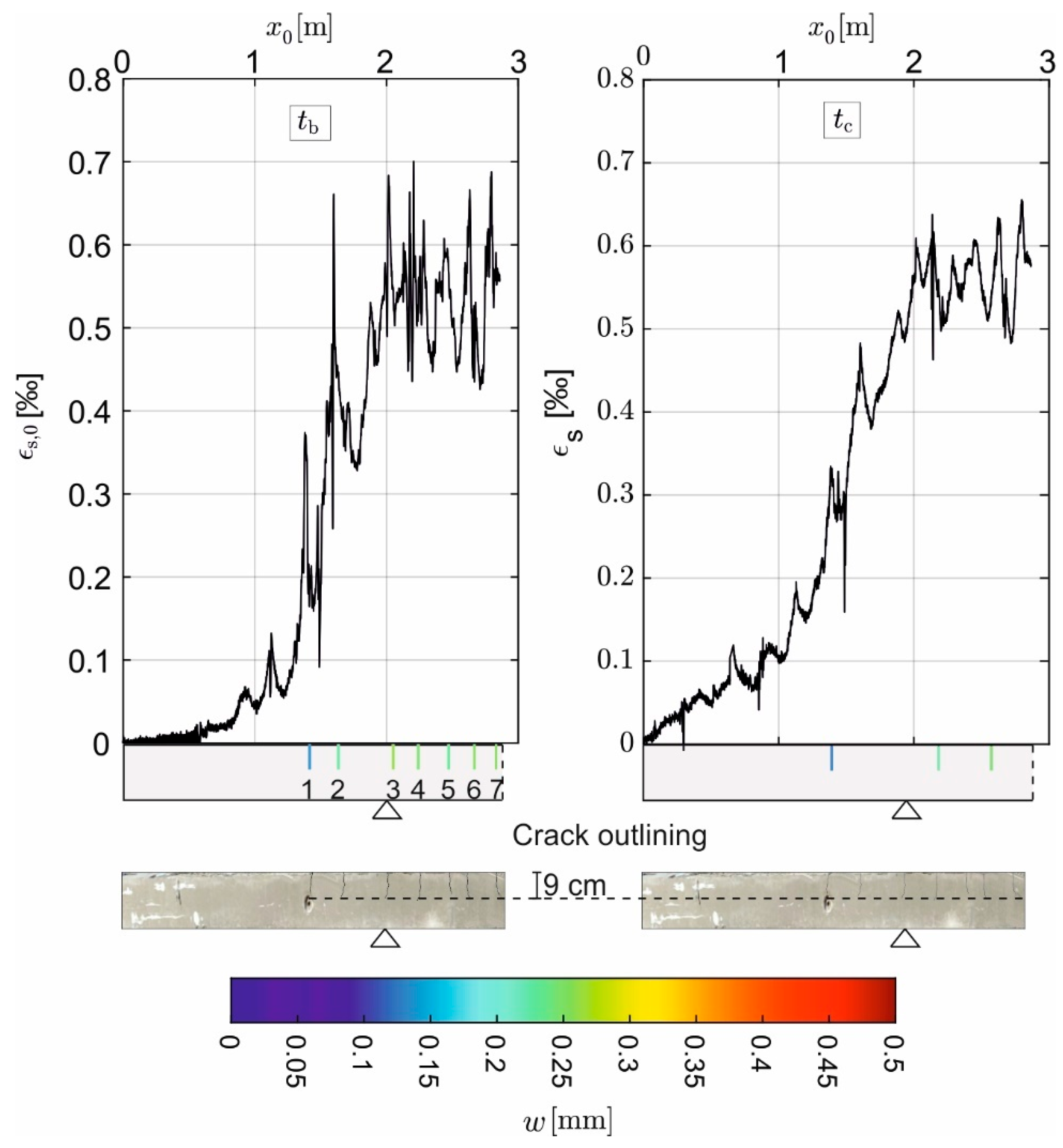
3.1. Strain in the Basic Reinforcement Due to Self-Weight at the Time of Strengthening
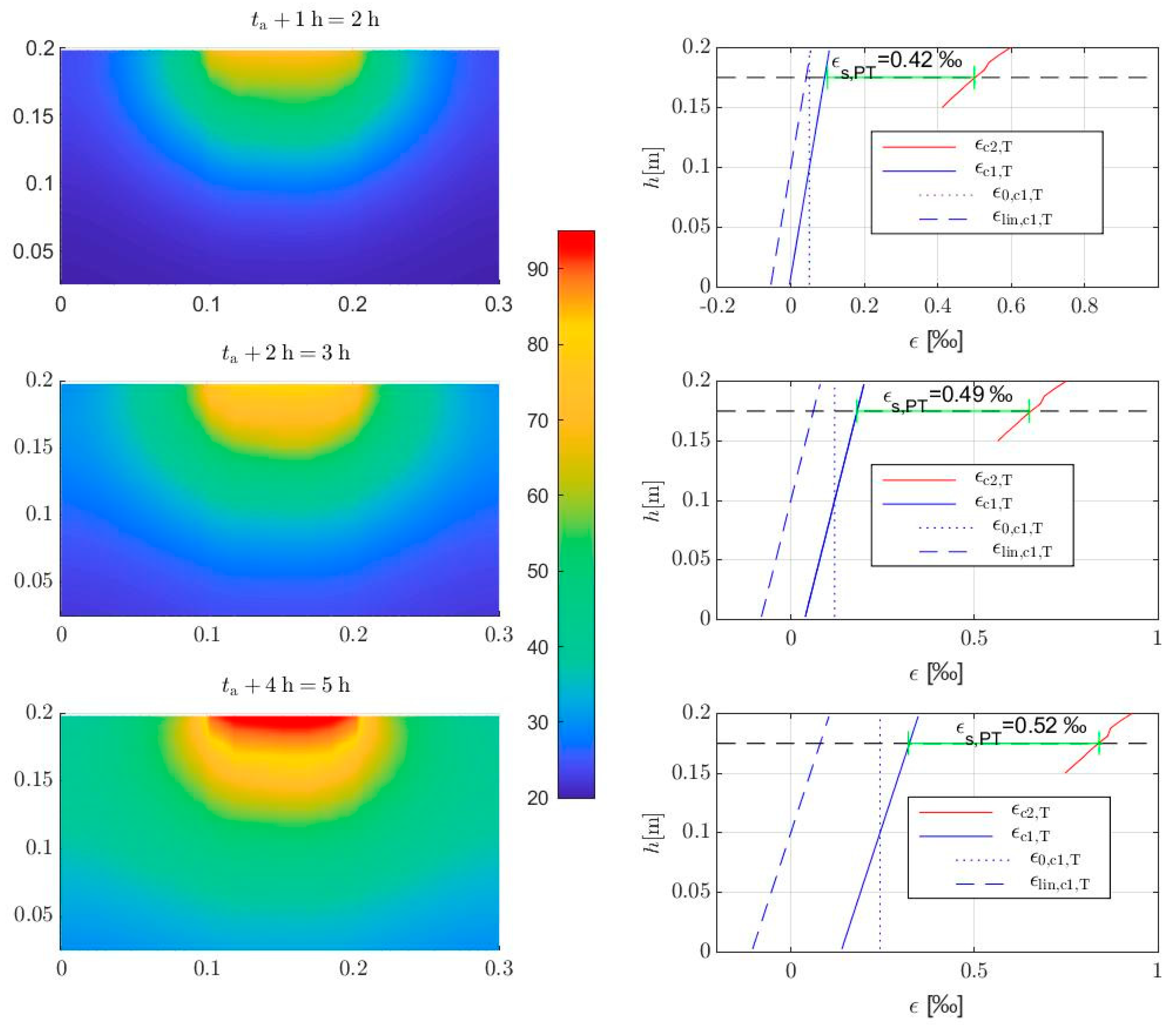
3.2. Thermal and Mechanical Strains in the Added Reinforcing Bar
4. Computational Model for Thermally Prestressed Reinforcement
5. Comparison of the Results of the Thermally Prestressed and the Reference Beams
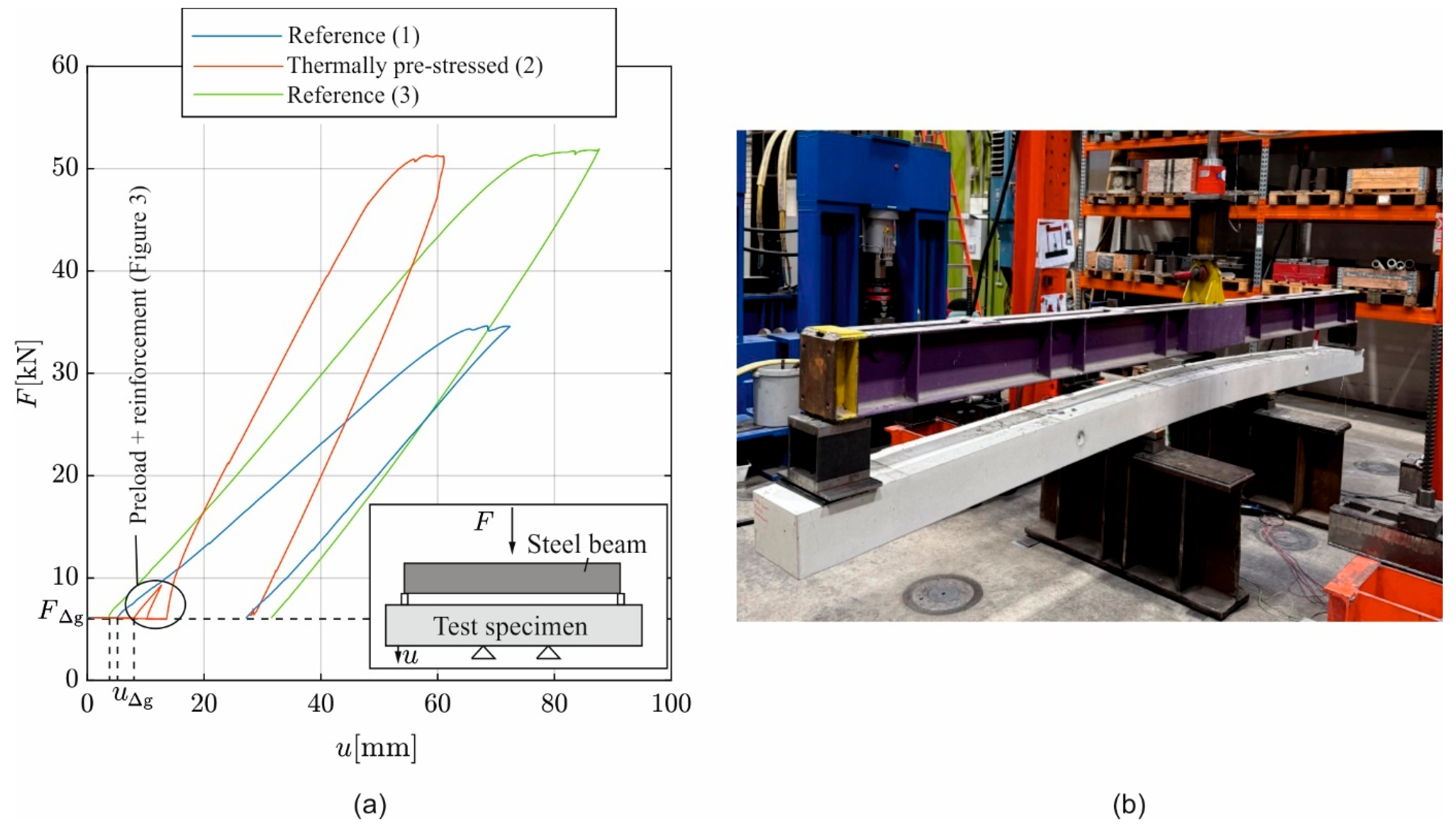
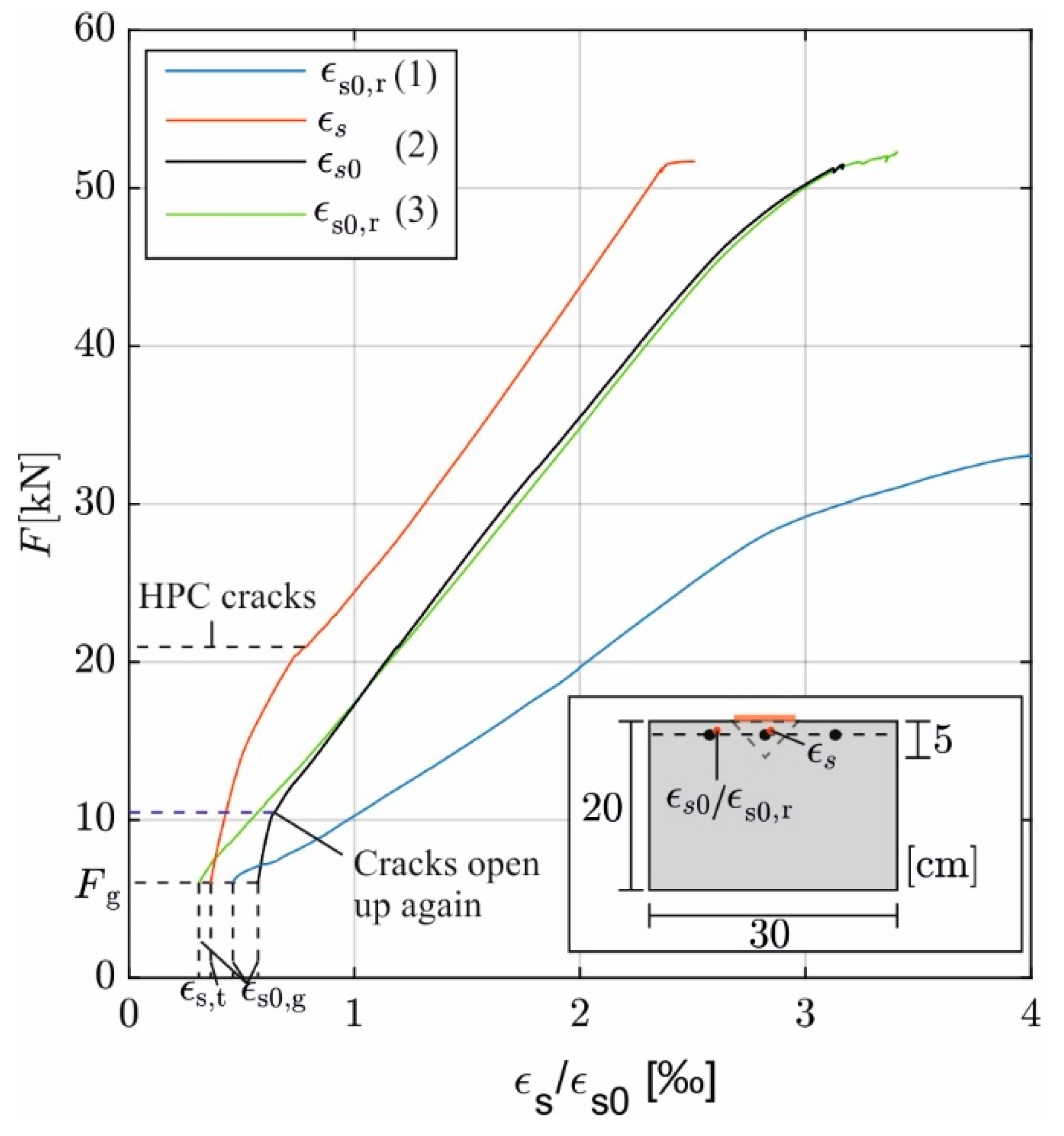
5.1. Relation of Load and Deflection
5.2. Comparison of the Strain Development in Thermally Prestressed and Initial Reinforcement
6. Discussion
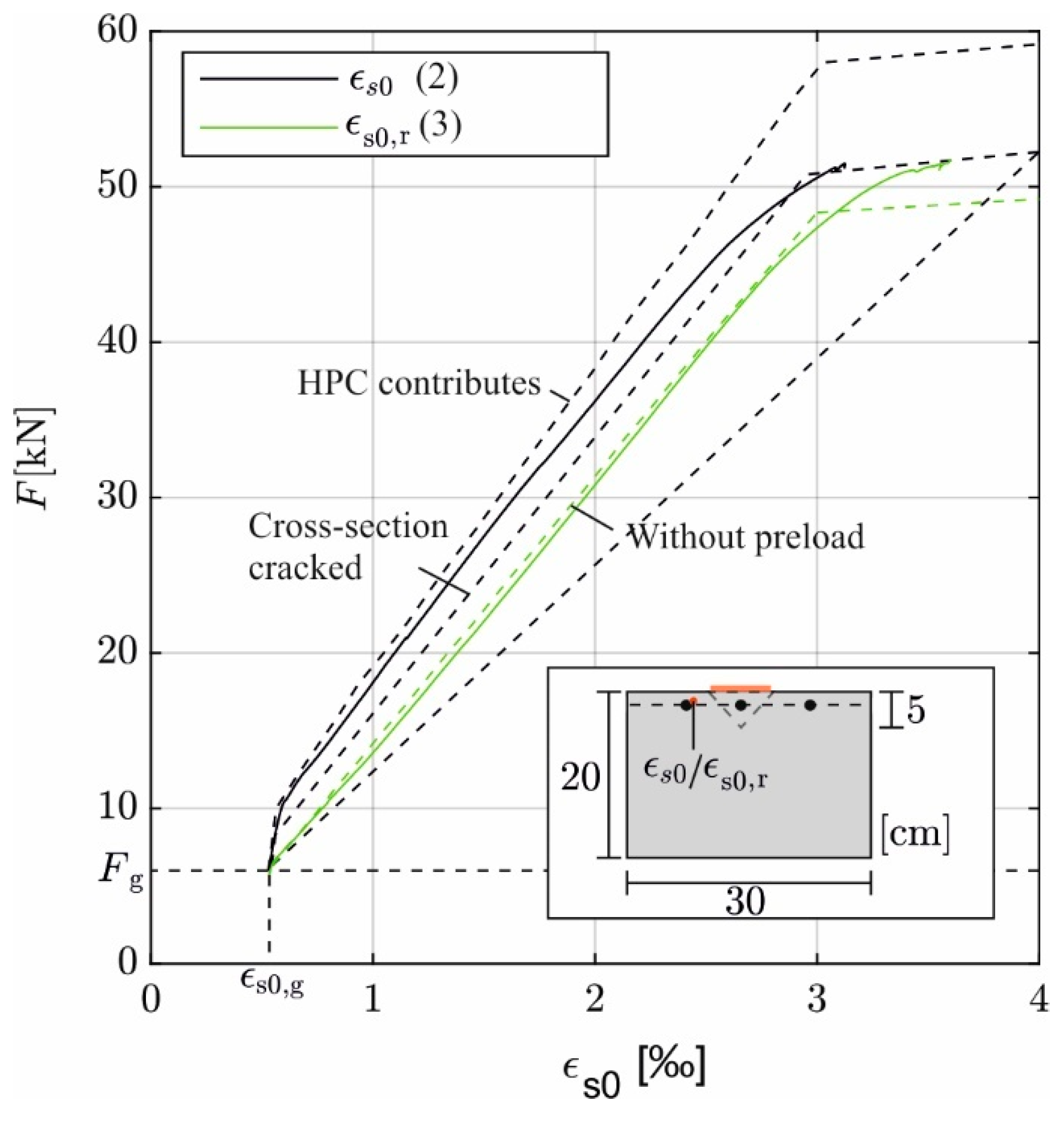
6.1. Impact of Thermal Prestressing on Cracking of Concrete
6.2. Comparison of the Measured and Numerically Predicted Mechanical Strain in the Reinforcement
6.3. Effectiveness of Strengthening in ULS and SLS
7. Conclusions
- The reinforcing bar could be thermally stretched by 0.4‰ through heating with mats at about 80 °C. Once the filler material is hardened, the new bar is bonded to the concrete and is jointly effective against increasing loads. Internal stresses are equally distributed to all reinforcing bars. The maximum load is virtually the same as that of the not-strengthened reference. Thus, strengthening is fully effective in ULS.
- Thermal prestressing significantly increases the stiffness of the beam. At the same maximum load, the deflection is approx. 33% lower than in the not-strengthened reference. Moreover, the crack depths at maximum load are significantly lower than in the reference, which is attributed to a lower utilization of the tensile zone.
- Inherently, prestressing the filler material also creates another benefit. Comparison of computational and measuring results with and without prestress proves that its contribution is fully effective up to 20% of the maximum load. With further load increase, it starts cracking, and the prestressing effect is mitigated. However, at serviceability load level or up to approx. 0.6 , the beneficial prestressing effect is still over 90% effective. But finally, at maximum load, just the thermally stretched bar remains effective.
- Subsequent thermal prestressing induces pressure into the cross-section, which partially closes existing cracks. After strengthening, the crack widths in the test are reduced by 45% on average.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Täljsten, B. FRP strengthening of concrete structures: New inventions and applications. Prog. Struct. Eng. Maths 2004, 6, 162–172. [Google Scholar] [CrossRef]
- Wu, C.; Li, V.C. CFRP-ECC hybrid for strengthening of the concrete structures. Compos. Struct. 2017, 178, 372–382. [Google Scholar] [CrossRef]
- Chen, Y.; Davalos, J.F.; Ray, I.; Kim, H.-Y. Accelerated aging tests for evaluations of durability performance of FRP reinforcing bars for concrete structures. Compos. Struct. 2007, 78, 101–111. [Google Scholar] [CrossRef]
- Huang, Y.; Grünewald, S.; Schlangen, E.; Luković, M. Strengthening of concrete structures with ultra high performance fiber reinforced concrete (UHPFRC): A critical review. Constr. Build. Mater. 2022, 336, 127398. [Google Scholar] [CrossRef]
- Siddika, A.; Mamun, M.A.A.; Ferdous, W.; Alyousef, R. Performances, challenges and opportunities in strengthening reinforced concrete structures by using FRPs—A state-of-the-art review. Eng. Fail. Anal. 2020, 111, 104480. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.; Hussein, H.H.; Chen, G. Flexural strengthening of reinforced concrete beams or slabs using ultra-high performance concrete (UHPC): A state of the art review. Eng. Struct. 2020, 205, 110035. [Google Scholar] [CrossRef]
- Gribniak, V.; Cervenka, V.; Kaklauskas, G. Deflection prediction of reinforced concrete beams by design codes and computer simulation. Eng. Struct. 2013, 56, 2175–2186. [Google Scholar] [CrossRef]
- Yu, Y.; Lee, S.; Cho, J.-Y. Deflection of reinforced concrete beam under low-velocity impact loads. Int. J. Impact Eng. 2021, 154, 103878. [Google Scholar] [CrossRef]
- Mishra, M.; Lourenço, P.B.; Ramana, G.V. Structural health monitoring of civil engineering structures by using the internet of things: A review. J. Build. Eng. 2022, 48, 103954. [Google Scholar] [CrossRef]
- van der Esch, A.; Wolfs, R.; Fennis, S.; Roosen, M.; Wijte, S. Categorization of formulas for calculation of crack width and spacing in reinforced concrete elements. Struct. Concr. 2024, 25, 32–48. [Google Scholar] [CrossRef]
- Jędrzejewska, A.; Zych, M.; Kanavaris, F.; Chen, F.; Ito, S.; Torrenti, J.M.; Schlicke, D.; Asamoto, S.; Azenha, M. Standardized models for cracking due to restraint of imposed strains—The state of the art. Struct. Concr. 2023, 24, 5388–5405. [Google Scholar] [CrossRef]
- Chai, L.-J.; Guo, L.-P.; Chen, B.; Sun, P.-Y.; Ding, C.; Liu, Z.-C.; Wang, L.-Y.; Wang, Y.-K. Design method of serviceability limit states of BFRP bar reinforced ecological high ductility concrete beam: Experimental and theoretical analysis. Structures 2022, 40, 855–865. [Google Scholar] [CrossRef]
- El Kechebour, B.; Zeloum, H. Choice between Retrofitting and Reconstruction of Buildings in Reinforced Concrete after an Earthquake. AMR 2015, 1119, 736–740. [Google Scholar] [CrossRef]
- Saeed, F.H.; Hejazi, F.; Rashid, R.S.M. Strengthening of reinforced concrete slabs using carbon fiber reinforced polymers rods and concrete jacket with a mechanical anchorage system. Constr. Build. Mater. 2024, 440, 137464. [Google Scholar] [CrossRef]
- Khaled, E.; Hassan, A.; Mahmoud, M.H.; El-Shafiey, T.F. Flexural behaviour of reinforced concrete slabs strengthened with textile-reinforced strain-hardening cementitious composites subjected to post-strengthening corrosion. Eng. Struct. 2025, 329, 119822. [Google Scholar] [CrossRef]
- Al-Yousuf, A.; Al-Kamaki, Y.S.S.; Lateef, H.A.; Ali, Y.A.; Assi, L.N.; Kareem, R.S.; Dekhn, H.C. The Behavior of Reinforced Concrete Slabs Strengthened by Different Patterns and Percentages of Carbon Fiber-Reinforced Polymer (CFRP) Plate. Constr. Mater. 2025, 5, 24. [Google Scholar] [CrossRef]
- Hamdy, A.E.; Abdalla, H.A.; Abdelhamed, G.D.; Elansary, A.A. Experimental and numerical behavior of strengthened reinforced concrete slabs. J. Eng. Appl. Sci. 2025, 72, 38. [Google Scholar] [CrossRef]
- Su, R.; Zhu, Y. Experimental and numerical studies of external steel plate strengthened reinforced concrete coupling beams. Eng. Struct. 2005, 27, 1537–1550. [Google Scholar] [CrossRef]
- Su, R.; Siu, W.H.; Smith, S.T. Effects of bolt–plate arrangements on steel plate strengthened reinforced concrete beams. Eng. Struct. 2010, 32, 1769–1778. [Google Scholar] [CrossRef]
- Barnes, R.A.; Baglin, P.S.; Mays, G.C.; Subedi, N.K. External steel plate systems for the shear strengthening of reinforced concrete beams. Eng. Struct. 2001, 23, 1162–1176. [Google Scholar] [CrossRef]
- Ghobarah, A.; El-Attar, M.; Aly, N.M. Evaluation of retrofit strategies for reinforced concrete columns. Eng. Struct. 2000, 22, 490–501. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, W.; Guo, X.; Sun, Q.; Tian, P.; Wu, Y. Development of theoretical model for predicting flexural behavior of GFRP reinforced concrete beams with CFRP grid-reinforced ECC. Struct. Concr. 2024, 25, 583–602. [Google Scholar] [CrossRef]
- Szczepański, K.; Kotynia, R. Bending moments redistribution in two-span reinforced concrete beams reinforced with FRP bars based on collected data research. Struct. Concr. 2024, 25, 1076–1091. [Google Scholar] [CrossRef]
- Abd elaziz, S.; Khalil, E.; Hadhoud, H. Strengthining of Reinforced Concrete Slabs Using Carbon Fiber Polymers. JES. J. Eng. Sci. 2023, 51, 242–254. [Google Scholar] [CrossRef]
- Feix, J.; Lechner, J. A new Post-Installed Reinforcement System to Extend Life Time of Existing Structures as Contribution to Sustainability. Ce Papers 2023, 6, 981–989. [Google Scholar] [CrossRef]
- Randl, N.; Kunz, J. Post-installed reinforcement connections at ultimate and serviceability limit states. Struct. Concr. 2014, 15, 563–574. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, Y.; Hussein, H.H.; Chen, G. Numerical modeling for damaged reinforced concrete slab strengthened by ultra-high performance concrete (UHPC) layer. Eng. Struct. 2020, 209, 110031. [Google Scholar] [CrossRef]
- Yang, J.; Chen, R.; Zhang, Z.; Zou, Y.; Zhou, J.; Xia, J. Experimental study on the ultimate bearing capacity of damaged RC arches strengthened with ultra-high performance concrete. Eng. Struct. 2023, 279, 115611. [Google Scholar] [CrossRef]
- Ahmed, F.B.; Biswas, R.K.; Sen, D.; Tasnim, S. Flexural and Shear Strengthening of Reinforced-Concrete Beams with Ultra-High-Performance Concrete (UHPC). Constr. Mater. 2024, 4, 468–492. [Google Scholar] [CrossRef]
- Saeed, F.H.; Hejazi, F. A Comprehensive Review of Retrofitted Reinforced Concrete Members Utilizing Ultra-High-Performance Fiber-Reinforced Concrete. Materials 2025, 18, 945. [Google Scholar] [CrossRef]
- Roh, Y.-J.; Kim, H.; Yune, D.-Y.; Eom, T.-S.; Kang, S.-M.; Kim, S.-H. Existing reinforced concrete slab strengthening by reinforced spray mortar and shear connectors. Eng. Struct. 2025, 343, 121030. [Google Scholar] [CrossRef]
- Ivanyi, G.; Buschmeyer, W. Reinforcement of prestressed concrete bridges with steel plates—Application criteria. Beton-Und Stahlbetonbau 1992, 87, 265–271. [Google Scholar] [CrossRef]
- Bierbrauer, K. Zur Ermittlung der Tragfähigkeit bestehender Brücken aus Stahlbeton: Abschätzung der Bewehrungsmengen. Beton-Und Stahlbetonbau 2005, 100, 13–16. [Google Scholar] [CrossRef]
- Schwarz, Y.; Sanio, D.; Mark, P. Calculation model for thermal pre-stressing of subsequentlyadded reinforcement. Beton-Und Stahlbetonbau 2024, 119, 894–907. [Google Scholar] [CrossRef]
- Löschmann, J.; Clauß, F.; Mark, P. Strengthening of reinforced concrete structures with temperature induction. Beton-Und Stahlbetonbau 2020, 115, 746–757. [Google Scholar] [CrossRef]
- Schwarz, Y.; Sanio, D.; Mark, P. Influence of heat treatment on the bond creep of high-strength concrete. Beton-Und Stahlbetonbau 2024, 119, 253–264. [Google Scholar] [CrossRef]
- Hoppe, J.; Schwarz, Y.; Stindt, J.; Forman, P.; Sanio, D.; Mark, P. Prozessbegleitende Ableitung mechanischer Eigenschaften hochfester Betone bei Schnellfertigung. Beton-Und Stahlbetonbau 2024, 119, 798–809. [Google Scholar] [CrossRef]
- Stindt, J.; Kempf, L.-A.; Forman, P.; Breitenbücher, R.; Mark, P. DEF of high-performance concrete with rapid, non-standard heat-treatment. Case Stud. Constr. Mater. 2023, 19, e02289. [Google Scholar] [CrossRef]
- Stindt, J.; Forman, P.; Mark, P. Influence of Rapid Heat Treatment on the Shrinkage and Strength of High-Performance Concrete. Materials 2021, 14, 4102. [Google Scholar] [CrossRef]
- Schwarz, Y.; Ratke, D.; Sanio, D.; Meurer, T.; Mark, P. An Experimental Method to Capture the Thermal Conductivity Coefficient of Fine-Grained. Materials 2024, 17, 2115. [Google Scholar] [CrossRef]
- Zdanowicz, K.; Gebauer, D.; Koschemann, M.; Speck, K.; Steinbock, O.; Beckmann, B.; Marx, S. Distributed fiber optic sensors for measuring strains of concrete, steel, and textile reinforcement: Possible fields of application. Struct. Concr. 2022, 23, 3367–3382. [Google Scholar] [CrossRef]
- Siwowski, T.; Rajchel, M.; Howiacki, T.; Sieńko, R.; Bednarski, Ł. Distributed fibre optic sensors in FRP composite bridge monitoring: Validation through proof load tests. Eng. Struct. 2021, 246, 113057. [Google Scholar] [CrossRef]
- Zhao, L.; Tang, F.; Li, G.; Lin, Z.; Li, H.-N. Crack monitoring of tension members with distributed fiber optic sensor considering substrate strain redistribution and coating/fiber interfacial slip. Eng. Struct. 2024, 300, 117267. [Google Scholar] [CrossRef]
- Woods, J.E.; Lau, D.T.; Bao, X.; Li, W. Measuring strain fields in FRP strengthened RC shear walls using a distributed fiber optic sensor. Eng. Struct. 2017, 152, 359–369. [Google Scholar] [CrossRef]
- Konertz, D.; Löschmann, J.; Clauß, F.; Mark, P. Faseroptische Messung von Dehnungs- und Temperaturfeldern. Bauingenieur 2019, 94, 292–300. [Google Scholar] [CrossRef]
- Schwarz, Y.; Ratke, D.; Sanio, D.; Meurer, T.; Mark, P. Thermal prestressing of subsequently slotted reinforcement—Experimental and numerical development and optimization of an induction method. Struct. Concr. 2025, 1–16. [Google Scholar] [CrossRef]
- Clauß, F.; Löschmann, J.; Ahrens, M.A.; Mark, P. Temperature induction into RC structures. Beton- Und Stahlbetonbau 2021, 116, 539–550. [Google Scholar] [CrossRef]
- Clauß, F.; Ahrens, M.A.; Mark, P. Thermo-mechanical experiments on reinforced concrete beams: Assessing thermal, mechanical, and mixed impacts on fiber optic measurements. Struct. Concr. 2022, 23, 3521–3537. [Google Scholar] [CrossRef]
- Deutscher Ausschuss für Stahlbeton. Verstärken von Betonbauteilen, 467th ed.; Beuth Verlag GmbH: Berlin, Germany, 1996; ISBN 978-3-410-65245-8. [Google Scholar]
- Sanio, D.; Mark, P.; Ahrens, M.A. Computation of temperature fields on bridges. Implementation by means of spread sheets. Beton- Und Stahlbetonbau 2017, 112, 85–95. [Google Scholar] [CrossRef]
- Zichner, T. Temperaturunterschied Infolge Witterungseinfluß und Beheizung von Massiven Brücken; Forschung Straßenbau und Straßenverkehrstechnik Heft 212: Bonn, Germany, 1976. [Google Scholar]
- Sanio, D.; Ahrens, M.A.; Mark, P. Lifetime predictions of prestressed concrete bridges—Evaluating parameters of relevance using Sobol’ indices. Civ. Eng. Des. 2022, 4, 143–153. [Google Scholar] [CrossRef]
- Richter, B.; Herbers, M.; Marx, S. Crack monitoring on concrete structures with distributed fiber optic sensors—Toward automated data evaluation and assessment. Struct. Concr. 2024, 25, 1465–1480. [Google Scholar] [CrossRef]
| Specimen | Reinforcement | Key Performance Indicators | |||
|---|---|---|---|---|---|
| Initial | Additional | Max. Deflection | Max. Load Capacity | Crack Development | |
| (1) “Reference” | 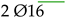 | - | umax(1) > umax(2) ≤ umax(3) | Fmax(1) < Fmax(2) ≥ Fmax(3) | w(1) > w(2) ≤ w(3) |
| (2) “Thermally Prestressed” | 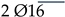 | 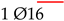 | |||
| (3) “Reference” | 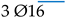 | - | |||
| Komponente | Normal Concrete C30/37 | HPC Based on Nanodur-Compound 5941 | ||
|---|---|---|---|---|
| Type | Mass [kg/m3] | Type | Mass [kg/m3] | |
| Sand | 0/2 | 711.0 | 0/2 | 426.0 |
| Basalt | - | - | 1/3 | 882.0 |
| Gravel | 2/8 | 356.0 | - | - |
| Gravel | 8/16 | 711.0 | - | - |
| Cement/Binder | CEM 1 42.5 R | 340.0 | Nanodur Compound 5941 (Dyckerhoff) | 1042.0 |
| Water | - | 204.0 | - | 159.8 |
| Superplasticizer | - | - | Master Glenium ACE 430 (Master Builders solutions, Mannheim, Germany) | 12.3 |
| Shrinkage Reducer | - | - | Eclipse Floor (gcp) | 8.0 |
| Hardening Accelerator | - | - | Master X-Seed 100 (Master Builders solutions) | 12.3 |
| Crack No. | Unreinforced at + | Thermally Prestressed at + | ||
|---|---|---|---|---|
| DFOS/Crack Mapping | DFOS/Crack Mapping | |||
| Crack Width w [mm] | Crack Position [m] | Crack Width w [mm] | Crack Position [m] | |
| 1 | 0.14/0.1 | 1.39/1.37 | 0.07/0.1 | 1.39/1.37 |
| 2 | 0.16/0.2 | 1.52/1.51 | -/0.1 | -/1.51 |
| 3 | 0.22/0.2 | 2.12/2.14 | -/0.1 | -/2.14 |
| 4 | 0.26/0.3 | 2.34/2.33 | 0.21/0.2 | 2.34/2.33 |
| 5 | 0.23/0.2 | 2.51/2.50 | -/0.1 | -/2.50 |
| 6 | 0.24/0.2 | 2.52/2.49 | -/0.1 | -/2.51 |
| 7 | 0.25/0.2 | 2.78/2.78 | 0.23/0.2 | 2.78/2.78 |
| Thermally Prestressed | Reference (1) | Reference (3) | ||
|---|---|---|---|---|
| Maximum Load [kN] | 51.2 | 34.5 | 51.7 | |
| Deflection at [mm] | 60.2 | 60.0 | 71.5 | |
| Mean Crack Width at g + [mm] | ||||
| 0.22 | 0.12 | - | 0.18 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schwarz, Y.; Sanio, D.; Mark, P. Experimental Study of the Effectiveness of Strengthening Reinforced Concrete Slabs with Thermally Prestressed Reinforcement. CivilEng 2025, 6, 49. https://doi.org/10.3390/civileng6030049
Schwarz Y, Sanio D, Mark P. Experimental Study of the Effectiveness of Strengthening Reinforced Concrete Slabs with Thermally Prestressed Reinforcement. CivilEng. 2025; 6(3):49. https://doi.org/10.3390/civileng6030049
Chicago/Turabian StyleSchwarz, Yannik, David Sanio, and Peter Mark. 2025. "Experimental Study of the Effectiveness of Strengthening Reinforced Concrete Slabs with Thermally Prestressed Reinforcement" CivilEng 6, no. 3: 49. https://doi.org/10.3390/civileng6030049
APA StyleSchwarz, Y., Sanio, D., & Mark, P. (2025). Experimental Study of the Effectiveness of Strengthening Reinforced Concrete Slabs with Thermally Prestressed Reinforcement. CivilEng, 6(3), 49. https://doi.org/10.3390/civileng6030049








