Next Article in Journal / Special Issue
Use of Fibre-Optic Sensors for Pipe Condition and Hydraulics Measurements: A Review
Previous Article in Journal
Concrete Overstrength: Assessment of Field Strength Seeking Insights for Overdesign Optimization
Previous Article in Special Issue
Experimental Study on the Reliability of Scaling Down Techniques Used in Direct Shear Tests to Determine the Shear Strength of Rockfill and Waste Rocks
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
CivilEng
Volume 3
Issue 1
10.3390/civileng3010005
civileng-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Experimental Study on the Minimum Required Specimen Width to Maximum Particle Size Ratio in Direct Shear Tests

by
Akram Deiminiat
,
Li Li
* and
Feitao Zeng
Research Institute on Mining and Environment, Department of Civil, Geological and Mining Engineering, Polytechnique Montreal, Montreal, QC H3T 1J4, Canada
*
Author to whom correspondence should be addressed.
CivilEng 2022, 3(1), 66-84; https://doi.org/10.3390/civileng3010005
Submission received: 15 November 2021 / Revised: 17 January 2022 / Accepted: 19 January 2022 / Published: 21 January 2022
(This article belongs to the Special Issue Early Career Stars in Civil Engineering)
Browse Figures
Versions Notes

Abstract

:
Conducting laboratory direct shear tests on granular materials is a common practice in geotechnical engineering. This is usually done by following the ASTM D3080/D3080M-11 (hereafter named ASTM), which stipulates a minimum required value of 10 for specimen width (W) to the maximum particle size (dmax) ratio. Recently, a literature review performed by the authors showed that the minimum required W/dmax ratio given in the ASTM is not large enough to eliminate the specimen size effect (SSE). The minimum required W/dmax ratio of ASTM needs to be revised. In this study, a critical analysis is first made on existing data in order to identify the minimum required W/dmax ratio. The analysis shows that more experimental data obtained on specimens having W/dmax ratios between 10 and 50 are particularly necessary. To complete this need, a series of direct shear tests were performed on specimens having different dmax by using three shear boxes of different dimensions. The results show once again that the minimum required W/dmax ratio of 10, defined in the ASTM, is not large enough to eliminate the SSE. Further analysis on these and existing experimental results indicates that the minimum required W/dmax ratio to remove the SSE of friction angles is about 60. These results along with the limitations of this study are discussed.

1. Introduction

The direct shear test is a very old but still regularly used method to determine the shear strength of geomaterials [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. For a given project, one usually needs to take samples from the project site. Specimens can then be prepared in a laboratory with a small portion of the samples. For the convenience of laboratory tests, tested specimens are preferred to be as small as possible. However, the method imposes a shear plane through the tested material between the upper and lower half parts of the shear box. When the specimen size is too small, the effect of individual particles along and near the imposed shearing plane can be amplified in terms of rotation, crushing, shearing, and dilation during direct shear tests. The distributions of stresses and strains can be non-uniform along the shearing plane [17,18,19,20]. The measured shear strength may be overestimated and not representative of that of the tested material in field conditions where the volume of the tested material can be very large [21]. The specimen size of tested material should not be too small.
Increasing the specimen size of the tested material reduces the effect of individual large particles and boundary effects associated with the stiff shear box walls. The measured shear strength can be closer to that of the tested material in field conditions. When the specimen size is large enough, the measured shear strength can then become constant with any further increase in the specimen size. The variation of shear strength as function of specimen size is known as specimen size effect or specimen scale effect (SSE). Finding the large enough specimen size to avoid any SSE is also known as a problem of representative volume element size [22,23,24].
Over the years, a number of studies have been published on the SSE of direct shear tests. Most of them were realized by performing laboratory tests [8,13,14,25,26,27,28,29,30,31,32,33,34]. A few studies have been realized through numerical modeling [35,36,37,38,39]. Each method has advantages and limitations. With experimental investigation, the test results are direct, tangible, and more convincing as long as the tests are properly realized. Its limitations are also obvious: shear box and specimen sizes are limited. The reliability of test results depends on the representativeness of assumptions, implicitly or explicitly used in the result interpretation. The accessibility to observe the movements of particles or other mechanical responses of the tested specimen during shear tests is difficult, if not impossible [40,41]. With numerical modeling, the stress and deformation anywhere through the modeled specimen can be visualized. This allows an insight to the micromechanical behavior, which can, in turn, lead to a better understanding of the macro mechanical behavior of material under direct shear test condition. However, all the numerical models, whatever continuum or discrete with or without meshes, are established with some discussable assumptions. Model calibrations are always necessary against experimental results to obtain model parameters. The representativeness of constitutive model or particle size distribution of granular material used in the numerical models depends on the reliability of the experimental results used for parameter calibration. In addition, ensuring the stability and reliability of numerical results is another challenging issue, especially at the zones of soil-wall interfaces and high gradient stress or deformation.
In this study, focus is given on the experimental study of SSE in direct shear tests.

2. Previous Laboratory Tests on SSE of Direct Shear Tests

In the past, a large number of experimental studies have been published on the SSE of direct shear tests. As the objective of the present study is to identify the minimum required specimen sizes to avoid SSE in direct tests, instead of an exhaustive literature review, analyses are only made on a few published works.
Over the years, several standards have been proposed to specify the minimum required ratios between the specimen sizes and maximum particle size (dmax) of tested material. Table 1 shows a few standards commonly used in geotechnical engineering with the specification of specimen sizes. For example, ASTM D3080/D3080M-11 [42] (hereafter named ASTM), the most used standard for direct shear tests all over the world, requires specimen width (W) to be at least 10 times dmax. In addition, specimen width W should not be smaller than 50 mm. For fine particle materials such as clay, silt, and sand with dmax not larger than 1 mm, the requirement of W ≥ 50 mm automatically results in W/dmax ≥ 50, a value largely exceeding the minimum required ratio. Respecting the standard of ASTM does not raise any problem of SSE. Problems appear when direct shear tests are needed with coarse particle materials such as rockfill and waste rocks.
Rockfill and chemically inert waste rocks are widely used to construct geotechnical infrastructures such as rockfill dikes of hydraulic reservoirs, waste rock piles [46,47], tailings dams [48,49], waste rock inclusions in tailings storage facilities [50,51,52,53], and waste rock barricades in underground mines to maintain backfill slurry in mine stopes [54,55,56,57]. The design of these infrastructures requires the knowledge of the shear strength of rockfill or waste works. Direct shear tests are then needed on these materials. However, rockfill and waste rocks usually contain fine particles as small as silts and coarse particles as large as boulders. Using a standard direct shear test box (6 cm for most cases) with field materials and respecting the minimum required specimen sizes to dmax ratio are impossible. Scaling down techniques are thus employed by removing oversized particles during sample preparation to make laboratory tests possible [16,58,59,60,61,62,63,64,65,66,67]. For most cases, the dmax of the resulting samples can still be too large compared to any available standard or nonstandard direct shear test apparatus. The minimum required specimen size to dmax ratio of 10 [42,68] has thus been universally used in direct shear tests [11,16,62,69,70,71,72,73,74] even though the validity of this minimum required value of 10 has never been verified. In other words, it remains unclear if the SSE of direct shear tests is eliminated with specimens having a width to dmax ratio of 10.
Parsons [25] studied the SSE of a crushed quartz and Ottawa sand with a dmax value of approximately 0.841 mm. Direct shear tests were conducted with small square (60 mm × 60 mm), medium rectangular (120 mm × 100 mm) and large rectangular (120 mm × 200 mm) shear boxes. Loose samples were poured in the shear boxes with a spoon at a constant falling height. The surface of the samples was smoothed to a standard thickness. The measured friction angles are presented in Table 2 along with the corresponding values of W/dmax. For the test results with the crushed quartz, it is difficult to evaluate if the minor diminution of friction angle is an exhibition of SSE or simply due to the precision of measurement, sample variation or shape effect. As the smallest W/dmax ratio of 71 is already much higher than 10, these results do not provide valuable information on the validity of the minimum required specimen size over dmax ratio of ASTM. For the test results with Ottawa sand, Table 2 indicates that the friction angle continues to change significantly as the W/dmax ratio increases from 71 to 143. These results tend to indicate that the minimum required ratios of ASTM are not large enough to eliminate the SSE even at W/dmax ratio of 71. However, this conclusion may not be strong enough because the test results may contain several uncertainties associated with the precision of measurement, sample variation from small to large box, and shape effect.
Similar tests to those of Parsons [25] have been conducted by Palmeira and Milligan [28] with one single normal stress of 30 kPa on a sand with dmax = 1.2 mm by using small square (60 mm × 60 mm × 32 mm), medium rectangular (252 mm × 152 mm × 152 mm), and large square (1000 mm × 1000 mm × 1000 mm) shear boxes. All the specimens were prepared by applying a pluviation technique with a constant falling height. The test results are shown in Table 3. One sees that the friction angles of the specimens remain almost constant when W/dmax increases from 50 to 833, values much larger than the minimum required W/dmax ratio of ASTM. These results tend to indicate that a W/dmax ratio of 50 is large enough to remove the SSE, but cannot help to evaluate if the minimum required ratios of ASTM are large enough to eliminate the SSE. In addition, it is unclear if W/dmax = 50 is the minimum required ratio or can be smaller to remove the SSE.
Rathee [26] investigated the SSE on the measurement of friction angle by direct shear tests. One tested material was made of pure gravel and another was a mixture of sand and gravel with the same portion. A small (60 mm × 60 mm) and a large (300 mm × 300 mm) shear box were used (the heights of the shear boxes were not provided in Rathee [26]). For the pure gravel material, only the large shear box was used to measure the friction angles of different samples having different dmax prepared by applying a scaling down technique. These results cannot be used to evaluate the SSE because each sample having a distinct value of dmax represents a distinct material. The variation of friction angle results from combined effects associated with the variation of dmax, particle size distribution, and specimen size to dmax ratio. The employed methodology is inappropriate to investigate the SSE. For the sand-gravel mixture material with dmax = 6.3 mm, both the small and large shear boxes were used by Rathee (1981) to measure the friction angle by direct shear tests. The experimental results showed that the friction angle decreases by about 1.7° when the W/dmax ratio increases from 10 to 48. These results clearly indicate that the SSE is not eliminated with a W/dmax ratio of 10. The minimum required specimen size to dmax ratio defined by ASTM is invalidated. However, as there are no results with W/dmax smaller or larger than 48, it is unclear if the W/dmax ratio of 48 is large enough to eliminate SSE.
The influence of specimen size on friction angle was further studied by Cerato and Lutenegger [8], who conducted direct shear tests with a small (59.9 mm × 59.9 mm × 26.4 mm), a medium (101.6 mm × 101.6 mm × 40.6 mm) and a large (304.8 mm × 304.8 mm × 177.8 mm) shear box on a sand and a gravel with different dmax and relative densities. For the specimen of gravel with dmax value of 5 mm, a known quantity of sample was placed in each box and compacted to achieve the desired relative density. Table 4 shows the measured friction angles of the gravel compacted to different relative densities. The experimental results clearly indicate that the W/dmax ratios of 12 and 20 are not large enough to remove the SSE, invalidating once again the minimum required W/dmax ratio of 10 given in ASTM. It is, however, unclear if the W/dmax ratio of 61 is large enough to remove the SSE.
Wu et al. [30] conducted direct shear tests on a sand with a dmax value of 0.42 mm with a small square (40 × 40 × 20 mm), a medium square (120 × 120 × 120 mm), a large square (300 × 300 × 300 mm) and a very large rectangular (800 × 500 × 600 mm) shear boxes. The minimum W/dmax ratio is 95. Among the numerous specimens, only two have close enough compactness and void ratio. The test results presented in Table 5 tend to indicate that the SSE is not eliminated even at W/dmax = 95. The minimum required W/dmax = 10, given in ASTM, is invalidated once again.
Mirzaeifar et al. [32] performed direct shear tests with a small (60 mm × 60 mm × 16 mm), a medium (100 mm × 100 mm × 30 mm), and a large (300 mm × 300 mm × 180 mm) shear box. The tested material is sand with a dmax value of 1.3 mm. Three samples were prepared, the first one at a density of 1.5 g/cm3, the second at 1.58 g/cm3, and the third at 1.67 g/cm3, respectively. Table 6 shows the friction angles obtained by the direct shear tests. The results tend to indicate that the W/dmax ratio of 46 is not large enough while a W/dmax ratio up to 77 may be necessary to remove the SSE. The minimum required W/dmax ratio of 10, stipulated by the standard of ASTM, is invalidated once again.
Ziaie Moayed et al. [34] studied the SSE on the friction angles of silty sand with a dmax value of 0.8 mm. The samples were prepared by mixing sand with different silt contents (Sand, 0%; Silty sand I, 10%; Silty sand II, 20%; Silty sand III, 30%). Small (60 mm × 60 mm × 24.5 mm), medium (100 mm × 100 mm × 35 mm), and large (300 mm × 300 mm × 154 mm) shear boxes were used to perform direct shear tests. Table 7 shows the friction angles obtained by only considering the direct shear test results of Ziaie Moayed et al. [34] with the normal stresses of 109, 163, and 218 kPa; the experimental results obtained with the normal stresses of 327 and 436 kPa were ignored due to the lack of tests using the large shear box with these two normal stresses. The friction angles were obtained by applying the linear fitting technique without imposing the straight lines passing through the origin in the shear stress–normal stress plane, resulting in apparent cohesions varying from 11 to 27 kPa with the small shear box tests and apparent cohesion ranging from −0.4 to 5 kPa with the large shear box tests. The results of the sand and silty sand I tend to show that the W/dmax ratio of 75 is not large enough to eliminate SSE, invalidating once again the minimum required W/dmax ratio of 10, stipulated by the standard of ASTM. With the test results of silty sand III, the W/dmax ratio of 75 seems to be large enough to avoid SSE. These results do not help to validate or invalidate the minimum required W/dmax ratio of 10, stipulated by the standard of ASTM.
More studies on the SSE of geomaterials can be found in the literature. For instance, Dadkhah et al. [75] studied the SSE of clayey sand. The SSE was clearly showed and the minimum required W/dmax ratio of 10 is invalidated again. However, the experimental results are difficult to be exploited because the values of dmax were not explicitly given (4.75 mm in a table and 10 mm in a figure of particle size distribution curves). In addition, it is unclear if the tested specimens were made of remoulded or unremoulded samples and how the designated densities of specimens were achieved. These results are thus not addressed further.
More recently, MotahariTabari and Shooshpasha [14] studied the SSE of a coarse grain material in direct shear tests. Similarly to Rathee [26], the test results involve the effects of several influencing factors such as dmax, fine and gravel contents and density. These results can neither be included in this study.
Table 8 shows a summarization of the previous analyses on the existing experimental results obtained to investigate the SSE. None of the existing experimental results shows validation of the minimum required W/dmax ratio of 10 by ASTM for direct shear tests. Rather, almost all of them show that SSE cannot be eliminated by using specimens having a W/dmax ratio of 10. The minimum required W/dmax ratio of 10 stipulated by ASTM is invalidated and needs to be revised.
Table 8 also shows that a W/dmax ratio of 50 is large enough based on some of the existing data while some other results indicate that even a specimen having W/dmax ratio as large as 75 is not large enough to remove SSE. In addition, more experimental results are particularly necessary with specimens having W/dmax ratio between 10 and 50. With fine particle materials, this is only possible with shear box smaller than the minimum required specimen size of 50 mm, stipulated by the ASTM. To fill this gap, a series of direct shear tests were performed on specimens with dmax in the range of 0.85 to 6 mm by using a mini shear box of 38 mm × 38 mm × 45 mm, a small shear box of 60 mm × 60 mm × 45 mm and a large shear box of 300 mm × 300 mm × 180 mm. The tested specimens then have a W/dmax ratio between 10 and 353. In this paper, the experimental results of these laboratory tests are first presented. Minimum required W/dmax ratio is identified and proposed to eliminate SSE.

3. Laboratory Tests

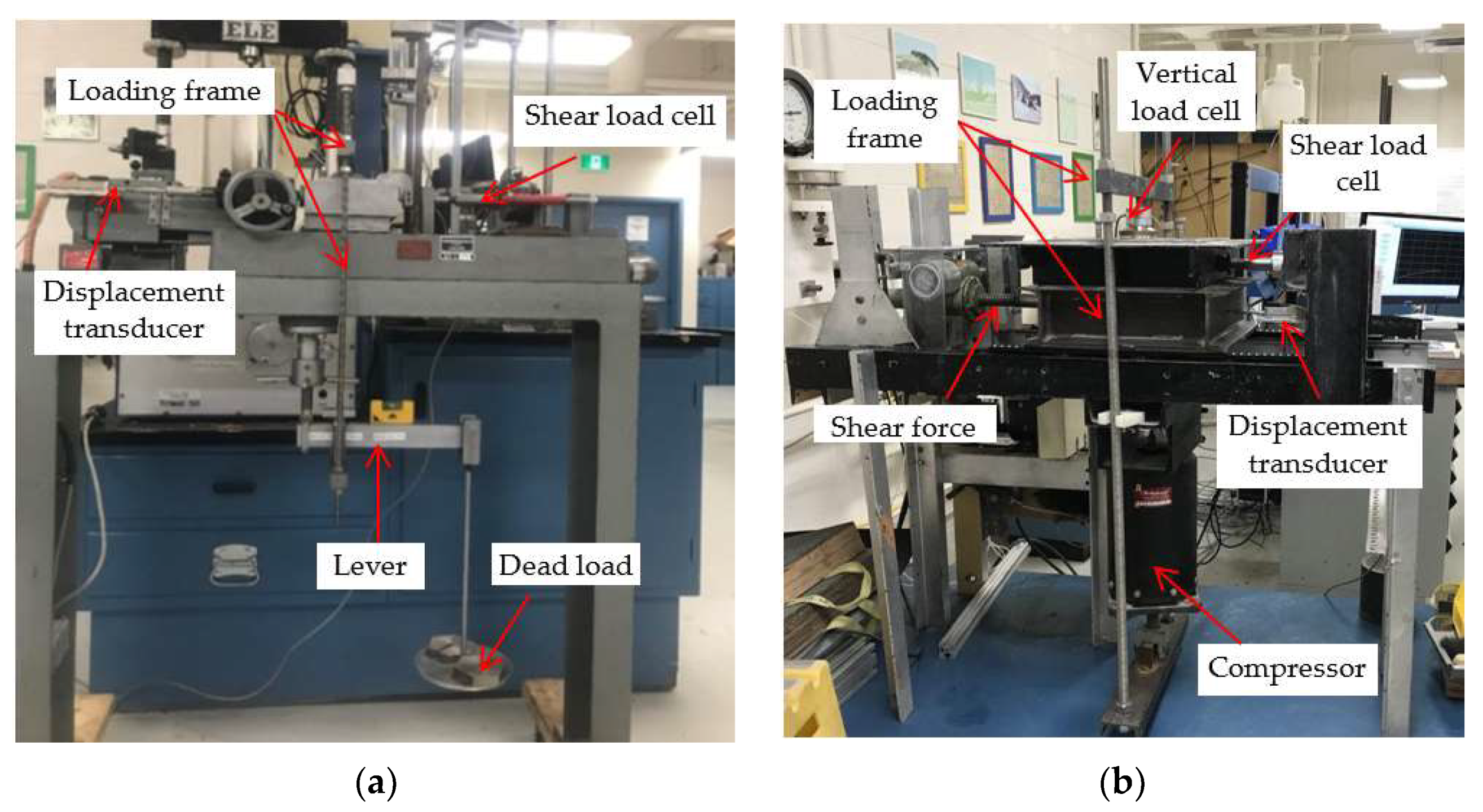
3.1. Test Apparatus

In the Geotechnical Laboratory of Polytechnique Montreal, there are a standard (Figure 1a) and a large (Figure 1b) direct shear test system. The standard direct shear test apparatus is equipped with a small (standard) shear box of 60 mm × 60 mm × 45 mm while the large direct shear apparatus is equipped with a large shear box of 300 mm × 300 mm × 180 mm. A mini shear box of 38 mm × 38 mm × 45 mm was designed and manufactured by the Geotechnical Laboratory of Polytechnique Montreal in order to test the SSE of fine particle materials with a W/dmax ratio smaller than 50 based on the critical review of Deiminiat et al. [76]. Figure 2 shows a picture of the three shear boxes used in this study. The mini shear box was made to have the same external dimensions as those of the small (standard) shear box in order for it to be compatible with the standard direct shear test system. The testing procedure is thus mainly the same as the standard one of ASTM with the small (standard) shear box. The only difference is in the normal stress loading system. The lever system is removed and the normal stress is applied by the self-weight of the loading frame and addition of dead load on the holding plate.

3.2. Materials and Testing Procedure

Keeping in mind that the scope of this study is to only analyze the SSE on the peak internal effective friction angle (hereafter called “friction angle” for the sake of simplicity) of granular material, it is very important to make sure that all the specimens prepared with a given material in the mini, small, and large shear boxes have the same compactness (density) and water content (dry).
The testing materials in this study are two types of waste rocks, called WR 1 and WR 2, respectively. These waste rocks contain sub-angular and sub-rounded particles. Figure 3 shows pictures of the original WR 1 (Figure 3a) and WR 2 (Figure 3b).
The two types of waste rocks were first sieved in different portions having particle sizes ranging from 0.08–0.85 mm, 0.85–1.19 mm, 1.19–1.4 mm, 1.4–2.36 mm, 2.36–3.36 mm, 3.36–5 mm, and 5–6 mm. Mixtures were made to obtain dry samples having a dmax of 0.85, 1.19, 1.4, 2.36, 3.36, 5, and 6 mm. Details of the different portions used to make the different mixtures are given in Table 9.
Figure 4 shows the target and obtained grain size distribution curves of samples having different dmax. The grain size distribution curves were also used to produce seven other materials by WR2. There are thus 14 samples prepared for the direct shear tests with the three different shear boxes. It should also be mentioned that the scope of this paper is to study the SSE, not the scaling-down techniques or the effect of dmax on the friction angle of granular materials. The different dmax values are thus used here as an identification of one material. Each dmax along with the type of waste rocks constitute a distinct material.
All the specimens for the mini, small, and large shear boxes were prepared with dry waste rocks in the loosest state in order to ensure that the variation of the test results is only associated with the variation of specimen sizes; the effects of other influencing factors (density, water content, particles shapes, etc.) on the test results are excluded. The specimen was prepared with a spoon by slowly placing waste rocks into each shear box without any compaction. The required mass of material was calculated according to the box volume and the desired dry density of 1450 kg/m3. After filling the box to the top edge of the upper box, the surface of the specimen was smoothed with a brush and the rigid plate was placed slowly to avoid any shock or compaction of the material.
Table 10 shows the shear boxes and specimen sizes to dmax ratios along with the maximum void ratios (emax) for the two types of waste rocks. The values of emax were estimated by following ASTM C29/C29M-17a [77]. One notes a decrease of emax with an increased dmax value. This is straightforward to understand. As seen in Figure 4, the materials with larger dmax have better gradations. With a well graded material, the pore or void spaces can easily be filled with fine particles, resulting in a denser material compared to a poorly graded material. This, along with the dense and heavy large particles associated with a large dmax value, results in a small emax. However, it should be noted that the scope of this study is to evaluate the SSE of direct shear tests. The value of dmax is only an identification of the material. Focus should be put on the variation of friction angle as function of specimen width for a given material (defined by the type of material and a dmax value), not on the variation of physical or mechanical properties as function of dmax value.
From Table 10, one sees that there are no tests planned with the mini box for the specimens with dmax of 5 and 6 mm in order to respect the minimum required specimen size to dmax ratio of 10 defined by ASTM. All the 19 specimen sizes meet the requirement of ASTM with W/dmax ranging from 10 to 353. Since each dmax along with the type of waste rocks is only used as an identification of a material, the testing program contains 14 materials (made of WR 1 and WR 2) completely different from each other.
As the shear strength of each specimen is obtained by direct shear tests with three normal stresses (50, 100, and 150 kPa), 57 direct shear tests were carried out for each type of waste rocks. A total number of 114 direct shear tests were realized for the two types of waste rocks. The direct shear tests were conducted by applying constant rates of 0.015 mm/s (0.9 mm/min) and 0.025 mm/s (1.5 mm/min) for the standard and large shear apparatuses, respectively.

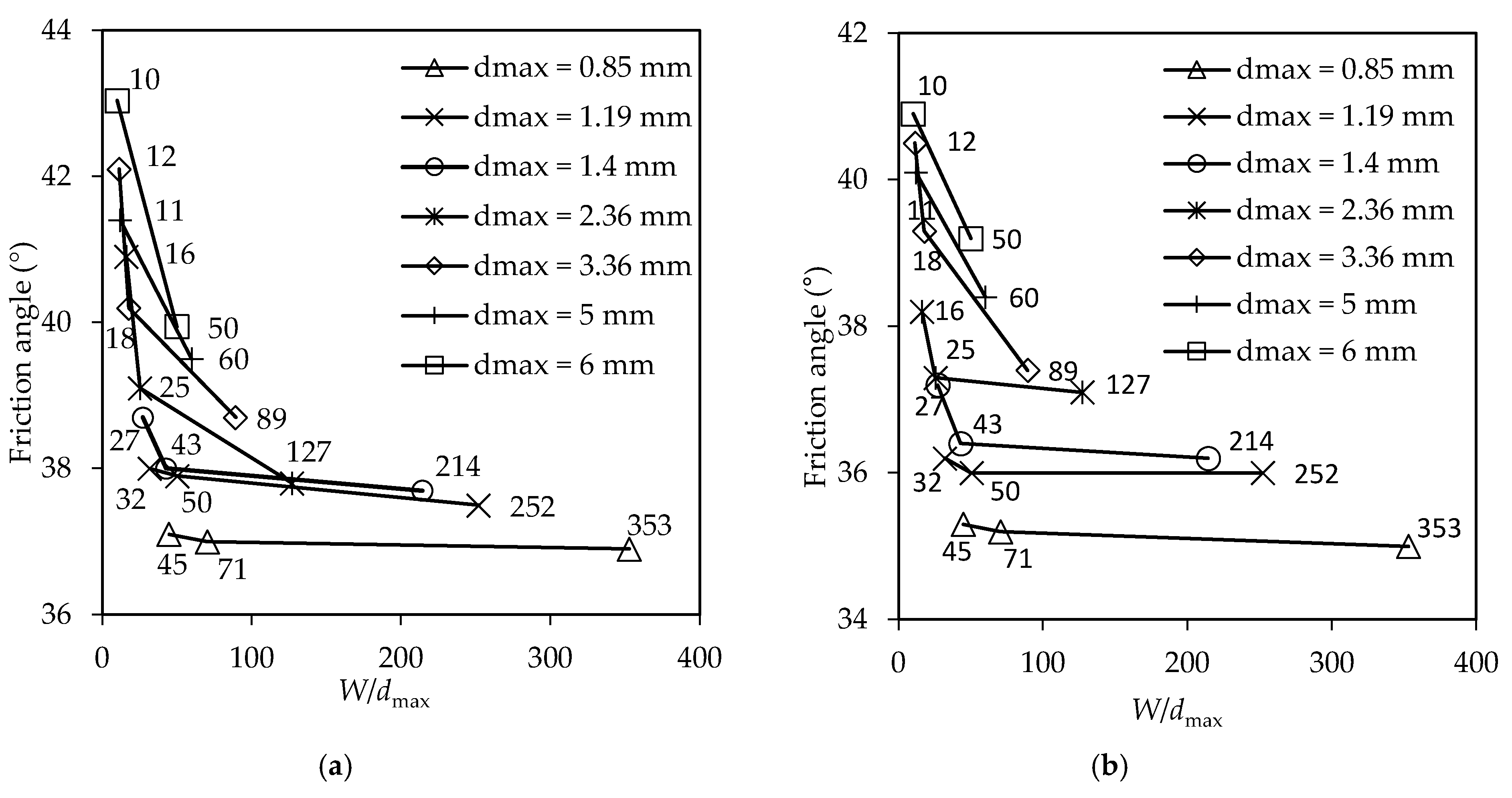
3.3. Test Results

Figure 5 shows some typical shear stress and shear displacement curves obtained by using the mini (Figure 5a), small (Figure 5b) and large (Figure 5c) shear boxes on WR 1 with a dmax value of 0.85 mm. It can be seen that material tested with different boxes at a given normal stress has the same mechanical behavior. For example, at a normal stress of 50 kPa, the material tested with the mini, small, and large boxes has a mechanical behavior of loose sand. At a normal stress of 150 kPa, the material tested with the three boxes starts to have a mechanical behavior of dense sand. These results indirectly indicate that the specimens prepared in the three different boxes have the same state and density. Subsequently, they have the same mechanical behavior under a given normal stress: loose sand under a normal stress of 50 kPa and slightly dense sand under a normal stress of 150 kPa.
By taking the peak value of shear stress for each curve, one then obtains three shear stresses at yield, each corresponding to one normal stress. The friction angle can then be obtained by applying the linear fitting technique without imposing the straight line passing to the origin in Mohr plane.
Table 11 shows the obtained friction angles of all the specimens with different dmax for WR 1 and WR 2. Once again, each dmax along with the type of waste rocks can only be considered as an identification of a material. The table thus presents the friction angles of 38 samples made of the 14 materials. It is unnecessary to analyze how the friction angles change with the value of dmax or with the type of waste rocks.
Figure 6 shows the variations of friction angles as function of W/dmax for the specimens made of WR 1 (Figure 6a) and WR 2 (Figure 6b), respectively. From Figure 6a, it is seen that the friction angle of the specimens with dmax = 0.85 mm remains constant as the W/dmax ratio increases from 45 to 353. For the specimens with dmax = 1.19 mm, the friction angle decreases by 0.1° as W/dmax increases from 32 to 50 and remains almost constant as W/dmax further increases to 252. For the specimens with dmax = 1.4 mm, the friction angle decreases by 0.7° when W/dmax increases from 27 to 43 and it remains almost constant when W/dmax further increases from 43 to 214. These results tend to indicate that a W/dmax ratio of 43 to 50 is large enough to remove the SSE while the minimum required W/dmax ratio of 10 suggested by the ASTM is too small for eliminating the SSE.
For the specimens with dmax = 2.36 mm, the friction angle decreases by 1.8° as W/dmax increases from 16 to 25 and then decreases by 1.2° when W/dmax further increases from 25 to 127. Similarly for the specimens with dmax = 3.36 mm, the friction angle decreases by at least 1.9° as W/dmax increases from 11 to 18 and decreases by 1.5° as W/dmax further increases from 18 to 89. These test results indicate that a W/dmax ratio of 18 or 25 is not large enough to eliminate the SSE. The minimum required W/dmax ratio of 10 defined by ASTM is invalidated again.
For the specimens with dmax = 5 mm, the friction angle decreases by 2.2° as W/dmax increases from 12 to 60. For the specimens with dmax = 6 mm, the friction angle decreases by 3.1° as W/dmax increases from 10 to 50. These results show once again that the minimum required W/dmax ratio of 10 defined by ASTM is not large enough to remove SSE.
All the above test results confirm what has been illustrated by Deiminiat et al. [76]. The minimum required W/dmax ratio of 10 defined in the ASTM is not validated for the fine particle material with a dmax value of 0.85 mm due to the lack of test results with W/dmax ratio in the range of 10 to 45, but is clearly invalidated for the coarse particle materials with dmax ranging from 3.36 to 6 mm. A W/dmax ratio of 10 is not large enough to eliminate the SSE on the friction angles of granular materials. The minimum required W/dmax ratio of ASTM should be revised.
Similar observations can be made on the experimental results shown in Figure 6b for WR 2. The friction angle of the specimens with dmax = 0.85 mm remains constant as W/dmax increases from 45 to 353. For the specimens with dmax = 1.19 mm, the friction angle decreases by 0.2° as W/dmax increases from 32 to 50 and remains almost constant as W/dmax further increases to 252. The friction angle of the specimens with dmax = 1.4 mm decreases by 0.8° when W/dmax increases from 27 to 43 and remains almost constant when W/dmax further increases from 43 to 214. For the specimens with dmax = 2.36 mm, the friction angle decreases by 0.9° as W/dmax increases from 16 to 25 and then decreases by 0.2° when W/dmax further increases from 25 to 127. The friction angle of the specimens with dmax = 3.36 mm decreases by at least 1.2° as W/dmax increases from 11 to 18 and decreases by 1.9° as W/dmax further increases from 18 to 89. For the specimens with dmax = 5 mm, the friction angle decreases by 1.7° as W/dmax increases from 12 to 60. The friction angle of the specimens with dmax = 6 mm decreases by 1.7° as W/dmax increases from 10 to 50. These results show once again that a W/dmax ratio of 43 to 50 is large enough to eliminate the SSE while a W/dmax ratio of 10 to 32 is too small to eliminate the SSE on the friction angles of granular materials. The minimum required W/dmax ratio of 10 defined in the ASTM needs to be revised [76].

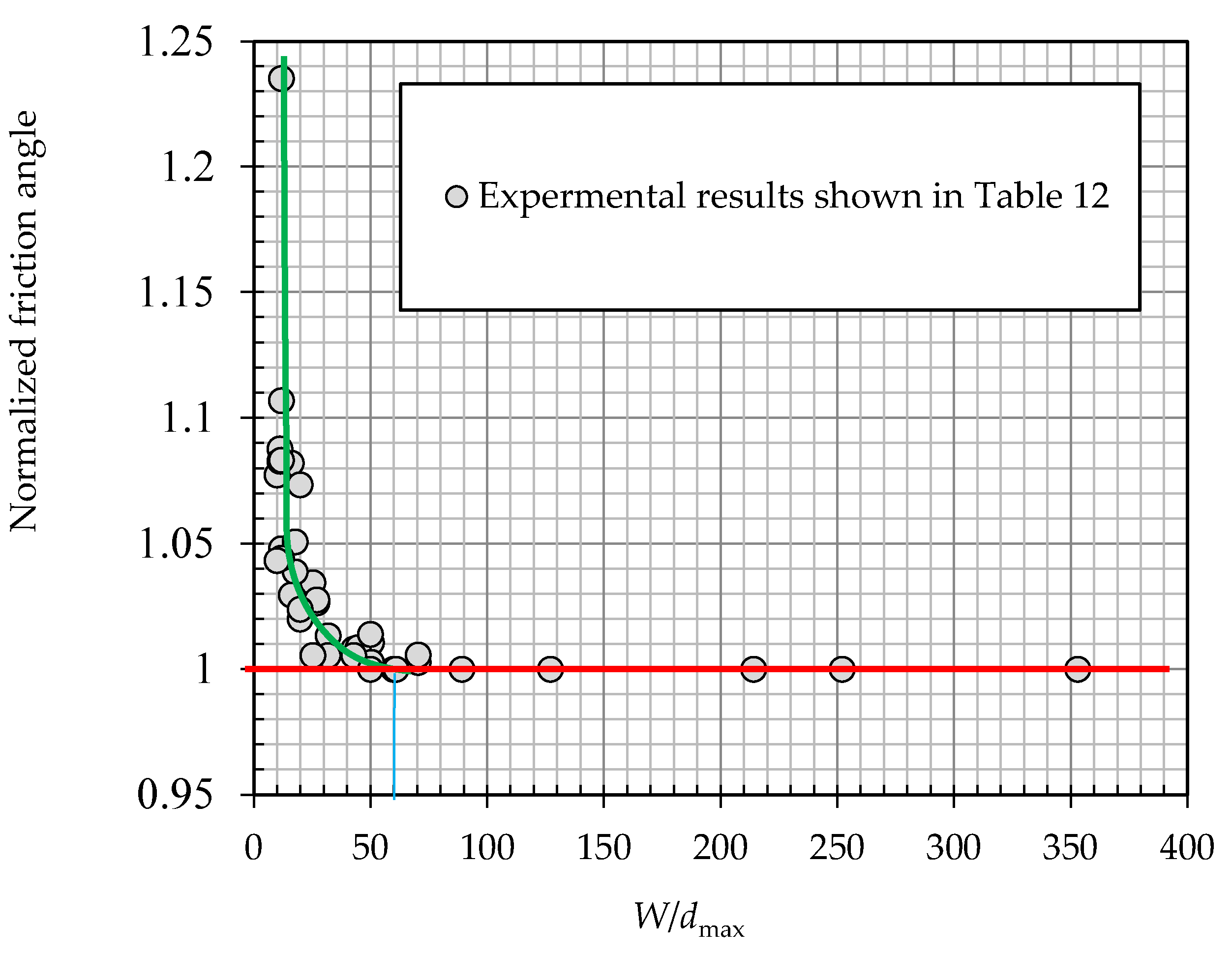
4. Identification of the Minimum Required W/dmax Ratio to Eliminate SSE

With the experimental results of fine particle materials with dmax values ranging from 0.83 to 1.4 mm shown in Figure 6, a W/dmax ratio of 43 to 50 seems to be large enough to eliminate the SSE on the friction angles of granular materials. It still remains unclear if these ratios can be applied to the specimens with dmax values ranging from 2.36 to 6 mm to remove the SSE.
One recalls that each dmax along with the type of waste rocks must be considered as the identification of one material. It is thus normal to see the test result points as a cloud, as shown in Figure 6. It is however very difficult, with such presentation, to identify a unique value respectively for the minimum required W/dmax ratio that can be considered as large enough to eliminate the SSE on the friction angle of granular materials.
Table 12 shows the friction angles of experimental results obtained in this study and those of existing data, normalized by the measured friction angle of sample having a large enough W/dmax ratio. Only a selected part of the existing data presented in Table 8 is included and presented in the table because the normalization can only be made on the experimental results with at least one specimen having W/dmax ratio large enough to eliminate the SSE. The experimental results of Rathee [26] and Wu et al. [30] are thus excluded.
Regarding the direct shear tests of Palmeira and Milligan [28], the results obtained with the rectangular shear box should be excluded in order to avoid any specimen shape effect. The remaining results should be included because it is difficult to justify that a specimen of 1 m by 1 m is still not large enough to eliminate the SSE with a tested material having a dmax = 1.2 mm and a W/dmax ratio of 833.
In this study, the experimental results of Ziaie Moayed [34] have also been excluded because their experimental results involve too many uncertainties pertaining to the SSE of friction angles. For example, their tested materials were prepared at optimum water contents. The very high apparent cohesions obtained with the small shear box can be well explained by the suction associated with the unsaturated state of the sample. However, the very small and even negative apparent cohesion obtained by the medium and large shear boxes cannot be explained by the unsaturated state of the samples. In addition, the shear stress–shear displacement curves clearly showed that the specimens in the small box received more compactness, having a mechanical behavior of dense sand while the specimens in the large box did not receive enough compactness, showing a mechanical behavior of loose sand. The problem of compactness can further be confirmed by the number of layers during their specimen preparation: three layers both in the small and medium sizes of shear box, five layers in the large shear box [34].
Regarding the experimental results of Mirzaeifar et al. [32], it is noted that the desired densities of 1.5, 1.58, and 1.67 g/cm3 were obtained by compacting the sand in 4, 6 and 8 layers, respectively. With the same number of layers in small, medium and large shear boxes, the resulting densities could be expected very different. Their test results thus not only involve the SSE, but also the effects of compactness or density. The experimental results of Mirzaeifar et al. [32] should thus also be excluded in the identification of the minimum required W/dmax ratio.
Figure 7 presents the variation of the normalized friction angles as a function of W/dmax of the experimental results obtained in this study and taken from the literature. It can be seen that the normalized friction angle varies from 1.12 to 1 depending on the W/dmax ratio. The normalized friction angle decreases as W/dmax increases from 10 to a certain value before it becomes constant when the W/dmax ratio further increases from this critical value to a value as high as 353. The critical value of W/dmax ratio beyond which the normalized friction remains constant is the searched minimum required W/dmax ratio to eliminate the SSE on friction angle of granular materials.
To identify these critical values, one first draws a horizontal line at normalized friction angles equal to 1. Eye-based best-fitted curves are then plotted to the experimental results having the W/dmax ratio between 10 and 50. One sees that the critical W/dmax ratio should be in the range of 50 to 70. One recommends a value of 60 for the minimum required W/dmax ratio, identified as large enough to eliminate the SSE. This value is chosen as a compromise between accuracy and practical convenience.

5. Discussions

The direct shear test is a very old but still regularly used method to determine the shear strength of geomaterials [1,2,3,4,5,6,7]. Unlike triaxial compression tests, a direct shear test imposes a sliding plane determined by upper and lower half boxes. Several shortages can be attributed to this imposed sliding plane. By following the standard of ASTM D3080 published in 1972, one can doubtlessly ensure higher quality of experimental results. Nevertheless, people are aware of the limitations. ASTM D3080 has to be regularly revised and updated every eight years. Recently, ASTM D3080/D3080M-11 [42] was temporarily withdrawn by the ASTM technical committees due to there being an excess of eight years since the last update. It seems that main concern of this update is related to the gap thickness to be left. One can expect that the updated version remains unchanged with respect to the minimum required specimen sizes. The current study is thus useful to inform its future updates.
This experimental study leads to a recommendation of a minimum required W/dmax ratio of 60. It is interesting to note that the same value was recommended by Wang and Gutierrez [39], who studied the SSE of direct shear tests through 2D discrete element modeling and made such a recommendation based on their experience (personal communication by email between the first author and Prof. Jianfeng Jerry Wang on 25 October 2021).
Despite the important and interesting discovery of this study, one has to point out that this experimental study involves several limitations.
In this study, the effect of specimen width was evaluated by trying to keep other influencing parameters constant. For one given material, all the shear tests with different shear boxes were performed with the same compact state and moisture content. However, due to a lack of shear boxes, the thickness of tested specimens meets the minimum required T/dmax ratio of ASTM, but is not constant. The influence of this parameter, the gap thickness between upper and lower half boxes as well as the specimen aspect ratio W/T were not taken into account [39,78]. More experimental work is thus necessary not only to verify the validity of the recommended value of the minimum required W/dmax ratio, but also to verify if the minimum required T/dmax ratio of ASTM is large enough to eliminate the SSE in direct shear tests [39].
Another limitation of this work is associated with the unique consideration of specimen sizes to dmax ratios. It is, however, well-known that the mechanical properties of geomaterials are not only controlled by the size of dmax, but also by the content of dmax. Two materials having the same dmax with different contents can behave differently. It is thus interesting and important to take into account other influencing factors, such as the portion of the coarsest particles, median size d50, coefficient of uniformity, particle shapes, contents of fine and coarse particles, and crushability of particles. It is also well-known that the friction angle of geomaterials depends on the compactness, water content, and confining pressure. More experimental work is necessary with more types of materials of different sources by taking into account these different influencing factors.
Finally, more experimental work can be necessary to evaluate if the minimum required specimen diameter over dmax ratio of 6 specified by ASTM D4767 [79] is large enough to eliminate SSE of triaxial compression tests by following the methodology presented in this study.

6. Conclusions

The minimum required specimen width to dmax ratio of ASTM has been revised based on an analysis on existing data and new experimental results. The following conclusions can be drawn:
  • The experimental results confirm what has been reported in [76], who showed that the minimum requirement of ASTM was not validated for fine particle materials due to the lack of experimental data with W/dmax ranging from 10 to 50, but invalidated for coarse particle materials. An update is necessary for the minimum required ratio between specimen sizes and dmax, stipulated by the ASTM D3080/D3080M [42] for direct shear tests.
  • The minimum required W/dmax ratio to eliminate the SSE on the shear strengths of granular materials is identified as equal to 60.
  • For fine particle materials having a dmax not larger than 1 mm, using the standard shear boxes having W = 60 mm automatically results in W/dmax ≥ 60. The obtained friction angles can be considered as fully representative to that of the tested material in field conditions. The ASTM D3080/D3080M-11 can thus continue to be applied without any problem of SSE.
  • For granular materials having dmax larger than 1 mm, applying the minimum requirements of ASTM D3080/D3080M-11 may result in a W/dmax ratio much smaller than the identified minimum required W/dmax ratio. The obtained friction angles can be erroneous.
More experimental works are necessary, not only with shear boxes of different sizes, but also with more materials by considering different testing conditions, including different densities, water contents, particle shapes, normal stresses, etc.

Author Contributions

Conceptualization, L.L. and A.D.; methodology, A.D. and L.L.; formal analysis, A.D., L.L. and F.Z.; investigation, A.D., F.Z. and L.L.; writing—original draft preparation, A.D. and F.Z.; writing—review and editing, L.L., A.D. and F.Z.; supervision, L.L.; project administration, L.L.; funding acquisition, L.L. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by Natural Sciences and Engineering Research Council of Canada (NSERC RGPIN-2018-06902), Fonds de recherche du Québec—Nature et Technologies (FRQNT 2017-MI-202860), and Mitacs (IT12569).

Data Availability Statement

Not applicable.

Acknowledgments

The authors acknowledge the financial support from the Natural Sciences and Engineering Research Council of Canada (NSERC RGPIN-2018-06902), Fonds de recherche du Québec—Nature et Technologies (FRQNT 2017-MI-202860), industrial partners of the Research Institute on Mines and the Environment (RIME UQAT-Polytechnique; http://rime-irme.ca/, accessed on 15 January 2022), and Mitacs Elevate Postdoctoral Fellowship (IT12569). Samuel Chenier, Eric Turgeon and Noura El-Harrak are gratefully acknowledged for their assistance in the laboratory work.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Goodrich, E.P. Lateral earth pressure and related phenomena. Trans. Am. Soc. Civil Eng. 1904, 53, 272–304. [Google Scholar] [CrossRef]
  2. Casagrande, A.; Albert, S.G. Research on the Shearing Resistance of Soils; Massachusetts Institute of Technology: Cambridge, MA, USA, 1932. [Google Scholar]
  3. Casagrande, A. Characteristics of cohesionless soils affecting the stability of slopes and earth fills. J. Boston Soc. Civ. Eng. 1936, 23, 13–32. [Google Scholar]
  4. Terzaghi, K. The shearing resistance of saturated soils and the angle between the planes of shear. In Proceedings of the 1st International Conference on Soil Mechanics and Foundation Engineering, Harvard, Boston, MA, USA, 22–26 June 1936; Volume 2, pp. 54–56. [Google Scholar]
  5. Cooling, L.F.; Smith, D.B. The shearing resistance of soils. In Proceedings of the 1st International Conference on Soil Mechanics and Foundation Engineering, Harvard, Boston, MA, USA, 22–26 June 1936; pp. 37–41. [Google Scholar] [CrossRef]
  6. Terzaghi, K.; Peck, R.B. Soil Mechanics in Engineering Practice; Wiley: New York, NY, USA, 1948. [Google Scholar]
  7. Hutchinson, J.N.; Rolfsen, E.N. Large scale field shear box test and quick clay. Adv. Civ. Eng. 1962, 28, 31–42. [Google Scholar]
  8. Cerato, A.B.; Lutenegger, A.J. Specimen size and scale effects of direct shear box tests of sands. Geotech. Test. J. 2006, 29, 1–10. [Google Scholar]
  9. Afzali-Nejad, A.; Lashkari, A.; Shourijeh, P.T. Influence of particle shape on the shear strength and dilation of sand-woven geotextile interfaces. Geotext. Geomembr. 2017, 45, 54–66. [Google Scholar] [CrossRef]
  10. Afzali-Nejad, A.; Lashkari, A.; Farhadi, B. Role of soil inherent anisotropy in peak friction and maximum dilation angles of four sand-geosynthetic interfaces. Geotext. Geomembr. 2018, 46, 869–881. [Google Scholar] [CrossRef]
  11. Zhang, Z.; Sheng, Q.; Fu, X.; Zhou, Y.; Huang, J.; Du, Y. An approach to predicting the shear strength of soil-rock mixture based on rock block proportion. Bull. Eng. Geol. Environ. 2019, 79, 2423–2437. [Google Scholar] [CrossRef]
  12. Cai, H.; Wei, R.; Xiao, J.Z.; Wang, Z.W.; Yan, J.; Wu, S.F.; Sun, L.M. Direct shear test on coarse gap-graded fill: Plate opening size and its effect on measured shear strength. Adv. Civ. Eng. 2020, 5750438. [Google Scholar] [CrossRef]
  13. Zahran, K.; Naggar, H.E. Effect of sample size on TDA shear strength parameters in direct shear tests. Transp. Res. Rec. 2020, 2674, 1110–1119. [Google Scholar] [CrossRef]
  14. Motahari Tabari, S.; Shooshpasha, I. Evaluation of coarse-grained mechanical properties using small direct shear test. Int. J. Geotech. Eng. 2021, 15, 667–679. [Google Scholar] [CrossRef]
  15. Xue, Z.F.; Cheng, W.C.; Wang, L.; Song, G. Improvement of the shearing behaviour of loess using recycled straw fiber reinforcement. KSCE J. Civ. Eng. 2021, 1–17. [Google Scholar] [CrossRef]
  16. Deiminiat, A.; Li, L. Experimental study on the reliability of scaling down techniques used in direct shear tests to determine the shear strength of rockfill and waste rocks. Civil Eng. 2022, 3, 35–50. [Google Scholar] [CrossRef]
  17. Jewell, R.A.; Wroth, C.P. Direct shear tests on reinforced sand. Géotechnique 1987, 37, 53–68. [Google Scholar] [CrossRef]
  18. Jewell, R.A. Direct shear test on sand. Géotechnique 1989, 39, 309–322. [Google Scholar] [CrossRef]
  19. Shibuya, S.; Mitachi, T.; Tamate, S. Interpretation of direct shear box testing of sands as quasi-simple shear. Géotechnique 1997, 47, 769–790. [Google Scholar] [CrossRef]
  20. Lings, M.L.; Dietz, M.S. An improved direct shear apparatus for sand. Géotechnique 2004, 54, 245–256. [Google Scholar] [CrossRef]
  21. Amirpour Harehdasht, S.; Karray, M.; Hussien, M.N.; Roubtsova, V.; Chekired, M. Influence of particle size and gradation on the stress-dilatancy behavior of granular materials during drained triaxial compression. Int. J. Geomech. 2017, 17, 1–20. [Google Scholar] [CrossRef]
  22. Drugan, W.J.; Willis, J.R. A micromechanics-based nonlocal constitutive equation and estimates of representative volume element size for elastic composites. J. Mech. Phys. Solids 1996, 44, 497–524. [Google Scholar] [CrossRef]
  23. Kanit, T.; Forest, S.; Galliet, I.; Mounoury, V.; Jeulin, D. Determination of the size of the representative volume element for random composites: Statistical and numerical approach. Int. J. Solids Struct. 2003, 40, 3647–3679. [Google Scholar] [CrossRef]
  24. Wen, R.; Tan, C.; Wu, Y.; Wang, C. Grain size effect on the mechanical behavior of cohesionless coarse-grained soils with the discrete element method. Adv. Civ. Eng. 2018, 2018, 4608930. [Google Scholar] [CrossRef]
  25. Parsons, J.D. Progress report on an investigation of the shearing resistance of cohesionless soils. In Proceedings of the 1st International Conference on Soil Mechanics and Foundation Engineering, Harvard, Boston, MA, USA, 22–26 June 1936; Volume 2, pp. 133–138. [Google Scholar]
  26. Rathee, R.K. Shear strength of granular soils and its prediction by modeling techniques. J. Inst. Eng. 1981, 62, 64–70. [Google Scholar]
  27. Vucetic, M.; Lacasse, S. Specimen size effect in simple shear test. ASCE J. Geotech. Eng. Div. 1982, 108, 1567–1585. [Google Scholar] [CrossRef]
  28. Palmeira, E.M.; Milligan, G.W.E. Scale effects in direct shear tests on sand. In Proceedings of the 12th International Conference on Soil Mechanics and Foundation Engineering, Rio De Janeiro, Brazil, 13–18 August 1989; Volume 1, pp. 739–742. [Google Scholar]
  29. Stone, K.J.; Wood, D.M. Effects of dilatancy and particle size observed in model tests on sand. Soils Found. 1992, 32, 43–57. [Google Scholar] [CrossRef] [Green Version]
  30. Wu, P.-K.; Matsushima, K.; Tatsuoka, F. Effects of specimen size and some other factors on the strength and deformation of granular soil in direct shear tests. Geotech. Test. J. 2008, 31, 1–20. [Google Scholar]
  31. Alonso, E.E.; Tapias, M.; Gili, J. Scale effects in rockfill behavior. Géotech. Lett. 2012, 2, 155–160. [Google Scholar] [CrossRef]
  32. Mirzaeifar, H.; Abouzar, A.; Abdi, M.R. Effects of direct shear box dimensions on shear strength parameters of geogrid-reinforced sand. In Proceedings of the 66th Canadian Geotechnical Conference and the 11th Joint CGS/IAH-CNC Groundwater Conference, GeoMontreal, Montrea, QC, Canada, 29 September–3 October 2013; pp. 1–6. [Google Scholar]
  33. Amirpour Harehdasht, S.; Hussien, M.N.; Karray, M.; Roubtsova, V.; Chekired, M. Influence of particle size and gradation on shear strength–dilation relation of granular materials. Can. Geotech. J. 2019, 56, 208–227. [Google Scholar] [CrossRef]
  34. Ziaie Moayed, R.; Alibolandi, M.; Alizadeh, A. Specimen size effects on direct shear test of silty sands. Int. J. Geotech. Eng. 2017, 11, 198–205. [Google Scholar] [CrossRef]
  35. Potts, D.M.; Dounias, G.T.; Vaughan, P.R. Finite element analysis of the direct shear box test. Géotechnique 1987, 37, 11–23. [Google Scholar] [CrossRef]
  36. Wang, J.; Dove, J.E.; Gutierrez, M.S. Discrete continuum analysis of shear band in the direct shear test. Géotechnique 2007, 57, 513–526. [Google Scholar] [CrossRef]
  37. Zhang, L.; Thornton, C. A numerical examination of the direct shear test. Géotechnique 2007, 57, 343–354. [Google Scholar] [CrossRef]
  38. Jacobson, D.E.; Valdes, J.R.; Evans, T.M. A numerical view into direct shear specimen size effects. Geotech. Test. J. 2007, 30, 512–516. [Google Scholar]
  39. Wang, J.; Gutierrez, M. Discrete element simulations of direct shear specimen scale effects. Géotechnique 2010, 60, 395–409. [Google Scholar] [CrossRef] [Green Version]
  40. DeJong, J.T.; Westgate, Z.J. Role of initial state, material properties, and confinement condition on local and global soil-structure interface behavior. J. Geotech. Geoenviron. Eng. 2009, 135, 1646–1660. [Google Scholar] [CrossRef]
  41. Lashkari, A.; Jamali, V. Global and local sand–geosynthetic interface behaviour. Géotechnique 2021, 71, 346–367. [Google Scholar] [CrossRef]
  42. ASTM D3080/D3080M-11; Standard Test Method for Direct Shear Test of Soils under Consolidated Drained Conditions (withdrawn 2020). ASTM International: West Conshohocken, PA, USA, 2011.
  43. Eurocode 7-07; Geotechnical Design; Part 1, General rules: EN 1997-1. The European Union Per Regulation: Brussels, Belgium, 2007.
  44. AS 1289.6.2.2-98; Soil Strength and Consolidation Tests-Determination of the Shear Strength of a Soil-Direct Shear Test Using a Shear Box. Standards Australia: Sydney, NSW, Australia, 1998.
  45. BS 1377-90; Methods of Test for Soils for Civil Engineering Purposes. Shear Strength Tests (total stress); Part 7. British Standard Institution: London, UK, 1990.
  46. McLemore, V.T.; Sweeney, D.; Dunbar, N.; Heizler, L.; Writer, E.P. Determining quantitative mineralogy using a modified MODAN approach on the Questa rock pile materials, New Mexico. In Proceedings of the Society of Mining, Metallurgy and Exploration Annual Convention, Denver, CO, USA, 22–25 February 2009; pp. 9–20. [Google Scholar]
  47. Zhai, Y.L.; Li, L.; Chapuis, R.P. Analytical, numerical and experimental studies on steady-state seepage through 3D rockfill trapezoidal dikes. Mine Water Environ. 2021, 40, 931–942. [Google Scholar] [CrossRef]
  48. Azam, S.; Li, Q. Tailings dam failures: A Review of the Last One Hundred Years. Geotech. News 2010, 28, 50–54. [Google Scholar]
  49. Owen, J.R.; Kemp, D.; Lèbre, É.; Svobodova, K.; Murillo, G.P. Catastrophic tailings dam failures and disaster risk disclosure. Int. J. Disaster Risk Reduct. 2020, 42, 101361. [Google Scholar] [CrossRef]
  50. Aubertin, M.; Bussière, B.; Bernier, B. Environnement et Gestion des Rejets Miniers; Manuel sur Cédérom; Presses Internationales Polytechnique: Montreal, QC, Canada, 2002. [Google Scholar]
  51. Azam, S.; Wilson, G.W.; Herasymuik, G.; Nichol, C.; Barbour, L.S. Hydrogeological behavior of an unsaturated waste rock pile: A case study at the Golden Sunlight Mine, Montana, USA. Bull. Eng. Geol. Environ. 2007, 66, 259–268. [Google Scholar] [CrossRef]
  52. Boudrias, G. Évaluation Numérique et Expérimentale du Drainage et de la Consolidation de Résidus Miniers à Proximité d’une Inclusion de Roches Stériles. Master’s Thesis, Polytechnique Montréal, Montreal, QC, Canada, 2018. [Google Scholar]
  53. Saleh-Mbemba, F.; Aubertin, M.; Boudrias, G. Drainage and consolidation of mine tailings near waste rock inclusions. In Sustainable and Safe Dams around the World; Taylor & Francis Group: London, UK, 2019; pp. 3296–3305. [Google Scholar]
  54. Li, L.; Ouellet, S.; Aubertin, M. A method to evaluate the size of backfilled stope barricades made of waste rock. In GeoHalifax; Canadian Geotechnical Society: Halifax, CA, Canada, 2009. [Google Scholar]
  55. Li, L.; Aubertin, M. Limit equilibrium analysis for the design of backfilled stope barricades made of waste rock. Can. Geotech. J. 2011, 48, 1713–1728. [Google Scholar] [CrossRef]
  56. Yang, P.Y.; Li, L.; Aubertin, M.; Brochu-Baekelmans, M.; Ouellet, S. Stability analyses of waste rock barricades designed to retain paste backfill. Int. J. Geomech. 2017, 17, 04016079. [Google Scholar] [CrossRef]
  57. Zhai, Y.L.; Yang, P.Y.; Li, L. Analytical solutions for the design of shotcreted waste rock barricades to retain slurried paste backfill. Constr. Build. Mater. 2021, 307, 124626. [Google Scholar] [CrossRef]
  58. Hall, E.B. A triaxial apparatus for testing large soil specimens. ASTM Triaxial Test. Soils Bitum. Mix. 1951, 106, 152–161. [Google Scholar]
  59. Holtz, W.; Gibbs, H.J. Triaxial shear tests on pervious gravelly soils. J. Soil Mech. Found. Div. 1956, 82, 1–22. [Google Scholar] [CrossRef]
  60. Leslie, D. Large scale triaxial tests on gravelly soils. In Proceedings of the Second Panamerican Conference on Soil Mechanics and Foundation Engineering, Sao Paulo, Brazil, 1 July 1963; Volume 1, pp. 181–202. [Google Scholar]
  61. Marachi, N.; Seed, H.; Chan, C. Strength characteristics of rockfill materials. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 25–29 August 1969; pp. 217–224. [Google Scholar]
  62. Marachi, N.D.; Chan, C.K.; Seed, H.B. Evaluation of properties of rockfill materials. J. Soil Mech. Found. Div. 1972, 98, 95–114. [Google Scholar] [CrossRef]
  63. Varadarajan, A.; Sharma, K.G.; Venkatachalam, K.; Gupta, A.K. Testing and modeling two rockfill materials. J. Geotech. Geoenviron. Eng. 2003, 129, 206–218. [Google Scholar] [CrossRef]
  64. Hamidi, A.; Azini, E.; Masoudi, B. Impact of gradation on the shear strength-dilation behavior of well graded sand-gravel mixtures. Sci. Iran. 2012, 19, 393–402. [Google Scholar] [CrossRef] [Green Version]
  65. Chang, W.J.; Phantachang, T. Effects of gravel content on shear resistance of gravelly soils. Eng. Geol. 2016, 207, 78–90. [Google Scholar] [CrossRef]
  66. Yang, G.; Jiang, Y.; Nimbalkar, S.; Sun, Y.; Li, N. Influence of particle size distribution on the critical state of rockfill. Adv. Civ. Eng. 2019, 2019, 1–7. [Google Scholar] [CrossRef]
  67. Ovalle, C.; Linero, S.; Dano, C.; Bard, E.; Hicher, P.-Y.; Osses, R. Data compilation from large drained compression triaxial tests on coarse crushable rockfill materials. J. Geotech. Geoenviron. Eng. 2020, 146, 06020013. [Google Scholar] [CrossRef]
  68. ASTM D3080-72; Direct Shear Test of Soils under Consolidated Drained Conditions. ASTM International: West Conshohocken, PA, USA, 1972.
  69. Varadarajan, A.; Sharma, K.G.; Abbas, S.M.; Dhawan, A.K. The role of nature of particles on the behavior of rockfill material. Soils Found. 2006, 46, 569–584. [Google Scholar] [CrossRef] [Green Version]
  70. Abbas, S.M. Behavior of Rockfill Materials Based on Nature of Particles; Lambert Academic Publishing: Saarbrücken, Germany, 2011. [Google Scholar]
  71. Pankaj, S.; Mahure, N.; Gupta, S.; Sandeep, D.; Devender, S. Estimation of shear strength of prototype rockfill materials. Int. J. Eng. Sci. 2013, 2, 421–426. [Google Scholar]
  72. Vasistha, Y.; Gupta, A.K.; Kanwar, V. Medium triaxial testing of some rockfill materials. Electron. J. Geotech. Eng. 2013, 18, 923–964. [Google Scholar]
  73. Honkanadavar, N.P.; Kumar, N.; Ratnam, M. Modeling the behavior of alluvial and blasted quarried rockfill materials. Geotech. Geol. Eng. 2014, 32, 1001–1015. [Google Scholar] [CrossRef] [Green Version]
  74. Xu, Y. Shear strength of granular materials based on fractal fragmentation of particles. Powder Technol. 2018, 333, 1–8. [Google Scholar] [CrossRef]
  75. Dadkhah, R.; Ghafoori, M.; Ajalloeian, R.; Lashkaripour, G.R. The effect of scale direct shear test on the strength parameters of clayey sand in Isfahan city. Can. J. Appl. Sci. 2010, 10, 2027–2033. [Google Scholar] [CrossRef] [Green Version]
  76. Deiminiat, A.; Li, L.; Zeng, F.; Pabst, T.; Chiasson, P.; Chapuis, R. Determination of the shear strength of rockfill from small scale laboratory shear tests: A critical review. Adv. Civ. Eng. 2020, 2020, 8890237. [Google Scholar] [CrossRef]
  77. ASTM C29/C29M-17a; Standard Test Method for Bulk Density (unit weight) and Voids in Aggregate. ASTM International: West Conshohocken, PA, USA, 2007.
  78. Hight, D.W.; Leroueil, S. Characterisation of soils for engineering purposes. Characterisation Eng. Prop. Nat. Soils 2003, 1, 255–360. [Google Scholar]
  79. ASTM D4767; Standard Test Method for Consolidated Undrained Triaxial Compression Test for Cohesive Soils. ASTM International: West Conshohocken, PA, USA, 2011.
Civileng 03 00005 g001 550
Figure 1. Direct shear apparatuses: (a) standard one for mini and small shear boxes; (b) large one for large shear box.
Figure 1. Direct shear apparatuses: (a) standard one for mini and small shear boxes; (b) large one for large shear box.
Civileng 03 00005 g001
Civileng 03 00005 g002 550
Figure 2. Shear boxes used in this study: (a) house-made mini square shear box (38 mm × 38 mm × 45 mm); (b) small (standard) square shear box (60 mm × 60 mm × 45 mm); (c) large square shear boxes (300 mm × 300 mm × 180 mm).
Figure 2. Shear boxes used in this study: (a) house-made mini square shear box (38 mm × 38 mm × 45 mm); (b) small (standard) square shear box (60 mm × 60 mm × 45 mm); (c) large square shear boxes (300 mm × 300 mm × 180 mm).
Civileng 03 00005 g002
Civileng 03 00005 g003 550
Figure 3. Photos of original (a) WR 1 and (b) WR 2.
Figure 3. Photos of original (a) WR 1 and (b) WR 2.
Civileng 03 00005 g003
Civileng 03 00005 g004 550
Figure 4. Grain size distribution curves of the samples with different dmax (same for WR 1 and WR 2).
Figure 4. Grain size distribution curves of the samples with different dmax (same for WR 1 and WR 2).
Civileng 03 00005 g004
Civileng 03 00005 g005 550
Figure 5. Shear stress vs. shear displacement curves of WR 1 specimens with dmax value of 0.85 mm under three normal stresses obtained with the mini (a), small (b) and large (c) shear boxes.
Figure 5. Shear stress vs. shear displacement curves of WR 1 specimens with dmax value of 0.85 mm under three normal stresses obtained with the mini (a), small (b) and large (c) shear boxes.
Civileng 03 00005 g005
Civileng 03 00005 g006 550
Figure 6. Variations of the friction angles of the specimens as a function of W/dmax for the specimens made of (a) WR 1 and (b) WR 2.
Figure 6. Variations of the friction angles of the specimens as a function of W/dmax for the specimens made of (a) WR 1 and (b) WR 2.
Civileng 03 00005 g006
Civileng 03 00005 g007 550
Figure 7. Variations of the normalized friction angles as a function of W/dmax of the experimental results obtained in this study and taken from the literature. The minimum required specimen size is identified as W/dmax = 60.
Figure 7. Variations of the normalized friction angles as a function of W/dmax of the experimental results obtained in this study and taken from the literature. The minimum required specimen size is identified as W/dmax = 60.
Civileng 03 00005 g007
Table
Table 1. Standards of direct shear tests regarding maximum particle size (dmax), specimen width (W) and thickness (T).
Table 1. Standards of direct shear tests regarding maximum particle size (dmax), specimen width (W) and thickness (T).
StandardRequired Shear Box SizeMaximum Allowed dmax
W (mm)T (mm)W/T
ASTM D3080/D3080M-11 [42]≥50≥13≥2Min{T/6, W/10}
Eurocode 7 [43]Not specifiedNot specifiedNot specifiedT/10
AS 1289.6.2.2 [44]Not specified≥12.5Not specifiedT/6
BS 1377–7 [45]602032 mm
1002542.5 mm
305150≈215 mm–20 mm
Table
Table 2. Variation of friction angle (ϕ) obtained by Parson (1936) with different specimen sizes through direct shear tests; L is the length of shear box.
Table 2. Variation of friction angle (ϕ) obtained by Parson (1936) with different specimen sizes through direct shear tests; L is the length of shear box.
L (mm) × W (mm)W/dmaxϕ (°)
Crushed QuartzOttawa Sand
60 × 607131.531.0
120 × 10011931.129.6
200 × 12014330.728.5
Table
Table 3. Friction angles of a sand with dmax = 1.2 mm, obtained by direct shear tests with three shear box sizes [28].
Table 3. Friction angles of a sand with dmax = 1.2 mm, obtained by direct shear tests with three shear box sizes [28].
L (mm) × W (mm) × T (mm)W/dmaxT/dmaxϕ (°)
60 × 60 × 32502750.1
252 × 152 × 15212712750.2
1000 × 1000 × 100083383349.4
Table
Table 4. Friction angles of gravel having a dmax value of 5 mm with different relative densities (Dr), obtained by direct shear tests with three shear box sizes [8].
Table 4. Friction angles of gravel having a dmax value of 5 mm with different relative densities (Dr), obtained by direct shear tests with three shear box sizes [8].
W (mm) × W (mm) × T (mm)W/dmaxT/dmaxϕ (°)
Dr = 25%Dr = 55%Dr = 85%
59.9 × 59.9 × 26.4125 42.0 44.5 45.5
101.6 × 101.6 × 40.64208 36.5 41.0 43.0
304.8 × 304.8 × 177.86136 34.0 40.242.0
Table
Table 5. Friction angles of the sand samples obtained by Wu et al. [30].
Table 5. Friction angles of the sand samples obtained by Wu et al. [30].
Void RatioW (mm) × W (mm) × T (mm)W/dmaxT/dmaxϕ (°)
0.65440 × 40 × 20954845.8
0.659120 × 120 × 12028528541.8
Table
Table 6. Friction angles of sand at three different densities, obtained by direct shear tests with three different size shear boxes [32].
Table 6. Friction angles of sand at three different densities, obtained by direct shear tests with three different size shear boxes [32].
W (mm) × W (mm) × T (mm)W/dmaxT/dmaxϕ (°)
at 1.5 (g/cm3)at 1.58 (g/cm3)at 1.67 (g/cm3)
60 × 60 × 16461235.437.939.7
100 × 100 × 30772333.334.535.2
300 × 300 × 18023113832.634.034.5
Table
Table 7. Friction angles of sand and silty sands, obtained by only considering the direct shear test results of Ziaie Moayed et al. [34] with the normal stresses of 109, 163, and 218 kPa.
Table 7. Friction angles of sand and silty sands, obtained by only considering the direct shear test results of Ziaie Moayed et al. [34] with the normal stresses of 109, 163, and 218 kPa.
W (mm) × W (mm) × T (mm)W/dmaxT/dmaxϕ (°)
Sand 1Silty Sand I 2Silty Sand II 3Silty Sand III 4
60 × 60 × 24.57530.643.939.734.430.4
100 × 100 × 3512543.839.031.431.231.0
300 × 300 × 154375192.534.933.730.831.3
Note: For sand and silty sand II, the peak shear stresses at the three normal stresses are taken from the stress-displacement curves to obtain the friction angles because the use of the peak shear stresses from Figure 10 of Ziaie Moayed et al. [34] may result in negative cohesion. For silty sand I and III, no stress-displacement curves were given in [34]. 1 Results based on Figure 5 of Ziaie Moayed et al. [34]; 2 Results based on Figure 10b of Ziaie Moayed et al. [34]; 3 Results based on Figure 6 of Ziaie Moayed et al. [34]; 4 Results based on Figure 10d of Ziaie Moayed et al. [34].
Table
Table 8. Summarization of the analyses on existing test data obtained to investigate the SSE.
Table 8. Summarization of the analyses on existing test data obtained to investigate the SSE.
ReferencesTested W/dmaxMinimum Require W/dmaxMinimum Tested W/dmax Large Enough to Remove SSEMinimum Required W/dmax of ASTM
Parsons [25]71, 119, 143~71Yes at 71Unknown
Rathee [26]10, 48UnknownNot at 10Invalidated
Cerato and Lutenegger [8]12, 20, 61UnknownNot at 20Invalidated
Wu et al. [30]95, 285UnknownNot at 95Invalidated
Mirzaeifar et al. [32]46, 77, 231~77Not at 46Invalidated
Palmeira and Milligan [28]50, 127, 833≤50Yes at 50Unknown
Ziaie Moayed et al. [34]Sand75, 125, 375UnknownNot at 75Invalidated
Silty sand I75, 125, 375UnknownNot at 75Invalidated
Silty sand II75, 125, 375~125Not at 75Invalidated
Silty sand III75, 125, 375≤75Yes at 75Unknown
Table
Table 9. Portions of waste rocks used to make the different mixtures.
Table 9. Portions of waste rocks used to make the different mixtures.
Ranges of Particle SizesMasse of Different Portions (g)
dmax = 6 mm5 mm3.36 mm2.36 mm1.4 mm1.19 mm0.85 mm
5 to 6 mm3618
3.36 to 5 mm58996190
2.36 to 3.36 mm431444325062
1.4 to 2.36 mm3272322725864663
1.19 to 1.4 mm52472178913342301
0.85 to 1.19 mm132613791603220222203283
0.63 to 0.85 mm121125369327154924016500
0.315 to 0.63 mm3703852914497108531440
0.16 to 0.315 mm345359408315539568590
0.08 to 0.16 mm106311057919727718321300
≤0.08 mm2942306025312691218623243550
Table
Table 10. Shear boxes and specimen size to dmax ratios, used in the direct shear tests on the two types of waste rocks.
Table 10. Shear boxes and specimen size to dmax ratios, used in the direct shear tests on the two types of waste rocks.
dmax (mm)emax38 mm × 38 mm × 45 mm60 mm × 60 mm × 45 mm300 mm × 300 mm × 180 mm
WR 1WR 2W/dmaxT/dmaxW/dmaxT/dmaxW/dmaxT/dmax
0.850.930.8445537153353212
1.190.870.7932385038252151
1.40.840.7327324332214129
2.360.880.751619251912776
3.360.850.74111318138954
5.00.800.77----1296036
6.00.780.72----1085030
Table
Table 11. Friction angles of the specimens obtained by extra small, small, and large shear boxes for WR 1 and WR 2.
Table 11. Friction angles of the specimens obtained by extra small, small, and large shear boxes for WR 1 and WR 2.
dmax (mm)38 mm × 38 mm × 45 mm60 mm × 60 mm × 45 mm300 mm × 300 mm × 180 mm
W/dmaxT/dmaxϕ (°)W/dmaxT/dmaxϕ (°)W/dmaxT/dmaxϕ (°)
WR 1WR 2WR 1WR 2WR 1WR 2
0.85455337.135.371533735.235321236.935.0
1.1932383836.2503837.936.125215137.536.0
1.4273238.737.2433238.036.421412937.736.2
2.36161940.938.2251939.137.31277637.937.1
3.36111342.140.5181340.239.3895438.737.4
5--------12941.440.1603639.538.4
6--------10843.040.9503039.939.2
Table
Table 12. Normalized friction angles of the experimental results obtained in this study and taken from the literature.
Table 12. Normalized friction angles of the experimental results obtained in this study and taken from the literature.
Id. of MaterialW/dmaxT/dmaxϕ (°)Normalized ϕId. of MaterialW/dmaxT/dmaxϕ (°)Normalized ϕReferences
WR 1,
dmax = 0.85 mm		455337.11.005WR 2,
dmax = 0.85 mm		455335.31.009This study
715337.01.003715335.21.006
35321236.9135321235.01
WR 1,
dmax = 1.19 mm		323838.01.013WR 2,
dmax = 1.19 mm		323836.21.006
503837.91.011503836.11.002
25215137.5125215136.01
WR 1,
dmax = 1.4 mm		273238.71.027WR 2,
dmax = 1.4 mm		273237.21.028
433238.01.008433236.41.006
21412937.7121412936.21
WR 1,
dmax = 2.36 mm		161940.91.082WR 2,
dmax = 2.36 mm		161938.21.030
251939.11.034251937.31.005
1277637.811277637.11
WR 1,
dmax = 3.36 mm		111342.11.088WR 2,
dmax = 3.36 mm		111340.51.083
181340.21.039181339.31.051
895438.71895437.41
WR 1,
dmax = 5 mm		12941.41.048WR 2,
dmax = 5 mm		12940.11.044
603639.51603638.41
Gravel,
dmax = 5 mm, Dr = 25%		12 5 42.0 1.235Gravel,
dmax = 5 mm,
Dr = 55%		12 5 44.51.107[8]
20 8 36.5 1.07420 8 41.01.020
61 36 34.0 161 36 40.21
Gravel,
dmax = 5 mm, Dr = 85%		12 5 45.5 1.083
20 8 43.0 1.024
61 36 42.01
Sand,
dmax = 1.2 mm		502750.11.014 [28]
83383349.41
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Deiminiat, A.; Li, L.; Zeng, F. Experimental Study on the Minimum Required Specimen Width to Maximum Particle Size Ratio in Direct Shear Tests. CivilEng 2022, 3, 66-84. https://doi.org/10.3390/civileng3010005

AMA Style

Deiminiat A, Li L, Zeng F. Experimental Study on the Minimum Required Specimen Width to Maximum Particle Size Ratio in Direct Shear Tests. CivilEng. 2022; 3(1):66-84. https://doi.org/10.3390/civileng3010005

Chicago/Turabian Style

Deiminiat, Akram, Li Li, and Feitao Zeng. 2022. "Experimental Study on the Minimum Required Specimen Width to Maximum Particle Size Ratio in Direct Shear Tests" CivilEng 3, no. 1: 66-84. https://doi.org/10.3390/civileng3010005

APA Style

Deiminiat, A., Li, L., & Zeng, F. (2022). Experimental Study on the Minimum Required Specimen Width to Maximum Particle Size Ratio in Direct Shear Tests. CivilEng, 3(1), 66-84. https://doi.org/10.3390/civileng3010005

Article Metrics

Back to TopTop