Study of the Bond Capacity of FRCM- and SRG-Masonry Joints
Abstract
1. Introduction
2. Experimental Program
2.1. Specimen Preparation
- The masonry block surface was wet with water to prevent absorption of the matrix water by the substrate.
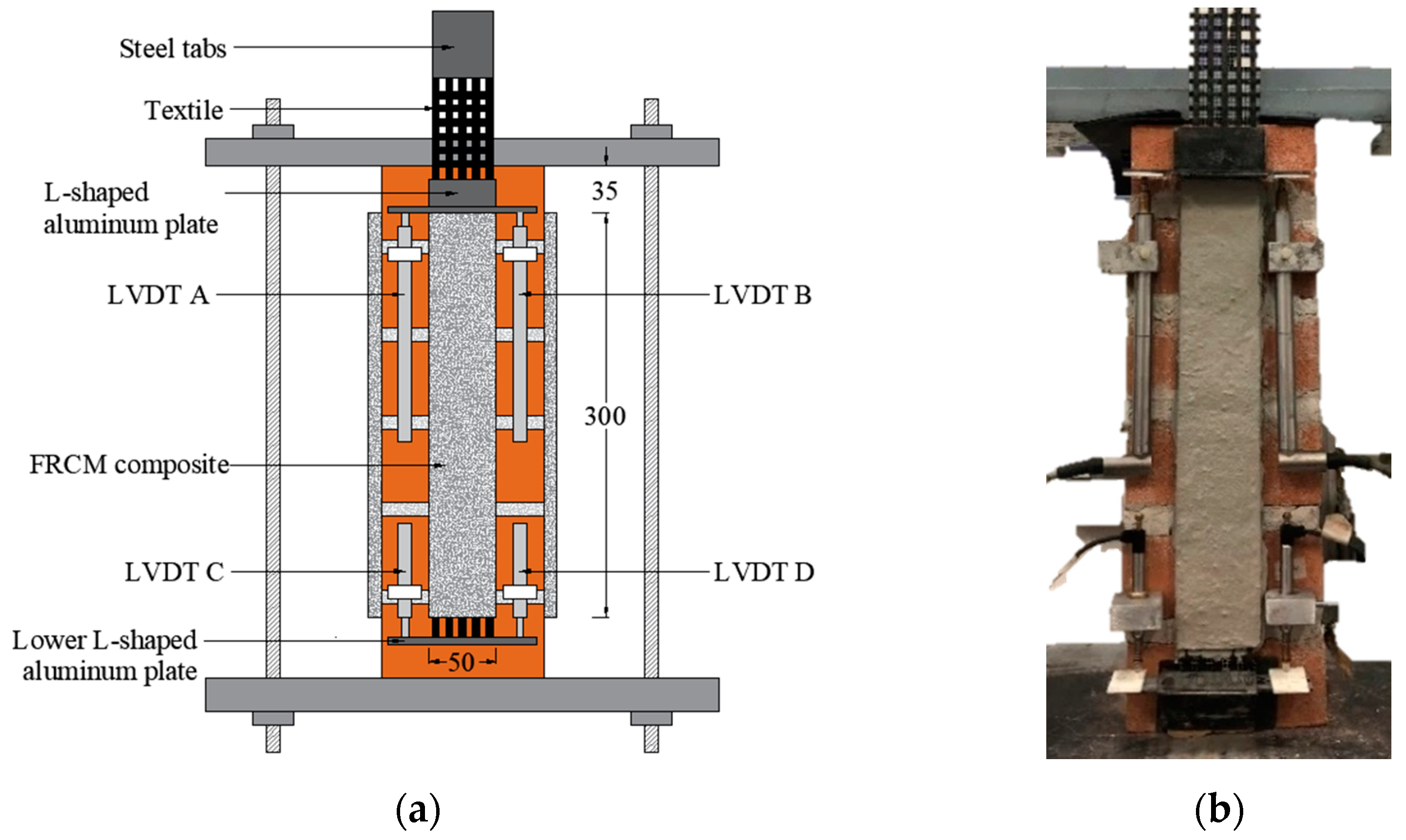
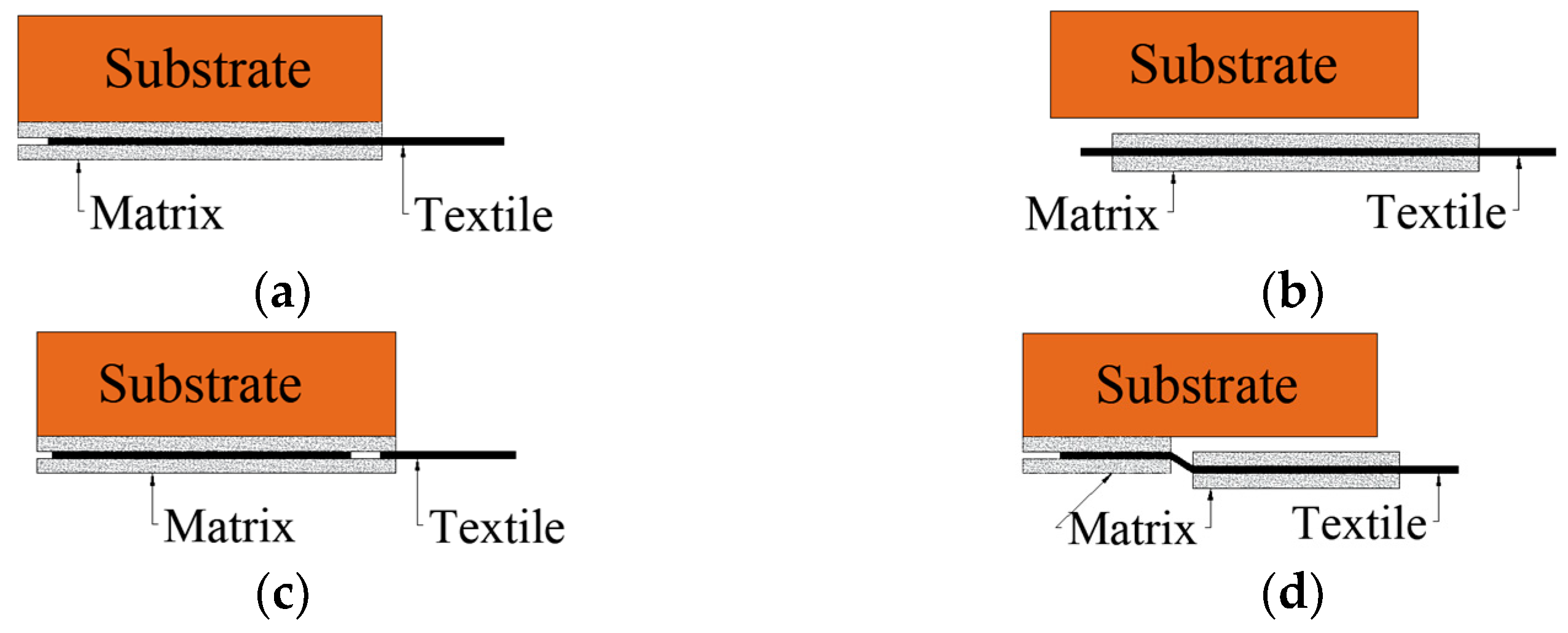
- A textile strip 630 mm long was gently pressed onto the internal matrix layer. The textile strip was left bare outside the loaded end for 310 mm and outside the free end for 20 mm. The bonded length started 35 mm far from the masonry block edge at the loaded end to prevent the substrate wedge failure [11]. The specimen geometry is shown in Figure 2.
- Finally, a second (external) layer of matrix with the same dimension of the matrix internal layer was applied over the textile again using a plastic mold to control its geometry.
2.2. Single-Lap Direct Shear Test Set-up
3. Results and Discussion
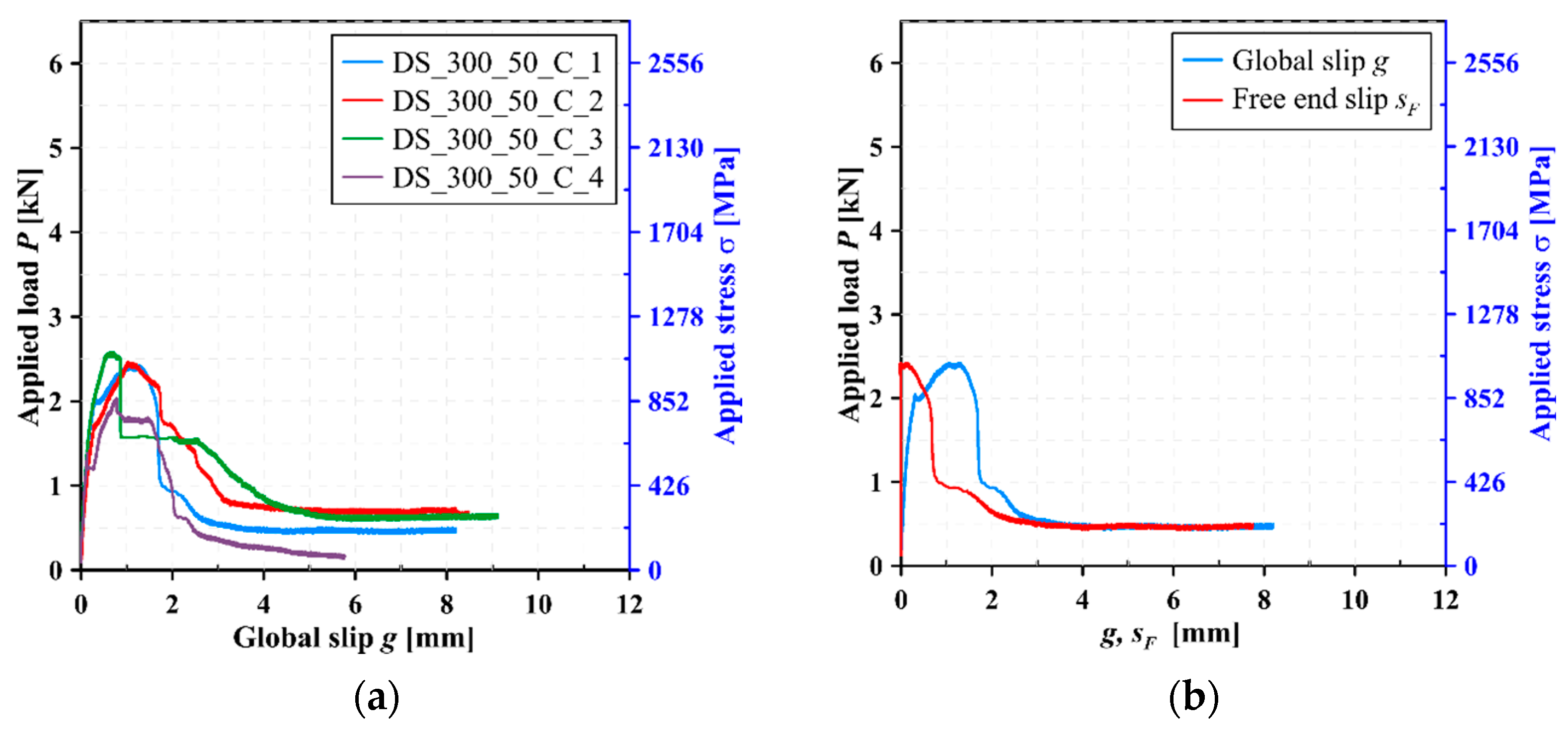
3.1. Bond Performance of Carbon FRCM-Masonry Joints
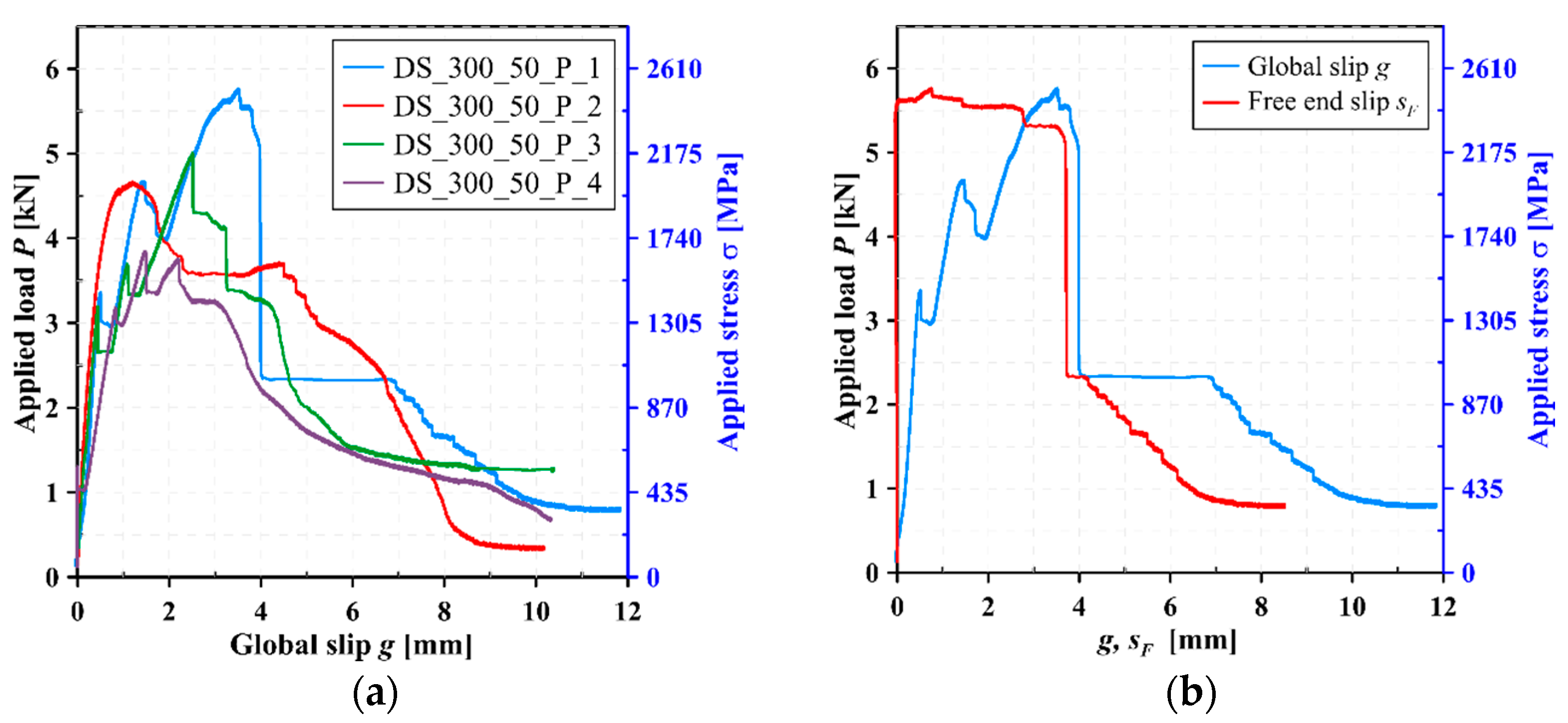
3.2. Bond Performance of PBO FRCM-Masonry Joints
3.3. Bond Performance of AR-Glass FRCM-Masonry Joints
3.4. Bond Performance of SRG-Masonry Joints
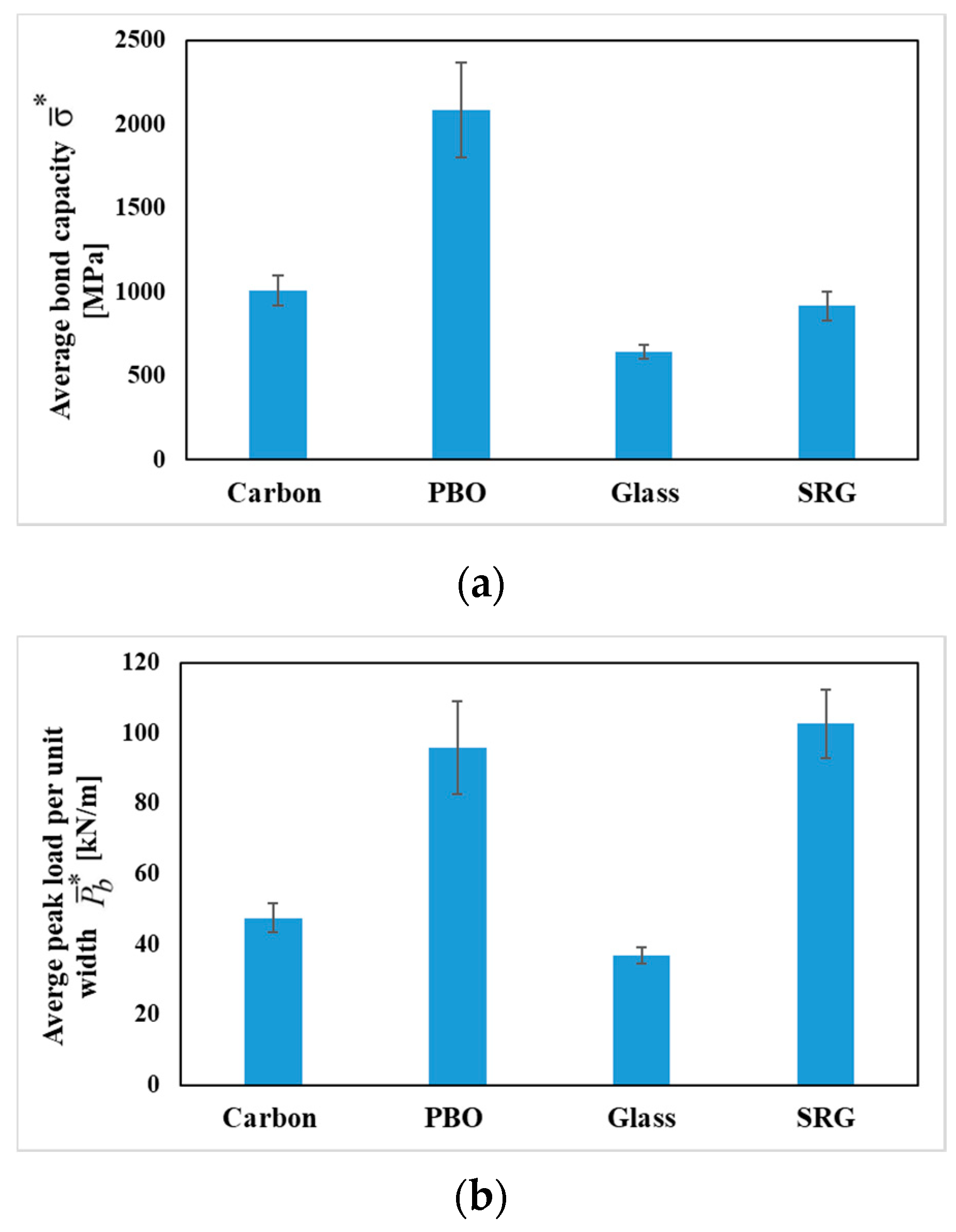
3.5. Comparison of the Bond Performance for the Various Composite Systems
4. Analytical Study
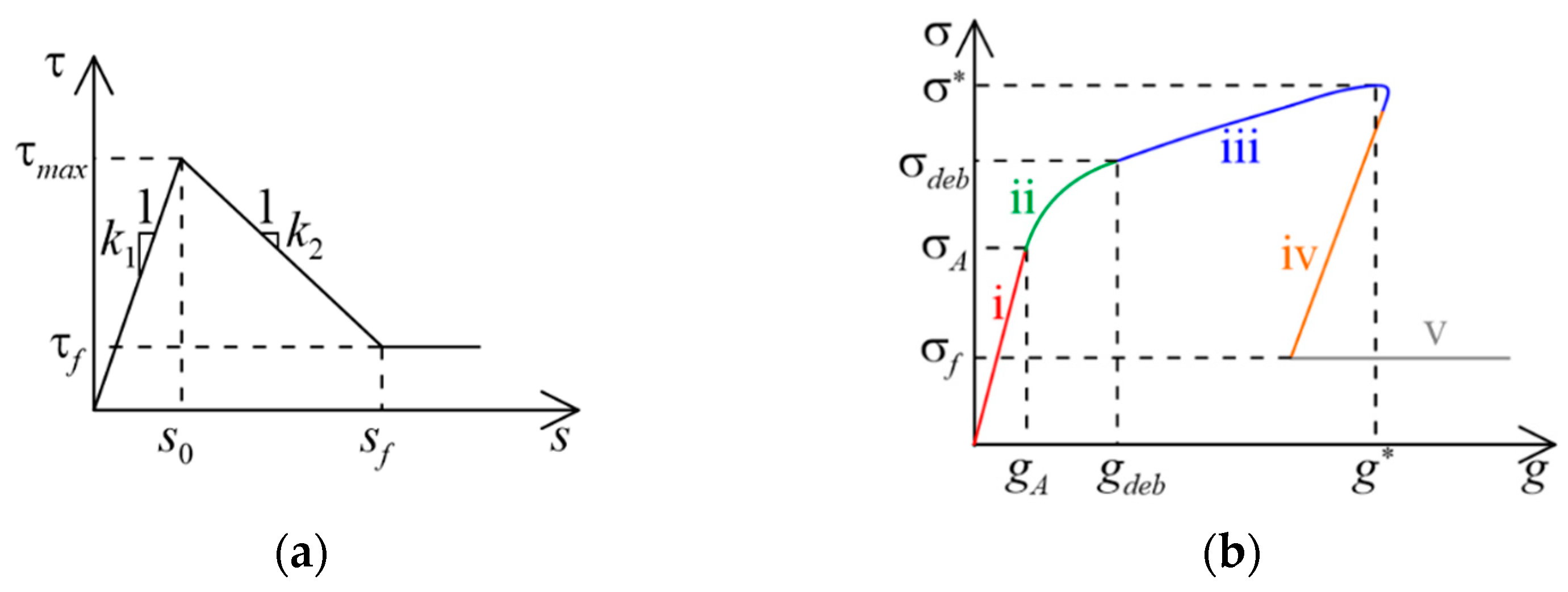
4.1. Governing Equations
4.2. Evaluation of the Effective Bond Length
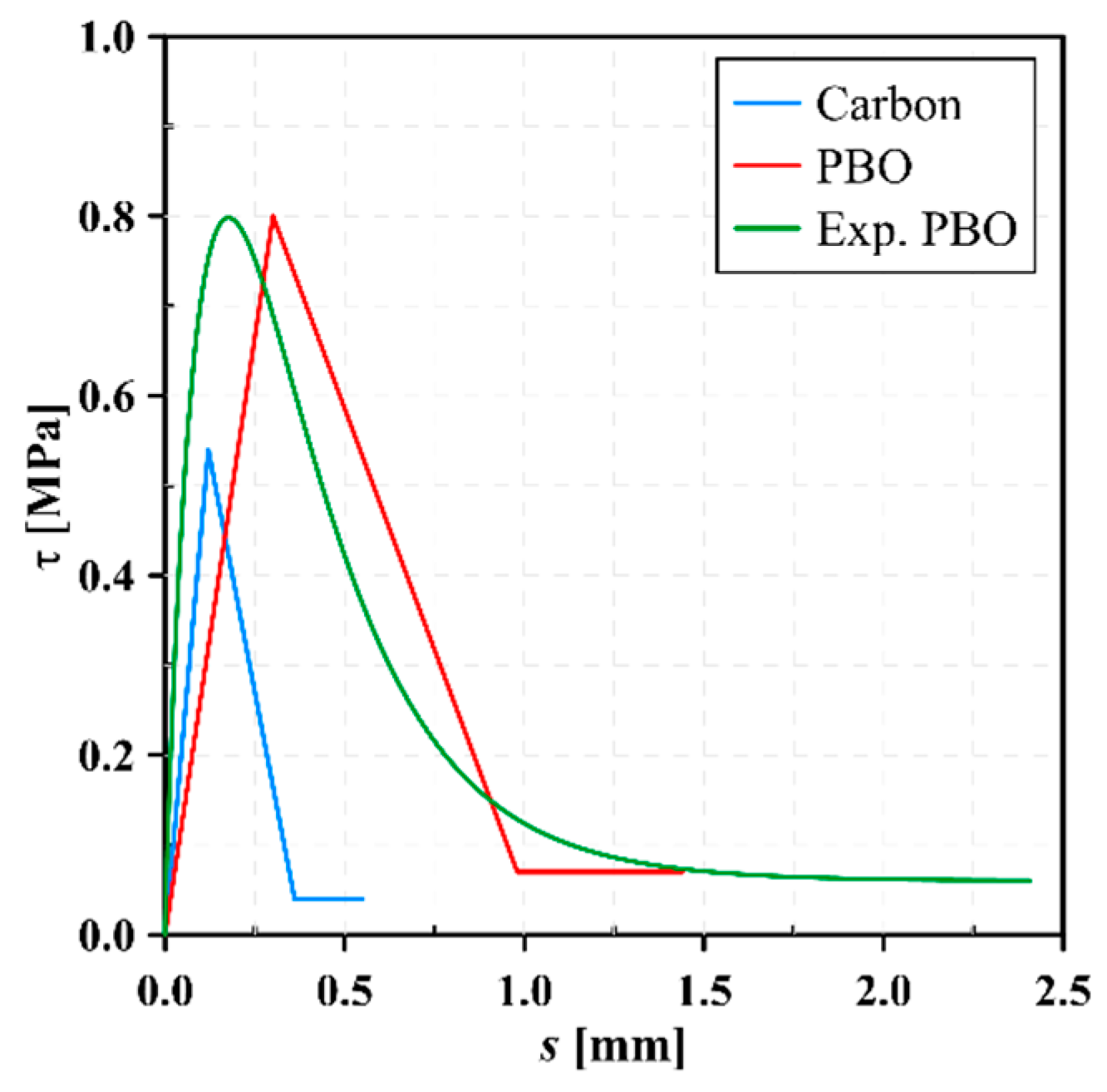
4.3. Estimation of the CML Parameters
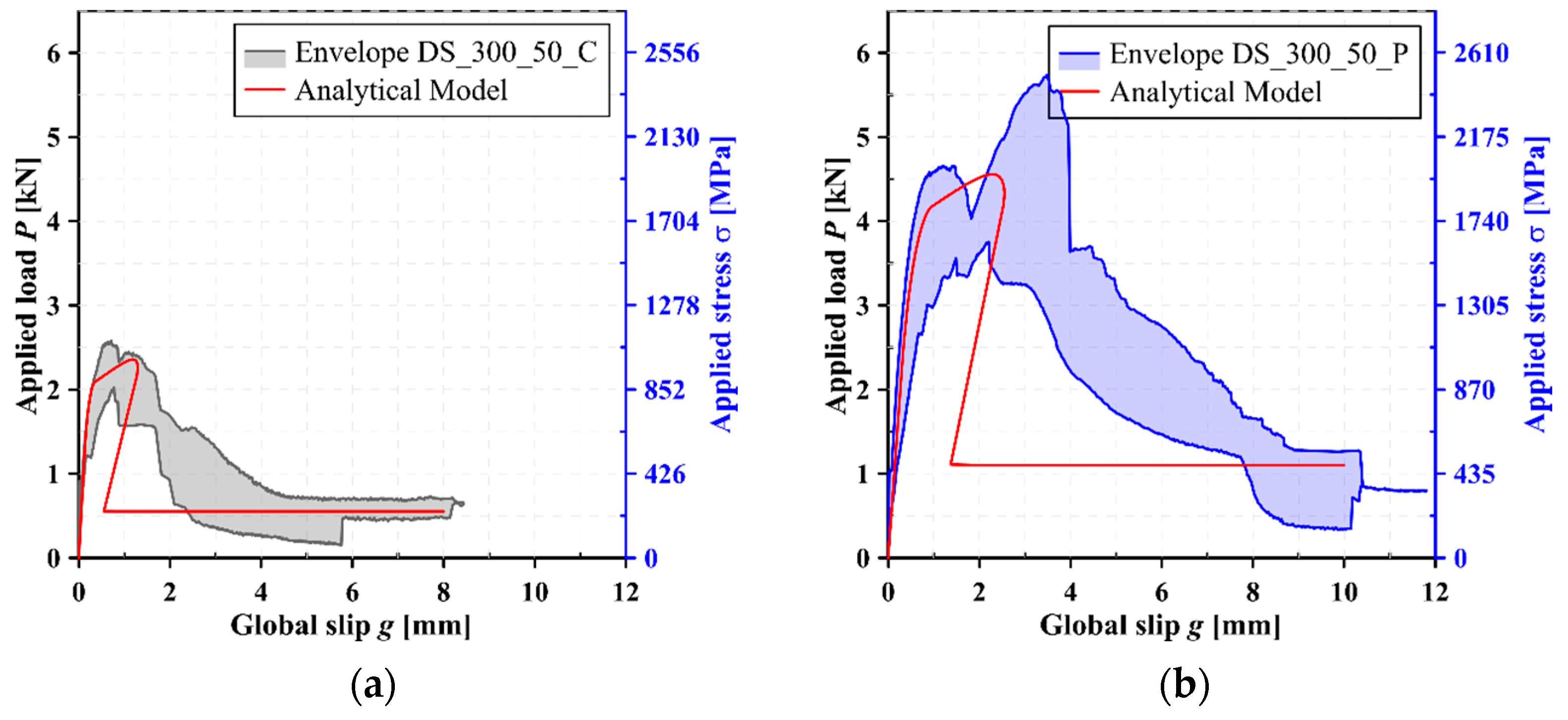
4.4. Simulation of the Load Response
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Abid, S.R.; Al-lami, K. Critical review of strength and durability of concrete beams externally bonded with FRP. Cogent Eng. 2018, 5. [Google Scholar] [CrossRef]
- Al-Lami, K.; Colombi, P.; D’Antino, T. Influence of hygrothermal ageing on the mechanical properties of CFRP-concrete joints and of their components. Compos. Struct. 2020, 238, 111947. [Google Scholar] [CrossRef]
- Heshmati, M.; Haghani, R.; Al-Emrani, M. Environmental durability of adhesively bonded FRP/steel joints in civil engineering applications: State of the art. Compos. Part B Eng. 2015, 81, 259–275. [Google Scholar] [CrossRef]
- Maljaee, H.; Ghiassi, B.; Lourenço, P.B.; Oliveira, D.V. FRP-brick masonry bond degradation under hygrothermal conditions. Compos. Struct. 2016, 147, 143–154. [Google Scholar] [CrossRef]
- Bencardino, F.; Condello, A.; Ashour, A.F. Single-lap shear bond tests on Steel Reinforced Geopolymeric Matrix-concrete joints. Compos. Part B Eng. 2017, 110, 62–71. [Google Scholar] [CrossRef]
- Franzoni, E.; Gentilini, C.; Santandrea, M.; Carloni, C. Effects of rising damp and salt crystallization cycles in FRCM-masonry interfacial debonding: Towards an accelerated laboratory test method. Constr. Build. Mater. 2018, 175, 225–238. [Google Scholar] [CrossRef]
- Carozzi, F.G.; Bellini, A.; D’Antino, T.; de Felice, G.; Focacci, F.; Hojdys, Ł.; Laghi, L.; Lanoye, E.; Micelli, F.; Panizza, M.; et al. Experimental investigation of tensile and bond properties of Carbon-FRCM composites for strengthening masonry elements. Compos. Part B Eng. 2017, 128, 100–119. [Google Scholar] [CrossRef]
- Koutas, L.N.; Tetta, Z.; Bournas, D.A.; Triantafillou, T.C. Strengthening of Concrete Structures with Textile Reinforced Mortars: State-of-the-Art Review. J. Compos. Constr. 2019, 23, 1–20. [Google Scholar] [CrossRef]
- ACI. 549.4R-20 Guide to Design and Construction of Externally Bonded Fabric-Reinforced Cementitious Matrix and Steel-Reinforced Grout Systems for Repair and Strengthening of Concrete Structures; American Concrete Institute: Farmington Hills, MI, USA, 2013. [Google Scholar]
- CNR. CNR-DT 215/2018 Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Existing Structures; National Research Council: Rome, Italy, 2018; Available online: https://www.cnr.it/en/node/12827 (accessed on 7 January 2021).
- CSLLPP. Linea Guida per la Identificazione, la Qualificazione ed il Controllo di Accettazione di Compositi Fibrorinforzati a Matrice Inorganica (FRCM) da Utilizzarsi per il Consolidamento Strutturale di Costruzioni Esistenti; Consiglio Superiore dei Lavori Pubblici: Rome, Italy, 2018; Available online: https://www.ruregold.com/wp-content/uploads/2019/01/linee-guida-frcm-2018.pdf (accessed on 7 January 2021). (In Italian)
- Ombres, L.; Verre, S. Flexural Strengthening of RC Beams with Steel-Reinforced Grout: Experimental and Numerical Investigation. J. Compos. Constr. 2019, 23, 04019035. [Google Scholar] [CrossRef]
- De Santis, S. Bond behaviour of Steel Reinforced Grout for the extrados strengthening of masonry vaults. Constr. Build. Mater. 2017, 150, 367–382. [Google Scholar] [CrossRef]
- Marcari, G.; Basili, M.; Vestroni, F. Experimental investigation of tuff masonry panels reinforced with surface bonded basalt textile-reinforced mortar. Compos. Part B Eng. 2017, 108, 131–142. [Google Scholar] [CrossRef]
- Caggegi, C.; Carozzi, F.G.; De Santis, S.; Fabbrocino, F.; Focacci, F.; Hojdys, Ł.; Lanoye, E.; Zuccarino, L. Experimental analysis on tensile and bond properties of PBO and aramid fabric reinforced cementitious matrix for strengthening masonry structures. Compos. Part B Eng. 2017, 127, 175–195. [Google Scholar] [CrossRef]
- D’Ambrisi, A.; Focacci, F.; Luciano, R.; Alecci, V.; De Stefano, M. Carbon-FRCM materials for structural upgrade of masonry arch road bridges. Compos. Part B Eng. 2015, 75, 355–366. [Google Scholar] [CrossRef]
- Arboleda, D. Fabric Reinforced Cementitious Matrix (FRCM) Composites for Infrastructure Strengthening and Rehabilitation: Characterization Methods. Ph.D. Thesis, University of Miami, Coral Gables, FL, USA, 2014; pp. 1–131. [Google Scholar]
- D’Antino, T.; Carozzi, F.G.; Colombi, P.; Poggi, C. Out-of-plane maximum resisting bending moment of masonry walls strengthened with FRCM composites. Compos. Struct. 2018, 202, 881–896. [Google Scholar] [CrossRef]
- Nobili, A. Durability assessment of impregnated Glass Fabric Reinforced Cementitious Matrix (GFRCM) composites in the alkaline and saline environments. Constr. Build. Mater. 2016, 105, 465–471. [Google Scholar] [CrossRef]
- Williams Portal, N.; Flansbjer, M.; Johannesson, P.; Malaga, K.; Lundgren, K. Tensile behaviour of textile reinforcement under accelerated ageing conditions. J. Build. Eng. 2016, 5, 57–66. [Google Scholar] [CrossRef]
- D’Antino, T.; Carloni, C.; Sneed, L.H.; Pellegrino, C. Matrix-fiber bond behavior in PBO FRCM composites: A fracture mechanics approach. Eng. Fract. Mech. 2014, 117, 94–111. [Google Scholar] [CrossRef]
- de Felice, G.; D’Antino, T.; De Santis, S.; Meriggi, P.; Roscini, F. Lessons Learned on the Tensile and Bond Behavior of Fabric Reinforced Cementitious Matrix (FRCM) Composites. Front. Built Environ. 2020, 6, 1–15. [Google Scholar] [CrossRef]
- Borri, A.; Castori, G.; Corradi, M. Shear behavior of masonry panels strengthened by high strength steel cords. Constr. Build. Mater. 2011, 25, 494–503. [Google Scholar] [CrossRef]
- Sneed, L.H.; D’Antino, T.; Carloni, C. Investigation of bond behavior of polyparaphenylene benzobisoxazole fiber-reinforced cementitious matrix composite-concrete interface. ACI Mater. J. 2014, 111, 569–580. [Google Scholar] [CrossRef]
- Calabrese, A.S.; D’Antino, T.; Colombi, P.; Poggi, C. Study of the influence of interface normal stresses on the bond behavior of FRCM composites using direct shear and modified beam tests. Constr. Build. Mater. 2020, 262, 120029. [Google Scholar] [CrossRef]
- Terreal Italia San Marco Vivo Red Bricks. Tech. Doc. Available online: https://www.sanmarco.it/scheda-prodotto.php?id-categoria=2&id-prodotto=36 (accessed on 3 November 2020).
- D’Antino, T.; Santandrea, M.; Carloni, C. Advances in Knowledge of the Fracture Properties of Cohesive Materials: Fired-Clay and Tuff Bricks. J. Eng. Mech. 2020, 146, 4020079. [Google Scholar] [CrossRef]
- FASSA BORTOLO MS 20, Malta cementizia fibrorinforzata per muratura ed intonaco, per interni ed esterni. Tech. Doc. 2019, 2–3. Available online: https://www.fassabortolo.it/it/prodotti/-/p/6/56/prodotti-tradizionali/ms-20-malta-cementizia-per-muratura-ed-intonaco-da-utilizzare-a-mano-per-interni-ed-esterni (accessed on 3 November 2020).
- Ruregold PBO-Mesh Gold 70/18 & PBO-MX GOLD MURATURA. Tech. Doc. 2019. Available online: https://www.ruregold.com/ (accessed on 3 November 2020).
- TCS B-STRUCTURA. Tech. Doc. 2020. Available online: https://www.tcscalce.it/en/prodotto/b-structura (accessed on 3 November 2020).
- Hausding, J.; Lorenz, E.; Ortlepp, R.; Lundahl, A.; Cherif, C. Application of stitch-bonded multi-plies made by using the extended warp knitting process: Reinforcements with symmetrical layer arrangement for concrete. J. Text. Inst. 2011, 102, 726–738. [Google Scholar] [CrossRef]
- Mazzucco, G.; D’Antino, T.; Pellegrino, C.; Salomoni, V. Three-dimensional finite element modeling of inorganic-matrix composite materials using a mesoscale approach. Compos. Part B Eng. 2018, 143, 75–85. [Google Scholar] [CrossRef]
- TCS Steel X800-A4. Tech. Doc. 2020, 1–3. Available online: https://www.tcscalce.it/en/prodotto/tcs-steel-x800-a4 (accessed on 3 November 2020).
- D’Ambrisi, A.; Feo, L.; Focacci, F. Experimental analysis on bond between PBO-FRCM strengthening materials and concrete. Compos. Part B Eng. 2013, 44, 524–532. [Google Scholar] [CrossRef]
- Askouni, P.D.; Papanicolaou, C.G. Experimental investigation of bond between glass textile reinforced mortar overlays and masonry: The effect of bond length. Mater. Struct. Constr. 2017, 50, 1–15. [Google Scholar] [CrossRef]
- Santandrea, M.; Focacci, F.; Mazzotti, C.; Ubertini, F.; Carloni, C. Determination of the interfacial cohesive material law for SRG composites bonded to a masonry substrate. Eng. Fail. Anal. 2020, 111, 104322. [Google Scholar] [CrossRef]
- Sika Sika MonoTop®-722 Mur. Tech. Doc. 2019, 1–4. Available online: https://ita.sika.com/it/edilizia/rinforzi-e-incollaggistrutturali/sistemi-antisfondellamentopersolai/sika-monotop-722mur.html (accessed on 3 November 2020).
- Carloni, C.; D’Antino, T.; Sneed, L.H.; Pellegrino, C. Role of the matrix layers in the stress-transfer mechanism of FRCM composites bonded to a concrete substrate. J. Eng. Mech. 2015, 141, 1–10. [Google Scholar] [CrossRef]
- D’Antino, T.; Colombi, P.; Carloni, C.; Sneed, L.H. Estimation of a matrix-fiber interface cohesive material law in FRCM-concrete joints. Compos. Struct. 2018, 193, 103–112. [Google Scholar] [CrossRef]
- Colombi, P.; D’Antino, T. Analytical assessment of the stress-transfer mechanism in FRCM composites. Compos. Struct. 2019, 220, 961–970. [Google Scholar] [CrossRef]
- Calabrese, A.S.; Colombi, P.; D’Antino, T. Analytical solution of the bond behavior of FRCM composites using a rigid-softening cohesive material law. Compos. Part B Eng. 2019, 174, 107051. [Google Scholar] [CrossRef]
- Wu, Z.; Yuan, H.; Niu, H.; Zhishen, W.; Hong, Y.; Hedong, N. Stress transfer and fracture propagation in different kinds of adhesive joints. J. Eng. Mech. 2002, 128, 562–573. [Google Scholar] [CrossRef]
- Dai, J.; Ueda, T.; Sato, Y. Development of the Nonlinear Bond Stress–Slip Model of Fiber Reinforced Plastics Sheet–Concrete Interfaces with a Simple Method. J. Compos. Constr. 2005, 9, 52–62. [Google Scholar] [CrossRef]
- Focacci, F.; Carloni, C. Periodic variation of the transferable load at the FRP-masonry interface. Compos. Struct. 2015, 129, 90–100. [Google Scholar] [CrossRef]
- Yuan, H.; Teng, J.G.; Seracino, R.; Wu, Z.S.; Yao, J. Full-range behavior of FRP-to-concrete bonded joints. Eng. Struct. 2004, 26, 553–565. [Google Scholar] [CrossRef]
- Dai, J.; Ueda, T.; Sato, Y. Unified analytical approaches for determining shear bond characteristics of FRP-concrete interfaces through pullout tests. J. Adv. Concr. Technol. 2006, 4, 133–145. [Google Scholar] [CrossRef]
- Carrara, P.; Ferretti, D. A finite-difference model with mixed interface laws for shear tests of FRP plates bonded to concrete. Compos. Part B Eng. 2013, 54, 329–342. [Google Scholar] [CrossRef]







| Composite | Textile Properties | Matrix Properties | |||||||
|---|---|---|---|---|---|---|---|---|---|
| d* [mm] | b* [mm] | t* [mm] | ff [MPa] | Ef [GPa] | εf | fc [MPa] | fr [MPa] | Ec† [GPa] | |
| Carbon FRCM | - | 5 | 0.094 | 1944 | 203 | 0.0095 | 25.0 | 6.1 | >7.5 † |
| PBO FRCM | - | 5 | 0.092 | 3014 | 206 | 0.0145 | 25.0 | 6.2 | >7.5 † |
| Glass FRCM | 1.11 | - | - | 874 | 65 | 0.0134 | 22.0 | 6.0 | ~7.6 † |
| SRG † | 1.01 | - | - | >2000 | 210 | - | 10.0 | - | - |
| Specimen Name | P* [kN] | [kN] | σ* [MPa] | FM | |||
|---|---|---|---|---|---|---|---|
| DS_300_50_C_1 | 2.42 | 2.37 (8.70) | 1030 | 1010 (8.70) | 48.4 | 47.5 (8.70) | MDmsDmf |
| DS_300_50_C_2 | 2.46 | 1047 | 49.2 | Dmf | |||
| DS_300_50_C_3 | 2.58 | 1098 | 51.6 | Dmf | |||
| DS_300_50_C_4 | 2.03 | 864 | 40.6 | Dmf | |||
| DS_300_50_P_1 | 5.67 | 4.80 (13.68) | 2465 | 2086 (13.68) | 113.4 | 96.0 (13.68) | Dmf |
| DS_300_50_P_2 | 4.66 | 2026 | 93.2 | Dmf | |||
| DS_300_50_P_3 | 5.01 | 2178 | 100.2 | Dmf | |||
| DS_300_50_P_4 | 3.85 | 1674 | 77.0 | Dmf | |||
| DS_300_50_G_1 | 1.77 | 1.85 (6.43) | 617 | 643 (6.43) | 35.4 | 36.9 (6.43) | MDmfR |
| DS_300_50_G_2 | 1.69 | 589 | 33.8 | MDmfR | |||
| DS_300_50_G_3 | 1.95 | 679 | 39.0 | MDmfR | |||
| DS_300_50_G_4 | 1.97 | 686 | 39.4 | MDmfR | |||
| DS_300_50_S_1 | 4.36 | 5.14 (9.47) | 778 | 916 (9.47) | 87.2 | 102.7 (9.47) | Dms |
| DS_300_50_S_2 | 5.28 | 942 | 105.6 | Dms | |||
| DS_300_50_S_3 | 5.2 | 928 | 104 | MRDmf | |||
| DS_300_50_S_4 | 5.7 | 1017 | 114 | MRDmf |
| Elastic stage (i) | |
| ; ; | |
| Elastic-softening stage (ii) | |
| Elastic-softening-debonding stage (iii) | |
| Softening-debonding stage (iv) | |
| Fully debonded stage (v) | |
| s0 [mm] | τmax [MPa] | sf [mm] | τf [MPa] | GF [N/mm3] | leff [Equation (3)] [mm] | l [Equation (4)] [mm] | |
|---|---|---|---|---|---|---|---|
| Carbon FRCM | 0.12 | 0.54 | 0.36 | 0.04 | 0.102 | 176 | 70 |
| PBO FRCM | 0.30 | 0.80 | 0.98 | 0.07 | 0.416 | 203 | 86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Lami, K.; D’Antino, T.; Colombi, P. Study of the Bond Capacity of FRCM- and SRG-Masonry Joints. CivilEng 2021, 2, 68-86. https://doi.org/10.3390/civileng2010005
Al-Lami K, D’Antino T, Colombi P. Study of the Bond Capacity of FRCM- and SRG-Masonry Joints. CivilEng. 2021; 2(1):68-86. https://doi.org/10.3390/civileng2010005
Chicago/Turabian StyleAl-Lami, Karrar, Tommaso D’Antino, and Pierluigi Colombi. 2021. "Study of the Bond Capacity of FRCM- and SRG-Masonry Joints" CivilEng 2, no. 1: 68-86. https://doi.org/10.3390/civileng2010005
APA StyleAl-Lami, K., D’Antino, T., & Colombi, P. (2021). Study of the Bond Capacity of FRCM- and SRG-Masonry Joints. CivilEng, 2(1), 68-86. https://doi.org/10.3390/civileng2010005






