Coumarin 153 Dynamics in Ethylammonium Nitrate: The Effects of Dilution with Methanol
Abstract
1. Introduction
2. Materials and Methods
3. Results
3.1. Bulk Properties-Viscosity
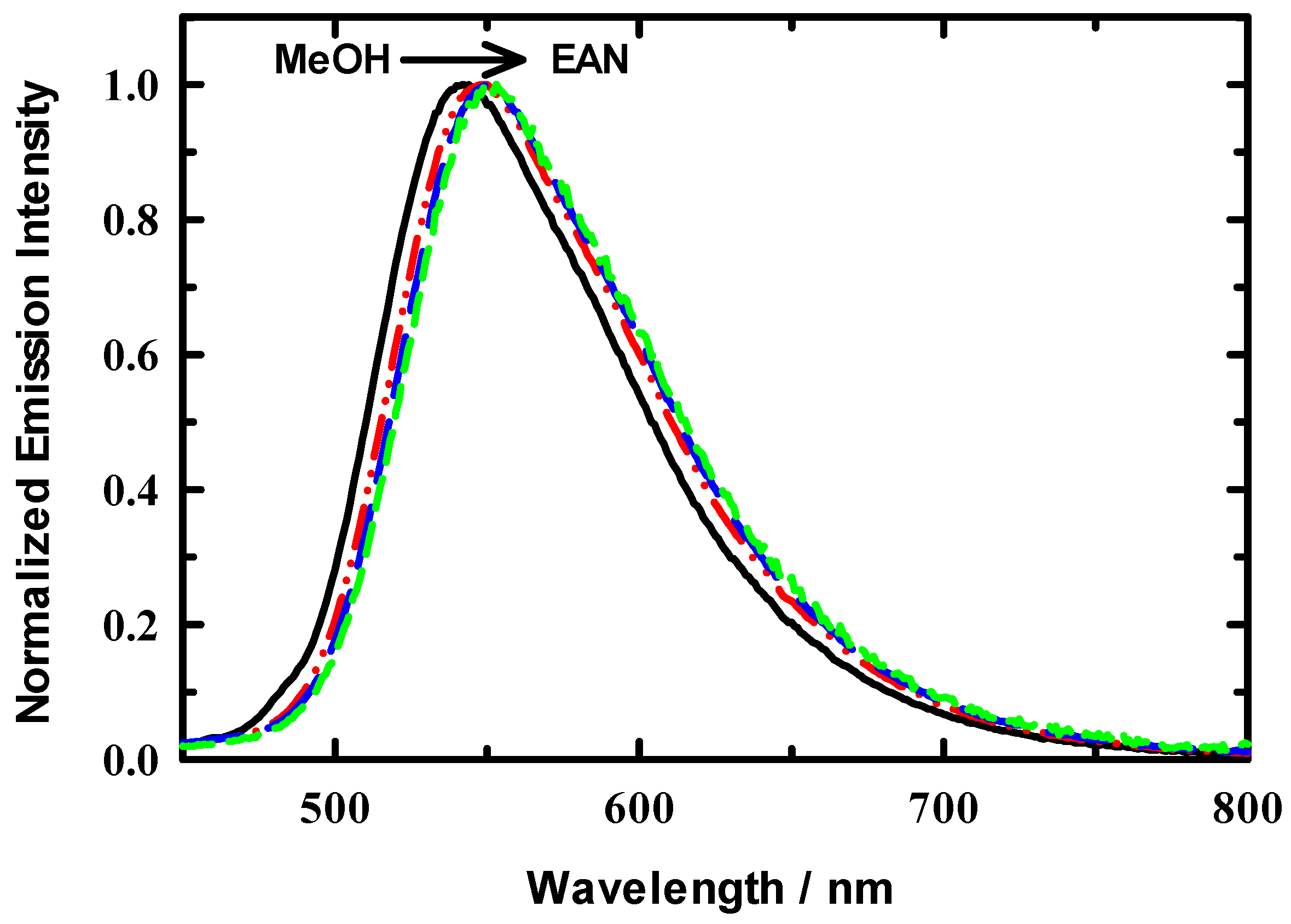
3.2. Steady State Spectroscopy
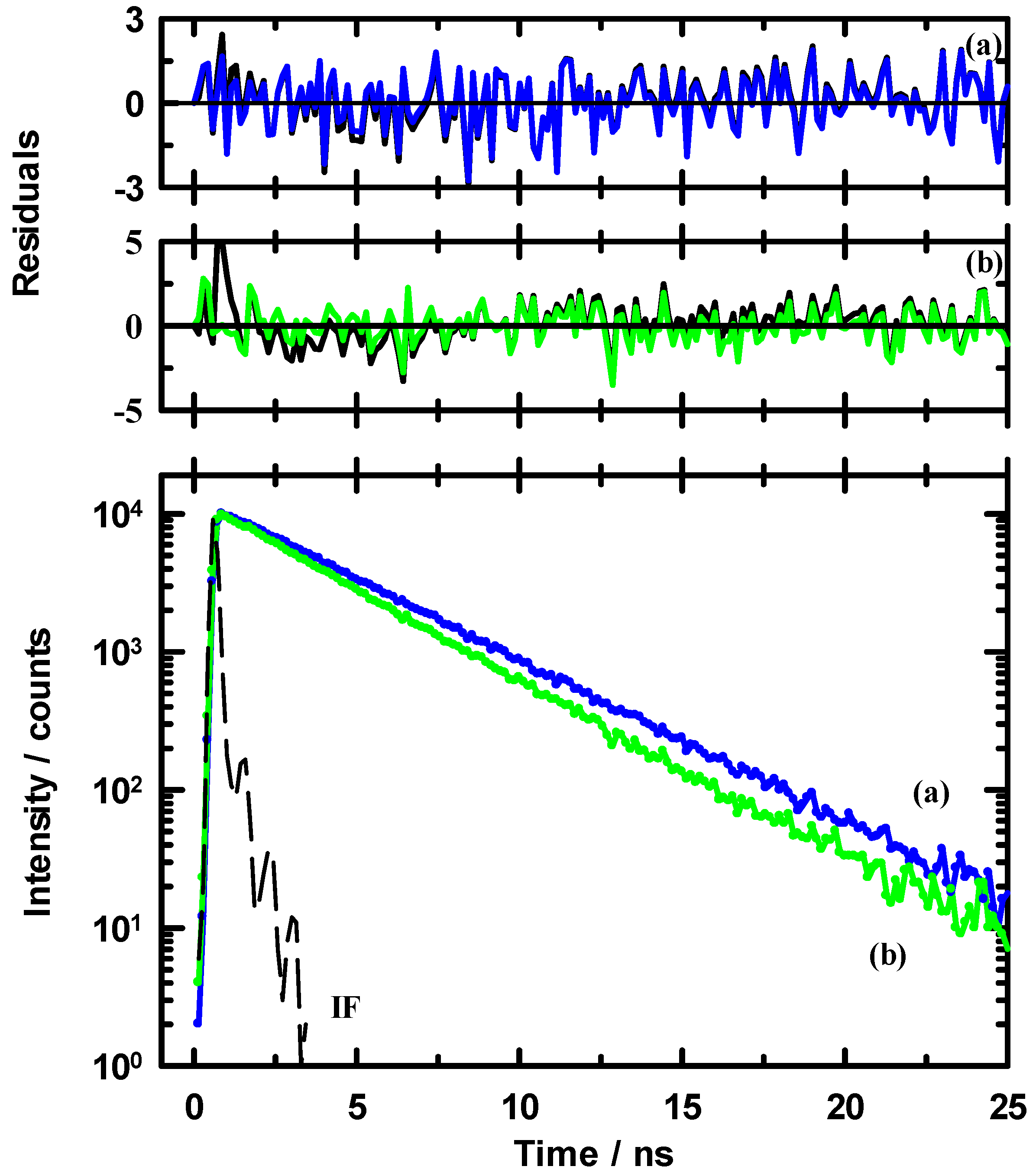
3.3. Time-Resolved Spectroscopy
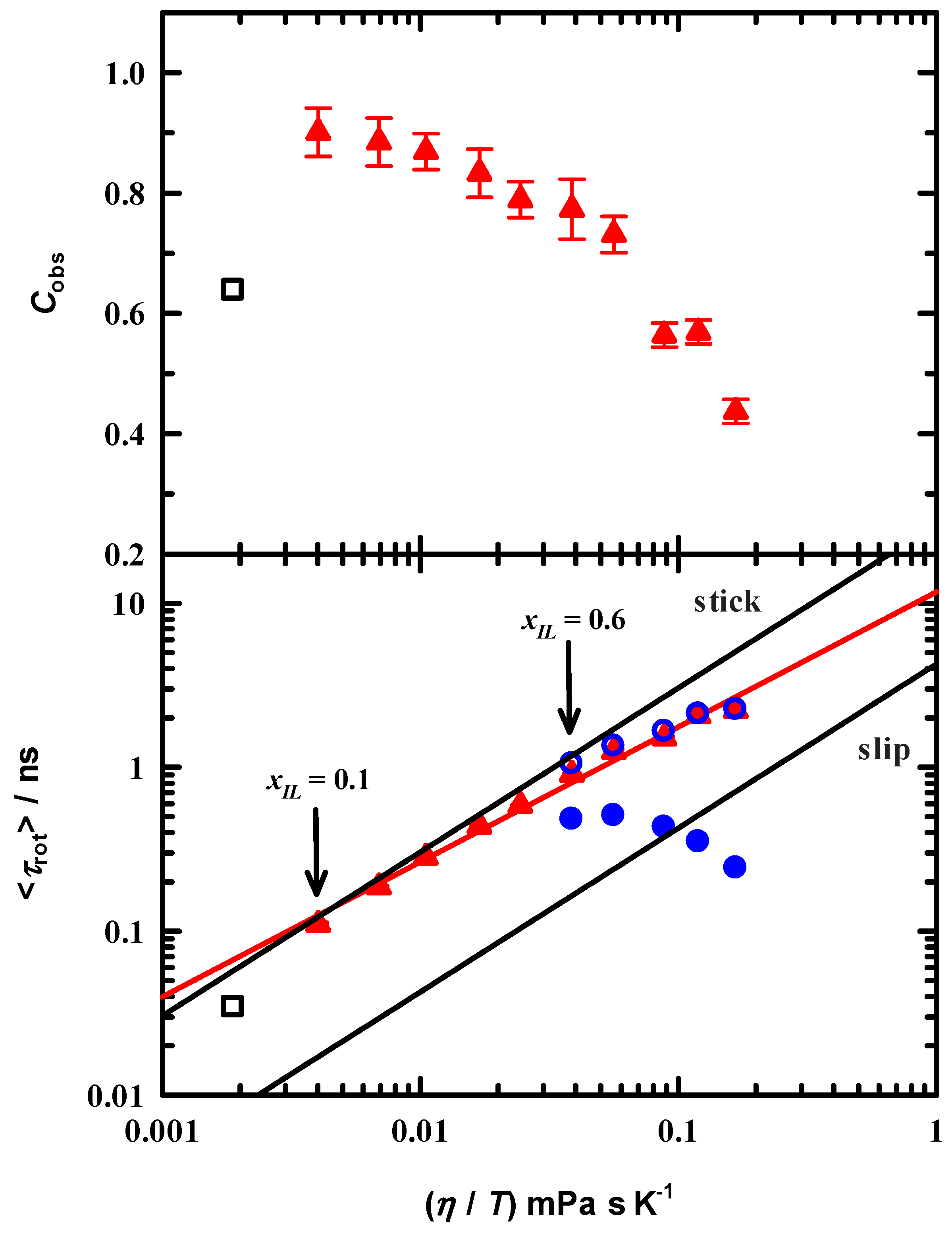
3.4. Rotational Dynamics
4. Discussion
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Welton, T. Ionic liquids: A brief history. Biophys. Rev. 2018, 10, 691–706. [Google Scholar] [CrossRef]
- Lei, Z.; Chen, B.; Koo, Y.-M.; MacFarlane, D.R. Introduction: Ionic Liquids. Chem. Rev. 2017, 117, 6633–6635. [Google Scholar] [CrossRef]
- Greaves, T.L.; Drummond, C.J. Protic Ionic Liquids: Evolving Structure–Property Relationships and Expanding Applications. Chem. Rev. 2015, 115, 11379–11448. [Google Scholar] [CrossRef]
- Castner, E.W.; Margulis, C.J.; Maroncelli, M.; Wishart, J.F. Ionic Liquids: Structure and Photochemical Reactions. Ann. Rev. Phys. Chem. 2011, 62, 85–105. [Google Scholar] [CrossRef] [PubMed]
- Edward, W.; Castner, J.; Wishart, J.F. Spotlight on ionic liquids. J. Chem. Phys. 2010, 132, 120901. [Google Scholar] [CrossRef]
- Greaves, T.L.; Drummond, C.J. Protic Ionic Liquids: Properties and Applications. Chem. Rev. 2008, 108, 206–237. [Google Scholar] [CrossRef] [PubMed]
- Mariani, A.; Caminiti, R.; Ramondo, F.; Salvitti, G.; Mocci, F.; Gontrani, L. Inhomogeneity in Ethylammonium Nitrate–Acetonitrile Binary Mixtures: The Highest “Low q Excess” Reported to Date. J. Phys. Chem. Lett. 2017, 8, 3512–3522. [Google Scholar] [CrossRef] [PubMed]
- Usula, M.; Matteoli, E.; Leonelli, F.; Mocci, F.; Marincola, F.C.; Gontrani, L.; Porcedda, S. Thermo-physical Properties of Ammonium-Based Ionic Liquid + N-methyl-2-pyrrolidone Mixtures at 298.15 K. Fluid Phase Equilib. 2014, 383, 49–54. [Google Scholar] [CrossRef]
- Docampo-Álvarez, B.; Gómez-González, V.; Méndez-Morales, T.; Carrete, J.; Rodríguez, J.R.; Cabeza, Ó.; Gallego, L.J.; Varela, L.M. Mixtures of protic ionic liquids and molecular cosolvents: A molecular dynamics simulation. J. Chem. Phys. 2014, 140, 214502. [Google Scholar] [CrossRef] [PubMed]
- Mariani, A.; Bonomo, M.; Wu, B.; Centrella, B.; Dini, D.; Castner, E.W.; Gontrani, L. Intriguing transport dynamics of ethylammonium nitrate–acetonitrile binary mixtures arising from nano-inhomogeneity. Phys. Chem. Chem. Phys. 2017, 19, 27212–27220. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.-P.; Fan, W.-H.; Roy, S.; Mazur, K.; Nazet, A.; Buchner, R.; Bonn, M.; Hunger, J. Ionic Liquids: Not only Structurally but also Dynamically Heterogeneous. Angew. Chem. Int. Ed. 2015, 54, 687–690. [Google Scholar] [CrossRef]
- Zarrougui, R.; Dhahbi, M.; Lemordant, D. Transport and Thermodynamic Properties of Ethylammonium Nitrate—Water Binary Mixtures: Effect of Temperature and Composition. J. Solution Chem. 2015, 44, 686–702. [Google Scholar] [CrossRef]
- Chagnes, A.; Tougui, A.; Carré, B.; Ranganathan, N.; Lemordant, D. Abnormal Temperature Dependence of the Viscosity of Ethylammonium Nitrate–Methanol Ionic Mixtures. J. Solution Chem. 2004, 33, 247–255. [Google Scholar] [CrossRef]
- Russina, O.; Mariani, A.; Caminiti, R.; Triolo, A. Structure of a Binary Mixture of Ethylammonium Nitrate and Methanol. J. Solution Chem. 2015, 44, 669–685. [Google Scholar] [CrossRef]
- Yalcin, D.; Christofferson, A.J.; Drummond, C.J.; Greaves, T.L. Solvation properties of protic ionic liquid—Molecular solvent mixtures. Phys. Chem. Chem. Phys. 2020, 22, 10995–11011. [Google Scholar] [CrossRef]
- Rumble, C.A.; Uitvlugt, C.; Conway, B.; Maroncelli, M. Solute Rotation in Ionic Liquids: Size, Shape, and Electrostatic Effects. J. Phys. Chem. B 2017, 121, 5094–5109. [Google Scholar] [CrossRef]
- Araque, J.C.; Yadav, S.K.; Shadeck, M.; Maroncelli, M.; Margulis, C.J. How Is Diffusion of Neutral and Charged Tracers Related to the Structure and Dynamics of a Room-Temperature Ionic Liquid? Large Deviations from Stokes—Einstein Behavior Explained. J. Phys. Chem. B 2015, 119, 7015–7029. [Google Scholar] [CrossRef]
- Usui, K.; Hunger, J.; Bonn, M.; Sulpizi, M. Dynamical heterogeneities of rotational motion in room temperature ionic liquids evidenced by molecular dynamics simulations. J. Chem. Phys. 2018, 148, 193811. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Zhou, G.; Li, Y.; Yang, Z.; Shi, M.; Wang, X.; Chen, X.; Zhang, F.; Li, W. Molecular Dynamics Simulations of Temperature-Dependent Structures and Dynamics of Ethylammonium Nitrate Protic Ionic Liquid: The Role of Hydrogen Bond. Chem. Phys. 2016, 472, 105–111. [Google Scholar] [CrossRef]
- Mariani, A.; Russina, O.; Caminiti, R.; Triolo, A. Structural Organization in a Methanol:Ethylammonium Nitrate (1:4) Mixture: A Joint X-ray/Neutron Diffraction and Computational Study. J. Mol. Liq. 2015, 212, 947–956. [Google Scholar] [CrossRef]
- Barra, K.M.; Sabatini, R.P.; McAtee, Z.P.; Heitz, M.P. Solvation and Rotation Dynamics in the Trihexyl(tetradecyl)phosphonium Chloride Ionic Liquid/Methanol Cosolvent System. J. Phys. Chem. B 2014, 118, 12979–12992. [Google Scholar] [CrossRef]
- Das, S.K.; Sarkar, M. Steady-state and time-resolved fluorescence behavior of coumarin-153 in a hydrophobic ionic liquid and ionic liquid–toluene mixture. J. Mol. Liq. 2012, 165, 38–43. [Google Scholar] [CrossRef]
- Das, S.K.; Sarkar, M. Solvation and rotational relaxation of coumarin 153 and 4-aminophthalimide in a new hydrophobic ionic liquid: Role of N–H…F interaction on solvation dynamics. Chem. Phys. Lett. 2011, 515, 23–28. [Google Scholar] [CrossRef]
- Ito, N.; Arzhantsev, S.; Heitz, M.; Maroncelli, M. Solvation Dynamics and Rotation of Coumarin 153 in Alkylphosphonium Ionic Liquids. J. Phys. Chem. B 2004, 108, 5771–5777. [Google Scholar] [CrossRef]
- Arzhantsev, S.; Ito, N.; Heitz, M.; Maroncelli, M. Solvation Dynamics of Coumarin 153 in Several Classes of Ionic Liquids: Cation Dependence of the Ultrafast Component. Chem. Phys. Lett. 2003, 381, 278–286. [Google Scholar] [CrossRef]
- Kashyap, H.K.; Biswas, R. Solvation Dynamics of Dipolar Probes in Dipolar Room Temperature Ionic Liquids: Separation of Ion−Dipole and Dipole−Dipole Interaction Contributions. J. Phys. Chem. B 2010, 114, 254–268. [Google Scholar] [CrossRef]
- Daschakraborty, S.; Ranjit, B. Stokes Shift Dynamics in (Ionic Liquid + Polar Solvent) Binary Mixtures: Composition Dependence. J. Phys. Chem. B 2011, 115, 4011–4024. [Google Scholar] [CrossRef] [PubMed]
- Daschakraborty, S.; Biswas, R. Composition Dependent Stokes Shift Dynamics in Binary Mixtures of 1-Butyl-3-methylimidazolium Tetrafluoroborate with Water and Acetonitrile: Quantitative Comparison between Theory and Complete Measurements. J. Phys. Chem. B 2014, 118, 1327–1339. [Google Scholar] [CrossRef]
- Pramanik, R.; Rao, V.G.; Sarkar, S.; Ghatak, C.; Setua, P.; Sarkar, N. To Probe the Interaction of Methanol and Acetonitrile with the Ionic Liquid N,N,N-Trimethyl-N-propyl Ammonium Bis(trifluoromethanesulfonyl) Imide at Different Temperatures by Solvation Dynamics Study. J. Phys. Chem. B 2009, 113, 8626–8634. [Google Scholar] [CrossRef]
- Horng, M.L.; Gardecki, J.A.; Maroncelli, M. Rotational Dynamics of Coumarin 153: Time-Dependent Friction, Dielectric Friction, and Other Nonhydrodynamic Effects. J. Phys. Chem. A 1997, 101, 1030–1047. [Google Scholar] [CrossRef]
- Hayes, R.; Imberti, S.; Warr, G.G.; Atkin, R. Amphiphilicity determines nanostructure in protic ionic liquids. Phys. Chem. Chem. Phys. 2011, 13, 3237–3247. [Google Scholar] [CrossRef]
- Dasari, S.; Mallik, B.S. Nondiffusive Rotational Jump Dynamics in Ethyl Ammonium Nitrate. J. Phys. Chem. B 2018, 122, 9738–9746. [Google Scholar] [CrossRef] [PubMed]
- Hunger, J.; Sonnleitner, T.; Liu, L.; Buchner, R.; Bonn, M.; Bakker, H.J. Hydrogen-Bond Dynamics in a Protic Ionic Liquid: Evidence of Large-Angle Jumps. J. Phys. Chem. Lett. 2012, 3, 3034–3038. [Google Scholar] [CrossRef] [PubMed]
- Kobrak, M.N. Characterization of the Solvation Dynamics of an Ionic Liquid via Molecular Dynamics Simulation. J. Chem. Phys. 2006, 125, 064502. [Google Scholar] [CrossRef]
- Samanta, A. Solvation Dynamics in Ionic Liquids: What We Have Learned from the Dynamic Fluorescence Stokes Shift Studies. J. Phys. Chem. Lett. 2010, 1, 1557–1562. [Google Scholar] [CrossRef]
- Schroer, W.; Triolo, A.; Russina, O. Nature of Mesoscopic Organization in Protic Ionic Liquid–Alcohol Mixtures. J. Phys. Chem. B 2016, 120, 2638–2643. [Google Scholar] [CrossRef]
- Kanzaki, R.; Mitsugi, T.; Fukuda, S.; Fujii, K.; Takeuchi, M.; Soejima, Y.; Takamuku, T.; Yamaguchi, T.; Umebayashi, Y.; Ishiguro, S.-I. Ion-ion interaction in room temperature ionic liquid 1-ethyl-3-methylimidazolium tetrafluoroborate studied by large angle X-ray scattering experiment and molecular dynamics simulations. J. Mol. Liq. 2009, 147, 77–82. [Google Scholar] [CrossRef]
- Paul, A.; Samanta, A. Effect of Nonpolar Solvents on the Solute Rotation and Solvation Dynamics in an Imidazolium Ionic Liquid. J. Phys. Chem. B 2008, 112, 947–953. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarty, D.; Chakraborty, A.; Seth, D.; Sarkar, N. Effect of Water, Methanol, and Acetonitrile on Solvent Relaxation and Rotational Relaxation of Coumarin 153 in Neat 1-Hexyl-3-methylimidazolium Hexafluorophosphate. J. Phys. Chem. A 2005, 109, 1764–1769. [Google Scholar] [CrossRef]
- Overbeck, V.; Schröder, H.; Bonsa, A.-M.; Neymeyr, K.; Ludwig, R. Insights into the translational and rotational dynamics of cations and anions in protic ionic liquids by means of NMR fast-field-cycling relaxometry. Phys. Chem. Chem. Phys. 2021, 23, 2663–2675. [Google Scholar] [CrossRef] [PubMed]
- Overbeck, V.; Appelhagen, A.; Rößler, R.; Niemann, T.; Ludwig, R. Rotational correlation times, diffusion coefficients and quadrupolar peaks of the protic ionic liquid ethylammonium nitrate by means of 1H fast field cycling NMR relaxometry. J. Mol. Liq. 2021, 322, 114983. [Google Scholar] [CrossRef]
- LaRocca, M.M.; Baker, G.A.; Heitz, M.P. Assessing rotation and solvation dynamics in ethaline deep eutectic solvent and its solutions with methanol. J. Chem. Phys. 2021, 155, 034505. [Google Scholar] [CrossRef] [PubMed]
- Johnson, C.A.; Parker, A.W.; Donaldson, P.M.; Garrett-Roe, S. An ultrafast vibrational study of dynamical heterogeneity in the protic ionic liquid ethyl-ammonium nitrate. I. Room temperature dynamics. J. Chem. Phys. 2021, 154, 134502. [Google Scholar] [CrossRef] [PubMed]
- Conway, B.; Uitvlugt, C.; Maroncelli, M. Simulations of 1-Butyl-3-methylimidazolium Tetrafluoroborate + Acetonitrile Mixtures: Force-Field Validation and Frictional Characteristics. J. Phys. Chem. B 2018, 122, 7385–7393. [Google Scholar] [CrossRef] [PubMed]
- Horng, M.L.; Gardecki, J.A.; Papazyan, A.; Maroncelli, M. Subpicosecond Measurements of Polar Solvation Dynamics: Coumarin 153 Revisited. J. Phys. Chem. 1995, 99, 17311–17337. [Google Scholar] [CrossRef]
- Reynolds, L.; Gardecki, J.A.; Frankland, S.J.V.; Horng, M.L.; Maroncelli, M. Dipole Solvation in Nondipolar Solvents: Experimental Studies of Reorganization Energies and Solvation Dynamics. J. Phys. Chem. 1996, 100, 10337–10354. [Google Scholar] [CrossRef]
- Kundu, N.; Roy, A.; Dutta, R.; Sarkar, N. Translational and Rotational Diffusion of Two Differently Charged Solutes in Ethylammonium Nitrate–Methanol Mixture: Does the Nanostructure of the Amphiphiles Influence the Motion of the Solute? J. Phys. Chem. B 2016, 120, 5481–5490. [Google Scholar] [CrossRef] [PubMed]
- Russina, O.; Schroer, W.; Triolo, A. Mesoscopic Structural and Dynamic Organization in Ionic Liquids. J. Mol. Liq. 2015, 210, 161–163. [Google Scholar] [CrossRef]
- Russina, O.; Sferrazza, A.; Caminiti, R.; Triolo, A. Amphiphile Meets Amphiphile: Beyond the Polar–Apolar Dualism in Ionic Liquid/Alcohol Mixtures. J. Phys. Chem. Lett. 2014, 5, 1738–1742. [Google Scholar] [CrossRef]
- McAtee, Z.P.; Heitz, M.P. Density, Viscosity and Excess Properties in the Trihexyltetradecylphosphonium Chloride Ionic Liquid/Methanol Cosolvent System. J. Chem. Thermodyn. 2016, 93, 34–44. [Google Scholar] [CrossRef]
- Jin, H.; Baker, G.A.; Arzhantsev, S.; Dong, J.; Maroncelli, M. Solvation and Rotational Dynamics of Coumarin 153 in Ionic Liquids: Comparisons to Conventional Solvents. J. Phys. Chem. B 2007, 111, 7291–7302. [Google Scholar] [CrossRef]
- Chakraborty, A.; Seth, D.; Chakrabarty, D.; Setua, P.; Sarkar, N. Dynamics of Solvent and Rotational Relaxation of Coumarin 153 in Room-Temperature Ionic Liquid 1-Butyl-3-methylimidazolium Hexafluorophosphate Confined in Brij-35 Micelles: A Picosecond Time-Resolved Fluorescence Spectroscopic Study. J. Phys. Chem. A 2005, 109, 11110–11116. [Google Scholar] [CrossRef]
- Ingram, J.A.; Moog, R.S.; Ito, N.; Biswas, R.; Maroncelli, M. Solute Rotation and Solvation Dynamics in a Room-Temperature Ionic Liquid. J. Phys. Chem. B 2003, 107, 5926–5932. [Google Scholar] [CrossRef]
- Bose, S.; Adhikary, R.; Mukherjee, P.; Song, X.; Petrich, J.W. Considerations for the Construction of the Solvation Correlation Function and Implications for the Interpretation of Dielectric Relaxation in Proteins. J. Phys. Chem. B 2009, 113, 11061–11068. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Funston, A.M.; Fadeeva, T.A.; Wishart, J.F.; Castner, E.W. Fluorescence Probing of Temperature-Dependent Dynamics and Friction in Ionic Liquid Local Environments. J. Phys. Chem. B 2007, 111, 4963–4977. [Google Scholar] [CrossRef]
- Hu, C.M.; Zwanzig, R. Rotational friction coefficients for spheroids with the slipping boundary condition. J. Chem. Phys. 1974, 60, 4354–4357. [Google Scholar] [CrossRef]
- Zwanzig, R.; Harrison, A.K. Modifications of the Stokes–Einstein formula. J. Chem. Phys. 1985, 83, 5861–5862. [Google Scholar] [CrossRef]
- Jiang, Y.; Nadolny, H.; Kashammer, S.; Weibels, S.; Schroer, W.; Weingartner, H. The ion speciation of ionic liquids in molecular solvents of low and medium polarity. Faraday Discuss. 2012, 154, 391–407. [Google Scholar] [CrossRef]
- Hu, X.; Lin, Q.; Gao, J.; Wu, Y.; Zhang, Z. Anion–cation and ion–solvent interaction of some typical ionic liquids in solvents with different dielectric constant. Chem. Phys. Lett. 2011, 516, 35–39. [Google Scholar] [CrossRef]
- Annapureddy, H.V.; Dang, L.X. Pairing mechanism among ionic liquid ions in aqueous solutions: A molecular dynamics study. J. Phys. Chem. B 2013, 117, 8555–8560. [Google Scholar] [CrossRef] [PubMed]
- Yee, P.; Shah, J.K.; Maginn, E.J. State of Hydrophobic and Hydrophilic Ionic Liquids in Aqueous Solutions: Are the Ions Fully Dissociated? J. Phys. Chem. B 2013, 117, 12556–12566. [Google Scholar] [CrossRef] [PubMed]
- Hunger, J.; Stoppa, A.; Buchner, R.; Hefter, G. From Ionic Liquid to Electrolyte Solution: Dynamics of 1-N-Butyl-3-N-methylimidazolium Tetrafluoroborate/Dichloromethane Mixtures. J. Phys. Chem. B 2008, 112, 12913–12919. [Google Scholar] [CrossRef]
- Hemmateenejad, B.; Safavi, A.; Dorostkar, S. Aggregation of imidazolium based ionic liquids in binary methanol–water solvents: A linear solvation free energy relationship study. J. Mol. Liq. 2011, 160, 35–39. [Google Scholar] [CrossRef]
- Mukherjee, P.; Crank, J.A.; Sharma, P.S.; Wijeratne, A.B.; Adhikary, R.; Bose, S.; Armstrong, D.W.; Petrich, J.W. Dynamic Solvation in Phosphonium Ionic Liquids: Comparison of Bulk and Micellar Systems and Considerations for the Construction of the Solvation Correlation Function, C(t). J. Phys. Chem. B 2008, 112, 3390–3396. [Google Scholar] [CrossRef] [PubMed]
- Hayes, R.; Warr, G.G.; Atkin, R. Structure and Nanostructure in Ionic Liquids. Chem. Rev. 2015, 115, 6357–6426. [Google Scholar] [CrossRef]
- Song, X.; Hamano, H.; Minofar, B.; Kanzaki, R.; Fujii, K.; Kameda, Y.; Kohara, S.; Watanabe, M.; Ishiguro, S.-I.; Umebayashi, Y. Structural Heterogeneity and Unique Distorted Hydrogen Bonding in Primary Ammonium Nitrate Ionic Liquids Studied by High-Energy X-ray Diffraction Experiments and MD Simulations. J. Phys. Chem. B 2012, 116, 2801–2813. [Google Scholar] [CrossRef]
- Das, A.; Biswas, R. Dynamic Solvent Control of a Reaction in Ionic Deep Eutectic Solvents: Time-Resolved Fluorescence Measurements of Reactive and Nonreactive Dynamics in (Choline Chloride + Urea) Melts. J. Phys. Chem. B 2015, 119, 10102–10113. [Google Scholar] [CrossRef]
- Hossain, S.S.; Paul, S.; Samanta, A. Liquid Structure and Dynamics of Tetraalkylammonium Bromide-Based Deep Eutectic Solvents: Effect of Cation Chain Length. J. Phys. Chem. B 2019, 123, 6842–6850. [Google Scholar] [CrossRef]
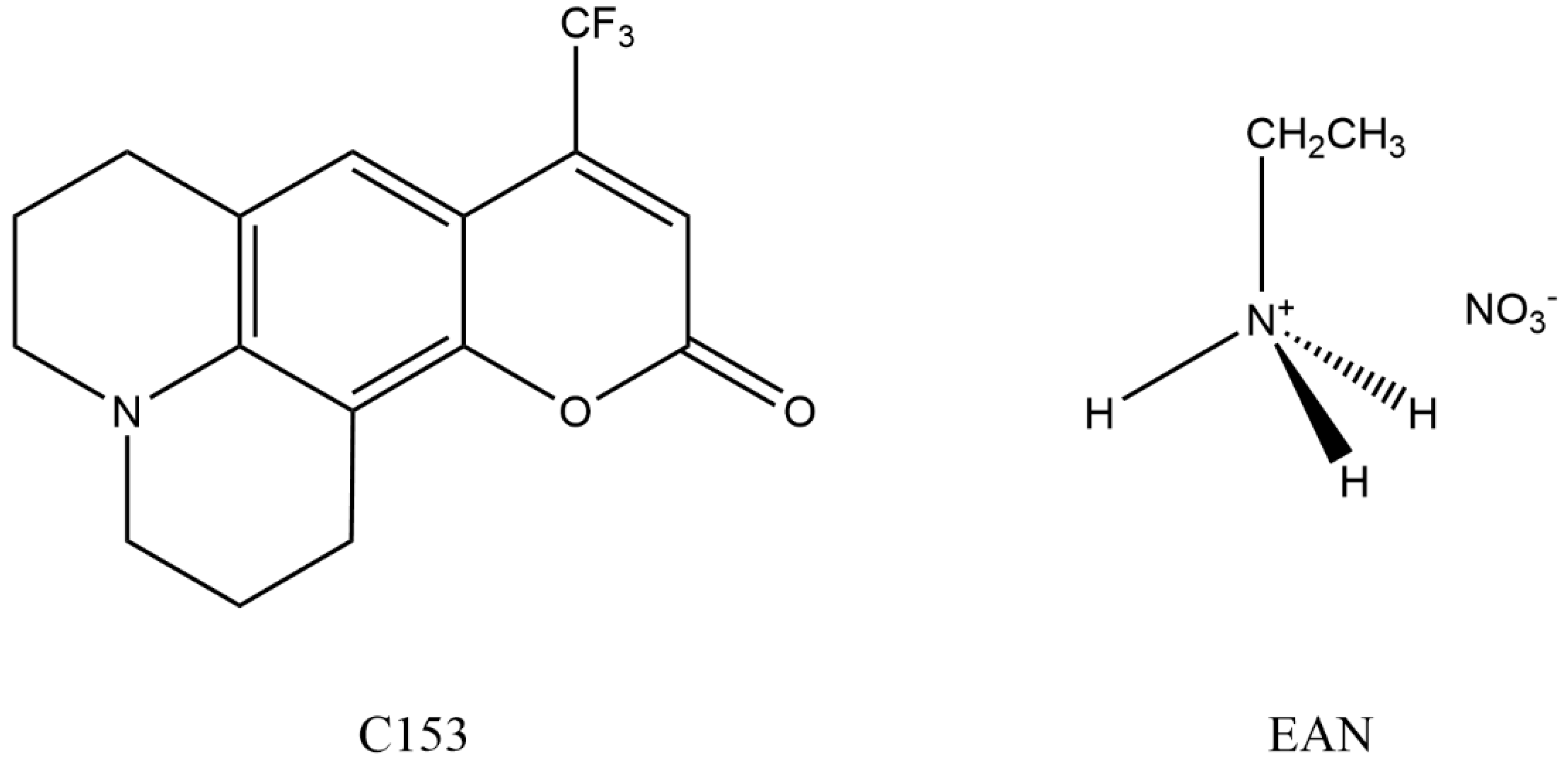




| xIL | f1 | f2 | τ1/ns | τ2/ns | χr2 | |
|---|---|---|---|---|---|---|
| 0 | 3.91 ± 0.05 | 3.91 | ||||
| 0.1 | 0.031 ± 0.005 | 0.968 ± 0.006 | 2.09 ± 0.36 | 3.70 ± 0.01 | 1.1 | 3.66 |
| 0.2 | 0.448 ± 0.024 | 0.551 ± 0.013 | 3.11 ± 0.15 | 3.92 ± 0.02 | 1.1 | 3.56 |
| 0.3 | 0.704 ± 0.089 | 0.295 ± 0.021 | 3.24 ± 0.33 | 3.99 ± 0.04 | 1.2 | 3.47 |
| 0.4 | 0.589 ± 0.018 | 0.410 ± 0.008 | 3.04 ± 0.07 | 3.89 ± 0.03 | 1.1 | 3.39 |
| 0.5 | 0.118 ± 0.016 | 0.881 ± 0.014 | 2.28 ± 0.30 | 3.49 ± 0.01 | 1.1 | 3.35 |
| 0.6 | 0.021 ± 0.001 | 0.978 ± 0.002 | 0.56 ± 0.03 | 3.35 ± 0.01 | 1.1 | 3.30 |
| 0.7 | 0.018 ± 0.001 | 0.981 ± 0.002 | 0.53 ± 0.04 | 3.31 ± 0.01 | 1.1 | 3.26 |
| 0.8 | 0.022 ± 0.001 | 0.977 ± 0.002 | 0.54 ± 0.03 | 3.28 ± 0.01 | 1.1 | 3.22 |
| 0.9 | 0.019 ± 0.001 | 0.980 ± 0.001 | 0.44 ± 0.01 | 3.24 ± 0.01 | 1.2 | 3.19 |
| 1 | 0.028 ± 0.002 | 0.971 ± 0.002 | 0.70 ± 0.05 | 3.25 ± 0.01 | 1.2 | 3.19 |
| xIL | η/mPa⋅s | r0 | f1a | τ1/ns | τ2/ns | χr2 | Cobs | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0.54 | 1.00 b | 0.04 ± 0.01 | 0.61 ± 0.09 | ||||
| 0.1 | 1.2 | 0.28 | 1.00 ± 0.04 | 0.11 ± 0.01 | 1.02 | 0.11 | 0.90 ± 0.04 | |
| 0.2 | 2.0 | 0.29 | 1.00 ± 0.02 | 0.18 ± 0.01 | 1.11 | 0.19 | 0.89 ± 0.04 | |
| 0.3 | 3.2 | 0.36 | 1.00 ± 0.01 | 0.28 ± 0.01 | 0.98 | 0.28 | 0.87 ± 0.04 | |
| 0.4 | 5.1 | 0.32 | 1.00 ± 0.01 | 0.43 ± 0.01 | 1.08 | 0.44 | 0.83 ± 0.03 | |
| 0.5 | 7.2 | 0.32 | 1.00 ± 0.01 | 0.58 ± 0.01 | 1.14 | 0.59 | 0.79 ± 0.03 | |
| 0.6 | 11.4 | 0.38 | 0.24 ± 0.04 | 0.47 ± 0.07 | 1.04 ± 0.02 | 1.07 | 0.91 | 0.77 ± 0.04 |
| 0.7 | 16.6 | 0.35 | 0.11 ± 0.01 | 0.50 ± 0.06 | 1.34 ± 0.01 | 0.95 | 1.25 | 0.73 ± 0.03 |
| 0.8 | 26.0 | 0.34 | 0.03 ± 0.01 | 0.42 ± 0.08 | 1.65 ± 0.01 | 1.00 | 1.51 | 0.56 ± 0.02 |
| 0.9 | 35.2 | 0.36 | 0.02 ± 0.01 | 0.35 ± 0.03 | 2.10 ± 0.01 | 1.06 | 2.07 | 0.57 ± 0.02 |
| 1 | 49.2 | 0.38 | 0.01 ± 0.01 | 0.24 ± 0.03 | 2.24 ± 0.01 | 1.09 | 2.22 | 0.44 ± 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heitz, M.P.; Sabo, T.J.; Robillard, S.M. Coumarin 153 Dynamics in Ethylammonium Nitrate: The Effects of Dilution with Methanol. Sustain. Chem. 2021, 2, 778-795. https://doi.org/10.3390/suschem2040041
Heitz MP, Sabo TJ, Robillard SM. Coumarin 153 Dynamics in Ethylammonium Nitrate: The Effects of Dilution with Methanol. Sustainable Chemistry. 2021; 2(4):778-795. https://doi.org/10.3390/suschem2040041
Chicago/Turabian StyleHeitz, Mark P., Tyler J. Sabo, and Stephanie M. Robillard. 2021. "Coumarin 153 Dynamics in Ethylammonium Nitrate: The Effects of Dilution with Methanol" Sustainable Chemistry 2, no. 4: 778-795. https://doi.org/10.3390/suschem2040041
APA StyleHeitz, M. P., Sabo, T. J., & Robillard, S. M. (2021). Coumarin 153 Dynamics in Ethylammonium Nitrate: The Effects of Dilution with Methanol. Sustainable Chemistry, 2(4), 778-795. https://doi.org/10.3390/suschem2040041







