Coordinating Day-Ahead and Intraday Scheduling for Bidirectional Charging of Fleet EVs

Abstract

The rapid growth of electric vehicles (EVs) and photovoltaic (PV) generation creates substantial power peaks that strain local electrical infrastructure. Coordinated bidirectional charging can mitigate these challenges while delivering benefits such as lower costs, improved PV utilization, and reduced emissions. This paper develops a framework for fleet charging that combines station assignment with a two-stage scheduling approach. A heuristic assignment method allocates EVs to uni- and bidirectional charging stations, ensuring efficient use of limited infrastructure. Building on these assignments, charging power is optimized in two stages: a Mixed-Integer Linear Program (MILP) generates day-ahead schedules from forecasts, while an intraday heuristic-based MILP adapts them to unplanned arrivals and forecast errors through lightweight re-optimization. A Python -based simulator is developed to evaluate the framework under stochastic PV, load, price, and EV conditions. Results show that the approach reduces costs and emissions compared to alternative methods, improves the utilization of bidirectional infrastructure, scales efficiently to large fleets, and remains robust under significant uncertainty, highlighting its potential for practical deployment.

1. Introduction

The transition to sustainable energy systems is motivated by the urgent need to mitigate climate change and reduce greenhouse gas emissions. Two prominent measures include the electrification of transport and the expansion of renewable energy generation. Electric vehicles (EVs) contribute to reduced tailpipe emissions and improved urban air quality, while photovoltaic (PV) systems provide cleaner electricity at declining costs. The adoption of these technologies is accelerating globally. In Germany, the number of registered EVs exceeded one million in 2024 and is projected to surpass ten million by 2030. Installed solar capacity is expected to more than double from 100 GW to 202 GW within the same period [1,2].

This rapid growth introduces both significant challenges and opportunities for the power system. On one hand, uncoordinated EV charging may intensify peak demand, while the distributed and variable nature of renewable energy generation can create local supply–demand imbalances [3]. These effects place stress on the transmission grid as well as local infrastructure, where existing power cables and distribution equipment are often not designed to handle sharp peaks. On the other hand, EVs are typically parked approximately 95% of the day, and charging stations are utilized less than 20% of the time. With ten million EVs and an average battery capacity of 60 kWh, the theoretical storage potential exceeds 600 GWh. Even under conservative assumptions regarding participation and usable State-of-Charge (SoC), tens of gigawatt-hours of flexibility could be made available to the grid. This flexibility facilitates the improved integration of renewable generation, reduces costs and emissions, and enhances grid reliability. These observations highlight the necessity for automated, coordinated bidirectional charging strategies that can enable EV fleets to function as active resources rather than passive loads [4,5].

Recent studies further emphasize the significance of such integration within broader contexts of energy storage and EV deployment [6,7]. Building on this potential, system-level studies have demonstrated the value of bidirectional charging [8,9,10]. Analyses across Europe indicate that EVs can reduce system costs by providing flexibility in both charging and discharging [11]. National studies and pilot projects in Germany similarly demonstrate that widespread adoption of these technologies can lower emissions and enhance grid stability [12]. Complementing these findings, local-level studies investigate smaller-scale scenarios in greater detail, exploring how smart charging can utilize EVs as flexible resources [13,14,15,16]. Objectives include reducing operational costs, shaving peaks, supporting grid stability, reducing battery degradation, and improving user satisfaction [17,18,19,20,21,22]. Research addresses both front-of-the-meter [13,14,23,24] and behind-the-meter applications [13,14,15,16,25], highlighting the diversity of contexts within which coordinated charging strategies are being evaluated.

Among these objectives, cost optimization and emission reduction have received considerable attention, as both economic and environmental considerations drive the adoption of EV smart charging. From an economic perspective, coordinated charging can substantially reduce electricity costs and generate revenue through market participation. These benefits depend on the structure of electricity markets. In Germany, these are the day-ahead and intraday electricity markets [26,27]. The day-ahead market [28] is cleared daily at noon, establishing hourly prices for the following day. The intraday market [29] features an auction at 3:00 PM and continuous trading until shortly before delivery, enabling adjustments to charging plans based on updated forecasts. From an environmental standpoint, charging decisions significantly influence carbon emissions, as the ${\mathrm{CO}}_2$ intensity of electricity varies with the mix of generation sources. Some studies utilize the Average Emission Factor (AEF), which reflects overall carbon intensity [30], but this approach may overlook short-term variations. Alternatively, the marginal emission factor (MEF) measures the emissions of the marginal power plant dispatched to meet additional demand, thus better capturing the immediate environmental consequences of charging decisions [31,32,33]. To achieve these objectives, researchers have studied a wide range of methods, including heuristic, mathematical programming, and data-driven approaches [34,35,36,37,38]. These methods are commonly applied to scheduling problems, determining when and how much EVs should charge or discharge, thereby translating strategic objectives into operational charging decisions.

Despite these advances, existing studies on EV smart charging remain limited in several respects. Few explicitly consider workplace fleets, despite their special importance. The simultaneous charging of multiple EVs can generate significant power flows. At the same time, cable capacity in workplace parking infrastructure is often insufficient to accommodate such peaks and has rarely been studied in detail. Station assignments [39] are also frequently overlooked. Since charging stations, particularly bidirectional models, are limited resources, the allocation of EVs to stations must be managed carefully. Additionally, only a small number of studies address day-ahead and intraday scheduling jointly, and even in those cases, the use of separate market price signals remains limited. Finally, the handling of unused day-ahead energy allocations in intraday operation is also often neglected, even though re-optimizing such allocations may enhance efficiency. The present study addresses the question of how coordinated day-ahead and intraday scheduling can improve both economic and environmental performance under infrastructure capacity limitations and operational uncertainty. The proposed framework differs from existing approaches by explicitly linking day-ahead optimization with event-driven intraday rescheduling, enhancing feasibility and robustness in real workplace charging environments. The main contributions of this paper are as follows:

• Modeling of workplace fleets with co-located PV generation and building loads, considering cable constraints via a hierarchical fuse tree; the analysis addresses both day-ahead and intraday electricity markets.
• Development of a charging station assignment method that accounts for the limited availability of bidirectional chargers and ensures efficient allocation of EVs.
• A two-stage optimization framework, comprising a day-ahead MILP that leverages forecasts and market prices, and an intraday heuristic-based MILP designed to adapt to EV behavioral uncertainty and estimation errors. This framework addresses multiple objectives, such as minimizing economic costs, reducing carbon emissions, and enhancing user satisfaction.
• Development of a discrete-event simulator that integrates day-ahead and intraday scheduling, modeling both forecasted and realized values to evaluate performance under realistic uncertainty conditions.

The paper is structured as follows: Section 2 reviews the related literature on day-ahead, intraday, and combined scheduling strategies for EV charging. Section 3 outlines the scenario and modeling assumptions, while Section 4 details the proposed methodology. Section 5 describes the simulation framework, and Section 6 presents the results. Section 7 concludes and provides directions for future research.

2. Related Work

Prior research on EV smart charging can be broadly divided into three categories based on the scheduling horizon. Some works focus on day-ahead scheduling, others on intraday adjustments, and a smaller set of studies on combined approaches. The following review discusses each category in turn.

Day-ahead scheduling provides an advanced plan based on forecasts of demand, renewable generation, and vehicle availability. For instance, ref. [40] combines day-ahead energy forecasting with demand response strategies, using an Ant Colony Optimization (ACO) algorithm supported by an Artificial Neural Network based on modified Enhanced Differential Evolution (ANN-mEDE) forecasting model to optimize energy consumption and microgrid operations, balancing local renewable generation with grid procurement while minimizing energy cost, peak-to-average ratio, carbon emissions, and user discomfort. In [41], the authors present a day-ahead scheduling model for microgrids with plug-in hybrid electric vehicles (PHEVs), employing a Modified Shuffled Frog Leaping Algorithm (MSFLA) to minimize operational costs by coordinating EV charging/discharging, renewable generation, and energy procurement based on forecasted electricity prices and renewable outputs. Another study  [42] develops a multimarket optimization model for EV aggregations, jointly scheduling charging for participation in the day-ahead energy market and frequency regulation services. Using a two-level centralized control framework, the model minimizes fleet-level operating costs while enhancing grid stability and demonstrating significant economic benefits from participating in ancillary services. At a regional scale, ref. [43] investigates EV smart charging in north-western Europe, developing a framework that integrates day-ahead market prices, marginal emission factors, charging flexibility, and grid constraints. The model minimizes electricity costs and CO₂ emissions, thereby assessing long-term trade-offs between economic and environmental objectives. Collectively, these studies demonstrate how day-ahead optimization enables cost-effective, market-responsive EV charging while supporting renewable integration and overall grid reliability.

On the contrary, intraday scheduling allows for adjustments closer to real-time, utilizing updated information on grid conditions, renewable generation, and user behavior. Several studies have focused on intraday optimization to manage the charging and discharging of EV fleets, highlighting adaptive scheduling in response to dynamic market and grid conditions. In [44], the authors propose an online Model Predictive Control (MPC) framework for optimizing uni- and bidirectional EV charging, aiming to reduce peak demand and minimize electricity costs. The approach operates in a rolling-horizon manner, leveraging short-term forecasts of load and renewable generation. Similarly, ref. [45] addresses hour-ahead scheduling for EV aggregators, integrating a local electricity market and using a Hybrid-Adaptive Differential Evolution with Decay Function (HyDE-DF) algorithm to minimize operational costs while comparing scenarios with and without local electricity market transactions. In another study, ref. [46] investigates real-time energy flexibility optimization with EVs and distributed energy resources, leveraging deep reinforcement learning (DRL) to continuously update energy schedules in response to changing demand, renewable generation, and electricity prices. Focusing on environmental objectives, ref. [47] explores intraday energy optimization for zero-carbon buildings, explicitly considering uncertainties in renewable generation and load while prioritizing indoor thermal comfort. Using a fuzzy chance-constrained, goal programming framework, this study dynamically updates intraday schedules across flexible resources, including EVs. These works highlight the crucial role of intraday and real-time optimization in improving operational efficiency, cost-effectiveness, and renewable energy utilization, while also facilitating carbon-conscious energy management through EV flexibility.

A combined day-ahead and intraday approach offers the benefits of both: a stable baseline plan established in advance, with the flexibility to adapt to uncertainties and fluctuations as they arise. The literature on EV charging optimization emphasizes this integrated approach. Ref. [48] proposes a two-stage framework for battery-assisted fast-charging EV hubs, where day-ahead bidding is optimized via MILP to minimize operational costs, followed by DRL to dynamically adjust schedules in real-time for efficiency and cost reduction. Aggregated intraday optimization is addressed in [49], employing evolutionary algorithms such as Differential Evolution and HyDE-DF to manage multiple resources under uncertain market conditions. While this complements day-ahead planning by adjusting energy use and market participation, the complex enhancements often reduce generalization ability and increase computational overhead, indicating a need for more balanced approaches. Extending this line of research, ref. [50] proposes a risk-aware day-ahead to intraday scheduling method for individual EVs and energy storage systems, incorporating extreme events through scenario generation and Conditional Value-at-Risk (CVaR). While intraday re-optimization mitigates deviations, reliance on metaheuristics may limit global optimality compared to mathematical models. Furthermore, ref. [51] proposes a real-time smart charging framework that integrates day-ahead and intraday scheduling within a fused distribution network topology; the approach remains restricted to unidirectional charging and assumes one single electricity market. Day-ahead schedules are initially generated via MILP and then updated in real-time to account for forecast errors and other uncertainties. In a related approach, ref. [52] develops a hybrid framework that schedules EV charging via centralized MILP in the day-ahead stage, followed by real-time adjustments through a distributed Genetic Algorithm (GA), balancing system reliability, load management, and user satisfaction. However, this study is constrained by fixed EV profiles, the absence of V2G/V2V and renewable coordination, and a simplified MILP and GA hybrid that may not capture real-world uncertainties.

Overall, these studies demonstrate the value of combining day-ahead planning with intraday flexibility, showing that such integration reduces operational costs, mitigates grid stress, and improves charging efficiency. Yet, despite these advances, much of the existing work remains constrained. Metaheuristic strategies, while adaptable, typically lack guarantees of global optimality. Additionally, many formulations oversimplify optimization models and user dynamics, often excluding bidirectional charging or renewable energy coordination. Moreover, most contributions do not address workplace fleets, infrastructure bottlenecks, or real-world market structures, leaving these areas underexplored. These limitations motivate a more comprehensive framework that captures both the stability of day-ahead planning and the responsiveness of intraday adaptation, while considering infrastructure constraints and user-driven performance.

In our earlier work [53], a heuristic algorithm was employed for bidirectional fleet charging, adapting intraday schedules based on real-time market prices while accounting for fuse limits. While this approach ensured cost efficiency and supported renewable energy utilization, it did not fully utilize day-ahead information and overlooked building load. It relied on a heuristic strategy that left room for improvement. These gaps motivate the integrated framework developed in this paper.

3. Scenario

To illustrate the potential of bidirectional charging, we consider a company site that integrates workplace charging, on-site PV generation, and building demand (Figure 1). This setting enables the coordinated control of substantial power flows while using existing parking infrastructure. Expanding the local electrical network to supply the simultaneous peak demand of all charging stations would be prohibitively expensive, emphasizing the need for coordinated smart charging strategies.

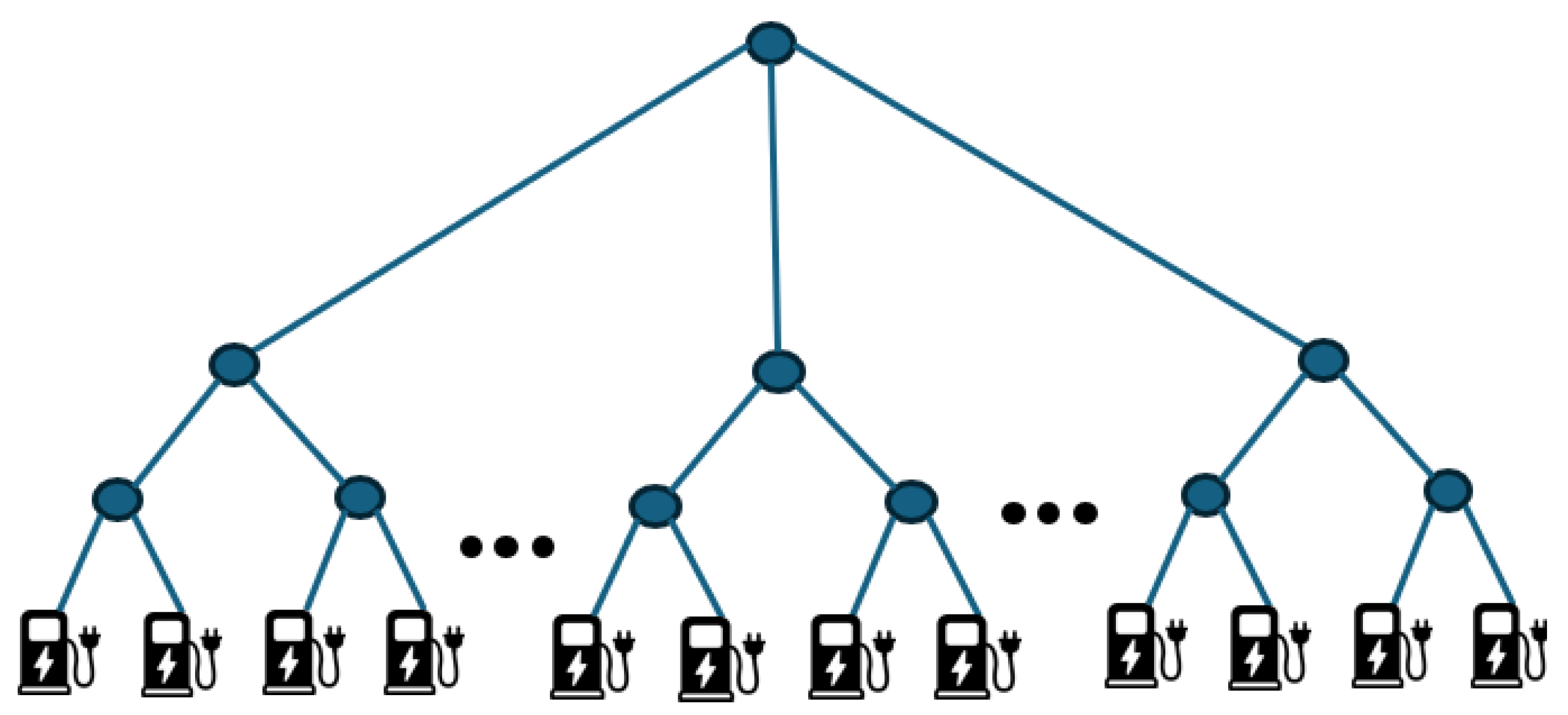
Each system component directly influences the scheduling process. The site features a parking lot equipped with both unidirectional and bidirectional charging stations, with power ratings ranging from 4 to 22 kW. The electrical cabling follows a three-level hierarchical fuse tree structure, where each node represents a fuse branching into downstream cables or charging stations, as shown in Figure 2. This structure reflects real-world installations and ensures that upstream fuse ratings constrain the aggregate load of all connected stations. The fleet consists of heterogeneous vehicle models with different battery sizes and charging capabilities: all vehicles support unidirectional charging, but only a subset are bidirectional capable. Battery behavior during charging is modeled linearly, following [54]. Arrival and departure patterns are derived from company fleet data and approximated by normal distributions with peaks at 08:00 and 17:00 and a standard deviation of one hour. Since the actual departure time of each EV is uncertain upon arrival, a fixed departure time of 17:00 is assumed for day-ahead prediction. Given the limited number of bidirectional chargers and the variability in vehicle flexibility, efficiently allocating EVs to charging stations is essential for optimal infrastructure use.

On-site PV generation and building load jointly define the local energy balance, which strongly influences charging decisions. PV generation is derived from weather conditions in Dresden, Germany, recorded in 2023 and scaled to a peak capacity of 340 kW. The data are discretized at 15 min resolution and treated as forecasts that are updated each timeslot to simulate prediction errors. Realized PV output is generated by adding Gaussian noise to the forecast using the prediction error rate as the standard deviation. Although more complex error models could be used, the Gaussian approach offers a transparent and efficient approximation that isolates scheduling effects from forecast modeling. 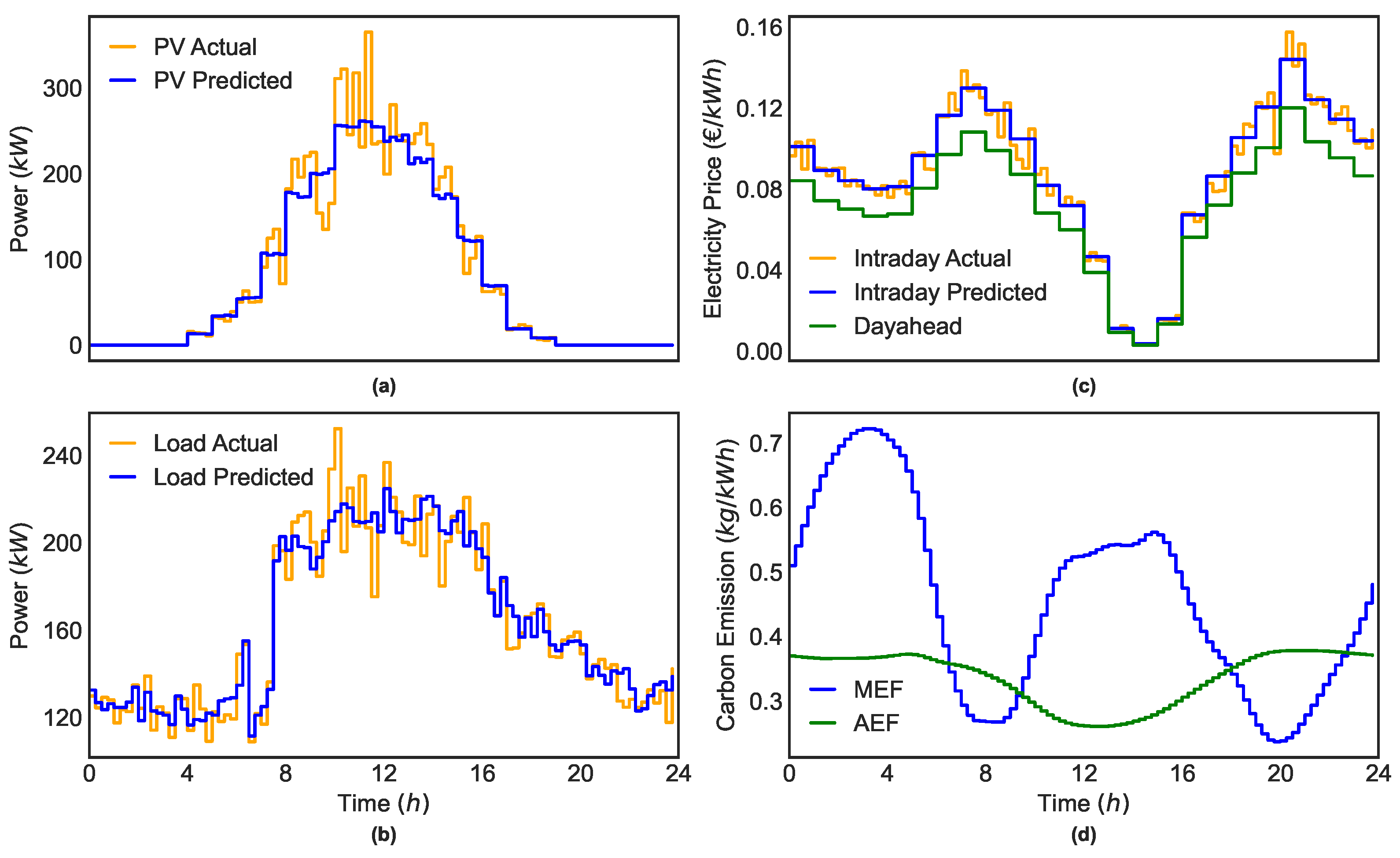Figure 3a shows a representative summer day with forecasted and realized generation. Building demand is based on workplace consumption data from the same period, scaled to the site and aligned with the PV and EV timescales to capture short-term variability. Forecasted load is likewise updated each timeslot to reflect prediction errors, as shown in Figure 3b. In the optimization framework, the building load acts as a passive demand that enters the overall power balance but is not actively controlled. This treatment allows the analysis to focus on EV scheduling while still accounting for the dynamic interaction between stochastic PV generation and baseline load, which together determine the available headroom for charging and discharging.

Electricity prices and environmental considerations also shape the operational objectives of the scheduling framework. Building on the PV and load dynamics described above, energy costs are determined by the German day-ahead and intraday electricity markets. The day-ahead market defines uniform clearing prices for each 15 min interval. In contrast, the intraday market is a continuous trading platform where transactions can occur at varying prices throughout the trading horizon. For modeling purposes, intraday prices are approximated as 20% higher than the corresponding day-ahead prices, representing an adverse price scenario. Energy costs are calculated using these prices and the total electricity consumed. Figure 3c shows the day-ahead clearing prices alongside predicted and realized intraday prices. It is worth noting that our analysis does not include system usage charges associated with peak consumption. In parallel, the environmental impact of charging is quantified using time-varying carbon-intensity data of the German electricity system at 15 min resolution. Both the AEF and MEF are calculated following [31]. While the AEF represents the overall carbon intensity of the grid, the MEF captures the incremental emissions caused by additional demand. The latter is adopted in this study, as it better reflects the short-term environmental consequences of EV charging and discharging decisions. The resulting emission profiles are illustrated in Figure 3d. It is important to note that the framework operates under a behind-the-meter configuration, where electricity export to the public grid is not considered. Such exports are currently restricted or compensated at very low rates in Germany, making them economically unattractive. This focus ensures that the proposed strategy remains practical, compliant with current regulations, and directly applicable to workplace charging environments.

Building upon the market signals, emission factors, and forecast-based inputs described above, the scheduling process operates in two stages. In the day-ahead stage, schedules are generated for all EVs using forecast data together with information submitted by drivers, including expected arrival and departure times, target SoC, minimum SoC, and maximum dischargeable energy. In the intraday stage, if an EV was not included in the day-ahead plan, a new charging plan is generated based on its actual arrival time, initial SoC, and updated departure information. Furthermore, if predefined re-optimization conditions are met (Section 4.2), the schedules of selected EVs are recalculated to reflect the current system state.

Together, the charging infrastructure, EV fleet characteristics, PV generation, building load, market prices, emission factors, and planning process form a realistic and implementable scenario for evaluating bidirectional smart charging strategies under both day-ahead and intraday conditions. This setup captures the practical challenges faced by companies operating EV fleets with on-site energy resources, where coordinated scheduling is essential to balance cost, emissions, and user requirements while avoiding costly grid reinforcement.

4. Method

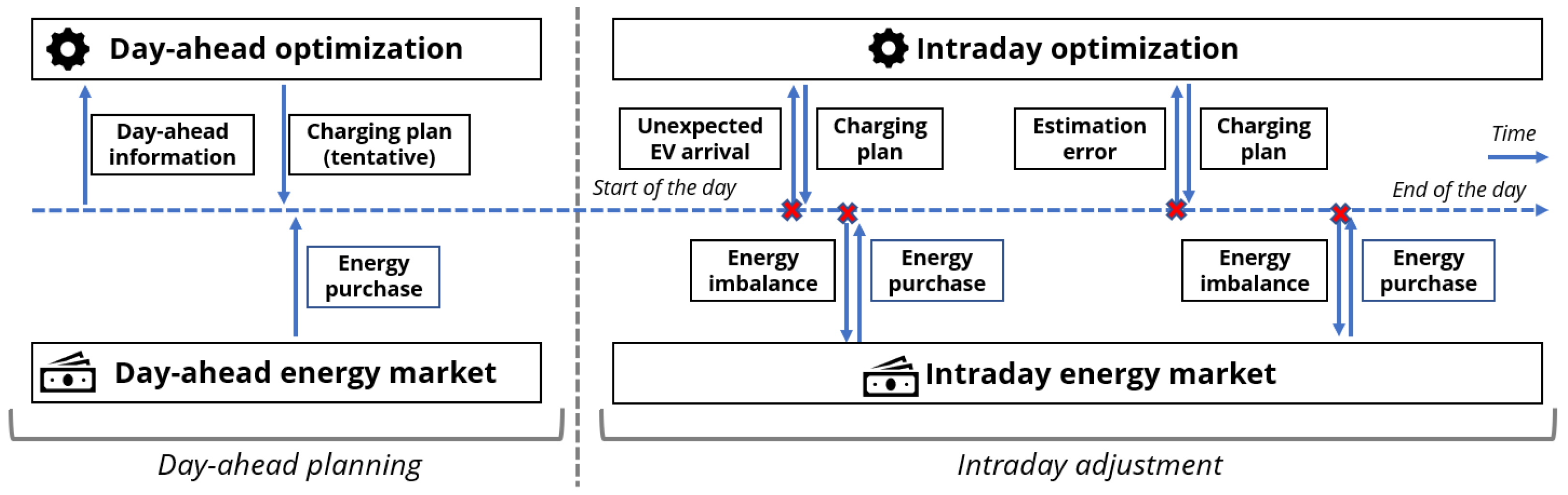
Our approach has two phases, as shown in Figure 4: (i) day-ahead planning and (ii) intraday adjustment. In the day-ahead phase, we collect forecasts and user inputs, assign EVs to charging stations using a priority-based heuristic, and subsequently compute the charging plan for each vehicle. Given the charging plan and forecasts of load and PV generation, purchase any expected shortfall from the day-ahead energy market, which typically offers lower prices and ensures a secure electricity supply. On the operation day, EVs that arrive as planned follow the day-ahead schedule. Deviations (early/late arrivals, different arrival SoC) and forecast errors in load or PV trigger a real-time heuristic that adapts the schedules on the fly. Any residual shortfall caused by these adaptations is procured from the intraday market.

4.1. Day-Ahead Optimization

This subsection describes the day-ahead scheduling of EV charging, including both the assignment of EVs to charging stations and the determination of their charging power profiles.

4.1.1. Day-Ahead Charging Station Assignment

Many existing works on smart charging neglect charging station assignment. Yet stations are a constrained resource, with bidirectional ones less available than unidirectional ones. Ignoring the assignment can lead to overestimated results and charging plans that are not implementable in practice. While charging station assignment and charging plans can be embedded in a single MILP, doing so greatly increases problem size. We therefore use a heuristic assignment that (i) is efficient at the day-ahead scale and (ii) can be reused intraday.

The algorithm is described in Algorithm 1: for each EV i, we estimate its arrival/departure time $t_i^{\mathrm{arr}},t_i^{\mathrm{dep}}$, dwell time $\Delta t_i$ and energy shortfall $\Delta E_i$. We then compute a charging priority score ${\sigma }_i^C$, taking into account EV’s max charging power $P_i^C$ and charging efficiency ${\eta }^{\mathrm{C}}$, as shown in Equation (1). The priority increases with required energy and decreases with longer parking time. This priority ranks all EVs, and the most urgent ones will be assigned to a charging station.

$$\begin{array}{c}\hfill {\sigma }_i^{\mathrm{C}}=min\left\{1,{\left[{\displaystyle \frac{\Delta E_i}{\Delta t_i{P}_i^{\mathrm{C}}{\eta }^{\mathrm{C}}}}\right]}_{+}\right\},\end{array}$$

(1)

Next, the algorithm decides which EV gets a bidirectional charging station. For bidirectional capable EVs, we estimate a discharging potential ${\sigma }_n^{\mathrm{D}}$, which is the maximum deliverable energy over the dwell time. As shown in Equation (2), $P_i^D$,${\eta }^{\mathrm{D}}$ are the discharging power and efficieny, $E_i^{\max }$ is the total capacity of the EV, and ${\varphi }_i$ is the equivalent full cycle (EFC) for discharge set by the user. EVs with higher discharging potential are prioritized for bidirectional stations, while the remainder are assigned to unidirectional stations. It is worth mentioning that charging priorities are measured in percentage of SoC, matching user perception, while discharging priority is reflected by dischargable energy, which is the relevant metric for the operator. Finally, we define $X_{i,j,t}=1$ if EV i is assigned to station j at time t, and 0 otherwise. The resulting assignment tensor $\left\{X_{i,j,t}\right\}$ is passed to the next stage. Algorithm 1’s computational complexity is dominated by the two sorting steps, resulting in overall $\mathcal{O}(nlogn)$ behavior and efficient performance for realistic fleet sizes.

$$\begin{array}{c}\hfill {\sigma }_i^{\mathrm{D}}=min\left\{{\varphi }_i{E}_i^{max},{\left[{\displaystyle \frac{P_i^{\mathrm{C}}\Delta t_i-{\displaystyle \frac{\Delta E_i}{{\eta }^{\mathrm{C}}}}}{{\displaystyle \frac{P_i^{\mathrm{C}}}{P_i^{\mathrm{D}}}}+{\displaystyle \frac{1}{{\eta }^{\mathrm{C}}{\eta }^{\mathrm{D}}}}}}\right]}_{+}\right\}\end{array}$$

(2)

Algorithm 1: Priority-based charging station assignment

4.1.2. Day-Ahead Power Assignment

This next stage builds on the station assignments by determining the charging power profiles. The decision variables $P_{i,t}^{\mathrm{ev}}$ are the power of each EV at each time t. The corresponding objectives and constraints can be expressed as linear or piecewise linear functions of these variables, which allows the problem to be formulated as an MILP [55]. The MILP framework has the advantage of mature, off-the-shelf solvers that guarantee optimality. Although MILPs can be computationally demanding for large-scale instances, runtime is acceptable in the day-ahead context, where schedules are computed in advance and sufficient time is available.

We design the objective from three perspectives (Equation (3)), economic cost, CO₂ emissions, and user satisfaction, with ${\omega }^{\mathrm{eco}},{\omega }^{\mathrm{env}}$, and ${\omega }^{\mathrm{soc}}$ as the weight factors. The economic cost component is given in Equation (4), where $P_t^{\mathrm{tot}+}$ denotes the positive part of the total power balance. This term represents the net energy drawn from the grid. The cost is obtained by multiplying this demand by the market price ${\pi }_t^{\mathrm{cost}}$ [€/kWh] and the timeslot length $\tau$ (15 min). The environmental impact is captured in Equation (5). It is analogous to the cost term but weighted by the marginal emission factor ${\pi }_t^{\mathrm{em}}$ [kgCO₂/kWh], which reflects the carbon intensity of electricity generation at time t. The user satisfaction term in Equation (6) rewards additional charging beyond the required target SoC. Specifically, it measures the surplus between the actual departure ${\mathrm{SoC}}_{i,t_i^{\mathrm{dep}}}$ and the target ${\mathrm{SoC}}_i^{\mathrm{tar}}$, weighted by ${\pi }^{\mathrm{soc}}$, which represents the utility gain per unit SoC increase.

We assume a behind-the-meter setup where no energy can be exported back to the grid; surplus PV generation is curtailed if not consumed locally. Accordingly, $P_t^{\mathrm{tot}+}$ in Equation (7) denotes the positive part of the total power balance, which combines building load $P_t^{\mathrm{load}}$, PV generation $P_t^{\mathrm{pv}}$, and EV charging power ${\sum }_i{P}_{i,t}^{\mathrm{ev}}$, as shown in Equation (8). The total power is constrained by the peak shaving target $P^{\mathrm{peak}}$ in Equation (9). In practice, operators are billed based on the highest peak demand observed over a given period (e.g., a year). Since our optimization horizon is only one day, minimizing peak demand in the objective would not guarantee compliance across periods. Therefore, we model the peak limit as a hard constraint rather than as an objective term.

SoC dynamics and bounds are defined in Equations (10) and (11). $P_{i,t}^{+}$ and $P_{i,t}^{-}$ denote charging and discharging power; ${\eta }^{\mathrm{C}}$ and ${\eta }^{\mathrm{D}}$ are the corresponding efficiencies; $E_i^{\max }$ is the battery capacity. The driver specifies a minimum SoC to guarantee sufficient battery reserve for emergencies. Arrival SoC is fixed in Equation (12), while departure SoC must reach at least the target in Equation (13).

Charging and discharging modes are separated in Equations (14)–(19). $P_{i,t}^{+}$ and $P_{i,t}^{-}$ represent the positive and negative parts of EV power, activated by binary variables ${\sigma }_{i,t}^{+}$ and ${\sigma }_{i,t}^{-}$. This separation allows us to model distinct charging and discharging efficiencies (${\eta }^{\mathrm{C}},{\eta }^{\mathrm{D}}$) and to enforce minimum and maximum power limits. Charging and discharging efficiency can be treated as approximately constant at higher power levels, but drops significantly below a certain threshold [56]. Therefore, a minimum power limit is imposed to prevent inefficient low-power operation. Battery degradation is primarily determined by the number of EFCs, regardless of whether they result from a single deep cycle or multiple shallow cycles [57]. Accordingly, Equation (20) limits the cumulative discharged energy to a fraction ${\varphi }_i$ of one EFC within the planning horizon, where the driver specifies ${\varphi }_i$.

EV power is also restricted by the capabilities of its assigned charging station, as enforced in Equation (21) through the charging station assignment $X_{i,j,t}$ and the station-specific power limits $[P_j^{\min },P_j^{\max }]$ (with $P_j^{\min }<0$ for bidirectional stations). From the charging station assignment, the set of EVs connected to each node in the fuse tree can be identified, and the corresponding fuse capacity constraints are then enforced in Equation (22).

$$\begin{array}{cc}\hfill \underset{P_{i,j,t}^{\mathrm{ev}}}{min}& {\omega }^{\mathrm{eco}}{J}^{\mathrm{cost}}+{\omega }^{\mathrm{env}}{J}^{\mathrm{em}}+{\omega }^{\mathrm{soc}}{J}^{\mathrm{soc}}\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill \mathrm{s}.\mathrm{t}.:& J^{\mathrm{cost}}=\sum _{t\in T}{P}_t^{\mathrm{tot}+}\tau {\pi }_t^{\mathrm{cost}}\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & J^{\mathrm{em}}=\sum _{t\in T}{P}_t^{\mathrm{tot}+}\tau {\pi }_t^{\mathrm{em}}\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & J^{\mathrm{soc}}=-\sum _{i\in I}({\mathrm{SoC}}_{i,t=t_i^{\mathrm{dep}}}-{\mathrm{SoC}}_i^{\mathrm{tar}}){\pi }^{\mathrm{soc}}\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & P_t^{\mathrm{tot}+}=\left\{\begin{array}{cc}{P}_t^{\mathrm{tot}},\hfill & P_t^{\mathrm{tot}}>0,\hfill \\ 0,\hfill & P_t^{\mathrm{tot}}\le 0,\hfill \end{array}\right.\forall t\in T\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & P_t^{\mathrm{tot}}=P_t^{\mathrm{load}}-P_t^{\mathrm{pv}}+\sum _{i\in I}{P}_{i,t}^{\mathrm{ev}},\forall t\in T\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & P_t^{\mathrm{tot}}\le P^{\mathrm{peak}},\forall t\in T\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & So{C}_{i,t+1}=So{C}_{i,t}+(P_{i,t}^{+}{\eta }^{\mathrm{C}}+{\displaystyle \frac{P_{i,t}^{-}}{{\eta }^{\mathrm{D}}}}){\displaystyle \frac{\tau }{E_i^{\max }}},\forall i\in I,\forall t\in T\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & So{C}_i^{\min }\le So{C}_{i,t}\le So{C}_i^{\max }\forall i\in I,\forall t\in T\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & So{C}_{i,t=t_i^{\mathrm{arr}}}=So{C}_i^{\mathrm{arr}},\forall i\in I\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill & So{C}_{i,t=t_i^{\mathrm{dep}}}\ge So{C}_i^{\mathrm{tar}},\forall i\in I\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill & {\sigma }_{i,t}^{+}=\left\{\begin{array}{cc}1,\hfill & P_{i,t}>0,\hfill \\ 0,\hfill & P_{i,t}\le 0,\hfill \end{array}\right.\forall i\in I,\forall t\in T\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill & P_{i,t}^{+}={\sigma }_{i,t}^{+}{P}_{i,t}\forall i\in I,\forall t\in T\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & {\sigma }_{i,t}^{+}{P}_i^{\min }\le P_{i,t}^{+}\le {\sigma }_{i,t}^{+}{P}_i^{\max }\forall i\in I,\forall t\in T\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & {\sigma }_{i,t}^{-}=\left\{\begin{array}{cc}1,\hfill & P_{i,t}<0,\hfill \\ 0,\hfill & P_{i,t}\ge 0,\hfill \end{array}\right.\forall i\in I,\forall t\in T\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & P_{i,t}^{-}={\sigma }_{i,t}^{-}{P}_{i,t}\forall i\in I,\forall t\in T\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill & -{\sigma }_{i,t}^{-}{P}_i^{\max }\le P_{i,t}^{-}\le -{\sigma }_{i,t}^{-}{P}_i^{\min }\forall i\in I,\forall t\in T\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & \sum _{t\in T}{\displaystyle \frac{-P_{i,t}^{-}}{{\eta }^{\mathrm{D}}}}\tau \le {\varphi }_i{E}_i^{\max }\forall i\in I\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill & \sum _{j\in J}{X}_{i,j,t}{P}_j^{\min }\le P_{i,t}\le \sum _{j\in J}{X}_{i,j,t}{P}_j^{\max }\forall i\in I,\forall t\in T\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & -P_{F_k}\le \sum _{i\in F_k}{P}_{i,t}\le P_{F_k},\forall k\in K,\forall t\in T\hfill \end{array}$$

(22)

Several constraints, such as Equations (7), (14), and (17), are nonlinear but can be linearized using the Big-M method. For example, Equation (14) is reformulated as

$$\begin{array}{cc}\hfill & P_{i,t}\le M{\sigma }_{i,t}^{+},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & P_{i,t}>-M(1-{\sigma }_{i,t}^{+}),\hfill \end{array}$$

(24)

with M chosen to be sufficiently large. The linearized formulation yields an MILP, which can be solved by mature commercial and open-source solvers. For a scenario with 25 EVs and 25 charging stations, the resulting model has on the order of 5000 binary variables, 10,000 continuous variables, and 25,000 constraints. This scale is manageable for day-ahead optimization, but it highlights the need for faster algorithms in the intraday setting.

4.2. Intraday Optimization

Precomputed schedules benefit from longer computation time to produce optimized results. Still they are fragile to real-world deviations: drivers may arrive or depart earlier or later than expected, the arrival SoC may differ, and load, PV, or prices can shift. Neglecting such deviations can lead to higher costs and emissions, insufficient charging for some EVs, or even violations of local power constraints. Other works address such deviations reactively, but typically underutilize the day-ahead knowledge available in advance [53]. Approaches that combine day-ahead and intraday scheduling in bidirectional smart charging are still limited. Our method fills this gap by using the day-ahead plan as a reference and adapting intraday plans with a MILP-based heuristic.

4.2.1. Intraday Charging Station Assignment

If an EV arrives and is already included in the day-ahead schedule, it normally retains its planned station assignment. If the arrival is delayed beyond a specified threshold (e.g., 30 min), the reservation will be canceled. For unplanned arrivals, we first check whether a station is available. If so, charging priority (Equation (1)) is compared with the lowest-priority EV in the day-ahead plan, while discharging potential (Equation (2)) is compared with the least-potential EV for bidirectional assignment. The results determine both whether the EV is assigned and, if so, whether it is assigned to a uni- or bidirectional station. A relaxation factor (e.g., $0.8$) scales the comparison thresholds, enabling opportunistic assignment. This allows for slightly lower-priority EVs to be accepted, reflecting the uncertainty of when or whether higher-priority EVs may arrive later.

4.2.2. Intraday Power Assignment

While station assignment determines which EVs are connected, intraday operation should also adjust their charging power in response to unexpected events and forecast errors. Such events can occur in every timeslot, including the arrival of an unplanned EV, early or delayed arrival or departure of expected EVs, deviations in arrival SoC, PV/load forecast errors, or intraday market price changes. Because intraday adjustments must be fast, thus limited in scope, only a subset of EVs is rescheduled at each step. The procedure is outlined in Algorithm 2.

When an unexpected EV $\widehat{i}$ arrives that is not included in the day-ahead plan, we generate a local schedule by solving the same model (Equations (3)–(22) with linearizations), while keeping all other EVs fixed to their current plans via Equation (25). In implementation, irrelevant constraints and variables are aggregated or removed, reducing the problem size from about 25,000 to 1000 constraints, which can be solved efficiently even as an MILP.

For other types of events l, we handle them individually but merge their effects into either a power increase or power decrease event. Multiple events within the same timeslot are thus aggregated into a single adjustment signal. Given such a signal, if the mismatch exceeds a predefined threshold $\theta$, we select the most suitable batch of EVs using the charging priority metric (Equation (1)) and re-optimize with the same MILP formulation (Equations (3)–(22) and (25)). The process is terminated once the remaining signal falls below $\theta$, the imbalance reduction between successive runs is less than $ϵ$, no further EVs remain for adjustment, or a maximum number of iterations is reached. With this setup, and small batch sizes (e.g., 2–5 EVs), each MILP remains small, allowing re-optimization to be solved fast enough for real-time operation.

$$\begin{array}{cc}\hfill & P_{i,t}=P_{i,t}^{\mathrm{Plan}},\forall i\in I\setminus \left\{\widehat{i}\right\},\forall t\in T\hfill \end{array}$$

(25)

Algorithm 2: Power assignment intraday: MILP-heuristic

Together, the day-ahead MILP and the intraday heuristic-based re-optimization form a two-stage framework: the day-ahead plan establishes a cost-effective and environmentally conscious baseline. In contrast, intraday adjustments ensure robustness against uncertainties and deviations in real operation.

5. Simulator

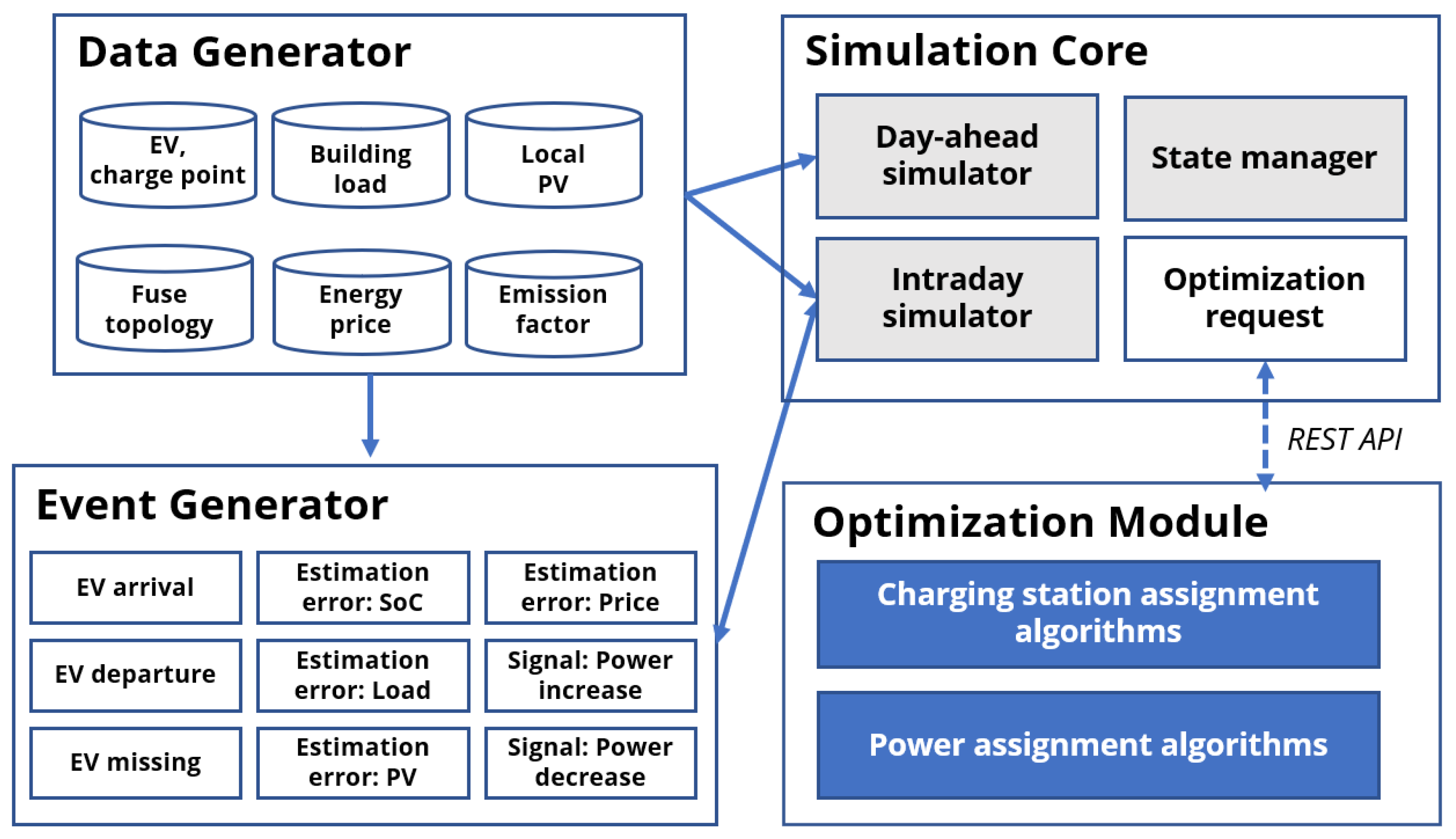
We developed a Python-based charging simulator to evaluate the interaction between day-ahead planning and intraday adaptation under randomized conditions. The simulator employs a discrete-event design and comprises four modules, as illustrated in Figure 5: a data generator, an event generator, a simulation core, and an optimization module.

Before each simulation run, the data generator creates predicted day-ahead input data based on configuration parameters. During intraday operation, realized data are produced in each timeslot by adding Gaussian noise to the predictions, thereby emulating forecast errors.

The event generator generates events such as EV arrivals and departures, and continuously monitors the comparison between realized and predicted data. If deviations exceed predefined thresholds, additional events are triggered. For each timeslot, all events are collected into a queue and passed to the simulator core.

The simulation core coordinates the data generator, event generator, and optimization module. It initializes from the day-ahead plan and, for each intraday timeslot, updates the system state to reflect the current environment. Multiple events occurring within the same timeslot are aggregated into a single adjustment signal (power increase or decrease) with a corresponding set of candidate EVs. When re-optimization is required, the simulation core creates a JSON representation of the current state containing only information available at that timeslot—for example, using updated data for arrived EVs and day-ahead plans for EVs not yet arrived. This design prevents any leakage of future information into the optimization process. The JSON file is then passed to the optimization module via REST API.

The optimization module receives the JSON state snapshot from the simulation core and solves the corresponding scheduling problem. The supported algorithms are listed in

Table 1. Implemented optimization algorithms in the simulator.

Category	Algorithms	Description
Charging station assignment	First-come-first-served	Assigns EVs to stations in order of arrival.
	Random assignment	Assigns EVs randomly among available stations.
	Heuristic	Based on Section 4.1.1 and Section 4.2.1.
Power assignment day-ahead	MILP	Based on Section 4.1.2.
Power assignment intraday	Greedy	EV charge with maximum power upon arrival.
	MILP-Heuristic	Based on Section 4.2.2.
	ReCo	Method proposed in [53].

. All optimizers share a standard input format and return charging station assignments and charging schedules as output. This modular design decouples the optimization logic from the rest of the simulator, allowing algorithms to be exchanged or extended without altering the simulation workflow. It also enables smooth integration into real-world testbeds via OCPP 2.1 [58].

The modular design of the simulator enables the systematic evaluation of different combinations of day-ahead and intraday strategies under controlled conditions. By separating data generation, event handling, simulation logic, and optimization, the framework ensures transparency, prevents information leakage, and allows flexible integration of alternative algorithms.

6. Result

All simulations are repeated with multiple random seeds to reduce stochastic noise, and results are reported as mean values with standard deviations. Experiments were conducted on a computer with Intel(R) Xeon(R) W-2125 CPU and 32 GB RAM, using Gurobi [59] as the MILP solver. The study evaluates several combinations of day-ahead and intraday optimization methods, summarized in

Table 2. Model configurations: day-ahead and intraday methodologies.

Stage	Proposed	Model1	Model2	Model3	Model4
Day-ahead	MILP	MILP	MILP	-	-
Intraday	MILP-Heuristic	ReCo	-	MILP-Heuristic	ReCo

. These configurations include the proposed two-stage framework as well as alternative baselines for comparison. Key simulation parameters are listed in

Table 3. Important simulation parameters.

Parameter	Value
Number of EVs, charging stations	25/25
Charging/discharging efficiency	95%/95%
Min/Max charging power	4/22 kW
Min/Max discharging power	4/22 kW
Max capacity of EV battery	42/62/66/82/85 kWh per model
Target SoC	80%
Min SoC	20%
Max discharged energy in SoC	50%
Parking lot fuse size	550/110/22 kW per level
Peak shaving including load and PV	420 kW
Estimation error	20%
Power threshold for re-optimization	11 kW
Intraday re-optimization batch size	5 EVs

.

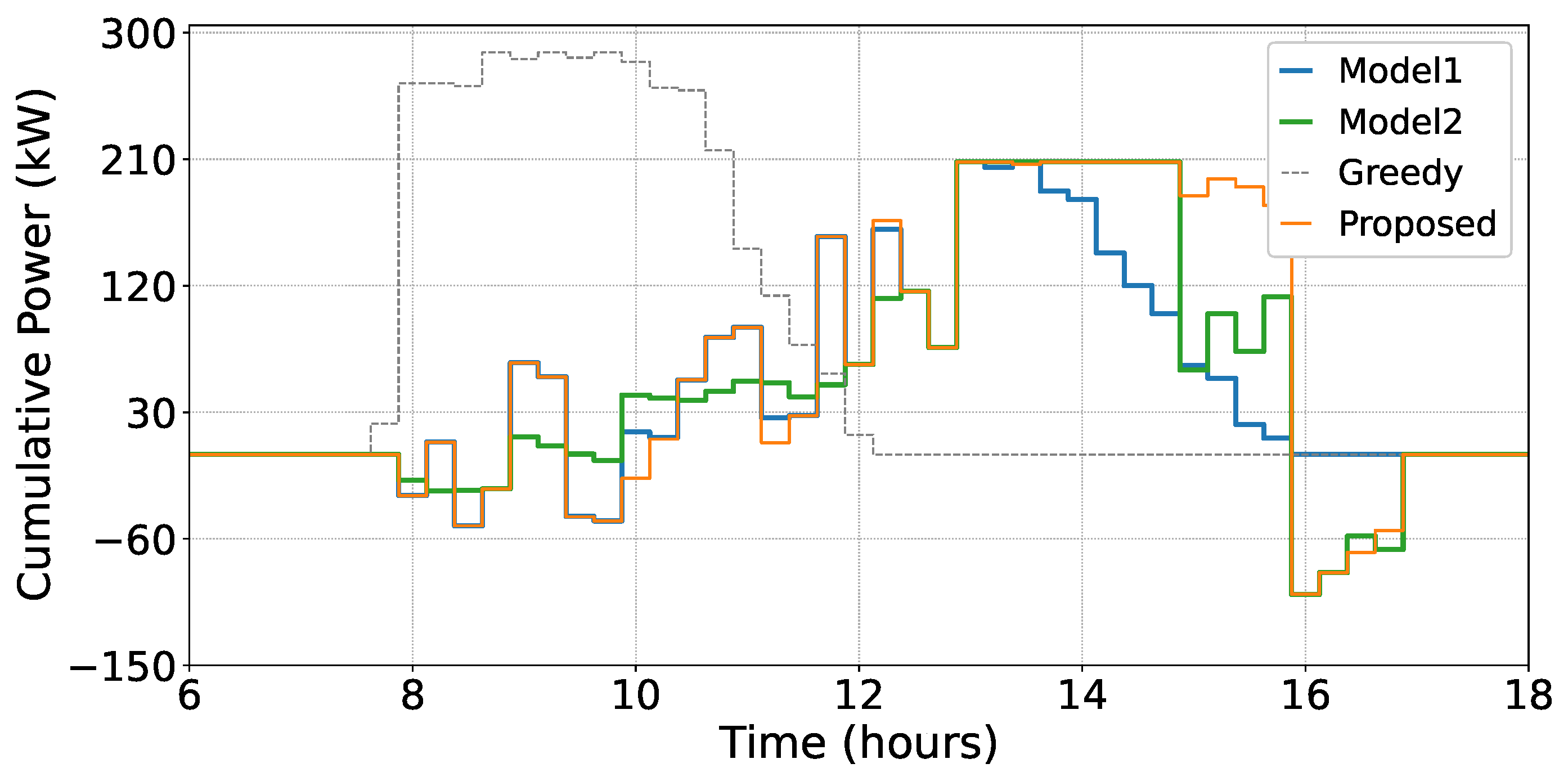
Figure 6 shows the cumulative charging profiles of EVs for a randomly selected day, comparing the performance of four optimization algorithms. The dotted gray line represents the greedy approach, which yields the highest peak demand by prioritizing immediate charging while disregarding the local power balance. The green line corresponds to the day-ahead planning strategy, which shifts charging to better align with system conditions but lacks flexibility to adapt to intraday variations. The orange line represents our proposed model, which combines day-ahead planning with an intraday MILP-based heuristic. It achieves better peak shaving than the greedy approach and adapts to renewable fluctuations, load variations, and intraday price changes, while still meeting the charging needs of drivers. Compared to Model 1 (day-ahead MILP with the intraday ReCo from [53]), it also provides stronger discharging capabilities, enabling improved bidirectional energy management.

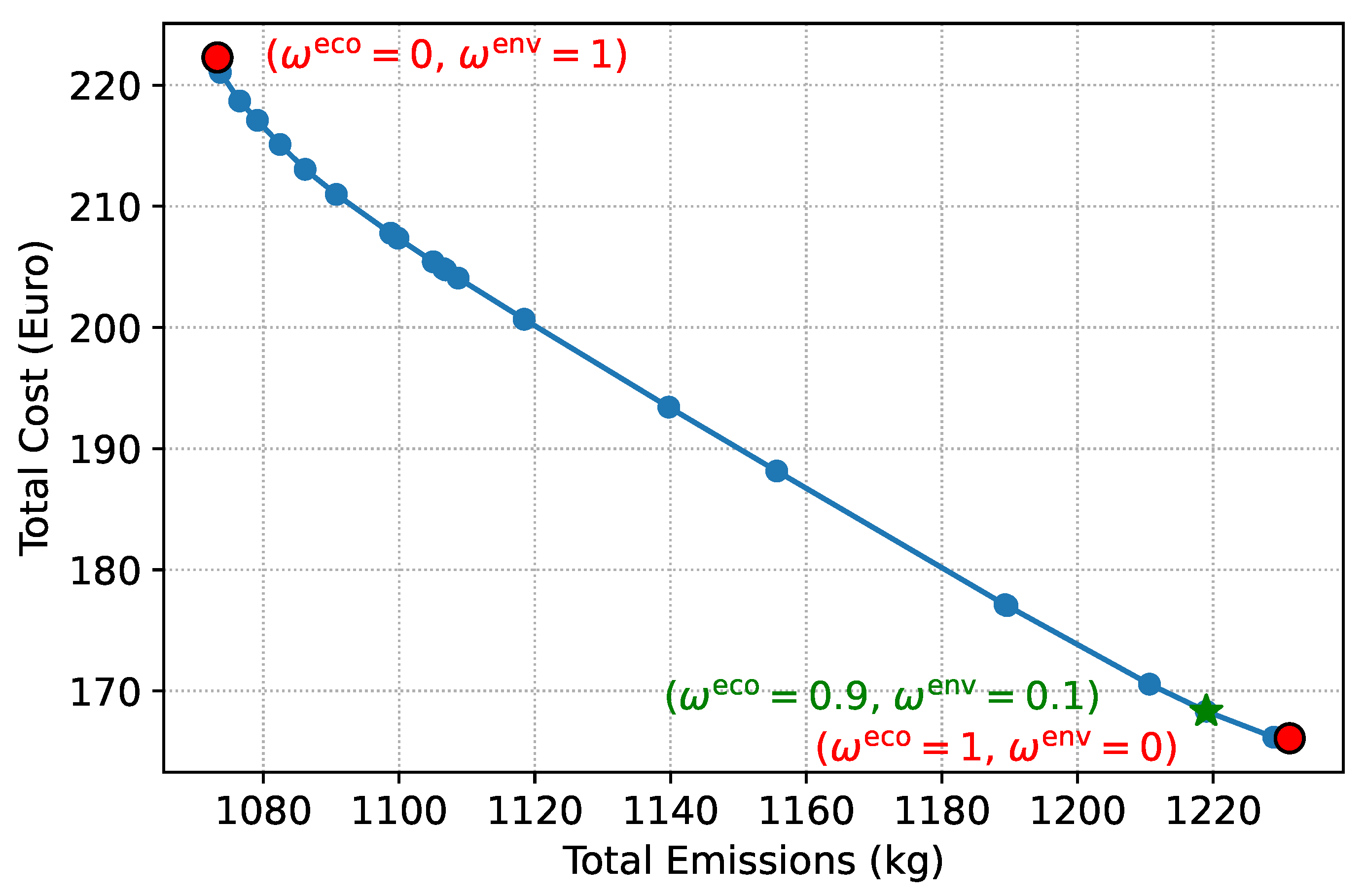
Figure 7 presents the Pareto front of total cost versus carbon emissions obtained from the proposed model using a weighted-sum approach, with user satisfaction given a small fixed weight (${\omega }^{\mathrm{soc}}=0.001$). This weight was chosen empirically to ensure that most EVs depart with a final SoC between 80% and 100%. The frontier is generated by varying the objective weights for cost (${\omega }^{\mathrm{eco}}$) and emissions (${\omega }^{\mathrm{env}}$) between 0 and 1. Red markers indicate the extreme weight allocations: dominant cost minimization (${\omega }^{\mathrm{eco}}=1,{\omega }^{\mathrm{env}}=0$) and dominant emission minimization (${\omega }^{\mathrm{eco}}=0,{\omega }^{\mathrm{env}}=1$). The green marker highlights the selected trade-off (${\omega }^{\mathrm{eco}}=0.9,{\omega }^{\mathrm{env}}=0.1$), which we adopt in this work as a cost-prioritized configuration. This choice significantly reduces total cost while keeping emissions at a reasonable level, demonstrating the model’s ability to balance economic, environmental, and user-oriented objectives.

Table 4. Comparative performance of different models under 20% prediction error.

Performance Indicators	Mean ± SD
	Model1	Model2	Model3	Model4	Proposed
Average SoC (%)	80.15 ± 0.12	84.57 ± 1.06	80.11 ± 0.04	84.70 ± 1.23	86.34 ± 1.31
Total Cost (Euro)	181.21 ± 1.05	180.77 ± 2.66	180.35 ± 1.20	180.24 ± 1.23	174.49 ± 1.24
PV Utilization (%)	85.60 ± 1.58	89.78 ± 1.38	97.03 ± 0.34	97.18 ± 0.42	94.91 ± 1.10
Energy from Grid—Day-ahead (kWh)	2640.02 ± 45.30	2640.02 ± 45.30	2084.56 ± 0.00	2084.56 ± 0.00	2640.02 ± 45.30
Energy from Grid—Intraday (kWh)	183.29 ± 4.64	162.41 ± 21.08	509.08 ± 72.57	563.72 ± 74.09	92.25 ± 13.20
Energy from PV (kWh)	1698.15 ± 11.14	1780.47 ± 8.47	1925.16 ± 25.98	1928.28 ± 27.60	1883.06 ± 23.81
Total Emissions (kg)	1342.85 ± 27.77	1331.60 ± 32.82	1212.56 ± 40.54	1242.60 ± 40.59	1303.67 ± 31.75

presents a comprehensive performance comparison across different models, derived from 50 independent simulation runs incorporating 20% prediction errors. The proposed methodology achieves the highest average departure SoC while simultaneously minimizing total costs, demonstrating robust performance across key metrics.

In terms of PV utilization, the proposed model achieves the best performance among approaches with day-ahead prediction (Models 1 and 2), reaching about 95% under nominal conditions. Its utilization is slightly lower than that of intraday-only models (Models 3 and 4), as day-ahead plans constrain flexibility and reduce the scope for aggressive, opportunistic use of solar energy.

Analysis of energy sourcing patterns reveals distinct operational characteristics across model categories. Day-ahead prediction models—including the proposed method and Models 1 and 2—purchase energy from the day-ahead market to cover both base load and anticipated EV charging demands, taking advantage of typically lower day-ahead prices. Models 3 and 4, however, restrict day-ahead purchases to base load requirements and procure EV charging energy from the intraday market, where prices are generally higher. By contrast, the proposed model strategically balances day-ahead commitments with intraday adjustments, leveraging its two-stage optimization to respond to prediction errors and unexpected events. This enables more accurate day-ahead planning while minimizing exposure to real-time price volatility, resulting in the lowest intraday energy requests among all day-ahead models.

Total emissions are marginally higher for the proposed method, a direct result of the selected weight prioritization that favors cost optimization over emission reduction. This trade-off can be easily adjusted by recalibrating the objective weights, allowing system operators to prioritize lower emissions at the expense of increased cost. Such flexibility enables alignment with varying environmental policies or economic constraints without structural model changes.

Figure 8 illustrates the performance of each model under increasing prediction uncertainty, ranging from 0% to 100% in load, PV, electricity price forecasts, EV schedules, and initial SoC, using a representative day for comparison. In terms of average SOC, the proposed model consistently outperforms all others, especially Model 2, which lacks intraday adjustment capabilities and exhibits significant performance degradation under uncertainty. Regarding total cost, Models 3 and 4, which rely solely on intraday optimization, incur substantially higher expenses due to their limited foresight and dependence on the volatile intraday market. In contrast, the proposed method achieves the lowest cost across all uncertainty levels, demonstrating the advantage of combining day-ahead planning with intraday recourse to adapt to unexpected variations. PV utilization declines across all models as prediction error increases, though intraday models maintain higher utilization by leveraging real-time PV availability. The proposed model achieves the highest PV utilization (75%) under extreme prediction error conditions among day-ahead-enabled approaches, demonstrating its ability to ensure robust renewable integration despite substantial uncertainty.

Beyond uncertainty handling, infrastructure availability also plays a critical role. Figure 9 investigates the impact of the number of bidirectional charging stations on average cost across different models over multiple days. Intraday-only models consistently incur higher costs, while the proposed model achieves the lowest average cost among day-ahead-based models. As the number of bidirectional stations increases, costs decrease but show only a slight additional improvement beyond 15 stations. Given the higher expense of bidirectional infrastructure, we select 10 bidirectional stations as a cost-effective choice. The figure also suggests that not all charging stations need to be bidirectional, since the cost reduction benefit levels off after a certain point.

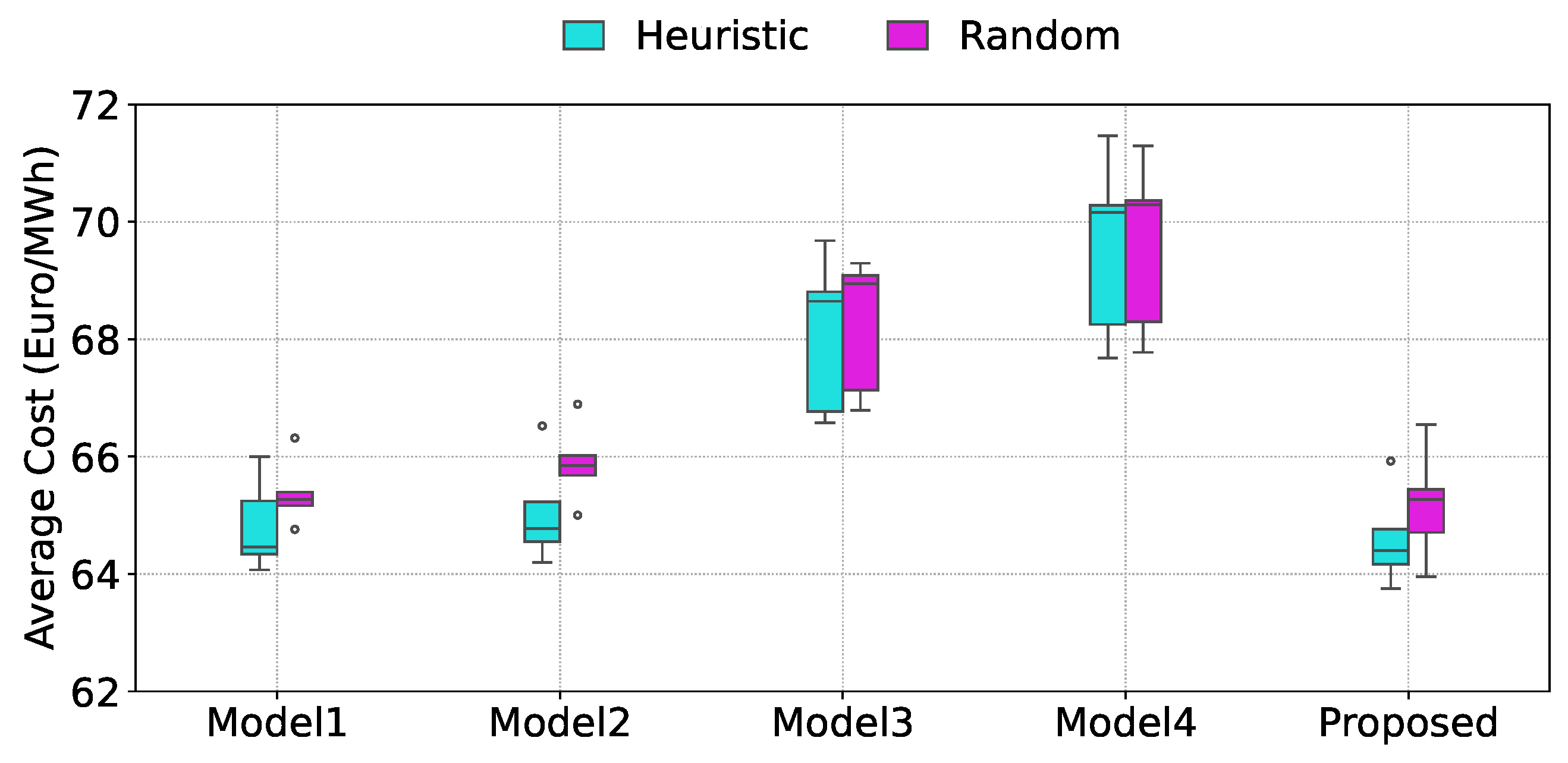
Given the limited number of bidirectional stations, Figure 10 compares two EV assignment strategies: random assignment and the proposed heuristic. Random assignment allocates EVs inefficiently, whereas the heuristic prioritizes vehicles with higher discharge potential, resulting in better utilization and lower average costs. Among all models, the proposed model with heuristic assignment achieves the lowest average cost.

To further investigate the proposed model, Figure 11 illustrates its performance under varying departure times. It can be observed that later departure times, especially after 17:00, lead to a notable reduction in average cost. This is attributed to the higher evening electricity prices, which allow the model to strategically schedule EV discharging and effectively leverage available capacity to minimize costs.

To assess scalability, we evaluate computational performance for fleet sizes ranging from 25 to 500 EVs (

Table 5. Average runtime (seconds) of proposed model across different fleet sizes.

Method	25 EVs	50 EVs	100 EVs	200 EVs	500 EVs
Day-ahead	4.48 s	10.03 s	24.28 s	97.51 s	1024.49 s
Intraday	0.65 s	1.14 s	2.45 s	3.68 s	6.44 s

). The day-ahead MILP becomes increasingly complex as the number of vehicles increases, resulting in both a higher number of decision variables and constraints. Nevertheless, because day-ahead optimization is performed offline with sufficient computation time, runtimes remain practical even for large fleets. In contrast, intraday re-optimization is designed to stay lightweight: only a small batch of EVs is adjusted at each iteration, so the problem size depends little on the total fleet size. Consequently, intraday runtimes stay short across all scenarios, ensuring responsiveness under real-time conditions. Overall, the results demonstrate that the proposed framework scales effectively to large fleets while preserving both computational tractability and real-time feasibility.

The results demonstrate that combining day-ahead and intraday scheduling yields both economic and environmental benefits, striking a balance between global optimization and real-time responsiveness. Scalability is ensured through lightweight intraday re-optimization, which keeps runtime low even for large fleets. The analysis also highlights the importance of charging station assignment, the limited benefit of installing large numbers of bidirectional stations, and robustness under prediction errors.

7. Conclusions

This paper has shown that combining day-ahead and intraday scheduling provides significant advantages for managing EV fleets with workplace charging and on-site PV. Uncoordinated charging can create large peaks, and upgrading cables and fuses to handle them is costly, making smart charging essential. Workplace fleets are particularly well-suited for coordinated scheduling, as their usage patterns are predictable and vehicles often remain parked for extended periods. PV generation adds further value, as its afternoon peak can be aligned with charging demand. In the proposed framework, day-ahead optimization establishes a consistent baseline plan, while intraday adjustments provide the flexibility to handle forecast errors and unplanned arrivals.

This dual approach comes with methodological trade-offs. Day-ahead MILP yields near global optimal schedules but grows rapidly in complexity with fleet size. By contrast, the intraday MILP-heuristic remains lightweight by limiting re-optimization to small EV batches, ensuring responsiveness under real-time conditions. Together, the stages deliver both economic and environmental benefits beyond those of single-horizon methods. The Pareto frontier further demonstrates how cost and emission objectives can be balanced, enabling operators to adjust priorities according to market or policy requirements.

The results also provide several practical insights. Infrastructure constraints are decisive: while increasing the number of bidirectional stations lowers costs, the benefit diminishes beyond a moderate level, making partial deployment a cost-effective strategy. Station assignment is likewise critical. Results show that our heuristic allocation based on charging urgency and discharging potential improves utilization and reduces costs compared to random assignment. Finally, robustness to uncertainty is essential: even under significant prediction errors in load, PV, prices, and EV schedules, the framework maintains stable performance compared to day-ahead-only methods, underscoring its suitability for real-world deployment.

A Python-based simulator was developed to support the analysis. It integrates both day-ahead and intraday planning, explicitly models forecasted and realized values, and incorporates stochastic EV behavior, PV generation, building load, and market prices. This modular design not only enables controlled experimentation but also provides a foundation for real-world integration.

Several limitations remain. The simulator abstracts from driver non-compliance, communication delays, and OCPP-level implementation details. Addressing these aspects in future work will be essential for translating the proposed approach into pilot deployments. In addition, although the imposed power and SoC limits effectively mitigate excessive battery degradation, the increased frequency of charging and discharging caused by the combined day-ahead and intraday scheduling may still contribute to long-term battery performance. Future studies could address this issue by constraining the frequency of plan adjustments or incorporating health-aware objectives when generating charging schedules. The current evaluation focuses on daily operational behavior but can be extended to longer horizons to capture cumulative performance and seasonal variations. Furthermore, the study does not quantify the cost–benefit trade-off between charger installation and operational savings. Extending the framework toward a techno-economic optimization of charger deployment and operation is a promising direction for future research. Nonetheless, the findings demonstrate the strong potential of coordinated day-ahead and intraday scheduling to enable cost-effective, sustainable, and practical charging strategies for fleets. The proposed coordination framework thus provides an actionable tool for fleet operators seeking to reduce energy costs and emissions while avoiding the need for additional grid expansion.