Tool Wear Prediction Using Machine-Learning Models for Bone Drilling in Robotic Surgery

Abstract

Bone drilling is a widely encountered process in orthopedic surgeries and keyhole neuro surgeries. We are developing a sensor-integrated smart end-effector for drilling for robotic surgical applications. In manual surgeries, surgeons assess tool wear based on experience and force perception. In this work, we propose a machine-learning (ML)-based tool condition monitoring system based on multi-sensor data to preempt excessive tool wear during drilling in robotic surgery. Real-time data is acquired from the six-component force sensor of a collaborative arm along with the data from the temperature and multi-axis vibration sensor mounted on the bone specimen being drilled upon. Raw data from the sensors may have noises and outliers. Signal processing in the time- and frequency-domain are used for denoising as well as to obtain additional features to be derived from the raw sensory data. This paper addresses the challenging problem of identification of the most suitable ML algorithm and the most suitable features to be used as inputs to the algorithm. While dozens of features and innumerable machine learning and deep learning models are available, this paper addresses the problem of selecting the most relevant features, the most relevant AI models, and the optimal hyperparameters to be used in the AI model to provide accurate prediction on the tool condition. A unique framework is proposed for classifying tool wear that combines machine learning-based modeling with multi-sensor data. From the raw sensory data that contains only a handful of features, a number of additional features are derived using frequency-domain techniques and statistical measures. Using feature engineering, we arrived at a total of 60 features from time-domain, frequency-domain, and interaction-based metrics. Such additional features help in improving its predictive capabilities but make the training and prediction complicated and time-consuming. Using a sequence of techniques such as variance thresholding, correlation filtering, ANOVA F-test, and SHAP analysis, the number of features was reduced from 60 to the 4 features that will be most effective in real-time tool condition prediction. In contrast to previous studies that only examine a small number of machine learning models, our approach systematically evaluates a wide range of machine learning and deep learning architectures. The performances of 47 classical ML models and 6 deep learning (DL) architectures were analyzed using the set of the four features identified as most suitable. The Extra Trees Classifier (an ML model) and the one-dimensional Convolutional Neural Network (1D CNN) exhibited the best prediction accuracy among the models studied. Using real-time data, these models monitored the drilling tool condition in real-time to classify the tool wear into three categories of slight, moderate, and severe.

1. Introduction

In orthopedic surgical procedures, such as internal fixation of fractures, precision bone drilling is a fundamental and critical step. Prior to the placement of fixation hardware, such as screws, plates, and intramedullary nails, it is essential to drill accurately positioned and dimensioned holes into the bone. The biomechanical stability of the fixation and the long-term healing outcome are highly dependent on the drilling accuracy, thermal damage control, and minimization of mechanical trauma to the surrounding bone tissue [1]. In conventional surgical drilling, complications such as thermal necrosis, microcracks, or misaligned trajectories may arise due to uncontrolled force application, excessive temperature rise (above the 47 °C threshold), or poor ergonomic control by the surgeon [2]. Therefore, robot-assisted bone drilling offers an ideal solution to achieve repeatable, accurate, and minimally invasive procedures.

Precision bone drilling is a fundamental and critical procedure in orthopedic surgery, particularly for the fixation of fractures using implants such as screws, plates, or intramedullary rods. The process demands not only geometric accuracy in the drilled hole but also the preservation of bone integrity and biological viability [3]. Improper drilling can lead to delayed healing due to complications such as microcracks [4], misalignment [5], and thermal necrosis [6] of bone tissue.

A key challenge in bone drilling is the generation of excessive heat due to friction between the drill bit and bone. Early studies [7] have pointed out how poor drill condition increases bone cell damage. It is well established that temperatures exceeding 47 °C can lead to thermal necrosis, permanently damaging bone structure, and affecting postoperative recovery [8]. The application of excessive axial force or torque may cause mechanical failure, such as microfractures, while insufficient force can lead to incomplete drilling or tool slippage [9].

Another critical factor influencing surgical success is tool wear, which accumulates progressively during drilling. A worn drill bit results in increased cutting forces, higher temperatures, poor hole quality, and longer drilling times [10]. Predicting and compensating for tool wear is therefore essential for ensuring consistent performance and minimizing intraoperative risks. Staroveski et al. [11] demonstrated that the wear of the cortical bone drill could be effectively classified using neural networks trained in the features of force, torque, and acoustic emission, demonstrating the feasibility of AI-assisted wear detection during surgery.

Additionally, vibrations generated during drilling, especially in dense cortical bone, can degrade the precision of drilling and cause discomfort or structural damage [12]. These vibrations, along with force, torque, and thermal feedback, provide vital information for real-time monitoring of the drilling state. Although the focus of the present work is surgical bone drilling, and surgery in general is a life-critical activity, the methodologies for characterization and tool wear prediction may be inspired by broader drilling research in manufacturing, which involve materials that are much stronger, such as metals and alloys, including those used in surgical implants [13], and much less homogeneous, such as composites [14].

Liu et al. [15] recently designed a deep learning-based tool wear monitoring system that uses vibration and cutting force signals to predict drill wear progression in bone drilling with high accuracy, highlighting the potential of integrating AI for risk reduction.

The convergence of robotics and sensor technology provides a platform for developing high-precision, minimally invasive surgical systems capable of overcoming the limitations of traditional manual drilling. Such systems offer repeatability, consistency, and data-driven decision support, marking a significant advancement in orthopedic surgical practice [16].

In the context of orthopedic bone drilling, tool wear is an increasingly recognized factor influencing both surgical accuracy and patient safety. Repeated usage of surgical drill bits, especially in high-speed or dense bone drilling scenarios, leads to progressive loss of sharpness, chipping, or flank wear, which can significantly degrade cutting efficiency [17]. As the tool wears, the required cutting force and torque increase, thermal energy rises, and hole quality deteriorates, contributing to longer operation times and increased risk of thermal necrosis [18]. Contamination may be a serious issue in the case of orthopedic implant surgeries if traditional coolants are used for machining in the custom-fitting of implants. Gómez-Escudero et al. [13] have presented a novel solution to this problem by using cryogenic carbon dioxide as the coolant. In the case of orthopedic surgeries, sterilized water is used as a coolant intermittently. Although the end-effector developed by us has provision for dispensing coolant water, coolant was not used in the drilling experiments as the focus is exclusively on tool condition monitoring.

Multiple studies in the field of manufacturing and biomedical engineering have addressed the importance of real-time tool wear monitoring and prediction. Techniques such as acoustic emission analysis, vibration signal monitoring, and cutting force modeling have been applied to industrial machining processes. These methods have shown potential for translation into surgical applications where predictive models can alert the system or surgeon about imminent tool failure or reduced performance. Peña et al. [19] have successfully implemented a novel method of preventing burr formation on aluminium alloy components during drilling using real-time monitoring of spindle torque and signal processing. Islam et al. [20] combined conventional analysis techniques with supervised ML algorithms to predict bone drilling temperatures using two different algorithms. Kung et al. [21] proposed a neural network model for immediate thermal visualization as a surgical assistive device for a human surgeon.

Recent research has explored the use of machine learning (ML) algorithms to correlate sensor-derived features (force, torque, vibration, and temperature) with the actual wear condition of drill bits [22,23]. These predictive frameworks, when combined with robotic systems, have been shown to reduce intraoperative risks, improve hole quality, and optimize tool replacement cycles, especially in constrained surgical environments where visual inspection is not feasible. Agarwal et al. [24] demonstrated that machine learning can effectively predict temperature elevation in conventional and rotary ultrasonic bone drilling. Extensive review of the literature on tool wear monitoring using AI [25] and big data [26] indicate the increasing research interest in and possible effectiveness of these modern techniques for tool condition monitoring. Due to the availability of innumerable ML models, identification of the most suitable model is a problem of plenty. Ensemble models that combine the results from multiple models are often employed. Bustillo et al. [27] have employed one such technique for the process optimization of friction drilling. Alajmi and Almeshal [28], using copper and cast-iron datasets, observe that the extreme gradient boosting algorithm with hyperparameter optimization performs better for predicting the tool wear as compared to support vector machines and multilayer perceptron, which are otherwise more popular. Our work attempts to analyze the performance of 47 different models, including a number of ensemble models, and the best few models are shortlisted for predicting real-time tool condition monitoring in bone drilling.

Despite these advances, the literature focused specifically on orthopedic surgical tool wear monitoring using real-time data acquisition for robotic surgery with sensor-integrated drilling tools is limited. This gap has motivated us to develop an end-effector capable of intelligently monitoring tool condition during bone drilling and automatically control the drilling process to maintain consistent performance and prevent complications.

This paper is organised as follows: Section 2 describes the experimental setup of the end-effector for robotic drilling for surgical applications. Section 3 discusses the signal processing on the multisensor data and the feature extraction from the sensory data for the purpose of machine learning. Section 4, Section 5, Section 6, Section 7 and Section 8 discusses the model training and hyperparameter tuning framework. Results are discussed in Section 9. Conclusions along with the scope and limitations of the current study are summarized in Section 10.

2. Experimental Setup

We have developed a sensor-integrated smart end-effector, specifically designed for precision bone drilling in robotic-assisted orthopedic surgery by a collaborative robot arm. The end-effector is engineered to meet the following objectives:

• Drill precisely aligned holes in cortical and cancellous bone structures, with minimal human intervention.
• Monitor drilling conditions in real-time, including force, torque, temperature, and vibration.
• Ensure thermal safety and mechanical precision, especially during high-speed operations or drilling in dense bone regions.

The experimental drilling setup consists of the collaborative robotic arm (Model UR5e from Universal Robots Inc., Odense, Denmark [29]) integrated with the end-effector developed by the authors for precision bone drilling. The experimental setup of the UR5e robot with the end-effector for robotic drilling is shown schematically in Figure 1, with wrist force sensors located on the robot arm providing force–torque data. The end-effector (shown in enlarged view) has provisions for optional external sensors (for vision and obstacle avoidance). Vibration data will be acquired from the sensors located on the bone to be drilled.

The objective of the experiment is to perform robotic drilling on the bone sample. The data are collected when drilling multiple holes with a depth of 3 mm while monitoring real-time force data and ensuring precise motor control.

2.1. Drilling Controller and Sensor Data Acquisition

The drilling controller is interfaced with the UR5e Robot Controller and acts as an interface for programmed actuation of the drilling tool. The configuration of the drilling controller is shown in Figure 2. The controller and sensors are integrated with the UR5e robot controller using the protocol prescribed by the UR5e robot manufacturer. This facilitates automatic control of the drilling processes and real-time data acquisition.

The drill bit is rotated by the DC motor, which may be controlled from the robot controller automatically. The motor driver that delivers the required power input to the motor supports a broad voltage range, ranging from 5 V to 35 V. The motor driver is interfaced with the UR5e robot controller through a microcontroller boards. The DC-DC converter ensures a safe level of the input voltage to the motor driver and the microcontroller board. A custom-made joystick interface is also provided for manual positioning of the tool by jogging. The joystick provides a convenient interface for manual motion control of the end-effector. The Left/Right input to the joystick moves the end-effector along the X-axis, while the Up/Down input to the joystick results in the vertical motion of the end-effector along the Z-axis. This helps in positioning or retraction of the drilling tool manually, if required.

The force data during the entire drilling cycle was captured using the UR5e’s built-in six-component wrist force sensor. The data acquisition was performed using the RTDE (Real-Time Data Exchange) interface [30]. The axial drilling force ($F_z$), the lateral forces ($F_x$ and $F_y$), and the torque values $(M_x,M_y,M_z)$ are acquired. The RTDE interface is configured for data acquisition at a sampling frequency of 125 Hz, enabling real-time monitoring and analysis of the drilling behavior and the forces involved in the tool–bone interaction, and the evaluation of tool wear indicators such as increasing force or torque during repeated cycles.

The force–torque data from the robot arm, drilling parameters from the drilling controller, and the temperature and vibration data from the bone being drilled are collectively acquired by the master controller. The master controller is a laptop running RTDE. Temperature and vibration sensors are located on the bone being drilled, and the data from these sensors are acquired directly by the laptop through a microcontroller interface.

2.2. Robot Motion and Drilling Sequence

Using the combination of the joystick and programmed monitoring by the infrared depth sensor, the robot is moved to a predefined starting position so that the distance between the tip of the tool and the bone surface is exactly 2 mm. This “ready” position allows safe tool engagement before spindle activation.

Once the UR5e robot positions the drill tip 2 mm away from the bone surface, the drill motor is activated. After contact with the bone, the robot advances the drill 3 mm along the tool axis, resulting in an actual drilled hole depth of 3 mm as shown in Figure 3. A hole depth of 3 mm was selected to simulate realistic cortical bone drilling in surgical applications.

Upon reaching the target depth, the robot retracted to the starting point (2 mm above the bone target) and the motor is turned OFF to complete the drilling cycle.

Titanium nitride-coated HSS drill bits the from Bosch Titanium drill bit set were used for the experiments. Ten holes each were drilled using the drill bits of diameters 2 mm and 3 mm with chisel edge drill geometry with a point angle of 135° and a helix angle of 30°. The cutting parameters are as follows: Spindle speeds of 1000 rpm and 1500 rpm, and feed rates of 30 mm/min and 50 mm/min. No coolant was used. The objective of the study was the real-time condition monitoring of a given tool under allowable drilling conditions. The dataset used for the machine learning methodology consisted solely of the sensory data resulting from the above experiments.

3. Machine Learning Methodology

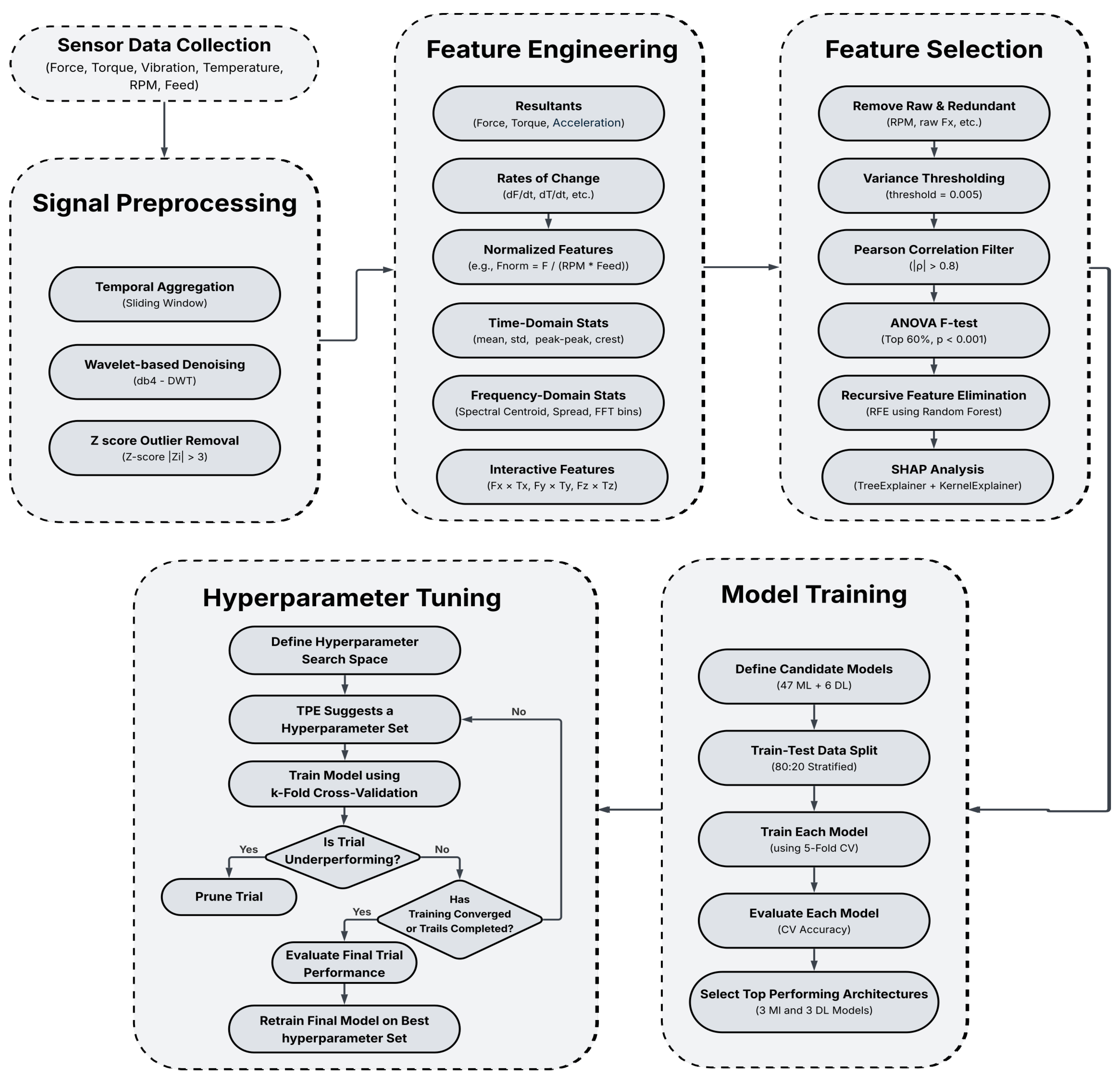
As the data from the sensors were collected at the sampling frequency of 125 HZ (every 8 ms), a large amount of raw data is created. Tool condition monitoring (TCM) relies on analyzing sensor signals such as force, vibration, torque, and thermal data to detect early signs of tool wear. As raw sensor data often contain high-frequency and noisy signals, making it difficult to establish clear links between the signals and the wear state of the tool, we adopt a sequence of processes involving signal pre-processing, feature extraction, and feature selection, as shown in Figure 4, which will be useful in training the ML model to classify tool wear.

In Signal Preprocessing, raw sensory data from different sensors are temporally aggregated over a period of time or a number of samples. The noise from the sensor data caused by external and unnecessary factors is removed using denoising techniques. The resulting data passes through outlier removal to make the sensor data more stable and reliable [31]. The Feature Engineering process helps in obtaining more features such as the resultant of the force vector, the rate of change of force, basic statistics, and time-domain and frequency-domain values of raw sensor data [32].

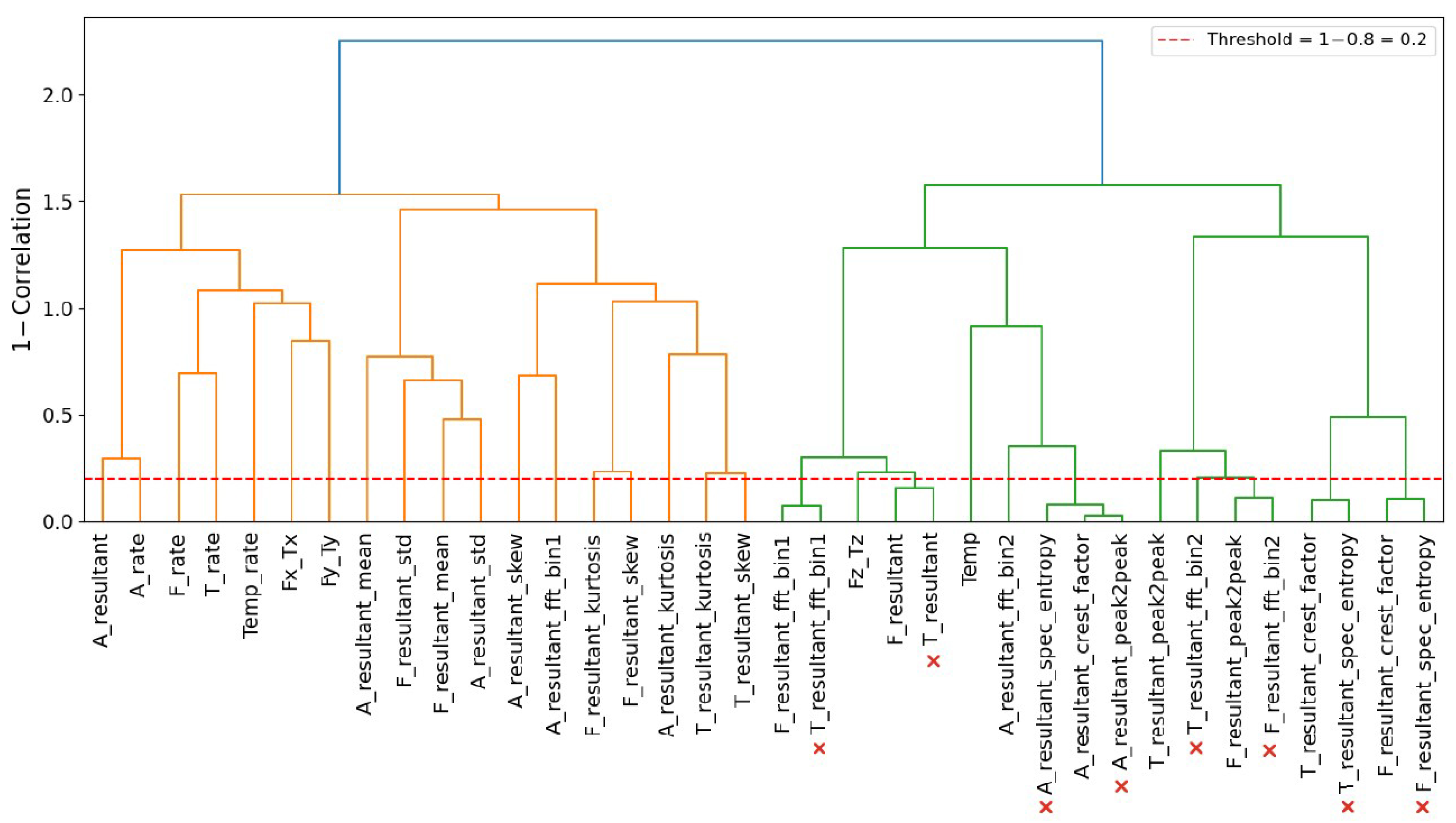
Finally, Feature Selection is employed to filter out the unnecessary features [33].

To select the best model for TCM, it is proposed to consider supervised learning algorithms based on both classical ML models and deep learning (DL) architectures. Three top-performing models with diverse architectures are selected from each of these two categories [23]. This approach ensures that the models show different improvements from optimization techniques like Bayesian and Hyperband optimization, implemented using Optuna [34], rather than having a single architecture outperform the others [35].

This multi-step approach with signal preprocessing, feature engineering, feature selection, and model selection and optimization ensures good model performance and reliable tool wear classification by cleaning the data, selecting important features, training models with diverse architecture, and optimizing them with techniques like Bayesian and hyperband optimization.

4. Data Preprocessing

Data preprocessing is a necessary step before being able to train models with the data collected from sensors, especially in TCM. Due to noise and other external factors in the signals collected during the experiment, it is challenging to establish a clear relationship between the raw signals and the tool wear state. Data preprocessing generally includes cleaning and transforming the raw sensor data to reduce noise and removing outliers to improve the performance of the trained model [31], as well as making sure the trained model does not overfit.

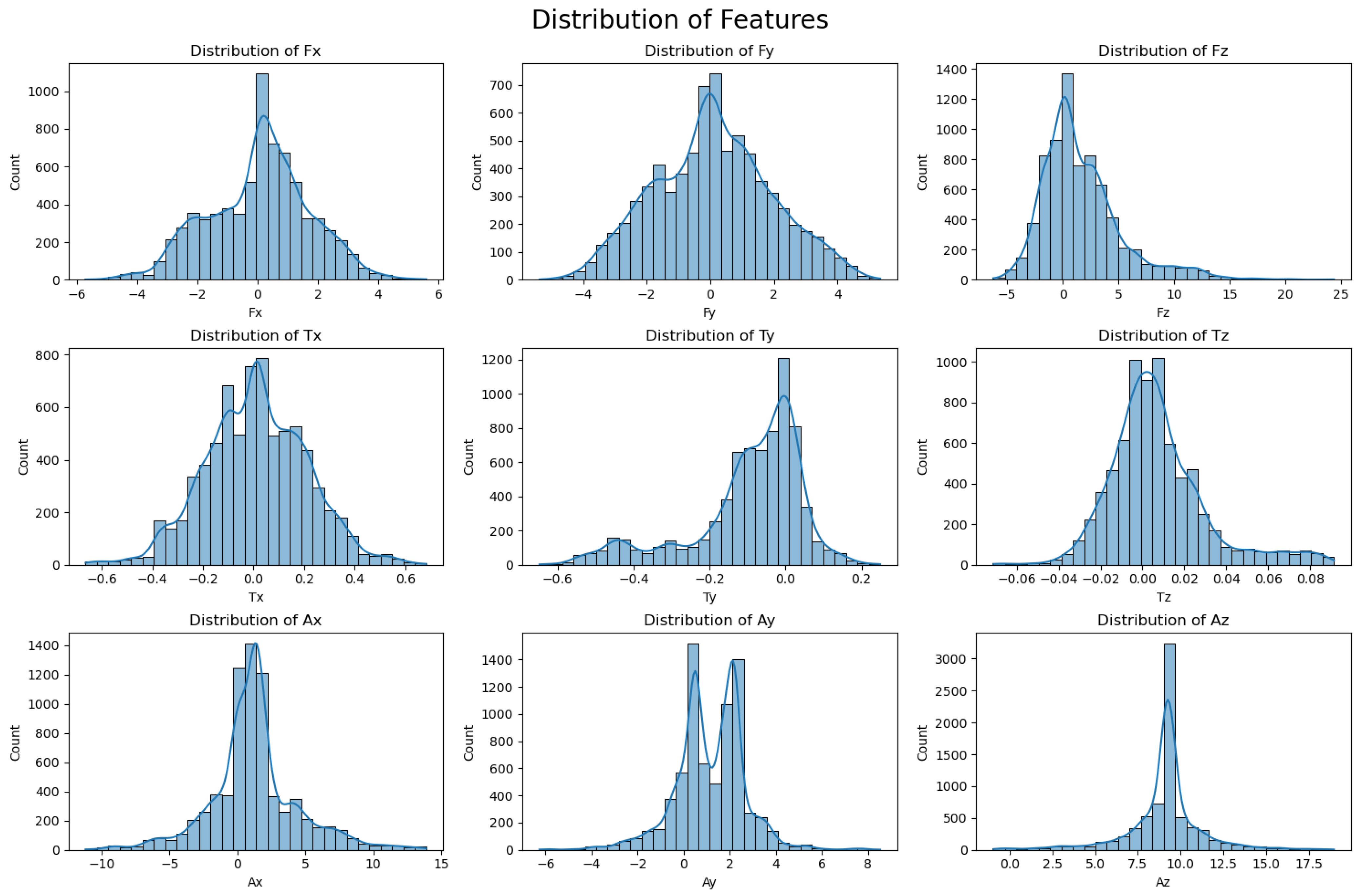
Before data preprocessing, we analyzed the distribution of raw features. Figure 5 shows the typical distribution of force ($F_x$, $F_y$, $F_z$), torque ($T_x$, $T_y$, $T_z$), and acceleration ($A_x$, $A_y$, $A_z$) features. In order to facilitate subsequent analysis such as outlier detection, the dimensionless Z-score of the raw features rather than the actual values of the raw features are used for obtaining the plots in Figure 5. The Z-score of a raw data x with mean $\mu$ and standard deviation $\sigma$ is defined as $(x-\mu )/\sigma$.

$F_x$ and $F_y$ are symmetric and centered near zero, indicating balanced lateral forces, while $F_z$ is right-skewed with high outliers due to vertical tool contact. Torque features show irregular patterns; $T_y$ is clearly multimodal, pointing to variable cutting dynamics. $A_x$ and $A_y$ display bimodal behavior, and $A_z$ peaks around 9.81 due to gravity, with added vibration. The non-Gaussian, skewed, and multimodal nature of these distributions highlights the need for robust preprocessing and careful feature selection.

4.1. Temporal Aggregation

In this study, the raw sensory data is subjected to temporal aggregation, which is a common signal smoothing and dimensionality reduction technique used in time-series signal processing. Temporal aggregation reduces high-frequency noise but retains hidden patterns or trends, preventing overfitting of trained models due to high noise and correlated consecutive samples. Temporal aggregation was applied on a sliding window of 5 consecutive data samples for the data from all sensors.

4.2. Denoising

Next, we applied denoising techniques to the temporally aggregated dataset. We used wavelet-based denoising with the Daubechies-4 (db4) wavelet; this was applied to all force, torque, acceleration in three axes, and temperature sensor data due to excellent time–frequency localization for nonstationary mechanical signals of db4. The denoising process follows the discrete wavelet transform (DWT) in which the input signal is decomposed, thresholded, and reconstructed, and then soft thresholding is applied to the detail coefficients at each level, with noise variance ${\sigma }^2$ estimated using the mean absolute deviation.

The DWT coefficients are decomposed by projecting the signal onto scaled and shifted wavelet bases:

$$W_{j,k}=\sum _{n}x\left[n\right]·{\psi }_{j,k}\left(n\right),{\psi }_{j,k}\left(n\right)=2^{-j/2}\psi (2^{-j}n-k)$$

(1)

To remove noise, soft thresholding is applied to the detail coefficients $D_j$:

$${\tilde{D}}_j\left(k\right)=\left\{\begin{array}{cc}\mathrm{sign}\left(D_j\left(k\right)\right)\left(\right|D_j\left(k\right)|-\lambda ),\hfill & \mathrm{if}|D_j\left(k\right)|>\lambda \hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(2)

where $\lambda$ is a scale-adaptive threshold chosen via universal thresholding.

$$\lambda =\sigma \sqrt{2logN}$$

(3)

where N is the signal length and the variance ${\sigma }^2$ estimates noise using the mean absolute deviation.

$$\sigma \approx \mathrm{median}\left(\right|D_1\left[k\right]\left|\right)/0.6745$$

(4)

The denoised signal is reconstructed via the inverse DWT:

$$\widehat{x}\left[n\right]=\mathrm{IDWT}(A_J\left[n\right],{\tilde{D}}_1\left[n\right],\dots ,{\tilde{D}}_J\left[n\right])$$

(5)

4.3. Outlier Removal

Finally, we removed the outliers from the datasets using Z-score outlier removal, where points with $|Z_i|>3$ as shown in Figure 5 are removed to avoid a skewed distribution and misrepresentative features that are due to events like tool crashes or sudden material changes [33]. The removal of outliers prevents classifier models from being biased toward extreme but misrepresentative patterns from sensor failure or machine glitches.

5. Feature Engineering

Feature engineering is the process of converting raw or pre-processed sensor data into structured features that capture patterns relevant to the target prediction [36]. In TCM, well-engineered features reflect the physical behaviour of tools under varying mechanical loads, vibrations, heat, and wear. These features are derived from signal transformations, time-domain, frequency-domain, and interaction-based data.

5.1. Time-Domain Features

To simplify analysis and reduce complexity, we calculate the resultants, which are combined values that are obtained by taking the magnitudes of the three spatial axes (X, Y, Z) and applying the Euclidean norm. These values represent the overall strength of the signal and indicate the total mechanical load, torsional moment, or vibration experienced by the tool [37]. By focusing on this scalar, we can eliminate directional noise. Further, temporal derivatives (rate of change with time) of the above magnitudes with time indicate sudden impacts and vibrations, which may indicate potential tool damage [38]. Rate of change of temperature is also used as another feature.

The values of force, torque, and acceleration are normalized by dividing them by the product of spindle speed (RPM) and feed rate, as in Equation (6). This allows for easier comparisons across different cutting conditions and different machining parameters [39].

$$F_{\mathrm{norm}}={\displaystyle \frac{F_{\mathrm{resultant}}}{\mathrm{RPM}·\mathrm{Feed}}},T_{\mathrm{norm}}={\displaystyle \frac{T_{\mathrm{resultant}}}{\mathrm{RPM}·\mathrm{Feed}}},A_{\mathrm{norm}}={\displaystyle \frac{A_{\mathrm{resultant}}}{\mathrm{RPM}·\mathrm{Feed}}}$$

(6)

In addition, six statistical parameters (mean, standard deviation, skewness, kurtosis, crest factor, and peak to peak) are used as as the time-domain features of the sensor signals [40].

5.2. Frequency-Domain Features

Frequency-domain features provide insight into the dominance of different frequencies in the signals. Frequency-domain features are derived either by using the frequency of the features or by converting sensor signals into the frequency spectrum using transformation techniques like the Fast Fourier Transform (FFT) [41]. These features are essential for finding hidden patterns such as periodic vibrations, harmonics, and noise that relate to phenomena like chatter, resonance, and micro-fractures, and, similar to time-domain, we apply the frequency-domain to resultants of force, torque, and vibration because they can summarize all 3 of them in three axes (X, Y, Z). Frequency-domain features listed in

Table 1. Frequency-domain features used in this study. and formulas of frequency-domain features.

Feature	Definition
Spectral Centroid [42]	Spectral Centroid represents the centre of mass of the frequency spectrum by weighting each frequency by its amplitude. A higher centroid indicates more energy at higher frequencies, often caused by wear-related vibrations or chatter.
Spectral Spread [43]	Spectral Spread measures how widely the spectral components are distributed around the centroid. A larger spread indicates greater variability in vibration frequencies, often caused by mechanical looseness or wear progression.
Spectral Entropy [44]	Spectral Entropy quantifies the randomness or disorder in the frequency spectrum. Higher entropy suggests a more uniform spectral energy distribution, often associated with unstable cutting or irregular vibrations.
FFT Bins (2 bins) [45]	FFT Bins divide the frequency spectrum into equal-width intervals and sum the energy within each bin. These bins highlight specific frequency regions where tool wear manifests due to imbalance, chatter, or breakage. Two bins were selected for this study to isolate prominent frequency bands.

are selected.

5.3. Interactive Features

Interactive features are combinations of multiple raw features in a multiplicative or composite manner to capture complex, non-linear relationships between them. In this study, we use three interactive features by multiplying force and torque components along the same corresponding axis (X, Y, and Z) to understand axis-wise mechanical coupling:

Fx_Tx $=F_x\times T_x$: Interaction between drilling force and torque in the X-direction.

Fy_Ty $=F_y\times T_y$: Interaction between drilling force and torque in the Y-direction.

Fz_Tz $=F_z\times T_z$: Interaction between drilling force and torque in the Z-direction.

After completion of all the feature extraction steps, we have a total of 60 features as listed in

Table 2. Feature extraction summary at each step.

Extraction Step	Extracted Features Count
Initial	14
Preprocessed and Derived	10 (3 × 3 + 1)
Time-Domain Statistical	18 (3 × 6)
Frequency-Domain Spectral	15 (3 × 5)
Interactive Feature	3
Total	60

. By excluding raw features, 47 statistical and engineered features [46] are retained as they are likely more relevant. Feature selection is employed to reduce the number of features further.

6. Feature Selection

Feature selection is the process of identifying and selecting only the most informative and not-redundant features to be used in the ML models. This reduces dimensionality, improves computational efficiency, and reduces the risk of overfitting [33]. We used multi-stage feature selection in an order we found to work the best with threshold, found by implementing cross-validation with multiple values. The sequence of steps used in the multi-stage feature selection is listed in Figure 4.

6.1. Variance Thresholding

In this multi-stage process, first we apply variance thresholding. This method removes features that have little to no variation across samples, as such features are unlikely to help in distinguishing between different wear classes [47]. Features with nearly constant values contribute little to class separation, so variance thresholding removes features with low statistical variability, often due to sensor saturation or measurement redundancy. By applying a variance threshold of 0.005, the number of features was reduced from 47 to 36, as shown in Figure 6.

6.2. Correlation Filter

Highly correlated features carry similar information, and thus add redundancy and unnecessary complexity to the model [48]. Pearson’s Correlation is one of the most used techniques to find the correlation between two features. The Pearson’s Correlation Coefficient $\rho (X,Y)$ between two features X and Y is given by [49]

$$\rho (X,Y)={\displaystyle \frac{E\left(XY\right)-E\left(X\right)E\left(Y\right)}{\sqrt{E\left(X^2\right)-E{\left(X\right)}^2)}\sqrt{E\left(Y^2\right)-E{\left(Y\right)}^2}}}.$$

(7)

The distance measure defined as $\delta (X,Y)=1-\left|\rho \right(X,Y\left)\right|$ is often used. When two features are highly correlated, their distance measure is low. Such a pair of features only provides overlapping information, and either of the features may be dropped. This step helps in reducing the number of features to be handled by the algorithm. This can also prevent issues such as multicollinearity, which can negatively affect the results and lead to unreliable coefficients.

We used a threshold of $\delta (X,Y)\le 0.2$ to designate such highly correlated features and plotted the results as a dendrogram in Figure 7. Features grouped closely below the threshold of 0.2 are redundant, while those separated above the threshold provide unique and useful information. This reduced the number of features from 36 to 28. The features that are eliminated in this process are marked with the × symbol in Figure 7.

6.3. ANOVA F-Test

Correlation-based feature selection is followed by ANOVA F-test, which evaluates how well each feature separates the classes in multiclass classification problems by comparing the inter-class variance (i.e., variance between different wear categories) with the intra-class variance (i.e., variance within each category) [50] using the F-score F.

Features with higher F-scores have stronger class-discriminatory power and are desired for training. The F-score is defined as:

$$F={\displaystyle \frac{{\displaystyle \sum _{k=1}^K}{n}_k{({\overline{x}}_k-\overline{x})}^2/(K-1)}{{\displaystyle \sum _{i=1}^N}{(x_i-{\overline{x}}_{c_i})}^2/(N-K)}}$$

(8)

where ${\overline{x}}_k$ is the mean of the feature values in class k, $\overline{x}$ is the overall mean of the feature values across all samples, $n_k$ is the number of samples in class k, $x_i$ is the $i\mathrm{th}$ sample, ${\overline{x}}_{c_i}$ is the mean of the class to which $x_i$ belongs, N is the total number of samples, and K is the total number of classes.

In this study, ANOVA F-test was used as a univariate feature selection filter, applied independently on each feature. Features ranked top 60% based on F-score and those with p value lower than 0.001 are retained. The details of the 17 features retained as a result of the ANOVA test are given in

Table 3. ANOVA F-Test results.

Features	F Score	p Value	${\mathrm{R}}^2$	$\widehat{\mathit{\eta }2}$	Cohen’s f	Contribution	Info Gain
Fz_Tz	846.120	$1.95\times {10}^{-246}$	0.300	0.361	0.752	37.146%	0.270
F Resultant FFT bin1	478.034	$3.34\times {10}^{-161}$	0.238	0.242	0.565	20.986%	0.362
F Resultant	392.437	$1.05\times {10}^{-137}$	0.180	0.208	0.512	17.228%	0.218
A Resultant Crest factor	123.732	$1.89\times {10}^{-50}$	0.142	0.076	0.288	5.432%	0.309
T Resultant Crest factor	103.090	$1.15\times {10}^{-42}$	0.028	0.064	0.263	4.526%	0.204
Fy_Ty	54.621	$1.28\times {10}^{-23}$	0.055	0.035	0.191	2.398%	0.131
F Resultant Mean	50.281	$7.36\times {10}^{-22}$	0.013	0.033	0.183	2.207%	0.350
A Resultant Mean	46.703	$2.12\times {10}^{-20}$	0.012	0.030	0.177	2.050%	0.308
A Resultant FFT bin1	41.657	$2.48\times {10}^{-18}$	0.010	0.027	0.167	1.829%	0.154
A Resultant FFT bin2	35.642	$7.56\times {10}^{-16}$	0.043	0.023	0.154	1.565%	0.129
F Resultant Crest factor	27.311	$2.24\times {10}^{-12}$	0.008	0.018	0.135	1.199%	0.122
T Resultant Peak-to-Peak	22.807	$1.75\times {10}^{-10}$	0.012	0.015	0.123	1.001%	0.844
F Resultant Peak-to-Peak	19.592	$3.99\times {10}^{-9}$	0.025	0.013	0.114	0.860%	0.829
A Resultant Skew	11.162	$1.54\times {10}^{-5}$	0.003	0.007	0.086	0.490%	0.300
A Resultant Std	8.999	$1.30\times {10}^{-4}$	0.002	0.006	0.078	0.395%	0.318
Fx_Tx	7.860	$4.02\times {10}^{-4}$	0.006	0.005	0.072	0.345%	0.034
F Resultant Std	7.803	$4.25\times {10}^{-4}$	0.002	0.005	0.072	0.343%	0.345

.

6.4. Recursive Feature Elimination

While tests and filters evaluate each feature independently, it is also important to consider how features interact when used together in a model. To capture this, we apply a wrapper-based method called Recursive Feature Elimination (RFE), which is a technique that identifies the features that contribute the most for the prediction of the output label and recursive removal of the least significant features [51]. It iteratively refits the model on the reduced set of features until the desired number of features is reached, as outlined in

Table 4. Algorithmic steps.

1	Train the estimator with a dataset containing all the features.
2	Rank the features based on their importance by the estimator.
3	Remove the least important features based on their ranked importance.
4	Train the estimator again with the new features list.
5	Repeat steps 2 to 4 until the number of remaining features matches the target number.

.

RFE captures model-specific feature relevance and interactions, unlike filter-based methods, which assess the features independently of the models; RFE trains the models then asses the features. As such, RFE can account for interactions between features that can improve the predictions of models but are overlooked by univariate test. In this study of TCM, a Random Forest (RF) model is trained as the estimator for RFE, where features are ranked based on their importance score from the RF model. After ranking the final features by importance, the top 60% of them are selected. Figure 8 shows the importance scores for the various features considered. The features that are not selected are indicated by red bars.

6.5. Shapley Additive Explanations

While RFE identifies important features based on their impact on model performance during training, it is equally valuable to understand and interpret the contribution of each feature toward individual predictions. To achieve this, Shapley Additive Explanation (SHAP) analysis was used as the final stage of feature evaluation.

SHAP assigns a Shapley value [52,53] to each feature for every prediction, regardless of whether the prediction is correct or incorrect. It determines the contribution of each feature by comparing the model’s prediction to the average prediction over all samples. The sum of all Shapley values for a sample equals the difference between the model’s prediction for that sample and the average prediction across all samples.

The Shapley value ${\varphi }_i$ for feature i is given by

$${\varphi }_i=\sum _{S\subseteq N\setminus \left\{i\right\}}{\displaystyle \frac{\left|S\right|!\left(\right|N|-|S|-1)!}{\left|N\right|!}}\left[f(S\cup \{i\left\}\right)-f\left(S\right)\right]$$

(9)

where S is the subset of features, $f\left(S\right)$ is the model prediction with subset S, and N is the full feature set.

For the SHAP analysis in this study, we used two models, Random Forest and Artificial Neural Network (ANN). For Random Forest, SHAP’s Tree Explainer [54] method was used, which is usually used and is optimized for tree-based models. For ANN, SHAP’s Kernel Explainer [55] was used. In both cases, feature importance was calculated by averaging the SHAP values across all samples to determine the importance of each feature. The importance scores from both models are compared, and only the features that are present in the top 60% of features based on their SHAP values were selected.

The stage-wise reduction in the number of features is shown in

Table 5. Results of the feature reduction stages.

Stage	Initial Features	Final Features
Variance Filter	47	36
Correlation Filter	36	28
ANOVA F-test	28	17
RFE	17	10
SHAP Analysis	10	4

. SHAP analysis is the final stage of the feature selection, resulting in just the following four 4 features: A Resultant Crest factor, T Resultant Peak-to-Peak, Fz_Tz, and F Resultant FFT bin1.

7. Model Training Framework

The preparation of a robust and reproducible model training framework is important to ensure a fair and accurate comparison of algorithm performance. So, we made sure that our dual-pipeline architecture can evaluate a diverse range of supervised learning algorithms, including both classical ML models and DL architectures [23].

The drilling experiment was conducted on an actual bone sample used in medical education. The amount of drilling data that may be acquired is limited as the workpiece in this case is a rare commodity. Unlike in industrial applications where the drilling process may last from a few minutes to even an hour, the bone drilling lasts for a few seconds. The size of the data that may be collected and the assessment of tool wear after every drill cycle pose challenges.

As the sensory data is collected every 8 ms (125 Hz) from various sensors and 20 holes were drilled, a good amount of sensory data is available. But, this data is unlabeled as the tool-wear labeling of the data for every time step (8 ms) is a difficult task. Tool force is known to be an important contributor towards tool wear. The perception of unusually large drilling force provides a cue on the tool wear in manual surgeries, too [15]. In view of this, it was decided to label the data based on the magnitude of the force vector sensed by the wrist force sensor. The maximum and minimum value of the force magnitude data was identified, and the range was divided into three categories based on the force magnitude: 0 (slight), 1 (moderate), and 2 (severe). This provides us with a reasonable dataset to be used with ML algorithms requiring a labeled dataset.

The dataset was randomized and an 80:20 train–test split that preserves the class distribution of the three tool wear categories was adopted. Multiple models (47 ML models and 6 DL models) were studied to select 3 models from each category, as described below.

7.1. Machine Learning Models

The following two-stage validation strategy was adopted for evaluating the various supervised ML classification models:

• Stratified k-Fold Cross-Validation [56] (k = 5), which ensures robust performance estimation while mitigating the risk of overfitting. Each fold maintains the original class proportions.
• Holdout Evaluation, where after cross-validation each model is retrained on the entire training set and evaluated on a previously unseen test set for generalization assessment.

• Each model is automatically wrapped in meta-classifiers such as One-vs-Rest or One-vs-One if native multiclass support is absent. Ensemble models including Voting Classifier and Stacking Classifier are built using diverse base learners to test the benefits of algorithmic heterogeneity [57]. Models with convergence issues (e.g., NuSVC) are supplied with adjusted parameters or dropped if unstable.

After training the 47 ML models and ranking their accuracy, the results obtained for the 15 most accurate models are shown in Figure 9a, from which, with the criteria of diverse architecture and good accuracy, the following 3 models are chosen for further optimization:

• Extra Trees Classifier.
• Hist Gradient Boosting Classifier.
• Cat Boost Classifier.

7.2. Deep Learning Models

Six custom-designed DL architectures were implemented using the PyTorch framework (Version 2.6.0). The models were trained with learning rates from ${10}^{-3}$ to ${10}^{-5}$ and batch sizes of 32 to 128 over a maximum of 100 epochs, employing early stopping to prevent overfitting [58].

After training and ranking based on the criteria of diverse architecture and high accuracy as show in Figure 9b, the following three DL models were chosen:

• CNN 1D Classifier
• Transformer Classifier
• DNN Classifer

7.3. Hyperparameters During the Training

Hyperparameters are variables that are set before training a DL model and remain constant during the training process; they determine the change from the current iteration to the next iteration. They are not learned from the data, but they significantly impact the model’s performance.

The key hyperparameters used were the learning rate of ${10}^{-3}$, the batch size of 16, and the gradient clipping of 1.0. Regularization techniques such as dropout (0.3–0.5), L2 weight decay, and batch normalization were used for better generalization [59], with ReLU activations for hidden layers and SoftMax for output.

The architecture and the optimizer used for different DL models are listed in

Table 6. Comparison of deep learning models.

Model	Architecture	Optimizer
DNN	2 hidden layers, 256 and 128 neurons per layer.	Adam
ANN	2 hidden layers, 256 and 128 neurons per layer.	RMSprop
CNN-1D	1D convolutional layers (kernel size = 4), fully connected output layer.	Adam
GRU	Single GRU layer with 128 hidden units, dense output layer.	Adam
LSTM	Single LSTM layer with 128 hidden units, dense output layer.	Adam
Transformer (Lightweight)	2 encoder layers, 2 attention heads, hidden size of 128, followed by dense layer.	AdamW

.

The choice of hyperparameters is decided through the hyperparameter tuning process discussed in Section 8. The hyperparameters obtained for all the three DL models were using the search space tailored to each hyperparameter and architecture [60]. The results are shown in Figure 10.

8. Hyperparameter Tuning

Hyperparameter tuning is the process of selecting the best set of hyperparameters for an algorithm and is specific to DL models. A random value is chosen within a sample space for each hyperparameter, and the DL model is trained with this set of hyperparameters. This process is repeated multiple times to select the hyperparameter set with the best target value for loss or accuracy. There are several techniques for computationally efficient hyperparameter tuning such as Grid Search and Random Search, etc. Intelligent tuning techniques such as Bayesian Optimization or Hyperband are also recommended with Optuna [34]. In this work, we used Bayesian Optimization with the Tree-structured Parzen Estimator (TPE) sampler [61], hyperband pruner, and early stopping if allowable for the model [62].

8.1. Bayesian Optimization

The primary objective of Bayesian Optimization is to identify the global minimum of the objective function:

$${\theta }^{*}=arg\underset{\theta \in \Theta }{min}f\left(\theta \right)$$

(10)

where $\theta$ is the set of hyperparameters, $f\left(\theta \right)$ is the objective function, and $\Theta$ is the search space. This is done by utilizing two main elements:

i.

A surrogate model (Equation (11)) to estimate the unknown objective function.

ii.

An acquisition function (Equation (12)) to determine the next set of hyperparameters to evaluate.

In this framework, TPE is used as the surrogate model, which separates the distribution of hyperparameter configurations as good and bad, and uses the Bayes rule to compute the probability of model performance improvement.

$$p\left(x\mid y\right)=\left\{\begin{array}{cc}l\left(x\right),& y^{″}<{\widehat{y}}^{*}\\ g\left(x\right),& y^{″}\ge {\widehat{y}}^{*}\end{array}\right.$$

(11)

where x is a hyperparameter configuration, y is the corresponding score, and ${\widehat{y}}^{*}$ is a performance threshold. The acquisition function, such as Expected Improvement (EI), determines which configuration to evaluate next based on the surrogate’s predictions:

$$EI\left(x\right)=E\left[max\left(f\left(x^{*}\right)-f\left(x\right),0\right)\right]$$

(12)

8.2. Hyperband Pruner

Hyperband pruner dynamically allocates the resources to enhance the efficiency of the hyperparameter tuning process by terminating the trials with no improvement. Hyperband evaluates models with limited resources initially, progressively allocating more resources to trials which are promising [35].

Additionally, for the models that support the Extra Trees Classifier, Hist Gradient Boosting Classifier, and Cat Boost Classifier, we added model-internal early stopping mechanisms during training, which stop the training when the model’s performance fails to improve on a validation set in a certain predefined number of iterations, thus preventing overfitting and not having to waste resources on them.

9. Results and Discussion

The main scope and contribution of this paper are the following:

• Identification of the most relevant features from the multi-sensor data;
• Identification the most suitable ML and DL models for analysing the data;
• Training the models using the most optimal hyperparameters;
• The assessment of the prediction accuracy of the models.

The results for the first two items were presented in Section 6, Section 7 and Section 8. The results of the latter two items are discussed here and the relevance of our work is compared with earlier attempts reported in the literature.

The hyperparameters for each model were optimized individually for 25 trials in each model, and the hyperparameters that had to be optimized were selected individually depending on their relevance to the model architecture and the sensitivity to the model performance [63]. The hyperparameter search space was carefully defined using domain knowledge and the observed results to include critical parameters such as the tree depth, the number of estimators, the learning rates, the regularization strength, and the splitting criteria. After applying this hybrid approach, we identified the best performing hyperparameters of each classifier obtained from the Optuna study [34].

Among the classical ML models, the Extra Trees Classifier resulted in the best prediction accuracy of 96.33% for TCM on the test set, while CNN 1D Classifier was the best among the DL models, with a prediction accuracy of 95.67%. The search space and the optimal value of the hyperparameters obtained from hyperparameter tuning for both these models are given in

Table 7. Hyperparameter tuning summary.

(a) Extra Trees Classifier
Hyperparameter	Search Space	Optimal Value
Max depth	Integer between 3 and 30	21
N estimators	Integer between 50 and 500	334
Criterion	{gini, entropy, log_loss}	gini
Max features	Float between 0.1 and 1.0	0.999
Min samples split	Integer between 2 and 20	5
(b) CNN 1D Classifier
Number of Filters	Integer between 16 and 128	110
Kernel Size	Integer between 2 and 4	4
Dropout Rate	Float between 0.0 and 0.5	0.049
Optimizer	{adam, adamw, rmsprop}	rmsprop
Epochs	Integer between 10 and 100	84
Learning Rate	Log-uniform between ${10}^{-5}$ and ${10}^{-2}$	0.001
Weight Decay	Log-uniform between ${10}^{-6}$ and ${10}^{-2}$	9.643

, and the classification reports for these two models are given in

Table 8. Classification report for the best-performing models with the optimized hyperparameter set.

(a) Extra Trees Classifier
	Precision	Recall	F1 Score	Support
0	0.96	0.99	0.97	150
1	0.95	0.97	0.96	103
2	1.00	0.87	0.93	47
Accuracy	—	—	0.966	300
Macro Average	0.97	0.94	0.96	300
Weighted Average	0.96	0.96	0.96	300
(b) CNN 1D Classifier
0	0.97	0.94	0.96	150
1	0.91	0.97	0.94	103
2	1.00	0.96	0.98	47
Accuracy	—	—	0.956	300
Macro Average	0.96	0.95	0.95	300
Weighted Average	0.95	0.95	0.95	300

. The CNN model’s optimization process involved tuning both architectural and training-related parameters. The hyperparameter search space was carefully bounded to enhance convergence and reduce overfitting.

The confusion matrices for the Extra Trees Classifier and the CNN 1D Classifier obtained after training with the set of hyperparameters after the hyperparameter tuning process are shown in Figure 11, where the distribution of correctly and incorrectly classified instances across all classes of TCM may be noted.

The results of this study show that combining a proper data preprocessing pipeline with well-selected features and comparing different model types can help detect tool wear during robotic bone drilling quite accurately. It may be further inferred that both traditional ML and DL models can perform well if used with the right data and approach.

Previous work using 1D CNNs also had good success in predicting tool wear from vibration and force signals. For example, models that combine CNN with temporal or frequency-domain processing have been shown to work well in noisy environments such as drilling [14,15,64]. But in most of those studies, the focus was mainly on raw signal inputs or just one signal type. Our approach, on the other hand, mixes different kinds of features, such as interaction-based and normalized values, making the model generalize better across samples.

Classical ML models are also useful for faster decision-making and identification of the most relevant features. Past research works have used such models for the prediction of bone drilling temperature or wear stages from vibration signals [20,65], but without full feature engineering and selection processes like ours. By adding a multi-stage methodology (ANOVA, RFE, SHAP), we are able to improve performance and reduce noise in predictions.

Overall, while earlier research focused on single models or features, our work stands out by combining engineered signals, strong model selection, and a clear validation process. This not only improves accuracy but also makes the system more reliable for real-time use in surgical settings.

10. Conclusions

In this study, we proposed a complete and real-time framework for Tool Condition Monitoring (TCM) in robotic bone drilling applications. Unlike traditional methods which mostly rely on limited models or single feature types, our approach combines signal preprocessing, domain-based feature engineering, multi-stage feature selection, and comparative model training across different supervised learning algorithms including both classical machine learning and deep learning models.

Using a UR5e robotic arm setup with a custom drilling end-effector, we collected multi-sensor data and performed preprocessing steps such as temporal aggregation, wavelet denoising, and outlier removal to make the raw signals more stable and meaningful. Feature engineering was done with a focus on resultant values, time-domain statistics, frequency-domain characteristics, and interaction-based signals which reflect the physical behaviour of the drilling process. Then, feature selection methods including ANOVA F-test, RFE, and SHAP were applied to pick the most important and relevant features which improved both model performance and interpretability.

After training and tuning a wide variety of models, Extra Trees Classifier showed the best performance among classical models, with a test accuracy of 96.33%, and CNN 1D Classifier was the best deep learning model, with a test accuracy of 95.33%. These results prove that a proper pipeline which uses data cleaning, smart feature extraction, and architecture-level diversity can lead to high accuracy and reliable predictions.

This framework can be very useful in real surgical setups where bone drilling is done in orthopaedic or neurosurgery. Although periodic drill bit replacement and regular machine maintenance are already part of standard protocol, still there can be unexpected problems like drill cracking, sudden breakage, or excessive heating due to local bone density differences or long operation times. Our model helps to detect these unexpected tool failures by analysing sensor signals in real-time, which can reduce the risk of tool breakage during operation and help avoid surgical errors.

This system can act like a second layer of safety by giving alerts when the tool condition starts to degrade, even if it is still under standard maintenance limits. This not only improves surgical safety but also helps in reducing unnecessary downtime and manual inspections.

Future Scope

This work is a part of an ongoing research in the development of end-effectors for robotic drilling. We are currently implementing real-time temperature sensing on the bone by locating sensors close to the drilling location. Currently, the IMU sensors to measure the vibration are located on the bone, which may not be possible in the case of a real patient. However, data may be collected by locating vibration sensors on the body of the patient or on a cadaver for further validation. TCM could be used for other surgical settings such as dental drilling, neurosurgery, and veterinary surgeries. Future work will consider contamination aspects and potential bone damage mechanisms, which are beyond the current focus on tool condition monitoring.