The Design of a Reaction Flywheel Speed Control System Based on ADRC

Abstract

The reaction flywheel is a crucial operational component within a satellite’s attitude control system. Enhancing the performance of the reaction flywheel speed control system holds significant importance for satellite attitude control. In this paper, an active disturbance rejection control (ADRC) approach is introduced to mitigate the impact of uncertain disturbances on reaction flywheel speed control precision. The reaction flywheel speed control system is designed as an ADRC controller due to the current challenge of measuring unknown disturbances accurately in the reaction flywheel system. To derive the rotor’s speed observation value and the estimated total disturbances value, the sampled data of the reaction flywheel rotor position and torque control signal are fed into the extended state observer. The estimated total disturbances value is compensated on feedforward control, which could mitigate significantly the effects of various nonlinear disturbances. The paper initially establishes the rationale behind the reaction flywheel ADRC controller through theoretical analysis, followed by analysis of the differences of performance of reaction flywheel control by the ADRC controller and the PID controller in MATLAB/SIMULINK. Simulation results demonstrate the evident advantages of the ADRC controller over the PID controller in terms of speed command tracking capability and disturbances suppression ability. Subsequently, the ADRC controller program and the PID controller program are implemented on the reaction flywheel control circuit, and experiments are conducted to contrast speed command tracking and disturbance suppression. Importantly, the experimental outcomes align with the simulation results.

1. Introduction

With the rapid development of the aerospace industry, there has been an increasing demand for the accuracy control and rapid response capabilities of spacecraft attitude control systems in recent years. The reaction flywheel, a critical component of satellite attitude control systems, has been used extensively in these systems due to its rapid response, high accuracy, stability, and energy efficiency. Its primary function is to control the motor speed of the reaction flywheel and provide angular momentum output to regulate satellite attitude.

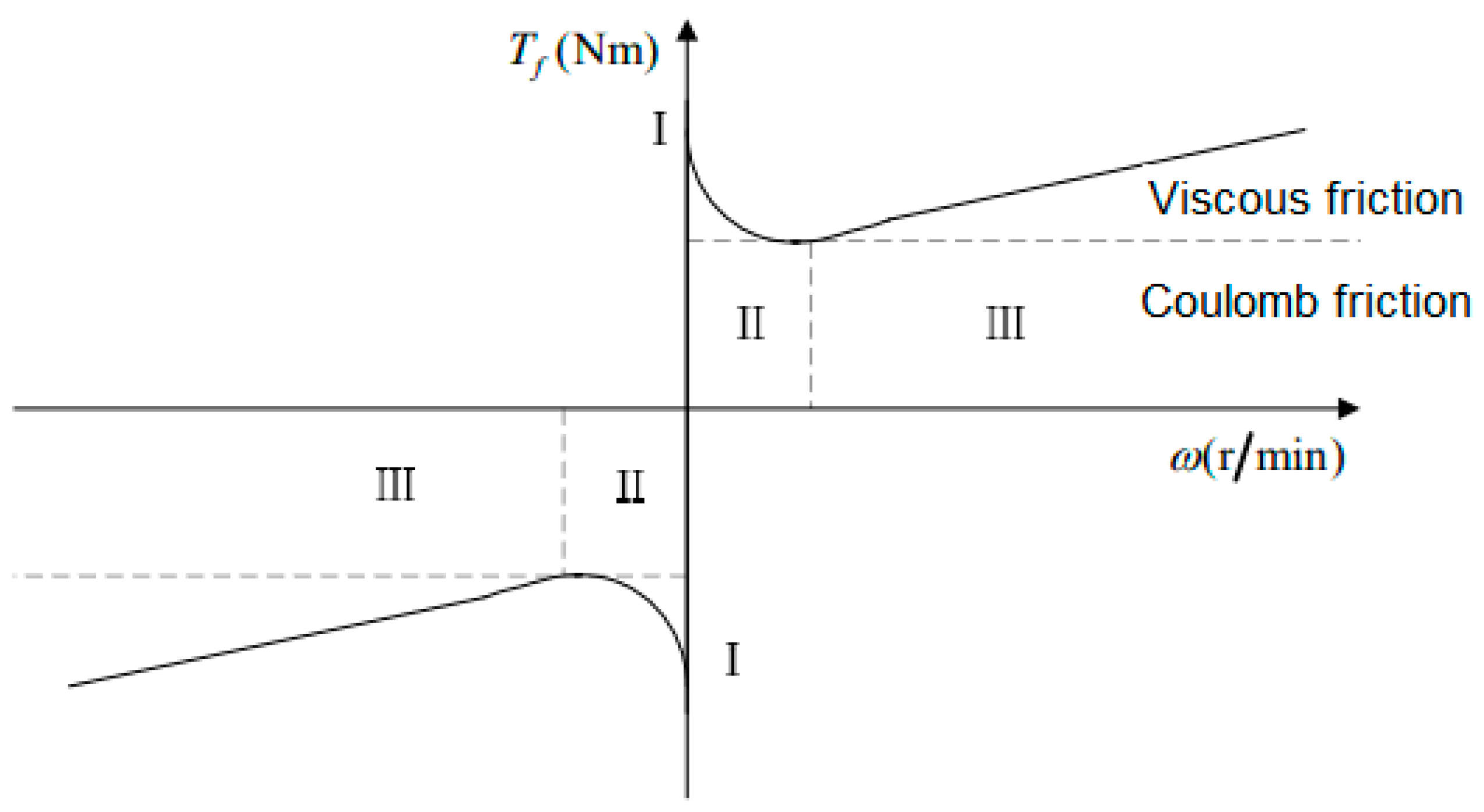
The reaction flywheel generally consists of a high-speed motor, bearings, and a control circuit. In engineering applications, it is essential to ensure that the high-speed motor and bearings exhibit good servo performance. However, various disturbances, which affect the high-speed motor and bearings, degrade the dynamic characteristics of the reaction flywheel system markedly. Disturbances such as friction torque, cogging torque, magnetic flux distortion, current ripple, and bearing noise torque [1] mainly impact the accuracy of reaction flywheel speed control. When the high-speed rotor of the reaction flywheel rotates, velocity fluctuations are generated and transferred to the spacecraft, ultimately affecting the spacecraft’s attitude control performance. Therefore, it is necessary to classify, analyze, and suppress these disturbances accurately to achieve high-accuracy velocity tracking control.

Currently, proportional–integral–derivative (PID) control is used widely in various motor drive systems. As a simple control method that provides good performance, PID controllers are not ideal for speed control of reaction flywheels, especially in the context of without using expensive bearings that have been strictly screened. To overcome disturbances and improve the speed control accuracy of reaction flywheels, more advanced control methods are required. Reference [2] has described disturbance estimation technology in the presence of parameter uncertainty and disturbance forces in detail. The use of a disturbance observer can enhance the motor speed control performance. Reference [3] employs a Linear Quadratic Regulator (LQR) with an observer, assuming the disturbance is periodic. Reference [4] employs feedback linearization and an extended high-gain observer to achieve high accuracy and fast response in the speed control of permanent magnet synchronous motors (PMSM). Reference [5] designs a disturbance observer that considers various disturbances, including cogging torque, load torque, friction torque, measurement error effects, dead time effects, and parameter disturbances. Most of these papers present experimental/simulation results showcasing the performance of these approaches.

Active disturbance rejection control (ADRC) is a fully-based control design method that builds upon the essence of PID control technology and incorporates achievements from modern control theory. The fundamental concept of ADRC involves treating the system’s nonlinear and unmeasurable disturbances as lumped unknown signals without any specific state variable structure, thereby simplifying the task of state and disturbance estimation [6]. By effectively estimating the sum of various disturbances in real time, their influence on the system’s closed loop is mitigated. The extended observer is a common tool for real-time disturbance estimation.

Motivated by these aforementioned observations, this paper focuses on the high-accuracy velocity control challenge of reaction flywheel systems subjected to multiple disturbances. The main contributions and enhancements of this paper are as follows:

(1) ADRC is introduced to enhance the reaction flywheel system’s anti-disturbance capability by integrating an extended state observer, which can be modeled as an exogenous system, while unmodeled disturbances are treated as a lumped term and estimated by the extended state observer.

(2) Based on the extended state observer, an ADRC system is designed. Compared to other control algorithms, this scheme enables the reaction flywheel system state to converge to the equilibrium point in finite time and achieves disturbance rejection. The corresponding composite anti-disturbance control algorithm is easy to implement due to the straightforward adjustment of controller parameters.

(3) The proposed control algorithm ensures a satisfactory reaction flywheel control performance even in the presence of different types of disturbances with relatively large amplitudes.

The remainder of this paper is organized as follows. Section 2 presents the problem formulation. The design process of the proposed ARRC system is outlined in Section 3. Section 4 verifies the effectiveness of the proposed control scheme through comparative simulation tests. In Section 5, the proposed control scheme’s effectiveness is verified through real tests. Finally, Section 6 concludes this paper.

2. System Disturbance and Noise

There are various nonlinear disturbances in the reaction flywheel system which seriously affect the performance of the reaction flywheel. The suppression effect of disturbances determines the control accuracy of the reaction flywheel system. It is necessary to analyze the various nonlinear disturbances in the reaction flywheel system.

2.1. Dynamic Model of Reaction Flywheel

According to Newton’s third law, the torque exerted by the reaction flywheel on the satellite, denoted as the reaction flywheel output torque T_r, is equal in magnitude but opposite in direction to the torque T_a applied to the reaction flywheel rotor. The dynamic equation of the reaction flywheel is expressed as shown in Equation (1):

$$J\frac{d\omega }{dt}=T_e-d_0$$

(1)

where the torque T_a acting on the reaction flywheel rotor is the difference between the electromagnetic torque T_e of the reaction flywheel motor and the disturbance torque d₀, which includes various components such as friction torque, cogging torque, magnetic flux distortion, current ripple, and bearing noise torque. J presents the inertia of the reaction flywheel rotor.

2.2. System Disturbances

There are various types of disturbances within the reaction flywheel system, which affect the performance of the reaction flywheel to different extents. These disturbances are illustrated in Figure 1, where the dashed box (1) represents cogging torque, magnetic flux distortion, current ripple, and other torques within the reaction flywheel motor body. The dashed box (2) represents bearing noise torque, and box (3) represents internal friction torque of the reaction flywheel.

2.2.1. Cogging Torque, Magnetic Flux Distortion, Current Ripple

In the reaction flywheel, pulsating disturbances arise due to cogging effects, magnetic flux distortion, current pulsations, and other factors. Based on engineering experience, these motor-induced pulsating disturbances can be effectively mitigated by adopting measures such as motor optimization design, magnetic flux compensation, torque closed-loop control, and optimization of current control strategies.

2.2.2. Bearing Noise Torque

Bearing noise torque is a significant source of disturbance for the reaction flywheel and has garnered substantial attention from researchers. The bearing components primarily consist of the cage, ball, and inner and outer rings. Due to factors such as processing, installation, deformation, and wear, these components cannot maintain an ideal state, leading to substantial noise-induced disturbance torque. Particularly, the bearing cage possesses six degrees of freedom, resulting in complex dynamic characteristics. The instability of the cage contributes to progressively larger noise interference torques. Additionally, dynamic behavior of lubricants contributes to bearing noise torque. However, the bearing noise torque caused by lubricant is a function of the lubricant’s intricate dynamic characteristics, which cannot be adequately expressed through simple analytical expressions. Hence, bearing noise torque necessitates indirect analysis and estimation. Reference [7] provides a test curve for bearing noise torque, depicted in Figure 2.

The disturbance caused by the instantaneous stop of the bearing cage is random and occurs at long intervals, which can result in a sudden deviation from the acceptable range of flywheel speed control accuracy. This kind of disturbance is challenging to address using conventional control methods due to its randomness, often leading to unpredictable deviations in flywheel speed control accuracy.

The disturbance caused by damage to the bearing steel ball is similar to the disturbance caused by contamination on the bearing steel ball, and its frequency is linked to the flywheel speed. Applying conventional PID control to address this type of disturbance proves difficult in adjusting control parameters, potentially necessitating the design of segmented PID controllers based on different flywheel rotational speeds, which could compromise system robustness.

The disturbance resulting from the deterioration of lubricant performance is random, and its frequency is tied to the flywheel speed. When the disturbance amplitude is significant, ensuring that the flywheel speed control accuracy remains within tolerance using conventional PID control becomes challenging.

2.2.3. Friction Torque

Typically, the friction torque in a motor system consists of Coulomb friction torque and Dahl friction torque, which is expressed in Equation (2):

$${\tau }_f=F_c\cdot sign(\omega )+F_v\omega +(F_s-F_c)\mathit{exp}(-(\frac{\omega }{{\omega }_s}{)}^2)\cdot sign(\omega )$$

(2)

$${\tau }_0=(F_s-F_c)\mathit{exp}(-(\frac{\omega }{{\omega }_s}{)}^2)\cdot sign(\omega )$$

(3)

where F_c represents the Coulomb friction torque, F_s is the maximum static friction torque, F_v is the coefficient of viscous friction torque, and ω_s is the critical speed of boundary lubrication (Stribeck speed). In the lubrication region where ω >> ω_s, the τ₀ as shown in Equation (3) exponentially decreases and can be approximately disregarded. At this point, the friction torque is predominantly represented by Coulomb friction torque and viscous friction torque [8], as illustrated in Figure 3.

As shown in Figure 3, At point I, the reaction flywheel’s speed is 0, and the only friction force present is static friction. In region II, the reaction flywheel speed is low, and the predominant friction force is the τ₀ component as described in Equation (3). In this region, the reaction flywheel’s friction is nonlinear. In region III, the reaction flywheel speed is high, and the τ₀ component decays rapidly. The main friction components are $F_c\cdot sign\left(\omega \right)+F_v\omega$, resulting in linear friction behavior for the flywheel.

2.3. Problem Description

Upon analyzing various disruptive forces within the reaction flywheel system, pulsating torques arising from cogging effects, magnetic flux distortion, current pulsations, and other factors generate periodic errors linked to the speed of the reaction flywheel motor [9]. These errors can be effectively mitigated by optimizing the motor structure [10].

Bearing noise torque originates from irregular cage, ball, and inner and outer ring movements within the reaction flywheel’s bearing assembly, along with dynamic behaviors of lubricant under different operational conditions. Disturbances to the reaction flywheel control system under varying speeds and conditions are nonlinear. When the bearing is in a satisfactory condition, the influence of bearing noise torque on the accuracy of reaction flywheel speed control can be disregarded. Thus, the prevailing method involves stringent screening of bearing components to reduce the impact of bearing noise torque on reaction flywheel speed control accuracy. However, this approach significantly escalates the manufacturing cost of the reaction flywheel.

The magnitude of friction torque is largely associated with the speed of the reaction flywheel, primarily characterized by Coulomb friction torque and viscous friction torque. Rapid changes in the reaction flywheel’s speed lead to substantial fluctuations in friction, significantly affecting the accuracy of speed command tracking for the reaction flywheel.

3. Control Law Design

In this section, the active disturbance rejection control (ADRC) controller for the reaction flywheel is designed, and an extended state observer is developed to estimate the reaction flywheel’s speed and total disturbances. Through modeling and derivation of mathematical formulas, the convergence of the estimation error for the extended state observer is proven. Finally, a reaction flywheel speed controller with feedforward compensation for total disturbances is designed, and the controller’s stability is demonstrated.

3.1. Design of Current Loop Controller

A proportional–integral (PI) controller is utilized for the current loop, yielding favorable outcomes. The desired control bandwidth for the current loop is denoted as ω_c, and the parameter configuration for the current PI controller is expressed as shown in Equation (4):

$$\left\{\begin{array}{c}{k}_{cp}={\omega }_{c}L\\ k_{ci}=R_s/L\end{array}\right.$$

(4)

where $k_{cp}$ represents the proportional gain coefficient of the controller, $k_{ci}$ represents the integral gain coefficient of the controller, while R_s represents Terminal resistance and L represents Terminal inductance.

At this juncture, the zero point of the current controller can nullify the poles of the motor model. The current loop is adjusted into a stable first-order low-pass system, with its closed-loop transfer function expressed as demonstrated in Equation (5):

$$G_i(s)=\frac{{\omega }_c}{s+{\omega }_c}$$

(5)

3.2. Design of Extended State Observer

In this section, we will design an extended state observer ${\widehat{x}}_1,\dots ,{\widehat{x}}_n$ to estimate the velocity and total disturbances of the reaction flywheel. Through modeling and mathematical formula derivation, we will demonstrate the convergence of the estimation error e₁, …, e_n of the extended state observer. Finally, we will design a reaction flywheel speed controller u(t) with feedforward compensation and establish the stability of the controller.

The ADRC controller employs a third-order linear extended state observer to dynamically monitor the speed of the reaction flywheel motor and the overall disturbances of the system in real time. The angular position of the reaction flywheel rotor is denoted as state x₁, the flywheel’s velocity is represented by state x₂, the cumulative disturbances within the system are captured as state x₃, and the derivative of x₃ is recorded as a(t):

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2\\ {\dot{x}}_2=u+x_3\\ {\dot{x}}_3=a\left(t\right)\end{array}\right.$$

(6)

The third-order extended state observer is designed as shown in Equation (7):

$$\{\begin{array}{c}{\dot{z}}_1=z_2+{\beta }_1(x_1-z_1)\\ {\dot{z}}_2=z_3+{\beta }_2(x_1-z_1)+u\\ {\dot{z}}_3={\beta }_3(x_1-z_1)\end{array}$$

(7)

where, z₁, z₂, z₃ are the observed values of reaction flywheel rotor position, speed, and total value of disturbances, respectively. β₁, β₂, β₃ are error gain values of each order. We define the matrix A and following vectors in Equation (8):

$$\begin{gathered} z=\left[\begin{array}{c}{z}_1\\ z_2\\ z_3\end{array}\right] \\ A=\left[\begin{array}{ccc}-{\beta }_1& 1& 0\\ -{\beta }_2& 0& 1\\ -{\beta }_3& 0& 0\end{array}\right] \\ {B}_1=\left[\begin{array}{c}{\beta }_1\\ {\beta }_2\\ {\beta }_3\end{array}\right] \\ {B}_2=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right] \\ c=\left[\begin{array}{ccc}0& 0& 1\end{array}\right] \end{gathered}$$

(8)

Then Equation (7) can be rewritten as in Equation (9):

$$\dot{z}=Az+B_1{x}_1+B_{2}u$$

(9)

System disturbances can be rewritten as in Equation (10):

$$d_0=Cz$$

(10)

The reaction flywheel motor speed state feedback control law adopts PI plus feedforward control. The proportional control parameter is K_p, the integral control parameter is K_i, the given command speed is x₀, the difference between the speed command and the speed is x₀–x₂, and the x₀–x₂ integral is set as x_c. The state feedback control law is designed as in Equation (11):

$$u=-z_3+K_P(x_0-x_2)+K_i{x}_c$$

(11)

The observer that includes the control input is expressed by Equation (12):

$$\left\{\begin{array}{c}{\dot{z}}_1=z_2+{\beta }_1(x_1-z_1)\\ {\dot{z}}_2=z_3+{\beta }_2(x_1-z_1)-z_3+K_P(x_0-x_2)+K_i{x}_c\\ {\dot{z}}_3={\beta }_3(x_1-z_1)\\ {\dot{x}}_c=x_0-x_1\end{array}\right.$$

(12)

We define the matrix A′, matrix B′, and the following vectors as presented in Equation (13):

$$\begin{gathered} z^{\prime }=\left[\begin{array}{c}{z}_1\\ z_2\\ z_3\\ x_c\end{array}\right] \\ {A}^{\prime }=\left[\begin{array}{cccc}-{\beta }_1& 1& 0& 0\\ -{\beta }_2& 0& 0& K_i\\ -{\beta }_3& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right] \\ {B}^{\prime }=\left[\begin{array}{cccc}{\beta }_1& 0& 0& 0\\ {\beta }_2& -K_P& 0& K_P\\ {\beta }_3& 0& 0& 0\\ -1& 0& 0& 1\end{array}\right] \\ {u}^{\prime }=\left[\begin{array}{c}{x}_1\\ x_2\\ x_3\\ x_0\end{array}\right] \\ {c}^{\prime }=\left[\begin{array}{cccc}0& 0& 1& 0\end{array}\right] \end{gathered}$$

(13)

Subsequently, Equation (12) can be rewritten as shown in Equation (14):

$${\dot{z}}^{\prime }=A^{\prime }{z}^{\prime }+B^{\prime }{u}^{\prime }$$

(14)

System disturbances can be redefined using Equation (15):

$$d_0=c^{\prime }{z}^{\prime }$$

(15)

Next, we analyze the performance of the disturbances’ observer. Based on the error dynamic equation of the disturbance observer given by Equations (16) and (17):

$$\dot{\widehat{x}}={\dot{z}}^{\prime }-{\dot{u}}^{\prime }=\left[\begin{array}{c}{\dot{z}}_1\\ {\dot{z}}_2\\ {\dot{z}}_3\\ x_0-x_2\end{array}\right]-\left[\begin{array}{c}{x}_2\\ x_3+u\\ z_3\\ 0\end{array}\right]=\left[\begin{array}{cccc}-{\beta }_1& 1& 0& 0\\ -{\beta }_2& 0& 1& 0\\ -{\beta }_3& 0& -1& 0\\ 0& 0& 0& 0\end{array}\right]z^{\prime }+\left[\begin{array}{cccc}{\beta }_1& -1& 0& 0\\ {\beta }_2& 0& -1& K_P\\ {\beta }_3& 0& 0& 0\\ -1& 0& 0& 1\end{array}\right]u^{\prime }$$

$$m\dot{\widehat{x}}=A_0\widehat{x}$$

(16)

$$A_0=\left[\begin{array}{cccc}-2{\beta }_1& 0& 0& 0\\ -2{\beta }_2& 0& 0& -K_p\\ -2{\beta }_3& 0& -1& 0\\ -1& 0& 0& 1\end{array}\right]$$

(17)

We select suitable values for β₁, β₂, β₃, and K_p to ensure the stability of A₀ to be Hurwitz; for any positive definite symmetric matrix Q > 0, there exists a unique positive definite symmetric matrix P > 0, as demonstrated in Equation (18):

$$P{A}_0+A_0^{T}P=-Q$$

(18)

Choose the Lyapunov function as shown in Equation (19):

$$V_0={\widehat{x}}^{T}P\widehat{x}>0$$

(19)

Differentiate Equation (19) and substitute Equation (18) into it to yield:

$$\dot{V_0}=-{\widehat{x}}^{T}Q{\widehat{x}}^T$$

(20)

Let γ₁ represent the minimum eigenvalue of the matrix. Based on Equation (20), we derive Equation (21):

$${\dot{V}}_0\le -{\gamma }_1{‖\widehat{x}‖}^2$$

(21)

The choice of Q determines its minimum eigenvalue γ₁. By selecting appropriate values for β₁, β₂, β₃, and K_p, rapid convergence can be achieved. Thus, the designed disturbances’ observer can configure the characteristic roots of the disturbance observer system to desired positions by choosing suitable parameters, achieving swift convergence of observation errors.

3.3. Design of Reaction Flywheel Speed Controller

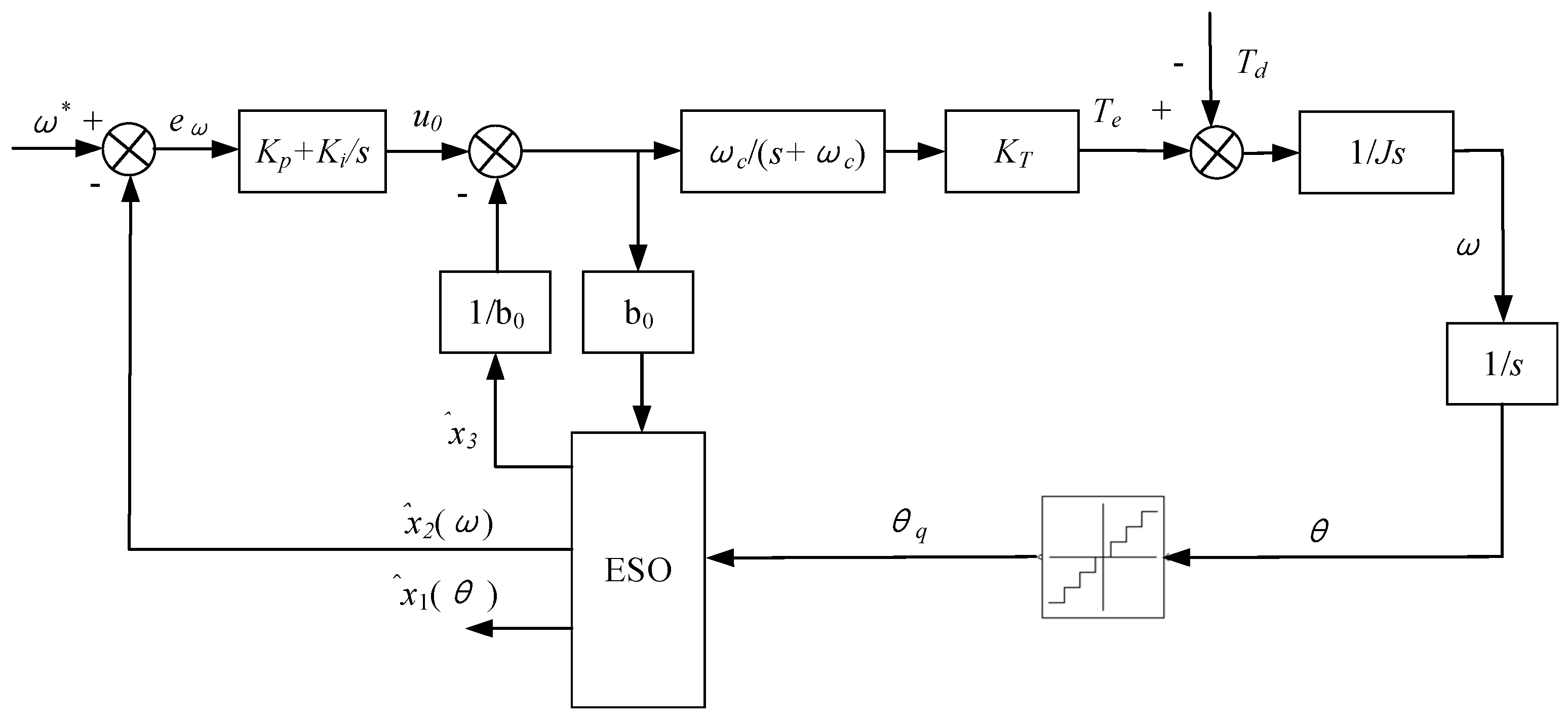
The observed disturbances are compensated through feedforward control. The control system block diagram of the reaction flywheel is depicted in Figure 4.

Reasonably design β₁, β₂, β₃, K_p, K_i parameters, and utilize MATLAB to calculate the model transfer function. The MATLAB commands are as follows:

[a,b,c,d] = linmod(‘Copy_of_test1_modified20211126’);

sys = tf(minreal(ss(a,b,c,d)));

The closed-loop system transfer function obtained is:

$$sys=\frac{205.3}{s^2+62.5s+205.3}$$

(22)

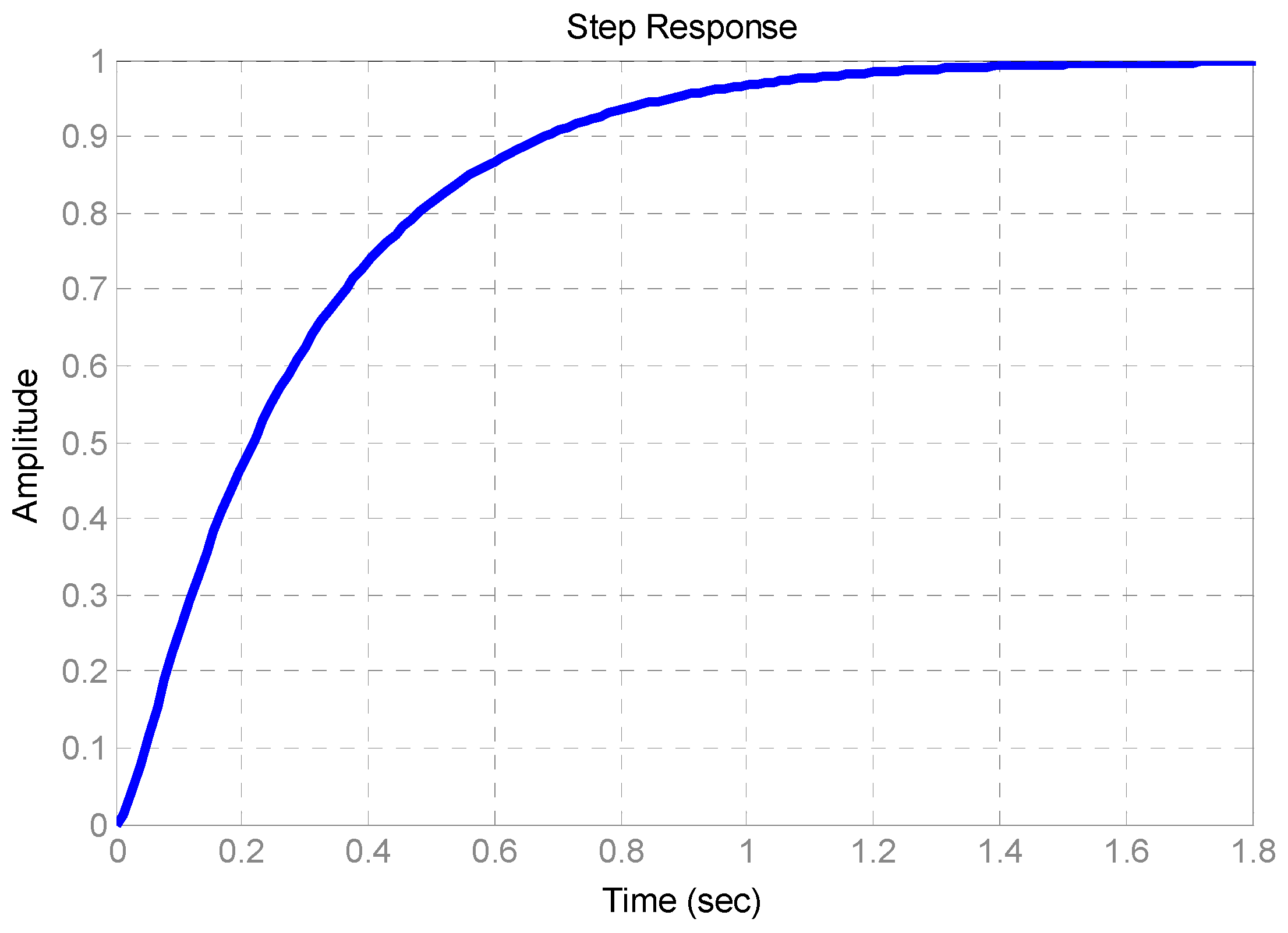
With roots of the denominator’s characteristic polynomial in the left half of the complex plane, the step response is shown in Figure 5. It can be observed that the reaction flywheel control system designed based on ADRC is stable and exhibits rapid convergence.

4. Simulation Results and Analysis

In this section, we compare the speed tracking and disturbance suppression performance of the reaction flywheel system using both PID controller and ADRC controller through simulations. The simulation parameters for the reaction flywheel are consistent with the actual system, as shown in

Table 1. Flywheel parameters.

Symbol	Parameters	Value
Rs	Terminal resistance, phase–phase	3.67 Ω
L	Terminal inductance, phase–phase	240 µH
kE	Back-EMF constant	4.335 mV/min−1
n	Number of pole pairs	2
J	Moment of inertia	0.000954 Kg·m2
kM	Torque constant	41.4 mNm/A
TM	Mechanical time constant	0.032 s

.

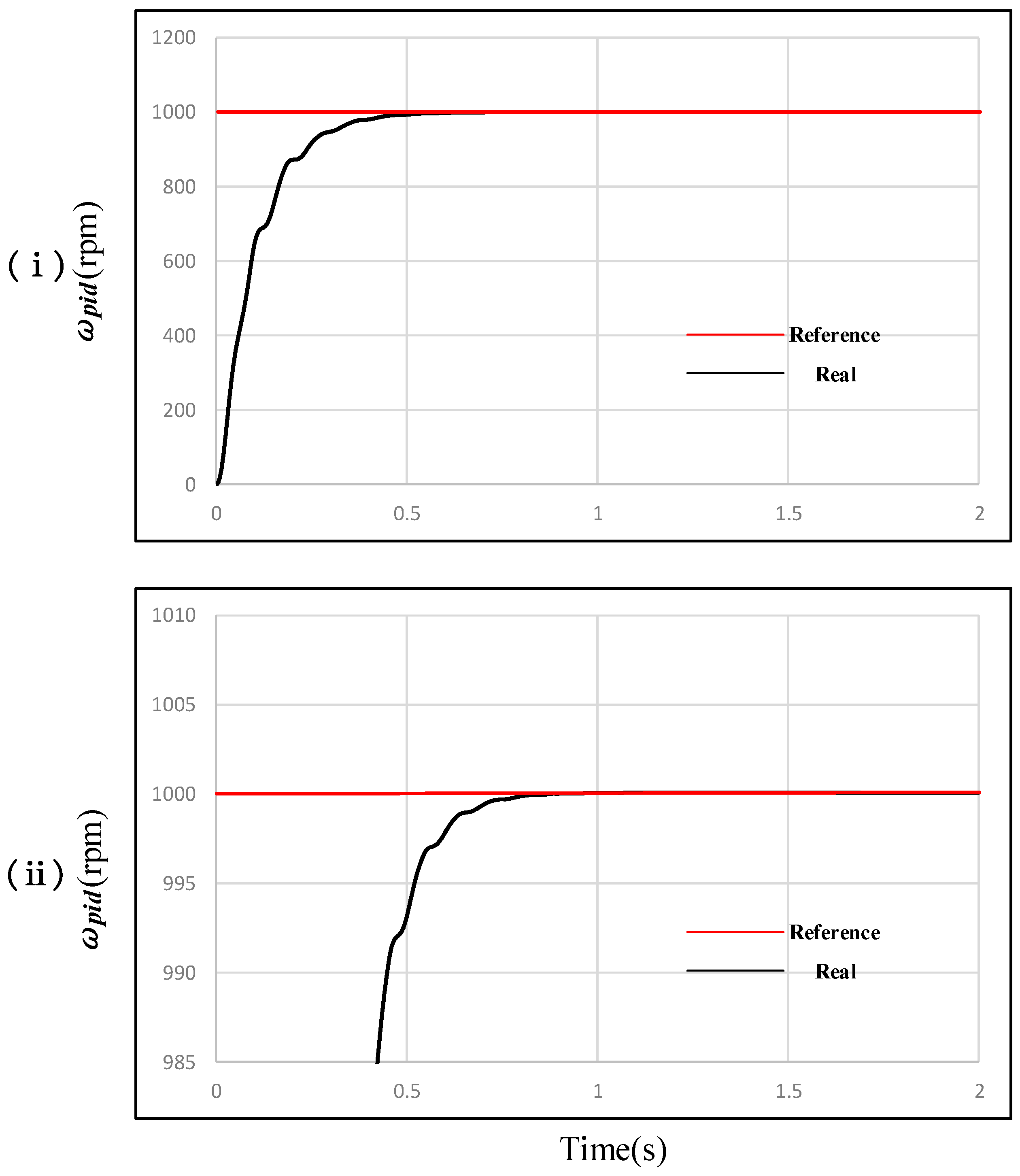
As depicted in Figure 6 and Figure 7, we simulate the speed-tracking capabilities of the two controllers. With a fixed speed command, it can be observed from the flywheel’s speed response curves that the response rates of the PID controller and the ADRC controller are essentially the same, but the PID controller exhibits a significant overshoot. On the other hand, the ADRC controller shows minimal overshoot, thereby effectively enhancing the system’s ability to rapidly track the speed command.

In the PID controller, K_p = 5, K_i = 0.05, K_d = 0. As shown in Figure 4, in the ADRC controller, K_p = 5, K_i = 0.05, K_d = 0, which are the same as the control parameters in the PID controller. By using the same control parameters, the ADRC controller is capable of suppressing overshoot and ensuring response speed by compensating for various disturbances, whereas the PID controller often compromises on overshoot suppression and response speed.

Subsequently, different types of bearing noise torque are simulated as disturbance inputs, and the suppression effects of both the PID controller and ADRC controller on different bearing noise torques are compared.

As shown in Figure 8, particle pollution or damage occurs on the steel ball within the flywheel bearing. The disturbance is depicted in Figure 8i with an amplitude of 4~5 mNm, which is a periodic signal. When the disturbance arises, if the PID controller is employed as shown in Figure 8ii, the reaction flywheel’s speed will drop by about 5 rpm. Conversely, with the use of the ADRC controller as shown in Figure 8iii, the speed fluctuation remains within 0.5 rpm. The disturbance suppression effect of the ADRC controller surpasses that of the PID controller by approximately an order of magnitude.

As illustrated in Figure 9, an instantaneous stop of the bearing cage occurs within the reaction flywheel bearing. The disturbance simulation is depicted in Figure 9i, with an amplitude of 4~5 mNm, representing a non-periodic signal. When a disturbance torque emerges, if the PID speed controller is utilized, as shown in Figure 9ii, the reaction flywheel’s speed will decrease by approximately 5 rpm. Conversely, with the utilization of the ADRC speed controller, as shown in Figure 9iii, the speed fluctuation remains within 0.5 rpm. The disturbance suppression effect of the ADRC controller surpasses that of the PID controller by about an order of magnitude.

As illustrated in Figure 10, the simulation curve of disturbances generated by the dynamic characteristics of the bearing lubricant is depicted in Figure 10i, with an amplitude of 4~5 mNm, constituting a non-periodic signal. In the presence of this disturbance, if the PID speed controller is utilized as shown in Figure 10ii, the reaction flywheel will experience a speed reduction corresponding to the disturbance torque, leading to a maximum speed error of 5 rpm. Alternatively, when the ADRC speed controller is employed, as demonstrated in Figure 10iii, the speed fluctuation remains within 0.5 rpm. The disturbance suppression effect of the ADRC controller on the dynamic characteristics of bearing lubricant is notably superior to that of the PID controller.

With the same control parameters, the ADRC controller can adaptively suppress different types of disturbances by compensating for various disruptions, while the PID controller is unable to adaptively suppress different types of disturbances.

5. Experimental Results

The practical performance of the proposed ADRC controller is assessed through two experiments. The first experiment aims to demonstrate the speed-tracking capability of the proposed ADRC controller. The second experiment tests the disturbance rejection ability of the proposed ADRC controller. Both experiments were compared with differences in control effects between the PID controller and ADRC controller. The parameters of the reaction flywheel motor used are consistent with the simulation experiments, as shown in Table 1.

In order to obtain optimal speed controller parameters β₁, β₂, β₃, K_p, and K_i, several experiments were conducted. In these experimental results, we only selected parameters with an overshoot ≤ 2%, effective disturbance suppression, and without oscillation [11,12].

The control algorithm is based on the reaction flywheel control system of the stm32f103 ARM chip. The reaction flywheel control circuit board is depicted in Figure 11 and is installed within the reaction flywheel. The current of the reaction flywheel is measured using high-precision sampling resistors. The position of the reaction flywheel rotor is determined through a 4096PPR incremental encoder [13,14], which is directly mounted at the end of the motor shaft.

All speed data acquired during the experiment were measured utilizing dedicated testing equipment designed for reaction flywheel products. Figure 12 presents a photograph of the experimental setup. The testing equipment encompasses a test computer, reaction flywheel testing software 2.0, power supply, and a multi-way flywheel switching device.

The black cube on the left side of Figure 12 is the reaction flywheel where the maximum angular momentum is 600 mNms, maximum output torque is 40 mNm, and the speed control accuracy is 2 rpm (2σ). The mass of the reaction flywheel is 1400 ± 100 g, with 24~30 voltage power supply and 30 watts maximum power consumption.

5.1. Experiment 1

In Experiment 1, the change time of the speed command is 0.25 s, and each beat’s increment is 20 rpm. We compare the tracking effects of the PID controller and the ADRC controller.

Figure 13i displays the curves of the reference command signal ω_ref, the actual speed ω_adrc of the ADRC controller, and the actual speed ω_PID of the PID controller. It can be observed that the ADRC controller can closely track the reference command signal, while the PID controller exhibits a significant overshoot. Figure 13ii further illustrates the performance difference between the ADRC controller and the PID controller. During the process of tracking the speed command ω_ref, the tracking error of the ADRC controller gradually decreases, and the speed stabilizes near the setpoint within 1 rpm, while the PID controller experiences noticeable overshoot and oscillation exceeds 10 rpm.

5.2. Experiment 2

In this experiment, the control effects of the ADRC controller and the PID controller are compared when the reaction flywheel runs at a constant speed and there are nonlinear and time-varying disturbances in the bearing. The reaction flywheel operates at a steady speed of 6000 rpm. In this scenario, the actual disturbance torque is significant, and the comparative effect is evident [15]. As shown in Figure 14, when the reaction flywheel runs at 6000 rpm using the PID controller, the flywheel experiences random speed loss, approximately 4–6 rpm. This phenomenon is similar to the one depicted in Figure 8 from the previous simulation. The bearing noise torque may result from particle pollution or damage to the bearing steel ball. The PID controller is unable to effectively suppress such nonlinear and time-varying disturbances. As illustrated in Figure 15, when the ADRC controller program is implemented on the same control circuit and the reaction flywheel runs at 6000 rpm, the control effect exhibits significant advantages. This outcome is consistent with the previous simulation effect, and the control accuracy can be maintained within 0.5 rpm.

Both experiments demonstrate that the proposed ADRC controller outperforms the PID controller in terms of tracking reaction flywheel speed commands and suppressing disturbances. The robustness of the proposed ADRC controller stems from its ability to estimate and eliminate the total disturbances within the control system. In Experiment 1, the disturbance is primarily attributed to friction torque, while in Experiment 2, the disturbance is primarily caused by bearing noise torque. The ADRC controller is capable of measuring disturbances and effectively suppressing them through feedforward compensation, yielding favorable control results.

6. Conclusions

This paper describes the design of a speed controller for a reaction flywheel based on ADRC. Compared to the PID controller, the ADRC-based controller achieves effective disturbance suppression and high-precision control of the flywheel speed through an extended state observer, particularly for disturbances from bearing friction torque and bearing noise torque. In scenarios where the reaction flywheel bearings are not rigorously selected, the control accuracy using a PID controller is difficult to maintain below 2 rpm. The fundamental reason is the trade-off between the rapid response characteristics of the flywheel and control precision. Increasing K_p can enhance rapid response characteristics but leads to increased overshoot; increasing K_i can improve control precision but worsens dynamic characteristics, and increasing K_d can enhance dynamic characteristics but reduces precision. The opposite is also true. However, with the ADRC control method proposed in this paper, using the extended state observer, disturbance from the flywheel bearing can be suppressed while achieving precise control of the flywheel speed. In the experiments from the previous section, the developed ADRC-based controller achieved rapid response characteristics better than 0.25 s and control accuracy better than 1 rpm.

In summary, theoretical analysis, mathematical simulation, and physical experiments collectively demonstrate the effectiveness of the ADRC controller in suppressing internal disturbances of the reaction flywheel bearing, improving speed control accuracy, and enhancing dynamic characteristics. In real-world applications, an ADRC-based control system approach can reduce the selection cost of reaction flywheel bearings and improve the pointing accuracy of satellite attitude control systems.