Speed Control Based on State Vector Applied for Electrical Drive with Elastic Connection
Abstract
:1. Introduction
2. A State Controller Applied for Speed Control of Electrical Drives with Elastic Shaft
2.1. Overall Description of the Control System
2.2. A State Controller with Fixed Parameters Implemented for the Two-Mass System
2.3. Scenario 1—Partial Adaptation of the Parameters Used in the State Controller
2.4. Scenario 2—A Novel Approach to the Adaptive State Space Controller—Indirect Adaptation of
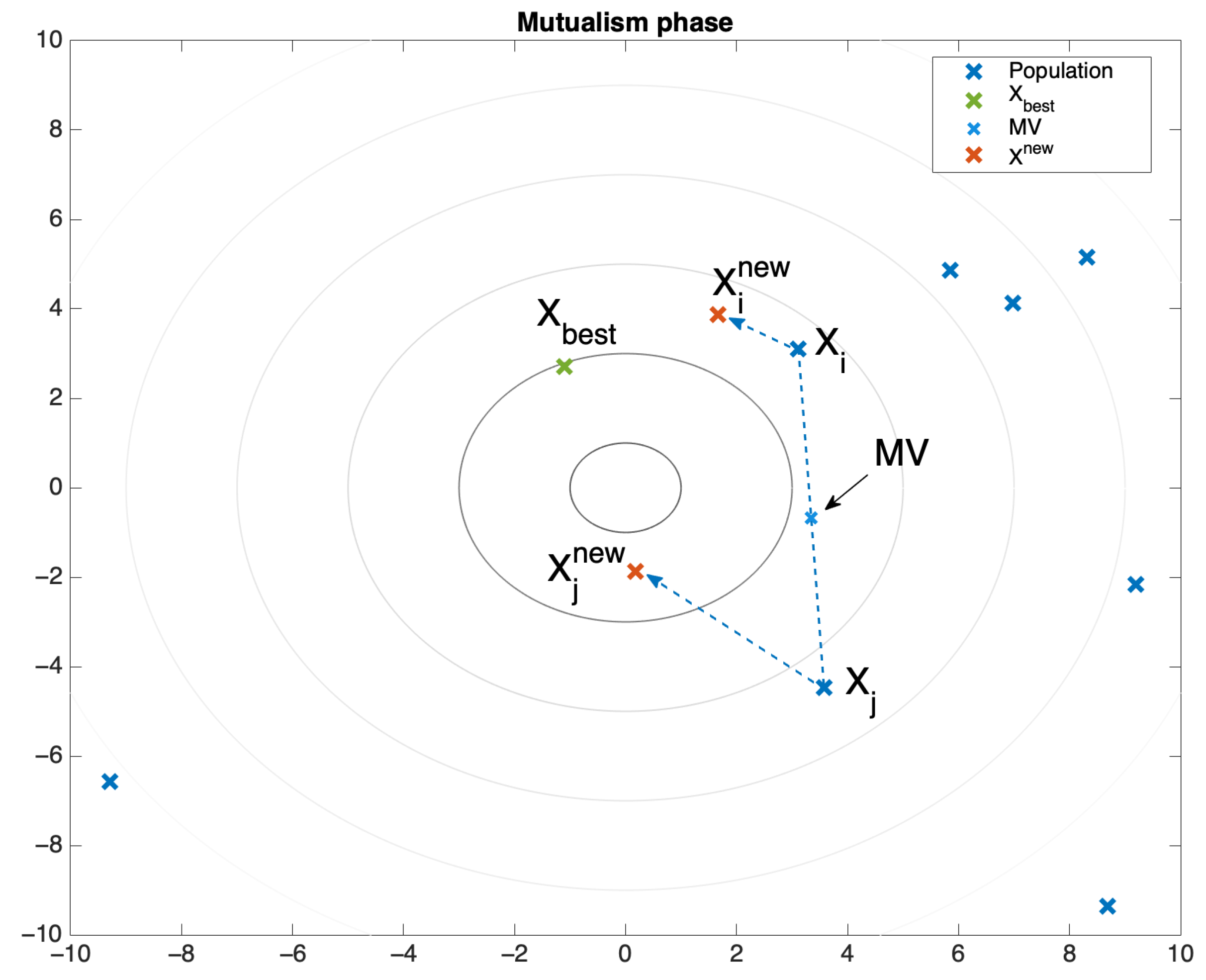
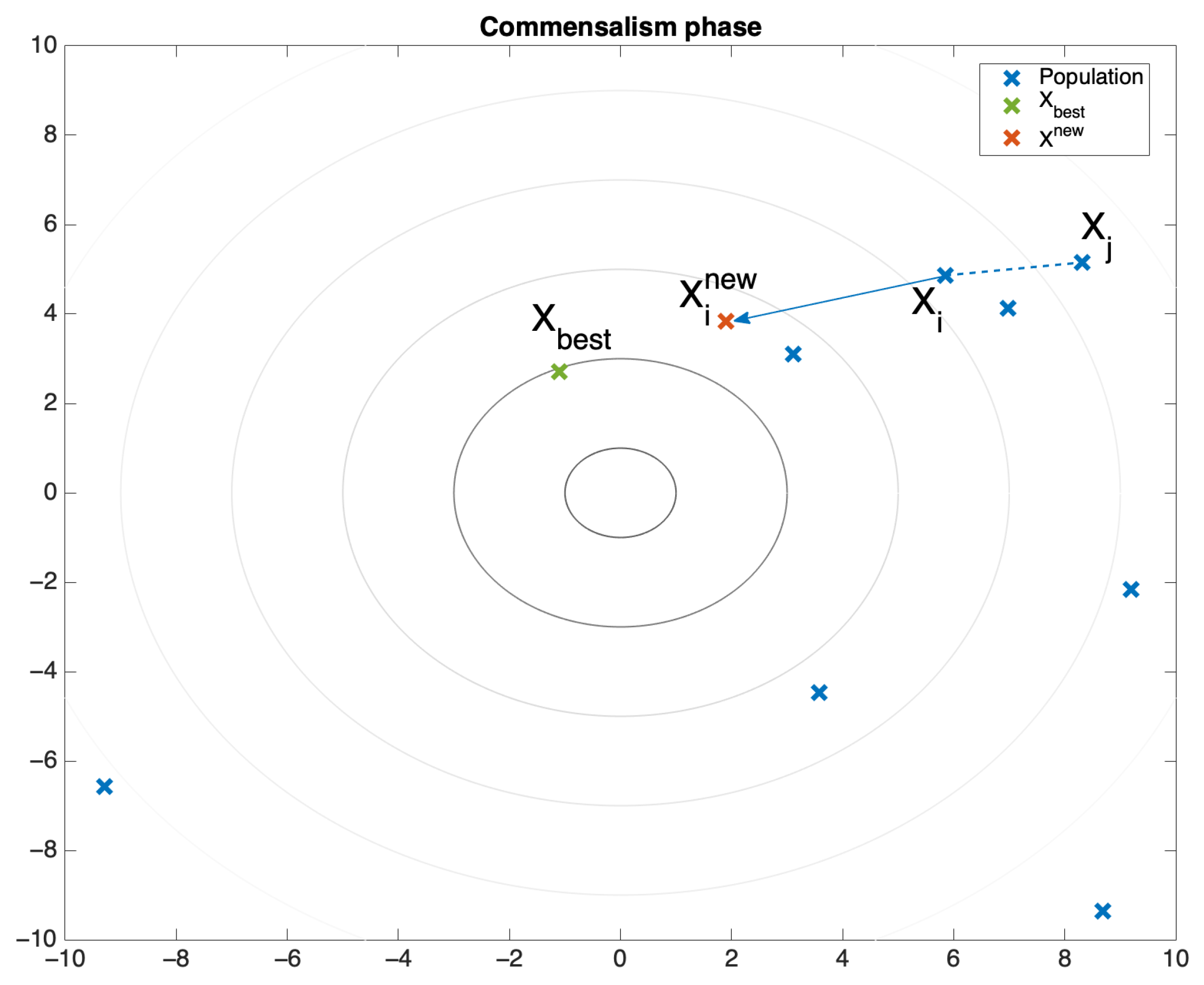
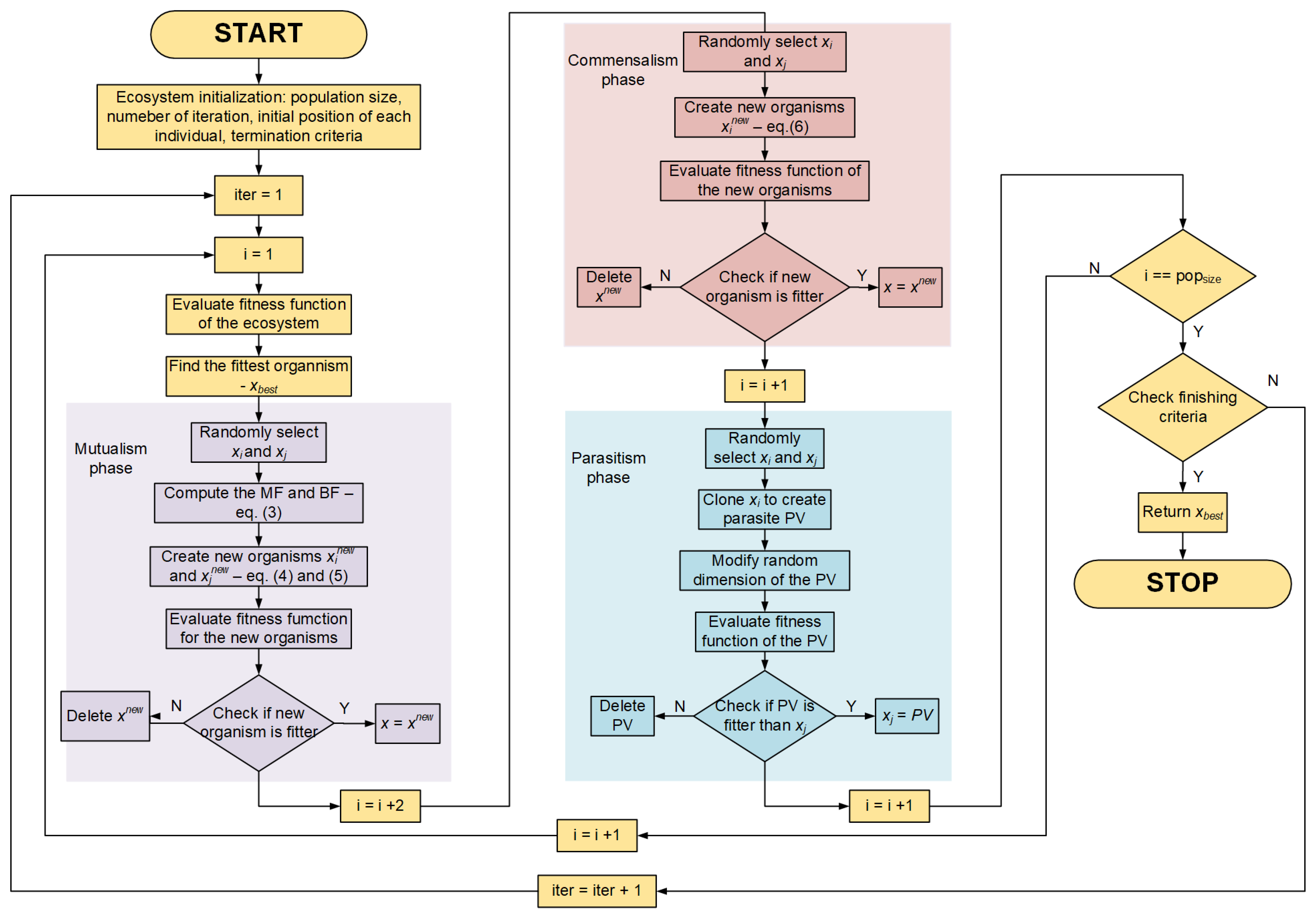
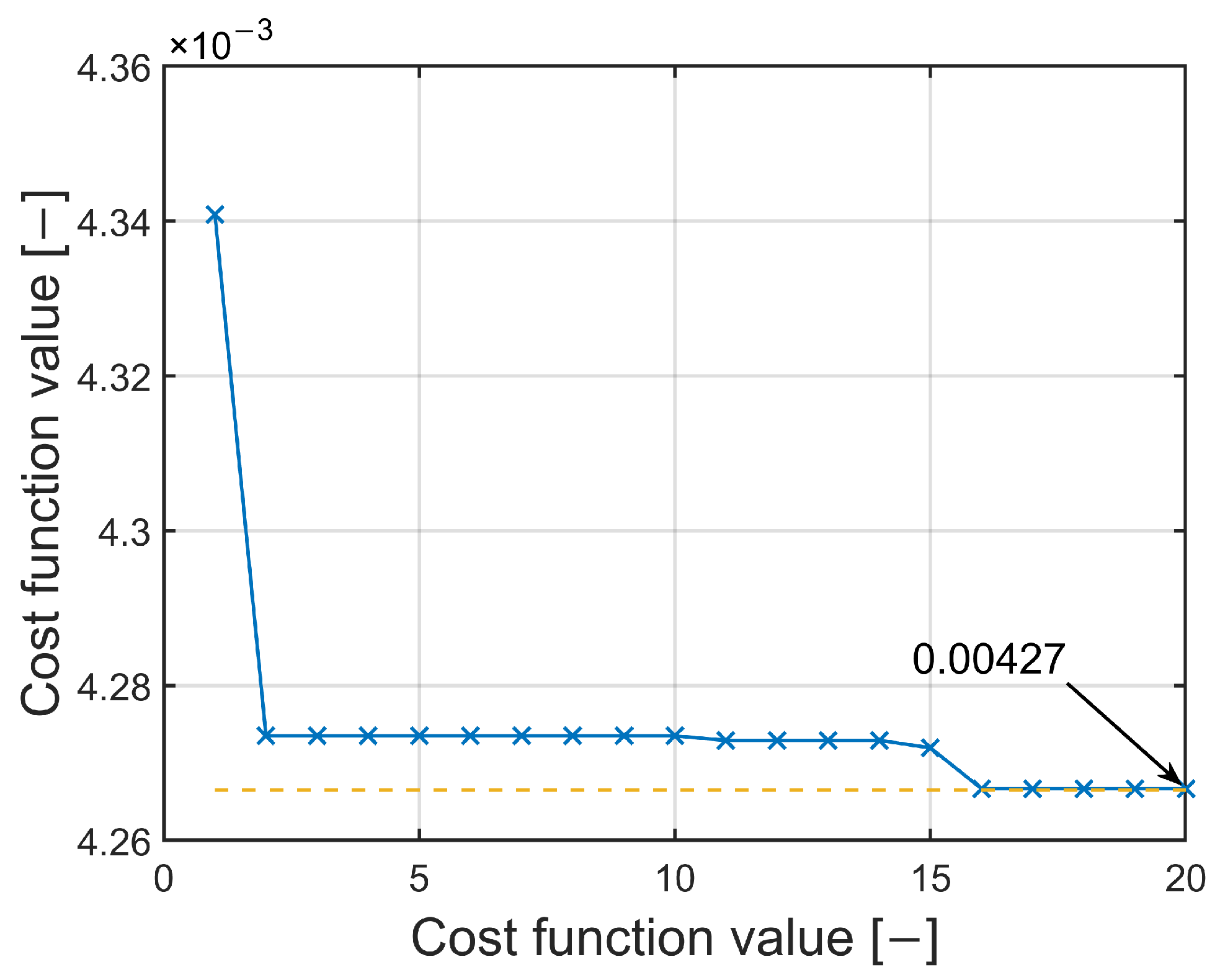
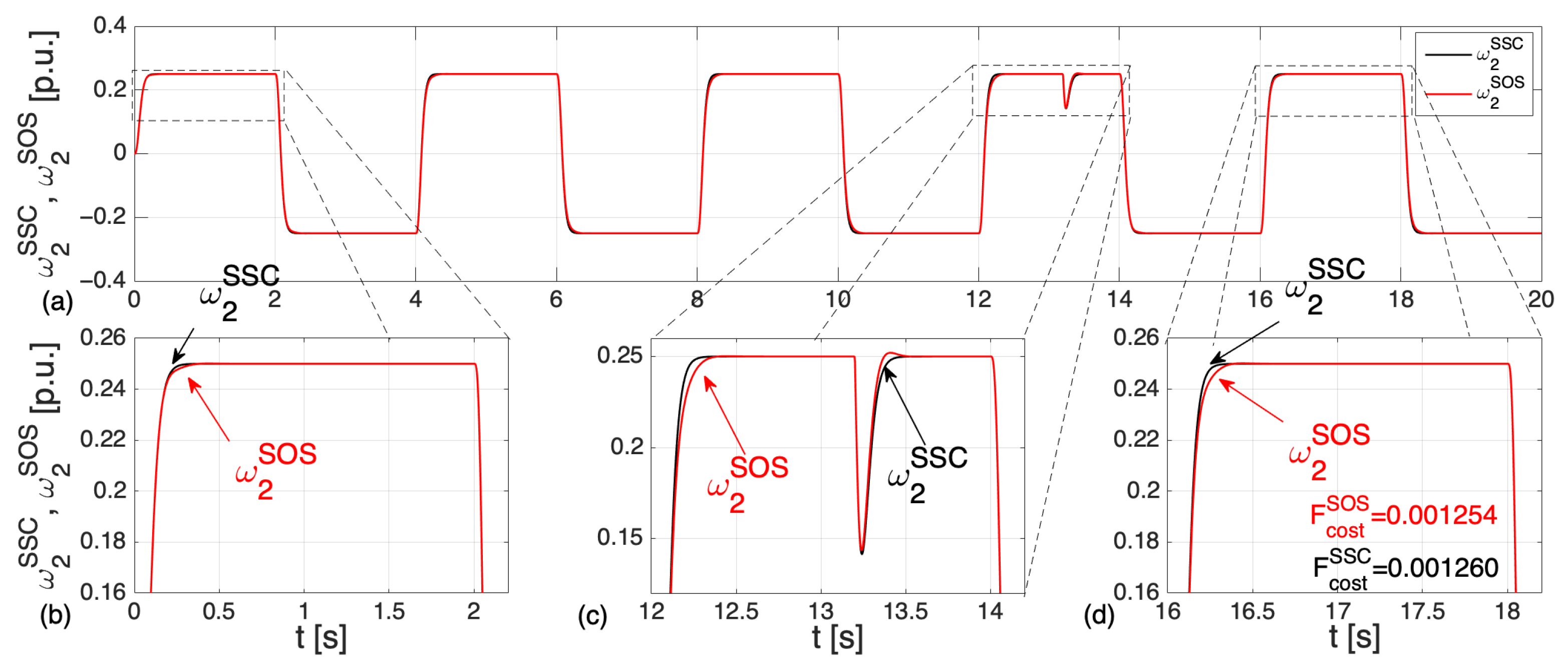
3. Nature Inspired Optimization Algorithm—The Symbiotic Organism Search
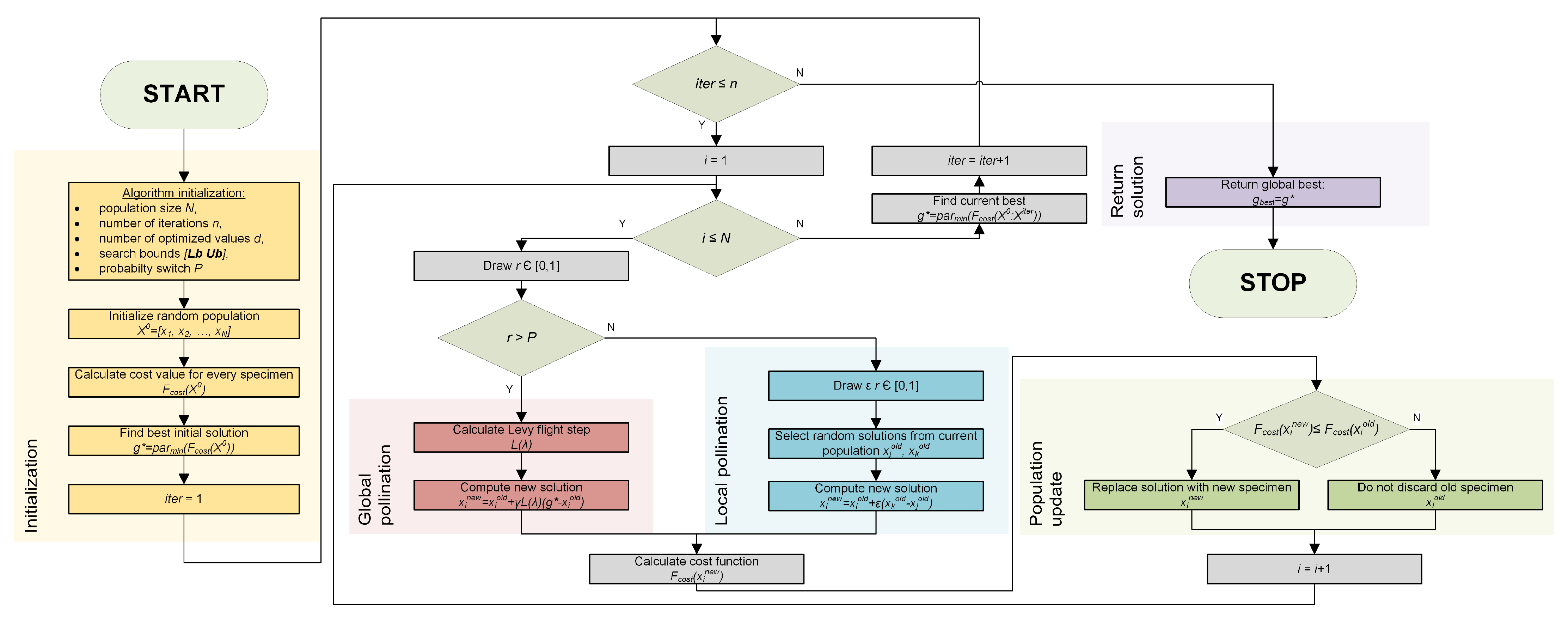
4. Nature Inspired Optimization Algorithm—The Flower Pollination Algorithm
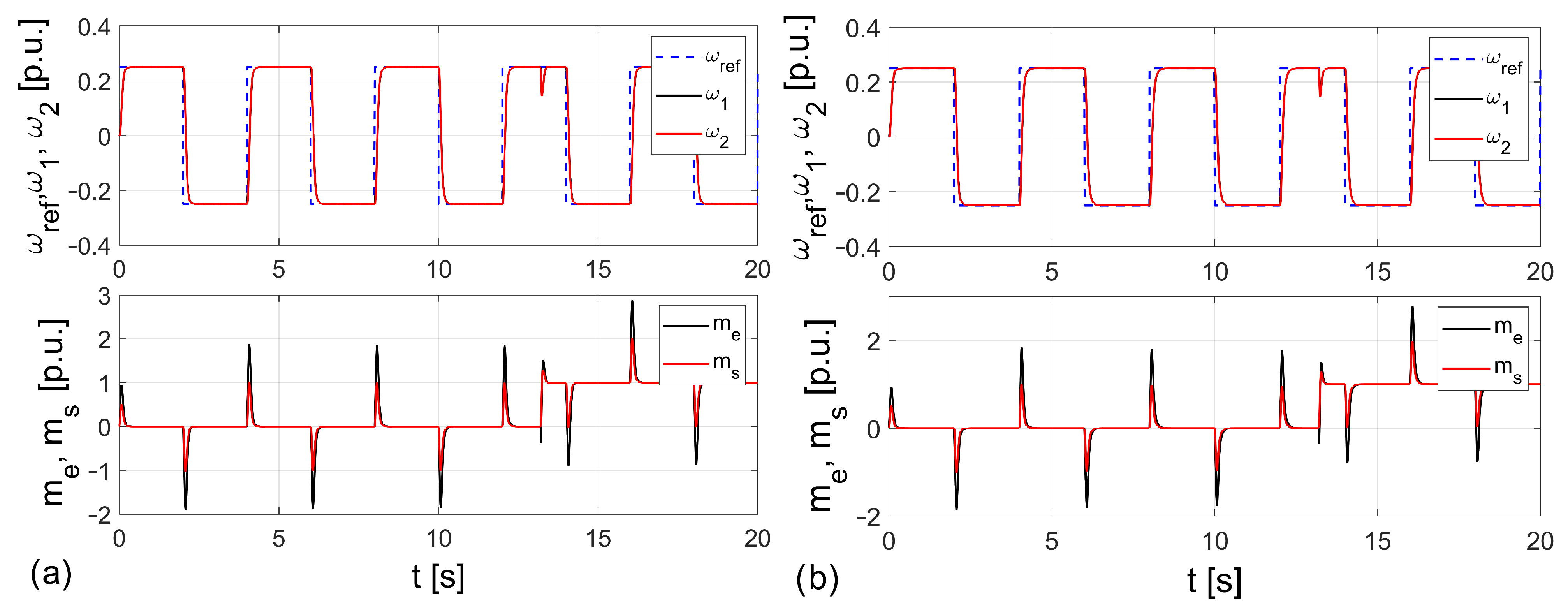
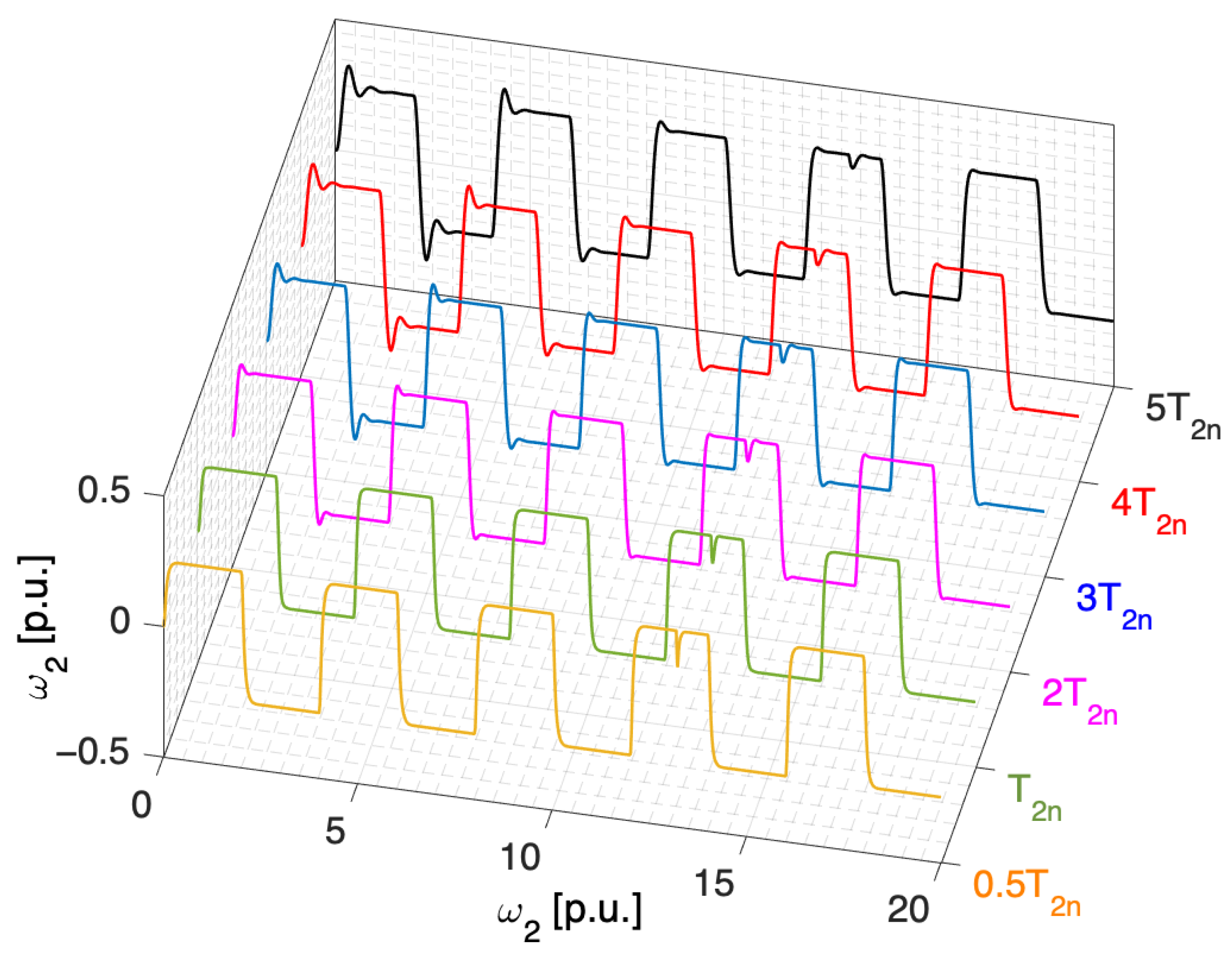
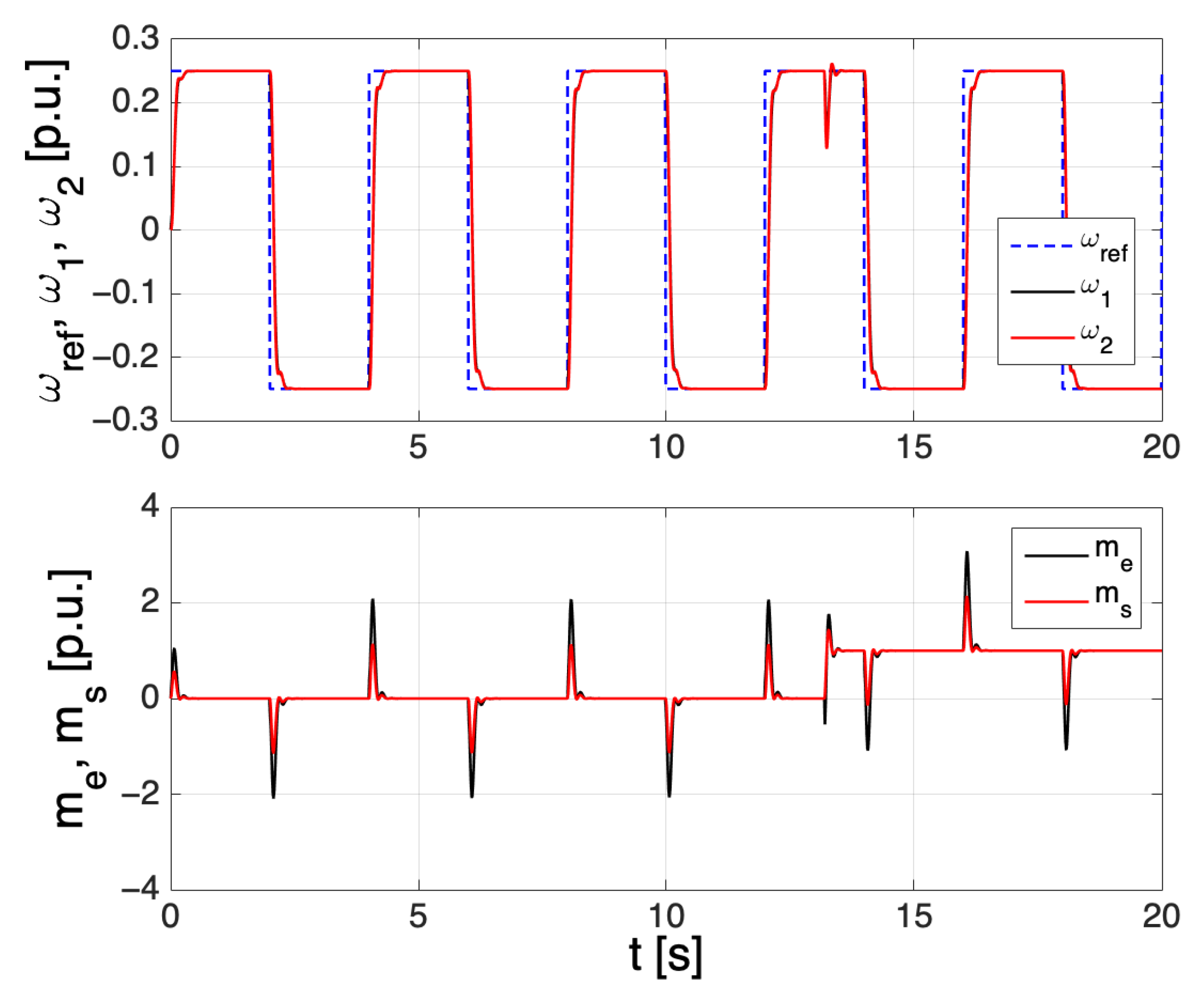
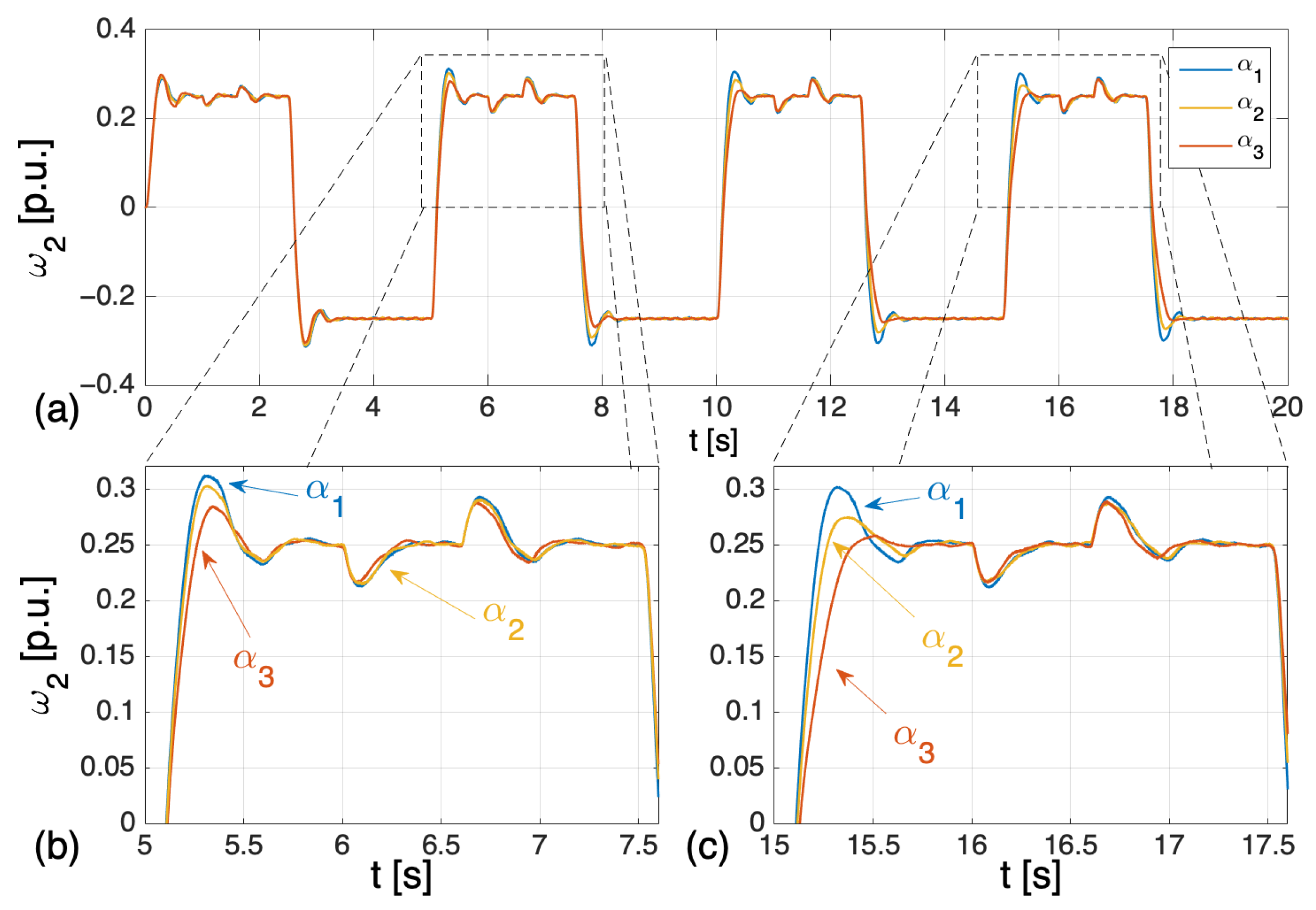
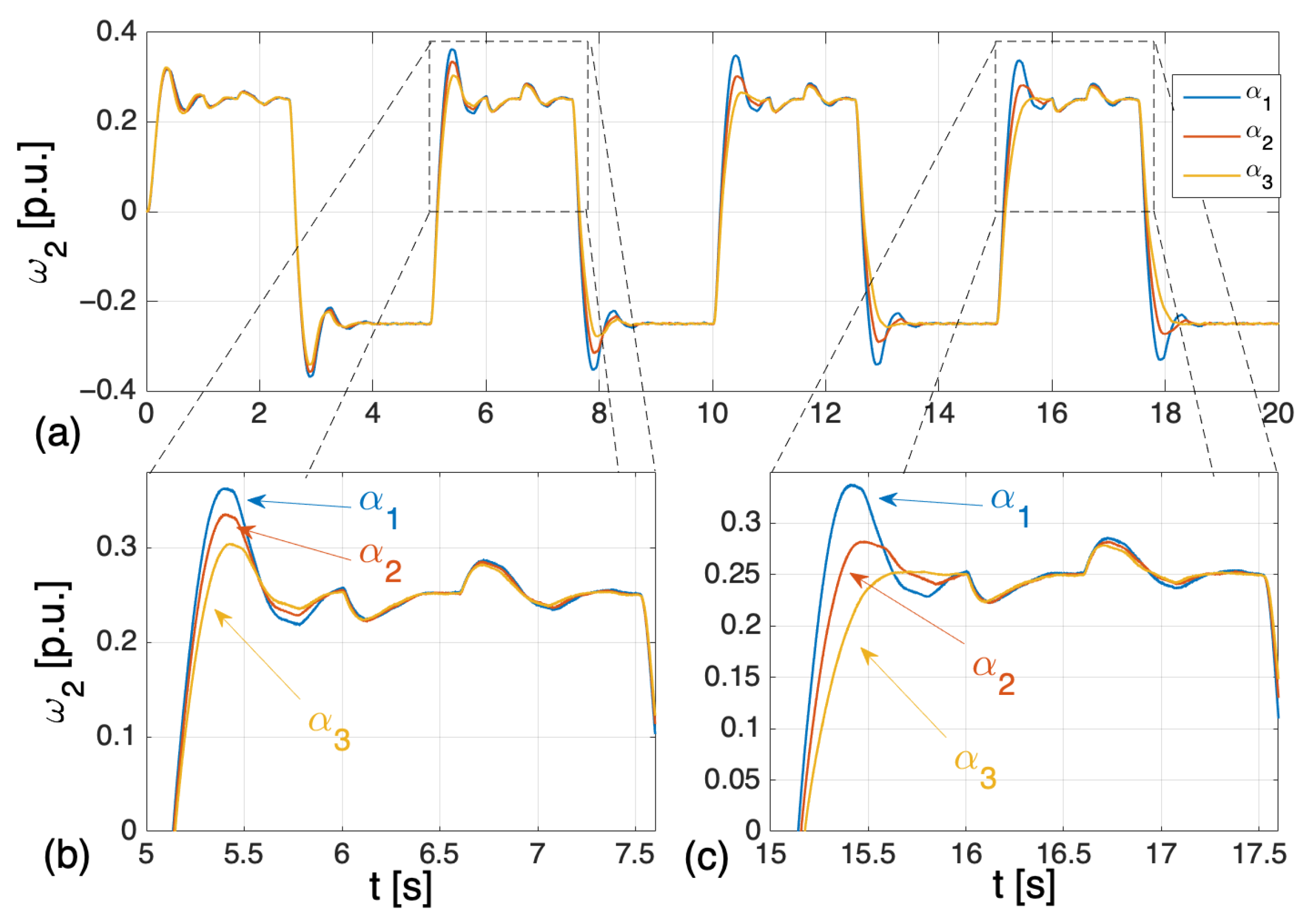
5. Simulation Tests
6. The Experimental Verification
7. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dhaouadi, R.; Kubo, K.; Tobise, M. Two-Degree-of-Freedom Robust Speed Controller for High Performance Rolling Mill Drives. In Proceedings of the Conference Record of the 1992 IEEE Industry Applications Society Annual Meeting, Houston, TX, USA, 4–9 October 1992. [Google Scholar] [CrossRef]
- Brock, S.; Łuczak, D.; Nowopolski, K.; Pajchrowski, T.; Zawirski, K. Two Approaches to Speed Control for Multi-Mass System With Variable Mechanical Parameters. IEEE Trans. Ind. Electron. 2017, 64, 3338–3347. [Google Scholar] [CrossRef]
- Brock, S.; Łuczak, D.; Pajchrowski, T.; Zawirski, K. Selected Methods for a Robust Control of Direct Drive with a Multi-mass Mechanical Load. In Advanced Control of Electrical Drives and Power Electronic Converters. Studies in Systems, Decision and Control, 75; Kabziński, J., Ed.; Springer: Cham, Switzerland, 2017; pp. 75–98. [Google Scholar] [CrossRef]
- Lukyanov, X.I.; Pishnograev, R.S.; Schvidchenko, N.V. Wide Strip Hot Rolling Mill Runout Roll Table Electric Drive Control System. In Proceedings of the IX International Conference on Power Drives Systems (ICPDS), Perm, Russia, 3–7 October 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Neshati, M.; Jersch, T.; Wenske, J. Model Based Active Damping of Drive Train Torsional Oscillations for a Full-Scale Wind Turbine Nacelle Test Rig. In Proceedings of the American Control Conference (ACC), Boston, MA, USA, 6–8 July 2016; pp. 2283–2288. [Google Scholar] [CrossRef]
- Hillsley, K.L.; Yurkovich, S. Vibration Control of a Two-Link Flexible Robot Arm. In Proceedings of the IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; pp. 2121–2126. [Google Scholar] [CrossRef]
- Cheng, X.; Zhang, Y.; Liu, H.; Wollherr, D.; Buss, M. Adaptive Neural Backstepping Control for Flexible-Joint Robot Manipulator with Bounded Torque Inputs. Neurocomputing 2021, 458, 70–86. [Google Scholar] [CrossRef]
- Jung, H.; Jeon, K.; Oh, S. Iterative Feedback Tuning of Cascade Control for Position and Velocity of Two-Mass System. IFAC-PapersOnLine 2020, 53, 8357–8362. [Google Scholar] [CrossRef]
- Zhang, R.; Yang, Y.; Chen, Z.; Tong, C. Torsional Vibration Suppression Control in the Main Drive System of Rolling Mill by State Feedback Speed Controller Based on Extended State Observer. In Proceedings of the IEEE International Conference on Control and Automation, Guangzhou, China, 30 May–1 June 2007; pp. 2172–2177. [Google Scholar] [CrossRef]
- Lin, M.-H.; Zhang, L.; Zhang, Y.-H.; Li, P.-F.; Wang, X.-H. Command Filter Backstepping Control with Error Compensation for Flexible-Joint Manipulator. In Proceedings of the Chinese Control And Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 3696–3701. [Google Scholar] [CrossRef]
- Yakub, M.F.H.; Martono, W.; Akmeliawati, R. Vibration control of two-mass rotary system using improved NCTF controller for positioning systems. In Proceedings of the IEEE Control and System Graduate Research Colloquium (ICSGRC 2010), Shah Alam, Malaysia, 22 June 2010; pp. 61–67. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T. Vibration Suppression in Two-Mass Drive System Using PI Speed Controller and Additional Feedbacks-Comparative Study. IEEE Trans. Ind. Electron. 2007, 54, 1193–1206. [Google Scholar] [CrossRef]
- Park, T.; Shin, E.; Oh, W.; Yoo, J. Robust Speed Control for Torsional Vibration Suppression of Rolling Mill Drive System. In Proceedings of the IECON’03, 29th Annual Conference of the IEEE Industrial Electronics Society (IEEE Cat. No.03CH37468), Roanoke, VA, USA, 2–6 November 2003; Volume 1, pp. 66–71. [Google Scholar] [CrossRef]
- Song, S.; Ji, J.; Sul, S.; Park, M. Torsional Vibration Suppression Control in 2-Mass System by State Feedback Speed Controller. In Proceedings of the IEEE International Conference on Control and Applications, Vancouver, BC, Canada, 13–16 September 1993; Volume 1, pp. 129–134. [Google Scholar] [CrossRef]
- Hara, K.; Hashimoto, S.; Funato, H.; Kamiyama, K. Robust comparison between state feedback-based speed control systems with and without state observers in resonant motor drives. In Proceedings of the Second International Conference on Power Electronics and Drive Systems, Singapore, 26–29 May 1997; Volume 1, pp. 371–376. [Google Scholar] [CrossRef]
- Tang, N.; Yang, M.; Hu, K.; Xu, D. Research on State Feedback of Two-Mass System Based on Weight Coefficient. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Radke, A.; Gao, Z. A Survey of State and Disturbance Observers for Practitioners. In Proceedings of the American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; pp. 5183–5188. [Google Scholar] [CrossRef]
- Sonawane, R.; Apte, A.A. Extended State Observer Based Speed Control Scheme for PMSM Drives. In Proceedings of the International Conference On Advances in Communication and Computing Technology (ICACCT), Sangamner, India, 8–9 February 2018; pp. 524–527. [Google Scholar] [CrossRef]
- Lagrioui, A.; Mahmoudi, H. Speed and Current Control for the PMSM Using a Luenberger Observer. In Proceedings of the 2011 International Conference on Multimedia Computing and Systems, Ouarzazate, Morocco, 7–9 April 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Li, Y.; Yang, M.; Long, J.; Liu, Z.; Xu, D. Current Sensorless Predictive Control Based on Extended Kalman Filter for PMSM Drives. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017; pp. 1–6. [Google Scholar] [CrossRef]
- Wei, M.; Liu, T. Design and Implementation of an Online Tuning Adaptive Controller for Synchronous Reluctance Motor Drives. IEEE Trans. Ind. Electron. 2013, 60, 3644–3657. [Google Scholar] [CrossRef]
- Chiang, H.; Hsu, K.; Li, I. Optimized Adaptive Motion Control Through an SoPC Implementation for Linear Induction Motor Drives. IEEE/ASME Trans. Mechatronics 2015, 20, 348–360. [Google Scholar] [CrossRef]
- Belov, M.P.; Lanh, N.V.; Khoa, T.D. State Observer based Elman Recurrent Neural Network for Electric Drive of Optical-Mechanical Complexes. In Proceedings of the 2021 IEEE Conference of Russian Young Researchers in Electrical and Electronic Engineering (ElConRus), Moscow, Russia, 26–29 January 2021; pp. 802–805. [Google Scholar] [CrossRef]
- Lukichev, D.V.; Demidova, G.L.; Brock, S. Fuzzy adaptive PID control for two-mass servo-drive system with elasticity and friction. In Proceedings of the 2015 IEEE 2nd International Conference on Cybernetics (CYBCONF), Gdynia, Poland, 24–26 June 2015; pp. 443–448. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Szabat, K. Damping of Torsional Vibrations in Two-Mass System Using Adaptive Sliding Neuro-Fuzzy Approach. IEEE Trans. Ind. Inform. 2008, 4, 47–57. [Google Scholar] [CrossRef]
- Song, G.; Tao, G. A Partial-State Feedback Model Reference Adaptive Control Scheme. IEEE Trans. Autom. Control 2020, 65, 44–57. [Google Scholar] [CrossRef]
- Al-Waeli, K.H.; Ramli, R.; Haris, S.M.; Zulkoffli, Z.B.; Amiri, M.S. Offline ANN-PID Controller Tuning on a Multi-Joints Lower Limb Exoskeleton for Gait Rehabilitation. IEEE Access 2021, 9, 107360–107374. [Google Scholar] [CrossRef]
- Lin, F.-J.; Wai, R.-J.; Duan, R.-Y. Neural-network controller for parallel-resonant ultrasonic motor drive. IEEE Trans. Control Syst. Technol. 1999, 7, 494–501. [Google Scholar] [CrossRef]
- Kodakkal, A.; Veramalla, R.; Kuthuri, N.R.; Salkuti, S.R. An ALO Optimized Adaline Based Controller for an Isolated Wind Power Harnessing Unit. Designs 2021, 5, 65. [Google Scholar] [CrossRef]
- Uçak, K. A Runge-Kutta MLP Neural Network Based Control Method for Nonlinear MIMO Systems. In Proceedings of the 2019 6th International Conference on Electrical and Electronics Engineering (ICEEE), Istanbul, Turkey, 16–17 April 2019; pp. 186–192. [Google Scholar] [CrossRef]
- Kaminski, M.; Szabat, K. Adaptive Control Structure with Neural Data Processing Applied for Electrical Drive with Elastic Shaft. Energies 2021, 14, 3389. [Google Scholar] [CrossRef]
- Lin, F.-J.; Chen, S.-Y.; Teng, L.-T.; Chu, H. Recurrent Functional-Link-Based Fuzzy Neural Network Controller With Improved Particle Swarm Optimization for a Linear Synchronous Motor Drive. IEEE Trans. Magn. 2009, 45, 3151–3165. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Y.; Cao, G.; Zhao, Y.; Zhang, J. Design of RBF Adaptive Sliding Mode Controller for A Supercavitating Vehicle. IEEE Access 2021, 9, 39873–39883. [Google Scholar] [CrossRef]
- Chen, S.-G.; Lin, F.-J.; Liang, C.-H.; Liao, C.-H. Intelligent Maximum Power Factor Searching Control Using Recurrent Chebyshev Fuzzy Neural Network Current Angle Controller for SynRM Drive System. IEEE Trans. Power Electron. 2021, 36, 3496–3511. [Google Scholar] [CrossRef]
- Pajchrowski, T.; Zawirski, K. Application of fuzzy logic techniques to robust speed control of PMSM. In Proceedings of the 2008 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; pp. 1198–1203. [Google Scholar] [CrossRef]
- Dyanamina, G.; Kakodia, S.K. Adaptive neuro fuzzy inference system based decoupled control for neutral point clamped multi level inverter fed induction motor drive. Chin. J. Electr. Eng. 2021, 7, 70–82. [Google Scholar] [CrossRef]
- Lin, C.; Li, H. TSK Fuzzy CMAC-Based Robust Adaptive Backstepping Control for Uncertain Nonlinear Systems. IEEE Trans. Fuzzy Syst. 2012, 20, 1147–1154. [Google Scholar] [CrossRef]
- Anderson, R.B.; Marshall, J.A.; L’Afflitto, A. Novel Model Reference Adaptive Control Laws for Improved Transient Dynamics and Guaranteed Saturation Constraints. J. Frankl. Inst. 2021, 358, 6281–6308. [Google Scholar] [CrossRef]
- Szabat, K. Direct and Indirect Adaptive Control of a Two-Mass Drive System—A Comparison. In Proceedings of the 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, 30 June–2 July 2008; pp. 564–569. [Google Scholar] [CrossRef]
- Etminaniesfahani, A.; Gu, H.; Salehipour, A. ABFIA: A hybrid algorithm based on artificial bee colony and Fibonacci indicator algorithm. J. Comput. Sci. 2022, 61, 101651. [Google Scholar] [CrossRef]
- Tarczewski, T.; Grzesiak, L.M. Artificial bee colony based auto-tuning of PMSM state feedback speed controller. In Proceedings of the 2016 IEEE International Power Electronics and Motion Control Conference, Varna, Bulgaria, 5–28 September 2016; pp. 1155–1160. [Google Scholar] [CrossRef]
- Rathod, N.; Wankhade, S. Optimizing neural network based on cuckoo search and invasive weed optimization using extreme learning machine approach. Neurosci. Inform. 2022, 2, 100075. [Google Scholar] [CrossRef]
- Knypiński, Ł.; Kuroczycki, S.; Márquez, F.P.G. Minimization of Torque Ripple in the Brushless DC Motor Using Constrained Cuckoo Search Algorithm. Electronics 2021, 10, 2299. [Google Scholar] [CrossRef]
- Zawirski, K.; Nowopolski, K.; Siwek, P. Application of Cuckoo Search Algorithm for Speed Control Optimization in Two-Sided Electrical Drive. In Proceedings of the 2018 IEEE 18th International Power Electronics and Motion Control Conference (PEMC), Budapest, Hungary, 26–30 August 2018; pp. 651–656. [Google Scholar] [CrossRef]
- Banaie-Dezfouli, M.; Nadimi-Shahraki, M.H.; Beheshti, Z. R-GWO: Representative-based grey wolf optimizer for solving engineering problems. Appl. Soft Comput. 2021, 106, 1–28. [Google Scholar] [CrossRef]
- Mishra, A.K.; Das, S.R.; Ray, P.K.; Mallick, R.K.; Mohanty, A.; Mishra, D.K. PSO-GWO Optimized Fractional Order PID Based Hybrid Shunt Active Power Filter for Power Quality Improvements. IEEE Access 2020, 8, 74497–74512. [Google Scholar] [CrossRef]
- Du, B.; Huang, S.; Guo, J.; Tang, H.; Wang, L.; Zhou, S. Interval forecasting for urban water demand using PSO optimized KDE distribution and LSTM neural networks. Appl. Soft Comput. 2022, 122, 108875. [Google Scholar] [CrossRef]
- Lin, X.; Li, K.; Wang, L. A driving-style-oriented adaptive control strategy based PSO-fuzzy expert algorithm for a plug-in hybrid electric vehicle. Expert Syst. Appl. 2022, 201, 117236. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Prayogo, D. Symbiotic organisms search algorithm: Theory, recent advances and applications. Expert Syst. Appl. 2019, 119, 184–209. [Google Scholar] [CrossRef]
- Zhou, Y.; Miao, F.; Luo, Q. Symbiotic organisms search algorithm for optimal evolutionary controller tuning of fractional fuzzy controllers. Appl. Soft Comput. 2019, 77, 497–508. [Google Scholar] [CrossRef]
- He, H.; Li, J.; Zhao, W.; Li, B.; Li, Y. Reactive power and voltage optimization of new-energy grid based on the improved flower pollination algorithm. Energies 2022, 15, 3653. [Google Scholar] [CrossRef]
- Tarczewski, T.; Grzesiak, L.M. An application of novel nature-inspired optimization algorithms to auto-tuning state feedback speed controller for PMSM. IEEE Trans. Ind. Appl. 2018, 54, 2913–2925. [Google Scholar] [CrossRef]
- Serkies, P.; Gorla, A. Implementation of PI and MPC-Based Speed Controllers for a Drive with Elastic Coupling on a PLC Controller. Electronics 2021, 10, 3139. [Google Scholar] [CrossRef]
- Łuczak, D.; Wójcik, A. The study of neural estimator structure influence on the estimation quality of selected state variables of the complex mechanical part of electrical drive. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. P.1–P.10. [Google Scholar] [CrossRef]
- Widrow, B.; Lehr, M.A. Perceptrons, Adalines, and Backpropagation. In Handbook of Brain Theory and Neural Networks; MIT Press: Cambridge, MA, USA, 1995; pp. 719–724. [Google Scholar]
- Kaminski, M. Application of the BAT algorithm in optimization of adaptive state space controller used for two-mass system. Przegląd Elektrotecniczny 2017, 93, 300–304. [Google Scholar] [CrossRef]
- Cheng, M.-Y.; Prayogo, D. Symbiotic Organisms Search: A new metaheuristic optimization algorithm. Comput. Struct. 2014, 139, 98–112. [Google Scholar] [CrossRef]
- Zainal, N.A.; Azad, S.; Zamli, K.Z. An Adaptive Fuzzy Symbiotic Organisms Search Algorithm and Its Applications. IEEE Access 2020, 8, 225384–225406. [Google Scholar] [CrossRef]
- Acharya, D.S.; Mishra, S.K. A multi-agent based symbiotic organisms search algorithm for tuning fractional order PID controller. Measurement 2020, 155, 107559. [Google Scholar] [CrossRef]
- Singh, S.P.; Prakash, T.; Singh, V.P. Coordinated tuning of controller-parameters using symbiotic organisms search algorithm for frequency regulation of multi-area wind integrated power system. Eng. Sci. Technol. Int. J. 2020, 23, 240–252. [Google Scholar] [CrossRef]
- Ezugwu, A.E.; Adeleke, O.J. Viriri, S. Symbiotic organisms search algorithm for the unrelated parallel machines scheduling with sequence-dependent setup Times. PLoS ONE 2018, 13, e0200030. [Google Scholar] [CrossRef]
- Kaminski, M.; Malarczyk, M. Hardware implementation of neural shaft torque estimator using low-cost microcontroller board. In Proceedings of the 2021 25th International Conference on Methods and Models in Automation and Robotics (MMAR), Międzyzdroje, Poland, 23–26 August 2021; Volume 10, pp. 372–377. [Google Scholar] [CrossRef]
- Wang, Z.; Qin, C.; Wan, B.; Song, W.W. A comparative study of common nature-inspired algorithms for continuous function optimization. Entropy 2021, 23, 874. [Google Scholar] [CrossRef]
- Yang, X.-S. Flower pollination algorithm for global optimization. arXiv 2012, arXiv:1312.5673. [Google Scholar]
- Bányai, T.; Illés, B.; Gubán, M.; Gubán, Á; Schenk, F.; Bányai, Á. Optimization of just-in-sequence supply: A flower pollination algorithm-based approach. Sustainability 2019, 11, 3850. [Google Scholar] [CrossRef] [Green Version]
- Dubey, H.M.; Pandit, M.; Panigrahi, B.K. A biologically inspired modified flower pollination algorithm for solving economic dispatch problems in modern power systems. Cogn. Comput. 2015, 7, 594–608. [Google Scholar] [CrossRef]
- Bekdaş, G.; Nigdeli, S.M.; Yang, X.-S. Sizing optimization of truss structures using flower pollination algorithm. Appl. Soft Comput. 2015, 37, 322–331. [Google Scholar] [CrossRef]
- Lalljith, S.; Fleming, I.; Pillay, U.; Naicker, K.; Naidoo, Z.J.; Saha, A.K. Applications of flower pollination algorithm in electrical power systems: A review. IEEE Access 2022, 10, 8924–8947. [Google Scholar] [CrossRef]
- Vallaeys, V.; Tyson, R.C.; Lane, W.D.; Deleersnijder, E.; Hanert, E. A Lévy-flight diffusion model to predict transgenic pollen dispersal. J. R. Soc. Interface 2017, 14, 126. [Google Scholar] [CrossRef] [PubMed]
- Kabzinski, J.; Mosiolek, P. Integrated, multi-approach, adaptive control of two-mass drive with nonlinear damping and stiffness. Energies 2021, 14, 5475. [Google Scholar] [CrossRef]














| Parameter | Value |
|---|---|
| Population size | 20 |
| Main loop iteration count | 20 |
| Max. time for a main loop | 120 min |
| Parameter | Value |
|---|---|
| Population size | 20 |
| Main loop iteration count | 20 |
| Probability switch P | 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malarczyk, M.; Zychlewicz, M.; Stanislawski, R.; Kaminski, M. Speed Control Based on State Vector Applied for Electrical Drive with Elastic Connection. Automation 2022, 3, 337-363. https://doi.org/10.3390/automation3030018
Malarczyk M, Zychlewicz M, Stanislawski R, Kaminski M. Speed Control Based on State Vector Applied for Electrical Drive with Elastic Connection. Automation. 2022; 3(3):337-363. https://doi.org/10.3390/automation3030018
Chicago/Turabian StyleMalarczyk, Mateusz, Mateusz Zychlewicz, Radoslaw Stanislawski, and Marcin Kaminski. 2022. "Speed Control Based on State Vector Applied for Electrical Drive with Elastic Connection" Automation 3, no. 3: 337-363. https://doi.org/10.3390/automation3030018
APA StyleMalarczyk, M., Zychlewicz, M., Stanislawski, R., & Kaminski, M. (2022). Speed Control Based on State Vector Applied for Electrical Drive with Elastic Connection. Automation, 3(3), 337-363. https://doi.org/10.3390/automation3030018







