Risk-Weight Calculation of Candidate Risk Factors for Incidental Osteoporotic Fracture in Patients with Rheumatic Diseases: A Potentially Accurate Approach
1
Department of Musculoskeletal Medicine, 6-7-5 Nakamura-Ohashidori, Shimanto-City 787-0033, Japan
2
Department of Rheumatology, Dohgo-Onsen Hospital Rheumatology Center, 21-21 HImetsuka-Otsu, Matsuyama 790-0858, Japan
3
Department of Rheumatology, Kochi Memorial Hospital, 4-13 Shiromi-cho, Kochi 780-0824, Japan
*
Author to whom correspondence should be addressed.
Osteology 2025, 5(1), 5; https://doi.org/10.3390/osteology5010005
Submission received: 28 November 2024
/
Revised: 27 December 2024
/
Accepted: 21 January 2025
/
Published: 27 January 2025
(This article belongs to the Topic Bone-Related Diseases: From Molecular Mechanisms to Therapy Development)
Abstract
:Background/Objectives: To assess the risk of osteoporotic fractures in patients with rheumatic diseases (RDs), we introduced a new approach for predicting incident osteoporotic fractures (OF), employing a risk-weight calculation for each candidate risk factor. Methods: RD outpatients were picked up, and their histories, including OFs, were studied. A Cox regression analysis that evaluated candidate risk factors was conducted with a multivariate model. The variants were selected as candidate risk factors that showed statistical significance using a univariate model. Using the risk ratio or the β-value and p-value, different approaches to acquire a total risk weight (TRW) for each patient were determined to compare the sensitivity and specificity among the approach methods. The cut-off index (COI) was determined using receiver operating characteristic analysis. Sensitivity and specificity for incident OFs were determined using the Kaplan–Meier survival analysis. Results: In a total of 1228 patients, incidental OF occurred in 179 (14.58%) who were included. Factors with significantly higher risk ratios were a history of vertebral and non-vertebral fractures (p < 0.001), cognitive impairment (p < 0.001), anti-osteoporosis drug intervention (p < 0.001), and rehabilitation (p < 0.001). The excellent approach to acquire the best sensitivity and specificity was to calculate the β-value multiplied by the logarithm of the p-value based on 0.05, including non-significant factors (sensitivity: 31.2%, specificity: 94.9%, and area under the curve (AUC): 0.774) compared to 29.4%, 91.6%, and 0.723, respectively, with a counted significant risk factors approach. Conclusions: This novel approach, which includes non-significant factors, can achieve a more accurate sensitivity and specificity to accidental OF in patients with RDs.
1. Introduction
Although already recognized worldwide, rheumatoid arthritis (RA) is an independent risk factor for osteoporotic fractures [1,2,3]. RA is an autoimmune and chronic inflammatory disease whose pathogenesis involves generating autoantibodies that tilt bone metabolism toward bone resorption. Deterioration of bone metabolism is also related to therapeutic drugs in RA. In RA cases, increased falls due to joint deformities and contractures are determined [4,5,6,7].
Similarly, rheumatic diseases (RDs) are also thought to increase the risk of osteoporotic fractures [8,9,10,11,12,13,14]. However, despite various reports on the extraction of risk factors, the accuracy in predicting the occurrence of osteoporotic fracture (OF) is far from high. Even FRAX®, a globally recognized fracture risk assessment site, has guidelines for therapeutic intervention of 15% over ten years [15].
Practical guidelines with high sensitivity and specificity for preventing incident OF (inc-OF) are needed. We have developed a novel risk calculation system that weighs each candidate risk factor for OF in RDs based on the β-value and p-value for the cut-off index (COI) obtained from Cox regression analysis. We have compared the area under the curve (AUC) using some novel methods to verify its accuracy in evaluating its sensitivity and specificity. This study aimed to assess the validity of the new approaches and the criteria separated by the COI that is determined with the approaches using retrospective cohort data.
2. Materials and Methods
2.1. Patients Recruit and Study Design
Outpatients with RDs who were treated in our institute from August 2010 to November 2021 and followed up for at least one year were selected for this study. The patients were followed up with blood tests, including cystatin-C, every three months. Bone mineral density (BMD) was measured at least annually using dual-energy X-ray absorptive densitometry. Time at the first measurement of the BMD was set as the baseline. Patients were followed up for at least one year in the institute. Patients were followed up until December 2022 unless censored by death, loss of follow-up, or dropping out due to admission to a nursing home. Patients who had been lost to follow-up one year after the baseline were excluded. The primary endpoint was the development of inc-OF. The presence of prevalent osteoporotic fracture (pr-OF) before baseline that had been harvested from medical records at baseline (yes/no: binary was picked up), and the presence of prevalent vertebral body fracture (pr-VF; yes/no: binary) and non-vertebral fracture (pr-nVF; yes/no: binary) were selected as candidate risk factors. Sex (male/female: binary), age (continuous number) at baseline, number of comorbidities except of RDs at baseline (nCom; constant number), estimated glomerular filtration rate measured with cystatin-C at baseline (eGFR_CysC; continuous number), T-score in the lumbar spine (LS; continuous number) and in the femoral neck (FN; constant number) at baseline, presence of lifestyle-related diseases (LSDs; yes/no: binary) such as diabetes mellitus (DM; yes/no: binary), hypertension (HT; yes/no: binary), hyperlipidemia (HL; yes/no: binary), chronic heart failure (CHF; yes/no: binary), chronic obstructive pulmonary diseases (COPD; yes/no: binary), insomnia (Insomnia; yes/no: binary), presence of conditions that induce hyper fallibility (Fallibility; yes/no: binary) such as osteoarthritis (OA; yes/no: binary), musculoskeletal ambulation disability symptom complex (MADS; yes/no: binary), joint contracture in the lower extremities (Contracture; yes/no: binary) and disuse status (Disuse; yes/no: binary), neuromuscular diseases (NMD; yes/no: binary), presence of cognitive impairment (CI; yes/no: binary), administration of anti-osteoporotic drugs (OPD; yes/no: binary), administration of glucocorticoid (GCs; yes/no: binary) during follow-up, total dose of glucocorticoids (total dose GCs; continuous number), rehabilitation administered during follow-up (Reha; yes/no: binary), and polypharmacy which is defined as no less than 6 kinds of tablet or capsule drug were administered during follow-up (PPs; yes/no: binary) were picked up as candidate risk factors. The authors diagnosed these comorbidities with specialists certified by the Japanese Society of Internal Medicine, the Japanese Orthopaedic Association, and the Japanese College of Rheumatology.
The Mann–Whitney U-test compared candidate risk factors between the groups in which an inc-OF developed and in whom no inc-OF developed (G-OF and G-nOF). The variables were also evaluated using a Cox regression analysis concerning the development of the inc-OF with a univariate model.
Several approaches were performed to determine each patient’s total risk weight (TRW).
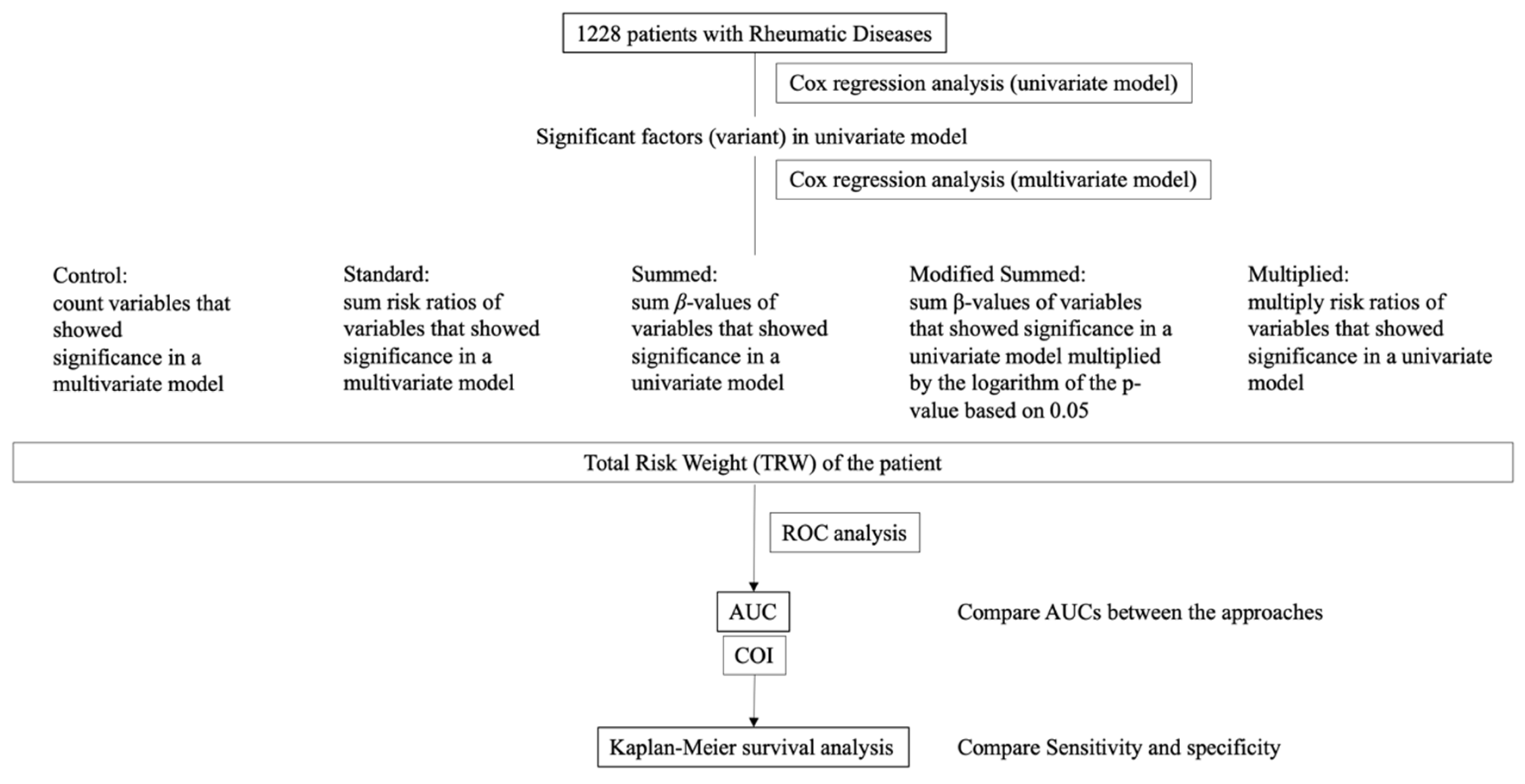
2.2. Approaches
2.2.1. Control Approach
Variables that showed a significant p-value using the multivariate model using a Cox regression analysis were counted as a control approach. A total summed number was determined as TRW for each patient.
2.2.2. Standard Approach with the Summed Risk Ratios
The risk ratios of each variable were summed. Variables were chosen to show a significant p-value using the multivariate model of a Cox regression analysis among the variables that showed significant p-values with the univariate model. The summed value was determined as the patient’s TRW.
2.2.3. Summed Approach with β-Value
β-Values of the variables that showed statistical significance in a univariate model with a Cox regression analysis were summed. These summed values were determined as the TRW of each patient.
2.2.4. Modified Summed Approach with a Combination of β-Value and p-Value
Variables that showed statistical significance in a univariate model with a Cox regression analysis were picked up. The β-value was multiplied by the logarithm of each p-value based on 0.05 calculated from the data in the multivariate model. The calculated value was determined as each variable’s primary risk weight (PRW). These PRWs of the variables were summed, and it was determined as the TRW of each patient.
2.2.5. Multiplied Approach
Variables that showed statistical significance in a univariate model with a Cox regression analysis were picked up. The risk ratios of each variable were multiplied by the value of each variable, and then these values of the variables in each patient were further multiplied. The calculated value was determined as the TRW of each patient.
2.3. Determining COI for Each Approach and Statistical Comparison
A COI and the area under the curve (AUC) for each approach were determined using a receiver operating characteristic analysis (ROC). A Kaplan–Meier survival analysis was used to calculate the hazard ratios, sensitivities, and specificities regarding the match/not-match of COI (G-TRW < COI and G-TRW ≥ COI) for inc-OF presence.
A schematic flowchart of this study is shown in Figure 1.
2.4. Statistical Procedures
All statistical procedures were performed with StatPlus:mac® (AnalystSoft Inc., Walnut, CA, USA).
2.5. Ethical Considerations
The Ethics Committee of the associated institute approved this study’s protocols and patient consent requirements (approval number: GC-2023-2). The subjects and their families were informed that the personal information obtained in this study was anonymous and would only be used for analysis.
3. Results
3.1. Patients’ Demographics
A total of 1228 patients in these 345 males and 883 females (female/male rate = 2.6) were included. The mean age at baseline was 77.7 ± 12.3 years old, and the mean follow-up length was 90.7 ± 76.9 months. The inc-OF presented in 179 (14.6%). Background RDs were 749 with rheumatoid arthritis (RA), 179 with psoriatic arthritis (PsA), 60 with ankylosing spondylitis (AS), 60 with Sjögren syndrome (SJS), 58 with pustulosis palmaris et plantaris (PPP), 28 with systemic lupus erythematosus (SLE), 26 with giant cell arteritis (GCA), 26 with polymyalgia rheumatica (PMR) (The cases in giant cell arteritis and polymyalgia rheumatica do not overlap), 15 with systemic sclerosis (SSc), 12 with Behçet’s disease (BD), 8 with polymyositis/dermatomyositis (PM/DM), 5 with adult-onset Still disease (AOSD), 1 with familial Mediterranean fever (FMF), and 1 with polyarteritis nodosa (PAN) (Table 1).
Mean age at baseline, GCs administration rate during follow-up, pr-OF rate at baseline, inc-OF rate during follow-up, and follow-up time length showed no significant differences among the disease groups. The female gender rate in AS was significantly lower than in RA (p < 0.05) and in SJS (p < 0.01), and the female gender rate in SJS was significantly higher than in Behçet disease (p < 0.05).
Female gender rate, age at baseline, pr-OF, pr-VF, and pr-nVF rate at baseline; nCom at baseline; eGFR_CysC at baseline; presence rates of DM, HT, HL, CHF, Insomnia, OA, MADS, Contracture, Disuse, NMD, CI, OPD, and Reha; follow-up length; and PPs showed greater significance, while the follow-up length was significantly shorter in the G-OF group than in the G-nonOF group (determined by the Mann–Whitney U-test) (Table 2).
Female gender, older age at baseline, presence of pr-VF and pr-nVF at baseline, higher number of comorbidities at baseline, lower eGFR_CysC at baseline, lower T-score in the LS at baseline, presence of CHF, insomnia, OA, MADS, Disuse, NMD, and CI, OPD administration, Rehabilitation intervened, follow-up length, and higher polypharmacy rate were the significant higher risk ratios using a Cox regression analysis with a univariate model. The β-values and 95% confidence interval, p-values, risk ratios in a univariate model, p-values, logarithms of each p-value, and the multiplied values using a multivariate model are shown in Table 3.
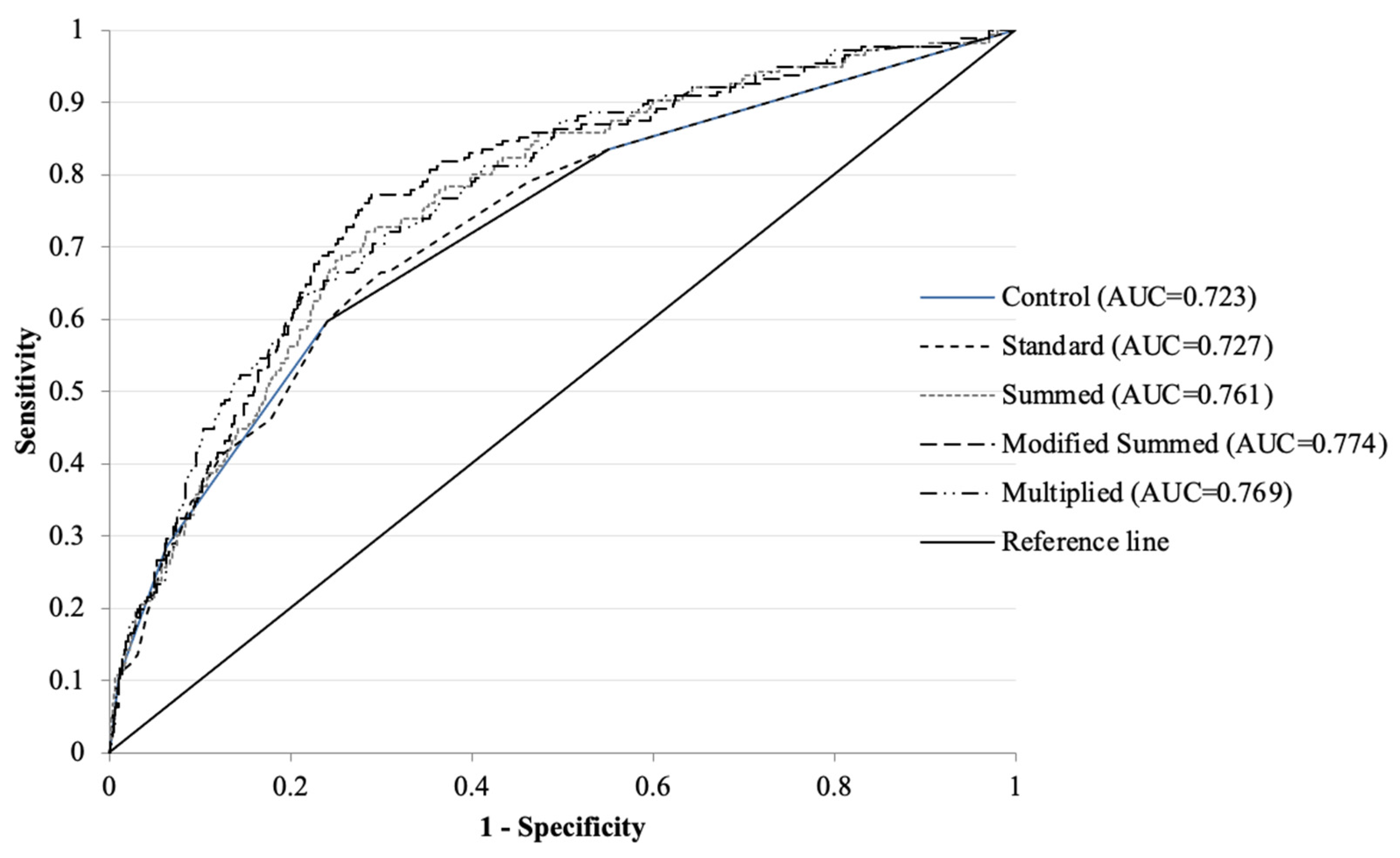
3.2. Comparison Among Approaches
The AUCs from the ROC curves for each approach were 0.723, 0.727, 0.761, 0.774, and 0.769 for the Control, Standard, Summed, Modified standard, and Multiplied approach, respectively (Figure 2 and Table 4). The AUC in the Control approach was significantly inferior to the other approaches but in the Standard approach. The standard approach had a significantly lower AUC than the other approaches besides the Control approach. The Summed approach had a significantly lower AUC than the Modified Summed and the Multiplied. The AUCs between the Modified Summed and the Multiplied showed no significant difference (Table 5).
The Kaplan–Meier survival curve resulted in statistically significant hazard ratios in all approaches with 3.89, 3.90, 5.16, 6.48, and 4.53 for the Control, Standard, Summed, Modified Summed, and Multiplied approaches, respectively. The sensitivities and specificities in each approach were 29.4% and 91.6%, 27.4% and 92.4%, 30.0% and 93.8%, 31.2% and 94.9%, and 33.5% and 92.5% for the Control, Standard, Summed, Modified Summed, and Multiplied approaches, respectively (Table 4).
4. Discussion
This study introduces a device to increase the prediction accuracy of OFs in patients with RDs. Many risk factors for OFs have been pointed out, but whether they were effectively utilized in clinical practice must be investigated. Even FRAX®, a globally acclaimed tool for predicting osteoporotic fractures, fails to incorporate LSDs as a risk factor, and the threshold for therapeutic intervention is 15% for a 10-year prediction [16]. In clinical practice, it would be more persuasive to patients if it could predict the occurrence of fractures with a higher probability, and the effectiveness of therapeutic intervention would increase if it could determine with greater accuracy how much risk each patient has.
Especially when there are many small, inconclusive risk factors, such as OP, there is a high possibility that the significant risk will change depending on the population. Even in such cases, it is more reasonable to determine the threshold (i.e., COI) by calculating each patient’s TRW and performing risk assessment by weighting the TRW.
Even though simply counting each patient’s significant risk variables as an indicator (the Control approach), ROC calculated the COI of the TRW, and the chi-square test compared the incidence of fractures in the two groups separated by the COI. The results showed 91.6% specificity and 29.4% sensitivity. The fracture incidence in this dataset was 179 out of 1228 (14.58%), and the approach to fracture incidence was approximately two times more accurate. However, we decided that while we might be satisfied with sensitivity, there was still room for improvement. Then, the Standard approach showed slightly better AUC than the Control approach. However, no significant difference was shown between the two approach methods.
When calculating TRW, the Modified Summed and Multiplied approaches calculate each factor’s risk ratio by combining β and p values. The basis for this is that the β value represents the risk ratio of false negatives, while the p-value represents the risk ratio of false positives. Therefore, we determined that the accuracy of each factor could be increased by combining these two. As a result, this attempt could exhibit higher accuracy.
The focus of interest is how much improvement there is in accuracy compared to the risk factor extraction methods that have already been developed. We used the same dataset to test the sensitivity and specificity of some different approaches. The multivariate model examined the significant risk factors extracted by the univariate model. The significantly extracted variables were counted as 1 if positive and 0 if negative. The relationship between the total score generated by adding them and inc-OP occurrence was determined using ROC. The COI was divided into two groups, and sensitivity and specificity were verified by the inc-OP event and the chi-square test (CST). Results showed that the multivariate model identified VF, nVF, CI, OPD, and Reha as significant risk factors. The average addition point for each component was 1.02, and the COI was one by ROC. When CST was divided into groups exceeding 1 (G > 1) and one or less (G ≤ 1), no inc-OP occurred in 793 of 866 (91.57%) patients in group G ≤ 1, and inc-OP occurred in 106 of 362 (29.28%) patients in group G > 1. This was about 0.1% less good than the temporary validation in the current study using the Control approach, but the specificity was about the same.
In this dataset, major risk factors for inc-OF were prevalent OFs in the vertebral and non-vertebral bodies and cognitive impairment. These were already known [17,18,19,20]. However, OPD and rehabilitation intervention were the newly presented risk factors. These were curious because these interventions might be ordered to prevent inc-OFs. A good explanation is that patients at high risk for OFs were given both therapeutic interventions, resulting in more fractures. This matter requires further analysis.
The approaches were focused on risk weight calculation. Then, risk weight calculations were performed in three different approaches. However, the selection method for significant variables was the same. We picked up variables as the risk factor extracted from the univariate model. Approaches varied according to the calculation methods. The reason for including significant variables in the multivariate and univariate models was that risk weight would be more in line with reality. The Summed approach already resulted in a better AUC than the Standard and Control approaches. However, further better approaches were shown in the Modified Summed and Multiplied approaches. The difference between the Summed and Modified Summed was to add logarithm in calculations. This technique gave a better AUC than a simple sum calculation. We adopted a combination of the β-value and the p-value technique in each candidate factor to represent the degree of hazard ratio [21]. In addition, the confounding of each other element was minimized by converting the p-value obtained by multivariate analysis into a logarithm based on the significance level of 5% [22,23]. This technique would be widely relevant in a dataset with numerous significant factors in a univariate model.
Surprisingly, the AUCs in the Modified Summed and the Multiplied approach showed no significant difference. However, the hazard ratio was superior in the Modified Summed approach. Multiply would enhance the risk weight, but more gimmick was afraid. The number of cases in the dataset was relatively small, and there was a risk of showing no statistical difference.
This analysis was performed on RDs but may also work effectively for primary osteoporosis. It was based on results from a single center, but more extensive research based on data from multiple centers and a national database would provide more reliable results. Bayesian statistics can also add or remove risk factors [24] and provide 95% confidence intervals while improving accuracy [25].
A novel assessment system for predicting osteoporotic fractures should be a numerical system that adds the risk weights of each candidate factor, as in this study. This approach will help in predicting the occurrence of OFs in the future. However, future studies to verify are necessary.
The limitation lies in the fact that in this single-center study, population bias was be included; the number of samples was small, so population bias was included; and unidentified risk factors were not included in this study, so this approach was not able to identify novel risk factors. However, we are confident that the approach introduced in this study would be beneficial for improving accuracy in predicting incident osteoporotic fracture.
5. Conclusions
A novel approach to evaluating risk factors for predicting incidental osteoporotic fractures calculated to summarize the risk weight in RDs was introduced, and its efficacy was validated. This approach could simultaneously achieve high sensitivity and specificity. This approach would be available when many candidate variables lie in the background in real-world practice.
Author Contributions
Conceptualization, I.Y.; methodology, I.Y. and N.S.; software, I.Y.; validation, I.Y., T.C. and N.S.; formal analysis, I.Y.; investigation, I.Y.; resources, I.Y., T.C. and N.S.; data curation, I.Y.; writing—original draft preparation, I.Y.; writing—review and editing, I.Y., T.C. and N.S.; visualization, I.Y.; supervision, T.C. and N.S.; project administration, I.Y.; funding acquisition, none. All authors have read and agreed to the published version of the manuscript.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Institutional Review Board Statement
This study was conducted according to the guidelines of the Declaration of Helsinki and approved by the Institutional Review Board (or Ethics Committee) of Yoshii Hospital ethics committee (approval number: Y-OP-2020-3, approved on 14 November 2020).
Informed Consent Statement
Informed consent was obtained from all subjects involved in this study. Anonymity was ensured for all patients and families who participated in this study, and no names and/or addresses were issued that could help identify these individuals.
Data Availability Statement
The datasets used and/or analyzed during the current study are available from the corresponding author on reasonable request.
Acknowledgments
Authors would like to thank Kaoru Kuwabara, Sayori Masuoka, Eri Morichika, and Aoi Yoshida for their dedicated data collection.
Conflicts of Interest
None of the authors or their families have shared any information regarding income, property, grants, or any other financial supports provided for this study.
Abbreviations
RA, rheumatoid arthritis; RDs, rheumatic diseases; OF, osteoporotic fracture; inc-OF, incident osteoporotic fracture; COI, cut-off index; pr-OF, prevalent osteoporotic fracture; BMD, bone mineral density; pr-VF, prevalent vertebral body fracture; pr-nVF, prevalent non-vertebral fracture; nCom, number of comorbidities; eGFR, estimated glomerular filtration rate; LS, lumbar spine; FN, femoral neck; LSDs, lifestyle-related diseases; DM, diabetes mellitus; HT, hypertension; HL, hyperlipidemia; CHF, chronic heart failure; COPD, chronic obstructive pulmonary diseases; Fallibility, conditions that induce hyper fallibility; OA, osteoarthritis; MADS, musculoskeletal ambulation disability symptom complex; Contracture, joint contracture in the lower extremities; Disuse, disuse status; NMD, neuromuscular diseases; CI, cognitive impairment; OPD, administration of anti-osteoporotic drugs; GCs, administration of glucocorticoid; Reha, rehabilitation administered during follow-up; PPs, polypharmacy, which is defined as no less than six kinds of tablet or capsule drugs were administered during follow-up; TRW, patient’s total risk weight; PRW, primary risk weight; AUC, area under the curve; ROC, receiver operating characteristic analysis; PsA, psoriatic arthritis; AS, ankylosing spondylitis; SJS, Sjögren syndrome, PPP, pustulosis palmaris et plantaris; SLE, systemic lupus erythematosus; GCA, giant cell arteritis; PMR, polymyalgia rheumatica; SSc, systemic sclerosis; BD, Behçet’s disease; PM/DM, polymyositis/dermatomyositis; AOSD, adult-onset Still disease; FMF, familial Mediterranean fever; PAN, polyarteritis nodosa; CST, chi-square test.
References
- Kim, S.Y.; Schneeweiss, S.; Liu, J.; Daniel, G.W.; Chang, C.-L.; Garneau, K.; Solomon, D.H. Risk of osteoporotic fracture in a large population-based cohort of patients with rheumatoid arthritis. Arthritis Res. Ther. 2010, 12, R154. [Google Scholar] [CrossRef] [PubMed]
- Raterman, H.G.; Lems, W.F. Pharmacological Management of Osteoporosis in Rheumatoid Arthritis Patients: A Review of the Literature and Practical Guide. Drugs Aging 2019, 36, 1061–1072. [Google Scholar] [CrossRef] [PubMed]
- Baker, R.; Narla, R.; Baker, J.F.; Wysham, K.D. Risk factors for osteoporosis and fractures in rheumatoid arthritis. Best. Pract. Res. Clin. Rheumatol. 2022, 36, 101773. [Google Scholar] [CrossRef]
- Gheita, T.; Fawzy, S.; Rizk, A.; Hussein, H. Impaired bone formation and osteoporosis in postmenopausal elderly onset rheumatoid arthritis patients. Egypt. Rheumatol. 2011, 33, 155–162. [Google Scholar] [CrossRef]
- Wafa, H.; Raja, A.; Dhia, K.; Nada, B.; Imene, Z.; Mohamed, K. Risk factors associated with bone loss and occurrence of fragility fractures in rheumatoid arthritis patients. Egypt. Rheumatol. 2019, 41, 1–5. [Google Scholar] [CrossRef]
- Sayed, S.; Darweesh, H.; Fathy, K.; Mourad, A.M. Clinical significance of bone mineral density in Ankylosing Spondylitis patients: Relation to disease activity and physical function. Egypt. Rheumatol. 2015, 37, 35–39. [Google Scholar] [CrossRef]
- Hafez, E.A.; ElBakry, S.A.; Ibrahim, S.I.; Morad, C.S.; Hamza, S.A.; El-Khalik, A. Assessment of fracture risk in a cohort of Egyptian female Systemic Lupus erythematosus patients. Egypt. Rheumatol. 2018, 40, 85–91. [Google Scholar] [CrossRef]
- Sinigaglia, L.; Varenna, M.; Girasole, G.; Bianchi, G. Epidemiology of osteoporosis in rheumatic diseases. Rheum. Dis. Clin. N. Am. 2006, 32, 631–658. [Google Scholar] [CrossRef]
- Maruotti, N.; Corrado, A.; Cantatore, F.P. Osteoporosis and rheumatic diseases. Rheumatismo 2014, 66, 125–135. [Google Scholar] [CrossRef]
- Ozen, G.; Pedro, S.; Wolfe, F.; Michaud, K. Medications associated with fracture risk in patients with rheumatoid arthritis. Ann. Rheum. Dis. 2019, 78, 1041–1047. [Google Scholar] [CrossRef]
- Adami, G.; Saag, K.G. Osteoporosis Pathophysiology, Epidemiology, and Screening in Rheumatoid Arthritis. Curr. Rheumatol. Rep. 2019, 21, 34. [Google Scholar] [CrossRef] [PubMed]
- Adami, G.; Fassio, A.; Rossini, M.; Caimmi, C.; Giollo, A.; Orsolini, G.; Viapiana, O.; Gatti, D. Osteoporosis in Rheumatic Diseases. Int. J. Mol. Sci. 2019, 20, 5867. [Google Scholar] [CrossRef] [PubMed]
- Adami, G.; Fassio, A.; Rossini, M.; Benini, C.; Pistillo, F.; Viapiana, O.; Bertelle, D.; Gatti, D. Bone loss in inflammatory rheumatic musculoskeletal disease patients treated with low-dose glucocorticoids and prevention by anti-osteoporosis medications. Arthritis Rheumatol. 2023, 75, 1762–1769. [Google Scholar] [CrossRef] [PubMed]
- Buttgereit, F.; Palmowski, A.; Bond, M.; Adami, G.; Dejaco, C. Osteoporosis and fracture risk are multifactorial in patients with inflammatory rheumatic diseases. Nat. Rev. Rheumatol. 2024, 20, 417–431. [Google Scholar] [CrossRef]
- Kanis, J.A.; Oden, A.; Johansson, H.; Borgström, F.; Ström, O.; McCloskey, E. FRAX® and its applications to clinical practice. Bone 2009, 44, 734–743. [Google Scholar] [CrossRef]
- Kanis, J.A.; Johansson, H.; Harvey, N.C.; McCloskey, E.V. A brief history of FRAX. Arch. Osteoporos. 2018, 13, 118. [Google Scholar] [CrossRef]
- Prieto-Alhambra, D.; Judge, A.; Arden, N.K.; Cooper, C.; Lyles, K.W.; Javaid, M.K. Fracture prevention in patients with cognitive impairment presenting with a hip fracture: Secondary analysis of data from the HORIZON Recurrent Fracture Trial. Osteoporos. Int. 2014, 25, 77–83. [Google Scholar] [CrossRef]
- Fernandez, M.A.; Griffini, X.L.; Costa, M.L. Management of hip fracture. Br. Med. Bull. 2015, 115, 165–172. [Google Scholar] [CrossRef]
- Diem, S.J.; Vo, T.N.; Langsetmo, L.; Schousboe, J.T.; Yaffe, K.; Ensrud, K.E.; for the Study of Osteoporotic Fractures (SOF) Research Group. Impact of competing risk of mortality on association of cognitive impairment with risk of hip fracture in older women. J. Bone Miner. Res. 2018, 33, 1595–1602. [Google Scholar] [CrossRef]
- Luo, J.; Su, L.; Ndeke, J.M.; Wang, F.; Hendryx, M. Gait speed, handgrip strength, and cognitive impairment among older women–A multistate analysis. Exp. Gerontol. 2022, 169, 111947. [Google Scholar] [CrossRef]
- Wikipedia. Proportional Hazards Model. Available online: https://en.wikipedia.org/wiki/Proportional_hazards_model (accessed on 20 April 2023).
- Boos, D.D.; Stefanski, L.A. P-Value Precision and Reproducibility. Am. Stat. 2011, 65, 213–221. [Google Scholar] [CrossRef]
- Cross Validated. What is the Name of a Plot of -log 10 of p Values in Multiple Testing? Available online: https://stats.stackexchange.com/questions/89644/what-is-the-name-of-a-plot-of-log-10-of-p-values-in-multiple-testing (accessed on 20 April 2023).
- Langseth, H.; Jensen, F.V. Bayesian networks in reliability. In Encyclopedia of Statistics in Quality and Reliability; Ruggeri, F., Kennett, R.S., Faltin, F.W., Eds.; Wiley: Hoboken, NJ, USA, 2007; Available online: https://vbn.aau.dk/en/publications/bayesian-networks-in-reliability-2 (accessed on 20 April 2023).
- Albert, J. Chapter #6 Markov chain Monte Carlo methods. In Bayesian Computation with R, 2nd ed.; Ishida, M.; Ishida, K., Translators; Springer: Tokyo, Japan, 2009. [Google Scholar]
Figure 1.
A schematic flowchart used in this study. Abbreviations: logP, logarithm of p-value based on 0.05.
Figure 1.
A schematic flowchart used in this study. Abbreviations: logP, logarithm of p-value based on 0.05.
Figure 2.
The receiver operating characteristics (ROC) analysis results in the approaches for the incident osteoporotic fracture development.
Figure 2.
The receiver operating characteristics (ROC) analysis results in the approaches for the incident osteoporotic fracture development.
Table 1.
Demographic characteristics of the background rheumatic diseases in the subjects.
| Disease Name | Female Gender (%) | Mean Age, Years Old | GCs Administered (%) | Prevalent OF at Baseline (%) | Incident OF During Follow-Up (%) | Follow-Up Length (Months) |
|---|---|---|---|---|---|---|
| RA (N=749) | 76.2 | 80.3 (11.4) | 11.9 | 36.7 | 13.4 | 85.3 (73.8) |
| PsA (N = 179) | 62.6 | 62.6 (12.7) | 8.9 | 33.7 | 15.1 | 97.2 (80.5) |
| AS (N = 60) | 46.7 | 69.9 (15.7) | 6.7 | 25.4 | 11.7 | 95.5 (74.6) |
| SJS (N = 60) | 91.7 | 69.9 (13.9) | 18.3 | 35.7 | 11.7 | 126.0 (80.0) |
| PAO (N = 58) | 56.9 | 75.4 (14.4) | 6.9 | 46.4 | 29.3 | 66.9 (67.9) |
| SLE (N = 28) | 85.7 | 64.3 (12.4) | 89.2 | 32.1 | 17.9 | 149.0 (75.1) |
| GCA (N = 26) | 69.2 | 77.5 (13.0) | 23.1 | 46.2 | 19.2 | 82.5 (74.1) |
| PMR (N = 26) | 73.1 | 81.2 (10.7) | 74.6 | 42.3 | 19.2 | 98.9 (80.7) |
| SSc (N = 15) | 80.0 | 73.9 (8.8) | 33.3 | 26.7 | 20.0 | 140.3 (82.5) |
| Behçet (N = 12) | 16.7 | 72.8 (14.8) | 16.7 | 25.0 | 0.0 | 74.3 (79.6) |
| PM/DM (N = 8) | 25.0 | 76.4 (8.6) | 37.5 | 50.0 | 12.5 | 14.0 (94.2) |
| ASD (N = 5) | 80.0 | 71.6 (8.5) | 20.0 | 40.0 | 20.0 | 64.2 (36.0) |
| FMF (N = 1) | 100.0 | 77.0 (0) | 100.0 | 0.0 | 0.0 | 12.0 (0) |
| PN (N = 1) | 100.0 | 91.0 (0) | 100.0 | 100.0 | 100.0 | 23.0 (0) |
| Total (N = 1228) | 71.9 | 77.7 (12.3) | 16.4 | 36.1 | 14.6 | 90.7 (76.9) |
In mean age and follow-up length, SDs were shown in parentheses. Abbreviations: GCs, glucocorticoid; OF, osteoporotic fracture; RA, rheumatoid arthritis; PsA, psoriatic arthritis; AS, ankylosing spondylitis; SJS, Sjogren syndrome; PAO, pustulotic arthro-osteitis; SLE, systemic lupus erythematosus; GCA, giant cell arthritis; PMR, polymyalgia rheumatica; SSc, systemic skin sclerosis; Behçet, Behçet disease; PM/DM, polymyositis/dermatomyositis; ASD, adult-onset Still disease; FMF, familial Mediterranean fever; PN, polyarteritis nodosa.
Table 2.
Demographic characteristics of the G-OF and G-nonOF.
| Factor | G-OF (n = 179) | G-nonOF (N = 1049) | p-Value |
|---|---|---|---|
| female gender (%) | 83.2 | 69.9 | <0.001 |
| age, years old | 78.5 (10.5) | 73.8 (14.0) | <0.001 |
| pr-VF at baseline (%) | 20.7 | 9.1 | <0.001 |
| pr-nonVF at baseline (%) | 26.8 | 9.9 | <0.001 |
| number of comorbidities | 12.2 (7.7) | 9.5 (6.1) | <0.001 |
| eGFR_CysC (mL/min/1.73 m2) | 56.7 (20.3) | 65.6 (25.6) | <0.001 |
| T-score in the LS | −2.3 (1.5) | −2.1 (1.8) | 0.35 |
| T-score in the FN | −2.2 (1.1) | −2.1 (1.2) | 0.23 |
| LSD (%) | 80.4 | 69.7 | <0.01 |
| DM (%) | 38.5 | 28.1 | <0.01 |
| HT (%) | 54.7 | 43.6 | <0.01 |
| HL (%) | 40.2 | 30.0 | <0.01 |
| CHF (%) | 40.2 | 24.4 | <0.001 |
| COPD (%) | 11.1 | 9.3 | 0.44 |
| insomnia (%) | 28.5 | 17.5 | <0.001 |
| Fallibility (%) | 78.2 | 54.8 | <0.001 |
| OA (%) | 62.0 | 43.6 | <0.001 |
| MADS (%) | 34.1 | 13.3 | <0.001 |
| Contracture (%) | 9.5 | 3.9 | <0.01 |
| Disuse (%) | 19.0 | 6.4 | <0.001 |
| NMD (%) | 6.7 | 2.7 | <0.01 |
| Cognitive impairment (%) | 22.3 | 11.1 | <0.001 |
| OPD administered (%) | 69.3 | 36.3 | <0.001 |
| GCs administered (%) | 15.4 | 15.3 | 0.93 |
| Rehabilitation (%) | 43.0 | 41.1 | <0.001 |
| follow-up length (months) | 52.8 (58.9) | 97.2 (77.8) | <0.001 |
| polypharmacy ratio (%) | 24.9 | 16.1 | <0.001 |
The values are presented as mean (SD) unless indicated otherwise. Abbreviations: G-OF, a patient group who have presented with incidental osteoporotic fractures during follow-up; G-nonOF, a patient group who have not presented with incidental osteoporotic fractures during follow-up; pr-VF, presence of prevalent vertebral body fracture; pr-nonVF, presence of non-vertebral body fracture; eGFR_CysC, estimated glomerular filtration ratio measured with cystatin C; LS, lumbar spine; FN, femoral neck; LSD, lifestyle-related diseases; DM, diabetes mellitus; HT, hypertension; HL, hyperlipidemia; CHF, chronic heart failure; COPD, chronic obstructive pulmonary diseases; Fallibility, a patient who has a hyper fallibility due to eligible reasons; OA, osteoarthritis; MADS, musculoskeletal ambulation disability complex; NMD, neuro-muscular diseases; OPD, anti-osteoporotic drugs; GCs, glucocorticoids.
Table 3.
Results of Cox regression analysis with univariate model and TRW using a multivariate model and cut-off index using an ROC.
Table 3.
Results of Cox regression analysis with univariate model and TRW using a multivariate model and cut-off index using an ROC.
| Univariate Model | Multivariate Model | ROC | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Variables | β-Value | 95%CI | p-Value | Risk Ratio | p-Value | Logarithm of p-Value (logP) | β-Value × logP | COI | AUC (LCL–UCL) |
| female gender (%) | 0.75 | 0.36–1.14 | <0.001 | 2.11 | 0.78 | 0.08 | 0.21 | female | 0.566 (0.536–0.597) |
| age, years old | 0.03 | 0.02–0.05 | <0.001 | 1.03 | 0.22 | 0.50 | 0.00 | >74 | 0.594 (0.553–634) |
| pr-VF at baseline (%) | 0.94 | 0.57–1.30 | <0.001 | 2.55 | 8.40 × 10−3 | 1.60 | 5.63 | positive | 0.558 (0.527–0.589) |
| pr-nonVF at baseline (%) | 0.87 | 0.64–1.31 | <0.001 | 2.65 | 3.00 × 10−5 | 3.50 | 11.02 | positive | 0.585 (0.551–0.618) |
| number of comorbidities | 0.03 | 0.02–0.05 | <0.001 | 1.04 | 0.46 | 0.26 | 0.00 | >11 | 0.603 (0.555–0.651) |
| eGFR_CysC (mL/min/1.73 m2) | −0.02 | −0.02–−0.01 | <0.001 | 0.98 | 0.40 | 0.31 | 0.00 | >48.0 | 0.605 (0.564–0.646) |
| T-score in the LS | −0.12 | −0.22–−0.02 | <0.05 | 0.89 | 0.33 | 0.37 | −0.09 | <−2.6 | 0.525 (0.473–0.578) |
| T-score in the FN | −0.14 | −0.29–0.01 | 0.07 | 0.87 | |||||
| LSD (%) | 0.30 | −0.07–0.67 | 0.11 | 1.35 | |||||
| DM (%) | 0.29 | −0.01–0.59 | 0.06 | 1.33 | |||||
| HT (%) | 0.27 | −0.03–0.56 | 0.07 | 1.31 | |||||
| HL (%) | 0.13 | −0.17–0.43 | 0.391 | 1.14 | |||||
| CHF (%) | 0.67 | 0.37–0.97 | <0.001 | 1.96 | 0.08 | 0.84 | 1.06 | present | 0.579 (0.541–0.617) |
| COPD (%) | 0.00 | −0.46–0.47 | 0.99 | 1.00 | |||||
| insomnia (%) | 0.36 | 0.04–0.69 | <0.05 | 1.43 | 0.28 | 0.43 | 0.03 | present | 0.555 (0.520–0.590) |
| Fallibility (%) | 0.78 | 0.42–1.13 | <0.001 | 2.17 | |||||
| OA (%) | 0.44 | 0.14–0.74 | <0.01 | 1.55 | 0.77 | 0.09 | 0.08 | present | 0.592 (0.554–0.631) |
| MADS (%) | 0.91 | 0.60–1.22 | <0.001 | 2.47 | 0.50 | 0.23 | 0.20 | present | 0.604 (0.568–0.640) |
| Contracture (%) | 0.45 | −0.05–0.96 | 0.08 | 1.57 | |||||
| Disuse (%) | 0.84 | 0.47–1.21 | <0.001 | 2.32 | 0.80 | 0.08 | 0.55 | present | 0.563 (0.533–0.593) |
| NMD (%) | 0.82 | 0.24–0.30 | <0.01 | 2.27 | 0.40 | 0.30 | 0.28 | present | 0.520 (0.501–0.539) |
| Cognitive impairment (%) | 0.97 | 0.61–1.32 | <0.001 | 2.63 | 9.03 × 10−3 | 1.57 | 3.97 | present | 0.561 (0.529–0.593) |
| OPD administered (%) | 1.13 | 0.82–1.45 | <0.001 | 3.11 | 0.05 | 1.03 | 5.08 | positive | 0.665 (0.628–0.702) |
| GCs administered (%) | −0.08 | −0.51–0.35 | 0.71 | 0.92 | |||||
| total dose of GCs (mg) † | −0.00 | −0.00–0.00 | 0.50 | 1.00 | |||||
| Rehabilitation (%) | 0.77 | 0.47–1.06 | <0.001 | 2.15 | 0.02 | 1.27 | 1.93 | never | 0.607 (0.569–0.646) |
| polypharmacy ratio (%) | 0.49 | 0.07–0.91 | <0.05 | 1.63 | 0.36 | 0.34 | 0.29 | >19.4% | 0.576 (0.535–0.616) |
†: prednisolone equivalent. Abbreviations: pr-VF, presence of prevalent vertebral body fracture; pr-nonVF, presence of non-vertebral body fracture; eGFR_CysC, estimated glomerular filtration ratio measured with cystatin C; LS, lumbar spine; FN, femoral neck; LSD, lifestyle-related diseases; DM, diabetes mellitus; HT, hypertension; HL, hyperlipidemia; CHF, chronic heart failure; COPD, chronic obstructive pulmonary diseases; Fallibility, a patient who has a hyper fallibility due to eligible reasons; OA, osteoarthritis; MADS, musculoskeletal ambulation disability complex; NMD, neuro-muscular diseases; OPD, anti-osteoporotic drugs; GCs, glucocorticoids.
Table 4.
Results of Cox regression, ROC, and Kaplan–Meier analysis for each approach.
| Approaches | Cox Regression of TRW | ROC | Kaplan–Meier Survival Analysis | ||||||
|---|---|---|---|---|---|---|---|---|---|
| TRW | Risk Ratio | 95%CI | COI | p-Value | AUC | Hazard Ratio | Sensitivity | Specificity | |
| Control | 1.00 ± 1.05 | 1.94 | 1.72–2.18 | >1 | <0.001 | 0.723 | 3.89 | 29.4% | 91.6% |
| Standard | 1.77 ± 1.90 | 1.43 | 1.34–1.52 | >1.92 | <0.001 | 0.727 | 3.90 | 27.4% | 92.4% |
| Summed | 3.77 ± 11.32 | 1.31 | 1.25–1.38 | >6.78 | <0.001 | 0.761 | 5.16 | 30.0% | 93.8% |
| Modified Summed | 7.79 ± 5.97 | 1.17 | 1.14–1.20 | >6.98 | <0.001 | 0.774 | 6.48 | 31.2% | 94.9% |
| Multiplied | 2848.2 ± 27,578.13 | 1.00 | 1.00–1.00 | >1.76 | <0.001 | 0.769 | 4.53 | 33.5% | 92.5% |
Approach methods: Control, a method that counts variables that showed significance in a multivariate model; Standard, a method that sums risk ratios of variables that showed significance in a multivariate model; Summed, a method that sums β-values of variables that showed significance in a univariate model; Modified Summed, a method that sums β-values of variables that showed significance in a univariate model multiplied by the logarithm of the p-value based on 0.05; Multiplied, a method that multiplies risk ratios of variables that showed significance in a univariate model. Abbreviations: ROC, receiver operating characteristics analysis; TRW, total risk weight; 95%CI, 95% confidence interval; COI, cut-off index; AUC, area under the curve.
Table 5.
Comparison of AUCs between approaches.
| Pair | Difference (LCL–UCL: 95% CI) | p-Value |
|---|---|---|
| Control vs. Standard | −0.00363 (−0.01181–0.00454) | 0.39 |
| Control vs. Summed | −0.03787 (−0.05143–−0.02432) | 4.3 × 10−8 |
| Control vs. Modified Summed | −0.05033 (−0.06431–−0.03635) | 1.7 × 10−12 |
| Control vs. Multiplied | −0.04572 (−0.05933–−0.03211) | 4.6 × 10−11 |
| Standard vs. Summed | −0.03424 (−0.04551–−0.02297) | 2.6 × 10−9 |
| Standard vs. Modified Summed | −0.04669 (−0.05883–−0.03456) | <1.0 × 10−12 |
| Standard vs. Multiplied | −0.04209 (−0.05352–−0.03066) | <1.0 × 10−12 |
| Summed vs. Modified Summed | −0.01245 (−0.01587–−0.00904) | <1.0 × 10−12 |
| Summed vs. Multiplied | −0.00785 (−0.01120–−0.00449) | 4.6 × 10−6 |
| Modified Summed vs. Multiplied | 0.00461 (−0.00044–0.00966) | 0.07 |
LCL: lower control limit; UCL: upper control limit; 95%CI: 95% confidence interval.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MDPI and ACS Style
Yoshii, I.; Sawada, N.; Chijiwa, T. Risk-Weight Calculation of Candidate Risk Factors for Incidental Osteoporotic Fracture in Patients with Rheumatic Diseases: A Potentially Accurate Approach. Osteology 2025, 5, 5. https://doi.org/10.3390/osteology5010005
AMA Style
Yoshii I, Sawada N, Chijiwa T. Risk-Weight Calculation of Candidate Risk Factors for Incidental Osteoporotic Fracture in Patients with Rheumatic Diseases: A Potentially Accurate Approach. Osteology. 2025; 5(1):5. https://doi.org/10.3390/osteology5010005
Chicago/Turabian StyleYoshii, Ichiro, Naoya Sawada, and Tatsumi Chijiwa. 2025. "Risk-Weight Calculation of Candidate Risk Factors for Incidental Osteoporotic Fracture in Patients with Rheumatic Diseases: A Potentially Accurate Approach" Osteology 5, no. 1: 5. https://doi.org/10.3390/osteology5010005
APA StyleYoshii, I., Sawada, N., & Chijiwa, T. (2025). Risk-Weight Calculation of Candidate Risk Factors for Incidental Osteoporotic Fracture in Patients with Rheumatic Diseases: A Potentially Accurate Approach. Osteology, 5(1), 5. https://doi.org/10.3390/osteology5010005
