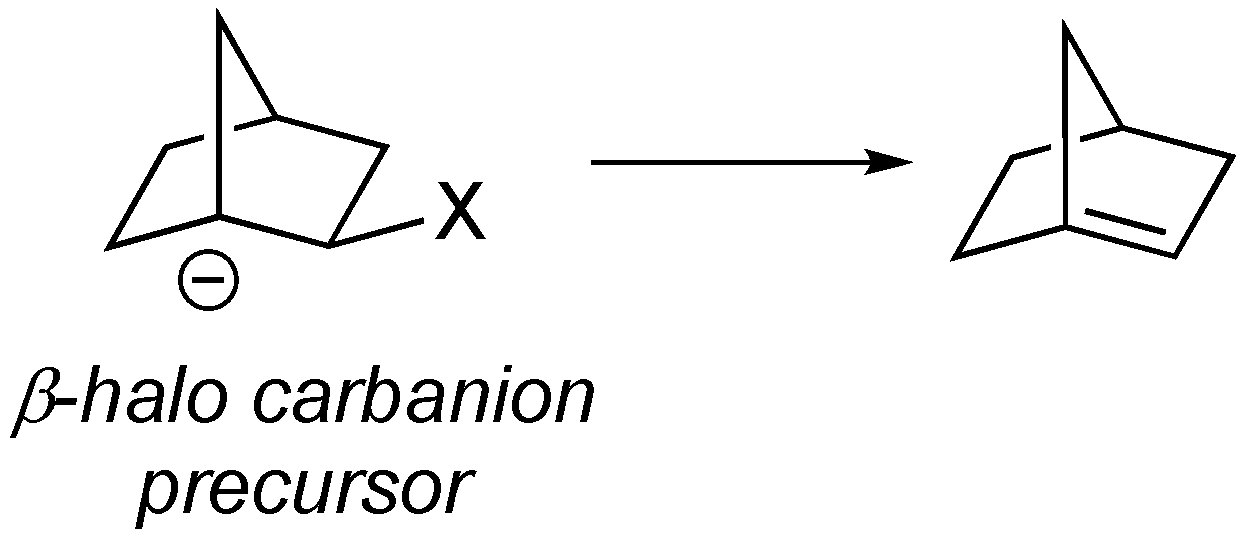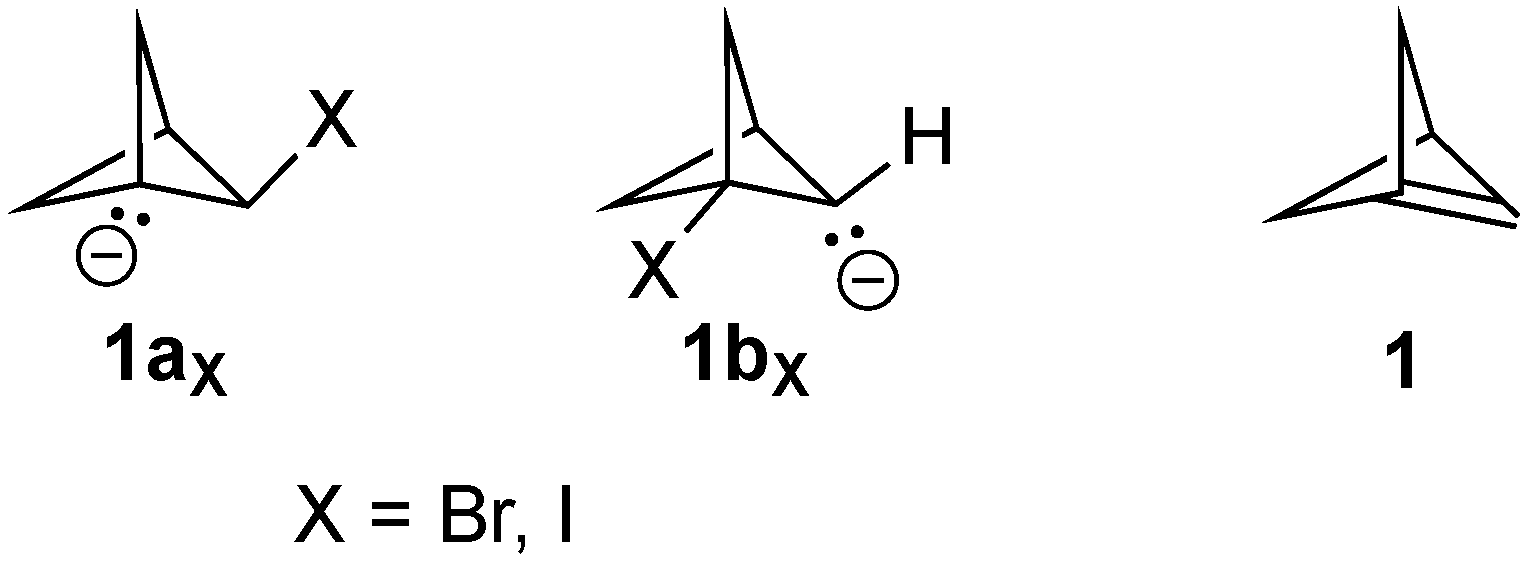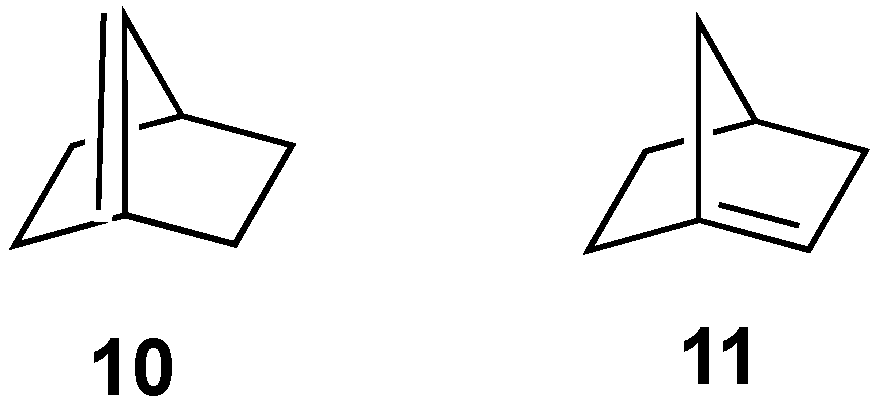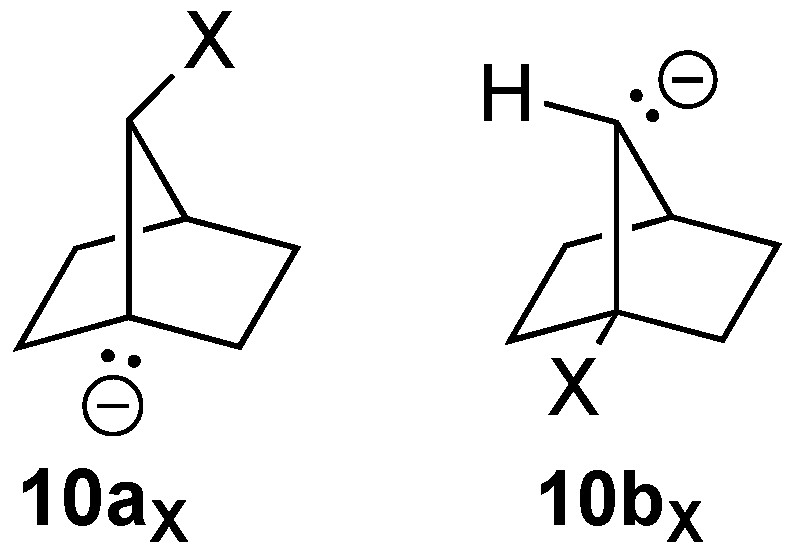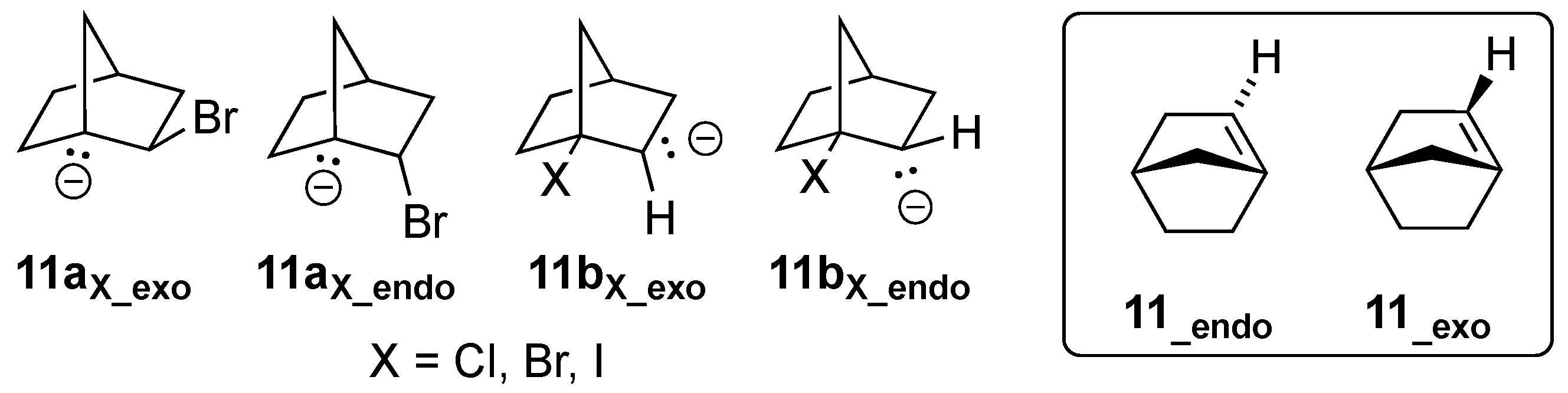Spontaneous Formation of Strained Anti-Bredt Bridgehead Alkenes upon Computational GeometryOptimization of Bicyclic β-Halo Carbanions

Abstract

Bridgehead alkenes are polycyclic molecules bearing at least one C=C bond that includes a bridgehead carbon atom. For small bicyclic systems, these bonds are highly strained due to geometric constraints placed on the sp² hybridized carbon atoms. These small, strained molecules have been termed “anti-Bredt” alkenes. β-halo carbanions have served as convenient precursors to bridgehead alkenes in experimental studies. We observed that upon attempted computational geometric optimizations (ωB97X-D/aug-cc-pVDZ) of the precursors, spontaneous elimination of the halide occurs along with formation of the anti-Bredt alkene in many cases. Such computational eliminations were shown to faithfully mimic experimentally obtained results. Computational elimination was not observed for [1.1.1] or [2.1.1] frameworks, in agreement with predictions that these bridgehead alkenes are too strained to be formed. However, computational elimination from the [2.2.1] framework was observed to form 1-norbornene, a compound suggested in experimental work to be a reactive intermediate. Similarly, [3.1.1] frameworks and higher led to eliminations upon computational geometric optimization, in agreement with experimental findings. Natural bond order (NBO) calculations of the starting geometries proved to be excellent predictors as to whether elimination would take place. Those precursor compounds exhibiting delocalization energies in the order of 10 kcal/mol between the lone-pair electrons of the carbon atom and σ*_C-Br were generally found to undergo elimination. Thus, computational optimization of β-halo substituted bicyclic precursor anions can be used to predict whether strained anti-Bredt alkenes are likely to be formed, thereby saving valuable time and costs in the experimental lab.

1. Introduction

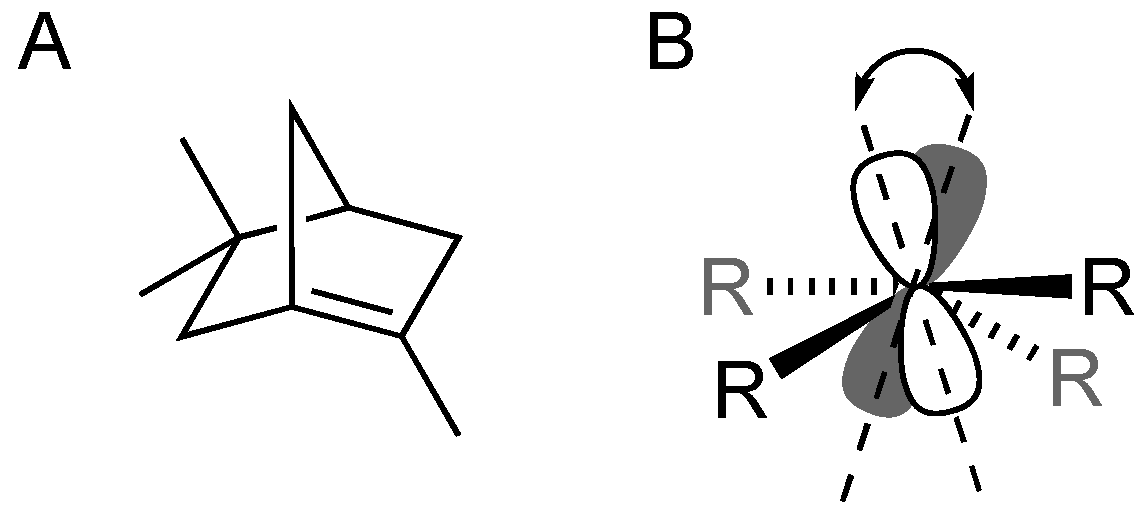
Stemming from his 1902 seminal work on bicyclic camphane and pinene substrates, Julius Bredt proposed his self-named “Bredt’s Rules” stating that C=C double bonds within bicyclic molecules cannot include one of the bridgehead carbon atoms (Figure 1A) [1,2]. Today we recognize that the problem with the substrates investigated by Bredt, and small bridgehead alkenes in general, is that to form a C=C bond involving a bridgehead carbon within a small bicyclic system requires considerable “twisting” from the preferred coplanarity of the two p-orbitals involved in formation of the pi-bond (Figure 1B) [3,4]. Therefore, the energies and reactivities of these bridgehead alkene compounds are generally significantly raised relative to their unstrained counterparts in which the two p-orbitals are properly aligned. Of course, enlarging the size of the substrates beyond the 1- and 2-carbon bridged molecules investigated by Bredt eventually allows sufficient relaxation of the geometries to lessen the twist of the two p-orbitals to enable the observation and/or isolation of many bridgehead alkenes [3,4].

Several methods for predicting which bicyclic alkenes will be stable (or at least observable) have been proposed based on (i) the number of bridging carbon atoms [5] and (ii) the extent of rotation of one p-orbital of the C=C bond relative to the other [6]. However, Schleyer developed what would probably be considered the most general method, based on the difference in strain energies (called the “olefin strain” or OS energy) between the bridged alkene of interest and the corresponding saturated derivative, as calculated via molecular mechanics [7,8]. Using this method, Schleyer proposed that bridged alkenes could be divided into one of three groups: isolable (OS < 17 kcal/mol), observable (21 > OS > 17 kcal/mol), or unstable (OS > 21 kcal/mol) [7]. Not surprisingly, physical organic chemists have taken pleasure in testing the limits of these predictions via the synthesis of bridgehead alkenes with increasingly shorter bridges [3]. The resulting highly strained alkenes have been termed “anti-Bredt” alkenes since they violate Bredt’s originally proposed limits of stability.

While bridgehead alkenes are of theoretical interest because they challenge commonly held perceptions of the limits of pi-bonding, bridgehead alkenes are also of practical importance since many examples of naturally occurring molecules with bridgehead double bonds have been discovered and described [9,10,11,12,13], and applications of strained bridgehead alkenes in organic synthesis have been developed [14,15,16]. Given the recent interest in applications of bridgehead alkenes in synthesis [14,15,16], it is reasonable to assume that increasing the number of potential bridgehead alkenes from which to choose would be welcomed by synthetic chemists. However, great time and cost would be expended in the attempted syntheses of such highly strained compounds. It would be convenient if there were a way to predict whether the target compounds had a high likelihood of being formed in the first place. Predictions such as those made by Schleyer are certainly important for judging the potential for the existence of anti-Bredt alkenes, but they do little to help predict the feasibility of their synthesis.

Several methods have been developed for synthesizing anti-Bredt alkenes, including cyclization reactions, carbene rearrangements, and ring contractions, among others [3,4]. However, one of the more commonly used methods to date has been via elimination of a β-substituted halogen from an adjacent carbanionic center (see Scheme 1) [3,4,5,17,18].

We were interested in computationally modelling this elimination process using standard computational procedures. However, we were surprised to find that in many cases, elimination took place spontaneously upon attempted geometry optimization of the carbanion precursor to form the bridgehead alkene directly, i.e., the carbanion precursor itself was not a stationary point. Such elimination suggests a barrierless, or low-barrier, elimination process to form the anti-Bredt bridgehead alkene from the precursor anions. Therefore, if elimination occurs during computational optimization, there is a possibility that such an alkene could be readily synthesized via this process. If elimination does not occur, then a larger energetic barrier to elimination may exist. These bridgehead alkenes may therefore be less easily formed (although it would not necessarily be impossible). Such preliminary computational studies might, therefore, easily predict which bridgehead alkenes are most promising to expend time and money pursuing in the lab. In this study, we experimentally tested this theory by computationally optimizing a number of precursor compounds to observe whether the results mimicked what is currently known.

2. Materials and Methods

Most calculations were performed at the ωB97X-D/aug-cc-pVDZ level of theory in the solvent THF via the polarizable continuum model (PCM) using the software package GAMESS (version = 30 JUN 2019, R1) [19,20] implemented through the ChemCompute.org website [21].

Default geometry optimization parameters were typically employed. A reviewer suggested that the default maximum size for an optimization step of 0.3 Bohr might have been too large, and that a possible transition state might have been missed. However, results identical to those using the default maximum step size were obtained when using a maximum step size of 0.1 Bohr when tested upon precursors 1a_Br, 1b_Br, 2a_Br_endo, 2a_Br_exo, 2b_Br_endo, 2b_Br_exo, 10a_Br, 10b_Br, 11a_Br_exo, 11a_Br_endo, 11b_Br_exo, 11b_Br_endo, 12a_{exo_exo}, 12a_{endo_exo}, 13a_ax, and 13a_eq. Therefore, the default optimization step size was used throughout for consistency.

Geometry pre-optimizations of the carbanion precursors were typically performed using the MMFF94 force field. A reviewer suggested that better pre-optimized geometries might be those of the DFT-optimized carbanions, for which the length of the C-Br bond was constrained so as to prevent elimination (we used the default bond length of 1.91 Å). However, results identical to those using the MM-optimized geometries were obtained upon complete optimization when tested upon precursors 1a_Br, 1b_Br, 2a_Br_endo, 2a_Br_exo, 2b_Br_endo, 2b_Br_exo, 10a_Br, 10b_Br, 11a_Br_exo, 11a_Br_endo, 11b_Br_exo, 11b_Br_endo, 12a_{exo_exo}, 12a_{endo_exo}, and 13a_ax. Elimination was observed to take place from 13a_eq using the DFT-optimized geometry, whereas it did not for the MMFF94-optimized geometry. However, it was not surprising that for the larger-sized, more flexible, precursors in which the C=C bond was formed in the larger ring, a subtle change in geometry could have an impact on the optimization. Generally, though, the much simpler MMFF94 geometries proved robust and predictive.

For calculations involving iodine, the program Spartan’20 [22] was employed, expanding the native basis set through addition of basis set parameters for iodine (aug-cc-pVDZ-PP including effective core potential) as obtained from the Basis Set Exchange website [23]. Details of this modified basis set are included in the Supplementary Materials. Frequency calculations were carried out at all stationary points to ensure the lack of imaginary frequencies. Natural bond order (NBO) calculations were performed with the NBO7 program at the same level of theory [24]. NBO orbital figures were created using Patek’s Jmol NBO light program [25].

3. Results and Discussion

3.1. General Computational Considerations

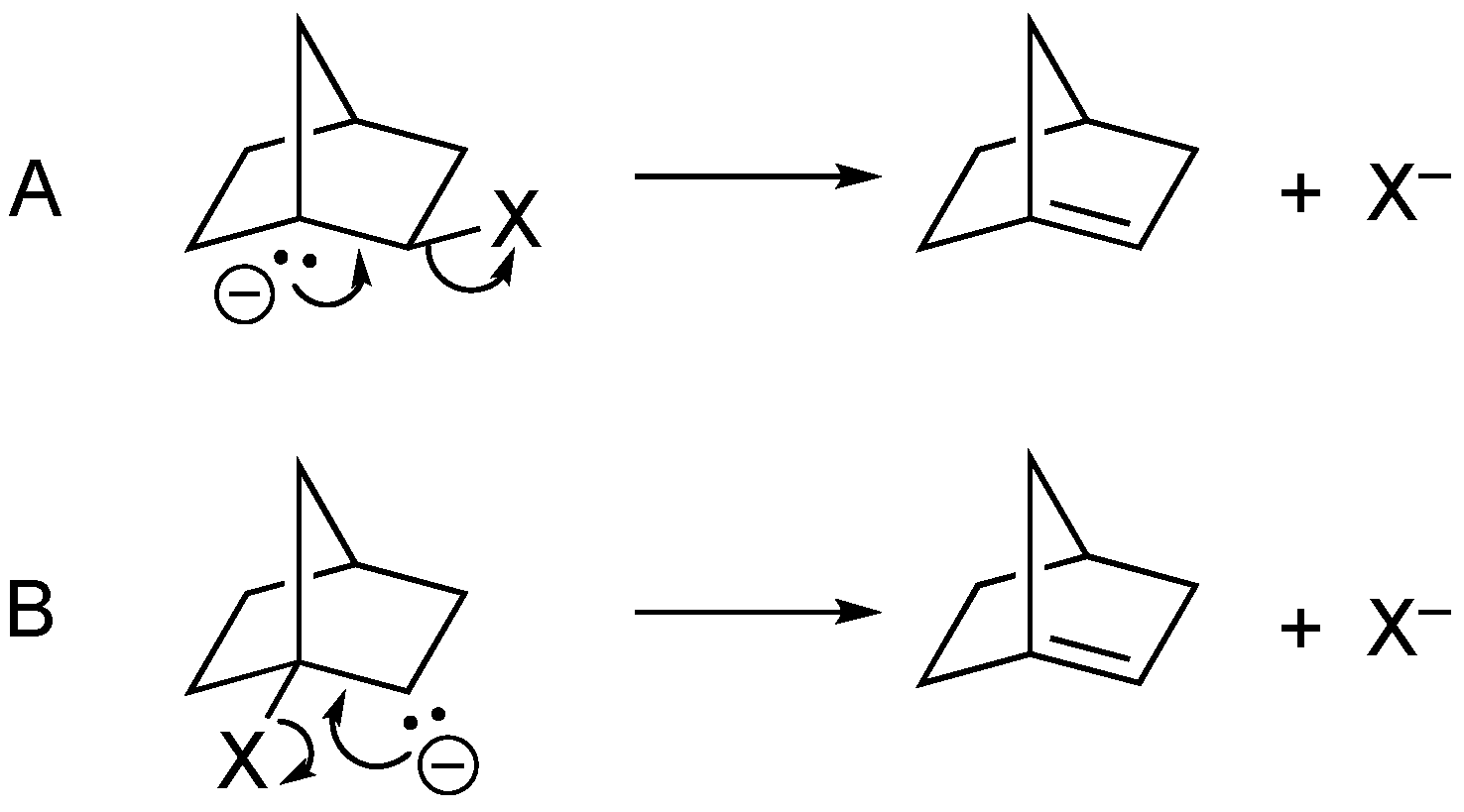
Initial models were created with the carbanionic center at both the bridgehead position (e.g, Scheme 2A) and with the carbon positioned β to the bridgehead halide (e.g., Scheme 2B). Geometry pre-optimizations of the carbanion precursors were typically performed using the MMFF94 force field (see Section 2).

Complete optimizations were conducted at the (U)ωB97X-D/aug-cc-pVDZ level of theory as it had proved robust for similar substrates in our previous works [26,27]. We selected THF as the solvent for optimization (employing the polarizable continuum model (PCM)) because it is a commonly used solvent for experimental work with carbanions [20].

3.2. [1.1.1]Bicyclopent-1-ene (1)

Experimentally, alkene 1 is an as-yet unknown compound, consistent with Novak’s DFT computational results that the predicted 1 is too strained to be formed [8]. Appropriate β-bromo carbanion precursors were modelled with the potential Br atom as the leaving group attached at both the bridging and the bridgehead positions (see Figure 2, X = Br) of the [1.1.1]bicyclopentane framework. Full geometric optimizations of both of these anions failed to result in elimination of a bromide atom to form the bridgehead alkene product 1. The same result was obtained using iodide as the potential leaving group (Figure 2, X = I). Therefore, both 1a_x and 1b_x were stationary points on the potential energy surface (PES), which was confirmed through conducting frequency calculations on each.

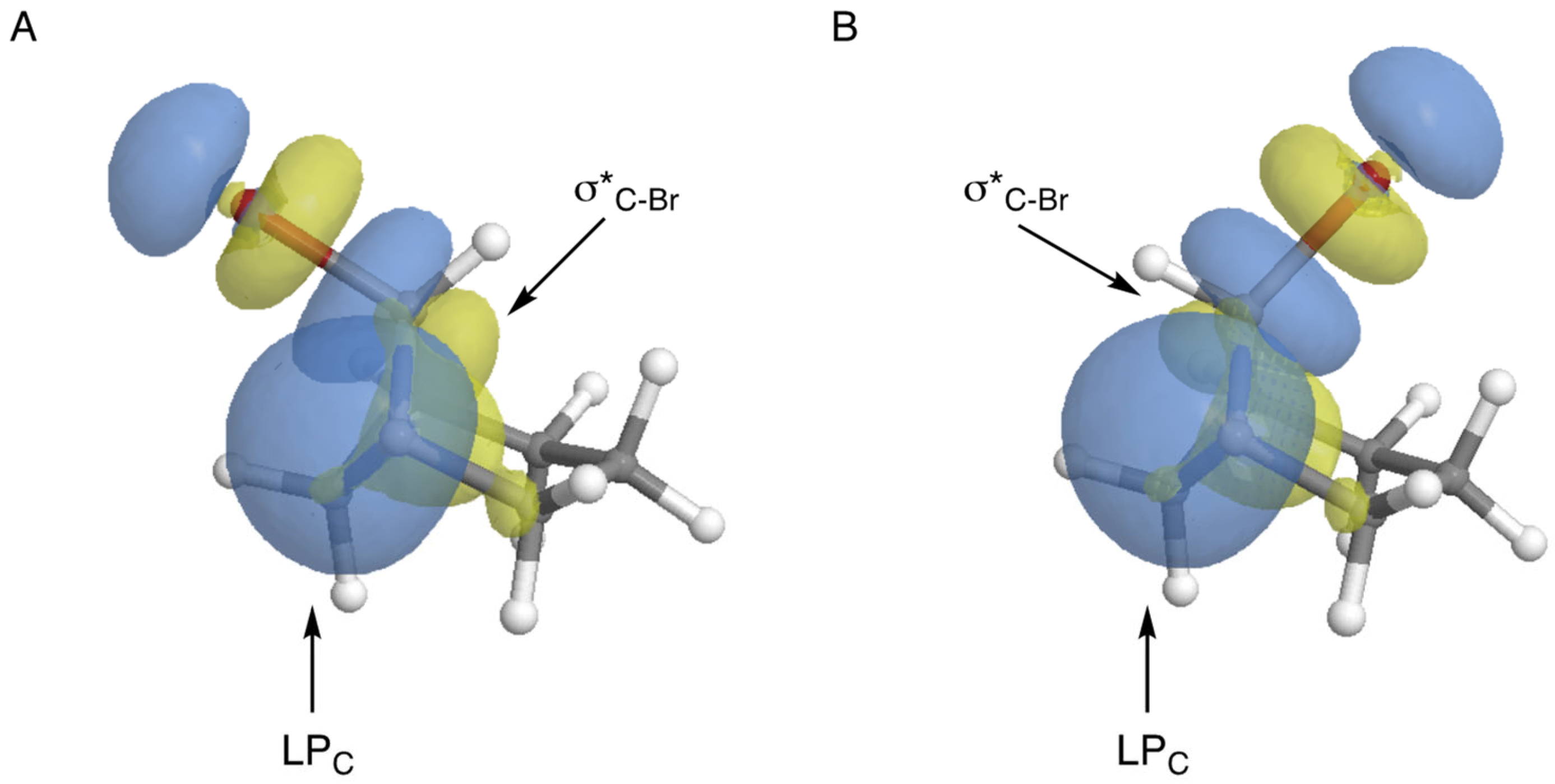
Failure to eliminate the bromide or iodide leaving group from 1a_x and 1b_x can be traced to the high strain energy that is inherent in anti-Bredt alkene 1, but natural bond order (NBO) calculations revealed that elimination was also greatly disfavored by the poor overlap of the carbon lone-pair electrons with the antibonding orbital of the C–X bond, as can be seen in Figure 3 for 1a_Br and 1b_Br [24]. Previous work from our labs demonstrated that such prior delocalization is a critical contributor towards promotion of the elimination process [27]. In fact, NBO calculations for 1a_Br and 1b_Br revealed absolutely no delocalization energy (derived from second-order perturbation energies) between the lone-pair orbital of the anionic carbon and the antibonding σ* orbital of the C-Br bond for either anion, since the geometry constrained the two orbitals to be essentially orthogonal to one another.

3.3. [2.1.1] Bicyclohexane Substrates

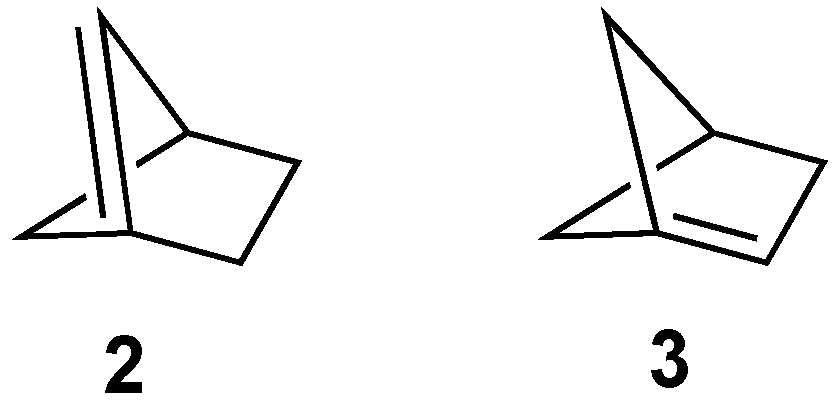
There are two anti-Bredt isomers that could potentially be formed from the [2.1.1]bicyclohexane framework: alkene 2, in which the double bond includes one of the carbons from a one-carbon bridge (i.e., [2.1.1]bicyclohex-1(5)-ene, Figure 4), and alkene 3, in which the double bond includes one of the carbons from the two-carbon bridge (i.e., [2.1.1]bicyclohex-1-ene, Figure 4). We discuss separately the potential formation of these two isomers from possible precursors.

3.3.1. [2.1.1]Bicyclohex-1(5)-ene (2)

The OS energy of alkene 2 as calculated via molecular mechanics (33.2 kcal/mol) places it comfortably in the category of “unstable” [7]. Independent computational studies by Novak and Wu suggested that not only would 2 be highly strained, but it would also likely exhibit strong diradical-like characteristics [8,28]. Given the expected strain in this molecule, it is not surprising that its formation has not been reported.

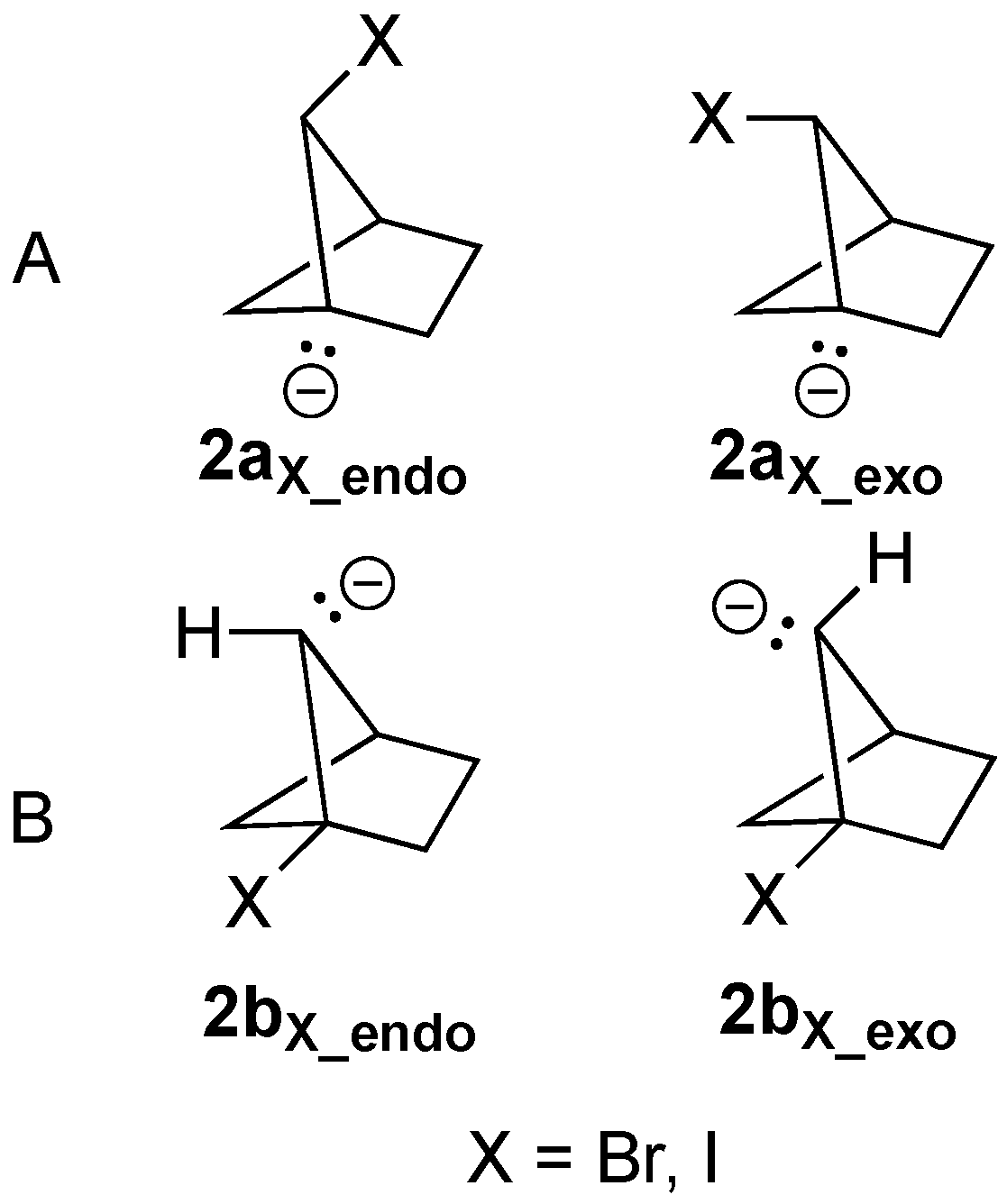
There are four possible anionic precursors for the formation of alkene 2 that differ in whether the anionic carbon or the C–X bond (X = Br or I) is located at the bridgehead position (2a versus 2b in Figure 5A and Figure 5B, respectively) and the orientation of the C–X bond or lone pair in relation to the one- or two-carbon bridge (2a_{X_endo/exo} and 2b_{X_endo/exo} Figure 5). We have taken the liberty to assign an “exo/endo” designation for the anion lone pairs in a manner consistent with orientation of the C–X bond, either towards the shorter bridge (exo) or the longer bridge (endo).

Optimization of all four isomeric potential precursors led to stationary points that failed to eliminate the Br^– or I^– leaving groups. As discussed above for 1a_Br and 1b_Br, the orientation of the lone-pair electrons relative to the σ* orbitals of the putative leaving group bonds remained essentially orthogonal and only minor delocalization energies were calculated with the NBO method (2a_{Br_endo}: 0.0 kcal/mol; 2a_{Br_exo}: 3.6 kcal/mol; 2b_{Br_endo}: 0.0 kcal/mol; 2b_{Br_exo}: 4.5 kcal/mol). Because a strong diradical character was predicted for 2 via the calculations [8,28], we repeated the optimizations of 2a_{Br_exo/endo} and 2b_{Br_exo/endo} in the absence of spin restriction (i.e., UωB97X-D). However, elimination was still not observed to occur. Given the expected high energy of 2 as discussed above, its resistance to formation from precursors 2a and 2b is not surprising and is consistent with previous predictions that 2 is not readily formed.

3.3.2. [2.1.1]Bicyclohex-1-ene (3)

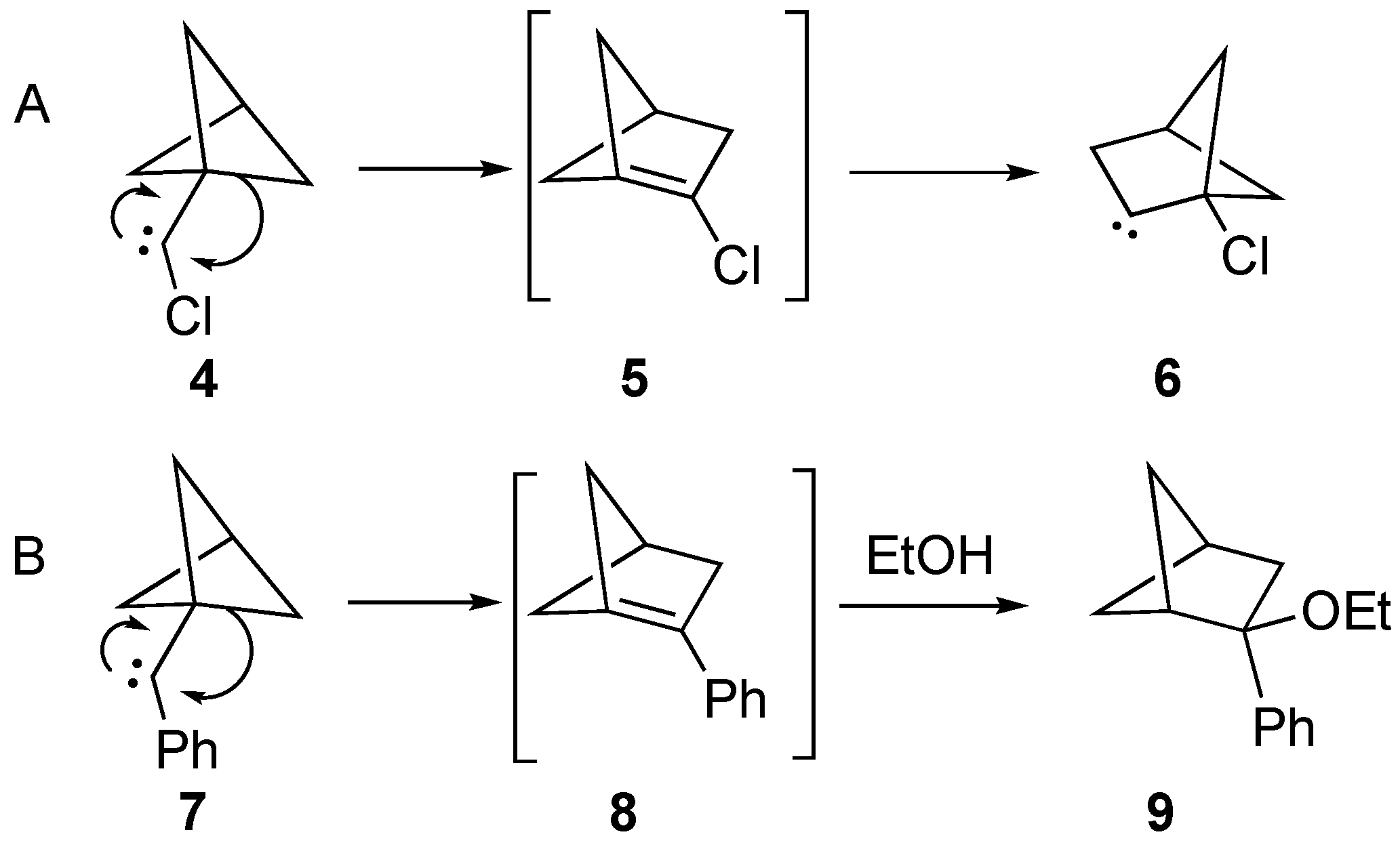
Alkene 3 was calculated by Schleyer to have significant strain (25.0 kcal/mol), placing it into the “unstable” category, but not as strained as the isomeric 2 (33.2 kcal/mol) [7]. Interestingly, Novak’s DFT calculations suggested 3 to have a strain energy even greater than that of 2 (by 3.7 kcal/mol) [8]. While parent alkene 3 still remains unknown, Szeimies reported his experimental results on the rearrangement of chloro-substituted carbene 4 to (presumably) bridgehead alkene 5, that subsequently rearranged to carbene 6 (Scheme 3A) [29,30]. Additionally, Wiberg proposed that the 2-phenyl derivative 8 may have been formed as an intermediate from a similar rearrangement of carbene 7, with the final observed product being ethanol-trapped 9 (Scheme 3B) [31]. However, to our knowledge, the syntheses of 3 (or substituted derivatives of 3) via an elimination route is still unknown.

There are two potential isomeric precursors to anti-Bredt alkene 3 (3a_X and 3b_X in Figure 6). In agreement with the high anticipated strain energy of compound 3, optimization of either of the precursors with X = Br or I failed to generate 3, even employing spin-unrestricted conditions. Frequency calculations confirmed the anionic precursors to be energetic minima. NBO calculations again suggested minimal delocalization of the lone pair into the σ* orbital of the C-Br bond (3a_Br, 1.2 kcal/mol; 3b_Br, 1.9 kcal/mol), potentially inhibiting C=C bond formation via elimination. Furthermore, optimization of precursors that could lead to substituted bridgehead alkenes 5 and 8 (compounds 5a/b and 8a/b in Figure 6) also failed to result in elimination.

3.4. [2.2.1]Bicyclohexane Substrates

There are two anti-Bredt isomers that could potentially be formed from the [2.2.1]bicycloheptane framework: alkene 10, in which the double bond includes one of the carbons from a one-carbon bridge (i.e., [2.2.1]bicyclohept-1(7)-ene, Figure 7), and alkene 11, in which the double bond includes carbon from one of the two-carbon bridges (i.e., [2.2.1]bicyclohept-1-ene, Figure 7).

3.4.1. [2.2.1]Bicyclohept-1(7)-ene (10)

Bridgehead alkene 10 is highly strained (Schleyer calculated an OS energy of 39.1 kcal/mol) [7], and Novak suggested it may have significant diradical character [8]. Not surprisingly, then, to our knowledge, there has been no report of the formation of 10 in the literature. Because of the symmetry of the [2.2.1] framework, there are only two possible precursors to alkene 10, i.e., 10a_X and 10b_X (Figure 8). Optimization of the geometries with X = Br (including without spin restriction) or X = I failed to eliminate the halide to form 10. NBO calculations again suggested only minor delocalizations of the carbon lone pair into the σ* orbital of the C-Br bond for either 10a_Br or 10b_Br (0.9 and 2.6 kcal/mol, respectively).

3.4.2. [2.2.1]Bicyclohept-1-ene (11)

There are four possible precursors to alkene 11, as shown in Figure 9. Again, the same convention that was used for compounds 2a/b for assigning the “exo/endo” stereochemistry of the anionic lone pairs has been applied.

In this case, optimization of the geometry of 11a_{Br_exo} resulted in spontaneous elimination of the bromine atom as Br^– and formation of bridgehead alkene 11. However, optimization of stereoisomeric 11a_{Br_endo} did not form 11 but instead proved to be an energetic minimum. NBO calculations on the MMFF-pre-optimized geometries revealed significant initial delocalization of the carbon lone pair into the C-Br antibonding orbital for 11a_{Br_exo} (10.8 kcal/mol, see Figure 10A), but very little delocalization within 11a_{Br_endo} (0.7 kcal/mol, see Figure 10B). Note that the C-C bond distances between the two interacting orbitals were essentially equivalent (i.e., 1.540 and 1.539 Å, respectively). The overlap of the two interacting orbitals is much better aligned for 11a_{Br_exo}, and therefore allows more efficient initial transfer of electron density for the formation of the C=C bond. For similar reasons of orbital alignment, optimization of 11b_{Br_exo} resulted in spontaneous formation of alkene 11, but optimization of 11b_{Br_endo} did not.

It should be noted that elimination from both 11a_{Br_exo} and 11b_{Br_exo} also directly gave rise to formation of the more stable stereoisomer 11_{_endo} (see inset, Figure 9). As has previously been pointed out by Wiseman [32], one of the two rings that contains the C=C bond of a bridgehead alkene must necessarily adopt a highly strained trans stereochemistry. In 11_{_endo,} the hydrogen atom of the C=C bond is tucked into the endo position, affording the six-membered ring trans stereochemistry rather than embedding it within the smaller five-membered ring. Note that elimination from 11a_{Br_endo} and 11b_{Br_endo} would lead to 11_{_exo}, in which the five-membered ring would be required to bear the strain. Indeed, as addressed earlier by Szeimies [33], the strain in 11_{_exo} is so high that it is not a stationary point on the PES; instead, it spontaneously isomerizes to 11_{_endo} upon attempted geometric optimization.

In all four cases, substitution of Br with I as the leaving group (i.e., 11a_I/11b_I) gave identical results, and formation of 11 was observed to spontaneously take place. We also attempted replacing the Br with the poorer leaving group Cl (11a_Cl/11b_Cl). However, all four structures failed to form alkene 11 upon geometric optimization. The reluctance of chloride to act as a leaving group under such computational geometric optimizations is consistent with our earlier findings on E1cb reactions [27].

Schleyer calculated an OS energy for 11 of 28.9 kcal/mol, placing it outside the energy limits of an “observable” bridgehead alkene [7]. However, several experimental studies have been reported that suggest the intermediacy of 11 [17,18,34,35,36]. Thus, the computationally obtained results correctly predicted the observed experimental data. In addition, experimental results suggested faster elimination of the bromide ion from 11a_{Br_exo} than from 11a_{Br_endo}, in complete agreement with our computational findings [17,34]. Finally, 11 was predicted to be more stable than isomeric 10 by 31 kcal/mol according to our calculations, consistent with the C=C bond being located within a six-membered ring rather than being restricted to being part of one of the two five-membered rings. Thus, the stronger driving force for formation of bridgehead alkene 11 compared with 10 is understandable.

3.5. [3.1.1]Bicycloheptane Substrates

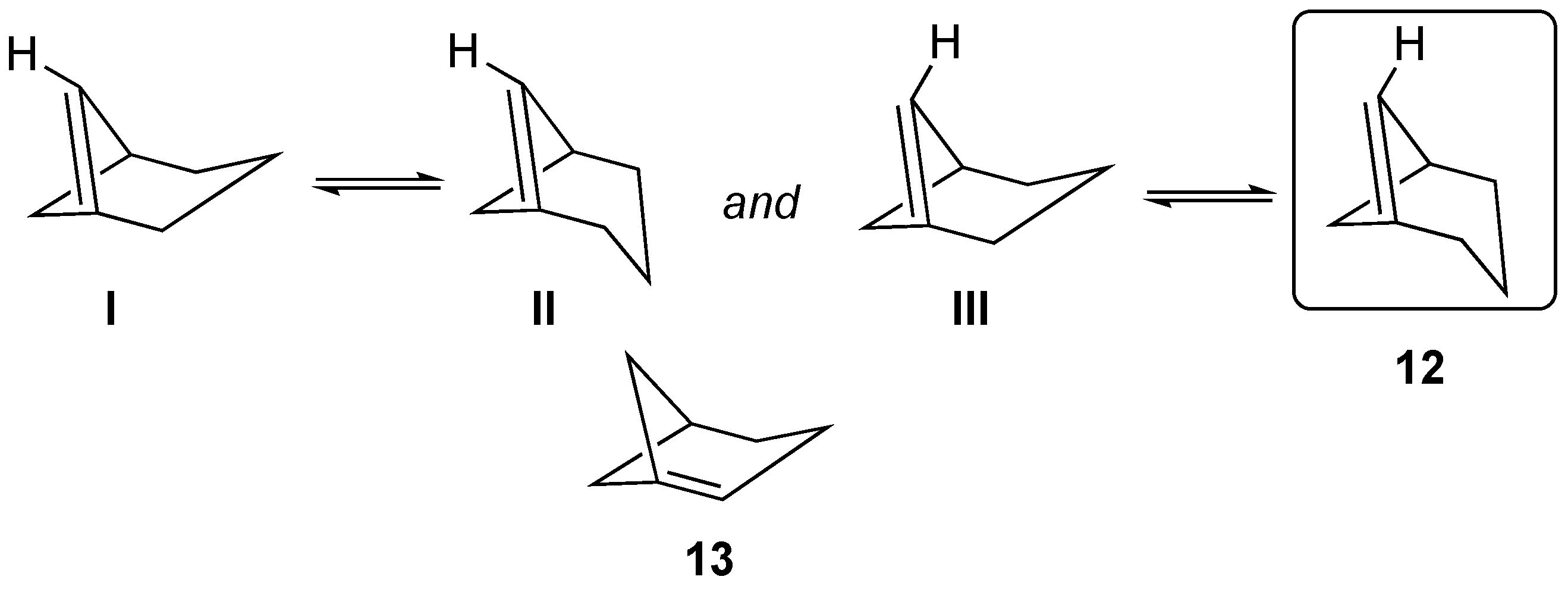
There are two anti-Bredt isomers that could potentially be formed from the [3.1.1]bicycloheptane framework. One of these is alkene 12, in which the double bond includes a carbon from one of the one-carbon bridges (i.e., [3.1.1]bicyclohept-1(6)-ene, Figure 11). There are four primary stereoisomers that can be drawn for 12, as shown in Figure 11. Two isomers (I and II) orient the hydrogen atom of the C=C double bond such that the four-membered ring component would be required to adopt trans stereochemistry (and the six-membered ring cis stereochemistry). These were unstable upon attempted geometric optimization, relative to formation of the system in which the four-membered ring adopted the preferred cis stereochemistry (and the larger six-membered ring adopted the trans stereochemistry), as shown in structures III and 12 (Figure 11). Furthermore, our attempted geometric optimization of III led spontaneously to formation of 12. The second possible bridgehead alkene is that of 13, in which the double bond includes a carbon from the three-carbon bridges (i.e., [3.1.1]bicyclohept-1-ene, Figure 11). Note that the structure of 13 precludes stereoisomers.

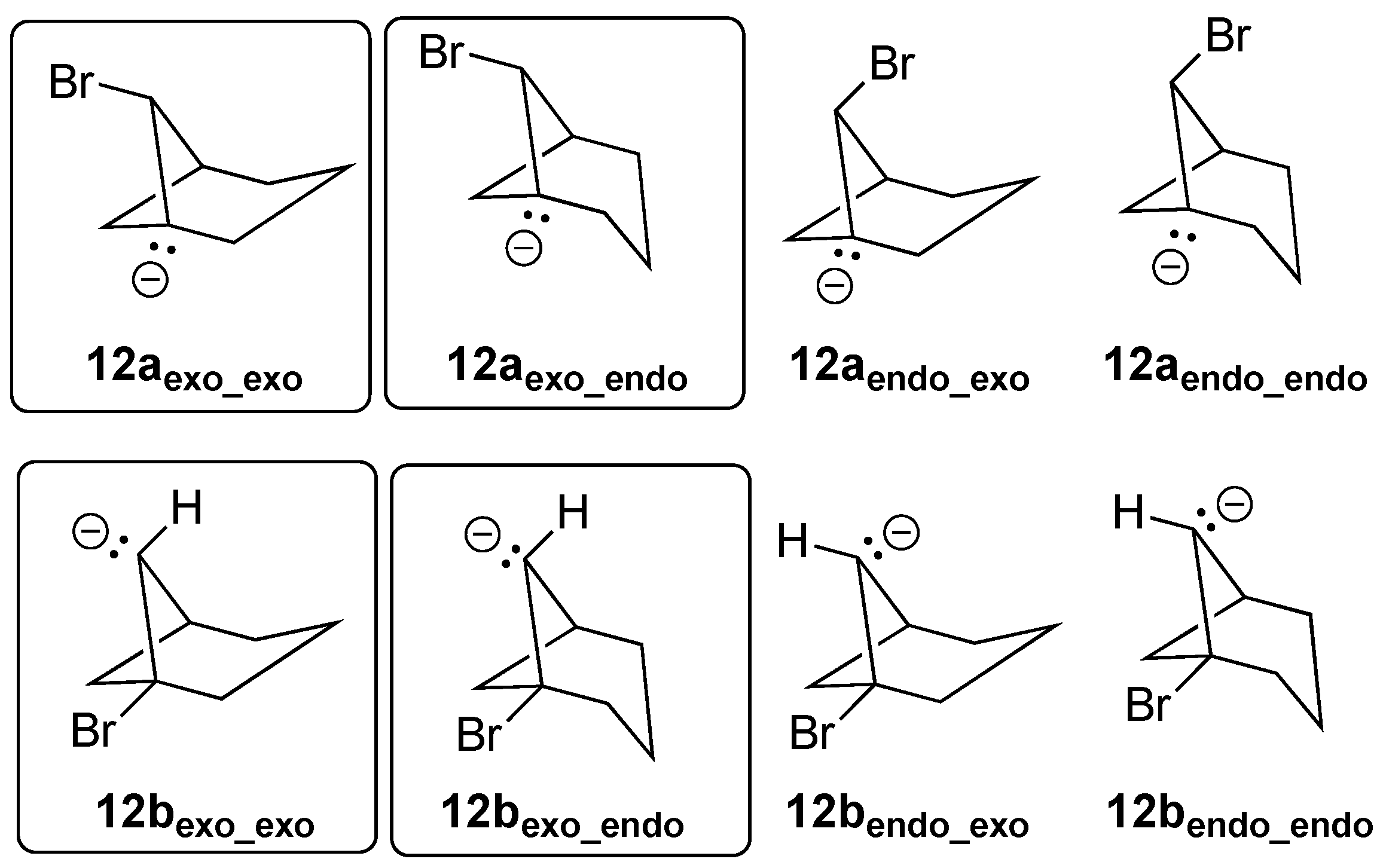
3.5.1. [3.3.1]Bicyclohept-1(6)-ene (12)

Having observed that iodine did not apparently lead to eliminations in cases where bromine did not, and that chlorine made for a generally poor leaving group, we decided to concentrate on bromine as a leaving group from this point on. There are a total of eight possible anionic precursors for the formation of alkene 12 that differ in whether the anionic carbon or the C–Br bond is present at the bridgehead position, the orientation of the C–Br bond or lone pair in relation to the one- or three-carbon bridges, and the conformation of the central CH₂ group of the three-carbon bridge (see Figure 12).

As described above for bridgehead alkene 11, the regio- and stereoisomers leading directly to III or 12 (see boxed structures in Figure 12) spontaneously eliminated bromine as a leaving group upon geometry optimization. When III was initially formed, it further optimized to 12. The remaining four isomers (unboxed in Figure 12) led directly to the highly strained structures I or II if elimination proceeded, and they therefore optimized as stationary points upon geometric optimization without elimination. NBO calculations supported these findings. For example, the delocalization energy for 12a_{exo_exo} (for which elimination occurred) was 11.2 kcal/mol, while that for stereoisomer 12a_{endo_exo} (for which elimination failed to occur) was a negligible 1.5 kcal/mol. The greater delocalization energy was not because the two orbitals were closer (the C-C bond distance for 12a_{endo_exo} was 1.558 Å, while that for 12a_{exo_exo} was 1.559 Å) but was due to more efficient orbital overlap of the back side of the anionic carbon lone pair orbital with the tail of the carbon–bromine antibonding orbital, as can be seen in Figure 13.

3.5.2. [3.2.1]Bicyclohept-1-ene (13)

Due to the symmetry of the final alkene product, there are only four precursors to bridgehead alkene 13 that need to be considered (see Figure 14). For these substrates, the endo/exo terminology does not readily apply, so we have designated them as “ax” or “eq” depending on whether the Br or lone pair initially resides in the axial or equatorial position of the six-membered ring that is configured in the chair conformation.

Perhaps not surprisingly, based on previous results, 13a_eq and 13b_eq both optimized to eliminate Br^– as the leaving group and formed bridgehead alkene 13, whereas both 13a_ax and 13b_ax did not. The success of the former two precursors was predicted based on the NBO calculations that revealed much greater delocalization of the lone-pair electrons into the C-Br antibonding orbital for 13a_eq and 13b_eq (9.4 and 11.7 kcal/mol, respectively) than for 13a_ax and 13b_ax (0 kcal/mol for both). As a side note, it was found that elimination occurred for these same stereoisomers even with Cl^– as a poorer leaving group.

Schleyer identified bridgehead alkenes 12 and 13 as having considerable OS energies (39.1 and 28.9 kcal/mol, respectively), placing both isomers into the predicted “unstable” category [7]. Interestingly, and as has been pointed out by Ermer [6], despite the difference in calculated OS energies, 12 was calculated to be slightly more stable than isomer 13 by 0.3 kcal/mol, according to our computational method. To our knowledge, neither compound 12 nor 13 has been reported, although computations by Szeimies suggested that 13 might conceivably be formed via an appropriate carbene precursor and could exhibit some stability relative to further rearrangement [33]. Our calculations suggest that both of these compounds could be viable synthetic targets.

3.6. [3.2.1]Bicycloheptane Substrates

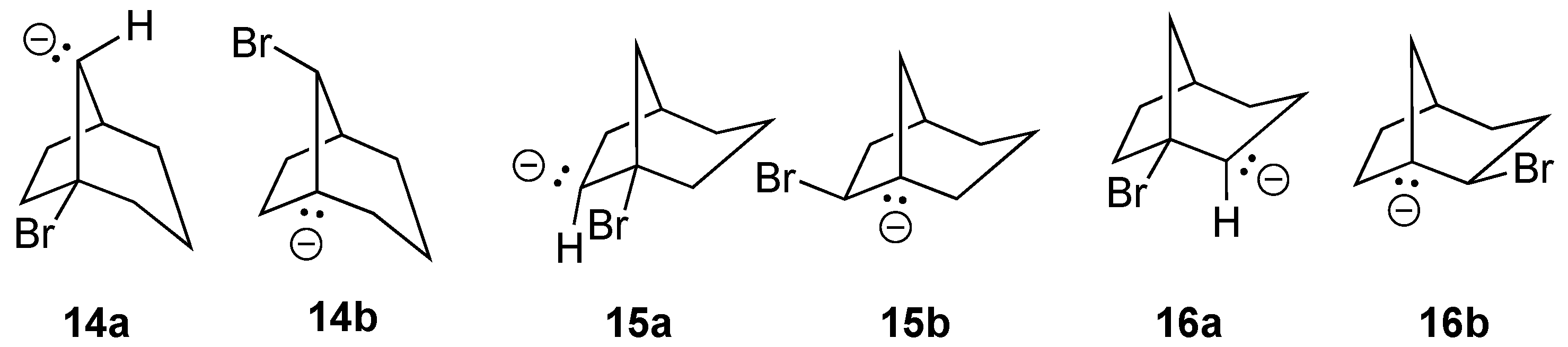
There are three anti-Bredt regioisomers that could potentially be formed from the [3.2.1]bicyclooctane framework, i.e., alkenes 14 ([3.2.1]bicyclooct-1(8)-ene), 15 ([3.2.1]bicyclooct-1(7)-ene), and 16 ([3.2.1]bicyclooct-1-ene). The most stable stereochemical and conformational isomer of each is illustrated in Figure 15.

To simplify the number of calculations required, and based on observed preferences for leaving group and carbon lone-pair orientation that led to successful eliminations as learned from earlier calculations, we considered only anionic β-bromo precursors that might lead directly to each of the more stable isomers upon elimination. As shown in Figure 16, all of the potential precursor compounds meeting these criteria successfully eliminated Br^– to form the corresponding bridgehead alkene, suggesting these to be viable routes for the synthesis of these strained anti-Bredt alkenes.

Of the three most stable bridgehead alkene isomers, 16, in which the C=C bond is located in the longer carbon bridge, was found to be more stable than both 14 and 15 by 4.7 and 18.6 kcal/mol, respectively. While bridgehead alkene 14 has not yet been reported, evidence for the formation of mixtures of 15 and 16 has been put forward by Wisemen [37]. Additionally, Kirmse has reported the synthesis of substituted versions of 15 and 16 [38], and Szeimies has provided evidence for the intermediacy of a dibromo-substituted 15 [33]. Thus, our computationally predicted results again paralleled experimental findings.

3.7. Other Known Bicyclic Substrates

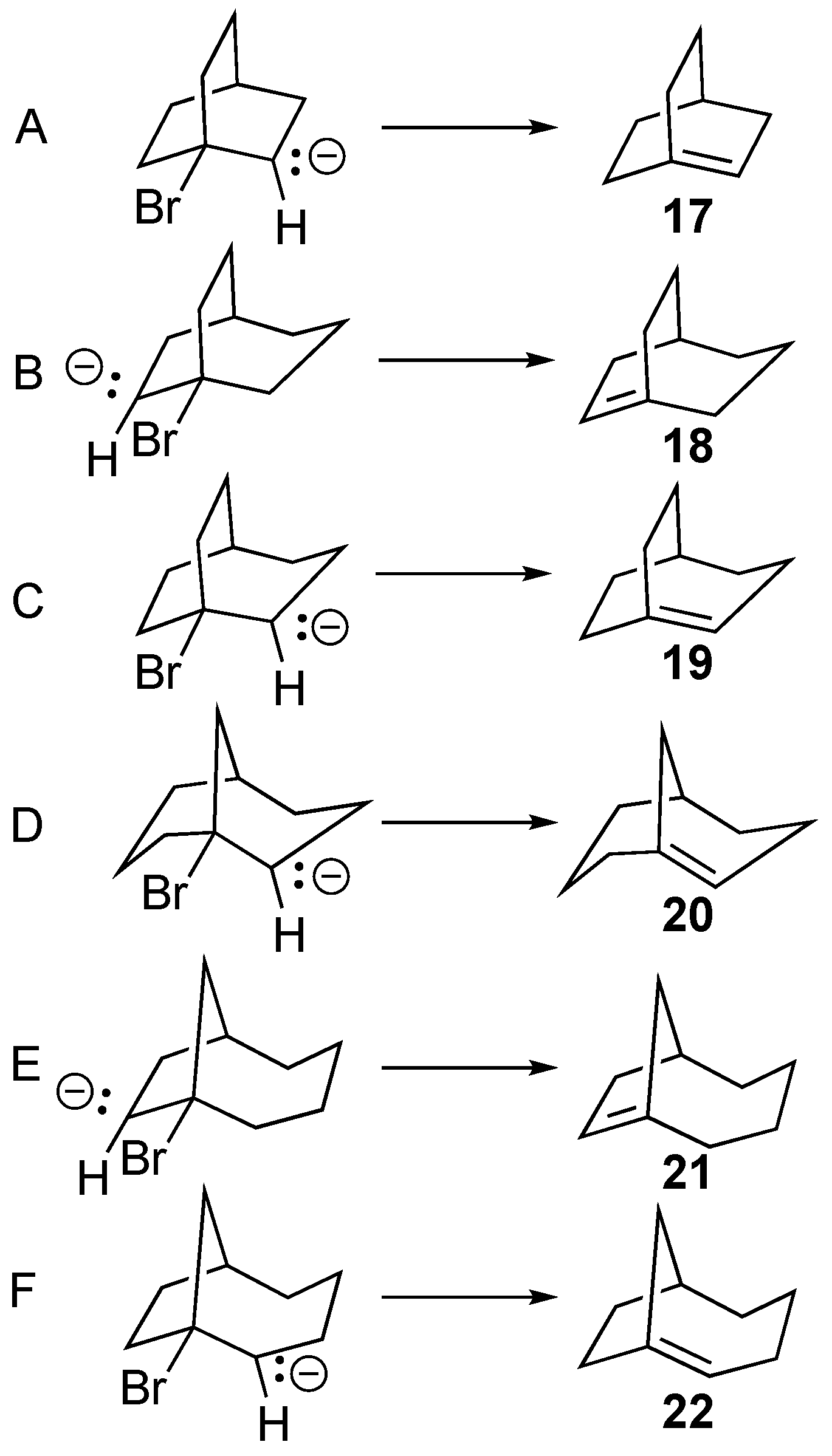
There are several other smaller-sized bridgehead alkenes (i.e., compounds 17–22) for which experimental evidence for their formation has been provided in the literature [39,40,41]. To test whether computational optimization of anionic β-bromo substrates would successfully predict the formation of these compounds, we modelled the six anionic bridgehead bromide substrates shown in Scheme 4, in which the lone pair was initially positioned to maximize interaction with σ*_C-Br. All of these precursors seamlessly optimized to the corresponding bridgehead alkene upon optimization.

4. Conclusions

In general, computational optimization of anionic β-bromides to form (or not form) bicyclic anti-Bredt bridgehead alkenes using the DFT method of (U)wB97X-D/aug-cc-pVDZ{THF} faithfully mimicked results obtained from earlier computational studies as well as available experimental results. Success in formation of the bridgehead alkenes upon geometric optimization was most readily predicted from NBO calculations according to the extent of delocalization of the carbon lone pair into σ*_C-Br. Delocalization energy in the range of 10 kcal/mol appears to be an indicator of successful elimination and formation of a C=C bond upon geometric optimization. Precursors unable to achieve such prior delocalization energies optimize instead to local minima without elimination. For especially small bicyclic systems (e.g., [1.1.1] and [2.1.1]) where the bridgehead alkenes have already been predicted to be too unstable to be formed, no elimination was observed upon optimization. However, for larger systems (e.g., [2.2.1], [3.1.1], etc.) for which there existed prior evidence (either computational or experimental) for the formation of such bridgehead alkene systems, optimization of the precursors successfully led to elimination. It should be noted that for some compounds (e.g., 12–14), while optimizations were successful, there does not yet exist any experimental evidence for their formation. However, this may well be because, to our knowledge, there have to date been no attempts at their synthesis. The computational results reported herein, however, suggest their synthesis to be viable via an elimination route. Finally, anionic bromides appear to be the most practical precursor targets. The corresponding chlorides are generally less prone to elimination, while iodides do not appear to provide any great advantage in terms of reactivity enhancement. Thus, computational optimization of appropriate β-substituted anionic precursors appears to be an excellent predictor of whether elimination will occur to form anti-Bredt bridgehead alkenes. Generally, these calculations require a fraction of the time that would otherwise be directed towards the attempted synthesis of the corresponding compound in the lab. In addition, the computational method is essentially cost-free. We believe this technique will be useful in predicting which bridgehead alkenes are promising targets for future synthetic work.