Theoretical Study on the Diels–Alder Reaction of Fullerenes: Analysis of Isomerism, Aromaticity, and Solvation
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
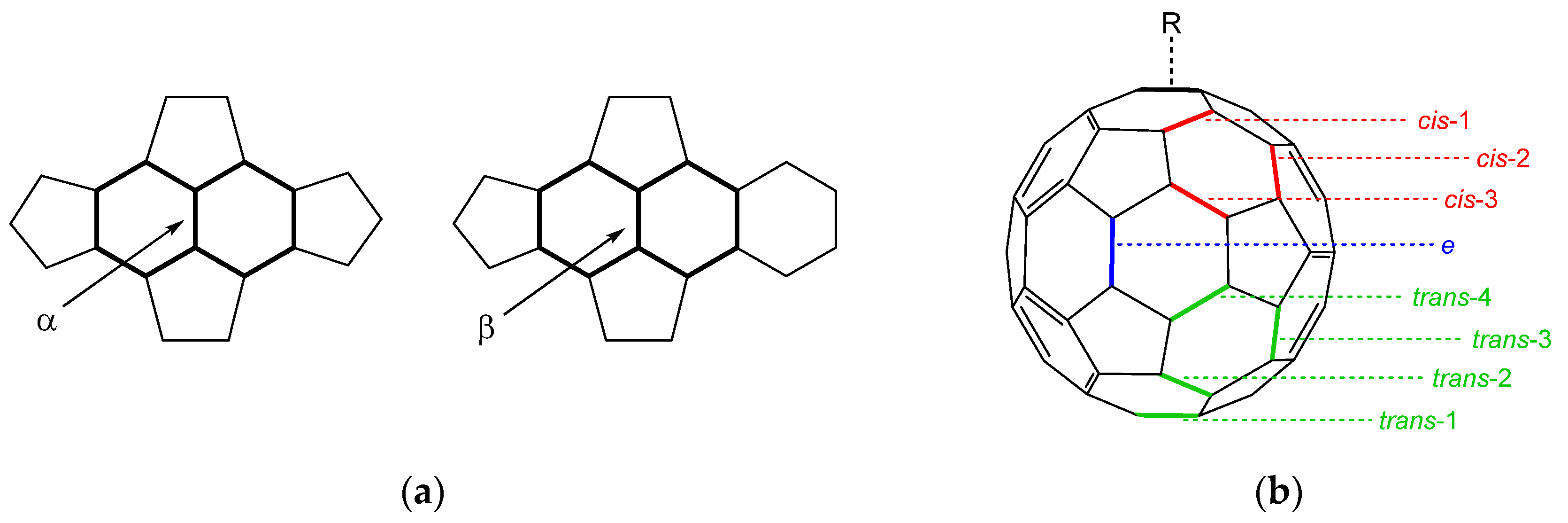
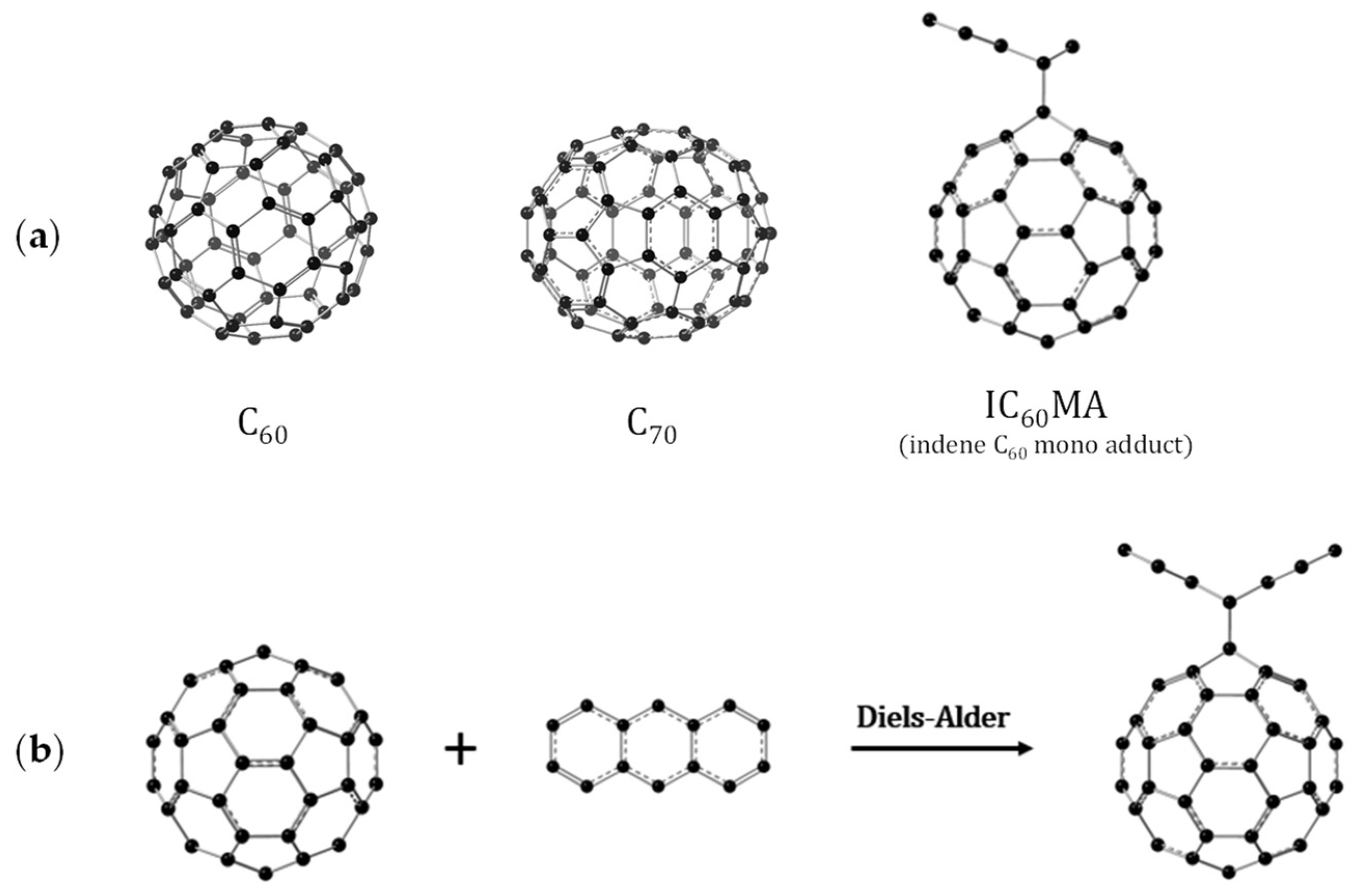
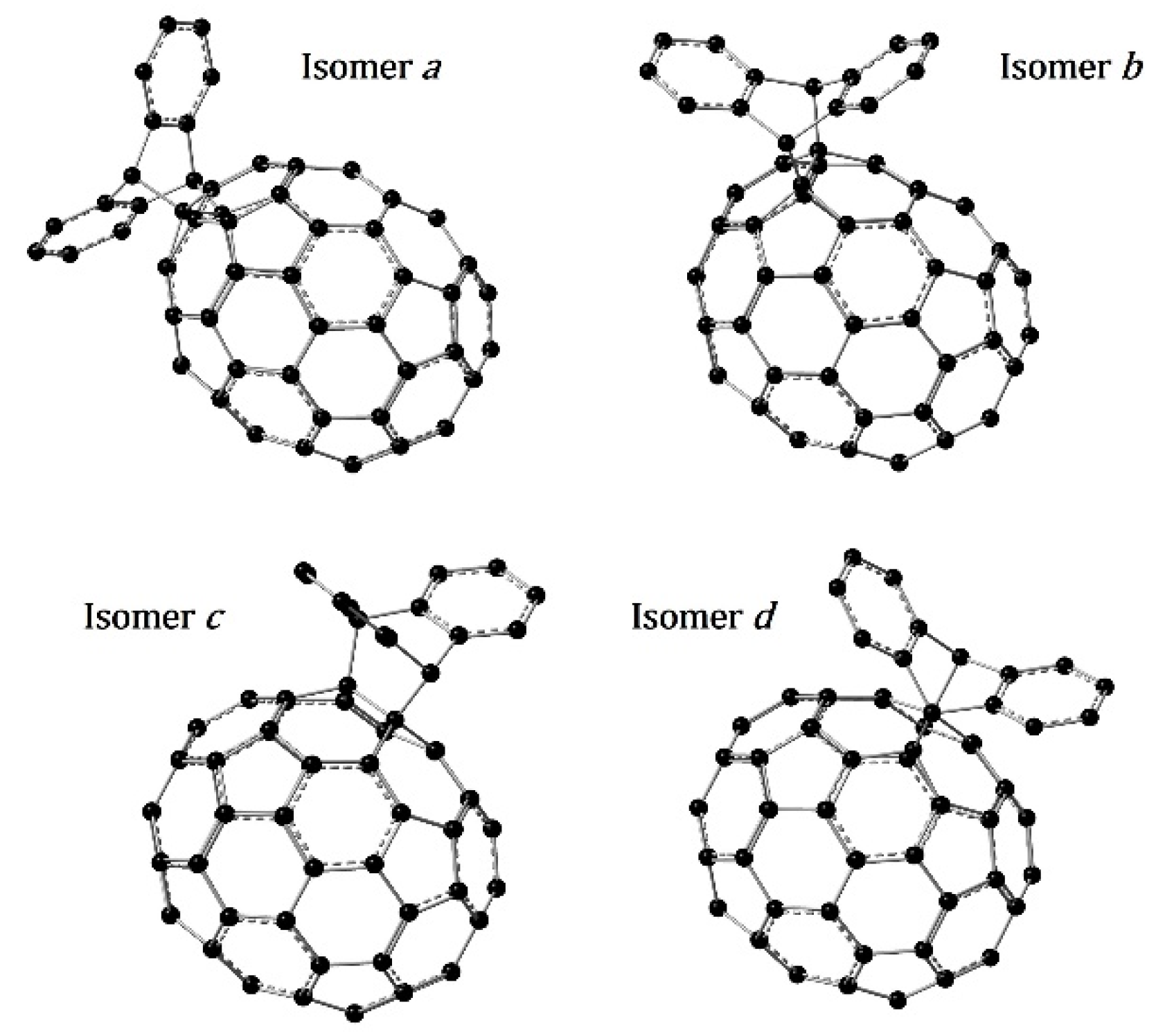
3.1. Optimized Molecular Structures and Isomers
3.2. Electronic Energies of Reaction in Vacuum
3.3. Effect of Computational Method and Basis-Set
3.4. Solvation Energies in M-Xylene. Enthalpies of Reaction at T = 298.15 K
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- De La Puente, F.L.; Nierengarten, J.-F. Fullerenes: Principles and Applications; Royal Society of Chemistry: London, UK, 2011. [Google Scholar]
- Taylor, R.; Walton, D.R.M. The chemistry of fullerenes. Nature 1993, 363, 685–693. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Fernandez, I.; Sola, M.; Bickelhaupt, F.M. Why do cycloaddition reactions involving C60 prefer [6, 6] over [5, 6] bonds? Chem. Eur. J. 2013, 19, 7416–7422. [Google Scholar] [CrossRef]
- Olah, G.A.; Bucsi, I.; Aniszfeld, R.; Prakash, G.S. Chemical reactivity and functionalization of C60 and C70 fullerenes. Carbon 1992, 30, 1203–1211. [Google Scholar]
- Yadav, B.; Kumar, R. Structure, properties and applications of fullerenes. Int. J. Nanotechnol. Appl. 2008, 2, 15–24. [Google Scholar]
- Hirsch, A. Addition reactions of buckminsterfullerene (C60). Synthesis 1995, 895–913. [Google Scholar] [CrossRef]
- Thilgen, C.; Herrmann, A.; Diederich, F. The covalent chemistry of higher fullerenes: C70 and beyond. Angew. Chem. Int. Ed. 1997, 36, 2268–2280. [Google Scholar] [CrossRef]
- Thilgen, C.; Diederich, F. The higher fullerenes: Covalent chemistry and chirality. In Fullerenes and Related Structures; Springer: Berlin/ Heidelberg, Germany, 1999; pp. 135–171. [Google Scholar]
- Hirsch, A.; Lamparth, I.; Karfunkel, H.R. Fullerene chemistry in three dimensions: Isolation of seven regioisomeric bisadducts and chiral trisadducts of C60 and di (ethoxycarbonyl) methylene. Angew. Chem. Int. Ed. 1994, 33, 437–438. [Google Scholar]
- Taylor, R. Addition reactions of fullerenes. C. R. Chim. 2006, 9, 982–1000. [Google Scholar] [CrossRef]
- Sarova, G.H.; Berberan-Santos, M.N. Kinetics of the Diels–Alder reaction between C60 and acenes. Chem. Phys. Lett. 2004, 397, 402–407. [Google Scholar] [CrossRef]
- Wang, G.W.; Saunders, M.; Cross, R.J. Reversible Diels−Alder Addition to Fullerenes: A Study of Equilibria Using 3He NMR Spectroscopy. J. Am. Chem. Soc. 2001, 123, 256–259. [Google Scholar]
- Frunzi, M.; Cross, R.J.; Saunders, M. Effect of xenon on fullerene reactions. J. Am. Chem. Soc. 2007, 129, 13343–13346. [Google Scholar] [CrossRef] [PubMed]
- Murata, M.; Maeda, S.; Morinaka, Y.; Murata, Y.; Komatsu, K. Synthesis and reaction of fullerene C70 encapsulating two molecules of H2. J. Am. Chem. Soc. 2008, 130, 15800–15801. [Google Scholar] [PubMed]
- Li, Y. Fullerene-Bisadduct Acceptors for Polymer Solar Cells. Chem. Asian J. 2013, 8, 2316–2328. [Google Scholar] [CrossRef] [PubMed]
- Yu, G.; Gao, J.; Hummelen, J.C.; Wudi, F.; Heeger, A.J. Polymer Photovoltaic Cells: Enhanced Efficiencies via a Network of Internal Donor-Acceptor Heterojunctions. Science 1995, 270, 1789–1791. [Google Scholar]
- Qian, X.; Umari, P.; Marzari, N. First-principles investigation of organic photovoltaic materials C60, C70, [C60]PCBM, and bis-[C60]PCBM using a many-body G0W0-Lanczos approach. Phys. Rev. B 2015, 91, 245105. [Google Scholar] [CrossRef]
- Lenes, M.; Wetzelaer, G.-J.A.H.; Kooistra, F.B.; Veenstra, S.C.; Hummelen, J.C.; Blom, P.W.M. Fullerene Bisadducts for Enhanced Open-Circuit Voltages and Efficiencies in Polymer Solar Cells. Adv. Mater. 2008, 20, 2116–2119. [Google Scholar] [CrossRef]
- He, Y.; Chen, H.-Y.; Hou, J.; Li, Y. Indene−C60 Bisadduct: A New Acceptor for High-Performance Polymer Solar Cells. J. Am. Chem. Soc. 2010, 132, 1377–1382. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Zhao, G.; Peng, B.; Li, Y. High-Yield Synthesis and Electrochemical and Photovoltaic Properties of Indene-C70 Bisadduct. Adv. Funct. Mater. 2010, 20, 3383–3389. [Google Scholar]
- Chikama, A.; Fueno, H.; Fujimoto, H. Theoretical Study of the Diels-Alder Reaction of C60. Transition-State Structures and Reactivities of CC Bonds. J. Phys. Chem. 1995, 99, 8541–8549. [Google Scholar] [CrossRef]
- Mestres, J.; Duran, M.; Sola, M. Theoretical Study of Diels−Alder Cycloadditions of Butadiene to C70. An Insight into the Chemical Reactivity of C70 as Compared to C60. J. Phys. Chem. 1996, 100, 7449–7454. [Google Scholar]
- Umeyama, T.; Imahori, H. Isomer effects of fullerene derivatives on organic photovoltaics and perovskite solar cells. Acc. Chem. Res. 2019, 52, 2046–2055. [Google Scholar] [CrossRef]
- Meng, X.; Zhao, G.; Xu, Q.; Tan, Z.A.; Zhang, Z.; Jiang, L.; Shu, C.; Wang, C.; Li, Y. Effects of fullerene bisadduct regioisomers on photovoltaic performance. Adv. Funct. Mater. 2014, 24, 158–163. [Google Scholar] [CrossRef]
- Sabirov, D.S.; Terentyev, A.O.; Cataldo, F. Bisadducts of the C60 and C70 fullerenes with anthracene: Isomerism and DFT estimation of stability and polarizability. Comput. Theor. Chem. 2016, 1081, 44–48. [Google Scholar] [CrossRef]
- Sabirov, D.S.H.; Garipova, R.R.; Bulgakov, R.G. What fullerene is more reactive toward peroxyl radicals? A comparative DFT Study on ROO• addition to C60 and C70 fullerenes. Fuller. Nanotub. Carbon Nanostruct. 2015, 23, 1051–1057. [Google Scholar]
- Ash, T.; Banerjee, S.; Debnath, T.; Das, A.K. Computational insights into the multi-Diels–Alder reactions of neutral C60 and its Li+ encapsulated analogue: A density functional theory study. Int. J. Quantum Chem. 2022, 122, e26824. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Revision A.02; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Josa, D.; Rodríguez-Otero, J.; Cabaleiro-Lago, E.M.; Rellán-Piñeiro, M. Analysis of the performance of DFT-D, M05-2X and M06-2X functionals for studying π⋯ π interactions. Chem. Phys. Lett. 2013, 557, 170–175. [Google Scholar]
- Denis, P.A. Theoretical investigation of the stacking interactions between curved conjugated systems and their interaction with fullerenes. Chem. Phys. Lett. 2011, 516, 82–87. [Google Scholar]
- Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J. Phys. Chem. B. 2009, 113, 6378–6396. [Google Scholar]
- Kiselev, V.D.; Konovalov, A.I. Internal and external factors influencing the Diels–Alder reaction. J. Phys. Org. Chem. 2009, 22, 466–483. [Google Scholar]
- Bühl, M.; Hirsch, A. Spherical aromaticity of fullerenes. Chem. Rev. 2001, 101, 1153–1184. [Google Scholar] [CrossRef]
- Chen, Z.; Wu, J.I.; Corminboeuf, C.; Bohmann, J.; Lu, X.; Hirsch, A.; von Rague Schleyer, P. Is C60 buckminsterfullerene aromatic? Phys. Chem. Chem. Phys. 2012, 14, 14886–14891. [Google Scholar]
- Krygowski, T.M. Crystallographic studies of inter-and intramolecular interactions reflected in aromatic character of. pi.-electron systems. J. Chem. Inf. Comput. Sci. 1993, 33, 70–78. [Google Scholar]
- Krygowski, T.M.; Cyrański, M. Separation of the energetic and geometric contributions to the aromaticity. Part IV. A general model for the π-electron systems. Tetrahedron 1996, 52, 10255–10264. [Google Scholar]
- Krygowski, T.M.; Cyrański, M. Separation of the energetic and geometric contributions to the aromaticity of π-electron carbocyclics. Tetrahedron 1996, 52, 1713–1722. [Google Scholar]
- Hirsch, A.; Lamparth, I.; Grösser, T.; Karfunkel, H.R. Regiochemistry of Multiple Additions to the Fullerene Core: Synthesis of a Th-Symmetric Hexakis adduct of C60 with Bis (ethoxycarbonyl) methylene. J. Am. Chem. Soc. 1994, 116, 9385–9386. [Google Scholar]
- Lamparth, I.; Maichle-Mössmer, C.; Hirsch, A. Reversible Template-Directed Activation of Equatorial Double Bonds of the Fullerene Framework: Regioselective Direct Synthesis, Crystal Structure, and Aromatic Properties of Th-C66 (COOEt) 12. Angew. Chem. Int. Ed. Engl. 1995, 34, 1607–1609. [Google Scholar]
- Osuna, S.; Swart, M.; Solà, M. Dispersion corrections essential for the study of chemical reactivity in fullerenes. J. Phys. Chem. A. 2011, 115, 3491–3496. [Google Scholar]
- Osuna, S.; Morera, J.; Cases, M.; Morokuma, K.; Solà, M. Diels−Alder reaction between cyclopentadiene and C60: An analysis of the performance of the ONIOM method for the study of chemical reactivity in fullerenes and nanotubes. J. Phys. Chem. A. 2009, 113, 9721–9726. [Google Scholar]
- Van Duijneveldt, F.B.; de Rijdt, J.G.V.D.-V.; van Lenthe, J.H. State of the art in counterpoise theory. Chem. Rev. 1994, 94, 1873–1885. [Google Scholar] [CrossRef]
- Lin, S.K. Correlation of entropy with similarity and symmetry. J. Chem. Inf. Comput. Sci. 1996, 36, 367–376. [Google Scholar]
- Estrada, E.; Avnir, D. Continuous symmetry numbers and entropy. J. Am. Chem. Soc. 2003, 125, 4368–4375. [Google Scholar] [CrossRef] [PubMed]
- Pollak, E.L.I.; Pechukas, P. Symmetry numbers, not statistical factors, should be used in absolute rate theory and in Bröensted relations. J. Am. Chem. Soc. 1978, 100, 2984–2991. [Google Scholar] [CrossRef]
- Parr, R.G.; Szentpály, L.V.; Liu, S. Electrophilicity index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar]
- Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R. Quantitative characterization of the global electrophilicity power of common diene/dienophile pairs in Diels–Alder reactions. Tetrahedron 2002, 58, 4417–4423. [Google Scholar]
- Domingo, L.R.; Aurell, M.J.; Pérez, P.; Contreras, R. Quantitative characterization of the local electrophilicity of organic molecules. Understanding the regioselectivity on Diels−Alder reactions. J. Phys. Chem. A 2002, 106, 6871–6875. [Google Scholar]
- Dewar, M.J.S.; Haselbach, E.; Worley, S.D. Calculated and observed ionization potentials of unsaturated polycyclic hydro-carbons; calculated heats of formation by several semiempirical scfmo methods. Proc. R. Soc. Lond. A 1970, 315, 431–442. [Google Scholar]
- Wojnarovits, L.; Foldiak, G. Electron capture detection of aromatic hydrocarbons. J. Chromatogr. Sci. 1981, 206, 511–519. [Google Scholar] [CrossRef]
- Hager, J.W.; Wallace, S.C. Two-laser photoionization supersonic jet mass spectrometry of aromatic molecules. Anal. Chem. 1988, 60, 5–10. [Google Scholar]
- Ando, N.; Mitsui, M.; Nakajima, A. Comprehensive photoelectron spectroscopic study of anionic clusters of anthracene and its alkyl derivatives: Electronic structures bridging molecules to bulk. J. Chem. Phys. 2007, 127, 234305. [Google Scholar] [PubMed]
- Boltalina, O.V.; Ioffe, I.N.; Sidorov, L.N.; Seifert, G.; Vietze, K. Ionization energy of fullerenes. J. Am. Chem. Soc. 2000, 122, 9745–9749. [Google Scholar]
- Huang, D.L.; Dau, P.D.; Liu, H.T.; Wang, L.S. High-resolution photoelectron imaging of cold C60(-) anions and accurate determination of the electron affinity of C60. J. Chem. Phys. 2014, 140, 224315. [Google Scholar]
- Wang, X.B.; Woo, H.K.; Huang, X.; Kappes, M.M.; Wang, L.S. Direct experimental probe of the on-site Coulomb repulsion in the doubly charged fullerene anion C70(2-). Phys. Rev. Lett. 2006, 96, 143002. [Google Scholar] [CrossRef]
- Nakanishi, R.; Nogimura, A.; Eguchi, R.; Kanai, K. Electronic structure of fullerene derivatives in organic photovoltaics. Org. Electron. 2014, 15, 2912–2921. [Google Scholar] [CrossRef]
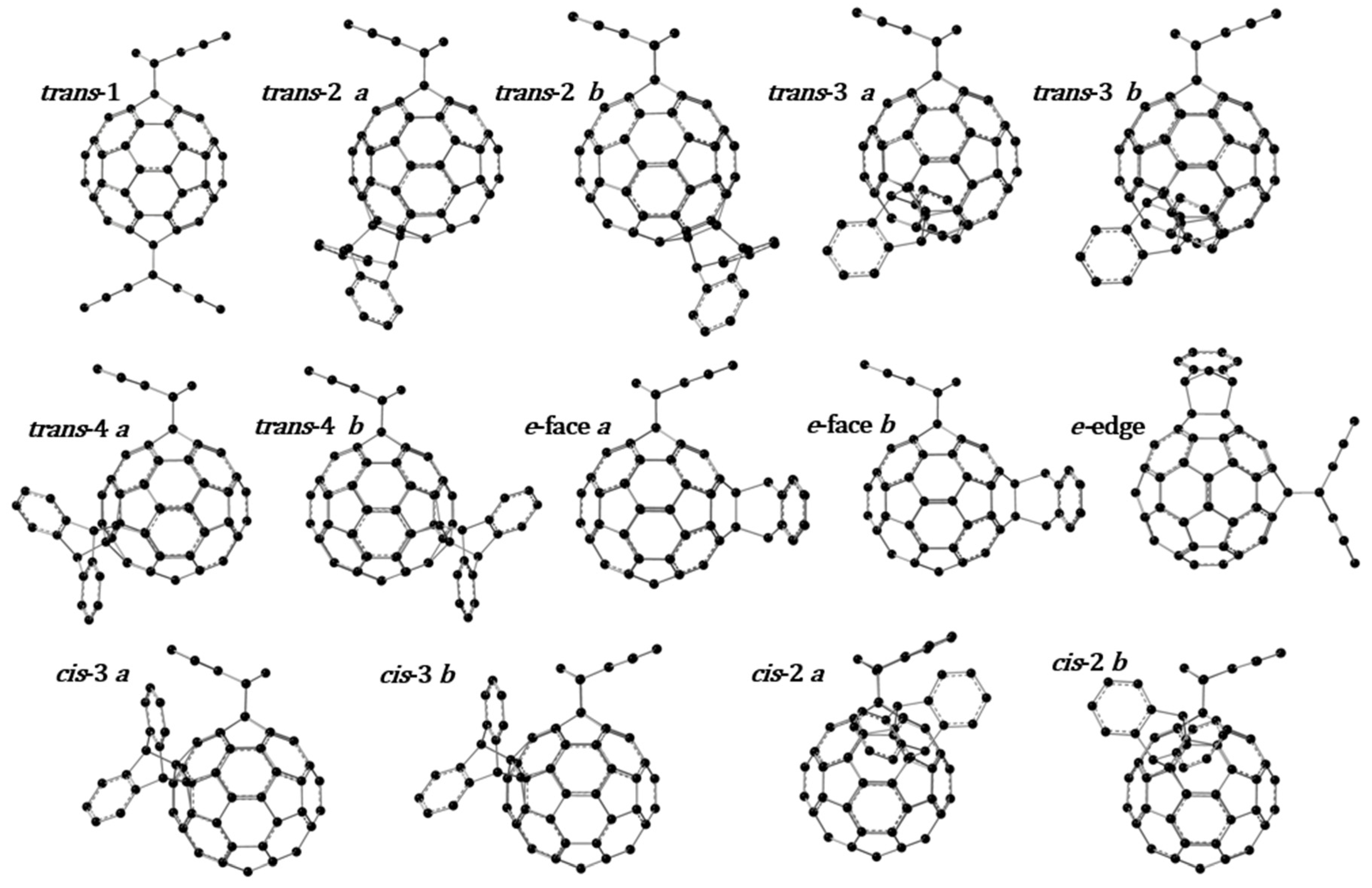
| Reaction | ∆rEel,m (g, 0 K)/kJ∙mol−1 | |||
|---|---|---|---|---|
| M06-2X/ 6-31+G(d) | M06-2X/ 6-311++G(2d,p) | B3LYP/ 6-31+G(d) | MP2/ cc-pVDZ 2 | |
| R1. C60 + Ind → IC60MA | −116.6 | −106.4 | −31.0 | −−− |
| R2. C60 + Ant → AC60MA | −95.4 | −85.4 | 7.8 | −165.5 (−30.2) |
| R3. C70 + Ant → AC70MA | ||||
| a | −96.6 | −86.4 | 8.2 | −−− |
| b | −91.6 | −80.4 | 20.9 | −−− |
| c | −19.5 | −9.2 | −−− | −−− |
| d | 95.5 | 105.6 | −−− | −−− |
| R4. IC60MA + Ant → AIC60BA 3 | ||||
| trans−1 | −91.2 | −81.1 | 14.6 | −−− |
| trans−2 a | −91.9 | −−− | −−− | −−− |
| trans−2 b | −92.1 | −−− | −−− | −−− |
| trans−3 a | −95.9 | −86.1 | 8.6 | −−− |
| trans−3 b | −95.0 | −−− | −−− | −−− |
| trans−4 a | −91.3 | −−− | −−− | −−− |
| trans−4 b | −91.2 | −−− | −−− | −−− |
| e-face a | −96.5 | −86.3 | 9.3 | −−− |
| e-face b | −96.1 | −−− | −−− | −−− |
| e-edge | −96.1 | −−− | −−− | −−− |
| cis−3 a | −79.9 | −−− | −−− | −−− |
| cis−3 b | −79.7 | −−− | −−− | −−− |
| cis−2 a | −64.9 | −−− | −−− | −−− |
| cis−2 b | −77.9 | −67.8 | 32.6 | −−− |
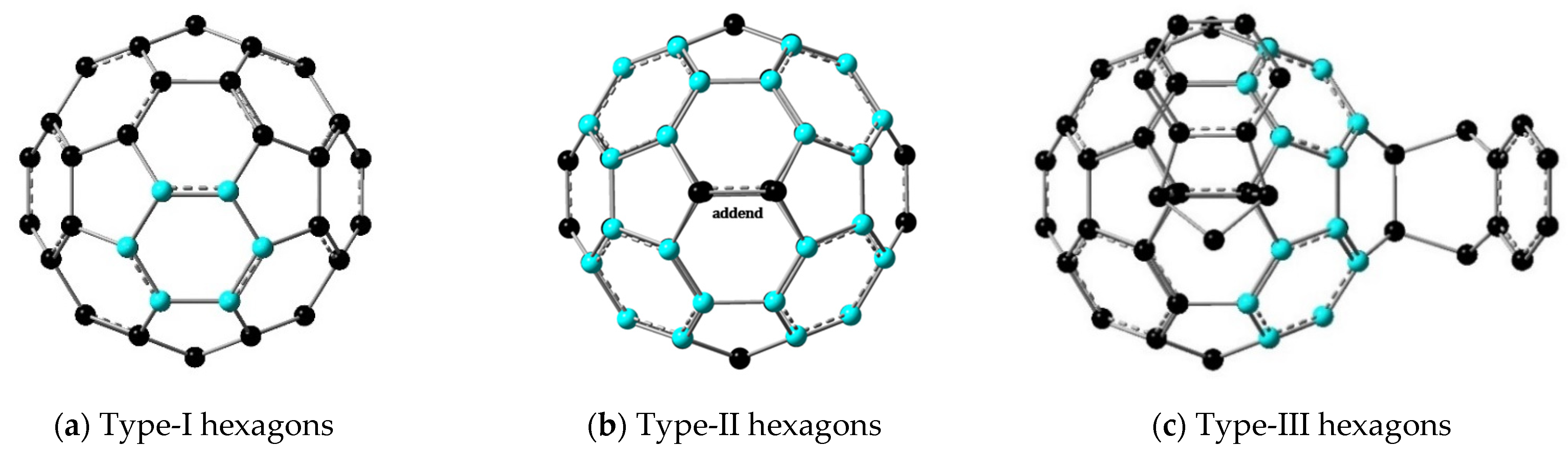
| Molecule | <EN> | <GEO> | <HOMA> | Hexagon Type (Qty.) 1 |
|---|---|---|---|---|
| C60 2 | 0.267 | 0.529 | 0.204 | I (20) |
| C70 | 0.219 | 0.462 | 0.319 | Ia (10) |
| 0.473 | 0.705 | −0.177 | Ib (10) | |
| 0.253 | 0.259 | 0.489 | Ic (5) | |
| IC60MA | 0.162 | 0.366 | 0.471 | II (4) |
| AC60MA 3 | 0.158 | 0.368 | 0.474 | II (4) |
| AC70MA isomer a | 0.126 | 0.299 | 0.575 | IIa (2) |
| 0.330 | 0.585 | 0.085 | IIb (2) | |
| AC70MA isomer b | 0.118 | 0.306 | 0.576 | IIa (2) |
| 0.178 | 0.199 | 0.624 | IIc (2) | |
| AIC60BA trans−1 | 0.160 | 0.354 | 0.486 | II (8) |
| AIC60BA trans−2 a | 0.163 | 0.363 | 0.474 | II (8) |
| AIC60BA trans−2 b | 0.163 | 0.363 | 0.474 | II (8) |
| AIC60BA trans−3 a | 0.168 | 0.368 | 0.464 | II (8) |
| AIC60BA trans−3 b | 0.167 | 0.367 | 0.465 | II (8) |
| AIC60BA trans−4 a | 0.080 | 0.217 | 0.703 | III (1) |
| 0.163 | 0.369 | 0.468 | II (6) | |
| AIC60BA trans−4 b | 0.083 | 0.228 | 0.690 | III (1) |
| 0.166 | 0.377 | 0.457 | II (6) | |
| AIC60BA e-face a | 0.084 | 0.222 | 0.694 | III (2) |
| 0.158 | 0.356 | 0.486 | II (4) | |
| AIC60BA e-face b | 0.086 | 0.232 | 0.682 | III (2) |
| 0.160 | 0.356 | 0.484 | II (4) | |
| AIC60BA e-edge | 0.085 | 0.226 | 0.689 | III (2) |
| 0.159 | 0.358 | 0.483 | II (4) |
| Molecule | ∆solvEel,m (m−xylene)/kJ∙mol−1 |
|---|---|
| Ind | −29.7 (−29.8) |
| Ant | −42.3 (−42.3) |
| C60 | −145.3 (−146.0) |
| C70 | −164.2 (−164.6) |
| IC60MA | −157.3 (−157.4) |
| AC60MA | −166.1 (−166.2) |
| AC70MA | |
| a | −186.4 |
| b | −187.0 (−187.0) |
| AIC60BA 1 | |
| trans−1 | −179.9 |
| trans−2 a | −180.8 |
| trans−2 b | −180.3 |
| trans−3 a | −180.8 |
| trans−3 b | −180.4 |
| trans−4 a | −179.4 |
| trans−4 b | −179.1 |
| e-face a | −180.2 (−180.3) |
| e-face b | −179.6 |
| e-edge | −181.4 |
| cis−3 a | −178.8 |
| cis−3 b | −180.7 |
| cis−2 a | −178.5 |
| cis−2 b | −180.0 |
| Reaction | ∆rEel,m (m−xylene) 1/kJ∙mol−1 | ||
|---|---|---|---|
| R1. C60 + Ind → IC60MA | −98.8 (−98.2) | −105.4 | −77 |
| R2. C60 + Ant → AC60MA | −74.0 (−73.4) | −85.6 | −54 |
| R3. C70 + Ant → AC70MA | |||
| a | −77.1 (−76.7) | −82.5 | −53 |
| b | −71.5 | −−− | −−− |
| R4. IC60MA + Ant → AIC60BA 3 | |||
| trans−1 | −71.6 | −−− | −−− |
| trans−2 a | −73.1 | −−− | −−− |
| trans−2 b | −72.8 | −−− | −−− |
| trans−3 a | −77.1 | −−− | −−− |
| trans−3 b | −75.9 | −−− | −−− |
| trans−4 a | −71.2 | −−− | −−− |
| trans−4 b | −70.7 | −−− | −−− |
| e-face a | −77.1 (−77.1) | −82.5 | −53 |
| e-face b | −76.1 | −−− | −−− |
| e-edge | −78.0 | −−− | −−− |
| cis−3 a | −59.1 | −−− | −−− |
| cis−3 b | −60.8 | −−− | −−− |
| cis−2 a | −43.9 | −−− | −−− |
| cis−2 b | −58.3 | −−− | −−− |
| Molecule | IP/eV | EA/eV | ω/eV |
|---|---|---|---|
| Ind | 8.14 ± 0.01 [51] (7.4) | 0.17 ± 0.03 [52] (−0.1) | 1.1 (0.9) |
| Ant | 7.44 ± 0.01 [53] (6.7) | 0.53 ± 0.02 [54] (1.2) | 1.1 (1.4) |
| C60 | 7.57 ± 0.01 [55] (7.5) | 2.684 ± 0.001 [56] (3.1) | 2.7 (3.1) |
| C70 | 7.36 ± 0.01 [55] (7.4) | 2.76 ± 0.02 [57] (3.1) | 2.8 (3.2) |
| IC60MA | 5.8 [58] (7.1) | 3.2 [58] (2.9) | 3.9 (3.0) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodrigues, D.J.L.; Santos, L.M.N.B.F.; Melo, A.; Lima, C.F.R.A.C. Theoretical Study on the Diels–Alder Reaction of Fullerenes: Analysis of Isomerism, Aromaticity, and Solvation. Organics 2022, 3, 364-379. https://doi.org/10.3390/org3040025
Rodrigues DJL, Santos LMNBF, Melo A, Lima CFRAC. Theoretical Study on the Diels–Alder Reaction of Fullerenes: Analysis of Isomerism, Aromaticity, and Solvation. Organics. 2022; 3(4):364-379. https://doi.org/10.3390/org3040025
Chicago/Turabian StyleRodrigues, Diogo J. L., Luís M. N. B. F. Santos, André Melo, and Carlos F. R. A. C. Lima. 2022. "Theoretical Study on the Diels–Alder Reaction of Fullerenes: Analysis of Isomerism, Aromaticity, and Solvation" Organics 3, no. 4: 364-379. https://doi.org/10.3390/org3040025
APA StyleRodrigues, D. J. L., Santos, L. M. N. B. F., Melo, A., & Lima, C. F. R. A. C. (2022). Theoretical Study on the Diels–Alder Reaction of Fullerenes: Analysis of Isomerism, Aromaticity, and Solvation. Organics, 3(4), 364-379. https://doi.org/10.3390/org3040025