Unveiling the Different Reactivity of Bent and Linear Three-Atom-Components Participating in [3 + 2] Cycloaddition Reactions
Abstract
:1. Introduction
2. Computational Methods
3. Results and Discussion
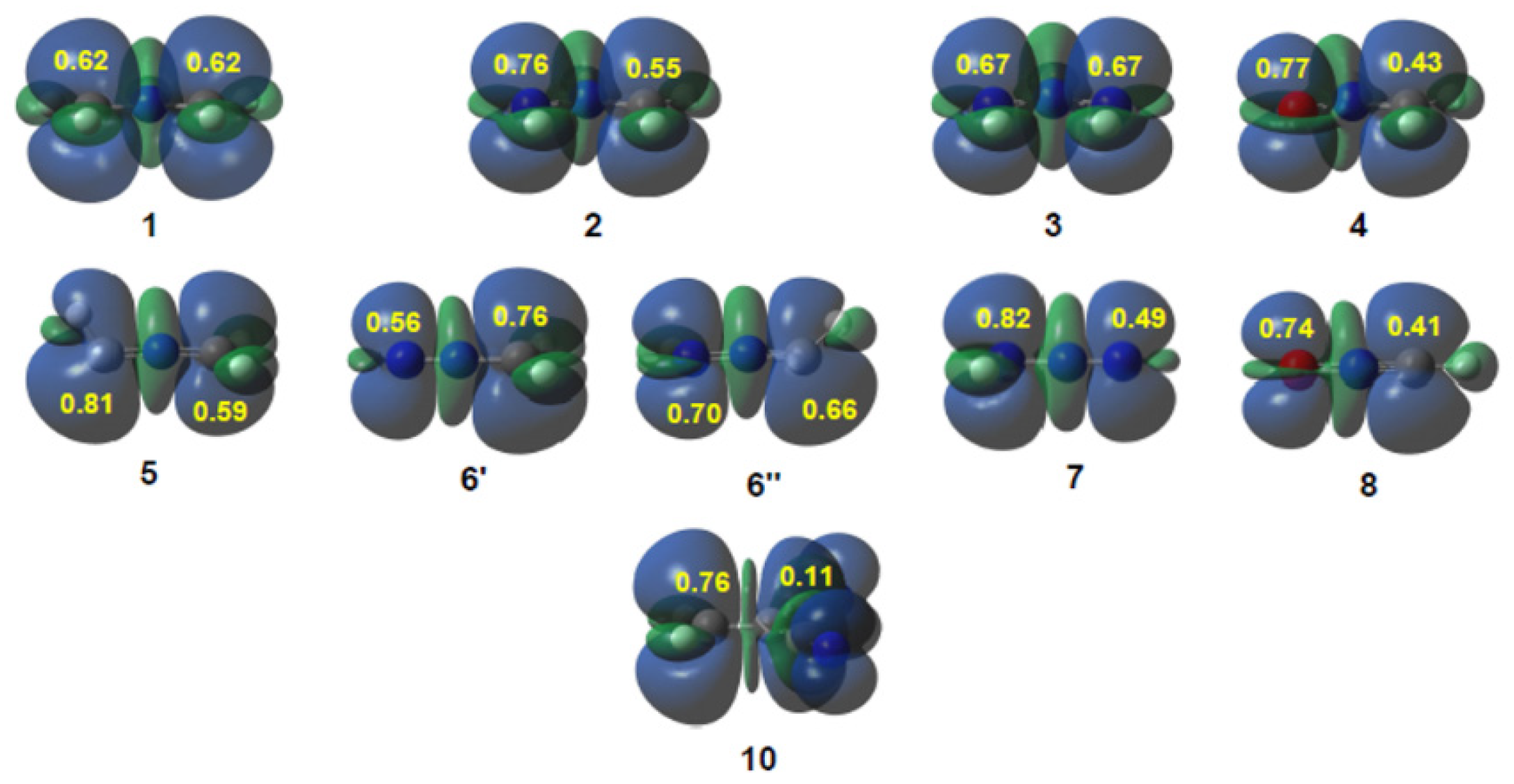
3.1. Comparison of the Electronic Structures of B-TACs and L-TACs
3.2. Analysis of CDFT Reactivity Indices at the Reagents
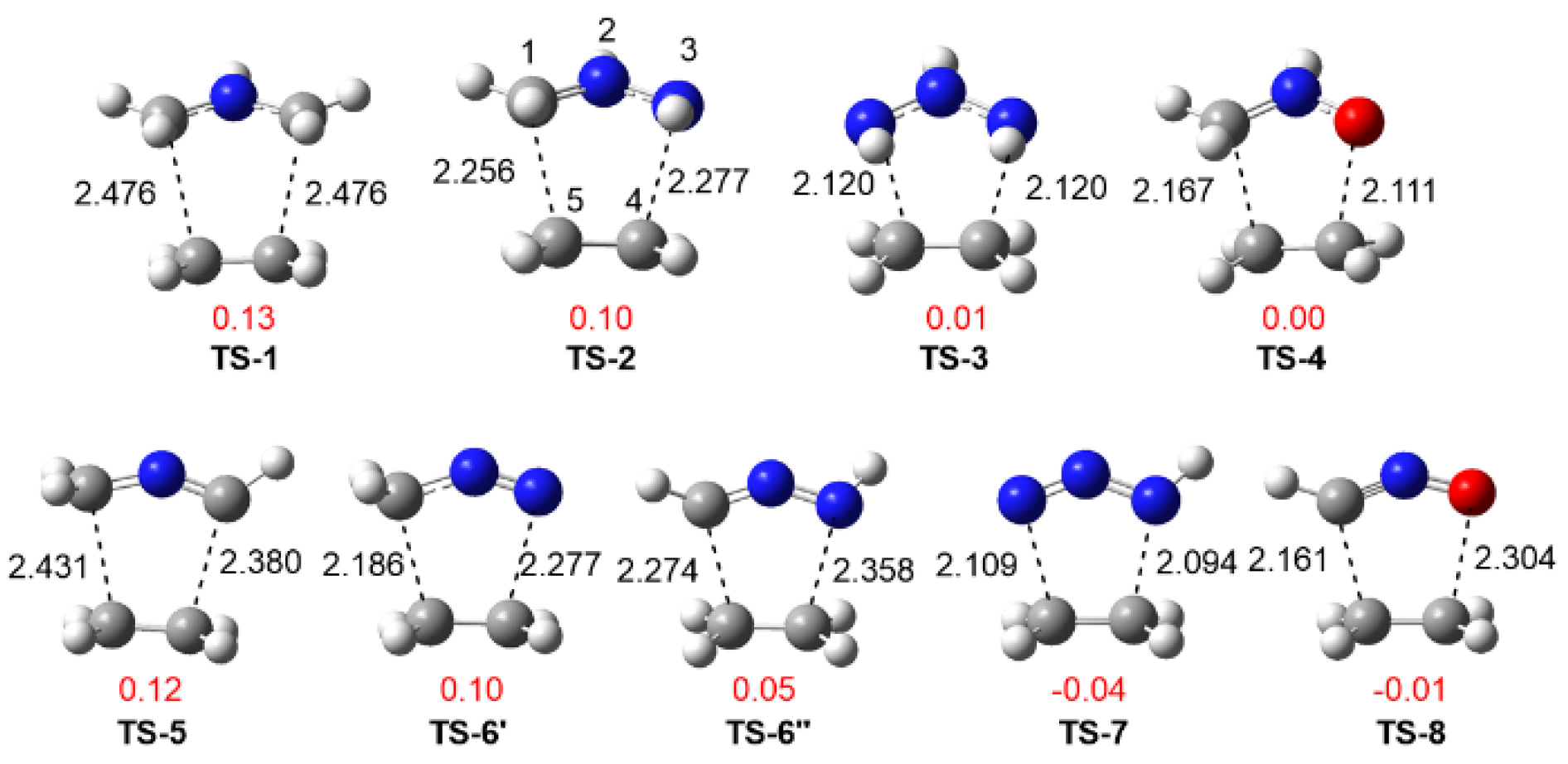
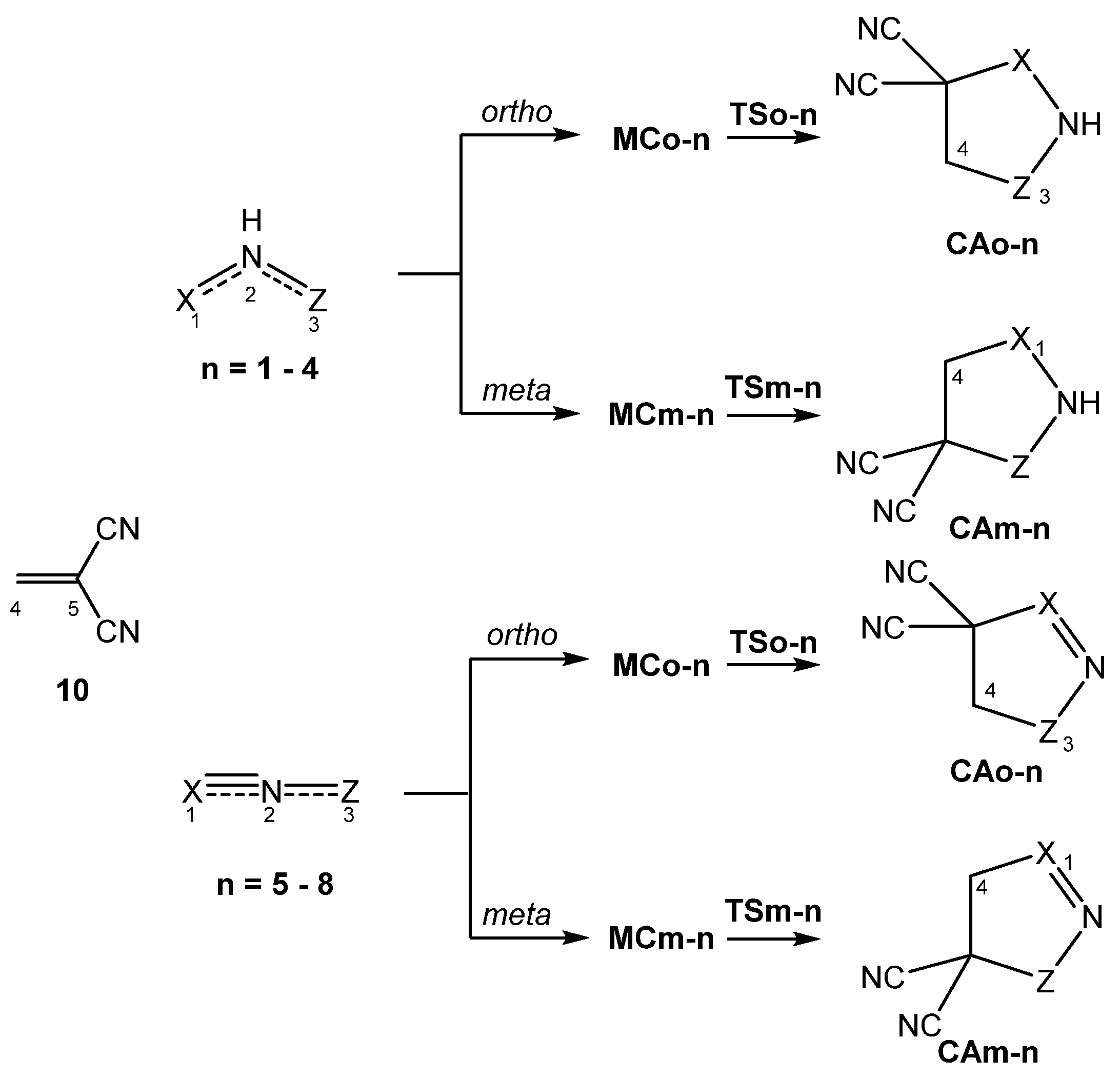
3.3. Study of the Reaction Paths Associated with the 32CA Reactions of TACs 1–8 with Ethylene 9 and with the Electrophilic DCE 10
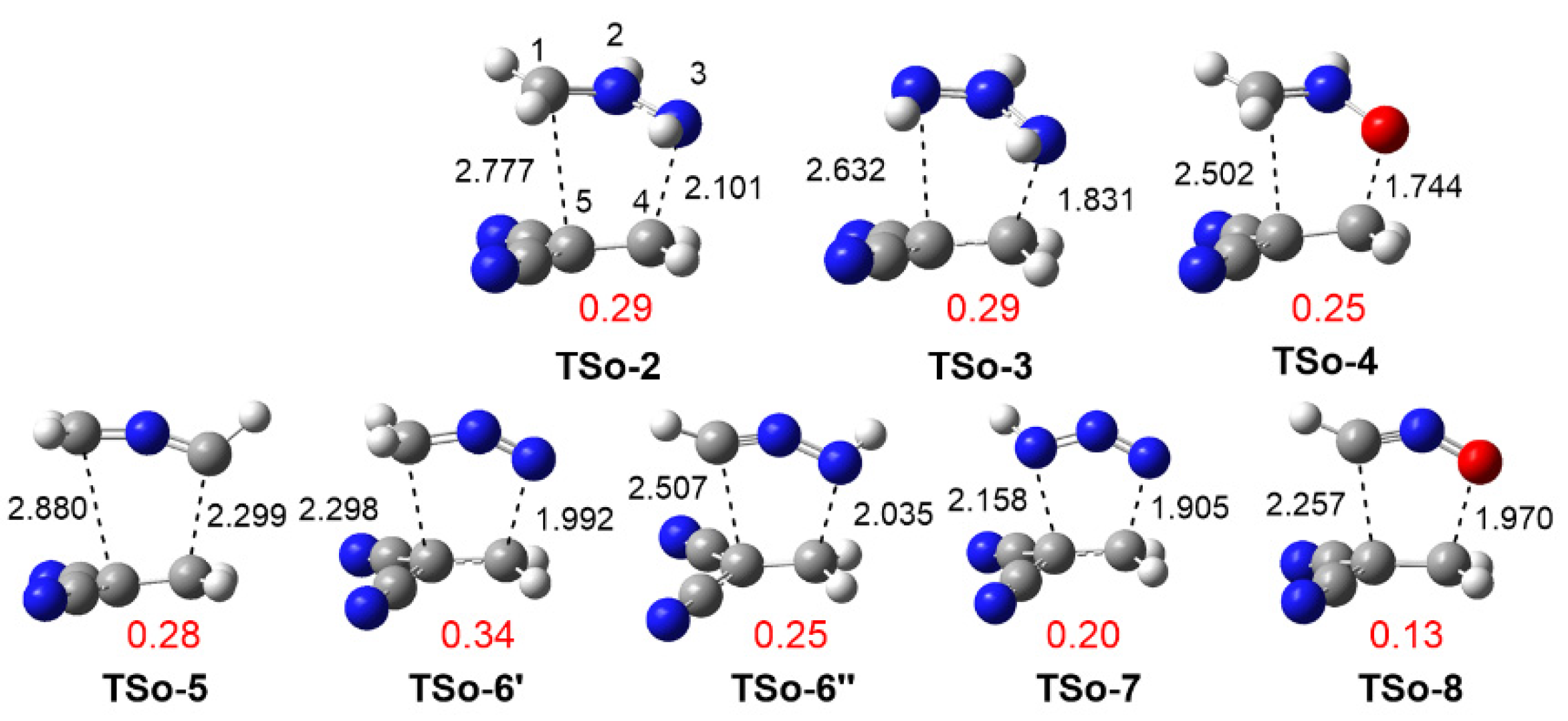
3.3.1. Study of the 32CA Reactions with Ethylene 9
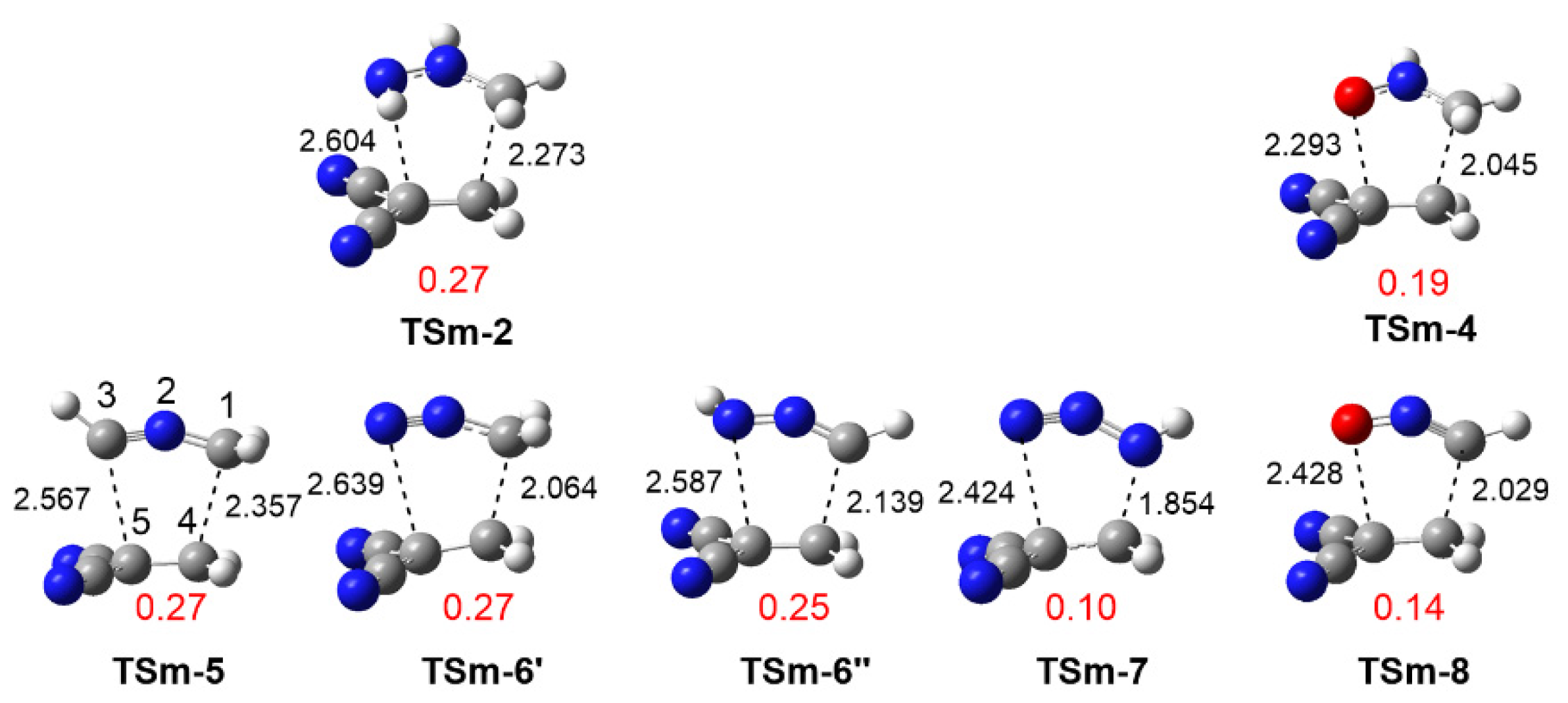
3.3.2. Study of the 32CA Reactions with Electrophilic DCE 10
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Moss, G.P.; Smith, P.A.S.; Tavernier, D. Glossary of class names of organic compounds and reactivity intermediates based on structure. Pure Appl. Chem. 1995, 67, 1307. [Google Scholar] [CrossRef]
- Carruthers, W. Cycloaddition Reactions in Organic Synthesis; Pergamon: Oxford, UK, 1990. [Google Scholar]
- Padwa, A. 1,3-Dipolar Cycloaddition Chemistry; Wileynterscience: New York, NY, USA, 1984; Volume 1–2. [Google Scholar]
- Domingo, L.R. Molecular electron density theory: A modern view of reactivity in organic chemistry. Molecules 2016, 21, 1319. [Google Scholar] [CrossRef]
- Ríos-Gutiérrez, M.; Domingo, L.R. Unravelling the mysteries of the [3 + 2] cycloaddition reactions. Eur. J. Org. Chem. 2019, 267–282. [Google Scholar] [CrossRef]
- Domingo, L.R.; Sáez, J.A. Understanding the mechanism of polar Diels–Alder reactions. Org. Biomol. Chem. 2009, 7, 3576–3583. [Google Scholar] [CrossRef]
- Domingo, L.R. A new C-C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415–32428. [Google Scholar] [CrossRef] [Green Version]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. How does the global electron density transfer diminish activation energies in polar cycloaddition reactions? A Molecular Electron Density Theory study. Tetrahedron 2017, 73, 1718–1724. [Google Scholar] [CrossRef]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. A Molecular Electron Density Theory Study of the Reactivity of Tetrazines in Aza-Diels-Alder Reactions. RSC Adv. 2020, 10, 15394–15405. [Google Scholar] [CrossRef] [Green Version]
- Domingo, L.R.; Kula, K.; Ríos-Gutiérrez, M. Unveiling the Reactivity of Cyclic Azomethine Ylides in [3 + 2] Cycloaddition Reactions within the Molecular Electron Density Theory. Eur. J. Org. Chem. 2020, 5938–5948. [Google Scholar] [CrossRef]
- Houk, K.N.; González, J.; Li, Y. Pericyclic reaction transition states: Passions and punctilios, 1935–1995. Acc. Chem. Res. 1995, 28, 81–90. [Google Scholar] [CrossRef]
- Sustmann, R.; Trill, H. Substituent Effects in 1,3-Dipolar Cycloadditions of Phenyl Azid. Angew. Chem. Int. Ed. Engl. 1972, 11, 838–840. [Google Scholar] [CrossRef]
- Domingo, L.R.; Mar Ríos-Gutiérrez, M.; Silvi, B.; Pérez, P. The Mysticism of Pericyclic Reactions: A Contemporary Rationalisation of Organic Reactivity Based on Electron Density Analysis. Eur. J. Org. Chem. 2018, 2018, 1107–1120. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Hybrid Meta Density Functional Theory Methods for Thermochemistry, Thermochemical Kinetics, and Noncovalent Interactions: The MPW1B95 and MPWB1K Models and Comparative Assessments for Hydrogen Bonding and van der Waals Interactions. J. Phys. Chem. A 2004, 108, 6908–6918. [Google Scholar] [CrossRef]
- Hehre, M.J.; Radom, L.; Schleyer, P.v.R.; Pople, J. Ab Initio Molecular Orbital Theory; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Schlegel, H.B. Optimization of equilibrium geometries and transition structures. J. Comput. Chem. 1982, 3, 214–218. [Google Scholar] [CrossRef]
- Schlegel, H.B. Modern Electronic Structure Theory; Yarkony, D.R., Ed.; World Scientific Publishing: Singapore, 1994. [Google Scholar]
- Fukui, K. Formulation of the reaction coordinate. J. Phys. Chem. 1970, 74, 4161–4163. [Google Scholar] [CrossRef]
- González, C.; Schlegel, H.B. Reaction path following in mass-weighted internal coordinates. J. Phys. Chem. 1990, 94, 5523–5527. [Google Scholar] [CrossRef]
- González, C.; Schlegel, H.B. Improved algorithms for reaction path following: Higher-order implicit algorithms. J. Chem. Phys. 1991, 95, 5853–5860. [Google Scholar] [CrossRef] [Green Version]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular-systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
- Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
- Parr, R.G.; Yang, W. Density Functional Theory of Atoms and Molecules; Oxford University Press: New York, NY, USA, 1989. [Google Scholar]
- Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the conceptual density functional indices to organic chemistry reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef] [Green Version]
- Parr, R.G.; Szentpaly, L.V.; Liu, S. Electrophilicity index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
- Parr, R.G.; Pearson, R.G. Absolute hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
- Domingo, L.R.; Chamorro, E.; Pérez, P. Understanding the reactivity of captodative ethylenes in polar cycloaddition reactions. A theoretical study. J. Org. Chem. 2008, 73, 4615–4624. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, 1133–1138. [Google Scholar] [CrossRef] [Green Version]
- Domingo, L.R.; Pérez, P.; Sáez, J.A. Understanding the local reactivity in polar organic reactions through electrophilic and nucleophilic Parr functions. RSC Adv. 2013, 3, 1486–1494. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Fox, D.J.; et al. (Eds.) Gaussian 16; Revision, A.03; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Noury, S.; Krokidis, X.; Fuster, F.; Silvi, B. Computational tools for the electron localization function topological analysis. Comput. Chem. 1999, 23, 597–604. [Google Scholar] [CrossRef]
- Gauss View; Version 6.0; Dennington, R.; Keith, T.A.; Millam, J.M. (Eds.) Semichem Inc.: Shawnee Mission, KS, USA, 2016. [Google Scholar]
- Huisgen, R. 1,3-Dipolar Cycloadditions. Proc. Chem. Soc. 1961, 2, 357. [Google Scholar]
- Chamorro, E.; Duque-Noreña, M.; Gutierrez-Sánchez, N.; Rincón, E.; Domingo, L.R. A close look to the oxaphosphetane formation along the Wittig reaction: A [2 + 2] cycloaddition? J. Org. Chem. 2020, 85, 6675–6686. [Google Scholar] [CrossRef] [PubMed]
- Aurell, M.J.; Domingo, L.R.; Pérez, P.; Contreras, R. A theoretical study on the regioselectivity of 1,3-dipolar cycloadditions using DFT-based reactivity indexes. Tetrahedron 2004, 60, 11503–11509. [Google Scholar] [CrossRef]
- Hammond, G.S. A Correlation of Reaction Rates. J. Am. Chem. Soc. 1955, 77, 334–338. [Google Scholar] [CrossRef]
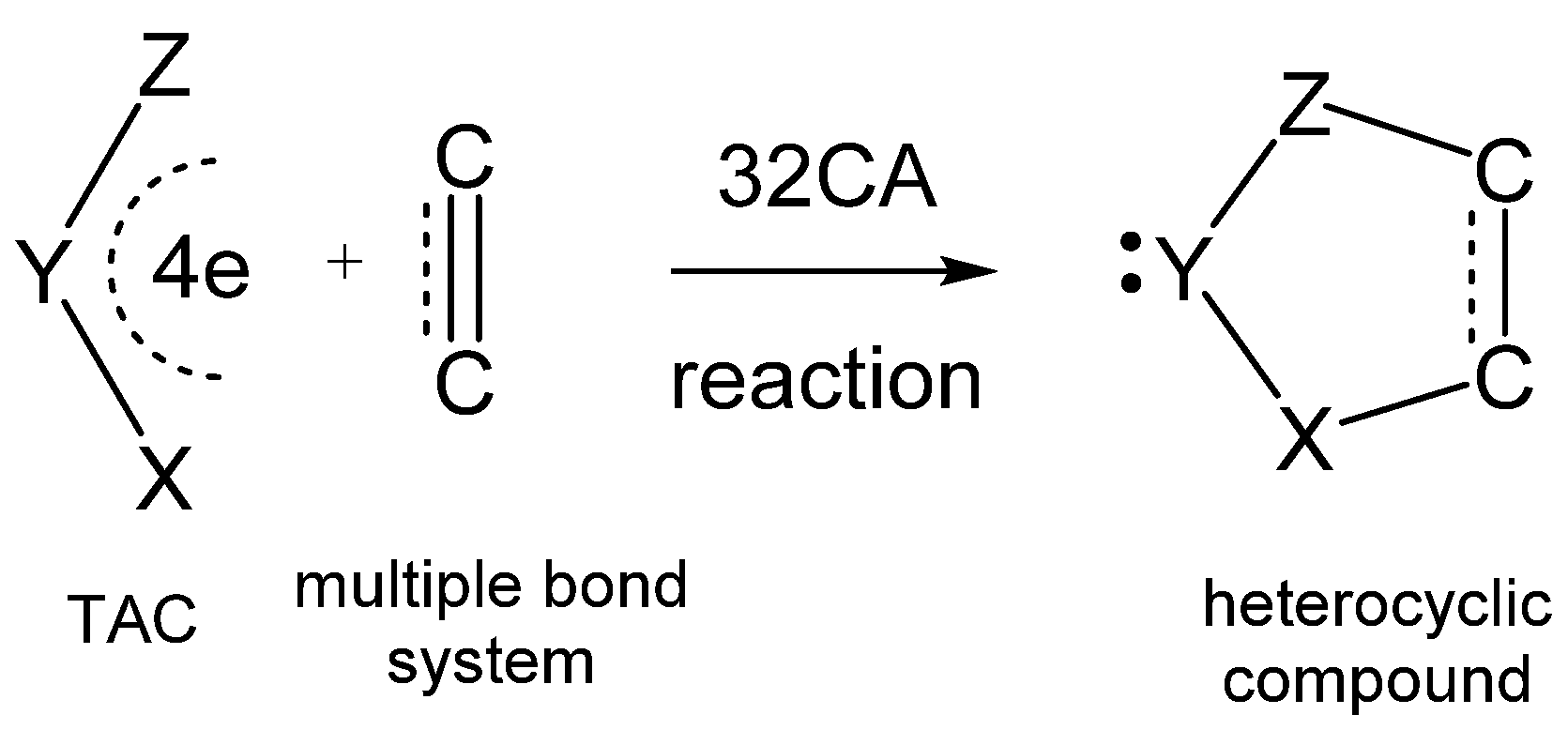


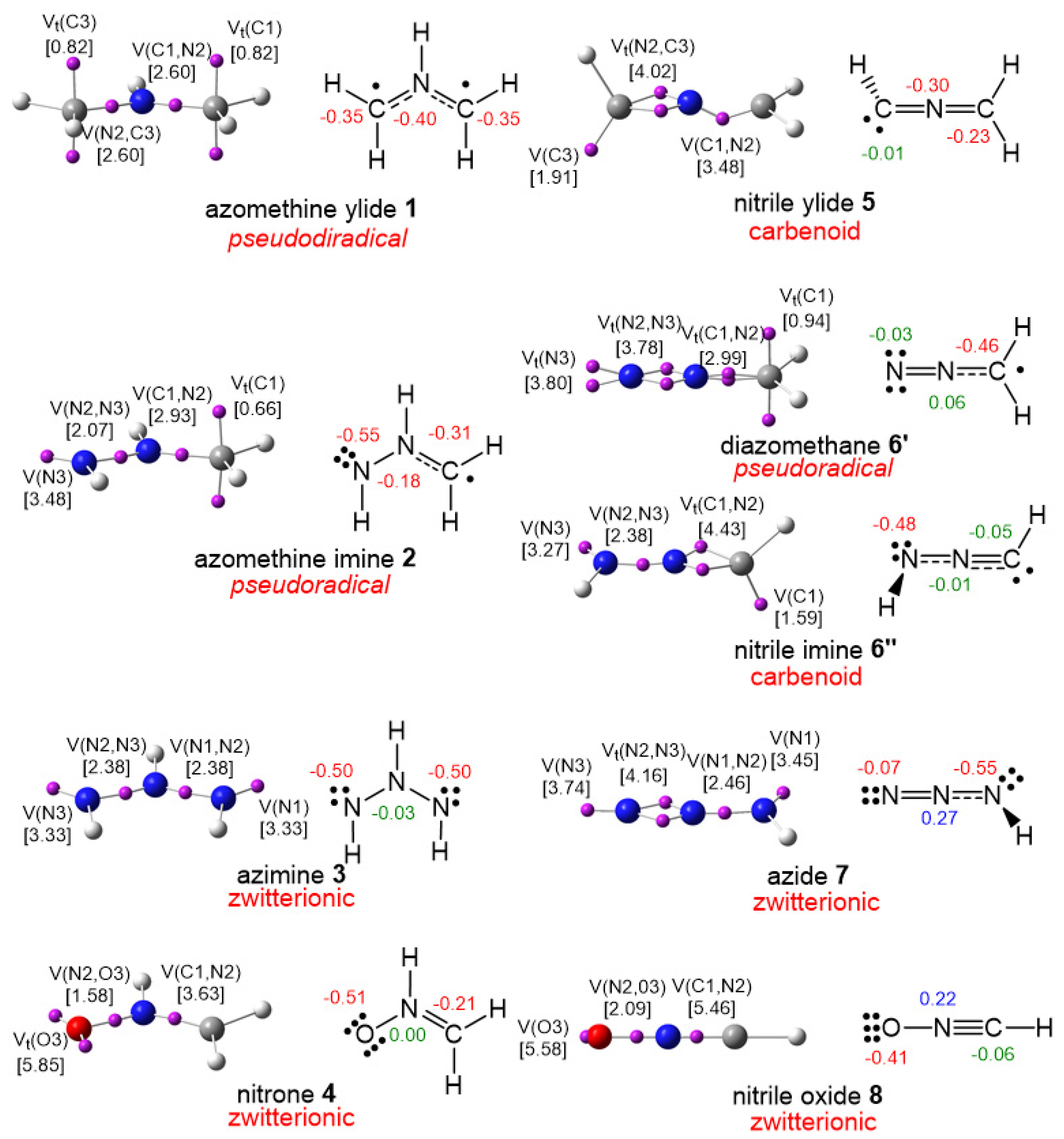

| B-TACs | L-TACs | ||||
|---|---|---|---|---|---|
| X1−N2−Z3 | Name | X1−N2−Z3 | Name | ||
| 1 | H2C−NH−CH2 | azomethine ylide | 5 | H2C−N−CH | nitrile ylide |
| 2 | H2C−NH−NH | azomethine imine | 6′ | H2C−N−N | diazomethane |
| 6″ | HC−N−NH | nitrile imine | |||
| 3 | NH−NH−NH | azimine | 7 | NH−N−N | azide |
| 4 | H2C−NH−O | nitrone | 8 | HC−N−O | nitrile oxide |
| Structure | μ | η | ω | N |
|---|---|---|---|---|
| TAC 1 | −1.81 | 4.47 | 0.37 | 5.07 |
| TAC 2 | −2.70 | 5.02 | 0.72 | 3.92 |
| TAC 3 | −3.70 | 5.62 | 1.22 | 2.61 |
| TAC 4 | −3.43 | 5.54 | 1.06 | 2.92 |
| TAC 5 | −2.90 | 5.45 | 0.77 | 3.50 |
| TAC 6′ | −3.64 | 4.73 | 1.40 | 3.11 |
| TAC 6″ | −3.54 | 5.87 | 1.07 | 2.64 |
| TAC 7 | −4.24 | 6.54 | 1.37 | 1.62 |
| TAC 8 | −3.40 | 7.94 | 0.73 | 1.75 |
| Ethylene 9 | −3.37 | 7.77 | 0.73 | 1.87 |
| DCE 10 | −5.64 | 5.65 | 2.82 | 0.65 |
| TAC | MC-n | TS-n | CA-n |
|---|---|---|---|
| 1 | −1.8 | 0.1 | −77.8 |
| 2 | −2.3 | 6.4 | −59.4 |
| 3 | −2.9 | 15.5 | −43.2 |
| 4 | −3.3 | 11.8 | −41.0 |
| 5 | −1.2 | 7.2 | −81.5 |
| 6′ | −1.0 | 16.3 | −42.6 |
| 6″ | −0.8 | 8.0 | −68.9 |
| 7 | −3.1 | 21.1 | −30.0 |
| 8 | −1.5 | 15.6 | −50.8 |
| ortho | meta | |||||
|---|---|---|---|---|---|---|
| TAC | MCo-n | TSo-n | CAo-n | MCm-n | TSm-n | CAm-n |
| 1 pdr | - | - | −76.5 | |||
| 2 pmr | −8.3 | −7.4 | −49.6 | −5.9 | −4.6 | −53.6 |
| 3 zw | −4.0 | 5.9 | −36.9 | |||
| 4 zw | −7.8 | −0.3 | −36.5 | −9.0 | 5.1 | −31.8 |
| 5 cb | −6.9 | −6.3 | −76.1 | −4.2 | −1.8 | −73.8 |
| 6′ pmr | −4.0 | 11.3 | −34.2 | −2.6 | 4.6 | −31.2 |
| 6″ cb | −5.2 | 1.0 | −60.9 | −4.8 | 0.2 | −61.1 |
| 7 zw | −2.5 | 21.9 | −19.0 | −5.6 | 16.4 | −18.6 |
| 8 zw | −4.0 | 15.3 | −38.3 | −1.5 | 13.6 | −38.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ríos-Gutiérrez, M.; Domingo, L.R.; Ghodsi, F. Unveiling the Different Reactivity of Bent and Linear Three-Atom-Components Participating in [3 + 2] Cycloaddition Reactions. Organics 2021, 2, 274-286. https://doi.org/10.3390/org2030014
Ríos-Gutiérrez M, Domingo LR, Ghodsi F. Unveiling the Different Reactivity of Bent and Linear Three-Atom-Components Participating in [3 + 2] Cycloaddition Reactions. Organics. 2021; 2(3):274-286. https://doi.org/10.3390/org2030014
Chicago/Turabian StyleRíos-Gutiérrez, Mar, Luis R. Domingo, and Fatemeh Ghodsi. 2021. "Unveiling the Different Reactivity of Bent and Linear Three-Atom-Components Participating in [3 + 2] Cycloaddition Reactions" Organics 2, no. 3: 274-286. https://doi.org/10.3390/org2030014
APA StyleRíos-Gutiérrez, M., Domingo, L. R., & Ghodsi, F. (2021). Unveiling the Different Reactivity of Bent and Linear Three-Atom-Components Participating in [3 + 2] Cycloaddition Reactions. Organics, 2(3), 274-286. https://doi.org/10.3390/org2030014









