Next Article in Journal
Pd-Based Polysaccharide Hydrogels as Heterogeneous Catalysts for Oxidation of Aromatic Alcohols
Next Article in Special Issue
The Role of the Catalyst on the Reactivity and Mechanism in the Diels–Alder Cycloaddition Step of the Povarov Reaction for the Synthesis of a Biological Active Quinoline Derivative: Experimental and Theoretical Investigations
Previous Article in Journal / Special Issue
Application of β-Phosphorylated Nitroethenes in [3+2] Cycloaddition Reactions Involving Benzonitrile N-Oxide in the Light of a DFT Computational Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Organics
Volume 2
Issue 1
10.3390/org2010004
organics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Theoretical Insight into the Reversal of Chemoselectivity in Diels-Alder Reactions of α,β-Unsaturated Aldehydes and Ketones Catalyzed by Brønsted and Lewis Acids

by
Lakhdar Benhamed
,
Sidi Mohamed Mekelleche
* and
Wafaa Benchouk
Laboratory of Applied Thermodynamics and Molecular Modeling, Department of Chemistry, Faculty of Science, University of Tlemcen, PB 119, Tlemcen 13000, Algeria
*
Author to whom correspondence should be addressed.
Organics 2021, 2(1), 38-49; https://doi.org/10.3390/org2010004
Submission received: 29 December 2020 / Revised: 2 February 2021 / Accepted: 2 March 2021 / Published: 5 March 2021
(This article belongs to the Special Issue Cycloaddition Reaction in Organic Synthesis)
Browse Figures
Versions Notes

Abstract

:
Experimentally, a reversal of chemoselectivity has been observed in catalyzed Diels–Alder reactions of α,β-unsaturated aldehydes (e.g., (2E)-but-2-enal) and ketones (e.g., 2-hexen-4-one) with cyclopentadiene. Indeed, using the triflimidic Brønsted acid Tf2NH as catalyst, the reaction gave a Diels–Alder adduct derived from α,β-unsaturated ketone as a major product. On the other hand, the use of tris(pentafluorophenyl)borane B(C6F5)3 bulky Lewis acid as catalyst gave mainly the cycloadduct of α,β-unsaturated aldehyde as a major product. Our aim in the present work is to put in evidence the role of the catalyst in the reversal of the chemoselectivity of the catalyzed Diels–Alder reactions of (2E)-but-2-enal and 2-Hexen-4-one with cyclopentadiene. The calculations were performed at the ωB97XD/6-311G(d,p) level of theory and the solvent effects of dichloromethane were taken into account using the PCM solvation model. The obtained results are in good agreement with experimental outcomes.

1. Introduction

Cycloadditions are one of the strongest bond-forming reactions to prepare (hetero)cyclic molecules in organic synthesis [1,2,3,4,5,6,7,8,9,10]. Their usefulness arises from their versatility and remarkable selectivity. Many synthetic routes to cyclic compounds are made possible through Diels–Alder (DA) reactions, which can involve a large variety of dienes and dienophiles [6,11,12]. In addition, various DA reactions have been studied theoretically using computational chemistry tools [13,14,15,16,17,18,19,20,21]. Notably the molecular electron density theory (MEDT) [22], proposed by Domingo in 2016, has recently become an important tool for the mechanistic study of cycloaddition reactions, about which an important number of papers were published in the last few years [23,24,25,26,27,28,29,30,31,32]. According to MEDT, changes in the electron density are responsible for the feasibility of an organic reaction in contrast to the frontier molecular orbital (FMO) theory [33], which uses molecular orbital interactions. Moreover, several quantum-chemical tools are used in MEDT, namely, reactivity indices derived from the conceptual density functional theory (CDFT) [34,35], the topological analysis of the electron localization function (ELF) [36], and the quantum theory of atoms in molecules (QTAIM) [37], to rigorously study organic chemical reactivity on the basis of electron density.
In order to make the cycloaddition feasible, various catalysts are introduced in reactions. Lewis acid (LA) and Brønsted acid (BA) catalysts [38,39,40,41,42] considerably extend the useful scope of DA reactions, enhancing the reaction rate and leading to significant changes in chemo-, regio-, and stereo-selectivities in comparison with the uncatalyzed process [43,44]. A large number of experimental works has been carried out to understand the effects of LA catalysts on the selectivity and the nature of molecular mechanisms of DA reactions [45,46,47,48]. As acidity of the BA can promote highly selectivity in DA cycloadditions, many works on this topic were also published [49,50,51,52,53,54]. Of note is that the design and development of powerful catalysts is one of the ongoing challenges in modern synthetic chemistry and is very important for the synthesis of natural products, pharmaceuticals, and agrochemicals [55,56,57,58].
In 2005, Yamamoto et al. [59] reported a famous work showing high chemoselectivity in the DA cycloaddition of α,β-unsaturated aldehydes 1 and α,β-unsaturated ketones 2 with cyclopentadiene (Cp), where an unexpected reversal of chemoselectivity, according to the choice of the acid catalyst, was observed (Scheme 1).
When a strong BA, such as Tf2NH, was used as a catalyst, the DA adduct derived from the α,β-unsaturated ketone was obtained as a major product. However, when a bulky LA, such as B(C6F5)3, was used as a catalyst, the cycloadduct derived from the α,β-unsaturated aldehyde was the major product. Yamamoto et al. [59] rationalized this reversal of chemoselectivity by the choice of the acid catalyst by consideration of the basicity of the electrophile and the steric hindrance of the acid catalyst. According to the experimentalist, a bulky LA such as B(C6F5)3 preferentially coordinates to the sterically less demanding α,β-unsaturated aldehyde, whereas aBA could be regarded as the smallest LA, which would be insensitive to the steric effect. Therefore, a BA selectively coordinates a more basic carbonyl group such as α,β-unsaturated ketone. To the best of our knowledge, the chemoselectivity between LA and BA on this type of DA reaction has not been studied theoretically. Our aim in this contribution is to explore the competitive reactions between the aldehyde 1 and ketone 2 with Cp catalyzed by BA and LA catalysts to shed light on the origin of catalytic efficiencies and chemoselectivity details of these reactions using DFT calculations. The competitive chemoselective pathways of this studied reaction are illustrated in Scheme 2.

2. Computational Details

All DFT calculations were carried out with the DFT/ωB97XD functional [60] combined with the 6-311G(d,p) basis set [61] implemented in the Gaussian 09 suite of programs [62]. This level of theory has shown to be suitable for geometry optimization and electronic property analysis of (3 + 2) cycloaddition and (4 + 2) DA reactions [17,63,64]. Optimizations were performed using the Berny analytical gradient optimization method [65,66] and the stationary points were characterized by frequency computations in order to verify that the transition states had one and only one imaginary frequency. Solvent effects were analyzed by optimizing the geometries in dichloromethane (DCM) through the polarizable continuum model (PCM) developed in the framework of the self-consistent reaction field (SCRF) [67,68,69,70]. The global electron density transfer (GEDT) [71] was computed as a sum of the natural atomic charge, obtained by a natural population analysis (NPA) [72,73] of the atoms belonging to each framework (f) at the TSs, i.e., GEDT (f) = ∑ q ∈ f q . Global reactivity indices derived from CDFT [74,75,76,77,78,79,80,81], namely the electrophilicity index ω and the nucleophilicity index N, were calculated using the following expressions [74]:
ω = μ 2 2 η N ≈ ε HOMO ( Nucleophile ) − ε HOMO ( TCE ) μ ≈ ( ε HOMO + ε LUMO ) / 2 η ≈ ε LUMO − ε HOMO
where TCE = tetracyanoethylene.

3. Results and Discussion

In order to explain the role of the catalyst on the reversal of the chemoselectivity of the catalyzed DA cycloaddition reaction of the α,β–unsaturated aldehyde 1 and α,β–unsaturated ketone 2 with Cp, all the chemoselective pathways were investigated (Scheme 2). The studied DA reactions were:
(i)
1 + Cp in the absence and presence of the BA/LA catalysts; and
(ii)
2 + Cp in the absence and presence of the BA/LA catalysts.
The quantum chemical calculations are based on the analysis of CDFT reactivity indices and calculated activation energies and free energies. The polarity of the cycloaddition processes is quantified by GEDT calculations at the located TSs.

3.1. Analysis of the Global CDFT-Based Reactivity Indexes

Global indexes defined in the context of the CDFT [34,35], namely, the electronic chemical potential µ, chemical hardness η, global electrophilicity ω, and nucleophilicity N, were calculated in terms of the one electron energies of the HOMO/LUMO frontier molecular orbitals at the ground states of the reactants in gas phase. The following table recapitulates the global reactivity indices for uncatalyzed reactants 1 and 2, BA-catalyzed reactants 1-BA and 2-BA, and LA-catalyzed reactants 1-LA and 2-LA (Table 1).
It turned out that the electronic chemical potential µ [34,82] of Cp, −0.123 eV, was higher than that of the uncatalyzed and catalyzed aldehyde and ketone, indicating that along the cycloaddition reaction the electron density will flux from the diene Cp to the dienophile aldehyde/ketone, being classified as the forward electron density flux (FEDF) [83]. The electrophilicity ω index [35] of Cp, 0.58 eV, being classified as a weak electrophile, was lower than that of uncatalyzed and catalyzed aldehyde and ketone. In the absence of catalysts, aldehyde 1 (ω = 1.02 eV) and ketone 2 (ω = 0.94 eV) can be classified as moderate electrophiles [74]. By introducing the BA catalyst, the electrophilicity of the dienophiles increased. It became 1.52 eV for BA-catalyzed aldehyde 1-BA and 1.40 eV for BA-catalyzed ketone 2-BA. By substituting the BA catalyst by the LA catalyst, the electrophilicities increased and reached 2.05 eV for LA-catalyzed aldehyde 1-LA and 1.89 eV for LA-catalyzed ketone 2-LA, which made them strong electrophiles although the aldehyde was predicted to be more electrophile than the ketone in the absence and presence of BA/LA catalysts.
The nucleophilicity N index [84,85] of Cp, 3.63 eV, was higher than that of the uncatalyzed aldehyde 1 (N = 2.56 eV) and ketone 2 (N = 2.76 eV), indicating that Cp acted as a nucleophile and dienophiles 1 and 2 acted as electrophiles. In the presence of BA, the nucleophilicity of the catalyzed aldehyde 1-BA and ketone 2-BA was reduced to 1.36 and 1.60 eV, respectively. Contrariwise, in the presence of LA, the nucleophilicity of the catalyzed aldehyde 1-BA and ketone 2-BA was increased to 2.91 and 2.94 eV, respectively. The difference in electrophilicity, Δω, for the DA reactions (1 + Cp), (1-BA + Cp), and (1-LA + Cp) were 0.44 eV, 0.94 eV, and 1.47 eV, respectively, indicating the largest polarity of the cycloaddition reaction between the aldehyde 1 and Cp corresponded to the 1-LA + Cp catalyzed reaction. The same trends were found for the DA reactions between the ketone 2 and Cp. In conclusion, compared to the uncatalyzed and BA-catalyzed DA reactions, the LA-catalyzed DA reactions were predicted to be the most polar ones.

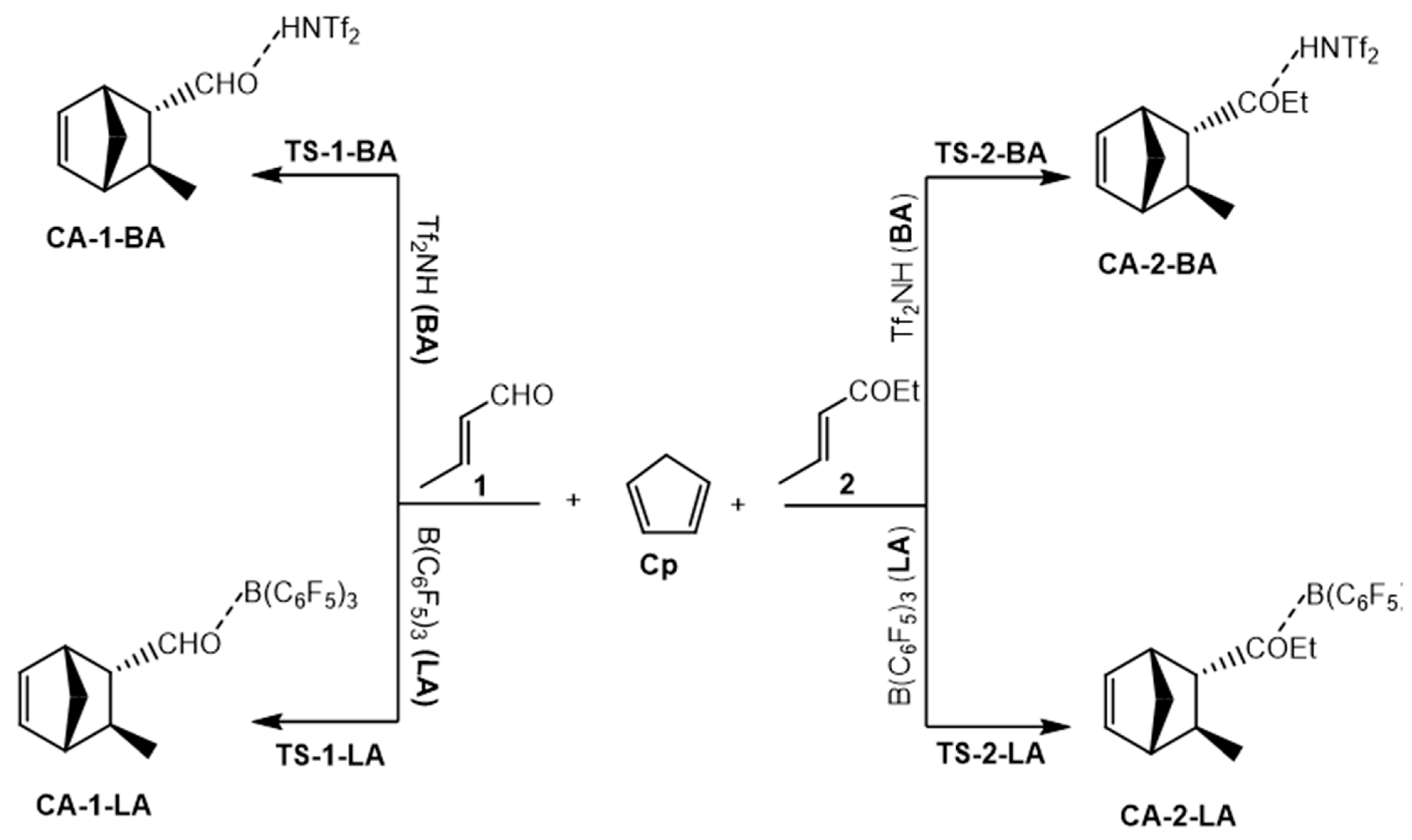
3.2. Analysis of the Potential Energy Surface of the Uncatalyzed and Catalyzed DA Reactions of 1 and 2

3.2.1. Competitive Uncatalyzed DA Reactions of 1 and 2 with Cp

The competitive DA reactions between α,β-unsaturated aldehyde 1 with Cp and between α,β-unsaturated ketone 2 with Cp (Scheme 1) were studied first in the absence of catalysts. The first DA reaction of 1 with Cp led to the formation of the cycloadduct CA-1 via TS-1 and the second DA reaction of 2 with Cp led to the formation of the cycloadduct CA-2 via TS-2. The gas phase energies and Gibbs free energies in DCM at −40 °C (experimental conditions of BA-catalyzed reaction) and at −20 °C (experimental conditions of LA-catalyzed reaction) are summarized in Table 2 and the chemical structures of the gas phase TSs, drawn using GaussView 5.0 [86], are given in Figure 1a.
The calculated activation barriers in gas phase and in DCM show that the second DA reaction (2 + Cp) was kinetically more favored than the first DA reaction (1 + Cp) by 0.9, 0.3, and 0.3 kcal/mol in gas phase, DCM at −40 °C, and DCM at −20 °C, respectively. We also noted that the second DA reaction was found to be more exergonic than the first one by 2.0 and 1.5 kcal/mol in DCM at −40 °C and −20 °C, respectively.

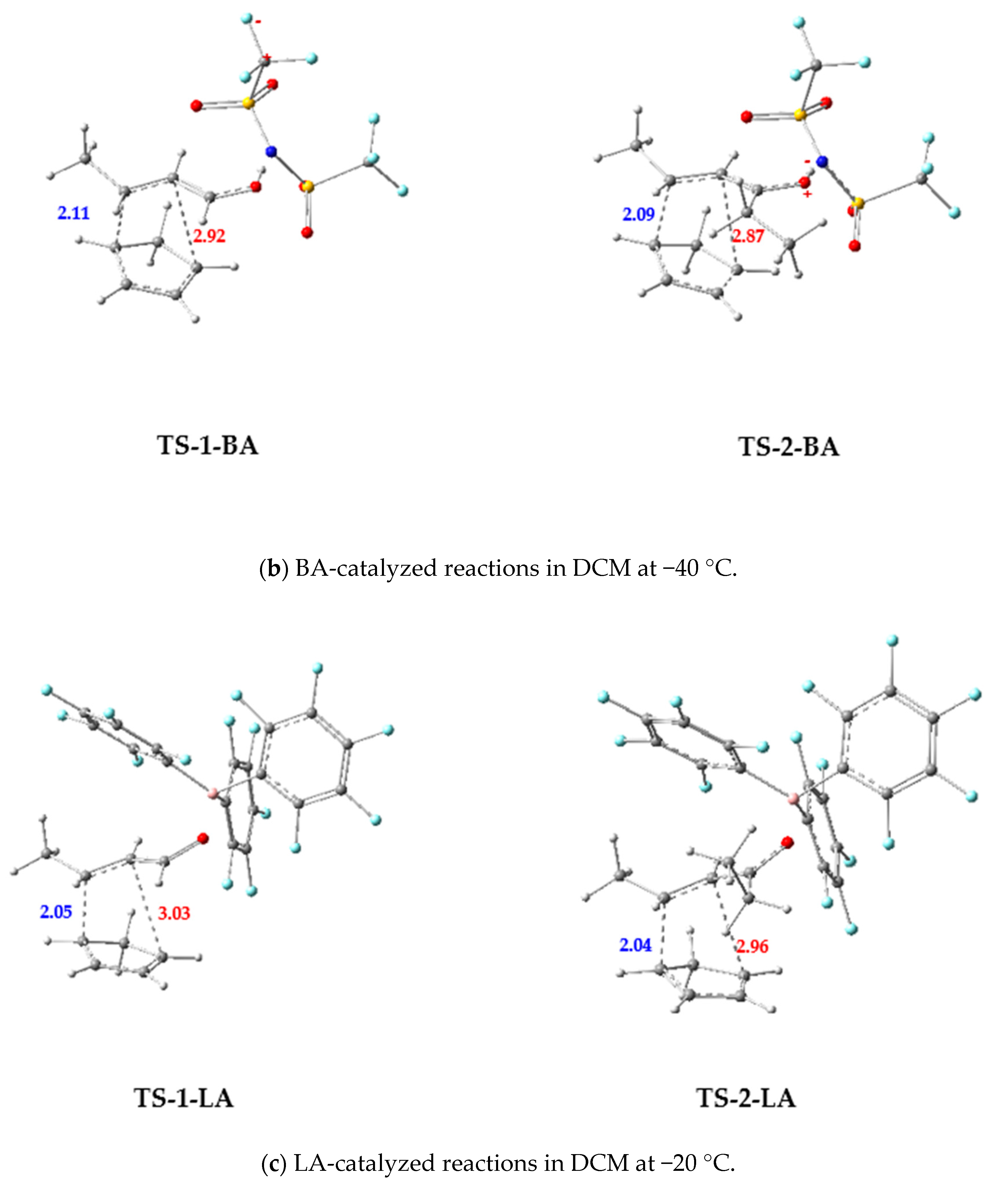
3.2.2. BA-Catalyzed DA Reactions of 1-BA and 2-BA with Cp

In the presence of the triflimide Tf2NH as a BA catalyst, the competitive DA reactions of BA-catalyzed aldehyde 1-BA and BA-catalyzed ketone 2-BA with Cp, giving CA-1-BA via TS-1-BA and CA-2-BA via TS-2-BA respectively, were studied. Calculations were carried out in gas phase and in DCM at −40 °C. The results are summarized in Table 3 and the chemical structures of TSs in solvent are given in Figure 1b.
Introducing Tf2NH as BA catalyst, the calculated activation barriers in gas phase and in DCM at −40 °C show that the second DA reaction (2-BA + Cp) was kinetically more favored than the first DA reaction (1-BA + Cp) by 0.5 and 0.7 kcal/mol in gas phase and DCM at −40 °C, respectively. We also noted that the second DA reaction was found to be more exergonic than the first one by 2.8 kcal/mol in DCM at −40 °C, which is in good agreement with experimental outcomes.

3.2.3. LA-Catalyzed Reaction of 1-LA and 2-LA with Cp

In the presence of the LA tris(pentafluorophenyl)borane B(C6F5)3, catalyzed DA reactions of aldehyde 1-LA and ketone 2-LA with Cp, giving cycloadduct CA-1-LA and CA-2-LA via TS-1-LA and TS-2-LA, respectively, were studied. Calculations were carried out in gas phase and in DCM at −20 °C. The results are summarized in Table 4 and the chemical structures of TSs in solvent are given in Figure 1c.
In opposition to the Tf2NH-catalyzed DA reactions, the B(C6F5)3-catalyzed DA reactions led to a reversed chemoselectivity. Indeed, in DCM at −20 °C, the calculated activation barriers indicate that the activation free energy for the DA reaction 1-LA + Cp, 15.7 kcal/mol, was lower than that of the DA reaction 2-LA + Cp, 16.5 kcal/mol, indicating that chemo pathway involving the catalyzed aldehyde was kinetically more favored than the chemo pathway involving the catalyzed ketone, in agreement with experiment. We noted that the calculations performed in gas phase did not reproduce the experimental finding, showing the importance of solvent effects in the calculation of activation barriers. We also noted that the two competitive chemo pathways were exergonic. It is important to note that intrinsic reaction coordinate (IRC) calculations indicated that the studied DA reactions followed a one-step mechanism and the eventuality of a stepwise mechanism was excluded. Indeed, the optimization of the last structures on the IRC curves in the forward direction gave structures identical to those of cycloadducts, indicating the absence of stable reaction intermediates.
To quantify the electronic and steric effects of BA and LA catalysts on the chemoselectivity of the studied DA reactions, we calculated the enthalpic and entropic contributions by partitioning ΔG° into two terms: ΔH° and −TΔS° (Table 3 and Table 4). According to the obtained results, we concluded that (i) both the steric and electronic effect are important in BA- and LA-catalyzed DA reactions; (ii) the steric contribution is more important than the electronic contribution in both BA- and LA-catalyzed reactions; (iii) the electronic contributions for LA-catalyzed reactions, 33.3 % and 30.4 % , are more important than those of BA-catalyzed reactions (17.5 % and 14.9 % ); (iv) for BA-catalyzed reactions, the steric contribution in TS-2-BA is more important than in TS-1-BA; and (v) in LA-catalyzed reactions, there is a decrease of steric contribution and increase of electronic contribution compared to BA-catalyzed reactions.

3.3. Relative Activation Free Energies and Boltzmann–Maxwell Populations

Table 5 summarizes the relative activation of Gibbs free energies, ΔΔG°, for the TSs corresponding to the four competitive chemo pathways, namely, 1-BA + Cp, 2-BA + Cp, 1-LA + Cp, and 2-LA + Cp reported in Table 3 and Table 4. The Maxwell–Boltzmann populations defined by [ B ] / [ A ] = exp ( − Δ Δ G / R T ) for the two equilibriums TS-1-BA ⇌ TS-2-BA and TS-1-LA ⇌ TS-2-LA were also calculated and are recapitulated in Table 5.
In the case of the BA-catalyzed reactions, the calculated Maxwell–Boltzmann populations shows that the population of TS-2-BA represented 82.86% of the mixture, whereas the population of TS-1-BA represented only 17.14%, indicating that chemo pathway 2-BA + Cp was kinetically more favored than the chemo pathway 1-BA + Cp in DCM at −40 °C. By contrast, in the case of the LA-catalyzed reactions, the calculated Maxwell–Boltzmann populations show that the population of TS-1-LA represented 83.07% of the mixture, whereas the population of TS-2-LA represented only 16.93%, indicating chemo pathway 1-LA + Cp was kinetically more favored than chemo pathway 2-LA + Cp in DCM at −20 °C. The obtained results put in evidence the crucial role played by the type of catalyst in the reversal of chemoselectivity in catalyzed DA reactions of α,β-unsaturated aldehydes.

3.4. GEDT Analysis and Polarity

The global electron density transfers (GEDTs) [71] were estimated from natural population analysis (NPA) [72,73] at the located TSs. The calculated GEDTs for uncatalyzed and BA/LA-catalyzed DA reactions are summarized in Table 6.
In the absence of catalysts, the GEDT values at TS-1 (0.13e) and TS-2 (0.12e) showed electron density fluxes from Cp to aldehyde 1 and ketone 2. The flux was two times greater in the presence of the BA catalyst and three times greater in the presence of the LA catalyst. These results clearly reveal that both the uncatalyzed and catalyzed studied DA reactions can be classified as polar processes. We noted that the calculated GEDTs (Table 6) correlated well with the calculated activation barriers (Table 2, Table 3 and Table 4). Indeed, when passing from the uncatalyzed reactions to BA- and LA-catalyzed reactions, an increase in the polarity led to a decrease in activation energies and free energies. We also noted that the calculated GEDTs (Table 6) also correlated well with the calculated electrophilicity differences Δω (Table 1). Indeed, when passing from the uncatalyzed reactions to BA- and LA-catalyzed reactions, the increase of Δω values led to an increase in polarity and consequently a decrease in activation barriers.

4. Conclusions

The chemoselectivity of the (un)catalyzed DA reactions of α,β-unsaturated aldehyde 1 and ketone 2 with Cp was investigated at the ωB97XD/6-311G(d,p) level of theory. The obtained results show that the most favored chemo pathway depends strongly on the type of the catalyst (Brønsted acid vs. bulky Lewis acid).
(i)
In the case of the uncatalyzed DA reactions, the 2 + Cp reaction was found to be kinetically more favored than the 1 + Cp reaction both in gas phase and in DCM.
(ii)
In the case of the DA reactions catalyzed by BA, the 2-BA + Cp reaction was found to be kinetically more favored than the 1-BA + Cp reaction both in gas phase and in DCM at −40 °C. Moreover, the calculated activation barriers, GEDTs at TSs, and electrophilicity differences (Δω) indicated that the BA-catalyzed reactions were predicted to be more polar and faster compared to the uncatalyzed reactions.
(iii)
In the case of the DA reactions catalyzed by LA, the 1-LA + Cp reaction was found to be kinetically more favored than the 2-LA + Cp reaction in DCM at −20 °C. In addition, the LA-catalyzed reactions were predicted to be more polar and faster compared to the uncatalyzed and BA-catalyzed reactions.
(iv)
The relative free energies and Maxwell–Boltzmann populations of the competitive TSs, calculated in DCM, put in evidence the reversal of the chemoselectivity when the BA catalyst Tf2NH -was replaced by the bulky LA catalyst B(C6F5)3, in agreement with the experimental findings.

Author Contributions

Conceptualization: S.M.M.; Investigation: L.B.; S.M.M. and W.B.; Methodology: L.B.; S.M.M.; Supervision: S.M.M.; Writing original draft: L.B. and S.M.M.; Writing—review & editing, L.B. and S.M.M.; All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Ministry of Higher Education and Scientific Research of the Algerian government for the project PRFU B00L01UN130120180001.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Huisgen, R. Cycloadditions—Definition, Classification, and Characterization. Angew. Chem. Int. Ed. 1968, 7, 321–328. [Google Scholar] [CrossRef]
  2. Padwa, A. 1,3-Dipolar Cycloaddition Chemistry; Padwa, A., Ed.; John Wiley and Sons: New York, NY, USA, 1984. [Google Scholar]
  3. Frühauf, H.-W. Metal-Assisted Cycloaddition Reactions in Organotransition Metal Chemistry. Chem. Rev. 1997, 97, 523–596. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  4. Kobayashi, S.; Jørgensen, K.A. Frontmatter and Index. In Cycloaddition Reactions in Organic Synthesis; Kobayashi, S., Jørgensen, K.A., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2001. [Google Scholar] [CrossRef]
  5. Nicolaou, K.C.; Snyder, S.A.; Montagnon, T.; Vassilikogiannakis, G. The Diels-Alder Reaction in Total Synthesis. Angew. Chem. Int. Ed. 2002, 41, 1668–1698. [Google Scholar] [CrossRef]
  6. Fringuelli, F.; Taticchi, A. The Diels-Alder Reaction: Selected Practical Methods; Fringuelli, F., Taticchi, A., Eds.; Wiley: Chichester, UK; New York, NY, USA, 2002. [Google Scholar]
  7. Konovalov, A.I.; Kiselev, V.D. Diels-Alder Reaction. Effect of Internal and External Factors on the Reactivity of Diene—Dienophile Systems. Russ. Chem. Bull. 2003, 52, 293–311. [Google Scholar] [CrossRef]
  8. Hodgson, D.M.; Labande, A.H.; Muthusamy, S. Cycloadditions of Carbonyl Ylides Derived from Diazocarbonyl Compounds. In Organic Reactions; Denmark, S.E., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2012; Chapter 2; pp. 133–496. [Google Scholar] [CrossRef]
  9. Ylijoki, K.E.O.; Stryker, J.M. [5+2] Cycloaddition Reactions in Organic and Natural Product Synthesis. Chem. Rev. 2013, 113, 2244–2266. [Google Scholar] [CrossRef]
  10. Martel, A.; Dhall, R.; Gaulon, C.; Laurent, M.Y.; Dujardin, G. Dihydrofurans by cycloadditions of oxadienes. In Organic Reactions, 1st ed.; Weinreb, S.M., Ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; Chapter 1; pp. 1–916. [Google Scholar] [CrossRef]
  11. Boger, D.L. Diels-Alder reactions of heterocyclic aza dienes. Scope and applications. Chem. Rev. 1986, 86, 781–793. [Google Scholar] [CrossRef]
  12. Hayashi, Y. Catalytic Asymmetric Diels-Alder Reactions. In Cycloaddition Reactions in Organic Synthesis; Kobayashi, S., Jørgensen, K.A., Eds.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2001; Chapter 1; pp. 5–55. [Google Scholar] [CrossRef]
  13. Houk, K.N.; Loncharich, R.J.; Blake, J.F.; Jorgensen, W.L. Substituent effects and transition structures for Diels-Alder reactions of butadiene and cyclopentadiene with cyanoalkenes. J. Am. Chem. Soc. 1989, 111, 9172–9176. [Google Scholar] [CrossRef]
  14. Jorgensen, W.L.; Lim, D.; Blake, J.F. Ab initio study of Diels-Alder reactions of cyclopentadiene with ethylene, isoprene, cyclopentadiene, acrylonitrile, and methyl vinyl ketone. J. Am. Chem. Soc. 1993, 115, 2936–2942. [Google Scholar] [CrossRef]
  15. Domingo, L.R.; Sáez, J.A. Understanding the mechanism of polar Diels-Alder reactions. Org. Biomol. Chem. 2009, 7, 3576–3585. [Google Scholar] [CrossRef] [PubMed]
  16. Morales-Bayuelo, A.; Vivas-Reyes, R. Understanding the Polar Character Trend in a Series of Diels-Alder Reactions Using Molecular Quantum Similarity and Chemical Reactivity Descriptors. J. Quantum Chem. 2014, 2014. [Google Scholar] [CrossRef] [Green Version]
  17. Cui, C.-X.; Liu, Y.-J. A thorough understanding of the Diels-Alder reaction of 1,3-butadiene and ethylene: Diels-Alder reaction of 1,3-butadiene and ethylene. J. Phys. Org. Chem. 2014, 27, 652–660. [Google Scholar] [CrossRef]
  18. Levandowski, B.J.; Houk, K.N. Theoretical Analysis of Reactivity Patterns in Diels-Alder Reactions of Cyclopentadiene, Cyclohexadiene, and Cycloheptadiene with Symmetrical and Unsymmetrical Dienophiles. J. Org. Chem. 2015, 80, 3530–3537. [Google Scholar] [CrossRef]
  19. Jasiński, R. A reexamination of the molecular mechanism of the Diels-Alder reaction between tetrafluoroethene and cyclopentadiene. React. Kinet. Mech. Catal. 2016, 119, 49–57. [Google Scholar] [CrossRef] [Green Version]
  20. Chen, S.; Yu, P.; Houk, K.N. Ambimodal Dipolar/Diels-Alder Cycloaddition Transition States Involving Proton Transfers. J. Am. Chem. Soc. 2018, 140, 18124–18131. [Google Scholar] [CrossRef]
  21. Jasiński, R.; Kwiatkowska, M.; Barański, A. Stereoselectivity and kinetics of [4+2] cycloaddition reaction of cyclopentadiene to para-substituted E-2-arylnitroethenes. J. Phys. Org. Chem. 2011, 24, 843–853. [Google Scholar] [CrossRef]
  22. Domingo, L. Molecular Electron Density Theory: A Modern View of Reactivity in Organic Chemistry. Molecules 2016, 21, 1319. [Google Scholar] [CrossRef] [PubMed]
  23. Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. A Molecular Electron Density Theory Study of the Competitiveness of Polar Diels-Alder and Polar Alder-ene Reactions. Molecules 2018, 23, 1913. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  24. Domingo, L.R.; Acharjee, N. Molecular Electron Density Theory: A New Theoretical Outlook on Organic Chemistry. In Frontiers in Computational Chemistry; Ul-Haq, Z., Wilson, A.K., Eds.; Bentham Science Publishers: Sharjah, UAE, 2020; Chapter 2; pp. 174–227. [Google Scholar] [CrossRef]
  25. Acharjee, N.; Banerji, A. A molecular electron density theory study to understand the interplay of theory and experiment in nitrone-enone cycloaddition. J. Chem. Sci. 2020, 132, 65. [Google Scholar] [CrossRef]
  26. Benhamed, L.; Mekelleche, S.M.; Benchouk, W.; Charif, I.E.; Ríos-Gutiérrez, M.; Domingo, L.R. Understanding the Influence of the Trifluoromethyl Group on the Selectivities of the [3+2] Cycloadditions of Thiocarbonyl S -methanides with α, β-Unsaturated Ketones. A MEDT study. ChemistrySelect 2020, 5, 12791–12806. [Google Scholar] [CrossRef]
  27. Domingo, L.R.; Ríos-Gutiérrez, M. On the nature of organic electron density transfer complexes within molecular electron density theory. Org. Biomol. Chem. 2019, 17, 6478–6488. [Google Scholar] [CrossRef]
  28. Emamian, S.; Domingo, L.R.; Javad Hosseini, S.; Ali-Asgari, S. A Study of the Effects of the Lewis Acid Catalysts on Oxa-Diels-Alder Reactions through Molecular Electron Density Theory. ChemistrySelect 2020, 5, 5341–5348. [Google Scholar] [CrossRef]
  29. Hosseini, S.J. Exploring effects of the trifluoromethyl substituent on the chemoselectivity and regioselectivity of [3+2] cycloadditions of thiocarbonyl S-methanides with α, β-unsaturated ketones. J. Chin. Chem. Soc. 2020, 67, 703–710. [Google Scholar] [CrossRef]
  30. Jalali, H.; Hosseini, S.J.; Ali-Asgari, S.; Izadi Nia, J. Stereoselective aziridination of imines via ammonium ylides: A molecular electron density theory study. J. Heterocycl. Chem. 2020, 57, 419–427. [Google Scholar] [CrossRef]
  31. Ríos-Gutiérrez, M.; Nasri, L.; Khorief Nacereddine, A.; Djerourou, A.; Domingo, L.R. A molecular electron density theory study of the [3+2] cycloaddition reaction between an azomethine imine and electron deficient ethylenes. J. Phys. Org. Chem. 2018, 31, e3830. [Google Scholar] [CrossRef]
  32. Barama, L.; Bayoud, B.; Chafaa, F.; Nacereddine, A.K.; Djerourou, A. A mechanistic MEDT study of the competitive catalysed [4+2] and [2+2] cycloaddition reactions between 1-methyl-1-phenylallene and methyl acrylate: The role of Lewis acid on the mechanism and selectivity. Struct. Chem. 2018, 29, 1709–1721. [Google Scholar] [CrossRef]
  33. Fukui, K. Molecular Orbitals in Chemistry, Physics, and Biology. In Index to Reviews, Symposia Volumes and Monographs in Organic Chemistry; Lowdin, P.O., Ed.; Academic Press: New York, NY, USA; London, UK, 1966. [Google Scholar] [CrossRef]
  34. Parr, R.G.; Pearson, R.G. Absolute hardness: Companion parameter to absolute electronegativity. J. Am. Chem. Soc. 1983, 105, 7512–7516. [Google Scholar] [CrossRef]
  35. Parr, R.G.; Szentpály, L.V.; Liu, S. Electrophilicity Index. J. Am. Chem. Soc. 1999, 121, 1922–1924. [Google Scholar] [CrossRef]
  36. Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
  37. Bader, R.F.W. Atoms in Molecules: A Quantum Theory; Clarendon Press: Oxford, UK; New York, NY, USA, 1990. [Google Scholar] [CrossRef]
  38. Carruthers, W.; Coldham, I. Modern Methods of Organic Synthesis; Carruthers, W., Coldham, I., Eds.; Cambridge University Press: Cambridge, UK, 2004; pp. 159–264. [Google Scholar]
  39. Yamamoto, H.; Boxer, M.B. Super Brønsted Acid Catalysis in Organic Synthesis. CHIMIA Int. J. Chem. 2007, 61, 279–281. [Google Scholar] [CrossRef]
  40. Cheon, C.H.; Yamamoto, H. Super Brønsted acid catalysis. Chem. Commun. 2011, 47, 3043. [Google Scholar] [CrossRef] [PubMed]
  41. Yamamoto, H. Acid Catalysis in Organic Synthesis. In Inventing Reactions; Gooßen, L.J., Ed.; Springer: Berlin/Heidelberg, Germany, 2012; pp. 315–334. [Google Scholar] [CrossRef]
  42. Ishihara, K. Chiral B (III) Lewis Acids. In Lewis Acids in Organic Synthesis; Yamamoto, H., Ed.; Wiley-VCH Verlag GmbH: Weinheim, Germany, 2000; pp. 135–190. [Google Scholar] [CrossRef]
  43. Fringuelli, F.; Piermatti, O.; Pizzo, F.; Vaccaro, L. Recent Advances in Lewis Acid Catalyzed Diels-Alder Reactions in Aqueous Media. Eur. J. Org. Chem. 2001, 17, 439–455. [Google Scholar] [CrossRef]
  44. Kagan, H.B.; Riant, O. Catalytic asymmetric Diels-Alder reactions. Chem. Rev. 1992, 92, 1007–1019. [Google Scholar] [CrossRef]
  45. Li, P.; Yamamoto, H. Lewis Acid Catalyzed Inverse-Electron-Demand Diels-Alder Reaction of Tropones. J. Am. Chem. Soc. 2009, 131, 16628–16629. [Google Scholar] [CrossRef] [Green Version]
  46. Shen, J.; Tan, C.-H. Brønsted-acid and Brønsted-base catalyzed Diels-Alder reactions. Org. Biomol. Chem. 2008, 6, 3229. [Google Scholar] [CrossRef]
  47. Pindur, U.; Lutz, G.; Otto, C. Acceleration and Selectivity Enhancement of Dlels-Alder Reactions by Special and Catalytic Methods. Chem. Rev. 1993, 93, 741–761. [Google Scholar] [CrossRef]
  48. Futatsugi, K.; Yamamoto, H. Oxazaborolidine-Derived Lewis Acid Assisted Lewis Acid as a Moisture-Tolerant Catalyst for Enantioselective Diels-Alder Reactions. Angew. Chem. Int. Ed. 2005, 44, 1484–1487. [Google Scholar] [CrossRef]
  49. Yamamoto, H. From designer Lewis acid to designer Brnsted acid towards more reactive and selective acid catalysis. Proc. Jpn. Acad. Ser. B 2008, 84, 134–146. [Google Scholar] [CrossRef] [Green Version]
  50. Jung, M.E.; Guzaev, M. Trimethylaluminum-Triflimide Complexes for the Catalysis of Highly Hindered Diels-Alder Reactions. Org. Lett. 2012, 14, 5169–5171. [Google Scholar] [CrossRef]
  51. Liu, L.; Kim, H.; Xie, Y.; Farès, C.; Kaib, P.S.J.; Goddard, R.; List, B. Catalytic Asymmetric [4+2]-Cycloaddition of Dienes with Aldehydes. J. Am. Chem. Soc. 2017, 139, 13656–13659. [Google Scholar] [CrossRef] [Green Version]
  52. Zhao, W.; Sun, J. Triflimide (HNTf2) in Organic Synthesis. Chem. Rev. 2018, 118, 10349–10392. [Google Scholar] [CrossRef] [PubMed]
  53. Held, F.; Grau, D.; Tsogoeva, S. Enantioselective Cycloaddition Reactions Catalyzed by BINOL-Derived Phosphoric Acids and N-Triflyl Phosphoramides: Recent Advances. Molecules 2015, 20, 16103–16126. [Google Scholar] [CrossRef] [Green Version]
  54. Dodziuk, H. Strained Hydrocarbons: Beyond the van-t Hoff and Le Bel Hypothesis, 1st ed.; Dodziuk, H., Ed.; Wiley-VCH Verlag Gmbh & Co. KGaA: Weinheim, Germany, 2009. [Google Scholar] [CrossRef]
  55. Park, S.; Sugiyama, H. DNA-Based Hybrid Catalysts for Asymmetric Organic Synthesis. Angew. Chem. Int. Ed. 2010, 49, 3870–3878. [Google Scholar] [CrossRef]
  56. Megens, R.P.; Roelfes, G. Asymmetric Catalysis with Helical Polymers. Chem. A Eur. J. 2011, 17, 8514–8523. [Google Scholar] [CrossRef] [Green Version]
  57. Rioz-Martínez, A.; Roelfes, G. DNA-based hybrid catalysis. Curr. Opin. Chem. Biol. 2015, 25, 80–87. [Google Scholar] [CrossRef]
  58. Raynal, M.; Ballester, P.; Vidal-Ferran, A.; van Leeuwen, P.W.N.M. Supramolecular catalysis. Part 1: Non-covalent interactions as a tool for building and modifying homogeneous catalysts. Chem. Soc. Rev. 2014, 43, 1660–1733. [Google Scholar] [CrossRef] [PubMed]
  59. Nakashima, D.; Yamamoto, H. Reversal of Chemoselectivity in Diels-Alder Reaction with α, β-Unsaturated Aldehydes and Ketones Catalyzed by Brønsted Acid or Lewis Acid. Org. Lett. 2005, 7, 1251–1253. [Google Scholar] [CrossRef]
  60. Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  61. Wiberg, K.B. Ab Initio Molecular Orbital Theory. J. Comput. Chem. 1986, 7, 379. [Google Scholar] [CrossRef]
  62. Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision A.1; Gaussian, Inc.: Wallingford, CT, USA, 2009. Available online: https://gaussian.com/g09citation/ (accessed on 1 November 2016).
  63. Li, Y.; Fang, D.-C. DFT calculations on kinetic data for some [4+2] reactions in solution. Phys. Chem. Chem. Phys. 2014, 16, 15224. [Google Scholar] [CrossRef] [PubMed]
  64. Fang, D.; Chen, Y. Theoretical Studies on the Mechanism of Cycloaddition Reaction between 1,2,4,5-Tetrazine and Cycloolefines. Acta Chim. Sin. 2014, 72, 253–256. [Google Scholar] [CrossRef] [Green Version]
  65. Schlegel, H.B. Optimization of equilibrium geometries and transition structures. J. Comput. Chem. 1982, 3, 214–218. [Google Scholar] [CrossRef]
  66. Schlegel, H.B. Some thoughts on reaction-path following. J. Chem. Soc. Faraday Trans. 1994, 90, 1569. [Google Scholar] [CrossRef]
  67. Tomasi, J.; Persico, M. Molecular Interactions in Solution: An Overview of Methods Based on Continuous Distributions of the Solvent. Chem. Rev. 1994, 94, 2027–2094. [Google Scholar] [CrossRef]
  68. Cossi, M.; Barone, V.; Cammi, R.; Tomasi, J. Ab initio study of solvated molecules: A new implementation of the polarizable continuum model. Chem. Phys. Lett. 1996, 255, 327–335. [Google Scholar] [CrossRef]
  69. Cancès, E.; Mennucci, B.; Tomasi, J. A new integral equation formalism for the polarizable continuum model: Theoretical background and applications to isotropic and anisotropic dielectrics. J. Chem. Phys. 1997, 107, 3032–3041. [Google Scholar] [CrossRef]
  70. Barone, V.; Cossi, M.; Tomasi, J. Geometry optimization of molecular structures in solution by the polarizable continuum model. J. Comput. Chem. 1998, 19, 404–417. [Google Scholar] [CrossRef]
  71. Domingo, L.R. A new C-C bond formation model based on the quantum chemical topology of electron density. RSC Adv. 2014, 4, 32415–32428. [Google Scholar] [CrossRef] [Green Version]
  72. Reed, A.E.; Weinstock, R.B.; Weinhold, F. Natural population analysis. J. Chem. Phys. 1985, 83, 735–746. [Google Scholar] [CrossRef]
  73. Reed, A.E.; Curtiss, L.A.; Weinhold, F. Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint. Chem. Rev. 1988, 88, 899–926. [Google Scholar] [CrossRef]
  74. Domingo, L.; Ríos-Gutiérrez, M.; Pérez, P. Applications of the Conceptual Density Functional Theory Indices to Organic Chemistry Reactivity. Molecules 2016, 21, 748. [Google Scholar] [CrossRef] [Green Version]
  75. Parr, R.G. Density-Functional Theory of the Electronic Structure of Molecules. Annu. Rev. Phys. Chem. 1995, 46, 701–728. [Google Scholar] [CrossRef]
  76. Chermette, H. Chemical reactivity indexes in density functional theory. J. Comput. Chem. 1999, 20, 129–154. [Google Scholar] [CrossRef]
  77. de Proft, F.; Geerlings, P. Conceptual and Computational DFT in the Study of Aromaticity. Chem. Rev. 2001, 101, 1451–1464. [Google Scholar] [CrossRef]
  78. Geerlings, P.; Proft, F.D.; Langenaeker, W. Conceptual Density Functional Theory. Chem. Rev. 2003, 103, 1793–1873. [Google Scholar] [CrossRef]
  79. Ayers, P.W.; Anderson, J.S.M.; Bartolotti, L.J. Perturbative perspectives on the chemical reaction prediction problem. Int. J. Quantum Chem. 2005, 101, 520–534. [Google Scholar] [CrossRef]
  80. Gázquez, J.L. Perspectives on the Density Functional Theory of Chemical Reactivity. J. Mex. Chem. Soc. 2008, 52, 3–10. [Google Scholar]
  81. Geerlings, P.; Fias, S.; Boisdenghien, Z.; de Proft, F. Conceptual DFT: Chemistry from the linear response function. Chem. Soc. Rev. 2014, 43, 4989–5008. [Google Scholar] [CrossRef]
  82. Calais, J.-L. Density-functional theory of atoms and molecules. Int. J. Quantum Chem. 1993, 47, 101. [Google Scholar] [CrossRef]
  83. Domingo, L.R.; Ríos-Gutiérrez, M.; Pérez, P. A molecular electron density theory study of the participation of tetrazines in aza-Diels-Alder reactions. RSC Adv. 2020, 10, 15394–15405. [Google Scholar] [CrossRef] [Green Version]
  84. Jaramillo, P.; Domingo, L.R.; Chamorro, E.; Pérez, P. A further exploration of a nucleophilicity index based on the gas-phase ionization potentials. J. Mol. Struct. THEOCHEM 2008, 865, 68–72. [Google Scholar] [CrossRef]
  85. Domingo, L.R.; Pérez, P. The nucleophilicity N index in organic chemistry. Org. Biomol. Chem. 2011, 9, 7168–7176. [Google Scholar] [CrossRef] [PubMed]
  86. Dennington, R.; Keith, T.; Millam, J. GaussView, Version 5.0.8; Semichem Inc.: Shawnee Mission, KS, USA, 2009. [Google Scholar]
Organics 02 00004 sch001 550
Scheme 1. Chemoselective DA reactions of (2E)-but-2-enal 1 and 2-hexen-4-one 2 with Cp. Only the endo cycloadducts were experimentally observed.
Scheme 1. Chemoselective DA reactions of (2E)-but-2-enal 1 and 2-hexen-4-one 2 with Cp. Only the endo cycloadducts were experimentally observed.
Organics 02 00004 sch001
Organics 02 00004 sch002 550
Scheme 2. Competitive chemoselective pathways of the BA-/LA-catalyzed DA reactions of (2E)-but-2-enal 1 and 2-hexen-4-one 2 with Cp.
Scheme 2. Competitive chemoselective pathways of the BA-/LA-catalyzed DA reactions of (2E)-but-2-enal 1 and 2-hexen-4-one 2 with Cp.
Organics 02 00004 sch002
Organics 02 00004 g001a 550Organics 02 00004 g001b 550
Figure 1. ωB97XD/6-311G(d,p) geometries of transition state structures involved in chemoselective DA reactions: (a) uncatalyzed reactions (1 + Cp) and (2 + Cp), (b) BA-catalyzed reactions (1-BA + Cp) and (2-BA + Cp), and (c) LA-catalyzed reactions (1-LA + Cp) and (2-LA + Cp). The bond lengths are given in Angstroms.
Figure 1. ωB97XD/6-311G(d,p) geometries of transition state structures involved in chemoselective DA reactions: (a) uncatalyzed reactions (1 + Cp) and (2 + Cp), (b) BA-catalyzed reactions (1-BA + Cp) and (2-BA + Cp), and (c) LA-catalyzed reactions (1-LA + Cp) and (2-LA + Cp). The bond lengths are given in Angstroms.
Organics 02 00004 g001aOrganics 02 00004 g001b
Table
Table 1. ωB97XD/6-311G(d,p) global electronic properties (chemical potential μ, chemical hardness η, electrophilicity ω, nucleophilicity N) of uncatalyzed reactants 1 and 2, BA-catalyzed reactants 1-BA and 2-BA, and LA-catalyzed reactants 1-LA and 2-LA, in gas phase.
Table 1. ωB97XD/6-311G(d,p) global electronic properties (chemical potential μ, chemical hardness η, electrophilicity ω, nucleophilicity N) of uncatalyzed reactants 1 and 2, BA-catalyzed reactants 1-BA and 2-BA, and LA-catalyzed reactants 1-LA and 2-LA, in gas phase.
Global Properties (in eV)
µηωNΔω 1
Cp−0.1230.3520.583.630.00
1−0.1620.3511.022.560.44
2−0.1560.3500.942.760.36
1-BA−0.2010.3621.521.360.94
2-BA−0.1930.3671.401.600.82
1-LA−0.1970.2562.052.911.47
2-LA−0.1920.2651.892.941.31
1 Relative to Cp.
Table
Table 2. Total energies E and relative energies ΔE in gas phase, and free energies G° and relative free energies ΔG° in solvent for the uncatalyzed DA reactions (1 + Cp) and (2 + Cp).
Table 2. Total energies E and relative energies ΔE in gas phase, and free energies G° and relative free energies ΔG° in solvent for the uncatalyzed DA reactions (1 + Cp) and (2 + Cp).
Gas PhaseIn DCM at −40 °CDCM at −20 °C
E
(in a.u.)		ΔE
(in kcal/mol)		G°
(in a.u.)		ΔG°
(in kcal/mol)		G°
(in a.u.)		ΔG°
(in kcal/mol)
Cp−194.081227 −194.010442 −194.012466
1−231.214513 −231.151897 −231.154155
2−309.848932 −309.732115 −309.734767
1 + Cp−425.2957400.0−425.1623390.0−425.1666210.0
2 + Cp−503.9301600.0−503.7425570.0−503.7472330.0
TS-1−425.26897116.8 1−425.11529929.5 1−425.11805330.5 1
TS-2−503.90475415.92−503.69597729.22−503.69909430.22
CA-1−425.337504−26.2 1−425.178925−10.4 1−425.176228−6.0 1
CA-2−503.975693−28.6 2−503.762314−12.4 2−503.759272−7.5 2
1 Relative to reactants (1 + Cp); 2 relative to reactants (2 + Cp).
Table
Table 3. Total energies E and relative energies ΔE in gas phase, and free energies G° and relative free energies ΔG° in solvent for the possible chemo pathways of DA reactions catalyzed by BA. The enthalpy and entropy contributions of ΔG° are included.
Table 3. Total energies E and relative energies ΔE in gas phase, and free energies G° and relative free energies ΔG° in solvent for the possible chemo pathways of DA reactions catalyzed by BA. The enthalpy and entropy contributions of ΔG° are included.
Gas PhaseIn DCM at −40 °C
E
(in a.u.)		ΔE
(in kcal/mol)		G°
(in a.u.)		ΔG°
(in kcal/mol)		ΔH°
(in kcal/mol)		−TΔS°
(in kcal/mol)
Cp−194.081227 −194.010442
1-BA−2058.968156 −2058.860635
2-BA−2137.604500 −2137.442545
1-BA + Cp−2253.0493840.0−2252.8710770.0
2-BA + Cp−2331.6857280.0−2331.4529870.0
TS-1-BA−2253.03318610.2 1−2252.84715315.0 12.6 (17.5%)12.4 (82.5%)
TS-2-BA−2331.6702059.72−2331.43022614.322.1 (14.9%)12.2 (85.1%)
CA-1-BA−2253.094037−28.0 1−2252.885020−8.7 1
CA-2-BA−2331.733508−30.0 2−2331.471355−11.5 2
1 Relative to reactants (1-BA + Cp); 2 relative to reactants (2-BA + Cp).
Table
Table 4. Total energies E and relative energies ΔE in gas phase, and free energies G° and relative free energies ΔG° in solvent for the possible chemo pathways of DA reactions catalyzed by LA. The enthalpy and entropy contributions of ΔG° are included.
Table 4. Total energies E and relative energies ΔE in gas phase, and free energies G° and relative free energies ΔG° in solvent for the possible chemo pathways of DA reactions catalyzed by LA. The enthalpy and entropy contributions of ΔG° are included.
Gas PhaseIn DCM at −20 °C
E
(in a.u.)		ΔE
(in kcal/mol)		G°
(in a.u.)		ΔG°
(in kcal/mol)		ΔH°
(in kcal/mol)		−TΔS°
(in kcal/mol)
Cp−194.081227 −194.010442
1-LA−2439.454482 −2439.272585
2-LA−2518.095162 −2517.856115
1-LA + Cp−2633.5357090.0−2633.2830270.0
2-LA + Cp−2712.1763890.0−2711.8665570.0
TS-1-LA−2633.5254056.5 1−2633.25804415.715.2 (33.3%)10.5 (66.7%)
TS-2-LA−2712.1690994.62−2711.84029416.5 25.0 (30.4%)11.5 (69.6%)
CA-1-LA−2633.576707−25.7 1−2633.295055−7.5 1
CA-2- LA−2712.223191−29.4 2−2711.882229−9.8 2
1 Relative to reactants (1-LA + Cp); 2 relative to reactants (2-LA + Cp).
Table
Table 5. Relative free energies ΔΔG° (in kcal/mol) between barrier free energies ΔG° of TSs in DCM and their corresponding Boltzmann–Maxwell populations (%).
Table 5. Relative free energies ΔΔG° (in kcal/mol) between barrier free energies ΔG° of TSs in DCM and their corresponding Boltzmann–Maxwell populations (%).
In DCM at −40 °Cin DCM at −20 °C
ΔΔG° pop(%)ΔΔG° pop(%)
TS-1-BA0.717.14
TS-2-BA0.082.86
TS-1-LA 0.083.07
TS-2-LA 0.816.93
Table
Table 6. GEDT (given in e) of the uncatalyzed and BA-/LA-catalyzed DA reactions.
Table 6. GEDT (given in e) of the uncatalyzed and BA-/LA-catalyzed DA reactions.
Uncatalyzed DA ReactionsBA-Catalyzed
DA Reactions		LA-Catalyzed
DA Reactions
TS-1TS-2TS-1-BATS-2-BATS-1-LATS-2-LA
GEDT0.130.120.260.230.380.33
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Benhamed, L.; Mekelleche, S.M.; Benchouk, W. Theoretical Insight into the Reversal of Chemoselectivity in Diels-Alder Reactions of α,β-Unsaturated Aldehydes and Ketones Catalyzed by Brønsted and Lewis Acids. Organics 2021, 2, 38-49. https://doi.org/10.3390/org2010004

AMA Style

Benhamed L, Mekelleche SM, Benchouk W. Theoretical Insight into the Reversal of Chemoselectivity in Diels-Alder Reactions of α,β-Unsaturated Aldehydes and Ketones Catalyzed by Brønsted and Lewis Acids. Organics. 2021; 2(1):38-49. https://doi.org/10.3390/org2010004

Chicago/Turabian Style

Benhamed, Lakhdar, Sidi Mohamed Mekelleche, and Wafaa Benchouk. 2021. "Theoretical Insight into the Reversal of Chemoselectivity in Diels-Alder Reactions of α,β-Unsaturated Aldehydes and Ketones Catalyzed by Brønsted and Lewis Acids" Organics 2, no. 1: 38-49. https://doi.org/10.3390/org2010004

APA Style

Benhamed, L., Mekelleche, S. M., & Benchouk, W. (2021). Theoretical Insight into the Reversal of Chemoselectivity in Diels-Alder Reactions of α,β-Unsaturated Aldehydes and Ketones Catalyzed by Brønsted and Lewis Acids. Organics, 2(1), 38-49. https://doi.org/10.3390/org2010004

Article Metrics

Back to TopTop