Utilization-Driven Performance Enhancement in Storage Area Networks
Abstract
1. Introduction
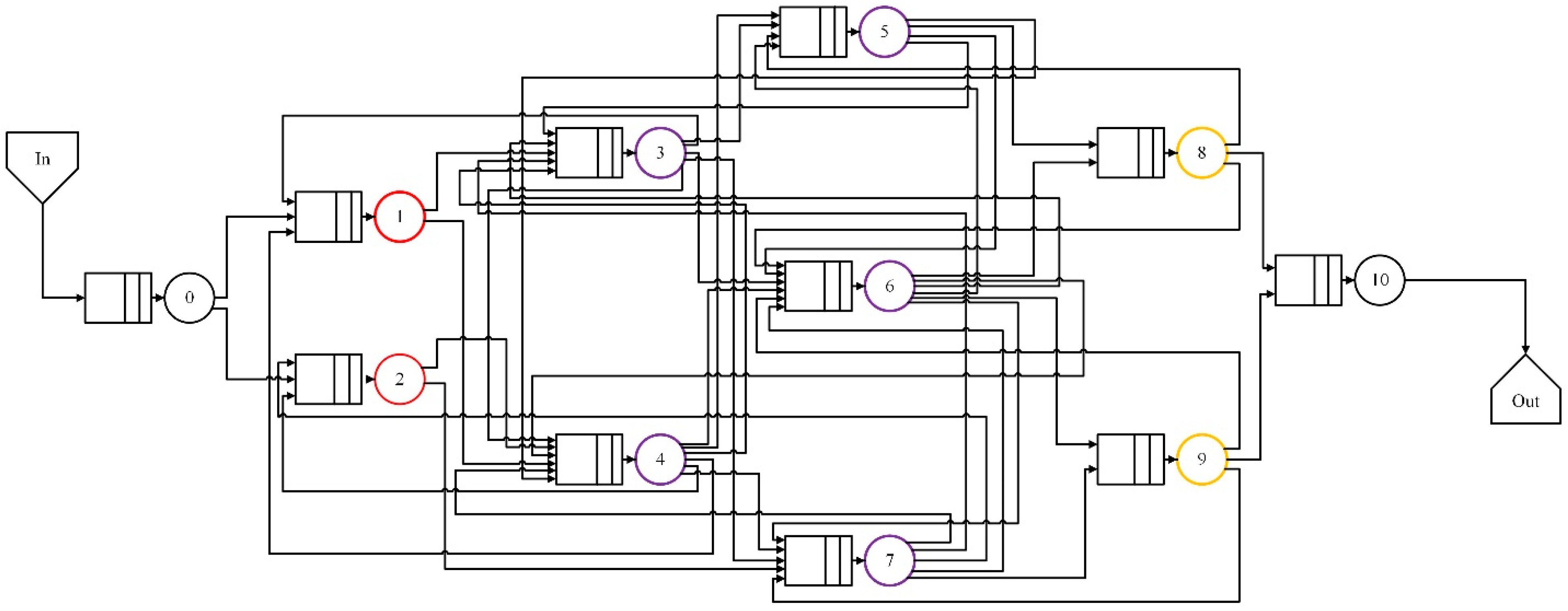
2. Jackson Queuing Network-Based Performance Evaluation
- 1.
- Each node k (k = 1, 2, …, K) consists of ck identical servers with service time following the exponential distribution characterized by a constant service rate μk.
- 2.
- Customers from outside the system arrive at node k following a Poisson process with arrival rate λk.
- 3.
- Once served at node k, a customer goes to node j (j = 1, 2, …, K) with probability Pkj; or leaves the network with probability . Thus, the average arrival rate to each node k, denoted by Λk, can be evaluated as
3. Utilization-Driven Performance Enhancement Strategy
3.1. Node Selection Rule
3.2. Transition Probability Adjustment Strategy
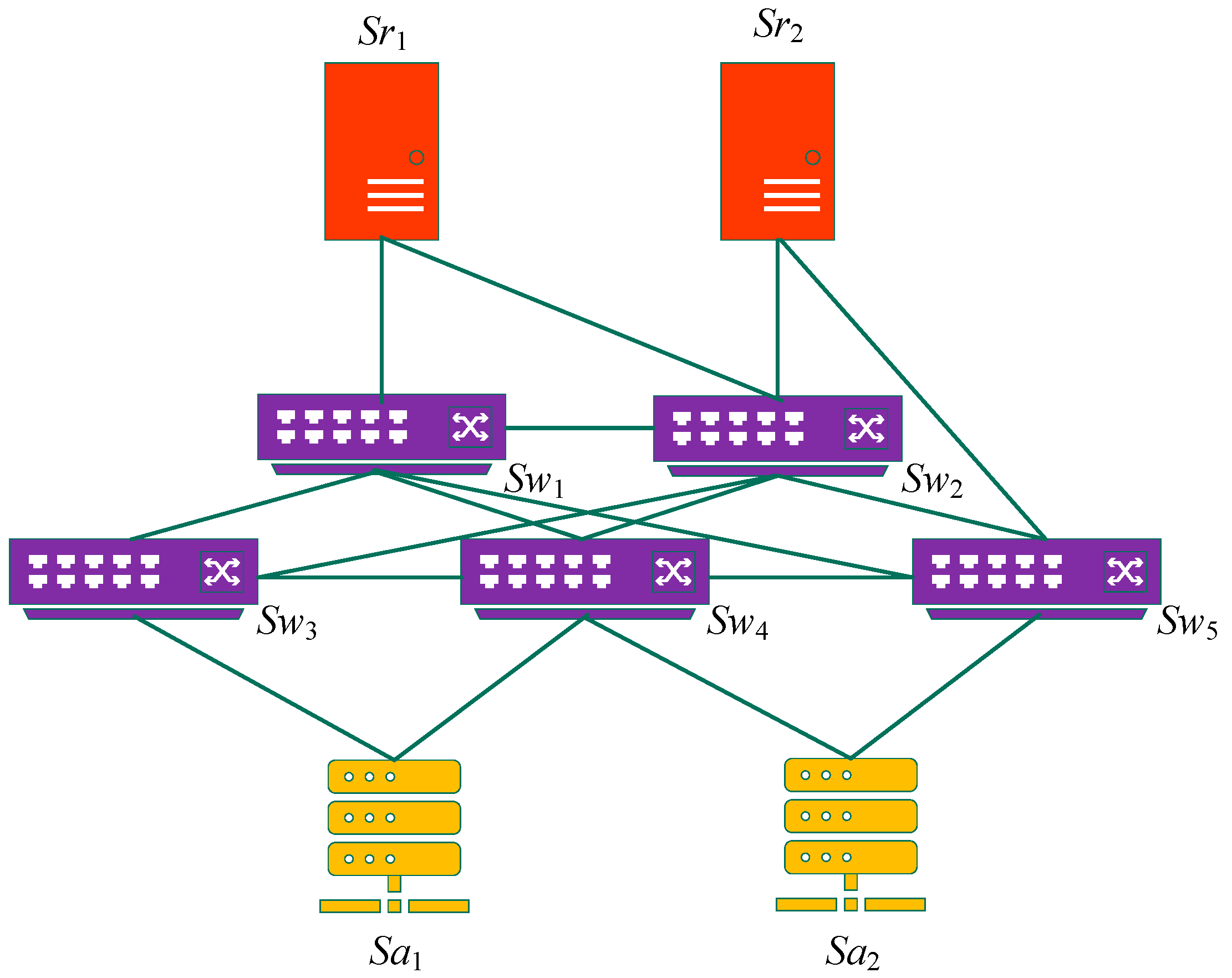
4. Illustrative Example
4.1. JQN Modeling
4.2. Initialization of Transition Probabilities
4.3. Problem Statement
5. Experiments and Results
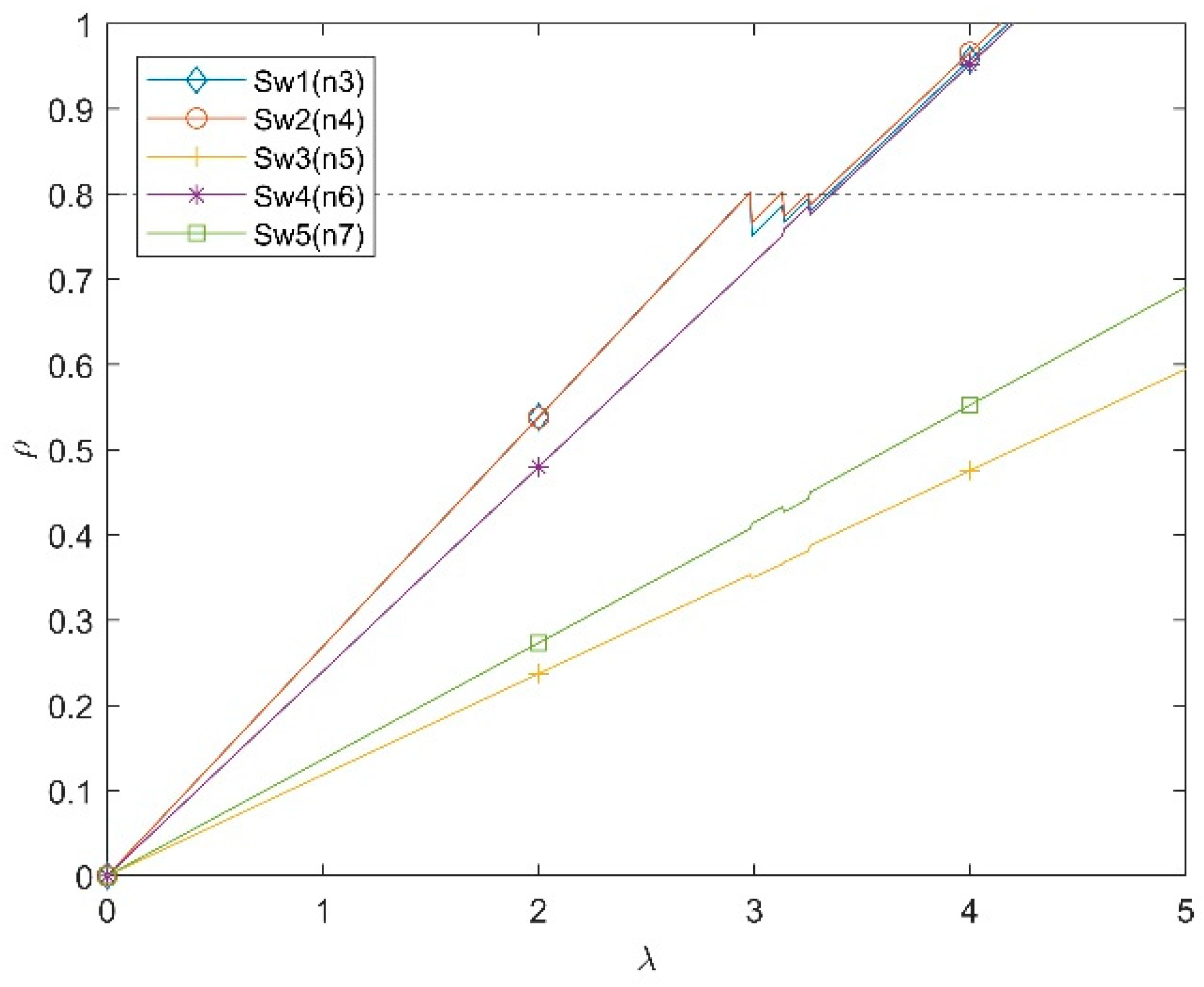
5.1. Effects of Adjustment Step Value s
5.1.1. Case 1: w = 0.02 and s = 0.01
5.1.2. Case 2: w = 0.02 and s = 0.05
5.1.3. Case 3: w = 0.02 and s = 0.07
5.1.4. Summary of Effects of Adjustment Step Value s
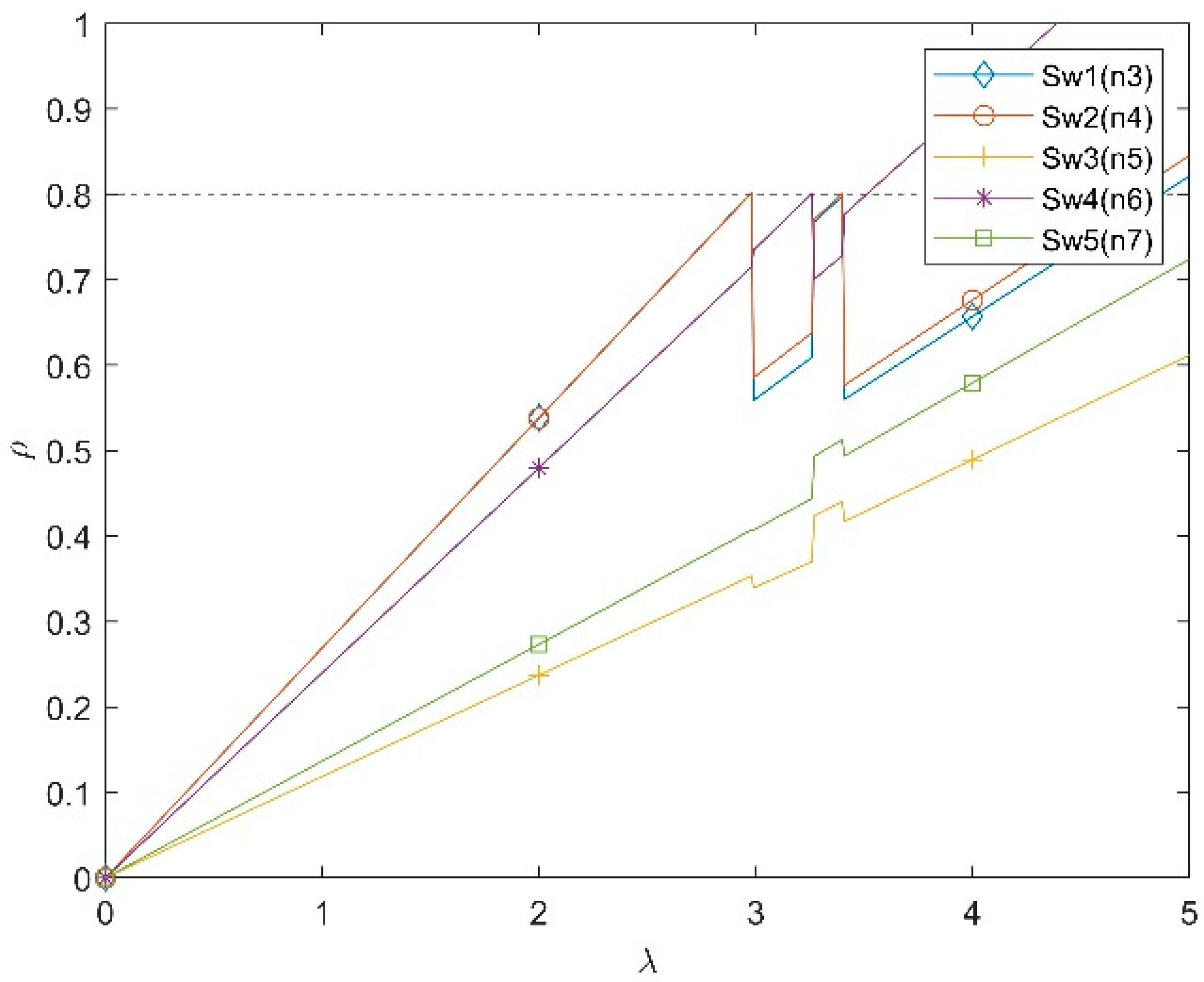
5.2. Effects of Selection Window Size w
5.2.1. Case 4: s = 0.07 and w = 0.1
5.2.2. Case 5: s = 0.07 and w = 0.2
5.2.3. Summary of Effects of Selection Window Size
6. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Notations
| K | Number of nodes in a queueing network |
| ck | Number of identical servers at node k |
| μk | Service rate of a server at node k |
| λk | Arrival rate to a server at node k |
| Pkj | Transition probability from node k to node j |
| Λk | Average arrival rate to node k |
| Utilization of node k | |
| (n1, n2, …, nK) | Joint steady state probability |
| Number of customers in node k | |
| Average response time at node k | |
| Average number of jobs in node k | |
| Overall mean response time of the entire queueing network | |
| ρ* | Pre-defined initial utilization threshold |
| w | Adjustment window size |
| Aj | Set of nodes selected for adjustment triggered by node j |
| Set of neighboring nodes for node j | |
| M | Total number of SAN servers |
| ln | Total number of paths through server n |
| Transition probability from dummy node 0 to server n | |
| Cardinality of set Nj | |
| ρavg | Average utilization of all switches in the example SAN |
| ρstd | Standard deviation of utilization of all switches in the example SAN |
| Wavg | Average response time of all switches in the example SAN |
| Wstd | Standard deviation of response time of all switches in the example SAN |
| IR | Improvement ratio |
References
- Margara, A.; Cugola, G.; Felicioni, B.; Cilloni, S. A Model and Survey of Distributed Data-Intensive Systems. ACM Comput. Surv. 2023, 56, 1–69. [Google Scholar] [CrossRef]
- Garber, L. Converged infrastructure: Addressing the efficiency challenge. Computer 2012, 45, 17–20. [Google Scholar] [CrossRef]
- Honma, S.; Morishima, H.; Tsukiyama, T.; Matsushima, H.; Oeda, T.; Tomono, Y. Computer System Using a Storage Area Network and Method of Handling Data in the Computer System. U.S. Patent US20040073677A1, 15 April 2004. Available online: https://www.google.com/patents/US20040073677 (accessed on 1 August 2025).
- Sharma, M.; Luthra, S.; Joshi, S.; Kumar, A. Developing a framework for enhancing survivability of sustainable supply chains during and post-COVID-19 pandemic. Int. J. Logist. Res. Appl. 2020, 25, 433–453. [Google Scholar] [CrossRef]
- Xing, L.; Tannous, M.; Vokkarane, V.M.; Wang, H.; Guo, J. Reliability modeling of mesh storage area networks for Internet of things. IEEE Internet Things J. 2017, 4, 2047–2057. [Google Scholar] [CrossRef]
- Liu, D.; Zhang, X.; Chi, K.T. Effects of high level of penetration of renewable energy sources on cascading failure of modern power systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 98–106. [Google Scholar] [CrossRef]
- Mishra, S.; Anderson, K.; Miller, B.; Boyer, K.; Warren, A. Microgrid resilience: A holistic approach for assessing threats, identifying vulnerabilities, and designing corresponding mitigation strategies. Appl. Energy 2020, 264, 114726. [Google Scholar] [CrossRef]
- Nguyen, T.; Liu, B.; Nguyen, N.; Dumba, B.; Chou, J. Smart Grid Vulnerability and Defense Analysis Under Cascading Failure Attacks. IEEE Trans. Power Deliv. 2021, 36, 2264–2273. [Google Scholar] [CrossRef]
- Xing, L. Cascading failures in Internet of Things: Review and perspectives on reliability and resilience. IEEE Internet Things J. 2021, 8, 44–64. [Google Scholar] [CrossRef]
- Bialek, J.; Ciapessoni, E.; Cirio, D.; Sanchez, E.; Dent, C.; Dobson, I.; Henneaux, P.; Hines, P.; Jardim, J.; Miller, S.; et al. Benchmarking and Validation of Cascading Failure Analysis Tools. IEEE Trans. Power Syst. 2016, 31, 4887–4900. [Google Scholar] [CrossRef]
- Shi, L.; Shi, Z.; Yao, L.; Ni, Y.; Bazarga, M. A review of mechanism of large cascading failure blackouts of modern power system. Power Syst. Technol. 2010, 34, 48–54. [Google Scholar]
- Xing, L. Reliability and Resilience in the Internet of Things; Elsevier: Amsterdam, The Netherlands, 2024. [Google Scholar]
- Huang, Q.; Shao, L.; Li, N. Dynamic detection of transmission line outages using hidden Markov models. IEEE Trans. Power Syst. 2015, 31, 2026–2033. [Google Scholar] [CrossRef]
- Ed-daoui, I.; El Hami, A.; Itmi, M.; Hmina, N.; Mazri, T. Resilience assessment as a foundation for systems-of-systems safety evaluation: Application to an economic infrastructure. Saf. Sci. 2019, 115, 446–456. [Google Scholar] [CrossRef]
- Dey, P.; Mehra, R.; Kazi, F.; Wagh, S.; Singh, N.M. Impact of topology on the propagation of cascading failure in power grid. IEEE Trans. Smart Grid 2016, 7, 1970–1978. [Google Scholar] [CrossRef]
- Rahnamay-Naeini, M.; Hayat, M.M. Cascading failures in interdependent infrastructures: An interdependent Markov-chain approach. IEEE Trans. Smart Grid 2016, 7, 1997–2006. [Google Scholar] [CrossRef]
- Liu, C.; Li, D.; Zio, E.; Kang, R. A modeling framework for system restoration from cascading failures. PLoS ONE 2014, 9, e112363. [Google Scholar] [CrossRef] [PubMed]
- Ghorbani-Renani, N.; González, A.D.; Barker, K.; Morshedlou, N. Protection-interdiction-restoration: Tri-level optimization for enhancing interdependent network resilience. Reliab. Eng. Syst. Saf. 2020, 199, 106907. [Google Scholar] [CrossRef]
- Dang, Y.; Yang, L.; He, P.; Guo, G. Effects of collapse probability on cascading failure dynamics for duplex weighted networks. Phys. A Stat. Mech. Its Appl. 2023, 626, 129069. [Google Scholar] [CrossRef]
- Li, J.; Wang, Y.; Zhong, J.; Sun, Y.; Guo, Z.; Chen, Z.; Fu, C. Network resilience assessment and reinforcement strategy against cascading failure. Chaos Solitons Fractals 2022, 160, 112271. [Google Scholar] [CrossRef]
- Al-Aqqad, W.; Hayajneh, H.; Zhang, X. A Simulation Study of the Resiliency of Mobile Energy Storage Networks. Processes 2023, 11, 762. [Google Scholar] [CrossRef]
- Lv, G.; Xing, L.; Wang, H.; Liu, H. Load Redistribution-based Reliability Enhancement for Storage Area Networks. Int. J. Math. Eng. Manag. Sci. 2023, 8, 1–14. [Google Scholar] [CrossRef]
- Lyu, G.; Xing, L.; Zhao, G. Static and Dynamic Load-Triggered Cascading Failure Mitigation for Storage Area Networks. Int. J. Math. Eng. Manag. Sci. 2024, 9, 697–713. [Google Scholar] [CrossRef]
- Alam, M.G.R.; Suma, T.M.; Uddin, S.M.; Siam, M.B.A.K.; Mahbub, M.S.B.; Hassan, M.M.; Fortino, G. Queueing theory based vehicular traffic management system through Jackson network model and optimization. IEEE Access 2021, 9, 136018–136031. [Google Scholar] [CrossRef]
- Liang, W.; Cui, L.; Tso, F.P. Low-latency service function chain migration in edge-core networks based on open Jackson networks. J. Syst. Arch. 2022, 124, 102405. [Google Scholar] [CrossRef]
- Doncel, J.; Assaad, M. Age of information of Jackson networks with finite buffer size. IEEE Wirel. Commun. Lett. 2021, 10, 902–906. [Google Scholar] [CrossRef]
- Mandalapu, J.; Jagannathan, K. The classical capacity of quantum Jackson networks with waiting time-dependent erasures. In Proceedings of the 2022 IEEE Information Theory Workshop (ITW), Mumbai, India, 1–9 November 2022; pp. 552–557. [Google Scholar]
- Allen, A.O. Probability, Statistics, and Queueing Theory; Academic Press: San Diego, CA, USA, 1990. [Google Scholar]
- Kleinrock, L. Queueing Systems: Theory; Wiley: Hoboken, NJ, USA, 1975; Volume 2. [Google Scholar]
- Dell Technologies. Dell EMC PowerEdge T150 Technical Guide. 2022. Available online: https://i.dell.com/sites/csdocuments/product_docs/en/dell-emc-poweredge-t150-technical-guide.pdf (accessed on 1 August 2025).
- Dell Technologies. Dell Unity XT HFA and AFA Storage. 2023. Available online: https://www.delltechnologies.com/asset/da-dk/products/storage/technical-support/h17713_dell_emc_unity_xt_series_ss.pdf (accessed on 1 August 2025).
- Dell Technologies. Connectrix B-Series DS-6600B Switches. 2024. Available online: https://www.delltechnologies.com/asset/en-us/products/storage/technical-support/h16567-connectrix-ds-6600b-switches-ss.pdf (accessed on 1 August 2025).
- Masich, I.S.; Tynchenko, V.S.; Nelyub, V.A.; Bukhtoyarov, V.V.; Kurashkin, S.O.; Gantimurov, A.P.; Borodulin, A.S. Prediction of Critical Filling of a Storage Area Network by Machine Learning Methods. Electronics 2022, 11, 4150. [Google Scholar] [CrossRef]
- Yang, Y.; Shi, Y.; Yi, C.; Cai, J.; Kang, J.; Niyato, D.; Shen, X. Dynamic Human Digital Twin Deployment at the Edge for Task Execution: A Two-Timescale Accuracy-Aware Online Optimization. IEEE Trans. Mob. Comput. 2024, 23, 12262–12279. [Google Scholar] [CrossRef]




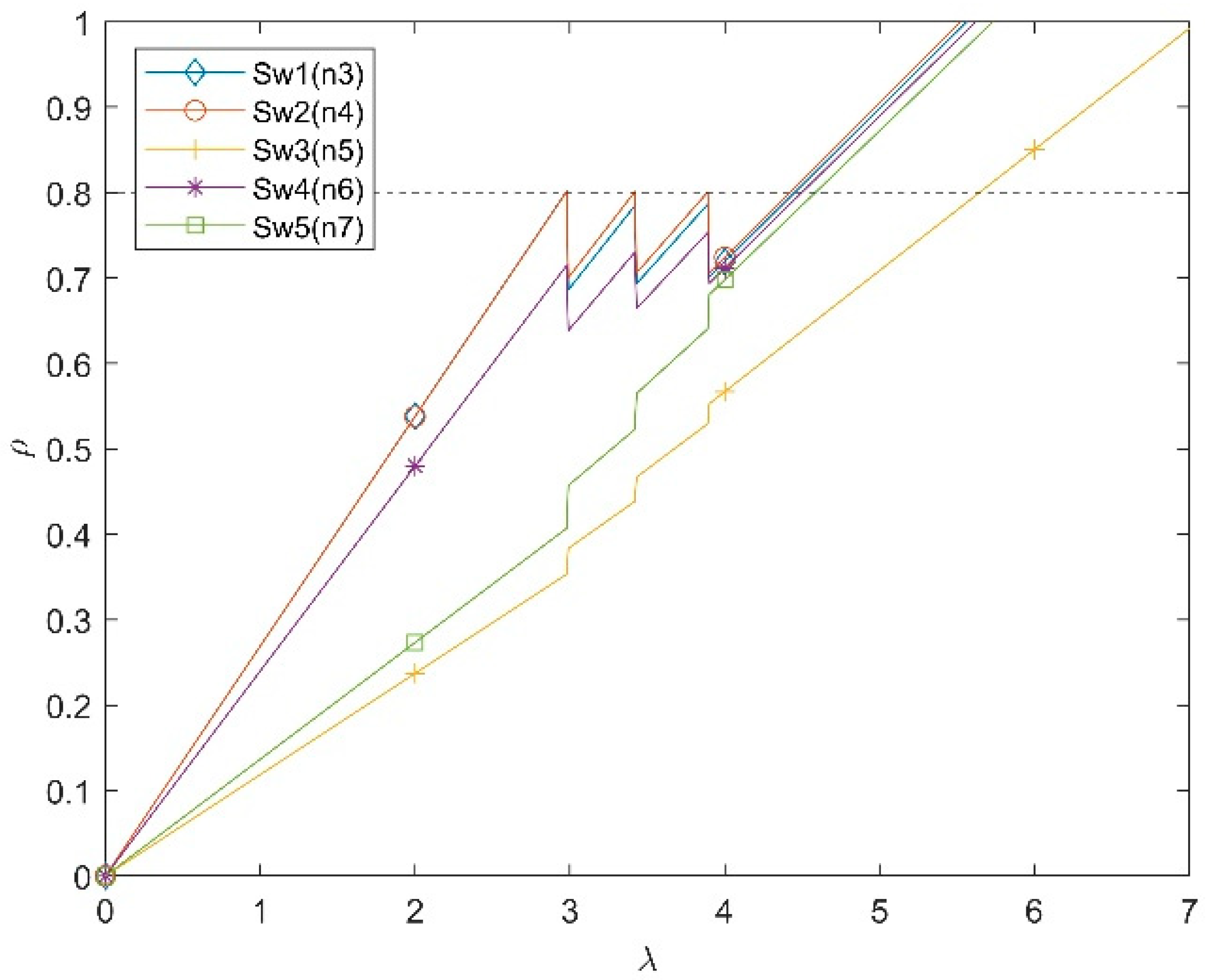
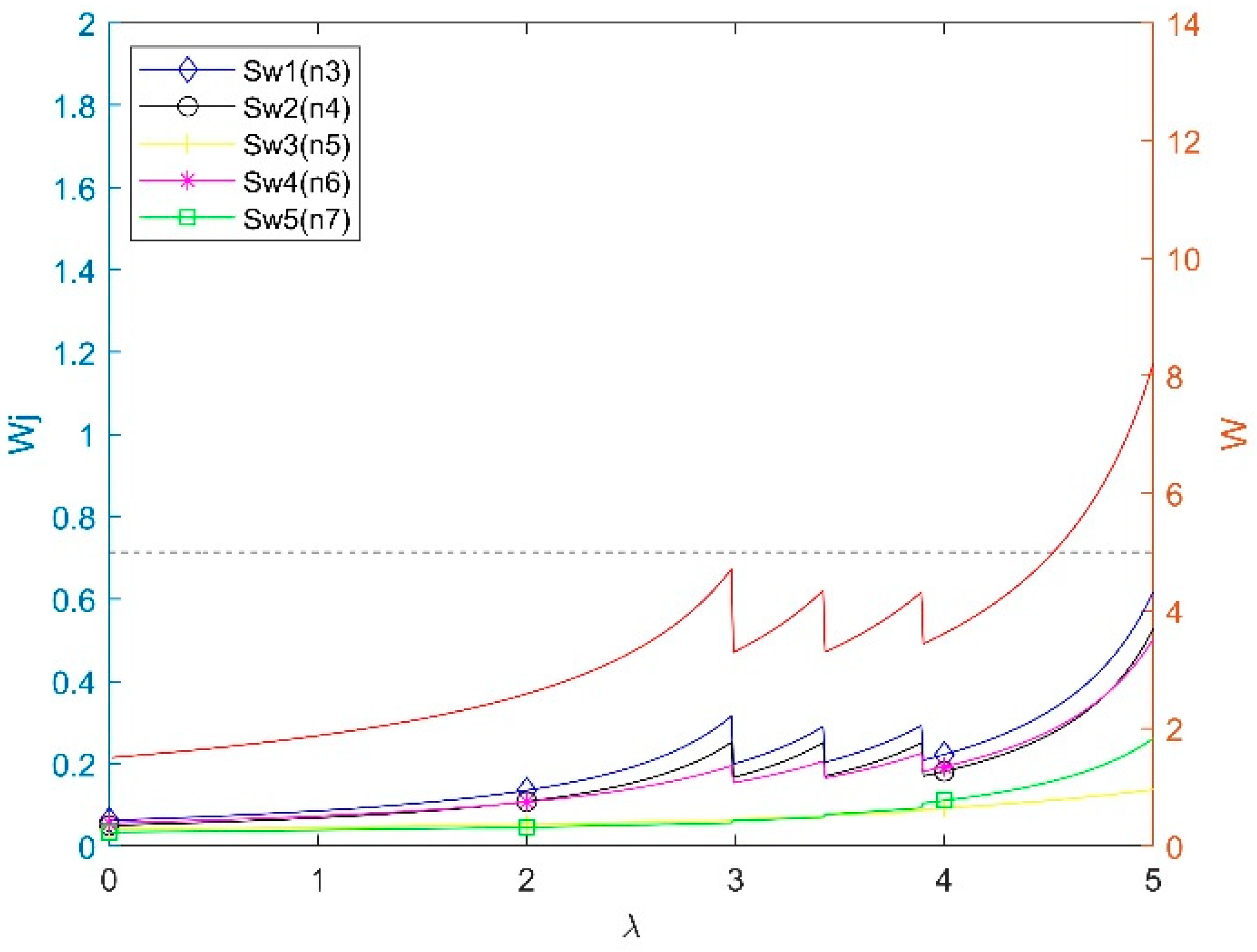


| Switch | Average Service Rate μ (Gb/s) |
|---|---|
| Sw1 | 16 |
| Sw2 | 20 |
| Sw3 | 25 |
| Sw4 | 18 |
| Sw5 | 30 |
| Redistribution | First | Second | Third | |||
|---|---|---|---|---|---|---|
| λ | 2.98 | 3.13 | 3.25 | |||
| before | after | before | after | before | after | |
| Sw1 | 0.799188 | 0.746299 | 0.783991 | 0.762454 | 0.791779 | 0.775559 |
| Sw2 | 0.798649 | 0.761487 | 0.799946 | 0.768714 | 0.798280 | 0.782550 |
| Sw3 | 0.352123 | 0.347071 | 0.364601 | 0.365864 | 0.379936 | 0.385192 |
| Sw4 | 0.712482 | 0.712791 | 0.748791 | 0.754322 | 0.783335 | 0.771306 |
| Sw5 | 0.405723 | 0.410676 | 0.431418 | 0.424570 | 0.440899 | 0.447452 |
| ρavg | 0.613633 | 0.595665 | 0.625749 | 0.615185 | 0.638846 | 0.632412 |
| ρstd | 0.194960 | 0.178844 | 0.187877 | 0.180618 | 0.187565 | 0.177568 |
| Redistribution | First | Second | Third | |||
|---|---|---|---|---|---|---|
| λ | 2.98 | 3.13 | 3.25 | |||
| before | after | before | after | before | after | |
| Sw1 | 0.311236 | 0.246353 | 0.28934 | 0.263107 | 0.300162 | 0.27847 |
| Sw2 | 0.248323 | 0.209632 | 0.249932 | 0.216183 | 0.247869 | 0.229938 |
| Sw3 | 0.061740 | 0.061262 | 0.062952 | 0.063078 | 0.064509 | 0.065061 |
| Sw4 | 0.193225 | 0.193433 | 0.221152 | 0.226132 | 0.256412 | 0.242926 |
| Sw5 | 0.056091 | 0.056562 | 0.058625 | 0.057928 | 0.05962 | 0.060327 |
| Wavg | 0.174123 | 0.153449 | 0.176401 | 0.165285 | 0.185714 | 0.175344 |
| Wstd | 0.101225 | 0.079085 | 0.096857 | 0.086987 | 0.102518 | 0.093353 |
| W | 4.6612 | 4.0329 | 4.5674 | 4.2172 | 4.6780 | 4.3893 |
| Redistribution | First | Second | Third | |||
|---|---|---|---|---|---|---|
| λ | 2.98 | 3.29 | 3.50 | |||
| before | after | before | after | before | after | |
| Sw1 | 0.799187 | 0.614231 | 0.678343 | 0.608058 | 0.646989 | 0.775742 |
| Sw2 | 0.798649 | 0.637256 | 0.703771 | 0.632921 | 0.673444 | 0.778516 |
| Sw3 | 0.352123 | 0.340244 | 0.375758 | 0.396116 | 0.421478 | 0.465316 |
| Sw4 | 0.712481 | 0.724201 | 0.79979 | 0.750534 | 0.798586 | 0.715498 |
| Sw5 | 0.405723 | 0.406378 | 0.448795 | 0.476845 | 0.507374 | 0.544798 |
| ρavg | 0.613633 | 0.544462 | 0.601291 | 0.572895 | 0.609574 | 0.655974 |
| ρstd | 0.194959 | 0.145984 | 0.161221 | 0.123993 | 0.131932 | 0.127761 |
| Redistribution | First | Second | Third | |||
|---|---|---|---|---|---|---|
| λ | 2.98 | 3.29 | 3.50 | |||
| before | after | before | after | before | after | |
| Sw1 | 0.311235 | 0.162014 | 0.194306 | 0.159462 | 0.177048 | 0.278697 |
| Sw2 | 0.248323 | 0.137838 | 0.168788 | 0.136211 | 0.153113 | 0.22575 |
| Sw3 | 0.061740 | 0.060628 | 0.064078 | 0.066238 | 0.069142 | 0.074811 |
| Sw4 | 0.193224 | 0.201435 | 0.277487 | 0.222698 | 0.275828 | 0.195273 |
| Sw5 | 0.056091 | 0.056153 | 0.060474 | 0.063716 | 0.067665 | 0.073228 |
| Wavg | 0.101224 | 0.057011 | 0.082366 | 0.05993 | 0.077306 | 0.082446 |
| Wstd | 0.174123 | 0.123614 | 0.153027 | 0.129665 | 0.148559 | 0.169552 |
| W | 4.6612 | 3.0654 | 3.7034 | 3.0559 | 3.4440 | 4.0638 |
| Redistribution | First | Second | Third | |||
|---|---|---|---|---|---|---|
| λ | 2.98 | 3.26 | 3.4 | |||
| ρ | before | after | before | after | before | after |
| Sw1 | 0.799188 | 0.554985 | 0.607306 | 0.762734 | 0.79559 | 0.556714 |
| Sw2 | 0.798649 | 0.581239 | 0.636036 | 0.765772 | 0.798759 | 0.573061 |
| Sw3 | 0.352123 | 0.337012 | 0.368784 | 0.42097 | 0.439104 | 0.414703 |
| Sw4 | 0.712482 | 0.729613 | 0.798399 | 0.696212 | 0.726203 | 0.772203 |
| Sw5 | 0.405723 | 0.404333 | 0.442452 | 0.490278 | 0.511397 | 0.490815 |
| ρavg | 0.613633 | 0.521436 | 0.570595 | 0.627193 | 0.654211 | 0.561499 |
| ρstd | 0.19496 | 0.138395 | 0.151442 | 0.143954 | 0.150155 | 0.119246 |
| Redistribution | First | Second | Third | |||
|---|---|---|---|---|---|---|
| λ | 2.98 | 3.26 | 3.4 | |||
| Wj | before | after | before | after | before | after |
| Sw1 | 0.311236 | 0.140445 | 0.159157 | 0.263417 | 0.305758 | 0.140993 |
| Sw2 | 0.248323 | 0.119402 | 0.137376 | 0.213468 | 0.248459 | 0.117113 |
| Sw3 | 0.061740 | 0.060333 | 0.063370 | 0.069081 | 0.071314 | 0.068341 |
| Sw4 | 0.193225 | 0.205467 | 0.275571 | 0.182876 | 0.202908 | 0.243881 |
| Sw5 | 0.056091 | 0.055960 | 0.059786 | 0.065395 | 0.068222 | 0.065464 |
| Wavg | 0.174123 | 0.116321 | 0.139052 | 0.158847 | 0.179332 | 0.127158 |
| Wstd | 0.101225 | 0.055347 | 0.078811 | 0.079104 | 0.095217 | 0.065088 |
| W | 4.6612 | 2.8168 | 3.3074 | 3.9541 | 4.3962 | 2.7690 |
| ρstd | ||||
| s | First | Second | Third | Average |
| 0.01 | −0.0827 | −0.0386 | −0.0533 | −0.0582 |
| 0.05 | −0.2512 | −0.2309 | −0.0316 | −0.1712 |
| 0.07 | −0.2901 | −0.0495 | −0.2059 | −0.1818 |
| Wstd | ||||
| s | First | Second | Third | Average |
| 0.01 | −0.2187 | −0.1019 | −0.0894 | −0.1367 |
| 0.05 | −0.4368 | −0.2724 | 0.0665 | −0.2142 |
| 0.07 | −0.4532 | 0.0037 | −0.3164 | −0.2553 |
| W | ||||
| s | First | Second | Third | Average |
| 0.01 | −0.1348 | −0.0767 | −0.0617 | −0.0911 |
| 0.05 | −0.3424 | −0.1748 | 0.1800 | −0.1124 |
| 0.07 | −0.3957 | 0.1955 | −0.3701 | −0.1900 |
| Redistribution | First | Second | Third | |||
|---|---|---|---|---|---|---|
| λ | 2.98 | 3.42 | 3.89 | |||
| before | after | before | after | before | after | |
| Sw1 | 0.799188 | 0.681535 | 0.782504 | 0.689241 | 0.784239 | 0.697394 |
| Sw2 | 0.798649 | 0.695682 | 0.798746 | 0.701763 | 0.798487 | 0.70243 |
| Sw3 | 0.352123 | 0.380847 | 0.437269 | 0.464034 | 0.527992 | 0.549905 |
| Sw4 | 0.712482 | 0.634236 | 0.728197 | 0.660232 | 0.751231 | 0.690172 |
| Sw5 | 0.405723 | 0.454048 | 0.521315 | 0.561399 | 0.638777 | 0.677011 |
| ρavg | 0.613633 | 0.56927 | 0.653606 | 0.615334 | 0.700145 | 0.663382 |
| ρstd | 0.194960 | 0.127737 | 0.146661 | 0.090276 | 0.102718 | 0.05738 |
| Redistribution | First | Second | Third | |||
|---|---|---|---|---|---|---|
| λ | 2.98 | 4.29 | 5.85 | |||
| before | after | before | after | before | after | |
| Sw1 | 0.311236 | 0.196254 | 0.287361 | 0.201120 | 0.289672 | 0.206539 |
| Sw2 | 0.248323 | 0.164302 | 0.248443 | 0.167652 | 0.248123 | 0.168028 |
| Sw3 | 0.061740 | 0.064604 | 0.074632 | 0.060085 | 0.084744 | 0.088870 |
| Sw4 | 0.193225 | 0.151889 | 0.204397 | 0.163510 | 0.223322 | 0.179311 |
| Sw5 | 0.056091 | 0.061055 | 0.069635 | 0.075999 | 0.092279 | 0.103203 |
| Wavg | 0.174123 | 0.127621 | 0.176893 | 0.133673 | 0.187628 | 0.149190 |
| Wstd | 0.101225 | 0.054858 | 0.089488 | 0.055381 | 0.083694 | 0.045397 |
| W | 4.6612 | 3.2605 | 4.3159 | 3.2683 | 4.2874 | 3.4054 |
| Redistribution | First | Second | Third | |||
|---|---|---|---|---|---|---|
| λ | 2.98 | 3.42 | 3.89 | |||
| before | after | before | after | before | after | |
| Sw1 | 0.799188 | 0.681535 | 0.782504 | 0.689241 | 0.784239 | 0.734402 |
| Sw2 | 0.798649 | 0.695682 | 0.798746 | 0.701763 | 0.798487 | 0.723097 |
| Sw3 | 0.352123 | 0.380847 | 0.437269 | 0.464034 | 0.527992 | 0.611864 |
| Sw4 | 0.712482 | 0.634236 | 0.728197 | 0.660232 | 0.751231 | 0.717596 |
| Sw5 | 0.405723 | 0.454048 | 0.521315 | 0.561399 | 0.638777 | 0.585046 |
| ρavg | 0.613633 | 0.569270 | 0.653606 | 0.615334 | 0.700145 | 0.674401 |
| ρstd | 0.194960 | 0.127737 | 0.146661 | 0.090276 | 0.102718 | 0.062821 |
| Redistribution | First | Second | Third | |||
|---|---|---|---|---|---|---|
| λ | 2.98 | 3.42 | 3.89 | |||
| before | after | before | after | before | after | |
| Sw1 | 0.311236 | 0.196254 | 0.287361 | 0.201120 | 0.289672 | 0.235318 |
| Sw2 | 0.248323 | 0.164302 | 0.248443 | 0.167652 | 0.248123 | 0.180568 |
| Sw3 | 0.061740 | 0.064604 | 0.074632 | 0.060085 | 0.084744 | 0.103057 |
| Sw4 | 0.193225 | 0.151889 | 0.204397 | 0.163510 | 0.223322 | 0.196724 |
| Sw5 | 0.056091 | 0.061055 | 0.069635 | 0.075999 | 0.092279 | 0.080330 |
| Wavg | 0.174123 | 0.127621 | 0.176893 | 0.133673 | 0.187628 | 0.159199 |
| Wstd | 0.101225 | 0.054858 | 0.089488 | 0.055381 | 0.083694 | 0.058363 |
| W | 4.6612 | 3.2605 | 4.3159 | 3.2683 | 4.2874 | 3.5538 |
| ρstd | ||||
| w | First | Second | Third | Average |
| 0.02 | −0.2901 | −0.0495 | −0.2059 | −0.1818 |
| 0.1 | −0.3448 | −0.3845 | −0.4414 | −0.3902 |
| 0.2 | −0.3448 | −0.3845 | −0.3884 | −0.3726 |
| Wstd | ||||
| w | First | Second | Third | Average |
| 0.02 | −0.4532 | 0.0037 | −0.3164 | −0.2553 |
| 0.1 | −0.4581 | −0.3811 | −0.4576 | −0.4323 |
| 0.2 | −0.4581 | −0.3811 | −0.3027 | −0.3806 |
| W | ||||
| w | First | Second | Third | Average |
| 0.02 | −0.3957 | 0.1955 | −0.3701 | −0.1900 |
| 0.1 | −0.3005 | −0.2427 | −0.2057 | −0.2497 |
| 0.2 | −0.3005 | −0.2427 | −0.1711 | −0.2381 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lyu, G.; Xing, L.; Zeng, Z. Utilization-Driven Performance Enhancement in Storage Area Networks. Telecom 2025, 6, 77. https://doi.org/10.3390/telecom6040077
Lyu G, Xing L, Zeng Z. Utilization-Driven Performance Enhancement in Storage Area Networks. Telecom. 2025; 6(4):77. https://doi.org/10.3390/telecom6040077
Chicago/Turabian StyleLyu, Guixiang, Liudong Xing, and Zhiguo Zeng. 2025. "Utilization-Driven Performance Enhancement in Storage Area Networks" Telecom 6, no. 4: 77. https://doi.org/10.3390/telecom6040077
APA StyleLyu, G., Xing, L., & Zeng, Z. (2025). Utilization-Driven Performance Enhancement in Storage Area Networks. Telecom, 6(4), 77. https://doi.org/10.3390/telecom6040077







