Message Passing-Based Assignment for Efficient Handover Management in LEO Networks

Abstract

As part of non-terrestrial networks (NTN), the Low Earth Orbit (LEO) plays a critical role in supporting high-throughput wireless communication. However, the high-speed mobility of LEO satellites, coupled with the high density of user terminals, makes efficient user assignment crucial in maintaining overall wireless performance. The suboptimal assignment from LEO satellites to user terminals can result in frequent unnecessary handovers, rendering the user terminal unable to receive the entire downlink signal. Consequently, it reduces user rate and user satisfaction metrics. However, finding the optimum user assignment to reduce handover issues is categorized as a non-linear programming problem with a combinatorial number of possible solutions, resulting in excessive computational complexity. Therefore, this study proposes a distributed user assignment for the LEO networks. By utilizing message-passing frameworks that map the optimization problem into a graphical representation, the proposed algorithm splits the optimization problem into a local mapping issue, thereby significantly reducing computational complexity. By exchanging small messages iteratively, the proposed algorithm autonomously determines the near-optimal solution. The extensive simulation results demonstrate that the proposed algorithm significantly outperforms the conventional algorithm in terms of user rate and user satisfaction metric under various wireless parameters.

1. Introduction

The massive increase in data, evolving from numeric formats to include images, videos, and high-dimensional sensor data, has resulted in a significant burden on traditional communication networks [1,2]. Global network traffic is predicted to reach 6641 exabytes per month by 2033, with video accounting for over 45% of this traffic [3]. This explosive growth in data size and demand significantly degrades the performance of terrestrial networks, which are limited by bandwidth, vulnerable to co-channel interference, and require high latency, especially in rural areas [4,5,6]. Consequently, relying only on terrestrial networks is insufficient to satisfy current and future communication demands. Therefore, Low Earth Orbit (LEO) satellites, as a part of non-terrestrial networks, are introduced as a novel solution to ensure reliable, low-latency, and wide-area coverage [6,7].

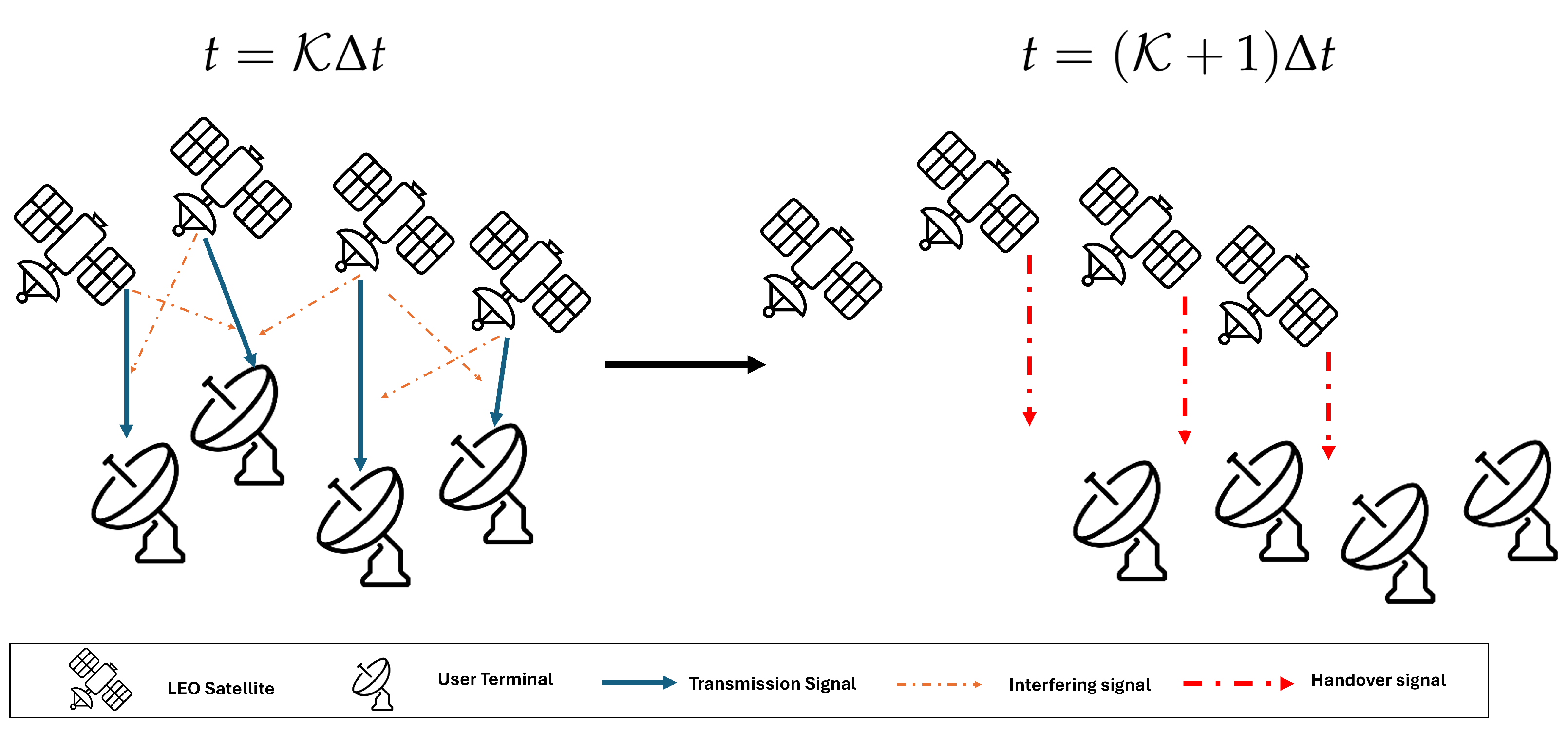
LEO networks refer to wireless communication systems that utilize satellite constellations orbiting the Earth at altitudes ranging from approximately 500 to 2000 kilometers [8]. Unlike traditional geostationary satellites, which remain fixed relative to a point on Earth at an altitude of approximately 35,786 kilometers [9], LEO satellites orbit the Earth at a rapid pace. Systematically, LEO satellites periodically transmit data to the user terminal (UT). However, the rapid movement of LEO satellites leads to frequent handover (HO) counts with very short preparation time, increasing the risk of timing mismatches that can cause data loss during the transition [10,11,12]. Additionally, the high dense UT can incur co-channel interference, which degrades overall wireless performance [12,13,14,15]. In the end, the user throughput and user satisfaction drastically drop. Accordingly, a new user assignment strategy is required to maintain the performance of LEO networks.

Over the past decade, numerous methods have been introduced to reduce the handover effect in LEO networks. A major concern is when UTs are assigned to satellites with short visibility windows, as this leads to frequent and unnecessary handovers, resulting in increased data loss, signaling overhead, and unstable connectivity [16,17]. A study in [18] proposes a graph-based approach that simultaneously maps satellite coverage. Here, the proposed approach utilizes nodes and links, where a node represents a satellite and a link indicates the overlap coverage between each pair of satellites. Then, this technique assigns link weights based on elevation angle and available channels. By computing the shortest path within the graph, each user can experience fewer handovers, improved channel quality, and more balanced traffic distribution. Another study in [19] introduces a bipartite graph that consists of weighted links. In this case, the weighted links are denoted by the time setting. If the satellite time falls within the user’s coverage range, then the weight equals the channel gain. Otherwise, the weight is equal to zero.

Another network flow technique in [20] formulates the satellite handover problem using a network flow graph, where a node represents a satellite and a UT. Additionally, weighted edges reflect the UT requests and the quality of satellite service. The handover process is optimized by computing the minimum-cost and maximum-flow within the graph, enabling multiple satellite-UT matchings under capacity constraints. To avoid negative cycles and infinite loops, a modified cost graph is proposed in this study. Simulation results demonstrate improved service quality and efficient UT handover management in large-scale LEO constellations.

Another study in [21] proposes a handover strategy for LEO satellite networks by formulating a utility function that captures two critical metrics: satellite coverage and propagation delay. The satellite coverage metric depends on both the duration of coverage and the elevation angle, while the delay component considers the propagation cost. In this method, the handover process is modeled as a bipartite graph to reflect the relationships between mobile terminals and candidate satellites. To enhance overall network performance and balance satellite workloads, a terminal random-access algorithm is introduced, aiming to maximize user space utility.

A study in [22] utilizes a weighted bipartite graph with the Kuhn–Munkres algorithm to achieve optimal matching with maximum weight. Subsequently, the hysteresis margin is employed to reduce unnecessary handover. The hysteresis margin mechanism is adjustable, providing flexibility in fulfilling various conditions. Another study in [23] proposes an enhanced message passing algorithm for LEO Satellite, which aimed to mitigate the inaccuracies caused by Taylor expansion errors in line of sight estimation. A combination of graph-based and neural network has also been introduced in [24] to tackle handover in LEO networks. This study employs a graph neural network to maximize the sum rate, while also considering load balancing concurrently. The method introduces a target satellite selection scheme, followed by an ACK decision policy to ensure load balancing at the satellites.

Recently, reinforcement learning methods have also been explored as a novel approach to address the handover issue in LEO network communication. A Q-learning study in [25] introduces an energy-aware technique to address the handover issue in LEO networks. By maximizing signal quality and minimizing associated energy costs, this study aims to reduce unnecessary handovers. However, this study is explicitly designed for single-user and remote scenarios. In another study, multi-agent reinforcement learning is proposed in [26] to address the high computational cost of handover. This study aims to minimize handover count by maximizing throughput and visible time under quality-of-service constraints.

However, conventional algorithms still leave major issues unsolved: (i) reliance on centralized processing, (ii) high computational complexity, and (iii) lack of adaptability to dynamic and large-scale LEO network environments. Centralized approaches often struggle with scalability and latency, particularly in rapidly evolving decision-making networks [27,28]. Furthermore, numerous existing methods rely on exhaustive computations, e.g., the global shortest path, which can become inefficient as the number of satellites increases significantly. Most critically, these approaches often assign UTs to satellites with short visibility durations. This practice accelerates the frequency of handovers, introduces instability, and contributes to uneven traffic distribution across the constellation.

To overcome this limitation, the proposed distributed algorithm simultaneously maximizes user rate and user satisfaction metrics in user assignment, thereby directly reducing the frequency of unnecessary handover. Using message passing frameworks, the proposed algorithm models the satellite-user network as a factor graph, where each node represents a relationship between a satellite and a UT. In addition, edges consist of weighted lines that direct the decision of the relationship based on specific constraints. Instead of relying on centralized processing, the message-passing mechanism enables each node to iteratively exchange local information via a message passing rule, allowing for the distributed computation of near-optimal decisions. This distributed framework significantly reduces processing overhead and computational complexity. As messages are propagated across the network, local decisions converge toward a near-optimum without requiring global topology awareness or a central coordinator. Compared to existing learning-based algorithms [29], which depend on implicit reward shaping and large amounts of training data, the proposed algorithm takes a different approach. It is fully message-passing-based, with objectives and constraints that are explicitly defined. Also, iterative message exchanges guide the message updates to remain feasible while ensuring a quick convergence rate. Accordingly, the proposed algorithm has a low computational load, is interpretable, and is well-suited for real-time user assignment in LEO networks. In addition, message passing techniques have been applied in numerous fields, including communication networks [30], power systems [31], manufacturing systems [32], and others.

Our main contributions in this work can be summarized as follows:

• Distributed user assignment for minimizing handover issue:
  This paper proposes a distributed user assignment strategy for LEO-UT communications. The proposed algorithm jointly maximizes both user rate and user satisfaction, thereby minimizing unnecessary handover issues. By enabling direct node-to-node message exchanges, the proposed algorithm eliminates reliance on a centralized controller, allowing each LEO satellite to determine its optimal solution autonomously based on local information. The evaluation results also show that the proposed algorithm outperforms the conventional algorithm in terms of user rate and user satisfaction metrics in various wireless parameters.
• Network-adaptable algorithm:
  The proposed algorithm adapts dynamically to variations in the number of UTs, satellite coverage, and wireless shadowing. With a low number of required iterations for local optimization, it can rapidly adjust the assignment structure without needing to gather all available messages. This ability to characterize and optimize the assignment in a highly responsive manner ensures that performance remains optimal even under rapidly changing network topologies, delivering consistent throughput and high satisfaction metrics to end-UTs.
• Low computational complexity algorithm:
  The user assignment problem is decomposed into localized optimization steps at each UT, resulting in a significant reduction in computational load compared to centralized approaches. By minimizing control message exchange and relying on lightweight calculations, the proposed algorithm supports rapid decision-making with minimal processing delay, making it well-suited for real-time operation in high-mobility LEO satellite networks.
  The rest of the manuscript is organized as follows. Section 2 presents the system models. The problem formulation is described in Section 3. The main idea and proposed algorithm are presented in Section 4. The comprehensive evaluation is presented in Section 5. Finally, a summary of this study is presented in Section 6.

2. System Models

Suppose a wireless satellite communication system consists of n LEO satellites and m UTs located on the ground. Each LEO satellite follows a deterministic orbital trajectory with a constant velocity v, allowing it to periodically cover different ground areas over time. Due to the dynamic nature of satellite motion, each satellite $i\in \{1,2,\dots ,n\}$ establishes intermittent communication attempts with UTs $j\in \{1,2,\dots ,m\}$. Thus, an invisible transmission window will exist during the handover process, leading to data loss. These communication attempts are characterized by two key parameters: the time availability ${\mathcal{T}}_{ij}$ and the elevation quality ${\varphi }_{ij}$ (see Section 2.2).

Figure 1 illustrates the dynamics of a UT’s association in a LEO satellite network. The left-hand panel shows a snapshot of transmissions and interference at a given time $t=\mathcal{K}\Delta t$, while the right-hand panel shows the snapshot of handover signal at time $t=(\mathcal{K}+1)\Delta t$, where the term $\mathcal{K}+1$ denotes the time-advancement representation, $\Delta t$ denotes a given fixed-time step, and $\mathcal{K}\in 0,1,2,\dots$ denotes a natural number. From the left-hand panel, the blue arrows represent the serving transmission from the selected satellite, and the orange dashed arrows indicate interfering signals from other satellites transmitting simultaneously. From the right-hand panel, as satellites move in orbit in an index time of $t=(\mathcal{K}+1)\Delta t$, the serving satellite changes, leading to handover events. At handover instants, a short gap may appear in which the UT cannot capture the downlink signaling, reflecting synchronization and switching delays that cause temporary service interruption. Therefore, it shows that the LEO satellite network experiences two significant challenges: (i) massive co-channel interference caused by ultra-dense LEO satellites that share the same channel; (ii) frequent handovers between satellites and UTs, which lead to invisible transmission windows where connections are temporarily lost. Accordingly, user rate, $R_{ij}$, and user satisfaction metrics, $H_{ij}$, are considered as main factors in LEO communication networks. By considering both instantaneous achievable sum rate and long-term user experience, the system can optimize overall network throughput performance while maintaining quality of service (QoS).

2.1. User Rate

The achievable data rate from the i-th LEO satellite to the j-th UT is characterized based on Shannon’s equation [33]. This formulation takes into account the co-channel interference from other LEO satellites that are simultaneously transmitting. In addition, the channel characteristics are also considered in this case. The data rate from the i-th LEO satellite to the j-th UT in bits per second (bps), i.e., $R_{ij}$, is computed as

$$R_{ij}=B{log}_2\left(1+{\displaystyle \frac{P_i{\mathcal{G}}_{ij}}{{\sum }_{g\in \xi \left(i\right)}{P}_g{\mathcal{G}}_{gj}+\sigma }}\right),$$

(1)

where B denotes the bandwidth of the communication channel, $P_i$ represents the transmit power of the i-th LEO satellite, ${\mathcal{G}}_{ij}$ denotes the channel gain between the i-th LEO satellite and the j-th UT, $\xi \left(i\right)$ represents the set of neighbor LEO satellites that potentially interfere the i-th LEO satellite in the same frequency band, and $\sigma$ is the background noise power. Finally, this formulation reflects a Signal-to-Interference-Noise Ratio (SINR)-based model [34], where the achievable rate depends on both the desired signal strength and the aggregate interference.

2.2. User Satisfaction

The time availability, ${\mathcal{T}}_{ij}$, denotes the fraction of the total observation period in which the i-th LEO satellite maintains a direct line-of-sight (LoS) communication link with the j-th UT. The altitude, orbital speed, and ground footprint of a satellite majorly affect the time availability and elevation angle to a UT. However, for the sake of simplicity, the detailed modeling of these orbital parameters is not included in this system model. Instead, the time availability and elevation angle are assumed to be precomputed and are directly utilized in the system model.

In addition, the elevation angle, ${\varphi }_{ij}$, represents the angle between the local horizontal plane at the j-th UT and the line connecting the i-th LEO satellite to the j-th UT. Higher elevation angles typically correspond to higher link quality due to reduced atmospheric path loss and signal distortion. As the satellite moves, its elevation dynamically changes, reaching a maximum of nearly $90°$ when it is close to the zenith and a minimum of nearly $0°$ when it is close to the horizon.

The LEO communication networks should be aware of user-centric metrics that consider the stability and quality of LEO satellite access over time. Accordingly, an integrated satisfaction index that jointly considers the service availability and the link elevation quality is introduced, as follows

$$H_{ij}=\eta {\mathcal{T}}_{ij}+(1-\eta ){\varphi }_{ij},$$

(2)

where $H_{ij}$ is the satisfaction index of j-th UT to the i-th LEO Satellite and $\eta \in [0,1]$ is a weighting factor that balances the contribution of time availability and elevation quality.

Here, the time availability is mathematically modeled as the fraction of time slots where the i-th LEO satellite successfully serves the j-th UT. This model is consistent with prior visibility-based analyses, where satellite-to-site availability is a fundamental factor of quality of service in LEO systems [35]. Accordingly, the notation is computed as

$${\mathcal{T}}_{ij}={\displaystyle \frac{{\mathcal{N}}_{ij}^{\mathrm{served}}}{{\mathcal{N}}_t}},$$

(3)

where ${\mathcal{N}}_{ij}^{\mathrm{served}}$ denotes the number of time slots during which the i-th LEO satellite transmits data to the j-th UT, and ${\mathcal{N}}_t$ indicates the total number of sampled time slots.

On the other side, the elevation quality is computed as the average normalized elevation angle across all served time slots. This indicates that higher elevation angles result in more substantial link budgets and reduced fading, whereas lower elevations experience higher attenuation. Such dependence of link reliability on elevation angle has been statistically characterized in recent LEO studies [36,37]. Thus, this formula is expressed as

$${\varphi }_{ij}={\displaystyle \frac{1}{{\mathcal{N}}_{ij}^{\mathrm{served}}}}\sum _{t\in {\tau }_{ij}}max\left({\displaystyle \frac{{\mathrm{El}}_{ij}\left(t\right)}{90°}},0\right),$$

(4)

where ${\mathrm{El}}_{ij}\left(t\right)$ denotes the elevation angle of the i-th LEO satellite relative to the j-th UT at time slot t. The set ${\tau }_{ij}$ represents the collection of time slots in which the link between the i-th LEO satellite and j-th UT is considered active, i.e., elevation above the visibility mask, and ${\mathcal{N}}_{ij}^{\mathrm{served}}=\left|{\tau }_{ij}\right|$ is the number of corresponding slots. The normalization by $90°$ ensures that ${\varphi }_{ij}\in [0,1]$, with unity corresponding to the satellite being directly overhead and zero corresponding to either horizon or non-visibility. If no valid serving slot exists, in this case, ${\mathcal{N}}_{ij}^{\mathrm{served}}=0$, then ${\varphi }_{ij}$ is defined as zero.

Finally, the integrated satisfaction index $H_{ij}$ represents both the continuity of service via availability and the geometry-induced link quality via elevation. This integrated mathematical rationale aligns with LEO networks design principles that jointly emphasize user-centric satisfaction metric and overall rate [20,38].

3. Problem Formulation

This section formulates the optimization of a downlink LEO satellite communication system. At any given time, a satellite can only serve UTs within its communication range. Therefore, these pairwise relationships are represented using the candidate sets, i.e., $\mathcal{M}\left(i\right)$ and $\mathcal{X}\left(j\right)$. Here, $\mathcal{M}\left(i\right)\subseteq \{1,2,\dots ,m\}$ denotes the set of UTs that can receive data from the i-th LEO satellite. In addition, $\mathcal{X}\left(j\right)\subseteq \{1,2,\dots ,n\}$ denotes the set of LEO satellites that can transmit data to the j-th UT.

A non-diagonal binary variable $C_{ij}\in \{0,1\}$ and diagonal binary variable $C_{jj}\in \{0,1\}$ are introduced to characterize the assignment decision. If the i-th LEO satellite is assigned to transmit to the j-th UT, $C_{ij}=1$; zero indicates otherwise. In addition, a self-assignment, $C_{jj}=1$, shows that the j-th UT is in an idle state, therefore actively enabled to receive data from any satellite; otherwise, the UT is in a busy state, thereby unable to receive data from any satellite.

The similarity metric, i.e., $S_{ij}$, is defined as a utility metric that combines user data rate and user satisfaction metrics across all satellite and UT pairs. Specifically, the proposed algorithm aims to simultaneously optimize two critical aspects: (i) the quality of signal transmission, measured by throughput, and (ii) the user satisfaction metric, represented by time availability and quality of elevation. Thus, the similarity metric is computed as follows:

$$S_{ij}=\left\{\begin{array}{cc}\sigma R_{ij}+(1-\sigma )H_{ij},\hfill & \mathrm{if}{C}_{ij}=1\mathrm{and}{C}_{jj}=1\hfill \\ 0,\hfill & \mathrm{if}\mathrm{otherwise}\hfill \end{array}\right..$$

(5)

where $\sigma$ indicates the weighting factor with a range of 0 and 1.

The main objective is to maximize the similarity metric, thereby enhancing the cumulative benefit derived from both the achievable data throughput and user satisfaction, as experienced by UTs. By maximizing $S_{ij}$, the mathematical framework naturally favors stable and high-quality assignments, thereby avoiding short-lived connections that trigger frequent or unnecessary handovers. This indirect handover optimization is consistent with recent LEO satellite research, where throughput-driven but stability-aware association policies have been shown to mitigate excessive handovers [20]. Furthermore, the emphasis on availability and elevation within $H_{ij}$ ensures alignment with LEO networks service continuity requirement [37,38]. However, this optimization must consider the load balancing among all involved LEO nodes. An unbalanced network, where only a subset of satellites are heavily utilized while others remain idle, can degrade overall performance. Moreover, it can magnify computational overhead and excessive resource utilization. To address this issue, the connection assignments should be fairly distributed to ensure that no individual satellite or UT is disproportionately burdened. Accordingly, the optimization problem is defined as

$$\begin{array}{cc}\hfill & \underset{C_{ij}}{max}\sum _{i=1}^n\sum _{j\in \mathcal{M}\left(i\right)}\left(S_{ij}\right)C_{ij},\hfill \end{array}$$

(6)

subject to

$$\begin{array}{cc}\hfill & \sum _{j\in \mathcal{M}\left(i\right)}{C}_{ij}=1,\forall i\in \{1,\dots ,n\},\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill & \sum _{i\in \mathcal{X}\left(j\right)}{C}_{ij}\le [C_{jj}=1],\forall j\in \{1,\dots ,m\}.\hfill \end{array}$$

(8)

Two constraints are established to guide the decision-making process for the objective function. Constraint (7) ensures that each satellite can transmit to exactly one UT among its set of candidate UTs. This constraint ensures that each satellite transmits exclusively, preventing any satellite from serving multiple UTs simultaneously during a given scheduling interval. This constraint design is motivated by both wireless and algorithmic considerations. From the wireless side, dedicating the complete resource of a satellite to one UT maximizes user rate and satisfaction metric under limited LEO power and bandwidth budgets [37,39], mitigates inter-beam interference [40], guarantees deterministic latency bounds in ultra-dense scenarios [38], and simplifies frequent handovers by reducing signaling overhead [41]. From the algorithmic side, the one-to-one mapping maintains factor-graph sparsity, ensuring convergence of the message-passing algorithm [42], lowers computational complexity [43], and improves interpretability of assignment decisions [44]. Constraint (8) controls the reception capability of the UTs. Each UT may or may not be ready to receive data, as indicated by a diagonal variable $C_{jj}$, where $C_{jj}=1$ implies that the j-th UT is ready to receive and $C_{jj}=0$ indicates otherwise. If $C_{jj}=1$, the UT can accept data from one and only one satellite within its candidate set $\mathcal{X}\left(j\right)$. This constraint also allows a UT not to receive any signal from the satellite; in this case, $C_{ij}=0$ and $C_{jj}=1$. For ready UTs, this constraint limits the number of transmitting satellites to exactly one, minimizing redundant allocations. In addition, for any UT not prepared to receive data, i.e., $C_{jj}=0$, no satellite is allowed to transmit to the corresponding UT.

The optimization of the objective function (6) falls under the category of nonlinear programming, which requires excessive computational resources due to its complex and non-convex nature. Finding the global optimum through conventional methods typically involves an exhaustive search, which can lead to scalability issues when applied to large-scale systems. To address this limitation, the proposed algorithm employs a distributed algorithmic framework that effectively decomposes the original large-scale optimization problem into local subproblems. Each local subproblem can then be solved independently, allowing for parallel processing and reducing the overall load on the system. Although this method does not always guarantee the global optimal solution, it typically yields a near-optimal outcome and achieves an efficient trade-off between solution quality and computational efficiency. As a result, both the computational burden and algorithmic complexity can be significantly reduced, making the approach suitable for real-time or resource-constrained environments.

4. Proposed Algorithm

To enable a distributed algorithm, a constrained optimization problem should be transformed into an unconstrained optimization problem. Therefore, the optimization problem is computed as

$$\begin{array}{cc}\hfill \mathrm{maximize}& \sum _{i,j}{S}_{ij}\left(C_{ij}\right)+\sum _i{F}_i\left(C_{ij}\right)+\sum _j{G}_j\left(C_{ij}\right)\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \mathrm{subject}\mathrm{to}& F_i\left(C_{ij}\right)=\left\{\begin{array}{cc}0,\hfill & \sum _{j\in \mathcal{M}\left(i\right)}{C}_{ij}=1\hfill \\ -\infty ,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill & G_j\left(C_{ij}\right)=\left\{\begin{array}{cc}0,\hfill & \sum _{i\in \mathcal{X}\left(j\right)}{C}_{ij}\le [C_{jj}=1]\hfill \\ -\infty ,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\hfill \end{array}$$

(11)

Here, two functions (10) and (11) are introduced to steer the decision of the objective function based on the constraints (7) and (8). Function (10) enforces the objective function on a LEO satellite to only transmit to one UT. If an objective function violates this function, then $F_i(C_{ij})$ has a value of minus infinity, and by maximization is never achieved. Otherwise, the $F_i(C_{ij})$ equal zero. In addition, Function (11) controls the matching problem, where the LEO satellite can only transmit if the UT is ready to receive data, $C_{jj}=1$. If this constraint is violated, the maximization result only oscillates iteratively without ever achieving convergent values.

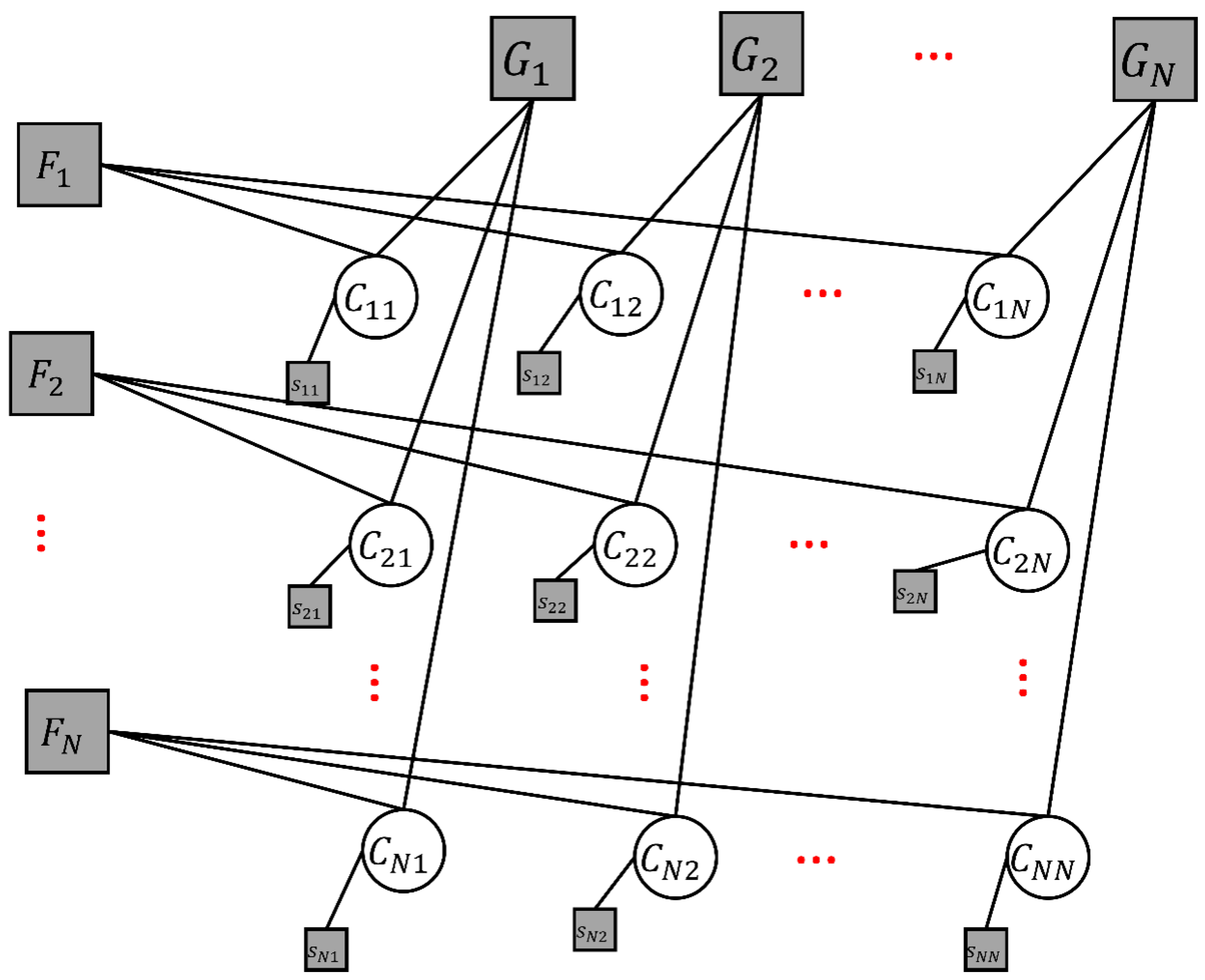
A graphical representation, specifically a factor graph, is used to structure the unconstrained optimization problem systematically. This factor graph models the dependencies among the variables and the constraints in the optimization. Accordingly, the flow of messages exchanged between nodes in the factor graph can be represented. Figure 2 presents the constructed factor graph that consists of variable nodes indicated by circles and function nodes indicated by squares. The function nodes $F_i$ correspond to the satellite-side constraint that is steered by constraint (7), i.e., ensuring that each satellite can serve at most one UT. Conversely, the function nodes $G_j$ represent the user-side constraint that enforces constraint (8), i.e., ensuring the reception capability of the UT. Each variable node is also linked to an objective function, $S_{ij}$ (6). The edges in the figure represent the logical and bias dependencies between variable nodes and function nodes. During the iterative message-passing process, satellites exchange small-sized messages with their candidate UTs, while UTs send back response messages reflecting their selection status. This iterative exchange enables distributed inference over the factor graph. Accordingly, the corresponding figure presents how the mathematical formulation of Equations (6)–(8) is mapped into a factor graph structure.

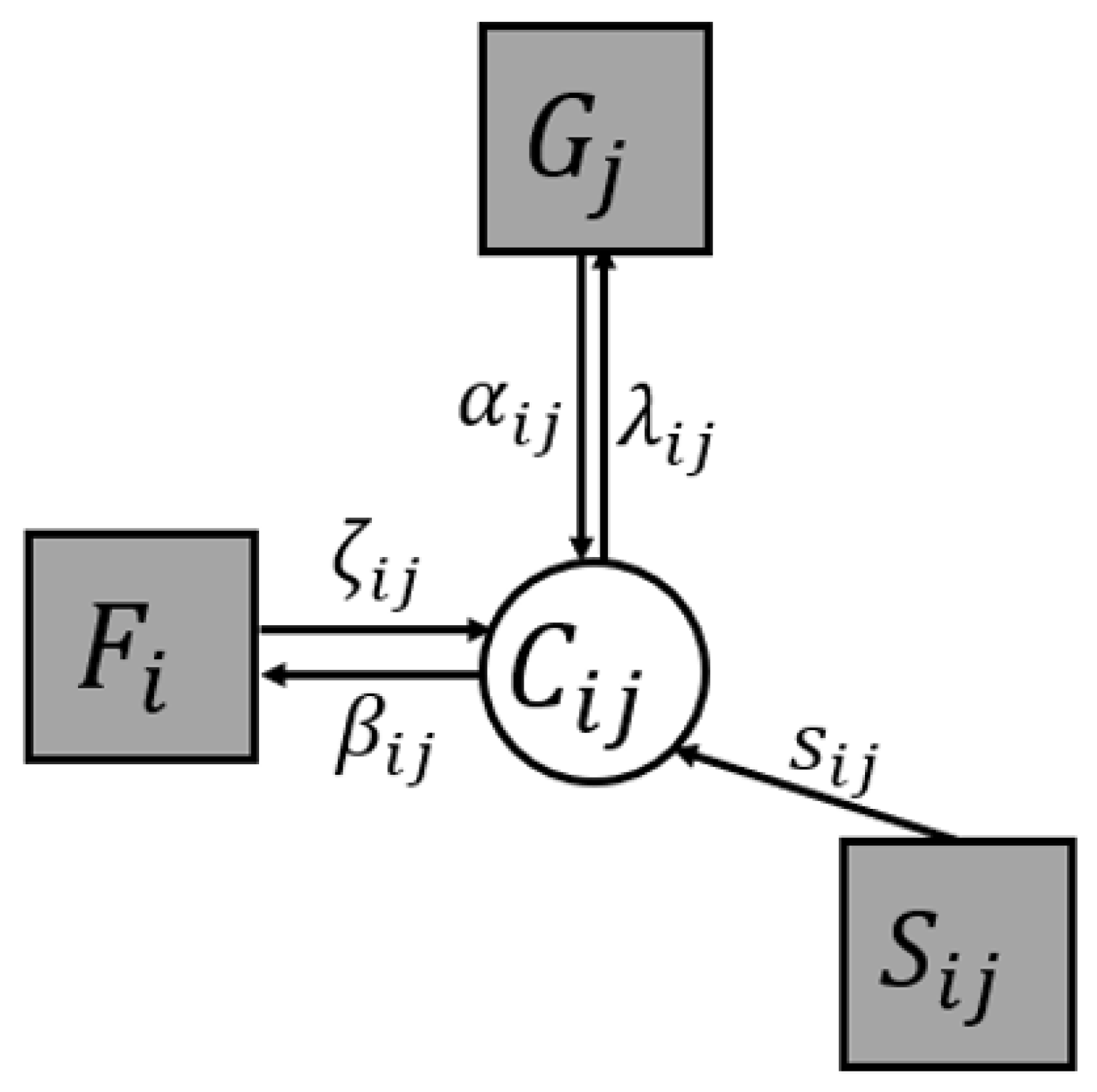
Figure 3 illustrates the detailed structure of a single node, denoted as $C_{ij}$, within the overall factor graph. This figure shows the local interactions between three key function nodes, i.e., $F_i$, $G_j$, and $S_{ij}$, each of which is connected to the variable node, i.e., $C_{ij}$. Initial messages are exchanged via the edges connecting these nodes, with ${\beta }_{ij}$ and ${\zeta }_{ij}$ representing the initial messages between $F_i$ and $C_{ij}$. In addition, the ${\alpha }_{ij}$ and ${\lambda }_{ij}$ denoting the initial messages between $G_j$ and $C_{ij}$. Also, $s_{ij}$ conveying information between $S_{ij}$ and $C_{ij}$. These messages reflect the probabilistic inference, where local computations update beliefs or costs iteratively across the factor graph. By utilizing this node-level structure, the overall problem can be decomposed into smaller and more manageable subproblems. By applying message passing rule [42,45,46], the initial messages ${\beta }_{ij}$, ${\zeta }_{ij}$, ${\alpha }_{ij}$, ${\lambda }_{ij}$ are exchanged iteratively by considering all involved messages and max-sum rule to produce final messages ${\tilde{\beta }}_{ij}$, ${\tilde{\zeta }}_{ij}$, ${\tilde{\alpha }}_{ij}$, and ${\tilde{\lambda }}_{ij}$. The transformation from initial messages into final messages is expressed by finding the marginal of binary preference values, as shown below:

$$\begin{array}{c}\hfill {\tilde{\beta }}_{ij}={\beta }_{ij}\left(1\right)-{\beta }_{ij}\left(0\right),\hfill \end{array}$$

(12)

$$\begin{array}{c}\hfill {\tilde{\zeta }}_{ij}={\zeta }_{ij}\left(1\right)-{\zeta }_{ij}\left(0\right),\hfill \end{array}$$

(13)

$$\begin{array}{c}\hfill {\tilde{\lambda }}_{ij}={\lambda }_{ij}\left(1\right)-{\lambda }_{ij}\left(0\right),\hfill \end{array}$$

(14)

$$\begin{array}{c}\hfill {\tilde{\alpha }}_{ij}={\alpha }_{ij}\left(1\right)-{\alpha }_{ij}\left(0\right),\hfill \end{array}$$

(15)

The initial messages ${\tilde{\beta }}_{ij}$ and ${\tilde{\zeta }}_{ij}$ represent the interaction between the variable node $C_{ij}$ and the function node $F_i$. Here, the message ${\tilde{\beta }}_{ij}$ is an incoming message from a variable node that is simply the summation of all the involved messages to the variable nodes, $C_{ij}$. Considering the preference of binary value; therefore, ${\tilde{\beta }}_{ij}$ is computed as

$${\tilde{\beta }}_{ij}={\tilde{s}}_{ij}+{\tilde{\alpha }}_{ij}.$$

(16)

In addition, the final message ${\tilde{\zeta }}_{ij}$ is characterized based on the preference value of the variable node, specifically the initial messages ${\zeta }_{ij}\left(1\right)$ and ${\zeta }_{ij}\left(0\right)$. The message ${\zeta }_{ij}\left(1\right)$ represents the maximum value obtained when the variable $C_{ij}$ is set to 1. Accordingly, by applying the max-sum message passing principle, the message ${\zeta }_{ij}\left(1\right)$ is represented as the maximum value between the associated local function node $F_i$ under the condition $C_{ik}=1$ with $k\ne j$ and the other incoming messages besides from j node, i.e., ${\zeta }_{ix}\left(C_{i}j\right)$. In this case, when the i-th LEO satellite transmits to the j-th UT; thus, the i-th LEO satellite can never transmit to any other nearby UTs. Accordingly, this formulation is expressed as follows:

$$\begin{array}{cc}{\zeta }_{ij}\left(1\right)\hfill & =\underset{C_{ik},k\ne j}{max}\left[F_i(C_{i1},\dots ,C_{ij}=1,\dots ,C_{iN})+\sum _{x\ne j}{\zeta }_{ix}\left(C_{i}x\right)\right]\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & =\sum _{i\ne s}{\beta }_{is}\left(0\right).\hfill \end{array}$$

(18)

On the other hand, the value ${\zeta }_{ij}\left(0\right)$ is obtained identically by setting $C_{ij}=0$ and maximizing over the remaining variables. In this case, when the i-th LEO satellite does not choose the j-th UT, then the i-th satellite can transmit to exactly one neighboring satellite in addition to the j-th UT. Therefore, the message $C_{ij}=0$ is represented as follows:

$$\begin{array}{cc}\hfill {\zeta }_{ij}\left(0\right)& =\underset{C_{ik},k\ne j}{max}\left[F_i(C_{i1},\dots ,C_{ij}=0,\dots ,C_{iN})+\sum _{x\ne j}{\zeta }_{ix}\left(C_i\right)\right]\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill & =\underset{i\ne s}{max}\left[{\beta }_{is}\left(1\right)+\sum _{m\in \ell (i,s)}{\beta }_{im}\left(0\right)\right]\hfill \end{array}$$

(20)

The final message ${\tilde{\zeta }}_{ij}$ is computed as the preference value of a binary choice, as follows

$$\begin{array}{cc}\hfill {\tilde{\zeta }}_{ij}& ={\zeta }_{ij}\left(1\right)-{\zeta }_{ij}\left(0\right)\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill & =\left[\sum _{i\ne s}{\beta }_{is}\left(0\right)\right]-\left[\underset{i\ne s}{max}\left({\beta }_{is}\left(1\right)+\sum _{m\in \ell (i,s)}{\beta }_{im}\left(0\right)\right)\right]\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & =-\underset{i\ne s}{max}\left[{\beta }_{is}\left(1\right)-{\beta }_{is}\left(0\right)\right]\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & =-\underset{i\ne s}{max}{\beta }_{is}\hfill \end{array}$$

(24)

The final message ${\tilde{\zeta }}_{ij}$ in (24) indicates the update mechanism, where each variable node updates its belief by combining local computations with other incoming messages.

The initial messages ${\lambda }_{ij}$ and ${\alpha }_{ij}$ are introduced as intermediary messages between variable nodes $C_{ij}$ and factor nodes $G_j$ in the factor graph. Similar to the final message ${\tilde{\beta }}_{ij}$, the final message ${\tilde{\lambda }}_{ij}$ also considers the binary preference value that quantify incoming values from other involved messages, i.e., ${\tilde{\zeta }}_{ij}$ and ${\tilde{s}}_{ij}$. Thus, the computed messages are expressed as

$${\tilde{\lambda }}_{ij}={\tilde{s}}_{ij}+{\tilde{\zeta }}_{ij}$$

(25)

In addition, the final message ${\tilde{\alpha }}_{ij}$ is affected by the function node $G_j$; therefore, it will consider the diagonal and non-diagonal variable nodes. Similar with previous messages, the final message ${\tilde{\alpha }}_{ij}$ need to consider the binary preference value: $C_{ij}=1$ and $C_{ij}=0$. For the non-diagonal variable nodes with $C_{ij}=1$, the i-th LEO satellite can only transmit data to the j-th UT; accordingly, there is no neighboring node of the i-th LEO satellite that allows it to transmit data to the j-th node. This logic is confirmed by the following equations, as shown below:

$$\begin{array}{cc}\hfill {\alpha }_{ij}\left(1\right)& =\underset{C_{ij}^{\mathrm{opt}}}{max}\left[g_i(C_{ij},\dots ,C_{ij}=1,\dots ,C_{nj})+\sum _{k\ne i}{\lambda }_{kj}\left(C_{tj}\right)\right]\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & ={\lambda }_{ij}\left(1\right)+\sum _{k\in E_{i\left(j\right)}}{\lambda }_{kj}\left(0\right)\hfill \end{array}$$

(27)

For non-diagonal variable nodes with $C_{ij}=0$, the i-th LEO satellite does not transmit data to the j-th UT. In this case, there are two possible options: (i) exactly one neighboring satellite can transmit the data to the j-th UT, or (ii) none of the satellites transmit to the j-th UT. Therefore, the message value ${\alpha }_{ij}\left(0\right)$ in this case is calculated as the maximum of two possible options. The first options is the sum of three parts: the message from i-th LEO satellite to the j-th user in the preference value of $C_{ij}=0$, the message from the neighbor m-th satellite to j-th UT in the state 1, and the sum of all other messages to the j-th UT from any neighboring of i-th LEO satellite, except the m-th satellite. The second option is the sum of all messages to the j-th UT from satellites other than the i-th LEO satellite, expressed as ${\sum }_{k\ne i}{\lambda }_{kj}\left(0\right)$. Accordingly, the ${\alpha }_{ij}\left(0\right)$ is defined as

$$\begin{array}{cc}\hfill {\alpha }_{ij}\left(0\right)& =max\left[{\lambda }_{ij}\left(0\right)+{\lambda }_{mj}\left(1\right)+\sum _{l\in E_{l\left(j\right),mj}}{\lambda }_{lj}\left(0\right),\sum _{k\ne i}{\lambda }_{kj}\left(0\right)\right]\hfill \end{array}$$

(28)

By considering the preference value, the final message ${\tilde{\alpha }}_{ij}$ is computed as

$$\begin{array}{cc}\hfill {\tilde{\alpha }}_{ij}& ={\alpha }_{ij}\left(1\right)-{\alpha }_{ij}\left(0\right)\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & =\left[{\lambda }_{ij}\left(1\right)+\sum _{k\in E_{i\left(j\right)}}{\lambda }_{kj}\left(0\right)\right]-\left[max\left[{\lambda }_{ij}\left(1\right)+{\lambda }_{mj}\left(1\right)+\sum _{l\in E_{l\left(j\right),mj}}{\lambda }_{lj}\left(0\right),\sum _{k\ne i}{\lambda }_{kj}\left(0\right)\right]\right]\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill & =min\left[{\lambda }_{mj}\left(0\right)-{\lambda }_{mj}\left(1\right),{\lambda }_{ij}\left(1\right)-{\lambda }_{ij}\left(0\right)\right]\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill & =min[-{\lambda }_{mj},{\lambda }_{ij}].\hfill \end{array}$$

(32)

Two binary preference values are also considered for the diagonal variable, $i=j$. For $C_{jj}=1$ that indicates the j-th UT is ready to receive the data, then there are two possible cases, i.e., (i) there is exactly one satellite that transmit to the j-th UT, and consequently, there is not another concurrent neighboring transmit to the j-th UT; (ii) none satellite transmit to the j-th UT due to optimization choice. Thus, the message ${\alpha }_{jj}\left(1\right)$ is expressed as follows:

$$\begin{array}{cc}\hfill {\alpha }_{jj}\left(1\right)& =max\left[{\lambda }_{ij}\left(1\right)+\sum _{k\in \mathcal{E}(i,j)}{\lambda }_{kj}\left(0\right),\sum _{k\ne j}{\lambda }_{kj}\left(0\right)\right]\hfill \end{array}$$

(33)

In the case of $C_{jj}=0$, i.e., the j-th UT is not ready to receive the data; therefore, no satellite allows transmitting to the j-th UT also. Accordingly, the formulation is computed as

$$\begin{array}{cc}\hfill {\alpha }_{jj}\left(0\right)& =\sum _{k\ne j}{\lambda }_{kj}\left(0\right)\hfill \end{array}$$

(34)

By finding the marginal of the binary preference value, the final message is computed as

$$\begin{array}{cc}\hfill {\tilde{\alpha }}_{jj}& ={\alpha }_{kj}\left(1\right)-{\alpha }_{ij}\left(0\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & =\left[max\left[{\lambda }_{ij}\left(1\right)+\sum _{k\in \mathcal{E}(i,j)}{\lambda }_{kj}\left(0\right),\sum _{k\ne j}{\lambda }_{kj}\left(0\right)\right]\right]-\left[\sum _{k\ne j}{\lambda }_{kj}\left(0\right)\right]\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill & =max\left[{\lambda }_{ij}\left(1\right)-{\lambda }_{ij}\left(0\right),0\right]\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill & =max[{\lambda }_{ij},0]\hfill \end{array}$$

(37)

In the final stage of the algorithm, the maximum a posteriori (MAP) criterion is employed to determine the optimal decision. In this case, the MAP decision rule is applied using the marginalized final messages obtained from the iterative message passing process. These marginal messages summarize the aggregated information from all relevant nodes. Therefore, the final decision is computed as follows:

$$\begin{array}{cc}\hfill & {\tilde{C}}_{jj}={\tilde{s}}_{ij}+{\tilde{\zeta }}_{ij}+{\tilde{\alpha }}_{jj}\hfill \end{array}$$

(38)

$$\begin{array}{cc}\hfill & {\tilde{C}}_{ij}={\tilde{s}}_{ij}+{\tilde{\zeta }}_{ij}+{\tilde{\alpha }}_{ij}\hfill \end{array}$$

(39)

The final decision (37) and (38) describe the final MAP-based decision metrics for diagonal and non-diagonal variables, respectively. Each decision metric, ${\tilde{C}}_{jj}$ or ${\tilde{C}}_{ij}$, is formed by summing the contributions from the messages ${\tilde{s}}_{ij}$, ${\tilde{\zeta }}_{ij}$, and the message based on diagonal and non-diagonal, ${\tilde{\alpha }}_{jj}$ or ${\tilde{\alpha }}_{ij}$. Algorithm 1 summarizes the procedure of the proposed algorithm.

Algorithm 1: Proposed distributed LEO satellite-UT algorithm.

Set $t\leftarrow 1$ and ${\tilde{\lambda }}_{jj}^{\left(t\right)}=0$ Repeat       For UT self-assignment:               Update ${\tilde{\alpha }}_{ij}^{\left(t\right)}$ and send to neighboring UTs via (38).               Update ${{\tilde{\zeta }}_{ij}}^{(t+1)}$ and send to neighboring UTs via (24).       For Satellite to UT assignment:               Update ${\tilde{\alpha }}_{ij}^{\left(t\right)}$ and send to neighboring UTs via (33).               Update ${{\tilde{\zeta }}_{ij}}^{(t+1)}$ and send to neighboring UTs via (24). Until all messages have been converged or max iteration reached. Compute ${\tilde{C}}_{ij}^{\left(t\right)}$ and ${\tilde{C}}_{jj}^{\left(t\right)}$ to determine the LEO satellite and UT assignments. If ${\tilde{C}}_{jj}^{\left(t\right)}=1$ and ${\tilde{C}}_{ij}^{\left(t\right)}=0$,               the j-th UT are ready to receive the data, however i-th LEO satellite transmit to another UT. If ${\tilde{C}}_{jj}^{\left(t\right)}=1$ and ${\tilde{C}}_{ij}^{\left(t\right)}=1$,               the j-th UT are ready to receive the data and i-th LEO satellite transmit to the j-th UT. If ${\tilde{C}}_{jj}^{\left(t\right)}=0$,               the j-th UT are not ready to receive the data.

5. Simulation Results

This section covers the evaluation results by comparing the proposed algorithm with the conventional algorithms. The simulation is developed in MATLAB R2024a and executed with an 11th Gen Intel^® Core™ i5-1135G7 CPU @ 2.40 GHz (8 logical cores) and 8 GB RAM. For benchmarking, three conventional algorithms are implemented: (i) graph: a bipartite graph matching approach to stabilize handovers [18]; (ii) netflow: a network-flows-based method that models handover as a flow optimization problem [20]; and (iii) greedy: algorithm that assigns satellites to UTs by the highest instantaneous throughput without long-term stability terms [17]. The user rate, user satisfaction metric, and handover (HO) count are evaluated under several variations, including user density, coverage, and shadowing. In addition, the computational complexity and algorithm convergence are also investigated in this section.

5.1. Simulation Parameters

The simulation models a low Earth orbit (LEO) satellite downlink under NTN (Non-Terrestrial Network) assumptions defined in 3GPP TR 38.811 [47] and TR 38.821 [48]. The network comprises n LEO satellites and m static UTs randomly distributed within the coverage area. Each UT is connected to at most one serving satellite at any arbitrary time.

Wireless propagation is modeled here using the 3GPP LOS-dominant Rician fading and a K-factor of 10–12 dB. Since UTs are considered static objects, the Doppler shift is caused only by satellite motion and is applied using the 3GPP NTN Doppler model.

The downlink transmission from the LEO satellite to the UT operates in the Ku-band, i.e., 12–12.7 GHz, with a carrier frequency of 12.2 GHz, a 100 MHz channel bandwidth, and a subcarrier spacing of 60 kHz. Large-scale fading includes free-space loss and clear-sky atmospheric absorption, while log-normal shadowing with a 2 dB standard deviation models LOS outdoor variations. Each satellite transmits at 30 dBW equivalent isotropically radiated power (EIRP) in the downlink, derived from a raw transmit power of 10 dBW and a satellite antenna gain of 20 dBi. The UT receiver has a system noise temperature of 200 K. Thus, the noise power calculation is expressed as

$$N=\mathcal{K}{\gamma }_{\mathrm{sys}}B,$$

(40)

where B is the channel bandwidth, ${\gamma }_{\mathrm{sys}}$ indicates receiver temparature, and $\mathcal{K}$ denotes Boltzmann constant. For the sake of simplicity, the Boltzmann constant is normalized to 1.

Here, LEO satellites are assumed to follow a constant-speed ground-track at altitude with a certain speed. Hence, the resulting angular drift is expressed as

$$\dot{\theta }={\displaystyle \frac{v_{\mathrm{sat}}}{R_{\oplus }+h}}{\displaystyle \frac{180}{\pi }},$$

(41)

where $v_{sat}$ is the orbital velocity in km/h unit, ${\mathcal{R}}_{\oplus }$ is the Earth’s radius, and $\mathcal{H}$ is the satellite altitude in km unit. The conversion factor ${\displaystyle \frac{180}{\pi }}$ converts radians per second into degrees per second. This formulation reflects the high relative angular speed of LEO satellites, which is a critical factor for evaluating handover frequency and mobility management in LEO networks’ constellation.”

For the constant–speed ground-track model, the satellite longitude and latitude are parametrized as

$$\begin{array}{cc}\hfill \mathrm{satLon}\left(t\right)& ={\mathrm{wrap}}_{180}\left(\mathrm{RAAN}+\theta \left(t\right)\right),\hfill \\ \hfill \mathrm{satLat}\left(t\right)& =\mathcal{I}cos\left(\theta \left(t\right)\right),\hfill \end{array}$$

(42)

where $\mathrm{RAAN}$ denotes the right ascension of the ascending node, $\mathcal{I}$ indicates the orbital inclination, $\theta \left(t\right)={\theta }_0+\dot{\theta }t$ indicates the pass phase, and ${\mathrm{wrap}}_{180}(·)$ transforms angles to the interval $[-180°,180°]$.

Table 1. Wireless and link budget parameters.

Parameters	Values
Carrier frequency	$f_c=12.2$ GHz
Channel bandwidth	$B=100$ MHz
Subcarrier spacing	$\Delta f=60$ kHz
Small-scale fading	Rician, $K=10$–12 dB
Shadowing	Log-normal, ${\sigma }_{\mathrm{sh}}=3$ dB
Satellite EIRP (per beam)	$P_i=30$ dBW
Receiver temperature	$T_{\mathrm{sys}}=200$ K
Noise power	$\sigma =k{T}_{\mathrm{sys}}B$ with $k=1$

and

Table 2. Geometry and motion parameters.

Parameters	Values
Earth radius	${\mathcal{R}}_{\oplus }=6371$ km
Altitude	$\mathcal{H}=1200$ km
Inclination	$\mathcal{I}=53°$
Satellite speed (constant)	$v_{\mathrm{sat}}=27,000$ km/h

correspondingly summarize the wireless-link budget parameter and geometry motion parameter.

5.2. Performance Under Different User Terminal Density

The number of UTs is a critical factor affecting the performance of LEO satellite networks. More involved UTs lead to increased co-channel interference, which can result in reduced per-user throughput, lower satisfaction metric requirements, and frequent unnecessary handovers. Moreover, the high number of UTs also enables several UTs to fail to allocate wireless resources. Therefore, the impact of UT density on overall network performance needs to be rigorously investigated.

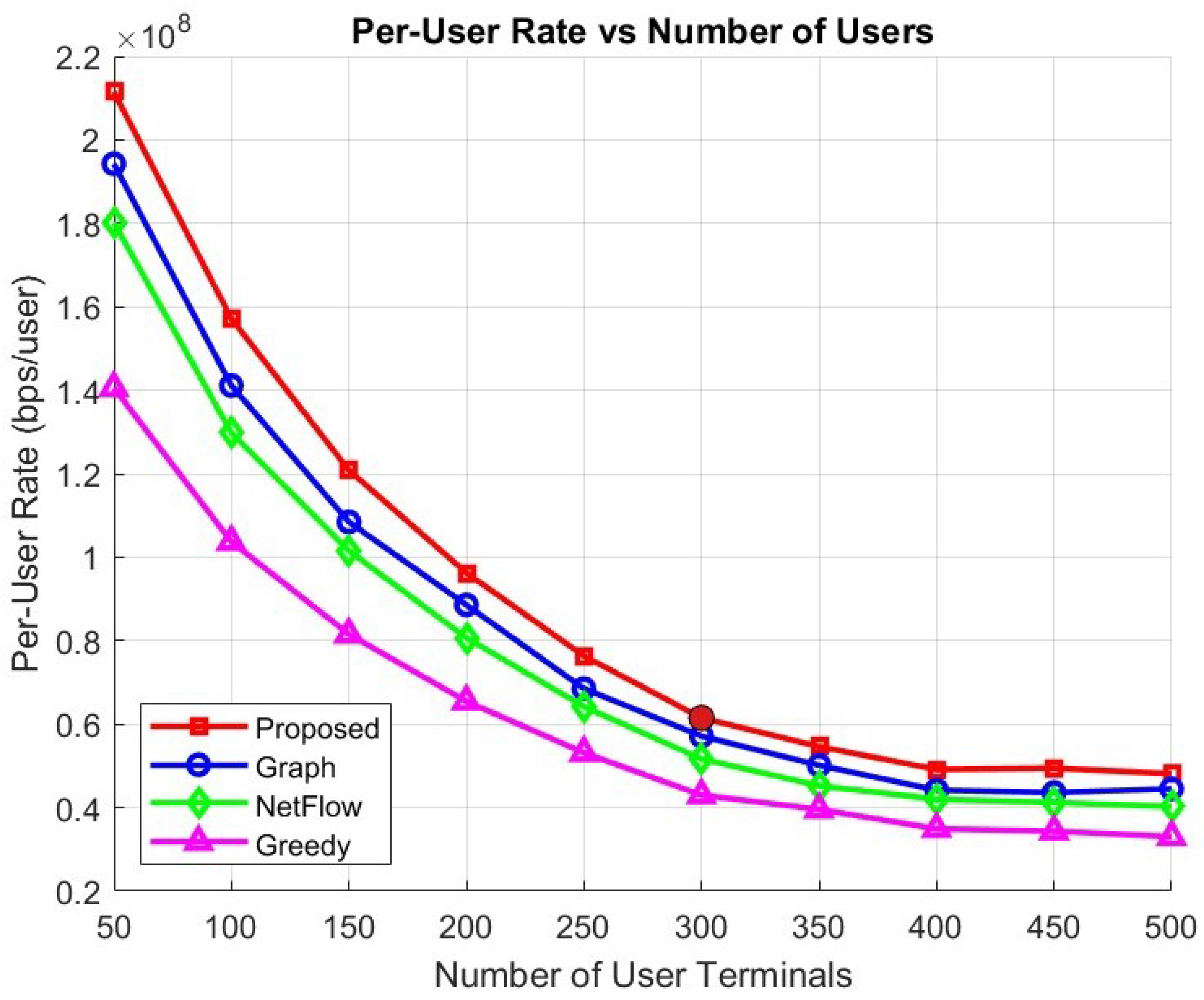
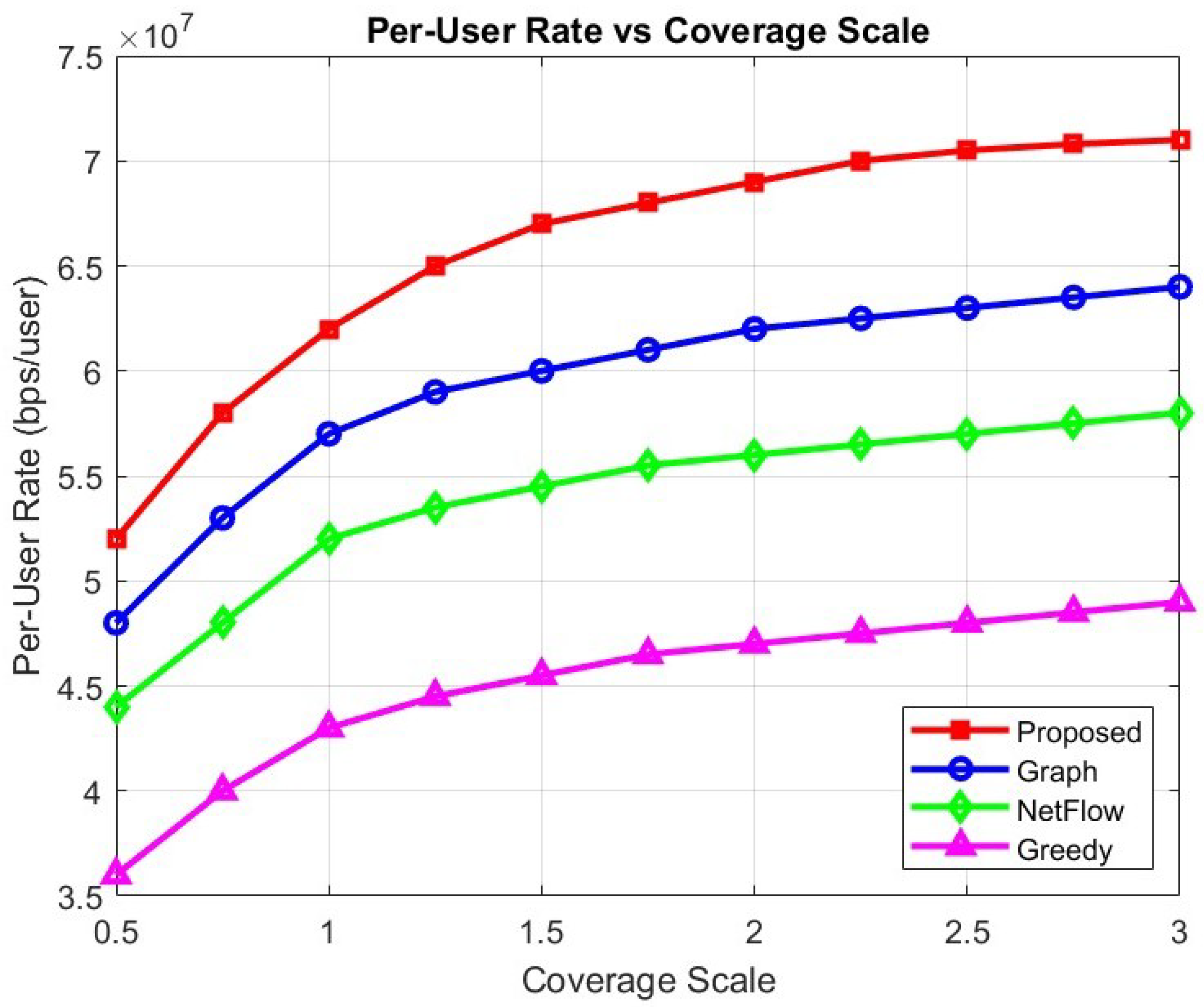
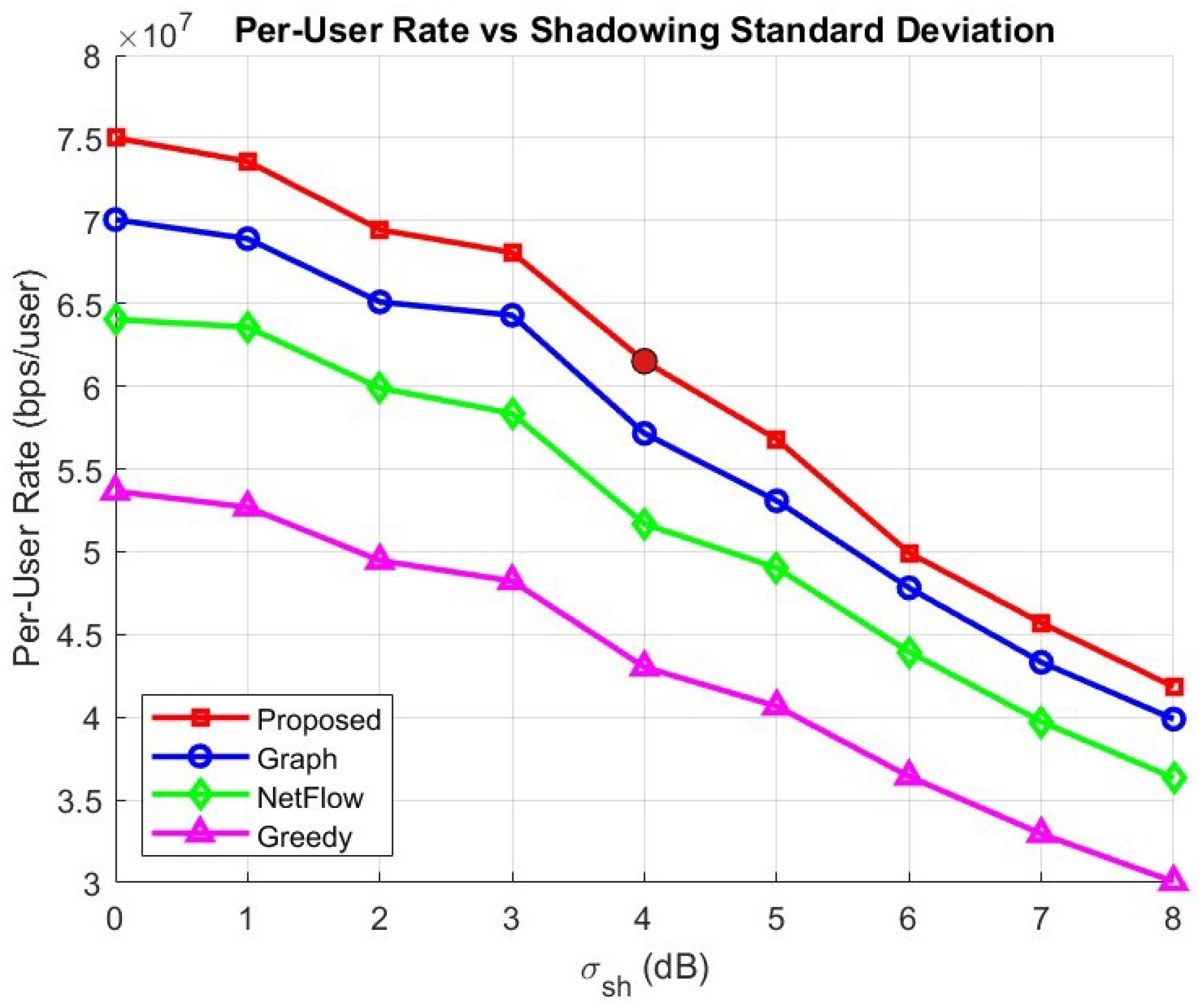
Figure 4 presents the per-user rate performance of all algorithms corresponding to the number of UTs; in this case, the number of LEO satellites is maintained at a fixed number, i.e., 80 satellites. The per-user rate naturally decreases with an increase in the number of UTs, as more UTs compete for the limited wireless resources. Moreover, co-channel interference also occurs frequently in ultra-dense environments, leading to data loss and distortion during transmission.

When the number of UTs is very small, in this case 50 UTs, the proposed algorithm achieves a high rate up to $2.11\times {10}^8$ bps/user. The proposed algorithm consistently outperforms conventional algorithms by approximately 8.76%, 17.09%, and 50.07% compared to the graph-based method, the NetFlow approach, and the greedy algorithm, respectively. When the network load increases to a medium-dense environment, i.e., 300 UTs, the per-user rate of the proposed algorithm dramatically decreases up to $0.62\times {10}^8$ bps/user. Although the proposed algorithm’s performance decreases significantly, it remains higher than that of the graph, NetFlow, and greedy methods by 7.7%, 18.9%, and 43.02%, respectively. Finally, under an ultra-dense scenario with 500 UTs, the proposed algorithm achieves only $0.48\times {10}^8$ bps/user, but still outperforms the graph, NetFlow, and greedy methods by approximately 8%, 19.65%, and 45.75%, respectively.

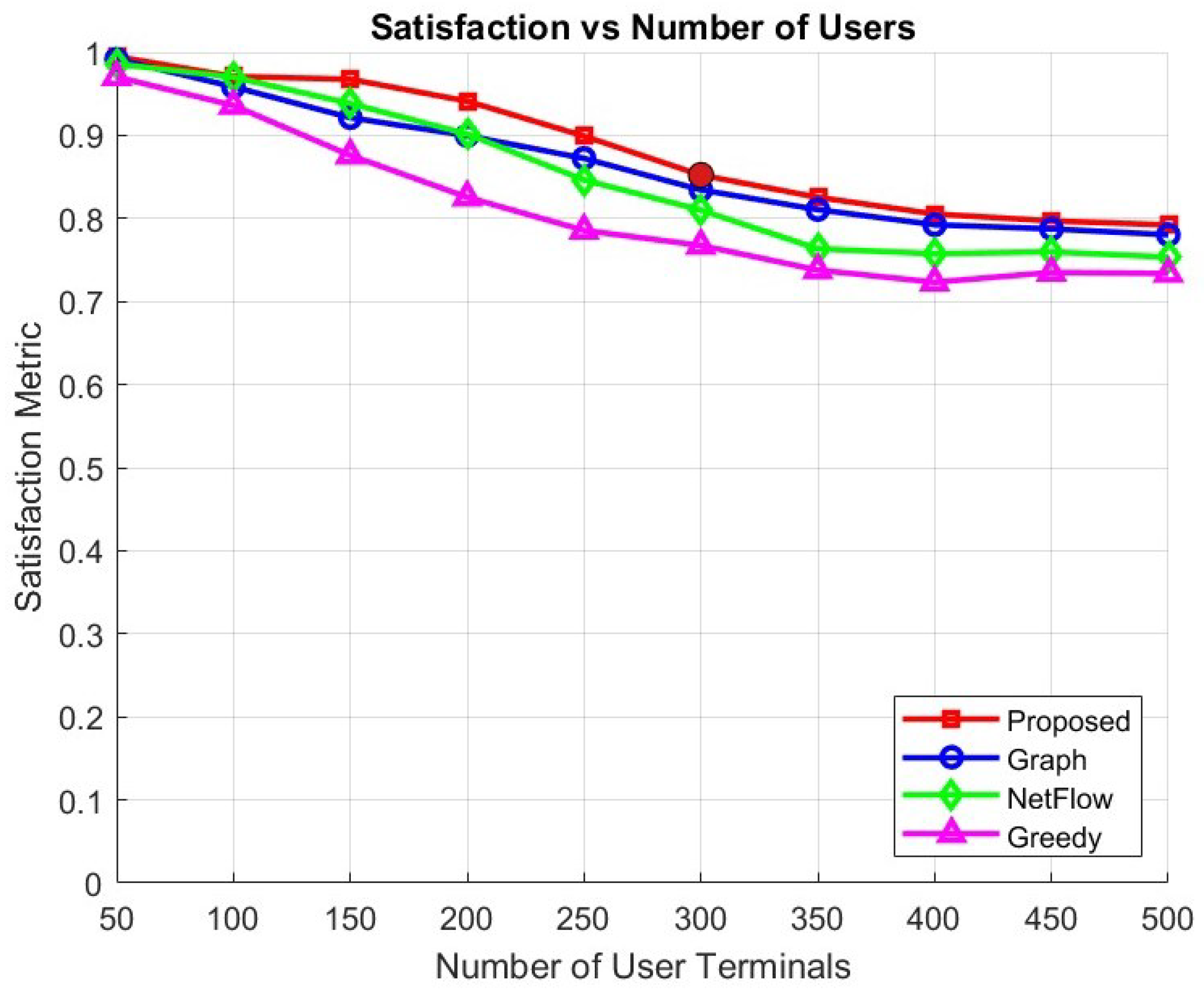
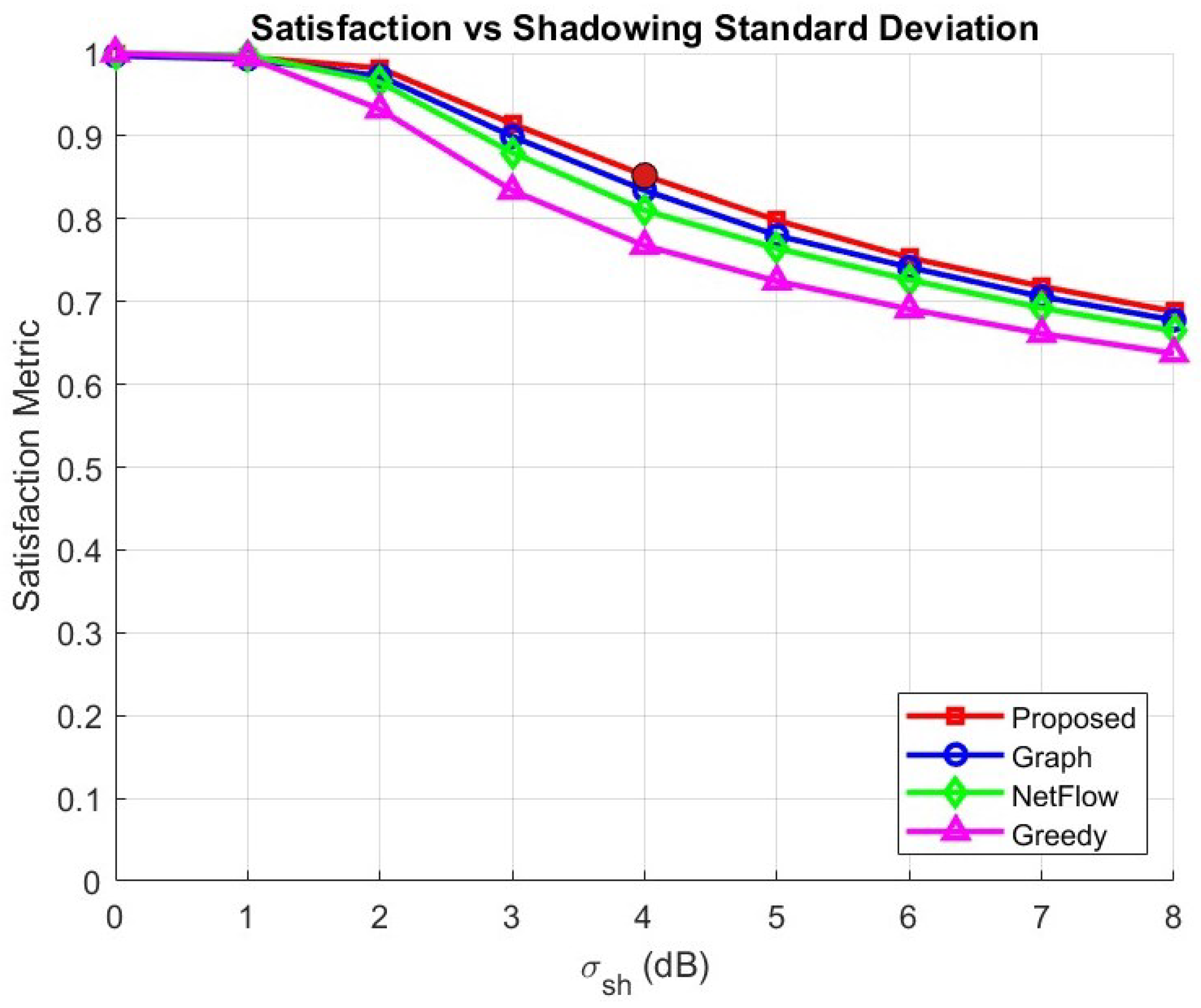
Figure 5 shows the satisfaction metric performance of all algorithms as the number of UTs increases from 50 to 500. In a typical wireless network, the satisfaction level decreases with increasing user density due to higher competition for limited resources. However, the proposed algorithm consistently achieves a higher satisfaction level compared to the conventional algorithms. When the number of UTs is relatively small, i.e., 50 UTs, all algorithms achieve satisfaction levels close to one, indicating that nearly all UTs can be served. As the number of UTs increases to 300, the satisfaction level of the proposed algorithm decreases approximately 0.85; this performance still outperforms conventional algorithms, providing improvements up to 3.5%, 7%, and 12% compared to the graph-based, NetFlow, and greedy algorithms, respectively. Even under heavy load conditions at 500 UTs, the proposed algorithm still achieves a satisfaction metric close to 0.79, whereas the graph-based, NetFlow, and greedy methods correspondingly drop to 0.77, 0.75, and 0.73.

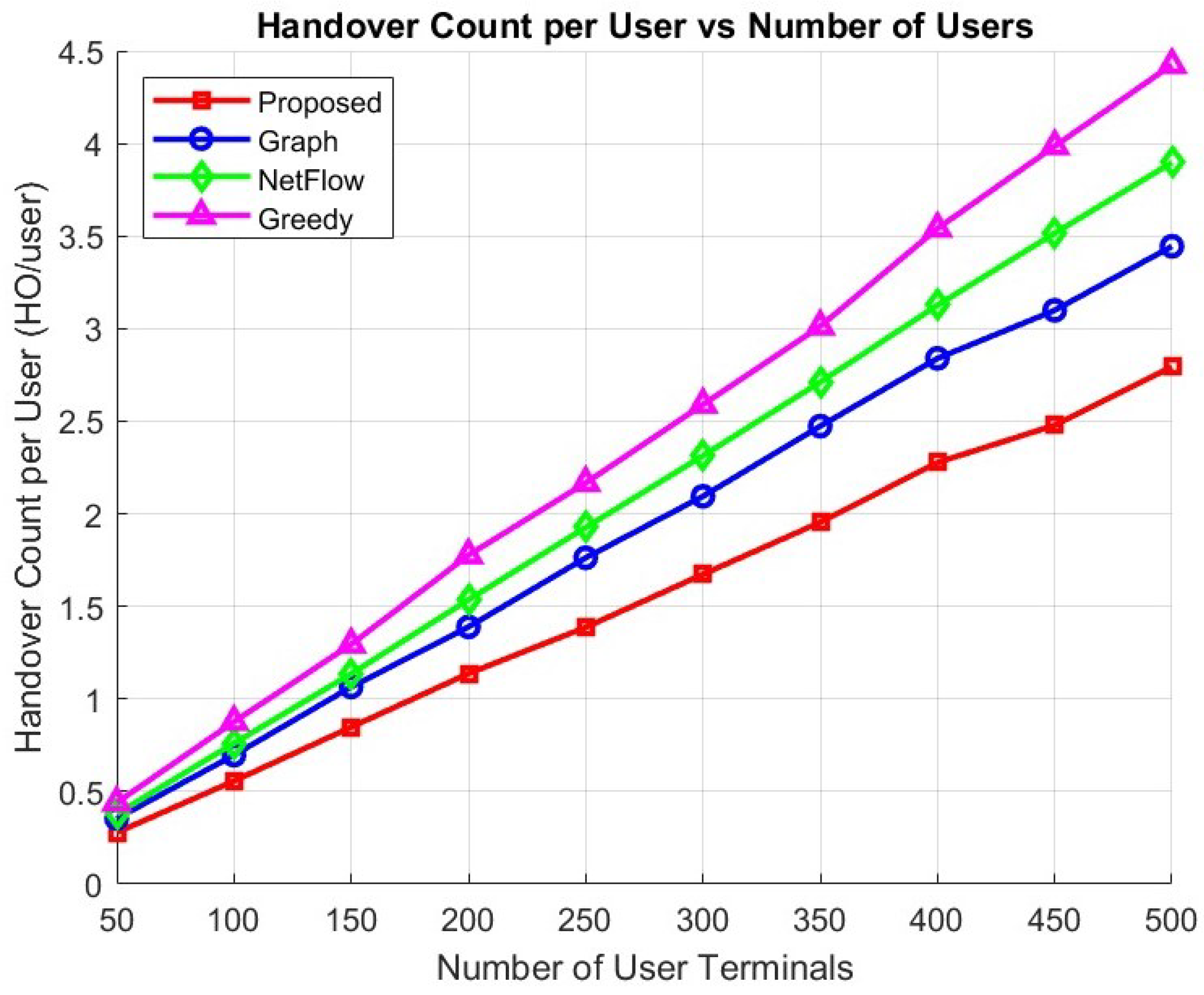
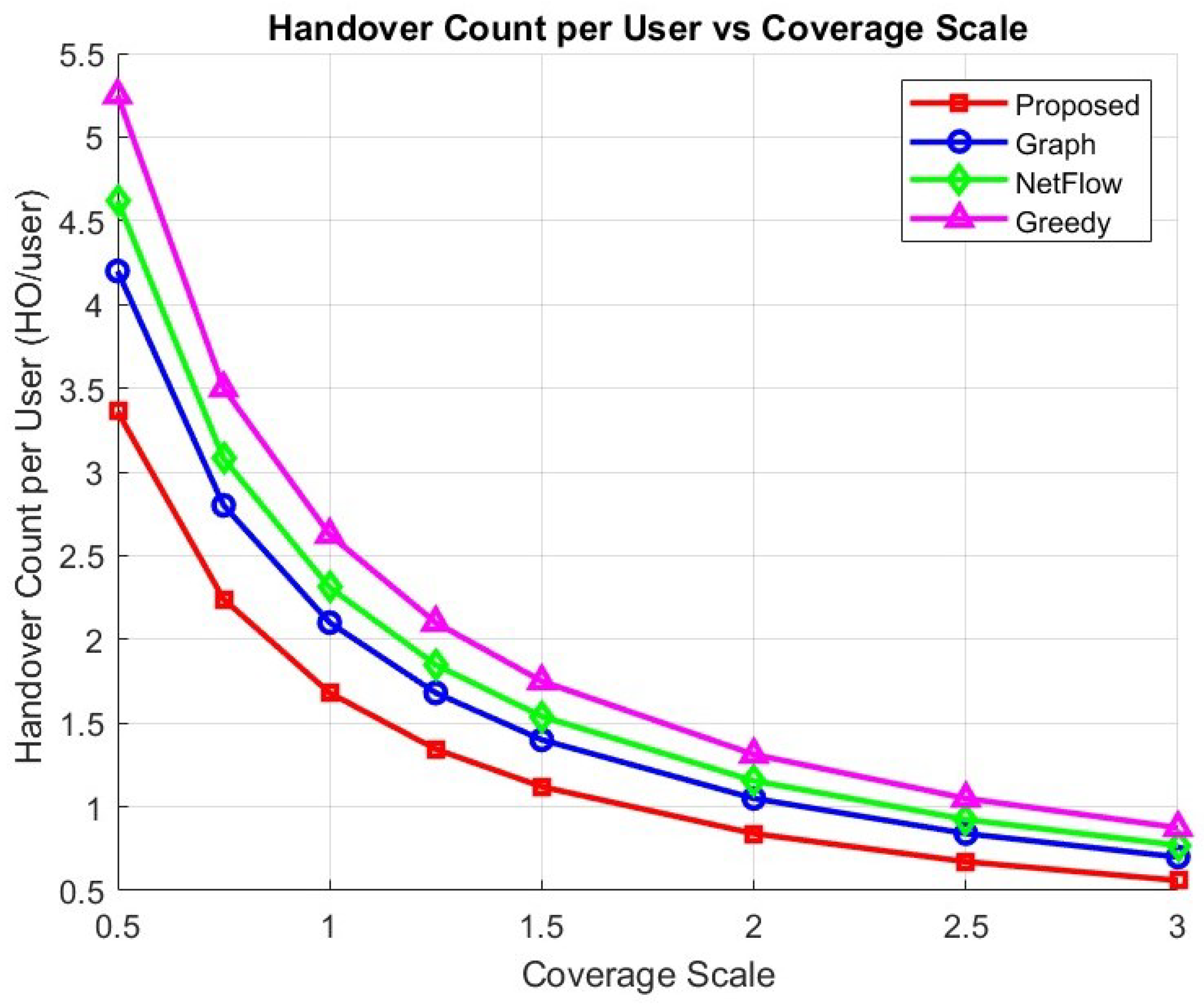
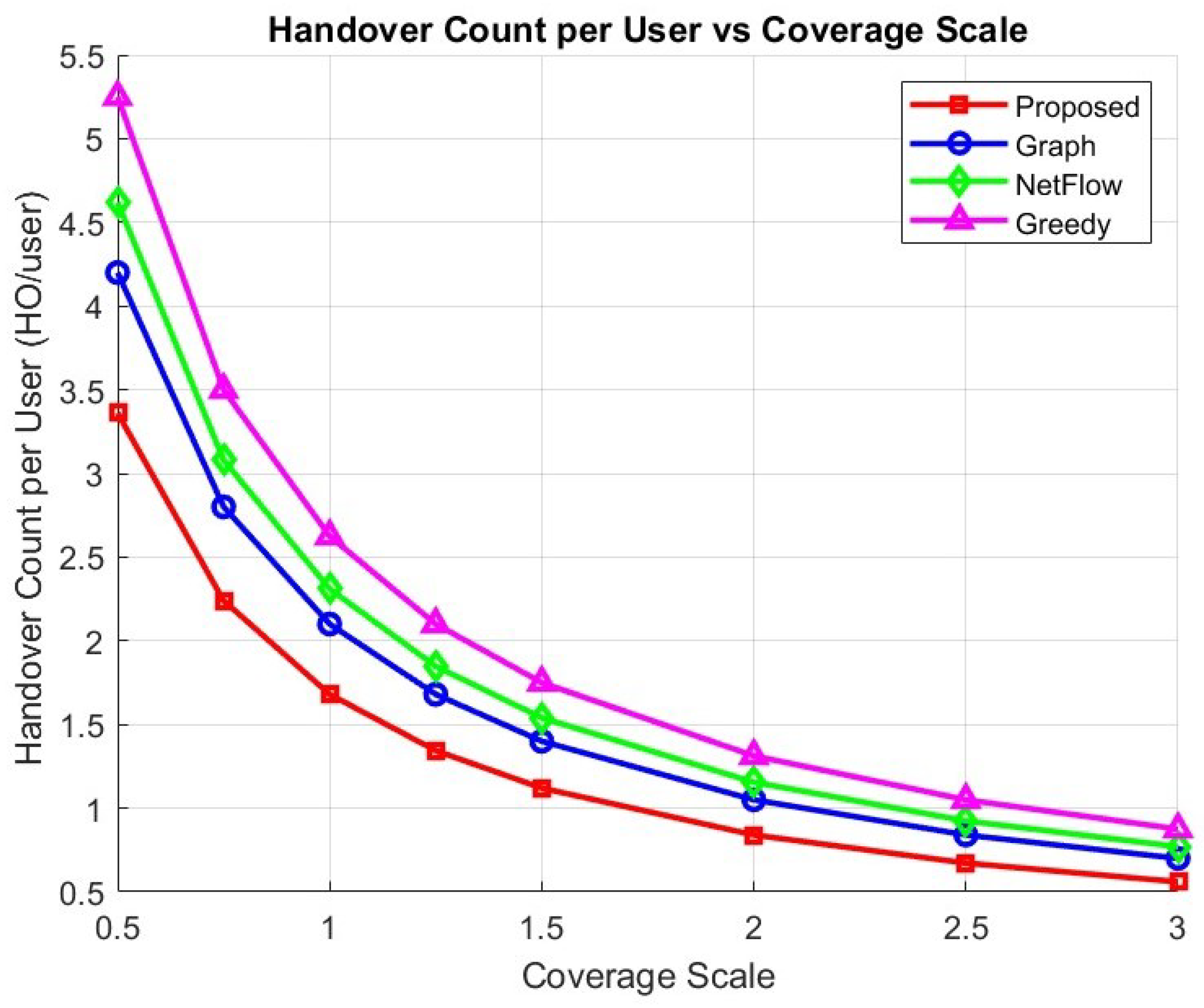
Figure 6 shows that the handover count per user increases almost linearly with the number of UTs. When the number of UTs equals 500, the proposed algorithm achieves about 2.79 handover counts per user, compared to 3.44 for the graph-based Graph method, 3.89 for NetFlow, and 4.42 for the greedy algorithm. Even in smaller-scale scenarios with only 100 UTs, the proposed algorithm maintains an advantage, with 0.27 HO/user versus 0.35 HO/user–0.44 HO/user for the other algorithms, confirming its efficiency across different load levels.

The consistent performance of the proposed algorithm is mainly due to its distributed optimization mechanism. Unlike conventional methods that rely on either centralized decisions or simplistic heuristics, the proposed algorithm performs iterative message exchanges only among nearby UTs and satellites. This localized interaction significantly reduces computational burden while enabling each satellite to make more informed scheduling decisions. As the number of UTs increases, the proposed algorithm utilizes local message exchanges to ensure that each satellite can still make informed scheduling decisions even under limited resource availability.

5.3. Performance Under Different Coverage

The coverage of an LEO satellite directly affects both the number of UTs that can be served simultaneously and the quality of their channel conditions. Expanding the coverage area enables satellites to reach more terminals, thereby potentially enhancing overall performance. However, at specific coverage scales, the performance gain begins to stabilize due to the influence of interference and path loss, which enables data to be lost and distorted.

Figure 7 shows that increasing the coverage scale leads to an increased per-user rate across all methods because of more favorable channel conditions. However, at higher coverage, all algorithm performance starts to converge due to path-loss and interference effects balancing out. In this case, the proposed algorithm consistently achieves the highest performance, starting from approximately $5.2\times {10}^7$ bps/user at a coverage scale of 0.5 and reaching nearly $7.1\times {10}^7$ bps/user at a coverage scale of 3.0. Compared to the graph-based, NetFlow, and greedy algorithms, the proposed method demonstrates a persistent improvement margin of 10–15%, 20–25%, and 40–45%, respectively, which confirms its robustness in diverse coverage scenarios.

Figure 8 shows that the satisfaction metric improves significantly as the coverage scale increases and then stabilizes at higher coverage values. At a coverage scale of 1.0, the proposed algorithm achieves a satisfaction metric of approximately 0.86, compared to 0.84, 0.82, and 0.78 for the graph-based, NetFlow, and greedy methods, respectively. When the coverage scale expands to 3, the proposed method maintains satisfaction levels around 0.92, while the graph-based and NetFlow methods remain near 0.90, and the greedy algorithm at about 0.84.

Figure 9 shows that enlarging the coverage scale significantly decreases the handover count per user. At the smallest coverage scale of $0.5$, the proposed algorithm records about 3.36 HO/user, compared to 4.2 for the graph-based method, 4.63 for NetFlow, and 5.25 for the greedy algorithm. As the coverage scale expands to $3.0$, all algorithms converge toward lower values, with the proposed algorithm experiencing about 0.56 HO/user. In contrast, the graph-based technique, NetFlow, and greedy algorithm remain slightly higher at 0.7, 0.77, and 0.82 HO/user, respectively. This result confirms that the proposed method consistently maintains the lowest handover count across both small and wide coverage conditions.

These results show that while all methods benefit from the additional coverage opportunities, only the proposed algorithm can simultaneously maximize throughput and ensure a higher proportion of satisfied UTs, highlighting its superior balance between efficiency and fairness in LEO satellite networks.

5.4. Performance Under Different Shadowing

Shadowing introduces random fluctuations in the received signal power caused by environmental obstacles such as terrain, buildings, or atmospheric conditions. Here, shadowing is modeled as a log-normal random process with zero mean and a standard deviation ${\sigma }_{sh}$, following commonly used LEO satellite channel assumptions. As the shadowing variance increases, the effective link quality degrades, resulting in a reduction in both per-user rates and satisfaction metrics. To assess the overall algorithm performance against shadowing,

Figure 10 shows that the per-user rate decreases continuously with increasing ${\sigma }_{sh}$. The proposed algorithm achieves approximately $7.5\times {10}^7$ bps/user at ${\sigma }_{sh}=0$ dB but declines to about $4.2\times {10}^7$ bps/user when ${\sigma }_{sh}=8$ dB. Despite this degradation, the proposed method consistently outperforms other algorithms, achieving 8.8%, 19.2%, and 44.2% per-user rate improvements compared to the graph-based, NetFlow, and greedy algorithms, respectively, at ${\sigma }_{sh}=4$ dB.

Similarly, Figure 11 illustrates that the satisfaction metric also degrades as shadowing increases. At ${\sigma }_{sh}=0$ dB, all methods achieve satisfaction levels close to 1.0. However, as shadowing grows severe, the satisfaction level of the proposed algorithm drops to around 0.69 at ${\sigma }_{sh}=8$ dB, while the graph-based, NetFlow, and greedy methods degrade to 0.67, 0.66, and 0.63, respectively.

Figure 12 illustrates the sensitivity of handover count to shadowing variance (${\sigma }_{sh}$). When ${\sigma }_{sh}=0$ dB, the proposed algorithm achieves about 1.2 HO/user, compared to 1.55 for the graph-based technique, 1.65 for NetFlow, and 1.875 for the greedy algorithm. As the shadowing variance increases to ${\sigma }_{sh}=8$ dB, the handover counts grow for all schemes: the proposed algorithm reaches about 2.16 HO/user, while Graph, NetFlow, and Greedy increase to 2.7, 2.97, and 3.38 HO/user, respectively. These results confirm that the proposed algorithm is the most robust to fading-induced variability, maintaining the lowest handover frequency under all shadowing conditions.

The proposed algorithm relies on the distributed optimization strategy, which adaptively exchanges messages among nearby UTs and satellites. This local message exchange enables mitigating the impact of deep fades and resource contention more effectively than conventional algorithms. Accordingly, the proposed algorithm achieves higher throughput and satisfaction metric, even under substantial shadowing performance.

5.5. Convergence Analysis

The convergence of the proposed algorithm is evaluated to ensure the stability of finding the final decision. Here, the convergence properties are analyzed under two scenarios: (i) the proposed algorithm and (ii) the proposed algorithm with a relaxed constraint model.

Figure 13 illustrates the normalized objective function across iterations for both cases. Under the one-to-one mapping of Constraint (7), the proposed algorithm demonstrates fast and stable convergence, achieving more than 95% of the normalized objective function within the first ten iterations, and reaching full convergence before 20 iterations. This behavior demonstrates that the one-to-one mapping constraint-enforced algorithm consistently renders the problem into an optimal solution. In contrast, when the relaxed constraint model is adopted, the algorithm fails to converge within the iteration budget. Instead, the objective function exhibits oscillatory behavior around a suboptimal region, with values fluctuating between 0.82 and 0.90 across iterations. This instability arises because the relaxed constraints allow multiple inconsistent assignment configurations, which prevent the iterative updates from reinforcing a single optimal solution. The comparison between the two scenarios shows the critical role of Constraint (7) in ensuring convergence: it prevents oscillations, guarantees the feasibility of assignments, and accelerates the stabilization of the algorithm. These results confirm that the proposed algorithm can converge with the minimum required iterations. This finding justifies the enforcement of strict constraints in practical deployments of the message-passing algorithm, especially for delay-sensitive LEO networks where stability and reliability are critical.

5.6. Computational Complexity

The proposed algorithm operates in an iterative and distributed manner, where only lightweight local messages are exchanged between UTs and their visible satellites. Messages such as ${\lambda }_{ij},{\beta }_{ij},{\alpha }_{ij},$ and ${\zeta }_{ij}$ are derived by accumulating small-sized information from neighboring nodes.

The computational complexity of the proposed scheme is compared with other baseline scheduling algorithms in

Table 3. Computational complexity of scheduling algorithms.

Method	Proposed Algorithm	Graph-Based Method	NetFlow Method	Greedy Method
Complexity	$O\left(m^2\right)$	$O\left(m^3\right)$	$O(m^{3}logm)$	$O\left(m^2\right)$

. The computational complexity of the proposed algorithm grows only quadratically with the number of UTs, i.e., $O\left(m^2\right)$. In contrast, the graph-based and NetFlow formulations require solving centralized optimization problems, which typically scale as $O\left(m^3\right)$ or $O(m^{3}logm)$, respectively. Meanwhile, the greedy heuristic achieves the same order of $O\left(m^2\right)$ complexity. The computational performance result shows that the proposed algorithm provides an effective balance between computational efficiency and network performance.

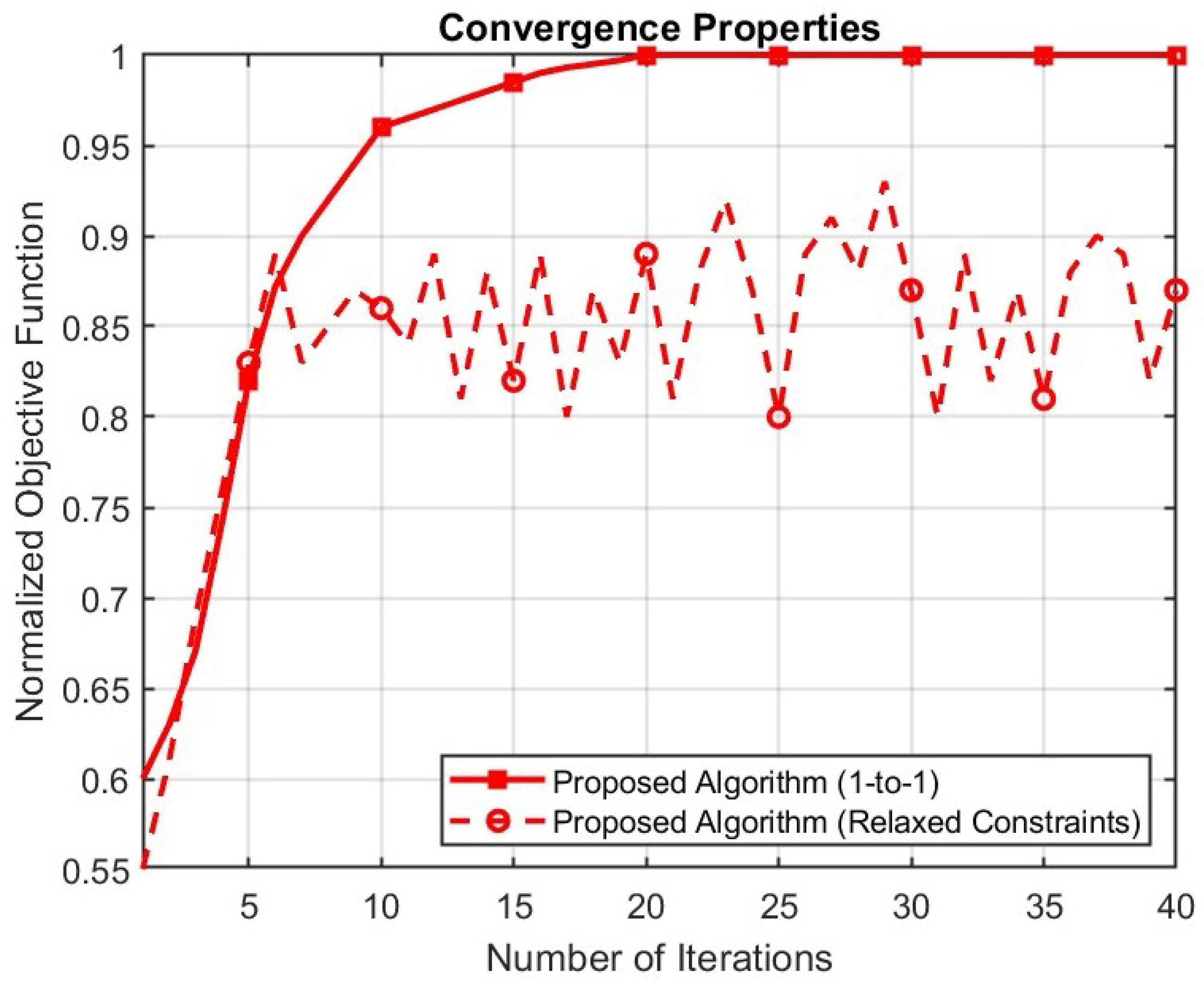
For the proposed algorithm, each iteration updates one message per satellite-UT edge, costing $O\left(mn\right)$. Because Constraint (7) enforces a one-to-one mapping, therefore, $m\simeq n$. Accordingly, it simplifies the computational complexity to $O\left(m^2\right)$. Convergence is reached within a bounded number of iterations, and the one-to-one mapping ensures that the factor graph remains sparse. The quadratic scaling, therefore, follows directly from the $m\times m$ edge structure in the factor graph.

For the bipartite graph, the cubic complexity arises from repeated augmenting-path searches. To complete the assignment, the algorithm must find m augmenting paths, one for each UT to be matched. Each path search requires updating feasibility labels and slack variables across the entire $m\times m$ cost matrix, which may involve scanning up to $O\left(m^2\right)$ entries. Hence, the total complexity is $m\times O\left(m^2\right)=O\left(m^3\right)$. The key insight of cubic computational complexity growth is that global feasibility is maintained and updated across all $m^2$ entries for every one of the m assignments.

For the network-flow formulation, the complexity becomes super-cubic. The assignment is formulated as a min-cost max-flow problem with $\left|V\right|=O\left(m\right)$ nodes and $\left|E\right|=O\left(m^2\right)$ arcs, which dominates all satellite–UT pairs. The successive shortest-path algorithm augments one unit of flow at a time, which requires computing a shortest path on the residual graph. Using Dijkstra with a binary variable, a single shortest-path run costs $O\left(\left|E\right|log\left|V\right|\right)=O\left(m^{2}logm\right)$. Because $O\left(m\right)$ augmentations are needed in one per UT, the total complexity becomes $O\left(m\right)\times O\left(m^{2}logm\right)=O\left(m^{3}logm\right)$. The $mlogm$ factor arises specifically from heap operations in Dijkstra, e.g., insert, decrease-key, extract-min. Thus, the additional logarithmic factor reflects the data structure cost in each shortest-path computation.

For the greedy algorithm, two cases must be distinguished. In the naïve version, each of the m assignment steps scans the full $m\times m$ utility matrix to find the maximum rate, costing $O\left(m^2\right)$ per step. With m steps in total, this results in $O\left(m\right)\times O\left(m^2\right)=O\left(m^3\right)$. In the optimized version, row and column maxima are maintained and updated after each assignment. Each update then requires only O(m) operations, reducing the total cost to $O\left(m\right)\times O\left(m\right)=O\left(m^2\right)$. However, while the optimized greedy algorithm achieves the same order as the proposed method, it is short-sighted, optimizing only local throughput at each step and lacking the convergence guarantees that message passing provides.

6. Conclusions

This paper develops an efficient user assignment framework to address the handover problem in LEO satellite communication networks. By jointly optimizing the user rate and satisfaction metric in a distributed manner, the proposed algorithm can find a final assignment decision with low computational complexity. Through a message-passing framework, the proposed algorithm enables UTs and satellites to exchange simple local messages iteratively, thereby making informed decisions with a limited involved parties and without relying on a central coordinator. The three contributions are achieved in this study. First, the distributed user assignment strategy is confirmed to minimize unnecessary handovers, as reflected in a significantly reduced handover count compared with the conventional algorithm. Under 500 UTs, the proposed algorithm achieves 2.79 HO/user, which improves the conventional algorithm by 18.89%. Second, the adaptability of the proposed method is validated by its ability to maintain performance under dynamic conditions. The proposed algorithm achieves $0.48\times {10}^8$ bps/user and a satisfaction metric of 0.79 when the number of UTs equals 500, improving upon the best conventional method by up to 8% in per-user rate and 2% in satisfaction. In the coverage scale of 3, the proposed algorithm achieves $7.1\times {10}^7$ bps/user and 0.92 of user satisfaction, improving the best conventional algorithm by up to 15% in per user rate and 2.2% in satisfaction metric. Under severe shadowing of 8 dB, the proposed algorithm still achieves $4.2\times {10}^7$ bps/user and 0.69 satisfaction, representing gains of 8.8% and 2.9%, respectively, over the best conventional algorithm. Third, the low-complexity design is validated by the derived quadratic, i.e., $O\left(m^2\right)$, that scales from the message-passing formulation, which outperforms the cubic and super-cubic complexities of conventional algorithms. Convergence analysis further shows that stable solutions are consistently reached within fewer than 20 iterations. A research direction can be further extended to model multi-UT assignments per satellite, which requires considering additional interference management, resource partitioning, and convergence challenges. Additionally, mobility-aware prediction and cross-layer optimization are crucial in future dynamic satellite constellations.