Abstract
The expected development of the future generation of wireless communications systems such as 6G aims to achieve an ultrareliable and low-latency communications (URLLCs) while maximizing the data rates. These requirements push research into developing new advanced technologies. To this end, massive multiple input multiple output (MMIMO) is introduced as a promising transmission approach to fulfill these requirements. However, maximizing the downlink-achievable sum rate (DASR) in MMIMO with a frequency division duplex (FDD) transmission mode and limited coherence time (LCT) is very challenging. To address this challenge, this paper proposes a DASR maximization approach using a feasible power allocation optimization method. The proposed approach is based on smartly allocating the total transmit power between the data transmission and training sequence transmission for channel estimation. This can be achieved by allocating more energy to the training signal than the data transmission during the channel estimation process to improve the quality of channel estimation without compromising more training sequence length, thus maximizing the DASR. Additionally, the theory of random matrix approach is exploited to derive an asymptotic closed-form expression for the DASR with a regularized zero-forcing precoder (RZFP), which allows the power optimization process to be achieved without the need for computationally complex Monte Carlo simulations. The results provided in this paper indicate that a considerable enhancement in the DASR performance is achieved using the proposed power allocation method in comparison with the conventional uniform power allocation method.
1. Introduction
The existing wireless communications systems will face significant challenges due to the rapid increase in the applications of the Internet of Things (IoT) that need ultrareliable and low-latency communication (URLLC) [1]. In particular, widely expected future services, such as smart healthcare systems, factory automation, and autonomous vehicles, will be critically reliant on providing URLLC while maximizing the data rates [2,3,4]. This necessitates finding massive communication systems with advanced techniques to meet the extremely high data rate requirements. To this end, massive multiple input multiple output (MMIMO) [5,6] is proposed as a promising technique to fulfill the aforementioned demands of future wireless communication systems [7]. This is because MMIMO technology has the potential to significantly increase both energy and spectral efficiencies.
However, from an information theoretic perspective, the system’s performance hinges on the precision channel state information (CSI) estimation. The accuracy of CSI acquisition and the overhead in the systems rely on the duplexing mode of operation. For example, there are the time division duplex mode (TDD) and the frequency division duplex (FDD) operation modes. In the TDD mode, the uplink CSI estimate is used in the downlink precoder design at the base station (BS) without the need for downlink CSI estimation. This is due to the uplink/downlink channel reciprocity that is obtained in TDD operation systems [8]. In this case, there is no overhead from CSI estimation, since it is proportional to the number of users and not to BS antennas N [9,10,11,12]. Despite the favorable outcomes of the TDD mode with downlink CSI estimation, most of the existing mobile networks operate in the FDD operation mode. For instance, the current wireless networks, which are advanced long-term evolution (A-LTE) networks, mostly operate with the FDD mode [13]. In addition, calibration errors in the uplink/downlink radio frequency (RF) chains and transceiver hardware limits are usually the source of the limitations of TDD operation systems [14,15,16,17]. Hence, this research concentrates on FDD transmission, where the downlink CSI estimation is determined using a dedicated downlink training sequence during the CSI estimation phase. Specifically, to acquire CSI estimation in the FDD mode, the BS needs to design a specific training sequence and direct this sequence to the users [18,19]. However, the BS with a MMIMO system operates with a large number of antenna elements, which poses a significant challenge in channel estimation, especially in FDD operation with limited coherence time (LCT).
To this end, several research works have investigated the downlink CSI estimation in FDD MMIMO systems, thereby taking into account the spatial correlation at the BS; see, e.g, [20,21,22,23,24,25,26,27,28]. Another area of study has been on CSI estimation utilizing methods based on compressed sensing (CS) [29,30,31,32,33,34]. In addition, a further advancement in CSI estimation is the application of hybrid two-stage precoding techniques in FDD MMIMO systems [35,36,37,38]. However, in the aforementioned research works, a uniform power allocation has been assumed, and the DASR has not been optimized with respect to power allocation. To the best of our knowledge, maximizing the DASR with respect to the optimized energy allocation has not been investigated in the literature.
1.1. Paper Contributions
This paper addresses the challenge of DASR maximization through power allocation optimization with LCT. To this end, a viable solution to design the training sequence, which is both low in complexity and suitable for LCT, is obtained. Additionally, a low-complexity power allocation optimization technique is employed to maximize the DASR of FDD MMIMO systems. The following is a summary of the main contributions of this research:
- This paper addresses the challenge of channel estimation with a very large antenna and short coherence time with an objective to maximize the DASR.
- This paper proposes a low-complexity solution for CSI estimation by utilizing the statistical information of the channel covariance matrix, which is considered to be locally stationary and varying more slowly than the instantaneous channel.
- Unlike previous works that have considered mean square error (MSE) minimization criteria, see, e.g., [20,21,22,23,24,39,40,41,42,43,44], this paper investigates the maximization of the DASR in LCT, which is crucial for many wireless system applications.
- This paper proposes a power allocation optimization strategy that is based on dividing the energy nonuniformly between the data transmission and training sequence transmission with LCT, with an objective function to maximize the DASR of MMIMO systems with the FDD transmission mode.
- We derive an analytical closed-form expression for the DASR with a regularized zero-forcing precoder (ZFBF) using a theory based on the random matrix method.
- This paper conducts comparisons for the DASR performance results between the proposed power optimization method and the conventional method with uniform power allocation. The results show that the proposed low-complexity power allocation optimization approach markedly improves the DASR over the conventional method across a wide range of configurations considered. This success in maximizing the DASR signifies the feasibility of applying the proposed method in practical systems utilizing URLLC and LCT scenarios.
1.2. Paper Organization and Notation
This work is delivered in the following organizational format. The system model description and the characterization of the SINR and the DASR are presented in Section 2. In Section 3, the CSI estimation and the training sequence design in the downlink MMIMO with the FDD mode are discussed, and the related formals are provided. In addition, the problem formulations of the DASR maximization are provided. Furthermore, the power allocation optimization is also developed in this section. In Section 4, an analytical solution of the RZFP is developed using the approach of random matrix theory. Section 5 presents performance evaluation results for the DASR with proposed power allocation optimization in comparison with the conventional method of uniform power allocation. Finally, Section 6 concludes the paper.
This research employs boldface symbols to represent matrices and lower boldface symbols for vectors. The Gaussian distribution is symbolized as , thus indicating a mean of zero and a covariance matrix of . The notation is utilized for the expectation operator, and denotes the absolute square, which is the power in the signal. Various mathematical operations are used in this paper, such as transpose, trace, and Hermitian transpose, which are given as , , and , respectively.
2. System Model of Downlink FDD MMIMO
In this study, a single-cell wireless communication system is considered in which the BS has an array of N antennas and connects with K single-antenna uncorrelated users in the downlink. The users’ single-antenna assumption makes low-cost, straightforward hardware with effective power consumption achievable as discussed in [10]. All users obtain the downlink transmission concurrently via the same time frequency resources. The number of users K is assumed to be limited and less than N, or , which is the typical assumption in MMIMO systems as described in [5]. We consider a single-frequency band FDD transmission mode in the downlink. In addition, this work also considers a block fading structure in which , where the channel with the LCT block is assumed as in the A-LTE mobile networks [45]. In the training phase, the downlink channel is employed per each coherence block, where the BS can transmit a training sequence in the downlink with a power of and a length . As a result, the remaining amount of power and time is dedicated for allocating the useful transmission data. The channel should be estimated in the downlink to beamform the data symbols correctly to the targeted uses. The main aim of this research is to investigate maximizing the DASR when the power is optimized with respect to the downlink training sequence and the data phase. A block diagram of the MMIMO systems at the BS with digital precoding is shown in Figure 1. The kth user’s received downlink data signal at the user’s side, which is denoted by , is provided as follows:
where the transmit power that is transmitted in the data phase is given as . The downlink transmit vector is represented by the parameter . This transmit vector includes the transmitting data symbols and the precoding vector that will be defined later in Equation (4). The additive noise is represented by the parameter , which is defined here as a Gaussian distribution with a zero mean. The actual downlink channel vector is denoted by . It can be modeled as
where is the downlink channel vector, and the covariance matrix at the transmitter is given as , which can be decomposed as in [46]:
Figure 1.
Block diagram of MMIMO systems with precoder at BS.
Therein, we use the eigenvalue decomposition (EVD) method with eigenvectors of and eigenvalues of . Note that the eigenvalues are given as . In practice, obtaining the channel covariance matrix involves either estimating it at the BS or determining the feedback of a quantized version of it from the users. Inaccuracies in estimating or defining the feedback of the covariance matrix can impact the system performance, thereby leading to suboptimal solutions and reduced overall system performance. Since the covariance matrix is represented by an expectation of the instantaneous channel vectors and relies on the scattering environment and the propagation geometry, it can be considered as locally stationary and varies much more slowly than the instantaneous channel of the coherence time [47,48,49]. Therefore, the channel covariance matrix can be accurately obtained in both the TDD and FDD transmission modes [50,51,52,53]. To this end, several research works have investigated the system performance when the channel covariance matrix is assumed to be unknown. For example, the work of [54] proposed a resampling method for obtaining the channel covariance matrix using cubic splines. In addition, a dictionary of known uplink/downlink covariance matrices was proposed in [55]. In this approach, upon encountering a new uplink covariance matrix, the associated downlink covariance matrix was approximated by interpolating across a Riemannian space, thereby utilizing the elements present in the dictionary. The works of [43,56,57] proposed a potential approach for estimating a high-dimensional covariance matrix with limited observations involving the application of regularization to the sample covariance matrix. The work of [58] proposed a spatial spectrum method for the quantization and the feedback of the covariance matrix. The work of [59] proposed a codebook-based approach to feedback quantized information with respect to the effective eigenvectors and eigenvalues of the channel covariance matrix. The work of [60] proposed an angle estimation with a power angular spectrum (PAS) that can be extracted from the instantaneous uplink channel estimate to obtain the uplink channel covariance matrix. Then, the downlink channel covariance matrix is reconstructed using the inference of the uplink one. Recently, a limited channel covariance feedback approach was proposed in [61], where the user feedback provided only partial information regarding the covariance matrix of the BS.
The investigations above have shown that the system performance using partial channel covariance knowledge suffers from minor losses compared to perfect channel covariance knowledge. It is worth noting that the proposed approach in this paper does not necessitate full knowledge of the channel covariance matrix. Instead, only the effective eigenvectors need to be obtained. Indeed, obtaining this partial information about the channel covariance matrix is more straightforward compared to dealing with the entire (complete) covariance matrix. Therefore, a more precise evaluation of the performance degradation under different levels of covariance matrix estimation errors can be investigated in the future. The transmitted signal is given by the vector , which is placed in Equation (1) and defined here as follows:
where denotes the useful data vector, which is modeled with a zero mean and a variable unit to satisfy , and represents the precoder at the BS, where the type of precoder used in this paper is defined later in (6). This precoder depends on the channel estimation. We need to normalize the power in order to satisfy and ensure the power used for the transmit data as . As such, the parameter given in Equation (4) is defined here, which represents the normalization coefficient to meet the above requirement as described in [11] so that
In this paper, a RZFP technique is used. To this end, the precoder matrix can be formulated as in [11]:
where represents the estimated channel with , and denotes the regularization parameter of the RZFP, which is considered to be , as given in [11]. The received signal at the kth user, which has been defined previously in Equation (1), can be written as
The DASR can be expressed as
where the received signal , by taking into account (7), can be written as [11,62]
where the nominator denotes the desired signal power, and the denominator represents the interference introduced by other users and the noise introduced at the user side that affects the received signal. Further details about the derivation of expression Equation (9) can be found in [62]. Furthermore, various channel realizations are used to calculate the expectations in Equation (9); these realizations are performed independently using massive Monte Carlo simulations. This is often considered to be a computationally intensive operation, because it is necessary to evaluate the SINR and the DASR for a range of values of N, where . However, the theory of the random matrix yields computationally realistic solutions for the SINR and the DASR, which are developed here to find an analytical solution for the SINR with RZFP. The downlink channel estimation, power allocation optimization procedure, and the problem formulation of the DASR in MMIMO systems with the FDD mode are provided in the following section.
3. Power Allocation Optimization and Problem Formulations
As presented in Equation (9), the performance of the DASR depends on the statistical information of the channel and the CSI estimation. The following subsection discusses channel estimation using the MMSE estimation method. The CSI estimation presented here differs from the channel estimation procedure performed in the uplink transmission such as in the TDD operation mode. In this case, channel reciprocity can be exploited to provide the precoder with the estimated channel.
3.1. MMSE Channel Estimation in Downlink FDD Systems
To obtain a CSI estimate in the downlink, in the training phase, the BS is required to transmit the training sequence with length to the users. Accordingly, the received signal, which is denoted here by , at the kth user side when the training phase is performed can be expressed as
where is the noise introduced at the training stage, which is modeled here as , and denotes the training sequence matrix and satisfies the power constraint with . The training matrix depends on essential parameters, which are the training sequence stricture, training sequence power and training sequence length . By taking advantage of traditional linear processing, the MMSE CSI estimate can be used as provided in [63]. Performing Bayesian channel estimation, such as minimum mean square error (MMSE) filters based on channel and noise statistics [63], can lead to a considerable improvement in the quality of channel estimation. To this end, the MMSE estimation can be expressed as
Upon applying the MMSE CSI estimate, the downlink CSI estimate is expressed as
where the received training signal is and given according to Equation (10). The error vector of the channel estimation can be represented as
where the CSI estimation of the MMSE covariance matrix can be given as , which is as expressed as
Our main objective in this paper is not to minimize the estimation error in the equation above but rather to maximize the DASR of FDD MMIMO systems. In particular, this paper investigates the maximization of the DASR of the MMIMO system through the optimization of the power allocation with respect to and .
3.2. Training Sequence Design in Downlink FDD Systems
The formulation in (14) describes the outcome of a channel estimator designed to minimize channel estimation error, and this outcome is contingent on the structure of the correlation matrix at the transmitter. This has led to the exploration of optimizing the training sequence by leveraging the statistical structure of the channel covariance matrix . Therefore, is constructed using the eigenvectors of length equal to . These eigenvectors represent the largest eigenvalues. To this end, the training matrix can be expressed as
A simplified analytical form for the MMSE CSI estimate can be obtained by substituting Equation (15) into Equation (14), which yields
Here, represents the eigenvalues of , where the eigenvalues are arranged as follows: . To constrain the downlink training sequence overhead, the channel energy, associated with the eigenvectors of , is omitted in the training sequence construction and consequently excluded from precoding. Using the proposed training sequence design in Equation (16), one can obtain a simplified formulation of the trace of the MMSE estimation as follows:
The expression in Equation (17) can be further simplified with the P-DoF model. In what follows, the proposed power allocation optimization procedure will be described.
3.3. Power Allocation Optimization Process
This subsection presents the methodology of power allocation to maximize the DASR of an FDD system. While several power allocation approaches have been investigated in the literature, see, e.g., [64,65,66,67,68,69,70], the concentrate was based on the TDD transmission mode. Here, we investigate the power allocation process to maximize the DASR in the FDD transmission mode using a simple straightforward approach. As mentioned earlier, the conventional method divides the power for channel training and data transmission equally without considering any optimization criteria. Equitable power allocation with respect to the training sequence phase and data phase is achieved through uniform power allocation. The work of [18] tried to characterize the tradeoff between DASR maximization and MSE minimization in FDD MMIMO systems. In [18], a uniform power allocation was assumed, and the DASR was not optimized with respect to power allocation but rather was optimized with respect to the training sequence length only. The authors in [18] clearly stated that optimizing the training power and data power with respect to DASR maximization could be investigated in the future. However, there is no characterization for the DASR in FDD MMIMO systems with respect to optimum power allocation. Therefore, our paper investigates the DASR performance with this desired scenario, and the results show that a considerable improvement can be achieved using the proposed power allocation approach, as we can see later in Section 5. To this end, a nonuniform power allocation strategy is performed, which allows for the maximization of the DASR of MMIMO FDD systems with LCT, which is the main objective function of this paper. In this case, the available coherence time and the available total transmit power are combined and divided nonuniformly between the data and training phase, as well as smartly allocated in such a way as to maximize the DASR per each transmission block. In this case, we are targeting the energy allocated per each coherence block and managing the power allocated to each phase (data transmission and channel estimation). This implies that allocating more power to the channel estimation while preserving some time duration for data transmission could help in improving the channel estimation quality while maximizing the DASR. This is because the training sequence length is more valuable due to the prelog fraction that is dedicated to transmitting useful data to the user.
3.4. Power Allocation Formulation
Let represent the total amount of energy at the base station. This is found by multiplying the available power at the base station —here, it is SNR—by the overall coherence time , as provided in Equation (18):
To perform downlink channel estimation in the training phase, the base station sends a training sequence length to the user per each transmission block. The remaining duration is dedicated to data transmission, which can be used to send useful data. Furthermore, the amount of the total transmit energy at the base station can be freely distributed with respect to the data phase and channel estimation phase. Therefore, the energy allocated to the training sequence can be expressed as
where represents the fraction of energy used for the channel estimation phase. As a result, the amount of energy that is still available for the data phase can be written as
where , and . In this case, by using the fraction of energy dedicated to the training , we are controlling the amount of energy dedicated to the channel estimation and data transmission. Hence, for example, we can allocate more energy to the channel estimation to improve the quality of estimation while perceiving some time duration to send useful data to the user. The connection between optimizing the energy allocation for the data transmission and channel estimation phase and maximizing the DASR in MMIMO systems with the FDD mode and LCT is illustrated clearly. In particular, improving training sequence energy becomes imperative to enhance CSI estimation accuracy in the downlink. This signifies that allocating an increased power to the training sequence during the training phase leads to an enhancement in CSI estimation accuracy. The obtained training sequence matrix must always satisfy to ensure constant power as transmitted by the base station. Therefore, the total energy allocated to the channel estimation is given as , which is equivalent to the energy expended during the downlink training period. The data transmission would use the remaining energy as explained clearly above. Note that in the realistic LCT scenarios, which are considered in this paper, increasing the training sequence length would reduce the DASR, since it will affect the remaining time for sending useful data to users. The main contribution in this present paper is derived from the maximization of the DASR using an optimized power allocation procedure. Specifically, by thoroughly going over every conceivable value for , the optimal power allocation that maximizes the DASR with each N is obtained. In the FDD transmission mode, the DASR is maximized for each value of N in relation to a suitable weighted energy value. Increasing the power allocation with respect to the training sequence phase can lead to an improvement in the DASR, as we will see later in the results section in Section 5. Note that machine learning (ML) algorithms can be integrated into the modeling framework of power allocation [64,71,72,73]. However, a recognizable challenge could be the potential lack of interpretability in the decision-making process, thus making it challenging to understand and validate the underlying reasoning behind power allocation choices. Therefore, this paper provides a feasible and tractable solution for optimizing the power allocation in the FDD system with straightforward implications. A block diagram of the MMIMO systems that demonstrates the power allocation for the training phase and the data phase is shown in Figure 2.
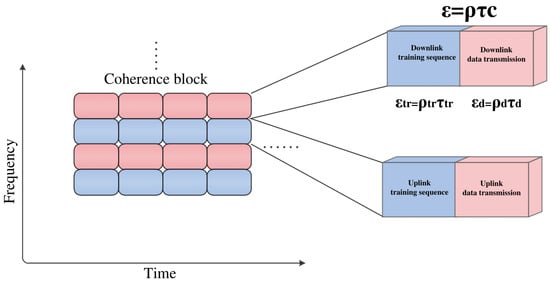
Figure 2.
A diagram that illustrates the power allocation for the training phase and the data phase.
3.5. Formulation of the DASR Maximization Problem
This subsection presents a formula for the DASR maximization for the problem considered in this paper. To this end, the DASR maximization of the MMIMO system in the FDD transition mode can be written as follows:
As was previously indicated, to fulfill the requiters for a high data rate, we need to maximize the possible DASR [74]. Hence, the main goal of this paper is to maximize the DASR. The expression in Equation (21) demonstrates that the length of the training sequence and the LCT, as well as the power allocation in the SINR, are the main factors that determine how much the DASR can be maximized. While the training sequence length and the LCT have a linear effect on the DASR, the power allocation, which is involved in the SINR, has a logarithmic effect on the DASR.
To sum up, unlike the conventional method where the performance of the DASR is investigated with equal power allocation, in this paper, we focus on optimizing the DASR with optimum power allocation. To the best of our knowledge, the power optimization to maximize the DASR performance of MMIMO systems in the FDD mode with LCT has not been investigated. The analyses developed above are valid for any channel model and precoding type. The formulation of the DASR problem in Equation (21) is computationally complex. This is due to the fact that in order to obtain the expectations in Equation (9), extensive Monte Carlo simulations over various channel realizations, different values of N, different correlation coefficients, different training sequence lengths, different SNR values, and different coherence times must be performed. This makes power allocation optimization very difficult without finding a feasible solution. Therefore, in this paper, we develop a computationally viable solution that is found by employing the theory of the random matrix method to address this problem. Specifically, an analytical expression of Equation (9) and the DASR are obtained in this study as using the theory of the random matrix method. Consequently, a low-complexity, simplified numerical evaluation of Equation (21) is obtained, which allows for power allocation optimization over a range of scenarios. The following section provides an analytical expression of the RZFP using the theory of the random matrix method.
4. Analytical Expression for the DASR of RZFP in FDD Systems
The SINR in the downlink is provided analytically here and is based on the theory of the random matrix method [11,75,76]. Let us assume that the users have a common correlation at the BS so that the covariance matrix is , and, hence, , as considered in [20,21,22,24]. Specifically, , an analytical expression of the SINR is calculated as . A straightforward system evaluation is obtained by replacing the SINR SINR term in Equation (9) with the approximation provided in this section thanks to the theory of the random matrix. Therefore, the results can be easily reproducible. The expression for SINR of the RZFP in the MMIMO system with the FDD mode is written as
where the fixed-point technique is used to find the parameter , and the variable is the analytical counterpart of the RZFP with
where the integer has the starting value , and is determined after the fixed-point technique in Equation (24) is converged. Thus, we have the following:
Once we obtain the value of in Equations (23) and (24), it is substituted into
with
with being obtained as
The SINR equation given in Equation (22) represents the analytical expression of the SINR, which applies to all models of channel correlation.
Simplified Analytical Expression for the DASR of RZFP
We use the P-DoF model to further simplify the analysis of the SINR and, consequently, the DASR. The correlations in the channel depend on how many degrees of freedom there are in this channel. Nevertheless, in MMIMO, the channel’s degrees of freedom may be substantially less than N. The P-DoF model as defined in [11,77,78,79] is presented in this subsection. Thus, using the P-DoF model, may be represented as
where matrix in Equation (32) is given as , which can be demonstrated as . Matrix in Equation (32) is denoted by , which can be obtained from of an matrix to satisfy with , which represents the correlation degree [11,77,78,79], and .
Using the P-DoF model and EVD, the expression of MMSE CSI estimation in Equation (16) can be formulated as
where if and is P if otherwise. The unitary matrix eigenvectors are given by . Now, recall the trace of the MMSE estimation in Equation (17), and, using the P-DoF model, the MMSE covariance matrix can be simplified as
The expression above can become a further simplified version of the MMSE estimation, which is defined as
Now, we have obtained a simplified version of the MMSE estimation, and the transmit covariance matrix can also be simplified using the P-DoF model; hence, we can apply these simplifications to further simplify the with the RZFP. The main findings of the RZFP in MMIMO systems with the FDD mode and the P-DoF model are summed up in the following:
where denotes a simplified expression of the fixed-point expressions in Equations (23) and (24) and yields
where the parameter in Equation(37) is given as , and and denote a simplified expression of Equations(28) and (29), which can be determined from Equations (38) and (39):
where is given as , which is used to simplify the above equation:
The SINR of the RZFP expression developed in this subsection allows the DASR of the FDD mode MMIMO system to be easily obtained without Monte Carlo simulations, and, hence, optimization with respect to power allocation becomes applicable. In the following section, we will use the closed-form analytical formula developed here for the SINR of the RZFP to investigate the DASR maximization over a wide range of scenarios.
5. Results of the Proposed Power Allocation Scheme
This section presents numerical findings that illustrate the DASR performance of the RZFP with different power allocations with respect to the training sequence phase and data phase. Hence, we compare the proposed method with optimized power allocation with the conventional method that uses uniform power allocation. Our objective is to maximize the DASR in MMIMO systems with the FDD operation. The lines represent an analytical expression for the SINR of the RZFP that has been developed in this paper and obtained based on the expression provided in Equation (36). The markers denote the simulation of the SINR that has been determined based on the expression in Equation (9).Both the lines and markers are combined in the figures for notation convenience.
Figure 3 depicts the DASR with the correlation coefficient, thereby comparing the proposed power optimization method with the conventional method, with , users, dB, and a correlation coefficient of 0.1, which implies a strong correlation, while 0.9 implies an uncorrelated channel. The red and black lines with markers depict the BS antennas of , while the magenta color and blue lines with markers illustrate the BS antennas of . The results demonstrate that with short coherence time and relatively strong correlation, the DASR was significantly increased and higher than that obtained when . The results also demonstrate that an improvement of around 9 bit/s/Hz in the DASR was achieved. In addition, the results presented here show that a marked improvement in the DASR was achieved with the proposed power optimization method. For example, when , around 3 bit/s/Hz was achieved with the proposed method across all the correlation coefficient ranges considered. In addition, when N was increased to , around 4 bit/s/Hz of improvement in the DASR was achieved at relatively high correlated scenarios. Furthermore, the results demonstrate that in order to achieve 30 bit/s/Hz, the proposed optimization method achieved a gain in power of around 3 dB, which signifies the applicability of the proposed method in a realistic scenario.
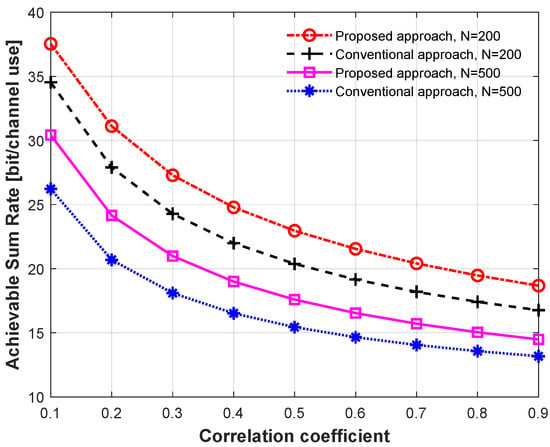
Figure 3.
DASR with correlation coefficient comparing different power allocation schemes with different numbers of BS antennas: and .
In order to observe the DASR performance with different total transmit power values, Figure 4 investigates the DASR performance of the proposed power allocation method in comparison with the conventional method using different SNR values. The configurations were chosen as users, , , and , and the correlation coefficient was 0.1. The results show that when the transmit power was reduced, i.e., dB, there was a slight improvement in the DASR for both of the scenarios considered. However, upon increasing the power, i.e., dB, dB, and dB, a significant improvement in the DASR was achieved using the proposed power allocation method.
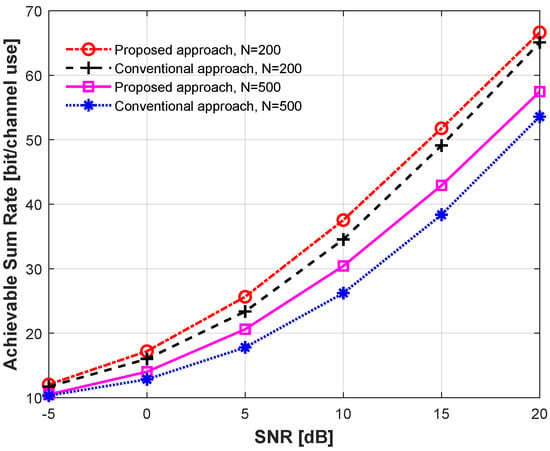
Figure 4.
DASR with in dB comparing different power allocation methods with different numbers of BS antennas: and .
Figure 5 investigates the DASR performance with varying amounts of N antennas comparing the proposed power optimization method with the conventional method when a different number of users K was considered. The configurations were , the average transmit power was considered so that dB, and the correlation coefficient was 0.1. The results show that a considerable enhancement in the DASR was achieved when the power was optimized, especially when N was increased to . For example, with and 500, approximately 8 bit/s/Hz of improvement in the DASR was achieved.
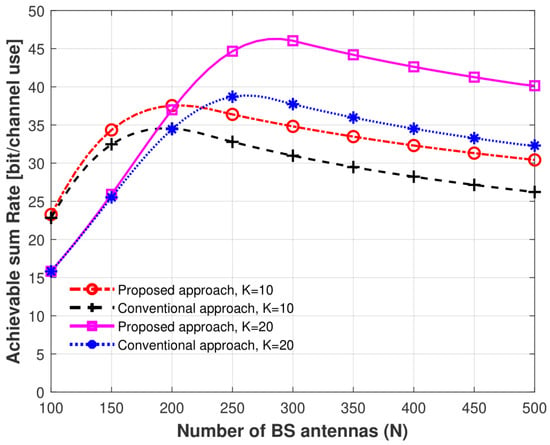
Figure 5.
DASR with different numbers of N antennas comparing different power allocation methods with different numbers of users antennas; and .
Figure 6 and Figure 7 investigate the DASR performance with coherence block time comparing the proposed power optimization method with the conventional method, with and , respectively. The configurations were , an average transmit power was considered, i.e., dB, and the correlation coefficient was 0.1. The results indicate that when the coherence time was increased, the DASR rose rapidly, thereby achieving an ∼53 rate at and an ∼67 rate at . In addition, the results demonstrate that the proposed power optimization scheme enhanced the DASR performance markedly over all the coherence time values considered. Note that the degradation in the DASR performance with a large number of BS antennas () was due to the residual interference caused by imperfect channel estimation. With increasing BS antennas, the RZF precoder’s interference cancellation capability diminishes, thus leading to heightened residual interference. Additionally, in a scenario with limited coherence time, where the prelog fraction designates the time allocated to channel estimation, a considerable impact on the DASR arises, since the number of N far exceeds the considered coherence time, thereby leaving insufficient time for transmitting useful data after CSI estimation.
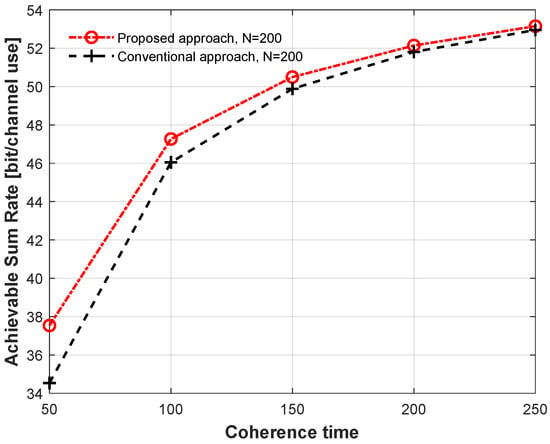
Figure 6.
DASR with coherence time comparing different power allocation methods, with .
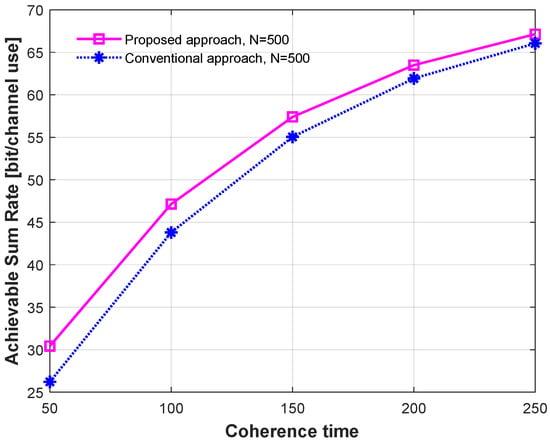
Figure 7.
DASR with coherence time comparing different power allocation methods, with .
Figure 8 investigates the DASR performance with N numbers of antennas comparing the proposed power optimization method with the conventional method when the coherence time was increased but with various N and different SNR values. The correlation coefficient was 0.1 and . The results indicate that increasing the SNR would significantly enhance the DASR. A peak DASR was achieved at , and an enhancement of 23 bits in the DASR was achieved when dB in comparison with dB. The results show that for both of the SNR values considered, the proposed power allocation optimization method improved the DASR performance outcomes, especially as . The results presented in the section clearly show the effectiveness of the proposed power optimization approach in improving the DASR performance.
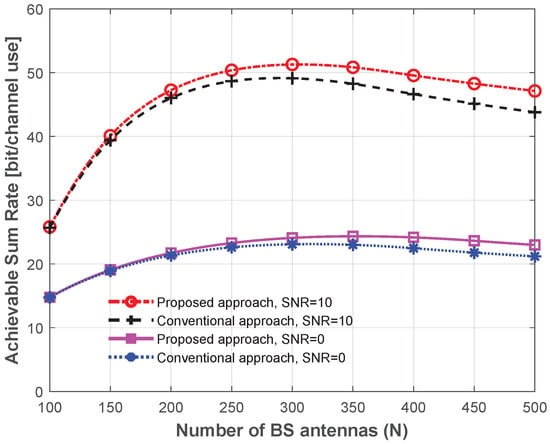
Figure 8.
DASR with different numbers of N comparing different power allocation methods with different SNR values, i.e., dB and dB.
6. Conclusions
This research addressed the problem of maximizing the DASR in the MMIMO with FDD systems considering URLLC scenarios, i.e., with LCT. To this end, a low-complexity power allocation optimization method was proposed for DASR maximization. In addition, this paper developed an analytical expression for the SINR and the DASR of the RZFP in FDD systems using the random matrix method. Different scenarios were examined to determine the effect of power optimization on the DASR of MMIMO with the FDD mode and LCT. The results demonstrated a precise alignment between the theoretical analysis (lines) and the simulated (markers) results, thereby substantiating the primary contributions of this paper. The results also indicated that a considerable enhancement in the DASR was obtained using the proposed power allocation method in comparison with the conventional uniform power allocation method. These findings allow for the implementation of FDD systems with high frequencies, especially in the scenarios of LCT. Future wireless communication systems, e.g., 6G, might adopt cell-free networks. Therefore, it is worthwhile to investigate a viable CSI estimation mechanism for the FDD systems with cell-free networks in the future. In addition, investigating the power allocation strategy for the aforementioned scenario may also be worth considering in the future.
Author Contributions
Conceptualization, M.A., M.I.S. and M.A.N.; methodology, M.A.; software, M.A. and M.I.S.; validation, M.A.N. and M.I.S.; formal analysis, M.A.; investigation, M.A.N.; resources, M.I.S.; writing—original draft preparation, M.A.N.; writing—review and editing, M.A. and M.I.S.; visualization, M.I.S.; supervision, M.A. and M.I.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The code used to generate the results in this paper is available upon request.
Conflicts of Interest
The authors want to make it clear that there are no conflicts of interest in this research.
References
- Alsabah, M.; Naser, M.A.; Mahmmod, B.M.; Abdulhussain, S.H.; Eissa, M.R.; Al-Baidhani, A.; Noordin, N.K.; Sait, S.M.; Al-Utaibi, K.A.; Hashim, F. 6G wireless communications networks: A comprehensive survey. IEEE Access 2021, 9, 148191–148243. [Google Scholar] [CrossRef]
- Simsek, M.; Aijaz, A.; Dohler, M.; Sachs, J.; Fettweis, G. 5G-enabled tactile internet. IEEE J. Sel. Areas Commun. 2016, 34, 460–473. [Google Scholar] [CrossRef]
- Zong, B.; Fan, C.; Wang, X.; Duan, X.; Wang, B.; Wang, J. 6G technologies: Key drivers, core requirements, system architectures, and enabling technologies. IEEE Veh. Technol. Mag. 2019, 14, 18–27. [Google Scholar] [CrossRef]
- Liu, H.; Deng, H.; Yi, Y.; Zhu, Z.; Liu, G.; Zhang, J. Energy Efficiency Optimization Based on Power Allocation in Massive MIMO Downlink Systems. Symmetry 2022, 14, 1145. [Google Scholar] [CrossRef]
- Marzetta, T.L. Noncooperative Cellular Wireless with Unlimited Numbers of Base Station Antennas. IEEE Trans. Wirel. Commun. 2010, 9, 3590–3600. [Google Scholar] [CrossRef]
- Rusek, F.; Persson, D.; Lau, B.K.; Larsson, E.G.; Marzetta, T.L.; Edfors, O.; Tufvesson, F. Scaling Up MIMO: Opportunities and Challenges with Very Large Arrays. IEEE Signal Process. Mag. 2013, 30, 40–60. [Google Scholar] [CrossRef]
- Gkonis, P.K.; Trakadas, P.T.; Kaklamani, D.I. A comprehensive study on simulation techniques for 5g networks: State of the art results, analysis, and future challenges. Electronics 2020, 9, 468. [Google Scholar] [CrossRef]
- Huh, H.; Caire, G.; Papadopoulos, H.C.; Ramprashad, S.A. Achieving “Massive MIMO” Spectral Efficiency with a Not-so-Large Number of Antennas. IEEE Trans. Wirel. Commun. 2012, 11, 3226–3239. [Google Scholar] [CrossRef]
- Jose, J.; Ashikhmin, A.; Marzetta, T.L.; Vishwanath, S. Pilot Contamination and Precoding in Multi-Cell TDD Systems. IEEE Trans. Wirel. Commun. 2011, 10, 2640–2651. [Google Scholar] [CrossRef]
- Ngo, H.Q.; Larsson, E.G.; Marzetta, T.L. Energy and spectral efficiency of very large multiuser MIMO systems. IEEE Trans. Commun. 2013, 61, 1436–1449. [Google Scholar]
- Hoydis, J.; Ten Brink, S.; Debbah, M. Massive MIMO in the UL/DL of Cellular Networks: How Many Antennas Do We Need? IEEE J. Sel. Areas Commun. 2013, 31, 160–171. [Google Scholar] [CrossRef]
- Omer, D.; Hussein, M.; Mina, L. Ergodic Capacity for Evaluation of Mobile System Performance. J. Eng. 2020, 26, 135–148. [Google Scholar] [CrossRef]
- Ericsson. Ericsson Mobility Report: On the Pulse of the Network Society. Technical Report. Ericsson. 2016. Available online: https://www.ericsson.com/assets/local/mobility-report/documents/2016/ericsson-mobility-report-november-2016.pdf (accessed on 25 October 2023).
- Kaltenberger, F.; Jiang, H.; Guillaud, M.; Knopp, R. Relative channel reciprocity calibration in MIMO/TDD systems. In Proceedings of the Future Network & Mobile Summit, Florence, Italy, 16–18 June 2010; pp. 1–10. [Google Scholar]
- Björnson, E.; Hoydis, J.; Kountouris, M.; Debbah, M. Hardware impairments in large-scale MISO systems: Energy efficiency, estimation, and capacity limits. In Proceedings of the 18th International Conference on Digital Signal Processing (DSP), Santorini, Greece, 1–3 July 2013; pp. 1–6. [Google Scholar]
- Mi, D.; Dianati, M.; Zhang, L.; Muhaidat, S.; Tafazolli, R. Massive MIMO performance with imperfect channel reciprocity and channel estimation error. IEEE Trans. Commun. 2017, 65, 3734–3749. [Google Scholar] [CrossRef]
- Vieira, J.; Rusek, F.; Edfors, O.; Malkowsky, S.; Liu, L.; Tufvesson, F. Reciprocity calibration for massive MIMO: Proposal, modeling, and validation. IEEE Trans. Wirel. Commun. 2017, 16, 3042–3056. [Google Scholar] [CrossRef]
- Alsabah, M.; Naser, M.A.; Mahmmod, B.M.; Noordin, N.K.; Abdulhussain, S.H. Sum rate maximization versus MSE minimization in FDD massive MIMO systems with short coherence time. IEEE Access 2021, 9, 108793–108808. [Google Scholar] [CrossRef]
- Alsabah, M.; Vehkapera, M.; O’Farrell, T. Non-Iterative Downlink Training Sequence Design Based on Sum Rate Maximization in FDD Massive MIMO Systems. IEEE Access 2020, 8, 108731–108747. [Google Scholar] [CrossRef]
- Kotecha, J.H.; Sayeed, A.M. Transmit signal design for optimal estimation of correlated MIMO channels. IEEE Trans. Signal Process. 2004, 52, 546–557. [Google Scholar] [CrossRef]
- Björnson, E.; Ottersten, B. A Framework for Training-Based Estimation in Arbitrarily Correlated Rician MIMO Channels with Rician Disturbance. IEEE Trans. Signal Process. 2010, 58, 1807–1820. [Google Scholar] [CrossRef]
- Noh, S.; Zoltowski, M.D.; Sung, Y.; Love, D.J. Pilot Beam Pattern Design for Channel Estimation in Massive MIMO Systems. IEEE J. Sel. Top. Signal Process. 2014, 8, 787–801. [Google Scholar] [CrossRef]
- Choi, J.; Love, D.J.; Bidigare, P. Downlink Training Techniques for FDD Massive MIMO Systems: Open-Loop and Closed-Loop Training With Memory. IEEE J. Sel. Top. Signal Process. 2014, 8, 802–814. [Google Scholar] [CrossRef]
- So, J.; Kim, D.; Lee, Y.; Sung, Y. Pilot Signal Design for Massive MIMO Systems: A Received Signal-To-Noise-Ratio-Based Approach. IEEE Signal Process. Lett. 2015, 22, 549–553. [Google Scholar] [CrossRef]
- Naser, M.A.; Alsabah, M.; Mahmmod, B.M.; Noordin, N.K.; Abdulhussain, S.H.; Baker, T. Downlink training design for FDD massive MIMO systems in the presence of colored noise. Electronics 2020, 9, 2155. [Google Scholar] [CrossRef]
- Naser, M.A.; Alsabah, M.Q.; Taher, M.A. A partial CSI estimation approach for downlink FDD massive-MIMO system with different base transceiver station topologies. Wirel. Pers. Commun. 2021, 119, 3609–3630. [Google Scholar] [CrossRef]
- Naser, M.A.; Abdul-Hadi, A.M.; Alsabah, M.; Mahmmod, B.M.; Majeed, A.; Abdulhussain, S.H. Downlink Training Sequence Design Based on Waterfilling Solution for Low-Latency FDD Massive MIMO Communications Systems. Electronics 2023, 12, 2494. [Google Scholar] [CrossRef]
- Alsabah, M.; Naser, M.A.; Mahmmod, B.M.; Abdulhussain, S.H. A Computationally Efficient Gradient Algorithm for Downlink Training Sequence Optimization in FDD Massive MIMO Systems. Network 2022, 2, 329–349. [Google Scholar] [CrossRef]
- Gao, Z.; Dai, L.; Dai, W.; Shim, B.; Wang, Z. Structured Compressive Sensing-Based Spatio-Temporal Joint Channel Estimation for FDD Massive MIMO. IEEE Trans. Commun. 2016, 64, 601–617. [Google Scholar] [CrossRef]
- Han, Y.; Lee, J.; Love, D.J. Compressed Sensing-Aided Downlink Channel Training for FDD Massive MIMO Systems. IEEE Trans. Commun. 2017, 65, 2852–2862. [Google Scholar] [CrossRef]
- Nouri, N.; Azizipour, M.J.; Mohamed-Pour, K. A Compressed CSI Estimation Approach for FDD Massive MIMO Systems. In Proceedings of the 2020 28th Iranian Conference on Electrical Engineering (ICEE), Tabriz, Iran, 4–6 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1–6. [Google Scholar]
- Shi, Y.; Jiang, Z.; Liu, Y.; Wang, Y.; Xu, S. A Compressive Sensing Based Channel Prediction Scheme with Uneven Pilot Design in Mobile Massive MIMO Systems. In Proceedings of the 2021 13th International Conference on Wireless Communications and Signal Processing (WCSP), Changsha, China, 20–22 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–6. [Google Scholar]
- Han, T.; Zhao, D. On the Performance of FDD Cell-Free Massive MIMO with Compressed Sensing Channel Estimation. In Proceedings of the 2021 IEEE 21st International Conference on Communication Technology (ICCT), Tianjin, China, 13–16 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 238–242. [Google Scholar]
- Mei, Y.; Gao, Z. CS-Based CSIT Estimation for Downlink Pilot Decontamination in Multi-Cell FDD Massive MIMO. In Proceedings of the 2021 IEEE/CIC International Conference on Communications in China (ICCC), Xiamen, China, 28–30 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Adhikary, A.; Nam, J.; Ahn, J.Y.; Caire, G. Joint Spatial Division and Multiplexing: The Large-Scale Array Regime. IEEE Trans. Inf. Theory 2013, 59, 6441–6463. [Google Scholar] [CrossRef]
- Nam, J.; Caire, G.; Ha, J. On the role of transmit correlation diversity in multiuser MIMO systems. IEEE Trans. Inf. Theory 2017, 63, 336–354. [Google Scholar] [CrossRef]
- Wu, X.; Yang, X.; Ma, S.; Zhou, B.; Yang, G. Hybrid Channel Estimation for UPA-Assisted Millimeter-Wave Massive MIMO IoT Systems. IEEE Internet Things J. 2021, 9, 2829–2842. [Google Scholar] [CrossRef]
- Mirzaei, J.; ShahbazPanahi, S.; Sohrabi, F.; Adve, R. Hybrid Analog and Digital Beamforming Design for Channel Estimation in Correlated Massive MIMO Systems. IEEE Trans. Signal Process. 2021, 69, 5784–5800. [Google Scholar] [CrossRef]
- Pang, J.; Li, J.; Zhao, L.; Lu, Z. Optimal Training Sequences for MIMO Channel Estimation with Spatial Correlation. In Proceedings of the IEEE Vehicular Technology Conference, Baltimore, MD, USA, 30 September–3 October 2007; pp. 651–655. [Google Scholar]
- Liu, Y.; Wong, T.F.; Hager, W.W. Training Signal Design for Estimation of Correlated MIMO Channels With Colored Interference. IEEE Trans. Signal Process. 2007, 55, 1486–1497. [Google Scholar] [CrossRef]
- Bjornson, E.; Ottersten, B. Training-based Bayesian MIMO channel and channel norm estimation. In Proceedings of the 2009 IEEE International Conference on Acoustics, Speech and Signal Processing, Taipei, Taiwan, 19–24 April 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 2701–2704. [Google Scholar]
- Shariati, N.; Wang, J.; Bengtsson, M. Robust training sequence design for correlated MIMO channel estimation. IEEE Trans. Signal Process. 2013, 62, 107–120. [Google Scholar] [CrossRef]
- Shariati, N.; Björnson, E.; Bengtsson, M.; Debbah, M. Low-complexity polynomial channel estimation in large-scale MIMO with arbitrary statistics. IEEE J. Sel. Top. Signal Process. 2014, 8, 815–830. [Google Scholar] [CrossRef]
- Biguesh, M.; Gazor, S.; Shariat, M.H. Optimal training sequence for MIMO wireless systems in colored environments. IEEE Trans. Signal Process. 2009, 57, 3144–3153. [Google Scholar] [CrossRef]
- Salman, M.I.; Abdulhasan, M.Q.; Ng, C.K.; Noordin, N.K.; Sali, A.; Mohd Ali, B. Radio resource management for green 3gpp long term evolution cellular networks: Review and trade-offs. IETE Tech. Rev. 2013, 30, 257–269. [Google Scholar] [CrossRef]
- Abdul-Hadi, A.M.; Naser, M.A.; Alsabah, M.; Abdulhussain, S.H.; Mahmmod, B.M. Performance evaluation of frequency division duplex (FDD) massive multiple input multiple output (MIMO) under different correlation models. PeerJ Comput. Sci. 2022, 8, e1017. [Google Scholar] [CrossRef]
- Stein, S. Fading channel issues in system engineering. IEEE J. Sel. Areas Commun. 1987, 5, 68–89. [Google Scholar] [CrossRef]
- Gao, X.; Edfors, O.; Rusek, F.; Tufvesson, F. Massive MIMO Performance Evaluation Based on Measured Propagation Data. IEEE Trans. Wirel. Commun. 2015, 14, 3899–3911. [Google Scholar] [CrossRef]
- Naser, M.A.; Salman, M.I.; Alsabah, M. The role of correlation in the performance of massive MIMO systems. Appl. Syst. Innov. 2021, 4, 54. [Google Scholar] [CrossRef]
- Liang, Y.C.; Chin, F.P.S. Downlink channel covariance matrix (DCCM) estimation and its applications in wireless DS-CDMA systems. IEEE J. Sel. Areas Commun. 2001, 19, 222–232. [Google Scholar] [CrossRef]
- Hochwald, B.M.; Maretta, T. Adapting a downlink array from uplink measurements. IEEE Trans. Signal Process. 2001, 49, 642–653. [Google Scholar] [CrossRef]
- Fang, J.; Li, X.; Li, H.; Gao, F. Low-Rank Covariance-Assisted Downlink Training and Channel Estimation for FDD Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2017, 16, 1935–1947. [Google Scholar] [CrossRef]
- Upadhya, K.; Vorobyov, S.A. Covariance matrix estimation for massive MIMO. IEEE Signal Process. Lett. 2018, 25, 546–550. [Google Scholar] [CrossRef]
- Jordan, M.; Dimofte, A.; Gong, X.; Ascheid, G. Conversion from uplink to downlink spatio-temporal correlation with cubic splines. In Proceedings of the VTC Spring 2009-IEEE 69th Vehicular Technology Conference, Barcelona, Spain, 26–29 April 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–5. [Google Scholar]
- Decurninge, A.; Guillaud, M.; Slock, D.T. Channel covariance estimation in massive MIMO frequency division duplex systems. In Proceedings of the 2015 IEEE Globecom Workshops (GC Wkshps), San Diego, CA, USA, 6–10 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Ledoit, O.; Wolf, M. A well-conditioned estimator for large-dimensional covariance matrices. J. Multivar. Anal. 2004, 88, 365–411. [Google Scholar] [CrossRef]
- Björnson, E.; Sanguinetti, L.; Debbah, M. Massive MIMO with imperfect channel covariance information. In Proceedings of the 2016 50th Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 6–9 November 2016; pp. 974–978. [Google Scholar]
- Liu, Y.; Li, G.Y.; Han, W. Quantization and feedback of spatial covariance matrix for massive MIMO systems with cascaded precoding. IEEE Trans. Commun. 2017, 65, 1623–1634. [Google Scholar] [CrossRef]
- Ghosh, S.; Rao, B.D.; Zeidler, J.R. Techniques for MIMO channel covariance matrix quantization. IEEE Trans. Signal Process. 2012, 60, 3340–3345. [Google Scholar] [CrossRef]
- Xie, H.; Gao, F.; Jin, S.; Fang, J.; Liang, Y.C. Channel estimation for TDD/FDD massive MIMO systems with channel covariance computing. IEEE Trans. Wirel. Commun. 2018, 17, 4206–4218. [Google Scholar] [CrossRef]
- Bazzi, S.; Xu, W. FDD Multiuser Massive MIMO Systems with Adaptive Channel Covariance Feedback. In Proceedings of the 2019 IEEE 30th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Istanbul, Turkey, 8–11 September 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–6. [Google Scholar]
- Björnson, E.; Hoydis, J.; Sanguinetti, L. Massive MIMO Networks: Spectral, Energy, and Hardware Efficiency; Now Publishers, Inc.: Delft, The Netherlands, 2017; Volume 11, pp. 154–655. [Google Scholar]
- Kay, S. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Sanguinetti, L.; Zappone, A.; Debbah, M. Deep learning power allocation in massive MIMO. In Proceedings of the 2018 52nd Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 28–31 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 1257–1261. [Google Scholar]
- Zhang, Q.; Jin, S.; McKay, M.; Morales-Jimenez, D.; Zhu, H. Power allocation schemes for multicell massive MIMO systems. IEEE Trans. Wirel. Commun. 2015, 14, 5941–5955. [Google Scholar] [CrossRef]
- Van Chien, T.; Björnson, E.; Larsson, E.G. Joint power allocation and user association optimization for massive MIMO systems. IEEE Trans. Wirel. Commun. 2016, 15, 6384–6399. [Google Scholar] [CrossRef]
- Ho, C.D.; Ngo, H.Q.; Matthaiou, M.; Nguyen, L.D. Power allocation for multi-way massive MIMO relaying. IEEE Trans. Commun. 2018, 66, 4457–4472. [Google Scholar] [CrossRef]
- Ren, H.; Pan, C.; Deng, Y.; Elkashlan, M.; Nallanathan, A. Joint pilot and payload power allocation for massive-MIMO-enabled URLLC IIoT networks. IEEE J. Sel. Areas Commun. 2020, 38, 816–830. [Google Scholar] [CrossRef]
- Van Chien, T.; Björnson, E.; Larsson, E.G. Joint power allocation and load balancing optimization for energy-efficient cell-free massive MIMO networks. IEEE Trans. Wirel. Commun. 2020, 19, 6798–6812. [Google Scholar] [CrossRef]
- Bobrov, E.; Chinyaev, B.; Kuznetsov, V.; Minenkov, D.; Yudakov, D. Power allocation algorithms for massive MIMO systems with multi-antenna users. Wirel. Netw. 2023, 29, 3747–3768. [Google Scholar] [CrossRef]
- Giannopoulos, A.; Spantideas, S.; Capsalis, N.; Gkonis, P.; Karkazis, P.; Sarakis, L.; Trakadas, P.; Capsalis, C. WIP: Demand-driven power allocation in wireless networks with deep Q-learning. In Proceedings of the 2021 IEEE 22nd International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Pisa, Italy, 7–11 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 248–251. [Google Scholar]
- Jo, S.; Jong, C.; Pak, C.; Ri, H. Multi-agent deep reinforcement learning-based energy efficient power allocation in downlink MIMO-NOMA systems. IET Commun. 2021, 15, 1642–1654. [Google Scholar] [CrossRef]
- Zhao, Y.; Niemegeers, I.G.; De Groot, S.M.H. Dynamic power allocation for cell-free massive MIMO: Deep reinforcement learning methods. IEEE Access 2021, 9, 102953–102965. [Google Scholar] [CrossRef]
- Chen, S.; Liang, Y.C.; Sun, S.; Kang, S.; Cheng, W.; Peng, M. Vision, requirements, and technology trend of 6G: How to tackle the challenges of system coverage, capacity, user data-rate and movement speed. IEEE Wirel. Commun. 2020, 27, 218–228. [Google Scholar] [CrossRef]
- Wagner, S.; Couillet, R.; Debbah, M.; Slock, D.T. Large System Analysis of Linear Precoding in Correlated MISO Broadcast Channels under Limited Feedback. IEEE Trans. Inf. Theory 2012, 58, 4509–4537. [Google Scholar] [CrossRef]
- Couillet, R.; Debbah, M. Random Matrix Methods for Wireless Communications; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Ngo, H.Q. Analysis of the pilot contamination effect in very large multicell multiuser MIMO systems for physical channel models. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 3464–3467. [Google Scholar]
- Payami, S.; Tufvesson, F. Channel measurements and analysis for very large array systems at 2.6 GHz. In Proceedings of the European Conference on Antennas and Propagation (EUCAP), Prague, Czech Republic, 26–30 March 2012; pp. 433–437. [Google Scholar]
- Ngo, H.Q.; Larsson, E.G.; Marzetta, T.L. The multicell multiuser MIMO uplink with very large antenna arrays and a finite-dimensional channel. IEEE Trans. Commun. 2013, 61, 2350–2361. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).