Dual Data Streaming on Tropospheric Communication Links Based on the Determination of Beam Pointing Dynamics Using a Modified Ray-Based Channel Model
Abstract
1. Introduction
1.1. Application of Tropo for Defense Communication
1.2. Problem Statement and Motivation
1.3. Research Methodology
1.4. Aims of the Work and Conclusions
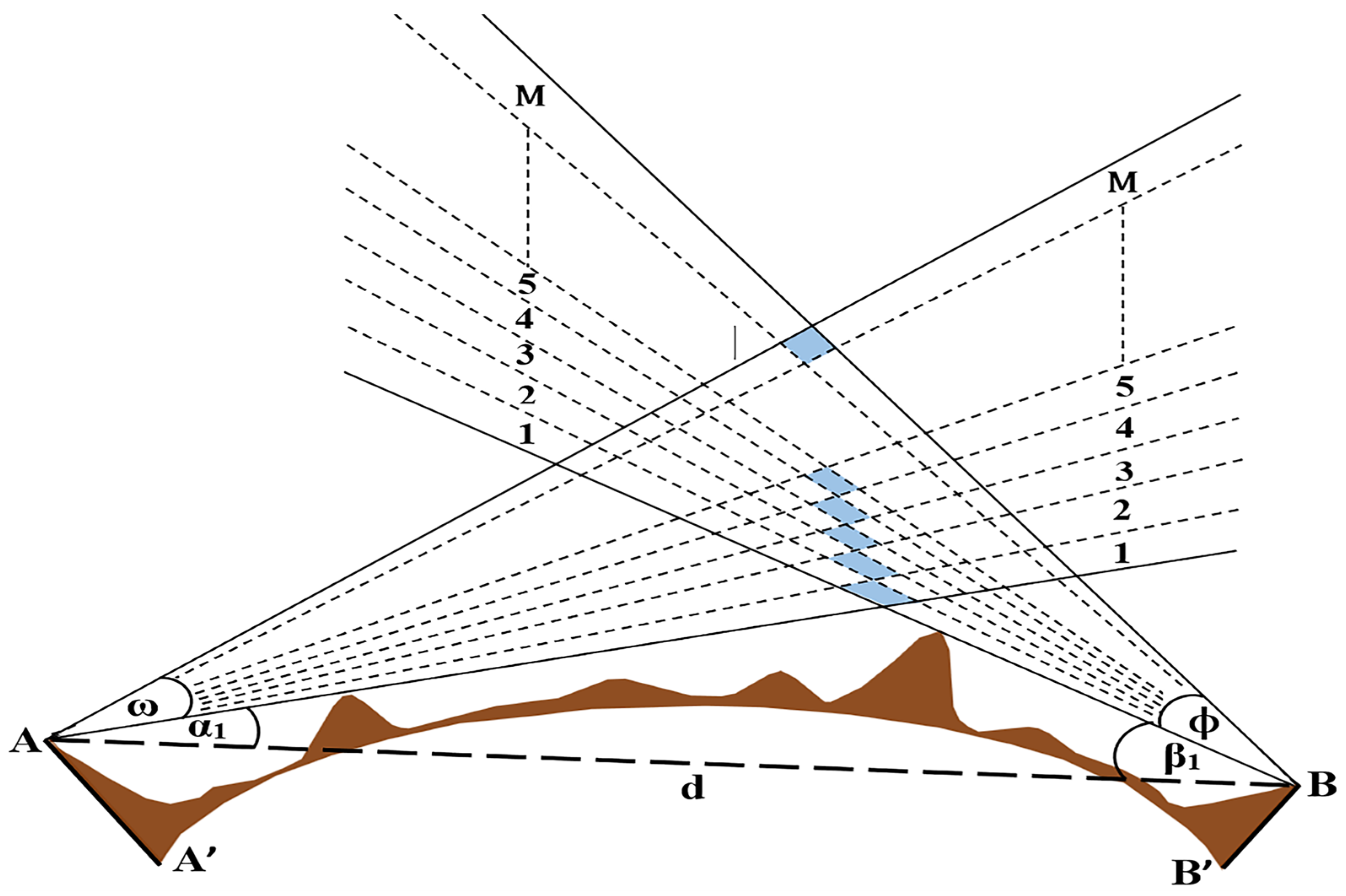
2. Methodology for Determination of Beam Pointing Dynamics
2.1. Derivation of Expression for Received Power
2.2. Dinc’s Ray-Based Model
2.3. Modified Model
3. Data Collection and Processing
4. Results and Discussions
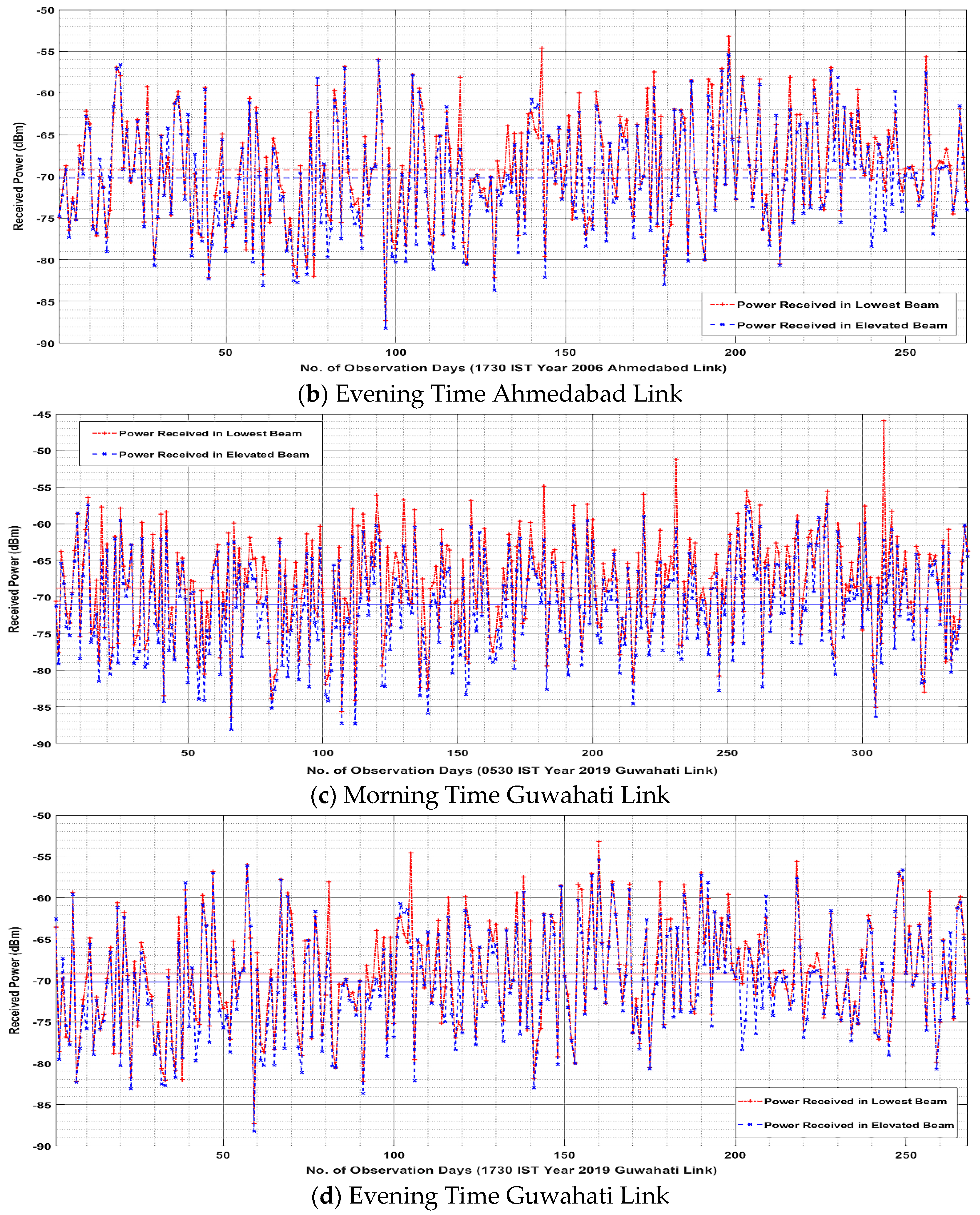
4.1. Results for Ahmedabad Link
4.2. Results for Guwahati Link
4.3. Discussions
4.4. Dual Data Streaming Design
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Calculation of Scatter Angle and Sub Volume Distances

Appendix B. Calculation of Vertical Gradient of Refractive Index
| Constant | Value ( > 0 °C) | Value ( ≤ 0 °C) |
|---|---|---|
| a′ | −4.9283 | −0.32286 |
| b′ | −2937.4 | −2705.21 |
| c′ | 23.5518 | 11.4816 |
| d′ | 273 | 273 |
Appendix C. Selection of Turbulence Wave Number
References
- Marconi, G. Radio communications by means of very short electric waves. IRE Trans. Antennas Propag. 1957, 5, 90–99. [Google Scholar] [CrossRef]
- Clavier, A.; Altovsky, V. Beyond-the-horizon 300-magacycle propagation tests in 1941. Elec. Commun. 1956, 33, 117–132. [Google Scholar]
- Katzin, M.; Bauchman, R.; Binnian, W. 3- and 9-centimeter propagation in low ocean ducts. Proc. IRE 1947, 35, 891–905. [Google Scholar] [CrossRef]
- Day, J.; Trolese, L. Propagation of short radio waves over desert terrain. Proc. IRE 1950, 38, 65–175. [Google Scholar] [CrossRef]
- Pekeris, C. Wave theoretical interpretation of propagation of 10- centimeter and 3-centimeter waves in low-level ocean ducts. Proc. IRE 1947, 35, 453–462. [Google Scholar] [CrossRef]
- Gunther, F.A. Tropospheric scatter communications past, present, and future. IEEE Spectr. 1966, 3, 79–100. [Google Scholar] [CrossRef]
- Roda, G. Troposcatter Radio Links, 1st ed.; Artech House Publishers: Norwood, MA, USA, 1988. [Google Scholar]
- Propagation Prediction Techniques and Data Required for the Design of Trans-Horizon Radio-Relay Systems. ITU-R Recommendation P.617-5(08/2019). Available online: https://www.itu.int/rec/R-REC-P.617-5-201908-I/en (accessed on 5 September 2023).
- Zhao, Q.; Zhang, R.; Lin, L.; Li, Q. The study of experiment on tropospheric scatter propagation at c-band. In Proceedings of the 12th International Symposium on Antennas, Propagation and EM Theory (ISAPE), Hangzhou, China, 3–6 December 2018; Volume 3. [Google Scholar] [CrossRef]
- Soi, S.; Singh, S.K.; Singh, R.; Kumar, A. Link analysis of ku band troposcatter communication. In Proceedings of the 2019 IEEE Mtt-s International Microwave and RF Conference (IMARC), Mumbai, India, 13–15 December 2019; pp. 1–5. [Google Scholar]
- Winters, J.H.; Luddy, M.J. Phased array applications to improve troposcatter communications. In Proceedings of the 2019 IEEE International Symposium on Phased Array System & Technology (PAST), Waltham, MA, USA, 15–18 October 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Winters, J.H.; Luddy, M.J. Wideband array transmission—Waveforms and phase notching. In Proceedings of the 2019 IEEE International Symposium on Phased Array System & Technology (PAST), Waltham, MA, USA, 15–18 October 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Booker, H.G.; Gordon, W.E. A theory of radio scattering in the troposphere. Proc. IRE 1950, 38, 401–412. [Google Scholar] [CrossRef]
- Friis, H.T.; Crawford, A.B.; Hogg, D.C. A reflection theory for propagation beyond the horizon. Bell Syst. Tech. J. 1957, 36, 627–644. [Google Scholar] [CrossRef]
- Bello, P. A troposcatter channel model. IEEE Trans. Commun. Technolog. 1969, 17, 130–137. [Google Scholar] [CrossRef]
- Rice, P.L.; Longley, A.G.; Barsis, A.P.; Norton, K.A. Transmission Loss Predictions for Tropospheric Communication Circuits; Ser. Technical Note no. 101; National Bureau of Standards, U.S. Department of Commerce: Gaithersburg, MD, USA, 1965.
- Prediction Procedure for the Evaluation of Interference between Stations on the Surface of the Earth at Frequencies Above about 0.1 GHz. ITU-R Recommendation P.452-17 (09/2021). Available online: https://www.itu.int/rec/R-REC-P.452-17-202109-I/en (accessed on 5 September 2023).
- A General Purpose Wide-Range Terrestrial Propagation Model in the Frequency Range 30 mhz to 50 ghz. ITU-R Recommendation P.2001-4 (09/2021). Available online: https://www.itu.int/rec/R-REC-P.2001-4-202109-I/en (accessed on 5 September 2023).
- Dinc, E.; Akan, O.B. A ray-based channel modeling approach for mimo troposcatter beyond-line-of-sight (b-los) communications. IEEE Trans. Commun. 2015, 63, 1690–1699. [Google Scholar] [CrossRef]
- NAMMA LIDAR Atmospheric Sensing Experiment (LASE). Available online: https://ghrc.nsstc.nasa.gov/uso/ds_docs/namma/namlase/namlase_dataset.html (accessed on 5 September 2023).
- Ishimaru, A. Wave Propagation and Scattering in Random Media; Ser. An IEEE OUP Classic Reissue; Wiley-IEEE Press: Hoboken, NJ, USA, 1999. [Google Scholar]
- Marzano, F.S.; d’Auria, G. Model-based prediction of amplitude scintillation variance due to clear-air tropospheric turbulence on earth-satellite microwave links. IEEE Trans. Antennas Propag. 1998, 46, 1506–1518. [Google Scholar] [CrossRef]
- Devasirvatham, D.M.J. Effects of Atmospheric Turbulence on Microwave and Millimeter Wave Satellite Communications Systems. Ph.D. Dissertation, Ohio State University, Columbus, OH, USA, May 1981. [Google Scholar]
- Tsang, L.; Kong, J.A.; Ding, K. Scattering of Electromagnetic Waves: Theories and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Prediction Procedure for the Evaluation of Interference between Stations Frequencies above about 0.1 ghz. ITU-R Recommendation P.452-15, Geneva, Switzerland, July 2015. Available online: https://www.itu.int/rec/R-REC-P.452/en (accessed on 5 September 2023).
- Parish, O.O.; Putnam, T.W. Equations for the Determination of Humidity from Dewpoint and Psychometric Data; NASA Technical Note D-8401; National Aeronautics and Space Administration: Washington, DC, USA, 1977.
- The Radio Refractive Index: Its Formula and Refractivity Data. Int. Telecommun. Union (ITU-R), Geneva, Switzerland, Rec. P.453-11, 2015. Available online: https://www.itu.int/rec/R-REC-P.453/en (accessed on 5 September 2023).








| System Parameters | Ahmedabad Link | Guwahati Link | Link Geometry Parameters | Ahmedabad Link | Guwahati Link |
|---|---|---|---|---|---|
| Transmission frequency (f) | 5 GHZ | 2 GHZ | Transmit antenna location * | 23.5776° N 72.7337° E | 26.1254° N 91.074° E |
| Transmission wavelength (λ) | 0.06 m | 0.15 m | Receive antenna location * | 22.6901° N 72.5525° E | 26.0757° N 92.0679° E |
| Band of operation | C | S | Transmit antenna height () | 130 m | 56.57 m |
| Signal bandwidth | 20 MHz | 10 MHz | Receive antenna height () | 23 m | 333.57 m |
| Total transmitted power | 2000 W | 2000 W | Straight line distance () | 100.52 Kms | 99.49 Kms |
| Power transmitted in sub-beam () | 200 W | 400 W | Effective Earth radius () | 9193.43 Kms | 8905.76 Kms |
| Noise Floor (1 Hz) | −174.00 dBm | −174.00 dBm | Elev. angle TX horizon () | −7.35 × 10−4 rad | 12.39 × 10−4 |
| Antenna type | Parabolic Dish | Parabolic Dish | Elev. angle RX horizon () | 23.52 × 10−4 rad | −25.23 × 10−4 rad |
| Antenna gain () ** | 7895.7 (≈39 dB) | 21,932.5 (43.4 dB) | Scatter angle | 125.46 × 10−4 rad | 98.84 × 10−4 rad |
| Antenna diameter | 2.4 m | 10 m | No. of elevation angle beam sets (N) *** | 11 | 11 |
| Antenna efficiency (, ) | 0.5 | 0.5 | No. of sub-beams for each elevation angle set (M) *** | 10 | 5 |
| Antenna beamwidth (, ) | 0.0305 rad | 0.0183 rad |
| Ahmedabad Link | Guwahati Link | |||||
|---|---|---|---|---|---|---|
| Beam Set | Beam Elevation Angle | Height Range (meters) | Beam Elevation Angle | Height Range (meters) | ||
| Transmit Beam (rad) | Receive Beam (rad) | Transmit Beam (rad) | Receive Beam (rad) | |||
| 1 | 5.8 × 10−3 | 6.8 × 10−3 | 249.3–1790.0 | 4.0 × 10−3 | 5.8 × 10−3 | 323.8–1217.8 |
| 2 | 8.9 × 10−3 | 9.8 × 10−3 | 404.4–1943.8 | 7.7 × 10−3 | 9.5 × 10−3 | 495.7–1399.7 |
| 3 | 11.9 × 10−3 | 12.9 × 10−3 | 558.8–2097.8 | 11.4 × 10−3 | 13.2 × 10−3 | 674.4–1581.9 |
| 4 | 15.0 × 10−3 | 15.9 × 10−3 | 712.8–2251.8 | 15.0 × 10−3 | 16.8 × 10−3 | 854.9–1764.2 |
| 5 | 18.0 × 10−3 | 19.0 × 10−3 | 866.8–2406.0 | 18.7 × 10−3 | 20.5 × 10−3 | 1036.1–1946.6 |
| 6 | 21.1 × 10−3 | 22.0 × 10−3 | 1020.6–2506.1 | 22.4 × 10−3 | 24.2 × 10−3 | 1217.8–2129.1 |
| 7 | 24.1 × 10−3 | 25.1 × 10−3 | 1174.5–2714.3 | 26.0 × 10−3 | 27.8 × 10−3 | 1399.7–2311.7 |
| 8 | 27.2 × 10−3 | 28.1 × 10−3 | 1328.3–2868.6 | 29.7 × 10−3 | 31.5 × 10−3 | 1581.9–2494.5 |
| 9 | 30.2 × 10−3 | 31.2 × 10−3 | 1482.2–3023.0 | 33.4 × 10−3 | 35.2 × 10−3 | 1764.2–2677.4 |
| 10 | 33.3 × 10−3 | 34.2 × 10−3 | 1636.0–3177.4 | 37.0 × 10−3 | 38.8 × 10−3 | 1946.6–2860.4 |
| 11 | 36.3 × 10−3 | 37.3 × 10−3 | 1790.0–3332.0 | 40.7 × 10−3 | 42.5 × 10−3 | 2129.1–3043.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garg, A.; Mishra, R.; Kalra, A.K.; Kapoor, A. Dual Data Streaming on Tropospheric Communication Links Based on the Determination of Beam Pointing Dynamics Using a Modified Ray-Based Channel Model. Telecom 2024, 5, 176-197. https://doi.org/10.3390/telecom5010009
Garg A, Mishra R, Kalra AK, Kapoor A. Dual Data Streaming on Tropospheric Communication Links Based on the Determination of Beam Pointing Dynamics Using a Modified Ray-Based Channel Model. Telecom. 2024; 5(1):176-197. https://doi.org/10.3390/telecom5010009
Chicago/Turabian StyleGarg, Amit, Ranjan Mishra, Ashok Kumar Kalra, and Ankush Kapoor. 2024. "Dual Data Streaming on Tropospheric Communication Links Based on the Determination of Beam Pointing Dynamics Using a Modified Ray-Based Channel Model" Telecom 5, no. 1: 176-197. https://doi.org/10.3390/telecom5010009
APA StyleGarg, A., Mishra, R., Kalra, A. K., & Kapoor, A. (2024). Dual Data Streaming on Tropospheric Communication Links Based on the Determination of Beam Pointing Dynamics Using a Modified Ray-Based Channel Model. Telecom, 5(1), 176-197. https://doi.org/10.3390/telecom5010009






