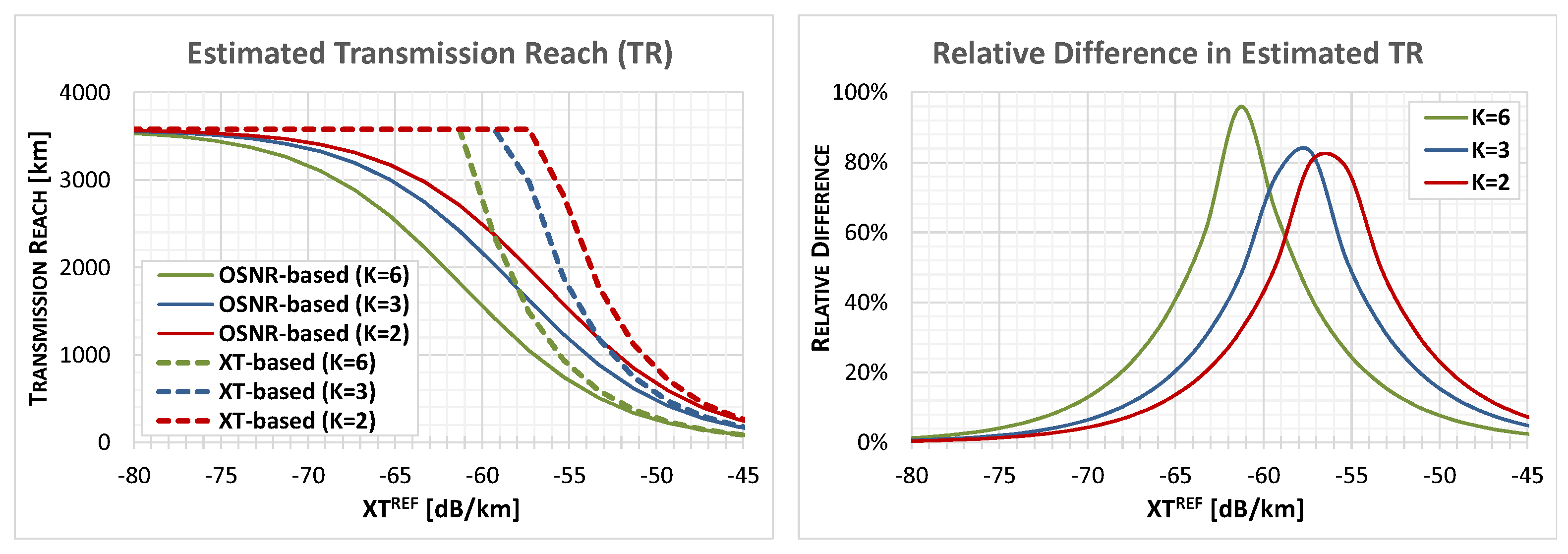
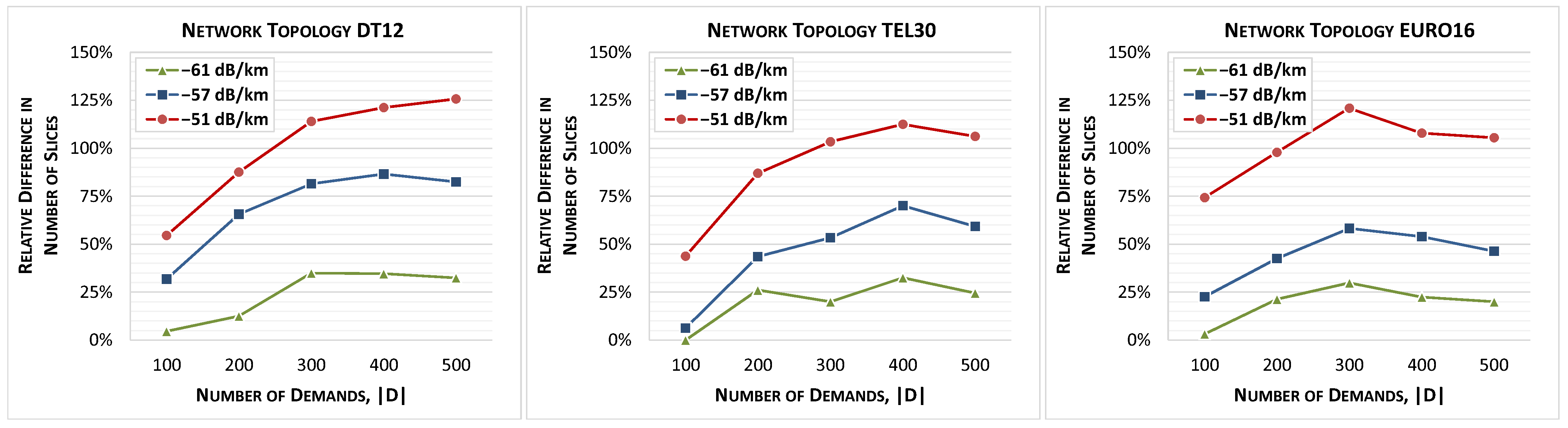
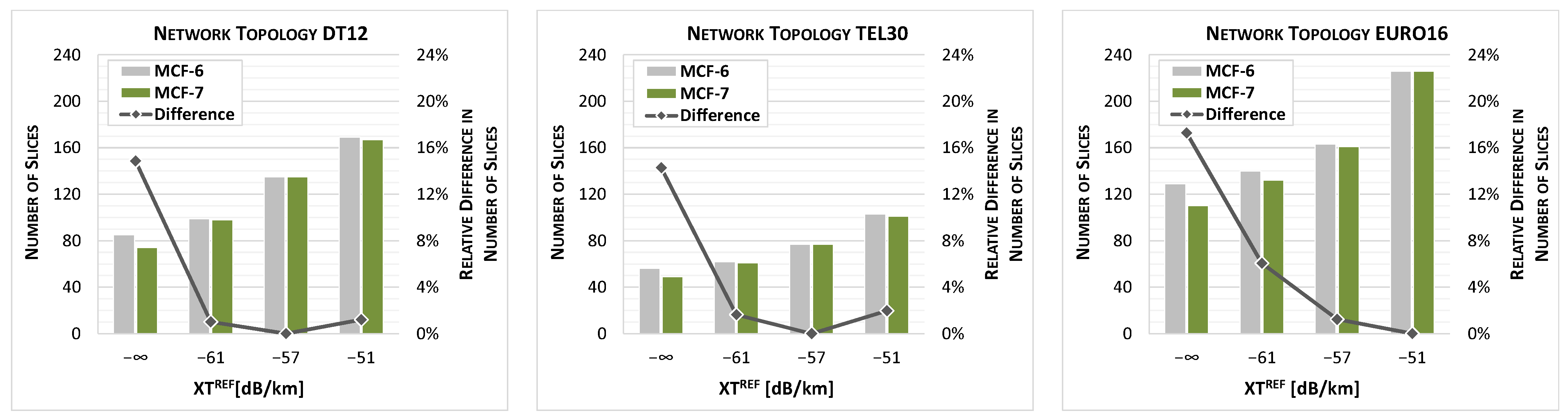
The core element of the optimization method is the OSRN-aware lightpath allocation (OSNR-LA) algorithm, which solves the problem of allocation of lightpaths satisfying given SNR requirements for an ordered set of traffic demands (denoted as
), which are processed one by one. The algorithm makes use of candidate routing paths
that are available for each demand
d. In OSNR-LA, the verification of SNR is performed both for each candidate lightpath and for all already allocated and possibly affected lightpaths based on the actual allocation status of spectral–spatial resources in network links, which is maintained in a network state matrix
A. In particular, the allocation status of frequency slices in cores of particular network links is represented using the maximal free-occupied block (MFOB) approach proposed in [
30] that utilizes a three-dimensional matrix
. Element
corresponds to slice
s in core
c of link
e, and it represents the allocation status of slice
s (free or busy) as well as contains the information about how many consecutive slices (beginning from
s) have the same status as slice
s. By reading element
, the algorithm is able to determine either whether the requested number of consecutive slices is available for allocation of a lightpath or which slice is worth checking next. As shown in [
30], the application of MFOB speeds up considerably the searching for free spectrum resources.
A pseudo-code of the OSNR-LA algorithm is shown in Algorithm 1. In lines 2 and 3, spectral–spatial resource allocation state matrix (
A), the set of allocated lightpaths (
), and the required number of slices (
z) are initialized. In line 3, a loop iterating over consecutive demands from the ordered set of demands (
) begins. In line 4, the best lightpath (
) selected for demand
d is initialized. In lines 5 and 6, respectively, loops iterating over candidate paths (
) for demand
d and available MCF cores (
) are started. The beginning frequency slice (
) of a candidate lightpath is initialized in line 7, and a “while” loop iterating over consecutive candidate slices starts in line 8. In line 9, frequency slot
f beginning from slice
and occupying
consecutive slices is initialized. Here,
represents the number of slices required to serve the bit rate of demand
d on path
p and core
c, assuming that the best modulation format that can be used on path
p is selected. In line 10, candidate lightpath
l is initialized with path
p, core
c, and frequency slot
f. In line 11, it is checked using the allocation state matrix (
A) whether spectral resources are available for lightpath
l in core
c in each link of path
p. If the resources are available, then subset
of the already selected lightpaths (
) that might be affected by lightpath
l is determined in line 12. In line 13, it is checked whether lightpath
l and all possibly affected lightpaths (
) satisfy the QoT requirement by calculating their inverse SNR values, using Model (
3), and comparing them with allowable limits, as discussed in
Section 3.2. If the QoT of lightpaths is acceptable, then it is checked (in line 14) whether candidate lightpath
l has a lower beginning slice index than the best lightpath (
) found so far for demand
d. If so, lightpath
is substituted with lightpath
l (in line 15) and the “while” loop is terminated (in line 16). Otherwise, if either spectral resources are not available or the QoT of some lightpath is not satisfied, then beginning slice
is updated to the next available slice (in line 18), and the candidate lightpath verification procedure (starting in line 9) is repeated. After all candidate path–core pairs have been processed, the best lightpath (
) found for demand
d is included into the set of allocated lightpaths (
) and network state (
A) is updated in line 19. In addition, in line 19, the required number of frequency slices (
z) is updated if the ending slice (
) of lightpath
exceeds
z. The algorithm terminates after all demands have been processed.
| Algorithm 1 OSNR-Aware Lightpath Allocation (OSNR-LA) |
| Require: ordered demands , candidate paths |
| 1: | Initialize resource allocation state matrix A |
| 2: | Allocated lightpaths , required number of slices |
| 3: | for all demand do |
| 4: | best lightpath |
| 5: | for all path do |
| 6: | for all core do |
| 7: | frequency slice |
| 8: | while do |
| 9: | frequency slot |
| 10: | lightpath |
| 11: | if spectral resources are available in A for lightpath l then |
| 12: | the lightpaths from that have a common link and a common slice and are carried on a neighbor core to l |
| 13: | if QoT estimated using Equation (3) is acceptable for all lightpaths in then |
| 14: | if then |
| 15: | |
| 16: | break |
| 17: | else |
| 18: | next available slice obtained from A |
| 19: | Include lightpath into , update network state in A, and update |
| Ensure: lightpaths satisfying QoT for demands in , the number of required slices (z)
|
Algorithm 1 returns a feasible allocation of lightpaths after processing the demands according to given order (). Since the lightpaths selected and spatial–spectral resources allocated may differ for different sequences of processed demands, the value of objective function (z), which represents the number of frequency slices required in the network, may differ as well. Therefore, as the value of z is subject to minimization, we execute Algorithm 1 a number of times, each time assuming a different order od demands , and we consider the solution with the lowest value of z as the best one and returned by the optimization method.
To drive the algorithm in its search toward the best order of demands, we apply a simulated annealing (SA) method [
31]. Namely, at each SA iteration, two randomly selected demands in
are swapped, and Algorithm 1 is executed for the resulting order of demands. If the obtained value of
z is improved, it is considered as the best one and order
is accepted as the current one; otherwise, order
is accepted with certain probability, which decreases after each SA iteration. To control the performance of SA, two parameters are used: temperature
determining the probability of accepting non-improving solutions and cooling rate
representing the speed of decreasing the temperature in consecutive iterations, where
. We consider that
is initialized with the product of the value of
z obtained in the first algorithm iteration and a temperature coefficient (denoted as
). After each SA iteration,
is updated and takes the value
. The probability of accepting non-improving solutions is calculated as
, where
z and
are objective function values corresponding, respectively, to the new and current solution. In
Section 6.2, we perform algorithm tuning to select the values of
and
that offer the best performance.
Eventually, to speed up the algorithm, we make use of multi-core CPU capabilities and run a number of parallel threads (one per a logical CPU core), where each thread executes an instance of the SA method described above. For algorithm parallelization, we apply the cooperative with solution exchange (CSE) approach proposed in [
30]. In CSE, the best global solution (namely, best order
and best value of
z) is shared between the threads. Whenever improved, this best global solution is updated and distributed among the parallel instances of SA that consider
as the current order of demands. As shown in [
30], a parallel simulated annealing (PSA) algorithm allows significantly decreasing computation times.
In the next section, we analyze the performance of the above presented OSNR-aware lightpath planning method—referred to as OSNR-LA-PSA—by means of numerical experiments run in various network scenarios.