Comprehensive Comparison of VNE Solutions Based on Different Coordination Approaches
Abstract
1. Introduction
2. VNE Problem Decomposition and Modeling
2.1. Problem Description
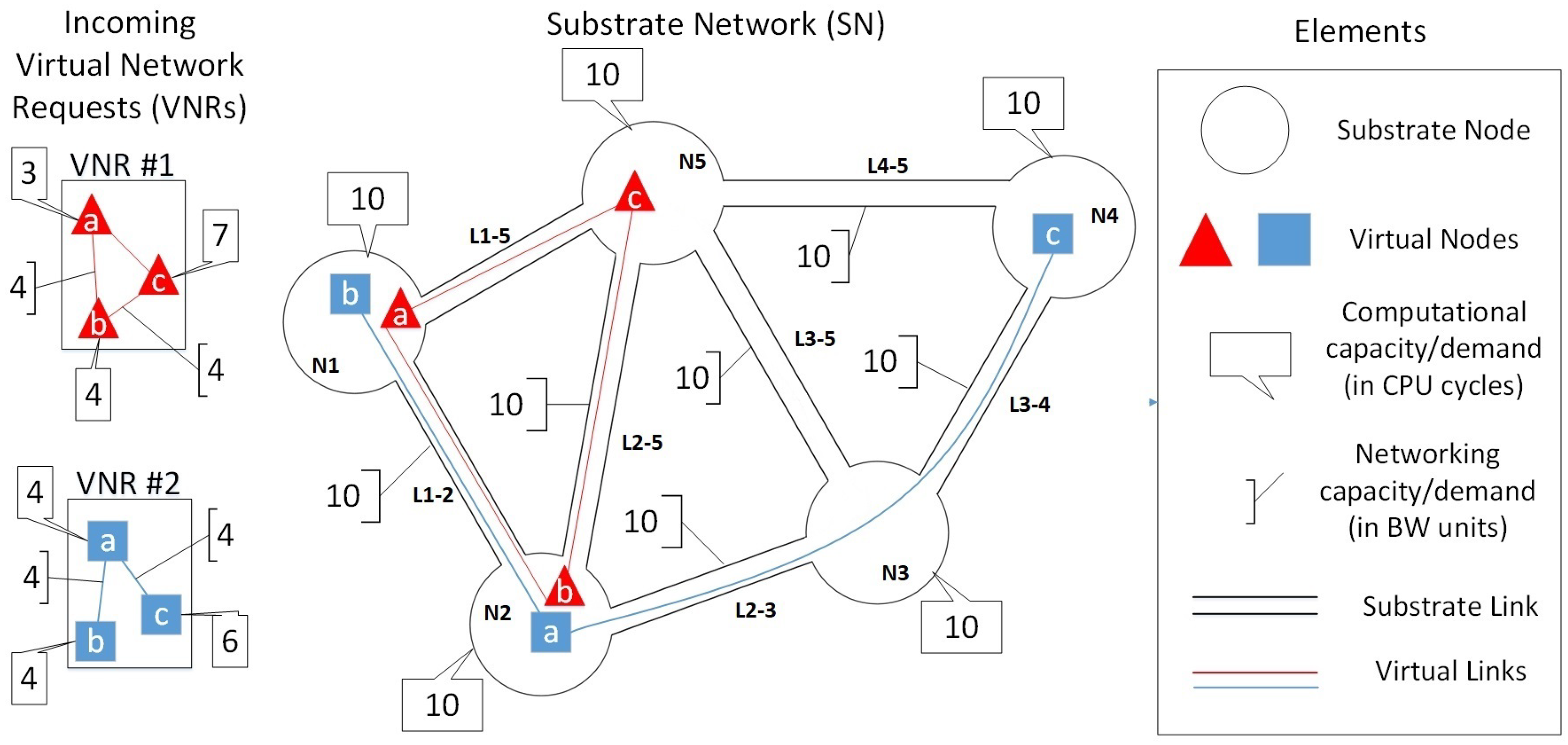
2.1.1. Modeling of the SN and VNR
2.1.2. Configuring the Element Parameters
2.1.3. Constraints Definition
2.1.4. Adopting an Embedding Objective
2.1.5. Execution of the Embedding Functions
2.1.6. Importance of Coordination
2.1.7. Outcome Evaluation
2.1.8. VNE Problem Complexity
3. Related Work-Coordination Analysis
3.1. Uncoordinated VNE
3.2. Coordinated VNE
3.2.1. Two Stages Coordination
3.2.2. One Stage Coordination
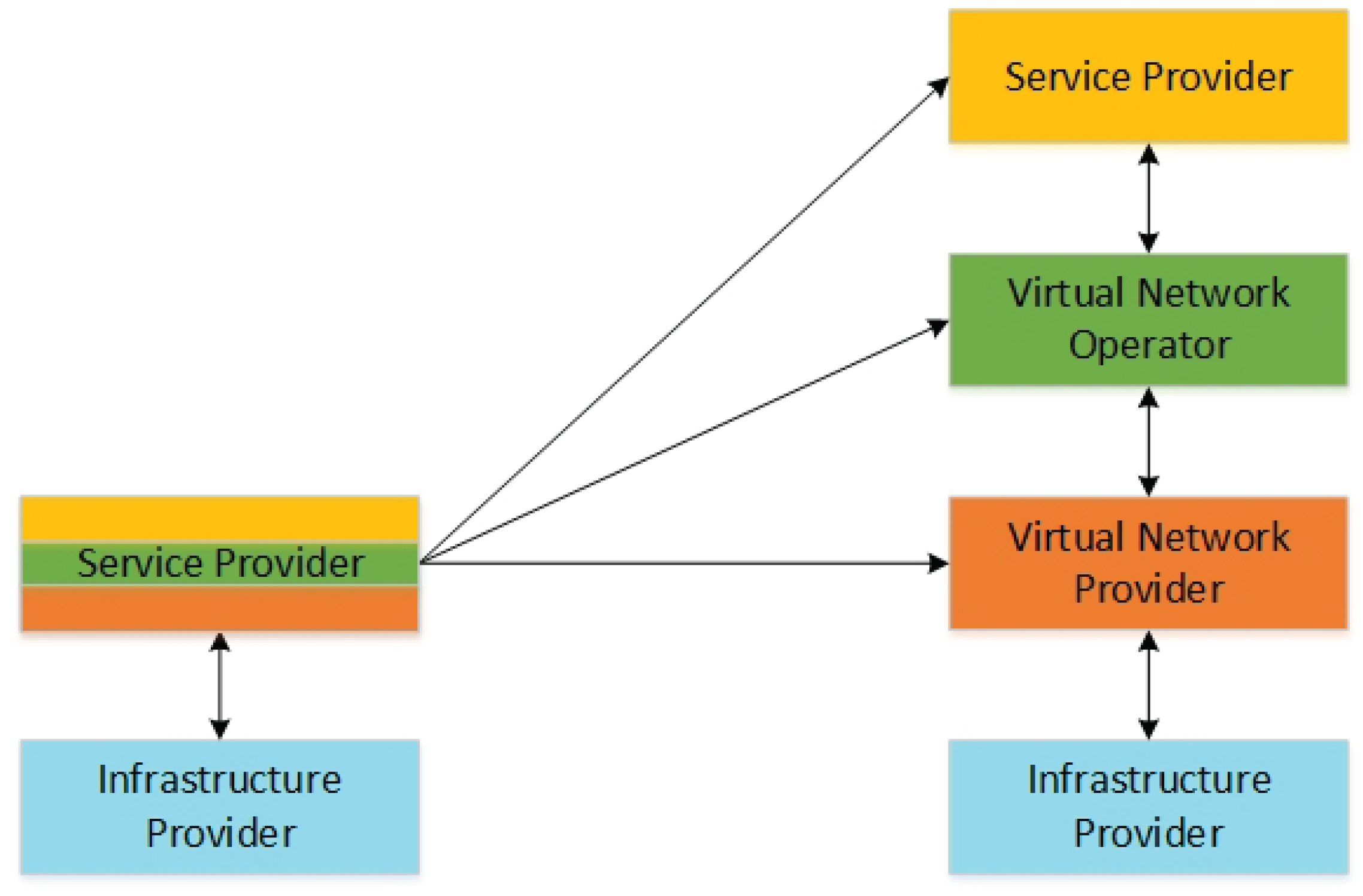
3.3. Inter-InP Coordination
3.4. Related Work Challenges
4. Evaluation of Examined Solutions
4.1. Adopted Objective Functions
4.2. Comparison Methodology
4.3. Simulation Environment
4.3.1. Configuring the SN
4.3.2. Configuring the VNRs
4.4. Performance Metrics
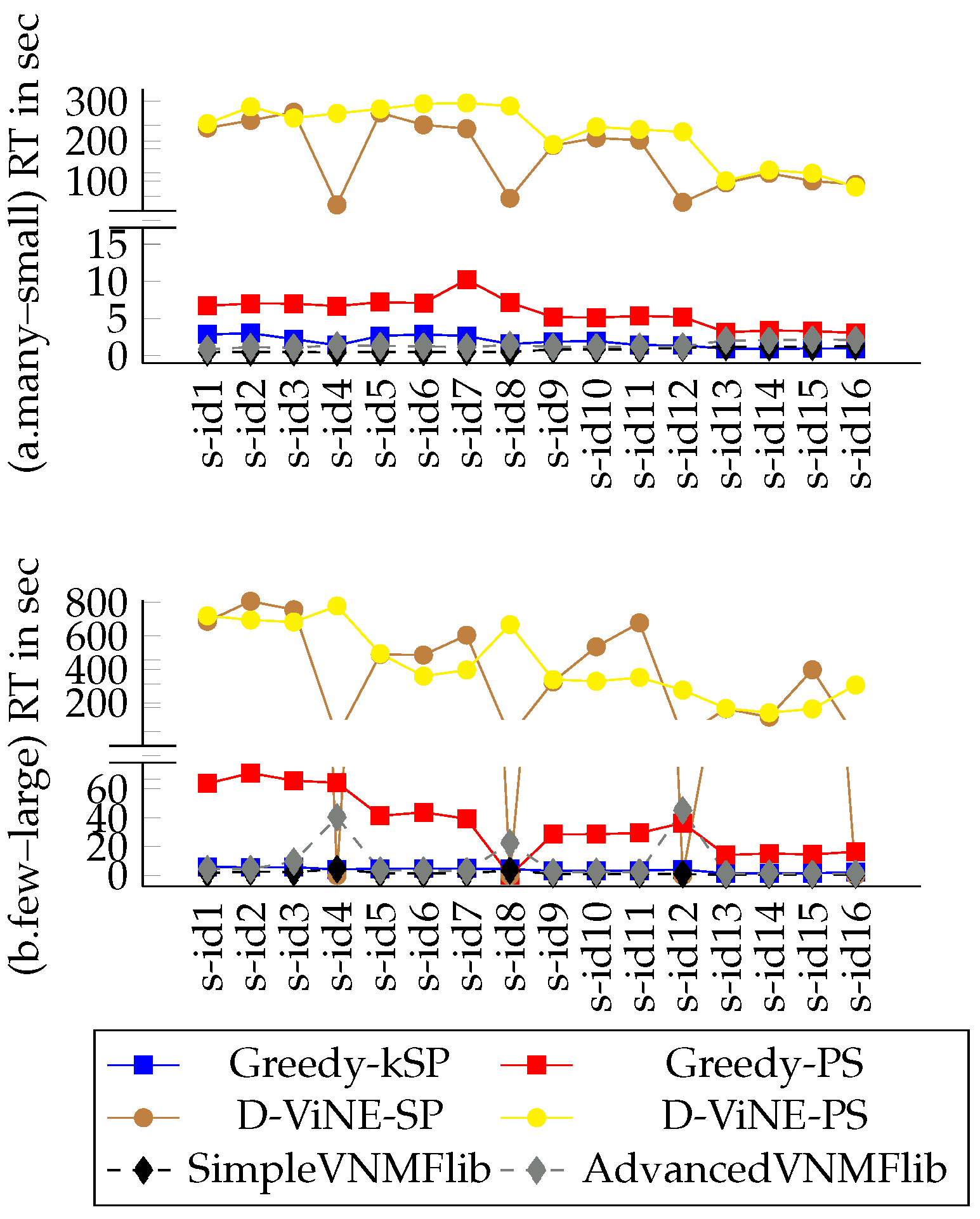
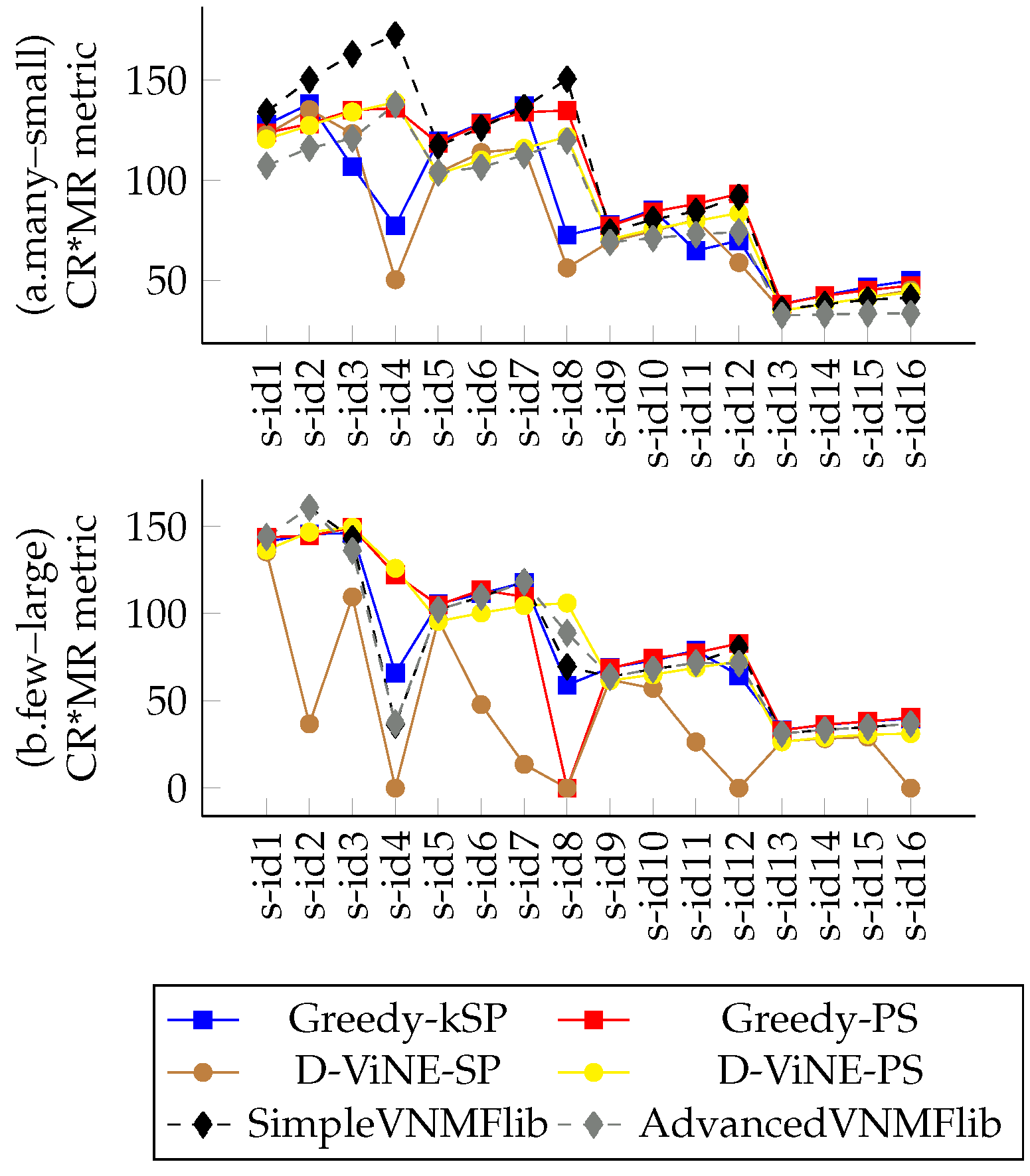
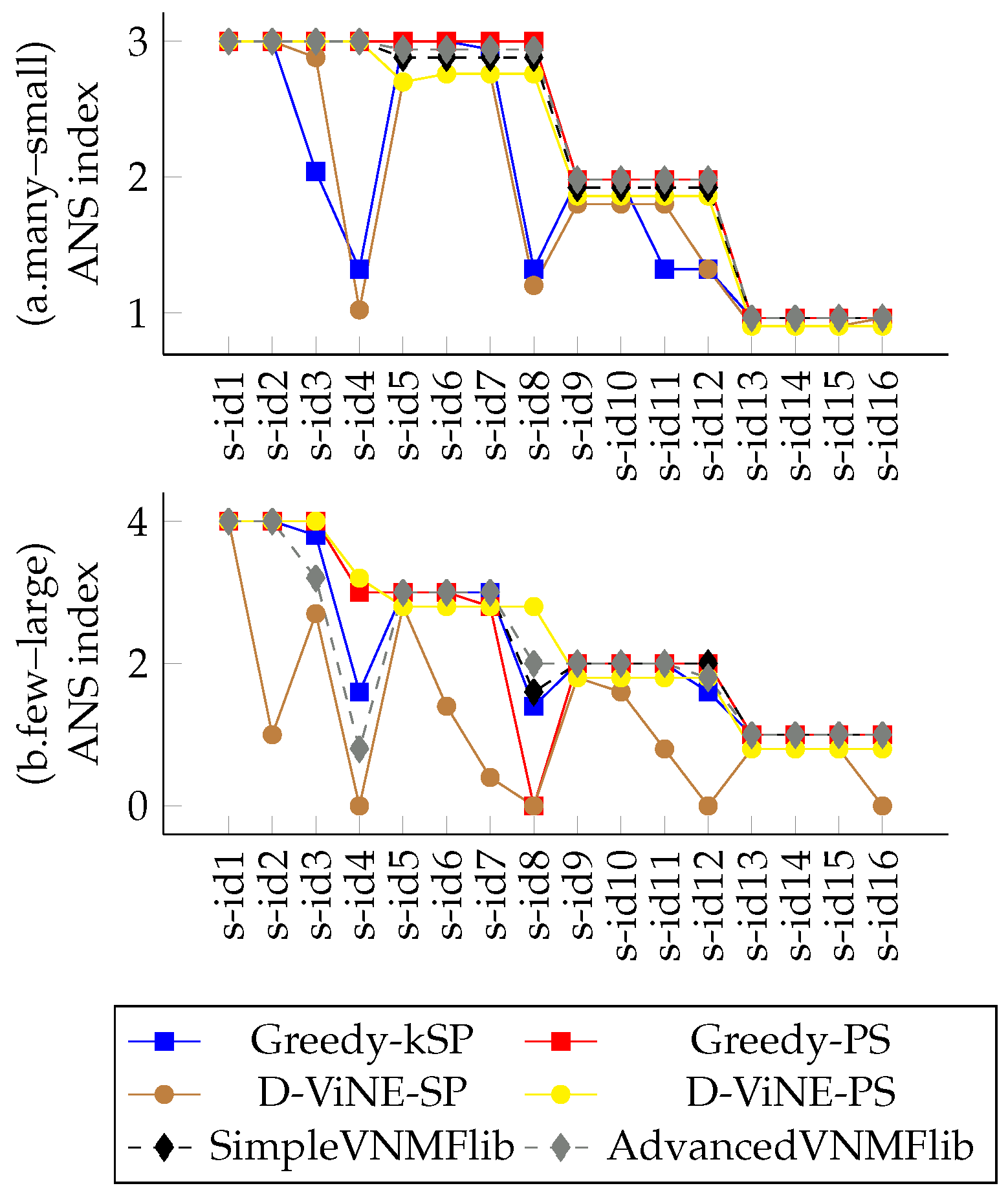
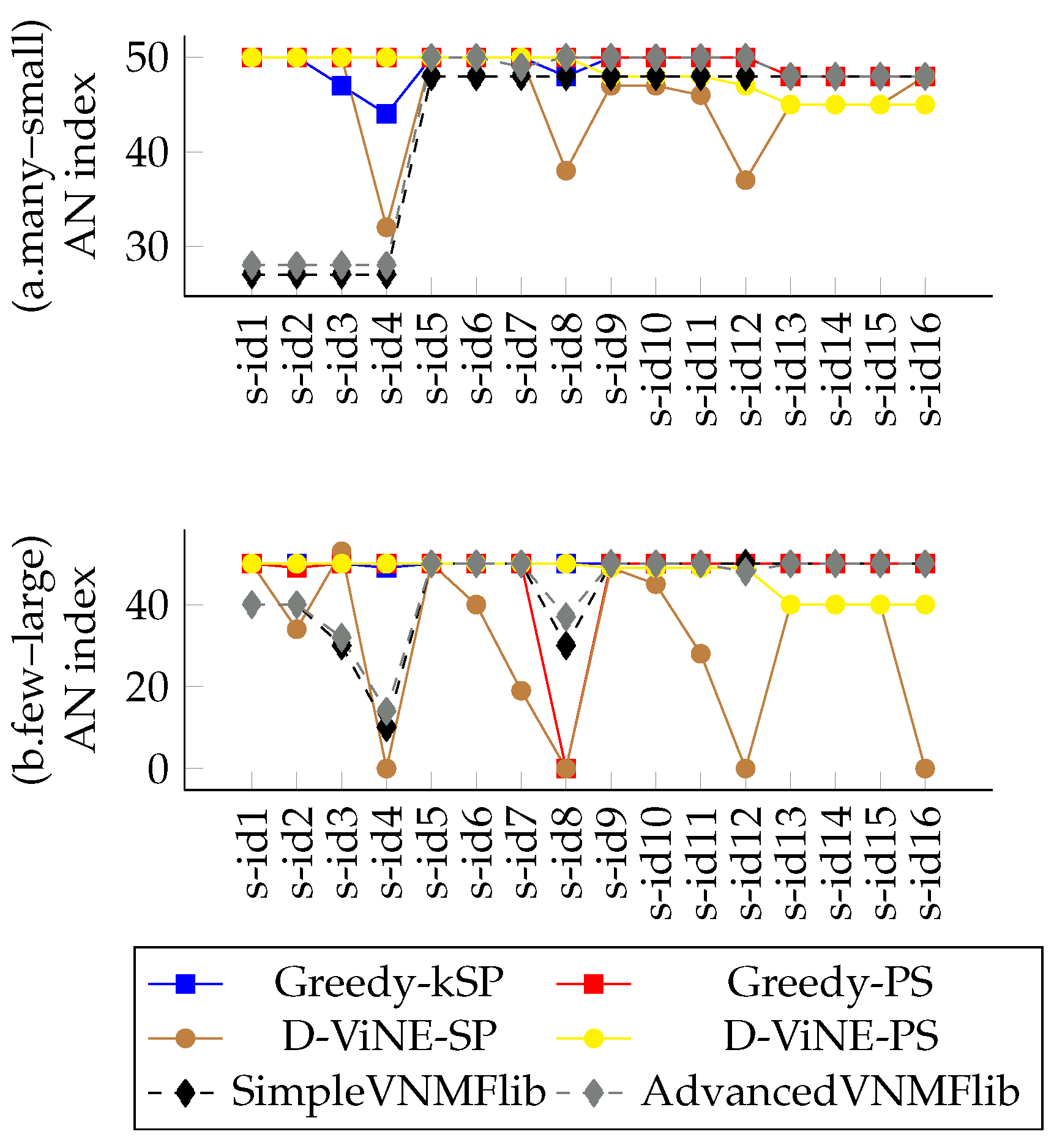
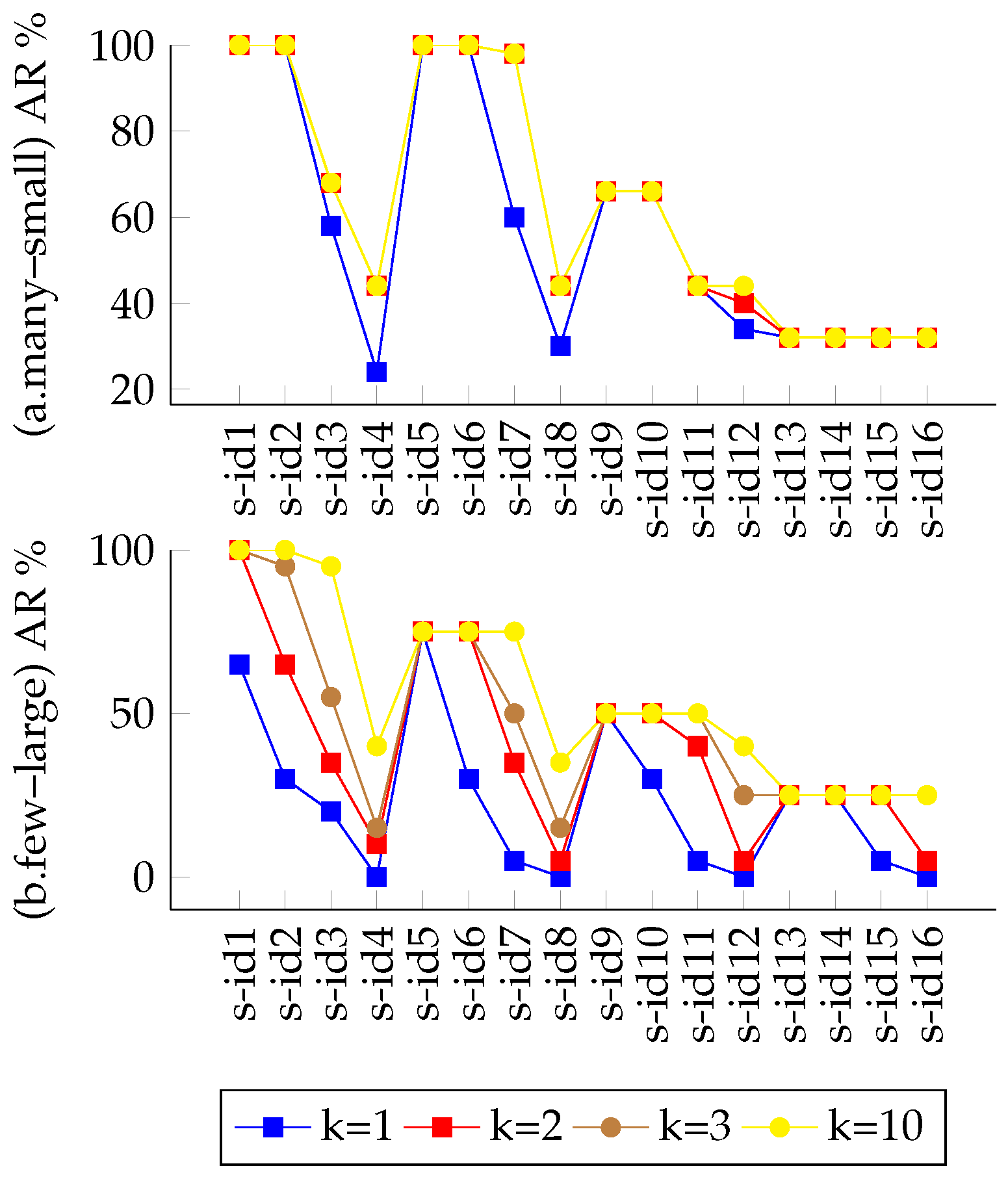
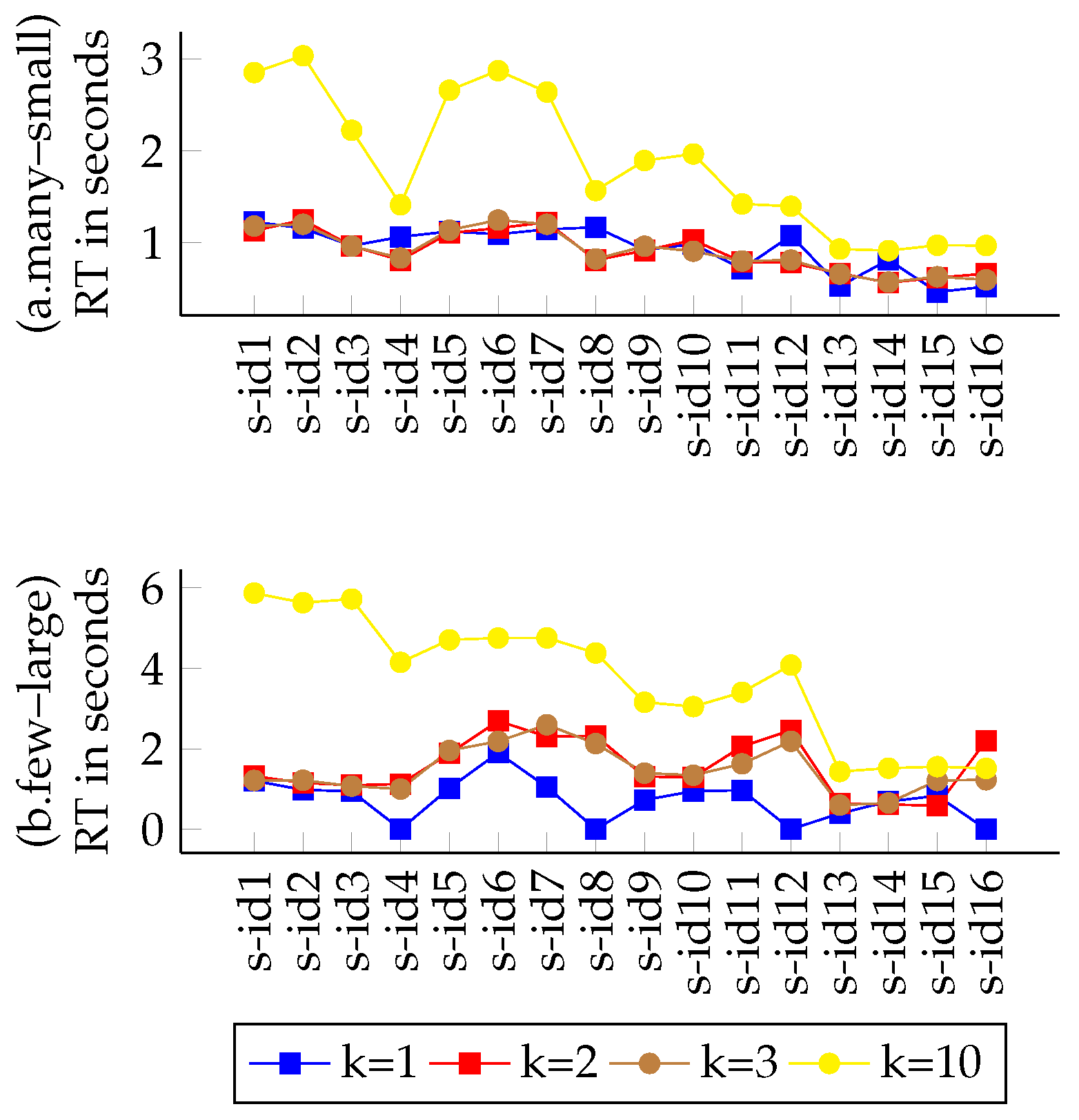
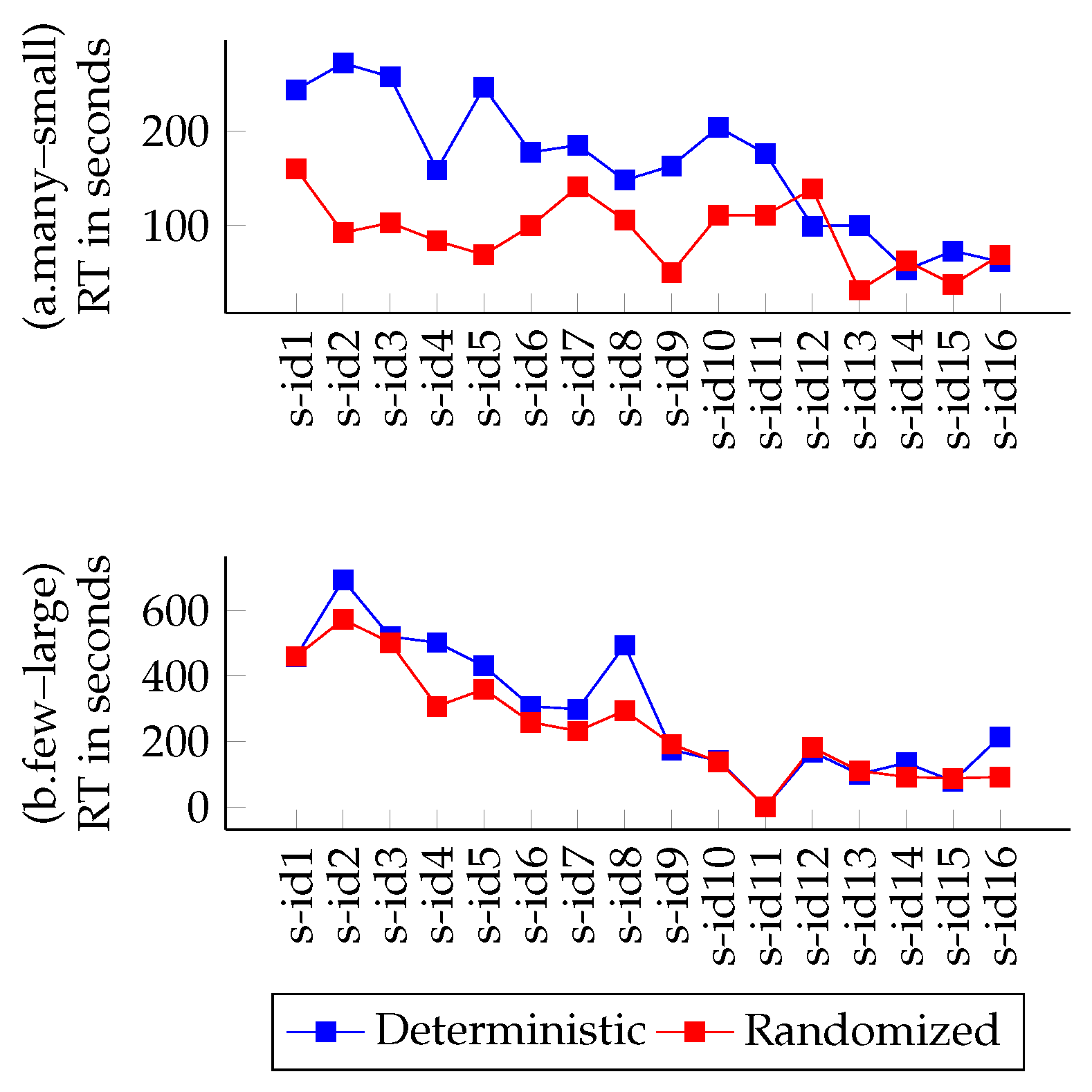
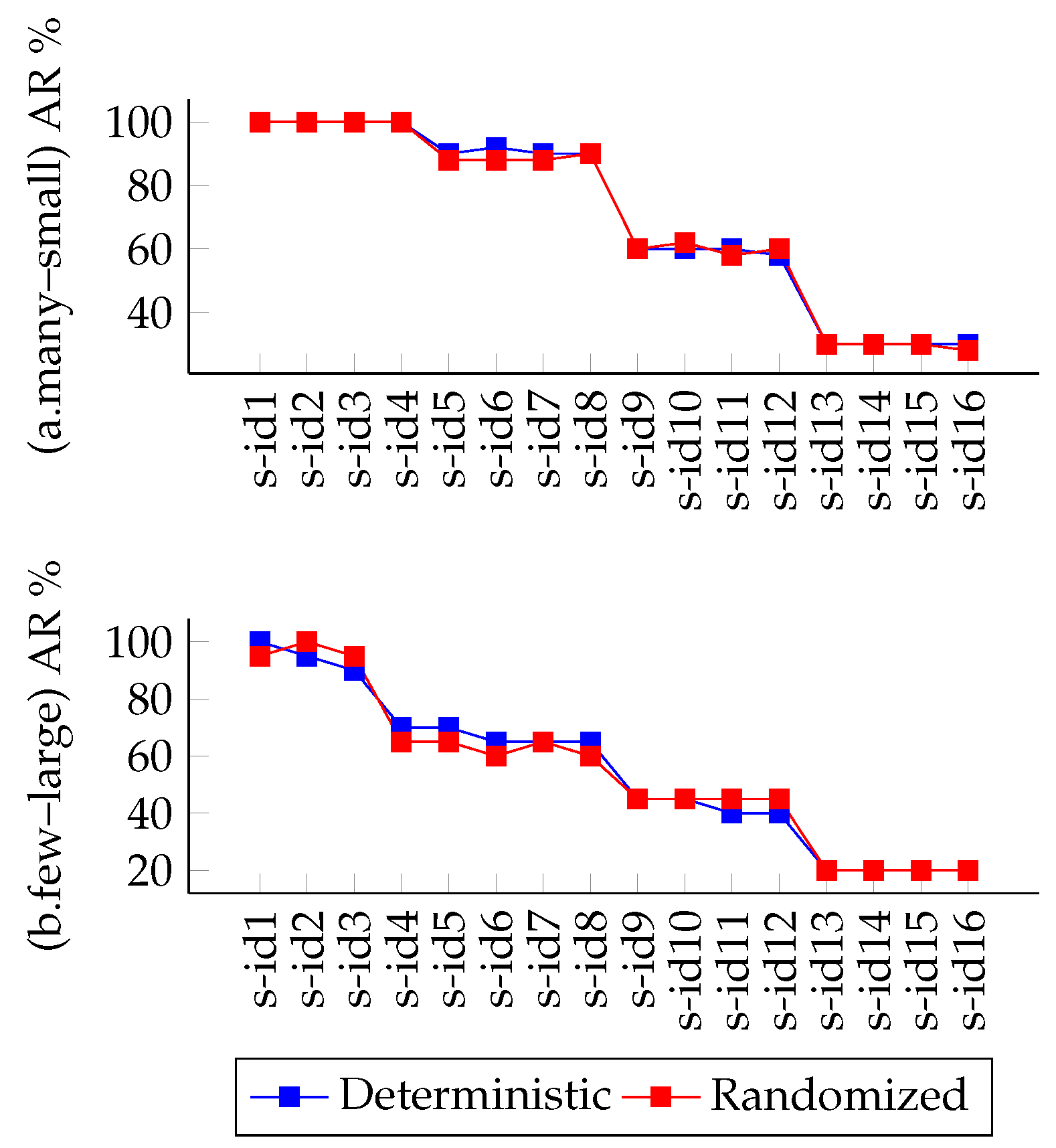
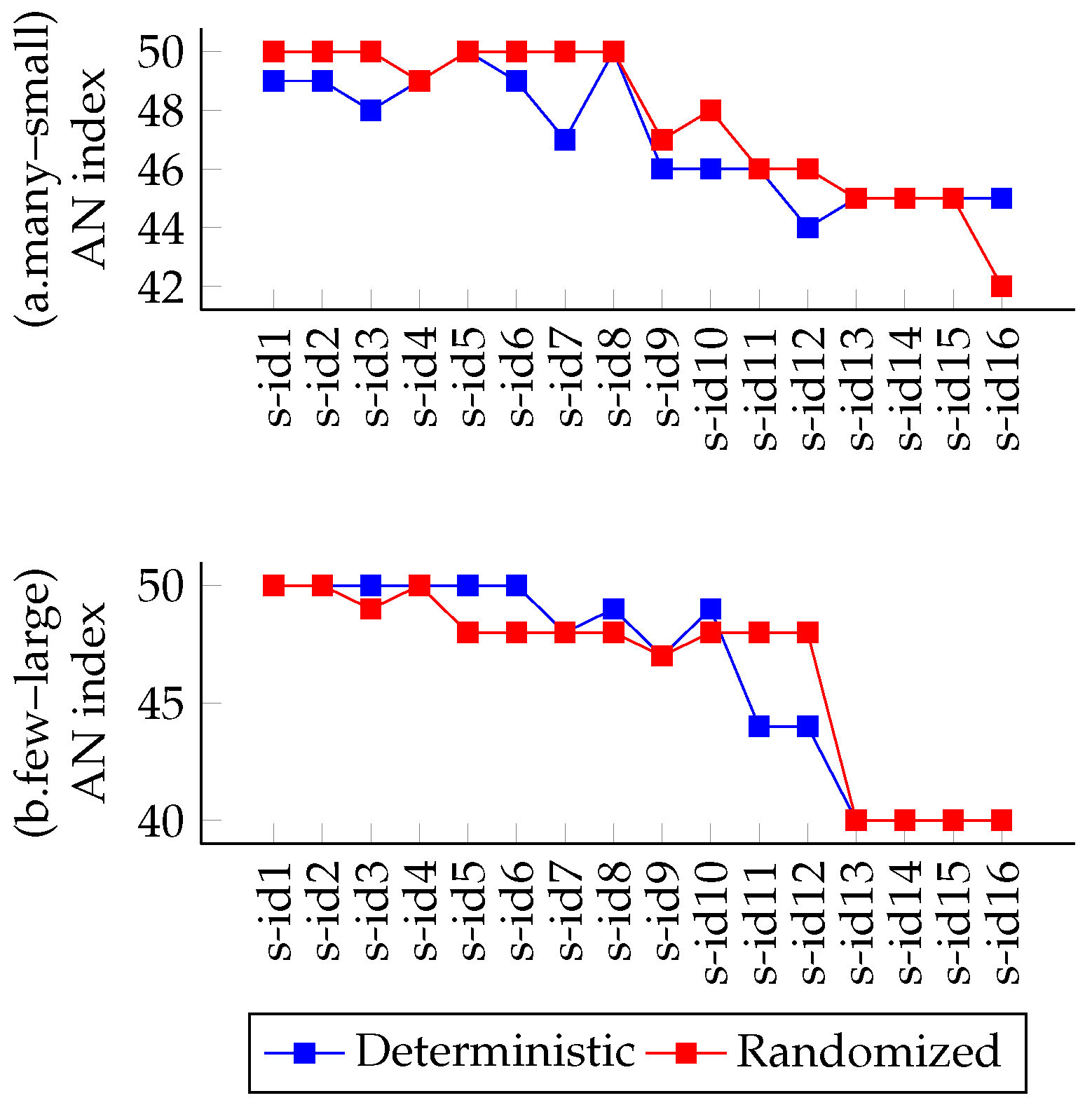
4.5. Evaluation Results
4.5.1. Variations on CPU and BW Demands
4.5.2. Variations on the “k” Parameter
5. Mixed Coordination Algorithm Proposal
| Algorithm 1 Mixed-stage algorithm concept. |
| while do |
| if then |
| else |
| end if |
| end while |
| return |
6. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tutschku, K.; Zinner, T.; Nakao, A.; Tran-Gia, P. Network virtualization: Implementation steps towards the future internet. Electron. Commun. EASST 2009, 17, 1–14. [Google Scholar] [CrossRef]
- Barham, P.; Dragovic, B.; Fraser, K.; Hand, S.; Harris, T.; Ho, A.; Neugebauer, R.; Pratt, I.; Warfield, A. Xen and the Art of Virtualization. SIGOPS Oper. Syst. Rev. 2003, 37, 164–177. [Google Scholar] [CrossRef]
- Alvarez, F.; Breitgand, D.; Griffin, D.; Andriani, P.; Rizou, S.; Zioulis, N.; Moscatelli, F.; Serrano, J.; Keltsch, M.; Trakadas, P.; et al. An Edge-to-Cloud Virtualized Multimedia Service Platform for 5G Networks. IEEE Trans. Broadcast. 2019, 65, 369–380. [Google Scholar] [CrossRef]
- Trakadas, P.; Karkazis, P.; Leligou, H.C.; Zahariadis, T.; Vicens, F.; Zurita, A.; Alemany, P.; Soenen, T.; Parada, C.; Bonnet, J. Comparison of management and orchestration solutions for the 5G era. J. Sens. Actuator Netw. 2020, 9, 4. [Google Scholar] [CrossRef]
- Peuster, M.; Schneider, S.; Zhao, M.; Xilouris, G.; Trakadas, P.; Vicens, F.; Tavernier, W.; Soenen, T.; Vilalta, R.; Andreou, G.; et al. Introducing Automated Verification and Validation for Virtualized Network Functions and Services. IEEE Commun. Mag. 2019, 57, 96–102. [Google Scholar] [CrossRef]
- Soenen, T.; Van Rossem, S.; Tavernier, W.; Vicens, F.; Valocchi, D.; Trakadas, P.; Karkazis, P.; Xilouris, G.; Eardley, P.; Kolometsos, S. Insights from SONATA: Implementing and integrating a microservice-based NFV service platform with a DevOps methodology. In Proceedings of the NOMS 2018-2018 IEEE/IFIP Network Operations and Management Symposium, Taipei, Taiwan, 23–27 April 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Zafeiropoulos, A.; Fotopoulou, E.; Peuster, M.; Schneider, S.; Gouvas, P.; Behnke, D.; Müller, M.; Bök, P.B.; Trakadas, P.; Karkazis, P. Benchmarking and Profiling 5G Verticals’ Applications: An Industrial IoT Use Case. In Proceedings of the 2020 6th IEEE Conference on Network Softwarization (NetSoft), Ghent, Belgium, 29 June–3 July 2020; pp. 310–318. [Google Scholar] [CrossRef]
- Rizou, S.; Athanasoulis, P.; Andriani, P.; Iadanza, F.; Trakadas, P.; Griffin, D.; Kheirkhah, M.; Breitgand, D.; Weit, A.; Ustok, R.F. Programmable Edge-to-Cloud Virtualization for 5G Media Industry: The 5G-MEDIA Approach. In Proceedings of the IFIP International Conference on Artificial Intelligence Applications and Innovations, Neos Marmaras, Greece, June 5–7 2020; pp. 95–104. [Google Scholar] [CrossRef]
- Trakadas, P.; Nomikos, N.; Michailidis, E.T.; Zahariadis, T.; Facca, F.M.; Breitgand, D.; Rizou, S.; Masip, X.; Gkonis, P. Hybrid Clouds for Data-Intensive, 5G-Enabled IoT Applications: An Overview, Key Issues and Relevant Architecture. Sensors 2019, 19, 3591. [Google Scholar] [CrossRef] [PubMed]
- Bhardwaj, S.; Jain, L.; Jain, S. Cloud computing: A study of infrastructure as a service (IAAS). Int. J. Eng. Inf. Technol. 2010, 2, 60–63. [Google Scholar]
- Manvi, S.S.; Krishna Shyam, G. Resource management for Infrastructure as a Service (IaaS) in cloud computing: A survey. J. Netw. Comput. Appl. 2014, 41, 424–440. [Google Scholar] [CrossRef]
- Caruso, G.; Nucci, F.; Gordo, O.P.; Rizou, S.; Magen, J.; Agapiou, G.; Trakadas, P. Embedding 5G solutions enabling new business scenarios in Media and Entertainment Industry. In Proceedings of the 2019 IEEE 2nd 5G World Forum (5GWF), Dresden, Germany, 30 September–2 October 2019; pp. 460–464. [Google Scholar] [CrossRef]
- Schaffrath, G.; Werle, C.; Papadimitriou, P.; Feldmann, A.; Bless, R.; Greenhalgh, A.; Wundsam, A.; Kind, M.; Maennel, O.; Mathy, L. Network Virtualization Architecture: Proposal and Initial Prototype. In Proceedings of the 1st ACM Workshop on Virtualized Infrastructure Systems and Architectures, VISA ’09, Barcelona, Spain, 17 August 2009; pp. 63–72. [Google Scholar] [CrossRef]
- Pol, A.; Roman, A.; Trakadas, P.; Karkazis, P.; Kapassa, E.; Touloupou, M.; Kyriazis, D.; Juan, L.; Alemany, P.; Vilalta, R. Advanced NFV features applied to multimedia real-time communications use case. In Proceedings of the 2019 IEEE 2nd 5G World Forum (5GWF), Dresden, Germany, 30 September–2 October 2019; pp. 323–328. [Google Scholar] [CrossRef]
- Shekhawat, Y.; Piesk, J.; Sprengel, H.; Gómez, I.D.; Vicens, F.; Carrillo, S.C.; Trakadas, P.; Karkazis, P.; Zahariadis, T.; Touloupou, M. Orchestrating Live Immersive Media Services Over Cloud Native Edge Infrastructure. In Proceedings of the 2019 IEEE 2nd 5G World Forum (5GWF), Dresden, Germany, 30 September–2 October 2019; pp. 316–322. [Google Scholar] [CrossRef]
- Botero, J.F.; Hesselbach, X.; Duelli, M.; Schlosser, D.; Fischer, A.; De Meer, H. Energy efficient virtual network embedding. IEEE Commun. Lett. 2012, 16, 756–759. [Google Scholar] [CrossRef]
- Liu, S.; Cai, Z.; Xu, H.; Xu, M. Security-aware virtual network embedding. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, NSW, Australia, 10–14 June 2014; pp. 834–840. [Google Scholar] [CrossRef]
- Yu, M.; Yi, Y.; Rexford, J.; Chiang, M. Rethinking virtual network embedding: Substrate support for path splitting and migration. SIGCOMM Comput. Commun. Rev. 2008, 38, 17–29. [Google Scholar] [CrossRef]
- Zhang, X.; Phillips, C.; Chen, X. An overlay mapping model for achieving enhanced QoS and resilience performance. In Proceedings of the 2011 3rd International Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT), Budapest, Hungary, 5–7 October 2011; pp. 1–7. [Google Scholar]
- Gong, L.; Wen, Y.; Zhu, Z.; Lee, T. Toward profit-seeking virtual network embedding algorithm via global resource capacity. In Proceedings of the IEEE INFOCOM 2014-IEEE Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 1–9. [Google Scholar] [CrossRef]
- Amaldi, E.; Coniglio, S.; Koster, A.M.; Tieves, M. On the computational complexity of the virtual network embedding problem. Electron. Notes Discret. Math. 2016, 52, 213–220. [Google Scholar] [CrossRef]
- Chowdhury, N.M.K.; Rahman, M.R.; Boutaba, R. Virtual network embedding with coordinated node and link mapping. In Proceedings of the IEEE INFOCOM 2009, Rio de Janeiro, Brazil, 19-25 April 2009; pp. 783–791. [Google Scholar] [CrossRef]
- Fajjari, I.; Aitsaadi, N.; Pujolle, G.; Zimmermann, H. Vnr algorithm: A greedy approach for virtual networks reconfigurations. In Proceedings of the 2011 IEEE Global Telecommunications Conference-GLOBECOM 2011, Houston, TX, USA, 5–9 December 2011; pp. 1–6. [Google Scholar] [CrossRef]
- Botero, J.F.; Hesselbach, X.; Duelli, M.; Schlosser, D.; Fischer, A.; De Meer, H. Flexible VNE algorithms analysis using ALEVIN. In Proceedings of the 11th Würzburg Workshop on IP: Joint ITG, ITC, and EuroNF Workshop “Visions of Future Generation Networks” (Euroview 2011), Würzburg, Germany, 1–2 August 2011. [Google Scholar] [CrossRef]
- Botero, J.F.; Hesselbach, X.; Fischer, A.; De Meer, H. Optimal mapping of virtual networks with hidden hops. Telecommun. Syst. 2012, 51, 273–282. [Google Scholar] [CrossRef][Green Version]
- Fischer, A.; Botero, J.F.; Beck, M.T.; De Meer, H.; Hesselbach, X. Virtual Network Embedding: A Survey. IEEE Commun. Surv. Tutor. 2013, 15, 1888–1906. [Google Scholar] [CrossRef]
- Lischka, J.; Karl, H. A Virtual Network Mapping Algorithm Based on Subgraph Isomorphism Detection. In Proceedings of the 1st ACM Workshop on Virtualized Infrastructure Systems and Architectures, VISA ’09, Barcelona, Spain, 17 August 2009; pp. 81–88. [Google Scholar] [CrossRef]
- Prekas, S.; Karkazis, P.; Trakadas, P. Comparison of Embedding Objectives for Next Generation Networks. In Proceedings of the Fifteenth International Multi-Conference on Computing in the Global Information Technology, Porto, Portugal, 18–22 October 2020; IARIA XPS Press: Wilmington, DE, USA, 2020; pp. 7–12. [Google Scholar]
- Prekas, S.; Karkazis, P.; Trakadas, P.; Nikolakakis, V. Comparison of VNE heuristic solutions with similar objective functions. In Proceedings of the 24th Pan-Hellenic Conference on Informatics, Athens, Greece, 20–22 November 2020. [Google Scholar] [CrossRef]
- Du, D.Z.; Ko, K.I. Theory of Computational Complexity, 2nd ed.; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Eppstein, D. Finding the k shortest paths. SIAM J. Comput. 1998, 28, 652–673. [Google Scholar] [CrossRef]
- Pióro, M.; Medhi, D. Routing, Flow, and Capacity Design in Communication and Computer Networks, 1st ed.; Elsevier: Morgan Kaufmann, 500 Sansome Street, Suite 400, San Francisco, CA, USA, 2004. [Google Scholar] [CrossRef]
- Chowdhury, M.; Samuel, F.; Boutaba, R. Polyvine: Policy-based virtual network embedding across multiple domains. In Proceedings of the Second ACM SIGCOMM Workshop on Virtualized Infrastructure Systems and Architectures, New Delhi, India, 3 September 2010; pp. 49–56. [Google Scholar] [CrossRef]
- Duelli, M.; Fischer, A.; Botero, J.F.; Diaz, L.; Schlosser, D.; Singeorzan, V.; Hesselbach, X. Alevin2-Tool for the evaluation of ALgorithms for Embedding VIrtual Networks. 2021. Available online: https://sourceforge.net/p/alevin/wiki/home/ (accessed on 10 September 2021).

| Formula | Description |
|---|---|
| is a substrate network, consisting of sets of nodes and links . | |
| represents a VNR as a set of i Virtual Networks. | |
| denotes the Virtual Network of an incoming VNR, consisting of nodes and links | |
| is the vector space of all the available resources, . | |
| is the function that assigns a capacity to an element of the substrate network. | |
| is the function that assigns a demand to an element of . | |
| is the function that maps a virtual node of to a substrate node. | |
| is the function that maps a virtual link of to a path (SP) in the substrate network. | |
| M is the generalized function, that maps a VNR denoted by onto the substrate network . |
| Notations | Embedding Solutions | Coordination |
|---|---|---|
| Greedy-kSP | Greedy Node Mapping and k shortest path Link Mapping | Uncoordinated |
| Greedy-PS | Greedy Node Mapping and Path Splitting Link Mapping | Uncoordinated |
| D-ViNE-SP | Coordinated Node and Link Mapping (kSP VLM w. DR) | Coordinated two-stage |
| D-ViNE-PS | Coordinated Node and Link Mapping (PS VLM w. DR) | Coordinated two-stage |
| R-ViNE-SP | Coordinated Node and Link Mapping (kSP VLM w. RR) | Coordinated two-stage |
| R-ViNE-PS | Coordinated Node and Link Mapping (PS VLM w. RR) | Coordinated two-stage |
| SimpleVNMFlib | Subgraph Isomorphism Detection (SID) w. SLL = 10 | Coordinated single-stage |
| AdvancedVNMFlib | Subgraph Isomorphism Detection (SID) w. SLL = {1 to 10} | Coordinated single-stage |
| Substrate Network | |||
|---|---|---|---|
| Scenario ID | Number of Nodes | CPU Cycles | BW Units |
| s-idn : n = 1, 2,…, 16 | 50 | 100 | 100 |
| Virtual Network | ||||
|---|---|---|---|---|
| Scenario ID | Number of VNRs | Nodes per VNR | CPU Cycles | BW Units |
| s-id1 | 50 | 3 | 15 | 15 |
| s-id2 | 50 | 3 | 15 | 30 |
| s-id3 | 50 | 3 | 15 | 50 |
| s-id4 | 50 | 3 | 15 | 70 |
| s-id5 | 50 | 3 | 30 | 15 |
| s-id6 | 50 | 3 | 30 | 30 |
| s-id7 | 50 | 3 | 30 | 50 |
| s-id8 | 50 | 3 | 30 | 70 |
| s-id9 | 50 | 3 | 50 | 15 |
| s-id10 | 50 | 3 | 50 | 30 |
| s-id11 | 50 | 3 | 50 | 50 |
| s-id12 | 50 | 3 | 50 | 70 |
| s-id13 | 50 | 3 | 70 | 15 |
| s-id14 | 50 | 3 | 70 | 30 |
| s-id15 | 50 | 3 | 70 | 50 |
| s-id16 | 50 | 3 | 70 | 70 |
| Virtual Network | ||||
|---|---|---|---|---|
| Scenario ID | Number of VNRs | Nodes per VNR | CPU Cycles | BW Units |
| s-id1 | 20 | 10 | 15 | 15 |
| s-id2 | 20 | 10 | 15 | 30 |
| s-id3 | 20 | 10 | 15 | 50 |
| s-id4 | 20 | 10 | 15 | 70 |
| s-id5 | 20 | 10 | 30 | 15 |
| s-id6 | 20 | 10 | 30 | 30 |
| s-id7 | 20 | 10 | 30 | 50 |
| s-id8 | 20 | 10 | 30 | 70 |
| s-id9 | 20 | 10 | 50 | 15 |
| s-id10 | 20 | 10 | 50 | 30 |
| s-id11 | 20 | 10 | 50 | 50 |
| s-id12 | 20 | 10 | 50 | 70 |
| s-id13 | 20 | 10 | 70 | 15 |
| s-id14 | 20 | 10 | 70 | 30 |
| s-id15 | 20 | 10 | 70 | 50 |
| s-id16 | 20 | 10 | 70 | 70 |
| Virtual Network | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario ID | Number of VNRs | Nodes per VNR | CPU Cycles | BW Units | Number of Links | Total Demand | Density Index | Absolute Intensity Index | Relative Intensity Index |
| s-id1 | 50 | 3 | 15 | 15 | 166 | 4740 | 0.06 | 284.4 | 0.0227 |
| s-id2 | 50 | 3 | 15 | 30 | 166 | 7230 | 0.06 | 433.8 | 0.0347 |
| s-id3 | 50 | 3 | 15 | 50 | 166 | 10,550 | 0.06 | 633 | 0.0506 |
| s-id4 | 50 | 3 | 15 | 70 | 166 | 13,870 | 0.06 | 832.2 | 0.0665 |
| s-id5 | 50 | 3 | 30 | 15 | 166 | 6990 | 0.06 | 419.4 | 0.0335 |
| s-id6 | 50 | 3 | 30 | 30 | 166 | 9480 | 0.06 | 568.8 | 0.0455 |
| s-id7 | 50 | 3 | 30 | 50 | 166 | 12,800 | 0.06 | 768 | 0.0614 |
| s-id8 | 50 | 3 | 30 | 70 | 166 | 16,120 | 0.06 | 967.2 | 0.0773 |
| s-id9 | 50 | 3 | 50 | 15 | 166 | 9990 | 0.06 | 599.4 | 0.0479 |
| s-id10 | 50 | 3 | 50 | 30 | 166 | 12,480 | 0.06 | 748.8 | 0.0598 |
| s-id11 | 50 | 3 | 50 | 50 | 166 | 15,800 | 0.06 | 948 | 0.0758 |
| s-id12 | 50 | 3 | 50 | 70 | 166 | 19,120 | 0.06 | 1147.2 | 0.0917 |
| s-id13 | 50 | 3 | 70 | 15 | 166 | 12,990 | 0.06 | 779.4 | 0.0623 |
| s-id14 | 50 | 3 | 70 | 30 | 166 | 15,480 | 0.06 | 928.8 | 0.0742 |
| s-id15 | 50 | 3 | 70 | 50 | 166 | 18,800 | 0.06 | 1128 | 0.0901 |
| s-id16 | 50 | 3 | 70 | 70 | 166 | 22,120 | 0.06 | 1327.2 | 0.1061 |
| Virtual Network | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Scenario ID | Number of VNRs | Nodes per VNR | CPU Cycles | BW Units | Number of Links | Total Demand | Density Index | Absolute Intensity Index | Relative Intensity Index |
| s-id1 | 20 | 10 | 15 | 15 | 166 | 5490 | 0.5 | 2745 | 0.0227 |
| s-id2 | 20 | 10 | 15 | 30 | 166 | 7980 | 0.5 | 3990 | 0.0330 |
| s-id3 | 20 | 10 | 15 | 50 | 166 | 11,300 | 0.5 | 5650 | 0.0468 |
| s-id4 | 20 | 10 | 15 | 70 | 166 | 14,620 | 0.5 | 7310 | 0.0605 |
| s-id5 | 20 | 10 | 30 | 15 | 166 | 8490 | 0.5 | 4245 | 0.0351 |
| s-id6 | 20 | 10 | 30 | 30 | 166 | 10,980 | 0.5 | 5490 | 0.0455 |
| s-id7 | 20 | 10 | 30 | 50 | 166 | 14,300 | 0.5 | 7150 | 0.0592 |
| s-id8 | 20 | 10 | 30 | 70 | 166 | 17,620 | 0.5 | 8810 | 0.0729 |
| s-id9 | 20 | 10 | 50 | 15 | 166 | 12,490 | 0.5 | 6245 | 0.0517 |
| s-id10 | 20 | 10 | 50 | 30 | 166 | 14,980 | 0.5 | 7490 | 0.0620 |
| s-id11 | 20 | 10 | 50 | 50 | 166 | 18,300 | 0.5 | 9150 | 0.0758 |
| s-id12 | 20 | 10 | 50 | 70 | 166 | 21,620 | 0.5 | 10,810 | 0.0895 |
| s-id13 | 20 | 10 | 70 | 15 | 166 | 16,490 | 0.5 | 8245 | 0.0683 |
| s-id14 | 20 | 10 | 70 | 30 | 166 | 18,980 | 0.5 | 9490 | 0.0786 |
| s-id15 | 20 | 10 | 70 | 50 | 166 | 22,300 | 0.5 | 11,150 | 0.0923 |
| s-id16 | 20 | 10 | 70 | 70 | 166 | 25,620 | 0.5 | 12,810 | 0.1061 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prekas, S.; Karkazis, P.; Nikolakakis, V.; Trakadas, P. Comprehensive Comparison of VNE Solutions Based on Different Coordination Approaches. Telecom 2021, 2, 390-412. https://doi.org/10.3390/telecom2040023
Prekas S, Karkazis P, Nikolakakis V, Trakadas P. Comprehensive Comparison of VNE Solutions Based on Different Coordination Approaches. Telecom. 2021; 2(4):390-412. https://doi.org/10.3390/telecom2040023
Chicago/Turabian StylePrekas, Stelios, Panagiotis Karkazis, Vasileios Nikolakakis, and Panagiotis Trakadas. 2021. "Comprehensive Comparison of VNE Solutions Based on Different Coordination Approaches" Telecom 2, no. 4: 390-412. https://doi.org/10.3390/telecom2040023
APA StylePrekas, S., Karkazis, P., Nikolakakis, V., & Trakadas, P. (2021). Comprehensive Comparison of VNE Solutions Based on Different Coordination Approaches. Telecom, 2(4), 390-412. https://doi.org/10.3390/telecom2040023









