Abstract
In this paper, a link of fixed capacity is considered that services calls from different service-classes. Calls arrive in the link according to a Poisson process, have an initial (peak) bandwidth requirement while their service time is exponentially distributed. We model this system as a multirate loss system and analyze two different multirate loss models. In the first model, named probabilistic retry loss model, if there is no available link bandwidth, a new call is blocked but retries with a lower bandwidth requirement and increased service time. To allow for the fact that a blocked call may be impatient, we assume that it retries with a probability. In the second model, named probabilistic threshold loss model, a call may reduce its bandwidth requirement (before blocking occurs) based on the occupied link bandwidth. To determine call blocking probabilities in both multirate loss models, we show that approximate but recursive formulas do exist that provide quite satisfactory results compared to simulation.
1. Introduction
Multirate loss models (MLMs) are widely adopted in the literature for the determination of call blocking probabilities (CBP), a significant performance index in contemporary multiservice networks [1,2]. Among the MLMs, the basis is considered to be the Erlang MLM (EMLM) not only because CBP can be efficiently determined via the Kaufman-Roberts recursive formula [3,4] but also due to the fact that it has been widely adopted for the CBP computation in various types of networks (from wired [4,5,6,7,8,9,10,11,12,13,14,15,16], to optical [17,18,19,20], wireless [21,22,23,24,25,26,27,28,29,30,31,32,33,34] and even satellite networks [35,36,37,38]).
The EMLM is used for the analysis of a link of certain capacity (in terms of bandwidth units (b.u.)) that services calls of different service-classes with various bandwidth requirements. The call arrival process in the link is Poisson while the available b.u. are shared via the complete sharing policy. According to this policy, a new call will be accepted in the link if there exist available b.u. at the time of the call’s arrival. Otherwise call blocking occurs. An accepted call remains in the link for a generally distributed service time. The fact that the steady state probabilities in the EMLM have a product form solution (PFS) is significant for the derivation of the classical Kaufman–Roberts formula, which leads to the accurate (compared to simulation) CBP computation [3,4].
In [39,40], two extensions of the EMLM are proposed. In the first extension, blocked calls may immediately retry to be accepted in the link with a reduced b.u. requirement and an increased service time. In that case, we have a retry loss model. Call blocking occurs if the reduced b.u. are not available. In the second extension, the b.u. requirement of a new call depends on the occupied link bandwidth. If the occupied link bandwidth is above a threshold (which is common for all service-classes), then the new call tries immediately to be accepted in the link with a reduced b.u. requirement and consequently an increased service time. In that case, we have a threshold loss model. Call blocking occurs if the reduced b.u. are not available. Conceptually, the main difference between the two loss models is that in a threshold loss model, a new call does not have to be blocked with its initial bandwidth requirement in order to retry with a reduced value. It is the value of the threshold and the occupied link bandwidth that decide with which bandwidth requirement (the initial or the reduced), a new call will try to be accepted in the link. Note that in both models, calls may have elastic bandwidth requirements but fixed bandwidth allocation (the initial or the reduced bandwidth requirement) during their service time. Because of this, we classify the models of [39,40] as models that consider stream traffic. This is different from the case of elastic traffic where the bandwidth of in-service calls fluctuates during their service time [2,13].
In this paper, we focus on both loss models and study the case where a call may wish to enter a system with a reduced b.u. requirement and consequently increased service time, with a predetermined probability. Such a probability expresses the fact that the increased service time may cause impatience to calls and therefore may decide not to enter a system, although the reduced b.u. are available. The steady-state probabilities in both loss models cannot be described via a PFS due to the existence of retry (in the retry loss model), the existence of the threshold (in the threshold loss model), and the incorporation of impatience (in both models). However, we propose approximate formulas for the recursive computation of the link occupancy distribution and consequently CBP whose accuracy is validated via simulation.
Note that the characteristic of impatient calls that retry has received attention in the literature under the assumption of queueing (and not loss) systems and single-rate (and not multirate) service-class calls, which require a single b.u. for their service. The interested reader may resort to [41,42,43,44] for the analysis of such queueing models.
The organization of this paper is the following: In Section 2, we review the probabilistic retry loss model of [45]. In Section 3, we propose the probabilistic threshold model and provide recursive formulas for the computation of both the link occupancy distribution and CBP. In Section 4, simulation and analytical results are provided so as to validate the accuracy of the proposed formulas. We conclude in Section 5. Finally, in Appendix A, we present a tutorial example in order to show the intermediate calculations for the CBP computation in the probabilistic threshold loss model.
2. The Probabilistic Retry Loss Model
In the probabilistic retry loss model, a link of capacity C b.u. services calls from K service-classes. Service-class k (k = 1, …, K) calls arrive in the link according to a Poisson process with an arrival rate and have an initial (peak) bandwidth requirement of b.u. If these b.u. are available, then a new service-class k call remains in the link for a service-time, which is exponentially distributed with mean . If the available link b.u. are less than , then the new call is blocked and may: (1) Abandon the link with probability 1 − or (2) immediately retry to be connected in the system with probability , reduced bandwidth requirement < and increased service time given by (see Figure 1, where the call admission mechanism of [39] does not include the grey parts).
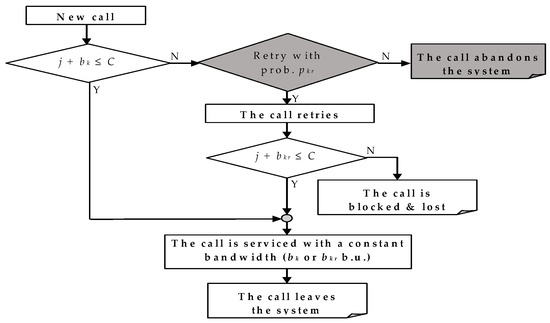
Figure 1.
The call admission mechanism for a new call in the probabilistic retry loss model.
The steady state probabilities in the probabilistic retry loss model cannot be determined via a PFS. However, it is proved in [45] that the computation of the link occupancy distribution, q(j), with j = 0, 1, …, C, is based on the following recursive formula:
where is the offered traffic-load of service-class k calls, is the retry offered traffic-load of service-class k calls accepted in the link with their reduced bandwidth requirement ( b.u.), is the retry probability of blocked calls of service-class k while when j > C − ( − ).
In order to derive (1), we assume that: (1) Local balance exists between adjacent states, which is correct in models whose steady state probabilities have a PFS and (2) retry calls do not exist in the link (i.e., the occupied link bandwidth from such calls is considered to be negligible) when the link occupancy j does not exceed the retry boundary, i.e., when j ≤ C − ( − ). The second assumption is expressed in (1) via .
Having computed, via (1), the unnormalized values of q(j)’s, we can now calculate the CBP of service-class k calls with their reduced bandwidth requirement of b.u., , as follows:
where G = is the normalization constant.
Similarly, we may also obtain the CBP of service-class k calls with their initial (peak) bandwidth requirement of b.u., , and the conditional CBP denoted as via (3) and (4), respectively:
Additionally, we can determine the mean number of in-service calls of service-class k, , accepted in the link with bk b.u. via the formula:
where refers to the mean number of service-class k calls with b.u. in state j.
The latter can be determined via the formula:
Similarly, we can compute the mean number of in-service calls of service-class k, , accepted in the link with b.u. via the formula:
where refers to the mean number of service-class k calls with b.u. in state j.
The latter can be determined via the formula:
The percentage of calls accepted in the system with b.u. can be obtained as .
3. The Proposed Probabilistic Threshold Loss Model
In the proposed probabilistic threshold loss model, a link of capacity C b.u. services calls from K service-classes. Service-class k (k = 1, …, K) calls arrive in the link according to a Poisson process with an arrival rate and have an initial (peak) bandwidth requirement of b.u. and a reduced bandwidth requirement of b.u. Contrary to the probabilistic retry loss model, in this model, it is the value of j (the occupied bandwidth of the link) together with the value of the threshold that are closely related to the bandwidth requirement (initial or reduced) a new call will use in order to enter the system. More specifically, the call admission mechanism applied in the case of a new service-class k call is the following: (a) Assuming that then the call will be accepted in the link with b.u. and will be serviced for an exponentially distributed service time with mean , and (b) assuming that then the call will: (b1) abandon the link with probability 1- or (b2) try to be connected in the system with probability , reduced bandwidth requirement < and increased service time computed as . Needless to say, if the b.u. are not available then the call will be blocked (see Figure 2, where the call admission mechanism of [38] does not include the grey parts).
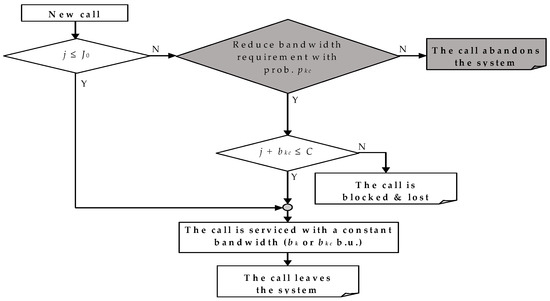
Figure 2.
The call admission mechanism for a new call in the probabilistic threshold loss model.
To determine the unnormalized values of q(j)’s, we initially consider the case of three service-classes whose calls are serviced by a link of capacity C and have the following call arrival parameters and service parameters . Assuming that , then calls of the third service-class have the choice to enter the system with probability , reduced bandwidth requirement < , and increased service time computed as . Contrary to the calls of the third service-class, calls of the first and second service-classes do not have the option to enter the system with a reduced bandwidth requirement.
The derivation of a recursive formula for the computation of q(j)’s, requires the assumption (approximation) that local balance exists between the adjacent states: (a) and j for k = 1, 2, 3 and (b) and j for k = 3. More precisely, we consider the following local balance equations for calls of the first two service-classes and j = 1, …, C:
where and refer to the average number of first and second service-class calls, respectively, that exist in the system in state j.
Regarding the local balance equations for calls of the third service-class, we have the following two equations for calls accepted with their initial bandwidth requirement and calls accepted with their reduced bandwidth requirement:
where refers to the average number of the third service-class calls with b.u. that exist in state j while refers to the average number of the third service-class calls with b.u. that exist in state j.
Based on (9)–(12) and since for k = 1, 2, 3 and for k = 3 are the corresponding offered traffic-loads, we can write the following equations:
In order to combine (13)–(15) into a single recursive formula for the computation of q(j)’s, two necessary approximations are adopted: (1) in (13), the value of when and (2) in (15), the value of when . Based on these approximations we can write the following recursive formula, assuming that expresses the second approximation and expresses the first approximation:
where , if and , or if and while when .
Assuming the general case where a link accommodates calls of K service-classes, Equation (16) takes the following form:
where , if and , or if and while when .
Having computed, via (17), the unnormalized values of q(j)’s in the probabilistic threshold loss model, we can now calculate the CBP of service-class k calls with their reduced bandwidth requirement of b.u., , as follows:
where G = is the normalization constant.
Similarly, we may also obtain the conditional CBP denoted as via:
The probabilistic threshold loss model provides the same CBP with those obtained via the probabilistic retry loss model if we set and .
Apart from the CBP, we can also determine the mean number of in-service calls of service-class k, , accepted in the link with b.u. via (5) where can be computed via:
Similarly, we can compute the mean number of in-service calls of service-class k, , accepted in the link with b.u. via the formula:
where refers to the mean number of service-class k calls with b.u. in state j.
The latter can be determined via the formula:
The percentage of calls accepted in the system with b.u. can be obtained as .
4. Performance Evaluation
In this section, we consider an application example of a single link and present both analytical and simulation CBP results of the proposed probabilistic threshold loss model as well as the corresponding analytical and simulation results of the probabilistic retry loss model. For reference we also present the corresponding analytical CBP results of the models of [39,40] together with those obtained via the EMLM. The simulation results presented in this section are mean values of seven runs and are based on Simscript III [46]. In each run, 1 million calls are generated while the initial 2% of these generated calls is not considered in the blocking probability results, so as to account for a warm-up period. Regarding reliability ranges, they are less than two orders of magnitude and therefore are not presented in the following figures.
In our application example, two service-classes are considered whose calls are accommodated in a link of 32 b.u. Calls of the first service-class have an initial bandwidth requirement of 6 b.u. and they do not have the option to retry with a reduced bandwidth requirement. On the other hand, calls of the second service-class have an initial (peak) bandwidth requirement of 24 b.u. In the case of the probabilistic retry loss model, blocked calls of this service-class retry with probability and a reduced bandwidth requirement of 8 b.u. In the case of the probabilistic threshold model, calls of this service-class try to be connected in the link with probability and a reduced bandwidth requirement of 8 b.u., when . The value of the threshold is set to 4 b.u. Regarding the values of p we consider the cases of: (a) = 0.2 and (b) = 0.6. Calls of both service-classes arrive in the link according to a Poisson process with arrival rates = 0.8 and = 0.1 while their service time is exponentially distributed with , and . Based on these values, the initial offered traffic-load values (in erl) are the following: , and .
In the x-axis of Figure 3, Figure 4, Figure 5 and Figure 6, we consider an increase in the value of in steps of 0.2 erl. Thus, point 1 (in the x-axis) is: and point 7 is: .
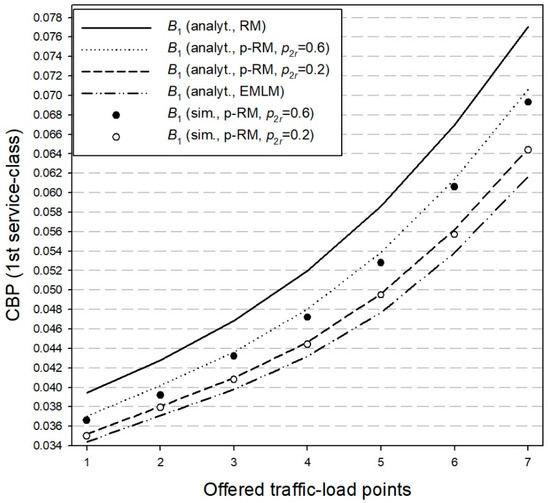
Figure 3.
CBP—First service-class (probabilistic retry loss model).
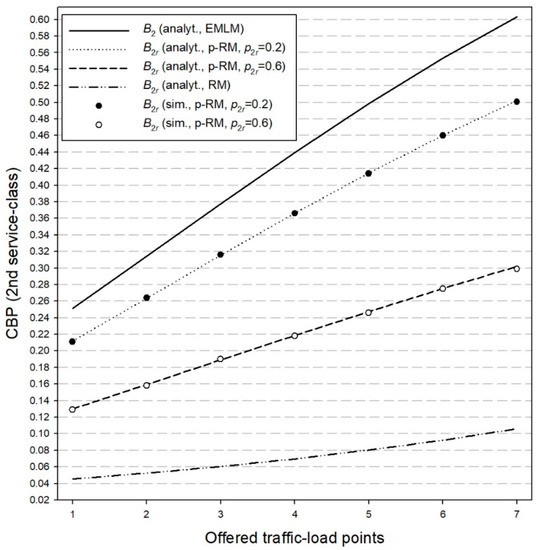
Figure 4.
CBP—Second service-class (probabilistic retry loss model).
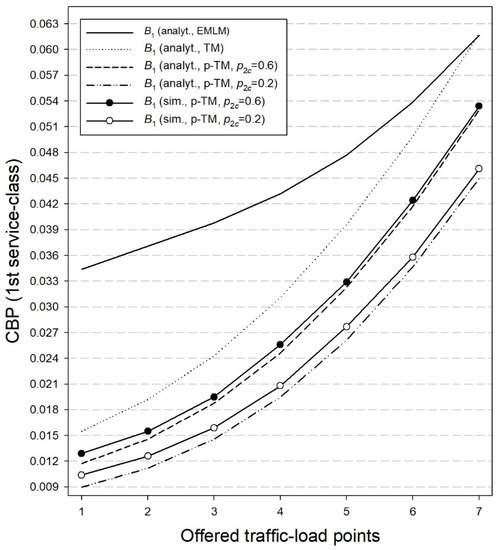
Figure 5.
CBP—First service-class (probabilistic threshold loss model).
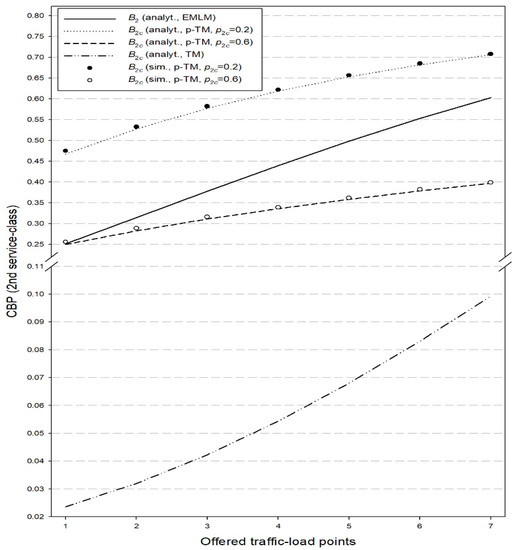
Figure 6.
CBP—Second service-class (probabilistic threshold loss model).
Figure 3 presents the analytical together with the simulation CBP of the first service-class calls assuming the probabilistic retry loss model (p-RM in Figure 3) for = 0.2 and = 0.6 and the corresponding analytical CBP for the retry loss model of [39] (RM in Figure 3) and the EMLM. On the same hand, in Figure 4, we present the corresponding CBP results of . Both figures show that the analytical results obtained via the probabilistic retry loss model are quite close to the corresponding CBP simulation results. Regarding Figure 3, we observe that decreasing results in a CBP decrease for the first service-class calls compared to the values of [39] or even the values of the EMLM (where retries are not permitted). As far as Figure 4 is concerned, we observe that a decrease of significantly increases the CBP of calls of the second service-class in the case of the probabilistic retry loss model, compared to the case of the model of [39]. Regarding the EMLM, it is obvious that it cannot capture the behavior of the proposed model or the model of [39].
In Figure 5, we present the analytical together with the simulation CBP of the first service-class calls assuming the probabilistic threshold loss model (p-TM in Figure 5) for = 0.2 and = 0.6 and the corresponding analytical CBP for the threshold loss model of [40] (TM in Figure 5) and the EMLM. On the same hand, in Figure 6, we present the corresponding CBP results of . In both figures, we see that the simulation results and the analytical results obtained via the probabilistic threshold loss model are quite close. Regarding Figure 5, we observe that decreasing results in a CBP decrease for the first service-class calls compared to the values of [40] or those obtained via the EMLM. In addition, the CBP of the first service-class are lower to the corresponding CBP results obtained via the probabilistic retry loss model (compare Figure 3 with Figure 5). This can be explained by the fact that in the probabilistic threshold loss model, calls from the second service-class may decide earlier (due to the value of = 4) not to enter the system, a fact that increases the available b.u. for calls of the first service-class. As far as Figure 6 is concerned, we observe that a decrease of significantly increases the CBP of calls of the second service-class in the case of the probabilistic threshold loss model, compared to the model of [40] or the probabilistic retry loss model (compare Figure 4 with Figure 6). Regarding the EMLM, it is obvious that it cannot capture the behavior of the proposed model or the model of [40]. As a general comment for both the probabilistic retry and the probabilistic threshold loss models, note that particular attention is necessary when choosing the values of and for calls of service-class k.
5. Conclusions
We propose multirate loss models for a single link that services different service-classes whose calls follow a Poisson process. New calls have an initial and a reduced bandwidth requirement. In the probabilistic retry loss model, calls that cannot be accepted in the link with their initial bandwidth requirement are allowed to retry with their reduced bandwidth requirement at the cost of an increased service time. The latter may lead some impatient calls to decide not entering the system. To this end, it is assumed that blocked calls retry with a predetermined probability. In the probabilistic threshold loss model, new calls may reduce their bandwidth requirement (before blocking takes place) based on the occupied link bandwidth. The proposed multirate loss models do not have a PFS. However, we show that recursive formulas do exist for the computation of CBP. The accuracy of the proposed formulas is quite satisfactory compared to simulation. As a future work, we will extend these models in order to incorporate the interesting case of elastic and adaptive multirate traffic, where the bandwidth given to in-service calls is not constant during their service time [47,48,49,50,51,52,53,54].
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
Appendix A
Calls of two service-classes are accommodated in a link whose capacity is 5 b.u. First service-class calls have a bandwidth requirement of 1 b.u. while calls of the second service-class require 3 b.u. and may use their reduced bandwidth requirement of 2 b.u., with probability = 0.4, when the occupied link bandwidth is above the threshold = 1. In that case, the increased service time will be . In addition, let .
Assuming that the in-service calls of both service-classes are denoted via n1, n2 and n2c (the latter expresses calls of the second service-class accepted in the system with ), then the state space of this multirate loss system consists of the following 16 states :
The computation of CBP for each service-class requires the solution of a system of 16 global balance equations, where the notation P(n) refers to the steady state probability of n:
P(1,0,0) + P(0,1,0) + 2/3 P(0,0,1) − 2P(0,0,0) = 0
P(0,1,1) + 4/3 P(0,0,2) + P(1,0,1) − (1.4 + 2/3) P(0,0,1) = 0
P(1,0,2) + 0.4 P(0,0,1) − 7/3 P(0,0,2) = 0
P(0,0,0) + P(1,1,0) +2/3 P(0,1,1) − 2.4 P(0,1,0) = 0
0.4P(0,1,0) − 5/3 P(0,1,1) = 0
2/3 P(1,0,1) + P(0,0,0) + 2P(2,0,0) + P(1,1,0) − 3 P(1,0,0) = 0
4/3 P(1,0,2) + P(0,0,1) + 2P(2,0,1) − (8/3 + 0.4) P(1,0,1) = 0
0.4P(1,0,1) + P(0,0,2) − 7/3 P(1,0,2) = 0
P(1,0,0) + P(0,1,0) + 2P(2,1,0) − 3P(1,1,0) = 0
P(2,1,0) + P(1,0,0) + 3P(3,0,0) + 2/3P(2,0,1) − 3.4P(2,0,0) = 0
0.4P(2,0,0) + P(1,0,1) + 3P(3,0,1) − 11/3 P(2,0,1) = 0
P(1,1,0) − 3P(2,1,0) = 0
2/3 P(3,0,1) + P(2,0,0) + 4P(4,0,0) − 4.4P(3,0,0) = 0
P(2,0,1) + 0.4P(3,0,0) − 11/3 P(3,0,1) = 0
5P(5,0,0) + P(3,0,0) − 5P(4,0,0) = 0
P(4,0,0) − 5P(5,0,0) = 0
P(0,1,1) + 4/3 P(0,0,2) + P(1,0,1) − (1.4 + 2/3) P(0,0,1) = 0
P(1,0,2) + 0.4 P(0,0,1) − 7/3 P(0,0,2) = 0
P(0,0,0) + P(1,1,0) +2/3 P(0,1,1) − 2.4 P(0,1,0) = 0
0.4P(0,1,0) − 5/3 P(0,1,1) = 0
2/3 P(1,0,1) + P(0,0,0) + 2P(2,0,0) + P(1,1,0) − 3 P(1,0,0) = 0
4/3 P(1,0,2) + P(0,0,1) + 2P(2,0,1) − (8/3 + 0.4) P(1,0,1) = 0
0.4P(1,0,1) + P(0,0,2) − 7/3 P(1,0,2) = 0
P(1,0,0) + P(0,1,0) + 2P(2,1,0) − 3P(1,1,0) = 0
P(2,1,0) + P(1,0,0) + 3P(3,0,0) + 2/3P(2,0,1) − 3.4P(2,0,0) = 0
0.4P(2,0,0) + P(1,0,1) + 3P(3,0,1) − 11/3 P(2,0,1) = 0
P(1,1,0) − 3P(2,1,0) = 0
2/3 P(3,0,1) + P(2,0,0) + 4P(4,0,0) − 4.4P(3,0,0) = 0
P(2,0,1) + 0.4P(3,0,0) − 11/3 P(3,0,1) = 0
5P(5,0,0) + P(3,0,0) − 5P(4,0,0) = 0
P(4,0,0) − 5P(5,0,0) = 0
The solution of this system of equations is the following:
P(0,0,0) = 0.173022, P(0,0,1) = 0.044023, P(0,0,2) = 0.012907, P(0,1,0) = 0.137834, P(0,1,1) = 0.03308, P(1,0,0) = 0.178861, P(1,0,1) = 0.040692, P(1,0,2) = 0.012507, P(1,1,0) = 0.135727, P(2,0,0) = 0.100354, P(2,0,1) = 0.032044, P(2,1,0) = 0.045242, P(3,0,0) = 0.031912, P(3,0,1) = 0.012221, P(4,0,0) = 0.007978, P(5,0,0) = 0.001596.
The normalized values of q(j)’s, denoted as Q(j)’s, are:
Based on the above, we compute and as follows (in the parenthesis we provide the corresponding values in the case of the probabilistic retry loss model):
For reference only, the CBP results in the EMLM are: = 0.09744, = 0.52077.
The corresponding recursive calculations in the case of the probabilistic threshold loss model are based on (17) and are the following (assuming that q(0) = 1, = 1.0 erl, erl while , for and , for j > 3).
and G = 5.37666 while:
Based on the previous values, we can compute the CBP of the two service-classes, as follows (in the parenthesis, we repeat the exact values obtained via the global balance equations):
References
- Stasiak, M.; Głąbowski, M.; Wisniewski, A.; Zwierzykowski, P. Modeling and Dimensioning of Mobile Networks: From GSM to LTE; John Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Moscholios, I.D.; Logothetis, M.D. Efficient Multirate Teletraffic Loss Models Beyond Erlang; John Wiley & IEEE Press: Hoboken, NJ, USA, 2019. [Google Scholar]
- Kaufman, J. Blocking in a shared resource environment. IEEE Trans. Commun. 1981, 29, 1474–1481. [Google Scholar] [CrossRef]
- Roberts, J. A service system with heterogeneous user requirements. Performance of Data Communications Systems and Their Applications; Springer: Amsterdam, The Netherlands, 1981; pp. 423–431. [Google Scholar]
- Berezner, S.; Krzesinski, A. An efficient stable recursion to compute multiservice blocking probabilities. Perf. Eval. 2001, 43, 151–164. [Google Scholar] [CrossRef]
- Moscholios, I.; Logothetis, M.; Kokkinakis, G. Connection dependent threshold model: A generalization of the Erlang multiple rate loss model. Perf. Eval. 2002, 48, 177–200. [Google Scholar] [CrossRef]
- Głąbowski, M.; Stasiak, M. Point-to-point blocking probability in switching networks with reservation. Ann. Telecommun. 2002, 57, 798–831. [Google Scholar]
- Moscholios, I.; Logothetis, M.; Nikolaropoulos, P. Engset multi-rate state-dependent loss models. Perf. Eval. 2005, 59, 247–277. [Google Scholar] [CrossRef]
- Iversen, V.; Stepanov, S. Derivatives of blocking probabilities for multi-service loss Systems and their applications. In Lecture Notes in Computer Science; Springer: Berlin, Germany, 2007; p. 4712. [Google Scholar]
- Huang, Q.; Ko, K.; Iversen, V. Approximation of loss calculation for hierarchical networks with multiservice overflows. IEEE Trans. Commun. 2008, 56, 466–473. [Google Scholar] [CrossRef]
- Głąbowski, M.; Kaliszan, A.; Stasiak, M. Modeling product-form state dependent systems with BPP traffic. Perf. Eval. 2010, 67, 174–197. [Google Scholar] [CrossRef]
- Moscholios, I.; Logothetis, M. The Erlang multirate loss model with batched Poisson arrival processes under the bandwidth reservation policy. Comp. Commun. 2010, 33, S167–S179. [Google Scholar] [CrossRef]
- Moscholios, I.; Vassilakis, V.; Vardakas, J.; Logothetis, M. Retry loss models supporting elastic traffic. Adv. Electr. Telecommun. 2011, 2, 8–13. [Google Scholar]
- Głąbowski, M.; Kaliszan, A.; Stasiak, M. Modelling overflow systems with distributed secondary resources. Comput. Netw. 2016, 108, 171–183. [Google Scholar] [CrossRef]
- Moscholios, I.; Logothetis, M.; Shioda, S. Performance evaluation of multirate loss systems supporting cooperative users with a probabilistic behavior. IEICE Trans. Commun. 2017, E100-B, 1778–1788. [Google Scholar] [CrossRef]
- Sagkriotis, S.; Pantelis, S.; Moscholios, I.; Vassilakis, V. Call blocking probabilities in a two-link multi rate loss system for Poisson traffic. IET Netw. 2018, 7, 233–241. [Google Scholar] [CrossRef]
- Kuppuswamy, K.; Lee, D. An analytical approach to efficiently computing call blocking probabilities for multiclass WDM networks. IEEE ACM Trans. Netw. 2009, 17, 658–670. [Google Scholar] [CrossRef]
- Vardakas, J.; Moscholios, I.; Logothetis, M.; Stylianakis, V. Performance analysis of OCDMA PONs supporting multi-rate bursty traffic. IEEE Trans. Commun. 2013, 61, 3374–3384. [Google Scholar] [CrossRef]
- Beyranvand, H.; Maier, M.; Salehi, J. An analytical framework for the performance evaluation of node-and network-wise operation scenarios in elastic optical networks. IEEE Trans. Commun. 2014, 62, 1621–1633. [Google Scholar] [CrossRef]
- Vardakas, J.; Moscholios, I.; Logothetis, M.; Stylianakis, V. Performance analysis of OCDMA PON configuration supporting multirate bursty traffic with retrials and QoS differentiation. Opt. Switch. Netw. 2014, 13, 112–123. [Google Scholar] [CrossRef]
- Cruz-Pérez, F.; Vázquez-Ávila, J.; Ortigoza-Guerrero, L. Recurrent formulas for the multiple fractional channel reservation strategy in multiservice mobile cellular networks. IEEE Commun. Lett. 2004, 8, 629–631. [Google Scholar] [CrossRef]
- Chen, J.; Chen, W. Call blocking probability and bandwidth utilization of OFDM subcarrier allocation in next-generation wireless networks. IEEE Comm. Lett. 2006, 10, 82–84. [Google Scholar] [CrossRef]
- Vassilakis, V.; Kallos, G.; Moscholios, I.; Logothetis, M. The wireless Engset multi-rate loss model for the call-level analysis of W-CDMA networks. In Proceedings of the 18th IEEE International Symposium on Personal, Indoor and Mobile Radio Communications, Athens, Greece, 3–7 September 2007. [Google Scholar]
- Pla, J.; Martinez-Bauset, J.; Casares-Giner, V. Comments on “call blocking probability and bandwidth utilization of OFDM subcarrier allocation in next-generation wireless networks”. IEEE Comm. Lett. 2008, 12, 349. [Google Scholar] [CrossRef]
- Widjaja, I.; La Roche, H. Sizing X2 bandwidth for inter-connected eNBs. In Proceedings of the 2009 IEEE 70th Vehicular Technology Conference Fall, Anchorage, AK, USA, 20–23 September 2009. [Google Scholar]
- Blaszczyszyn, B.; Karray, M. Dimensioning of the downlink in OFDMA cellular networks via an Erlang’s loss model. In Proceedings of the European Wireless Conference, Aalborg, Denmark, 17–20 May 2009. [Google Scholar]
- Karray, M. Analytical evaluation of QoS in the downlink of OFDMA wireless cellular networks serving streaming and elastic traffic. IEEE Trans. Wirel. Commun. 2010, 9, 1799–1807. [Google Scholar] [CrossRef]
- Paik, C.; Suh, Y. Generalized queueing model for call blocking probability and resource utilization in OFDM wireless networks. IEEE Commun. Lett. 2011, 15, 767–769. [Google Scholar] [CrossRef]
- Parniewicz, D.; Stasiak, M.; Zwierzykowski, P. Traffic engineering for multicast connections in multiservice cellular networks. IEEE Trans. Ind. Inform. 2013, 9, 262–270. [Google Scholar] [CrossRef]
- Avramova, A.; Iversen, V. Radio access sharing strategies for multiple operators in cellular networks. In Proceedings of the IEEE ICC Workshop on 5G & Beyond, London, UK, 8–12 June 2015. [Google Scholar]
- Hanczewski, S.; Stasiak, M.; Zwierzykowski, P. Modelling of the access part of a multi-service mobile network with service priorities. EURASIP J. Wirel. Commun. Netw. 2015, 194. [Google Scholar] [CrossRef]
- Moscholios, I.; Vassilakis, V.; Logothetis, M.; Boucouvalas, A. A probabilistic threshold-based bandwidth sharing policy for wireless multirate loss networks. IEEE Wirel. Commun. Lett. 2016, 5, 304–307. [Google Scholar] [CrossRef]
- Moscholios, I.; Vassilakis, V.; Logothetis, M.; Boucouvalas, A. State-dependent bandwidth sharing policies for wireless multirate loss networks. IEEE Trans. Wirel. Commun. 2017, 16, 5481–5497. [Google Scholar] [CrossRef]
- Panagoulias, P.; Moscholios, I. Congestion probabilities in the X2 link of LTE networks. Telecommun. Syst. 2019, 71, 585–599. [Google Scholar] [CrossRef]
- Wang, Z.; Mathiopoulos, P.; Schober, R. Performance analysis and improvement methods for channel resource management strategies of LEO-MSS with multiparty traffic. IEEE Trans. Veh. Technol. 2008, 57, 3832–3842. [Google Scholar] [CrossRef]
- Wang, Z.; Mathiopoulos, P.; Schober, R. Channeling partitioning policies for multi-class traffic in LEO-MSS. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1320–1334. [Google Scholar] [CrossRef]
- Moscholios, I.; Vassilakis, V.; Sarigiannidis, P.; Sagias, N.; Logothetis, M. An analytical framework in LEO mobile satellite systems servicing batched Poisson traffic. IET Commun. 2018, 12, 18–25. [Google Scholar] [CrossRef]
- Moscholios, I.; Vassilakis, V.; Sagias, N.; Logothetis, M. On channel sharing policies in LEO mobile satellite systems. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1628–1640. [Google Scholar] [CrossRef]
- Kaufman, J. Blocking in a completely shared resource environment with state dependent resource and residency requirements. In Proceedings of the IEEE INFOCOM, Florence, Italy, 4–8 May 1992; pp. 2224–2232. [Google Scholar]
- Kaufman, J. Blocking with retrials in a completely shared resource environment. Perf. Eval. 1992, 15, 99–113. [Google Scholar] [CrossRef]
- Artalejo, J.; Gomez-Corral, A. Retrial Queueing Systems: A Computational Approach; Springer: Berlin, Germany, 2008. [Google Scholar]
- Wang, K.; Li, N.; Jiang, Z. Queueing system with impatient customers: A review. In Proceedings of the IEEE International Conference Service Operations and Logistics and Informatics, Qingdao, China, 15–17 July 2010. [Google Scholar]
- Wu, M.; Tan, L. An infinite-source M/M/S retrial queuing network model with balking and impatient customers. In Proceedings of the IEEE Global High Tech Congress on Electronics, Shenzhen, China, 17–19 November 2013. [Google Scholar]
- Danilyuk, E.; Moiseeva, S.; Nazarov, A. Asymptotic analysis of retrial queueing system M/GI/1 with collisions and impatient calls. In International Conference on Information Technologies and Mathematical Modelling; Springer: Cham, Switzerland, 2019; Volume 1109, pp. 230–242. [Google Scholar]
- Moscholios, I.; Logothetis, M. A single retry multirate loss model for impatient calls. In Proceedings of the IEEE/IET CSNDSP, Porto, Portugal, 20–22 July 2020. [Google Scholar]
- Simscript III. Available online: http://www.simscript.com (accessed on 26 January 2021).
- Fodor, G.; Rácz, S.; Telek, M. On providing blocking probability and throughput guarantees in a multi-service environment. Int. J. Commun. Syst. 2002, 15, 257–285. [Google Scholar] [CrossRef]
- Vassilakis, V.; Kallos, G.; Moscholios, I.; Logothetis, M. Call-level analysis of W-CDMA networks supporting elastic services of finite population. In Proceedings of the IEEE International Conference Communications (ICC), Beijing, China, 19–23 May 2008. [Google Scholar]
- Moscholios, I.; Vardakas, J.; Logothetis, M.; Boucouvalas, A. A batched Poisson multirate loss model supporting elastic traffic under the bandwidth reservation policy. In Proceedings of the IEEE International Conference Communications (ICC), Kyoto, Japan, 5–9 June 2011. [Google Scholar]
- Głąbowski, M.; Hanczewski, S.; Stasiak, M. Modelling load balancing mechanisms in self-optimising 4G mobile networks with elastic and adaptive traffic. IEICE Trans. Commun. 2016, E99-B, 1718–1726. [Google Scholar]
- Głąbowski, M.; Kmiecik, D.; Stasiak, M. Modelling of multiservice networks with separated resources and overflow of adaptive traffic. Wirel. Commun. Mob. Comput. 2018, 7870164. [Google Scholar] [CrossRef]
- Vassilakis, V.; Moscholios, I.; Logothetis, M. Quality of service differentiation of elastic and adaptive services in CDMA networks: A mathematical modelling approach. Wirel. Netw. 2018, 24, 1279–1295. [Google Scholar] [CrossRef]
- Nowak, B.; Piechowiak, M.; Stasiak, M.; Zwierzykowski, P. An analytical model of a system with priorities servicing a mixture of different elastic traffic streams. Bull. Pol. Acad. Sci. Tech. Sci. 2020, 68, 263–270. [Google Scholar]
- Hanczewski, S.; Stasiak, M.; Weissenberg, J. A model of a system with stream and elastic traffic. Accept. Publ. IEEE Access 2021, 9, 7789–7796. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).